Vibration and deflection analysis of thin cracked and submerged orthotropic plate under thermal environment using strain gradient theory

Abstract

Based on a non-classical plate theory, a nonlinear analytical model is proposed to analyze transverse vibration of thin partially cracked and submerged orthotropic plate in the presence of thermal environment. The governing equation for the cracked plate is derived using the Kirchhoff’s thin plate theory in conjunction with the strain gradient theory of elasticity. The effect of centrally located surface crack is deduced using appropriate crack compliance coefficients based on the simplified line spring model, whereas the effect of thermal environment is introduced using moments and in-plane forces. The influence of fluidic medium is incorporated in the governing equation in the form of fluid forces associated with its inertial effects. The equation has been solved by transforming the lateral deflection in terms of modal functions. The shift in primary resonance due to crack, length scale parameter and temperature has also been derived with central deflection. To demonstrate the accuracy of the present model, a few comparison studies are carried out with the published literature. The variation in fundamental frequency of the cracked plate is studied considering various parameters such as crack length, plate thickness, level of submergence, temperature and length scale parameter. It has been concluded that the frequency is affected by crack length, temperature and level of submergence. A comparison has also been made for the results obtained from the classical plate theory and Strain gradient theory. Furthermore, the variation in frequency response and peak amplitude of the cracked plate is studied using method of multiple scales to show the phenomenon of bending hardening or softening as affected by level of submergence, temperature, crack length and length scale parameter .

1 Introduction

Thin plates or shells are one of the essential structural components in marine building applications which expose them to work under fluidic medium of varying temperature. Thus, the knowledge of dynamic characteristics of such thin structures under fluidic medium with temperature variation is necessary for reliable design. It becomes more interesting to understand the effect of temperature under fluidic medium when these structures contain various flaws in the form of holes and cracks. In the literature, a lot of efforts have been dedicated on vibrations of intact plates under fluidic medium and thermal environment individually. However, a little study on vibration problems of cracked plates in considering the effect of both surrounding fluid medium and thermal environment are found in the relevant literature. Concerning the influence of surrounding fluid medium on vibration analysis of plates, it is observed that the fluidic medium essentially diminishes the fundamental frequency of plate structures in correlation with those figured in vacuum medium, it is because of the presence of fluid nearby the plate structures which causes increment in the kinetic energy of whole structural system without a relating increment in the strain energy. Utilizing the Rayleigh’s strategy Lamb [1] performed for the first time on vibrations of circular plate coupled with water. The developed method was based on a calculation of the kinetic energy of water. Kwak [2] proposed an approximate formula for added virtual mass incremental (AVMI) factor to determine the fundamental frequency of plate in water from the frequency of the plate in vacuum. Kwak and Kim [3] and Amabali et al. [4] investigated the influence of fluidic medium on axisymmetric vibrations of circular and annular plate coupled with water. Haddara and Cao [5] developed an approximate relation for the virtual added mass to study the vibration response of intact plates vibrating under fluid. Their results are investigated experimentally as well as analytically for different submergence levels and boundary conditions. For analysis of the plate–fluid interaction problems, Kerboua et al. [6] worked on the free vibration problems of isotropic plate coupled with water and developed a mathematical model based on the Sander’s shell theory and FEM technique. Recently, Hosseini Hashemi et al. [7] developed an analytical model for thick horizontal plates partially and totally submerged in fluid. They used the Mindlin’s plate hypothesis for deriving the model. Vibration problems of plates considering the effect of both crack and fluidic medium are found in few investigations. Liu et al. [8] analyzed the natural vibration problems of perforated plates using the finite element method (FEM). They studied the influence of through crack on the vibration characteristics of a circular plate coupled with fluid. Recently, Si et al. [9, 10] proposed a computational approach based on FEM method for vibration analysis of cracked circular and rectangular plates vibrating under water. They investigated the effect of fluidic medium and side crack on fundamental frequency of cracked circular plate for different modes of vibration.

Similarly, for the effect of thermal environment on vibration problems of plates, it is seen that the presence of thermal stress decreases the stiffness of plate which results in reduction of natural frequency. Murphy and Ferreira [11] and Yang and Shen [12] studied the vibration problems of isotropic and FGM rectangular plates by taking the consideration of thermal environment. The analysis of vibration problems for functionally graded plates subjected to thermal heating is presented by Li et al.[13]. They utilized three-dimensional theory of elasticity to model the FGM plates in nearness of thermal environment. Kim [14] and Viola et al. [15] have also worked on vibration analysis of intact and cracked FGM rectangular plates under thermal environment using finite element method. Natarajan et al. [16] performed a detail study on vibration and buckling analysis of a functionally graded plate containing internal discontinuities in form of cracks using FEM and first-order shear deformation (FSDT) theory. They showed the effect of increase in crack length and temperature gradient the natural frequency of cracked plate.

In recent literature on study of microstructures, it has been found that it affects the vibration response of plate structures [17,18,19,20]. Different theories which catches the size effect on the analysis of the gradient elastic plates are developed in recent works, among them, the strain gradient theory (SGT) which was proposed by Mindlin and Eshel [21] are found to be efficient one. They [21] considered a single length scale of microstructure to catch size effect of plate in their developed theory. Papargyri-Beskou and Beskos [17] developed a sixth-order governing equation of gradient elastic plate using the force and moment equilibrium equations. In their model, they considered two length scale parameters to capture size effect and to make the model more effective. Tsiatas [19] developed a new mathematical model for micro-plates based on the modified couple stress theory (MCST). In their study, they used a material scale parameter to demonstrate the size effect of microstructure. By employing the Hamilton’s principle, Gao and Zhang [22] deduced the new governing equation of motion in which they used a material length scale constant to catch the size effect of microstructure. They also observed that their results for natural frequency obtained by the non-classical plate model (MCST) are higher than that of the classical plate model for very thin plates. Most recently, Gupta et al. [23] used the vibration model of intact micro-plate of Yin et al. [20] to build up an analytical model for vibration problem of partially cracked thin isotropic and functionally graded micro-plate. Further, they demonstrated the impact of fiber orientation on vibration characteristics of cracked specially orthotropic micro-plate [24].

Surface cracks are the most widely recognized imperfection in any sorts of shells and plates; henceforth, the issue of free vibration problem of the cracked plate has been broadly considered in the current decades. It is observed in recent literature that many of researchers used the Line Spring Model (LSM) to find an approximate analytical solution of cracked plates containing a part-through surface crack. This concept was first introduced by Rice and Levy [25], for investigating the analytical solution of cracked plates based on Kirchhoff’s thin plate theory. They represented the surface crack as persistent line spring with stretching, bending and twisting compliances. Utilizing the line spring model, the first approximate mathematical model for vibration problem of cracked isotropic plates is suggested by Israr et al. [26]. They studied the influence of crack length on frequency response of plate for different boundary conditions (SSSS, CCSS and CCFF). Ismail and Cartmell [27] extended the previously developed model of Israr et al. [26] for plate with variably orientated crack by founding relations for bending moments and membrane forces. It is observed from their work that for all the edge conditions, the frequency of plate is decreased with increase in orientation and crack length. Joshi et al. [28] introduced the mathematical models for vibration analysis of partially cracked orthotropic plate with two perpendicular internal and surface cracks located at its center. Extending their work, they also studied the buckling and vibration analysis of thin orthotropic [29] cracked plates taking the consideration of thermal environment. Recently, Soni et al. [30, 31] studied the effect of fluidic medium on vibration characteristics of cracked isotropic [30] and magneto-electro-elastic (MEE) [31] plates by incorporating the inertial effect of fluids forces on previously developed models.

On the one hand, it is known from relevant literature that the microstructure plays an important role in stiffness of structures. On the other hand, the external environment such as thermal environment and fluidic medium cannot be neglected as it affects the dynamics. Thirdly, recent literature shows the effect of crack on vibration behavior. The aim of the present work is to combine the research in these related areas and present comprehensive effect of microstructure, thermal environment, partial crack and surrounding fluid on the vibration behavior of specially orthotropic plates.

Fig. 1

Partially cracked orthotropic plate submerged in a fluid tank

The literature lacks in the outcomes for free vibration problems of specially cracked and submerged orthotropic plates thinking about the effect of microstructure and thermal environment. Thus, to develop theoretical understanding of influence of surface crack on vibration problem of submerged plate subjected to thermal environment becomes significant. The present work fills this gap by proposing a new analytical model and addresses the following novel points;

• 1. An analytical model is presented for first time which is so inclusive that it caters not only to free and forced vibrations of partially cracked orthotropic plate, but it considers the presence of thermal environment, surrounding fluidic medium and microstructure by employing strain gradient theory.

• 2. Another unique contribution of the present work is that it presents a classical relation for central deflection for orthotropic plate as affected partial crack, thermal environment, microstructure and surrounding fluid.

• 3. Parametric study is presented for fundamental frequency of cracked orthotropic plate as a function of crack length, temperature, length scale of microstructure, plate thickness and level of submergence.

• 4. The nonlinearity in frequency response presented in this work is more expansive; it not only includes the effect of crack but includes the effect of temperature, microstructure and level of submergence.

• 5. The present work presents a comparison of classical plate theory and strain gradient theory for nonlinear vibration of partially cracked orthotropic plate in the presence of thermal and fluidic environment”

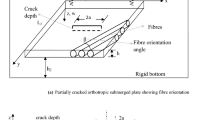
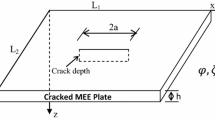
In the present study, an analytical model has been presented for cracked orthotropic rectangular plate in light of a non-classical approach. The differential governing equation of the plate derived using strain gradient theory is found to be of $6{\mathrm{th}}$ order rather than the $4{\mathrm{th}}$ order found in the classical plate theory. The moment equilibrium equations for cracked orthotropic plate are derived by taking the consideration of thermal environment and microstructure. The effect of crack is introduced in the form of additional membrane force and bending moment using the line spring model. The effect of fluidic medium is integrated in the model in the form of added virtual mass with help of Bernoulli’s equation and velocity potential function. Apart from the membrane forces due to elasticity, the in-plane forces due to effect of microstructure and thermal environment are also considered in the present model. Fig. 1 shows the orthotropic plate configuration with unidirectional fibers along x axis. The in-plane dimensions of the plate are taken as $l_{1}$ and $l_{2}$ in x and y direction separately. The plate thickness is denoted by h. 2a is the length of crack at plate center, and the depth of the crack is less than the thickness. To study the effect of various parameters such as rise in temperature, crack length, length scale parameter and level of submergence on vibration characteristics. CCSS (Two adjacent edges clamped and the other two simply supported) and SSSS (All sides simply supported), these two boundary conditions are considered in present work. Finally, new results for fundamental frequencies, frequency response and peak amplitude of the partially cracked and submerged orthotropic plate are presented. The central deflection of the cracked plate has also been studied as affected by length of crack and temperature variation. A comparison of these results with the classical plate theory has also been established.

Fig. 2

Submerged plate element showing all moments and transverse forces

2 Governing equation

In this section, the differential governing equation for a partially cracked and submerged orthotropic plate subjected to uniform heating (as shown in Fig. 1) is formulated based on classical plate theory in conjunction with strain gradient theory of elasticity. The assumptions involved in the modeling are: (1) The plate is presumed as thin, homogenous and impeccably elastic composed of orthotropic material (2) The mid-plane stays unstrained consequent to bending, for that reason the normal strain $(\varepsilon _{z})$, resulting from transverse loading, might be discarded. (3) The normal stress $(\sigma _{z})$ acting in the lateral direction of plate is neglected from constitutive relations in the modeling, because its magnitude is thought to be diminutive compared to the other stress components of model. (4) Effects of shear deformation and rotary inertia are neglected. (5) The temperature variation is thought to be linear all through the thickness of the plate; $T(z)=T_\mathrm{avg} +((\Delta {T}){z})/2$, where $\Delta T=T_\mathrm{t}-T_\mathrm{b}$ is the temperature difference between the top and the bottom surface of the plate and $T_\mathrm{avg} =(T_\mathrm{t}+T_\mathrm{b})/2$ is average temperature.

The constitutive relations for an isotropic intact plate using the principle of strain gradient theory of elasticity has been obtained in Ref. [17], based on the above assumptions and accommodating the orthotropic nature of the plate, the relations in the presence of thermal environment can be written as:

$$\begin{aligned} \sigma _{x}= & {} \frac{E_{x}}{1-\nu _{x}\nu _{y}}(\varepsilon _{x}+\nu _{y} \varepsilon _{y})\nonumber \\&-g^{2}\frac{E_{x}}{1-\nu _{x}\nu _{y}} \nabla ^{2}(\varepsilon _{x}+\nu _{y}\varepsilon _{y})\nonumber \\&-\frac{E_{x}}{1-\nu _{x}\nu _{y}}(\alpha _{x}+\nu _{y}\alpha _{y})\Delta T \end{aligned}$$

(1)

$$\begin{aligned} \sigma _{y}= & {} \frac{E_{x}}{1-\nu _{x}\nu _{y}}(\varepsilon _{y}+\nu _{x} \varepsilon _{x})\nonumber \\&-g^{2}\frac{E_{x}}{1-\nu _{x}\nu _{y}} \nabla ^{2}(\varepsilon _{y}+\nu _{x}\varepsilon _{x})\nonumber \\&-\frac{E_{y}}{1-\nu _{x}\nu _{y}}(\alpha _{y}+\nu _{x}\alpha _{x})\Delta T \end{aligned}$$

(2)

$$\begin{aligned} \tau _{xy}= & {} \tau _{yx}=G_{xy}\gamma _{xy}-g^{2}G_{xy}\nabla ^{2}\gamma _{xy} \end{aligned}$$

(3)

where $g^{2}$ is the volumetric gradient coefficient with g being the internal length scale of the microstructure of the plate. $\sigma _{x}$, $\sigma _{y}$ and $\varepsilon _{x}$, $\varepsilon _{y}$ are the normal stresses and strains in x and y direction respectively. Similarly, $\tau _{xy}$ and $\gamma _{xy}$ denotes the shear stress and strain in the x–y plane and $\nabla ^{2}=\left( {\frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}} \right)$. $E_{x}$, $E_{y}$ and ${\nu }_{{{x}}}$, ${\nu }_{{{y}}}$ represents the modulus of elasticity and Poisson’s ratio along two principle directions of orthotropy coinciding with x and y axes. $G_{xy}$ is the shear modulus. $\alpha _{x}$ and $\alpha _{y}$ are the thermal expansion coefficients in x and y direction, respectively. $\Delta T$ is the rise in temperature above stress free temperature of plate.

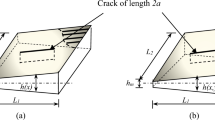
Consider a submerged orthotropic plate element containing a part-through crack of length 2a at its center as represented in Fig. 2. The bending moments and internal forces acting on middle surface of the plate due to volumetric gradient coefficient, thermal environment and crack are considered according to established classical thin plate theory. On resolving the internal forces along z axis and taking moment about x and y axes, one obtains the required equilibrium equation as,

$$\begin{aligned}&\frac{\partial ^{2}M_{x}}{\partial x^{2}}+\frac{\partial ^{2}M_{x}^{g} }{\partial x^{2}}+\frac{\partial ^{2}M_{y} }{\partial y^{2}}+\frac{\partial ^{2}M_{y}^{g}}{\partial y^{2}}+\frac{\partial ^{2}M_{xy} }{\partial x\partial y}\nonumber \\&\qquad +\frac{\partial ^{2}M_{xy}^{g} }{\partial x\partial y}+\frac{\partial ^{2}M_{yx} }{\partial x\partial y}+\frac{\partial ^{2}M_{yx}^{g}}{\partial x\partial y}\nonumber \\&\qquad +\frac{\partial ^{2}m_{y} }{\partial y^{2}}+\frac{\partial ^{2}M_{Tx} }{\partial x^{2}}+\frac{\partial ^{2}M_{Ty} }{\partial y^{2}}\nonumber \\&\quad =\rho h\frac{\partial ^{2}w}{\partial t^{2}}+\Delta P-P_{z} \end{aligned}$$

(4)

where $M_{x}$, $M_{y}$ and $M_{xy}=M_{yx}$ are the internal bending and twisting moments, respectively. Similarly, $M_{x}^{g}$, $M_{y}^{g}$ and $M_{xy}^{g}=M_{yx}^{g}$ are bending and twisting moments due to the microstructure of the plate. $M_{Tx}$ and $M_{Ty}$ are the moments due to thermal environment. $m_{y}$ represents additional moment which shows the effect of crack as deduced in the line spring model [26, 27, 30]. $\Delta P$ is the fluid dynamic pressure difference between the upper and lower surface of the plate. $\rho h\frac{\partial ^{2}w}{\partial t^{2}}$ denotes the inertia force of vibrating plate. $\rho$ and h are the density and thickness of plate, and $P_{z}$ represents the transverse load per unit area.

On expressing the bending moments in form of transverse deflection (see “Appendix A”), Eq. (4) can be written as,

$$\begin{aligned}&D_{x}\frac{\partial ^{4}w}{\partial x^{4}}+2B\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+D_{y}\frac{\partial ^{4}w}{\partial y^{4}}\nonumber \\&\qquad -\,g^{2}\left\{ D_{x}\frac{\partial ^{6}w}{\partial x^{6}}+D_{y} \frac{\partial ^{6}w}{\partial y^{6}}+(D_{x} +2B) \frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}\right. \nonumber \\&\qquad \left. +\,(D_{y}+2B)\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}} \right\} \nonumber \\&\quad =-\rho h\frac{\partial ^{2}w}{\partial t^{2}}-\Delta P+\frac{\partial ^{2}M_{Tx} }{\partial x^{2}}+\,\frac{\partial ^{2}M_{Ty} }{\partial y^{2}}\nonumber \\&\qquad +\,\frac{\partial ^{2}m_{y}}{\partial y^{2}}+P_{z} \end{aligned}$$

(5)

where $D_{x} =\frac{E_{x} h^{3}}{12(1-\nu _{x}\nu _{y})}$, $D_{y}=\frac{E_{y}h^{3}}{12(1-\nu _{x}\nu _{y})}$ and $D_\mathrm{t} =G_{xy}\frac{h^{3}}{12}$ represents the flexural and torsional rigidities, respectively. $B=\frac{1}{2}(\nu _{y}D_{x}+\nu _{x}D_{y}+4D_\mathrm{t})$ is the effective torsional rigidity.

When the displacements in both x and y direction of any plate structure being restricted then the pre-stressing of the plate causes in-plane forces [23]. In this present study for cracked orthotropic plates, apart from the in-plane force due to the crack, the in-plane forces due to effect of microstructure and temperature are also considered. The literature [27, 30] shows that the equilibrium of forces along z axis for an isotropic plate, for an arbitrary boundary condition results in a transverse force $(\sum F_{z})$, to be added to the moment equilibrium equations. Considering an arbitrary boundary condition as two adjacent edges free and the other two clamped, and employing summation of forces along z direction leads to,

$$\begin{aligned} \sum F_{z}= & {} R_{x}\frac{\partial ^{2}w}{\partial x^{2}}+R_{x}^{g} \frac{\partial ^{2}w}{\partial x^{2}}+R_{Tx} \frac{\partial ^{2}w}{\partial x^{2}}+R_{y} \frac{\partial ^{2}w}{\partial y^{2}}\nonumber \\&+R_{y}^{g} \frac{\partial ^{2}w}{\partial y^{2}}+R_{Ty} \frac{\partial ^{2}w}{\partial y^{2}}+r_{y} \frac{\partial ^{2}w}{\partial y^{2}}\nonumber \\&+2(R_{xy} +R_{xy}^{g}) \frac{\partial ^{2}w}{\partial x\partial y} \end{aligned}$$

(6)

where $R_{x}$, $R_{y}$, $R_{xy}=R_{yx}$ are the in-plane stretching forces and $R_{x}^{g}$, $R_{y}^{g}$, $R_{xy}^{g}=R_{yx}^{g}$ are the in-plane or membrane forces due to microstructure of plate. $R_{Tx}$ and $R_{Ty}$ are the thermal in-plane compressive forces. In this work, the shear force $(R_{Txy})$ is neglected because the temperature variation does not affect the shear stress [32]. $r_{y}$ represents the additional in-plane force due to line crack. Israr et. al. [26] in their formulation for cracked isotropic plate neglected the in-plane forces $N_{y}$ and $N_{xy}$ due to the crack parallel to x axis. In the present model also due to discontinuity across y direction, the in-plane forces $R_{y}$, $R_{y}^{g}$, $R_{xy}$ and $R_{xy}^{g}$ are neglected for equilibrium. Equation (6) represents the lateral force to be added to the required governing equation, Eq. (5). Thus, the governing equation of a cracked orthotropic micro-plate becomes,

$$\begin{aligned}&D_{x}\frac{\partial ^{4}w}{\partial x^{4}}+2B\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+D_{y} \frac{\partial ^{4}w}{\partial y^{4}}\nonumber \\&\quad -\,g^{2}\left\{ D_{x} \frac{\partial ^{6}w}{\partial x^{6}}+D_{y} \frac{\partial ^{6}w}{\partial y^{6}}+({D_{x} +2B}) \frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}\right. \nonumber \\&\quad \left. +\,(D_{y}+2B)\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}\right\} =-\rho h\frac{\partial ^{2}w}{\partial t^{2}}-\Delta P\nonumber \\&\quad +\,\frac{\partial ^{2}M_{Tx} }{\partial x^{2}}+\frac{\partial ^{2}M_{Ty} }{\partial y^{2}}+R_{x} \frac{\partial ^{2}w}{\partial x^{2}}+R_{x}^{g} \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\quad +\,R_{Tx} \frac{\partial ^{2}w}{\partial x^{2}}+R_{Ty} \frac{\partial ^{2}w}{\partial y^{2}}+\frac{\partial ^{2}m_{y} }{\partial y^{2}}+r_{y} \frac{\partial ^{2}w}{\partial y^{2}}+P_{z}\nonumber \\ \end{aligned}$$

(7)

The crack terms ($m_{y}$ and $r_{y}$) are obtained using simplified line spring model given by Rice and Levy [25]. It gives the relationship between the limiting effect produced by the net ligament stresses and the bending and tensile moments at far edges of the plate. Israr et al. [26] proposed the relationship of tensile and bending stresses at crack tips and far edges of plate for an isotropic plate. These relations were further modified and applied to a specially orthotropic plate by Joshi et al. [28]. Recently, Soni et al. [30, 31] presented the above relationship of the bending and tensile loads at the crack location and at the far sides of the plate in presence of fluidic medium for the isotropic and MEE plates. Similar relations for the cracked and submerged orthotropic plate incorporating the moments and in-plane forces due to internal microstructure and thermal environment can be presented as,

$$\begin{aligned} r_{y}= & {} -\frac{2a}{(6\alpha _\mathrm{bt}+\alpha _\mathrm{tt}) (1-\nu _{x}^{2})h+2a}(R_{y}{+}R_{y}^{g}{+}R_{Ty}) \end{aligned}$$

(8)

$$\begin{aligned} m_{y}= & {} -\frac{2a}{3\left( \frac{\alpha _\mathrm{bt}}{6}+\alpha _\mathrm{bb}\right) (3+\nu _{x})(1-\nu _{x})h+2a}\nonumber \\&(M_{y}+M_{y}^{g}+M_{Ty}) \end{aligned}$$

(9)

where the terms $\alpha _\mathrm{bb}, \alpha _\mathrm{tt},\alpha _\mathrm{bt}=\alpha _\mathrm{tb}$ are crack compliance coefficients for bending, stretching and bending-tensile, respectively. The crack compliance coefficients depend on the ratio of crack depth to its thickness, and they can be found in the literature [26]. On employing Eqs. (8) and (9) in Eq. (7) and expressing the moment $M_{y}$ and $M_{y}^{g}$ in form of transverse deflection (“Appendix A”), one obtains the required governing equation of motion of cracked orthotropic micro-plate as,

$$\begin{aligned}&D_{x}\frac{\partial ^{4}w}{{\partial x}^{4}}+2B\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+D_{y}\frac{\partial ^{4}w}{{\partial y}^{4}}\nonumber \\&\qquad -\,g^{2}\left\{ D_{x}\frac{\partial ^{6}w}{{\partial x}^{6}}+D_{y}\frac{\partial ^{6}w}{{\partial y}^{6}}+\left( D_{x}+2B \right) \frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}\right. \nonumber \\&\qquad \left. +\,\left( D_{y}+2B \right) \frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}\right\} \nonumber \\&\quad =-\rho h\frac{\partial ^{2}w}{{\partial t}^{2}}-\Delta P\nonumber \\&\qquad +\,\frac{2a}{3\left( \frac{\alpha _\mathrm{bt}}{6}+\alpha _\mathrm{bb} \right) \left( 3+\nu _{x})(1-\nu _{x} \right) h+2a}\nonumber \\&\qquad \left[ D_{y}\left\{ \left( \frac{\partial ^{4}w}{{\partial y}^{4}}+\nu _{x}\frac{\partial ^{4}w}{{\partial x}^{2}{\partial y}^{2}} \right) -g^{2}\left( \frac{\partial ^{6}w}{{\partial y}^{6}}\right. \right. \right. \nonumber \\&\qquad \left. \left. +\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}+\nu _{x}\left( \frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}+\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}} \right) \right) \right\} \nonumber \\&\qquad \left. -\frac{\partial ^{4}M_{Ty}}{\partial y^{4}} \right] +\frac{\partial ^{2}M_{Tx}}{\partial x^{2}} +\frac{\partial ^{2}M_{Ty}}{\partial y^{2}}\nonumber \\&\qquad +R_{x}\frac{\partial ^{2}w}{{\partial x}^{2}}+R_{x}^{g}\frac{\partial ^{2}w}{\partial x^{2}}+R_{Tx}\frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\qquad +R_{Ty} \frac{\partial ^{2}w}{\partial y^{2}}-\frac{2a}{\left( {6\alpha _\mathrm{bt} +\alpha _\mathrm{tt} } \right) \left( {1-\nu _{x}^{2}} \right) h+2a}\nonumber \\&\qquad (R_{y} +R_{y}^{g} +R_{Ty} )\frac{\partial ^{2}w}{\partial y^{2}}+P_{z} \end{aligned}$$

(10)

When a plate is submerged in a fluid, it is known from the literature [30] that a thin layer of fluid vibrates along with the plate which increases the mass of the plate–fluid system. In this proposed work, fluid forces acting on plate surface are stated in the form of virtual added mass accompanying with the inertia of the surrounding fluid which helps to form the final differential governing equation of a coupled fluid–plate system. Soni et al. [30] in their work formulated the fluid forces in form of virtual added mass using potential flow theory and presented the influence of fluid medium on vibration response of cracked isotropic plate. They used the velocity potential function along with Bernoulli’s equation to express the fluid dynamic pressures acting on the plate. Similar approach has been adopted here to find the fluid pressure for cracked orthotropic plate with the following assumptions:

• 1. The fluid flow is assumed to be small, incompressible, homogeneous and irrotational.

• 2. The dynamic fluid pressure is normal to the surface of the plate and shear forces are neglected as the fluid is inviscid.

• 3. Interaction between the cracked plate and fluid and influence of nonlinearity at plate–fluid interface is neglected.

• 4. As the orthotropic plate is considered thin, the effect of fluid forces is ignored in the derivation of in-plane forces.

• 5. The fluid behaves like a thermal reservoir and the rise in temperature does not affect the fluid properties.

The fluid–plate coupled system for calculating the fluid dynamic pressures ($P_\mathrm{u}$ and $P_\mathrm{l}$) acting on upper and lower surface of plate is shown in Fig. 3.

Fig. 3

Plate–fluid model bounded by a rigid wall (A submerged plate)

Consider a plate element submerged in fluid horizontally as shown in Fig. 3. Expressing the velocity potential function in terms of Laplace equation and then using Bernoulli’s equation for the dynamic pressure at fluid–plate interaction in terms of potential function, applying the method of separation of variables with the assumption that a permanent contact exists among the fluid and plate so that the out of plane velocity of fluid is equal to the instantaneous velocity of plate in the transverse direction, the potential function can be expressed in terms of plate’s transverse deflection. Applying the kinematic boundary conditions [30] for fluid free surface and rigid container bottom, the resulting potential function becomes second order which can be solved for simply supported boundary condition using the deflection in form of the modal functions. Thus, the fluid dynamic pressure acting on the plate’s upper surface $(P_\mathrm{u})$ can be stated as [30]:

$$\begin{aligned} P_\mathrm{u}=-\frac{\rho _\mathrm{f}}{\mu }\left[ \frac{1+C\mathrm{e}^{2\mu h_{1}}}{1-C\mathrm{e}^{2\mu h_{1}}}\right] \frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(11)

where $C=\frac{{g}_{\mathrm{a}}\mu -\omega ^{2}}{{g}_{\mathrm{a}} \mu -\omega ^{2}}$ in which $\omega$ denotes the frequency of wave motion at free surface of fluid and ${g}_{\mathrm{a}}$ is the acceleration due to gravity. $\rho _\mathrm{f}$ is fluid density per unit volume and $\mu$ is plane wave number which is taken as independent of boundary condition, and it can be determined as $\mu =\pi \sqrt{\frac{1}{l_{1}^{2}} +\frac{1}{l_{2}^{2}}}$ [6, 30]. Kerboua et al. [6] in their formulation, showed that the value of parameter C tends asymptotically toward $-1$ to avoid nonlinearity at fluid–plate interface. This is true for most of the plate aspect ratios. In the present work, the plate aspect ratio is taken as 1, for which Kerboua et al. [6] has shown that the parameter ${C}=-1$ and hence, it is assumed that ${C}=-1$. Here, $\frac{\partial ^{2}w}{\partial t^{2}}$ represents the inertia of the surrounding fluid that forces it to oscillate when the plate vibrates. $h_{1}$ is height of fluid above the surface of plate whereas $h_{2}$ is the level of fluid below the plate surface. The detailed derivation for fluid modeling can be referred from “Appendix B”.

Similarly, the fluid dynamic pressure at lower surface of the plate $(P_\mathrm{l})$ can be written as [30]:

$$\begin{aligned} P_\mathrm{l}=-\frac{\rho _\mathrm{f}}{\mu }\left[ \frac{1+\mathrm{e}^{-2\mu h_{2}}}{1-\mathrm{e}^{-2\mu h_{2}}}\right] \frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(12)

For fully submerged plate (as shown in Fig. 3.), the net fluid dynamic pressure can be determined using above two expressions Eqs. (11) and (12). The resulting fluid dynamic pressure difference $(\Delta P)$ for the fully submerged plate can be given as:

$$\begin{aligned} \Delta P= & {} P_\mathrm{u}-P_\mathrm{l}\nonumber \\= & {} -\frac{\rho _\mathrm{f}}{\mu } \left[ \frac{1+C\mathrm{e}^{2\mu h_{1}}}{1-C\mathrm{e}^{2\mu h_{1}}} -\frac{1+\mathrm{e}^{-2\mu h_{2}}}{1-\mathrm{e}^{-2\mu h_{2}}}\right] \frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(13)

$$\begin{aligned} \Delta P= & {} m_\mathrm{add}\frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(14)

where $m_\mathrm{add}=-\frac{\rho _\mathrm{f}}{\mu }\left[ {\frac{1+C\mathrm{e}^{2\mu h_{1}}}{1-C\mathrm{e}^{2\mu h_{1}}}-\frac{1+\mathrm{e}^{-2\mu h_{2}}}{1-\mathrm{e}^{-2\mu h_{2}}}}\right]$ is the additional virtual mass of submerged plate due to surrounding fluid. Thus, for the case of submerged plate vibrations, the mass of the plate is increased due to a layer of fluid vibrating with the plate. This added mass is referred to as virtual added mass.

Employing the expression of net dynamic pressure of fluid $(\Delta P)$ from Eq. (14), the required governing equation of motion for cracked orthotropic plate in presence of fluid medium given by Eq. (10) becomes:

$$\begin{aligned}&D_{x} \frac{\partial ^{4}w}{\partial x^{4}}+2B\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+D_{y} \frac{\partial ^{4}w}{\partial y^{4}}\nonumber \\&\qquad -g^{2}\left\{ D_{x} \frac{\partial ^{6}w}{\partial x^{6}}+D_{y} \frac{\partial ^{6}w}{\partial y^{6}}\right. \nonumber \\&\left. \qquad +\left( {D_{x} +2B} \right) \frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}+\left( {D_{y}+2B}\right) \frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}\right\} \nonumber \\&\qquad -\frac{2a}{3\left( {\frac{\alpha _\mathrm{bt} }{6}+\alpha _\mathrm{bb}}\right) \left( {3+\nu _{x} )(1-\nu _{x} } \right) h+2a}\nonumber \\&\qquad \left[ D_{y} \left\{ \left( {\frac{\partial ^{4}w}{\partial y^{4}}+\nu _{x} \frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}} \right) -g^{2}\left( \frac{\partial ^{6}w}{\partial y^{6}}\right. \right. \right. \nonumber \\&\qquad \left. \left. +\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}+\nu _{x} \left( {\frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}+\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}} \right) \right) \right\} \nonumber \\&\qquad \left. -\frac{\partial ^{4}M_{Ty} }{\partial y^{4}}\right] -\frac{\partial ^{2}M_{Tx} }{\partial x^{2}}-\frac{\partial ^{2}M_{Ty} }{\partial y^{2}}\nonumber \\&\quad =-\left( {\rho h+m_\mathrm{add} } \right) \frac{\partial ^{2}w}{\partial t^{2}}+R_{x} \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\qquad +R_{x}^{g} \frac{\partial ^{2}w}{\partial x^{2}}+R_{Tx} \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\qquad +R_{Ty} \frac{\partial ^{2}w}{\partial y^{2}}-\frac{2a}{\left( {6\alpha _\mathrm{bt} +\alpha _\mathrm{tt} } \right) \left( {1-\nu _{x}^{2}} \right) h+2a}\nonumber \\&\qquad (R_{y} +R_{y}^{g} +R_{Ty} )\frac{\partial ^{2}w}{\partial y^{2}}+P_{z} \end{aligned}$$

(15)

Equation (15) shows the final form of governing equation of cracked and submerged orthotropic plate in the presence of thermal environment based on strain gradient theory.

3 General solution for governing equation

The presence of external environment like rise in temperature has been included in the differential governing equation of cracked and submerged orthotropic plate in the terms of thermal bending moments and in-plane compressive forces. The present work restricts itself to the solution of final governing equation for the case of uniformly heated plates (${M}_{{Tx}}={M}_{{Ty}}=0)$. Since, in majority of engineering applications thin plate structures having good thermal conductivity are used, there is little temperature gradient along the plate thickness and they can be considered as uniformly heated plates. The characteristic functions which depends on the boundary conditions of plates can be selected for general solution of governing equation as [26,27,28],

$$\begin{aligned} w (x,y,t)=\sum \limits _{m=1}^{\infty }\sum \limits _{n=1}^{\infty } A_{mn}X_{m}Y_{n}\psi _{mn} (t) \end{aligned}$$

(16)

where $X_{m}$ and $Y_{n}$ are the characteristic functions, $\psi _{mn} (t)$ is time-dependent characteristic modal term and $A_{mn}$ is arbitrary amplitude of vibration. The characteristic functions $X_{m}$ and $Y_{n}$ for the two boundary conditions considered in this work can be found from the literature [26, 32].

It is well known that the in-plane or membrane forces depends on the boundary conditions and they can be expressed in form of mid-surface strains as found in the literature [26, 28].

$$\begin{aligned} R_{x}= & {} \frac{12D_{x}}{h^{2}}\left[ \frac{\partial u}{\partial x}+\nu _{y} \frac{\partial v}{\partial y}+\frac{1}{2}\left( \left( \frac{\partial w}{\partial x}\right) ^{2}\right. \right. \nonumber \\&\left. \left. +\nu _{y} \left( {\frac{\partial w}{\partial y}} \right) ^{2}\right) \right] \end{aligned}$$

(17)

$$\begin{aligned} R_{y}= & {} \frac{12D_{y}}{h^{2}}\left[ \frac{\partial v}{\partial y}+\nu _{x} \frac{\partial u}{\partial x}+\frac{1}{2}\left( \left( \frac{\partial w}{\partial y}\right) ^{2}\right. \right. \nonumber \\&\left. \left. +\nu _{x} \left( \frac{\partial w}{\partial x}\right) ^{2}\right) \right] \end{aligned}$$

(18)

$$\begin{aligned} R_{x}^{g}= & {} -\frac{12D_{x} }{h^{2}}g^{2}\nabla ^{2}\left[ \frac{\partial u}{\partial x}+\nu _{y}\frac{\partial v}{\partial y}+\frac{1}{2}\left( \left( \frac{\partial w}{\partial x}\right) ^{2}\right. \right. \nonumber \\&\left. \left. +\nu _{y}\left( \frac{\partial w}{\partial y}\right) ^{2}\right) \right] \end{aligned}$$

(19)

$$\begin{aligned} R_{y}^{g}= & {} -\frac{12D_{y} }{h^{2}}g^{2}\nabla ^{2}\left[ \frac{\partial v}{\partial y}+\nu _{x} \frac{\partial u}{\partial x}+\frac{1}{2}\left( \left( \frac{\partial w}{\partial y}\right) ^{2}\right. \right. \nonumber \\&\left. \left. +\nu _{x} \left( \frac{\partial w}{\partial x}\right) ^{2}\right) \right] \end{aligned}$$

(20)

$$\begin{aligned} R_{Tx}= & {} -\frac{E_{x}h\Delta T}{1-\nu _{x}\nu _{y}}(\alpha _{x}+\nu _{y}\alpha _{y}) \end{aligned}$$

(21)

$$\begin{aligned} R_{Ty}= & {} -\frac{E_{y}h\Delta T}{1-\nu _{x}\nu _{y}}(\alpha _{y}+\nu _{x}\alpha _{x}) \end{aligned}$$

(22)

where $R_{x}$, $R_{y}$ represent the in-plane forces per unit length on mid-plane of plate along x and y axis and $R_{x}^{g}$, $R_{y}^{g}$ are the in-plane forces due to effect of microstructure. $R_{Tx}$ and $R_{Ty}$ are in-plane compressive forces induced due to thermal heating.

On multiplying Eqs. (17)–(20) by dxdy and integrating over the surface of the plate, invoking the conditions that in-plane deflections u and v vanish at the location of the crack and at the far sides of the plate due to symmetry, the in-plane forces can be written as:

$$\begin{aligned} R_{x}= & {} \frac{6D_{x}}{h^{2}l_{1}l_{2}}\int _{0}^{l_{1}} \int _{0}^{l_{2}}\left[ \left( \frac{\partial w}{\partial x} \right) ^{2}+{\nu _{y}\left( \frac{\partial w}{\partial y}\right) }^{2}\right] {\hbox {d}}x\,{\hbox {d}}y \end{aligned}$$

(23)

$$\begin{aligned} R_{y}= & {} \frac{6D_{y}}{h^{2}l_{1}l_{2}}\int _{0}^{l_{1}} \int _{0}^{l_{2}}\left[ \left( \frac{\partial w}{\partial y}\right) ^{{2}}+{\nu _{x}\left( \frac{\partial w}{\partial x} \right) }^{2}\right] {\hbox {d}}x\,{\hbox {d}}y \end{aligned}$$

(24)

$$\begin{aligned} R_{x}^{g}= & {} -\frac{6D_{x}}{h^{2}l_{1}l_{2}}{2g}^{2}\int _{0}^{l_{1}} \int _{0}^{l_{2}} \left[ \left( \frac{\partial ^{2}w}{\partial x^{2}} \right) ^{2}+\left( \frac{\partial ^{2}w}{\partial x\partial y} \right) ^{2}\right. \nonumber \\&\left. +\frac{\partial w}{\partial x}\left( \frac{\partial ^{3}w}{\partial x^{3}}+\frac{\partial ^{3}w}{\partial x\partial y^{2}}\right) +\nu _{y}\left\{ \left( \frac{\partial ^{2}w}{\partial y^{2}}\right) ^{2}\right. \right. \nonumber \\&\left. \left. +\left( \frac{\partial ^{2}w}{\partial x\partial y} \right) ^{2}+\frac{\partial w}{\partial y}\left( \frac{\partial ^{3}w}{\partial y^{3}}+\frac{\partial ^{3}w}{\partial y\partial x^{2}} \right) \right\} \right] {\hbox {d}}x\,{\hbox {d}}y \end{aligned}$$

(25)

$$\begin{aligned} R_{y}^{g}= & {} -\frac{6D_{y}}{h^{2}l_{1}l_{2}}{2g}^{2}\int _{0}^{l_{1}} \int _{0}^{l_{2}}\left[ \left( \frac{\partial ^{2}w}{\partial y^{2}} \right) ^{2}+\left( \frac{\partial ^{2}w}{\partial x\partial y} \right) ^{2}\right. \nonumber \\&\left. +\frac{\partial w}{\partial y}\left( \frac{\partial ^{3}w}{\partial y^{3}}+\frac{\partial ^{3}w}{\partial y\partial x^{2}}\right) +\nu _{x}\left\{ \left( \frac{\partial ^{2}w}{\partial x^{2}}\right) ^{{2}}\right. \right. \nonumber \\&\left. \left. +\left( \frac{\partial ^{2}w}{\partial x\partial y}\right) ^{2} +\frac{\partial w}{\partial x}\left( \frac{\partial ^{3}w}{\partial x^{3}}+\frac{\partial ^{3}w}{\partial x\partial y^{2}}\right) \right\} \right] \, {\hbox {d}}x\,{\hbox {d}}y\nonumber \\ \end{aligned}$$

(26)

On substitution of the in-plane forces from Eqs. (21) to (26) into Eq. (15), applying the general solution of lateral deflection from Eq. (16), multiplying each term of Eq. (15) by the characteristic functions $X_{m}$ and $Y_{n}$, and then integrating over the plate area, the required governing equation can be written as:

$$\begin{aligned}&(\rho h+m_\mathrm{add})\sum \limits _{n=1}^{\infty } \sum \limits _{m=1}^{\infty } A_{mn} \int _{0}^{l_{1}}\int _{0}^{l_{2}} {X_{m}^{2}Y_{n}^{2}} {\hbox {d}}x\,{\hbox {d}}y\frac{\partial ^{2}\psi _{mn}(t)}{{\partial t}^{2}}+\sum \limits _{n=1}^{\infty }\sum \limits _{m=1}^{\infty } A_{mn}\psi _{mn}(t)\int _{0}^{l_{1}}\int _{0}^{l_{2}}\nonumber \\&\qquad \left\{ (D_{x}X_{m}^\mathrm{iv}Y_{n}+2B X_{m}^\mathrm{ii}Y_{n}^\mathrm{ii} +D_{y}Y_{n}^\mathrm{iv}X_{m})-g^{2}{(D_{x}X}_{m}^\mathrm{vi}Y_{n}+( D_{x}+2B)X_{m}^\mathrm{iv}Y_{n}^\mathrm{ii}+(D_{y}+2B)X_{m}^\mathrm{ii}Y_{n}^\mathrm{iv} \right. \nonumber \\&\qquad \left. +{D_{y}Y_{n}}^\mathrm{vi}X_{m})-\frac{2aD_{y}\left\{ (\nu _{x}X_{m}^\mathrm{ii}Y_{n}^\mathrm{ii}+Y_{n}^\mathrm{iv}X_{m}) -g^{2}\left( X_{m}^\mathrm{ii}Y_{n}^\mathrm{iv}+X_{m}Y_{n}^\mathrm{vi}+\nu _{x} (X_{m}^\mathrm{iv}Y_{n}^\mathrm{ii}+X_{m}^\mathrm{ii}Y_{n}^\mathrm{iv})\right) \right\} }{3\left( \frac{\alpha _\mathrm{bt}}{6}+\alpha _\mathrm{bb} \right) (3+\nu _{x})(1-\nu _{x})h+2a}\right. \nonumber \\&\qquad \left. +\left( \frac{E_{x}h\Delta T}{1-\nu _{x}\nu _{y}} (\alpha _{x}+\nu _{y}\alpha _{y})X_{m}^\mathrm{ii}Y_{n} +\frac{E_{y}h\Delta T}{1-\nu _{x}\nu _{y}} (\alpha _{y}+\nu _{x}\alpha _{x}) \frac{(1+2a)Y_{n}^\mathrm{ii}X_{m}}{( 6\alpha _\mathrm{bt}+\alpha _\mathrm{tt})(1-\nu ^{2})h+2a}\right) \right\} X_{m}Y_{n}{\hbox {d}}x\,{\hbox {d}}y \nonumber \\&\qquad +\sum \limits _{n=1}^{\infty } \sum \limits _{m=1}^{\infty }A_{mn}^{3}\psi _{mn} (t)^{3}\int \limits _{0}^{l_{1}}\int \nolimits _{0}^{l_{2}} \left\{ \frac{2aB_{2mn}Y_{n}^\mathrm{ii}Y_{n} X_{m}^{2}}{(6\alpha _\mathrm{bt} +\alpha _\mathrm{tt})(1-\nu _{x}^{2})h+2a}-B_{1mn} X_{m}^\mathrm{ii}X_{m} Y_{n}^{2}\right\} {\hbox {d}}x\,{\hbox {d}}y\nonumber \\&\quad =\int \nolimits _{0}^{l_{1}} \int \nolimits _{0}^{l_{2}}P_{z} X_{m} Y_{n} {\hbox {d}}x\,{\hbox {d}}y \end{aligned}$$

(27)

where

$$\begin{aligned} B_{1mn}= & {} \frac{6D_{x}}{h^{2}l_{1}l_{2}}\sum \limits _{n=1}^\infty \sum \limits _{m=1}^\infty \int _{0}^{l_{1}} \int _{0}^{l_{2}}\left[ \left( X_{m}^\mathrm{i}Y_{n} \right) ^{2}\right. \\&\left. +\nu _{y}\left( Y_{n}^\mathrm{i}X_{m} \right) ^{2}-{2g}^{2}\left\{ \left( X_{m}^\mathrm{ii}Y_{n} \right) ^{2}\right. \right. \nonumber \\&\left. \left. +\left( X_{m}^\mathrm{i}Y_{n}^\mathrm{i} \right) ^{2}+X_{m}^\mathrm{i}Y_{n}\left( X_{m}^\mathrm{iii}Y_{n}+X_{m}^\mathrm{i}Y_{n}^\mathrm{ii} \right) \right. \right. \\&\left. \left. +\nu _{y}\left( \left( X_{m}Y_{n}^\mathrm{ii} \right) ^{2}+\left( X_{m}^\mathrm{i}Y_{n}^\mathrm{i} \right) ^{2}\right. \right. \right. \nonumber \\&\left. \left. \left. +X_{m}Y_{n}^\mathrm{i}\left( X_{m}Y_{n}^\mathrm{iii}+X_{m}^\mathrm{ii}Y_{n}^\mathrm{i} \right) \right) \right\} \right] {\hbox {d}}x\,{\hbox {d}}y\\ B_{2mn}= & {} \frac{6D_{y}}{h^{2}l_{1}l_{2}}\sum \limits _{n=1}^\infty \sum \limits _{m=1}^\infty \int _{0}^{l_{1}} \int _{0}^{l_{2}} \left[ \left( Y_{n}^\mathrm{i}X_{m} \right) ^{2}\right. \\&\left. +\nu _{x}\left( X_{m}^\mathrm{i}Y_{n} \right) ^{2}-{2g}^{2}\left\{ \left( X_{m}Y_{n}^\mathrm{ii} \right) ^{2}\right. \right. \nonumber \\&\left. \left. +\left( X_{m}^\mathrm{i}Y_{n}^\mathrm{i} \right) ^{2}+X_{m}Y_{n}^\mathrm{i}\left( X_{m}Y_{n}^\mathrm{iii}+X_{m}^\mathrm{ii}Y_{n}^\mathrm{i} \right) \right. \right. \nonumber \\&\left. \left. +\nu _{x}\left( \left( X_{m}^\mathrm{ii}Y_{n} \right) ^{2}+\left( X_{m}^\mathrm{i}Y_{n}^\mathrm{i} \right) ^{2}\right. \right. \right. \nonumber \\&\left. \left. \left. +X_{m}^\mathrm{i}Y_{n}\left( X_{m}^\mathrm{iii}Y_{n}+X_{m}^\mathrm{i}Y_{n}^\mathrm{ii} \right) \right) \right\} \right] {\hbox {d}}x\,{\hbox {d}}y \end{aligned}$$

Based on the application of the appropriate delta function, the lateral load $P_{z}$ can be readily expressed as [26],

$$\begin{aligned} P_{z}=P_{0} (t)\delta (x-x_{0})\delta (y-y_{0}) \end{aligned}$$

(28)

where $P_{0} (t)$ denotes the time-dependent lateral load and ($x_{0}$, $y_{0}$) is the position coordinate of load.

On substituting $P_{z}$ from Eq. (28) into Eq. (27), the force term of Eq. (27) can be expressed as:

$$\begin{aligned} P_{mn}= & {} P_{0} (t)\int \nolimits _{0}^{l_{1}}\int \nolimits _{0}^{l_{2}} \delta (x-x_{0})\delta (y-y_{0}) X_{m} Y_{n} {\hbox {d}}x\,{\hbox {d}}y\nonumber \\ P_{mn}= & {} P_{0}(t)X_{m} (x_{0})Y_{n} (y_{0})\nonumber \\ P_{mn}= & {} P_{0}(t)Q_{mn} \end{aligned}$$

(29)

where $Q_{mn} =X_{m} (x_{0})Y_{n} (y_{0})$ shows the position of lateral load $(P_{0} (t))$ on plate for different boundary conditions.

Using Eq. (29), the governing equation Eq. (27) containing nonlinear term can be expressed as.

$$\begin{aligned}&(M_{mn} +M_\mathrm{add})\frac{\partial ^{2}\psi _{mn} (t)}{\partial t^{2}}+ K_{mn} \psi _{mn} (t)+ G_{mn} \psi _{mn} (t)^{3}\nonumber \\&\quad = P_{mn} \end{aligned}$$

(30)

where

$$\begin{aligned} M_{mn}= & {} \rho h\sum \limits _{n=1}^{\infty } \sum \limits _{m=1}^{\infty } A_{mn} \int _{0}^{l_{1}}{\int _{0}^{l_{2}}{X_{m}^{2}Y_{n}^{2}}{\hbox {d}}x\,{\hbox {d}}y} \end{aligned}$$

(31)

$$\begin{aligned} M_\mathrm{add}= & {} m_\mathrm{add}\sum \limits _{n=1}^{\infty } \sum \limits _{m=1}^{\infty } A_{mn} \int _{0}^{l_{1}} {\int _{0}^{l_{2}} {X_{m}^{2}Y_{n}^{2}} {\hbox {d}}x\,{\hbox {d}}y} \end{aligned}$$

(32)

$$\begin{aligned} K_{mn}= & {} \sum \limits _{n=1}^{\infty } \sum \limits _{m=1}^{\infty } A_{mn} \int _{0}^{l_{1}}\int _{0}^{l_{2}} \left\{ (D_{x}X_{m}^\mathrm{iv}Y_{n}+2B X_{m}^\mathrm{ii}Y_{n}^\mathrm{ii} +{D_{y}Y_{n}}^\mathrm{iv}X_{m}) .-g^{2}{(D_{x}X}_{m}^\mathrm{vi}Y_{n} +(D_{x}+2B)X_{m}^\mathrm{iv}Y_{n}^\mathrm{ii}+(D_{y}\right. \nonumber \\&+\,2B)X_{m}^\mathrm{ii}Y_{n}^\mathrm{iv} {+}{D_{y}Y_{n}}^\mathrm{vi}X_{m}){-}\frac{2aD_{y}\left\{ (\nu _{x}X_{m}^\mathrm{ii}Y_{n}^\mathrm{ii}{+}Y_{n}^\mathrm{iv}X_{m}){-}g^{2}( X_{m}^\mathrm{ii}Y_{n}^\mathrm{iv}+X_{m}Y_{n}^\mathrm{vi}{+}\nu _{x}( X_{m}^\mathrm{iv}Y_{n}^\mathrm{ii}+X_{m}^\mathrm{ii}Y_{n}^\mathrm{iv}))\right\} }{3( \frac{\alpha _\mathrm{bt}}{6}+ \alpha _\mathrm{bb})(3+\nu _{x})(1-\nu _{x})h+2a}\nonumber \\&+\,\left( \frac{E_{x}h\Delta T}{1-\nu _{x}\nu _{y}}(\alpha _{x}+\nu _{y}\alpha _{y})X_{m}^\mathrm{ii} Y_{n}\left. +\frac{E_{y}h\Delta T}{1-\nu _{x}\nu _{y}}(\alpha _{y}+\nu _{x}\alpha _{x})\frac{(1+2a) Y_{n}^\mathrm{ii}X_{m}}{(6\alpha _\mathrm{bt}+\alpha _\mathrm{tt}) (1-\nu ^{2})h+2a}\right) \right\} X_{m}Y_{n}{\hbox {d}}x\,{\hbox {d}}y \end{aligned}$$

(33)

$$\begin{aligned} G_{mn}= & {} \sum \limits _{n=1}^{\infty }\sum \limits _{m=1}^{\infty } A_{mn}^{3}\int \limits _{0}^{l_{1}}\int \nolimits _{0}^{l_{2}} \left\{ \frac{2aB_{2mn} Y_{n}^\mathrm{ii}Y_{n} X_{m}^{2}}{(6\alpha _\mathrm{bt}+\alpha _\mathrm{tt})(1-\nu _{x}^{2})h+2a}-B_{1mn} X_{m}^\mathrm{ii}X_{m}Y_{n}^{2}\right\} {\hbox {d}}x\,{\hbox {d}}y \end{aligned}$$

(34)

$M_{mn}$ and $M_\mathrm{add}$ represent the actual and virtual mass of cracked plate. $K_{mn}$ denotes the plate stiffness and $G_{mn}$ represents the nonlinear term of governing equation [26, 32].

Damping of plate structures submerged in fluid is yet another area of research. In the recent work of Luo and Karney [33], he determined the damping ratios for plate structure submerged in fluid. In the present work, the fluid–plate system is assumed to be affected by linear viscous damping $(\mu _\mathrm{o})$. For such condition of classical damping occurs due to the fluidic medium, the differential governing equation [Eq. (30)] can be expressed as:

$$\begin{aligned}&\frac{\partial ^{2}\psi _{mn}(t)}{\partial t^{2}}+2\mu _\mathrm{o} \frac{\partial \psi _{mn}(t)}{\partial t}+\omega _{mn}^{2} \psi _{mn}(t)\nonumber \\&\quad +\frac{G_{mn}}{(M_{mn}+M_\mathrm{add})} \psi _{mn}(t)^{3}=\frac{{Q_{mn}P}_{0}(t)}{{(M}_{mn}+M_\mathrm{add})} \end{aligned}$$

(35)

where $\omega _{mn}$ represents the natural frequency of partially cracked and submerged orthotropic plate subjected to thermal environment and it can be given by,

$$\begin{aligned} \omega _{mn}^{2}=\frac{K_{mn}}{{(M}_{mn}+M_\mathrm{add})} \end{aligned}$$

(36)

In the above equation [Eq.(36)], the virtual added mass $(M_\mathrm{add})$ clearly shows the effect of surrounding fluid medium on the natural frequency of cracked orthotropic plate.

4 Frequency response and peak amplitude

In the present work, a perturbation technique, namely Method of Multiple Scales, is employed for determining the approximated solution of nonlinear governing equation [Eq. (35)]. In the literature, this method is used by many researchers [26,27,28] to find the approximate solutions for partially cracked rectangular plates in vacuum. Here, this approach is modified to incorporate the influence of fluid medium for better understanding of the nonlinear behavior of cracked and submerged orthotropic plate. The detailed derivation can be referred from Ref. [28, 30]. The final relation for frequency response of cracked and submerged orthotropic plate can be written as:

$$\begin{aligned}&e_{mn}=\frac{3G_{mn}}{8(M_{mn}+M_\mathrm{add}) \omega _{mn}}J^{2}\nonumber \\&\quad \underline{+}\,\, \sqrt{\left( \frac{Q_{mn}^{2}}{4(M_{mn}+M_\mathrm{add})^{2} \omega _{mn}^{2}J^{2}}P_{0}^{2}-\mu _\mathrm{o}^{2}\right) } \end{aligned}$$

(37)

where $e_{mn}$ denotes the detuning parameter, $P_\mathrm{o}$ and J represents the amplitude of external excitation force and the amplitude of frequency response, respectively. The peak amplitude of frequency response can be given by [30],

$$\begin{aligned} J_{P}=\frac{Q_{mn}}{2{(M}_{mn}+M_\mathrm{add})\omega _{mn}\mu _\mathrm{o}}P_{0} \end{aligned}$$

(38)

The new term $M_\mathrm{add}$ in the nonlinear part $\left( \frac{3G_{mn}}{{8(M}_{mn}+M_\mathrm{add})\omega _{mn}}J^{2}\right)$ of Eq. (37) shows the influence of fluidic medium on the frequency response of the partially cracked orthotropic plate. Similarly, in case of the peak amplitude [Eq. (38)], it is seen that it is also affected by the surrounding fluid medium.

5 Relation for central deflection of plate

Consider a cracked orthotropic plate with all sides simply supported, subjected to a lateral uniformly distributed dynamic load $(P_{z})$ harmonically varying with time. For a plate in the absence of thermal moments $({M}_{{Tx}}={M}_{{Ty}}=0)$ and the presence of constant in-plane forces (${R}_{{{Tx}}}$ and ${R}_{{Ty}}$) due to thermal environment only [Eqs. (21 and 22)], the governing equation [Eq. (15)] becomes

$$\begin{aligned}&D_{x}\frac{\partial ^{4}w}{{\partial x}^{4}}+2B\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+D_{y}\frac{\partial ^{4}w}{{\partial y}^{4}}\nonumber \\&\quad -\,g^{2}\left\{ D_{x}\frac{\partial ^{6}w}{{\partial x}^{6}}+D_{y}\frac{\partial ^{6}w}{{\partial y}^{6}}\right. \nonumber \\&\quad \left. +\,(D_{x}+2B)\frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}+(D_{y}+2B)\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}\right\} \nonumber \\&\quad -\,\frac{2a}{3\left( \frac{\alpha _\mathrm{bt}}{6}+ \alpha _\mathrm{bb} \right) \left( 3+\nu _{x})(1-\nu _{x} \right) h+2a}\nonumber \\&\qquad D_{y}\left\{ \left( \frac{\partial ^{4}w}{{\partial y}^{4}}+\nu _{x}\frac{\partial ^{4}w}{{\partial x}^{2}{\partial y}^{2}} \right) -g^{2}\left( \frac{\partial ^{6}w}{{\partial y}^{6}}\right. \right. \nonumber \\&\quad \left. \left. +\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}}+\nu _{x}\left( \frac{\partial ^{6}w}{\partial x^{4}\partial y^{2}}+\frac{\partial ^{6}w}{\partial x^{2}\partial y^{4}} \right) \right) \right\} \nonumber \\&\quad +\frac{E_{x}\Delta Th}{1-\nu _{x}\nu _{y}}\left( \alpha _{x}+\nu _{y}\alpha _{y} \right) \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\quad +\left( 1+\frac{2a}{\left( 6\alpha _\mathrm{bt}+\alpha _\mathrm{tt} \right) \left( 1-\nu _{x}^{2} \right) h+2a} \right) \nonumber \\&\qquad \frac{E_{y}\Delta Th}{1-\nu _{x}\nu _{y}}\left( \alpha _{y}+\nu _{x}\alpha _{x} \right) \frac{\partial ^{2}w}{\partial y^{2}}\nonumber \\&\quad +\left( \rho h+m_\mathrm{add} \right) \frac{\partial ^{2}w}{{\partial t}^{2}}=P_{z} \end{aligned}$$

(39)

Assuming the solution for lateral deflection as,

$$\begin{aligned} w(x,y,t)=W_{mn}{{\sin }} \left( \frac{m\pi x}{l_{1}}\right) {{\sin }} \left( \frac{n\pi y}{l_{2}}\right) {{\sin }} (\omega t) \end{aligned}$$

(40)

where $\omega$ is the vibrational frequency. The above expression is only applicable for the classical case with very week nonlinear effects. Now for the case of forced vibrations, the applied lateral dynamic load $P_{z} =P_{z}(x,y,t)$ can be expressed as

$$\begin{aligned} P_{z} (x,y,t)=P_{mn} {{\sin }} \left( \frac{m\pi x}{l_{1}}\right) {{\sin }} \left( \frac{n\pi y}{l_{2}}\right) \sin (\varnothing t) \end{aligned}$$

(41)

With $\varnothing$ being the forcing frequency of the load. Substituting the general solution of lateral deflection (w) from Eq. (40) with $\omega$ being replaced by $\varnothing$ and the lateral dynamic load $(P_{z})$ from Eq. (41) into the governing equation [Eq. (39)] results in an expression for $W_{mn}$. Thus, the classical relation for central deflection of cracked and submerged orthotropic plate subjected to uniform heating can be proposed as:

$$\begin{aligned} W_{mn}= & {} \frac{P_{mn}}{\begin{array}{c} \pi ^{4}\left( D_{x}\left( \frac{m}{l_{1}}\right) ^{4}+2B \left( \frac{m}{l_{1}}\right) ^{2} \left( \frac{n}{l_{2}}\right) ^{2}+D_{y} \left( \frac{n}{l_{2}}\right) ^{4}\right) \\ +\,\pi ^{6}g^{2}\left( D_{x}\left( \frac{m}{l_{1}}\right) ^{6} +(D_{x}+2B)\left( \frac{m}{l_{1}}\right) ^{4} \left( \frac{n}{l_{2}}\right) ^{2} +D_{y}\left( \frac{n}{l_{2}}\right) ^{6} +(D_{y}+2B)\left( \frac{m}{l_{1}}\right) ^{2} \left( \frac{n}{l_{2}}\right) ^{4}\right) \\ -\,\frac{2a}{H_{2}}\pi ^{4}D_{y}\left[ \left( \frac{n}{l_{2}} \right) ^{4}+\nu _{x}\left( \frac{m}{l_{1}}\right) ^{2}\left( \frac{n}{l_{2}} \right) ^{2}+\pi ^{2}g^{2}\left\{ \left( \frac{n}{l_{2}}\right) ^{6} +\nu _{x}\left( \frac{m}{l_{1}}\right) ^{4}\left( \frac{n}{l_{2}} \right) ^{2}+\left( 1+\nu _{x}\right) \left( \frac{m}{l_{1}} \right) ^{2}\left( \frac{n}{l_{2}}\right) ^{4}\right\} \right] \\ -\,\pi ^{2}\left[ \frac{E_{x}\Delta Th}{1-\nu _{x}\nu _{y}}\left( \alpha _{x}+\nu _{y}\alpha _{y} \right) \left( \frac{m}{l_{1}} \right) ^{2}+\left( 1+\frac{2a}{H_{1}} \right) \frac{E_{y}\Delta Th}{1-\nu _{x}\nu _{y}}\left( \alpha _{y}+\nu _{x}\alpha _{x} \right) \left( \frac{n}{l_{2}} \right) ^{2} \right] -{\varnothing }^{2}\left( \rho h+m_\mathrm{add} \right) \\ \end{array}} \end{aligned}$$

(42)

where

$$\begin{aligned} H_{2}= & {} 3\left( \frac{\alpha _\mathrm{bt}}{6}+\alpha _\mathrm{bb}\right) (3+\nu _{x})(1-\nu _{x})h+2a\\ H_{1}= & {} (6\alpha _\mathrm{bt}+\alpha _\mathrm{tt})(1-\nu _{x}^{2})h+2a \end{aligned}$$

For a special case of a square plate with side $l_{1}$ and $m=n=1$, the central deflection $W_{11}$ takes the form which clearly shows the presence of crack and temperature terms.

$$\begin{aligned} W_{11}= & {} \frac{P_{11}}{\begin{array}{c} \frac{\pi ^{4}}{l_{1}^{4}}\left[ \left( 1+2\pi ^{2} \left( \frac{g}{l_{1}}\right) ^{2}\right) \left\{ (D_{x} +2B+D_{y})-\frac{2a}{H_{2}}D_{y} (1+\nu _{x})\right\} \right] \\ -\frac{\pi ^{2}}{l_{1}^{2}}\left\{ \frac{E_{x}\Delta Th}{1-\nu _{x}\nu _{y}}(\alpha _{x}+\nu _{y}\alpha _{y}) +\left( 1+\frac{2a}{H_{1}}\right) \frac{E_{y}\Delta Th}{1-\nu _{x}\nu _{y}} (\alpha _{y}+\nu _{x}\alpha _{x})\right\} -\varnothing ^{2}(\rho h+m_\mathrm{add})\\ \end{array}}\nonumber \\ \end{aligned}$$

(43)

The results for central deflection of a cracked orthotropic plate without influence of thermal environment $(\Delta {T} = 0)$, Eq. (43) can be expressed as:

$$\begin{aligned}&W_{11}^{{\mathrm{cracked}}}=\frac{P_{11}}{\frac{\pi ^{4}}{l_{1}^{4}} \left[ \left( 1+2\pi ^{2}\left( \frac{g}{l_{1}}\right) ^{2}\right) \left\{ (D_{x}+2B+D_{y})-\frac{2a}{H_{2} }D_{y} (1+\nu _{x})\right\} \right] -\varnothing ^{2}(\rho h+m_\mathrm{add})} \end{aligned}$$

(44)

Similarly, the result for central deflection of a uniformly heated intact orthotropic plate without influence of any crack $({a} = 0)$, Eq. (43) can be expressed as:

$$\begin{aligned}&W_{11}^{\mathrm{heated}} =\frac{P_{11}}{\begin{array}{c} \frac{\pi ^{4}}{l_{1}^{4}}\left[ \left( {1+2\pi ^{2} \left( \frac{g}{l_{1}}\right) ^{2}}\right) \left( D_{x} +2B+D_{y}\right) \right] \\ -\frac{\pi ^{2}}{l_{1}^{2}}\left\{ \frac{E_{x}\Delta Th}{1-\nu _{x} \nu _{y}}\left( \alpha _{x}+\nu _{y}\alpha _{y}\right) +\frac{E_{y} \Delta Th}{1-\nu _{x}\nu _{y}}(\alpha _{y} +\nu _{x}\alpha _{x})\right\} -\varnothing ^{2}(\rho h+m_\mathrm{add})\\ \end{array}}\nonumber \\ \end{aligned}$$

(45)

The result for central deflection of an intact submerged orthotropic plate without influence of any crack $({a} = 0)$ and thermal environment $(\Delta {T} = 0)$, Eq. (43) can be expressed as:

$$\begin{aligned}&W_{11}^\mathrm{SGT}\; {\hbox {or}} \; W_{11}^{\mathrm{intact}}\nonumber \\&\quad =\frac{P_{11}}{\frac{\pi ^{4}}{l_{1}^{4}}\left[ \left( 1+2\pi ^{2} \left( \frac{g}{l_{1}}\right) ^{2}\right) (D_{x} +2B+D_{y})\right] -\varnothing ^{2}\left( \rho h+m_\mathrm{add}\right) }\nonumber \\ \end{aligned}$$

(46)

Similarly, the central deflection of an intact submerged orthotropic plate without influence of any crack, temperature and length scale parameter (${a} = 0, \Delta {T} = 0$ and $g = 0$) can be expressed as:

$$\begin{aligned} W_{11}^\mathrm{CPT}=\frac{P_{11}}{\frac{\pi ^{4}}{l_{1}^{4}} \left[ (D_{x} +2B+D_{y})\right] -\varnothing ^{2}(\rho h+m_\mathrm{add})} \end{aligned}$$

(47)

The central deflection ratio $W_{11}^{\mathrm{cracked}}/W_{11}^{\mathrm{intact}}$ can be obtained by dividing Eqs. (44) and (46) as:

$$\begin{aligned} \frac{W_{11}^{\mathrm{cracked}}}{W_{11}^{\mathrm{intact}}} =\frac{\frac{\pi ^{4}}{l_{1} ^{4}}\left[ \left( 1+2\pi ^{2}\left( \frac{g}{l_{1}}\right) ^{2}\right) (D_{x} +2B+D_{y})\right] -\varnothing ^{2} (\rho h+m_\mathrm{add})}{\frac{\pi ^{4}}{l_{1}^{4}} \left[ \left( 1+2\pi ^{2}\left( \frac{g}{l_{1}}\right) ^{2}\right) \left\{ (D_{x}+2B+D_{y})-\frac{2a}{H_{2}}D_{y} (1+\nu _{x})\right\} \right] -\varnothing ^{2}(\rho h+m_\mathrm{add})} \end{aligned}$$

(48)

Or

$$\begin{aligned} \frac{W_{11}^{\mathrm{cracked}}}{W_{11}^{\mathrm{intact}}} =\frac{1-(\varnothing /\omega _{11}^\mathrm{SGT})^{2}}{1-\frac{\frac{2a}{H_{2}}D_{y} (1+\nu _{x})}{(D_{x} +2B+D_{y})}-(\varnothing /\omega _{11}^\mathrm{SGT})^{2}} \end{aligned}$$

(49)

where $\omega _{11}^\mathrm{SGT} =\sqrt{\frac{\frac{\pi ^{4}}{l_{1}^{4}} \left[ \left( 1+2\pi ^{2}\left( \frac{g}{l_{1}}\right) ^{2}\right) (D_{x}+2B+D_{y})\right] }{(\rho h+m_\mathrm{add})}}$ is the natural frequency of intact submerged orthotropic plate based on strain gradient theory.

Similarly, the central deflection ratio $W_{11}^{\mathrm{heated}}/W_{11}^{\mathrm{intact}}$ can be obtained by dividing Eqs. (45) and (46) as;

$$\begin{aligned} \frac{W_{11}^{\mathrm{heated}}}{W_{11}^{\mathrm{intact}}} =\frac{1-\left( \varnothing /\omega _{11}^\mathrm{SGT}\right) ^{2}}{1-\frac{\frac{l_{1}^{2}}{\pi ^{2}} \left\{ \frac{E_{x} \Delta Th}{1-\nu _{x}\nu _{y}} (\alpha _{x} +\nu _{y}\alpha _{y}) +\frac{E_{y}\Delta Th}{1-\nu _{x} \nu _{y}} (\alpha _{y}+\nu _{x}\alpha _{x})\right\} }{\left[ \left( 1+2\pi ^{2} \left( \frac{g}{l_{1}}\right) ^{2}\right) (D_{x} +2B+D_{y})\right] } -\left( \varnothing /\omega _{11}^\mathrm{SGT}\right) ^{2}} \end{aligned}$$

(50)

The central deflection ratio $W_{11}^\mathrm{SGT}/W_{11}^\mathrm{CPT}$ can be obtained by dividing Eqs. (46) and (47) as,

$$\begin{aligned} \frac{W_{11}^\mathrm{SGT}}{W_{11}^\mathrm{CPT}} =\frac{\frac{\pi ^{4}}{l_{1}^{4}} \left[ (D_{x} +2B+D_{y})\right] -\varnothing ^{2}(\rho h+m_\mathrm{add})}{\frac{\pi ^{4}}{l_{1}^{4}} \left[ \left( 1+2\pi ^{2}\left( \frac{g}{l_{1}}\right) ^{2}\right) (D_{x} +2B+D_{y})\right] -\varnothing ^{2}(\rho h+m_\mathrm{add})} \end{aligned}$$

(51)

Table 1 Non-dimensional frequency parameter for intact and cracked orthotropic plate in vacuum (${m} = {n} = 1$, ${g} = 0$, $\Delta {T} = 0$)

Table 2 Comparison of fundamental frequency parameter $({\omega }_{{ mn}}{l}_{1}^{2}\sqrt{{\rho }{h}/{D}})$ for cracked isotropic plate as a function of fluid level and half crack length (${g} = 0$, $\Delta {T} = 0$)

Or

$$\begin{aligned} \frac{W_{11}^\mathrm{SGT}}{W_{11}^\mathrm{CPT}}=\frac{1-(\varnothing /\omega _{11}^\mathrm{CPT})^{2}}{1+2\pi ^{2}\left( \frac{g}{l_{1}}\right) ^{2} -(\varnothing /\omega _{11}^\mathrm{CPT})^{2}} \end{aligned}$$

(52)

where $\omega _{11}^\mathrm{CPT}=\sqrt{\frac{\frac{\pi ^{4}}{l_{1}^{4}} \left[ (D_{x} +2B+D_{y})\right] }{(\rho h+m_\mathrm{add})}}$ is the natural frequency of intact submerged orthotropic plate based on classical plate theory.

6 Results and discussions

In this section, the analytical results for vibration characteristics and central deflection for partially cracked and submerged orthotropic rectangular plate subjected to thermal heating are presented and discussed for the two boundary conditions. As per the author’s knowledge, the literature lacks in analytical results for cracked and submerged orthotropic plate considering the effect of temperature variation and hence new results for vibration characteristics of cracked orthotropic plate are presented as a function crack length $(a/l_{1})$, rise in temperature $(\Delta {T})$, length scale parameter $(g/l_{1})$, fluid level $(h_{1}/l_{1})$ and plate thickness (h). The literature [30] shows the results for isotropic plate as affected by crack and submergence level in the absence of any temperature variation, whereas the effect of crack on natural frequency of orthotropic plate in vacuum is also known [28]. Therefore, for validation of the present results, they are compared with these results of the literature [28, 30]. Table 1 represents the comparison of natural frequency of an intact and cracked orthotropic plate for different crack length and different boundary conditions, in vacuum medium, neglecting the effect of strain gradient and temperature. The material constants of orthotropic plate for this validation table are used from Ref. [28]. From Table 1, it is seen that the proposed results are in exact agreement with the published one which verifies the correctness of our proposed model.

To compare the effect of level of submergence and thermal environment, the present model is applied to a partially cracked isotropic plate and the results for fundamental frequency parameter are shown in Tables 2 and 3. The material constants and plate dimensions are taken from Ref [30] for Table 2 and Ref. [34] for Table 3. Again here the exact agreement of the proposed and existing results indicates that the proposed model deduces to the model developed in Ref [30] and Ref. [34] when the model is applied for isotropic plate.

Table 3 Comparison of non-dimensional frequency parameter $({\omega }_{{mn}}{l}_{1}^{2} \sqrt{{\rho }{h}/{D}})$ for cracked isotropic CCSS plate in vacuum as a function of temperature and half crack length $({m} ={n} = 1$, ${l}_{1}/{l}_{2}=1$, ${g} =0)$

For the results presented in Tables 1,  2 and 3, the effect of length scale parameter $(g/l_{1})$ has been neglected and to show its effect on fundamental frequency, a comparison is presented in Fig. 4. It shows exact agreement as the material and geometric properties for comparison are taken from Ref. [17]. Thus, it is known that the length scale parameter increases the frequencies of intact isotropic plate.

Fig. 4

Comparison of natural frequency $(\omega _{11}/\omega _{11}^{c})$ as a function of length scale parameter $(g/l_{1})$ for intact isotropic SSSS plate

New results for non-dimensional frequency parameter $(F=\omega _{mn} l_{1}^{2}\sqrt{\rho h/D_{x}})$ of cracked orthotropic plate considering the level of submergence $(h_{1} /l_{1})$, thermal environment $(\Delta {T})$, crack length $(a/l_{1})$ and length scale parameter $(g/l_{1})$ are presented here. The material considered is Boron–Epoxy with properties as: Young’s modulus $E_{x}=208\,\hbox {GPa}$, $E_{y}= 18.9\,\hbox {GPa}$, Shear modulus ${G}_{{xy}} = 5.7\,\hbox {Gpa}$, material density $\rho =2000\,\hbox {kg-m}^{{-3}}$, Poisson’s ratio $\nu _{x}=0.23$, $\nu _{y}= 0.0208$, $l_{{1}} = 1\,\hbox {m}$, $l_{{2}}= 1\,\hbox {m}$ and thickness ${h} = 0.01\,\hbox {m}$. The coefficients of thermal expansion are taken ${\upalpha }_{\mathrm{x}}=7.10\text{ e }{-}06/^{\circ }\hbox {C}$ and ${\upalpha }_{\mathrm{y}}=2.3\text{ e }{-}05/^{\circ }\hbox {C}$. The fluid density is $1000\,\hbox {kg}\,\hbox {m}^{{-3}}$. The dimensions of reservoir tank is assumed as $5\,\hbox {m} \times 5\,\hbox {m}\,\times 5\,\hbox {m}$. The depth of crack is taken 6 mm, and thickness of plate is taken 10 mm throughout the work. A lateral load of 30 N, acting at point $x_\mathrm{o}$, $y_\mathrm{o} = 0.375, 0.75$ is used for calculation of peak amplitude and frequency response. The influence of fluid medium on fundamental frequencies of the plate is analyzed by placing the plate horizontally in a fluid tank with various depth of submergence $(h_{1}/l_{1})$.

By employing the strain gradient theory, results for frequency parameter as a function of fluid level ($h_{1}/l_{1}= 0.1$ to 0.5), crack length ($a/l_{1}= 0$ to 0.1) and length scale parameter ($g/l_{1} = 0$ to 0.3) are presented in Tables 4 and 5 for SSSS and CCSS boundary conditions in the absence of thermal environment. It is observed from both the tables that for a given length of crack and length scale parameter, as the plate goes deeper into the fluid tank with increase in depth of submergence, the frequency of the plate decreases for both intact and cracked plate. This is because of increase in virtual added mass which increases with $h_{1}/l_{1}$. The increase in virtual added mass is independent of boundary conditions and hence the decrease in frequency parameter is same for both the SSSS and CCSS boundary conditions. Such phenomenon of variation in frequency is also found in the literature Refs. [7, 30] for intact and cracked isotropic plate respectively. Similarly, it is also observed that for a given level of submergence and length scale parameter, as the crack length increases, the frequency parameter decreases for both the boundary conditions. This is due to reduction in stiffness of plate seen from Eq. (33). Thus, here, we can be concluded that the presence of crack in decreases the frequency and this decrease is augmented by the submergence level.

Table 4 Fundamental frequency parameter for cracked orthotropic plate as a function of fluid level, length scale parameter and crack length for SSSS boundary condition $(\Delta {T}= 0)$

Table 5 Fundamental frequency parameter for cracked orthotropic plate as a function of fluid level, length scale parameter and crack length for CCSS boundary condition ($\Delta {T} = 0$)

Table 6 Fundamental frequency parameter for SSSS cracked orthotropic plate subjected to temperature rise $({h}_{1}/{l}_{1} =0.1)$

Comparing the results obtained from CPT ($g = 0$) and SGT ($g\ne 0$), it is observed that as the length scale parameter increases from $g/l_{1}= 0$ to 0.3, the natural frequency increases due to increase in stiffness owing to the strain gradients of elasticity . This type of variation is observed in the literature Ref. [17] for intact plate without any influence of surrounding fluid medium. Tables 4 and 5 show that such variation is observed to be valid in case of partially cracked and submerged orthotropic plate also. Thus, the consideration of effect of microstructure in form of length scale parameter is significant. It is important to mention that the frequency decreases due to the presence of crack, whereas it increases for the internal length scale parameter. The effect of internal scale parameter depends on the boundary condition and is more pronounced in case of CCSS boundary condition than SSSS.

For a given level of submergence, the variation in frequency for cracked orthotropic plate with uniform temperature rise ($\Delta {T} = 0$ to $8\,^{\circ }\hbox {C}$) for both the boundary conditions is shown in Tables 6 and 7. It is known that the rise in temperature of isotropic plate reduces the frequencies [34]. Such a reduction in frequency due to decrease in stiffness is observed to be valid for cracked orthotropic plate. Again it is observed that the increase in length of crack and temperature decreases the frequency, whereas the length scale parameter increases it. In order to understand the combined effect of crack length, change in length scale parameter and temperature on the natural frequency of plate, some results from Tables 4 and 6 are rearranged as shown in Fig. 5. It shows that for all values of ‘${a}/l_{1}$’ and ‘$\Delta {T}$’, the increase in length scale parameter increases the frequency, while for all values of $g/l_{1}$, the increase in length of crack and rise in temperature decreases the frequency.

Table 7 Frequency parameter for CCSS cracked orthotropic plate subjected to temperature rise (${h}_{1}/{l}_{1}=0.1)$

From Fig. 5a, b, it is observed that the effect of internal length scale parameter is same for submerged plate than for the plate vibrating in vacuum. Similarly, from Fig. 5c, d, it is seen that the effect of variation in internal length scale parameter and temperature on fundamental frequency for a given crack length is also same for submerged plate and plate in vacuum. This is due to the assumption that the internal length scale parameter and rise in temperature do not affect the virtual added mass. Again for higher values of length scale parameter ($g/l_{1} = 0.3$), the effect of increase in temperature on frequency decreases owing to the substantial contribution of internal scale parameter to the stiffness. Comparing the decrease in frequency for the two boundary conditions from Tables 6 and 7, it is concluded that the CCSS plate is more vulnerable to rise in temperature than the SSSS plate. The rise in temperature gives rise to in-plane compressive forces which are more for CCSS boundary condition, thus making it more prone to rise in temperature. The dependence of in-plane forces on boundary conditions can be visualized from the fact that for same maximum lateral deflection, the deflected surface length is more in case of CCSS plate than SSSS plate, resulting in higher magnitude of in-plane forces.

Fig. 5

Fundamental frequency parameter as a function of crack length $({a}/l_{1})$, temperature $(\Delta {T})$ and length scale parameter $(g/l_{1})$ for SSSS boundary condition (for in fluid, $h_{1}/l_{1}= 0.1$)

The results for fundamental frequency in vacuum as affected of plate thickness, using the classical plate theory and the Strain gradient theory are compared in Fig. 6 for $l_{1}/h ={100}$. It captures the size effect and the significance of internal scale parameter. Figure 6a shows such variation for intact isotropic plate, whereas Fig. 6b shows the variation for intact orthotropic plate. For an isotropic plate, the outcomes of natural frequency as affected by plate thickness and internal scale parameter are shown in the literature [23]. The present model when applied for an intact isotropic plate in absence of thermal environment and fluid medium deduces to the model developed by Gupta et al. [23]. It is established in the literature [23] that the effect of length scale of microstructure is more significant for very thin plates and as the plate thickness increases this effect reduces, this observation is observed to be valid for orthotropic plate using the strain gradient theory as seen from Fig. 6. To study the dependence of fundamental frequency on plate thickness in the presence of crack, thermal environment and surrounding fluid medium, results are presented in Fig. 7a–f for $l_{{1}}/h =100$. It is seen from that for all values of plate thickness, the increase in length of crack, depth of submergence (fluid level) and rise in temperature decreases the frequency. Figure 7a, b shows that the classical thin plate theory cannot capture the size effect for the cracked plate and the effect of microstructure is very well incorporated by the length scale parameter for very thin plates. Thus, it is concluded that as the cracked plate becomes smaller in size, it is important to consider the effect of microstructure. Similarly, the effect of level of submergence and rise in temperature on size effect is shown in Fig 7c–f. It is interesting to know that consideration of the microstructure increases the frequency for submerged plate under thermal environment. Thus, it can be concluded that the presence of fluid medium, thermal environment and partial crack affects the frequency and the size effect can be captured by the length scale parameter.

Fig. 6

Fundamental frequency $(\omega )$ as a function of plate thickness (h) and length scale parameter (g) for $l_{1} /h =100$, ${a}/l_{1} = 0$ and $\Delta {T} = 0$, in vacuum

Fig. 7

Natural frequency $(\omega )$ as a function of plate thickness (h) and length scale parameter (g) for $l_{1} /h=100$

Figure 8 shows the variation of ratio of deflection of cracked plate to intact orthotropic plate. In order to investigate the primary resonance, the ratio of forcing frequency to fundamental frequency of intact plate based on strain gradient theory is varied from 0.92 to 1.04. It is interesting to know that the presence of crack shifts the primary resonance and it takes place well below $\varnothing /\omega _{11}^\mathrm{SGT} =1$. This is due to reduction in stiffness of plate due to centrally located crack. The results for variation of deflection ratio of intact plate with and without temperature rise are shown in Fig. 9. With the rise in temperature of plate, it is known that the fundamental frequencies decrease, such a fact seen in the literature is validated from the results in Fig. 9. As expected, the rise of temperature decreases fundamental frequency of plate, thereby increasing the deflection. The shift in primary resonance can be attributed to the reduction in stiffness due to temperature rise. Figure 10 shows the ratio of deflections $W_{11}^\mathrm{SGT}/W_{11}^\mathrm{CPT}$ versus $(\varnothing /\omega _{11}^\mathrm{CPT})^{2}$ for different values of length scale parameter $(g/l_{1})$. It is seen that increasing values of g result in shifting the primary resonance position of the classical case $(\varnothing /\omega _{11}^\mathrm{CPT} =1)$ to higher values of $(\varnothing /\omega _{11}^\mathrm{CPT})$. The shift in primary resonance can be attributed to the increase in stiffness due to length scale parameter. Thus, it can be concluded that the primary resonance occurs at higher values of forcing frequency $(\varnothing )$. Figures 8, 9 and 10 along with Eqs. (42)–(52) represents the effect of temperature, crack length and length scale parameter on deflection and primary resonance of cracked and submerged orthotropic plate.

Fig. 8

Central deflection ratio $W_{11}^\mathrm{cracked}/W_{11}^\mathrm{intact}$ versus the normalized operational frequency $(\varnothing /\omega _{11}^\mathrm{SGT})^{2}$ for various values of crack length $({a}/l_{1})$, SSSS

Fig. 9

Central deflection ratio $W_{11}^\mathrm{heated}/W_{11}^\mathrm{intact}$ versus the normalized operational frequency $(\varnothing /\omega _{11}^\mathrm{SGT})^{2}$ for various values of rise in temperature (‘$\Delta {T}$’ in $^{\circ }\hbox {C}$), SSSS

Fig. 10

Central deflection ratio $W_{11}^\mathrm{SGT}/W_{11}^\mathrm{CPT}$ versus the normalized operational frequency $(\varnothing /\omega _{11}^\mathrm{CPT})^{2}$ for various values of length scale parameter $(g/l_{1})$, SSSS

The results for peak amplitude $(J_\mathrm{p})$ of uniformly heated cracked orthotropic plate vibrating under fluid medium are evaluated in the present study. Tables 8 and 9 show the results of peak amplitude as affected by various fluid level $(h_{1} /l_{1})$, crack length $({a}/l_{1})$, temperature $(\Delta {T})$ and length scale parameter $(g/l_{1})$ for the submerged orthotropic plate. It is seen from Table 8 that for the cracked orthotropic plate in the absence of temperature variation, the peak amplitude increases with the increase in length of crack. This corresponds to the decrease in frequency as shown in Tables 4,  5,  6 and 7 which satisfies one’s physical understanding. Also as the length scale parameter increases, the peak amplitude of vibration decreases owing to increase in fundamental frequency as seen from Tables 4 and 5.

Table 8 Peak amplitude (mm) for simply supported cracked and submerged orthotropic plate $(\Delta {T} = 0)$

It is seen from Table 4 that as the level of submergence increases, the fundamental frequency decreases. From Table 8, it is interesting to know that with increase in the submergence level, the peak amplitude also decreases. Thus, as the plate goes deep into the fluid, both the peak amplitude and fundamental frequency decreases. This is due to increase in virtual added mass and the resistance offered by the surrounding fluid to the vibration of the plate. This phenomenon is unlike the vibration in vacuum and has been presented in the recent work by Soni et al. [30] on submerged isotropic plate. It is important to mention here that this is the first attempt to model peak amplitude and fundamental frequency of cracked and submerged orthotropic plate, thereby modeling the fluid–structure interaction. The effect of increase in temperature, crack length and length scale parameter for a given level of submergence on the peak amplitude is shown in Table 9. It is seen that as the temperature of the plate increases, the peak amplitude of vibration increases owing to decrease in fundamental frequency as seen from Table 6. This increase in peak amplitude is arrested by the increase in internal scale parameter which increases the stiffness of the cracked plate.

Table 9 Peak amplitude (mm) for simply supported cracked and submerged orthotropic plate subjected to temperature rise $({h}_{1} /{l}_{1} =0.1)$

To study the nonlinear behavior of the coupled plate–fluid system, the response curves are plotted as per the frequency response relation proposed in Eq. (37) and are shown in Fig. 11. The geometrically nonlinear ($\frac{G_{mn}}{(M_{mn} +M_\mathrm{add})}<0$, soft spring and $\frac{G_{mn}}{(M_{mn}+M_\mathrm{add})}>0$, hard spring) response curves of a cracked and submerged orthotropic plate subjected to temperature rise are figured for given damping ($\mu _\mathrm{o} =0.061$ for fluid and $\mu _\mathrm{o} =0.05$ for vacuum [33] and excitation of 30N acting at ($x_{0}, y_{0}$). The concept of bending hardening/bending softening is studied for various length scale parameter, crack length and temperature in two different surrounding environments (Vacuum and fluid).

Figure 11b shows the nonlinear frequency response curves for simply supported boundary condition, for a fixed length scale parameter $(g/l_{1} = 0.1)$, temperature $(\Delta {T} = 0)$ and fluid level $(h_{1} /l_{1} = 0.1)$. Response curves plotted for vacuum (Fig. 11a) are also given for comparison. The curves show a nonlinear phenomenon of bending hardening in submerged plate due to presence of crack, such a hard spring behavior is evident in recent literature [30] for plate vibrating in vacuum. But this nonlinearity is less in fluid as compared to vacuum due to the virtual added mass which appears in the cubic nonlinear term as seen from Eq. (35). Thus, it leads to the conclusion that hard spring softens due to the presence of fluidic medium.

Figure 11c, d shows the nonlinear response curves for a given temperature ($\Delta {T} = 0$), fluid level ($h_{1} /l_{1} =0.1$) and crack length ($a/l_{1} = 0.01$) as affected by length scale parameter. It is observed that the increase in length scale parameter reduces the nonlinearity for both in vacuum and in fluid. Such phenomenon of reduction in nonlinearity is also evident in recent literature [23] for cracked isotropic plate vibrating in vacuum.

Fig. 11

Nonlinear response curves for cracked orthotropic plate with varying crack length, length scale parameter and temperature for simply supported boundary conditions. (For in fluid $h_{1}/l_{1} = 0.1$), (dashed line) stable branch, (solid line) unstable branch

The effect of rise in temperature on the frequency response of the fluid–plate interaction system is shown in Fig. 11e, f for a given fluid level, crack length and length scale parameter. It is seen from Fig. 11a–d that the increase in length of crack and length scale parameter decreases the nonlinearity but with the rise in temperature the hardening increases as seen from Fig. 11e, f. The nonlinearity (hardening) is seen to be more in plate at $\Delta {T}= 4\,^{\circ }\hbox {C}$ as compared to plate at $\Delta {T}=0\,^{\circ }\hbox {C}$. This is because of decrease in frequency due to rise in temperature. It is important to mention that the nonlinear term [${G}_{{mn}}$ (Eq. (34)] is not affected by the temperature rise but affects the stiffness. Again as per the authors’ knowledge, this is the first attempt to investigate the effect of rise in temperature on the hardening behavior of submerged plate.

Fig. 12

Plate specimens

Fig. 13

The experimental setup

7 Experimental validations

In order to verify the trend in analytical results, experimental measurements are carried out in this section to estimate the effect of partial crack, temperature, level of submergence. The experimental setup consists of a FFT (fast Fourier transform) analyzer, heavy boundary condition foundation, water tank, heating coil, thermometer, excitation hammer, accelerometer and plate specimens for testing. In this work, two different boundary conditions SSSS (all sides simply supported) and CCSS (two adjacent sides clamped and other two sides simply supported) are chosen. A computer connected with the fast Fourier transform (FFT) analyzer is used to analyze the frequency spectrum. In order to raise the temperature of plate specimen uniformly, two plate heaters are placed on the top and bottom surfaces of the plate. When a steady state desired temperature is achieved, the heaters are removed and accelerometer is place for measurements.

Jute fiber reinforced epoxy plate specimens having dimension $200\,\times \,200\,\times \,5$ mm are taken for experimental analysis as shown in Fig. 12. The material properties of plate specimen are $E_{x}= 8.94\,\hbox {GPa}$, $E_{y}= 3.5\,\hbox {GPa}$, Shear modulus ${G}_{{xy}}=0.805\,\hbox {Gpa}$, material density $\rho = 1337.5\,\hbox {kg-m}^{{-3}}$, Poisson’s ratio $\nu _{x}= 0.264$, $\nu _{y} = 0.021$. A crack of depth 3 mm and width 1 mm is generated by Laser Beam Machining. The volume fraction of fibers is considered while selecting the above properties.

Figure 13 shows the experimental setup consisting of the FFT analyzer and a sensitive accelerometer. Care has been taken so that the vibrations of the boundary condition structure and other ambient vibrations do not interfere in the measurements. On triggering the vibration of plate using excitation hammer, one obtains a frequency spectrum and corresponding to the first peak of the spectrum, first mode frequency is measured as shown in Fig.14. For each plate specimen, multiple readings are taken for a position of accelerometer and the first peak in the spectrum is noted for the fundamental frequency. Averaging of these readings is done to arrive at a single value of frequency. This procedure is repeated for different positions of the accelerometer. Finally, averaging of the averaged reading is taken as the fundamental frequency. Readings for both intact and cracked plates are obtained in this way.

Fig. 14

Frequency spectrum for partially cracked and submerged plate under thermal environment ($h_{1} /l_{1} =0.1$, ${a}= 0.01\,\hbox {m}$, $\Delta {T} = 20\,^{\circ }\hbox {C}$); a SSSS, b CCSS

Table 10 Comparison between the experimental and theoretical results for the fundamental frequency of cracked and submerged orthotropic plate under thermal environment ($h_{1} /l_{1} =0.1$, $g/l_{1} = 0$)

The comparison of results obtained using the present analytical model and the experimental work are shown in Table 10. It is observed that the experimental results are lower than the analytical; this is due to ambient vibrations of the setup and unavoidable-inherent geometric distortion of the specimen and micro-burs formed during machining of the crack would have played a role. Another probable reason is that the analytical model neglects the nonlinear fluid–structure interaction. Considering these facts the comparison shows good agreement between the theoretical and experimental results with maximum error in prediction of about 7.93% in SSSS boundary condition and 8.80 % in CCSS boundary condition. The frequency spectrums obtained for cracked plate with crack length ${a}= 0.01\,\hbox {m}$, fluid level ${h}_{1}/{l}_{1}= 0.1$ and rise in temperature $\Delta {T} = 20\,^{\circ }\hbox {C}$ are shown in Fig. 14 for two different boundary conditions.

8 Conclusions

In the present work, an analytical fluid–structure–temperature interaction model is presented for vibration analysis of a partially cracked and submerged orthotropic plate subjected to uniform heating, based on strain gradient theory of elasticity. It is established that the fundamental frequency of plate decreases by the presence of crack and thermal environment and this decrease in frequency is further augmented by the presence of surrounding fluid medium in present study. It has been established that the length scale parameter has a significant effect for micro-plates. A classical relation for central deflection of cracked and submerged orthotropic plate is also proposed. The effect of varying forcing frequency, crack length, length scale parameter and change in temperature on deflection has been established which shows a shift in primary resonance. The rise in temperature and increase in crack length shift the resonance to lower values of forcing frequency, whereas the internal scale parameter shift the resonance to higher values. Another important conclusion is that as the level of submergence of the plate increases, both the fundamental frequency and peak amplitude decrease. The nonlinear frequency response curves shows that the presence of crack, increase in length scale parameter and fluid level decreases the bending hardening. Out of these three factors which affect the hardening, it is concluded that the level of submergence decreases the nonlinearity more. It is also concluded that the rise in temperature increases the bending hardening. To the best of the authors’ knowledge, this is the first attempt to model fluid–structure interaction vibrations of a cracked orthotropic plate in the presence of thermal environment, and hence, it would be instructive to formulate the model based on some higher-order theory.

Appendices

Appendix A

On the basis of Kirchhoff’s thin classical plate theory, the mid-surface strains ($\varepsilon _{x}, \varepsilon _{y}$ and $\gamma _{xy}$) can be given in terms of transverse deflection (w) as,

$$\begin{aligned} \varepsilon _{x}= & {} -z\frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\ \varepsilon _{y}= & {} -z\frac{\partial ^{2}w}{\partial y^{2}}\nonumber \\ \gamma _{xy}= & {} -2z\frac{\partial ^{2}w}{\partial x\partial y} \end{aligned}$$

(A1)

Using the constitutive relations [Eqs. (1)–(3)] and Eq. (A1), the expressions for bending moment become,

$$\begin{aligned} M_{x}^{*}= & {} \int \nolimits _{-\frac{h}{2}}^{+\frac{h}{2}}\sigma _{x} z{\hbox {d}}z\nonumber \\= & {} M_{x} +M_{x}^{g} +M_{Tx} \end{aligned}$$

(A2)

$$\begin{aligned} M_{y}^{*}= & {} \int \nolimits _{-\frac{h}{2}}^{+\frac{h}{2}}\sigma _{y} z{\hbox {d}}z\nonumber \\= & {} M_{y}+M_{y}^{g} +M_{Ty} \end{aligned}$$

(A3)

$$\begin{aligned} M_{xy}^{*}= & {} \int \nolimits _{-\frac{h}{2}}^{+\frac{h}{2}}\tau _{xy}\, z{\hbox {d}}z\nonumber \\= & {} M_{xy} +M_{xy}^{g} \nonumber \\ M_{x}= & {} -D_{x} \left( {\frac{\partial ^{2}w}{\partial x^{2}}+\nu _{y} \frac{\partial ^{2}w}{\partial y^{2}}} \right) \nonumber \\ M_{x}^{g}= & {} g^{2}D_{x} \left( {\frac{\partial ^{4}w}{\partial x^{4}}+\nu _{y} \frac{\partial ^{4}w}{\partial y^{4}}+\left( {1+\nu _{y} } \right) \frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}} \right) \nonumber \\ M_{y}= & {} -D_{y} \left( {\frac{\partial ^{2}w}{\partial y^{2}}+\nu _{x} \frac{\partial ^{2}w}{\partial x^{2}}} \right) \nonumber \\ M_{y}^{g}= & {} g^{2}D_{y} \left( {\frac{\partial ^{4}w}{\partial y^{4}}+\nu _{x} \frac{\partial ^{4}w}{\partial x^{4}} +\left( {1+\nu _{x} } \right) \frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}} \right) \nonumber \\ M_{xy}= & {} -2D_\mathrm{t} \left( {\frac{\partial ^{2}w}{\partial x\partial y}} \right) \nonumber \\ M_{xy}^{g}= & {} g^{2}2D_\mathrm{t} \left( {\frac{\partial ^{4}w}{\partial x^{3}\partial y}+\frac{\partial ^{4}w}{\partial x\partial y^{3}}} \right) \nonumber \\ M_{Tx}= & {} -\frac{E_{x} }{1-\nu _{x} \nu _{y} }(\alpha _{x} +\nu _{y} \alpha _{y})\int \nolimits _{h/2}^{-h/2}(\Delta T)z{\hbox {d}}z\nonumber \\ M_{Ty}= & {} -\frac{E_{y} }{1-\nu _{x}\nu _{y}} (\alpha _{y} +\nu _{x}\alpha _{x})\int \nolimits _{h/2}^{-h/2} (\Delta T)z{\hbox {d}}z\nonumber \\ \end{aligned}$$

(A4)

where $M_{x}$, $M_{y}$ and $M_{xy} =M_{yx}$ are the internal bending and twisting moments respectively. Similarly, $M_{x}^{g}$, $M_{y}^{g}$ and $M_{xy}^{g} =M_{yx}^{g}$ are bending and twisting moments due to the microstructure of the plate. $M_{Tx}$ and $M_{Ty}$ are the moments due to thermal environment.

Appendix B

The velocity potential function $\phi (x, y, z, t)$ satisfying the Laplace’s equation can be expressed in the Cartesian coordinate system as:

$$\begin{aligned} \nabla ^{2}\phi =\frac{\partial ^{2}\phi }{\partial x^{2}}+\frac{\partial ^{2}\phi }{\partial y^{2}}+\frac{\partial ^{2}\phi }{\partial z^{2}}=0 \end{aligned}$$

(B1)

Using Bernoulli’s equation, the fluid dynamic pressure at any point of plate–fluid boundary can be given by:

$$\begin{aligned} P_\mathrm{u}= & {} P_{z=0}=-\rho _\mathrm{f} \left( \frac{\partial \phi }{\partial t}\right) _{z=0} \end{aligned}$$

(B2)

$$\begin{aligned} P_\mathrm{l}= & {} P_{z=-h}=-\rho _\mathrm{f} \left( \frac{\partial \phi }{\partial t}\right) _{z=-h} \end{aligned}$$

(B3)

where $\rho _\mathrm{f}$ is fluid density per unit volume.

Assuming $\phi$ be the function of two discrete variables.

$$\begin{aligned} \phi (x,y,z,t)=F(z)S(x,y,t) \end{aligned}$$

(B4)

where S(x, y, t) and F(z) are the two discrete functions.

For the assumption of a permanent contact between the surface of plate and fluid layer, the kinematic boundary conditions at the fluid–plate interface can be written as [30],

$$\begin{aligned}&\left( \frac{\partial \phi }{\partial z}\right) _{z=0}=\frac{\partial w}{\partial t} \end{aligned}$$

(B5)

$$\begin{aligned}&\left( \frac{\partial \phi }{\partial z}\right) _{z=-h}=\frac{\partial w}{\partial t} \end{aligned}$$

(B6)

On introducing Eqs. (B4), (B5) and (B6), we get

$$\begin{aligned} S(x,y,t)= & {} \frac{1}{({\hbox {d}}F(z)/{\hbox {d}}z)}_{z=0}\frac{\partial w}{\partial t} \end{aligned}$$

(B7)

$$\begin{aligned} S(x,y,t)= & {} \frac{1}{({\hbox {d}}F(z)/{\hbox {d}}z)}_{z=-h}\frac{\partial w}{\partial t} \end{aligned}$$

(B8)

By substituting Eqs. (B7) and (B8) in Eq. (B4), the $\phi$ on fluid–plate interfaces (i.e., upper and lower surface of plate) can be stated as

$$\begin{aligned} \phi (x,y,z,t)= & {} \frac{F(z)}{({\hbox {d}}F(z)/{\hbox {d}}z)_{z=0}}\frac{\partial w}{\partial t} \end{aligned}$$

(B9)

$$\begin{aligned} \phi (x,y,z,t)= & {} \frac{F(z)}{({\hbox {d}}F(z)/{\hbox {d}}z)_{z=-h}}\frac{\partial w}{\partial t} \end{aligned}$$

(B10)

The following differential equation of $2{\mathrm{nd}}$ order can be obtained by putting above Eqs. (B9) or (B10) into Eq. (B1).

$$\begin{aligned} \frac{{\hbox {d}}^{2}F(z)}{{\hbox {d}}z^{2}}-\mu ^{2}F(z)=0 \end{aligned}$$

(B11)

where $\mu$ represents wave number, which can be determined by $\mu =\pi \sqrt{\frac{1}{l_{1}^{2}}+\frac{1}{l_{2}^{2}}}$ [6]

The general solution for the differential equation [Eq. (B11)] can be expressed as:

$$\begin{aligned} F(z)=A\mathrm{e}^{\mu z}+B\mathrm{e}^{-\mu z} \end{aligned}$$

(B12)

On substituting Eq. (B12) into Eqs. (B9) and (B10), we get an expression for $\phi$ on plate- fluid interface as shown:

$$\begin{aligned} \phi (x,y,z,t)= & {} \frac{A\mathrm{e}^{\mu z}+B\mathrm{e}^{-\mu z}}{({\hbox {d}}F(z)/{\hbox {d}}z)_{z=0}} \frac{\partial w}{\partial t} \end{aligned}$$

(B13)

$$\begin{aligned} \phi (x,y,z,t)= & {} \frac{A\mathrm{e}^{\mu z}+B\mathrm{e}^{-\mu z}}{({\hbox {d}}F(z)/{\hbox {d}}z)_{z=-h}}\frac{\partial w}{\partial t} \end{aligned}$$

(B14)

Here, A and B denote the unknown constants which can be resolved utilizing two extreme limit conditions at plate–fluid interface and at fluid extremity surfaces $z=h_{1}$ and $z =(h+h_{2})$.

Assuming the disturbance because of free surface wave motion of liquid is irrelevant, the accompanying boundary condition can be applied for velocity potential at the free surface of liquid [6], see Fig. 4.

$$\begin{aligned} \left( \frac{\partial \phi }{\partial z} \right) _{z=h_{1}} =-\frac{1}{{g}_\mathrm{a}} \left( \frac{\partial ^{2}\phi }{\partial t^{2}}\right) _{z=h_{1}} \end{aligned}$$

(B15)

where ‘${g}_\mathrm{a}$’ denotes the gravity acceleration. Substitution of Eq. (B13) into the above Eqs. (B15) and (B5) gives the expression for velocity potential $\phi$ as,

$$\begin{aligned} \phi (x,y,z,t)=\frac{1}{\mu }\left[ \frac{\mathrm{e}^{\mu z}+C\mathrm{e}^{-\mu (z-2h_{1})}}{1-C\mathrm{e}^{2\mu h_{1}}}\right] \frac{\partial w}{\partial t} \end{aligned}$$

(B16)

where $C=\frac{{g}_\mathrm{a} \mu -\omega ^{2}}{{g}_\mathrm{a}\mu -\omega ^{2}}$ and $\omega$ represents wave motion frequency at free surface of fluid.

The fluid pressure acting on plate’s upper surface can be obtained by substituting above Eq. (B16) of velocity potential into Eq. (B2) as:

$$\begin{aligned} P_\mathrm{u}=-\frac{\rho _\mathrm{f}}{\mu }\left[ \frac{1+C\mathrm{e}^{2\mu h_{1}}}{1-C\mathrm{e}^{2\mu h_{1}}}\right] \frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(B17)

The boundary condition at the rigid base of tank represented in Fig. 5 is referred as null-frequency condition and can be written as:

$$\begin{aligned} \left( \frac{\partial \phi }{\partial z}\right) _{z=-(h+h_{2})}=0 \end{aligned}$$

(B18)

On substituting Eq. (B14) into Eqs. (B18) and (B6), the expression for $\phi$ is obtained as

$$\begin{aligned} \phi (x,y,z,t)=\frac{1}{\mu }\left[ \frac{\mathrm{e}^{\mu z}+\mathrm{e}^{-2\mu (h+h_{2})}\mathrm{e}^{-\mu z}}{\mathrm{e}^{-\mu h}-\mathrm{e}^{-2\mu (h+h_{2})}\mathrm{e}^{\mu h}}\right] \frac{\partial w}{\partial t}\nonumber \\ \end{aligned}$$

(B19)

From Eqs. (B19) and Eq. (B3), the fluid pressure at plate’s lower surface can be expressed as

$$\begin{aligned} P_\mathrm{l}=-\frac{\rho _\mathrm{f}}{\mu }\left[ \frac{1+\mathrm{e}^{-2\mu h_{2}}}{1-\mathrm{e}^{-2\mu h_{2}}}\right] \frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(B20)

The resulting fluid dynamic pressure for the plate fully submerged in fluid is written as:

$$\begin{aligned} \Delta P= & {} P_\mathrm{u}-P_\mathrm{l}\nonumber \\= & {} -\frac{\rho _\mathrm{f}}{\mu } \left[ \frac{1+C\mathrm{e}^{2\mu h_{1}}}{1-C\mathrm{e}^{2\mu h_{1}}}-\frac{1+\mathrm{e}^{-2\mu h_{2}}}{1-\mathrm{e}^{-2\mu h_{2}}}\right] \frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(B21)

$$\begin{aligned} \Delta P= & {} m_\mathrm{add}\frac{\partial ^{2}w}{\partial t^{2}} \end{aligned}$$

(B22)

where $m_\mathrm{add}=-\frac{\rho _\mathrm{f}}{\mu } \left[ \frac{1+C\mathrm{e}^{2\mu h_{1}}}{1-C\mathrm{e}^{2\mu h_{1}}} -\frac{1+\mathrm{e}^{-2\mu h_{2}}}{1-\mathrm{e}^{-2\mu h_{2}}}\right]$ represents the virtual added mass of submerged plate.