1 Introduction

The vibration isolation is crucial to ensure the stability of the sensitive device, and is widely used in ships [1, 2], vehicles [3,4,5], ultra-precision machining [6] and other fields. For example, the nanoscale precision processing task of lithography machine cannot be completed without isolating the interference of low frequency vibration on the ground. With the improvement of precision, the traditional technology can no longer meet the increasing requirements of isolation performance [7]. Vibration isolation technology can be divided into passive [8, 9], active [10, 11], and semi-active technologies [12]. A passive vibration isolator has a simple structure and reliable performance [13], but its performance is limited by its inherent properties. An active isolator suppresses the vibration response by controlling the output of the actuator [14], which has better performance, but the application is limited by the output force and high cost. A semi-active vibration isolator replaces or increases the variable stiffness or variable damping mechanism in the passive isolator. Isolation performance close to that of an active isolator could be achieved through the real-time adjustment of stiffness or damping. Moreover, a semi-active vibration isolator has higher reliability because it can still work in passive mode when the control system is damaged [13].

Semi-active damping control is studied more deeply, such as electrorheological fluid [15], magnetorheological fluid [16] and piezoelectric [17]. However, adjustable damping affects only a narrow frequency band, and the adjustable stiffness which can improve the isolation performance over a wider frequency band should be considered [18]. Traditional stiffness control methods can be divided into two types, one is to change the geometry of the elastic mechanism, such as the effective structure [19], or the force transmission angle [20], and the other is to change the properties of the material, such as magnetorheological elastomers (MREs) [21]. It should be noted that, the common adjustable stiffness components can only be adjusted in the positive stiffness range and often need to support the load. Consequently, the equilibrium position of the load may be changed once the stiffness is adjusted [22].

The negative stiffness mechanism (NSM) which does not produce force at the working point should be considered, so that the working point will not be changed even if the stiffness is adjusted. The force generated by the NSM is opposite to the restoring force of the positive stiffness. Connecting the NSM in parallel with the isolator can reduce the dynamic stiffness near the working point and expand the isolation frequency band, while maintaining high static stiffness and stability, that is, to achieve high-static-low-dynamic stiffness (HSLDS) characteristic. The HSLDS isolator solves the contradiction between load stability and vibration isolation frequency band, and has been widely used in low frequency vibration isolation. Many NSMs have been proposed, such as hinged bars [23, 24], inclined springs [25,26,27], cam-rollers [28, 29] and magnets [30,31,32]. However, most NSMs are not adjustable, which limits the performance of the isolator to a certain extent. For example, the passive HSLDS isolator will resonate at the reduced natural frequency. The adjustable NSM is an emerging adjustable stiffness component, and it can realize negative stiffness control by adding actuators in NSM, or adding control means such as air pressure and current. Palomares et al. [33] put the pneumatic actuator symmetrically in the lateral direction and converted the pressure to the vertical direction to produce negative stiffness, which can be controlled by air pressure. Churchill et al. [34] adjusted the negative stiffness by using a piezo actuator to adjust the lateral preload of Euler buckling beams. Tan et al. [35] proposed an adjustable negative stiffness mechanical metamaterial with a unique cavity architecture that can be adjusted through pneumatic actuation without further sealing treatment. Mechanical NSMs have a complex structure and backlash. The electromagnetic NSMs use the non-contact electromagnetic force to produce stiffness, which can be easily controlled online by current, and has the advantages of compact structure and no wear. Yuan et al. [36] proposed a linear electromagnetic spring which contains three toroidal coils arranged coaxially with a ring magnet. Zhou et al. [37] designed a NSM configured with two electromagnetic springs in parallel. Ding et al. [38] proposed an electromagnetic NSM with a concentric nested configuration consisting of two pairs of magnet rings and coils. It provided a low linear composite stiffness and neutralized the positive stiffness in the geophone. Ma et al. [39] designed "8"-shaped electromagnetic equivalent magnetic circuit for an electromagnetic NSM, which improved the adjustable range of the negative stiffness. Nonetheless, the existing electromagnetic NSMs have problems such as low energy efficiency and low response speed, which are not conducive to real-time control. However, existing electromagnetic NSMs do not fully utilize the magnetic field, resulting in low energy efficiency in generating negative stiffness, which means that more wire turns are needed to generate the required negative stiffness. This results in low response speed and is not conducive to real-time control.

Semi-active control strategy is also important for isolators. There has been some research on the semi-active control of the traditional adjustable stiffness components with positive stiffness. Rustighi et al. [40] used a PD controller to improve the performance of an adjustable vibration absorber with shape memory alloy elements. Williams et al. [41] designed a nonlinear PI controller with integrator reset for a shape memory alloy adaptive adjusted vibration absorber and a second Lyapunov analysis was used to demonstrate stability of the system. Gu et al. [42] used a classical LQR controller and a learning-based inverse model to realise semi-active control of an MRE-based isolation system. A Lyapunov-based control strategy [43] was employed in an MRE-based isolator to reduce the acceleration and relative displacement of the building floors. Furthermore, fuzzy logic control [44,45,46] has attracted abundant attention in the semi-active control of MREs since it allows imprecise resolution or uncertain information. However, there are still relatively few studies on the semi-active control of mechanisms with adjustable negative stiffness. Zhou and Liu [47] studied the method of switching the natural frequency according to the disturbance frequency distribution to avoid resonance, and Ledezma-Ramirez et al. [48] proposed a method of switching the stiffness based on the motion state to attenuate the post-shock response.

Min et al. [49] used a method called equivalence in control to obtain the steady state response of the serial-switch-stiffness-system. However, the control method is mainly on–off control, and the advantage that the electromagnetic NSMs can be continuously adjusted within the range of positive and negative stiffness has not been brought into play. This limits the application scenarios and performance of vibration control.

To improve the low-frequency vibration control performance, a new electromagnetic negative stiffness mechanism (ENSM) is proposed, whose stiffness can be continuously adjusted within the positive and negative range. To improve the stiffness adjustable range and response speed of the ENSM, the magnetic field distribution around the magnet is analyzed and it is found that the radial magnetic flux density near the inner and outer edges of the magnet is higher. Then a new configuration of a radial array of ring magnets and coils is proposed to fully utilize the magnetic field and improve the stiffness generation efficiency. A double-layer vibration isolator based on the ENSM is designed and the nonlinear dynamic characteristics are analyzed. Further, a semi-active control algorithm based on suboptimal control is proposed. The actual control force is generated by the ENSM adjusting stiffness according to the relative displacement. More importantly, expanding the adjustable range of stiffness to negative stiffness can effectively reduce the required stiffness adjustable range in semi-active vibration isolation.

The remainder of this paper is organized as follows. In Sect. 2, an improved ENSM is introduced first, the electromagnetic force model of the ENSM is given and verified by measurements, and then parameter analysis is performed. In Sect. 3, a double-layer vibration isolator based on the ENSM is designed and the nonlinear dynamic characteristics are analyzed. In Sect. 4, a semi-active control method based on suboptimal control theory is proposed, and the advantages of the ENSM in semi-active control are verified in simulations. The effectiveness of the control method is verified in the experiments in Sect. 5. Finally, conclusions are given in Sect. 6.

2 Design and analysis of the ENSM

The adjustable stiffness mechanism is the basis of semi-active stiffness control isolator. In this section, an improved ENSM is proposed, which can adjust the stiffness within the range of positive and negative stiffness. The electromagnetic force model of the ENSM is established using the filament method, and then the experimental verification and parameter analysis are carried out.

2.1 Design of the ENSM

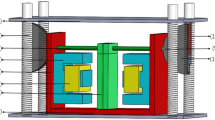
Figure 1a shows the configuration of the coils and ring magnets in the ENSM. It consists of three coaxial coil groups and two ring magnets, all of which are arranged coaxially. All the coils are fixed to each other and move axially relative to the two magnets. Each coil group has top, middle, and bottom coils. For example, coil group A is composed of coil At, coil Am and coil Ab. The axial heights of the top, middle, and bottom layer coils in each coil group are equal. According to the Fleming’s rule, the axial forces between the coils and the magnets are generated by the radial flux. As shown in Fig. 1b, the radial magnetic flux density near the inner and outer edges of the ring magnets is the largest. Therefore, the axial height of the middle coils is consistent with that of the magnet to achieve the maximum negative stiffness. The current direction of the top and bottom coils is opposite to that of the middle coil. The current direction of the coil on the inside of the ring magnet is opposite to that on the outside. To conveniently control the input current, all coils are connected in series. When the input current is positive (as shown in Fig. 1a), the ENSM works in the negative stiffness range. The middle coils of the coil groups repel the ring magnets; the top and bottom coils attract the ring magnets. Once the ring magnets deviate from the equilibrium position, the electromagnetic force make them deviate further and cannot be restored without other external forces. Similarly, when the input current is negative, these electromagnetic forces are reversed, and the ENSM works in the positive stiffness range. When the ENSM is in the equilibrium position, the repulsive force and the attractive force on the ring magnets are always zero due to symmetry. So, it would not affect the working point of the load under adjustment.

Fig. 1
figure 1

Concept of the proposed ENSM: a structure, b radial magnetic flux density

Full size image

2.2 Analysis model of the electromagnetic force

To obtain an accurate response in the semi-active control of the double-layer vibration isolator, the analysis model of the electromagnetic force is established first. The force generated by the ENSM is the sum of the electromagnetic forces of the three coil groups on the two ring magnets:

$$ F(x_{d} ) = F_{WA} + F_{VA} + F_{WB} + F_{VB} + F_{WC} + F_{VC} $$
(1)

An axially magnetized ring magnet can be considered equivalent to two thin-walled solenoids with a reverse current on the internal and external cylindrical surfaces [50]. Therefore, ring magnet W is equivalent to a thin-walled solenoid Wi and a thin-walled solenoid Wo. The electromagnetic force of each coil group on a ring magnet is the sum of the electromagnetic force of the top, middle, and bottom coils on the two solenoids:

$$ F_{WA} = F^{{W_{i} /A_{t} }} + F^{{W_{i} /A_{m} }} + F^{{W_{i} /A_{b} }} + F^{{W_{o} /A_{t} }} + F^{{W_{o} /A_{m} }} + F^{{W_{o} /A_{b} }} $$
(2)

The electromagnetic force between coil At and thin-walled solenoid Wi can be obtained as the sum of the interaction forces of all the pairs of Maxwell’s coils, calculated using the filament method [51]:

$$ F^{{W_{i} /A_{t} }} = \sum\limits_{{n^{Wi} = 1}}^{{N^{W} }} {\sum\limits_{{n_{a}^{{A_{t} }} = 1}}^{{N_{a}^{t} }} {\sum\limits_{{n_{r}^{{A_{t} }} = 1}}^{{N_{r}^{A} }} {f(i(W_{i} ),i(A_{t} ),r(W_{i} ),r(n_{r}^{{A_{t} }} ),z(n^{{W_{i} }} ),z(n_{a}^{{A_{t} }} ))} } } $$
(3)

where \(i(W_{i} ) = - i(W_{o} ) = \frac{{B_{r} H_{W} }}{{\mu_{0} N^{W} }}\), \(- i(A_{t} ) = i(A_{m} ) = - i(A_{B} ) = I\), \(r(W_{i} ) = r_{w}\). Br is the polarization of the ring magnets and \(\mu_{0} = 4\pi \times 10^{ - 7}\) H/m is the vacuum permeability.

\(r(n_{r}^{{A_{t} }} ) = r_{a} + \frac{{2n_{r}^{{A_{t} }} - 1}}{{2N_{r}^{A} }}(R_{a} - r_{a} )\), \(z(n^{Wi} ) = x_{d} - \frac{{H_{W} }}{2} + \frac{{2n^{Wi} - 1}}{{2N^{W} }}H_{W}\), \(z(n_{a}^{{A_{t} }} ) = \frac{{H_{m} }}{2} + \frac{{2n_{a}^{{A_{t} }} - 1}}{{2N_{a}^{t} }}H_{t}\). where \({\text{x}}_{\text{d}}\) represents the relative displacement of the coils and the ring magnets. The calculation of the force between other coils and magnets is similar to Eq. (3).

The interaction force between two coaxial Maxwell’s coils can be calculated by the following equation [52]:

$$ f(i_{1} ,i_{2} ,r_{1} ,r_{2} ,z_{1} ,z_{2} ) = \frac{{\mu_{0} i_{1} i_{2} (z_{1} - z_{2} )k}}{{4\sqrt {r_{1} r_{2} } }}\left[ {2K(k) - \frac{{2 - k^{2} }}{{1 - k^{2} }}E\left( k \right)} \right]. $$
(4)

where the functions \(K(k) = \int_{0}^{{\frac{\pi }{2}}} {\frac{{{\text{d}}\theta }}{{\sqrt {1 - k^{2} \sin^{2} \theta } }}}\) and \(E(k) = \int_{0}^{{\frac{\pi }{2}}} {\sqrt {1 - k^{2} \sin^{2} \theta } {\text{d}}\theta }\) are the complete first and second elliptic integrals respectively with parameter k, and \(k^{2} = \frac{{4r_{1} r_{2} }}{{(r_{1} + r_{2} )^{2} + (z_{1} - z_{2} )^{2} }}\).

The electromagnetic force model of the ENSM can be obtained by superimposing the forces between the turns of all coils and the equivalent current loops of two magnets. The above analysis model indicates that the electromagnetic force generated by the ENSM is proportional to the input current I, which is convenient for controller design. The stiffness can change continuously with the current, which can improve the vibration control performance. Moreover, changing the direction of the input current can adjust the stiffness of the ENSM in the positive and negative ranges, further expanding the stiffness adjustable range.

The expression of the electromagnetic force obtained by Eq. (1) ~ (4) is relatively complicated and inconvenient to use. It can often be approximated as a cubic polynomial for the relative displacement \({\text{x}}_{\text{d}}\) and the input current I [52, 53]:

$$ F(x_{d} ,I) = a_{1} Ix_{d} + a_{2} Ix_{d}^{3} $$
(5)

The axial stiffness generated by the ENSM is the derivative of force to displacement:

$$ k\left( {x_{d} ,I} \right) = - a_{1} I - 3a_{2} Ix_{d}^{2} $$
(6)

where \({\text{a}}_{1}\) and \({\text{a}}_{2}\) are fitting parameters computed by the polyfit function in MATLAB.

2.3 Testing of the electromagnetic force

The parameters of the ring magnets and coils are shown in Table 1. The ring magnets and coils in the ENSM are fixed on the fixed end and the moving end of the universal testing machine, respectively. The universal testing machine is used to measure the electromagnetic force under different input currents I. Figure 2 shows the measurement, calculation, and fitting results. The calculation results are basically consistent with the experimental results, which proves the accuracy of the modeling. Moreover, the fitting results are also close to the experimental results, indicating that the cubic polynomial expression has sufficient accuracy and can be used for modeling and control. The fitting parameters are obtained as a1 = 6350 Nm−1A−1, a2 = -3.75 × 108 Nm−3A−1. Thus, when the relative displacement \({\text{x}}_{\text{d}}\) is known, the expected electromagnetic force can be output by controlling the input current I.

Table 1 Parameters of the ring magnets and coils
Full size table
Fig. 2
figure 2

Measurement, calculation, and fitting of electromagnetic force generated by the ENSM

Full size image

Table 2 compares the proposed ENSM with electromagnetic NSMs proposed by other studies. It is obvious that the ENSM produces the largest stiffness adjustable range at a relatively small number of ampere-turns, which proves that it has higher stiffness generation efficiency. This is because that the ENSM makes full use of the area with high radial magnetic flux density around the edge of the ring magnet by adding coils (Am and Bm) inside the ring magnet and adding coils (like At and Ab) on the both ends of the middle coils. Furthermore, the ENSM has the smallest size. This is because the radial arrangement of magnets makes full use of the radial space and makes the structure more compact.

Table 2 Compare with previous studies
Full size table

2.4 Parametric study

The influence of the ENSM parameters on stiffness fitting parameters was analyzed, and the results are shown in Fig. 3. To make full use of the magnetic field to generate negative stiffness, the wire turns are arranged as close to the ring magnets as possible. In the parametric study, the configuration of the ENSM is kept unchanged, including: the radial thickness of the inner and outer ring coil groups remains unchanged, and the radial thickness of the central coil group follows the radial spacing between the magnets to ensure a consistent air gap; the axial height of the top coils and bottom coils remains unchanged, and the axial height of the middle coils is consistent with the magnet. The current used in the parametric study is the maximum current 1 A, which represents the stiffness adjustable range.

Fig. 3
figure 3

Parametric study of the ENSM: a force–displacement curves and b stiffness fitting parameters at different magnet axial heights; c force–displacement curves and d stiffness fitting parameters at different magnet radial spacing; e force–displacement curves and f stiffness fitting parameters at different magnet radii

Full size image

As shown in Fig. 3a, b, as the axial height of the ring magnets increases, the negative stiffness increases. It should be noted that the increase in negative stiffness is not obvious after the axial height increases to a certain level. This shows that increasing the axial height of the magnets cannot effectively improve the negative stiffness adjustable range. In addition, the negative stiffness stroke increases with axial height of the magnets, which indicates that the axial height of the magnet should be designed according to the need for negative stiffness stroke in the vibration environment.

\(R_{g} = r_{w} - R_{v}\) represents the radial spacing between the two ring magnets. When the radial thickness of the magnets is kept constant and the spacing between the magnets is increased, the inner and outer radii of the outer ring magnets will increase simultaneously. Figure 3c, d show that the linear stiffness a1 and nonlinear stiffness a2 generated by the ENSM increases as the spacing increases. Then, keeping the magnet spacing constant and increasing the magnet radial thickness, the outer radius of both magnets will increase. As shown in Fig. 3e, f, the electromagnetic negative stiffness increases with the radius of the two ring magnets, and the increments of both linear stiffness coefficient a1 and nonlinear stiffness coefficient a2 are proportional to the increments of the magnetic ring radius. These two results indicate that increasing the inner or outer diameter of the magnet can increase the stiffness adjustable range. It is worth mentioning that the radial multi-layer combination can reduce the required volume while maintaining the stiffness adjustable range of the ENSM.

3 Design and analysis of the isolator

To verify the effect of the ENSM in vibration isolator, a double-layer isolator is designed and dynamic analysis is carried out in this section.

3.1 Design of the double-layer vibration isolator

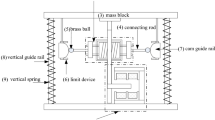
As shown in Fig. 4a, the double-layer vibration isolator consists of two mass-spring-damper systems connected in series, while the ENSM is connected in parallel with the upper system. In the lower layer of the isolator, there are two helical springs to support the upper layer. The helical springs are sleeved on the lower shaft and two fixed collars are used to compress the helical springs. The lower shaft is limited by a linear bushing to move in the vertical direction, and its upper end is connected to the intermediate block. The upper layer of the isolator consists of the ENSM in parallel with a mass-spring-damper system. The coils of the ENSM are glued to the load and the ring magnets are glued to the intermediate block. The upper shaft is also limited by a linear bushing to move in the vertical direction. The fine-adjustment nuts are not only used to preload the spring, but also to adjust the initial relative position of the coils and magnets in the ENSM to achieve the equilibrium position.

Fig. 4
figure 4

Structure of the double-layer vibration isolator: a assembly model, b simplified model

Full size image

When the ENSM is in equilibrium, the force of the ENSM is zero and the load is fully supported by the helical springs; thus, the ENSM will not affect the load-carrying capacity of the isolator. Moreover, adjusting the stiffness of the ENSM will not change the equilibrium position. When the load is disturbed, the helical springs provide a restoring force to the load. The negative stiffness provided by the ENSM will offset the positive stiffness and decrease the dynamic stiffness of the isolator, then the natural frequency would be decreased and the isolation frequency band would be expanded. By changing the direction of the current, the ENSM can work in the positive stiffness range, which will increase the overall stiffness. The bi-directional adjustment of positive and negative stiffness expands the adjustable range of the isolator. According to the relative displacement of the coils and magnets, the current in the coils can be controlled to generate control force in real-time. This semi-active control can further improve vibration control performance.

The parameters of the double-layer vibration isolator are listed in Table 3. The first and second natural frequency of the isolator are 8.6 Hz and 16.6 Hz, respectively. Due to the limitation of coil heating, the input current is limited within ± 1 A, then the stiffness adjustable range of the ENSM is from − 6350 N/m to 6350 N/m. With the ENSM is connected in parallel with the upper spring, the adjustable range of the total stiffness of the upper layer is from − 2710 N/m to 9990 N/m.

Table 3 Parameters of the double-layer vibration isolator
Full size table

3.2 Nonlinear dynamics modeling and analysis of the isolator

Figure 4b shows the simplified model of the double-layer vibration isolator. When a base excitation \(z = Z\cos \omega t\) is applied to the system, the load and intermediate block produce exhibit oscillations. The nonlinear dynamic model of the double-layer isolator can be described as follows:

$$ \begin{array}{*{20}c} {\ddot{x}_{1} m_{1} = - (k_{1} - a_{1} I_{n} )(x_{1} - x_{2} ) + a_{2} I_{n} (x_{1} - x_{2} )^{3} - c_{1} (\dot{x}_{1} - \dot{x}_{2} )} \\ {\ddot{x}_{2} m_{2} = (k_{1} - a_{1} I_{n} )(x_{1} - x_{2} ) - a_{2} I_{n} (x_{1} - x_{2} )^{3} + c_{1} (\dot{x}_{1} - \dot{x}_{2} ) - k_{2} (x_{2} - z) - c_{2} (\dot{x}_{2} - \dot{z})} \\ \end{array} $$
(7)

where \(I_{n}\) represents the current in the coils used to generate negative stiffness.

The relative displacement of the coils and magnets in the ENSM is \(x_{d} = x_{1} - x_{2}\). The linear stiffness supporting the load is \(k_{l} = k_{1} - a_{1} I_{n}\), and the nonlinear stiffness is \(k_{s} = - 3a_{2} I_{n} x_{d}^{2}\). With the displacement of the intermediate block relative to the base being \(x_{b} = x_{2} - z\), the proceeding equation can be nondimensionalized as:

$$ \begin{array}{*{20}c} {\hat{x}_{b}^{\prime \prime } + \hat{x}_{d}^{\prime \prime } + \hat{x}_{d} + 2\zeta_{1} x_{d}^{\prime } + \alpha \hat{x}_{d}^{3} = \varphi_{1}^{2} \cos (\varphi_{1} \tau )} \\ {\hat{x}_{b}^{\prime \prime } - \beta \hat{x}_{d} - 2\beta \zeta_{1} x_{d}^{\prime } - \beta \alpha \hat{x}_{d}^{3} + \left( {\frac{{\varphi_{1} }}{{\varphi_{2} }}} \right)^{2} \hat{x}_{b} + 2\zeta_{2} \left( {\frac{{\varphi_{1} }}{{\varphi_{2} }}} \right)\hat{x}_{b}^{\prime } = \varphi_{1}^{2} \cos (\varphi_{1} \tau )} \\ \end{array} $$
(8)

where \(\omega_{1} = \sqrt {\frac{{k_{l} }}{{m_{1} }}}\), \(\omega_{2} = \sqrt {\frac{{k_{2} }}{{m_{2} }}}\), \(\zeta_{1} = \frac{{c_{1} }}{{2m_{1} \omega_{1} }}\), \(\zeta_{2} = \frac{{c_{2} }}{{2m_{2} \omega_{2} }}\), \(\beta = \frac{{m_{1} }}{{m_{2} }}\), \(\alpha = \frac{{ - a_{2} I_{n} }}{{k_{l} }}Z^{2}\), \(\varphi_{1} = \frac{\omega }{{\omega_{1} }}\), \(\varphi_{2} = \frac{\omega }{{\omega_{2} }}\), \(\tau = \omega_{1} t\), \({\text{x}}_{\text{d}}\) and \({\text{x}}_{\text{b}}\) can be nondimensionalized as \(\hat{x}_{d} = \frac{{x_{d} }}{Z}\) and \(\hat{x}_{b} = \frac{{x_{b} }}{Z}\), thus \(\dot{x}_{d} = Z\omega_{1} \hat{x}^{\prime}_{d}\) and \(\ddot{x}_{d} = Z\omega_{1}^{2} \hat{x}^{\prime\prime}_{d}\)(the primes ′ denote the derivatives with respect to the dimensionless time \(\tau\)). \(\alpha\) is the nonlinear term, which is obviously related to stiffness nonlinearity a2 and excitation amplitude Z.

The dimensionless periodic response is assumed to be \(\hat{x}_{d} = a_{10} + a_{11} \sin (\varphi_{1} \tau ) + b_{11} \cos (\varphi_{1} \tau )\) and \(\hat{x}_{b} = a_{20} + a_{21} \sin (\varphi_{1} \tau ) + b_{21} \cos (\varphi_{1} \tau )\), and the numerical solution will be obtained using the harmonic balance method [54] and Newton's iteration method, ignoring high harmonic frequencies. The dimensionless absolute displacement of the load is given by:

$$ \hat{x}_{1} = a_{10} + a_{11} \sin (\varphi_{1} \tau ) + b_{11} \cos (\varphi_{1} \tau ) + a_{20} + a_{21} \sin (\varphi_{1} \tau ) + b_{21} \cos (\varphi_{1} \tau ) + \cos (\varphi_{1} \tau ) $$
(9)

Thus, the transmissibility from the base to the load is:

$$ T_{r} = 20\log \left| {\hat{x}_{1} } \right| = 20\log \left( {\sqrt {\left( {a_{11} + a_{21} } \right)^{2} + \left( {b_{11} + b_{21} + 1} \right)^{2} } + a_{10} + a_{20} } \right) $$
(10)

Then, the influence of different conditions on the transmissibility of the vibration isolator is analyzed. As shown in Fig. 5a, with the increase in the current In, the two natural frequencies decrease, and the effective vibration isolation band is extended to lower frequency. Moreover, the peak value of transmissibility decreases significantly, because the increase in negative stiffness reduces the comprehensive stiffness and leads to the increase in damping ratio.

Fig. 5
figure 5

Transmissibility of the isolator: a different input currents In, b different excitation amplitudes Z, c different damping ratio \(\zeta_{1}\), d different damping ratio \(\zeta_{2}\)

Full size image

Figure 5b shows that the transmissibility increases with the excitation amplitude, because the nonlinear response is more significant due to the increase in the nonlinear term \(\alpha = \frac{{ - a_{2} I_{n} }}{{k_{l} }}Z^{2}\). This shows that the nonlinear vibration isolator may worsen the vibration isolation performance under large excitation. It is worth mentioning that increasing the nonlinear term of stiffness a2 alone has a similar effect.

As shown in Fig. 5c, d, increasing the damping coefficient of the system can suppress the resonance and nonlinear response, but will deteriorate the high-frequency performance of the isolator.

To suppress the resonance that still exists after reducing the natural frequency, while maintaining the high-frequency vibration isolation performance, a semi-active control method using the ENSM to generate control force is proposed in this paper.

4 Semi-active stiffness control of double-layer isolator

Aiming at the problem of the resonance behavior of the double-layer vibration isolator and the nonlinearity caused by the ENSM, a semi-active control strategy based on suboptimal control theory is proposed in this section. Furthermore, it is proven that expanding the adjustable stiffness to negative stiffness range can effectively improve the semi-active vibration isolation performance in simulations.

4.1 Design of the semi-active controller

Equation (7) can be converted to a state-space equation by defining a state vector as \({\varvec{x}} = \left[ {\begin{array}{*{20}c} {\dot{x}_{1} } & {\dot{x}_{2} } & {x_{1} } & {x_{2} } \\ \end{array} } \right]^{T}\). Furthermore, the control input is defined as \(u = F\), and the disturbance input is defined as \({\varvec{w}} = [\begin{array}{*{20}c} z & {\dot{z}} \\ \end{array} ]\). the discrete state-space equation can be given based on zero-order hold method as follows:

$$ {\varvec{x}}(n + 1) = {\varvec{A}}_{d} {\varvec{x}}(n) + {\varvec{B}}_{1d} u(n) + {\varvec{B}}_{2d} {\varvec{w}}(n) + {\varvec{\theta}} $$
(11)

where the subscript d indicates that the matrix is applied to the discrete system. And.

\({\varvec{A}} = \left[ {\begin{array}{*{20}c} { - \frac{{c_{1} }}{{m_{1} }}} & {\frac{{c_{1} }}{{m_{1} }}} & { - \frac{{k_{l} }}{{m_{1} }}} & {\frac{{k_{l} }}{{m_{1} }}} \\ {\frac{{c_{1} }}{{m_{2} }}} & { - \frac{{c_{1} + c_{2} }}{{m_{2} }}} & {\frac{{k_{l} }}{{m_{2} }}} & { - \frac{{k_{l} + k_{2} }}{{m_{2} }}} \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{array} } \right]\), \({\varvec{B}}_{1} = \left[ {\begin{array}{*{20}c} {\frac{1}{{m_{1} }}} \\ { - \frac{1}{{m_{2} }}} \\ 0 \\ 0 \\ \end{array} } \right]\), \({\varvec{B}}_{2} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\frac{{k_{2} }}{{m_{2} }}} \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\frac{{c_{2} }}{{m_{2} }}} \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \right]\), \({\varvec{\theta}} = \left[ {\begin{array}{*{20}c} {\frac{{a_{2} I_{n} x_{d}^{3} }}{{m_{1} }}} \\ { - \frac{{a_{2} I_{n} x_{d}^{3} }}{{m_{2} }}} \\ 0 \\ 0 \\ \end{array} } \right]\),

\({\varvec{A}}_{d} = \sum\limits_{q = 0}^{\infty } {\frac{{{\varvec{A}}^{q} T^{q} }}{q!}}\), \({\varvec{B}}_{id} = \sum\limits_{q = 0}^{\infty } {\frac{{{\varvec{A}}^{q} T^{q + 1} }}{{\left( {q + 1} \right)!}}} {\varvec{B}}_{i}\), \(i = 1,2\), T represents the sampling time of the discrete system.

The total current \({\text{I}}_{\text{o}}\) output to the ENSM can be divided into \({\text{I}}_{\text{n}}\) for generating negative stiffness and \({\text{I}}_{\text{c}}\) for generating control force. When \({\text{I}}_{\text{n}}\) is not 0, the isolator has nonlinear stiffness due to the existence of θ. Nonlinear stiffness may lead to unwanted nonlinear responses, such as bifurcations and jumps, especially under large excitation. Therefore, the feedback linearization method is used to design the controller. Part of the control force \({\text{F}}_{e}\) is used to cancel the nonlinear part of the system, and effectively turn it back into a linear system, while the other part of the control force \({\text{F}}_{\text{c}}\) is used for feedback control. The control structure of the semi-active vibration isolator is shown in Fig. 6. The force \({\text{F}}_{\text{e}}\) can be obtained by \({{\varvec{\theta}}+{\text{B}}_{{1}{\text{d}}}{\text{F}}}_{\text{e}}={0}\), so \({\text{F}}_{\text{e}}=-{\text{a}}_{2}{{\text{I}}}_{\text{n}}{{\text{x}}_{\text{d}}}^{3}\). This will eliminate the nonlinearity of the system, so that the controller of the linear system can be applied to the system. The expected control force \({\text{F}}_{\text{c}}=-{\text{K}}{\text{x}}_{p}\), where K is suboptimal feedback gain and \({\text{x}}_{\text{p}}\) is partial state variables. Then, the control current \({\text{I}}_{\text{c}}\) of the ENSM is given by Eq. (5) according to the measured relative displacement \({\text{x}}_{\text{d}}\). To prevent the coils from overheating, the total current is limited to ± 1 A before outputting into the ENSM. Its constraint law is as follows:

$$ I_{o} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 1,} & {I_{c} + I_{n} \le - 1} \\ \end{array} } \\ {\begin{array}{*{20}c} {I_{c} + I_{n} ,} & {\left| {I_{c} + I_{n} } \right| < 1} \\ \end{array} } \\ {\begin{array}{*{20}c} {1,} & {I_{c} + I_{n} \ge 1} \\ \end{array} } \\ \end{array} } \right. $$
(12)
Fig. 6
figure 6

Semi-active control strategy of the double-layer vibration isolator

Full size image

The actual electromagnetic force is generated through the relative displacement and stiffness change of the ENSM. This process ultimately improves the isolation performance of the double-layer vibration isolator.

The suboptimal feedback gain K is obtained based on the linear quadratic regulator (LQR) control, which is a control strategy that allows the system to work at minimum cost. The definition of its cost function is related to the input and output of the system, and the weights of the input and output in the cost function are controlled by the weighting matrices Q and R. The general form of the cost function is:

$$ J = \mathop \sum \limits_{n = 1}^{\infty } ({\varvec{x}}[n]^{T} {\varvec{Qx}}[n] + {\varvec{u}}[n]^{T} {\varvec{Ru}}[n]) $$
(13)

where:

\({\varvec{Q}} = {\varvec{Q}}^{T} \ge 0\),\({\varvec{R}} = {\varvec{R}}^{T} > 0\).

The increasing in Q will accelerate the convergence speed of states x. The increasing in R will lead to the reduction of the control input u. Q and R should be designed to improve control performance as much as possible while ensuring system stability and not exceeding the output range of the ENSM.

Once the state matrix \({\text{A}}_{\text{d}}\) and input matrix \({\text{B}}_{\text{d}}\) of the system are established and the weighting matrices Q and R are determined, the matrix P can be obtained by solving the following Riccati equation:

$$ {\varvec{A}}_{d}^{T} {\varvec{PA}}_{d} - {\varvec{P}} - {\varvec{A}}_{d}^{T} {\varvec{PB}}_{d} ({\varvec{B}}_{d}^{T} {\varvec{PB}}_{d} + {\varvec{R}})^{ - 1} {\varvec{B}}_{d}^{T} {\varvec{PA}}_{d} + {\varvec{Q}} = 0 $$
(14)

The optimal full-state feedback gain is given by taking the matrix P into Eq. (15):

$$ {\varvec{L}} = ({\varvec{B}}_{d}^{T} {\varvec{PB}}_{d} + {\varvec{R}})^{ - 1} {\varvec{B}}_{d}^{T} {\varvec{PA}}_{d} . $$
(15)

The optimal controller with full-state feedback has good performance. However, the measurement of absolute displacement requires a constant reference point, which is often difficult to obtain. Therefore, if feedback control can be carried out using only the easily measured velocity state variables, the control system will be greatly simplified. Next, the importance of the velocity variable in a double-layer isolator is examined to ensure that suboptimal control of the velocity feedback is still well controlled.

The relative importance of the state variables is obtained by calculating the second-order sensitivity of the cost function with respect to the optimal feedback gain:

$$ \frac{{\partial^{2} J}}{{\partial^{2} {\varvec{L}}}} = 2\hat{\user2{R}}({\varvec{R}} + {\varvec{B}}_{d}^{T} \hat{\user2{S}}\user2{B}_{d} ) $$
(16)

The parameters in Eq. (16) are calculated as follows:

$$ \hat{\user2{H}} = {\varvec{A}}_{d} - {\varvec{B}}_{d} {\varvec{L}} $$
(17)
$$ \hat{\user2{Q}} = {\varvec{Q}} + {\varvec{L}}^{T} {\varvec{RL}} $$
(18)
$$ \hat{\user2{S}} = \hat{\user2{H}}^{T} {\hat{\user2 S}\hat{\user2 H}} + \hat{\user2{Q}} $$
(19)
$$ \hat{\user2{R}} = {\hat{\user2 H}\hat{\user2 R}\hat{\user2 H}}^{T} + {\varvec{I}} $$
(20)

\(\Delta{\text{J}}_{\text{i}}\) represents the increment of the cost function J when the i-th state variable is removed. The value of \(\Delta {\text{J}}_{\text{i}}\) represents the relative importance of the i-th state variable to the control performance. It can be calculated as follows:

\(\Delta J_{i} \approx \frac{1}{2}\frac{{\partial^{2} J}}{{\partial L_{i}^{2} }}L_{i}^{2}\), \(i = 1,2,3,4\)(21). where \({\text{L}}_{\text{i}}\) represents the i-th feedback gain corresponding to the i-th state variable.

After verifying the influence of the selected state variables on the control performance, the output matrix \({\text{C}}_{\text{d}}\) is obtained. The iterative method [55] can be used to calculate the suboptimal partial-state feedback gain K. As shown in Fig. 7, the initial value \({\text{K}}_{0}\) can be obtained from Eq. (22). Then, we take \({\text{K}}_{0}\) into Eq. (23) and Eq. (24) to solve \(\hat{\user2{S}}_{1}\) and \(\hat{\user2{R}}_{1}\). Then, \(\hat{\user2{S}}_{1}\) and \(\hat{\user2{R}}_{1}\) are substituted into Eq. (25) to obtain \({\text{K}}_{1}\) for the next iteration. The value of \({\text{K}}_{{\rm i}}\) converges, and when \(\Delta{\text{K}}\) is less than 0.1%, a final solution to \({\text{K}}_{{\rm i}}\) can be obtained.

Fig. 7
figure 7

Iterative calculation flow chart

Full size image

4.2 Simulation analysis

To investigate the effect of expanding the adjustable stiffness to negative stiffness range on semi-active vibration isolation, a simulation model of semi-active control of the double-layer isolator was established in MATLAB/Simulink, and four groups of simulations were performed, including the ENSM adjusted in passive (0 A), positive–negative stiffness range (-1 ~ 1 A), positive stiffness range (-1 ~ 0 A), negative stiffness range (0 ~ 1 A).

Considering that velocity is usually used as the main control objective in vibration control, and there is only one control input, so the weight matrix Q and R are set to:

\({\varvec{Q}} = \left[ {\begin{array}{*{20}c} {2000} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\), \({\varvec{R}} = 1/10\).

The full-state feedback gain in Eq. (15) is calculated as L = [109.89, 14.86, -303.88, 1952.80]. Then, the relative importance of the state variables can be obtained using Eqs. (16) ~ (21) as \(\Delta J = [23.71,3.65,0.25,11.74] \times 10^{6}\). The state variable \({\dot{\text{x}}}_{1}\) has the greatest influence on the cost function, and other state variables have less of an effect. Therefore, using the state variables \({\dot{\text{x}}}_{1}\) and \({\dot{\text{x}}}_{2}\) for feedback control will not significantly affect the control performance. When partial-state feedback is used, the control gain vector can be obtained as \({\varvec{K}} = [155.36,8.98]\).

Figure 8 shows the simulation results obtained by adjusting the current of ENSM in different ranges. The required force refers to the control force calculated from the LQR algorithm and the load velocity, and the required current refers to the current required to generate the required force, which is calculated based on the displacement and electromagnetic force model. The actual current is the current after limiting the required current to the allowable range of the coil, and the actual force is the control force that the actual current can produce.

Fig. 8
figure 8

Control force and input current during the simulation: the required force and the actual force when the ENSM is adjusted a in negative stiffness range, c in positive stiffness range, and e in positive and negative stiffness range; the required current and the actual current when the ENSM is adjusted b in negative stiffness range, d in positive stiffness range, and f in positive and negative stiffness range

Full size image

In Fig. 8a, e, the required force are almost overlapping with the actual force. This is because when the ENSM is adjusted in the negative stiffness range or the positive–negative stiffness range, the required control force is relatively small and is within the capabilities of the ENSM. As can be seen from Fig. 8b, f, the actual current is consistent with the required current most of the time. There are only a few short moments when the required current is not reached, because the current required to generate the control force is too large when the ENSM is close to equilibrium position. As for Fig. 8c, when the stiffness can only be adjusted within the positive stiffness range, the required control force is larger and exceeds the capability of the ENSM, so the actual force is smaller than the required force, which can be seen from Fig. 8d, the actual current is less than the required current. This demonstrates that extending stiffness semi-active control into the negative stiffness range can reduce the need for stiffness adjustable range.

Figure 9 shows the transmissibility of the isolator when the ENSM is adjusted in different stiffness ranges. Compared with passive vibration isolators, when the ENSM is adjusted in the negative stiffness range, the peak transmissibility drops by 18.1 dB, while when adjusted in the positive stiffness range, the drop is only 2.5 dB. Vibration isolators with adjustable negative stiffness mechanisms have better performance than isolators that can only be adjusted in the positive stiffness range, which proves the superiority of the ENSM in semi-active vibration isolation.

Fig. 9
figure 9

Transmissibility of the double-layer isolator under different stiffness adjustable range (positive–negative stiffness curve and negative stiffness curve nearly overlap)

Full size image

5 Semi-active vibration isolation experiment

To verify the practical performance of the ENSM and the suboptimal control strategy in vibration isolation, a double-layer isolator was manufactured, and a vibration testing platform was built. Both passive and semi-active isolation performance under different disturbances were tested, and the performance of passive isolators with negative stiffness in parallel was also considered. It should be noted that the negative stiffness reduces the overall stiffness of the system. Correspondingly, the control gain also needs to be reduced. Matrix \({\text{Q}}_{\text{n}}\) and matrix \({\text{R}}_{\text{n}}\) are set as follows:

\({\varvec{Q}}_{n} = \left[ {\begin{array}{*{20}c} {300} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\),\({\varvec{R}}_{n} = 1/10\),

and the control gain vector is \({\varvec{K}}_{n} = [39.96,9.59]\).

5.1 Experimental setup

As shown in Fig. 10, the isolator was installed on the center of a shaking table. The vibration generated by the exciter was transmitted to the shaking table through a thin shaft and then to the isolator and load. The excitation signal was generated by the NI-PXI platform and amplified by the power amplifier to drive the exciter. Two acceleration sensors were glued to the load and the intermediate block. The velocity feedback signals could be obtained by filtering and integrating the signals of the acceleration sensors. A laser displacement sensor was installed on the intermediate block to measure the relative displacement of the load and intermediate block. The measured signals were collected by the NI PXIe-6363 data acquisition (DAQ) card and transmitted to the computer embedded in NI-PXI platform. According to the semi-active control algorithm described in Sect. 3, the required control force and the input current of the ENSM was calculated by the computer. The actual input current is limited from -1 A to 1 A. The actual control voltage was output to the driver through the NI PXIe-6363 DAQ card. Then, it was converted to the input current of the ENSM by the driver.

Fig. 10
figure 10

Experimental platform of the semi-active vibration isolation

Full size image

5.2 Experimental results

5.2.1 Sweep vibration isolation experiment

To reduce the influence of test noise, the ENSM is supposed to work in a larger stroke in the sweep vibration isolation experiment. The exciter generated a variable-amplitude sweep vibration in the frequency range of 5 to 25 Hz. Figure 11a, b show the effect of introducing semi-active control in isolators without negative stiffness (\({\text{I}}_{\text{n}}\)= 0) and isolators with negative stiffness (\({\text{I}}_{\text{n}}\)= 0.4 A), respectively. The semi-active stiffness control significantly reduces the vibration response of the load and improves vibration isolation performance at the whole frequency band. Transmissibility results in Fig. 11c show that the parallel connection of negative stiffness effectively reduces the natural frequency of the double-layer isolator. The first-order natural frequency is reduced from 9.23 to 7.69 Hz, and the second-order natural frequency is reduced from 16.92 to 13.08 Hz, and the effective isolation frequency band is also widened. However, the resonance still exists while the natural frequency is reduced. The semi-active control can significantly suppress resonance while improve the performance of high frequency vibration isolation. This resolves the contradiction between resonance suppression and high frequency attenuation in passive systems. With the introduction of semi-active control, the peak transmissibility is reduced from 13.29 to 0.67 dB.

Fig. 11
figure 11

Sweep vibration isolation experimental results: a without negative stiffness, b with negative stiffness, c transmissibility

Full size image

5.2.2 Single-frequency vibration isolation experiment

To further verify the performance of the isolator, two single-frequency tests of 8 Hz and 16 Hz were carried out. In 0 ~ 2 s, there is no current in the coils (\({\text{I}}_{\text{n}}\)= 0, \({\text{I}}_{\text{c}}\)= 0), and the isolator works passively and without negative stiffness. At 2 s, the first experiment turned on the negative stiffness (\({\text{I}}_{\text{n}}\)= 0.4 A), while the second experiment turned on the semi-active control (\({\text{I}}_{\text{c}}\) in control). At 7 s, the first experiment turned on the semi-active control on the basis of the negative stiffness parallel system (\({\text{I}}_{\text{n}}\)= 0.4 A and \({\text{I}}_{\text{c}}\) in control). The results in Fig. 12a show that the response of the passive system with negative stiffness in parallel is larger than that of the original system under 8 Hz excitation. This is because the system resonates at the natural frequency reduced by the negative stiffness. However, the semi-active system effectively attenuates the vibration. As shown in Fig. 12b, both the negative stiffness parallel system and the semi-active system effectively isolate the vibration.

Fig. 12
figure 12

Response of the load under single-frequency vibration excitation: a 8 Hz and b 16 Hz

Full size image

5.2.3 White noise vibration isolation experiment

Figure 13 shows the control effect of the double-layer isolator on noise vibration of 0.1 to 60 Hz. From Fig. 13a, b, after applying the semi-active control, the decline of the root mean square of the load velocity reaches 54.3% and 62.4%, respectively. It is proven that the vibration control performance is effectively improved by the semi-active control strategy. From the power spectral density in Fig. 13c, it can be seen that the passive system with negative stiffness in parallel improves the high-frequency vibration isolation performance, but the semi-active stiffness control system obviously has higher vibration isolation performance, especially at low frequencies.

Fig. 13
figure 13

White noise vibration isolation experimental results: a without negative stiffness, b with negative stiffness, c PSD estimate

Full size image

5.2.4 Impact isolation experiment

To further verify the impact isolation performance of the double-layer isolator under semi-active stiffness control, the following experiment was conducted. At 1 s, a half-period sinusoidal excitation signal with a period of 0.1 s is generated by the NI-PXI platform so that the exciter produces an impact on the isolator. The velocity response of the load is shown in Fig. 14. Compared with the passive response, the maximum value of the load velocity response is reduced from 0.205 to 0.071 m/s, a drop of 65.4%.

Fig. 14
figure 14

Response of the load under impact

Full size image

In summary, the double-layer vibration isolator designed in this paper and the semi-active control strategy based on suboptimal control have shown better performance than passive vibration isolators in single-frequency vibration, sweep vibration, white noise vibration, and impact experiments. The advantages of the designed ENSM and suboptimal control strategy are proven.

6 Conclusion

In this paper, a novel ENSM is proposed. Through the analysis of the magnetic field, it is found that there is a higher radial flux density near the inner and outer edges of the magnet, and the magnet and coil configuration of the radial multi-layer array is proposed to make full use of it, which effectively improves the stiffness adjustable range (± 6350 Nm−1) and generation efficiency (4.65 Nm−1A−1). When the current of the ENSM is constant, it will produce a stiffness proportional to the current, and can be adjusted bidirectionally within the range of positive and negative stiffness. Then, a double-layer vibration isolator is designed based on the ENSM, and a semi-active control method based on a suboptimal control strategy is proposed. When the current of the ENSM is adjusted in real time according to the desired control force and relative displacement, an active control effect can be produced. In the simulations, expanding the range of stiffness adjustment to negative stiffness can effectively reduce the required stiffness adjustable range and effectively improve the semi-active vibration isolation performance. The effectiveness of the ENSM and the semi-active control method is verified in single-frequency vibration, sweep vibration, white noise vibration, and impact experiments. The negative stiffness produced by the ENSM effectively reduces the natural frequency of the double-layer vibration isolator and extends the effective isolation frequency band. The introduction of semi-active control further suppresses resonance and improves vibration isolation performance. In the sweep vibration experiment, the peak transmissibility is reduced from 13.29 to 0.67 dB with the introduction of semi-active control. In the white noise vibration experiment, the root mean square of the load velocity drops by 54.3% and 62.4%, respectively. However, there are more external disturbances in the actual environment that may affect the stability of the system. In the future, we will focus on a more robust controller design for semi-active vibration isolation.