A new association coefficient measure for the conflict management and its application in medical diagnosis

Abstract

Conflicts in the evidence are addressed through various functions based on distance and similarity measure etc. Some complications and irrationality in existing distance measure is an open issue as how to address its conflicting degree. In this paper, we have introduced a new association coefficient measure primarily based on the modification of Jaccard’s similarity matrix with related properties and examples. In this paper, firstly the initial belief functions are constructed by using the fuzzy soft sets and information structure image matrix. Secondly, we used the proposed association coefficient measure to pre-process the initial belief function. Finally, Dempster’s combination rule is implemented to combine the modified belief function and rank the alternatives based on their final belief measure. The study is validated through various examples and a case study in medical diagnosis with the comparison of the existing two methods. The proposed association coefficient is efficient in representing the degree of association between the belief functions and modifying the belief function.

1 Introduction

Decision-making in the world of uncertainty involves the knowledge and information about the decision environment, however, suitable fusion of information and its exchange helps in decision-making to reduce uncertainty. Several theories namely probability theory, fuzzy set theory, fuzzy soft set theory, evidence theory have been developed for a few decades to address the uncertainty depending on randomness, lack of knowledge, imprecision etc. Evidence theory or Dempster–Shafer theory is extensively used in real-life applications of decision-making problems of medical diagnosis [16, 22, 33], fault diagnosis [2, 8], target and pattern recognition [29], sensor data fusion [14, 39] etc. Dempster–Shafer evidence theory (DSET) is often recognized as the generalized form of Bayesian probability theory jointly developed by Dempster in 1967 and Shafer in 1976, capable of handling uncertainty without prior knowledge about the events. Despite a lot of advantages in this theory, its well-known combination rule of multiple pieces of evidence has some difficulties encountered in the evidence fusion of some set of evidence which was first pointed out by Zadeh [41]. Zadeh’s demonstration about the conflicts attracted many researchers towards this theory to develop some other combination methods to overcome the difficulties. Many researchers proposed evidence fusion rules among which [9, 11, 31, 40, 42], etc. are a few fusion methods in this direction of developing Dempster’s combination rule. However, conflicts and the counter-intuitive nature of evidence can also be handled by simple averaging [28] without acknowledging the importance of the evidence or weighted averaging of the evidence. In weighted average mass, the weight or importance of the evidence is an important factor in evidence combination. Several researchers [6, 8, 10, 15, 35, 39] used the approach of the weighted average mass of the evidence where the Jousselme’s distance [17] and belief entropy are broadly used to find the weight of the evidence.

The various distance measure [17, 18], similarity measures [38], correlation measures [12], association coefficient measure [29], and divergence measure [43], etc. are widely used in various fields of decision-making problems. Chen et al. [1] proposed an improved combination method in multi-sensor data fusion using the modified Minkowski distance and betting-commitment distance function. Zhu et al. [45] proposed a power set distribution probability function and introduced a distance based on the power set distributions betting commitments. Cheng and Xiao [4] proposed a new distance measure based on the new similarity coefficient and used it in the sensor data fusion of the target recognition problem. Deng and Wang [7] proposed the method based on Hellinger distance measure and evidence angle. Sun et al. [32] proposed a method based on the pignistic probability distance and Deng entropy of evidence. Li et al. [21] proposed the Hellinger distance measure and applied it to the fault diagnosis problem. Xhu and Xiao [44] defined a new belief Hellinger distance measure with related properties and applied it in the classification problem of the Iris data set. Khalaj and Khalaj [20] proposed three well-known similarity measures namely Jaccard similarity, Cosine similarity, and Dice similarity on the novel belief set and applied it in multicriteria decision-making.

Particularly in medical diagnosis, several researchers used the concept of Dempster–Shafer theory along with the other mathematical tools in medical diagnosis problems [16, 24,25,26, 36]. Recently, Li et al. [22] presented an incorporated approach of the fuzzy soft set, grey relation analysis, and DSET with a diagnostic application. Wang et al. [33] presented another method where the tools like fuzzy soft set are used for parameterization, ambiguity measure for uncertainty, and Dempster’s rule for evidence combination respectively. Xiao [37] also introduced the fuzzy soft set approach by means of fuzzy preference relation, Deng entropy, and evidence theory. Chen et al. [3] used the distance function and improved belief entropy to modify the evidence in the medical diagnosis problems. Zhou et al. [43] proposed the new Pythagorean fuzzy divergence measure distance in the medical diagnosis where the Pythagorean fuzzy set is used is in form BPA. Khalaj and Khalaj [19] proposed the concept of the new belief set and defined the cosine similarity measure in medical diagnosis problems.

1.1 Motivation of the study

• Mathematical modelling [3, 16, 22, 33] plays a significant role in establishing the relationship between the disease and symptoms in diagnosing the disease of a patient. Symptoms are assessed by the decision-maker from multiple sources and its fusion is much preferable to the single due to change in the symptoms which can be handled through the evidence theory efficiently.

• The conflicting evidence is modified by utilizing different types of functions. Existing distance measure gives some irrational results for some pieces of evidence. Basically, Jousselme’s distance fails to reflect the conflicts between two evidence containing singleton focal elements; especially the distance remains unaltered with the alteration of the singleton subset by the other singleton subset. This motivates us to develop a new association coefficient measure based on the new similarity index to deal with the difficulties caused by the Jousselme distance measure and develop WAM by using the proposed association coefficient measure in medical evidence fusion.

• The distance measures [4, 17], correlation measure [12, 13] and association coefficient measure [29] are defined based on the similarity index. However, the evaluation of similarity between two sets from a greater number of factors has high convergence speed motivates us to use a new similarity index. The similarity degree is estimated from the ratio of cardinality numbers that is common with the collection of possible subsets to the product of both individual subsets as well as the subset of their union.

In order to deal with the issue of conflict in evidence fusion and obtained a modified belief function, a new association coefficient measure is introduced based on the modification of Jaccard’s similarity index and use some examples to show its efficiency in showing conflicts between two belief functions. The proposed association coefficient measure is treated as a similarity measure to pre-process the evidence efficiently. The present paper is structured on the basis of the construction of the initial belief functions using information structure image matrix, determination of the initial weight of the evidence by using the new association coefficient measure, and combined the weighted average mass of the evidence to evaluate the belief measure of the decision alternatives. Finally, a case study from Li et al. [22] is taken for the validation of the methodology in medical diagnosis and compared with the existing methods.

The present paper is prepared as follows: In Sect. 2, preliminaries of soft set and fuzzy soft set with their “AND” & “OR” operations are discussed with a numerical example. In addition, the information structure image matrix is defined in the same section. Section 3providedthe fundamental idea of Dempster–Shafer theory and some important definitions of existing distance measures, correlation measures and association coefficient measures. In this section, we have proposed a new measure of the association coefficient and put forward some properties with examples. In Sect. 4, methodology and algorithm are introduced for the construction of the initial mass assignment of the decision alternatives in medical diagnosis. Section 5 illustrates the conclusion of the paper with the future direction of the study.

2 Preliminaries

In this section, we have put forward various preliminary definitions of soft set theory [27], fuzzy soft sets [23]with related operations and examples.

2.1 Fuzzy soft set and some important operations

Definition 1

(Molodtsov [27]). Consider $U$ denotes the universal set and $P$ be the set parameters over $U$. A pair $\left( {f,A} \right)$ where $f:A \to 2^{U}$ is a function is referred to as the soft set, provided $A$ is subset of $P$.

Definition 2

(Maji et al. [23]). Suppose, ${\mathcal{F}}(U)$ be the collection of fuzzy sets over the universal set $U$ and $A \subseteq P$. A fuzzy soft set over $U$ is a pair $\left( {\widetilde{f},A} \right)$, where $\tilde{f}$ is a function given by $\widetilde{f}: \, A \to {\mathcal{F}}(U)$.

2.2 Operations on fuzzy soft set

Definition 3

(Maji et al. [23]). Consider $(f,{\rm X}_{1} )$ and $(g,{\rm X}_{2} )$ represents the two distinct fuzzy soft sets over $U$, we have

• (i) AND operation ($\wedge$) The “AND” operation between $(f,{\rm X}_{1} )$ and $(g,{\rm X}_{2} )$ is defined as:

  $$(f,{\rm X}_{1} ) \wedge \left( {g,{\rm X}_{2} } \right) = \left( {h,{\rm X}_{1} \times {\rm X}_{2} } \right),$$

where $h(x_{1} ,x_{2} ) = f(x_{1} )\tilde{ \cap }g(x_{2} )$, $\forall x_{1} \in {\rm X}_{1}$ and $x_{2} \in {\rm X}_{2}$.

• (ii) (OR) operation ($\vee$) The “OR” operation between $(f,{\rm X}_{1} )$ and $(g,{\rm X}_{2} )$ is defined as:

  $$(f,{\rm X}_{1} ) \vee (g,{\rm X}_{2} ) = (h,{\rm X}_{1} \times {\rm X}_{2} ),$$

where $h(x_{1} ,x_{2} ) = f(x_{1} )\tilde{ \cup }g(x_{2} )$, $\forall x_{1} \in {\rm X}_{1}$ and $x_{2} \in {\rm X}_{2}$.

Example 1

Consider $U = \{ \tau_{1} ,\tau_{2} ,\tau_{3} ,\tau_{4} \} \,$ be the universal set of four choices of alternatives. Let $P = \{ \rho_{1} ,\rho_{2} ,...,\rho_{5} \}$ be the set of selection parameters over $U$. Let $X_{1} = \left\{ {\rho_{1} ,\rho_{2} } \right\}$ and $X_{2} = \left\{ {\rho_{3} ,\rho_{4} } \right\} \subseteq P$ such that

$$(f,{\rm X}_{1} ) = \left\{ {f(\rho_{{1}} ){ = }{ \{ }\tau_{{1}} {/0}{{.65, }}\tau_{{2}} {/0}{{.10, }}\tau_{3} {/0}{{.20, }}\tau_{{4}} {/0}{{.35}}{\} ,}} \right.f(\rho_{{2}} ){ = }{\{ }\tau_{{1}} {/0}{{.85, }}\tau_{{2}} {/0}{{.25, }}\tau_{3} {/0}{{.20, }}\tau_{{4}} {/0}{{.55}}{\} \} }$$

$$\left( {g,{\rm X}_{2} } \right) = \left\{ {g(\rho_{3} ){ = }{ \{ }\tau_{{1}} {/0}{{.45, }}\tau_{{2}} {/0}{{.65, }}\tau_{3} {/0}{{.35, }}\tau_{{4}} {/0}{{.40}}{\} },} \right.g(\rho_{4} ){ = }\left. {{\{ } \, \tau_{{1}} {/0}{{.75, }}\tau_{{2}} {/0}{{.10, }}\tau_{3} {/0}{{.25, }}\tau_{{4}} {/0}{{.40}}{\} }} \right\}$$

Then $(f,{\rm X}_{1} )$ and $(g,{\rm X}_{2} )$ represents the fuzzy soft sets over $U$. Now, we have

$$(f,{\rm X}_{1} ) \wedge (g,{\rm X}_{2} ) = (h,{\rm X}_{1} \times {\rm X}_{2} )$$

Therefore, $h(\rho_{i} ,\rho_{j} ){ = }f(\rho_{i} )\tilde{ \cap }g(\rho_{j} )$ for all $\rho_{i} \in {\rm X}_{1}$ and $\rho_{j} \in {\rm X}_{2}$ is given in Table 1.

Table 1 AND operation of FSSs $(f,{\rm X}_{1} )$ and $(g,{\rm X}_{2} )$

Definition 4

(Li et al. [22]). Let $M = [ {\mu_{ij} } ]_{m \times n}$ be finite information matrix through the membership degree of alternative $x_{i}$ with respect to parameters $e_{j}$. Then, the information structure image matrix $\widetilde{M}$ is defined as

$$\begin{gathered} \begin{array}{*{20}c} {\,\,\qquad\qquad e_{1} } & {\,\,\, e_{2} } & {\,\, \cdots } & {\,\,e_{n} } \\ \end{array} \hfill \\ \widetilde{M} = \begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{m} } \\ \end{array} \left[ {\begin{array}{*{20}c} {\tilde{\mu }_{11} } & {\tilde{\mu }_{12} } & \cdots & {\tilde{\mu }_{1n} } \\ {\tilde{\mu }_{21} } & {\tilde{\mu }_{22} } & \cdots & {\tilde{\mu }_{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {\tilde{\mu }_{n1} } & {\tilde{\mu }_{m1} } & \ldots & {\tilde{\mu }_{mn} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(1)

where $\tilde{\mu }_{ij} = \frac{{\mu_{ij} }}{{\sum\nolimits_{i = 1}^{m} {\mu_{ij} } }}$ for some parameters $e_{j}$. Then, the sequence $\tilde{\mu }_{ij} = \left\{ {\tilde{\mu }_{1j} ,\tilde{\mu }_{2j} ,...,\tilde{\mu }_{mj} } \right\}$ is called the information structure image sequence.

3 Basic concepts of Dempster–Shafer evidence theory

In this section, we have put forward some basic concepts of DSET. In the framework of decision-making, a set $X = \{ x_{1} ,x_{2} ,...,x_{N} \}$ under consideration for judgement is a collection of $N$ mutually exclusive and collectively exhaustive elements is termed as the frame of discernment (FOD in short). The power set of $X \ne \phi$ denoted by $2^{X}$ is called as the set of hypotheses:

$$2^{X} = \{ \phi ,\{ x_{1} \} ,...,\{ x_{N} \} ,\{ x_{1} ,x_{2} \} ,...,X\} = \{ H_{1} ,H_{2} ,...,H_{i} ,...,H_{{2^{N} }} \}$$

where $H_{i}$ represents a hypothesis among $2^{N} - 1$ non-empty hypotheses.

Definition 5

(Dempster [5] and Safer [30]). Let $X$ denotes the FOD and A function $m:2^{X} \to [0,1]$ is referred to as the basic probability assignment shortly BPA with the condition

$$m(\phi ) = 0\quad {\text{and}}\quad \sum\limits_{{H_{i} \in 2^{X} }}^{{2^{N} - 1}} {m(H_{i} )} = 1$$

(2)

The set of all such possible subsets $H$ of $X$ with the mass function $m(H) > 0$ forms a body of evidence (BOE) denoted by $F = \{ H:m(H) > 0, \, \forall \, H \in 2^{X} \}$ and every element $H \subseteq X$ is known as the focal element.

Definition 6

(Dempster [5] and Safer [30]). Let $m$ is a BPA on the FOD $X$. The Belief measure of any focal element $H$ is a function $Bel:2^{X} \to [0,1]$ such that

$$Bel(\phi ) = 0,\quad Bel(H) = \sum\limits_{{H_{i} \subseteq \, H}} {m(H_{i} )}$$

(3)

Plausibility measure of $H$ is a function $Pl:2^{X} \to [0,1]$ which satisfies the condition

$$Pl(\phi ) = 0,\quad Pl(H) = \sum\limits_{{H \cap H_{i} \ne \phi }} {m(H_{i} )}$$

(4)

where the functions namely $Bel(H)$ represents the exact support and $Pl(H)$ represents the possible support to $H$. The bounded interval $[Bel(H),Pl(H)]$ can be considered as interval of lower probability and upper probability to which $H$ is supported, and the difference $Pl(H) - Bel(H)$ represents the uncertainty of the focal element.

Definition 7

(Dempster [5] and Safer [30]). The Dempster’s combinational rule for combining two BPAs $m_{1}$ and $m_{2}$ is a function $m_{1} \oplus m_{2} :2^{X} \to [0,1]$ defined by

$$(m_{1} \oplus m_{2} )(\phi ) = 0\quad {\text{and}}\quad (m_{1} \oplus m_{2} )(H) = \frac{{\sum\nolimits_{{H_{i} \cap H_{j} = H}} {m_{1} (H_{i} )m_{2} (H_{j} )} }}{1 - K}$$

(5)

where $H_{i} ,H_{j} \in 2^{X}$ and $K = \sum\nolimits_{{H_{i} \cap H_{j} = \phi }} {m_{1} (H_{i} )m_{2} (H_{j} )}$ represents the conflict coefficient and the normalization factor $1 - K$ is interpreted as the conflict coefficient between two distinct evidence.

The two pieces of evidence is said to be in conflicts whenever $K = 1$. Several researchers focus on the issue of conflicts management through different types of conflict coefficient measures defined as below.

3.1 Some important conflict management measures

In this section, we have discussed various conflict measurement functions like distance measure, correlation coefficient and similarity measure that can express the degree of significance between the BPAs.

Definition 8

(Jousselme et al. [17]). Consider $m_{1}$ and $m_{2}$ be two basic probability assignments defined in the FOD $X$. The Jousselme’s evidence distance between two BPA is defined as:

$$d(m_{1} ,m_{2} ) = \sqrt {\frac{1}{2}(\vec{m}_{1} - \vec{m}_{2} )^{t} \underline{\underline{D}} (\vec{m}_{1} - \vec{m}_{2} )} ,$$

(6)

where $\vec{m}_{1}$ and $\vec{m}_{2}$ be the BPAs in vector form. The matrix $\underline{\underline{D}}$ in Eq. (6) is the Jaccard’s matrix of order $2^{N} \times 2^{N}$ where the entries $\underline{\underline{D}} (H_{i} ,H_{j} )$ are the Jaccard’s similarity coefficient defined as:

$$\underline{\underline{D}} (H_{i} ,H_{j} ) = \frac{{\left| {H_{i} \cap H_{j} } \right|}}{{\left| {H_{i} \cup H_{j} } \right|}};\quad \forall \, H_{i} ,H_{j} \in 2^{X}$$

(7)

Definition 9

(Jiang [12]). The correlation coefficient measure between two basic probability assignment $m_{1}$ and $m_{2}$ is defined as:

$$r(m_{1} ,m_{2} ) = \frac{{c(m_{1} ,m_{2} )}}{{\sqrt {c(m_{1} ,m_{1} )} \sqrt {c(m_{2} ,m_{2} )} }},$$

(8)

where

$$c(m_{1} ,m_{2} ) = \sum\limits_{i = 1}^{{2^{N} - `1}} {\sum\limits_{j = 1}^{{2^{N} - 1}} {m_{1} (H_{i} )m_{2} (H_{j} ) \times \frac{{|H_{i} \cap H_{j} |}}{{|H_{i} \cup H_{j} |}}} }$$

(9)

Definition 10

(Pan and Deng [29]). The association coefficient between $m_{1}$ and $m_{2}$ is defined as:

$$a_{BPA} (m_{1} ,m_{2} ) = \frac{{r(m_{1} ,m_{2} )}}{{\frac{1}{2}\{ r(m_{1} ,m_{1} ) + r(m_{2} ,m_{2} )\} }},$$

(10)

where

$$r(m_{1} ,m_{2} ) = \sum\limits_{i = 1}^{{2^{N} - 1}} {\sum\limits_{j = 1}^{{2^{N} - 1}} {m_{1} (H_{i} )m_{2} (H_{j} ) \times \left( {\frac{{2^{{|H_{i} \cap H_{j} |}} - 1}}{{2^{{|H_{i} |}} - 1}}} \right)} } \times \left( {\frac{{2^{{|H_{i} \cap H_{j} |}} - 1}}{{2^{{|H_{j} |}} - 1}}} \right)\quad {\text{or}}\quad r(m_{1} ,m_{2} ) = \vec{m}_{1}^{t} D_{d} \vec{m}_{2}$$

(11)

where $\left| {H_{i} } \right|$ denotes the cardinality of the subset $H_{i}$, and $D_{d}$ is the positive-definite matrix of order $(2^{N} - 1) \times (2^{N} - 1)$ whose elements are given by

$$D_{d} (H_{i} ,H_{j} ) = \left( {\frac{{2^{{\left| {H_{i} \cap H_{j} } \right|}} - 1}}{{2^{{\left| {H_{i} } \right|}} - 1}}} \right) \times \left( {\frac{{2^{{\left| {H_{i} \cap H_{j} } \right|}} - 1}}{{2^{{\left| {H_{j} } \right|}} - 1}}} \right)$$

(12)

3.2 Proposed association coefficient measure

Let $m_{1}$ and $m_{2}$ denotes the BPAs in the FOD $X$ consisting of $N$ elements. The association coefficient measure between $m_{1}$ and $m_{2}$ is defined as:

$a(m_{1} ,m_{2} ) = \frac{{r(m_{1} ,m_{2} )}}{{\frac{1}{2}\{ r(m_{1} ,m_{1} ) + r(m_{2} ,m_{2} )\} }},$ where

$$\begin{aligned}r(m_{1} ,m_{2} ) &= \sum\limits_{i = 1}^{{2^{N} - 1}} {\sum\limits_{j = 1}^{{2^{N} - 1}} {m_{1} (H_{i} )m_{2} (H_{j} ) } } \\ &\quad \times \frac{{(2^{{|H_{i} \cap H_{j} |}} - 1)^{3} }}{{(2^{{|H_{i} |}} - 1)(2^{{|H_{j} |}} - 1)(2^{{|H_{i} \cup H_{j} |}} - 1)}}\end{aligned}$$

(14)

which can also be expressed as $r(m_{1} ,m_{2} ) = m_{1} (H_{i} )Dm_{2} (H_{j} )$ with the similarity index as follows:

$$D(H_{i} ,H_{j} ) = \frac{{(2^{{|H_{i} \cap H_{j} |}} - 1)^{3} }}{{(2^{{|H_{i} |}} - 1)(2^{{|H_{j} |}} - 1)(2^{{|H_{i} \cup H_{j} |}} - 1)}},$$

(15)

where $D$ is a positive-definite matrix of order $(2^{N} - 1) \times (2^{N} - 1)$ can be expressed as the product of the invertible matrix and its transpose i.e.,$D = Q^{t} Q$.

3.3 Properties

The proposed association coefficient measure $a(m_{1} ,m_{2} )$ between two distinct belief functions will holds the following properties:

• 1. $a(m_{1} ,m_{2} ) = a(m_{2} ,m_{1} )$

• 2. $0 \le a(m_{1} ,m_{2} ) \le 1$

• 3. $m_{1} = m_{2} \Leftrightarrow a(m_{1} ,m_{2} ) = 1$

• 4. $a(m_{1} ,m_{2} ) = 0 \Leftrightarrow H_{i} \cap H_{j} = \phi$ for all $H_{i} ,H_{j} \in 2^{X}$

• (1) Proof:

  Suppose the two pieces of evidences $m_{1}$ and $m_{2}$ are in vector form as follows:

  $$\vec{m}_{1} = \left( {\begin{array}{*{20}l} {m_{1} (H_{1} )} \hfill & {m_{1} (H_{2} )} \hfill & \ldots \hfill & {m_{1} (H_{{2^{N} }} )} \hfill \\ \end{array} } \right)^{t} ,\quad \vec{m}_{2} = \left( {\begin{array}{*{20}l} {m_{2} (H_{1} )} \hfill & {m_{2} (H_{2} )} \hfill & \ldots \hfill & {m_{2} (H_{{2^{N} }} )} \hfill \\ \end{array} } \right)^{t} .$$

By definition of association coefficient measure, we have

$$a(m_{1} ,m_{2} ) = \frac{{r(m_{1} ,m_{2} )}}{{\frac{1}{2}\{ r(m_{1} ,m_{1} ) + r(m_{2} ,m_{2} )\} }}$$

It is sufficient to proof that $r(m_{1} ,m_{2} )$ is symmetric i.e., $r(m_{1} ,m_{2} ) = \, r(m_{2} ,m_{1} )$. We have

$$\begin{aligned} r(m_{1} ,m_{2} ) & = \sum\limits_{i = 1}^{{2^{N} - 1}} {\sum\limits_{j = 1}^{{2^{N} - 1}} {m_{1} (H_{i} )m_{2} (H_{j} ) \times \frac{{(2^{{|H_{i} \cap H_{j} |}} - 1)^{3} }}{{(2^{{|H_{i} |}} - 1)(2^{{|H_{j} |}} - 1)(2^{{|H_{i} \cup H_{j} |}} - 1)}}} } \\ & = \sum\limits_{i = 1}^{{2^{N} - 1}} {\sum\limits_{j = 1}^{{2^{N} - 1}} {m_{1} (H_{j} )m_{2} (H_{i} ) \times \frac{{(2^{{|H_{i} \cap H_{j} |}} - 1)^{3} }}{{(2^{{|H_{i} |}} - 1)(2^{{|H_{j} |}} - 1)(2^{{|H_{i} \cup H_{j} |}} - 1)}}} } = \, r(m_{2} ,m_{1} ) \\ & \Rightarrow a(m_{1} ,m_{2} ) = a(m_{2} ,m_{1} ) \\ \end{aligned}$$

Therefore, the proposed association coefficient measure is symmetric.

Before proceeding for the proof of properties 2 and 3, we first put forward the statement of the Cauchy–Schwartz triangular inequality for any two nonzero vectors.

Lemma 3.1

For any two vectors $\vec{x} \ne 0$ and $\vec{y} \ne 0$ satisfies the inequality $\left\| {x + y} \right\| \le \left\| x \right\| + \left\| y \right\|$, where $\vec{x} = (x_{1} ,x_{2} ,...,x_{n} )^{t}$ and $\vec{y} = (y_{1} ,y_{2} ,...,y_{n} )^{t}$. The inequality holds equality iff $x$ is scalar multiple of $y$.

• (2) Proof:

  From Cauchy–Schwarz triangle inequality of two nonzero vectors of BPA, we have

  $$\begin{aligned} & \left\| {Q(m_{1} + m_{2} )} \right\|^{2} = \left( {\left\| {Qm_{1} } \right\| + \left\| {Qm_{2} } \right\|} \right)^{2} \\ & \quad \Rightarrow (Q(m_{1} + m_{2} ))^{t} (Q(m_{1} + m_{2} )) \le \left( {\sqrt {m_{1}^{t} Q^{t} Cm_{1} } + \sqrt {m_{2}^{t} Q^{t} Qm_{2} } } \right)^{2} \\ & \quad \Rightarrow (m_{1} + m_{2} )^{t} Q^{t} Q(m_{1} + m_{2} ) \le m_{1}^{t} Q^{t} Qm_{1} \\&\quad + m_{2}^{t} Q^{t} Qm_{2} + 2\sqrt {m_{1}^{t} Q^{t} Qm_{1} } \cdot \sqrt {m_{2}^{t} Q^{t} Qm_{2} } \\ & \quad \Rightarrow m_{1}^{t} Q^{t} Qm_{2} \le \sqrt {m_{1}^{t} Q^{t} Qm_{1} } \sqrt {m_{2}^{t} Q^{t} Qm_{2} } \le \frac{{(m_{1}^{t} Q^{t} Qm_{1} ) + (m_{2}^{t} Q^{t} Qm_{2} )}}{2} \\ & \quad \Rightarrow \, \frac{{2m_{1}^{t} Q^{t} Qm_{2} }}{{(m_{1}^{t} Q^{t} Qm_{1} ) + (m_{2}^{t} Q^{t} Qm_{2} )}} \, \le \, 1 \\ & \quad \Rightarrow \, a(m_{1} ,m_{2} ) \le 1 \\ \end{aligned}$$

Since all the BPAs $m_{1} (H_{i} ),m_{2} (H_{i} ) \ge 0$ and $D$ positive definite matrix, we have $a(m_{1} ,m_{2} ) \ge 0$. Therefore, the degree of association lies in the interval $\left[ {0,1} \right]$ i.e.,$0 \le a(m_{1} ,m_{2} ) \le 1$.

• (3) Proof:

  We have, $a(m_{1} ,m_{2} ) = 1$

  $$\begin{aligned} & \Rightarrow \, \frac{{r(m_{1} ,m_{2} )}}{{\frac{1}{2}\{ r(m_{1} ,m_{1} ) + r(m_{2} ,m_{2} )\} }} = 1 \\ & \quad \Rightarrow \, m_{1}^{t} Q^{t} Qm_{2} = \frac{1}{2}\{ m_{1}^{t} Q^{t} Qm_{1} + m_{2}^{t} Q^{t} Qm_{2} \} \quad (\because \, D_{pro} = Q^{t} Q) \\ & \quad \Rightarrow { (}Qm_{1} )^{t} Qm_{2} = \frac{1}{2}\{ (Qm_{1} )^{t} Qm_{1} + (Qm_{2} )^{t} Qm_{2} \} \\ & \quad \Rightarrow { ||}Q(m_{1} + m_{2} )|| = \frac{1}{2}\left\{ {||Qm_{1} || + ||Qm_{2} ||} \right\} \le \left\| {Qm_{1} } \right\| + \left\| {Qm_{2} } \right\| \\ \end{aligned}$$

which holds equality (according to Lemma 3.1) if $Qm_{1} = kQm_{2}$. Since $Q$ is an invertible matrix implies $m_{1} = km_{2}$, where $k$ is any scalar quantity. Therefore, $a(m_{1} ,m_{2} ) = 1 \Leftrightarrow m_{1} = m_{2}$.

• (4) Proof:

  Let us assume $a(m_{1} ,m_{2} ) = 0$ for any two BPAs $m_{1}$ and $m_{2}$, we have

  $$\begin{aligned} & \Rightarrow \, \frac{{r(m_{1} ,m_{2} )}}{{\frac{1}{2}\{ r(m_{1} ,m_{1} ) + r(m_{2} ,m_{2} )\} }} = 0 \\ & \quad \Rightarrow \sum\limits_{i = 1}^{{2^{N} - 1}} {\sum\limits_{j = 1}^{{2^{N} - 1}} {m_{1} (H_{i} )m_{2} (H_{j} ) \times \frac{{(2^{{|H_{i} \cap H_{j} |}} - 1)^{3} }}{{(2^{{|H_{i} |}} - 1)(2^{{|H_{j} |}} - 1)(2^{{|H_{i} \cup H_{j} |}} - 1)}}} } = 0 \\ & \quad \Rightarrow \, \frac{{(2^{{|H_{i} \cap H_{j} |}} - 1)^{3} }}{{(2^{{|H_{i} |}} - 1)(2^{{|H_{j} |}} - 1)(2^{{|H_{i} \cup H_{j} |}} - 1)}} = 0 \\ \end{aligned}$$

If both $m_{1} (H_{i} ) > 0$ and $m_{2} (H_{j} ) > 0$ so that $m_{1} (H_{i} )m_{2} (H_{j} ) \ne 0$, then it must follow

$$=> \, |H_{i} \cap H_{j} | = 0$$

$$=>\,H_i\cap H_j=\phi,\quad\forall\,H_i,H_j\in2^X.$$

i.e., $a_{BPA} (m_{1} ,m_{2} ) = 0 \Leftrightarrow H_{i} \cap H_{j} = \phi$ for all $H_{i} ,H_{j} \in 2^{X}$.

If the distance measure between two BPAs is zero, then BPAs are identical whereas if distance measure is one, they are completely distinct or doesn’t support to each other. The increase in degree of association effects in the decrease of the distance measure between the two evidences. Based on this distance principle, the conflict coefficient measure between two distinct BPAs based on new association coefficient measure is defined as follows:

$$C(m_{1} ,m_{2} ) = 1 - a(m_{1} ,m_{2} ),$$

(16)

where $C(m_{1} ,m_{2} )$ in Eq. (16) represents the conflict coefficient measure between two BPAs. The proposed association coefficient measure is based on the new similarity index where the similarity between two sets is estimated from ratio of the common element to the product of non-trivial power set of two set and nontrivial power set of its union respectively.

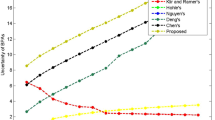
For any two sets $A = \{ x_{1} \}$(fixed) and another with variable set $B = \{ x_{1} \}$,$\{ x_{1} ,x_{2} \}$,…,$\{ x_{1} ,x_{2} ...,x_{10} \}$, the similarity index is observed and compared with the similarity index given by Eqs. (9) to (12) that used in [12] and [29]. In Fig. 1, it is seen that the convergence of association of the all the decreases with the increasing $B$ and the proposed coefficient measure is speed convergence in reflecting the association between two sets than the other similarity index.

Fig. 1

Comparison of association degree between two sets that used in [12] and [29]

The validity of the conflict coefficient measure based on the proposed association coefficient measure is discussed with some numerical examples.

Example 2

Consider the set $X = \{ 1,2,3,4\}$ as the frame of discernment and the BPAs are as follows:

$m_{1} (\{ 1\} ) = 0.4,\;m_{1} (\{ 2\} ) = 0.6,\;m_{1} (\{ 3\} ) = 0,\;m_{1} (\{ 4\} ) = 0.$

$$m_{2} (\{ 1\} ) = 0,\;m_{2} (\{ 2\} ) = 0,\;m_{2} (\{ 3\} ) = 0.7,\;m_{2} (\{ 4\} ) = 0.3.$$

$$m_{3} (\{ 1\} ) = 0.30,\;m_{3} (\{ 2\} ) = 0.25,\;m_{3} (\{ 3\} ) = 0.25,\;m_{3} (\{ 4\} ) = 0.20.$$

$$m_{4} (\{ 1\} ) = 0.30,\;m_{4} (\{ 2\} ) = 0.25,\;m_{4} (\{ 3\} ) = 0.25,\;m_{4} (\{ 4\} ) = 0.20.$$

In this example, the BPAs $m_{1}$ supports the event $(\{ 2\} )$ whereas $m_{2}$ is in favour of the event $(\{ 3\} )$ which is conflicting to each other. In Table 2, it has been seen that the Jousselme’s evidence distance between $m_{1}$ and $m_{2}$ is 0.7416 which is not much reasonable as the BPAs are completely counter intuitive to each other. The rest of the conflict coefficient other than Jousselme’s distance is 1 for the evidence $m_{1}$ and $m_{2}$.

Table 2 Conflict coefficient measure of different measures.

Table 3 Focal elements with variable BPA and fixed BPA

In case of $m_{3}$ and $m_{4}$, the Dempster’s conflict coefficient is 0.745 which is again not reasonable as the evidence are identical while all the other conflicts are zero. Therefore, since $m_{1} \ne m_{2}$ and $m_{3} = m_{4}$ the respective BPAs satisfies the property of extreme conflict coefficients by the proposed association coefficient measure.

Example 3

Let $F = \{ x_{1} ,x_{2} ,x_{3} \}$ be the frame of discernment and two basic probability assignments for the bodies of evidence with $0 < a < 1$_, respectively are as follows.

In Table 3, consider two BPAs where $m_{2}$ is fixed real number and $m_{1}$ depends on the values of $a$. Here, the association coefficient measure is increases with the increasing value of $a$ which seems that the proposed association coefficient is logical for representing the association between two evidences. The association coefficient measure $a(m_{1} ,m_{2} )$ between $m_{1}$ and $m_{2}$ is given by the Eq. (17) and shown in Fig. 2 below:

$$a(m_{1} ,m_{2} ) = \frac{8889a + 1111}{{8889a^{2} - 8889a + 10000}}$$

(17)

Fig. 2

The association coefficient when one BPA changes with parameter a while the other is fixed

Example 4

Let $F = \{ x_{1} ,x_{2} ,x_{3} \}$ be the frame of discernment and two basic probability assignment for the bodies of evidence with $0 < a < 1$ and $0 < b < 1$_, respectively are as follows (Table 4).

Table 4 Focal elements with two BPA depends upon the different parameters

The Example 4 deals with the case where the evidence $m_{1}$ depends on the change of the parameter $a$ and $m_{2}$ depends on the parameter $b$ respectively. For different values of the parameters $a$ and $b$, the surface of the association coefficient measure between the belief functions $m_{1}$ and $m_{2}$ is given by the Eq. (18) and shown in the Fig. 3 below:

$$a(m_{1} ,m_{2} ) = \frac{2(1633a - 1837)(b - 1)}{{8889a^{2} - 8889a + 9796b^{2} - 9796b + 10000}}$$

(18)

Fig. 3 

The association coefficient where both the BPAs are vary with two different parameters

Example 5

Let $F = \{ x_{1} ,x_{2} ,x_{3} \}$ be the frame of discernment and two basic probability assignment for the bodies of evidence with $0 < a < 1$, $0 < b < 1$ and $a + b = 1$_, respectively are as follows (Table 5).

Table 5 Focal elements with fixed BPA and other varies with two parameters

In the Example 3, the BPA $m_{1}$ assigns fixed real number for all the focal elements and $m_{2}$ depends on the variables $a$ and $b$. The behaviour of the association coefficient measure between the BPAs $m_{1}$ and $m_{2}$ is shown in the Fig. 4 .

Fig. 4

The association coefficient with one BPA is fixed while the other depends upon the two parameters

Example 6

Consider $X = \{ 1,2,...,12\}$ be a FOD. The BPAs $m_{1}$ and $m_{2}$ for the focal elements are given by

$$m_{1} (\{ 1,2,3\} ) = 0.05,\;m_{1} (\{ 7\} ) = 0.05,\;m_{1} (A) = 0.8,\;m_{1} (X) = 0.1$$

$$m_{2} (\{ 1,2,...,5\} ) = 1$$

In this example, consider a set $A$ whose elements varies from {1}, {1, 2},…{1,2,…,12} respectively. The conflict coefficient between the couple of BPAs are measured from the Eqs. (5) to (15) with the changing behaviour of $A$.

We have noticed in Table 6 that the conflict coefficient between $m_{1}$ and $m_{2}$ changes with the variable set $A = \{ 1\}$ to $A = \{ 1,2,...,12\}$. The degree of conflict attains its minimum value for $A = \{ 1,2,...,5\}$ and increased with the addition of elements in $A$. The proposed association coefficient is also changing its pattern with the change in $A$ with high association coefficient degree than others. However, Dempster’s conflict coefficient degree remains constant for all $A$. The comparative analysis of the conflict coefficient of the existing functions is shown in the Fig. 5 below.

Table 6 Comparisons with the existing conflicts measurement

Fig. 5

Comparison of conflicts when the behaviour of A changes

4 Application in medical diagnosis decision making

In this section, we have implemented the association coefficient measure in order to determine the modified initial mass function of the decision alternatives from the dataset that put forward in the existing paper [3, 22].

4.1 Methodology and algorithm

Consider E be the universal set of parameters consists of two sets of decision parameters $A = \{ e_{1} ,e_{2} ,...,e_{m} \}$ and $B = \{ f_{1} ,f_{2} ,...,f_{n} \}$, where $A$ be the set of the symptoms and $B$ stands for the decision-making tools other than symptoms. The building steps for the generation of the basic probability assignment for the diseases $X = \{ x_{1} ,x_{2} ,...,x_{k} \}$ are as follows.

Step 1: Construct the fuzzy soft sets $(f,A)$ and $(g,B)$ represents the symptoms and decision-making tools of the disease such that

$$f(e_{M} ) = \left\{ {\frac{{x_{k} }}{{u_{ki} }}:u_{ki} \in [0,1]; \, i = 1,2,...,m} \right\}\quad {\text{and}}\quad g(s_{j} ) = \left\{ {\frac{{x_{k} }}{{v_{kj} }}:\nu_{kj} \in [0,1]; \, j = 1,2,...,n} \right\},$$

for $k = 1,2,...,p$ and $u_{ki} ,\nu_{kj}$ are the membership degree of $x_{k}$ for the parameters $e_{i}$ and $s_{j}$ respectively. In the matrix form, we have

$$\begin{gathered}\begin{array}{*{20}c} {\qquad\qquad\quad\,\,\, e_{1} } & { \,\, e_{2} } & \,\ldots & { \, e_{m} } \hfill \\ \end{array} \, \begin{array}{*{20}c} {\qquad\qquad\qquad\qquad\,\,\, s_{1} } \hfill & {\,s_{2} } \hfill & { \,\, \ldots } \hfill & {\,s_{n} } \hfill \\ \end{array} \hfill \\ (F,A) = \begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ \vdots \hfill \\ {x_{k} } \hfill \\ \end{array} \left[ {\begin{array}{*{20}l} {u_{11} } \hfill & {u_{12} } \hfill & \ldots \hfill &{u_{1m} } \hfill \\ {u_{21} } \hfill & {u_{22} } \hfill &\ldots \hfill & {u_{2m} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {u_{k1} } \hfill & {u_{k2} } \hfill & \ldots \hfill & {u_{km} } \hfill \\ \end{array} } \right]{\text{ and (}}G,B{)} = \begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ \vdots \hfill \\ {x_{k} } \hfill \\ \end{array} \left[ {\begin{array}{*{20}l} {v_{11} } \hfill & {v_{12} } \hfill & \ldots \hfill & {v_{1n} } \hfill \\ {v_{21} } \hfill & {v_{22} } \hfill & \ldots \hfill & {v_{2n} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {v_{k1} } \hfill & {v_{k2} } \hfill & \ldots \hfill & {v_{kn} } \hfill \\ \end{array} } \right] \hfill \\ \end{gathered}$$

Step 2: Construct the matrix $M = [c_{ij} ]_{k \times t}$, where $c_{ij}$ be the joint membership degree of $x_{i}$ for $t = mn$ possible parameters formed by $e_{i}$ and $s_{j}$ as follows:

$$\begin{gathered} \hfill \\ \, \begin{array}{*{20}l} {\qquad\qquad p_{1} } \hfill & {\,p_{2} } \hfill & \,\ldots \hfill & {p_{t} } \hfill \\ \end{array} \hfill \\ M = \begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ \vdots \hfill \\ {x_{k} } \hfill \\ \end{array} \left[ {\begin{array}{*{20}l} {c_{11} } \hfill & {c_{12} } \hfill &\ldots \hfill & {c_{1t} } \hfill \\ {c_{21} } \hfill &{c_{22} } \hfill &\ldots \hfill & {c_{2t} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {c_{k1} } \hfill &{c_{k2} } \hfill &\ldots \hfill & {c_{kt} } \hfill \\ \end{array} } \right] \hfill \\ \end{gathered}$$

where $c_{ij} = \min (u_{ij} ,v_{ij} )$, and the information structure image matrix $\widetilde{M} = [\tilde{c}_{ij} ]_{k \times t}$ is defined as:

$$\begin{gathered} \begin{array}{*{20}l} {\qquad\qquad \,p_{1} } \hfill & {\,p_{2} } \hfill &\,\ldots \hfill &{p_{t} } \hfill \\ \end{array} \hfill \\ M = \begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ \vdots \hfill \\ {x_{k} } \hfill \\ \end{array} \left[ {\begin{array}{*{20}l} {\tilde{c}_{11} } \hfill & {\tilde{c}_{12} } \hfill & \ldots \hfill & {\tilde{c}_{1t} } \hfill \\ {\tilde{c}_{21} } \hfill &{\tilde{c}_{22} } \hfill & \ldots \hfill & {\tilde{c}_{2t} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\tilde{c}_{k1} } \hfill & {\tilde{c}_{k2} } \hfill & \ldots \hfill & {\tilde{c}_{kt} } \hfill \\ \end{array} } \right] \hfill \\ \end{gathered}$$

Step 3: Build $t$ pieces of initial BPAs defined as follows:

$$\begin{array}{*{20}l} {m_{1} \{ x_{1} \} = \tilde{c}_{11} ,} \hfill & {m_{1} \{ x_{2} \} = \tilde{c}_{21} ,} \hfill & \ldots \hfill & {m_{1} \{ x_{j} \} = \tilde{c}_{j1} ,} \hfill & \ldots \hfill & {m_{1} \{ x_{k} \} = \tilde{c}_{k1} } \hfill \\ {m_{2} \{ x_{1} \} = \tilde{c}_{12} ,} \hfill & {m_{2} \{ x_{2} \} = \tilde{c}_{22} } \hfill & \ldots \hfill & {m_{2} \{ x_{j} \} = \tilde{c}_{j2} ,} \hfill & \ldots \hfill & {m_{2} \{ x_{k} \} = \tilde{c}_{k2} } \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & {} \hfill & \vdots \hfill & \vdots \hfill \\ {m_{i} \{ x_{1} \} = \tilde{c}_{1i} ,} \hfill & {m_{i} \{ x_{2} \} = \tilde{c}_{2i} ,} \hfill & \ldots \hfill & {m_{i} \{ x_{j} \} = \tilde{c}_{ji} ,} \hfill & \ldots \hfill & {m_{i} \{ x_{k} \} = \tilde{c}_{ki} } \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & {} \hfill & \vdots \hfill & \vdots \hfill \\ {m_{t} \{ x_{1} \} = \tilde{c}_{1t} } \hfill & {m_{t} \{ x_{2} \} = \tilde{c}_{2t} } \hfill & \ldots \hfill & {m_{t} \{ x_{j} \} = \tilde{c}_{jt} } \hfill & \ldots \hfill & {m_{t} \{ x_{k} \} = \tilde{c}_{kt} } \hfill \\ \end{array}$$

Step 4: The association coefficient matrix of the body of evidence is defined as:

$$\begin{gathered} \begin{array}{*{20}c} { \qquad\qquad m_{1} } & {\,m_{2} } & {\,...} & {\,m_{t} } \\ \end{array} \hfill \\ A = \begin{array}{*{20}c} {m_{1} } \\ {m_{1} } \\ \vdots \\ {m_{t} } \\ \end{array} \left[ {\begin{array}{*{20}c} 1 &{a_{12} } & {...} & {a_{1t} } \\ {a_{21} } & 1 & {...} & {a_{2t} } \\ { \, \vdots } & { \, \vdots } & \ddots & { \, \vdots } \\ {a_{t1} } & {a_{t2} } & {...} &1 \\ \end{array} } \right],\quad {\text{where}}\;a_{ij} = a(m_{i} ,m_{j} ). \hfill \\ \end{gathered}$$

Step 5: The support degree $Sup(m_{i} )$ and credibility degree $Crd(m_{i} )$ of any $m_{i}$ is defined as:

$$Sup(m_{i} ) = \sum\limits_{j = 1,j \ne i}^{n} {a(m_{i} ,m_{j} )} \quad {\text{and}}\quad Crd(m_{i} ) = \frac{{Sup(m_{i} )}}{{\sum\limits_{i = 1}^{n} {Sup(m_{i} )} }},$$

where $Crd(m_{i} )$ is the weight of the evidence, and $\sum\nolimits_{i = 1}^{n} {Crd(m_{i} )} = 1$ implies that the BPAs are evident.

Step 6: The weighted average mass WAM(m) of the evidences $m_{i}$ is given by

$$WAM(m) = \sum\limits_{i = 1}^{n} {crd(m_{i} ) \times m_{i} }$$

Step 7: Finally, WAM(m) is combined for $(n - 1)$ times by Dempster’s combination rule and rank the decision alternatives based on the final belief measure.

4.2 Case study in medical diagnosis

In the diagnostic support system, we take the case study that put forward in [3, 22], a patient is under observation have noticed some symptoms among the several symptoms $s_{1}$—fever, $s_{2}$—running nose, $s_{3}$—weakness, $s_{4}$—oro-facial pain, $s_{5}$-nausea or vomiting, $s_{6}$—swelling, $s_{7}$—trismus etc. A decision-maker assessed the patient based the three symptoms $s_{1}$, $s_{2}$ and $s_{4}$ with decision-making tools $h$—history, $p$—physical examination, $l$—lab investigation etc. Consider $X = \{ x_{1} ,x_{2} ,x_{3} ,x_{4} \}$ be the set of possible disease associated with the symptoms, where $x_{1}$, $x_{2}$, $x_{3}$ and $x_{4}$ stands for the disease Acute dental abscess, Migraine, Acute sinusitis and Peritonsillar abscess respectively.

Let $E$ be the set of parameters formed by the symptoms and decision-making tools with $A = \{ s_{1} ,s_{2} ,...,s_{7} \}$ represents the set of symptoms and $B = \{ h,p,l\}$ be the decision-making tools of diseases such that

$$(f,A) = \{ f(s_{1} ),f(s_{2} ),...,f(s_{7} )\} \quad {\text{and}}\quad (g,B) = \{ g(h), \, g(p), \, g(l)\} .$$

be the fuzzy soft set whose membership degree is given in the Tables 7 and 8 respectively.

Table 7 Tabular representation $(f,A)$ for symptoms

Table 8 Tabular representation $(g,B)$ for decision-making tools

The patient is suffered from a disease and assessed based on the symptoms fever, running noise, facial pain. Thus, patient’s symptoms and decision-making tool forms the nine possible pairs of parameters or evidence as $(s_{1} ,h)$, $(s_{1} ,p)$, $(s_{1} ,l)$, $(s_{2} ,h)$, $(s_{2} ,p)$, $(s_{2} ,l)$, $(s_{4} ,h)$, $(s_{4} ,p)$, $(s_{4} ,l)$ respectively. Consider $X = \{ x_{1} ,x_{2} ,x_{3} ,x_{4} \}$ be the set of four diseases as the frame of discernment and their assessment is obtained as shown in Table 9.

Table 9 Tabular forms of pairs of symptom and decision-making tool $(F,A) \wedge (G,B)$

The initial BPAs $m_{j}^{in}$ can be generated from the parameters according as in Step 1–3 and arranged as follows:

$(s_{1} ,h):$ $m_{1}^{in} (\{ x_{1} \} ) = 0.40$, $m_{1}^{in} (\{ x_{2} \} ) = 0.1333$, $m_{1}^{in} (\{ x_{3} \} ) = 0.20$, $m_{1}^{in} (\{ x_{4} \} ) = 0.2667$.

$(s_{1} ,p):$ $m_{2}^{in} (\{ x_{1} \} ) = 0.40$, $m_{2}^{in} (\{ x_{2} \} ) = 0.1333$, $m_{2}^{in} (\{ x_{3} \} ) = 0.20$, $m_{2}^{in} (\{ x_{4} \} ) = 0.2667$.

$(s_{1} ,l):$ $m_{3}^{in} (\{ x_{1} \} ) = 0.3333$, $m_{3}^{in} (\{ x_{2} \} ) = 0.1667$, $m_{3}^{in} (\{ x_{3} \} ) = 0.25$, $m_{3}^{in} (\{ x_{4} \} ) = 0.25$.

$(s_{2} ,h):$ $m_{4}^{in} (\{ x_{1} \} ) = 0$, $m_{4}^{in} (\{ x_{2} \} ) = 0$, $m_{4}^{in} (\{ x_{3} \} ) = 1$, $m_{4}^{in} (\{ x_{4} \} ) = 0$.

$(s_{2} ,p):$ $m_{5}^{in} (\{ x_{1} \} ) = 0$, $m_{5}^{in} (\{ x_{2} \} ) = 0$, $m_{5}^{in} (\{ x_{3} \} ) = 1$, $m_{5}^{in} (\{ x_{4} \} ) = 0$.

$(s_{2} ,l):$ $m_{6}^{in} (\{ x_{1} \} ) = 0$, $m_{6}^{in} (\{ x_{2} \} ) = 0$, $m_{6}^{in} (\{ x_{3} \} ) = 1$, $m_{6}^{in} (\{ x_{4} \} ) = 0$.

$(s_{4} ,h):$ $m_{7}^{in} (\{ x_{1} \} ) = 0.2143$, $m_{7}^{in} (\{ x_{2} \} ) = 0.2857$, $m_{7}^{in} (\{ x_{3} \} ) = 0.2857$, $m_{7}^{in} (\{ x_{4} \} ) = 0.2143$.

$(s_{4} ,p):$ $m_{8}^{in} (\{ x_{1} \} ) = 0.3636$, $m_{8}^{in} (\{ x_{2} \} ) = 0.1364$, $m_{8}^{in} (\{ x_{3} \} ) = 0.1818$, $m_{8}^{in} (\{ x_{4} \} ) = 0.3182$.

$(s_{4} ,l):$ $m_{9}^{in} (\{ x_{1} \} ) = 0.20$, $m_{9}^{in} (\{ x_{2} \} ) = 0.30$, $m_{9}^{in} (\{ x_{3} \} ) = 0.35$, $m_{9}^{in} (\{ x_{4} \} ) = 0.15$.

The association coefficient measure between any two BPAs is obtained based on the step 4 and the association coefficient matrix whole set of evidence is given by

$$\begin{gathered} \, \begin{array}{*{20}l} {\qquad\qquad\quad m_{1} } \hfill & { \quad\,\, m_{2} } \hfill & {\quad\,\,\,\, m_{3} } \hfill & {\quad\,\,\,\,m_{4} } \hfill & {\quad\,\,\,\, m_{5} } \hfill & {\quad\,\,\,\, m_{6} } \hfill & {\quad\,\,\,\, m_{7} } \hfill & {\quad\,\,\,\, m_{8} } \hfill & {\quad\,\,\,\, m_{9} } \hfill \\ \end{array} \hfill \\ A = \begin{array}{*{20}l} {m_{1} } \hfill \\ {m_{2} } \hfill \\ {m_{3} } \hfill \\ {m_{4} } \hfill \\ {m_{5} } \hfill \\ {m_{6} } \hfill \\ {m_{7} } \hfill \\ {m_{8} } \hfill \\ {m_{9} } \hfill \\ \end{array} \left[ {\begin{array}{*{20}c} 1 & 1 & {0.{9849}} & {0.{31}0{3}} & {0.{31}0{3}} & {0.{31}0{3}} & {0.{8754}} & {0.{9925}} & {0.{8157}} \\ 1 & 1 & {0.{9849}} & {0.{31}0{3}} & {0.{31}0{3}} & {0.{31}0{3}} & {0.{8754}} & {0.{9925}} & {0.{8157}} \\ {0.{9849}} & {0.{9849}} & 1 & {0.{3956}} & {0.{3956}} & {0.{3956}} & {0.{94}0{5}} & {0.{9797}} & {0.{8969}} \\ {0.{31}0{3}} & {0.{31}0{3}} & {0.{3956}} & 1 & 1 & 1 & {0.{4553}} & {0.{2829}} & {0.{549}0} \\ {0.{31}0{3}} & {0.{31}0{3}} & {0.{3956}} & 1 & 1 & 1 & {0.{4553}} & {0.{2829}} & {0.{549}0} \\ {0.{31}0{3}} & {0.{31}0{3}} & {0.{3956}} & 1 & 1 & 1 & {0.{4553}} & {0.{2829}} & {0.{549}0} \\ {0.{8754}} & {0.{8754}} & {0.{94}0{5}} & {0.{4553}} & {0.{4553}} & {0.{4553}} & 1 & {0.{8775}} & {0.{9836}} \\ {0.{9925}} & {0.{9925}} & {0.{9797}} & {0.{2829}} & {0.{2829}} & {0.{2829}} & {0.{8775}} & 1 & {0.{8}0{34}} \\ {0.{8157}} & {0.{8157}} & {0.{8969}} & {0.{549}0} & {0.{549}0} & {0.{549}0} & {0.{9836}} & {0.{8}0{34}} & 1 \\ \end{array} } \right] \hfill \\ \end{gathered}$$

Now, the support degree of BPAs and the corresponding credibility degrees are obtained based on the Step 5and is given below

$$\begin{aligned} & Sup(m_{1} ) = 5.5996,Sup(m_{2} ) = 5.5995,Sup(m_{3} ) = 5.9738,Sup(m_{4} ) = 4.3035,Sup(m_{5} ) = 4.3035, \\ & Sup(m_{6} ) = 4.3035,Sup(m_{7} ) = 5.9182,Sup(m_{8} ) = 5.4944,Sup(m_{9} ) = 5.9625 \\ \end{aligned}$$

and

$$\begin{aligned} & Crd(m_{1} ) = 0.1180,Crd(m_{2} ) = 0.1180,Crd(m_{3} ) = 0.1259,Crd(m_{4} ) = 0.0907,Crd(m_{5} ) = 0.0907, \\ & Crd(m_{6} ) = 0.0907,Crd(m_{7} ) = 0.1247,crd(m_{8} ) = 0.1158,Crd(m_{9} ) = 0.1256. \\ \end{aligned}$$

The weighted average mass of each alternative is obtained as shown in the Step 8 and, we have

$$m(\{ x_{1} \} ) = 0.2303,\;m(\{ x_{2} \} ) = 0.1415,\;m(\{ x_{3} \} ) = 0.4515,\;m(\{ x_{4} \} ) = 0.1768.$$

Finally, the WAM(m) of the alternatives are combined for eight times to itself by using Dempster’s combination rule and final belief measure for each alternative are obtained as shown below:

$Bel\left( {\{ x_{1} \} } \right) = 0.0023$, $Bel\left( {\{ x_{2} \} } \right) = 0.0000$, $Bel\left( {\{ x_{3} \} } \right) = 0.9974$ and $Bel\left( {\{ x_{4} \} } \right) = 0.0002$.

4.3 Comparison and results

From the final belief measure of the alternatives, the disease $x_{3}$ has the high degree of belief and we conclude that the patient has the high possibility of suffering from the disease $x_{3}$. However, in comparison to the existing method of Li et al. [22], Wang et al. [33] and Chen et al. [3],the belief measure of disease alternatives is shown in the Fig. 6and Table 10 below.

Fig. 6

Belief measures of alternatives from different methods

Table 10 Comparison of final belief measure top ranked alternatives with existing method

In Table 10, the ranking order of alternatives remains same with the high belief degree in support of disease $x_{3}$ and it is increases up to 0.9974 which is better performance than existing two methods [22, 33]. Also, the belief measure of $x_{3}$ is lower than the Chen et al. [3] method nevertheless the use of new association coefficient measure in proposed methodology makes the decision-process more reasonable.

5 Conclusion

Conflict management is an essential factor in appropriate decision-making in the evidence theory. In literature, various conflict measurement functions such as distance measure, similarity measure and association coefficient measure etc. are widely used to describe the significance in between two distinct evidences. To address the difficulties in the existing conflict coefficient and distance, we proposed a new association coefficient measure with desirable properties and some numerical examples to show its effectiveness. In this paper, proposed association coefficient is used in the construction of initial BPAs by using information structure image matrix, evaluating the weighted average mass and combined the mass by the Dempster’s rule of combination. Finally, the belief measure in medical diagnosis is analysed and compared with the existing related works.

In future direction, association coefficient measure may be used on the generalised fuzzy number such as Intuitionistic fuzzy number, Pythagorean fuzzy number and q-rung fuzzy number etc. in place of discrete number to handle the uncertainty more efficiently.