Interval Arithmetic Power Flow Analysis of Radial Distribution System with Probabilistic Load Model and Distributed Generation

Abstract

The variations in load and generation result in higher degree of uncertainty in power flow calculation and create new challenge for the system operator to develop new tools to assess the current and future state of the system. Therefore, the incorporation of the system uncertainties plays a vital role for sustainable planning of the power system. This paper demonstrates the combined application of the probabilistic and possibilistic approach to address line, load and distributed generation (DG) uncertainties in a radial distribution system. The uncertainty in load demand is represented as a Gaussian distribution function, whereas line and DG uncertainty are varied at a fixed proportion. The load is modelled as composite. Type I (penetrates real power), Type II (penetrates reactive power) and Type IV (penetrates both real and reactive power) DG are considered depending upon the type of power injected. The efficacy of improved power flow techniques with the inclusion of various types of DG and its effect on power losses is verified by four test cases on three IEEE test systems: 33-bus, 34-bus and 69-bus. The obtained results are compared to the possibilistic-only approach and found out to be superior. The convergence characteristic is also analysed at various degree of belongingness. The technique converges in smaller number of iterations as compared to other methods. The lower interval width signifies the numerical stability. The statistical analysis of power losses reduction with DG penetration is also carried out.

Introduction

Motivation

The distribution system is ill-conditioned because most of it is radial structure, low X/R ratio due to the smaller inductance of line and determinant of admittance matrix being small due to sparsity. Thus, the methods for solving power flow in the transmission system such as Newton–Raphson and Gauss–Seidel fail to converge, in most cases in a radial distribution system (RDS). Moreover, the deterministic power flow methods require precise values of generation and load to find bus voltage and power flows for only specific system configuration and operating conditions at a given instant and thus do not contribute to optimal planning and operation. Due to social, economic, technical and environmental concerns, the emphasis is to incorporate distributed generation (DG) in the power distribution system. At distribution level, DG serves as a small-scale power generation using renewable (wind, micro/mini/small hydropower, biomass, solar, etc.) or non-renewable (gas turbine, etc.) resources and technologies. The generation of these resources exhibits stochastic behaviour and introduces significant uncertainty in total power production. These uncertainties should be considered in future planning to meet the growing energy needs of the consumer, hence, grabbing the focus of the system operators towards sustainable development of the power system.

Real-world systems are complex due to its non-linearity and inability of the system to express its variables in precise terms whose complexity can be reduced by either making certain assumptions about the system or allowing some degree of uncertainty in its description. The propositions obtained from this simplified system are less precise but their relevance to the original system is fully maintained. In actual power grid operations, the input parameters (system line, load and transformer data) are assumed to be fixed but are practically uncertain. The uncertainty in system line data is because of an error in the estimation of resistance and reactance due to variation in temperature and ageing effects of conductors. The uncertainties in load data are because of an error in assumed load demand (load forecasting) due to unscheduled outages, uncertain load switching and change in status data of various protective devices. Uncertainty in hydropower is due to climate change and water runoff. The sensitivity to temperature brings uncertainty in a fuel cell as temperature variation has a greater effect at higher currents (Noorkami et al. 2014). This influences the analysis and subsequent results of the RDS.

Therefore, these uncertainties are modelled using either as a probabilistic or possibilistic approach. Monte Carlo simulation (MCS) and stochastic methods fall under the probabilistic domain, whereas fuzzy sets and Interval Arithmetic (IA) are possibilistic approaches. IA provides a strict bound of all plausible system conditions that could have been obtained by thousands of repeated MCS which increases the computation time considerably and makes the analysis difficult. IA is able to obtain good quality results with a lower computational effort. Probabilistic modelling is quantitative through stochastic randomness (Wang and Alvarado 1992) and is preferred where adequate historical information of uncertain parameter or their probability density function (PDF) is available such as load pattern, solar irradiation and wind speed (Aiena et al. 2014), whereas possibilistic modelling is qualitative in nature (Wang and Alvarado 1992) and is desirable when there is inadequate information for operators and planners to establish PDF of the variables such as line data, controllable gas turbine DG power output and battery charge in an electric vehicle (Aiena et al. 2014). Both approaches are cooperative and their use may lead to a more realistic approximation to system modelling.

Literature Review

The uncertainties in input parameters were first introduced in the power transmission system by Wang and Alvarado (1992) and in the distribution system by Das (2002). Effect of load uncertainties on the system’s performance is analysed in (Ersavas and Karatepe 2017). Vidovic and Saric (2017) developed a correlated interval-based backward/forward power flow algorithm to account uncertainties in renewable energy resources. To deal with uncertainties of the system a novel midpoint-radius interval-based algorithm is developed in (Marin et al. 2017), which eliminates the factorization of the interval Jacobian matrix. Wang et al. (2017) demonstrate the impact of intermittent energy sources and uncertainty in load on the power flow solution and found out to be superior in precision and computation aspects. To attain more realistic interval solutions, the interval-based power flow models are converted into the interval optimization problem in (Ding et al. 2015) which reduces the conservatism of the interval solutions. In (Pereira et al. 2012), the Krawczyk technique is presented for solving the interval power flow equations. An Affine Arithmetic approach is projected in (Vaccaro et al. 2010) to incorporate uncertainties. The proposed method is not dependent on the level and the types of uncertainties present in the system data. A probabilistic distribution-based IA method is simulated in (Chaturvedi et al. 2006) to incorporate load demand uncertainty in conventional power flow. Parihar and Malik (2017) projected the IA-based power flow analysis considering uncertainties in line and load data. Das (2009) proposed the application of IA to introduce fixed line and load uncertainties in the RDS considering voltage-dependent loads. A similar method is used in (Attari et al. 2015) to forecast accurate operational conditions of the distribution system considering input uncertainties. Wang et al. (2009) demonstrated an interval-based fast-decoupled power flow algorithm for large-scale power system analysis. Abdelkader et al. (2014) developed a Fuzzy Arithmetic Algorithm (FAA) for introducing fixed load and line uncertainties in RDS. Triangular Fuzzy Number method is proposed in (Esmaeili et al. 2016) for introducing uncertainties in the distribution system but with a higher system loss. A probabilistic approach is shown in Carpinelli et al. (2015) to analyse the behaviour of the electrical distribution system considering wind and photovoltaic generators in the presence of system uncertainties. The effect of uncertainty on optimal placement of capacitor in distribution system is analysed in (Das and Malakar 2020). (Raj and Kumar 2019) presented a modified affine approach for the power flow analysis in the RDS considering DG.

Paper Contribution

It has been observed from the published literature that the combined application of the IA and the probabilistic approach to determine the load interval width variations for solving the power flow problem considering different types of DG has not been evaluated before. This article contributes to the existing body of knowledge by making use of the hybrid possibilistic–probabilistic approach. This article presents a direct technique to simulate results for Type I, Type II and Type IV DG with a composite load (CL) model considering uncertainties in system input parameters (both line and load). All input variables (line and loads) and generation in the system are defined as random variables with load uncertainty as Gaussian distribution function, whereas line variables and DG uncertainty are varied at fixed proportion. Further, the results of previous literature and the proposed technique are compared and the significant improvement in the voltage profile is observed by installing DG at different buses. The proposed method is also found out be less conservative as compared to the published methods. Various case studies for uncertainty in load models with and without DG have been presented in Sect. 6. The summarized contributions of this article are given below:

• A combined application of the IA and probabilistic approach to incorporate load uncertainty is presented for analysing the performance of the proposed method to obtain more realistic and accurate state of the distribution system.

• Uncertainty in both system parameter and different types of DGs (Type I and IV DG) is considered.

• The effect of system uncertainties is also analysed in the presence of different DGs and load models by directly integrating them into the Interval-based backward-forward power flow algorithm.

• The analysis of system’s performance in the presence of DGs is carried out considering system uncertainties which actually helps the distribution system operators (DSO) in future planning.

• The results signified that the proposed technique is efficient and feasible to design larger systems with a high degree of uncertainty.

Interval Arithmetic

In this method, any number can be written in the form of a confidence interval (CI) either closed, open or a combination as opposed to a point estimate for a parameter of the system which suffers from the disadvantage that the estimated result cannot cover all possible solution space. An interval number can be defined as a set of real numbers. Let K and L be the two interval numbers (of real numbers) with their supporting interval [k₁, k₂] and [l₁, l₂], respectively. Here, the k₁, l₁ and k₂, l₂ represent the lower and upper interval limits (end points), respectively. The interval width of K and L is k₂-k₁ and l₂-l_1, respectively. The mathematical operations of addition, multiplication, subtraction, division, maximum and minimum can be applied to intervals numbers (Alefeld and Herzeberger 1983).

$$K+L=[{k}_{1}+{l}_{1},{k}_{2}+{l}_{2}]$$

(1)

$$K-L=[{k}_{1}-{l}_{2},{k}_{2}-{l}_{1}]$$

(2)

$$K*L=\left[{min.(k}_{1}*{l}_{1},{k}_{1}*{l}_{2},{k}_{2}*{l}_{1},{k}_{2}*{l}_{2}\right),{max.(k}_{1}*{l}_{1},{k}_{1}*{l}_{2},{k}_{2}*{l}_{1},{k}_{2}*{l}_{2})]$$

(3)

$$\frac{K}{L}=K*{L}^{-1}$$

(4)

where ${L}^{-1}$= [1/l_2, 1/l₁] with 0 ∉ [l₁, l₂].

The distance between two interval numbers, K and L is given as

$$d\left(K,L\right)=max\left[\left|{k}_{1}-{l}_{1}\right|,\left|{k}_{2}-{l}_{2}\right|\right]$$

(5)

Complex uncertainty can be expressed by projecting real numbers to the complex domain. Any complex number whose real and imaginary parts are interval numbers can be expressed as a complex interval number. Using the above fundamental operations for the real numbers, the relationship between uncertain variables in terms of complex interval numbers is calculated for the power flow study. The uncertainties present in the system data are handled using IA. Therefore, resistance, reactance, system power and bus voltages are considered as interval numbers rather than  a fixed value. Here, load at any bus is varied over a certain range based on Gaussian distribution (continuous probability distribution) rather than fixed variation as discussed in Sect. 3.2.

Mathematical Modelling

Line Variation Model

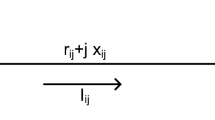
The equivalent diagram of one branch connected between i-1th and ith bus in a single-line diagram (SLD) of a RDS of Fig. 1 is shown in Fig. 2. The line-to-ground capacitance is very small for short line model in RDS and therefore neglected (Parihar and Malik 2020).

Fig. 1

SLD of a sample RDS

Fig. 2

Equivalent diagram of a single branch of Fig. 1

From Fig. 2, we get

$${P}_{i}+j{Q}_{i}={V}_{i}*{I}_{i}^{*}$$

(6)

where V_i is receiving-end bus voltage and V_i-1 is sending-end bus voltage. Q_i and P_i represent total downstream reactive and real power load fed by the bus i, respectively. The initial voltage estimated at every bus including source bus is taken as [1.0,1.0] + j [0.0,0.0] p.u. As both voltage and power are complex interval quantities, the subsequent current at bus i (${I}_{i}$) is also found as a complex interval quantity given in Eq. (7) and can be evaluated using division operation as in Eq. (4).

$${I}_{i}=\frac{\left[{P}_{{i}_{lo}},{P}_{{i}_{up}}\right]-\mathrm{ j }\left[{Q}_{{i}_{lo}},{Q}_{{i}_{up}}\right] }{{{V}_{i}}^{*}}$$

(7)

where ${P}_{{i}_{lo}}$, ${Q}_{{i}_{lo}}$ and ${P}_{{i}_{up}}$, ${Q}_{{i}_{up}}$ are the lower and the upper limit for real and reactive power load at bus i, respectively. The branch real power loss (${P}_{loss}$) and reactive power loss (${Q}_{loss}$) are expressed as

$${P}_{loss}(i-1,i)=\frac{\left({{P}_{i}}^{2}+{Q}_{i}^{2}\right)}{{{|V}_{i}|}^{2}}*R$$

(8)

$${Q}_{loss}(i-1,i)=\frac{\left({{P}_{i}}^{2}+{Q}_{i}^{2}\right)}{{{|V}_{i}|}^{2}}*X$$

(9)

where X is the branch reactance and R is the branch resistance. The uncertainty in line parameter at a fixed proportion can be introduced as

$${X}_{lo}\left(i\right)=\left(1-\%(X)\right)X\left(i\right)$$

(10)

$${X}_{up}\left(i\right)=\left(1+\%(X)\right)X\left(i\right)$$

(11)

$${R}_{lo}\left(i\right)=\left(1-\%(R)\right)R\left(i\right)$$

(12)

$${R}_{up}\left(i\right)=\left(1+\%(R)\right)R\left(i\right)$$

(13)

where ${R}_{lo}(i)$, ${X}_{lo}(i)$ and ${R}_{up}(i)$, ${X}_{up}(i)$ are the lower and the upper limit of resistance and reactance, respectively.

Load Variation Model

Generally, the load model chosen is complex power type but in practice, load is a combination of various voltage-dependent load models, therefore, modelling load as the composite load is more appropriate which includes three practical voltage-dependent loads in addition to the constant power load. Analysis of the effect of these load models in the distribution system is very useful for DSOs in different planning scenarios. Mathematically, these load models can be given as

$${P}_{i}={P}_{ino}\times \left(a+b\left|V\right|+c{\left|V\right|}^{2}+{d\left|V\right|}^{{x}_{1}}\right)$$

(14)

$${Q}_{i}={Q}_{ino}\times ({a}_{1}+{b}_{1}\left|V\right|+{c}_{1}{\left|V\right|}^{2}+{{d}_{1}\left|V\right|}^{{x}_{2}})$$

(15)

The 1^st term of (14) and (15) represents the constant power (CP) load, the 2^nd term signifies the constant current (CC) load, the 3^rd term shows the constant impedance (CZ) load and the last term indicates the exponential load. ${P}_{ino}$ is the nominal real power load and ${Q}_{ino}$ is the nominal reactive power load at bus i. The values of the participating coefficients may vary as per the locality and nature of load connected. The coefficients considered for the analysis purpose are $a$ = ${a}_{1}$= 0.2,$b$ = ${b}_{1}$= 0.3, $c$ = ${c}_{1}$= 0.25 and $d$ = ${d}_{1}$= 0.25 for both test systems (Ranjan et al. 2003). The values of the exponents chosen for the exponential load are ${x}_{1}$=1.38 and ${x}_{2}$ = 3.22 (Ranjan et al. 2003) for both test systems. The random fluctuations in the model parameters such as reactive and real power load demand are fairly represented by the normal distribution and is expected to change as per the Gaussian distribution function because we have a large sample size for the power load in IEEE bus system and so central limit theorem kicks in. As the distribution system with uncertainties provides many random solutions, hence, Gaussian distribution function is used to model load over other distribution functions. The Gaussian distribution is a bell-shaped distribution which is symmetric about its mean value and is defined as in (16)

$$f\left( {yi} \right) = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}e^-{\frac{1}{2}} \frac{{\left( {yi - \mu } \right)^{2} }}{{\sigma^{2} }}$$

(16)

where distribution parameters μ and ${\sigma }^{2}$ are the mean (expected) value and the variance of the base loads, respectively, and are considered as random variables. The variance captures the width/spread of the probability distribution, i.e. how far the random variable is expected to vary (specific percentage) from its mean value. The normalized value of the real or reactive power load ($yi$) at the ith bus is given as (Chaturvedi et al. 2006)

$$yi=\frac{{P}_{i}}{{P}_{ino}} \mathrm{and}\ yi=\frac{{Q}_{i}}{{Q}_{ino}}$$

(17)

where ${P}_{i}$ and ${Q}_{i}$ are defined in (14) and (15), respectively.

The degree of belongingness for real and reactive power load is denoted by ${\alpha }_{pl}(k)$ and ${\alpha }_{ql}(k)$, where k represents the number of degree of belongingness varying from 1 through N, where N is taken as the number of points of linearization of the Gaussian curve. The degree of belongingness will have a value from $\frac{{{\alpha }_{pl}}_{max}}{N}$ (minimum degree of belongingness) to ${{\alpha }_{pl}}_{max}$ (highest possible degree of belongingness) for the specified number of intervals N. The Gaussian distribution curve of real power load is shown in Fig. 3 (Chaturvedi et al. 2006). From the characteristic curve of the load illustrated in Fig. 3, the mean value of the normalized system power load is 1.0 for the degree of belongingness 1.0.

Fig. 3

Gaussian distribution of load

Equation (16) can be rewritten as

$${\alpha }_{pl}\left(k\right)=f\left[\frac{{P}_{i}}{{P}_{ino}}\right]=\frac{1}{\sqrt{2\pi {\sigma }^{2}}}{e}^{{{\left[\frac{{P}_{i}}{{P}_{ino}} -\mu \right]}^{2}}\left/ {2{\sigma }^{2}}\right.}$$

(18)

From the above equation, we get $\sigma$ = 0.399 for $\mu$ = 1.0 and ${\alpha }_{pl}\left(k\right)$ = 1.0.

Using $\sigma$ = 0.399 as a fixed standard deviation throughout the study and using $\mu$ = 1.0 in (18), we get

$$\frac{{P}_{i}}{{P}_{ino}}-1=\pm \sqrt{\frac{-\mathrm{ln}\left({\alpha }_{pl}\left(k\right)\right)}{\pi }}\mathrm{ for }\frac{{P}_{i}}{{P}_{ino}}\ne 1$$

(19)

Similarly, for reactive load

$$\frac{{Q}_{i}}{{Q}_{ino}}-1=\pm \sqrt{\frac{-\mathrm{ln}({\alpha }_{ql}(k))}{\pi }\mathrm{ for }}\frac{{Q}_{i}}{{Q}_{ino}}\ne 1$$

(20)

Right-hand side of (19) and (20) is given as

$$\sqrt{\frac{-\mathrm{ln}({\alpha }_{pl}(k))}{\pi }}={\alpha }_{K}=\sqrt{\frac{-\mathrm{ln}({\alpha }_{ql}(k))}{\pi }}$$

(21)

Thus, (19) can be rewritten as

$$\frac{{P}_{i}}{{P}_{ino}}=1\pm {\alpha }_{K}$$

(22)

$${P}_{i}={P}_{ino} (1\pm {\alpha }_{K})$$

(23)

where ± sign provides a lower limit and an upper limit of real and reactive power load at the i^th bus.

$${P}_{{i}_{lo}}={P}_{ino}(1-{\alpha }_{K})$$

(24)

$${P}_{{i}_{up}}={P}_{ino}(1+{\alpha }_{K})$$

(25)

$${Q}_{{i}_{lo}}={Q}_{ino}(1-{\alpha }_{K})$$

(26)

$${Q}_{{i}_{up}}={Q}_{ino}\left(1+{\alpha }_{K}\right)\mathrm{ where\ k}=1, 2,\dots .,\mathrm{ N}$$

(27)

Linearization at different values of k of the above equations results in k distinct load intervals in bounded form. The  linearization conducted at three different points as shown in Fig. 3 provides three distinct load intervals (D-regions) as given below.

$${D}_{1}\to \left\{{P}_{ino}[1-{\alpha }_{1}],{P}_{ino}[1+{\alpha }_{1}]\right\} point\ interval\ for\ k=1$$

(28)

$${D}_{2}\to \left\{{P}_{ino}[1-{\alpha }_{2}],{P}_{ino}[1+{\alpha }_{2}]\right\} \mathrm{for\ k}=2$$

(29)

$$D_{3} \to \left\{ {P_{ino} \left[ {1 - \alpha_{3} } \right],P_{ino} \left[ {1 + \alpha_{3} } \right]} \right\} {\text{for k}} = 3$$

(30)

Equations (28–30) clearly reflect that the D_1, D₂ and D₃ are definitely in bounded form. Therefore, IA operation must be applied to integrate these variations in power flow.

Distributed Generators Modelling

The DG resources of small size generally operate in constant power mode, that is, the generator bus is being modelled as a constant negative PQ load. According to IEEE 1547 Standard (2003), the utilities do not recommend the DG units to regulate bus voltages in order to avoid their conflict with the existing voltage control schemes (Walling et al. 2008). In addition to this, as the amount of reactive power delivered by the generator depends upon the system configuration and cannot be stated in advance. Therefore, the DG is modelled as PQ load. On the basis of power delivering capability, DG is classified as (Jagtap and Khatod 2016).

• Type I (injects real power, power factor (PF) = 1): Ex. photovoltaic, battery, fuel cell

• Type II (injects reactive power, PF = 0): Ex. synchronous capacitor

• Type III (injects real power, consumes reactive power, PF is leading): Ex. induction generator

• Type IV (injects reactive and real power at lagging PF): Ex. synchronous generator, wind power

The system performance in terms of bus voltage enhancement and loss reduction attained from Type III DG is found out to be worst amongst all other DG types (Pradeepa et al. 2015). The total load demand is reduced by the power injected by the DG at that bus. If a DG is placed at bus i, then the equivalent load at the same bus can be articulated as

$${P}_{i}^{eq}={P}_{i}-{P}_{gi}$$

(31)

$${Q}_{i}^{eq}={Q}_{i}-{Q}_{gi}$$

(32)

where ${P}_{gi}$ and ${Q}_{gi}$ represent the real and reactive power penetrated by any DG connected at bus i, respectively. As uncertainty may also be present in the distribution system due to variation in generation, therefore, it is important to consider uncertainty in DG units as well. The uncertainty in Type I and Type IV DG is considered to vary at fixed proportion in this paper.

Interval-Based Backward/Forward Power Flow Solution Methodology

A direct power flow solution (Teng 2003) of RDS is obtained by the multiplication of the BCBV (Branch Current to Bus Voltage) matrix and BIBC (Bus Incidence to Branch current) matrix. This technique is free from the substitution of the admittance matrix, Jacobian matrix and matrix decomposition because of which this technique is found to be superior to other methods. To articulate the BIBC matrix, branch currents are expressed as a function of the equivalent bus current injection. From Fig. 1, we get

$$\left[\begin{array}{c}B1\\ B2\\ B3\\ B4\\ B5\\ B6\\ B7\\ B8\end{array}\right]=\left[\begin{array}{cccccccc}1& 1& 1& 1& 1& 1& 1& 1\\ 0& 1& 1& 1& 1& 1& 1& 1\\ 0& 0& 1& 1& 0& 0& 1& 1\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}I2\\ I3\\ I4\\ I5\\ I6\\ I7\\ I8\\ I9\end{array}\right]$$

(33)

The above formulated matrix is an upper triangular matrix having values 0 and 1. Thus (33) can be given as

$$\left[\begin{array}{c}B\end{array}\right]=\left[\begin{array}{c}BIBC\end{array}\right]\left[\begin{array}{c}I\end{array}\right]$$

(34)

For BCBV matrix formulation, the bus voltages are expressed in terms of branch current, branch impedance and the substation bus voltage. Hence, its relationship can be given as (35)

$$\left[\begin{array}{c}V1\\ V1\\ V1\\ V1\\ V1\\ V1\\ V1\\ V1\end{array}\right]-\left[\begin{array}{c}V2\\ V3\\ V4\\ V5\\ V6\\ V7\\ V8\\ V9\end{array}\right]=\left[\begin{array}{cccccccc}Z12& 0& 0& 0& 0& 0& 0& 0\\ Z12& Z23& 0& 0& 0& 0& 0& 0\\ Z12& Z23& Z34& 0& 0& 0& 0& 0\\ Z12& Z23& Z34& Z45& 0& 0& 0& 0\\ Z12& Z23& 0& 0& Z36& 0& 0& 0\\ Z12& Z23& 0& 0& Z36& Z67& 0& 0\\ Z12& Z23& Z34& 0& 0& 0& Z48& 0\\ Z12& Z23& Z34& 0& 0& 0& Z48& Z89\end{array}\right]\left[\begin{array}{c}B1\\ B2\\ B3\\ B4\\ B5\\ B6\\ B7\\ B8\end{array}\right]$$

(35)

The above matrix is a lower triangular matrix represented by branch impedances. The above (35) can be rewritten as (36)

$$\left[ {\begin{array}{*{20}c} {\Delta V} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {BCBV} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} B \\ \end{array} } \right]$$

(36)

where $\Delta V$ is defined as a vector of system bus voltage differences compared to the substation bus voltage (1.0 p.u). By substituting (34) in (36),

$$\left[ {\begin{array}{*{20}c} {\Delta V} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {BCBV} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {BIBC} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} I \\ \end{array} } \right]$$

(37)

$$\left[ {\begin{array}{*{20}c} {\Delta V} \\ \end{array} } \right] = \left[ {DPF} \right]\left[ {\begin{array}{*{20}c} I \\ \end{array} } \right]$$

(38)

where DPF stands for distribution power flow matrix which gives a direct solution for the power flow problem by multiplying BIBC and BCBV matrices. Therefore, the iterative formula used for the solution of a power flow problem is given by (39) and (40).

$$\left[ {\Delta V_{i}^{n} } \right] = \left[ {DPF} \right]\left[ {\begin{array}{*{20}c} {I_{i}^{n - 1} } \\ \end{array} } \right]$$

(39)

$$\left[ {V_{i}^{n} } \right] = \left[ {V_{i}^{0} } \right] + \left[ {\begin{array}{*{20}c} {\Delta V_{i}^{n} } \\ \end{array} } \right]$$

(40)

where ${V}_{i}^{0}$ is the initial voltage [1.0,1.0] + j [0.0,0.0] p.u.

As ${V}_{i}^{n}$ and ${V}_{i}^{0}$ are both complex interval numbers, they can be expressed as ${V}_{i}^{n}={A}_{1}+i{A}_{2}$ and ${V}_{i}^{0}={B}_{1}+i{B}_{2}$, where ${A}_{1}$, ${A}_{2}$, ${B}_{1}$ and ${B}_{2}$ are all interval numbers.

$${{V}_{i}^{n}-V}_{i}^{0}=\mathrm{max}\left[d\left({A}_{1},{B}_{1}\right), d({A}_{2},{B}_{2})\right]$$

(41)

where $d\left({A}_{1},{B}_{1}\right)$ and $d({A}_{2},{B}_{2})$ are calculated using Eq. (5).

The bus voltage magnitude and system losses are determined as per the given steps:

• Step I: Read system load and line data at various buses.

• Step II: Find the degree of belongingness ${\alpha }_{pl}(k)$ and ${\alpha }_{ql}(k)$ for the specified number of intervals N.

• Step III: All buses including the source bus are initialized to a flat voltage start of [1.0,1.0] + j [0.0,0.0] p.u. Real and reactive system power losses are initially set to zero. Slack bus angle and iteration count are set to zero.

• Step IV: Compute the equivalent real power load and reactive power load at the bus where the DG has been installed using (31) and (32).

• Step V: Define the variation in line and load data and determine their respective closed intervals using (10) through (13) and (24) through (27), for the different degree of belongingness.

• Step VI: Update the bounded intervals for real and reactive power load for the composite nature of load using (14) and (15).

• Step VII: Formulate BIBC, BCBV and DPF matrices.

• Step VIII: Calculate bus current and bus voltage using Eqs. (7) and (40) using subtraction, division, multiplication and addition operation of the complex interval numbers as explained in Sect. 2.

• Step IX: If $\mathrm{max}\left[d\left({A}_{1},{B}_{1}\right), d({A}_{2},{B}_{2})\right]<0.0001$ for all the buses then go to step X, otherwise go to step V.

• Step X: Determine system power losses using Eqs. (8) and (9).

• Step XI: Obtain the results for a particular value of ${\alpha }_{pl}(k)$ and ${\alpha }_{ql}(k)$.

• Step XII: If k = N terminates the programme, else give increment to the counter and jump to step II.

Figure 4 illustrates the complete work flow of the proposed approach to solve Interval-based backward/forward power flow problem.

Fig. 4

Flow chart of Interval-based backward/forward power flow solution methodology

Simulation Test Result and Discussion

To illustrate the performance of the IA-based power flow algorithm, it has been extensively stimulated on three IEEE distribution test systems having different configuration, size and complexity level to authenticate its robustness. The single-line diagram of IEEE 33-bus and the 69-bus RDS is illustrated in Figs. 5 and 6, respectively, whereas the complete system data for 33-bus, 34-bus and 69-bus RDS are taken from Baran and Wu (1989a), Salama and Chikhani (1993) and Baran and Wu (1989b), respectively. The power demand of 69-bus RDS is 3.803 + j2.693 MVA. The single-line diagram of the IEEE 34-bus system is taken from Salama and Chikhani (1993).

Fig. 5

SLD of 33-bus RDS

Fig. 6

SLD of 69-bus RDS

The base kV and MVA taken for 33-bus and 69-bus RDS are 12.66 kV & 100 MVA, respectively, and for IEEE 34-bus system as 11 kV & 5 MVA, respectively. The IEEE bus feeders were tested on MATLAB. A tolerance of 10^–4 p.u in bus voltage difference in two successive iterations at all the buses is considered as the stopping criteria.

Power Flow with DG for Different Load Models

The voltage magnitude and system losses for the IEEE 33-bus system were calculated by considering two different cases: without and with DG. The DG is located at bus 33 with DG power penetration of 25% of total real power load of the RDS as in (Jagtap and Khatod 2016). The bus voltages obtained for the IEEE 33-bus system for CP model before and after installation of Type I DG are tabularized in Table 1. Figure 7 exemplifies the convergence of the voltage magnitude with and without DG. It is obvious from the results that by installing DG the minimum voltage obtained at bus 18 is raised from 0.9131 p.u to 0.9274 p.u.

Table 1 Base case power flow results for 33-bus RDS with and without DG

Fig. 7

Voltage profile of a 33-bus distribution system

The impact of various load models on real and reactive system losses is analysed and tabulated in Table 2. The results depict the reduction in real and reactive losses of the system with DG integration for all the types of load models. The comparative study is carried out with previously published results (Jagtap and Khatod 2016) and found comparable in every respect. The CPU time for bus voltages computation for the constant power load model in IEEE 33-bus system obtained from the proposed method is 0.05 s.

Table 2 Performance comparison for 33-bus RDS with published results

Uncertainties in Line and Load Data (Without DG)

In 33-bus system, the line and load uncertainties for the CP load model are taken as 1% and 5%, respectively, as in (Abdelkader et al. 2014). The interval width and percentage reduction in it at minimum bus voltage for line and load uncertain parameters are calculated and tabulated in Table 3. The results obtained from the proposed probabilistic–possibilistic approach are further compared with the FAA (Abdelkader et al. 2014), which clearly illustrates that the interval width attained from the proposed approach is narrower and hence the solution is found out to be less conservative and superior than the possibilistic approach alone. It was also observed that the incorporation of load uncertainty in the system leads to a greater voltage drop than with the line uncertainty.

Table 3 Interval width of minimum bus voltage for CP load model in IEEE 33-bus system

The bus voltage convergence for the CP model and CL model for the 34-bus RDS is presented in Fig. 8. For the given system, the minimum bus voltage attained is 0.8834 p.u at bus 27 for a constant power model and is 0.8961 p.u for the CL model. However, since the practical RDS has all types of load and system power losses are voltage-dependent, it is more appropriate to consider the CL model. In addition to CL modelling, the disparity in input parameters is also considered for this case study using IA.

Fig. 8

Bus voltage profile for CP and CL model for 34-bus RDS

The degree of belongingness varies from 0 to 1.0. To exemplify the application of IA, the total real and reactive power fed and system power losses at three different degree of belongingness obtained for 34-bus RDS are depicted and compared with Chaturvedi et al. (Chaturvedi et al. 2006) in Table 4. The proposed approach takes four iterations less and is found to be in close agreement with the published results. Here, all four types of loads are considered for the CL model. The interval width in p.u and its reduction in % for power fed and system power losses in 34-bus RDS at α = 0.6 and 0.2 are calculated and given in Table 5. The obtained results demonstrate that the interval width obtained from the proposed method is narrower and hence the solution is found out to be less conservative than the published results.

Table 4 Total Real and Reactive power fed and losses with the CL model for 34-bus RDS

Table 5 Interval width at different degree of belongingness in IEEE 34-bus system

Figure 9 illustrates the lower and upper limits of the voltage magnitude with different load parameters at α = 0.2, 0.6 and 1.0. It can be recognized from the figure that the interval of voltage variation rises with a decline in the degree of belongingness. The voltage magnitude at each bus is within the interval attained by the IA power flow solution. The variation in minimum bus voltage for the 34-bus system at different degree of belongingness (0.1 through 1.0) has been displayed in Fig. 10, which shows that the interval width of voltage magnitude at bus 27 reduces as degree of belongingness increases.

Fig. 9

Voltage magnitude variation at different degree of belongingness

Fig. 10

Voltage magnitude variation at a bus with minimum voltage|V₂₇⃒

The interval width of voltage magnitude in IEEE 69-bus system considering fixed load variation of ± 5% was calculated for CP load model in (Nogueira et al. 2021). The interval width obtained in this study is 0.0001 p.u at bus 29 and 0.0097 p.u at bus 63, which is found to be less as compared to 0.0002 p.u at 29 and 0.0098 p.u at bus 63 as mentioned in Nogueira et al. (2021).

Uncertainties in Line and Load Data (with Different Types of DG)

In this case, independent placement of Type I, Type II and Type IV DG is presented for the IEEE 69-bus system. The variation of ± 3% is taken in the line parameter, whereas variation in load parameter is taken as per the Gaussian distribution function. The DG is located at bus 61 as in Ali et al. (2018). The real and reactive power penetration are assumed to be 25% of the total real and reactive power load demand, respectively.

For the CL model, value of V_min is upgraded from 0.9181 p.u to 0.9522, 0.9272 and 0.9588 p.u at bus 65 after penetration of Type I, II and IV DG with the percentage voltage improvement of 3.7%, 1% and 4.4%, respectively, for fixed line and load data. The deterministic CPU time determined for bus voltages computation with the CL model in 69-bus RDS for the base case (no DG) and with Type I, Type II and Type IV DG is 0.03 s and 0.043 s, 0.047 s and 0.040 s, respectively. Table 6 tabularizes the simulated results for minimum bus voltage, total system losses (real and reactive) of 69-bus RDS with Type I, Type II and Type IV DG penetration for the deterministic case as well as when uncertainties occur in line and load parameter at a different degree of belongingness. Based on the lower and the upper bounds of the minimum voltage magnitude, the interval width for Type I, II and IV DG are 0.0022 p.u, 0.0043 p.u and 0.0024 p.u, respectively, at α = 1. The voltage magnitude interval at bus 65 is narrower for Type I and IV DG than that obtained from Type II DG installation. This concludes that the Type I and Type IV DG installation provides more realistic results in contrast to Type II DG.

Table 6 Results for 69-bus RDS with line and load uncertainty and DG penetration

Figure 11 demonstrates the consequence of introducing uncertainties (both line and load) on the voltage profile of the 69-bus RDS by considering CL model and different degree of belongingness, i.e. α = 0.2, 0.6 and 1. As expected, the voltage magnitude at each bus for the deterministic input parameter always lies within the possible system states obtained by variation in input parameters.

Fig. 11

Voltage profile with Type IV DG at different degree of belongingness with fixed and varying line and load parameters

Figure 12 shows the variation of total P_loss and Q_loss for CL model at various degree of belongingness with and without considering Type IV DG in 69-bus RDS. It demonstrates that the power losses reduced significantly with the installation of Type IV DG for the IEEE 69-bus system. It can be recognized from Fig. 12 that the interval of power losses decreases with an increase in the degree of belongingness.

Fig. 12

Variation of system power losses at various degree of belongingness

For 69-bus RDS, statistical analysis for ${P}_{loss}$ reduction due to DG introduction has been carried out and found that the reduction in the value of coefficient of variation (CV) in power loss is maximum for Type IV DG with respect to other DG types as mentioned in Table 7. This demonstrates that the Type IV DG is capable of reducing the variation in system power losses in distribution feeders around its mean value much more effectively than other DG types and therefore gives better security against overheating of the distribution feeders. The mean, standard deviation (Std), coefficient of variation, minimum (min) and maximum (max) of real power loss lies between their lower and upper limits for α = 1.0, 0.6 and 0.2 but has been shown for α = 1.0 only, in Table 7. It was also found out that the higher DG penetration level increases the CV due to a higher degree of uncertainty.

Table 7 Statistical analysis for power loss due to DG penetration in 69-bus RDS with CL model and uncertainty

Uncertainties in DG output

The power generation by DG units brings additional uncertainties in the system. Solar PV system (Type I DG) and wind power (Type IV DG) output are uncertain because of variability in solar insolation and wind speed, respectively. The non-stochastic controllable DG such as gas turbine output is also uncertain as it depends upon the decision of private DG owner. Therefore, Sect. 5.3 is extended to include uncertainty in the DG output power and is taken as ± 5% as in Vidovic and Saric (2017). The equivalent real and reactive power load at uncertain DG output power can be obtained using

$${P}_{i}^{eq}(lo,up)={P}_{i}-{P}_{gi}\pm (0.05)P_{gi}$$

(42)

$${Q}_{i}^{eq}(lo,up)={Q}_{i}-{Q}_{gi}\pm (0.05){Q}_{gi}$$

(43)

The results attained for 69-bus RDS with the line, load and DG uncertainty are determined and tabulated in Table 8 for minimum bus voltage magnitude and system losses at a different degree of belongingness. The bus voltage magnitude and system power losses obtained for deterministic input parameters are found to lie within the possible system states.

Table 8 Results for 69-bus RDS with the line, load and DG uncertainty

Conclusion

Modern RDS is subjected to many uncertainties due to variations in load demand and new generation technologies, which motivates operators to develop new tool for incorporating these uncertainties in the system. In this context, a hybrid probabilistic–possibilistic method for solving the power flow problem with different types of DGs is presented to investigate the impact of line, load and DG uncertainties in the RDS. The probabilistic approach is implemented to introduce load uncertainty in distribution system using Gaussian distribution function. Four numerical test cases have been developed and solved for different complexity levels of the power flow problem. The voltage characteristic of the RDS for a different degree of belongingness is obtained without and with considering DG and is found to be affected by voltage-dependent load models. The proposed approach provides tighter solution interval and comprises all possible states of the system thus signifying numerical stability and robustness of the method, especially for large-scale RDS when compared with the possibilistic approach (FAA) alone. The robustness of the method for solving distribution power flow was demonstrated on IEEE 33-bus, 34-bus and 69-bus RDS. It has also been statistically acknowledged from the test cases that the algorithm gives more realistic and consistent results in terms of lowest power losses, better voltage profile and less overheating of feeders. The percentage reduction in the interval width of 34-bus system losses is 2.2% and 3.2% for 0.6 and 0.2 degree of belongingness, respectively, when compared with the published result. The interval width of bus voltage magnitude in 69-bus system considering line uncertainty is 0.0027 p.u, 0.0378 p.u and 0.0665 p.u at 1, 0.6 and 0.2 degree of belongingness, respectively. The results demonstrated the significant influence of uncertainties on results and hence cannot be neglected. The qualitative information from the solution is essential to the DSOs for the planning and expansion of the RDS. Here, the analysis has been carried out without optimally allocating DG in the system. The proposed technique can be further extended to evaluate possible system states in the presence of optimally allocated DG.