Abstract
The present paper comprises a review of kinetic instabilities that may be operative in the solar wind, and how they influence the dynamics thereof. The review is limited to collective plasma instabilities driven by the temperature anisotropies. To limit the scope even further, the discussion is restricted to the temperature anisotropy-driven instabilities within the model of bi-Maxwellian plasma velocity distribution function. The effects of multiple particle species or the influence of field-aligned drift will not be included. The field-aligned drift or beam is particularly prominent for the solar wind electrons, and thus ignoring its effect leaves out a vast portion of important physics. Nevertheless, for the sake of limiting the scope, this effect will not be discussed. The exposition is within the context of linear and quasilinear Vlasov kinetic theories. The discussion does not cover either computer simulations or data analyses of observations, in any systematic manner, although references will be made to published works pertaining to these methods. The scientific rationale for the present analysis is that the anisotropic temperatures associated with charged particles are pervasively detected in the solar wind, and it is one of the key contemporary scientific research topics to correctly characterize how such anisotropies are generated, maintained, and regulated in the solar wind. The present article aims to provide an up-to-date theoretical development on this research topic, largely based on the author’s own work.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The purpose of this review is to lay out a systematic exposition of various theoretical methods to study the temperature anisotropy-driven instabilities and their consequences on the solar wind plasma. This research topic is highly relevant to the contemporary solar wind physics as the US and European space agencies will shortly launch inner heliospheric spacecraft missions called the Parker Solar Probe (NASA) and Solar Orbiter (ESA). One of the aims of such missions is to map the spatio-temporal evolution of temperature anisotropies associated with the proton, electron and minor heavy ions from the solar source to near-Earth orbit.
Since the main objective of the present review is to discuss the theoretical development in a pedagogic manner, the literature review will not be exhaustive. When the literature is overviewed, it will be done mainly for setting up the scientific motivations and for the purpose of giving the readers an overall and rough sense of historical backdrop for this particular research area. So, the literature review will be selective, and the choices will be made mostly on the basis of those that have impacted the present author’s research priorities. Apologies to colleagues are preemptively offered in case the present author missed any major published works that, in the reader’s opinion, should have been cited.
If the reader is interested in historic and early reviews of plasma instabilities including those driven by the temperature anisotropy, a classic example may be that by Vedenov et al. (1961). In the context of space physics, the classic and excellent early review papers on plasma instabilities may be those by Hasegawa (1971) and by Schwartz (1980).
From a technical perspective, the present review will rely on the Vlasov linear kinetic theory of temperature anisotropy instabilities in magnetized plasmas based upon the assumption of bi-Maxwellian velocity distribution functions for plasma particles—mostly for protons, but some discussions of electron physics will also be included. The review will also include quasilinear kinetic theory of these instabilities. The collisional effects on these instabilities as well as the influence of large-scale inhomogeneity will be discussed. The linear theory of waves and instabilities are well known such that, it probably is a standard research tool for any practitioner of plasma physics. Hence, it is deemed that no specific references on general theory are necessary. In contrast, quasilinear kinetic theory is far less practiced in the community. Instead, these days, direct numerical simulation is preferred. In the view of the present author, however, quasilinear theory, when properly used, is a powerful and efficient tool. Early works on quasilinear kinetic theory in magnetized plasmas, especially in the context of space physics may be those by Kennel and Petschek (1966) and Kennel and Engelmann (1966). There are many textbooks on plasma physics, but the excellent two-volume monographs by Baumjohann and Treumann (1997) and Treumann and Baumjohann (1997) are specifically dedicated to space applications. One may also add an excellent general textbook on space physics by Parks (2003).
At the dawn of space exploration, scientists realized that the velocity distributions of charged particles in space do not follow the law of thermodynamic equilibrium theory. That is, instead of the well-known Maxwell–Boltzmann–Gauss distribution, the observed velocity distributions featured tenuous populations of highly energetic particles near the tail of the Gaussian distribution, that are best fitted by inverse power law distributions. It was also quite common that the temperature defined in directions perpendicular to the local magnetic field was different from that of the parallel or field-aligned direction, that is, anisotropic velocity distribution functions are pervasively observed in space. Examples of early observations, which indicate that the solar wind plasma particles possessed anisotropic velocity distribution functions may be papers by Hundhausen et al. (1967a, b), Hundhausen and Bame (1967) and Montgomery et al. (1968). These observations were made near the Earth orbit, that is 1 AU. Systematic observations of solar wind plasma thermal anisotropy from 1 AU and extended toward the inner heliosphere, as close to the Sun as 0.3 AU, became available with the Helios solar probes mission (Marsch et al. 1982; Schwenn and Marsch 1990, 1991).
In this review, we will be concerned with plasma instabilities excited by thermal anisotropies and their impact on the solar wind dynamics. We will not consider instabilities generated by field-aligned drift, i.e., the beam, as such a topic probably deserves a separate treatise. This is a particularly limiting assumption as the solar wind electrons (and sometimes protons too) are often observed with bulk drift speeds and beams. However, in order to limit the range of discourse, the present review will be restricted to kinetic instabilities driven only by the temperature anisotropies. We will also ignore the impact of non-bi-Maxwellian velocity distributions, especially those features associated with energetic quasi-power-law tail population. Often, such a feature is represented by the kappa distribution (Livadiotis 2017).
The main body of the present review will systematically explore the properties of various temperature anisotropy instabilities as understood by the present author such that, after providing a scientific backdrop in the present section, no expansive and conscious effort will be made to direct the readers to published works every time a new equation, topic, or a new theory is introduced. Instead, the subsequent presentation will be in the style of lecture notes. However, if one is interested in early theories of plasma instabilities associated with thermal anisotropies in the solar wind, see, e.g., the papers by Scarf et al. (1967) or Kennel and Scarf (1968), just to name a couple.
The present review will also discuss large-scale models of the solar wind in which macroscopic quantities are subject to adiabatic effects that come from large-scale spatial inhomogeneities, but small kinetic-scale wave–particle interactions affect the local dynamics. Historically, some early efforts along such a line, namely, the macroscopic model of the solar wind including the effects of temperature anisotropy-driven instabilities were discussed by Eviatar and Schulz (1970), Hollweg (1978), and Schwartz et al. (1981). These are representative examples, and they may be considered as precursors to more sophisticated later models, see, e.g., more recent papers by Jasperse et al. (2006a, b), Passot and Sulem (2007), Chandran et al. (2011), and Yoon and Seough (2014).
In the macro–micro or fluid–kinetic model of the solar wind, the wave–particle interaction will be incorporated into the equation that governs large-scale quantities, namely, the density, momentum, and temperatures. Perpendicular and parallel temperatures are constructed from the velocity moments of the distribution function. The Vlasov theory of linear waves and quasilinear kinetic theory depend on the particle distribution function, but in general, it is not so straightforward to incorporate the information associated with the kinetic-scale particle distribution function directly into the equations governing large-scale velocity space integrated quantities. To facilitate the coupling between large- and small-scale quantities and physics, we will adopt and extensively utilize the method pioneered by Davidson and Ogden (1975), in which velocity moments are taken over the particle kinetic equation under the assumption of bi-Maxwellian distribution function. Such a method may be termed the quasilinear “moment” theory, or macroscopic quasilinear theory.
As it will be shown subsequently, the macroscopic quasilinear model of the solar wind, when applied to inhomogeneous density and magnetic field intensity, will describe how the solar wind plasma evolves in various spatial location from the solar source to the observed points in the heliosphere. Observations show that near the solar coronal source as well as almost everywhere along the spatial location up to 1 AU and beyond, the perpendicular temperature can be much higher than that predicted by fluid theories. This has prompted many to suggest that local perpendicular heating by pre-existing Alfvénic fluctuations must be operative. Examples of early suggestion of local perpendicular ion heating may be those by Schwartz et al. (1981) and by Bame et al. (1975), just to name two most representative papers. In the present review, however, we will not discuss the issue of local perpendicular heating.
As far as the systematic kinetic instability analysis of the temperature anisotropy is concerned, the contribution by S. Peter Gary probably deserves a special mention. Gary’s lifelong work on kinetic plasma instabilities laid foundations for many subsequent works (Gary 1993). See, e.g., the early paper by Gary et al. (1976) on proton instabilities, which contains the temperature anisotropy versus parallel beta marginal stability curve, which will become very popular decades later. For general references on various plasma instabilities, see e.g., the monographs by Baumjohann and Treumann (1997) and by Treumann and Baumjohann (1997), which we already mentioned, but also the excellent monograph by Gary (1993). Among the temperature anisotropy instabilities, the mirror mode is still not completely understood, especially its nonlinear development. For discussions on mirror instabilities, see the works by Southwood and Kivelson (1993), series of papers by Pokhotelov et al. (2000, 2002, 2003), and other related works, e.g., papers by Treumann et al. (2004) and Porazik and Johnson (2013a). For other instabilities in the context of space plasmas, see also the early work by Hasegawa (1971).
The problem of how various plasma instabilities regulate the temperature anisotropy of space plasma particles actually began with observations made in the magnetosheath. Representative papers on this topic may be by Anderson et al. (1991, 1994, 1996), Anderson and Fuselier (1993, 1994), Phan et al. (1994), Lacombe and Belmont (1995), Tan et al. (1998), Samsonov et al. (2007), Remya et al. (2013), etc. Theoretical analysis of thermal anisotropy instabilities in the magnetosheath was spearheaded by Gary and his colleagues, who built upon his early work (Gary et al. 1976), and analyzed the problem by making use of the linear Vlasov theory of small-amplitude perturbations in magnetized plasmas including the proton and helium cyclotron instabilities (Gary et al. 1993b, c). Thus, in the decade of 1990s the problem of temperature anisotropy instabilities began to receive an intense interest, and numerical simulations of the anisotropy-driven instabilities have been also carried out in order to understand the nonlinear evolution. These works are ongoing. For instance, McKean et al. (1992, 1993, 1994), Gary et al. (1993c, 1996a, b), Gary and Winske (1993), Gary and Saito (2003), Shoji et al. (2009), Omidi et al. (2010), and Bortnik et al. (2011) performed mirror and ion-cyclotron (or EMIC) instabilities with parameters relevant to the magnetosheath and magnetosphere. Later, however, with applications to the solar wind and other astrophysical situations in mind, further simulations were carried out by Califano et al. (2008), Camporeale and Burgess (2008, 2010), Génot et al. (2009), Hellinger et al. (2009, 2014), Porazik and Johnson (2013b), and Ahmadi et al. (2016). Firehose instability driven by excessive parallel temperature anisotropy was also simulated (Gary and Nishimura 2003). Gary et al. (1993a, 1995, 1997) compared the theory, simulation, and observation made in the magnetosheath in order to establish the role of anisotropy-driven instabilities in regulating the thermal anisotropies.
An important development around this time period is that the concept of empirical relationship between the observed anisotropic temperature ratio, \(T_\perp /T_\parallel\) (where \(T_\perp\) and \(T_\parallel\) are perpendicular and parallel temperatures with respect to the ambient magnetic field, respectively) and parallel component of the plasma beta, \(\beta _\parallel =8\pi nT_\parallel /B^2\) (where n and B are ambient density and magnetic field intensity) emerged. Anderson et al. (1994), Gary et al. (1994a, b, c), and Fuselier et al. (1994) thus introduced the empirical relationship between the temperature ratio and parallel beta, known as the temperature anisotropy versus beta inverse relationship. The relationship is often expressed as
where S and \(\alpha\) are empirical fitting parameters for each instability, and (1.1) represents the marginal stability condition. Gary et al. (1994d) extended the marginal stability analysis, or the inverse relationship, to include helium cyclotron anisotropy instability in the magnetosheath. Scime et al. (2000) confirmed the validity of the inverse relationship on the basis of laboratory plasma experiment. Pantellini and Schwartz (1995) and Pokhotelov et al. (2000) extended the model to include isotropic electrons and anisotropic ions. Most of the efforts up to this point in time were restricted to ions and low-frequency instabilities, but the empirical fitting of marginal stability conditions were also extended to include high-frequency electromagnetic electron-cyclotron (EMEC) or whistler instability by Gary and Wang (1996).
The magnetosheath temperature anisotropy instability problem was first extended to the solar wind proper and solar corona, by Gary et al. (2001a, b). Many subsequent works followed including those by Gary et al. (2003), Kasper et al. (2003, 2008, 2013), Marsch et al. (2004, 2006), Hellinger et al. (2006, 2011, 2013), Hellinger and Trávníček (2014), Matteini et al. (2007, 2012, 2013), Bale et al. (2009), Bourouaine et al. (2010, 2013), Maruca et al. (2011, 2012), Osman et al. (2011, 2012, 2013), Marsch (2012), Maneva et al. (2014), Adrian et al. (2016), and others that the present review might have missed. These works further investigated the effects of temperature anisotropy instabilities in the solar wind by analyzing data obtained from an armada of spacecraft including Helios, Ulysses, WIND, ACE, Stereo, etc. The empirical marginal stability relationship of the type (1.1) became very popular and useful in characterizing and analyzing the solar wind data.
One of the most cited and representative empirical model of the proton temperature anisotropy marginal condition may be that by Hellinger et al. (2006), who introduced an additional parameter \(\beta _0\) in order to fine-tune the fitting,
Other extensions include inverse correlations using non-Maxwellian models by Xiao et al. (2006, 2007), Lazar et al. (2011), and Lazar (2012); empirical inverse correlations for electrons and high-frequency instabilities by Gary et al. (2005) and Štverák et al. (2008); modification of the inverse correlation by including binary collisional effects by Schlickeiser et al. (2011); efforts to rigorously calculate the inverse correlation by Isenberg (Isenberg 2012; Isenberg et al. 2013) who sought to obtain a rigorous asymptotic solution of the plasma subjected to linear instability condition; including the effects of streaming population on the stability condition by Hadi et al. (2014), Schlickeiser and Yoon (2014), and Vafin et al. (2015); the mutual dynamical influence of electrons and ions, considered by Michno et al. (2014), Maneva et al. (2016), and Shaaban et al. (2016, 2017), etc.
As an example of observations near 1 AU and to illustrate the usefulness of the empirical relation (1.1), we plot in Fig. 1, the proton data distribution obtained near 1 AU, in \((\beta _{\parallel i}, T_{\perp i}/T_{\parallel i})\) parameter space. Figure 1 is adopted from the paper by Michno et al. (2014), where perpendicular and parallel temperatures as well as the density and magnetic field intensity in the solar wind are calculated using data from WIND SWE and MFI instruments (through the SPDF CDAWeb service) (Bale et al. 2009; Ogilvie et al. 1995; Lepping et al. 1995). We then constructed the proton temperature ratio and the parallel plasma beta. The result is displayed in Fig. 1. Each bin corresponds to a logarithmically spaced \(100\times 100\) grid in the intervals \(10^{-1}<T_{\perp i}/T_{\parallel i}< 10\) and \(10^{-3}<\beta _{\parallel ,i}<10^2\). We discarded data with errors larger than \(10\%\) in the thermal speed, and when the spacecraft was too close to the Earth’s bow shock.
The empirical marginal stability threshold contours computed according to formula (1.1) are superposed, where for reasons that will become obvious later, we chose the fitting parameters
for mirror instability,
for electromagnetic ion-cyclotron (EMIC) or proton-cyclotron instability, and
for (parallel) proton firehose (PFH) instability. Note how the above marginal stability curves quite nicely account for the upper-right and lower-right outer boundaries of the data distribution. An outstanding issue is whether the outer boundaries of the same data distribution that are apparent in the upper-left and lower-left parts can also be accounted for on the basis of some fundamental plasma physics or not. At present, this issue is not resolved.
Note also that quite besides the issue of the regulation of the temperature anisotropy by instabilities, or equivalently, the upper and lower bounds in the parameter region \((T_\perp /T_\parallel ,\beta _\parallel )\), a separate issue has to do with the physical origin of magnetic fluctuations in the same parameter space, which corresponds to the stable regime. If the temperature anisotropy is sufficiently low such that no instability is expected, then what is the reason for observed magnetic field fluctuations? One possibility is the remnant solar wind turbulence, whose origin may reside with the surface region of the Sun, but which is observed to exist pervasively in the solar wind. Alternatively, the spontaneous emission of low-frequency electromagnetic fluctuations by thermal plasmas may also be the physical origin. In this regard, Araneda et al. (2012), Navarro et al. (2014, 2015), and Viñas et al. (2014, 2015) suggested such a mechanism. On the other hand, Camporeale (2012) invoked a transient effect known as the nonmodal linear theory to explain the same observation. In a novel approach, Servidio et al. (2014) considered the observed data distribution in \((T_\perp /T_\parallel ,\beta _\parallel )\) from a distinct perspective. They employed a hybrid simulation of large-amplitude plasma turbulence in order to explain not only the source of magnetic fluctuations, but also the observed data distribution. Recently, Verscharen et al. (2016) invoked the pervasive compressional turbulence in the solar wind to explain why the solar wind plasma is predominantly measured to be well within the quasi-isotropic state.
To investigate the nonlinear behavior of plasma instabilities generally requires theories that go beyond the linear theory, since linear theory only describes the condition for initial exponential growth. Ideally computer simulations are most accurate and rigorous. However, simulations are strictly speaking, numerical experiments that require interpretations in the light of theory. In this regard, the simplest nonlinear theory, i.e., quasilinear kinetic theory, is a suitable choice for studying the nonlinear evolution of the plasma system subject to instabilities. Quasilinear theory of the anisotropy-driven instabilities of the type pioneered by Davidson and Ogden (1975) was first extended to include the mirror and ion-cyclotron instabilities by the present author (Yoon 1992). The present review will extensively rely on such a formalism to include other unstable modes along the same line of theoretical approach as taken in Davidson and Ogden (1975) and Yoon (1992). Thus far, such an effort has been quite successful, except that the quasilinear moment theory for the so-called oblique firehose instability has not been done, so this review will have to leave it out. Note that there exist alternative models of the macroscopic theory that incorporate microscopic physics. For instance, the FLR-Landau model (Hunana et al. 2011, 2016; Passot et al. 2012) has been employed to discuss the mirror mode constraint on proton temperature anisotropy (Laveder et al. 2011). Recently, Hunana and Zank (2017) formulated CGL-Hall-FLR theory in order to describe parallel and oblique firehose instabilities.
Kinetic approach to the oblique firehose instability for the protons was first discussed by Yoon et al. (1993), but they made simplifying assumptions. More complete discussion of the oblique proton firehose instability, based upon full numerical solution of the transcendental linear dispersion relation, and complemented by hybrid simulation, was carried out by Hellinger and Matsumoto (2000, 2001), and also recently by Seough and Nariyuki (2016). However, as mentioned, Hunana and Zank (2017) employed an advanced two-fluid model to reformulate the parallel and oblique firehose instabilities. Consequently, it appears that both kinetic and fluid models yield similar results. Discussion of the oblique electron firehose instability was first carried out by Paesold and Benz (1999), Li and Habbal (2000), and Messmer (2002). Recently, Hellinger and Trávníček (2011), Hellinger et al. (2014), Camporeale and Burgess (2010), Hellinger (2017), and Maneva et al. (2016) further carried out theoretical discussion as well as numerical simulation of the proton oblique firehose instability. However, the quasilinear theory based upon taking the velocity moments of the particle kinetic equation has not been developed to this date.
A macroscopic model of the solar wind that contains the influence of anisotropy instabilities was first discussed by Eviatar and Schulz (1970), Hollweg (1978), and Schwartz et al. (1981), as mentioned, but later Denton et al. (1994) revisited the problem with specifically invoking the temperature anisotropy versus beta inverse relationship as a closure scheme. Recently, Chandran et al. (2011) further developed a more sophisticated model of the solar wind in which similar anisotropy–beta closure is also used for the temperature equations. Marsch and Tu (2001) constructed a comprehensive macroscopic model of the solar wind, in which the wave–particle interaction effects are incorporated, but the self-consistent wave dynamics was not included.
Hybrid simulations of the expanding system were carried out by Hellinger et al. (2003), Matteini et al. (2006, 2012), Trávníček et al. (2007), Hellinger and Trávníček (2008, 2011, 2013, 2015), Camporeale and Burgess (2010), Ofman et al. (2011, 2014), and Moya et al. (2012), which are in many ways equivalent to the macroscopic–kinetic model of the solar wind. Of course, numerical simulations are more rigorous in that they contain full nonlinear physics, but fluid/kinetic model is an efficient way to investigate the large-scale physics and its coupling to small kinetic-scale processes. The approach taken in the present review is to adopt the analytical model based upon the quasilinear theory. One should keep in mind, however, that quasilinear approach, especially with the simplifying assumption of bi-Maxwellian model of the particle distribution functions for all time, is a simplification that must be validated against more rigorous models such as the particle-in-cell or hybrid simulations.
In general, for plasmas with perpendicular temperature higher than parallel temperature, there are several plasma instabilities that may be excited. If the excessive perpendicular thermal anisotropy resides with the protons, then it is well known that electromagnetic proton (or ion) cyclotron—EMIC for short—instability and proton mirror instability are operative. If, on the other hand, the perpendicular temperature anisotropy is associated with the electrons, then the whistler or electromagnetic electron-cyclotron—EMEC for short—instability and electron mirror instability will be excited. For the opposite case of parallel temperature higher than the perpendicular temperature, generally firehose instability is excited. However, if the free energy source is in the protons, then the firehose instability excited in such a case is called the proton firehose (PFH) instability. Similarly, if the excessive parallel temperature anisotropy is in the electrons, then it is called the electron firehose (EFH) instability. Both types of firehose instability are, in fact, made of two distinct branches, parallel and oblique. In the present review, we will systematically discuss the parallel branch only.
The quasilinear moment theory to be employed in the present review is not only restricted to instabilities, where the free energy initially resides in the particles. It was also successfully employed by Moya et al. to discuss solar wind heating (Moya et al. 2012, 2011, 2014), for which the free energy resides with finite amplitude waves while the particles are initially isotropic. The recent application of such a method to the solar wind temperature anisotropy instability was initiated by the present author and his colleagues (Seough and Yoon 2012; Yoon and Seough 2012; Seough et al. 2013, 2015a, b; Stockem Novo et al. 2015; Yoon et al. 2015). We also recently initiated a research program to test and verify the accuracy and reliability of the quasilinear moment method by comparing the theoretical calculation against particle-in-cell simulation (Seough et al. 2014). Recently, the present author also began a systematic investigation of macroscopic quasilinear theory that includes large- to intermediate-scale inhomogeneities (Yoon and Seough 2014; Yoon 2016a, b; Yoon and Sarfraz 2017). The model being developed as of the present writing differs from earlier discussions and models, say, by Eviatar and Schulz (1970), Hollweg (1978), Schwartz et al. (1981), Jasperse et al. (2006a, b), Passot and Sulem (2007), and Chandran et al. (2011), in that the author’s model emphasizes the self-consistent wave dynamics.
In the remainder of the present review, we will systematically discuss the various temperature anisotropy instabilities for protons, from a simple case of parallel propagation, then move on to include instabilities with arbitrary propagation direction. Then we will discuss instabilities operative in inhomogeneous solar wind-like plasmas. We will also consider the effect of binary collisions. Next, we will discuss the dynamical interplay between the electrons and ions. Finally, we will conclude and summarize the present review.
2 Quasilinear moment theory of waves and instabilities in magnetized plasmas
2.1 Quasilinear kinetic theory for magnetized plasmas
The discussion presented herewith is meant to be pedagogic, but also as a brief overview. The detailed conditions for the validity of the theory, the definition of collective versus collisional plasmas, etc., can be found in the standard literature, so we will omit them. The readers are assumed to be already familiar with the basic notion of plasma physics. Let us start from the fully nonlinear Vlasov equation,
where \({\mathbf {E}}\) and \({\mathbf {B}}\) are electric and magnetic field vectors that satisfy Maxwell’s equation. The label a represents species, \(e_a=e\) for protons (\(a=i\)), \(e_a=-e\) for electrons (\(a=e\)). The proton and electron masses are denoted by \(m_i\) and \(m_e\), respectively. Here, the particle distribution function is normalized according to \(\int {\mathrm{d}}{\mathbf{v}}f_a({\mathbf {r}},{\mathbf {v}},t)=n_a({\mathbf{r}})\), where \(n_a({\mathbf {r}})\) is the local density. For spatially uniform system, \(n_a({\mathbf {r}})=n_0\), where \(n_0\) is the total number density. We assume that there is no net electric field in the system, but the plasma is immersed in slowly varying ambient magnetic field, \({\mathbf {B}}_0\), which could adiabatically depend on t or \({\mathbf {r}}\). We assume that \({\mathbf {B}}_0\) is directed along z axis. Let us separate physical quantities into the averages and fluctuations,
In what follows, we will omit the slow spatio-temporal variations associated with \(f_{a0}({\mathbf {r}},{\mathbf {v}},t)\) and \({\mathbf {B}}_0({\mathbf {r}},t)\), so that we may write \(f_{a0}({\mathbf {r}},{\mathbf {v}},t)=f_{a0}({\mathbf {v}})\) and \({\mathbf {B}}_0({\mathbf {r}},t)={\mathbf {B}}_0=\mathrm{const}\).
Inserting (2.2) to (2.1), we obtain
Taking the ensemble average on both sides, we obtain the formal particle kinetic equation,
where
is the cyclotron (or gyro) frequency. If we further assume that \(f_{a0}({\mathbf {v}})\) is independent of the velocity gyrophase angle \(\varphi\) (i.e., gyrotropic), where \(\varphi\) is defined by \({\mathbf {v}}=(v_\perp \cos \varphi ,v_\perp \sin \varphi ,v_\parallel )\) in cylindrical velocity coordinate system, then we may average (2.4) over \(\varphi\),
This is the gyrophase angle averaged formal particle kinetic equation. In the above \(f_{a0}({\mathbf {v}})\) is assumed to depend slowly on t.
Inserting (2.4) back to (2.3), we have
In the quasilinear closure, we ignore nonlinear terms on the right-hand side of (2.7), and thus we are left with
The field perturbations \(\delta {\mathbf {E}}({\mathbf {r}},t)\) and \(\delta {\mathbf {B}}({\mathbf {r}},t)\) satisfy Maxwell’s equation,
Solving (2.8) formally using the method of characteristics, we have
where going from the first to second equality, we have ignored the initial perturbation, and replaced the lower limit of the \(t'\) integral by \(-\infty\). In (2.9), \({\mathbf {r}}(t')\) and \({\mathbf {v}}(t')\) are the characteristics, satisfying
along the \(t'\) integral, but satisfying the requirement \({\mathbf {r}}(t'=t)={\mathbf {r}}\) and \({\mathbf {v}}(t'=t)={\mathbf {v}}\) when \(t'=t\). Note that the momentum equation in (2.11) reduces to
It is straightforward to show that the characteristics (2.11) and (2.12) are explicitly given by
In the quasilinear theory, the perturbed physical quantities can be represented in spectral transformation, where the time dependence is assumed to be proportional to \(\propto \exp (-i\omega t)\), where \(\omega\) satisfy the instantaneous or adiabatic linear dispersion relation, \(\omega =\omega _{\mathbf {k}}+i\gamma _{\mathbf {k}}\). Consequently, fluctuating physical quantities are represented by the Fourier transformation of the form
Making use of (2.13) and (2.14) we write the formal solution (2.10) in spectral representation, and also combine the Maxwell’s equation (2.9) by means of vector algebra, which leads to
In what follows, we assume \({\mathbf {k}}=k_\perp {\mathbf {e}}_x+k_\parallel {\mathbf {e}}_z\), without loss of generality. The detailed manipulations of (2.15) and (2.16) by making use of the Bessel function identities,
where \(J_n(b)\) is the Bessel function of the first kind of order n, are a standard exercise in any advanced graduate plasma physics course, so we leave the detailed task for the readers. The result is
In what follows, we use \(k_\parallel\), \(v_\parallel\) and \(k_z\), \(v_z\) interchangeably. Combining (2.18) with the field equation (2.16), we obtain the instantaneous or adiabatic dispersion equation,
where \({\mathbf {b}}={\mathbf {B}}_0/|{\mathbf {B}}_0|={\mathbf {e}}_z\), \(F_{a0}=f_{a0}/n_0\) is the distribution function with the ambient density taken out of the definition so that it is normalized to unity (\(\int {\mathrm{d}}{\mathbf {v}}F_{a0}=1\)), and \(\omega _{\mathrm{pa}}\) is the plasma frequency defined by
The wave kinetic equation follows trivially from the definition (2.14), and is given by
where \(\delta {\mathbf {E}}_{\mathbf {k}}^*=\delta {\mathbf {E}}_{-{\mathbf {k}}}\), and we have made use of the symmetry properties, \(\omega _{\mathbf {k}}=-\omega _{-{\mathbf {k}}}\) and \(\gamma _{\mathbf {k}}=\gamma _{-{\mathbf {k}}}\).
To construct the particle kinetic equation, consider the following quantity that appears on the right-hand side of the formal gyrophase angle averaged particle kinetic equation (2.6):
Abbreviating
we may rewrite the quantity I as follows:
In the above, those terms that contain the derivative \(\partial /\partial \varphi\) will vanish after the average over \(\varphi\). Consequently, we may ignore these terms at the outset. Upon inserting (2.18), we obtain
Upon inserting I to (2.6), and performing the gyrophase angle average, we arrive at the desired particle kinetic equation expressed in terms of \(F_{a0}=f_{a0}/n_0\),
An alternative expression is
The instantaneous dispersion relation determined from (2.19), the wave kinetic equation (2.21), and the particle kinetic equation (2.26), or equivalently, (2.27), form a self-consistent set of quasilinear kinetic theory.
2.2 Dielectric tensor for bi-Maxwellian velocity distribution function
It is useful to consider the specific form of dispersion equation (2.19) for bi-Maxwellian velocity distribution function,
Making use of the standard definite integrals involving Bessel functions and exponential functions,
where \(I_n(x)\) is the modified Bessel function of the first kind of order n, as well as the definition for plasma dispersion (or Fried–Conte) function and its derivatives,
we obtain
where \(\chi _{ij}^a({\mathbf {k}},\omega )\) is the linear dielectric susceptibility tensor and
Of course, the general dispersion relation is obtained from the solution of equation, which is given by
where
2.3 Moment kinetic equation for bi-Maxwellian model
We now derive the moment kinetic equation that describes the time evolution of the bi-Maxwellian plasma temperatures. The starting point is the definition of kinetic temperatures,
Upon taking the velocity moments of the kinetic equation (2.27), we obtain
With the definition for the diffusion coefficient, \(D_{\alpha \beta }\), we have
For the bi-Maxwellian distribution (2.28) the velocity integrals on the right-hand side of (2.37) and (2.38) can be computed in closed form, and we have
In this approach, instead of actually solving the particle kinetic equation (2.26) or (2.27), by assuming that the particle distribution function maintains the bi-Maxwellian form (2.28) for all time, we may simply solve for the evolution of the temperatures. Such an assumption is, of course an approximation, and in fact the validity of such an assumption must be tested. Such a caveat notwithstanding, in what follows, we will make use of the quasilinear moment kinetic equation in order to discuss the temperature anisotropy instabilities.
The advantages of employing such a simple method are several. First, this method obviously reduces computational efforts greatly when compared with direct particle-in-cell or hybrid numerical simulations or even when compare with the full numerical partial differential equation solution which the particle kinetic equation (2.26) or (2.27) is. Another advantage has to do with the fact that this method can easily be incorporated into macroscopic models of the solar wind in which large-scale quantities may vary in both space and time, and indeed, we will discuss such an approach later. In contrast, computer simulations are limited not only by spatial dimensions, but also it is not so trivial to simulate the spatial inhomogeneity. For this reason large-scale inhomogeneous solar wind dynamics is usually studied by means of the so-called expanding box simulation (Matteini et al. 2012; Hellinger and Trávníček 2008), which is a method to simulate what is essentially a uniform plasma but with arbitrarily expanding the simulation domain. The disadvantages of the use of simple quasilinear method with the assumed particle distribution function (in this case, bi-Maxwellian) are multiple. It ignores nonlinear mode coupling physics. Also, the distortion of velocity phase space as a result of local wave–particle dynamics is not captured. For instance, in the textbook problem of electrostatic bump-on-tail instability and subsequent velocity space plateau formation by quasilinear relaxation, the local distortion of the particle distribution cannot be modeled by any assumed form of particle distribution function. Fortunately for the anisotropy-driven instabilities, bulk of the particles participate in the wave–particle interaction so that the bi-Maxwellian model is at least acceptable as a first step. Quasilinear theory also ignores certain coherent nonlinear physics, such as the particle trapping by finite amplitude wave. In short, the present quasilinear moment kinetic theory must be applied judiciously, and guided by certain physical intuition. Moreover, the basic assumptions must be verified against more rigorous computer simulations (Seough et al. 2015a, b; Stockem Novo et al. 2015; Yoon et al. 2015).
3 Proton temperature anisotropy instabilities for parallel propagation
As shown in Fig. 1, the proton-cyclotron or electromagnetic ion-cyclotron (EMIC) instability is one of the unstable modes that provides a partial upper bound for the proton data distribution near 1 AU. When a parcel of solar wind plasma approaches the Earth’s magnetosphere, it may undergo a slight compression. The compression leads to an increase of perpendicular pressure, which leads to the excessive perpendicular temperature anisotropy, \(T_{\perp a}/T_{\parallel a}>1\) for each particle species labeled a. For protons, this condition leads to the excitation of two types of instability. For relatively low beta conditions, the left-hand circularly polarized electromagnetic ion-cyclotron (EMIC) instability is predominantly excited, while for relatively high beta values, the oblique aperiod mirror mode instability is also excited in addition to the EMIC instability, and compete for the available free energy. In general, the expanding solar wind generates excessive parallel temperature anisotropy, \(T_{\perp a}/T_{\parallel a}<1\), which leads to the excitation of firehose instability. As discussed in the Introduction, the firehose mode has two unstable branches, one is the so-called parallel firehose instability, and the second is the oblique aperiodic firehose instability. In the present review, we will limit ourselves to the parallel firehose modes only. In this section, we discuss instabilities characterized by parallel propagation. For parallel propagation, the dispersion relation for purely transverse electromagnetic mode for bi-Maxwellian plasma can be shown to greatly simplify, and is given by
3.1 Electromagnetic ion-cyclotron (EMIC) instability
The electromagnetic ion-cyclotron (EMIC) instability operates on the left-hand circularly polarized branch of (3.1). As a simple approximation, let us ignore the displacement current and thermal effects for the electrons. We may also assume \(\omega ^2\ll \varOmega _e^2\), so that we may approximate \(\omega -\varOmega _e\approx |\varOmega _e|\). This leads to the dispersion relation that supports EMIC instability,
Shown in Fig. 2 is the real frequency and growth rate versus normalized wave number for various temperature ratios and for fixed parallel beta. The temperature anisotropy-driven instabilities, including the EMIC instability, is determined by two dimensionless parameters, the temperature ratio, \(T_{\perp i}/T_{\parallel i}\), and parallel beta, \(\beta _{\parallel i}\), which is why the anisotropy–beta relationship, (1.1) or (1.2), and the data distribution plotted in the format shown in Fig. 1, are so useful and widely referred to in the literature.
We next discuss the nonlinear evolution of plasmas subject to the excitation of left-hand EMIC instability. For this purpose, we make use of the moment kinetic equations (2.39) and (2.40), which in the limit of \(k_\perp \rightarrow 0\), and for proton temperatures, are given by the following upon retaining only the contribution from the left-hand mode,
where the spectral wave energy density associated with the wave electric field is defined by
Of course, the wave kinetic equation is given by
Upon making use of the dispersion relation (3.2), the moment kinetic equations (3.3a) and (3.3b) may be simplified as follows:
where
is the square of the Alfvén speed, \(\omega _\mathrm{r}\) is the real part of the complex frequency, \(\gamma\) is the growth/damping rate (or the imaginary part of the complex frequency), and \(\delta B^2(k_\parallel )=|c^2k_\parallel^2/\omega^2| \delta \mathscr{E} (k_\parallel)\) is the magnetic field spectral intensity.
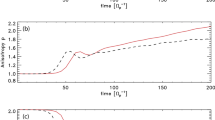
Figure 3 displays three cases of EMIC instability and its quasilinear evolution. From left to right, we considered initial states characterized by \(T_{\perp i}(0)/T_{\parallel i}(0)=2\) and three different initial betas, \(\beta _{\parallel i}(0)=0.1\), 1, and 10. The bottom panels represent the normalized wave energy \(\delta B^2/B_0^2\equiv \int {\mathrm{d}}k_\parallel \delta B^2(k_\parallel )/B_0^2\). The horizontal axis represents normalized time \(\tau =\varOmega _it\).
According to Fig. 3 it is seen that the initial temperature anisotropy, \(T_{\perp i}/T_{\parallel i}\), which is equal to 2 for all three cases, gets reduced as a result of instability excitation. In contrast, the parallel beta for all three cases increases as time progresses. The wave energy density associated with the unstable left-hand EMIC mode exponentially increases from the initial low level of intensity, until the mode gradually approaches saturated value. In the first case shown on the left top and bottom panels, the wave energy density monotonically increases until it reaches quasi-saturation stage. The full saturation is not shown since the computation was terminated before the wave intensity reaches the plateau stage. The true saturated plateau in the wave intensity can be seen in the middle two panels. For the third case of high initial beta, shown on the right, the wave exponentially increases, reaches the saturation, but subsequently the wave energy is partially reabsorbed by the protons, so the wave intensity exhibits the overshoot–undershoot behavior. This behavior is often seen in the particle simulation, and was often attributed to nonlinear mode coupling, but the present quasilinear analysis shows that the explanation can be provided within the quasilinear paradigm.
In Fig. 4, we display the maximum growth rate for EMIC instability in \(\beta _{\parallel i}\) versus \(T_{\perp i}/T_{\parallel i}\) phase space, and comparison with empirical fitting formula (1.1) with the coefficients \(S=0.65\) and \(\alpha =0.4\)—Eq. (1.4). This is the formula suggested by Gary et al. (1994a, b, c), and the fitting formula agrees excellently with the numerical maximum growth rate contour for \(\gamma _\mathrm{max}/\varOmega _i=10^{-2}\). Recall that this was the same formula superposed in Fig. 1 to indicate the rough upper-right boundary of the proton data distribution.
3.2 Parallel proton firehose instability
The firehose instability is excited in general for expanding solar wind since the expansion naturally leads to the parallel temperature anisotropy as a result of the conservation of first adiabatic invariant. To discuss the parallel proton firehose instability, we start from (3.1) but consider the lower sign,
Shown in Fig. 5 is the numerical solution for several combinations of input parameters. The dimensionless quantities are
In Fig. 6, we display the maximum growth rate for parallel proton firehose instability in the same \(\beta _{\parallel i}\) versus \(T_{\perp i}/T_{\parallel i}\) phase space as in Fig. 4 except for different plotting ranges, and we make the comparison with the empirical fitting formula (1.1) with \(S=-1.53\) and \(\alpha =0.74\), i.e., Eq. (1.5), which is the formula suggested by Gary et al. (1998), and the fitting formula agrees rather well with the numerical maximum growth rate \(\gamma _\mathrm{max}/\varOmega _i=10^{-1}\). This was the same formula for the marginal firehose stability curve superposed in Fig. 1 to indicate the rough lower-right boundary of the proton data distribution.
Quasilinear moment kinetic equation for parallel propagation, which is applicable for parallel proton firehose instability, can be discussed by again considering the limit of \(k_\perp =0\) in (2.39) and (2.40) and by limiting to the right-hand mode,
which upon making use of the dispersion relation (3.8) can be further simplified by
Figure 7 plots the solutions of quasilinear moment kinetic equations (3.11a) and (3.11b) for four different initial conditions, \(T_{\perp i}(0)/T_{\parallel i}(0)=0.1\) and \(\beta _{\parallel i}(0)=1\), 5, 10, and 20. The perpendicular and parallel betas, temperature ratio, as well as the wave energy density are plotted as a function of normalized time, \(\tau /\tau _\mathrm{max}\), where \(\tau =\varOmega _it\) and \(\tau _\mathrm{max}=1\times 10^4\), 60, 40, and 40, respectively, for the four different initial betas.
Figure 7 shows how the firehose instability relaxes the parallel temperature anisotropy. The perpendicular temperature, which is initially lower than the parallel temperature, undergoes an increase, as the upper-left panel shows. The initially high parallel temperature, on the other hand, decreases, as the upper-right panel shows. The temperature ratio \(T_{\perp i}/T_{\parallel i}\), which was less than unity at \(t=0\), increases toward unity as the instability develops (lower-left panel). The magnetic wave energy density exponentially increases, followed by saturation. In the present case of parallel firehose instability, the quasilinear behavior is generally the plateau formation in the saturation stage, although for \(\beta _\parallel (0)=20\), there is a weak overshoot–undershoot behavior, but when compared with EMIC instability case shown in Fig. 3, the reabsorption of the wave energy by the particles beyond the saturation stage is generally weak.
3.3 Validity of quasilinear moment theory
The assumption of bi-Maxwellian distribution for all times is clearly an approximation. Also, in the simple quasilinear paradigm nonlinear mode coupling or nonlinear wave–particle interaction (nonlinear Landau damping) is ignored. In order to test whether such an assumption is valid we have carried out one-dimensional particle-in-cell simulations (Seough et al. 2014, 2015a). We found that the agreement between the simplified quasilinear theory and PIC simulation is quite good in the case of proton-cyclotron instability, but for parallel proton firehose instability the agreement became poorer. The results for EMIC instability is shown in Fig. 8, where it can be seen that the agreement between the theory and simulation is quite good.
The details of the 1D PIC simulation setup are described in Seough et al. (2014, 2015a), so we will not repeat them here. In Fig. 8 it can be seen that the comparison between the quasilinear moment method and PIC simulation for proton firehose instability shows generally favorable agreement. It is noteworthy that the overshoot–undershoot behavior mentioned in regard to Fig. 3, which is explained by partial reabsorption of wave energy by the protons during the overshoot–undershoot process associated with the waves, is reproduced in the simulation.
Figure 9 shows the comparison between the quasilinear moment method and PIC simulation for proton firehose instability. In this case the agreement is appreciably poorer than the case of EMIC instability. The disagreement is more pronounced for the waves, although the early exponential growth phase is excellently reproduced by theory. The post-saturation phase of the wave growth is not very well described by quasilinear theory. Note that the PIC code simulation shows pronounced overshoot–undershoot, followed by multiple intensity undulations. As for the particle quantities, the agreement between the theory and simulation is actually quite good for \(\beta _{\parallel i}(0)=5\) and 10, which correspond to moderate and high betas. At the present moment, the precise reason for the differences showcased in Fig. 9 is not entirely clear. One possible cause is that the left-hand EMIC mode is highly dispersive, meaning that the wave phase speed \(v_\varphi =\omega /k_\parallel\) greatly varies over the unstable range of wave numbers, such that there are multiple particle pitch-angle scattering centers in the velocity space. As particles diffuse along the arc defined with respect to each multiple pitch-angle centers, the overall bi-Maxwellian form of the distribution function is maintained in the case of EMIC instability. However, for the parallel proton firehose instability, the wave phase speed is defined only over a very narrow range such that all particles pitch-angle scatter about the nearly identical paths defined in the wave frame. This contributes to the distortion of the initial bi-Maxwellian form into a dumb-bell shape distribution (Astfalk and Jenko 2017), and leads to the premature quenching of the instability. The time evolution of the initially bi-Maxwellian distribution in PIC code runs is discussed in Seough et al. (2014, 2015a), and shows that indeed, for EMIC case, the quasi-bi-Maxwellian shape is maintained throughout most of the simulation time. In contrast, for PFH case, the bi-Maxwellian form gets distorted quite early on, even though later on, the quasi-bi-Maxwellian shape appears to be restored. Another cause for the less-than-favorable comparison between the theory and simulation in the case of PFH instability is that, unlike the case for EMIC instability, the PIC simulation generates longitudinal electrostatic fluctuations, which were shown to possess ion acoustic mode characteristics. This indicates the presence of nonlinear wave–wave decay interaction, which the quasilinear theory does not have.
4 Mirror instability and competition with EMIC instability
When the solar wind plasma is compressed against the Earth’s magnetosphere, excessive perpendicular temperature anisotropy can be spontaneously generated. This leads to conditions favorable for the excitation of EMIC and mirror instabilities. We have already discussed the linear and quasilinear properties of EMIC instability. In this section, we consider the obliquely-propagating, aperiodic mirror instability.
4.1 Mirror instability
Returning to (2.31), consider isotropic cold electrons. Then we may approximate for electrons,
For ions we assume \(\omega /\varOmega _i\ll 1,\) so that only \(n=0\) terms may be retained and higher gyro-harmonic terms can be ignored,
This is because the mirror instability is a low-frequency mode satisfying \(\omega /\varOmega _i\ll 1\). As a consequence, we may ignore terms of order \(\omega /\varOmega _i\), and electron response for xy and yz components. Moreover, we may assume \(\xi \ll 1\) for the ions. This implies that yz and zz components among the ion response can be ignored upon making use of the ordering, \(Z'(\xi )\gg \xi \,Z'(\xi )\gg \xi ^2\,Z'(\xi )\). This leads to the dispersion relation, which is expressed as
From this we obtain the mirror mode dispersion relation
Figure 10 plots a typical growth rate for the purely growing (or aperiod) mirror instability in the case of \(T_{\perp i}(0)/T_{\parallel i}(0)=2\) and \(\beta _{\parallel i}(0)=10\). As the plot shows, the peak growth rate takes place at an oblique angle so that to describe the mirror instability one must consider both \(k_\parallel\) and \(k_\perp\).
The contour plot of maximum growth rate for mirror instability as well as the empirical fitting function (1.1) with parameters \(S=0.87\) and \(\alpha =0.56\), or Eq. (1.3) (which are the same choices used in Fig. 1) are displayed in Fig. 11.
Quasilinear theory for mirror instability can be discussed on the basis of the generic form of temperature evolution equations (2.39) and (2.40), except that we only consider the ion temperatures, and retain only the y component electric field,
For low-frequency mirror mode we may ignore all cyclotron harmonics and only consider the Landau resonance (\(n=0\)),
Making use of the dispersion relation (4.4) we may further simplify (4.7) and (4.8),
Figure 12 plots the time evolution of perpendicular and parallel betas in response to the excitation and saturation of the mirror instability (top panel). The lower panel shows the magnetic field energy density associated with the mirror instability. The overall dynamical consequences of the mirror mode instability on the particle quantities, that is, the temperatures, are similar to that of the EMIC instability. The instability is saturated via the reduction of perpendicular temperature and concomitant increase of parallel temperature. This is because both EMIC and mirror mode instabilities are driven by the same free energy source. Consequently, in general both instabilities will be simultaneously excited and in the nonlinear (or quasilinear) stage, they will compete for the same available free energy. We turn to this problem next.
4.2 Competition between mirror and EMIC instabilities
To describe the competition between EMIC and mirror instabilities, we now discuss the two (or with cylindrical symmetry, three) dimensional theory of EMIC instability. From (2.31), we impose the same simplification (4.1) for the electrons. For the ions we assume \(\omega /\varOmega _i\sim 1\) so that only \(n=1\) terms may be retained and all other gyro-harmonic terms and Landau resonance terms can be ignored,
In the above we ignored xz and zx components since the EMIC mode is predominantly quasi-parallel mode characterized by \(k_\parallel > k_\perp\). This leads to
From this we obtain the 2D EMIC dispersion relation
In the velocity moment kinetic equation (2.39) and (2.40), we again consider only ions, and ignore the z component of the electric field fluctuation. We retain only the \(n=1\) term and ignore \(2\lambda \varLambda '_n\) associated with the y component of the electric field fluctuation,
Making use of the dispersion relation (4.13), we simplify the above equations,
To discuss quasilinear development of combined mirror and EMIC instability, we add the terms on the right-hand sides of (4.9) and (4.10), which represents the effects of mirror instability, and the terms on the right-hand sides of (4.16) and (4.17), which represents the effects of EMIC instability on the temperatures. Shown in Fig. 13 is the 2D EMIC instability dispersion surface (mesh plots) and growth rate (surface plots underneath). The input parameters are described in the caption. Figure 14 shows the mirror mode growth rate for the same set of input parameters. In the quasilinear development, both EMIC and mirror modes will affect the evolution of temperatures.
Dispersion relation for unstable 2D EMIC mode. The input parameters are (top left) \(T_{\perp i}/T_{\parallel i}=4\) and \(\beta _{\parallel i}=0.5\), (top right) \(T_{\perp i}/T_{\parallel i}=4\) and \(\beta _{\parallel i}=1\), (bottom left) \(T_{\perp i}/T_{\parallel i}=4\) and \(\beta _{\parallel i}=1.5\), and (bottom right) \(T_{\perp i}/T_{\parallel i}=4\) and \(\beta _{\parallel i}=2\)
Growth rate for unstable mirror mode. The input parameters are the same as Fig. 13
We show in Fig. 15, the result of quasilinear calculations of combined proton-cyclotron and mirror instabilities. For \(\beta _{\parallel i}(0)=0.5\), the EMIC mode completely dominates the wave amplification process. For the case of \(\beta _{\parallel i}(0)=2\), in contrast, the total wave energy density almost completely comprises mirror mode waves. In the intermediate case of \(\beta _{\parallel i}(0)=1\), initially both the cyclotron and mirror modes grow with comparable exponential amplification behavior. However, for time steps around \(\tau =\varOmega _it\approx 25\) to \(\tau \approx 75\) or so, the mirror mode overshoots the EMIC mode in terms of their relative wave energy density. Beyond \(\tau \approx 75\) or so, the proton-cyclotron mode catches up with the mirror mode in wave intensity, and eventually the cyclotron mode ends up with higher wave energy density at the saturation stage.
Upper panels show the time evolution of temperature anisotropy \(T_{\perp i}/T_{\parallel i} =\beta _{\perp i}/\beta _{\parallel i}\) (solid lines) and parallel beta \(\beta _{\parallel i}\) (dashes). Lower panels display the time evolution of wave energy density \(\int {\mathrm{d}}{\mathbf {k}}\;W({\mathbf {k}}) =\int {\mathrm{d}}{\mathbf {k}}\;\delta B^2({\mathbf {k}})/B_0^2\). Solid lines represent the total (proton-cyclotron plus mirror) wave energy density, dotted curves show the wave energy density corresponding to the cyclotron mode, \(\int {\mathrm{d}}{\mathbf {k}}\;W_C({\mathbf {k}})\), and the mirror mode wave energy density, \(\int {\mathrm{d}}{\mathbf {k}}\;W_M({\mathbf {k}})\), is shown with dashes. For all three cases, the initial anisotropy is \(\beta _{\perp i}(0)/\beta _{\parallel i}(0)=4\), and three cases of initial parallel betas are considered, \(\beta _{\parallel i}(0)=0.5\) (left), 1 (middle), and 2 (right)
5 Proton temperature anisotropy instabilities in inhomogeneous solar wind
Having discussed the linear and quasilinear properties of the various anisotropy-driven instabilities, we may incorporate the influence of these instabilities on the global dynamics of the solar wind. In this section, we thus discuss the effects of kinetic instabilities on the large-scale solar wind plasma that is characterized by large-scale inhomogeneities. The adiabatic forcing on macroscopic quantities is an important factor that determines the large-scale properties. For expanding solar wind, the adiabatic forcing effect will lead to the generation of parallel excessive temperature (or more accurately, pressure) anisotropy, which the excitation of kinetic-scale firehose instability will eventually counter-balance. Suppose that the magnetic field geometry is largely radial. That is, magnetic field intensity varies along the field. For axially varying magnetic field, it is well known that there are two adiabatic invariants, the magnetic moment \(\mathcal{M}\) and the Hamiltonian \(H_a\),
This means that the Vlasov equation in the absence of wave–particle interaction is given by
For inhomogeneous plasma with diverging or converging magnetic field the left-hand side of the kinetic equation for particles must be modified in accordance with (5.2). For the sake of simplicity, let us restrict ourselves to parallel propagation. We also ignore the electrostatic field. In this case, we have
The moments of the distribution function are defined by
Let us take the moments of the kinetic equation (5.3):
Specifically, if we focus on the ions (\(a=i\)). Upon making use of explicit definition for diffusion tensor, we obtain
For the electrons we simply adopt the fluid approximation without the wave–particle interaction,
where we have assumed the bi-Maxwellian distribution function. The wave dispersion relation is the same as EMIC or PFH instability dispersion relations, (3.2) or (3.8).
In what follows, let us assume \(V_i=V_e\), and we work in the moving plasma frame so that in computing the right-hand sides of (5.9a)–(5.9d), we may ignore \(V_i\). Suppose that we are interested in a stationary problem, \(\partial /\partial t=0\), and that the magnetic field and density profile are given by a Lorentzian model,
We also assume constant solar wind speed, \(V_i=V_e=V=\mathrm{const}\). Then from the electron fluid equations we obtain,
The Lorentzian models for density and magnetic field intensity with constant speed are chosen above for the sake of simple illustration. The more sophisticated calculation requires the full consideration of continuity and momentum equations, but for the present purpose of illustrating the effects of large-scale adiabatic forcing versus the local wave–particle interaction effects (that is, instability), the simple Lorentzian model (or any other suitable model) suffices.
In order to solve the steady-state version of Eqs. (5.9a)–(5.9d), we introduce the normalized quantities,
where \(V_{\mathrm{A}0}\) is the Alfvén speed at \(x=0\). Note that local proton betas are defined by
We solved (5.9a)–(5.9d) numerically for \(L_*=10^4\) and \(u=3\). We call the spatial boundary \(X=0\) “the source region”, and we solve the set of Eqs. (5.9a)–(5.9d) up to normalized distance \(X\equiv \varOmega _{i0}r/V=4\times 10^5\). We conveniently name this boundary “the Earthward boundary”.
(Top) Spatial structure of the temperature ratio \(T_{\perp i}/T_{\parallel i}\) (green), perpendicular and parallel betas, \(\beta _{\perp i}\) (blue) and \(\beta _{\parallel i}\) (red), versus normalized distance. Dotted lines represent adiabatic theory without the wave–particle interaction taken into account, while solid lines depict the influence of kinetic instabilities. (Bottom) Spatial distribution of perturbed magnetic field intensities associated with EMIC (\(W_c\)) and parallel firehose (\(W_F\)) instabilities
Figure 16 displays the numerical solution. The sunward boundary condition is \(\beta _{\perp i}(0)/\beta _{\parallel i}(0)=8\) and \(\beta _{\parallel i}(0)=0.02\). Top panel shows particle quantities, the temperature ratio \(T_{\perp i}/T_{\parallel i}\) (green), perpendicular beta \(\beta _{\perp i}\) (blue), and parallel beta \(\beta _{\parallel i}\) (red). The bottom panel displays perturbed magnetic field intensities associated with EMIC (\(W_c\)) and parallel firehose (\(W_F\)) instabilities. Figure 16 displays the stationary spatial distribution of these quantities as a function of normalized distance.
Near the source, at some distance away from the source, the convective growth of the proton-cyclotron or EMIC (C) instability takes place owing to the excessive perpendicular temperature anisotropy present at the source. However, as the observer moves along the field lines away from the source region, the combination of adiabatic and quasilinear relaxation leads to the saturation of mode C. Furthermore, this combined effects result in the increase in the parallel beta and reduction of the anisotropy. The initially excited and saturated wave energy density associated with proton-cyclotron mode gradually decreases and then reaches the noise level (bottom panel). According to the strict adiabatic expansion model, the perpendicular beta is supposed to remain unchanged (dotted blue curve). However, as the wave–particle interaction leads to perpendicular cooling and parallel heating, the parallel beta increases, until the combined adiabatic and quasilinear process leads to a situation where the parallel beta is higher than the perpendicular beta. In this situation, the plasma becomes unstable to the parallel firehose instability (F). As the firehose instability is excited, the parallel beta gets reduced while the perpendicular beta abruptly increases.
Beyond the spatial location at which the firehose instability begins to be excited, one can observe that the quasilinear relaxation dominates over the double-adiabatic expansion effects. It is therefore apparent that the kinetic wave–particle interaction must be incorporated in order to properly model the solar wind. The overall situation is that the temperature ratio becomes nearly 1, while the parallel beta monotonically increases as one approaches the “Earthward” boundary. Near the “Earthward” boundary, the firehose instability operates in a marginal state in which the quasilinear relaxation is critically balanced by the adiabatic effects. This can be seen by the fact that the firehose wave energy density undergoes irregular and repeated increase followed by decrease, and increase again (see the bottom panel). Note that even though we are concerned with a steady-state situation, if one views the present numerical model as representing the moving solar wind frame, then the present computational results can be interpreted in the dynamical sense as well.
The trajectory of the “solar wind” in \((\beta _\parallel ,T_\perp /T_\parallel )\) space, whose “Sunward” position and “Earthward” state are indicated. Various empirical threshold conditions (EMIC), mirror (M), parallel firehose (PFH), and oblique firehose (ObFH) conditions are indicated for reference
It is instructive to re-plot the spatial evolution of the physical quantities in the anisotropy–beta diagram. Such a plot reveals the dynamical behavior associated with the solar wind subject to combined adiabatic and quasilinear effects in a new light. Thus we plot in Fig. 17, the trajectory of the solar wind in \((\beta _\parallel ,T_\perp /T_\parallel )\) space, characterized by the “initial” condition, \([\beta _\parallel (0),T_\perp (0)/T_\parallel (0)]=(0.02,8)\). For a visual guide, we also plot the marginal stability conditions obtained from the linear stability theory for the proton-cyclotron (solid) and mirror (dashed) instabilities in the case \(T_\perp >T_\parallel\), and for the parallel (dotted) and oblique (dash-dotted) firehose instabilities in the case \(T_\parallel >T_\perp\) (Hellinger et al. 2006), namely, Eq. (1.2), where \((S,\beta _0,\alpha )\) are fitting parameters empirically determined as (0.43, 0.0004, 0.42) for the proton-cyclotron, (0.77, 0.016, 0.76) for mirror, \((-0.47, -0.59, 0.53)\) for parallel firehose, and \((-1.4, 0.11, 1)\) for the oblique firehose instabilities. The scheme to determine these parameters by empirical means on the basis of numerical solution of linear dispersion relations is explained in Hellinger et al. (2006), so we will simply adopt these parameters. The normalized wave magnetic field energy density, \(\delta B^2/B_0^2\), is depicted by the color map scale. The thin white line in the middle of the phase space trajectory aids visualize the details of the trajectory. The adiabatic trajectory without the influence of instability is also plotted with red dashes, which overlaps with the actual trajectory within the stable region, but becomes visible outside the marginal firehose threshold area. Since we chose initially unstable state subject to the proton-cyclotron instability, the proton-cyclotron mode is excited near the sunward boundary. However, as can be seen from the fact that the actual path largely overlaps the adiabatic trajectory, the influence of the EMIC excitation is not too dramatic.
As the solar wind plasma evolves toward the marginal stability threshold for parallel firehose instability, the plasma does not settle down close to the parallel firehose instability threshold, but instead it overshoots the marginal stability curve. The trajectory then abruptly changes course in \((\beta _{\parallel i},T_{\perp i}/T_{\parallel i})\) space, and crosses the marginal parallel firehose curve again. The trajectory subsequently undergoes undulations near the threshold crossing the curve multiple times. During these oscillatory phases, the adiabatic effects compete with quasilinear relaxation process. Similar behavior near the firehose instability threshold is also found in expanding box hybrid simulations for firehose instabilities (Matteini et al. 2006; Hellinger and Trávníček 2008).
6 Collisional age effects on kinetic instabilities operative in expanding solar wind
As the previous section shows, the expanding solar wind naturally generates the temperature anisotropy, but the kinetic instabilities are excited in order to reduce the anisotropy to an upper bound. However, while the instability theory is useful for explaining the existence of the upper and lower bounds of the temperature ratio, an outstanding issue is that most of the actual solar wind plasma resides far away from the marginal stability boundary (see Fig. 1), and is best described as in a quasi-isotropic condition. One of the possible mechanisms that counteracts the expansion force is the cumulative collisional effect called the collisional age. In the literature, when binary collisions are discussed, the collisional operator of Landau type is often used. However, the Landau equation is applicable for unmagnetized plasmas, whereas the solar wind is magnetized. The present author (Yoon 2016c) correctly formulated the collisional relaxation of bi-Maxwellian temperatures. For the sake of completeness, we briefly outline the derivation.
6.1 Collisional kinetic equation for magnetized plasmas
For the derivation of a collisional operator for magnetized plasmas, we assume the electrostatic approximation, for which the formal solution of the perturbed phase space density within the Klimontovich formalism is given by
Here \(\delta N_{{\mathbf {k}},\omega }^{a0}({\mathbf {v}})\) represents the phase density perturbation owing to the discrete nature of the particles. In the purely collisionless Vlasov formalism this quantity is absent. In the Klimontovich theory, however, this quantity contributes to the collisionality of the plasma. For electrostatic problem, we may write
Assuming \({\mathbf {k}}=k_\perp {\mathbf {e}}_z+k_\parallel {\mathbf {e}}_z\), we may carry out the \(\tau\) integral, as before,
Inserting this to the Poisson equation we have
From this we find that
In the Klimontovich formalism the fluctuation that arises from the discrete nature of the particles is described by the ensemble average of the products of perturbed phase space distribution, which is given by
where \({\mathbf {r}}(t-t')\) and \({\mathbf {v}}(t-t')\) are given by (2.13). Taking the Fourier spectral transformation, we obtain
Inserting (6.7) to (6.5), we obtain
From this, we also have
The collisional kinetic equation under electrostatic approximation, and gyro-averaged, is thus given by
Upon writing
we arrive at the desired collisional kinetic equation,
This equation generalizes the Balescu–Lenard equation for unmagnetized plasmas. The collisional relaxation of bi-Maxwellian temperatures can be discussed on the basis of the above equation.
6.2 Collisional relaxation for anisotropic temperatures
From (6.12), if we approximate by assuming \(\varepsilon ({\mathbf {k}},k_\parallel v_\parallel )\approx 1\), then we have the Landau equation for magnetized case. Taking the density out of \(f_{a0}=n_aF_{a0}\), we make use of the definition for effective perpendicular and parallel temperatures, and take the velocity moments of the kinetic equation,
If we assume bi-Maxwellian \(F_{a0}\), then after some lengthy calculations, the details of which can be found in Yoon (2016c), we have
where
and
In the above
and \(E_1(x)=\int _x^\infty t^{-1}\mathrm{e}^{-t}\,{\mathrm{d}}t\) is the exponential integral.
Yoon (2016a) systematically derived the simplified form of the collisional relaxation equation from (6.15) and (6.16). Here, we present the final form
This is the equation for temperature relaxation purely on the basis of collisional interaction.
For numerical computation, we define
Numerical integrations show that
6.3 Wave–particle and collisional relaxation of temperature anisotropy for inhomogeneous plasmas
Now that we have derived the collisional relaxation equation, we may add the right-hand sides of (6.21a)–(6.21d) to the macro-kinetic equation (5.9a)–(5.9d). We adopt the same density (and B field intensity) form factor given by the Lorentzian function,
where r represent spatial variable, and \(r_0\) is some reference point on the sunward boundary. The equations to solve are then those for the temperatures and waves,
In the above, the mode designation \(\sigma =-1\) corresponds to the proton-cyclotron mode, which we will denote as mode C subsequently, and the mode corresponding to \(\sigma =+1\) represents the firehose mode (F). Note that mode C is driven by excessive perpendicular temperature anisotropy, \(T_{\perp i}/T_{\parallel i}>1\), while mode F is driven unstable by excessive parallel temperature anisotropy, \(T_{\perp i}/T_{\parallel i}<1\).
A dimensionless quantity that determines the degree of collisionality is
where \(\rho _i\) is the thermal gyroradius. Figure 18 displays the numerical solution in the format of solar wind “data” trajectories in \((\beta _{\parallel i}, T_{\perp i}/T_{\parallel i})\) space. Different choices for the “sunward” boundary conditions are shown with open circles. Figure 18 is for purely collision-free situation with \(g=0\). This figure is essentially the same as Fig. 17, except that in Fig. 17 only a single initial configuration is considered, whereas in the present Fig. 18, we consider an ensemble of initial points near the sunward boundary.
Consider the top panel. The wave energy density is depicted in terms of color level. Near the “sunward” source, convective growth of the proton-cyclotron (C), or equivalently, electromagnetic ion-cyclotron (EMIC) instability takes place because of excessive perpendicular temperature anisotropies associated with source boundary conditions. The proton-cyclotron (C) mode subsequently undergoes stabilization by combined effects of quasilinear saturation, reabsorption of wave energy by the particles, and adiabatic expansion. The expansion spontaneously generates excessive parallel temperature anisotropy, which leads to the excitation of parallel firehose mode. Eventually, quasilinear relaxation by the firehose instability causes the solar wind protons in \((\beta _{\parallel i}, T_{\perp i}/T_{\parallel i})\) space to bounce back to the inner region of the stability boundary. Subsequently, the trajectories are seen to move in and out of the parallel firehose threshold curve. Over long distances, the solar wind data points all reside in between the parallel and oblique firehose threshold conditions, which is interesting since we do not consider the oblique firehose instability in the present calculation. So, the fact that asymptotic solar wind data are sandwiched between the two firehose instability thresholds is purely coincidental. Note that we have superposed marginal stability conditions for the mirror, proton-cyclotron (EMIC), parallel, and oblique firehose instabilities, as empirically constructed by Hellinger et al. (2006), as visual guides.
Consider next the bottom panel, which shows the same numerical result except that the logarithm of \(T_{\perp i}/T_{\parallel i}\) is plotted versus normalized distance X. From the bottom panel, spatial scales associated with the adiabatic processes that lead to the reduction of the temperature ratio, and the spatial scale associated with subsequent increase of \(T_{\perp i}/T_{\parallel i}\) as a result of excitation of parallel firehose instability, can be gleaned.
(Top) Spatial distribution of the “solar wind data” in \((\beta _{\parallel i},T_{\perp i}/T_{\parallel i})\) space, whose “sunward” boundary conditions are shown with open circles. This case is for purely collision-free situation with \(g=0\). (Bottom) The same numerical result as the top panel except that the logarithm of the temperature ratio is plotted versus normalized distance X
In Fig. 19, we consider finite collisionality by choosing \(g=0.01\). In this case, one may discern the deviation of the trajectories in \((\beta _{\parallel i}, T_{\perp i}/T_{\parallel i})\) space from the collision-free case toward isotropic states. Some trajectories overshoot the firehose marginal stability condition substantively before turning back and settling down near the firehose threshold curves. Since actual observations made near 1 AU show that most data points do not exceed the firehose threshold curves, the overshoot behavior is not consistent with actual data, implying that the choice of \(g=0.01\) is probably too high and not realistic. Nevertheless, the important point here is that collisional age can in principle contribute to the isotropization of the solar wind protons, provided the parameter g can be sufficiently high. However, as we will discuss below, it is unlikely that for typical solar wind the collisional age effect is important.
The same as Fig. 20, except \(g=0.01\)
Near 1 AU the typical number density is \(n\sim 3.4\) \(\mathrm{cm}^{-3}\). magnetic field strength of \(B\sim 6.2\) nT \(=6.2\times 10^{-5}\) gauss is also typical. The proton temperature can be typically \(T_i\sim 1.2\times 10^5\) K \(=10.34\) eV. From this, we have \(v_\mathrm{A}\sim 2.18\times 10^{11}n^{-1/2}B_{[\mathrm{{gauss}}]} \sim 7.3301\times 10^6\) (cm/s), perpendicular proton thermal speed, \(v_{T\perp i}\sim 9.79\times 10^5T_i^{1/2}{}_{[\mathrm{{eV}}]}\) \(\sim 3.1482\times 10^6\) (cm/s), and \(\varOmega _i=9.58\times 10^3B_{[\mathrm{{gauss}}]}\sim 0.5940\) (rad/s). This leads to \(n\rho _i^3(v_\mathrm{A}/c)^4=n(\alpha _{\perp i}/\varOmega _i)^3 (v_\mathrm{A}/c)^4\sim 1.8041\times 10^6\), and thus g is of the order \(10^{-6}\) to \(10^{-4}\), which is too low when compared with the arbitrary choice of \(g=10^{-2}\) considered in Fig. 21. This shows that unless the plasma is unusually collisional, the collisional age effect is generally not expected to be important, at least not for the protons. However, as Yoon (2016c) shows, the collisional relaxation of the temperature anisotropy for the electrons proceeds on a much faster time scale so that the collisional age effect may actually be important for the electrons. This is a subject matter that deserves a separate investigation, which is beyond the scope of the present review.
7 Effects of dynamic electrons and isotropization of solar wind protons
In this section, we relax the assumption of cold and isotropic electrons and investigate the dynamical interplay of electrons and protons via the electron anisotropy instability excitation that takes place in an inhomogeneous medium. In order to simplify the matter, we consider only left-hand circularly polarized modes propagating parallel to the ambient magnetic field. For such a mode, the excessive parallel electron temperature anisotropy, \(T_{\parallel e}>T_{\perp e}\), excites the parallel electron firehose mode under a high beta condition, while for excessive perpendicular proton temperature anisotropy, \(T_{\perp p}>T_{\parallel p}\), the proton-cyclotron or electromagnetic ion-cyclotron (EMIC) instability is excited. Consequently, the two unstable modes may influence both species of charged particles as the instability develops in the framework of quasilinear theory. It turns out that the electron–proton coupling leads to an effective counter-balancing force against the adiabatic forcing term that operates in expanding solar wind.
While the solar wind data distribution boundaries are partially explained by plasma instability theories, the majority of actual data points are broadly distributed in various states that can be described as being quasi-isotropic, \(T_{\perp a}\sim T_{\parallel a}\)—see Fig. 1. Macroscopic–kinetic models (Denton et al. 1994; Hellinger and Trávníček 2008; Chandran et al. 2011; Yoon and Seough 2014) or expanding box hybrid simulations (Hellinger and Trávníček 2008; Matteini et al. 2012) predict that expanding solar wind should rapidly and inexorably evolve toward the marginal firehose state such that most data points should accumulate near the boundary in \((\beta _{\parallel a},T_{\perp a}/T_{\parallel a})\) phase space, which is at variance with actual observation. This implies that some processes are operative in order to counter-balance the effects of radial expansion. In the literature, a number of possible causes have been put forth: perpendicular heating by intrinsic large-amplitude Alfvénic fluctuations, ion-cyclotron waves, and/or kinetic Alfvén waves, collisional age effect (but this effect has shown to be ineffectual in the previous section, at least for the protons), intermediate-scale spatio-temporal variations for density and magnetic field intensity that are either intrinsic (Seough et al. 2013) or are generated by low-frequency compressive turbulence (Verscharen et al. 2016), and large-scale non-monotonic structures (Yoon 2016b). Against this backdrop, the dynamical coupling of protons and electrons through the instability process constitutes yet another mechanism, which may contribute toward the resolution of the isotropization problem (Yoon and Sarfraz 2017). Before we discuss this issue, let us extend the quasilinear moment kinetic theory to electron anisotropy instabilities.
7.1 Quasilinear theory of electromagnetic electron-cyclotron (EMEC) instability
Let us now adapt the quasilinear moment kinetic equations (2.39), (2.40), and the dispersion relation (3.1) to electrons. For the solar wind electrons, the assumption of a single bi-Maxwellian model is not appropriate since it is well known that the solar wind electrons are made of several different components. In the present discussion, let us therefore assume that the solar wind electrons are made of a Maxwellian core (c) with low temperature and high density, and a hot halo (h) component with high temperature and low density. In such a model, we may write down the temperature equations for both species,
The instantaneous dispersion relation for the electromagnetic electron-cyclotron (EMEC) wave and instability, which is a right-hand circularly polarized mode, is given by
Figure 20 shows unstable EMEC mode (Saeed et al. 2017). One group of solutions is for the case when the core temperature anisotropy is \(T_{\perp c} / T_{\parallel c} = 1\) and the halo anisotropy \(T_{\perp h} / T_{\parallel h}\) varies from 2 to 4, and the other group of solutions is for the case when the halo is isotropic and the ore anisotropy varies as \(T_{\perp c} / T_{\parallel c} = 2, 3, 4\). Other input parameters are specified in the figure caption. Figure 20 shows that growth rate of the EMEC mode is higher when the anisotropy resides in the core, although halo electron anisotropy also contributes to the growth of EMEC instability. This conclusion is based upon the input parameters adopted in Fig. 20 and it is by no means general. For very low core temperatures the halo temperature anisotropy may in fact be the dominant source of instability.
Quasilinear evolution of the core and halo temperatures (or betas) as well as the wave energy density associated with the EMEC instability is shown in Fig. 21 (Sarfraz et al. 2016). In Fig. 21, the left-most panel is for initial values of \(T_{\perp h}(0)/T_{\parallel h}(0)=3\), \(\beta _{\parallel h}(0)=0.36\), and \(\beta _{\perp c}(0) =\beta _{\parallel c}(0)=0.04\); the middle panels are for \(T_{\perp h}(0)/T_{\parallel h}(0)=4\), \(\beta _{\parallel h} (0)=0.38\), and \(\beta _{\perp c}(0)=\beta _{\parallel c} (0)=0.05\); and the right-hand panels are for \(T_{\perp h}(0)/T_{\parallel h}(0)=6\), \(\beta _{\parallel h}(0)=0.40\), and \(\beta _{\perp c}(0)=\beta _{\parallel c}(0)=0.06\).
Time evolution of normalized temperatures (betas) for core component, \(\beta _{\perp c}\) and \(\beta _{\parallel c}\) (top), for halo component, \(\beta _{\perp h}\) and \(\beta _{\parallel h}\) (middle), and wave energy density \(\delta B^2/B_0^2\) (bottom), versus normalized time, \(\tau =\varOmega _et\), for initially isotropic core electrons. Left-hand panels are for initial halo anisotropy \(\beta _{\perp h}(0)/\beta _{\parallel h}(0)=3\), \(\beta _{\parallel h}(0)=0.36\), and \(\beta _{\perp c}(0)=\beta _{\parallel c}(0)=0.04\); the middle panels are for \(\beta _{\perp h}(0)/\beta _{\parallel h}(0)=4\), \(\beta _{\parallel h} (0)=0.38\), and \(\beta _{\perp c}(0)=\beta _{\parallel c} (0)=0.05\); the right-hand panels represent the initial condition \(\beta _{\perp h}(0)/\beta _{\parallel h}(0)=6\), \(\beta _{\parallel h}(0)=0.40\), and \(\beta _{\perp c}(0)=\beta _{\parallel c}(0)=0.06\)
The purpose the discussion on EMEC instability in this subsection is for the purpose of completeness. The EMEC instability is a high-frequency mode, which does not influence the protons in any significant manner. As such, electrons with excessive perpendicular temperature does not couple with the protons in any appreciable way. However, when the temperature anisotropy for the electrons is with the parallel component, then the electron firehose (EFH) instability, which operates near the proton-cyclotron frequency, has a dynamical impact on the protons. We discuss the electron parallel firehose instability next.
7.2 Quasilinear theory of parallel electron firehose (EFH) instability
In this subsection we discuss the parallel electron firehose instability in a uniform plasma. In the next section we will discuss the dynamic interplay between the electrons and protons, which contributes to the isotropization of the protons. Before we do that, however, it is instructive to discuss the case of a uniform plasma. The instantaneous dispersion relation and the temperature evolution equations for the parallel electron firehose instability can be derived from the generic transverse dispersion equation (3.1) and the moment kinetic equation (2.39) and (2.40). For the sake of simplicity, let us treat the solar wind electrons as a single component bi-Maxwellian distribution. Unlike the EMEC instability, the parallel proton firehose instability operates on the left-hand mode branch, and it is a low-frequency mode. Consequently, the electron FH instability interacts with the protons. The relevant equations are
together with the trivial wave kinetic equation. A sample calculation is shown in Fig. 22. The input parameters and physical descriptions are self-explanatory (Sarfraz et al. 2017). The important point here is that one of the consequences of the excitation of electron firehose instability is that the protons are heated in the perpendicular direction while along the parallel direction, the proton beta also changes. This is the key to explaining how dynamic electrons can lead to isotropization of the solar wind electrons.
(Left) Time evolution of normalized temperatures (betas) for electrons, \(\beta _{\perp e}\) and \(\beta _{\parallel e}\) (top), for protons, \(\beta _{\perp i}\) and \(\beta _{\parallel i}\) (middle), and wave energy density \(\delta B^2/B_0^2\) (bottom), versus normalized time, \(\tau =\varOmega _it\). (Right) Instantaneous dispersion relation for the parallel electron firehose instability
7.3 Dynamic electrons and isotropization of the solar wind protons
In this subsection, we consider the macroscopic–kinetic model of the solar wind, which is similar to Yoon and Seough (2014) for the proton temperatures. We do not consider collisional dissipation. The basic equations are the left-hand mode local dispersion relation that supports the combined electron firehose and proton-cyclotron or EMIC modes,
and the steady-state macro-kinetic equations for the temperatures,
The density and magnetic field intensity form factor,
is the same Lorentzian form as considered before.
(Upper-left) Spatial evolution of local proton betas, \(\beta _{\perp p}=\theta _{\perp p}/f\) and \(\beta _{\parallel p}=\theta _{\parallel p}/f\); (middle-left) local electron betas, \(\beta _{\perp e}=\theta _{\perp e}/f\) and \(\beta _{\parallel e}=\theta _{\parallel e}/f\); (upper-right) temperature ratios for protons and electrons; (middle-right) local wave energy density versus normalized spatial variable \(X=\varOmega _{p0}r/V\). (Bottom two panels) Paths of protons and electrons in \(\beta _{\parallel a},T_{\perp a}/T_{\parallel a})\) space
We also adopt the same normalization convention as in (5.13). In what follows, we adopt \(u=1\) and \(X_0=0\) for convenience. The first case considered is a situation where at the sunward boundary, \(X_0=0\), the protons are unstable to the excitation of the left-hand proton-cyclotron (or EMIC) mode, with input parameters, \(T_{\perp p}/T_{\parallel p}=2\) and \(\beta _{\parallel p}=0.5\), and the electrons are unstable to the parallel electron firehose mode, which is also a left-hand mode, with input parameters, \(T_{\perp e}/T_{\parallel e}=0.3\), and \(\beta _{\parallel e}=3\). The upper-left panel of Fig. 23 plots the spatial evolution of the local proton betas,
versus normalized spatial variable \(X=\varOmega _{p0}r/V\). Very close to \(X=0\), it can be seen that the proton perpendicular beta slightly decreases while parallel beta increases accordingly, although the vertical plotting range makes it difficult to discern such features very well. This can be interpreted as the instability excitation and quasilinear saturation of the proton-cyclotron mode, which is a local process. As one moves away from the sunward boundary \(X=0\), the expansion leads to a gradual increase of \(\beta _{\parallel p}\), until around \(X\sim 1\), the perpendicular proton beta abruptly increases while there is a concomitant decrease in the parallel beta. This turns out to coincide with the electrons crossing the marginal electron firehose instability boundary, which leads to perpendicular proton heating. Without the electron instability excitation and the dynamic interplay, the protons would be unaffected and simple adiabatic expansion would proceed until the protons cross the parallel proton firehose threshold condition. However, because of the electron instability and interaction with the protons, the progression toward the proton firehose stability curve is arrested.
The middle-left panel plots the local electron betas,
in the same format as the upper-left panel. It can be seen that very close to \(X=0\), there is a sudden reduction of \(\beta _{\parallel e}\) and the corresponding increase of \(\beta _{\perp e}\). This is owing to the excitation and subsequent quasilinear saturation of the parallel electron firehose instability. Around \(X\sim 1\), the electrons cross the marginal parallel electron firehose boundary for the second time, and abrupt changes in the beta values are seen. Subsequently, electrons cross the parallel electron firehose boundary multiple times, as will be discussed below.
The upper-right panel plots the temperature ratios for protons and electrons, \(T_{\perp p}/T_{\parallel p}\) and \(T_{\perp e}/T_{\parallel e}\) versus normalized distance \(X=\varOmega _{p0}s/V\). This panel recapitulates the results shown in the previous two panels, except that the results are shown in terms of temperature ratio. The temperature ratio plots are useful since they can be used to check whether the right-hand modes are expected to be generated or not. That is, one can tell on the basis of this plot whether conditions for parallel proton firehose instability, which requires \(T_{\parallel p}>T_{\perp p}\) and high \(\beta _{\parallel p}\), or electromagnetic electron-cyclotron (EMEC) instability, which requires \(T_{\perp e}>T_{\parallel e}\), are spontaneously generated or not. In the present case, neither of these conditions arise. This justifies our approach of ignoring the right-hand mode at the outset.
The middle-right panel plots the local wave energy density versus normalized spatial variable \(X=\varOmega _{p0}r/V\). By “local” wave energy density,
we mean the normalized wave energy density divided by the square of the form factor \(f^2\), since the local magnetic field intensity scales by the same factor, \(B=fB_0\). In the plot, the abrupt increase near \(X=0\) corresponds to the excitation of proton-cyclotron (EMIC) instability by the proton perpendicular anisotropy, combined with the electron firehose instability by electron parallel anisotropy. These initial instabilities are rather rapidly saturated, but as a result of expansion, electrons cross the stability boundary for the second time, which results in subsequent re-excitation of parallel firehose instability near \(X\sim 1\). After the second excitation is rather quickly stabilized, the electrons undergo multiple crossing of the stability boundary. The quasilinear evolution of the wave energy density does not follow any known pattern of exponential increase followed by smooth saturation, but the wave intensity changes rather abruptly. This is the result of adiabatic forcing, which spontaneously generates the free energy source for the instability, i.e., the parallel temperature anisotropy, and the action of instability that removes the free energy source. The competition between the two processes leads to rather non-uniform and sudden changes in the wave intensity.
Finally, the bottom two panels plot the paths of protons and electrons in \((\beta _{\parallel a},T_{\perp a}/T_{\parallel a})\) space. In the left-hand panel, the initial proton position is shown with an open circle, and the values of \((\beta _{\parallel a},T_{\perp a}/T_{\parallel a})\) at \(X=0\) are indicated. The final state is also indicated by an open circle with the corresponding final values of \((\beta _{\parallel a},T_{\perp a}/T_{\parallel a})\) indicated. The curves designated with “EMIC” and “PFH” are the empirical marginal stability curves for EMIC and (parallel) proton firehose instabilities (Hellinger et al. 2006). Proton states above the curve designated by EMIC are unstable, while below this curve, protons are stable to the excitation of EMIC instability. Similarly, proton states below the curve denoted as PFH are unstable to the parallel proton firehose excitation, but above this curve, they are stable. Consequently, the area bounded from above by EMIC and from below by PFH corresponds to a stable and quasi-isotropic region. The present computation shows that the final proton state is situated below the stability curve for EMIC instability and above the proton firehose threshold condition. It is important to compare Fig. 23 with Fig. 17. In Fig. 17 it is shown that, without the electron dynamics, the trajectory of protons in \((\beta _{\parallel p},T_{\perp p}/T_{\parallel p})\) space is an almost diagonal straight line until the protons reach the parallel firehose condition. Beyond such a point, the proton bounce back and forth around the marginal firehose threshold. In contrast, in Fig. 23 where the electrons are allowed to dynamically interact with the protons, one can see that the proton trajectory exhibits a zig-zag pattern within the stable region, with the final state situated well within the two instability threshold curves. This finding thus amounts to a strong evidence that the dynamical interplay between the electrons and protons leads to a counter-balancing effect that opposes the expansion force, and so the present mechanism may possibly contribute to the resolution of the solar wind proton isotropy problem.
Moving on to the electron phase space (bottom right), it can be seen that the electron state at \(X=0\), which is shown with an open circle, is outside the marginal electron parallel firehose condition, hence unstable. The lower curve corresponds to the empirical parallel electron firehose (EFH) instability (Lazar et al. 2014). The marginal stability curve for electromagnetic electron-cyclotron (EMEC) mode is also indicated as a visual guide. As the parallel firehose instability is excited, the electrons rapidly move upward and cross the stability boundary to a stable state. However, the expansion forces the electrons to recross the stability curve and re-emerge into an unstable domain. Subsequently, the electron firehose instability is reignited, which corresponds to sudden changes in betas and temperature ratios, as shown in the upper panels. This causes the electrons to cross the marginal stability curve once more into the stable regime. As a byproduct, the protons also turn around in their respective phase space (bottom-left panel). The electrons eventually move in and out of the threshold curve repeatedly, as the bottom-right panel shows. The colormap indicates the normalized wave intensity. Note that the empirical stability boundary for the EFH mode does accurately trace the electron trajectory.
8 Summary and discussion
In the present review, kinetic instabilities driven by bi-Maxwellian plasma temperatures that may be operative in the solar wind are discussed. The discussion is outlined within the context of linear and quasilinear Vlasov kinetic theories. The anisotropic temperatures associated with charged particles are pervasively detected in the solar wind, and it is one of the key contemporary scientific research topics to correctly characterize how such anisotropies are generated, maintained, and regulated in the solar wind. This problem of solar wind plasma temperature anisotropy is a part of a larger science of studying the solar corona and wind, which has always received intense research interest in the community, but is likely to receive even greater amount interest in the near future, as the space science community will shortly witness the launching of historic inner heliospheric missions, Parker Solar Probe and Solar Orbiter. With such a pair of missions, humanity will return, via artificial satellite, to the inner heliosphere. The purpose of the present article has been to provide an up-to-date theoretical development on this research topic, but largely based on the author’s own work. There is a vast body of works that approach similar research topics based upon computer simulations and data analysis. Some of the existing literature has been cited in the reference, but the main body of the present article had been based upon theoretical methodology.
After Sect. 1, Sect. 2 was devoted to a fundamental theoretical discussion of Vlasov kinetic theory and the quasilinear moment method. Section 3 was devoted to discussion of proton temperature anisotropy instabilities, namely, electromagnetic ion-cyclotron (EMIC) and parallel proton firehose instabilities and their quasilinear development. In Sect. 4, two- or with cylindrical symmetry, three-dimensional proton instabilities, which includes mirror instability, was discussed. The actual application of the theories developed in the previous sections were applied to an inhomogeneous solar wind model in Sect. 5, where the expanding solar wind model is considered, in which, the adiabatic effect continuously and spontaneously generates the parallel temperature anisotropy, while the excitation of the proton firehose instability was shown to oppose the increase in parallel temperature anisotropy; hence, the proton firehose instability regulates the temperature anisotropy upper and lower bounds.
One of the outstanding issues associated with the observed proton (and electron) anisotropic temperatures is that, while the upper and lower bounds of observed temperature ratios, \(T_{\perp a}/T_{\parallel a}\), are partially explained by marginal stability conditions for various plasma instabilities, the fact that the majority of data points in \((\beta _{\parallel a},T_{\perp a}/T_{\parallel a})\) phase space are actually broadly distributed near isotropic conditions and sufficiently far away from the marginal stability conditions cannot be explained easily. This implies that there must be a cause or multiple causes that counter-balance the effects of adiabatic expansion. Among possible causes are local perpendicular heating, significant heat flux, local small- or intermediate-scale spatio-temporal variations of number density and magnetic field, cumulative effects of binary collisions along the passage of solar wind parcel to the observation point, known as the “collisional age effect”, and large-scale density and magnetic field strength that are intrinsic to the solar wind expansion trajectories.
In Sect. 6, we developed a first principle theory of collisional age effects, and by combining the collisional friction with an expanding solar wind model that contains the influence of wave–particle interaction, we demonstrated that finite collisionality does indeed contribute to the isotropization of the solar wind protons, if the solar wind happens to be characterized by high collisionality. Nevertheless, the collisional age effect, in and of itself, is not sufficient to retard the inexorable progression of the solar wind toward marginal firehose stability state. This is especially true if we consider typical solar wind parameters, which leads to generally extremely low collisionality.
In Sect. 7, we explored another possibility, namely the dynamic interplay between the electrons and protons, mediated by instability excitation. It was shown that the interaction of electrons and protons through excitation of the electron parallel firehose and EMIC instabilities is quite efficient, and it plays a role as a counter-balancing force to contain the expansion force, thus contributing greatly toward the isotropization of the protons. Specifically, it was shown that the electron firehose mode excitation is very efficient in slowing down the progression of the protons toward the parallel firehose marginal state.
References
M.L. Adrian, A.F. Viñas, P.S. Moya, D.E. Wendel, Solar wind magnetic fluctuations and electron non-thermal temperature anisotropy: survey of WIND-SWE-VEIS observations. Astrophys. J. 833, 49 (2016)
N. Ahmadi, K. Germaschewski, J. Raeder, Effects of electron temperature anisotropy on proton mirror evolution. J. Geophys. Res. 121, 5350–5365 (2016)
B.J. Anderson, S.A. Fuselier, Magnetic pulsations from 0.1 to 4.0 Hz and associated plasma properties in the Earth’s subsolar magnetosheath and plasma depletion layer. J. Geophys. Res. 98, 1461–1479 (1993)
B.J. Anderson, S.A. Fuselier, Response of thermal ions to electromagnetic ion cyclotron waves. J. Geophys. Res. 99, 19413–19425 (1994)
B.J. Anderson, S.A. Fuselier, D. Murr, Electromagnetic ion cyclotron waves observed in the plasma depletion layer. Geophys. Res. Lett. 18, 1955–1958 (1991)
B.J. Anderson, S.A. Fuselier, S.P. Gary, R.E. Denton, Magnetic spectral signatures in the Earth’s magnetosheath and plasma depletion layer. J. Geophys. Res. 99, 5877–5891 (1994)
B.J. Anderson, R.E. Denton, G. Ho, D.C. Hamilton, S.A. Fuselier, R.J. Strangeway, Observational test of local proton cyclotron instability in the Earth’s magnetosphere. J. Geophys. Res. 101, 21527–21543 (1996)
J.A. Araneda, H. Astudillo, E. Marsch, Interactions of Alfvén-cyclotron waves with ions in the solar wind. Space Sci. Rev. 172, 361–372 (2012)
P. Astfalk, F. Jenko, LEOPARD: A grid-based dispersion relation solver for arbitrary gyrotropic distributions. J. Geophys. Res. 122, 89–101 (2017). doi:10.1002/2016JA023522
S.D. Bale, J.C. Kasper, G.G. Howes, E. Quataert, C. Salem, D. Sundkvist, Magnetic fluctuation power near proton temperature anisotropy instability threshold in the solar wind. Phys. Rev. Lett. 103, 211101 (2009)
S.J. Bame, J.R. Asbridge, W.C. Feldman, S.P. Gary, M.D. Montgomery, Evidence for local ion heating in solar wind high speed streams. Geophys. Res. Lett. 2, 373–375 (1975)
W. Baumjohann, R.A. Treumann, Basic Space Plasma Physics (Imperial College Press, London, 1997)
J. Bortnik, N. Omidi, L. Chen, R.M. Thorne, R.B. Horne, Saturation characteristics of electromagnetic ion cyclotron waves. J. Geophys. Res. 116, A09219 (2011). doi:10.1029/2011JA016638
S. Bourouaine, E. Marsch, F.M. Neubauer, Correlations between the proton temperature anisotropy and transverse high-frequency waves in the solar wind. Geophys. Res. Lett. 37, L14104 (2010). doi:10.1029/2010GL043697
S. Bourouaine, D. Verscharen, B.D.G. Chandran, B.A. Maruca, J.C. Kasper, Limits on alpha particle temperature anisotropy and differential flow from kinetic instabilities: solar wind observations. Astrophys. J. Lett. 777, L3 (2013)
F. Califano, P. Hellinger, E. Kuztnetsov, T. Passot, P.L. Sulem, P.M. Trávníček, Nonlinear mirror mode dynamics: simulations and modeling. J. Geophys. Res. 113, A08219 (2008). doi:10.1029/2007JA012898
E. Camporeale, Nonmodal linear theory for space plasmas. Space Sci. Rev. 172, 397–409 (2012)
E. Camporeale, D. Burgess, Electron firehose instability: kinetic linear theory and two-dimensional particle-in-cell simulations. J. Geophys. Res. 113, A07107 (2008). doi:10.1029/2008JA013043
E. Camporeale, D. Burgess, Electron temperature anisotropy in an expanding plasma: particle-in-cell simulations. Astrophys. J. 710, 1848–1856 (2010)
B.D.G. Chandran, T.J. Dennis, E. Quataert, S.D. Bale, Incorporating kinetic physics into a two-fluid solar-wind model with temperature anisotropy and low-frequency Alfvén-wave turbulence. Astrophys. J. 743, 197 (2011). doi:10.1088/0004-637X/743/2/197
R.C. Davidson, J.M. Ogden, Electromagnetic ion cyclotron instability driven by ion energy anisotropy in high-beta plasmas. Phys. Fluids 18, 1045–1050 (1975)
R.E. Denton, B.J. Anderson, S.P. Gary, S.A. Fuselier, Bounded anisotropy fluid model for ion temperatures. J. Geophys. Res. 99, 11225–11241 (1994)
A. Eviatar, M. Schulz, Ion-temperature anisotropies and the structure of the solar wind. Planet. Space Sci. 18, 321–332 (1970)
S.A. Fuselier, B.J. Anderson, S.P. Gary, R.E. Denton, Inverse correlations between the ion temperature anisotropy and plasma beta in the Earth’s quasi-parallel magnetosheath. J. Geophys. Res. 99, 14931–14936 (1994)
S.P. Gary, Theory of Space Plasma Microinstabilities (Cambridge University Press, Cambridge, 1993)
S.P. Gary, K. Nishimura, Resonant electron firehose instability: particle-in-cell simulations. Phys. Plasmas 10, 3571–3576 (2003)
S.P. Gary, S. Saito, Particle-in-cell simulations of Alfvén-cyclotron wave scattering: proton velocity distributions. J. Geophys. Res. 108(A5), 1194 (2003). doi:10.1029/2002JA009824
S.P. Gary, J. Wang, Whistler instability: electron anisotropy upper bound. J. Geophys. Res. 101, 10749–10754 (1996)
S.P. Gary, D. Winske, Simulations of ion cyclotron anisotropy instabilities in the terrestrial magnetosheath. J. Geophys. Res. 98, 9171–9179 (1993)
S.P. Gary, M.D. Montgomery, W.C. Feldman, D.W. Forslund, Proton temperature anisotropy instabilities in the solar wind. J. Geophys. Res. 81, 1241–1246 (1976)
S.P. Gary, B.J. Anderson, R.E. Denton, S.A. Fuselier, M.E. McKean, D. Winske, Ion anisotropies in the magnetosheath. Geophys. Res. Lett. 20, 1767–1770 (1993a)
S.P. Gary, S.A. Fuselier, B.J. Anderson, Ion anisotropy instabilities in the magnetosheath. J. Geophys. Res. 98, 1481–1488 (1993b)
S.P. Gary, M.E. McKean, D. Winske, Ion cyclotron anisotropy instabilities in the magnetosheath: theory and simulations. J. Geophys. Res. 98, 3963–3971 (1993c)
S.P. Gary, M.A. Lee, The ion cyclotron anisotropy instability and the inverse correlation between proton anisotropy and proton beta. J. Geophys. Res. 99, 11297–11301 (1994a)
S.P. Gary, B.J. Anderson, R.E. Denton, S.A. Fuselier, M.E. McKean, A limited closure relation for anisotropic plasmas from the Earth’s magnetosheath. Phys. Plasmas 1, 1676–1683 (1994b)
S.P. Gary, M.E. McKean, D. Winske, B.J. Anderson, R.E. Denton, S.A. Fuselier, The proton cyclotron instability and the anisotropy/\(\beta\) inverse correlation. J. Geophys. Res. 99, 5903–5914 (1994c)
S.P. Gary, P.D. Convery, R.E. Denton, S.A. Fuselier, B.J. Anderson, Proton and helium cyclotron anisotropy instability thresholds in the magnetosheath. J. Geophys. Res. 99, 5915–5921 (1994d)
S.P. Gary, M.F. Thomsen, L. Yin, D. Winske, Electromagnetic proton cyclotron instability: interactions with magnetospheric protons. J. Geophys. Res. 100, 21961–21972 (1995)
S.P. Gary, M.E. McKean, D. Winske, Proton temperature anisotropy in the magnetosheath: hybrid simulations. Geophys. Res. Lett. 23, 2887–2890 (1996a)
S.P. Gary, V.M. Vazquez, D. Winske, Electromagnetic proton cyclotron instability: proton velocity distributions. J. Geophys. Res. 101, 13327–13333 (1996b)
S.P. Gary, J. Wang, D. Winske, S.A. Fuselier, Proton temperature anisotropy upper bound. J. Geophys. Res. 102, 27159–27169 (1997)
S.P. Gary, H. Li, S. O’Rouke, D. Winske, Proton resonant firehose instability: temperature anisotropy and fluctuating field constraints. J. Geophys. Res. 103, 14567 (1998)
S.P. Gary, R.M. Skoug, J.T. Steinberg, C.W. Smith, Proton temperature anisotropy constraint in the solar wind: ACE observations. Geophys. Res. Lett. 28, 2759–2762 (2001a)
S.P. Gary, Y. Lin, D. Winske, L. Ofman, Electromagnetic heavy ion cyclotron instability: anisotropy constraint in the solar corona. J. Geophys. Res. 106, 10715–10722 (2001b)
S.P. Gary, B.E. Goldstein, M. Neugebauer, Signatures of wave-ion interactions in the solar wind: Ulysses observations. J. Geophys. Res. 107(A8), 1169 (2002). doi:10.1029/2001JA000269
S.P. Gary, B. Lavraud, M.F. Thomsen, B. Lefebvre, S.J. Schwartz, Electron anisotropy constraint in the magnetosheath: cluster observations. Geophys. Res. Lett. 32, L13109 (2005)
V. Génot, E. Budnik, P. Hellinger, T. Passot, G. Belmont, P.M. Trávníček, P.-L. Sulem, E. Lucek, I. Dandouras, Mirror structures above and below the linear instability threshold: cluster observations, fluid model and hybrid simulations. Ann. Geophys. 27, 601–615 (2009)
F. Hadi, M.F. Bashir, A. Qamar, P.H. Yoon, R. Schlickeiser, On the ordinary mode instability for low beta plasmas. Phys. Plasmas 21, 052111 (2014)
A. Hasegawa, Instabilities in the Magnetosphere. Rev. Geophys. Space Phys. 9, 703–772 (1971)
P. Hellinger, Proton fire hose instabilities in the expanding solar wind. J. Plasma Phys. 83, 70583015 (2017)
P. Hellinger, H. Matsumoto, New kinetic instability: oblique Alfvén fire hose. J. Geophys. Res. 105, 10519–10526 (2000)
P. Hellinger, H. Matsumoto, Nonlinear competition between the whistler and Alfvén fire hoses. J. Geophys. Res. 106, 13215–13218 (2001)
P. Hellinger, P.M. Trávníček, Oblique proton fire hose instability in the expanding solar wind: hybrid simulations. J. Geophys. Res. 113, A10109 (2008). doi:10.1029/2008JA013416
P. Hellinger, P.M. Trávníček, Proton core-beam system in the expanding solar wind: hybrid simulations. J. Geophys. Res. 116, A11101 (2011). doi:10.1029/2011JA016940
P. Hellinger, P.M. Trávníček, Proton and alpha particles in the expanding solar wind: hybrid simulations. J. Geophys. Res. 118, 5421–5430 (2013)
P. Hellinger, P.M. Trávníček, Solar wind protons at 1 AU: trends and bounds, constraints and correlations. Astrophys. J. Lett. 784, L15 (2014)
P. Hellinger, P.M. Trávníček, Proton temperature-anisotropy-driven instabilities in weakly collisional plasmas: hybrid simulations. J. Plasma Phys. 81, 305810103 (2015)
P. Hellinger, P. Trávníček, A. Mangeney, R. Grappin, Hybrid simulations of the expanding solar wind: temperatures and drift velocities. Geophys. Res. Lett. 30(5), 1211 (2003). doi:10.1029/2002GL016409
P. Hellinger, E.A. Kuznetsov, T. Passot, P.L. Sulem, P.M. Trávníček, Mirror instability: from quasi-linear diffusion to coherent structures. Geophys. Res. Lett. 36, L06103 (2009). doi:10.1029/2008GL036805
P. Hellinger, P. Trávníček, J.C. Kasper, A.J. Lazarus, Solar wind proton temperature anisotropy: linear theory and WIND/SWE observations. Geophys. Res. Lett. 33, L09101 (2006). doi:10.1029/2006GL025925
P. Hellinger, L. Matteini, Š. Štverák, P.M. Trávníček, E. Marsch, Heating and cooling of protons in the fast solar wind between 0.3 and 1 AU: Helios revisited. J. Geophys. Res. 116, A09105 (2011). doi:10.1029/2011JA016674
P. Hellinger, P.M. Trávníček, Š. Štverák, L. Matteini, M. Velli, Proton thermal energetics in the solar wind: Helios reloaded. J. Geophys. Res. 118, 1351–1365 (2013)
P. Hellinger, P.M. Trávníček, V.K. Decyk, D. Schriver, Oblique electron fire hose instability: particle-in-cell simulations. J. Geophys. Res. 119, 59–68 (2014)
J.V. Hollweg, Some physical processes in the solar wind. J. Geophys. Res. 16, 689–720 (1978)
P. Hunana, D. Laveder, T. Passot, P.L. Sulem, D. Borgogno, Reduction of compressibility and parallel transfer by Landau damping in turbulent magnetized plasmas. Astrophys. J. 743, 128 (2011). doi:10.1088/0004-637X/743/2/128
P. Hunana, G.P. Zank, M.L. Goldstein, G.M. Webb, L. Adhikari, CGL description revisited. AIP Conf. Proc. 1720, 030002 (2016)
P. Hunana, G.P. Zank, On the parallel and oblique firehose instability in fluid models. Astrophys. J. 839, 13 (2017). doi:10.3847/1538-4357/aa64e3
A.J. Hundhausen, S.J. Bame, Solar wind thermal anisotropies: Vela 3 and IMP 3. J. Geophys. Res. 72, 5265–5274 (1967)
A.J. Hundhausen, J.R. Asbridge, S.J. Bame, H.E. Gilbert, I.B. Strong, Vela 3 satellite observations of solar wind ions: a preliminary report. J. Geophys. Res. 72, 87–100 (1967a)
A.J. Hundhausen, J.R. Asbridge, S.J. Bame, I.B. Strong, Vela satellite observations of solar wind ions. J. Geophys. Res. 72, 1979–1987 (1967b)
P.A. Isenberg, A self-consistent marginally stable state for parallel ion cyclotron waves. Phys. Plasmas 19, 032116 (2012)
P.A. Isenberg, B.A. Maruca, J.C. Kasper, Self-consistent ion cyclotron anisotropy–beta relation for solar wind protons. Astrophys. J. 773, 164 (2013)
J.R. Jasperse, B. Basu, E.J. Lund, M. Bouhram, Gyrotropic guiding-center fluid theory for turbulent inhomogeneous magnetized plasma. Phys. Plasmas 13, 072903 (2006a). doi:10.1063/1.2220006
J.R. Jasperse, B. Basu, E.J. Lund, M. Bouhram, Gyrotropic guiding-center fluid theory for the turbulent heating of magnetospheric ions in downward Birkeland current regions. II. Phys. Plasmas 13, 112902 (2006b). doi:10.1063/1.2364475
J.C. Kasper, A.J. Lazarus, S.P. Gary, A. Szabo, Solar wind temperature anisotropies, in Solar Wind Ten: Proceedings of the Tenth International Solar Wind Conference, ed. by M. Velli, R. Bruno, F. Malara (American Institute of Physics, College Park, 2003), pp. 538–541
J.C. Kasper, A.J. Lazarus, S.P. Gary, Hot solar-wind helium: direct evidence for local heating by Alfvén-cyclotron dissipation. Phys. Rev. Lett. 101, 261103 (2008)
J.C. Kasper, B.A. Maruca, M.L. Stevens, A. Zaslavsky, Sensitive test for ion-cyclotron resonant heating in the solar wind. Phys. Rev. Lett. 110, 091102 (2013)
C.F. Kennel, F. Engelmann, Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9, 2377–2388 (1966)
C.F. Kennel, H.E. Petschek, Limit on stably trapped particle fluxes. J. Geophys. Res. 71, 1–28 (1966). doi:10.1029/JZ071i001p00001
C.F. Kennel, F.L. Scarf, Thermal anisotropies and electromagnetic instabilities in the solar wind. J. Geophys. Res. 73, 6149–6165 (1968)
C. Lacombe, G. Belmont, Waves in the Earth’s magnetosheath: observations and interpretations. Adv. Space Res. 15, 329–340 (1995)
D. Laveder, L. Marradi, T. Passot, P.L. Sulem, Fluid simulations of mirror constraints on proton temperature anisotropy in solar wind turbulence. Geophys. Res. Lett. 38, L17108 (2011). doi:10.1029/2011GL048874
M. Lazar, The electromagnetic ion-cyclotron instability in bi-kappa distributed plasma. A&A 547, A94 (2012)
M. Lazar, S. Poedts, R. Schlickeiser, Proton firehose instability in bi-kappa distribution plasmas. A&A 534, A116 (2011)
M. Lazar, S. Poedts, R. Schlickeiser, The interplay of Kappa and core populations in the solar wind: electromagnetic electron cyclotron instability. J. Geophys. Res. 119, 9395 (2014)
R.P. Lepping, M.H. Acũna, L.F. Burlaga, W.M. Farrell, J.A. Slavin, K.H. Schatten, F. Mariani, N.F. Ness, F.M. Neubauer, Y.C. Whang, J.B. Byrnes, R.S. Kennon, P.V. Panetta, J. Scheifele, E.M. Worley, Space Sci. Rev. 71, 207 (1995)
X. Li, S.R. Habbal, Electron kinetic firehose instability. J. Geophys. Res. 105, 27377–27385 (2000)
G. Livadiotis (ed.), Kappa Distributions. Theory and Applications in Plasmas, 1st edn. (Elsevier, Amsterdam, 2017) (ISBN:9780128046388)
M.E. McKean, D. Winske, S.P. Gary, Mirror and ion cyclotron anisotropy instabilities in the magnetosheath. J. Geophys. Res. 97, 19421–19432 (1992)
M.E. McKean, S.P. Gary, D. Winske, Kinetic physics of the mirror instability. J. Geophys. Res. 98, 21313–21321 (1993)
M.E. McKean, D. Winske, S.P. Gary, Two-dimensional simulations of ion anisotropy instabilities in the magnetosheath. J. Geophys. Res. 99, 11141–11153 (1994)
Y.G. Maneva, J.A. Araneda, E. Marsch, Regulation of ion drifts and anisotropies by parametrically unstable finite-amplitude Alfvén-cyclotron waves in the fast solar wind. Astrophys. J. 783, 139 (2014)
Y. Maneva, M. Lazar, A. Viñas, S. Poedts, Mixing the solar wind proton and electron scales: effects of electron temperature anisotropy on the oblique proton firehose instability. Astrophys. J. 832, 64 (2016)
E. Marsch, Helios: evolution of distribution functions 0.3–1 AU. Space Sci. Rev. 172, 23–39 (2012)
E. Marsch, C.-Y. Tu, Heating and acceleration of coronal ions interacting with plasma waves through cyclotron and Landau resonance. J. Geophys. Res. 106, 277–238 (2001)
E. Marsch, K.-H. Mühlhäuser, R. Schwenn, H. Rosenbauer, W. Pilipp, F.M. Neubauer, Solar wind protons: three-dimensional velocity distributions and derived plasma properties measured between 0.3 and 1 AU. J. Geophys. Res. 87, 52–72 (1982)
E. Marsch, X.-Z. Ao, C.-Y. Tu, On the temperature anisotropy of the core part of the proton velocity distribution function in the solar wind. J. Geophys. Res. 109, A04102 (2004). doi:10.1029/2003JA010330
E. Marsch, L. Zhao, C.-Y. Tu, Limits on the core temperature anisotropy of solar wind protons. Ann. Geophys. 24, 2057–2063 (2006)
B.A. Maruca, J.C. Kasper, S.D. Bale, What are the relative roles of heating and cooling in generating solar wind temperature anisotropies? Phys. Rev. Lett. 107, 201101 (2011)
B.A. Maruca, J.C. Kasper, S.D. Bale, Instability-driven limits on helium temperature anisotropy in the solar wind. Astrophys. J. 748, 137 (2012)
L. Matteini, S. Landi, P. Hellinger, M. Velli, Parallel proton fire hose instability in the expanding solar wind: hybrid simulations. J. Geophys. Res. 111, A10101 (2006). doi:10.1029/2006JA011667
L. Matteini, S. Landi, P. Hellinger, F. Pantellini, M. Maksimovic, M. Velli, B.E. Goldstein, E. Marsch, Evolution of the solar wind proton temperature anisotropy from 0.3 to 2.5 AU. Geophys. Res. Lett. 34, L250105 (2007). doi:10.1029/2007GL030920
L. Matteini, P. Hellinger, S. Landi, P.M. Trávníček, M. Velli, B.E. Goldstein, E. Marsch, Ion kinetics in the solar wind: coupling global expansion to local microphysics. Space Sci. Rev. 172, 373–396 (2012)
L. Matteini, P. Hellinger, B.E. Goldstein, S. Landi, M. Velli, M. Neugebauer, Signatures of kinetic instabilities in the solar wind. J. Geophys. Res. 118, 2771–2782 (2013)
P. Messmer, Temperature isotropization in solar flare plasmas due to the electron firehose instability. A&A 382, 301–311 (2002)
M.J. Michno, M. Lazar, P.H. Yoon, R. Schlickeiser, Effects of electrons on the solar wind proton temperature anisotropy. Astrophys. J. 781, 49 (2014)
M.D. Montgomery, S.J. Bame, A.J. Hundhausen, Solar wind electrons: Vela 4 measurements. J. Geophys. Res. 73, 4999–5003 (1968)
P.S. Moya, V. Muñoz, J. Rogan, J.A. Valdivia, Study of the cascading effect during the acceleration and heating of ions in the solar wind. J. Atmos. Solar-Terr. Phys. 73, 1890–1397 (2011)
P.S. Moya, A.F. Viñas, V. Muñoz, J.A. Valdivia, Computational and theoretical study of the wave–particle interaction of protons and waves. Ann. Geophys. 30, 1361–1369 (2012)
P.S. Moya, R. Navarro, A.F. Viñas, V. Muñoz, J.A. Valdivia, Weak turbulence cascading effects in the acceleration and heating of ions in the solar wind. Astrophys. J. 781, 76 (2014)
R.E. Navarro, P.S. Moya, V. Muñoz, J.A. Araneda, A.-F. Viñas, J.A. Valdivia, Solar wind thermally induced magnetic fluctuations. Phys. Rev. Lett. 112, 245001 (2014). doi:10.1103/PhysRevLett.112.245001
R.E. Navarro, V. Muñoz, J. Araneda, A.-F. Viñas, P.S. Moya, J.A. Valdivia, Magnetic Alfvén-cyclotron fluctuations of anisotropic nonthermal plasmas. J. Geophys. Res. 120, 2382–2396 (2015)
L. Ofman, A.-F. Viñas, P.S. Moya, Hybrid models of solar wind plasma heating. Ann. Geophys. 29, 1071–1079 (2011)
L. Ofman, A.-F. Viñas, Y. Maneva, Two-dimensional hybrid models of \({\rm H}^+\)-\({\rm He}^{++}\) expanding solar wind plasma heating. J. Geophys. Res. 119, 4223–4238 (2014)
K.W. Ogilvie, D.J. Chornay, R.J. Fritzenreiter, R. Hunsaker, J. Keller, J. Lobell, G. Miller, J.D. Scudder, E.C. Sittler Jr., R.B. Torbert, D. Bodet, G. Needell, A.J. Lazarus, J.T. Steinberg, J.H. Tappan, A. Mavretic, E. Gergin, Space Sci. Rev. 71, 55 (1995)
N. Omidi, R.M. Thorne, J. Bortnik, Nonlinear evolution of EMIC waves in a uniform magnetic field: 1. Hybrid simulation. J. Geophys. Res. 115, A12241 (2010). doi:10.1029/2010JA015607
K.T. Osman, W.H. Matthaeus, A. Greco, S. Servidio, Evidence for inhomogeneous heating in the solar wind. Astrophys. J. Lett. 727, L11 (2011)
K.T. Osman, W.H. Matthaeus, B. Hnat, S.C. Chapman, Kinetic signatures and intermittent turbulence in the solar wind plasma. Phys. Rev. Lett. 108, 261103 (2012)
K.T. Osman, W.H. Matthaeus, K.H. Kiyani, B. Hnat, S.C. Chapman, Proton kinetic effects and turbulent energy cascade rate in the solar wind. Phys. Rev. Lett. 111, 201101 (2013)
G. Paesold, A.O. Benz, Electron firehose instability and acceleration of electrons in solar flares. Astron. Astrophys. 351, 741–746 (1999)
F.G.E. Pantellini, S.J. Schwartz, Electron temperature effects in the linear proton mirror instability. J. Geophys. Res. 100, 3539–3549 (1995)
G. Parks, Physics of Space Plasmas: An Introduction, 2nd edn. (Westview Press, Boulder, 2003)
T. Passot, P.L. Sulem, Collisionless magnetohydrodynamics with gyrokinetic effects. Phys. Plasmas 14, 082502 (2007). doi:10.1063/1.2751601
T. Passot, P.L. Sulem, P. Hunana, Extending magnetohydrodynamics to the slow dynamics of collisionless plasmas. Phys. Plasmas 19, 082113 (2012)
T.-D. Phan, G. Paschmann, W. Baumjohann, N. Sckopke, H. Lühr, The magnetosheath region adjacent to the dayside magnetopause: AMPTE/IRM observations. J. Geophys. Res. 99, 121–141 (1994)
O.A. Pokhotelov, M.A. Balikhin, H. St-C, K. Alleyne, O.G. Onishchenko, Mirror instability with finite electron temperature effects. J. Geophys. Res. 105, 2393–2401 (2000)
O.A. Pokhotelov, R.A. Treumann, R.Z. Sagdeev, M.A. Balikhin, O.G. Onishchenko, V.P. Pavlenko, I. Sandberg, Linear theory of the mirror instability in non-Maxwellian space plasmas. J. Geophys. Res. 107(A10), 1312 (2002). doi:10.1029/2001JA009125
O.A. Pokhotelov, I. Sandberg, R.Z. Sagdeev, R.A. Treumann, O.G. Onishchenko, M.A. Balikhin, V.P. Pavlenko, Slow drift mirror modes in finite electron-temperature plasma: hydrodynamic and kinetic drift mirror instabilities. J. Geophys. Res. 108(A3), 1098 (2003). doi:10.1029/2002JA009651
P. Porazik, J.R. Johnson, Linear dispersion relation for the mirror instability in context of the gyrokinetic theory. Phys. Plasmas 20, 104501 (2013a)
P. Porazik, J.R. Johnson, Gyrokinetic particle simulation of nonlinear evolution of mirror instability. J. Geophys. Res. 118, 7211–7218 (2013b)
B. Remya, R.V. Reddy, B.T. Tsurutani, G.S. Lakhina, E. Echer, Ion temperature anisotropy instabilities in planetary magnetosheaths. J. Geophys. Res. 118, 785–793 (2013)
S. Saeed, P.H. Yoon, M. Sarfraz, M.N.S. Qureshi, Characteristics of heat flux and electromagnetic electron-cyclotron instabilities driven by solar wind electrons. MNRAS 466, 4928–4936 (2017)
A.A. Samsonov, O. Alexandrova, C. Lacombe, M. Maksimovic, S.P. Gary, Proton temperature anisotropy in the magnetosheath: comparison of 3-D MHD modeling with Cluster data. Ann. Geophys. 25, 1157–1173 (2007)
M. Sarfraz, S. Saeed, P.H. Yoon, G. Abbas, H.A. Shah, Macroscopic quasi-linear theory of electromagnetic electron cyclotron instability associated with core and halo solar wind electrons. J. Geophys. Res. 121, 9356–9368 (2016)
M. Sarfraz, P.H. Yoon, S. Saeed, G. Abbas, H.A. Shah, Macroscopic quasilinear theory of parallel electron firehose instability associated with solar wind electrons. Phys. Plasmas 24, 012907 (2017)
F.L. Scarf, J.H. Wolfe, R.W. Silva, A plasma instability associated with thermal anisotropies in the solar wind. J. Geophys. Res. 72, 993–1005 (1967)
R. Schlickeiser, P.H. Yoon, On the marginal instability threshold condition of the aperiodic ordinary mode. Phys. Plasmas 21, 072119 (2014)
R. Schlickeiser, M.J. Michno, D. Ibscher, M. Lazar, T. Skoda, Modified temperature-anisotropy instability thresholds in the solar wind. Phys. Rev. Lett. 105, 201102 (2011)
E.E. Scime, P.A. Keiter, M.M. Balkey, R.F. Boivin, J.L. Kline, M. Blackburn, S.P. Gary, Ion temperature anisotropy limitation in high beta plasmas. Phys. Plasmas 7, 2157–2165 (2000)
S.J. Schwartz, Plasma instabilities in the solar wind: a theoretical review. Rev. Geophys. Space Phys. 18, 313–336 (1980)
S.J. Schwartz, W.C. Feldman, S.P. Gary, The source of proton anisotropy in the high-speed solar wind. J. Geophys. Res. 86, 541–546 (1981)
R. Schwenn, E. Marsch (eds.), Physics of the Inner Heliosphere I, Large-Scale Phenomena (Springer, Berlin, 1990)
R. Schwenn, E. Marsch (eds.), Physics of the Inner Heliosphere II, Particles, Waves and Turbulence (Springer, Berlin, 1991)
J. Seough, Y. Nariyuki, Effects of alpha-proton drift velocity on alpha particle firehose instability. Phys. Plasmas 23, 082113 (2016)
J. Seough, P.H. Yoon, Quasilinear theory of anisotropy–beta relations for proton cyclotron and parallel firehose instabilities. J. Geophys. Res. 117, A08101 (2012)
J. Seough, P.H. Yoon, K.-H. Kim, D.-H. Lee, Solar wind proton anisotropy versus beta relation. Phys. Rev. Lett. 110, 071103 (2013)
J. Seough, P.H. Yoon, J. Hwang, Quasilinear theory and particle-in-cell simulation of proton cyclotron instability. Phys. Plasmas 21, 062118 (2014)
J. Seough, P.H. Yoon, J. Hwang, Simulation and quasilinear theory of proton firehose instability. Phys. Plasmas 22, 012303 (2015a)
J. Seough, P.H. Yoon, J. Hwang, Y. Nariyuki, Simulation and quasilinear theory of aperiodic ordinary mode instability. Phys. Plasmas 22, 082122 (2015b)
S. Servidio, K.T. Osman, F. Valentini, D. Perrone, F. Calidano, S. Chapman, W.H. Matthaeus, P. Veltri, Proton kinetic effects in Vlasov and solar wind turbulence. Astrophys. J. Lett. 781, L27 (2014)
S.M. Shaaban, M. Lazar, S. Poedts, A. Elhanbaly, The interplay of the solar wind proton core and halo populations: EMIC instability. J. Geophys. Res. 121, 6031–6047 (2016)
S.M. Shaaban, M. Lazar, S. Poedts, A. Elhanbaly, Shaping the solar wind temperature anisotropy by the interplay of electron and proton instabilities. Astrophys. Space Sci. 362, 13 (2017)
M. Shoji, Y. Omura, B.T. Tsurutani, O.P. Verkhoglyadova, B. Lembege, Mirror instability and L-mode electromagnetic ion cyclotron instability: competition in the Earth’s magnetosheath. J. Geophys. Res. 114, A10203 (2009). doi:10.1029/2008JA014038
D.J. Southwood, M.G. Kivelson, Mirror instability: 1. Physical mechanism of linear instability. J. Geophys. Res. 98, 9181–9187 (1993)
A. Stockem Novo, P.H. Yoon, M. Lazar, R. Schlickeiser, S. Poedts, J. Seough, Quasilinear saturation of the aperiodic ordinary mode streaming instability. Phys. Plasmas 22, 092301 (2015)
Š. Štverák, P. Trávníček, M. Maksimovic, E. Marsch, A.N. Fazakerley, E.E. Scime, Electron temperature anisotropy constraints in the solar wind. J. Geophys. Res. 113, A03103 (2008). doi:10.1029/2007JA012733
L.C. Tan, S.F. Fung, R.L. Kessel, S.-H. Chen, J.L. Green, T.E. Eastman, Ion temperature anisotropies in the Earth’s high-latitude magnetosheath: Hawkeye observations. Geophys. Res. Lett. 25, 587–590 (1998)
P. Trávníček, P. Hellinger, M.G.G. Taylor, C.P. Escoubet, I. Dandouras, E. Lucek, Magnetosheath plasma expansion: hybrid simulations. Geophys. Res. Lett. 34, L15104 (2007). doi:10.1029/2007GL029728
R.A. Treumann, W. Baumjohann, Advanced Space Plasma Physics (Imperial College Press, London, 1997)
R.A. Treumann, C.H. Jaroschek, O.D. Constantinescu, R. Nakamura, O.A. Pokhotelov, E. Georgescu, The strange physics of low frequency mirror mode turbulence in high temperature plasma of the magnetosheath. Nonlinear Proc. Geophys. 11, 647–657 (2004)
S. Vafin, R. Schlickeiser, P.H. Yoon, Linear theory of low frequency magnetosonic instabilities in counterstreaming bi-Maxwellian plasmas. Phys. Plasmas 22, 092131 (2015)
D. Verscharen, B.D.G. Chandran, K.G. Klein, E. Quataert, Collisionless isotropization of the solar-wind protons by compressive fluctuations and plasma instabilities. Astrophys. J. 831, 128 (2016)
A.A. Vedenov, E.P. Velikov, R.Z. Sagdeev, Stability of plasma. Sov. Phys. Uspekhi 4, 332–369 (1961)
A.F. Viñas, P.S. Moya, R. Navarro, J.A. Araneda, The role of higher-order modes on the electromagnetic whistler-cyclotron wave fluctuations of thermal and non-thermal plasmas. Phys. Plasmas 21, 012902 (2014)
A.F. Viñas, P.S. Moya, R. Navarro, J.A. Valdivia, J.A. Araneda, V. Muñoz, Electromagnetic fluctuations of the whistler-cyclotron and firehose instabilities in a Maxwellian and Tsallis-kappa-like plasma. J. Geophys. Res. 120, 3307–3317 (2015)
F. Xiao, Q. Zhou, H. He, H. Zheng, S. Wang, Whistler instability threshold condition of energetic electrons by kappa distribution in space plasmas. J. Geophys. Res. 111, A08208 (2006)
F. Xiao, Q. Zhou, H. He, H. Zheng, S. Wang, Electromagnetic ion cyclotron waves instability threshold condition of suprathermal protons by kappa distribution. J. Geophys. Res. 112, A07219 (2007)
P.H. Yoon, Quasilinear evolution of Alfvén-ion-cyclotron and mirror instabilities driven by ion temperature anisotropy. Phys. Fluids B 4, 3627–3637 (1992)
P.H. Yoon, Proton temperature relaxation in the solar wind by combined collective and collisional processes. J. Geophys. Res. 121, 10665–10676 (2016a)
P.H. Yoon, On the isotropization of solar wind protons. Astrophys. J. 833, 106 (2016b)
P.H. Yoon, Collisional relaxation of bi-Maxwellian plasma temperatures in magnetized plasmas. Phys. Plasmas 23, 072114 (2016c)
P.H. Yoon, M. Sarfraz, Interplay of electron and proton instabilities in expanding solar wind. Astrophys. J. 835, 246 (2017)
P.H. Yoon, J. Seough, Quasilinear theory of anisotropy–beta relations for combined mirror and proton cyclotron instabilities. J. Geophys. Res. 117, A08102 (2012)
P.H. Yoon, J. Seough, Proton-cyclotron and firehose instabilities in inhomogeneous plasmas. J. Geophys. Res. 119, 7108–7119 (2014)
P.H. Yoon, C.S. Wu, A.S. de Assis, Effect of finite ion gyroradius on the fire-hose instability in a high beta plasma. Phys. Fluids B 5, 1971–1979 (1993)
P.H. Yoon, J. Seough, J. Hwang, Y. Nariyuki, Macroscopic quasi-linear theory and particle-in-cell simulation of helium ion anisotropy instabilities. J. Geophys. Res. 120, 6071–6084 (2015)
Acknowledgements
The author acknowledges NSF Grant AGS1550566 to the University of Maryland, and the BK21 plus program from the National Research Foundation (NRF), Korea, to Kyung Hee University. Part of this work was carried out while P.H.Y. was visiting Ruhr University Bochum, Germany, which was made possible by the support from the Ruhr University Research School PLUS, funded by Germany’s Excellence Initiative (DFG GSC 98/3), and by a Mercator fellowship awarded by the Deutsche Forschungsgemeinschaft through the Grant Schl 201/31-1. The author acknowledges use of Wind SWE (Ogilvie et al. 1995) ion data, and Wind MFI (Lepping et al. 1995) magnetic field data from the SPDF CDAWeb service: http://cdaweb.gsfc.nasa.gov/. The author also acknowledges many collaborators including J. Seough, K.-H. Kim, D.H. Lee, M. Sarfraz, S. Saeed, R. Schlickeiser, M. Lazar, and others.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The corresponding author states that he has no conflict of interest.
Rights and permissions
About this article
Cite this article
Yoon, P.H. Kinetic instabilities in the solar wind driven by temperature anisotropies. Rev. Mod. Plasma Phys. 1, 4 (2017). https://doi.org/10.1007/s41614-017-0006-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41614-017-0006-1