Shaping the solar wind temperature anisotropy by the interplay of electron and proton instabilities

Abstract

A variety of nonthermal characteristics like kinetic, e.g., temperature, anisotropies and suprathermal populations (enhancing the high energy tails of the velocity distributions) are revealed by the in-situ observations in the solar wind indicating quasistationary states of plasma particles out of thermal equilibrium. Large deviations from isotropy generate kinetic instabilities and growing fluctuating fields which should be more efficient than collisions in limiting the anisotropy (below the instability threshold) and explain the anisotropy limits reported by the observations. The present paper aims to decode the principal instabilities driven by the temperature anisotropy of electrons and protons in the solar wind, and contrast the instability thresholds with the bounds observed at 1 AU for the temperature anisotropy. The instabilities are characterized using linear kinetic theory to identify the appropriate (fastest) instability in the relaxation of temperature anisotropies $A_{e,p} = T_{e,p,\perp}/ T _{e,p,\parallel} \ne1$. The analysis focuses on the electromagnetic instabilities driven by the anisotropic protons ($A_{p} \lessgtr1$) and invokes for the first time a dynamical model to capture the interplay with the anisotropic electrons by correlating the effects of these two species of plasma particles, dominant in the solar wind.

1 Introduction

Due to a continuous presence of observational missions in space, the solar wind is currently exploited as a natural laboratory for studying the plasma mechanisms and effects including kinetic instabilities driven locally by the temperature anisotropy of plasma particles. The existence and viability of these mechanisms of instability are confirmed by a recent combined analysis of the plasma particle distributions and the enhanced wave fluctuations observed in the solar wind, see Gary et al. (2016). Instead, the back effects of the growing fluctuating fields scattering the plasma particles and limiting their anisotropy remain controversial, especially the role played in the relaxation process by the cyclotron electromagnetic fluctuations usually dominating the direction parallel to the stationary magnetic field (Kasper et al. 2003; Hellinger et al. 2006; Bale et al. 2009).

Driven by an excess of perpendicular temperature $T_{\perp} > T_{ \parallel}$ cyclotron modes grow faster than other instabilities like mirror instability which may develop in the same conditions. Resonant interactions, i.e., cyclotron resonance with plasma particles, are therefore expected to be effective in the relaxation of temperature anisotropy in this case. The interest to explain these effects and their consequences in the solar wind has been boosted after the simulations suggested that the mirror instability is not an effective pitch angle scatterer of protons (McKean et al. 1992, 1994; Gary et al. 1993) and the cyclotron anisotropy instability may be assumed the primary mechanism to constrain the proton anisotropy (Gary and Lee 1994). Further confirmation of this constraint can also be obtained in a straightforward way, namely, by fitting the instability thresholds predicted by the linear theory with the anisotropy limits reported by the observations (see explanatory arguments and references in Gary et al. (1994)). However, the instability thresholds derived from simplified models assuming plasma particles bi-Maxwellian distributed and minimizing the effects of electrons considering them isotropic, do not provide a good agreement with the observations. Thus, thresholds of the electromagnetic ion (proton) cyclotron (EMIC) instability simply do not align to the limits of the proton temperature anisotropy in the solar wind, but are markedly lower than these limits, which instead appear to be better described by the thresholds of the mirror (aperiodic) modes instability (Hellinger et al. 2006). In the opposite case, an excess of parallel temperature $T_{\perp} < T_{ \parallel}$ may ignite two branches of firehose instability, one destabilizing the electromagnetic cyclotron modes propagating mainly in the parallel direction but with an opposite polarization, i.e., right-handed (RH) if driven by protons and left-handed (LH) if driven by electrons, and the other one destabilizing highly oblique and aperiodic modes. Again, when the firehose thresholds are derived with simplified models the temperature anisotropy in the solar wind is better constrained by the aperiodic instability (Hellinger et al. 2006), which, however, cannot undergo cyclotron resonant interactions with plasma particles. In both these two cases, the anisotropy thresholds derived for the instabilities of cyclotron modes lie below the anisotropy limits reported by the observations in the solar wind, seeming that the instability thresholds may be overestimated by using simplified models for the velocity distributions of plasma particles and neglecting their interplay. Two distinct classes of mechanisms may be at work in the solar wind generating temperature anisotropies of plasma particles. These are either the large scale mechanisms like adiabatic expansion (leading to $A = T_{\perp} / T_{\parallel} < 1$) and magnetic compression (leading to $A > 1$), or the small scale heating and acceleration of plasma particles by their resonant interactions with electromagnetic fields fluctuations. Large scale mechanisms act in the same manner on both species, electrons and protons (subscripts $e$ and $p$, respectively), expecting to provide a direct correlation between their anisotropies measured in the solar wind, i.e., both species with $A_{e,p} > 1$, or both with $A_{e,p} < 1$. Binary collisions are not efficient enough to reduce the anisotropy and affect this correlation of the electron and proton anisotropies, but the small scale mechanisms like the wave-particle interactions, usually conditioned by the presence of different wave fluctuations may accelerate plasma particles preferentially, e.g., in direction perpendicular to the magnetic field by the cyclotron resonance (leading to $A > 1$), or in parallel direction by the Landau (transit-time) damping (leading to $A < 1$). Moreover, the electrons mainly resonate with the high-frequency waves while the protons react to the low-frequency modes. An anti-correlation between the electron and proton anisotropies, i.e., $A_{e} \gtrless1$ and $A_{p} \lessgtr1$, can therefore result from local mechanisms involving either microinstabilities or damping of small scale fluctuations.

A quantitative analysis with systematic evidences and estimations of these correlations between the electron and proton anisotropies in space plasmas is not reported yet, at least to our knowledge, but some qualitative elements can however be extracted. Thus, an implication of the large scale mechanisms in generating temperature anisotropy of plasma particles seems to be confirmed by the observations, which show a radial evolution of the temperature anisotropy from an exclusive $A = T_{\perp} / T_{\parallel} > 1$ at low heliocentric distances $\sim0.3~\mbox{AU}$ (Matteini et al. 2007), where the interplanetary magnetic field is more intense, to a dominant $A<1$ after the expansion at large radial distances $\sim1~\mbox{AU}$ (Kasper et al. 2003; Štverák et al. 2008). On the other hand, the anisotropy-driven instabilities enhance the small-scale fluctuations, which may play two distinct roles, either to maintain the anisotropy correlation of the electrons and protons, e.g., by cyclotron electromagnetic instabilities, or to transfer the free energy between plasma species, e.g., by firehose instability, and eventually induce an anti-correlation of their anisotropies. Indeed, radial profile of the temperature anisotropy departs from CGL predictions (Matteini et al. 2007) suggesting perpendicular heating by wave turbulence, while a parallel cooling may likely be related to microinstabilities connected with the structure of the proton velocity distribution function (Hellinger et al. 2013).

The present paper presents an advanced description of these instabilities on the basis of a refined and, tentatively, more realistic model, which takes into account the effects of suprathermal electrons, ubiquitous in the solar wind, as well as different couplings between the electron and proton anisotropies. The dispersion formalism is provided in Sect. 2 on the basis of a Vlasov kinetic approach for a plasma of electrons and protons described by (bi-)Kappa distribution functions. Kappa power-laws are generalized models empirically introduced to describe with accuracy the velocity distributions measured in space plasmas (Vasyliunas 1968; Maksimovic et al. 1997; Christon et al. 1989). Standard (bi-)Maxwellian models can reproduce only the low-energy core of the measured distributions, while (bi-)Kappa can also incorporate the high-energy tails of the distributions, which are markedly enhanced by the suprathermal populations. The unstable solutions are discussed in Sect. 3 for different situations mainly conditioned by the interplay of anisotropic electrons and protons. We focus on the electromagnetic instabilities driven by the anisotropic protons and invoke for the first time a dynamical model to include the effects of anisotropic electrons. In Sect. 4 we contrast the instability thresholds with the observations, and perform a comparative analysis with the previous results from simplified approaches. Conclusions are presented in Sect. 5.

2 Dispersion-stability formalism: transverse modes

For a collisionless and homogeneous electron-proton plasma, the electromagnetic modes in a direction parallel to the stationary magnetic field ($\mathbf{k} \parallel{\mathbf{B}}$) decouple from the electrostatic oscillations, and their instabilities may display maximum growth rates, e.g., cyclotron instabilities (Kennel and Petschek 1966). Provided by a linear Vlasov-Maxwell dispersion formalism (Krall and Trivelpiece 1973), the dispersion relations for these electromagnetic modes read

$$\begin{aligned} &1+\sum_{\alpha=e,p}\frac{\omega_{p,\alpha}^{2}}{\omega^{2}} \biggl[ \frac{\omega}{k\; u_{\alpha,\parallel}} Z_{\alpha,\eta} \bigl(\xi_{\alpha,\eta}^{\pm} \bigr) \\ &\quad {}+ ( A_{\alpha}-1 )\bigl\{ 1+\xi_{\alpha,\eta}^{\pm} \; Z_{\alpha,\eta}\bigl( \xi_{\alpha,\eta}^{\pm} \bigr) \bigr\} \biggr] =\frac{c^{2}k^{2}}{\omega^{2}}, \end{aligned}$$

(1)

where $\omega$ is the wave-frequency, $k$ is the wave-number, $c$ is the speed of light, $\omega_{p,\alpha}^{2}= 4\pi n_{\alpha}e^{2}/m _{\alpha}$ are the plasma frequencies for protons (subscript $\alpha=p$) and electrons (subscript $\alpha=e$), $A_{\alpha}=T _{\alpha, \perp}/T_{\alpha, \parallel}$ are the temperature anisotropies, ± denote the circular polarizations, right-handed (RH) and left-handed (LH), respectively. $Z_{\alpha,\eta} ( \xi_{\alpha,\eta}^{\pm} )$ may denote either the plasma dispersion function for (bi)-Maxwellian (subscript $\eta=M$) distributed plasmas (Fried and Conte 1961), or the modified dispersion function for Kappa (subscript $\eta= \kappa$) distributed plasmas as derived in Lazar et al. (2008), and $u_{\alpha,\parallel}$ are the corresponding thermal velocities (Lazar et al. 2015). See Appendix A for the explicit definitions of these quantities.

Since the presence of anisotropic ($A_{e} \ne1$) electrons can change the dispersive properties of the electromagnetic modes, including those destabilized by the proton anisotropy $A_{p} \ne1$ (Kennel and Scarf 1968; Lazar et al. 2011; Michno et al. 2014; Shaaban et al. 2015, 2016), here we propose a dynamical model for the interplay of the electrons and protons by correlating their temperature anisotropies $A_{e,p}\neq1$, as well as their plasma parallel betas $\beta_{e,p,\parallel}$. Previous studies carried out by Kennel and Scarf (1968), Lazar et al. (2011), Michno et al. (2014), Shaaban et al. (2015, 2016) have assumed constant values of the electron anisotropy $A_{e}$ and plasma beta $\beta_{e,\parallel}$, independent of proton properties. On the other hand, our present analysis includes the effects of the suprathermal populations of electrons, which are ubiquitous in the solar wind.

In order to proceed and make the analysis more transparent, we rewrite the linear dispersion relation (1) in terms of normalized quantities

$$\begin{aligned} \tilde{k}^{2} =&\mu ( {A_{e}}-1 ) +\mu\frac{{A_{e}} ( \tilde{\omega}\mp\mu ) \pm\mu}{\tilde{k}\sqrt{\mu \beta_{e,\parallel}}} Z_{e,\eta} \biggl( \frac{\tilde{\omega}\mp \mu}{\tilde{k}\sqrt{\mu\beta_{e,\parallel}}} \biggr) \\ &{}+A_{p}-1+ \frac{ A_{p} ( \tilde{\omega}\pm1 ) \mp1}{\tilde{k}\sqrt{\beta_{p,\parallel}}}Z_{p, \eta} \biggl( \frac{ \tilde{\omega}\pm1}{\tilde{k}\sqrt{\beta_{p,\parallel}}} \biggr) \end{aligned}$$

(2)

where $\tilde{\omega}=\omega/\varOmega_{p}$, $\tilde{k}= kc/\omega_{p,p}$, $\mu= m_{p}/m_{e}$ is the proton/electron mass ratio, $\beta_{\alpha, \parallel} = 8 \pi n_{e} k_{B} T_{ \alpha,\parallel} / B^{2}$ are the parallel plasma betas for protons (subscript $\alpha=p$) or electrons (subscript $\alpha=e$). Now we assume that the electron and proton temperature anisotropies are correlated

$$\begin{aligned} A_{e}= A_{p}^{\delta} \end{aligned}$$

(3)

with a correlation index $\delta$, eventually indicated by the observations. The correlation index may be either positive $\delta>0$ when both species have the same type of anisotropy with respect to the stationary magnetic field $\mathbf{B}$, i.e., if $A_{p} \gtrless1$ then $A_{e} \gtrless1$, or negative $\delta< 0$, when electrons and protons have opposite anisotropies, i.e., if $A_{p}\gtrless1$ then $A_{e}\lessgtr1$. In the following calculations our reference is the classical case with isotropic electrons, i.e., $A_{e}=1$, that here is obtained for a correlation index $\delta=0.0$.

3 Unstable solutions: interplay of protons and electrons

In this section we examine the electromagnetic instabilities driven by proton anisotropies $A_{p}\neq1$ under the influence of anisotropic electrons by means of the correlation-index $\delta$. For the electrons the velocity distributions measured in space plasmas may be considerably enhanced by the suprathermal populations and we therefore consider them (bi-)Kappa distributed. The proton data invoked in our analysis is measured by SWE/WIND (Ogilvie et al. 1995) with velocities corresponding to a kinetic energy in the range of $150\mbox{ eV}$ to $8\mbox{ keV}$ excluding suprathermal populations. In general, the presence of suprathermal protons is indeed less significant and we can assume the protons to be more thermalized and bi-Maxwellian distributed.

We divide our analysis into two distinct classes of instabilities according to the proton anisotropy. First we consider the instabilities developed by an excess of parallel temperature, i.e., $A_{p} > 1$. Among these, the firehose instability is the fastest growing mode and is RH circularly polarized when is propagating in direction parallel to the magnetic field. In the opposite situation, when protons exhibit an excess of perpendicular temperature, i.e., $A_{p} < 1$, the fastest developing instability is that of the electromagnetic ion cyclotron (EMIC) instability propagating in direction parallel to the magnetic field and with a LH circular polarization.

3.1 Solar wind protons with $T_{p,\parallel}>T_{p,\perp}$

The effects of the new correlation-index $\delta$ on the growth rates of the PFHI are displayed in Fig. 1(a). The unstable solutions are computed, for $A_{p}=0.4$, $\beta_{e,\parallel}= \beta_{p,\parallel}=3$, and for different values of $\delta= 1.0,0.0,-0.37$ (implying different electron anisotropies, respectively, $A_{e}=0.4, 1.0, 1.4$). The growth rates display two distinct peaks when the electrons are anisotropic, i.e., $\delta= 1.0, -0.37$. The first peak at low wavenumbers corresponds to the PFHI, while the second peak may represent either the electron FHI (EFHI), see the solid (red) line, when the correlation-index $\delta=1$, or the whistler instability (WI), see the dotted (blue) line, when the correlation-index $\delta=-0.37$. Driven by an electron anisotropy $A_{e}<1$ the EFHI propagating parallel to the magnetic field is LH circularly polarized and has a frequency in the range of $\omega_{p}<\omega_{r}\ll\vert \varOmega_{e}\vert$, while the WI is a RH circularly polarized mode destabilized by the anisotropic electrons with $A_{e}>1$ and with the frequency $\omega_{p}< \omega_{r}<\vert\varOmega_{e}\vert$. Results in Fig. 1(a) show that the growth rates of the PFHI are inhibited by anisotropic electrons described by a negative $\delta$-index (implying $A_{e}>1$), while the same growth rates are stimulated by a positive $\delta$-index (implying $A_{e}<1$). Physically, under the inhibiting effect of a negative $\delta<0$ on the PFHI, the instability needs higher values of the anisotropy $A_{p}$ or higher values of the parallel plasma beta $\beta_{p,\parallel}$ to achieve the same growth rate. We should therefore expect that the PFHI thresholds will move towards higher values of plasma beta $\beta_{p,\parallel}$, and shape better the anisotropy limits observed in the solar wind (see Sect. 4). For the opposite case, when $\delta>0$, the instability is stimulated and threshold conditions should diminish towards lower values of plasma beta $\beta_{p,\parallel}$.

Fig. 1

Effects of $\delta\mbox{-index} =-0.37,0.0,1.0$ (top), and the $\kappa\mbox{-index}=2,3,6,\infty$ with $\delta=-0.3$ (bottom) on the growth rates of PFHI instability. The plasma parameters are explicitly given in each panel

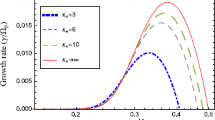
Based on these premises, the effect of the suprathermal electrons is shown in Fig. 1(b) only for a negative correlation-index $\delta=-0.3$. The growth rates are computed for $A_{p}=0.47$, $\beta_{e,\parallel}=\beta_{p,\parallel} = 2$, and for different values of the power-index $\kappa_{e}=2, 3, 6, \infty$. The PFHI growth rates are suppressed by increasing the suprathermal population, i.e., lowering $\kappa$, see the subplot (zoomed) in Fig. 1(b), while the WI growth rates are enhanced. In other words, the inhibiting effect of the anisotropic electrons described by a negative $\delta<0$ on the PFHI is enhanced by the suprathermal electrons. Moreover, this instability may be completely suppressed with decreasing the power-index, e.g., for $\kappa_{e}=2$, only the WI develops (blue dotted line) at electron scales. Note that the growth rate of the WI obtained for $A_{p}=0.47$ cannot distinguish from that obtained with isotropic protons $A_{p}=1$ (not shown here). These new results apparently contradict those obtained by Lazar et al. (2011) in a study of the PFHI cumulatively driven by the anisotropic protons $A_{p}<1$ and electrons $A_{e}>1$ (see Fig. 5 in Lazar et al. 2011). In their study the WI growth rates were found to decrease with increasing the electron suprathermal population as a result of a different Kappa approach with a $\kappa$-independent temperature that recently was proven inappropriate for such an analysis (Lazar et al. 2015). More results on the kinetic instabilities using approaches with a $\kappa$-dependent temperature, as used in the present paper, can be found in Leubner and Schupfer (2000, 2001), Lazar et al. (2015), and Shaaban et al. (2016).

For a complete picture, Fig. 2 displays the real frequencies corresponding to the unstable solutions in Fig. 1. When the anisotropies of protons and electrons are correlated by a positive $\delta=1$, i.e., $A_{e} < 1$, the wave-frequencies in panel (a) confirm a conversion of the RH-polarized PFH modes to the LH-polarized EFH modes (solid red line) by changing the sign in between the PFHI and EFHI peaks. At these low frequencies, the LH and Rh branches are relatively close to each other making possible a conversion, determined in this case by the interplay of the PFH and EFH instabilities. Otherwise, the RH branch (which is destabilized at low frequencies by the PFHI) extends smoothly (monotonically increasing dispersion) to electron scales (dashed and dotted lines), where the anisotropic electrons with an anti-correlated anisotropy $A_{e} > 1$, as given by a negative $\delta=-0.37$, may drive the instability of whistler modes (WI with dotted line). In panel (b) we show that wave-frequencies corresponding to the growth rates in Fig. 1(b) are not markedly influenced by the presence of suprathermal electrons.

Fig. 2

Wave-frequencies of the unstable modes in Fig. 1. The plasma parameters are mentioned in each panel

3.2 Solar wind protons with $T_{p,\perp}>T_{p,\parallel}$

The electromagnetic ion cyclotron (EMIC) instability is triggered by the anisotropic protons with $A_{p}>1$ (i.e., $T_{p,\perp}> T_{p,\parallel }$). This instability develops first in direction parallel to the magnetic field, where the EMIC modes are LH circularly polarized. In Fig. 3(a) we display the growth rates of this instability driven by a temperature anisotropy $A_{p}=1.4$ for $\beta_{e,\parallel }=\beta_{p,\parallel} = 6$, and different values of the $\delta=1.0,0.0,-1.0$, with mention that first value $\delta=1$ is carefully chosen to produce the same anisotropy of the electrons $A_{e}=1.4$ as in Fig. 1(a). In this case the growth rates display two peaks only for a negative correlation-index, e.g., for $\delta=-1.0$ (implying $A_{e}=0.714$) the EMIC peak obtained at low wavenumbers is followed by the peak of the EFHI, see solid (red) line. For a positive $\delta> 0$, implying $A_{e} >1$, the WI is absent, as it belongs to another branch with opposite (RH) polarization and much higher frequency ($\omega_{r} \gg\varOmega_{p}$). The EMIC instability is inhibited by increasing $\delta$ from negative values, implying protons and electrons with anti-correlated anisotropies ($A_{p} > 1$, $A_{e} < 1$) to positive values when these anisotropies are correlated ($A_{p,e} > 1$). Therefore, in Fig. 3(b) we describe the influence of suprathermal electrons only for a direct correlation of the proton and electron anisotropies by a positive $\delta=0.8$. Growth-rates are plotted for a proton anisotropy $A_{p}=2.7$, the same plasma beta parameter for protons and electrons $\beta_{e,\parallel}= \beta_{p,\parallel}= 0.1$, and different values $\kappa=1.8,2,3, \infty$. In the vicinity of the instability threshold level $\gamma_{m}/\varOmega_{p}=10^{-2}$ the instability inhibits by increasing the suprathermal population of electrons.

Fig. 3

Effect of $\delta=1,0.0,-1$ (top) and the $\kappa\mbox{-index} =1.8,2,3,\infty$ with $\delta=0.8$ (bottom) on the growth rates of EMIC instability. The plasma parameters are explicitly given in each panel

Figure 4 presents the real frequencies corresponding to the unstable solutions in Fig. 3. Unlike the growth rates, the wave-frequencies of the EMIC modes are enhanced by increasing the correlation index $\delta$, see panel (a). However, the anisotropy of protons is modest (not very large) and after the EMIC saturation the wave-frequency changes the sign, converting to the RH branch under the influence of electrons, which are expected to manifest important kinetic effects in this case, due to their high $\beta_{e,\parallel} = 6$. The same high value of $\beta_{e,\parallel}$ may stimulate a LH EFHI to develop (at larger wave-numbers) when the electron anisotropy is anti-correlated, i.e., $\delta= -1$ (red solid line), and this is confirmed by the wave-frequency which becomes again positive, i.e., LH-polarized. In panel (b) we show that wave-frequency of the EMIC modes are slightly enhanced by the presence of suprathermal electrons, but in this case the effects of electrons are minimal due to their small $\beta_{e,\parallel} = 0.1$.

Fig. 4

Wave-frequencies of the unstable modes in Fig. 3. The plasma parameters are mentioned in each panel

The results in Sects. 3.1 and 3.2 already suggest that instabilities thresholds can be enhanced, namely, by a negative correlation-index $\delta<0$ for the PFHI and a positive $\delta>0$ for the EMIC instability. An analysis of these thresholds is presented in Sect. 4.

3.3 Insights from resonance conditions

In these section we will try to identify the physical mechanisms behind these effects. Basic explanations for the electron anisotropy effects on the PFHI are offered by Kennel and Scarf (1968) and later by Michno et al. (2014), namely, that for isotropic electrons the protons are weakly resonant, while for anisotropic electrons with $A_{e}>1$ the phase velocity is increased and, consequently, the protons become less resonant leading to lower growth rates of PFHI. This explanation is confirmed here by studying the resonance conditions $\vert\xi_{p} ^{+}\vert= \vert\ (\tilde{\omega}+1)/(\tilde{k}\sqrt{ \beta_{p,\parallel}})\vert$ given by the arguments of plasma dispersion function in Appendix A, Eq. (7). We call these quantities resonant factors, and Figs. 5(a) and (b) display them for protons and electrons, respectively, for the same plasma parameters as in Fig. 1(a). The zoomed plot in Fig. 5(a) provides details on the proton resonant factor $\vert\xi_{p}^{+}\vert$ for different values of $\delta$-index at wavenumbers $\tilde{k}$ corresponding to the peaks of the PFHI growth rates as $(\delta, \tilde{k}, \vert\xi_{p}^{+}\vert)= (-0.37,0.42, 2.15), (0.0,0.41,1.98), (1.0,0.5,1.6)$. It becomes now clear that in the presence of anisotropic electrons with $A_{e}>1$, the resonant factor increases $(\vert\xi_{p}^{+}\vert=2.15 > 1)$ and the protons become less resonant with the resulting PFHI. With increasing the wave-number the resonant factors $\vert\xi_{p} ^{+}\vert$ drops down to a minimum value, and then, for large enough $\tilde{k}>1$ their values rise again since the real frequency (not shown here) is rapidly increased. For $\delta=0.0,-0.37$ these minimum values remain above unity. Comparison can be made to a simplified approach with isotropic electrons, i.e., $\delta=0.0$. For a negative correlation-index $\delta=-0.37$ the protons become less resonant ($\vert\xi_{p}^{+}\vert>1$) due to a significant increase of the real frequency by coupling to the high-frequency WI with the same RH polarization, see also Fig. 1(a). As normalized quantities, both the wave-frequency and the resonant factor remain much larger than unity with increasing the wave-number. In the opposite case, namely, for a positive correlation-index $\delta=1.0$, the EFHI arises at (slightly) higher wavenumbers, Fig. 3(a), with an opposite (LH) polarization, i.e., the wave-frequency changes the sign (Michno et al. 2014). The turning point (singularity given by the cold-plasma resonance $\Re(\xi_{p}^{+}) =0$), where the resonant factor takes a minimum value $\vert\xi_{p}^{+}\vert_{\mathrm{min}}=\vert \tilde{\gamma}/ (\tilde{k} \sqrt{\beta_{p,\parallel}})\vert \ll1$, is followed by the resonance of protons with the EFHI, i.e., $\vert\xi_{p}^{+}\vert\sim1$, and with increasing the wave-number the resonant factor increases again.

Fig. 5

The resonant conditions for protons $\vert\xi_{p}^{+} \vert$ (top) and electrons $\vert\xi_{e}^{+}\vert$ (bottom) for the same plasma parameters in Fig. 1(a)

Figure 5(b) shows the electron resonant factor $\vert\xi_{e} ^{+}\vert$ at wave-numbers corresponding to the peaks of the EFHI and WI as $(\delta,\tilde{k},\vert\xi_{e}^{+}\vert)=(1.0,6.85,3.6),(-0.37,18.5, 1.06)$. The electrons are clearly non-resonant with the EFHI since $\vert\xi_{e} ^{+}\vert>1$, and strongly non-resonant near the peak of the PFHI where $\vert\xi_{e}^{+}\vert\gg 1$. However, the electrons become resonant with the WI when $\vert\xi_{e}^{+}\vert\gtrsim 1$.

Additional insights can be provided for the EMIC instability in order to understand the recent results which show that anisotropic electrons with $A_{e}>1$ may increase the wave-frequency of these modes but inhibit the growth rates of the instability (Shaaban et al. 2015), while these effects are stimulated by the suprathermal electrons (Shaaban et al. 2016). Our dynamical model which correlates the main kinetic properties of protons and electrons reconfirms these effects, e.g., in Fig. 3. The resonant factors for protons ($\vert\xi _{p}^{-}\vert$) and electrons ($\vert\xi_{e}^{-}\vert$) are plotted in Fig. 6, panels (a) and (b), respectively. These factors are computed for the same parameters as in Fig. 3(b) to show the influence of suprathermal electrons quantified by the power-index $\kappa=1.8, 2,3,\infty$. For protons, four values of the resonant factor are explicitly given corresponding to the peaks of the EMIC growth rates as $(\kappa_{e}, \tilde{k},\vert\xi_{p}^{-}\vert) = (1.8,1.705), (0.78,1.675), (0.81,1.62), (0.825,1.598)$. According to the zoomed plot in Fig. 6(a), the protons become less resonant $(\vert\xi_{p}^{-}\vert=1.705)$ with increasing the suprathermal population of electrons $(\kappa_{e}=1.8)$, which explains the inhibiting effect of the EMIC instability. Note that maximum growth rate for $\kappa_{e}=3$ is near the threshold level $\gamma_{m}/\varOmega _{p}=10^{-2}$, and the corresponding value of the proton resonant factor $\vert\xi_{p}^{-}\vert=1.62$ is in a good agreement with the results obtained by Gary and Lee (1994). The proton resonant factor $\vert\xi_{p}^{-}\vert= \vert\ (\tilde{\omega}-1)/(\tilde{k}\sqrt{ \beta_{p,\parallel}})\vert$ decreases with increasing the wave-number until is drops abruptly down reaching a minimum value $\vert\xi_{p} ^{-}\vert_{\mathrm{min}}= \vert\tilde{\gamma}/(\tilde{k}\sqrt{ \beta_{p,\parallel}})\vert\ll1$ at the turning point (singularity of cold-plasma resonance $\Re(\xi_{p}^{-}) =0$). Beyond this point the real frequencies are saturated and the modes are strongly damped with an increasing damping rate $-\tilde{\gamma}$, making the proton resonant factor (as absolute value) to increase.

Fig. 6

The resonant conditions for protons $\vert\xi_{p}^{-} \vert$ (top) and electrons $\vert\xi_{e}^{-}\vert$ (bottom) for the same plasma parameters in Fig. 3(b)

Figure 6(b) shows that the electrons are highly non-resonant near the peaks of the EMIC instability, with $\vert\xi_{e}^{-}\vert \gg 1$, and remain non-resonant $\vert\xi_{e}^{-}\vert\simeq10$, even for the wave-numbers corresponding to the electron scales. It becomes also clear that the EMIC branch cannot connect to the high-frequency whistler (electron cyclotron) modes, which have a different (RH) polarization and which is resonantly destabilized by the (anisotropic) electrons, e.g., the whistler instability (WI) discussed above, also known as the electron-cyclotron instability.

4 Instabilities thresholds vs. observations

The anisotropy thresholds may provide a straightforward confirmation for the constraining role played by the kinetic instability in collision-poor plasmas from space, namely, when these thresholds fit the limits of the temperature anisotropy reported by the observations. Derived for different levels of maximum growth-rates $\gamma_{m}/ \varOmega_{p}= 10^{-3}, 10^{-2}, 10^{-1}$ and for an extended range of the plasma beta parameter $0.005\leqslant\beta_{p,\parallel}\leqslant 100$, the instability thresholds may also provide a general picture of the instability and the new effects triggered by the interplay of electrons and protons. In the present work we analyze the isocontours of anisotropy thresholds ($A_{p}$) derived for $\gamma_{m}= 10^{-3} \varOmega_{p}$ (a sufficiently low level also adopted in similar investigations), and represented as an inverse correlation law of the proton plasma beta $\beta_{p,\parallel}$ (Hellinger et al. 2006)

$$ A_{p}=1+\frac{a}{ ( \beta_{p,\parallel}-\beta_{0} ) ^{b}}. $$

(4)

For the instability thresholds derived in Figs. 7–9 fitting parameters $a$, $b$, and $\beta_{0}$ are tabulated in Tables 1 and 2 in Appendix B. The standard inverse correlation introduced by Gary and Lee (1994) may be recovered for $\beta_{0}=0$. Thresholds are compared with the observations in the slow solar wind ($v_{sw}\leqslant 600~\mbox{km}/\mbox{s}$), i.e., protons measured by SWE (Ogilvie et al. 1995) and MFI (Lepping et al. 1995) on the WIND spacecraft at 1 AU (Kasper et al. 2002; Hellinger et al. 2006; Michno et al. 2014).

Fig. 7

The influence of the correlation-index $\delta=0.0,-0.5,-0.8$ (top), and the power-index $\kappa=3,6,\infty$ with $\delta=-0.5$ (bottom) on the PFHI thresholds ($\gamma_{m} =10^{-3} \varOmega_{p}$). Thresholds are compared with the proton (core) anisotropy at 1 AU in the solar wind and the plasma parameters are explicitly given in each panel

The PFHI thresholds are displayed in Fig. 7, in panel (a) for different correlation-indices $\delta= 0.0, -0.5, -0.8$ (implying different electron anisotropy $A_{e}= A_{p}^{\delta}$), and in panel (b) for different power-indices $\kappa_{e}=3, 6, \infty$ and same $\delta= -0.5$. Simplified approaches usually adopt $\delta=0.0$ when the electrons are assumed isotropic $A_{e}=1$ (blue dotted line in Fig. 5(a)). The inhibiting effect obtained for a negative correlation index $\delta<0$ (i.e., $A_{e}>1$), see Fig. 1(a), is confirmed by the thresholds with $\delta= -0.5,-0.8$ moving towards higher values of the proton plasma beta $\beta_{p,\parallel}$. By increasing this anti-correlation between protons and electrons, i.e., decreasing negative values of $\delta$, the instability thresholds are enhanced and can markedly improve their fit with the limits of the temperature anisotropy observed in the solar wind. In the second panel (b) we can observe that these thresholds are further boosted by the suprathermal electrons: for lower values of $\kappa_{e}$ the PFHI thresholds are moved to higher plasma beta exceeding the limits observed for the proton anisotropy confirming the results in Fig. 1(b).

Figure 8 shows the influence of the anisotropic electrons with $A_{e}>1$ on the EMIC instability, and compares to the idealized case with isotropic electrons ($A_{e}=1$, dotted blue line). For $\beta_{e,\parallel}=\beta_{p,\parallel}$ the instability thresholds do not change much to improve fitting to the observations, even for $\delta=1$ (i.e., $A_{p}=A_{e}$), see the short-dashed (orange) line. However, Shaaban et al. (2015, 2016) have recently shown that inhibiting effect induced by the anisotropic electrons is stimulated by increasing $\beta_{e,\parallel}$. Thus, for an average value $\beta_{e,\parallel}=1$ indicated by the observations (Štverák et al. 2008), also commonly invoked in similar investigations (Hellinger et al. 2006; Matteini et al. 2013), the EMIC threshold can increase considerably constraining more observational data, see dashed (green) line. On the other hand, the fit with the observations is considerably improved in the presence of suprathermal electrons, i.e., the instability thresholds enhance with decreasing the power-index $\kappa_{e}$ confirming the results in Fig. 3. In this case, the EMIC thresholds are plotted for $A_{e}=A_{p}$ (i.e., $\delta=1$), $\beta_{e,\parallel}=1$, $\kappa_{e}=2$ (long-dashed brown line), and $\kappa_{e}=1.8$ (solid red line).

Fig. 8

Thresholds conditions ($\gamma_{m} =10^{-3} \varOmega_{p}$) for the EMIC instability compared with the proton (core) anisotropy at 1 AU in the solar wind. The plasma parameters are explicitly given in each panel

For the sake of completeness, Fig. 9 compares the best of our results with the those obtained by Michno et al. (2014) for parallel PFHI ($C_{e}=2$), and Hellinger et al. (2006) for the aperiodic $(\omega_{r}=0)$ instabilities, namely, the aperiodic proton firehose (APFH) and mirror instabilities. Most interesting appear to be the new instability thresholds obtained in panel (a) for the EMIC instability in the presence of suprathermal electrons and with a direct (positive) correlation $\delta= 1$ between the proton and electron anisotropies ($A_{e}=A_{p}$). These isocontours show a good alignment to the observations, similar to the mirror instability. The presence of suprathermal electrons, which are ubiquitous in the solar wind, is critical and may considerably enhance the role played by the EMIC instability in the low-beta regimes (e.g., for $\kappa_{e}=1.8$). Moreover, these results are obtained for a common (average) value of the electron beta parameter, namely, $\beta_{e,\parallel} =1$ indicated by the observational data cumulation (Štverák et al. 2008), and for a direct correlation of the electron and proton anisotropies given by a positive $\delta= 1 > 0$. As already explained in the Introduction we do not dispose of systematic observational analyses to confirm a direct correlation of electron and proton anisotropies, but this condition may in general be ensured by the mechanisms always at work in space plasmas, e.g., solar wind expansion, magnetic focusing, and it seems therefore more plausible than an anti-correlation of the anisotropies. Based on these arguments, the fits obtained in panel (a) can be considered robust enough to support the implication of the EMIC instability in constraining the proton temperature anisotropy and explain the observations. In panel (b) we compare the new thresholds obtained for the PFHI with those derived by Michno et al. (2014) or Hellinger et al. (2006) for the APFH instability, and can conclude that anisotropic electrons may influence the PFHI thresholds and determine them to align better to the observations, e.g., the long-dashed brown line obtained for $\delta=-0.8$. However, in this case the best-aligned thresholds are conditioned by an anti-correlation between the proton and electron anisotropies as required by a negative $\delta< 0$.

Fig. 9

Thresholds of the aperiodic ($\omega_{r} = 0$) instabilities, i.e., mirror and the aperiodic PFH (APFH), as provided by Hellinger et al. 2006, and the instabilities of our periodic modes, i.e., EMIC and PFH, are compared with the proton core data at 1 AU in the solar wind

5 Conclusions

In a collisionless electron-proton plasma the temperature anisotropy, and, implicitly, the distribution function should be regulated by the resulting instabilities and electromagnetic fluctuations through the wave-particle interaction. For anisotropic protons, the theory and simulations predict a dominance of the cyclotron modes driven unstable by the PFH and EMIC instabilities, which may develop fast enough leading to an important pitch angle scattering of protons toward isotropy (Kennel and Scarf 1968; Gary 1992). However, predictions made by the simplified approaches for the anisotropy thresholds of these instabilities appear to be overestimated by comparison to the temperature anisotropy measured in-situ in the solar wind. Instead, these observations seem to be better constrained by the aperiodic instabilities, e.g., APFHI and mirror instability (Hellinger et al. 2006).

In this paper we have aimed to resolve this paradigm and provide more realistic predictions from an advanced modeling that accounts for the interplay of protons and electrons, and the presence of suprathermal electrons. New regimes are thus found for the PFH and EMIC instabilities, which are mainly controlled by the cumulative effects of protons and electrons by correlating either their anisotropies, e.g., $A_{e}=A_{p}^{\delta}$, via the parameter $\delta$, or/and their plasma beta parameters, $\beta_{e}=\beta_{p}$. Similarities and differences among these regimes are highlighted in Sect. 3, always comparing with the idealized approaches which consider electrons isotropic, i.e., $\delta= 0$. We have studied the effects of these correlation factors on the growth-rates and provided physical explanations by studying the resonant conditions for both the protons and electrons.

A comparative analysis of these new regimes enabled us to identify conditions that may inhibit the instabilities and make their thresholds to adjust better to the observations. Thus, the PFHI is driven by a proton anisotropy $A_{p}<1$, and can be inhibited by anisotropic electrons with anti-correlated anisotropies $A_{e}=A_{p}^{\delta} > 1$ given by a negative $\delta< 0$. In the opposite situation when protons exhibit a temperature anisotropy $A_{p}>1$, the EMIC instability is inhibited only for a positive $\delta> 0$ meaning electrons with a direct correlated anisotropy $A_{e}=A_{p}^{\delta} > 1$. Moreover, in both these two cases the inhibiting effect is boosted by the suprathermal electrons. The explanation is provided by the resonant factors, which indicate that protons become less resonant inhibiting the instability and leading to higher anisotropy thresholds. These results confirm the expectations from the previous studies carried out by Kennel and Scarf (1968), Lazar et al. (2011), Michno et al. (2014), Shaaban et al. (2015, 2016).

To provide a complete picture, in Sect. 4 we have studied the instability thresholds, and recovered the inhibiting effects on the PFH and EMIC instabilities for an extended range of the plasma beta parameter $0.005 <\beta_{p,\parallel} < 100$. These thresholds are compared to the proton anisotropy data observed in the (slow) solar wind at 1 AU. The PFHI thresholds decrease moving towards higher plasma beta $\beta_{p,\parallel}$ with decreasing the $\delta$-index and with increasing the suprathermal electron population. For the EMIC instability, the threshold conditions in the low-beta regimes are only weakly affected by the anisotropic electrons, but can be significantly lowered by increasing the electron plasma beta $\beta_{e,\parallel}=1$ and the presence of suprathermal electrons. To conclude, we have identified the conditions for the instability thresholds to align and shape the limits of the temperature anisotropy reported by the observations. These agreements with the observations can be even better than those obtained before for the aperiodic instabilities, but are highly conditioned by the electron properties, i.e., the anisotropy (correlated or anti-correlated with the proton anisotropy), plasma beta parameter, and their suprathermal populations.

Suprathermal electrons are ubiquitous in space plasmas but the main question arising now concerns the existence of the plasma states with protons and electrons having anisotropies either direct correlated and roughly described by a positive $\delta> 0$, or anti-correlated by a negative $\delta< 0$. As already discussed in the Introduction, we do not dispose of any systematic evidences and estimations of these correlations from the observations, but there are some qualitative indications which appear to be more favorable to direct correlated anisotropies of electrons and protons, i.e., $A_{e,p} > 1$ at low heliocentric distances for both species, or $A_{e,p} < 1$ at higher radial distances, again for both species. These states may naturally result from the large-scale processes which generate temperature anisotropy in the solar wind, e.g., adiabatic expansion, magnetic field compression, while the other states with anti-correlated anisotropies may be established most probably, locally, by the small-scale mechanisms of particle energization involving the electromagnetic fluctuations. For a correct interpretation of the kinetic effects, like dissipation or instabilities, in space plasmas, a self-consistent treatment of plasma particles and electromagnetic fluctuations is therefore crucial and needs to be supported by the observations. From this point of view, the advanced approach proposed in the present paper may be considered as an important progress towards a realistic interpretation of the interplay of electrons and protons and their effects in the solar wind.

Appendices

Appendix A: Distributions and dispersion functions

For a plasma of electrons and protons with bi-Maxwellian velocity distribution functions (VDFs)

$$ F_{\alpha,M} ( v_{\parallel},v_{\perp} ) =\frac{1}{\pi ^{3/2}u_{\alpha,\perp}^{2} u_{\alpha,\parallel}}\exp \biggl( -\frac{v _{\parallel}^{2}}{u_{\alpha,\parallel}^{2}}-\frac{v_{\perp }^{2}}{u _{\alpha,\perp}^{2}} \biggr) , $$

(5)

where thermal velocities $u_{\alpha,\parallel, \perp}$ are defined by the components of the anisotropic temperature

$$\begin{aligned} &T_{\alpha,\parallel}^{M}=\frac{m}{k_{B}} \int d\textbf{v} v_{\parallel}^{2} F_{\alpha}(v_{\parallel}, v_{\perp})=\frac{m u_{\alpha,\parallel}^{2}}{2 k_{B}} \end{aligned}$$

(6)

$$\begin{aligned} &T_{\alpha,\perp}^{M}=\frac{m}{2 k_{B}} \int d\textbf{v} v_{\perp} ^{2} F_{\alpha}(v_{\parallel}, v_{\perp})=\frac{m u_{\alpha,\perp}^{2}}{2 k_{B}}, \end{aligned}$$

(7)

the plasma dispersion function in Eq. (1) takes the standard form (Fried and Conte 1961)

$$ Z_{\alpha,M} \bigl( \xi_{\alpha,M}^{\pm} \bigr) = \frac{1}{\pi^{1/2}} \int_{-\infty }^{\infty}\frac{\exp ( -x^{2} ) }{x-\xi_{\alpha,M}^{\pm}}dt,\quad \Im \bigl( \xi_{\alpha,M}^{\pm} \bigr) >0 $$

(8)

of argument $\xi_{\alpha,M}^{\pm}= ( \omega\pm\varOmega_{ \alpha} ) / ( ku_{\alpha,\parallel,} )$

To include suprathermal population, the electrons can be described by a bi-Kappa VDF (Summers and Thorne 1991)

$$\begin{aligned} F_{e,\kappa} =& \frac{1}{\pi^{3/2}u_{e, \perp}^{2}u_{e, \parallel}} \frac{\varGamma ( \kappa_{e} +1 ) }{\varGamma ( \kappa_{e} -1/2 )} \\ &{}\times\biggl[ 1+\frac{v_{\parallel}^{2}}{\kappa_{e} u_{e, \parallel}^{2}}+\frac{v_{\perp}^{2}}{\kappa_{e} u_{e, \perp}^{2}} \biggr] ^{-\kappa_{e} -1} \end{aligned}$$

(9)

which is normalized to unity $\int d^{3}vF_{e,\kappa}= 1$, and is written in terms of thermal velocities $u_{e,\parallel, \perp}$ defined by the components of the effective temperature (for a power-index $\kappa_{e} >3/2$)

$$ T_{e,\parallel}^{K}=\frac{2 \kappa_{e}}{2 \kappa_{e}-3}\frac{m_{e} u _{e ,\parallel}^{2} }{2 k_{B}}, \quad \quad T_{e,\perp}^{K}=\frac{2 \kappa_{e}}{2 \kappa_{e}-3}\frac{m_{e} u_{e , \perp}^{2}}{2 k_{B}}. $$

(10)

Suprathermals enhance the electron temperature, and implicitly the plasma beta parameter (Leubner and Schupfer 2000, 2001; Lazar et al. 2015)

$$ \begin{aligned} &T_{e,\parallel, \perp}^{K}=\frac{2 \kappa_{e}}{2 \kappa_{e}-3}T_{e,\parallel,\perp}^{M} > T_{e,\parallel,\perp}^{M}, \\ &\beta_{e,\parallel, \perp}^{K}=\frac{2 \kappa_{e}}{2 \kappa_{e}-3} \beta_{e,\parallel,\perp} > \beta_{e,\parallel,\perp}, \end{aligned} $$

(11)

and for the modified Kappa dispersion function (8) we use in Eq. (1) the form (Lazar et al. 2008)

$$\begin{aligned} Z_{e,\kappa} \bigl( \xi_{e,\kappa}^{\pm}\bigr) =& \frac{1}{\pi^{1/2}\kappa_{e}^{1/2}}\frac{\varGamma ( \kappa_{e} ) }{\varGamma ( \kappa_{e} -1/2 )} \\ &{}\times \int_{-\infty}^{\infty}\frac{ ( 1+x^{2}/\kappa_{e} ) ^{-\kappa_{e}}}{x-\xi_{e,\kappa}^{\pm}}dx,\ \Im \bigl(\xi_{e,\kappa}^{\pm} \bigr) >0, \end{aligned}$$

(12)

of argument $\xi_{e,\kappa}^{\pm}= (\omega\pm\varOmega_{e})/(k u_{e,\parallel,})$.

Appendix B: Fitting parameters for Eq. (4)

Table 1 Fitting parameters for PFH thresholds in Figs. 7 and 9(b)

Table 2 Fitting parameters for EMIC thresholds in Figs. 8 and 9(a)