A four-way decision-making approach using interval-valued fuzzy sets, rough set and granular computing: a new approach in data classification and decision-making

Abstract

In this paper, a novel method is presented to solve the problems of classification and decision-making by employing the interval-valued fuzzy set, rough set and granular computing (GrC) concepts. The proposed method can classify the objects available in a system, called an interval-valued fuzzy decision table into the four distinct regions as interval-valued fuzzy-positive region, interval-valued fuzzy-negative region, interval-valued completely fuzzy region and interval-valued gray fuzzy region. These four regions constitute a new space for decision-making, which is termed as a four-way interval-valued decision space (4WIVDS). Based on the classified objects, various decision rules are generated from the distinct regions of the 4WIVDS. The study shows that the interval-valued gray fuzzy region has included most prominent decision rules. For taking precise level of decisions based on this particular region, this study utilizes the GrC to extract granular level of decision rules which are prominent by nature. The proposed 4WIVDS method is verified and validated with various benchmark datasets. Experimental results include statistical and comparison analyses which signify the efficiency of the proposed method in classifying the objects and generating the decision rules.

1 Introduction

Classification of information and decision-making is the process of correlating the relationships between the input and output attributes (Theodoridis and Koutroumbas 2008). In information classification, input attributes are often called as the conditional attributes, whereas output attribute is called as the decision attribute. Basically, in the soft computing-based methods (Singh 2015), i.e., methods based on fuzzy set (Zadeh 1965) and rough set (Pawlak 1982), have gained popularity in the scientific community for solving the problem of information classification and decision-making. The concept of fuzzy sets as proposed by Zadeh (1965) has been applied in many different fields including data analysis and decision-making (Bezdek and Pal 1992; Chen et al. 2001, 2012; Wang and Chen 2008; Chen and Tanuwijaya 2011; Chen and Chang 2011). It is almost incomprehensible for mathematical- or statistical-based models for making appropriate decisions due to the poor characterization of conditions associated with conditional attributes. Therefore, it is favorable to utilize a fuzzy concept instead of a crisp concept to reach to a specific decision or solution (Szmidt and Kacprzyk 1996). In literature, among several types of fuzzy sets, interval-valued fuzzy set (IVFS) presented by Zadeh (1975) has been observed to be appropriate for managing uncertainty. In many real-world applications, due to an unconfirmed degree of memberships of the elements, it is more appropriate to define the degree of memberships in terms of IVFS (Yang et al. 2009). For the representation of higher order imprecision and vagueness, various interval-valued memberships are also suggested based on type-2 fuzzy set (Castillo and Melin 2008; Guh et al. 2009; Sanchez et al. 2015a, b; Cervantes and Castillo 2015; Castillo et al. 2016a, b; Ontiveros-Robles et al. 2018), which are better than real membership values.

In these articles (Chen et al. 1997; Chen and Hsiao 2000), authors have presented a bidirectional approximate reasoning method based on IVFS by utilizing fuzzy production rules for knowledge representation. Bustince (2000) studied IVFS-based methods in inference approximate reasoning. Yang et al. (2009) proposed a new decision-making model by combining IVFS with soft set. Zhang et al. (2009a) proposed a new axiomatic definition of the entropy of IVFS. For group decision-making, Chen et al. (2013) proposed interval-valued hesitant preference relations. Bustince et al. (2009) show the application of IVFS in the edge detection of the image. Jiang et al. (2010) introduced interval-valued intuitionistic fuzzy soft set theory by integrating interval-valued intuitionistic fuzzy set theory and a soft set theory. By combining rough set theory with IVFS, Zhang et al. (2009b) proposed the concept of interval-valued fuzzy rough sets on two universe of discourses. To fit real-life uncertainty in algebraic form, Pal (2015) proposed matrix having row and column in the form of interval-valued fuzzy elements. Takác̆ (2016) proposed a measure or an inclusion indicator for IVFS, which is based on the aggregation of fuzzy interval implications. Yu (2017) introduced the method for multi-criteria decision-making using hesitant fuzzy Heronian mean operators. Zhang et al. (2016) presented an approach for multi-criteria decision-making using interval-valued intuitionistic fuzzy set.

It is obvious that IVFS can be used to represent the uncertainty of the data, and to solve the problems associated with information classification and decision-making. However, to classify the information into more granular level to take a granular level of decision, a new computational technique is used, which is termed as a granular computing (GrC). Nowadays, GrC is evolving as an emerging technique for information processing (Peters and Weber 2016). GrC is used to extract fine-grain information from the complex information or data. It is applied in various domains, such as data discretization (Lingras et al. 2016), data classification (Antonelli et al. 2016), partition of universe to solve complex problems (Zadeh 1997), analysis of non-geometric patterns (Livi and Sadeghian 2016), and decision-making (Xu and Wang 2016). GrC techniques can be regarded as an indispensable part of information granulation, rough sets, and interval computations (Pedrycz 2013). GrC is also used in data mining for rule representation, rule mining, and soft computing (especially in fuzzy and rough sets) (Yao 2006). In fuzzy sets, information granulation means discretization of the basis of information or source of information into a fine-grain level to extract optimal results (Singh and Dhiman 2018). Based on fuzzy set, rough set and GrC concepts, novel four-way decision-making systems have been proposed (Singh et al. 2018; Singh and Rabadiya 2017, 2018).

Literature review evaluation indicates that there is a still requirement of a complex decision-making system that can completely deal with the uncertain and vague nature of information. By motivating this, we present a novel method to solve the problems of uncertain information classification and decision-making by employing the IVFS, rough set and GrC concepts, which is termed as a “four-way interval-valued decision space (4WIVDS)”. This 4WDS classifies objects available in information system into four distinct regions and generates decision rules from them by following means as

• Step 1: Representation of information using IVFS Initially, available information corresponding to each attribute is fuzzified using the IVFS and transferred into a system, which is termed as an interval-valued fuzzy information system (IVFIS). Then, a decision table is designed, which is called as an interval-valued fuzzy decision table (IVFDT).

• Step 2: Generate three regions using rough set Rough set is applied in the IVFDT to classify the objects into three regions, viz., lower approximation (LA), upper approximation (UA) and boundary region (BR).

• Step 3: Region level partitioning or granularization using proposed method In this phase, granularization is applied into the three regions of rough set to evolve more precise regions with classified information. By applying granularization, initially objects available in the LA and UA are classified into two separate granular regions as interval-valued fuzzy-positive region and interval-valued fuzzy-negative region, respectively. During granularization, two more regions are discovered, which are named as an interval-valued completely fuzzy region and interval-valued gray fuzzy region. By combining these four granular regions, a new decision-making space is defined, which is entitled as a four-way interval-valued decision space (4WIVDS).

• Step 4: Granularization of the interval-valued gray fuzzy region Among the four regions of the 4WIVDS, the interval-valued fuzzy-positive and interval-valued fuzzy-negative regions comprise binary relations with decision, whereas the interval-valued gray fuzzy region comprises information that is inherited from both interval-valued fuzzy-positive and interval-valued fuzzy-negative regions. In most of the cases, these two regions comprise identical decision rules that can obviously affect on decision-making process. So, there is a requirement of further granularization of this particular region, so that insignificant information can be filtered out from the significant information. For this purpose, granularization is applied on the interval-valued gray fuzzy region to discover more precise and significant information. Finally, information available in the four regions of the 4WIVDS are represented in the form of decision rules, and their significance is analyzed using various statistical parameters.

Applications of the proposed 4WIVDS are shown in benchmark datasets (Lichman 2013), which include Pima Indians diabetes, Thyroid disease, Fisher’s Iris and Spambase. Experimental results demonstrate that the proposed 4WIVDS concept is not only able to classify the objects available in the IVFDT into the four distinct regions, but also able to take the granular level of decisions from them.

The remainder of this article is structured as follows. In Sect. 2, the proposed 4WIVDS is presented. In Sect. 3, decision rule evaluation parameters are discussed. Experimental results are discussed in Sect. 4. Conclusion is presented in Sect. 5.

2 The proposed four-way interval-valued decision space (4WIVDS)

The proposed 4WIVDS follows four sequential steps (as discussed in Sect. 1) for the classification of objects and generation of decision rules from information systems. This section provides an illustration of these four steps of the proposed 4WIVDS in the following subsections.

2.1 Representation of information using IVFS

The IVFS is an extension of fuzzy set, which can be defined as follows:

Definition 1

(Interval-valued fuzzy set (IVFS)) (Gorzałczany 1987) Let the universe of discourse$U=\{({d}_1, {d}_2, \ldots , {d}_k)\}$ consist of non-empty finite set of objects; $D=\{{X}_1, {X}_2, \ldots , {X}_k\}$ is a non-empty finite set of attributes. Then, an IVFS $\tilde{A}$ on the universe of discourse U is a mapping, such that

$$\tilde{A}:U \to {\text{Int}}\,([0,1]).$$

(1)

Here, Int ([0, 1]) represents for the set of all closed sub-intervals of [0, 1]. The set of all IVFS on the universe U is denoted by I (U).

Let $I_1=[lb_{1}, ub_{1}]$, $I_2=[lb_{2}, ub_{2}]$, $\ldots$, $I_n=[lb_{n}, ub_{n}]$ be the set of sub-intervals for each of the tuples that belong to the U. Now, if $\tilde{A} \in I(U)$, then the corresponding degree of membership for each tuple can be bounded between lower and upper degrees of membership as $[\mu _{\tilde{A}}(I_i)_*, \mu _{\tilde{A}}(I_i)^*]$, where $0 \le \mu _{\tilde{A}}(I_i)_*\le \mu _{\tilde{A}}(I_i)^*\le 1$. The lower and upper degrees of membership for each $I_{i}$ w.r.t. U can be computed as

$$\mu _{{\tilde{A}}} (I_{i} )_{*} = \frac{{lb_{i} - \min \,(U)}}{{\max \,(U) - \min \,(U)}}$$

(2)

$$\mu _{{\tilde{A}}} (I_{i} )^{*} = \frac{{ub_{i} - \min \,(U)}}{{\max \,(U) - \min \,(U)}}.$$

(3)

Here, ${lb}_{i}$ and ${ub}_{i}$ represent the lower and upper bounds of the sub-interval $I_{i}$, where $I_{i} \in U$. In Eqs. (2) and (3), min (U) and max (U) return the minimum and maximum values of the k-tuples that belong to the universe of discourse U, respectively.

In this study, each tuple associated with the attributes is represented using an interval-valued fuzzified linguistic variable (IVFLV). Therefore, IS in which each tuple is represented using the IVFLV is called as an interval-valued fuzzy information system (IVFIS). In the IVFIS, each row may represent event (i.e., a case, an event, a patient, etc.) and every column may represent attribute (i.e., a variable, an observation, a property, etc.). We can define the IVFIS based on IVFS next.

Definition 2

(Interval-valued fuzzy information system (IVFIS)) Assume that ${\mathbb {F}}\,(D)$ is the set of all IVFLV for the D, then an interval-valued fuzzy information system (IVFIS) can be defined as a function $f_{i}\,(i=1,2, \ldots , n)$, such that $\forall d_{i}: D \longrightarrow {\mathbb {F}}\,(D)$.

Table 1 Multi-attribute information system for the daily stock index price of Yahoo Inc. for the period 3/1/2000–31/1/2000

Table 2 A list of IVFLVs used to fuzzify the daily stock index price of Yahoo Inc. for the period 3/1/2000–31/1/2000

In the following, an example is illustrated using the daily stock index price of Yahoo Inc. for the period 3/1/2000–31/1/2000. This dataset is shown in Table 1 and collected from the website: http://in.finance.yahoo.com.

Example 1

Dataset as shown in Table 1 comprises 20 objects (i.e., $1, 2, 3, \ldots , 20$), where all of them belong to the universe of discourse U (refer to Definition 1). In this table, various crisp information in context of the daily used financial attributes, such as “Open”, “High”, “Low”, “Close”, and “Final Price”, have been shown. The attributes “Open”, “High”, “Low”, and “Close” are called as the conditional attributes, whereas “Final Price” is called as the decision attribute. For each of the tuples, their corresponding memberships are determined using Eqs. (2) and (3), respectively. Then, they are represented using IVFLVs. A list of IVFLVs used to represent each of the tuples corresponding to their attributes are shown in Table 2. In Table 2, each $I_{ji}\,(i=1,2,3~\text{ for } \text{ j=1, } \text{ and } \text{ so } \text{ on })$ represents an IVFLV for each of the corresponding attributes. For example, in Table 1, dated on 3/1/2000, the stock index price for the attribute “Open” is 110.73. This stock index price belongs to the interval $I_{13}=(0.69, 1)$ (refer to Table 2); hence, this crisp information is represented by IVFLV $I_{13}$. In this way, all the crisp information available in Table 1 is represented using the list of IVFLVs (as given in Table 2). Hence, a system is prepared for each of the tuples contained in Table 1 using the IVFLVs, which is shown in Table 3. This newly evolved system is called as an interval-valued fuzzy decision table (IVFDT).

Table 3 The IVFDT for the daily stock index price of Yahoo Inc. for the period 3/1/2000–31/1/2000

The interval-valued fuzzy information system (IVFIS) can be classified into two disjoint classes of attributes, called as conditional and decision (actions) attributes, respectively. Such a system is called an interval-valued fuzzy decision table (IVFDT), which is defined next.

Definition 3

(Interval-valued fuzzy decision table (IVFDT)) An interval-valued fuzzy decision table (IVFDT) is an IVFIS, which is augmented with a special attribute ${X}_j \in D$, known as the decision attribute, whereas attributes other than $X_j$ are called the conditional attributes. It can be denoted by $\mathbb {T}$.

Example 2

In Example 1, we have seen that how crisp values can be represented in terms of the IVFLVs. Now, information contained in Table 3 can be regarded as the IVFDT. In Table 3, last column “Final Price” represents the decision attribute. Remaining attributes are considered as the conditional attributes. Now, this IVFDT can be used for object classification and decision rule generation.

Definition 4

(Interval-valued fuzzy equivalence class (IVFEC)) An interval-valued fuzzy equivalence class (IVFEC) is a set of objects from the $U=\{({d}_1, {d}_2, \ldots , {d}_k)\}$ such that their tuple values are identical in terms of conditional and decision attributes of the IVFDT.

Definition 5

(Interval-valued fuzzy equivalence class (IVFEC)) It is a set of all objects like $d_{j} ,d_{k}$, so that $d_{j} ,d_{k}$ have similar conditional and decision attributes in the IVFDT (${\mathbb {T}}$). It can be denoted as ${\mathbb {E}}$ and can be represented by

$${\mathbb{E}} = \{ d_{j} ,d_{k} \in {\mathbb{T}\mid }D(d_{j} ) = D(d_{k} )\}.$$

(4)

Example 3

From Table 3, we want to explain the attribute “Final Price” in terms of objects 1–20. In this table, when all the conditional as well as decision attributes are considered, then total four IVFECs are explored as ${\mathbb {E}}_{c}$ = {3, 7, 8, {9, 13}, {4, 5}, {1, 2, 6}, {10, 11, 12, 14, 15, 16, 17, 18, 19, 20}}. Among all these IVFECs, there are three particular objects, viz., 3, 7 and 8 can be distinguished from one another based on the corresponding attributes.

Example 4

Decision rules can often be presented as implications, called “if...then ...” rules. An example of decision rule induced from the IVFDT (as shown in Table 3) is given as follows:

$$1:if({\text{Open}},I_{{13}} ),({\text{High}},I_{{23}} ),({\text{Low}},I_{{33}} ),({\text{Close}},I_{{43}} ),\,{\text{then}}\,({\text{Final Price}},I_{{53}} ).$$

Here, $I_{13}$, $I_{23}$, $I_{33}$, and $I_{43}$ represent the IVFLVs corresponding to their corresponding conditional attributes for the object 1 (as shown in Table 3).

2.2 Generate three regions using rough set

In this subsection, rough set theory is applied to classify the objects available in the IVFDT into three regions as LA, UA and BR. Before initiating the classification using rough set theory, an interval-Valued equivalence relation is required to obtain for the objects available in the IVFDT, which can be defined as

Definition 6

(Interval-Valued Equivalence Relation (IVER)) Let R be an interval-valued equivalence relation (IVER) over U, then the family of all IVFEC of R is represented by U/R.

Based on the IVER, three regions, viz., LA, UA and BR, can be defined for the objects available in the IVFDT. These three regions are defined next.

Definition 7

(Lower approximation (LA)) It is a set of all objects $d_{i}$ that completely belong to the set I(U). The lower approximation (LA) of $d_{i}$ (i.e., $\underline{R}({d}_{i})$) can be defined as

$$\underline{R}({d}_{i})=\cup \{{d}_{i} \in I(U) \mid [{d}_{i}]_R \subseteq I(U)\}.$$

(5)

Definition 8

(Upper approximation (UA) It is a set of all objects $d_{i}$ that possibly belong to the set I (U). The interval-valued upper approximation (IVUA) of $d_{i}$ (i.e., $\bar{R}({d}_{i})$) can be defined as

$$\bar{R}({d}_{i})=\cup \{{d}_{i} \in I(U) \mid [{d}_{i}]_R \cap I(U) \ne \emptyset \}.$$

(6)

Definition 9

(Boundary region (BR)) The set of all objects $d_{i} \in I(U)$, which can be decisively classified neither as members of $\bar{R}({d}_{i})$ nor as members of $\bar{R}({d}_{i})$ w.r.t. R is called the boundary region (BR) of a set I(U) w.r.t.R, and denoted by $RS_B$.

$$RS_{B}=\bar{R}({d}_{i})-\underline{R}({d}_{i}).$$

(7)

Based on the above notions, we can formulate the definition of rough set as:

Definition 10

(Rough set (RS)) A set I(U) is called rough set (RS) (inexact) w.r.t.R, if and only if the BR of I(U) is nonempty.

Example 5

We want to explain the attribute “Final Price” for the decision $I_{51}$ in terms of objects {9, 13, 14, 15, 16, 17, 18, 19, 20} as

• The $\underline{R}({u}_{i})$ of the set of objects having decision $I_{51}$w.r.t. the “Final Price” is the set {10, 11, 12} (based on Eq. 5).

• The $\overline{R}({u}_{i})$ of the set of objects having decision $I_{51}$w.r.t. the “Final Price” is the set {3, 7, 8, {9, 13}, {4, 5}, {1, 2, 6}, {10, 11, 12, 14, 15, 16, 17, 18, 19, 20}} (based on Eq. 6).

• The set {10, 11, 12} is the $RS_{B}$ for the attribute “Final Price” having decision $I_{51}$ (based on Eq. 7).

Using rough set theory (Pawlak 1982), set of objects available in the IVFDT can be classified into three regions as LA, UA and BR. This approach of classification indicates that

• 1. if an object belongs to the LA, then it must be prominent for the decision,

• 2. if an object belongs to the complement of UA, then it must be non-prominent for the decision, and

• 3. if an object belongs to the BR, then it must be indecisive for the decision.

From such classification of objects, one cannot state that the primary cause of this decision is because of this specific attribute’s value. Rough set approach is also not able to classify objects precisely in terms of prominent or non-prominent if their representation is itself fuzzy. Therefore, in the next subsection, a novel method has been presented for the object classification and decision-making.

2.3 Region level partitioning or granularization using proposed approach

In this subsection, we introduce the four-way interval-valued decision space (4WIVDS) method for the object classification and decision-making. This method initially classifies the set of objects available in the IVFDT into the four distinct regions as (a) interval-valued fuzzy-positive region $(IVFPR^{+})$, (b) interval-valued fuzzy-negative region $(IVFNR^{-})$, (c) interval-valued completely fuzzy region $(IVCFR^{+-})$ and (d) interval-valued gray fuzzy region $(IVGFR^{+-})$. The 4WIVDS can be defined as follows:

Definition 11

(Four-way interval-valued decision space (4WIVDS)) A 4WIVDS can be defined by a five-tuple ${\mathbb {S}}$ = $\langle U,IVFPR^{+},IVFNR^{-},IVCFR^{+-},IVGFR^{+-}\rangle$ on the IVFDT, where U is called the universe of discourse, $IVFPR^{+}$ the interval-valued fuzzy-positive region, $IVFNR^{-}$ the interval-valued fuzzy-negative region, $IVCFR^{+-}$ the interval-valued completely fuzzy region, and $IVGFR^{+-}$ is called the interval-valued gray fuzzy region.

Definitions and mathematical representations of the four regions, viz., $IVFPR^{+}$, $IVFNR^{-}$, $IVCFR^{+-}$ and $GFR^{+-}$, are presented next.

Definition 12

(Interval-valued fuzzy-positive region$(IVFPR^{+})$) The $IVFPR^{+}$ region can be defined as the set of $d_{i} (i=1,2, \ldots ,n)$ from the IVFDT that completely belongs to the $\underline{R}({d}_{i})$, i.e., $d_{i} \in \underline{R}({d}_{i})$. Mathematically, it can be represented by

$$IVFPR^{+}=\{d_{i} \in I(U) \mid d_{i} \in \underline{R}({d}_{i}) \wedge d_{i} \notin \overline{R}({d}_{i})\}.$$

(8)

Definition 13

(Interval-valued fuzzy-negative region$(IVFNR^{-})$) The $IVFNR^{-}$ region can be defined as the set of $d_{i} (i=1,2,\ldots ,n)$ from the IVFDT that completely belongs to the $\overline{R}({d}_{i})$, i.e., $d_{i} \in \overline{R}({d}_{i})$. Mathematically, it can be represented by

$$IVFNR^{-}=\{d_{i} \in I(U) \mid d_{i} \in \overline{R}({d}_{i}) \wedge d_{i} \notin \underline{R}({d}_{i})\}.$$

(9)

Definition 14

(Interval-valued completely fuzzy region$(IVCFR^{+-})$) The $IVCFR^{+-}$ region can be defined as the set of $d_{i} (i=1,2,\ldots ,n)$ from the IVFDT that not belong to either of the $\underline{R}({d}_{i})$ and $\overline{R}({d}_{i})$. Mathematically, it can be represented by

$$IVCFR^{+-}=\{d_{i} \in I(U) \mid d_{i} \notin \underline{R}({d}_{i}) \vee d_{i} \notin \overline{R}({d}_{i})\}.$$

(10)

Definition 15

(Interval-valued gray fuzzy region$(IVGFR^{+-})$) The $IVGFR^{+-}$ region can be defined as the set of $d_{i} (i=1,2,\ldots ,n)$ from the IVFDT that belongs to both $\underline{R}({d}_{i})$ and $\overline{R}({d}_{i})$. Mathematically, it can be represented by

$$IVGFR^{+-}=\{d_{i} \in I(U) \mid d_{i} \in \underline{R}({d}_{i}) \wedge d_{i} \in \overline{R}({d}_{i})\}.$$

(11)

Fig. 1

The figure showing the granularization of three regions of rough set into four distinct regions of the 4WIVDS. Here, left-hand side of the figure indicates three regions of rough set, and right-hand side of the figure indicates four regions of the 4WIVDS obtained through the granularization

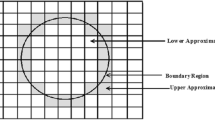
In Fig. 1, it has been demonstrated the granularization of three regions of rough set (i.e., LA, UA and BR) into four distinct regions of the 4WIVDS, viz., $IVFPR^{+}$, $IVFNR^{-}$, $IVCFR^{+-}$ and $IVGFR^{+-}$. These four regions are associated with four kinds of objects, which can be defined as

Definition 16

(Fuzzy-positive interval-valued object (FPIVO)) If set $X_{P}$ contains such $d_{i}$ from the IVFDT that satisfies the property of $IVFPR^{+}$, then it is called as a fuzzy-positive interval-valued object (FPIVO). Mathematically, it can be represented by

$$X_{P}=\{(d_{i} \in IVFPR^{+}) \wedge (d_{i} \notin IVFNR^{-}) \mid d_{i} \in I(U) \}.$$

(12)

Definition 17

(Fuzzy-negative interval-valued object (FNIVO)) If set $X_{N}$ contains such $d_{i}$ from the IVFDT that satisfies the property of $IVFNR^{-}$, then it is called as a fuzzy-negative interval-valued object (FNIVO). Mathematically, it can be represented by

$$X_{N} = \{ (d_{i} \notin IVFPR^{ + } ) \wedge (d_{i} \in IVFNR^{ - } ){\mid }d_{i} \in I(U)\} .$$

(13)

Definition 18

(Completely fuzzy interval-valued object (CFIVO)) If set $X_{C}$ contains such $d_{i}$ from the IVFDT that does not satisfy the properties of $IVFPR^{+}$ and $IVFNR^{-}$, then it is called as a completely fuzzy interval-valued object (CFIVO). Mathematically, it can be represented by

$$X_{C} = \{ (d_{i} \notin IVFPR^{ + } ) \wedge (d_{i} \notin IVFNR^{ - } ){\mid }d_{i} \in I(U)\} .$$

(14)

Definition 19

(Gray fuzzy interval-valued object (GFIV)) If set $X_{G}$ contains such $d_{i}$ from the IVFDT that satisfies the properties of both $IVFPR^{+}$ and $IVFNR^{-}$, then it is called as a gray fuzzy interval-valued object (GFIVO). Mathematically, it can be represented by

$$X_{G}=\{(d_{i} \in IVFPR^{+}) \wedge (d_{i} \in IVFNR^{-}) \mid d_{i} \in I(U)\}.$$

(15)

Example 6

Information available in Table 3 can be classified into four distinct parts as discussed above. For example, in terms of the decision $I_{51}$w.r.t objects {9, 13, 14, 15, 16, 17, 18, 19, 20} for the decision attribute “Final Price” (refer to Table 3), the four distinct regions can be defined as

• By referring to Table 3, the $X_{P}$ is the set of objects, which have decision $I_{51}$ for the decision attribute “Final Price” and prominent for decision-making. Hence, we have $X_{P}=${10, 11, 12}. Based on Definition 16, all the tuples that belong to objects of $IVFPR^{+}$ can be considered as the FPIVs. Now, these FPIVs constitute a region, which is called the $IVFPR^{+}$ (based on Definition 12). This region can be shown in Fig. 1.

• By referring to Table 3, the $X_{N}$ is the set of objects, which have decision $I_{51}$ for the decision attribute “Final Price” and important and insignificant for decision-making. Hence, we have $X_{N}=${{9, 13}, {10, 11, 12, 14, 15, 16, 17, 18, 19, 20}}. Based on Definition 17, all the tuples that belong to objects of $IVFNR^{-}$ can be considered as the FNIVs. Now, these FNIVs constitute a region, which is called the $IVFNR^{-}$ (based on Definition 13). This region can be shown in Fig. 1.

• Based on Definition 18, all other objects {3, 7, 8, {4, 5}, {1, 2, 6}} w.r.t. the decision $I_{51}$ for the decision attribute “Final Price” can be considered as the CFIVs. It is the most insignificant for decision-making. Now, these CFIVs constitute a region, which is called the $IVCFR^{+-}$ (based on Definition 14).

• Based on Definition 19, the objects {10, 11, 12} can be considered as the GFIVs and most prominent decision rules, which have the decision $I_{51}$ for the decision attribute “Final Price”. Now, these GFIVs constitute a region, which is called the $IVGFR^{+-}$ (based on Definition 15).

Hence, the significance of the four regions in terms of decision-making is given as follows:

• The $IVFPR^{+}$ comprises those decision rules, which can be considered as a prominent for decision-making.

• The $IVFNR^{-}$ contains both important and insignificant decision rules.

• The $IVCFR^{+-}$ region constitutes of such decision rules, which are the most insignificant for decision-making.

• The $IVGFR^{+-}$ signifies region, which contains the most prominent decision rules, through which efficient decision-making can be performed.

Various properties associated with the 4WIVDS are presented in “Appendix”.

2.4 Granularization of the interval-valued gray fuzzy region

On the basis of GrC, a new granular level of region can be defined based on the interval-valued gray fuzzy region ($IVGFR^{+-}$) (refer to Definition 15). Due to granularization of the $IVGFR^{+-}$, two more sub-regions are obtained, which are termed as a gray fuzzy interval-valued granular-positive region (GFIVGPR) and gray fuzzy interval-valued granular-negative region (GFIVGNR). Both GFIVGPR and GFIVGNR are denoted as $GFIVGPR^{+}$ and $GFIVGNR^{-}$, respectively. Both these two sub-regions are defined next.

Definition 20

($GFIVGPR^{+}$ and $GFIVGNR^{-}$) If $X_{G}^{P}({d}_{i})$ contains such $d_{i}$ from the $X_{G}$ (refer to Definition 19) that satisfies properties of the $IVFPR^{+}$, then it is called the $GFIVGPR^{+}$. Similarly, if $X_{G}^{N}({d}_{i})$ contains such $d_{i}$ from the $X_{G}$ (refer to Definition 19) that satisfies properties of the $IVFNR^{-}$, then it is called the $GFIVGNR^{-}$. Mathematical representations of both $GFIVGPR^{+}$ and $GFIVGNR^{-}$ are given in Eqs. (16) and (17), respectively.

$$X_{G}^{P}({d}_{i})=\{{d}_{i} \in GFIVGPR^{+}) \mid {d}_{i} \in X_{G}\},$$

(16)

$$X_{G}^{N}({d}_{i})=\{{d}_{i} \in GFIVGNR^{-}) \mid {d}_{i} \in X_{G}\}.$$

(17)

Definition 21

(Gray fuzzy interval-valued granular boundary region (GFIVGR)) It is a set $X_{GR}({d}_{i})$, which contains those objects $d_{i}$ from the $IVGFR^{+-}$ that satisfies the following condition:

$$X_{GR}({d}_{i})=\{X_{G}^{N}({d}_{i})-X_{G}^{P}({d}_{i}) \mid X_{G}^{P}({d}_{i}),X_{G}^{N}({d}_{i}) \in X_G\}.$$

(18)

Example 7

From Example 6, we have the set of objects in $X_{G}$ as :{10, 11, 12}. Now, we select pair set of IVFEC as objects {10, 11} from the $IVGFR^{+-}$ for taking granular-level decision. Based on Eqs. (16) and (17), we have $X_{G}^{P}({d}_{i})$ = {12} and $X_{G}^{N}({d}_{i})$ = {10, 11, 12}. Hence, from Eq. (18), we get $X_{GR}({d}_{i})$ = {10, 11}.

Granularization of the IVFDT provides a new insight into the patterns inherited in the data. Therefore, more granularization of objects that belong to the IVFDT may lead to evolve various inherited information. By summarizing the definitions and theories of the 4WIVDS, an algorithm is presented to classify objects available in the IVFDT. This algorithm is referred as a granular-level classification and decision-making algorithm (GLCDMA), which is presented in Fig. 2.

Fig. 2

Granular-level classification and decision-making algorithm (GLCDMA)

A complete process of information classification and decision-making using the proposed GLCDMA is shown in Fig. 3.

Fig. 3

A complete process of information classification and decision-making based on the proposed 4WIVDS

3 Decision rule evaluation

To examine whether decision rules are classified accurately in terms of regions associated with the 4WIVDS, following parameters are defined.

Definition 22

(Measure of accuracy) The measure of accuracy ($\alpha _{R} (d_{i} )$) in terms of $X_{P}$ and $X_{N}$ can be defined as

$$\alpha _{R} (d_{i} ) = \frac{{\left| {X_{P} } \right|}}{{\left| {X_{N} } \right|}}.$$

(19)

Here, $\left| {d_{i} } \right|$ denotes the cardinality of $d_{i}$. Here, $\alpha _B({d}_{i})$ lies between the ranges $0\le \alpha _B({d}_{i}) \le 1$. An object $d_{i}$ can easily be differentiated from crisp to rough based on $\alpha _B({d}_{i})$ value as follows:

• If $\alpha _R({d}_{i})\le 1$, then $d_{i}$ is prominent for decision.

• If $\alpha _R({d}_{i})= 0$, then $d_{i}$ is non-prominent for decision.

Example 8

Here, we demonstrate an example for Definition 22. From Example 5, we have the $X_{P}$ as {10, 11, 12} and the $X_{N}$ as {{10, 11, 12, 14, 15, 16, 17, 18, 19, 20}, {9, 13}}. Now, based on Eq. (19), the accuracy of approximation is $\alpha_{R}$(“Final Price”) $=\frac{3}{12}=0.25 <1$. It indicates that the decision $I_{51}$ for the decision attribute “Final Price” can be characterized partially employing conditional attributes {Open, High, Low, Close} w.r.t. objects {9, 13, 14, 15, 16, 17, 18, 19, 20} and can be considered as prominent for decision.

Based on this accuracy of approximation concept, a four-way decision evaluation function is defined as follows:

Definition 23

(Degree of association (DA)) Any $d_{i}$ can be associated with one of the four regions of the decision space ${\mathbb {D}}$ with a certain degree of percentage, which can be evaluated as

• Condition 1: If $\bigcup \nolimits _{i=1}^n{\tilde{d}_i}= K \subseteq {\mathbb {D}}$, and $DA(\%)=\frac{\mid K \cap X_P\mid }{\mid X_P\mid } > 0$, then the objects of K belong to the $IVFPR^{+}$ with the certain degree of percentage (obtained through the DA).

• Condition 2: If $\bigcup \nolimits _{i=1}^n{\tilde{d}_i}= K \subseteq {\mathbb {D}}$, and $DA(\%)=\frac{\mid K \cap X_N\mid }{\mid X_N\mid } > 0$, then the objects of K belong to the $IVFNR^{-}$ with the certain degree of percentage (obtained through the DA).

• Condition 3: If $\bigcup \nolimits _{i=1}^n{\tilde{d}_i}= K \subseteq {\mathbb {D}}$, and $DA(\%)=\frac{\mid K \cap X_C\mid }{\mid X_C\mid } > 0$, then the objects of K belong to the $IVCFR^{+-}$ with the certain degree of percentage (obtained through the DA).

• Condition 4: If $\bigcup \nolimits _{i=1}^n{\tilde{d}_i}= K \subseteq {\mathbb {D}}$, and $DA(\%)=\frac{\mid K \cap X_G\mid }{\mid X_G\mid } > 0$, then the objects of K belong to the $IVGFR^{+-}$ with the certain degree of percentage (obtained through the DA).

Example 9

Here, we demonstrate an example for Definition 23. From Example 6, we have the objects in the following 4WIVDS as (a) {10, 11, 12} $\in X_P$, (b) {{10, 11, 12, 14, 15, 16, 17, 18, 19, 20}, {9, 13}} $\in X_{N}$, (c) {10, 11, 12} $\in X_{G}$, and (d) {3, 7, 8, {4, 5}, {1, 2, 6}} $\in X_{C}$. Now, we will take $K=${10, 11} to verify that the objects {10, 11} are classified correctly or not into the $\in X_{P}$. By following Condition 1 of the DA, we have $DA(\%)=\frac{\mid K \cap X_P\mid }{\mid X_P\mid }= \frac{2}{3}=0.67>0$. This 0.67 value indicates the association of the objects {10, 11} with the $IVFPR^{+}$ having $67\%$ of DA.

The term cardinality helps to measure the uniqueness of the objects $d_{i} \in U$ contained in an IVFDT. The higher the cardinality, the less replicated objects $d_{i} \in U$ in the 4WIVDS. Thus, if any of the four regions of the 4WIVDS have the identical cardinality, then these objects $d_{i}$ that are classified into these four regions can have almost same feature patterns.

Definition 24

The cardinality of two different regions, viz., $IVFPR^{+}$ and $IVFNR^{-}$ can be represented by $\phi (X_P)$ and $\phi (X_N)$, respectively, and can be defined as follows:

$$\phi (X_{P} ) = \frac{{\left| {d_{i} } \right|}}{{\left| U \right|}},$$

(20)

$$phi (X_{N} ) = \frac{{\left| {d_{j} } \right|}}{{\left| U \right|}}.$$

(21)

Here, these two objects $d_{i}$ and $d_{j}$ belong to the $IVFPR^{+}$ and $IVFNR^{-}$, respectively. The cardinality for the remaining two regions can be calculated in a similar manner.

Example 10

From Table (3), we have the objects in the four regions of the 4WIVDS as follows: (a) {10, 11, 12} $\in X_P$, (b) {{10, 11, 12, 14, 15, 16, 17, 18, 19, 20}, {9, 13}} $\in X_N$, (c) {10, 11, 12} $\in X_G$, and (d) {3, 7, 8, {4, 5}, {1, 2, 6}} $\in X_C$. Now, based on Eqs. (20) and (21), we have the cardinality for the above discussed four regions as

$$\begin{aligned} & \phi (X_P)=\frac{\mid 3 \mid }{\mid 20 \mid }=0.15\\ & \phi (X_N)=\frac{\mid 12 \mid }{\mid 20 \mid }=0.6\\ & \phi (X_G)=\frac{\mid 3 \mid }{\mid 20 \mid }=0.15\\ & \phi (X_C)=\frac{\mid 8 \mid }{\mid 20 \mid }=0.4. \end{aligned}$$

Here, the cardinality of the $X_{P}$ and $X_{G}$ is identical to each other. It indicates that these two distinct regions have the similar feature patterns in their corresponding regions.

Theorem 1

Every object ${d}_{i} (i=1,2,\ldots ,n)$ of U that also belongs to the $IVFPR^{+}$ and $IVGFR^{+-}$ have always similar cardinality.

Proof

It is obvious from Example (10). $\square$

4 Experimental results

The proposed 4WIVDS method can be applicable in decision-making of various kinds of real-world problems. In this section, we demonstrate the applications of the proposed 4WIVDS method by employing real-world datasets of (a) Pima Indians diabetes dataset, (b) Thyroid disease dataset, and (c) Fisher’s Iris dataset, and (d) Spambase dataset. These datasets are obtained from the UCI repository (Lichman 2013).

To evaluate the performance of the proposed 4WIVDS, it has been compared with various well-known classification methods, such as PART, JRip, Decision table, NaiveBayes, BayesNet, OneR, ZeroR, J48, LMT and rough set (Witten et al. 2016). Statistics which are adopted to compare the performance of the proposed 4WIVDS with existing competing methods are Kappa ($\kappa$), mean absolute error (MAE), root mean square error (RMSE), relative absolute error (RAE) and root relative squared error (RRSE) (Witten et al. 2016). All these parameters are defined as follows:

$$\kappa =\frac{p_o-p_e}{1-p_e},$$

(22)

$${\text{MAE}}=\frac{1}{n} \sum _{i=1}^{n} \mid p_o - p_e \mid ,$$

(23)

$${\text{RMSE}}=\sqrt{\frac{1}{n} \sum _{i=1}^{n} (p_o - p_e)^2},$$

(24)

$${\text{RAE}}=\frac{ \sum _{i=1}^{n} \mid p_o - p_e|}{\sum _{i=1}^{n} \mid p_e- \bar{p}_e\mid }\%,$$

(25)

$${\text{RRSE}}=\sqrt{\frac{{ \sum _{i=1}^{n} (p_o - p_e)^2}}{\sum _{i=1}^{n} (p_e- \bar{p}_e)^2}}\%.$$

(26)

In Eqs. (22–26), $p_{o}$ indicates observed value and $p_{e}$ indicates expected value for the same. In Eq. (22), the value of the kappa $\kappa$ is interpreted as value near to 1 is almost perfect fit model compared to the model having $\kappa \approx 0$. The MAE in Eq. (23) measures the average of absolute value of the errors present in classification. The RMSE (refer to Eq. 24) shows the average error, and if RMSE > 0 then it shows that there is an error present in classification. The RMSE will always be larger or equal to the MAE. In Eq. (25), $\bar{p}_{e}$ is the mean value of all $p_{e}$ values. For a perfect classification, the RAE is equal to 0 and $0< {\text{RAE}} < \infty$. Similarly, in Eq. (26), $\bar{p}_e$ is the mean value of all $p_{e}$ values. For a perfect fit of the model, the RRSE is equal to 0 and $0< {\text{RRSE}} < \infty$.

Table 4 A comparison of the proposed 4WIVDS with existing classification models for the Pima Indians diabetes dataset

Table 5 A comparison of the proposed 4WIVDS with existing classification models for the Thyroid disease dataset

Table 6 A comparison of the proposed 4WIVDS with existing classification models for the Fisher’s Iris dataset

Table 7 A comparison of the proposed 4WIVDS with existing classification models for the Spambase dataset

Tables 4, 5, 6 and 7 present various statistics of the different classification methods, such as PART, JRip, decision table, NaiveBayes, BayesNet, OneR, ZeroR, J48, LMT, rough set and the proposed 4WIVDS. From Tables 4, 5, 6 and 7, it has been shown that the proposed 4WIVDS gives maximum correctly classified instances and minimum incorrectly classified instances. Hence, amongst all the existing methods, the proposed 4WIVDS performs effectively in classification. For the proposed method, Kappa statistics for all four datasets are closer to 1 in comparison with existing methods. It indicates that the proposed 4WIVDS is better for classification compared to all other existing methods. While comparing the performance of the proposed 4WIVDS with the existing methods, it seems that the MAE and RMSE values for all four datasets are closer to 0 as well as less than the other existing methods. Hence, the proposed method is far better than all existing methods of classification. In Tables 4, 5, 6 and 7, values of other parameters, such as RAE (%), and RRSE (%) are very less as compared to all other classification methods that are considered for the comparison purpose. Hence, the proposed 4WIVDS outperforms and generates effective results in comparison with the well-known classification methods (as listed in Tables 4, 5, 6, 7).

5 Conclusion

This study presented a new method for solving the problem of object classification and decision-making. The proposed method, which is entitled as the 4WIVDS, is designed based on the IVFS, rough set and GrC concepts. The rough set theory can only classify the objects into three regions as lower approximation, upper approximation and boundary region. On the other hand, the proposed 4WIVDS can able to classify the objects into four distinct regions as interval-valued fuzzy-positive region $(IVFPR^{+})$, interval-valued fuzzy-negative region $(IVFNR^{-})$, interval-valued completely fuzzy region $(IVCFR^{+-})$ and interval-valued gray fuzzy region $(IVGFR^{+-})$.

In real world, most of the objects are overlapped to each other in terms of decision attributes. The rough set theory simply classifies such kind of objects as partially accepted and rejected objects. But, the 4WIVDS classified such kind of unclear boundary objects as the $IVGFR^{+-}$. This study applied the GrC approach on this particular region to discover a precise level of decision rules, which could help the decision makers to filter the prominent decision rules from the non-prominent decision rules. Experimental results showed that the four regions of the 4WIVDS have their own distinct classified objects. Based on these classified objects, various decision rules can be generated. Applicability of the proposed 4WIVDS was shown in various benchmark datasets (Lichman 2013), such as Pima Indians diabetes, Thyroid disease, Fisher’s Iris and Spambase datasets. The main advantage of the proposed 4WIVDS is its ability of preserving the property of fuzziness by crisply classifying the uncertain boundary information into the four well-defined regions.

Appendix

The 4WIVDS exhibits various properties, which are discussed as follows:

• (i) $RS_{B} \in X_N$

• (ii) $X_{N} \ne \emptyset$

• (iii) For $IVFPR^{+}$, it has the following conditions:

  $$\begin{aligned} X_P = {\left\{ \begin{array}{ll} \ne \emptyset; &{} \quad \text{ if } \text{ it } \text{ satisfies } \text{ Eq. } {8}. \\ =\emptyset; &{} \quad \text{ Otherwise. } \end{array}\right. } \end{aligned}$$

• (iv) $X_P \subseteq X_N$

• (v) $X_P \cup X_N \cup X_C \cup X_G = U$

• (vi) $RS_{B} \cap X_G = \emptyset$

• (vii) $X_P \cap X_C = \emptyset$

• (viii) $X_N \cap X_C = \emptyset$

• (ix) $RS_{B} \cap X_C = \emptyset$

• (x) $\overline{(X_P \cup X_N \cup X_G)}=X_C$

• (xi) If $RS_{B} \subseteq X_N$, then each ${d}_{i} \in RS_{B}$ and ${d}_{i} \in X_N$.

Theorem 2

For each of the non-empty sets $X_{P}$ , $X_{N}$ , and $X_{G},$ there exists a set $X_{C}$ if it holds

$$U-(X_{P}\cup X_{N} \cup X_G)=X_{C}.$$

Proof

With reference to Fig. 1, it is considered that $X_{P} \ne \emptyset$, $X_{N} \ne \emptyset$, and $X_{G} \ne \emptyset$. Now, we define three different regions in the 4WIVDS as $\gamma_{1}$, $\gamma_{2}$, and $\gamma_{3}$, based on the following set-theoretic operations:

$$U-X_P=\gamma_{1}$$

(27)

$$\gamma_1-X_{N}=\gamma_{2}$$

(28)

$$\gamma _2-X_{G}=\gamma_{3}.$$

(29)

Here, $\gamma_{3}$ represents the $X_{C}$ in the 4WIVDS, where $\gamma _1 \cap \gamma _2 \cap \gamma _3=X_C.$$\square$