Hesitant probabilistic fuzzy set based time series forecasting method

Abstract

Uncertainties due to randomness and fuzziness coexist in the system simultaneously. Recently probabilistic fuzzy set has gained attention of researchers to handle both types of uncertainties simultaneously in a single framework. In this paper, we introduce hesitant probabilistic fuzzy sets in time series forecasting to address the issues of non-stochastic non-determinism along with both types of uncertainties and propose a hesitant probabilistic fuzzy set based time series forecasting method. We also propose an aggregation operator that uses membership grades, weights and immediate probability to aggregate hesitant probabilistic fuzzy elements to fuzzy elements. Advantages of the proposed forecasting method are that it includes both type of uncertainties and non-stochastic hesitation in a single framework and also enhance the accuracy in forecasted outputs. The proposed method has been implemented to forecast the historical enrolment student’s data at University of Alabama and share market prizes of State Bank of India (SBI) at Bombay stock exchange (BSE), India. The effectiveness of the proposed method has been examined and tested using error measures.

1 Introduction

Time series forecasting has been an important area of research since age. Profound applications of time series forecasting are found in many fields that includes finance, engineering, medicines and management science, etc. Regression analysis, autoregressive integration moving average, simple moving average and simple exponential smoothing are few statistical models which are commonly used in conventional time series forecasting. However, these models touch the issue of probabilistic uncertainty of time series data, but fail to include non-probabilistic uncertainty that arises due to inaccuracies in measurement and linguistic representation. Need of fuzzy sets (Zadeh 1965) was felt in time series forecasting to overcome the limitations of conventional time series forecasting methods and to arrive a realistic results with higher accuracy rate in forecasted output with linguistic representation of time series data.

Song and Chissom (1993a, b, 1994) proposed time series forecasting models based on fuzzy sets (Zadeh 1965) to deal uncertainty in time series forecasting that arises due to vague, inaccurate and linguistic representation of time series data. Chen (1996) proposed simple arithmetic operators rather than complex max–min compositions operators used by Song and Chissom (1993a, b, 1994). Afterwards, many researchers (Chen and Hwang 2000; Huarng 2001; Song 2003; Lee and Chou 2004; Liu 2007; Cheng et al. 2008, 2016; Huarng and Yu 2006; Chen et al. 2009; Chen and Tanuwijaya 2011) proposed various fuzzy time series forecasting models with the innovation either in partitioning the universe of discourse or in fuzzy logical relations to enhance the accuracy in forecast. Chen and Chen (2014), Chen and Chen (2015), Chen and Phuong (2017), Wang and Mishra (2018) proposed various forecasting methods using granular computing, adaptive and intelligent fuzzy time series forecasting models. Chen and Chen (2011), Chen (2014), Ye et al. (2016), Yolcu et al. (2016), Kocak (2017) and Efendi et al. (2018) have proposed the high order fuzzy time series forecasting method based on fuzzy logic relations for stock trading. Recently, Bas et al. (2018) proposed ridge regression for forecasting using type 1 fuzzy function. Granular computing is intended as a convergence of numerous modeling approaches (Pedrycz and Chen 2011, 2015a, b). Various researchers (Livi and Sadeghian 2016; Wilke and Portmann 2016; Liu and Cocea 2017; D’Aniello et al. 2017) have used granular computing approach in modeling and computing with uncertainty, human-data interaction, machine learning and approximate reasoning. Deng et al. (2016) and Maciel et al. (2016) proposed time series forecasting models using multi-granularity and granular analytics.

Although fuzzy time series methods have achieved great success in forecasting in environment of non-probabilistic uncertainty, but failed to handle non-determinism. Non-determinism in fuzzy time series forecasting occurs due to hesitation. This hesitation is non-probabilistic and is due to single function in fuzzy set for both membership and non-membership and cannot be handled by random probability distribution. To deal with this non-probabilistic non-determinism in fuzzy time series forecasting, many researchers (Joshi and Kumar 2012a, b; Gangwar and Kumar 2014; Kumar and Gangwar 2015, 2016; Wang et al. 2016) developed intuitionistic fuzzy sets (Atanassov 1986) based time series forecasting models. Another non-probabilistic non-determinism in fuzzy time series forecasting occurs when time series data can be fuzzified using multiple valid fuzzification methods. Since difficulty of creating a common membership grade is not due to margin of error or possible distribution values, therefore, this non-determinism cannot be handled using IFS and type-2 fuzzy sets. Torra and Narukawa (2009) and Torra (2010) introduced the hesitant fuzzy set (HFS) as a new generalization of fuzzy sets to address this particular non-determinism. HFS provides an effective tool to eliminate the compromise among the membership grades of time series datum during fuzzification using multiple fuzzy sets. Bisht and Kumar (2016) proposed HFS based fuzzy time series forecasting model and claimed it’s out performance in financial time series forecasting. Recently, hesitant fuzzy linguistic sets have also been used by many researchers (Chen and Hong 2014; Lee and Chen 2015a, b; Joshi and Kumar 2018a, b; Joshi et al. 2018) in decision-making problems.

Probabilistic and non-probabilistic uncertainties are two conceptually different kinds of uncertainties which occur simultaneously in the system. One of the main advantages of fuzzy time series forecasting methods is their ability to handle non-stochastic uncertainty. However, these forecasting models do not possess the capabilities to handle stochastic uncertainties. Meghdadi (2001) introduced probabilistic fuzzy set (PFS) to consider both uncertainties in a single framework. Due to its main advantage of combining interpretability of fuzzy set with statistical properties, Liu and Li (2005) proposed a probabilistic fuzzy logic system for the modeling and control problems. Applications of PFS were explored by many researchers (Almeida et al. 2009; Hinojosa et al. 2011; Li and Huang 2012; Huang et al. 2012; Fialho et al. 2016) in various fields where probabilistic uncertainty plays equal and important role as non-probabilistic uncertainty. Xu and Zhou (2017) associated probabilistic to the elements of HFS and defined hesitant probabilistic fuzzy set (HPFS).

The motivation and contribution of this paper are to propose a novel time series forecasting method that can include both stochastic and non-stochastic uncertainties in hesitant fuzzy environment. Since profound applications of HPFS are found in decision making problem (Zhou and Xu 2017; Li and Wang 2017; Ding et al. 2017) to include both types of uncertainties, therefore, we develop a novel time series forecasting method using HPFS for the same reasons. Advantage of proposed forecasting method is its ability to handle uncertainties that are caused by randomness and fuzziness simultaneously and also increases flexibility of using more than one fuzzification method. Another advantage of proposed forecasting method is that it addresses issue of non-statistical non-determinism (hesitation) which arises due to the presence of multiple valid fuzzification methods for time series data. In this paper, non-determinism is included using two different methods of discretization of universe of discourse with equal and unequal length partitions. HPFS is constructed using a probability distribution function that associates probabilities to possible membership grades of time series data in multiple fuzzy sets. We propose an aggregation operator to aggregate the hesitant probabilistic fuzzy elements (HPFEs) using weights and immediate probabilities. Performance of proposed forecasting method is tested using bench mark problem of data of University of Alabama enrolments. As statistical uncertainty is an inherent characteristic of financial time series data, performance of proposed method is also tested on a financial time series data of SBI share price at BSE, India.

Rest of the paper is organized as follows: Basic definitions of fuzzy set, PFS, fuzzy time series, HFS and HPFS are presented in Sect. 2. In Sect. 3, we define the max min composition operator and aggregation operator and also include few examples to understand max–min composition operator and aggregation process for HPFS. This section also includes algorithm of proposed HPFS-based time series forecasting method. Efficiency of proposed forecasting method is tested using dataset of University of Alabama enrolments and SBI share prices in Sect. 4. This section also includes comparison of forecasted enrolments and SBI prices with few other existing forecasting methods. Finally, conclusions are presented in Sect. 5.

2 Preliminaries

In this section, we review the definitions of fuzzy set (Zadeh 1965), PFS (Liu and Li 2005) and fuzzy time series (Song and Chissom 1993a, b; Chen 1996). Definitions of HFS (Torra and Narukawa 2009; Torra 2010), HPFS (Xu and Zhou 2017) are also reviewed in this section.

Definition 1

(Zadeh 1965) Let $U=\{ {u_1},{u_2},{u_3}, ... ,{u_n} \}$ be a finite and fixed universe of discourse. A fuzzy set A on $U=\{ {u_1},{u_2},{u_3}, ... ,{u_n} \}$ is defined as follows:

$$A\;=\;\left\{ {\left\langle {u,\;{\mu _A}(u)} \right\rangle \left| {\forall u \in U} \right.} \right\}$$

(1)

Here ${\mu _A}\;:\;U\; \to \;\left[ {0,\;1} \right]$ and ${\mu _A}(u)$ represents degree of membership of u in A.

Definition 2

(Liu and Li 2005) Probabilistic fuzzy set (PFS) $\tilde {A}$ for a variable $u \in U$ and its fuzzy membership grade $\mu \in [0,1]$ can be expressed by a probability space $({V_u},\wp ,P).$ Here ${V_u}$ and $\wp \;$ are the set of all possible events $\{ \mu \in [0,1]\} {\text{and}}\;\sigma$ field respectively. The probability P is defined on $\wp$ for all element event E_i in ${V_u}$ satisfies the following conditions:

$$P({E_i}) \geqslant 0,\;\;\;P\left( {\sum {{E_i}} } \right)=\sum {P({E_i})} \;\;\;P({V_u})=1$$

(2)

Here ${E_i}$ is corresponding to an event $\mu ={\mu _i} \subseteq [0,1]$ and P(E_i) is probability for the event E_i. $\tilde {A}$ can also be expressed as the union of finite sub probability space as follows:

$$\tilde {A}\; \equiv \;\bigcup\limits_{{u \in U}} {({V_u},\wp ,P)} .$$

(3)

Definition 3

(Song and Chissom 1993a, b; Chen 1996) Let $Y(t)(t =... , 0,1,2,. ..)$ be subset of real numbers. A fuzzy time series F(t) on Y(t) is a collection of fuzzy sets ${f_i}(t)(i=1,2, ...)$. If there exists a fuzzy relation$R(t-1, t)$ such that $F(t)=F(t-1) \circ R(t-1, t)$, ($\circ$ is the max–min composition operator) then relation $F(t-1) \to F(t)$ indicates that F(t) is caused by only F(t − 1). This is called first-order model of fuzzy time series forecasting model F(t). If F(t) is caused by$F(t-1), F(t-2),..., F(t-n),$ then this fuzzy relationship is an nth-order fuzzy time series$F(t-n),..., F( t-2 ), F( t-1 ) \to F(t ).$

Definition 4

(Torra and Narukawa 2009; Torra 2010) Let $U=\{ {u_1},{u_2},{u_3}, ... ,{u_n} \}$ be a fixed set and ${h_A}\;:\;U\; \to P\;[0,\;1]$ be a function from U to the collection of subsets of $[0,\;1]$. An HFS H on U is a mathematical object of following form:

$$H\;=\;\left\{ {\left\langle {u,\;{h_A}(u)} \right\rangle \left| {\forall u \in U} \right.} \right\}$$

(4)

Here ${h_A}(u)$ is a collection of membership degrees of an element $u \in U$to the set H in $[0,\;1]$. Elements of HFS are called hesitant fuzzy element (HFE). Basic operations of union, intersection and complement on HFEs are defined as follows:

• ${h_1}^{c}\;=\;\left\{ {1 - \gamma \left| {\gamma \in {h_1}} \right.} \right\}$

• ${h_1} \cup {h_2}\;=\;\left\{ {{\gamma _1} \vee {\gamma _2}\left| {{\gamma _1} \in {h_1},\;} \right.{\gamma _2} \in {h_2}} \right\}$

• ${h_1} \cap {h_2}\;=\;\left\{ {{\gamma _1} \wedge {\gamma _2}\left| {{\gamma _1} \in {h_1},\;} \right.{\gamma _2} \in {h_2}} \right\}$

Here $\vee$ and $\wedge$ are max and min operators.

Definition 5

(Xu and Zhou 2017) Let R be a fixed set. HPFS on R is expressed as ${H_p}=\left\{ {{{\left\langle {\bar {h}({{{\gamma _i}} \mathord{\left/ {\vphantom {{{\gamma _i}} {{p_i}}}} \right. \kern-0pt} {{p_i}}})} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\bar {h}({{{\gamma _i}} \mathord{\left/ {\vphantom {{{\gamma _i}} {{p_i}}}} \right. \kern-0pt} {{p_i}}})} \right\rangle } {{\gamma _i},\;{p_i}}}} \right. \kern-0pt} {{\gamma _i},\;{p_i}}}} \right\}$ where $\bar {h}({{{\gamma _i}} \mathord{\left/ {\vphantom {{{\gamma _i}} {{p_i}}}} \right. \kern-0pt} {{p_i}}})$ is a set of elements in ${{{\gamma _i}} \mathord{\left/ {\vphantom {{{\gamma _i}} {{p_i}}}} \right. \kern-0pt} {{p_i}}}$${\gamma _i} \in R,\;0 \leqslant {\gamma _i} \leqslant 1,\;i=1,2,...,\# \bar {h},$ where $\# \bar {h}$ is the number of possible elements in $\bar {h}({{{\gamma _i}} \mathord{\left/ {\vphantom {{{\gamma _i}} {{p_i}}}} \right. \kern-0pt} {{p_i}}}).$${p_i} \in [0,1]$ is the hesitant probability of ${\gamma _i}$ and $\sum\nolimits_{{i=1}}^{{\# \bar {h}}} {{p_i}} \;=\;1$.

3 Proposed hesitant probabilistic fuzzy time series forecasting method

In the proposed forecasting method, time series data are fuzzified using two different fuzzification methods to construct HFS. HFS is converted into HPFS using a suitable probability distribution function. Proposed method utilizes a novel immediate probabilities based aggregation operator to aggregate HPFEs to fuzzy set and max–min composition operator on fuzzy logical relations which are defined as follows:

3.1 Max–min composition operator for fuzzy set

Let R₁ and R₂ be two fuzzy relations on fuzzy sets A₁, A₂, A₃ such that ${R_1} \subseteq {A_1} \times {A_2}\,$ and ${R_2} \subseteq {A_2} \times {A_3}$. The max min composition (${R_1} \circ {R_2}$) of two relations ${R_1}$ and ${R_2}$ is expressed by the relation from A₁ to A₃ as follows:

For $(a,\,b) \in {A_1} \times {A_2},\,(b,\,c) \in {A_2} \times {A_3}$

$$\begin{gathered} {\mu _{{R_1} \circ {R_2}}}(a,\,c)=\mathop {\hbox{max} }\limits_{b} \left[ {\hbox{min} ({\mu _{{R_1}}}(a,\,b),\,{\mu _{{R_2}}}(b,\,c))} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\mathop \vee \limits_{b} \left[ {{\mu _{{R_1}}}(a,\,b) \wedge {\mu _{{R_2}}}(b,\,c)} \right] \hfill \\ \end{gathered}$$

(5)

Here $\vee ,\; \wedge$ are maximum and minimum operations, respectively.

Max–min composition operation is illustrated by following example.

Example 1

If ${R_1}={\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0.21}&{0.51}&{0.19} \end{array}} \\ {\begin{array}{*{20}{c}} {0.37}&{0.92}&{0.76} \end{array}} \\ {\begin{array}{*{20}{c}} {0.71}&{0.97}&{0.39} \end{array}} \\ {\begin{array}{*{20}{c}} {0.91}&{0.42}&{0.81} \end{array}} \end{array}} \right]_{4 \times 3}}\;{\text{and}}\;{R_2}={\left[ {\begin{array}{*{20}{c}} {0.29}&{0.97}&{0.86} \\ {0.35}&{0.75}&{0.49} \\ {0.17}&{0.29}&{0.68} \end{array}} \right]_{3 \times 3}}$ are two fuzzy relations, then ${R_1} \circ {R_2}=\left[ {{c_{ij}}} \right];\;\;\left( {i=1,2,3,4\,\;{\text{and}}\,\;j=1,2,3} \right)={\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{{c_{13}}} \end{array}} \\ {\begin{array}{*{20}{c}} {{c_{21}}}&{{c_{22}}}&{{c_{23}}} \end{array}} \\ {\begin{array}{*{20}{c}} {{c_{31}}}&{{c_{32}}}&{{c_{33}}} \end{array}} \\ {\begin{array}{*{20}{c}} {{c_{41}}}&{{c_{42}}}&{{c_{43}}} \end{array}} \end{array}} \right]_{4 \times 3}}$

$$\begin{gathered} {c_{11}}=\hbox{max} [\hbox{min} (0.21,\,0.29),\hbox{min} (0.51,\,0.35),\hbox{min} (0.19,\,0.17)] \hfill \\ \;\;\;\;\,=\hbox{max} [0.21,\,0.35,\,0.17]=0.35 \hfill \\ \end{gathered}$$

3.2 Aggregation operator

Let H_p be a HPFS on reference set U and let ${h_{Hp}} :U \to P[0, 1]$ be a function that determines HPFEs. A mapping $O:P[0, 1] \to [0, 1]$ which is defined as follows is an aggregation operator that gives a fuzzy set ${H_{{A_i}}}\;=\;\left\{ {\left\langle {u,O({h_H}(u))} \right\rangle \left| {\forall {u_i} \in U} \right.} \right\}$

$$O\left\{ {{\mu _{{A_i}}}} \right\}\;=\;\frac{{\prod\nolimits_{{i=1}}^{n} {{{(1+(1 - {\omega _i}){\mu _{{A_i}}})}^{{{\hat {p}}_{{A_i}}}}} - \prod\nolimits_{{i=1}}^{n} {{{(1 - {\mu _{{A_i}}})}^{{{\hat {p}}_{{A_i}}}}}} } }}{{\prod\nolimits_{{i=1}}^{n} {{{(1+(1 - {\omega _i}){\mu _{{A_i}}})}^{{{\hat {p}}_{{A_i}}}}}+(1 - {\omega _{im}})\prod\nolimits_{{i=1}}^{n} {{{(1 - {\mu _{{A_i}}})}^{{{\hat {p}}_{{A_i}}}}}} } }}$$

(6)

Here ${\hat {p}_{{A_i}}}$ and ${\omega _i}$ are immediate probability (Yager et al. 1995) and weights of the membership grades ${\mu _{{A_i}}}$ and are defined as follows:

$${\hat {p}_{{A_i}}}\;=\;\frac{{{\omega _i}.{p_{{A_i}}}({\mu _{{A_i}}})}}{{\sum\nolimits_{{i=1}}^{n} {{\omega _i}.{p_{{A_i}}}({\mu _{{A_i}}})} }}\,$$

(7)

$${\omega _{\text{i}}}=\;\frac{{{d_i}}}{{\sum\nolimits_{{i=1}}^{n} {{d_i}} }}$$

(8)

Immediate probabilities and weights of the membership grades satisfy the condition of ${\text{ }}\sum\nolimits_{{i=1}}^{n} {{{\hat {p}}_{{A_i}}}} \;=\;1$ and $\sum\nolimits_{{i=1}}^{n} {{\omega _i}} \;=\;1$. ${\omega _{im}}$ is weight of maximum membership grades ${\mu _{{A_i}}}$. ${p_{{A_i}}}({\mu _{{A_i}}})$ is probability of the membership grades ${\mu _{{A_i}}}$ and is calculated using following Gaussian probability distribution function (Huang et al. 2012).

$${p_{{A_i}}}({\mu _{{A_i}}})\;=\;\frac{{{\xi _i}}}{{\sqrt {2\pi } {\varsigma _i}}}\left( {{e^{ - \frac{{({u_k} - ({\mu _{{A_i}}} - 1){\xi _i} - {m_i})}}{{2{\varsigma _i}^{2}}}}}+{e^{ - \frac{{({u_k} - (1 - {\mu _{{A_i}}}){\xi _i} - {m_i})}}{{2{\varsigma _i}^{2}}}}}} \right),\;\;\;{\text{(}}i=1,2,...{\text{, }}n{\text{)}}$$

(9)

Here${\mu _{{A_i}}}$, ${\xi _i}$, ${\varsigma _i}$ and ${m_i}$ are the membership grades, width, standard deviation, and mean of the fuzzy sets ${A_i}$, respectively.

Aggregation operator (Eq. 6) satisfies following property:

$$\hbox{min} \{ {\mu _{{A_i}}} \} \leqslant O\{ {\mu _{{A_i}}} \} \leqslant \hbox{max} \{ {\mu _{{A_i}}} \} ; \forall {\mu _{{A_i}}} \in [0,1]$$

Following example illustrates the process of construction of HPFS and aggregation of HPFEs using proposed aggregation operator.

Example 2

Let $H=\left\{ {\left\langle {1219,\{ 0.429, 0.473\} } \right\rangle , \left\langle {1123, \{ 0.739, 0.774\} } \right\rangle } \right\}$ be a HFS on reference set $U = \{ 1219, 1123\}$ which is constructed using two fuzzy sets ${A_1}=[732,1042,1352]$and ${A_2}=[732,1051,1370]$. Using weights${\omega _{\text{1}}}{\text{ = 0}}{\text{.493,}}\;{\omega _{\text{2}}}{\text{ = 0}}{\text{.507}}$, standard deviation of (732, 1042, 1352) and Eq. (9) probability of ${\mu _{{A_1}}}(1219)=0.429$ is calculated as follows:

$${p_{{A_1}}}(0.429)\;=\;\frac{{310}}{{\sqrt {2 \times 3.14} \times 253.11}}\left( {{{\text{e}}^{ - \frac{{\left( {1219 - (0.429 - 1) \times 310 - 1042} \right)}}{{2 \times 64066.67}}}}+{{\text{e}}^{ - \frac{{\left( {1219 - (1 - 0.429) \times 310 - 1042} \right)}}{{2 \times 64066.67}}}}} \right)=0.673$$

Similarly, other probabilities of membership grades are calculated and following HPFS is obtained.

$$H_{p}=\left\{ {\left\langle {1219,\{ 0.429(0.673), 0.473(0.686)\} } \right\rangle , \left\langle {1123, \{ 0.739(0.897), 0.774(0.908)\} } \right\rangle } \right\}$$

Using Eq. (7) corresponding immediate probabilities of membership grades are computed as follows:

$${\hat {p}_{{A_1}}}(0.429) =\frac{{0.493 \times 0.673}}{{(0.493 \times 0.673+0.507 \times 0.686)}}=0.488\quad {\text{and}} \quad {\hat {p}_{{A_1}}}(0.473) =\frac{{0.507 \times 0.686}}{{(0.493 \times 0.673+0.507 \times 0.686)}}=0.512,$$

$${\hat {p}_{{A_2}}}(0.739) =\frac{{0.493 \times 0.897}}{{(0.493 \times 0.897+0.507 \times 0.908)}}=0.49\quad {\text{and}}\quad {\hat {p}_{{A_2}}}(0.774) =\frac{{0.507 \times 0.908}}{{(0.493 \times 0.897+0.507 \times 0.908)}}=0.51$$

Using weights, immediate probabilities of membership grades and Eq. (6) HPFEs are aggregated to ${H_{{A_1}}}\,{\text{and}}\,{H_{{A_2}}}$ as follows:

$${H_{{A_1}}}=\frac{{((({{(1+(1 - 0.493) \times 0.429)}^{0.488}} \times {{(1+(1 - 0.507) \times 0.473)}^{0.512}}{\text{ }})-({{(1-0.429)}^{0.488}} \times {{(1-0.473)}^{0.512}}{\text{ }})))}}{{((({{(1+(1 - 0.493) \times 0.429)}^{0.488}} \times {{(1+(1 - 0.507) \times 0.473)}^{0.512}}{\text{ }})+(1 - 0.507)({{(1-0.429)}^{0.488}} \times {{(1-0.473)}^{0.512}}{\text{ }})))}}=0.453$$

$${H_{{A_2}}}=\frac{{((({{(1+(1 - 0.493) \times 0.739)}^{0.49}} \times {{(1+(1 - 0.507) \times 0.774)}^{0.51}}{\text{ }})-({{(1-0.739)}^{0.49}} \times {{(1-0.774)}^{0.51}}{\text{ }})))}}{{((({{(1+(1 - 0.493) \times 0.739)}^{0.49}} \times {{(1+(1 - 0.507) \times 0.774)}^{0.51}}{\text{ }})+(1 - 0.507)({{(1-0.739)}^{0.49}} \times {{(1-0.774)}^{0.51}}{\text{ }})))}}=0.758$$

Finally aggregated fuzzy set ${H_A}=\left\{ {\left\langle {1219,0.453} \right\rangle ,\left\langle {1123,0.758} \right\rangle } \right\}$ is obtained.

3.3 Algorithm of proposed HPFS-based time series forecasting method

Proposed HPFS-based time series forecasting method uses following algorithm.

Algorithm for proposed HPFS-based time series forecasting method

• 1. Define the universe of discourse and include hesitancy by constructing different types of fuzzy sets to fuzzify time series data.

• 2. Assign weights to membership grades of time series data in different types of fuzzy sets.

• 3. Assign probability to membership grades using Gaussian probability distribution function.

• 4. Calculate the immediate probability of membership grades and determine aggregated fuzzy set using aggregation operator.

• 5. Use max–min operations on FLR to have fuzzified outputs and defuzzify them numerical forecast by centroid average formula.

Each step of above algorithm is further described in detail as follows:

Step 1: Define universe of discourse as $U=\,[{D_{\hbox{min} }}\; - \;\sigma ,\;{D_{\hbox{max} }}\;+\;\sigma ]$, where ${D_{\hbox{min} }}$ and ${D_{\hbox{max} }}$ are the minimum and maximum observed value and $\sigma$ is the standard deviation of the data. Fuzzify time series data using more than one valid fuzzification methods. In this paper, universe of discourse is partitioned into equal and unequal intervals and length of unequal intervals are determined using CPDA approach. Collection $\left\langle {u,\,{\mu _1}(u),{\mu _2}(u)} \right\rangle$ is an HFE; where $\,{\mu _1}(u)\,{\text{and}}\,{\mu _2}(u)$ are membership grades of a time series datum (u) in fuzzy sets with equal intervals ${A_{{e_i}}}$ and unequal intervals ${A_{u{e_i}}}$, respectively.

Step 2: Compute the weights to the triangular membership function ${\omega _i}$ using following expression.

$${\omega _i}\;=\;\frac{{{d_i}}}{{\sum\nolimits_{{i=1}}^{n} {{d_i}} }}$$

Here ${d_i}$ is length of corresponding intervals of fuzzy sets ${A_i}$.

Step 3: Take membership grade as random variable and use following probability distribution function (Huang et al. 2012) to associate probabilities.

$${p_{{A_i}}}({\mu _{{A_i}}})\;=\;\frac{{{\xi _i}}}{{\sqrt {2\pi } {\varsigma _i}}}\left( {{{\text{e}}^{ - \frac{{({u_k} - ({\mu _{{A_i}}} - 1){\xi _i} - {m_i})}}{{2{\varsigma _i}^{2}}}}}+{{\text{e}}^{ - \frac{{({u_k} - (1 - {\mu _{{A_i}}}){\xi _i} - {m_i})}}{{2{\varsigma _i}^{2}}}}}} \right),\;{\text{(}}i = {\text{1,2, }}...{\text{, }}n{\text{)}}$$

Here${\mu _{{A_i}}}$, ${\xi _i}$, ${\varsigma _i}$ and ${m_i}$ are, respectively, membership grades, width, standard deviation and mean of data that lies in fuzzy sets ${A_i}$.

Step 4: Compute immediate probability of membership grades for fuzzy sets ${A_i}$ is ${\hat {p}_{{A_i}}}$ using following expression.

$${\hat {p}_{{A_i}}}\;=\;\frac{{{\omega _i}.{p_{{A_i}}}({\mu _{{A_i}}})}}{{\sum\nolimits_{{i=1}}^{n} {{\omega _i}.{p_{{A_i}}}({\mu _{{A_i}}})} }}$$

Apply aggregation operator (Eq. 6) to have aggregated fuzzy set. Time series data is again fuzzified using following simple algorithm.

Step 5: Fuzzy logical relations (FLRs) are defined on fuzzy sets that are obtained using aggregation of HPFEs and is denoted as ${H_{{A_i}}} \to {H_{{A_j}}}$, where ${H_{{A_i}}}$ is the fuzzy production of the year n as current state and ${H_{{A_j}}}$ is the fuzzy production of the year n + 1 as next state.

Use max–min operations (Eq. 5) on FLR to have fuzzified outputs and defuzzify them numerical forecast by following centroid average formula:

$${\text{Numerical forecast}} =\frac{{\sum\nolimits_{{i=1}}^{n} {{f_i}{c_i}} }}{{\sum\nolimits_{{i=1}}^{n} {{f_i}} }}$$

(10)

Here ${f_i}$ is fuzzified output and ${c_i}$ is average of centroids for equal and unequal intervals.

For error measure RMSE and AFE are the general tools in fuzzy time series forecasting. RMSE, AFE, correlation coefficient and coefficient of determination are applied to estimate the execution of forecasting model. Following error measures, correlation coefficient and coefficient of determination are defined as:

$${\text{RMSE}}= \sqrt {\frac{{\sum\nolimits_{{i=1}}^{n} {{{({O_i}-{F_i})}^2}} }}{n}}$$

(11)

$${\text{Forecasting error}} ({\text{in}} \% ) =\;\frac{{\left| {{F_i}-{O_i}} \right|}}{{{O_i}}} \times 100$$

(12)

$${\text{AFE}} ({\text{in}} \% ) =\frac{{{\text{sum of forecasting error}}}}{n}$$

(13)

$${\text{Coefficient of correlation}} (R)=\frac{{n\sum {{O_i}{F_i}\;-\;\left( {\sum {{O_i}} } \right)\left( {\sum {{F_i}} } \right)} }}{{\sqrt {n\left( {\sum {{O_i}^{2}} } \right)-{{\left( {\sum {{O_i}} } \right)}^2}} \sqrt {n\left( {\sum {{F_i}^{2}} } \right)-{{\left( {\sum {{F_i}} } \right)}^2}} }}$$

(14)

$${\text{Coefficient of determination}} = {R^2}$$

(15)

Here ${O_i}$ and ${F_i}$ denote the observed and forecasted time series data, n is the number of data points and $\sigma$ is standard deviation of the given data. Positive and negative value of R indicates positive and negative linear correlation, respectively, between forecasted and observed time series data and it is lies between − 1 and 1 and R² is a non-negative value.

4 Experimental results

In this section, we apply the proposed fuzzy time series forecasting method in the hesitant probabilistic fuzzy environment for forecasting the enrolments of University of Alabama (Song and Chissom 1993b) and the SBI share prizes at BSE, India (Joshi and Kumar 2012a).

4.1 Forecasting historical enrolments data with proposed method

In this subsection the proposed HPFS-based forecasting method is implemented on historical data of the enrolments at University of Alabama (Table 1).

Table 1 Historical enrolments data of University of Alabama

Step 1: ${D_{\hbox{min} }}$ and ${D_{\hbox{max} }}$ are the observed from Table 1 to define universe of discourse for historical data of student’s enrolments of University of Alabama. Using standard deviation $\sigma =1775$, universe of discourse for University of Alabama enrolment time series data is defined as $U=\,\left[ {11,280,\;21,112} \right]$. The lower and upper bound of probabilities for historical enrolments data of University of Alabama are computed using CPDA approach. The universe of discourse has been partitioned into 14 unequal intervals as given in Table 2.

Table 2 Lower and upper bound of probability for historical enrolments data of University of Alabama

Fourteen equal length intervals of universe of discourse are as follows:

$$\begin{gathered} {e_1}= [11,280,11,982.29],\;\;{e_2}= [11,982.29,12,684.57], \;\;{e_3}= [12,684.57,13,386.86], \hfill \\ {e_4}= [13,386.86,14,089.14],\;\; {e_5}= [14,089.14,14,791.43], \;\;{e_6}= [14,791.43,15,493.71], \hfill \\ {e_7}= [15,493.71,16,196],\;\;{e_8}= [16,196,16,898.29],\;\; {e_9}= [16,898.29,17,600.57], \hfill \\ {e_{10}}= [17,600.57,18,302.86], \;\;{e_{11}}= [18,302.86,19,005.14],\;\; {e_{12}}= [19,005.14,19,707.43], \hfill \\ {e_{13}}= [19,707.43,20,409.71], \;\;{e_{14}}= [20,409.71,21,112] \hfill \\ \end{gathered}$$

The historical enrolments data of University of Alabama follows the normal distribution; universe of discourse is partitioned into 14 unequal lengths of intervals using CPDA approach.

Following 14 triangular fuzzy sets${A_{{e_i}}}(i=1,2,3,... ,14)$ are constructed in accordance with equal length intervals.

$$\begin{gathered} {A_{{e_1}}}= [11,\;280,\;11,\;982.29,12,\;684.57],\;\;{A_{{e_2}}}= [11,\;982.29,\;12,684.57,\;13,\;386.86],\;{A_{{e_3}}}= [12,\;684.57,\;13,\;386.86,\;14,\;089.14],\;\;\; \hfill \\ {A_{{e_4}}}= [13,\;386.86,\;14,\;089.14,\;14,\;791.43],\;{A_{{e_5}}}= [14,\;089.14,\;14,\;791.43,\;15,\;493.71],\;{A_{{e_6}}}= [14,\;791.43,\;15,\;493.71,\;16,\;196],\;\hfill \\ {A_{{e_7}}}= [15,\;493.71,\;16,\;196,\;16,\;898.29],{A_{{e_8}}}= [16,\;196,\;16,\;898.29,\;17,\;600.57],{A_{{e_9}}}= [16,\;898.29,\;17,\;600.57,\;18,\;302.86],\;\hfill \\ {A_{{e_{10}}}}= [17,\;600.57,\;18,\;302.86,\;19,\;005.14],{A_{{e_{11}}}}= [18,\;302.86,\;19,\;005.14,\;19,\;707.43],\;{A_{{e_{12}}}}= [19,\;005.14,\;19,\;707.43,\;20,\;409.71],\;\; \hfill \\ {A_{{e_{13}}}}= [19,\;707.43,\;20,\;409.71,\;21,\;112],\;\;\;{A_{{e_{14}}}}= [20,\;409.71,\;21,\;112,\;21,\;112]. \hfill \\ \end{gathered}$$

Following 14 triangular fuzzy sets ${A_{u{e_i}}}(i=1,2,3,... ,14)$ are constructed in accordance with unequal length intervals.

$$\begin{gathered} {A_{u{e_1}}}= [11,\;280,\;12,\;436.72,\;13,\;593.39],\;{A_{u{e_2}}}= [12,\;994.31,\;13,\;646.78,\;14,\;299.24],\;{A_{u{e_3}}}= [13,\;989.87,\;14,\;389.45,\;14,\;789.02],\;\;\; \hfill \\ {A_{u{e_4}}}= [14,\;559.72,\;14,\;874.67,\;15,\;189.62],\;{A_{u{e_5}}}= [14,\;996.96,\;15,\;270.65,\;15,\;544.34],\;{A_{u{e_6}}}= [15,\;371.11,\;15,\;622.88,\;15,\;874.66],\;\hfill \\ {A_{u{e_7}}}= [15,\;711.59,\;15,\;952.89,\;16,\;194.18],{A_{u{e_8}}}= [16,\;035.07,\;16,\;274.39,\;16,\;513.71],\;{A_{u{e_9}}}= [16,\;353.30,\;16,\;598.66,\;16,\;844.02],\;\hfill \\ {A_{u{e_{10}}}}= [16,\;676.77,\;16,\;937.3,\;17,\;198.74],{A_{u{e_{11}}}}= [17,\;017.26,\;17,\;308.30,\;17,\;599.34],\;{A_{u{e_{12}}}}= [17,\;391.40,\;17,\;740.26,\;18,\;089.12],\;\; \hfill \\ {A_{u{e_{13}}}}= [17,\;828.64,\;18,\;311.81,\;18,\;794.97],{A_{u{e_{14}}}}= [18,\;398.50,\;19,\;755.25,\;21,\;112]. \hfill \\ \end{gathered}$$

Step 2: Weights of equal and unequal intervals are calculated using Eq. (8) and are shown in Table 3.

Table 3 Weights of the equal and unequal intervals

Step 3: Membership grades of each enrolment in triangular fuzzy sets with equal and unequal intervals are calculated. Probabilities that are to be associated with the membership grades are also computed to construct the 14 HPFSs ${H_{pi}}(i=1,2,3,... ,14)$ (Table 4). Immediate probability of membership grades are computed using probability and weights of equal and unequal intervals. HPFEs are aggregated using proposed aggregation operator (Eq. 6) to have 14 fuzzy sets ${H_{{A_i}}}(i=1,2,3,... ,14)$ (Table 5).

Table 4 HPFS of membership grades of enrolment for equal and unequal intervals

Table 5 Aggregated hesitant fuzzified data of University of Alabama

Step 4: University of Alabama enrolment time series data are fuzzified using the algorithm for fuzzification which is described in the previous Sect. 3. FLRs are determined and fuzzy logical relationship groups (FLRGs) are computed (Table 6).

Table 6 FLRs and FLRGs for the data of University of Alabama

Step 5: Using max–min operations (Eq. 5) on FLR and forecast the time series data of University of Alabama from Eq. (10). A sample of calculation for the year 1979 enrolment forecast is as follows:

For enrolment of year 1978, hesitant probabilistic fuzzy sets are ${H_{p6}}=\left\langle {15861,\{ 0.477014(0.70386),0.054253(0.522124)\} } \right\rangle$ and ${H_{p7}}=\left\langle {15861,\{ 0.522986(0.735674),0.619184(0.805042)\} } \right\rangle$.

Here 0.477014, 0.054253, 0.522986, 0.619184 are the membership grades of the enrolment 15,861 in fuzzy sets ${A_{{e_6}}},{A_{u{e_6}}},{A_{{e_7}}},{A_{u{e_7}}}$ respectively. 0.736098 and 0.263902 are the weights in Table 3 of${A_{{e_6}}},{A_{u{e_6}}}$. Immediate probabilities, ${\hat {p}_{{A_{{e_6}}}}}$ and ${\hat {p}_{{A_{u{e_6}}}}}$ for enrolment of the year 1978 are computed as follows:

$$\begin{gathered} {{\hat {p}}_{{A_{{e_6}}}}}=\frac{{0.736098 \times 0.70386}}{{0.736098 \times 0.70386+0.263902 \times 0.522124}}=0.789923, \hfill \\ {{\hat {p}}_{{A_{u{e_6}}}}}=\frac{{0.263902 \times 0.522124}}{{0.736098 \times 0.70386+0.263902 \times 0.522124}}=0.210077 \hfill \\ \end{gathered}$$

Membership grades of the enrolment of the year 1978 (15,861) in H_p6 are aggregated using Eq. (6) as follows:

$$\frac{{((({{(1+(1 - 0.736098) \times 0.477014)}^{0.789923}} \times {{(1+(1 - 0.263902) \times 0.054253)}^{0.210077}}{\text{ }})-({{(1-0.477014)}^{0.789923}} \times {{(1-0.054253)}^{0.210077}}{\text{ }})))}}{{((({{(1+(1 - 0.736098) \times 0.477014)}^{0.789923}} \times {{(1+(1 - 0.263902) \times 0.054253)}^{0.210077}}{\text{ }})+(1 - 0.477014) \times ({{(1-0.738507)}^{0.789923}} \times {{(1-0.054253)}^{0.210077}}{\text{ }})))}}={\text{ }}0.398$$

Immediate probabilities ${\hat {p}_{{A_{{e_7}}}}}$and ${\hat {p}_{{A_{u{e_7}}}}}$ for enrolment of the year 1978 are computed using weights 0.744278 and 0.255722 as follows:

$$\begin{gathered} {{\hat {p}}_{{A_{{e_7}}}}}=\frac{{0.744278 \times 0.735674}}{{0.744278 \times 0.735674+0.255722 \times 0.805042}}=0.726755, \hfill \\ {{\hat {p}}_{{A_{u{e_7}}}}}=\frac{{0.255722 \times 0.805042}}{{0.744278 \times 0.735674+0.255722 \times 0.805042}}=0.273245 \hfill \\ \end{gathered}$$

Membership grades of the enrolment of the year 1978 (15,861) in H_p7 are aggregated using Eq. (6) as follows:

$$\frac{{((({{(1+(1 - 0.744278) \times 0.522986)}^{0.726755}} \times {{(1+(1 - 0.255722) \times 0.619184)}^{0.273245}}{\text{ }})-({{(1-0.522986)}^{0.726755}} \times {{(1-0.619184)}^{0.273245}}{\text{ }})))}}{{((({{(1+(1 - 0.744278) \times 0.522986)}^{0.726755}} \times {{(1+(1 - 0.255722) \times 0.619184)}^{0.273245}}{\text{ }})+(1 - 0.744278)({{(1-0.522986)}^{0.726755}} \times {{(1-0.619184)}^{0.273245}}{\text{ }})))}}={\text{ }}0.6079$$

Since max(0.398, 0.6079) = 0.6079, hence ${H_{{A_7}}}$ is assigned to 15,861, i.e., the enrolment of the year 1978.

FLR ${H_{{A_7}}} \to {H_{{A_8}}}$ is used to forecast the enrolment for the year 1978. Following row vector is obtained using max–min operation (Eq. 5).

0

0

0

0

0.615294

0.799093

0.155614

0.799093

0.150882

0.799093

0

0

0

0

Since the centroids of the fuzzy set with equal interval ${A_{{e_1}}}$ and unequal intervals ${A_{u{e_1}}}$ are 11,982.29 and 12,436.7, respectively, therefore, average centroid is

$${c_1}=\frac{{11,982.29+12,436.7}}{2}=12,209.49$$

Similarly other average centroids ${c_2},{c_3},...,{c_{14}}$ are calculated.

Numerical forecast for the year 1979 is calculated using Eq. (10) and is as follows:

$$\frac{{0.615294 \times 15031.04+0.799093 \times 15558.3+0.155614 \times 16074.44+0.799093 \times 16586.34+0.150882 \times 17099.62+0.799093 \times 17620.31}}{{0.615294+0.799093+0.155614+0.799093+0.150882+0.799093}}={\text{16298.77}}$$

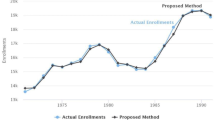
Other enrolments of University of Alabama are also computed in similar way and are shown in Table 7. Proposed hesitant probabilistic fuzzy time series forecasting method is compared with previous proposed forecasting method of Chen (1996), Cheng et al. (2006, 2008), Huarng (2001), Joshi and Kumar (2012a), Kumar and Gangwar (2016), Lee and Chou (2004), Qiu et al. (2011), Song and Chissom (1993a, b, 1994) and Yolcu et al. (2009) using error measures, correlation coefficient, and coefficient of determination (Table 15).

Table 7 Forecasted enrolments

4.2 Proposed method for forecasting market price of SBI share

In this subsection, proposed forecasting method is implemented on market prices of SBI share at BSE, India (Table 8).

Table 8 Actual market prices of SBI share at BSE, India

Step 1: ${D_{\hbox{min} }}$ and ${D_{\hbox{max} }}$ are observed from Table 8 to define universe of discourse for data of SBI share prices. Using standard deviation $\sigma =391.07$, universe of discourse for SBI share price is defined as $U=\,[741.18,2891.07]$. The lower and upper bound of probabilities for market prices of SBI share at BSE, India are computed using CPDA approach. The universe of discourse has been partitioned into 14 unequal intervals as given in Table 9.

Table 9 Lower bound and upper bound of probability for market prices of SBI share at BSE, India

Fourteen equal length intervals of universe of discourse are as follows:

$$\begin{gathered} {e_1}= [741.18,\;894.75],\;{e_2}= [894.75,\;1048.31], {e_3}= [1048.31,\;1201.87], {e_4}= [1201.87,\;1355.44], \hfill \\ {e_5}= [1355.44,\;1509], \;{e_6}= [1509,\;1662.56], {e_7}= [1662.56,\;1816.13],\;{e_8}= [1816.13,\;1969.69], \hfill \\ {e_9}= [1969.69,\;2123.25], {e_{10}}= [2123.25,\;2276.81], {e_{11}}= [2276.81,\;2430.38], \hfill \\ {e_{12}}= [2430.38,\;2583.94], {e_{13}}= [2583.94,\;2737.5], {e_{14}}= [2737.5,\;2891.07] \hfill \\ \end{gathered}$$

Universe of discourse of market prices of SBI share at BSE, India is partitioned into 14 unequal lengths of intervals using CPDA approach.

Step 2: Weights of equal and unequal intervals are calculated using Eq. (8) and are shown in Table 10.

Table 10 Weights of the equal and unequal intervals

Step 3: Membership grades of SBI share price in triangular fuzzy sets with equal and unequal intervals are calculated. Probabilities that are to be associated with the membership grades are also computed to construct the 14 HPFSs ${H_{pi}}(i=1,2,3,... ,14)$(Table 11). Immediate probability of membership grades are computed using probability and weights of equal and unequal intervals. HPFEs are aggregated using proposed aggregation operator (Eq. 6) to have 14 fuzzy sets ${H_{{A_i}}}(i=1,2,3,... ,14)$(Table 12).

Table 11 HPFS of Membership grades of the data of share market prices of SBI for equal and unequal intervals

Table 12 Aggregate hesitant fuzzified data of share prices of SBI

Step 4: SBI share price data are fuzzified using the algorithm for fuzzification which is described in the previous Sect. 3. FLRs are determined and fuzzy logical relationship groups (FLRGs) are computed (Table 13).

Table 13 FLRs and FLRGs for data of share price of SBI

Step 5: Using max–min operations (Eq. 5) on FLR and forecast the time series data of SBI share price from Eq. (10) (Table 14).

Table 14 Forecasted SBI share prices data

We compare forecasted enrolments and SBI share prices using error measures, correlation coefficient and coefficient of determination with few existing fuzzy time series forecasting methods. RMSE and AFE in forecasting both enrolments and SBI share prices are found less compared to previous forecasting methods. Additionally, actual and forecasted data (Tables 15, 16) are found highly correlated compared to previous forecasting methods proposed by various researchers.

Table 15 Error measure, correlation coefficient and coefficient of determination verification of propose method in forecasted enrolments of University of Alabama

Table 16 Error measure, correlation coefficient and coefficient of determination verification of propose method in forecasted data of share prices data of SBI at BSE, India

5 Conclusions

Probabilistic and non-probabilistic uncertainties occur in the system simultaneously. This paper contributes a methodology for a novel HPFS-based time series forecasting model to include both probabilistic and non-probabilistic uncertainties along with hesitant information. In proposed forecasting method, HFS is converted into HPFS by assigning probability to membership grades using Gaussian probability distribution function. We also propose an aggregation operator that uses immediate probability, weights and membership grades to aggregate HPFEs of HPFS. To verify the performance of proposed forecasting method, it is implemented to time series data of University of Alabama and SBI share price at BSE India. RMSE and AFE in forecasting both University of Alabama enrolments and SBI share price using proposed HPFS-based time series forecasting method are found less than that of previous forecasted methods. Even though RMSE in forecasting University of Alabama using proposed forecasting method is slightly higher than that of the methods proposed by Chen (2014) and Bisht and Kumar (2016), but inherent characteristic of HPFS of handling probabilistic uncertainty is an added advantage of proposed forecasting method. It is also observed that coefficient of correlation between actual and forecasted data is almost in accordance with the methods proposed by Bisht and Kumar (2016) and Joshi and Kumar (2012a) (Table 15). Reduced RMSE and AFE in forecasting SBI share prices (Table 16) confirm the out performance of proposed forecasting method over other forecasting methods that were proposed by Chen (1996), Pathak and Singh (2011), Joshi and Kumar (2012a). Although proposed HPFS based forecasting method slightly under perform in forecasting SBI share compared to the methods proposed by Huarng (2001), Kumar and Gangwar (2016), but it is competent enough to handle both types of uncertainties of financial time series forecasting.

As HPFS includes the prominent characteristic of both hesitant and probabilistic fuzzy set, it makes proposed HPFS-based forecasting method more competent in handling both probabilistic and non-probabilistic uncertainties along with non-deterministic hesitation that may arise due to multiple fuzzification of time series data.