1 Introduction

Granular modeling is an important tool for system modeling, analysis, and applications (Pedrycz 2013). Often, an information granule is understood as a collection of objects put together by indistinguishability, similarity, proximity, and functionality. Examples of information granules include intervals, rough sets, probability densities, fuzzy sets, and possibility distributions (Zadeh 1997).

In system modeling, the use of partial differential equations (PDE) with fuzzy parameters reflects the need to account for the imprecise nature of real world phenomena. Contrary to the usual expectations and assumptions, actual values of the model parameters rarely are known precisely. System models are much more expressive if the inaccurate nature of the observations and measurements are intrinsically accounted by the modeling approach. The values of measurements are inaccurate because they depend on the experimental set-up, the nature of the system, and on the observer. For instance, physical parameters are estimated using measurements made during different tests with distinct materials. The values measured depend on the energy intensity, the degree of freedom of Brownian motion, as in the case of the diffusion coefficient of the heat equation. The diffusion coefficient depends on the phase, temperature, and molecule size. In practice, values of phase, temperature, and molecule size measurements are imprecise.

Probabilistic and statistical methods have been used to compute parameter variability of the heat and mass transfer models (Jirka and Socolofsky 2012; Chakraverty and Nayak 2012; Bart et al 2011), but currently techniques to convey parameter variability information into solutions of PDE are unavailable. The use of statistical analysis in numerical solutions of differential equations is reviewed in Conrad et al (2017). Different methods have been developed to solve fuzzy differential equations with fuzzy parameters. Examples include Hukuhara and generalized derivatives, Zadeh extension of the classic solution, fuzzy differential inclusions, and extensions of the derivative operator (Takata et al 2015). However, these methods are mainly theoretical. The attempt is to obtain analytical solutions of fuzzy differential equations.

The framework of fuzzy information granulation, especially the concepts of linguistic variables, fuzzy if-then rules, and fuzzy graphs play a major role in many applications of fuzzy set theory (Ahmad and Pedrycz 2017; Liu et al 2017). The idea of fuzzy graph was introduced as a way to account for granular functional dependences (Zadeh 1971, 1974). A fuzzy graph can be understood as a collection of fuzzy if-then rules (Zadeh 1994). Applications of fuzzy graph are many. For instance, Batyrshin (2002) develop a method to solve a granular initial value problem by granulating the directions field, and propagating fuzzy constraints. An alternative method to approach PDE modeling is to construct local models in the form of functional if-then fuzzy rules with partial differential equations in the consequents. Combination of the local models employing fuzzy inference produces a PDE equation as a global model. This method can be seen as a way to obtain a granular global model from the aggregation of local granular models (Silveira and Barros 2015; Wang et al 2012; Wu et al 2012).

Granular approximations of solutions of PDE with fuzzy parameters in the form of fuzzy graphs have not, to the best of the authors knowledge, been addressed yet in the literature. This is the major contribution of the paper. The idea can be understood as follows. First, consider the PDE

$$\begin{aligned} P(x, d, u(x),\partial u(x),\partial ^2u(x))=0, \end{aligned}$$
(1)

where P is a function, \(x\in \mathcal X \subset \mathbb {R}\), \(\mathcal X\) is the domain of the PDE, \(\partial u(x)\) and \(\partial ^2 u(x)\) denote the partial derivative, and the partial derivative of order 2 with respect to the variable x, and d is a known real-valued parameter.

Assume that \(u_d(x)=G(x, d)\) is the unique solution of Eq. (1), and that G is a uniformly continuous function that assigns to each pair (x, d) in a bounded set the real value \(u_d(x)\).

The novel granular method to approximate the solutions of PDE fuzzy parameter can be summarized as follows. Suppose that fuzzy set D replaces the real-valued parameter d in Eq. (1). The PDE shown in Eq. (1) becomes

$$\begin{aligned} P(x, D, u(x),\partial u(x), \partial ^2 u(x))=0. \end{aligned}$$
(2)

In particular, let D be a fuzzy number with support \([D]^0=\{d\in \mathcal{D}, D(d) > 0\}\), and core \(D^p=\{d\in \mathcal{D}, \mu _D(d)=1\}\). Denote the solution \(u_{d^p}\) of the PDE of Eq. (1) when \(d=d^p\) as the preferable solution. Consider the interval \(\mathcal{I}_{x}=[x-\delta _1, x+\delta _2]\). Because G is uniformly continuous, given an arbitrary \(\epsilon >0\), there exists a \(\delta _1,\delta _2>0\), depending on \(\epsilon\) only, such that for every \(x'\) in \(\mathcal{I}_{x}\), the distance between \(G(x',\cdot )\) and \(G(x,\cdot )\) is less than \(\epsilon\). If we denote by \(\widehat{G}_{x}(D)\) the Zadeh extension of the function \(G(x,d^p)\), then we may construct the following fuzzy rule:

$$\begin{aligned} \text{ If } x' \text{ is } \mathcal{I}_{x} \text{ then } G(x',d^p) \text{ is } \widehat{G}_{x}(D)\text{. } \end{aligned}$$
(3)

Intuitively, Eq. (3) means that whenever the value of the variable x is within a neighborhood specified by the interval \(\mathcal{I}_{x}\), the solution of the PDE with fuzzy parameter shown in Eq. (2) is around the corresponding preferred solution \(G(x,d^p)\). The meaning of around is specified by the fuzzy set found by the extension \(\widehat{G}_{x}(D)\) of \(G(x',d^p)\). Therefore, to build a granular approximation of the function \(G(x, d^p)=u_{d^p}\) we granulate the domain \(\mathcal X\) into n disjoint intervals \(\mathcal{I}_{x_i}=[x_i-\delta _1,x_i+\delta _2]\), \(i=1,\ldots ,n\), compute the extension of \(G(x_i, \cdot )\) using D to obtain the fuzzy number \(\widehat{G}_{x_i}(D)\), and construct a granule for each \(\mathcal{I}_{x_i}\) in the form of the fuzzy rule as explained in Eq. (3). The collection of these n rules forms a fuzzy graph. The fuzzy graph produced by the rule base gives a granular approximation of the preferred solution in the sense of Zadeh (1997).

In what follows, after a short remind of fuzzy set theory basics, an algorithm to construct the collection of fuzzy if-then rules to form a granular approximation of the solution of Eq. (2) is developed in Sect. 3. Illustrative examples are given in Sect. 4. Section 5 concludes the paper and suggests issues for further research.

2 Fuzzy sets

This section gives a short review on the basic notions needed to develop the granular approximation of PDE with fuzzy parameter algorithm. A more detailed coverage is found in Zadeh (1975), Barros et al (1997) and Pedrycz and Gomide (1998).

A fuzzy number is a convex and normal fuzzy set of the real line. Zadeh extension: if X and Y are sets, then the image of fuzzy set A in X under function \(f:X\rightarrow Y\), is the fuzzy set \(B=f(A)\) in Y whose membership function is \(\mu _B(y)= \sup\nolimits_{x\in X}\mu _A(x)\) for each \(y\in Y\) such that \(y=f(x)\). Let \(\mathcal D\) and Z be nonempty metric spaces, D a fuzzy set of \(\mathcal D\), and \(f:\mathcal D\rightarrow Z\) be a continuous function. Then for every \(\alpha\), \(0\le \alpha \le 1\), \(\left[ f(D)\right] ^\alpha =f\left( \left[ D\right] ^\alpha \right)\), where \([D]^\alpha =\{d\in \mathcal{D}, D(d)\ge \alpha \}\). A t-norm is a function \(T:[0,1]\times [0,1] \rightarrow [0,1]\) that is commutative, associative, and monotone with boundary conditions \(T(0,x)=0\), and \(T(1,x)=x\). An example of \(t-\)norm is \(T_\mathrm{min}(a,b)=\min \{a,b\}\). A s-norm is a function \(S:[0,1]\times [0,1]\rightarrow [0,1]\) that is commutative, associative, and monotone with boundary conditions \(S(0,x)=x\), and \(S(1,x)=1\). An example of a \(s-\)norm is \(S_\mathrm{max}(a,b)=\max \{a,b\}\). A Fuzzy graph \(F^*\) is a fuzzy subset of the Cartesian product \(X \times Y\) whose membership function is

$$\begin{aligned} \mu _{F^*}(x,y)=S\left( T(\mu _{M_j}(x),\mu _{N_j}(y))\right) , \qquad j=1, \ldots , k \end{aligned}$$
(4)

where \(M_j\) is a fuzzy set on X, and \(N_j\) is fuzzy set on Y, \(k \in \mathbb {N}\). In what follows we use the t-norm \(T=T_\mathrm{min}\) and the s-norm \(S=S_\mathrm{max}\).

3 Granular approximation of the solution of PDE with fuzzy parameter

This section details the algorithm to construct a granular approximation of the PDE of Eq. (2). We assume that the PDE of Eq. (1) has a unique solution \(u_{d}(x)=G(x,d)\), \(d \in [D]^0\), D is a triangular fuzzy number with core \(D^p=\{d^p\}\), and that function G(x, d) is uniformly continuous with respect to x and d. The steps to develop the granular approximation of Eq. (2) are the following:

  • Step 1: let \(\epsilon\) be an arbitrary positive number. Because G is uniformly continuous, there exists a \(\delta >0\) such that \(|(x,d)-(x',d')|<\delta\), then \(|G(x,d)-G(x',d')|<\epsilon\). In particular,

    $$\begin{aligned} |G(x,d)-G(x',d)|<\epsilon \text{ for } \text{ each } d\in [D]^0. \end{aligned}$$
    (5)

  • Step 2: let \(x_i\in \mathcal{X}\), \(i=1,\ldots ,n\), such that \(\mathcal{X}=\bigcup \nolimits _{i=1}^n[x_i-\delta _1,x_i+\delta _2]\) with \(\delta _1+\delta _2=\delta\), and \([x_i-\delta _1,x_i+\delta _2]\) pairwise disjoint intervals.

  • Step 3: choose intervals \(\mathcal{I}{x_i}=[x_i-\delta _1,x_i+\delta _2]\), \(i=1,\ldots ,n\);

  • Step 4: fix \(x_i\) and compute the extension of \(G(x_i, \cdot )\) using D to obtain the fuzzy number \(\widehat{G}_{x_i}(D)\). The zero-cut of \(\widehat{G}_{x_i}(D)\) is the compact interval \([G(x_i,d^p)-\beta _1, G(x_i,d^p)+\beta _2]\), \(\beta _1,\ \beta _2 \ge 0\). Figure 1 illustrates the Step 4.

  • Step 5: construct n fuzzy rules as follows

    $$\begin{aligned} \text {If}\, x_i \,\text {is}\, \mathcal{I}_{x_i}\, \text {then} \,G(x_i,d^p)\, \text {is} \,\widehat{G}_{x_i}(D), i=1, \ldots , n. \end{aligned}$$

  • Step 6: the granular approximation is the fuzzy graph

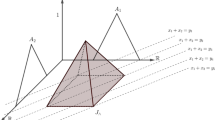
    $$\begin{aligned} \mu _{F^*}(x,G(x,d^p))=S\left( T(\mu _{\mathcal{I}_{x_i}}(x),\mu _{\widehat{G}_{x_i}(D)}(G(x,d^p)))\right) , \ i=1, \ldots , n. \end{aligned}$$
    (6)

    Figure 2 illustrates Step 6.

Fig. 1
figure 1

Fuzzy set D (magenta) and the Zadeh extension \(\widehat{G}_{x_i}(D)\) (red). Because of the relation detailed in Eq. (5), the parametric form of \(G(x_j,d)\) is between the dashed blue lines, representing \(G(x_i,d)-\epsilon\) (lower blue line), and \(G(x_i,d)+\epsilon\) (upper blue line)

Full size image
Fig. 2
figure 2

Fuzzy graph of the granular approximation

Full size image

It should be emphasized that the algorithm can be extended to address the case in which Eq. (1) has local uniformly continuous solutions \(G_i(x_i,d^p)\). All that is needed is to follow the same algorithm steps replacing \(G(x_i,d^p)\) by \(G_i(x_i,d^p)\). This means that the rule consequents are found using the Zadeh extension of each local solution \(G_i(x_i,d^p)\).

4 Granular approximation of PDE solution with fuzzy parameter: Examples

The algorithm of Sect. 3 is used to develop granular approximations of the heat, wave, and Poisson PDEs with fuzzy parameter. These equations are representative of numerous applications of thermodynamics, communication, and electrical engineering.

4.1 Granular approximation of the solution of a heat equation

The heat equation considered is the following:

$$\begin{aligned} \partial _tu(x,t)&= d~\partial ^2_{x x} u(x,t),\ (x,t)\in (0,L)\times (0,T),\nonumber \\ u(x,0)&= u_0(x),\ x\in (0,L),\nonumber \\ u(0,t)&= u(L,t)=0,\quad {\text {for}}\quad t\in (0,T), \end{aligned}$$
(7)

where \(d>0\) is the molecular diffusion coefficient, and \(u_0(x)=\sin (\pi x)\).

The solution of Eq. (7) with the initial condition \(u(x,0)=u_0(x)\) is given by the Fourier series (Jost 2002)

$$\begin{aligned} u_d(x,t)=\int _0^Lu_0(y)\sum \limits _{n=1}^{+\infty }a_n(x,y) \exp \left( {-\frac{d n^2\pi ^2 }{L^2}t}\right) {\text {d}}y, \end{aligned}$$
(8)

where

$$\begin{aligned} a_n(x,y)=\sin \left( \frac{n\pi y}{L}\right) \sin \left( \frac{n\pi x}{L}\right) . \end{aligned}$$
(9)

Assume that the parameter d shown in Eq. (7) is the fuzzy number D shown in Fig. 3 instead.

Fig. 3
figure 3

Fuzzy number D.

Full size image

Let us first check the hypothesis concerning the uniform continuity required by function G. It has been proved in Bertone et al (2013) that G is continuous with respect to d. Here we show that G is, fixing t, uniformly continuous with respect x as well. Let \(\mathcal X=[0,L]\). From Eqs. (8), (9), and taking x and \(x'\) in \(\mathcal X\), we get

$$\begin{aligned}& |u_d(x,t)-u_{d}(x',t)|\\ &\quad=\left| \int \limits _0^1 u_0(y) \sin (\pi y){\text {d}}y(\sin (\pi x)-\sin (\pi x')) \right| \\ &\quad\le |-\frac{1}{2}\int \limits _0^1(\cos (2\pi y)-1){\text {d}}y||\sin (\pi x)-\sin (\pi x')|\\ &\quad=\frac{1}{2}|\sin (\pi x)-\sin (\pi x')|\\ &\quad=\left| \sin \left( \frac{\pi x-\pi x'}{2}\right) \cos \left( \frac{\pi x +\pi x'}{2}\right) \right| \\ &\quad\le \left| \frac{\pi x-\pi x'}{2}\right| . \end{aligned}$$

Because \(d>0\), the supremum of the function \(\eta (d)=\exp \left( -\frac{d~n^2\pi ^2}{L^2}\right)\) is equal to 1. Hence, denoting \(K_n=\int _0^L u_0(y) \sin \left( \frac{n\pi y}{L}\right) {\text {d}}y\), we have

$$\begin{aligned} &|u_d(x,t)-u_d(x',t)| \\ &\quad \le\displaystyle \sum _{n=1}^{+ \infty } \left| K_n\right| \left| \sin (\frac{n\pi x}{L})-\sin (\frac{n\pi x'}{L}) \right| \\ &\quad=\displaystyle \sum _{n=1}^{+ \infty }|K_n|2\left| \sin \left( \frac{n\pi x-n\pi x'}{2L}\right) \cos \left( \frac{n\pi x+n\pi x'}{2L}\right) \right| \\ &\quad\le 2~\displaystyle \sum _{n=1}^{+ \infty }|K_n|\left| \frac{n\pi x-n\pi x'}{2L}\right| \\ &\quad\le \frac{\pi }{L}\left| x-x' \right| \displaystyle \sum _{n=1}^{+ \infty }n|K_n|.\end{aligned}$$
(10)

For the functions \(u_0(x)\) for which the series \(\sum \nolimits _{n=1}^{+\infty }n|K_n|\) converges to a positive real number l, there exists \(\delta (\epsilon )=\frac{\epsilon ~ L}{\pi ~l}\) such that for values of x and \(\overline{x}\) that verify \(|x-x'|<\delta\) we have \(|G(x,d)-G(x',d)|<\epsilon\). As a consequence, G is uniformly continuous with respect to the variable x for those type of functions \(u_0(x)\).

There exits an enumerated set of these functions, namely,

$$\begin{aligned} u_0(x)=\sin \left( \frac{k\pi y}{L}\right) , k\in \mathbb {N}. \end{aligned}$$

As a particular case, we use the function \(u_0(x)=\sin (\pi x)\) as the initial condition in the numerical examples. In addition, for this particular initial value it is possible to find an appropriate value of \(\delta\). If \(n\ne 1\), then \(u_0\) is orthogonal with respect to \(\sin (n\pi y)\). We get

$$\begin{aligned} & |u_d(x,t)-u_d(x',t)| \\&\quad =\left| \int \limits _0^1 u_0(y) \sin (\pi y){\text {d}}y(\sin (\pi x)-\sin (\pi x')) \right| \\ & \quad\le|-\frac{1}{2}\int \limits _0^1(\cos (2\pi y)-1){\text {d}}y||\sin (\pi x)-\sin (\pi x')|\\ &\quad= \frac{1}{2}|\sin (\pi x)-\sin (\pi x')| \\ &\quad=\left| \sin \left( \frac{\pi x-\pi x'}{2}\right) \cos \left( \frac{\pi x +\pi x'}{2}\right) \right| \\ &\quad\le\left| \frac{\pi x-\pi x'}{2}\right| . \end{aligned}$$

The fuzzy graph constructed using the algorithm, keeping t fixed, is depicted in Fig. 4.

Fig. 4
figure 4

Granular approximation of the solution of the heat equation with fuzzy parameter D. The yellow points assemble the preferable solution. t is fixed

Full size image

We have that Eq. (10) is valid for all \(t\in (0, T)\). Figure 5 shows the function \(G(x,d^p)\) at different time instants.

Fig. 5
figure 5

Granular approximation of the solution of heat equation with fuzzy parameter D. The yellow points are the values of the function \(G(x,d^p)\) at different time instants

Full size image

4.2 Granular approximation of the solution of a wave equation

The wave equation considered here is:

$$\begin{aligned} \partial _{tt}u(x,t)= &\, {} d~\partial _{xx} u(x,t),\ (x,t)\in [0,1]\times \mathbb R_+,\nonumber \\ u(x,0)= &\, {} m(x),\ u_t(x,0)=n(x),\ x\in [0,1],\nonumber \\ u(0,t)= &\, {} 0 \text{ and } u(1,t)=0. \end{aligned}$$
(11)

The parameter d of the wave equation shown in Eq. (11) is the speed of the wave, whose value depends on the environment through which the wave propagates.

The solution of Eq. (11) has the following analytic form:

$$\begin{aligned} u_d(x,t)=\frac{M(x+{\text {d}}t)+M(x-{\text {d}}t)}{2}+\frac{1}{2d}\int _{x-{\text {d}}t}^{x+{\text {d}}t}N(s){\text {d}}s, \end{aligned}$$
(12)

where functions M and N are

$$\begin{aligned} M(x)&= m(x) \quad\text{ if } x\in [0,1], M(x+k)=m(x),\ k\in \mathbb {Z},\\ N(x)&= n(x) \quad\text{ if } x\in [0,1], N(x+k)=n(x),\ k\in \mathbb {Z}. \end{aligned}$$

For t fixed, M and N are continuous functions because the domain of the variable x is the compact interval [0, 1].

Consider equation shown in Eq. (11) with fuzzy parameter expressed by fuzzy number D of Fig. 3 instead of a real-valued d. Its granular approximation obtained following the steps of Sect. 3 is shown in Fig. 6.

Fig. 6
figure 6

Granular approximation of the wave equation solution with fuzzy parameter D. t is fixed

Full size image

The granular approximation of the wave equation explicit in Eq. (11) fuzzy parameter D at distinct time instants shown in Fig. 7.

Fig. 7
figure 7

Granular approximation of the wave equation solution with fuzzy parameter D. The yellow points are the values of the function \(G(x,d^p)\) at different time instants

Full size image

4.3 Granular approximation of solution of a Poisson equation

The Poisson equation is:

$$\begin{aligned} \partial _{xx}u+ \partial _{yy}u= &\, {} d~j(x,y),\ (x,y)\in Q=[0,a]\times [0,a],\nonumber \\ u(x,y)= &\, {} k(x,y),\ x\in \partial Q,\nonumber \\ \end{aligned}$$
(13)

where j and k are continuous functions in the square Q of side a and boundary \(\partial Q\). Parameter d is the permittivity, a measure of the resistance encountered when forming an electric field in a medium.

We have that Eq. (13) has the following analytic solution (Butkovskiy 1982)

$$\begin{aligned} u_d(x,y)&=\displaystyle \int _0^a\int _0^a d~j(\xi ,\eta ){\text {GR}}(x,y,\xi ,\eta ){\text {d}}\eta ~{\text {d}}\xi \\ &\quad+\displaystyle \int _0^a~k(\eta )\partial _\xi \left( {\text {GR}}(x,y,0,\eta )-{\text {GR}}(x,y,a,\eta )\right) {\text {d}}\eta \\ &\quad\displaystyle \int _0^a~k(\xi )\partial _\eta \left( {\text {GR}}(x,y,\xi ,0)-{\text {GR}}(x,y,\xi ,a)\right) {\text {d}}\xi , \end{aligned}$$
(14)

where GR is the Green function

$${\text {GR}}(x,y,\xi ,\eta )=2/a\sum _{n=1}^{\infty }(\sin (p_nx)\sin (p_n\xi ))/(p_n\sinh (p_na))H_n(y,\eta ),$$

\(p_n=\pi n/a\), and \(H_n\) is the function

$$\begin{aligned} H_n(y,\eta )= \left\{ \begin{array}{lcl} \sin h(p_n\eta )\sin h(p_n(a-y))&\quad \text{ for } &a\ge y>\eta \ge 0,\\ \sin h(p_n\eta )\sin h(p_n(a-\eta ))&{}\quad \text{ for } &a\ge \eta >y\ge 0. \end{array} \right. \end{aligned}$$
(15)

The solution of Eq. (13) is infinitely smooth (analytic in the sense of complex variables (Rudin 1987). Because the domain is compact (a square of length a), the solution with respect to x (or y) is uniformly continuous.

Consider the PDE of Eq. (13) with the fuzzy number D of Fig. 3 as a parameter instead of the real-valued parameter d. The algorithm of Sect. 3 produces, keeping y fixed, the granular approximation shown in Fig. 8. The granular approximation for different values of y is shown in Fig. 9.

Fig. 8
figure 8

Granular approximation of the Poisson equation solution with fuzzy parameter D. y is fixed

Full size image
Fig. 9
figure 9

Granular approximation of the solution of the Poisson equation with fuzzy parameter D. The yellow points are the values of the function \(G(x,d^p)\) for different values of y.

Full size image

5 Conclusion

A novel algorithm to derive granular approximation of the solutions of partial differential equations with fuzzy numbers as parameters has been developed. The granular approximation is built in the form of a fuzzy graph. The fuzzy graph is a collection of fuzzy if-then rules constructed from a granulation of the domain of the variables, and from the extension principle on the fuzzy parameter. The algorithm is also applicable when the partial differential equations have local uniformly continuous solutions only. Illustrative examples have been offered using the fuzzy parameter counterparts of a heat, wave, and Poisson partial differential equations. The task of developing granular solutions for granular differential equations still remains a challenge to be addressed in the future.