1 Introduction

Proper numerical modelling of the shear walls under seismic loads has been a very important research subject for decades. Although there are many experimental studies in the literature which investigate the behaviour of reinforced concrete (RC) shear walls against lateral loading, there are still uncertainties with regard to the best numerical approach and the best damping ratio in the modelling of shear walls [1,2,3]. These uncertainties should be investigated, and some recommendations should be made for designers of RC shear wall structures. The seismic performance of RC shear walls has been simulated using different modelling approaches [4,5,6,7]. Beam-column elements comprised of nonlinear rotational and axial springs were used in the most common modelling approach. These elements were located at the centreline of the wall in the vertical direction. Changing the neutral axis location, rocking the wall and rotating the fixed end are some of the deficiencies of the beam-column element model. These deficiencies were addressed by the use of a three-vertical-line-element model (TVLEM) based on the beam-column element model. TVLEM consisted of two vertical line elements at both sides and a vertical line element at the centreline of the wall. The element at the centreline of the wall includes three different nonlinear springs in the bottom side of the wall (vertical, horizontal and rotational). These vertical line elements were connected to rigid beams at their ends.

The multiple-vertical-line-element model (MVLEM), a modified version of TVLEM, was developed [8]. This model refined the definition of the flexural response of the wall by using multiple uniaxial elements in parallel. Another analytical model based on MVLEM which is similar to the macroscopic fibre model was developed by Orakcal [8]. In this model, a series of uniaxial elements called “macro fibres” were used to simulate the flexural behaviour of the RC shear wall. The force–displacement relations and the stiffness properties of the macro fibres were defined using cyclic constitutive models and the area assigned for these uniaxial elements. The definition of the cross-section of the shear wall was further refined by the use of additional uniaxial elements. The fibre element model used in this study is based on the nonlinear behaviour of uniaxial elements (fibres). Therefore, we investigate the effectiveness of using fibre elements on the numerical modelling of the shear walls structures.

A lumped plastic hinge model and a distributed plastic hinge model are used for the numerical modelling of nonlinear behaviour of the RC structural elements. The lumped plastic hinge modelling approach is preferred in most modelling programs because of its simplicity and the reduced computational time used. Recently, the distributed plastic hinge model has been developed for the more accurate prediction of the nonlinear behaviour of RC structural elements. In the distributed plastic hinge model, the cross-section of the structural elements is divided into steel and concrete fibre elements. In the model, the core concrete, the cover concrete and the steel reinforcement in the cross-section of each element are taken into account using the linear superposition principle. The nonlinear behaviour of these sections enables a more precise calculation of the behaviour of structural elements. This model, which is based on both force-based and displacement-based formulations, is also known as the fibre element model.

The Fibre Element Model was used in several numerical studies to observe the nonlinear behaviour of RC structural elements (i.e., beams, columns or shear walls) [9,10,11,12]. Although these previous studies converged numerically, there are still uncertainties about the following aspects of the model: the damping type and ratio of the structure, the number of fibres in the element cross-section and the number of integration points in the direction of the element axis.

Though some recommendations are given in the literature, there are still uncertainties about the damping ratio of RC shear wall structures. In most modelling programs, seismic design spectra are defined according to a 5% damping ratio, which also commonly assumed in structural analyses. However, some researchers recommended a damping ratio of 3% as appropriate for all vibration modes in the design stage of the RC shear wall structures under the seismic loading by accepting the findings of Fritz et al. [13, 14]. In an experimental study which investigated the dynamic properties of RC shear wall structures, damping ratios of 27 RC shear wall structures ranged between 1 and 4%. This experimental study was reported according to ambient vibration test results. A mean damping ratio of 2% was calculated from 107 damping values. It was stated that the damping ratio is critical between 3 and 4%. Moreover, the damping ratio was shown to be independent of the building height, the number of stories and the natural frequency of corresponding mode [14].

In this study, the displacement-based fibre element formulation is used for nonlinear seismic analysis of the RC shear walls. The optimal number of fibre elements in the cross-section of the wall is investigated. Two different RC shear wall structures were analysed against two sample earthquake loadings. We determined the optimal number of fibre elements and the optimal damping ratio for three different damping types. The feasible range of the damping ratio of RC shear wall structures is also investigated by comparing previous experimental results with new numerical results. The number of integration points is taken as a constant in the numerical solutions. Nonlinear time-history analyses are conducted by SeismoStruct software [15]. This software is commonly utilized in the literature and gives good agreement between experimental and numerical results [16, 17].

2 Fibre Element Method

The Fibre Element Method uses beam-column elements consisting of longitudinal fibres in each cross-section of the element. In this approach, cross-sections which are planar before bending are assumed to remain planar after bending. The sections are perpendicular to the reference axis. The effects of cracking and tension stiffening are included by modifying the stress–strain relation of RC based on the smeared crack concept of finite element analysis. The method does not consider cracking and bond-slip effects.

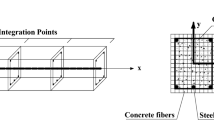
The geometric centroids of the sections are treated as a straight line which coincides with the reference axis due to the reference axis being fixed. Any element which does not coincide with the reference axis is divided into sub-elements. These sub-elements connect the centroids of the sections [18]. A fibre beam-column element is divided into cross-sections which are located at the numerical integration points. A schematic view of the fibre beam-column element and integration sections is shown in Fig. 1. The behaviours of the element and the structure are affected by the number of sections in the element and the number of fibres in the section.

Fig. 1
figure 1

The schematic view of fibre beam-column element, integration points and cross-sections [15]

Full size image

2.1 Fibre Element Formulation of the Beam-Column Element

In this section, the displacement-based fibre element (DBFE) formulation of the beam-column element is introduced. The formulation is based on a three-dimensional law for the concrete and steel fibre elements in the cross-section. In the elements, axial and bending responses are obtained by decoupling the elements from the shear responses of the section. The section stiffness matrix is obtained by using the areas, coordinates and tangent elasticity modulus of each fibre and layer (i.e., concrete and reinforcement) in each segment. The tangent elasticity modulus of each concrete/reinforcement pair can be calculated using the uniaxial stress–strain relationship of each material. The linear superposition rule is used to incorporate the different fibre material properties in the section. The resulting section forces and section tangent stiffness matrix can be written as follows:

$${\mathbf{k}}(x) = \left[ {\begin{array}{*{20}c} {\sum\limits_{f = 1}^{n} {E_{f} A_{f} } } & 0 & 0 & 0 & {\sum\limits_{f = 1}^{n} {E_{f} A_{f} z_{f} } } & { - \sum\limits_{{{\text{fiber}} = 1}}^{n} {E_{f} A_{f} y_{f} } } \\ 0 & {GA_{{S_{y} }} } & 0 & { - GA_{{S_{y} }} z_{c} } & 0 & 0 \\ 0 & 0 & {GA_{{S_{z} }} } & { - GA_{{S_{z} }} y_{c} } & 0 & 0 \\ 0 & { - GA_{{S_{y} }} z_{c} } & { - GA_{{S_{z} }} y_{c} } & {GJ\left( {A_{{S_{z} }} y_{c}^{2} + A_{Sy} z_{c}^{2} } \right)} & 0 & 0 \\ {\sum\limits_{f = 1}^{n} {E_{f} A_{f} z_{f} } } & 0 & 0 & 0 & {\sum\limits_{f = 1}^{n} {E_{f} A_{f} z_{f}^{2} } } & {\sum\limits_{f = 1}^{n} {E_{f} A_{f} y_{f} z_{f} } } \\ { - \sum\limits_{{{\text{fiber}} = 1}}^{n} {E_{f} A_{f} y_{f} } } & 0 & 0 & 0 & {\sum\limits_{f = 1}^{n} {E_{f} A_{f} y_{f} z_{f} } } & {\sum\limits_{f = 1}^{n} {E_{f} A_{f} y_{f}^{2} } } \\ \end{array} } \right]$$
(1)

where \(n\) is the number of fibres in the section; \({\sigma }_{f}\), \({A}_{f}\) and \({E}_{f}\) are the stress, area and tangent elasticity modulus of each fibre, respectively; \({y}_{f}\) and \({z}_{f}\) are the distance between the centroid of the fiber and the centroid of the section; \(G\) is the shear modulus; \({A}_{{S}_{y}}\) and \({A}_{{S}_{z}}\) are the reduced areas for shear stress in directions of \(y\) and \(z,\) respectively; \({y}_{c}\) and \({z}_{c}\) are the local coordinates of the shear centre of the section; and \(J\) is the polar moment of inertia of the section [18, 19].

The nonlinear response of the fibre beam-column element depends on the nonlinear response of the fibres. The material models of the fibres have more importance for the validity of the numerical solutions. In this study, the modified version of Menegotto and Pinto steel model [22] and Mander-Priestley-Park model [21] are selected to model the nonlinear behaviour of the reinforcement and the concrete, respectively (Fig. 2).

Fig. 2
figure 2

a Modified Menegotto and Pinto steel model [20] and b Mander-Priestley-Park concrete model [21]

Full size image

2.2 Geometric Nonlinearity of the Beam-Column Element

The geometrically nonlinear behaviour of the reinforced concrete frame elements is taken into account as P-Δ effects. Using a total co-rotational formulation, the deformations relative to the chord of the frame are included in the calculation [23]. The formulation is based on the kinematic transformations related to the three-dimensional displacement and rotations. Additionally, small deformations relative to the chord of the frame are considered, in spite of large nodal displacement and rotations. The frame element has six degrees of freedom in the local coordinate axis system as seen in Fig. 3a. The displacement in the direction of the element axis is Δ and each node has three rotational degrees of freedom around the 1, 2 and 3 local axes. The internal forces are calculated using these degrees of freedom (Fig. 3b).

Fig. 3
figure 3

a Local degrees of freedom and (b) internal forces of the beam-column frame element

Full size image

3 Numerical Investigation

In this study, numerical analyses of shear walls were investigated using Fibre Element Method which includes displacement-based formulations. The method was applied to two shear wall structures: CAMUS I and NEES-UCSD. CAMUS I and NEES-UCSD are a 5-story shear wall structure scaled by 1/3 and a full-scale seven-story shear wall structure, respectively. Shaking table test results of the shear wall structures were compared with numerical analysis results. SeismoStruct software was used for nonlinear seismic (dynamic) analyses of the walls. Geometric non-linearity was included in all solutions of the shear wall structures [24, 25].

3.1 Dynamic Solution Algorithm of the Structures

The equation of motion for the building including the linear elastic material assumption can be written as:

$$\left[ M \right]\,\left\{ a \right\} + \left[ C \right]\,\left\{ v \right\} + \left[ K \right]\,\left\{ u \right\} = \left[ M \right]\,\left\{ \iota \right\}\,a_{g}$$
(2)

where \(\left\{ a \right\}\),\(\left\{ v \right\}\) and \(\left\{ u \right\}\) are the relative acceleration, velocity and displacement and for the building, respectively; \(\left\{ \iota \right\}\) is the influence vector; \(a_{g}\) is the ground acceleration; and \(\left[ M \right]\), \(\left[ C \right]\) and \(\left[ K \right]\) are the mass matrix, damping matrix and stiffness matrix of the building.

In the nonlinear behaviour model, an improved form of Eq. (2) according to Hilber-Hughes-Taylor-α (HHT-α) integration method can be written as,

$$\left[ M \right]\,\left\{ a \right\}_{i + 1} + (1 + \alpha )\,\left[ C \right]_{i + 1} \,\left\{ v \right\}_{i + 1} - \alpha \left[ C \right]_{i} \left\{ v \right\}_{i} + (1 + \alpha )\left\{ F \right\}_{i + 1} - \alpha \left\{ F \right\}_{i + 1} = (1 + \alpha )\left\{ {F_{g} } \right\}_{n + 1} - \alpha \left\{ {F_{g} } \right\}_{n}$$
(3)

where \(\left\{ F \right\}\) is the internal load vector; \(\left\{ {F_{g} } \right\}^{{}}\) is the external load due to ground acceleration vectors; subscripts i and n are the indices of the nonlinear solution and external load step, respectively; and \(\alpha\) is a parameter controlling the numerical dissipation. To ensure second-order accuracy and unconditional stability, these parameters should be chosen such that,

$$\alpha \in \left[ { - \frac{1}{3},0} \right];\;\beta = \frac{1}{4}(1 - \alpha )^{2} ;\;\gamma = \frac{1}{2} - \alpha$$
(4)

In this study, \(\alpha\) is − 0.10 and \(\beta\) and \(\gamma\) are the Newmark parameters. \(\left[ C \right]_{i}\), the changing damping matrix in each iteration step, is obtained by

$$\left[ C \right]_{i} = \alpha_{c} \cdot \left[ M \right] + \beta_{c} \cdot \left[ K \right]_{i}$$
(5)

where \({\alpha }_{c}\) and \({\beta }_{c}\) are the mass matrix and the stiffness matrix coefficients for Rayleigh damping (both) [26]. These coefficients are defined by the natural frequencies of the two effective modes. The damping matrix can also be calculated using only the mass matrix, only the stiffness matrix or a combination of both matrices. For all three types of damping, these coefficients are calculated using only the natural frequency of the mode with the highest mass participation ratio.

3.2 Numerical Modelling of CAMUS I Shear Wall

The CAMUS I shear wall structure was tested on the shaking table at Azalée (France). The structure consisted of two identical RC shear walls parallel to each other. These shear walls were connected by rigid diaphragms. The structure has 5 floors and the height of each floor is 0.9 m. The footing height of the wall is 0.6 m. Thus, the total height of the shear wall is 5.1 m from the base. The thickness and width of the shear walls are 0.06 m and 1.7 m, respectively. Slabs measuring 1.7 × 1.7 m were placed between the two parallel shear walls. Reinforcement details for each floor are given in Fig. 4. Four different longitudinal reinforcement bars were used whose diameters were 4.5, 5.0, 6.0, and 8.0 mm. In the modelling process, 5 mm diameter steel bars at 170 mm spacing were used for stirrups instead of 3 mm diameter with 60 mm spacing to provide an equal shear reinforcement ratio. The tensile strengths of steel bars changed between 430 and 570 MPa according to tensile test results. In the numerical model, the mean of this value, 500 MPa was used for the tensile strength of the steel reinforcement [19].

Fig. 4
figure 4

Reinforcement details of the CAMUS I structure [19]

Full size image

The compressive strength and elasticity modulus of the concrete were taken as 35 MPa and 28,000 MPa, respectively [19]. Tensile strength \({f}_{\mathrm{t}}\) is calculated by;

$$f_{{\text{t}}} = 0.5563\,\sqrt {f_{{{\text{ck}}}} }$$
(6)

where \({f}_{\mathrm{ck}}\) is the uniaxial compressive strength of the concrete [27]. The units in Eq. (6) are MPa. The tensile strength of the concrete was calculated to be 3.291 MPa by using this equation.

The recorded motion of the 1957 San Francisco earthquake was the third earthquake load studied in the experimental investigation. This earthquake has high accelerations in a narrow time interval and the PGA (peak ground acceleration) of the earthquake is 1.11 g. The acceleration values and the time axis of the 1957 San Francisco earthquake were scaled by a factor of 2 and \(1/\sqrt 3\) in the experimental program, respectively (Fig. 5). The maximum acceleration value is 1.11 g [24]. The absolute maximum values of displacement at the top of the structure, shear force and bending moment at the base level (at 0.0 m altitude) were recorded as 13.20 mm, 112 kN and 324 kN m, respectively.

Fig. 5
figure 5

Acceleration time-history graph of 1957 San Francisco earthquake [24]

Full size image

We carried out time-history analyses of the shear wall using SeismoStruct. In the software, the finite element method is used for the global solutions of the walls and the fibre element method is used for the calculation of the nonlinear behaviour of the cross-sections of the structural elements. The finite element model of the shear wall is given in Fig. 6. In this model, 14 nodes and 12 elements were used. In the fibre element model calculations, 4 integration points were selected. However, different numbers of fibre elements were used to observe the effect on numerical solutions. The maximum iteration numbers chosen for the global solution and for the element solutions were 50 and 300, respectively.

Fig. 6
figure 6

Finite element model of CAMUS I structure and discretization of the shear wall

Full size image

Top displacement time-history graphs of the RC shear wall structure from experimental and numerical analysis results were compared. The damping ratio, the damping type and the number of fibre element were used as variable parameters for the comparison process. In the first solution phase, the number of fibre elements was initially set to 250. This value was varied to investigate the effectiveness of the fibre element method on shear walls. The cross-section of the shear wall and discretization of the fibre elements are shown in Fig. 6. In the figure, \({l}_{\mathrm{f}}\) represents the mean length of fibre elements and \({L}_{\mathrm{w}}\) represents the length of shear wall.

The natural frequencies of the structure were calculated using eigenvalue analysis. Effective modal mass percentages are given in Table 1, where, \({U}_{x}\), \({U}_{y}\) and \({U}_{z}\) are the displacements for the effective modal mass in the x, y and z directions, respectively. \({R}_{x}\), \({R}_{y}\) and \({R}_{z}\), the rotations for effective modal mass around x, y and z axes, are also given. Table 1 shows that the mass participation ratio of mode 3 is the highest among the modes. Therefore, the natural frequency of mode 3 was used in the stiffness- and mass- proportional damping calculations. In the Rayleigh damping calculation, the natural frequency of mode 1 was used, since it has the second-highest mass participation ratio among all modes.

Table 1 Effective modal mass pe rcentages of CAMUS I structure
Full size table

In a typical RC structure, the damping ratio generally changes between 1 and 10%. In some special cases, damping ratio may exceed 15% [28]. Therefore, in the first solution phase of the study, numerical results were obtained using 2%, 3% and 5% damping ratios. The model was calibrated by changing the damping ratio based on these obtained results. All the solutions of the first phase were obtained according to stiffness-proportional, mass-proportional and Rayleigh damping calculations. The tangent stiffness matrix was used for the structural damping calculation. Top displacement time-history graphs of the shear wall were obtained under the San Francisco earthquake loading for the three damping ratios and the results are given in Figs. 7, 8 and 9. According to the numerical results, solutions with the damping ratio of 2% converged until t = 4.58 s, t = 4.11 s and t = 4.33 s for stiffness-proportional, mass-proportional and Rayleigh damping, respectively. After these times, solutions were not obtained due to divergence. Additionally, solutions for stiffness-proportional, mass-proportional and Rayleigh damping at 3% damping ratio were divergent at t = 4.94 s, t = 4.35 s and t = 4.79 s, respectively. Although the solution for mass-proportional damping completed for 5% damping ratio, solutions for stiffness-proportional and Rayleigh damping types cannot be obtained after t = 5.02 s and t = 5.19 s, respectively.

Fig. 7
figure 7

Comparison of experimental results with numerical analysis results of CAMUS I obtained for (a) stiffness-proportional, (b) mass-proportional and (c) Rayleigh damping types at 2% damping ratio

Full size image
Fig. 8
figure 8

Comparison of experimental results with numerical analysis results of CAMUS I obtained for (a) stiffness-proportional, (b) mass-proportional and (c) Rayleigh damping types at 3% damping ratio

Full size image
Fig. 9
figure 9

Comparison of experimental results with numerical analysis results of CAMUS I obtained for (a) stiffness-proportional, (b) mass-proportional and (c) Rayleigh damping types at 5% damping ratio

Full size image

Differences between experimental and numerical results are shown in Table 2 for the three damping types and the ratios. As seen in this table, the minimum differences between experimental and numerical results were obtained as 5.74% for the stiffness-proportional damping type at 2% damping ratio, 11.67% for the mass-proportional damping type at 3% damping ratio, as 6.77% for the Rayleigh damping type at 2% damping ratio. The best approximation within these nine solutions was obtained for stiffness-proportional damping type at 2% damping ratio.

Table 2 Comparison of experimental results with numerical analysis results of CAMUS I structure obtained for 2%, 3% and 5% damping ratios
Full size table

The model was refined by changing the damping type and the damping ratio for the best approximation to the experimental results. Therefore, different damping ratio values from 2%, 3% and 5% were used for the three damping types. According to the numerical results, a difference of 0.04% from the experimental data was obtained for the stiffness-proportional damping type at 2.31% damping ratio. Numerical solution steps for this model could be obtained until 4.60 s. For the mass-proportional damping type at 3.20% damping ratio, a difference of 1.71% was calculated and numerical solution steps could be obtained until 4.68 s (Fig. 10).

Fig. 10
figure 10

Comparison of experimental results with numerical analysis results of CAMUS I obtained for (a) stiffness-proportional damping type at 2.31% damping ratio and (b) mass-proportional damping type at 3.20% damping ratio

Full size image

Combinations of 2.31% and 3.20% damping ratios and the natural frequencies of mode 1 and mode 3 were used for the calculation of Rayleigh damping coefficients. The first combination used mode 1 for the first natural frequency with a 2.31% damping ratio and mode 3 for the second natural frequency with a 3.20% damping ratio. The difference between experimental and numerical results was calculated as 1.62% for the first combination. The second combination used mode 3 with a 3.20% damping ratio for the first natural frequency and mode 1 with a 2.31% damping ratio for the second natural frequency. The difference between experimental and numerical results was observed as 20.81% for this combination. Numerical solution steps of the first and the second combinations could be also obtained until 4.44 s and 4.91 s, respectively (Fig. 11).

Fig. 11
figure 11

Comparison of experimental results with numerical analysis results of CAMUS I obtained for (a) 2.31–3.20% damping ratios and (b) 3.20–2.31% damping ratios for Rayleigh damping type

Full size image

Time-history graphs of the numerical solutions coincided more with the experimental results, especially between the time interval of t = 2.5–3.1 s. Differences between frequencies and amplitudes were observed after t = 3.1 s. Consequently, this time interval was used in the comparison stage of the time-history graphs.

Comparisons of damping types were carried out according to differences between experimental and numerical analysis results in terms of absolute maximum top displacement, base shear force and base bending moment (Fig. 12). For top displacements, if the damping ratio selected is between 2.5% and 3%, the differences obtained between experimental and numerical analysis results for all three damping types are less than 16% (Fig. 12a). The differences are defined as less than 59% (less than 3% except for mass-proportional damping) and 6% for base shear force and bending moment for the same interval of damping ratio, respectively. The maximum difference observed was for mass-proportional damping type when calculating the base shear force.

Fig. 12
figure 12

Comparisons of differences between experimental with numerical results obtained for different damping types of CAMUS I structure in terms of (a) top displacement, (b) base shear force and (c) bending moment

Full size image

Both the minimum differences between absolute maximum top displacement values and the minimum differences between the overlaps of time-history graphs were taken into consideration in the comparison stage. These minimum differences were observed in three different conditions; stiffness-proportional damping with 2.31% damping ratio, mass-proportional damping with 3.20% damping ratio and Rayleigh damping with 2.31–3.20% damping ratios. In the investigation phase of the optimal fibre element length ratio, the mean length of one fibre element \(({l}_{\mathrm{f}})\) was divided by longitudinal length of the shear wall \(({L}_{\mathrm{w}})\). The three conditions which provide the best approximation in all solutions were considered whilst investigating the \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}\) ratio. Therefore, the number of fibre elements was changed to 100, 500, 750 and 1000 from the conventional value of 250. Numerical results according to the \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}\) ratios are given in Table 3.

Table 3 The effect of fiber element number on the solutions for the CAMUS I
Full size table

The optimal ratio of \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}\) for stiffness-proportional and Rayleigh damping was determined to be 2.78% for 250 fibre elements. This optimal ratio was identified as 0.62% for 1000 fibre elements for mass-proportional damping. Minimum differences between top displacement values of the shear wall obtained from experimental and numerical analysis results for the stiffness-proportional, mass-proportional and Rayleigh damping solutions were calculated as: 0.037% at 2.31% damping ratio, 0.376% at 3.20% damping ratio and 1.622% at 2.31–3.20% damping ratios, respectively. The best approximation was obtained by the stiffness-proportional damping at 2.31% damping ratio. On the other hand, when stiffness-proportional damping and mass-proportional damping are selected for the CAMUS I structure, the resulting top displacement differences using the DBFE method are less than 0.6% for 0.76% ratio of \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}\).

3.3 Numerical Modelling of NEES-UCSD Shear Wall

A full-scale seven-story reinforced concrete shear wall structure, built by the University of California at San Diego (UCSD), NEES (network for earthquake engineering simulation) Consortium and Portland Cement Association (PCA) was tested on a shaking table [19]. The structure consisted of two types of shear walls which had pier columns at each corner of the structure. The shear walls, referred to as the flange wall and the web wall, are perpendicular to each other. The flange wall was connected to the slab. The shear walls were connected to each other via slotted connections. The basement height is 0.76 m and the height of each floor is 2.74 m. The structure is fixed at basement level. The total height and total mass of the structure are 19.96 m and 226 tons. Two different cross-sections were defined for the flange wall and web wall. The widths of the flange wall and web walls are 4.88 m and 3.65 m. The flange wall thicknesses are 203 mm for the 7th floor and 152 mm for the other floors. The web wall thicknesses are 203 mm for the 1st and the 7th floor and 152 mm for other floors. The shear walls and pier columns supported 3.65 × 8.13 m slabs for each floor. Precast piers (post-tensioned) were connected to the web wall and slabs through bracing. A view of the NEES-UCSD shear wall structure and its details is shown in Fig. 13.

Fig. 13
figure 13

View of NEES-UCSD shear wall structure [19]

Full size image

For longitudinal reinforcement, 12.7 and 15.9 mm diameter steel bars were used in the web wall, but only 12.7 mm diameter steel bars were used the flange wall. At the ends of both the flange wall and the web wall, a 9.5 mm diameter steel bar with 101.6 mm spacing was used for stirrups. The mean yield strength of the steel bars was defined as 458.63 MPa. This value was calculated as the mean of tensile test results of 11 specimens. The elasticity modulus and compressive strength of the concrete were also calculated as 29.24 GPa and 41.39 MPa. These values were defined by mean of uniaxial compressive strength test results of 10 specimens [19]. Thus, the uniaxial tensile strength of the concrete was computed to be 3.580 MPa using Eq. (6). For the seismic input, the record of the1994 Northridge earthquake taken at the Sylmar Olive View Medical Centre was used. The acceleration time-history graph of the 1994 Northridge earthquake is given in Fig. 14. The earthquake had a magnitude of 6.7, measured by released energy. The earthquake had high accelerations in a narrow time interval. The maximum acceleration value is 0.83 g [19]. Absolute maximum values of displacement, shear force and bending moment from the experimental results were recorded as: 395 mm at the top of the structure, 1184.7 kN and 11,839.4 kN·m at the base level, respectively.

Fig. 14
figure 14

The acceleration time-history graph of the 1994 Northridge earthquake [15]

Full size image

In this section of the study, the seismic performance of the NEES-UCSD shear wall structure was investigated using the DBFE method. The NEES-UCSD shear wall structure was modelled with 56 nodes and 14 elements. The finite element model of the structure is shown in Fig. 15. The number of integration points for each element was selected as 4. The maximum iteration numbers chosen for the global solution and for the element solutions were 50 and 300, respectively.

Fig. 15
figure 15

Finite Element model of the NEES-UCSD shear wall structure

Full size image

Numerical analysis results were compared with experimental results according to top displacement time-history graphs. For the numerical analyses, variable parameters were specified as the damping type, the damping ratio and the number of fibre elements. The first solution stage used 250 fibre elements were used. Subsequently, the number of fibre elements was changed to determine the optimal fibre element length ratio.

The natural frequencies of the structure were specified with respect to effective modal mass percentages. Obtained results by using eigenvalue analysis are given in Table 4. The table shows that the mass participation ratio of mode 3 is the highest among the modes. Therefore, the natural frequency of mode 3 was used in the stiffness- and mass-proportional damping calculations. In the Rayleigh damping calculation, the natural frequencies of mode 3 and mode 4 were used, since mode 4 has the second-highest mass participation ratio among all modes.

Table 4 Effective modal mass percentages of NEES-UCSD structure
Full size table

Numerical solutions were obtained for damping ratios of 2%, 3% and 5%. The damping matrix of the structure was calculated using its tangent stiffness matrix. Comparisons of experimental results with numerical analysis results are given in Figs. 16, 17 and 18 for these three damping ratios with stiffness-proportional, mass-proportional and Rayleigh damping types. Seismic analyses of the NEES-UCSD structure converged for all solution steps.

Fig. 16
figure 16

Comparison of experimental results with numerical analysis results of NEES-UCSD structure obtained for (a) stiffness-proportional, (b) mass-proportional and (c) Rayleigh damping types at 2% damping ratio

Full size image
Fig. 17
figure 17

Comparison of experimental results with numerical analysis results of NEES-UCSD structure obtained for (a) stiffness-proportional, (b) mass-proportional and (c) Rayleigh damping types at 3% damping ratio

Full size image
Fig. 18
figure 18

Comparison of experimental results with numerical analysis results of NEES-UCSD structure obtained for (a) stiffness-proportional, (b) mass-proportional and (c) Rayleigh damping types at 5% damping ratio

Full size image

In Table 5, the differences between experimental and numerical results are shown for the three damping types and ratios. The minimum differences between experimental and numerical analysis results for stiffness-proportional, mass-proportional and Rayleigh damping types were 5.77%, 0.25% and 1.29%, respectively at 3% damping ratio. The best approximation within these nine solutions was given by the mass-proportional damping type at a 3% damping ratio.

Table 5 Comparison of numerical analysis results with experimental results of NEES-UCSD structure for 2%, 3% and 5% damping ratios
Full size table

The model was calibrated by changing the damping type and the damping ratio for the best approximation to the experimental results. Damping ratios of 2%, 3% and 5% were used for the three damping types. A difference of 0.375% was obtained between experimental and numerical analysis results by using stiffness-proportional damping type at 3.91% damping ratio. A difference of 0.412% was also obtained by using damping ratio of 3.08% for mass-proportional damping type. The resulting time-history graphs of these two cases are given in Fig. 19. For the calculation of the Rayleigh damping coefficients, combinations of 3.91% and 3.08% damping ratios and natural frequencies of mode 3 and mode 4 were used. For the first combination, a natural frequency of mode 3 having a damping ratio of 3.91% and a natural frequency of mode 4 having a damping ratio of 3.08% were selected. The resulting difference for this is 6.201%. In the second combination, a natural frequency of mode 3 having a damping ratio of 3.08% and a natural frequency of mode 4 having aa damping ratio of 3.91% were used. The difference between numerical and experimental results is 1.704%. Time-history graphs obtained from results of the first and the second combinations are given in Fig. 20.

Fig. 19
figure 19

Comparison of experimental results with numerical analysis results of NEES-UCSD structure obtained for (a) stiffness-proportional damping type at 3.91% damping ratio and (b) mass-proportional damping type at 3.08% damping ratio

Full size image
Fig. 20
figure 20

Comparison of experimental results with numerical analysis results of NEES-UCSD structure obtained for (a) 3.91–3.08% damping ratios and (b) 3.08–3.91% damping ratios for Rayleigh damping type

Full size image

Differences between experimental and numerical analysis results in terms of the absolute maximum top displacement, the base shear force and the bending moment were investigated for defining the effectiveness of damping types in Fig. 21. For top displacements, if the damping ratio selected is between 2.5% and 3.5%, the differences between experimental and numerical analysis results for all three damping types is less than 8% as seen Fig. 21a. The differences are defined as less than 34% for the base shear force and less than 38% for the bending moment for the same interval of damping ratio. Maximum differences were seen in the base shear force and the bending moment calculations.

Fig. 21
figure 21

Comparisons of differences between experimental with numerical results obtained for different damping types of NEES-UCSD structure in terms of (a) top displacement, (b) base shear force and (c) the bending moment

Full size image

Time-history graphs of the numerical solutions coincided best with experimental results between the t = 4–10 s time interval. Frequency and amplitude differences were observed after t = 10 s. This time interval was taken into consideration in the comparison stage of the time-history graphs. The minimum differences of the top displacement values and the minimum divergences of frequency/amplitude contents (closest time-history graphs) were observed at 3.91% damping ratio for stiffness-proportional damping, at 3.08% damping ratio for mass-proportional damping and at 3.08–3.91% damping ratios for Rayleigh damping. For the investigation of optimal fibre element number, these three conditions were used. Numbers of fibre elements of 70, 80, 90, 100, 250, 500, 750 and 1000 were tested to obtain the optimal number. The \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}\) ratios and obtained numerical results according to the fiber element numbers are given in Table 6. Minimum differences were obtained of 0.146% at 3.91% damping ratio for stiffness-proportional damping, 0.072% at 3.08% damping ratio for mass-proportional damping and 1.601% at 3.08–3.91% damping ratios for Rayleigh damping. The best approximation was obtained with the stiffness-proportional damping at 3.91% damping ratio.

Table 6 The effect of fiber element number on solutions for the NEES-UCSD
Full size table

The optimal ratio of \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}\) for stiffness-proportional and mass-proportional damping was 10.87% using 100 fibre elements. Moreover, the optimal ratio was 0.98% for 750 fibre elements and Rayleigh damping. On the other hand, when stiffness-proportional damping and mass-proportional damping were used for the NEES-UCSD structure, top displacement differences resulting from the DBFE method are less than 0.5% for all numbers of fibre elements. Provided that the fibre element length is less than 21.75% of the longitudinal length of the shear wall, the differences are less than 1% for all numerical solutions obtained by using stiffness-proportional and mass-proportional damping types for DBFE method.

3.4 Comparison of CAMUS I and NEES-UCSD Shear Wall Structures

The differences between experimental and numerical results of CAMUS I and NEES-UCSD shear wall structures were compared with respect to the top displacement, the base shear force and the bending moment for each damping type and damping ratio for investigation of the effectiveness of numerical solutions.

The differences of the top displacement, the base shear force and the bending moment results obtained for damping ratios between 2.0% and 2.5% are less than 13%, 22% and 32% for stiffness-proportional damping, respectively (Fig. 22). The differences of the top displacement, the base shear force and the bending moment results obtained for the same damping ratio interval are less than 11%, 29% and 36% for Rayleigh damping, respectively (Fig. 23). Ho wever, the differences of the top displacement, the base shear force and the bending moment for damping ratios between 4.5% and 5.0%, were less than 14%, 34% and 39% for mass-proportional damping, respectively (Fig. 24).

Fig. 22
figure 22

Comparisons of differences between experimental with numerical results obtained for stiffness-proportional damping in terms of (a) top displacement, (b) base shear force and (c) the bending moment

Full size image
Fig. 23
figure 23

Comparisons of differences between experimental with numerical results obtained for Rayleigh damping in terms of (a) top displacement, (b) base shear force and (c) the bending moment

Full size image
Fig. 24
figure 24

Comparisons of differences between experimental with numerical results obtained for Mass-proportional damping in terms of (a) top displacement, (b) base shear force and (c) the bending moment

Full size image

In the DBFE method, deformations are calculated in the first phase. The base shear force and the bending moment are calculated using the deformation values. Therefore, the differences calculated for the base shear force and the bending moment are greater than the top displacement differences.

4 Conclusions

In this study, the effect of DBFE method on numerical solutions of RC shear wall structures has been investigated. Several time-history analyses were performed for the CAMUS I and NEES-UCSD (Network for Earthquake Engineering Simulation and University of California at San Diego) shear wall structures. These shear wall structures were subjected to the 1957 San Francisco and 1994 Northridge earthquake loadings, respectively. These earthquakes have high accelerations in a narrow time interval and the maximum acceleration value of the earthquakes is between 0.83 and 1.11 g. Furthermore, modal analyses were performed to obtain the natural frequencies of the structures. Our numerical results have been compared with previously performed experimental shaking table test results on these two shear wall structures. Comparisons are carried out in terms of both absolute maximum values and time-history graphs of the top displacements. In the first stage of the comparison, which includes the top displacement, the base shear force and the bending moment, results at 2%, 3% and 5% damping ratios were used for stiffness-proportional, mass-proportional and Rayleigh damping types. Different damping ratios were investigated to obtain the optimal damping ratio for each damping type until minimum differences were observed between the experimental and numerical results. The number of fibre elements was first selected as 250 for numerical solutions. In order to obtain the optimal fibre element length ratio, the fibre element number in each cross-section of the shear walls was changed to 70, 80, 90, 100, 250, 500, 750 and 1000. The ratio of the mean length of fibre elements to the longitudinal length of shear wall \({(l}_{\mathrm{f}}/{L}_{\mathrm{w}})\) is also taken into consideration. In the DBFE method, obtained results from this research can be summarized as follows:

  • The differences of the top displacement, the base shear force and the bending moment results obtained for a damping ratio between 2.0% and 2.5% are less than 13%, 22% and 32%, respectively for stiffness-proportional damping.

  • The differences of the top displacement, the base shear force and the bending moment results obtained for a damping ratio between 2.0% and 2.5% are less than 11%, 29% and 36%, respectively for Rayleigh damping.

  • The differences of the top displacement, the base shear force and the bending moment for a damping ratio between 4.5% and 5.0% are less than 14%, 34% and 39%, respectively for mass-proportional damping.

  • Within the damping types, the Rayleigh damping model had the minimum difference (11%) between experimental and numerical analysis results.

  • The minimum differences of the top displacement between experimental and numerical analysis results for the CAMUS I and NEES-UCSD structures are calculated at 2.31% and at 3.91% damping ratios, respectively, for the stiffness-proportional damping. However, the minimum differences for the CAMUS I and NEES-UCSD structures are determined to be 3.2% and 3.08% damping ratios, respectively, for the mass-proportional damping.

  • The optimal number of fibre elements is determined according to the ratio of \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}=0.76\mathrm{\%}\) for the CAMUS I structure and according to the ratio of \({l}_{\mathrm{f}}/{L}_{\mathrm{w}}=21.75\mathrm{\%}\) for the NEES-UCSD structure. When the ratio is smaller than 3%, the differences between experimental and numerical analysis results for both shear wall structures are calculated as less than 2% at the optimal damping ratios.

  • The base shear force and the bending moment are computed by using the deformations that are obtained in the first solution phase. Therefore, the differences between base shear force and the bending moment are greater than displacement differences.

  • The DBFE method is usable for nonlinear seismic analysis of reinforced concrete shear wall structures.

This subject can be extended for different soil by considered soil-structure interaction in future studies.