Moving Contact Problem of an Unbonded Layer in the Presence of Body Force

Abstract

In this study, moving continuous and discontinuous contact problems of a layer were examined in the presence of body force. The unbonded layer was pressed to a rigid foundation by a rigid cylindrical punch that moved over the layer steadily. In the presence of body force, for the moving contact problem, the general stress and displacement expressions were derived using the theory of elasticity and Fourier integral transforms, without using the superposition technique. Through applying the boundary conditions of the problem, the singular integral equations in which the contact stresses and contact areas were unknown were obtained for both the continuous and discontinuous contact cases. The singular integral equations were solved numerically using the Gauss–Chebyshev integration formula. Numerical results for critical load, initial separation distance, the separation region, contact stress distributions under the punch and between the layer, and foundation were given for various dimensionless quantities.

1 Introduction

Since loads are transmitted through contacting components in many practical engineering applications, contact problems have gained an important role in solid mechanics. Contact stress, contact area, contact type, and deformation at the contact surfaces remarkably affect the behavior of engineering structures such as road pavements, foundations, railway ballasts, brake disks, and abradable seals in gas turbine components.

Studies related to the contact problem can be classified into four groups based on the separation types: bonded contact, receding contact, continuous contact, and discontinuous contact.

In bonded contact problems, it is assumed that contacting bodies are fully bonded to each other and the separation of them is not possible whatever the value of the load is. Recent studies related to contact problems have focused on functionally graded materials (FGMs). FGMs are a new class of composite materials whose compositions and microstructures vary continuously in any direction. Assuming the exponential variation of the shear modulus, Guler and Erdogan (2004, 2007) investigated the plane strain sliding contact problem of an FG layer bonded to a homogeneous half plane. The loading is provided by a rigid cylindrical or flat punch. Ke and Wang (2006, 2007) and Yang and Ke (2008) developed the multilayered model for the frictional and frictionless contact problems with arbitrary varying material properties. In this model, the FGM was divided into sublayers in which the shear modulus varied linearly from one surface to another. The axisymmetric contact problem of an FM layer bonded to a homogeneous half plane was studied by Liu and Wang (2008) and Liu et al. (2008) using the Hankel transform technique. In the study of Chen and Chen (2012), the layer was assumed as linearly graded. The layer is indented by a concentrated normal force or by a rigid cylindrical stamp. Choi (2009) examined the frictional contact problem of a single FG layer bonded to a rigid foundation. Çömez and Guler (2017) studied the sliding contact problem of an FG bilayer indented by a rigid cylindrical punch. Chen et al. (2017) and Chen et al. (2019) investigated the interfacial analysis of a thin film bonded to a finite-thickness graded substrate under different loading conditions. Chen et al. (2018) examined a thin piezoelectric actuator attached to a graded half plane with an adhesive layer under electrical loading. Peng et al. (2019) investigated a frictional contact problem of an arbitrarily oriented substrate loaded by a rigid flat indenter.

In receding contact problems, contacting components are not bonded to each other, and the body forces are ignored. Thus, the separation begins when the effect of the external load vanishes. Because the body force is ignored, the separation lasts infinitely. Receding double-contact problems of two layers bonded to a rigid foundation and indented by a rigid cylindrical punch were solved by Comez et al. (2004), Yan and Li (2015), and Çömez et al. (2016). The layers were assumed as homogeneous by Comez et al. (2004), the upper layer as FG and the lower layer as homogeneous by Yan and Li (2015), and both layers as FG by Çömez et al. (2016). The plane receding contact problem between the layer and a homogeneous half plane was investigated by Kahya et al. (2007a, b) and El-Borgi et al. (2006). The layer was assumed as anisotropic (Kahya et al., 2007a, b) and FG (El-Borgi et al., 2006). The axisymmetric receding contact problem between the FG layer and a homogeneous half plane was solved by Rhimi et al. (2009) and Liu et al. (2016) using the Hankel transform technique. Adıyaman et al. (2016) investigated the receding contact problem of a homogeneous or FG layer resting on a quarter plane and loaded by a symmetrical distributed load. Adibelli et al. (2013) and Yan and Mi (2017a, 2017b) studied the bilayer resting on a half plane. Frictional receding contact problems are more complex than frictionless contact problems because the unknown contact areas increase, and there are not many studies about this issue. Çömez (2010), El-Borgi et al. (2014), El-Borgi and Çömez (2017), and Yilmaz et al. (2018) investigated the frictional receding contact problem between a FG/homogeneous layer and a homogeneous half plane/FG layer. Parel and Hills (2016) studied the frictional receding contact problem between a homogeneous layer and a half plane when the layer was loaded by a semi-infinite uniform normal surface pressure.

In the studies mentioned before, the body forces are neglected. However, in continuous and discontinuous (CDC) contact problems, body forces are taken into account, and it is assumed that contacting components are not bonded to each other. Hence, two types of contact occur depending on the value of the external load: continuous contact and discontinuous contact. When the external load is less than a certain critical value, no separation occurs between the contacting bodies, and the contact will be continuous throughout the components interface. Thus, the main problem of the continuous contact issue is to find the critical load that causes separation. If the external load exceeds the certain critical value, separation occurs between contacting components, and this type of contact is called discontinuous. In the study of Civelek and Erdogan (1975), the elastic layer lying on a rigid foundation was subjected to the concentrated vertical lifting force. Gecit and Erdogan (1978) extended this study to the axisymmetric case. The elastostatic problem of a layer resting on a half space was studied by Gecit (1980). The layer was subjected to the uniform clamping pressure as well as the concentrated vertical line load. Çakıroğlu et al. (2001) studied the CDC contact problem of two layers resting on a half plane. They examined the separation regions between the upper and lower layer and between the lower layer and half plane. Kahya et al. (2007a, b) studied the continuous contact problem of two orthotropic layers indented by a rigid flat-ended stamp. Ozsahin and Taşkıner (2013) investigated the CDC contact problem of a layer lying on a half plane. The layer was loaded via three rigid flat punches. Öner et al. (2017) and Adıyaman et al. (2017) examined the CDC contact problem of an FG layer. Çömez (2019) studied the CDC contact problem of an FG layer pressed to a rigid foundation by a rigid cylindrical punch. Polat et al. (2018) and Kaya et al. (2020) studied the CDC problem of an FG layer indented by two rigid flat punches.

Although there are many studies related to static contact problems in the literature, moving continuous and discontinuous contact problems have not been discussed yet. In this study, the effects of velocity on continuous and discontinuous contact problems are examined when the layer is indented by a rigid cylindrical punch, and stress and displacement expressions are derived without using the superposition technique.

2 General Equations for Stresses and Displacements

In this part, general expressions for the stresses and the displacements will be obtained without asserting the superposition method used by the previous researchers.

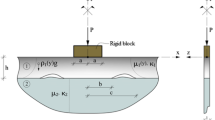
The geometries of the continuous and discontinuous contact problems of an isotropic and homogeneous layer are shown in Figs. 1 and 2, respectively. The layer with the height $h$ is subjected to a concentrated normal force $P$ by means of a rigid cylindrical punch with radius $R$. The rectangular coordinates $(x_{1} ,y_{1} )$ are fixed in the layer, and the translating coordinates $(x,y)$ are attached to the rigid punch.

Fig. 1

Geometry of the continuous moving contact problem

Fig. 2

Geometry of the discontinuous moving contact problem

The differential equations of motion for the case of plane strain may be written as

$$\frac{{\partial \sigma_{x} }}{{\partial x_{1} }} + \frac{{\partial \tau_{xy} }}{{\partial y_{1} }} = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}$$

(1)

$$\frac{{\partial \tau_{yx} }}{{\partial x_{1} }} + \frac{{\partial \sigma_{y} }}{{\partial y_{1} }} - \rho g = \rho \frac{{\partial^{2} v}}{{\partial t^{2} }}$$

(2)

where $\rho$ is the mass density per unit volume of the layer and $g$ is the gravitational acceleration.

The layer is assumed to be homogeneous, isotropic, and linearly elastic. Hence, for the plane strain contact problem, stress–displacement relation can be written as follows:

$$\sigma_{x} (x,y) = \frac{\mu }{\kappa - 1}\left[ {(\kappa + 1)\frac{\partial u}{{\partial x_{1} }} + (3 - \kappa )\frac{\partial v}{{\partial y_{1} }}} \right]$$

(3)

$$\sigma_{y} (x,y) = \frac{\mu }{\kappa - 1}\left[ {(3 - \kappa )\frac{\partial u}{{\partial x_{1} }} + (\kappa + 1)\frac{\partial v}{{\partial y_{1} }}} \right]$$

(4)

$$\tau_{xy} = \mu \left[ {\frac{\partial u}{{\partial y_{1} }} + \frac{\partial v}{{\partial x_{1} }}} \right]$$

(5)

where $u$ and $v$ are the $x_{1}$ and $y_{1}$ components of the displacement vector, $\nu$ is the Poisson's ratio, and $\kappa = 3 - 4\nu$ for the plane strain case. $\mu$ is the shear modulus of the layer.

The dynamic contact problem can be reduced to the steady contact problem by using the following coordinate transformation:

$$x = x_{1} - Vt\;y = y_{1}$$

(6)

Substituting Eqs. (2) and (3) into the equilibrium Eqs. (1) and (2), the following partial differential equations are obtained in terms of $u(x,y)$ and $v(x,y)$:

$$(\kappa + 1)\frac{{\partial^{2} u}}{{\partial x^{2} }} + (\kappa - 1)\frac{{\partial^{2} u}}{{\partial y^{2} }} + 2\frac{{\partial^{2} v}}{\partial x\partial y} - (\kappa - 1)\frac{{V^{2} \rho }}{\mu }\frac{{\partial^{2} u}}{{\partial x^{2} }} = 0$$

(7)

$$(\kappa - 1)\frac{{\partial^{2} v}}{{\partial x^{2} }} + (\kappa + 1)\frac{{\partial^{2} v}}{{\partial y^{2} }} + 2\frac{{\partial^{2} u}}{\partial x\partial y} - (\kappa - 1)\frac{{V^{2} \rho }}{\mu } = (\kappa - 1)\frac{\rho g}{\mu }$$

(8)

Using the Fourier integral transforms, the system of the partial differential equations can be reduced to the ordinary differential equations. Therefore, the displacement components are taken as the following transformed form:

$$u(x,\,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\tilde{u}(\alpha ,{\kern 1pt} {\kern 1pt} y){\kern 1pt} {\kern 1pt} e^{ - I\alpha x} d\alpha }$$

(9)

$$v(x,\,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\tilde{v}(\alpha ,{\kern 1pt} {\kern 1pt} y){\kern 1pt} {\kern 1pt} e^{ - I\alpha x} d\alpha }$$

(10)

where $I{\kern 1pt}$ denotes the imaginary unit, and $\tilde{u}(\alpha ,y){\kern 1pt}$ and $\tilde{v}(\alpha ,y){\kern 1pt}$ are the Fourier transforms of $u(x,y)$ and $v(x,y)$, respectively. Applying the Fourier transforms (5) to Eqs. (4) and (7) with respect to $x$, the following ordinary differential equation system is obtained:

$$(\kappa - 1)\frac{{d^{2} \tilde{u}}}{{dy^{2} }} - 2I\alpha \frac{{d\tilde{v}}}{dy} - \alpha^{2} (\kappa + 1)\tilde{u} + \alpha^{2} (\kappa - 1)\frac{{V^{2} \rho }}{\mu }\tilde{u} = 0$$

(11)

$$(\kappa + 1)\frac{{\partial^{2} \tilde{v}}}{{\partial y^{2} }} - 2I\alpha \frac{{\partial \tilde{u}}}{\partial y} - \alpha^{2} (\kappa - 1)\,\tilde{v} + \alpha^{2} (\kappa - 1)\frac{{V^{2} \rho }}{\mu }\tilde{v} = (\kappa - 1)\frac{\rho g}{\mu }\delta (\alpha )$$

(12)

where $\delta$ denotes the Dirac delta function. After some lengthy but straightforward mathematical operations shown in Eq. (6), the following nonhomogeneous ordinary differential equation is achieved:

$$(\kappa + 1)\frac{{d^{4} \tilde{v}}}{{dy^{4} }} + L_{1} \frac{{d^{2} \tilde{v}}}{{dy^{2} }} + L_{2} \tilde{v} = - \alpha^{2} \frac{\rho g}{\mu }(1 + \kappa + (1 - \kappa )\frac{{V^{2} \rho }}{\mu })\delta (\alpha )$$

(13)

where

$$L_{1} = 2\alpha^{2} \left( {\kappa \left( { - 1 + \frac{{V^{2} \rho }}{\mu }} \right) - 1} \right)$$

(14)

$$L_{2} = - \alpha^{4} \left( { - 1 + \frac{{V^{2} \rho }}{\mu }} \right)\left( {\kappa + 1 - (\kappa - 1)\frac{{V^{2} \rho }}{\mu }} \right)$$

(15)

The solution of Eqs. (11 and 12) can be obtained as

$$\tilde{v}(\alpha ,y) = A_{1} e^{{n_{1} \left| \alpha \right|y}} + A_{2} e^{{n_{2} \left| \alpha \right|y}} + A_{3} e^{{n_{3} \left| \alpha \right|y}} + A_{4} e^{{n_{4} \left| \alpha \right|y}} - \frac{\rho g/\mu }{{\alpha^{2} (1 - V^{2} \rho /\mu )}}\delta (\alpha )$$

(16)

where

$$n_{1} = - n_{2} = \sqrt {1 - \frac{{V^{2} \rho }}{\mu }}$$

(17)

$$n_{3} = - n_{4} = \sqrt {1 - (\frac{\kappa - 1}{{\kappa + 1}})\frac{{V^{2} \rho }}{\mu }}$$

(18)

Using Eq. (16) and (9 and 10), the tangential displacement $\tilde{u}(\alpha ,y){\kern 1pt}$ can be written as follows:

$$\tilde{u}(\alpha ,y) = I\frac{\left| \alpha \right|}{\alpha }\left( { - A_{1} n_{1} e^{{n_{1} \left| \alpha \right|y}} + A_{2} n_{2} e^{{n_{2} \left| \alpha \right|y}} + \frac{1}{{n_{3} }}A_{3} e^{{n_{3} \left| \alpha \right|y}} + \frac{1}{{n_{4} }}A_{4} e^{{n_{4} \left| \alpha \right|y}} } \right)$$

(19)

Substituting Eqs. (9, 10, 11) into Eq. (5), the displacement expressions for the layer are obtained as

$$u(x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {I\frac{\left| \alpha \right|}{\alpha }\left( { - A_{1} n_{1} e^{{n_{1} \left| \alpha \right|y}} + A_{2} n_{2} e^{{n_{2} \left| \alpha \right|y}} + \frac{1}{{n_{3} }}A_{3} e^{{n_{3} \left| \alpha \right|y}} + \frac{1}{{n_{4} }}A_{4} e^{{n_{4} \left| \alpha \right|y}} } \right)} \right]} \,e^{ - I\alpha x} d\alpha$$

(20)

$$v(x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {A_{1} e^{{n_{1} \left| \alpha \right|y}} + A_{2} e^{{n_{2} \left| \alpha \right|y}} + A_{3} e^{{n_{3} \left| \alpha \right|y}} + A_{4} e^{{n_{4} \left| \alpha \right|y}} - \frac{\rho g/\mu }{{\alpha^{2} (1 - V^{2} \rho /\mu )}}\delta (\alpha )} \right]} \,e^{ - I\alpha x} d\alpha$$

(21)

Substituting Eqs. (20 and 21) into Eqs. (3, 4, 5), the stress components for the layer can be obtained as follows:

$$\frac{{\sigma_{x} (x,y)}}{\mu } = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left| \alpha \right|\left[ { - 2A_{1} n_{1} e^{{n_{1} \left| \alpha \right|y}} - 2A_{2} n_{2} e^{{n_{2} \left| \alpha \right|y}} + A_{3} \frac{1}{{n_{3} }}m_{1} e^{{n_{3} \left| \alpha \right|y}} + A_{4} \frac{1}{{n_{4} }}m_{1} e^{{n_{4} \left| \alpha \right|y}} } \right]} e^{ - I\alpha x} d\alpha$$

(22)

$$\frac{{\sigma_{y} (x,y)}}{\mu } = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left| \alpha \right|\left[ {2A_{1} n_{1} e^{{n_{1} \left| \alpha \right|y}} - 2A_{2} n_{2} e^{{n_{2} \left| \alpha \right|y}} - A_{3} \frac{1}{{n_{3} }}m_{2} e^{{n_{3} \left| \alpha \right|y}} + A_{4} \frac{1}{{n_{4} }}m_{2} e^{{n_{4} \left| \alpha \right|y}} } \right]} e^{ - I\alpha x} d\alpha$$

(23)

$$\frac{{\tau_{xy} (x,y)}}{\mu } = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\alpha I\left[ {A_{1} m_{2} e^{{n_{1} \left| \alpha \right|y}} + A_{2} m_{2} e^{{n_{2} \left| \alpha \right|y}} - 2A_{3} e^{{n_{3} \left| \alpha \right|y}} + A_{4} e^{{n_{4} \left| \alpha \right|y}} + \frac{\rho g/\mu }{{\alpha^{2} (1 - V^{2} \rho /\mu )}}\delta (\alpha )} \right]} e^{ - I\alpha x} d\alpha$$

(24)

where

$$m_{1} = \left( {\frac{\kappa - 3}{{\kappa + 1}}} \right)\frac{{V^{2} \rho }}{\mu } - 2,\;m_{2} = V^{2} \rho /\mu - 2$$

(25)

where $A_{j}$ $(j = 1,\ldots 4)$ are the unknowns and will be determined based on the boundary conditions of the problems.

3 The Boundary Conditions and the Singular Integral Equation in the Continuous Contact Case

When the external load $P$ is less than the critical value $P_{cr}$, the contact between the layer and the foundation will be continuous, and there will be no separation along the interface. Thus, the vertical displacement of the layer will be “0” at the interface. Also, the fact that the shear stress between the contacting components is “0” will result in frictionless contact. Therefore, the continuous contact problem should be solved under the following boundary conditions:

$$\sigma_{y} (x,h) = \left\{ \begin{gathered} - p(x)\quad - a < x < a \hfill \\ \quad 0\quad x \le - a,\,\,\,x \ge a \hfill \\ \end{gathered} \right\}$$

(26)

$$\tau_{xy} (x,h) = 0\quad ( - \infty \le x < \infty )$$

(27)

$$v(x,0) = 0\quad \,( - \infty \le x < \infty )$$

(28)

$$\tau_{xy} (x,0) = 0{\kern 1pt} \quad \,( - \infty \le x < \infty )$$

(29)

where $p(x){\kern 1pt}$ is a priori unknown contact stress between the rigid punch and the layer on the contact area $( - a,a)$. Performing the boundary conditions given above, four of the unknown functions $A_{j}$ can be obtained in terms of the unknown function $p(x){\kern 1pt}$ as follows:

$$A_{j} = \frac{1}{\mu }\int\limits_{ - a}^{a} {p(t)} A_{j}^{p} e^{I\alpha t} dt + \rho g\delta (\alpha )A_{j}^{W} \quad (j = 1, \ldots ,4)$$

(30)

The unknown contact pressure $p(x){\kern 1pt}$ is determined based on the following condition:

$$\frac{\partial v(x,h)}{{\partial x}} = \frac{x}{R}\quad ( - a < x < a)$$

(31)

Substituting the $A_{j}$ into the mixed condition (31), the following singular integral equation can be obtained:

$$\frac{1}{\pi }\int\limits_{ - a}^{a} {p(t)} \left[ {\frac{1}{t - x} + k_{1} (x,t)} \right]dt - \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\frac{\mu }{{\varphi_{1} }}} \left[ {\rho gW_{1} (\alpha )\delta (\alpha )} \right]e^{ - I\alpha x} d\alpha = \frac{\mu }{{\varphi_{1} }}\frac{x}{R}$$

(32)

Note that the expressions related to the body forces vanish.

$$\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\delta (\alpha )W_{1} (\alpha )} e^{ - I\alpha x} d\alpha = \mathop {\lim }\limits_{\alpha \to 0} \;W_{1} (\alpha ) = 0$$

(33)

Thus, the singular integral equation is reduced to the following structure:

$$\frac{1}{\pi }\int\limits_{ - a}^{a} {p(t)} \left[ {\frac{1}{t - x} + k_{1} (x,t)} \right]dt = \frac{\mu }{{\varphi_{1} }}\frac{x}{R}$$

(34)

where

$$k_{1} (x,t) = \frac{1}{{\varphi_{1} }}\int\limits_{0}^{\infty } {(M_{1} (\alpha ) - \varphi_{1} } )\sin \alpha (t - x)d\alpha$$

(35)

The expressions for $M_{1} (\alpha )$, $W_{1} (\alpha )$, and $\varphi_{1}$ are given in Appendix A1.

To complete solution of the problem, contact stress $p(x)$ must satisfy the following equilibrium condition:

$$\int\limits_{ - a}^{a} {p(t)} dt = P$$

(36)

The integral Eq. (31) can be solved taking into account the equilibrium condition (36). However, the solution is only valid if the external load is less than $P_{cr}$ ($0 < P < P_{cr} {\kern 1pt}$) which has not been determined yet. Thus, to determine the critical load $P_{cr}$, the contact stress between the layer and foundation $\sigma_{y} (x,0)$ should be evaluated. Substituting the $A_{j}$ into (23), the contact stress on the interface is found as follows:

$$\sigma_{y} (x,0) = \frac{1}{\pi }\int\limits_{ - a}^{a} {p(t)} k_{2} (x,t)dt + \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\delta (\alpha )} \left[ {\rho gW_{2} (\alpha )} \right]e^{ - I\alpha x} d\alpha$$

(37)

Note that

$$\mathop {\lim }\limits_{\alpha \to 0} \;\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\delta (\alpha )W_{2} (\alpha )} e^{ - I\alpha x} d\alpha = - h$$

(38)

Thus, Eq. (37) becomes

$$\sigma_{y} (x,0) = \frac{1}{\pi }\int\limits_{ - a}^{a} {p(t)} k_{2} (x,t)dt - \rho gh$$

(39)

where

$$k_{2} (x,t) = \int\limits_{0}^{\infty } {M_{2} (\alpha )} \cos \alpha (t - x)d\alpha$$

(40)

The expressions for $M_{2} (\alpha )$, $W_{2} (\alpha )$ are given in Appendix A2.

Introducing the following transformations

$$t = ar,\quad x = as$$

(41)

$$\alpha = z/h\quad \phi (r) = \frac{{p(r)}}{\mu }$$

(42)

the integral Eq. (34), the equilibrium condition (36), and the contact stress between the layer and foundation (39) may be expressed in the following forms:

$$\frac{1}{\pi }\int\limits_{ - 1}^{1} {\phi (r)} \left[ {\frac{1}{r - s} + \frac{a}{h}k_{1} (s,r)} \right]dr = \frac{1}{{\varphi_{1} }}\frac{a/h}{{R/h}}s\quad \left| r \right| \le 1$$

(43)

$$\frac{a}{h}\int\limits_{ - 1}^{1} {\phi (r)} dr = \frac{P}{\mu h}$$

(44)

$$\frac{{\sigma_{y} (x,0)}}{\mu } = \frac{1}{\pi }\int\limits_{ - 1}^{1} {\phi (r)} \frac{a}{h}k_{2} (x,r)dr - \frac{\rho gh}{\mu }$$

(45)

Because the contact stress vanishes at the end points $x = - a,$$x = a$, the index of the integral Eq. (43) is −1 (Erdogan 1978). The solution of the integral equation can be expressed as

$$\varphi (r) = G(r)(1 - r^{2} )^{1/2}$$

(46)

By using the Gauss–Chebyshev formulas (Erdogan 1978), the integral Eq. (43) can be converted to the system of algebraic equations as follows:

$$\sum\limits_{i = 1}^{N} {W_{i}^{N} \left[ {\frac{1}{{r_{i} - s_{k} }} + \frac{a}{h}k_{1} (s_{k} ,r_{i} )} \right]} \,G(r_{i} ) = \frac{1}{{\varphi_{1} }}\frac{a/h}{{R/h}}s_{k} \quad k = 1, \ldots N + 1$$

(47)

where $r_{i}$ and $s_{k}$ are the roots of related Chebyshev polynomials and $W_{i}^{N}$ is the weighting constant

$$r_{i} = \cos \left( {\frac{i\pi }{{N + 1}}} \right)\quad i = 1, \ldots N$$

(48)

$$s_{k} = \cos \left( {\frac{\pi }{2}\frac{2k - 1}{{N + 1}}} \right)\quad k = 1, \ldots N + 1$$

(49)

$$W_{i}^{N} = \frac{{1 - r_{i}^{2} }}{N + 1}$$

(50)

Similarly, the equilibrium condition (44) and contact stress between the layer and foundation (45) become

$$\frac{a}{h}\pi \sum\limits_{i = 1}^{N} {W_{i}^{N} g(r_{i} )} = \frac{P}{\mu h}$$

(51)

$$\frac{{\sigma_{y} (x,0)}}{\mu } = \frac{a}{h}\sum\limits_{i = 1}^{N} {W_{i}^{N} k_{2} (x,r_{i} )} \,G(r_{i} ) - \frac{\rho gh}{\mu }$$

(52)

It can be shown that the $N/2 + 1$ equation in (47) is automatically satisfied and results in the symmetry of the contact widths. Therefore, Eqs. (47) and (51) provide $N + 1$ equations to determine the $N + 1$ unknowns $G(r_{i} )$ and $a/h$. The system of equation is linear in terms of the $G(r_{i} )$ but highly nonlinear in terms of variable $a/h$. Therefore, considering the equilibrium condition (51), an iterative method is used to obtain unknowns. In addition, the solution must also ensure that the maximum contact stress between the layer and foundation (47) is equal to “0”:

$$Max[\frac{{\sigma_{y} (x,0)}}{\mu }] = 0$$

(53)

Thus, to find the unknowns, $P_{cr} /(\mu h)$ and $a/h$ are estimated at first. Then, $G(r_{i} )$ can be computed based on (47), and (51) and (53) are checked. The iteration keeps on until the “desired accuracy” obtained in (51) and (53) is reached. The value of $P/(\mu h)$ that satisfies Eq. (53) is the critical load $P_{cr} /(\mu h)$ and corresponding $x/h$ is the location at which the interface separation begins ($x_{cr} /h$).

4 Boundary Conditions and the Singular Integral Equations in the Discontinuous Contact Case

Since the layer and foundation are not bonded to each other, the separation occurs for $P > P_{cr}$. The boundary conditions for the discontinuous moving contact problem can be written as follows:

$$\sigma_{y} (x,h) = \left\{ \begin{gathered} - p(x){\kern 1pt} \quad - a < x < a \hfill \\ \quad 0\quad x \le - a,\,\,\,x \ge a \hfill \\ \end{gathered} \right\}$$

(54)

$$\tau_{xy} (x,h) = 0\quad ( - \infty \le x < \infty )$$

(55)

$$\frac{d}{dx}v(x,0) = f(x)\quad (b \le x < c,\, - c \le x < - b)$$

(56)

$$\tau_{xy} (x,0) = 0\quad \,( - \infty \le x < \infty )$$

(57)

where $f(x)$ is an unknown function that defines the separation between the layer and foundation on the separation region $(b,c)$.

Taking the Fourier transforms of the boundary conditions (54–57), four of the unknown functions $A_{j}$ can be obtained in terms of the unknown functions $p(x){\kern 1pt}$ and $f(x){\kern 1pt}$ as follows:

$$A_{j} = \frac{1}{\mu }\int\limits_{ - a}^{a} {p(t)} A_{j}^{p} e^{I\alpha t} dt + \int\limits_{ - \infty }^{\infty } {f(x)} A_{j}^{m} e^{I\alpha x} dx + \rho g\delta (\alpha )A_{j}^{F}$$

(56)

The unknown functions $p(x){\kern 1pt}$ and $f(x){\kern 1pt}$ will be determined by employing the following conditions:

$$\frac{\partial v(x,h)}{{\partial x}} = \frac{x}{R}\quad ( - a < x < a)$$

(57)

$$\sigma_{y} (x,0) = 0\quad (b \le x < c,\, - c \le x < - b)$$

(58)

Substituting $A_{j}$ into the conditions (57) and (58), the following singular integral equation system is obtained:

$$\begin{gathered} \frac{1}{\pi }\int\limits_{ - a}^{a} {p(t_{1} )} \left[ {\frac{1}{{t_{1} - x_{1} }} + k_{11} (x_{1} ,t_{1} )} \right]dt_{1} + \mu \frac{1}{\pi }\int\limits_{b}^{c} {f(t_{2} )} \left[ {k_{12} (x_{1} ,t_{2} )} \right]dt_{2} \hfill \\ - \frac{\mu }{{\beta_{1} }}\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\delta (\alpha )} \left[ {\rho gW_{11} (\alpha )} \right]e^{{ - I\alpha x_{1} }} d\alpha = \frac{\mu }{{\beta_{1} }}\frac{{x_{1} }}{R} \hfill \\ \end{gathered}$$

(59)

$$\begin{gathered} \frac{1}{\pi }\int\limits_{ - a}^{a} {p(t_{1} )} \left[ {k_{21} (x_{1} ,t_{1} )} \right]dt_{1} + \mu \frac{1}{\pi }\int\limits_{b}^{c} {f(t_{2} )} \left[ {\frac{{\beta_{2} }}{2}\left( {\frac{1}{{t_{2} + x_{2} }} - \frac{1}{{t_{2} - x_{2} }}} \right) + k_{22} (x_{2} ,t_{2} )} \right]dt_{2} \hfill \\ - \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\delta (\alpha )} \left[ {\rho gW_{12} (\alpha )} \right]e^{{ - I\alpha x_{2} }} d\alpha = 0 \hfill \\ \end{gathered}$$

(60)

Note that

$$\mathop {\lim }\limits_{\alpha \to 0} \;\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\delta (\alpha )W_{11} (\alpha )} e^{ - I\alpha x} d\alpha = 0$$

(61)

$$\mathop {\lim }\limits_{\alpha \to 0} \;\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\delta (\alpha )W_{12} (\alpha )} e^{ - I\alpha x} d\alpha = - h$$

(62)

Hence, the singular integral equations become

$$\frac{1}{\pi }\int\limits_{ - a}^{a} {p(t_{1} )} \left[ {\frac{1}{{t_{1} - x_{1} }} + k_{11} (x_{1} ,t_{1} )} \right]dt_{1} + \mu \frac{1}{\pi }\int\limits_{b}^{c} {f(t_{2} )} \left[ {k_{12} (x_{1} ,t_{2} )} \right]dt_{2} = \frac{\mu }{{\beta_{1} }}\frac{{x_{1} }}{R}$$

(63)

$$\frac{1}{\pi }\int\limits_{ - a}^{a} {p(t_{1} )} \left[ {k_{21} (x_{1} ,t_{1} )} \right]dt_{1} + \mu \frac{1}{\pi }\int\limits_{b}^{c} {f(t_{2} )} \left[ {\frac{{\beta_{2} }}{2}\left( {\frac{1}{{t_{2} + x_{2} }} - \frac{1}{{t_{2} - x_{2} }}} \right) + k_{22} (x_{2} ,t_{2} )} \right]dt_{2} = \rho gh$$

(64)

where

$$k_{11} (x_{1} ,t_{1} ) = \frac{1}{{\beta_{1} }}\int\limits_{0}^{\infty } {(M_{11} (\alpha ) - \beta_{1} } )\sin \alpha (t_{1} - x_{1} )d\alpha$$

(65)

$$k_{12} (x_{1} ,t_{2} ) = \frac{1}{{\beta_{1} }}\int\limits_{0}^{\infty } {M_{12} (\alpha )} \cos \alpha x_{1} \cos \alpha t_{2} d\alpha$$

(66)

$$k_{21} (x_{2} ,t_{1} ) = \int\limits_{0}^{\infty } {M_{21} (\alpha )} \cos \alpha (t_{1} - x_{2} )d\alpha$$

(67)

$$k_{22} (x_{2} ,t_{2} ) = \int\limits_{0}^{\infty } {M_{22} (\alpha )} \sin \alpha x_{2} \cos \alpha t_{2} d\alpha$$

(68)

The expressions for $M_{1i} (\alpha )$,$M_{2i} (\alpha )$, $\beta_{i}$ are given in Appendix B.

For a complete solution of the problem, the following equilibrium and single-value conditions must be satisfied:

$$\int\limits_{ - a}^{a} {p(t_{1} )} dt_{1} = P$$

(69)

$$\int\limits_{b}^{c} {f(t_{2} )} dt_{2} = 0$$

(70)

For the numerical solution, the following normalizations are introduced:

$$t_{1} = ar_{1} ,\quad x_{1} = as_{1}$$

(71)

$$t_{2} = \frac{c - b}{2}r_{2} + \frac{c + b}{2},\quad x_{2} = \frac{c - b}{2}s_{2} + \frac{c + b}{2}$$

(72)

$$\phi (r_{1} ) = p(r_{1} )/\mu$$

(73)

Applying the normalizations, the integral equations become

$$\frac{1}{\pi }\int\limits_{ - 1}^{1} {\phi (r_{1} )} \left[ {\frac{1}{{r_{1} - s_{1} }} + \frac{a}{h}k_{11} (s_{1} ,r_{1} )} \right]dr_{1} + \frac{1}{\pi }\int\limits_{ - 1}^{1} {f(r_{2} )} \left[ {\frac{c - b}{{2h}}k_{12} (s_{1} ,r_{2} )} \right]dr_{2} = \frac{1}{{\beta_{1} }}\frac{a/h}{{R/h}}s_{1} \quad \left| {r_{i} } \right| \le 1$$

(74)

$$\frac{1}{\pi }\int\limits_{ - 1}^{1} {\phi (r_{1} )} \left[ {\frac{a}{h}k_{21} (s_{1} ,r_{1} )} \right]dr_{1} + \frac{1}{\pi }\int\limits_{b}^{c} {f(r_{2} )} \left[ {\frac{{\beta_{2} }}{2}\left( {\frac{1}{{r_{2} + s_{2} + 2\frac{c + b}{{c - b}}}} - \frac{1}{{r_{2} - r_{2} }}} \right) + \frac{c - b}{{2h}}k_{22} (s_{2} ,r_{2} )} \right]dr_{2} = \frac{\rho gh}{\mu }$$

(75)

Similarly, the equilibrium and single-value conditions become

$$\frac{a}{h}\int\limits_{ - 1}^{1} {\phi (r)} dr = \frac{P}{\mu h}$$

(76)

$$\int\limits_{ - 1}^{1} {f(r_{2} )} dr_{2} = 0$$

(77)

Because of the smooth contact, at the end points ($\mp a$,$\mp b$, and $\mp c$), the index of the integral Eqs. (74–75) is −1 (Erdogan 1978). The solution of the integral equations can be expressed as

$$\varphi (r_{1} ) = G(r_{1} )(1 - r_{1}^{2} )^{1/2}$$

(78)

$$f(r_{2} ) = H(r_{2} )(1 - r_{2}^{2} )^{1/2}$$

(79)

Applying the Gauss–Chebyshev integration formulas (Erdogan 1978), the integral Eqs. (74–75) can be reduced to the system of algebraic equations as follows:

$$\sum\limits_{\xi = 1}^{N} {W_{\xi }^{N} \left[ {\frac{1}{{r_{\xi } - s_{k} }} + \frac{a}{h}k_{11} (s_{k} ,r_{\xi } )} \right]G(r_{\xi } )} + \sum\limits_{\xi = 1}^{N} {W_{\xi }^{N} \left[ {\frac{c - b}{{2h}}k_{12} (s_{k} ,r_{\xi } )} \right]H(r_{\xi } )} = \frac{1}{{\beta_{1} }}\frac{a/h}{{R/h}}s_{k} \quad k = 1,...N + 1$$

(80)

$$\sum\limits_{\xi = 1}^{N} {W_{\xi }^{N} \left[ {\frac{a}{h}k_{21} (s_{k} ,r_{\xi } )} \right]G(r_{\xi } )} + \sum\limits_{\xi = 1}^{N} {W_{\xi }^{N} \left[ {\frac{{\beta_{2} }}{2}(\frac{1}{{r_{\xi } + s_{k} + 2\frac{c + b}{{c - b}}}} - \frac{1}{{r_{\xi } - s_{k} }}) + \frac{c - b}{{2h}}k_{22} (s_{k} ,r_{\xi } )} \right]H(r_{\xi } )} = \frac{\rho gh}{\mu }\quad k = 1,...N + 1$$

(81)

Similarly, the equilibrium (76) and single-value conditions (77) become

$$\frac{a}{h}\pi \sum\limits_{\xi = 1}^{N} {W_{\xi }^{N} G(r_{\xi } )} = \frac{P}{\mu h}$$

(82)

$$\sum\limits_{\xi = 1}^{N} {W_{\xi }^{N} H(r_{\xi } )} = 0$$

(83)

Since the contact area under the punch is symmetrical, the $N/2 + 1$ equation in (80) is automatically satisfied. In (81), the additional equation (provided by $s_{1} , \ldots s_{N + 1}$) is equivalent to the consistency conditions of the integral equation, and an equation corresponding to one of the $s_{k}$’s will be used to determine $a$,$b$, and $c$ with the equilibrium condition (82) and single-value condition (83). Thus, $2N + 3$ unknowns, which are $G(r_{\xi } )$,$H(r_{\xi } )$, $a,b,c$, can be determined with $2N + 3$ equations. The system of equations is linear in terms of $G(r_{\xi } )$ and $H(r_{\xi } )$ but highly nonlinear in terms of variables $a$,$b$, and $c$. Therefore, an iterative method should be used to obtain unknowns. In the iterative method, random initial values of $a$,$b$, and $c$ are selected first. The system of Eqs. (80–81) is solved for $G(r_{\xi } )$ and $H(r_{\xi } )$ with these values. Then, Eqs. (82), (83), and consistency condition are checked by substituting $G(r_{i} )$ and $H(r_{i} )$ into them. The iteration keeps on until the desired accuracy is obtained. The accuracy selected as $10^{ - 10}$ for the problem and iteration procedure is used based on the Newton–Raphson method.

Once $G(r_{\xi } )$,$H(r_{\xi } )$, $a,b,c$ are determined, the displacement components $v(x,0)$ can be obtained easily.

5 Numerical Results

In this part, numerical results for critical load, initial separation distance, separation regions, displacement on the interface, contact area under the punch, contact stress distributions under the punch and between the layer, and foundation are given for various dimensionless quantities such as moving velocity, body force, punch radius, and external load. Poisson’s ratio is taken as $\nu = 0.25$(that is, $\kappa = 2$) in the following analysis. The values of $\mu$ and $h$ should be considered fixed because they are related to more than one dimensionless quantity.

Note that if the sliding speed is chosen as $V = 0$, this problem is reduced to the static continuous and discontinuous contact problem of a layer (Çömez, 2019). Table 1 presents a comparison of the present study results and the results of Çömez (2019). It is seen that the present results are in line with the results of Çömez (2019).

Table 1 Comparison of the contact area under the punch and separation regions with those from Çömez (2019) $(V^{2} \rho /\mu = 0,\;\rho gh/\mu = \, 1x10^{ - 6} ,\;R/h = 5,\;P/(\mu h) = 0.2 \times 10^{ - 3} )$

Table 2 shows the variation of the critical load, initial separation distance, and contact area under the punch for various values of the moving velocity in the continuous contact case. Enhancing the moving velocity $V$ causes the magnitude of the critical load to be small. In other words, the layer separates from the foundation readily when the punch moves faster. In addition, the contact area under the punch and the initial separation distance decrease with the increasing moving velocity. Table 3 shows the variation of the critical load, initial separation distance, and contact area under the punch for various values of the punch radius $R$. Increasing the punch radius ($R$) provides a wider contact area under the punch. As seen in Table 3, the magnitude of the critical load and initial separation distance does not change with the punch radius.

Table 2 Variations of the contact width under the punch $a/h$, initial separation distance $x_{cr} /h$ and critical load $P_{cr} /(\mu h)$ versus the moving velocity $V^{2} \rho /\mu$ $(\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;R/h = 5,\;\kappa = 2)$ (continuous contact)

Table 3 Variations of the contact width under the punch $a/h$, initial separation distance $x_{cr} /h$ and critical load $P_{cr} /(\mu h)$ versus the punch radius $R/h$ $(\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;V^{2} \rho /\mu = 0.4,\;\kappa = 2)$ (continuous contact)

Figures 3, 4 and 5 delineate the contact stress distribution under the punch and between the layer and rigid foundation when the external load is less than the critical load. Note that contact stress between the layer and foundation equals the body force when the distance from the external load increases. From Fig. 3, it can be concluded that the contact stress under the punch decreases when the punch moves faster. An inverse relation can be observed in terms of the contact stress between the layer and foundation. Unlike other parameters, both the contact area and contact stress under the punch increase with the increase in the external load (Fig. 4). Note that the fact that the maximum value of the contact stress between the layer and foundation is zero for the critical load confirms the solution.

Fig. 3

Variations of the contact stress under the punch $p(x)/\mu$ and between the layer and substrate $\sigma_{y} (x,0)/\mu$ versus the moving velocity $V^{*} = V^{2} \rho /\mu$ $(P/(\mu h) = 0.1 \times 10^{ - 6} ,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;R/h = 5)$ (continuous contact)

Fig. 4

Variations of the contact stress under the punch $p(x)/\mu$ and between the layer and substrate $\sigma_{y} (x,0)/\mu$ versus the external load $P^{*} = P/(\mu h)$$(V^{2} \rho /\mu = 0.4,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;R/h = 5)$(continuous contact)

Fig. 5

Variations of the contact stress under the punch $p(x)/\mu$ and between the layer and substrate $\sigma_{y} (x,0)/\mu$ versus the punch radius $R^{*} = R/h$$(V^{2} \rho /\mu = 0.4,\;P/(\mu h) = 0.1 \times 10^{ - 6} ,\;\rho gh/\mu = 0.5 \times 10^{ - 6} )$ (continuous contact)

Figure 5 shows the variation of the contact stresses for various values of the punch radius $R$. When the punch radius increases, the external load is distributed over a larger area, and as a result, the peak value of the contact stress under the punch decreases. Another interesting result is that the contact stress between the layer and foundation does not change with the punch radius.

Table 4 shows the variation of the contact area under the punch and separation regions depending on the external load in the discontinuous contact case. When the external load increases, the punch penetrates the layer more, and the contact area under the punch increases. The layer begins to separate from the layer easily with increasing external load values, and consequently, $b/h$ decreases and $c/h$ increases. Note that if the external load equals the critical load, the separation region closes (that is, $b/h = c/h$).

Table 4 Variation of the contact area under the punch and separation regions for various values of external load $(V^{2} \rho /\mu = 0.4,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;R/h = 5)$(discontinuous contact)

The variation of the contact area under the punch and separation regions with moving velocity is given in Table 5. When the punch moves faster, contact area under the punch increases and the separation starts more easily. Table 6 shows the variation of the contact area and separation region with punch radius. Note that the punch radius has not any influence on the separation region. However, the contact area under the punch increases with increasing values of the punch radius.

Table 5 Variation of the contact area under the punch and separation regions for various values of moving velocity $(P/(\mu h) = 30 \times 10^{ - 6} ,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;R/h = 5)$(discontinuous contact)

Table 6 Variation of the contact area under the punch and separation regions for various values of punch radius $(P/(\mu h) = 30 \times 10^{ - 6} ,\;V^{2} \rho /\mu = 0.2,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6} )$(discontinuous contact)

The variations of the contact stress between the punch and the layer $p(x)/\mu$, separation function $f(x)$, contact stress between the layer and foundation $\sigma_{y} (x,0)/\mu$, and the displacements on the interface $v(x,0)/h$ versus load $P^{*} = P/(\mu h)$ are shown in Fig. 6. Note that, unlike other parameters, both the peak values of the contact stress under the punch and the contact area increase with increasing values of the external load (Fig. 6a). The derivation of the vertical displacement $f(x)$ that defines the separation between the layer and foundation on the separation region $(b,c)$ is not symmetrical (Fig. 6b). Thus, in the second integral equation, the N/2 + 1 equation should be considered as done in this study. The larger the value of external load, the longer the separation region (Fig. 6c). As expected, the vertical displacement $v(x,0)$ increases with the increasing values of the external load. Note that if the external load is equal to the critical load, the separation closes, and vertical displacement does not occur, as expected.

Fig. 6

Variations of the contact stress between the punch and the upper layer $p(x)/\mu$, $f(x)$, contact stress between the layer and substrate $\sigma_{y} (x,0)/\mu$, the displacements on the interface $v(x,0)/h$ versus load $P^{*} = P/(\mu h)$ with fixed parameters $V^{2} \rho /\mu = 0.4,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;R/h = 5$. $(P_{cr} = {6}{\text{.837585x10}}^{{ - 6}} )$ (discontinuous contact)

Figure 7 shows the variations of the contact stress between the punch and the layer $p(x)/\mu$, separation function $f(x)$, contact stress between the layer and foundation $\sigma_{y} (x,0)/\mu$, and the displacements on the interface $v(x,0)/h$ with the moving velocity $V^{2} \rho /\mu$. The peak values of the contact stress under the punch decrease when the punch moves faster (Fig. 7a). The separation region spreads with increasing values of moving velocity, and large displacement occurs at the interface (Fig. 7b–d). As the punch radius increases, the stress distributes over a wider area, and consequently, the peak values of the contact stress decrease (Fig. 8a). Note that the contact stress and vertical displacement at the interface do not change with the punch radius (Fig. 8b–d).

Fig. 7

Variations of the contact stress between the punch and the upper layer $p(x)/\mu$, $f(x)$, contact stress between the layer and substrate $\sigma_{y} (x,0)/\mu$, the displacements on the interface $v(x,0)/h$ versus moving velocity $V^{*} = V^{2} \rho /\mu$ with fixed parameters $P/(\mu h) = 30 \times 10^{ - 6} ,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6} ,\;R/h = 5$ (discontinuous contact)

Fig. 8

Variations of the contact stress between the punch and the upper layer $p(x)/\mu$, $f(x)$, contact stress between the layer and substrate $\sigma_{y} (x,0)/\mu$, the displacements on the interface $v(x,0)/h$ versus punch radius $R^{*} = R/h$ with fixed parameters $P/(\mu h) = 30 \times 10^{ - 6} ,\;V^{2} \rho /\mu = 0.2,\;\rho gh/\mu = \, 0.5 \times 10^{ - 6}$ (discontinuous contact)

6 Conclusions

In this study, the dynamic continuous and discontinuous contact problems were discussed in the framework of the linear elasticity theory. The layer was indented by a rigid cylindrical punch, and body force was taken into account. General stress and displacement expressions for the moving continuous and discontinuous contact problems were obtained without using the superposition technique. Based on this study, the following conclusions can be outlined:

• 1. The critical load decreases when the moving velocity increases; that is, the layer easily separates from the foundation when the punch moves faster.

• 2. Both the contact area under the punch and the initial separation distance decrease when the punch moves faster.

• 3. The separation region and vertical displacement at the interface increase when the punch moves faster.

• 4. The punch radius does not influence the contact stress and vertical displacement at the interface.

• 5. Unlike other parameters, both the peak values of the contact stress and the contact area between the punch and layer increase with increasing values of the external load.

Appendices

Appendix

1.1 A1

The expressions of $M_{1} (\alpha )$, $W_{1} (\alpha )$, and $\varphi_{1}$ appearing in (26–29) and (32) are given as follows:

$$M_{1} (\alpha ) = - \mathop {\lim }\limits_{y \to 0} \;\alpha \sum\limits_{j = 1}^{4} {A_{j}^{p} e^{{n_{j} \left| \alpha \right|y}} }$$

(84)

$$W_{1} (\alpha ) = - \mathop {\lim }\limits_{y \to 0} \;\alpha \left( {\alpha \sum\limits_{j = 1}^{4} {A_{j}^{F} e^{{n_{j} \left| \alpha \right|y}} } - \frac{\rho g/\mu }{{\alpha^{2} (1 - V^{2} \rho /\mu )}}\delta (\alpha )} \right)$$

(85)

$$\varphi_{1} = \mathop {\lim }\limits_{\alpha \to \infty } \;M_{1} (\alpha )$$

(86)

1.2 A2

The expressions for $M_{21} (\alpha )$ and $W_{2i} (\alpha )$ appearing in (34) and (37) are given as follows:

$$M_{2} (\alpha ) = {\text{Re}} \left[ {\mathop {\lim }\limits_{y \to 0} \;\left| \alpha \right|\left[ {2A_{1}^{p} n_{1} e^{{n_{1} \left| \alpha \right|y}} - 2A_{2}^{p} n_{2} e^{{n_{2} \left| \alpha \right|y}} - A_{3}^{p} \frac{1}{{n_{3} }}m_{2} e^{{n_{3} \left| \alpha \right|y}} + A_{4}^{p} \frac{1}{{n_{4} }}m_{2} e^{{n_{4} \left| \alpha \right|y}} } \right]} \right]$$

(87)

$$W_{2} (\alpha ) = {\text{Re}} \left[ {\mathop {\lim }\limits_{y \to 0} \;\left| \alpha \right|\left[ {2A_{1}^{F} n_{1} e^{{n_{1} \left| \alpha \right|y}} - 2A_{2}^{F} n_{2} e^{{n_{2} \left| \alpha \right|y}} - A_{3}^{F} \frac{1}{{n_{3} }}m_{2} e^{{n_{3} \left| \alpha \right|y}} + A_{4}^{F} \frac{1}{{n_{4} }}m_{2} e^{{n_{4} \left| \alpha \right|y}} } \right]} \right]$$

(88)

Appendix B

The expressions of $M_{1i} (\alpha )$,$M_{2i} (\alpha )$, $\beta_{i}$ ($i = 1,2$) appearing in (66–68) are given as follows:

$$M_{11} (\alpha ) = \mathop {\lim }\limits_{y \to 0} \;\alpha (A_{1}^{p} e^{{n_{1} \left| \alpha \right|y}} + A_{2}^{p} e^{{n_{2} \left| \alpha \right|y}} + A_{3}^{p} e^{{n_{3} \left| \alpha \right|y}} + A_{4}^{p} e^{{n_{4} \left| \alpha \right|y}} )$$

(89)

$$M_{12} (\alpha ) = 2{\text{Re}} [\mathop {\lim }\limits_{y \to 0} \;\alpha (A_{1}^{m} e^{{n_{1} \left| \alpha \right|y}} + A_{2}^{m} e^{{n_{2} \left| \alpha \right|y}} + A_{3}^{m} e^{{n_{3} \left| \alpha \right|y}} + A_{4}^{m} e^{{n_{4} \left| \alpha \right|y}} )]$$

(90)

$$M_{21} (\alpha ) = \mu {\text{Re}} \left[ {\mathop {\lim }\limits_{y \to 0} \left| \alpha \right|(2A_{1}^{p} n_{1} e^{{n_{1} \left| \alpha \right|y}} - 2A_{2}^{p} n_{2} e^{{n_{2} \left| \alpha \right|y}} - A_{3}^{p} \frac{1}{{n_{3} }}m_{2} e^{{n_{3} \left| \alpha \right|y}} + A_{4}^{p} \frac{1}{{n_{4} }}m_{2} e^{{n_{4} \left| \alpha \right|y}} )} \right]$$

(91)

$$M_{21} (\alpha ) = 2\mu {\text{Im}} \left[ {\mathop {\lim }\limits_{y \to 0} \left| \alpha \right|(2A_{1}^{p} n_{1} e^{{n_{1} \left| \alpha \right|y}} - 2A_{2}^{p} n_{2} e^{{n_{2} \left| \alpha \right|y}} - A_{3}^{p} \frac{1}{{n_{3} }}m_{2} e^{{n_{3} \left| \alpha \right|y}} + A_{4}^{p} \frac{1}{{n_{4} }}m_{2} e^{{n_{4} \left| \alpha \right|y}} )} \right]$$

(92)

$$\beta_{1} = \mathop {\lim }\limits_{\alpha \to \infty } \;M_{11} (\alpha )$$

(93)

$$\beta_{2} = \mathop {\lim }\limits_{\alpha \to \infty } \;M_{22} (\alpha )$$

(94)