Analytical solution to continuous contact problem for a functionally graded layer loaded through two dissimilar rigid punches

Abstract

A continuous contact problem of functionally graded layer resting on an elastic semi-infinite plane, which is loaded with through two different blocks is addressed in this study. The elasticity theory and integral transformation techniques are used in solution of the problem. The problem is reduced to a system of singular integral equations, and solved numerically by the aid of appropriate Gauss–Chebyshev integration formula. It is assumed that the elastic semi-infinite homogeneous plane is isotropic and all surfaces are frictionless and continuous. The shear modulus and the mass density of the FG layer vary exponentially along the thickness direction.

1 Introduction

The contact problems have found a wide application area in various engineering disciplines. The building and machine elements in particular, are made up of systems that contain contact. Knowing of the character and length of contact as well as stress distribution over the contact area in these systems provide convenience in design and production of materials for engineers.

New generation materials with improved physical and mechanical properties are used for today’s structures, which are more complex than older ones. Composite materials, which combine the best properties of more than one material in particular, provide an ideal solution at this point. In this respect, functionally graded materials (FGM), which functionally change from one surface of the material to the other, have begun to be used.

Functionally graded materials are widely preferred especially in aerospace, defense and automotive industries due to their thermal resistance and high strength properties. Various studies have been done about FG layers in recent years.

Giannakopoulos and Suresh studied contact stresses in axial symmetric functionally graded materials loaded with frictionless flat, conical, and spherical rigid pointed tips [1]. Dağ and Erdoğan solved the contact and surface cracks problems of a semi-infinite functionally graded plane under the effect of frictional rigid punch with any profile [2]. Güler and Erdoğan solved the contact problem of a functionally graded coating on a homogeneous body [3]. El Borgi et al. examined the receding contact problem between a functionally graded layer and a homogeneous layer in their study [4]. Ke and Wang examined the moving and frictional contact problem of an elastic half-plane covered with a functionally graded layer [5]. Yang and Ke analytically examined the two-dimensional contact problem of a functionally graded layer, which is covered by a homogeneous layer loaded through a rigid cylindrical punch and resting on an elastic semi-infinite plane [6]. Dağ examined fracture and contact mechanics of orthotropic functionally graded materials [7]. Rekik et al. analytically studied a crack problem of a functionally graded layer on a homogeneous semi-infinite plane [8]. Elloumi et al. addressed a two-dimensional nonlinear sliding contact problem between a nonhomogeneous and isotropic functionally graded half-plane and an arbitrarily shaped punch subjected to normal load [9]. Rhimi et al. analytically analyzed the axial symmetric double receding contact problem of an elastic functionally graded layer loaded with a rigid spherical punch and resting on a homogeneous half-plane [10]. Küçüksucu performed the analysis of the contact mechanics of orthotropic graded materials [11]. Güler et al. investigated the contact mechanics of thin films bonded to functionally graded coatings both mechanically and numerically [12]. El Borgi et al., analyzed the frictional and receding contact problem of a FGM layer resting on a homogeneous plane [13]. Yaylacı et al. compared the results by solving a receding contact problem according to the elasticity theory and the finite element method [14]. Chen et al. examined the frictional contact problem of a functionally graded layer directed randomly, and cylindrical punches [15]. Çömez examined the contact problem of a functionally graded layer loaded by means of a moving rigid block [16]. Liu et al. made the axial symmetric stress analysis of the receding contact problem belonging to functionally graded with random gradation loaded by a circular and rectangular block, separately [17]. Güler et al. examined the frictional contact problem of a cylindrical rigid punch sliding on a cylindrical functionally graded orthotropic medium [18]. Öner et al. solved the symmetric and continuous contact problem of the functionally graded layer resting on an elastic semi-infinite plane loaded by a rigid block according to the elasticity theory [19]. Polat et al. analyzed the frictionless and continuous contact problem of a FG layer lying over an elastic semi-infinite plane by the finite element method [20, 21]. Kaya et al. solved the continuous contact problem on a FG layer loaded with three flat rigid blocks and resting on an elastic semi-infinite plane by the finite element method [22].

When the literature is examined in general, it can be seen that there are various studies about the contact problem of FG layers. The main purpose of this study is to analytically investigate how the stress distribution of a FG layer loaded by two different blocks changes depending on the interaction between the blocks, and calculate the first separation loads and distances, accordingly. These calculations are done according to an exponential change both the shear modulus and mass density of the FG layer. The elasticity theory and Fourier integral transform technique are used for the solution of the problem. The problem is reduced to a system of singular integral equations, and solved numerically with the appropriate Gauss–Chebyshev qaudrature.

2 Formulation of continuous contact problem

2.1 Case without the body forces

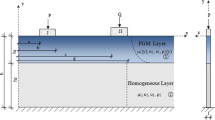
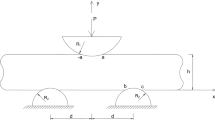
Geometry of the continuous contact problem is given in Fig. 1. This study includes the solution of the continuous contact problem of a functionally graded layer resting on a homogeneous half-plane, loaded with two blocks according to the elasticity theory. It is assumed that all surfaces are frictionless and the width of the layer is unit. FG layer extends in the range of $( - \,\infty , + \,\infty )$. It is assumed that the blocks are rigid and the contact surfaces can only transmit the compressive stresses. Shear modulus change of the FG layer material along its height h;

$$\mu_{1} (y) = \mu_{0} e^{\beta y} \quad - h < y \le 0$$

(1)

where $\mu_{0}$ is the shear modulus on the upper surface of the layer. $\beta$ is a non-zero inhomogeneity parameter of the FG material.

Fig. 1

FG layer loaded with two rigid flat blocks resting on the elastic semi-infinite plane

Equilibrium equations when the body forces are neglected are written as follows:

$$\frac{{\partial \sigma_{1x} }}{\partial x} + \frac{{\partial \tau_{1xy} }}{\partial y} = 0$$

(2)

$$\frac{{\partial \tau_{1yx} }}{\partial x} + \frac{{\partial \sigma_{1y} }}{\partial y} = 0$$

(3)

Stress–strain expressions can be written as

$$\sigma_{1x} = \frac{{\mu_{1} \left( y \right)}}{{\kappa_{1} - 1}}\left[ {\left( {\kappa_{1} + 1} \right)\frac{{\partial u_{1} }}{\partial x} + \left( {3 - \kappa_{1} } \right)\frac{{\partial v_{1} }}{\partial y}} \right]$$

(4)

$$\sigma_{1y} = \frac{{\mu_{1} \left( y \right)}}{{\kappa_{1} - 1}}\left[ {\left( {3 - \kappa_{1} } \right)\frac{{\partial u_{1} }}{\partial x} + \left( {\kappa_{1} + 1} \right)\frac{{\partial v_{1} }}{\partial y}} \right]$$

(5)

$$\tau_{1xy} = \mu_{1} \left( y \right)\left[ {\frac{{\partial u_{1} }}{\partial y} + \frac{{\partial v_{1} }}{\partial x}} \right]$$

(6)

u₁ and v₁ in Eqs. (4–6), denote the displacements in the x- and y- directions, respectively, and $\kappa$ denotes the Kolosov constant, which is taken to be $3 - 4\upsilon$ in plane strain problems. It is also assumed that the Poisson’s ratio ($\upsilon$) does not change. Substituting Eqs. (4–6) into Eqs. (2, 3), after some manipulations, following equations are obtained:

$$\begin{aligned} & \left( {\kappa_{1} + 1} \right)\frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} + \left( {\kappa_{1} - 1} \right)\frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} + 2\frac{{\partial^{2} v_{1} }}{\partial x\partial y} \\ & \quad + \,\beta \left( {\kappa_{1} - 1} \right)\frac{{\partial u_{1} }}{\partial y} + \beta \left( {\kappa_{1} - 1} \right)\frac{{\partial v_{1} }}{\partial x} = 0 \\ \end{aligned}$$

(7)

$$\begin{aligned} & \left( {\kappa_{1} - 1} \right)\frac{{\partial^{2} v_{1} }}{{\partial x^{2} }} + \left( {\kappa_{1} + 1} \right)\frac{{\partial^{2} v_{1} }}{{\partial y^{2} }} + 2\frac{{\partial^{2} u_{1} }}{\partial x\partial y} \\ & \quad + \beta \left( {3 - \kappa_{1} } \right)\frac{{\partial u_{1} }}{\partial x} + \beta \left( {\kappa_{1} + 1} \right)\frac{{\partial v_{1} }}{\partial y} = 0 \\ \end{aligned}$$

(8)

That the Navier equations given above form a set of partial differential equations makes the solution difficult. Navier equations are converted from a set of partial differential equations into a set of ordinary differential equations by applying Fourier integral transform to the displacement statements u₁ and v₁ in order to make the solution easier. Fourier transform of displacements;

$$u_{1} \left( {x,y} \right) = \frac{1}{2\pi }\mathop \int \limits_{ - \infty }^{ + \infty } \phi_{1} \left( {\xi ,y} \right)e^{i\xi x} d\xi$$

(9)

$$v_{1} \left( {x,y} \right) = \frac{1}{2\pi }\mathop \int \limits_{ - \infty }^{ + \infty } \psi_{1} \left( {\xi ,y} \right)e^{i\xi x} d\xi$$

(10)

Inverse Fourier transform of these statements are obtained as follows;

$$\phi_{1} \left( {\xi ,y} \right) = \mathop \int \limits_{ - \infty }^{ + \infty } u_{1} \left( {x,y} \right)e^{ - i\xi x} dx$$

(11)

$$\psi_{1} \left( {\xi ,y} \right) = \mathop \int \limits_{ - \infty }^{ + \infty } v_{1} \left( {x,y} \right)e^{ - i\xi x} dx$$

(12)

where $\xi$ indicates the transform variable. Substituting the statements in (11, 12) are applied to the Navier Eqs. (7) and (8), following sets of ordinary differential equations are obtained:

$$\begin{aligned} & - (\kappa_{1} + 1)\xi^{2} \phi_{1} + (\kappa_{1} - 1){\kern 1pt} \frac{{d^{2} \phi_{1} }}{{dy^{2} }} + 2i\xi {\kern 1pt} {\kern 1pt} \frac{{d\psi_{1} }}{dy} \\ & \quad + \,\beta (\kappa_{1} - 1){\kern 1pt} \frac{{d\phi_{1} }}{dy} + \beta (\kappa_{1} - 1){\kern 1pt} i\xi {\kern 1pt} \psi_{1} {\kern 1pt} = 0 \\ \end{aligned}$$

(13)

$$\begin{aligned} & - (\kappa_{1} - 1)\xi^{2} \psi_{1} + (\kappa_{1} + 1){\kern 1pt} \frac{{d^{2} \psi_{1} }}{{dy^{2} }} + 2i\xi {\kern 1pt} {\kern 1pt} \frac{{d\phi_{1} }}{dy} \\ & \quad + \,\beta (\kappa_{1} + 1){\kern 1pt} \frac{{d\psi_{1} }}{dy}{\kern 1pt} {\kern 1pt} {\kern 1pt} + \beta (3 - \kappa_{1} ){\kern 1pt} i\xi {\kern 1pt} \phi_{1} {\kern 1pt} = 0 \\ \end{aligned}$$

(14)

The solution of the differential equation system can be in the form:

$$\phi_{1} = \sum\limits_{j = 1}^{4} {M_{j} {\kern 1pt} e^{{s_{j} y}} }$$

(15)

$$\psi_{1} = \sum\limits_{j = 1}^{4} {M_{j} n_{j} e^{{s_{j} y}} }$$

(16)

where $M_{j} (j = 1, \ldots ,4)$ in these statements are unknown constants and will be obtained by use of the boundary conditions of the problem. Substituting Eqs. (15) and (16) into Eqs. (13) and (14), the characteristic equation is obtained as follows:

$$(s^{2} + \beta s - \xi^{2} )^{2} + \xi^{2} \beta^{2} \left( {\frac{{3 - \kappa_{1} }}{{\kappa_{1} + 1}}} \right) = 0$$

(17)

Roots of the characteristic equation are obtained as follows:

$$s_{1} = - \frac{1}{2}\beta - \frac{1}{2}\sqrt {4\xi^{2} + \beta^{2} + 4i\xi \eta }$$

(18)

$$s_{2} = - \frac{1}{2}\beta - \frac{1}{2}\sqrt {4\xi^{2} + \beta^{2} - 4i\xi \eta }$$

(19)

$$s_{3} = - \frac{1}{2}\beta + \frac{1}{2}\sqrt {4\xi^{2} + \beta^{2} + 4i\xi \eta }$$

(20)

$$s_{4} = - \frac{1}{2}\beta + \frac{1}{2}\sqrt {4\xi^{2} + \beta^{2} - 4i\xi \eta }$$

(21)

where $\eta$ is defined as:

$$\eta = \left| \beta \right|\sqrt {\frac{{3 - \kappa_{1} }}{{1 + \kappa_{1} }}}$$

(22)

In Eq. (16), $n_{j} {\kern 1pt} (j = 1, \ldots ,4)$ is defined as follows:

$$n_{j} = \frac{{ - 2\xi is_{j} + \xi i\beta (\kappa_{1} - 3)}}{{\xi^{2} i^{2} (\kappa_{1} - 1) + (\kappa_{1} + 1)\left( {s_{j} \beta + s_{j}^{2} } \right)}}$$

(23)

Thus, the general equations for displacements and stresses of the FG layer are obtained as

$$u_{1h} (x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\sum\limits_{j = 1}^{4} {M_{j} {\kern 1pt} e^{{s_{j} y + i\xi x}} } } d\xi$$

(24)

$$v_{{1_{hm} }} (x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\sum\limits_{j = 1}^{4} {M_{j} {\kern 1pt} n_{j} e^{{s_{j} y + i\xi x}} } } d\xi$$

(25)

$$\sigma_{{1x_{hm} }} (x,y) = \frac{{\mu_{1} (y)}}{{(\kappa_{1} - 1)}}\frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\sum\limits_{j = 1}^{4} {\left[ \begin{aligned} i\xi (\kappa_{1} + 1) + \hfill \\ (3 - \kappa_{1} )n_{j} s_{j} \hfill \\ \end{aligned} \right]} } M_{j} e^{{s_{j} y + i\xi x}} d\xi$$

(26)

$$\sigma_{{1y_{hm} }} (x,y) = \frac{{\mu_{1} (y)}}{{(\kappa_{1} - 1)}}\frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\sum\limits_{j = 1}^{4} {\left[ \begin{aligned} i\xi (3 - \kappa_{1} ) + \hfill \\ (\kappa_{1} + 1)n_{j} s_{j} \hfill \\ \end{aligned} \right]} } M_{j} e^{{s_{j} y + i\xi x}} d\xi$$

(27)

$$\tau_{{1xy_{hm} }} (x,y) = \mu_{1} (y)\frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\sum\limits_{j = 1}^{4} {\left[ {s_{j} + i\xi n_{j} } \right]} } M_{j} e^{{s_{j} y + i\xi x}} d\xi$$

(28)

The solution of homogeneous elastic plane is also found in the same way, and given by

$$u_{{2_{hm} }} (x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\left[ {A_{3} \frac{\left| \xi \right|}{\xi } + A_{4} \left( {\frac{\kappa }{\xi } + \frac{\left| \xi \right|}{\xi }y} \right)} \right]} {\kern 1pt} {\kern 1pt} ie^{\left| \xi \right|y + i\xi x} d\xi$$

(29)

$$v_{{2_{hm} }} (x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\left[ {A_{3} + A_{4} y} \right]} {\kern 1pt} {\kern 1pt} e^{\left| \xi \right|y + i\xi x} d\xi$$

(30)

$$\sigma_{{2x_{hm} }} = - \frac{{\mu_{2.} }}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\left\{ {2A_{3} \left| \xi \right| + A_{4} \left[ {\left( {\kappa_{2} + 3} \right) + 2\left| \xi \right|y} \right]} \right\}} {\kern 1pt} e^{\left| \xi \right|y + i\xi x} d\xi$$

(31)

$$\sigma_{{2y_{hm} }} = \frac{{\mu_{2} }}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\left\{ {2A_{3} \left| \xi \right| + A_{4} \left[ {\left( {\kappa_{2} - 1} \right) + 2\left| \xi \right|y} \right]} \right\}} {\kern 1pt} e^{\left| \xi \right|y + i\xi x} d\xi$$

(32)

$$\tau_{{2xy_{hm} }} = \frac{{i\mu_{2.} }}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\left\{ {2\xi A_{3} + A_{4} \left[ {\left( {\kappa_{2} + 1} \right)\frac{\left| \xi \right|}{\xi } + 2\xi y} \right]} \right\}} {\kern 1pt} e^{\left| \xi \right|y + i\xi x} d\xi$$

(33)

The indices 1 and 2 in these equations represent the FG layer and the homogeneous semi-infinite plane, respectively, and the hm represents the state where the body forces are neglected. In addition, $\mu_{2}$ and $\kappa_{2}$ are the shear modulus of the semi-infinite plane and the Kolosov constant, respectively.

2.2 Case with the body forces of functionally graded layer

The general expressions for the functionally graded layer under the influence of body forces are found in this section. The body forces of the layer are taken as X = 0 and $Y = - \rho_{1} (y)g$. In these equations, g represents the acceleration of the gravity, $\rho_{1} (y)$ represents the density of the functionally graded layer and given by

$$\rho_{1} (y) = \rho_{0} \,e^{\gamma y}$$

(34)

where $\rho_{0}$ indicates the density of the layer at y =0 and $\gamma$ indicates the density parameters that vary along the layer thickness.

Equilibrium equations when the body forces are taken into account are given by

$$\frac{{\partial \sigma_{1x} }}{\partial x} + \frac{{\partial \tau_{1xy} }}{\partial y} + X = 0$$

(35)

$$\frac{{\partial \tau_{1yx} }}{\partial x} + \frac{{\partial \sigma_{1y} }}{\partial y} + Y = 0$$

(36)

The stress components of the functionally graded layer are given in Eqs. (4–6). If the derivatives of the stress statements in Eqs. (4–6) are taken and rewritten in Eqs. (35, 36), the Navier equations are as follows;

$$\begin{aligned} & \left( {\kappa_{1} + 1} \right)\frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} + \left( {\kappa_{1} - 1} \right)\frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} + 2\frac{{\partial^{2} v_{1} }}{\partial x\partial y} \\ & \quad + \beta \left( {\kappa_{1} - 1} \right)\frac{{\partial u_{1} }}{\partial y} + \beta \left( {\kappa_{1} - 1} \right)\frac{{\partial v_{1} }}{\partial x} = 0 \\ \end{aligned}$$

(37)

$$\begin{aligned} & \left( {\kappa_{1} - 1} \right)\frac{{\partial^{2} v}}{{\partial x^{2} }} + \left( {\kappa_{1} + 1} \right)\frac{{\partial^{2} v}}{{\partial y^{2} }} + 2\frac{{\partial^{2} u}}{\partial x\partial y} \\ {\kern 1pt} & \quad + \,\beta \left( {3 - \kappa_{1} } \right)\frac{\partial u}{\partial x} + \beta \left( {\kappa_{1} + 1} \right)\frac{\partial v}{\partial y} = {\kern 1pt} \frac{{\rho_{0\,} e^{{\left( {\gamma - \beta } \right)y}} g\left( {\kappa_{1} - 1} \right)}}{{\mu_{0} e^{\beta y} }} \\ \end{aligned}$$

(38)

The displacement statements in these equations are taken as u = u(x) and v = v(y).

The boundary conditions are as follows:

$$u_{1} \left( 0 \right) = 0$$

(39)

$$v_{1} \left( { - h} \right) = 0$$

(40)

$$\sigma_{1y} = \int\limits_{y}^{0} { - \rho_{0} g{\kern 1pt} {\kern 1pt} e^{\gamma y} {\kern 1pt} dy}$$

(41)

$$\int\limits_{ - h}^{0} {\sigma_{1x} dy} = 0$$

(42)

Thus in the Eq. (43) the required stress statement $\sigma_{y} (x,y)$ is generally obtained by adding the body forces.

$$\begin{aligned} \sigma _{{1y}} (x,y) & = \left\{ {\begin{array}{*{20}l} {2P\frac{{e^{{\beta y}} }}{{\kappa _{1} - 1}}\int\limits_{0}^{{ + \infty }} {\sum\limits_{{j = 1}}^{4} {\left[ {i\xi \left( {3 - \kappa _{1} } \right) + \left( {\kappa _{1} + 1} \right)n_{j} s_{j} } \right]M_{j} e^{{s_{j} y}} \left[ {\cos \xi \left( {t - x} \right)} \right]d\xi } } } \hfill \\ {\quad + 2Q\frac{{e^{{\beta y}} }}{{\kappa _{1} - 1}}\int\limits_{0}^{{ + \infty }} {\sum\limits_{{j = 1}}^{4} {\left[ {i\xi \left( {3 - \kappa _{1} } \right) + \left( {\kappa _{1} + 1} \right)n_{j} s_{j} } \right]M_{j} e^{{s_{j} y}} \left[ {\cos \xi \left( {t - x} \right)} \right]d\xi } } } \hfill \\ \end{array} } \right\} + \frac{{\rho _{0} g\left( {e^{{\gamma y}} - 1} \right)}}{\gamma } \\ & \quad - h < y \le 0 \\ \end{aligned}$$

(43)

2.3 Numerical solution of singular integral equation

The boundary conditions of the problem can be written as

$$\tau_{1xy} (x,0) = 0\quad - \infty < x < \infty$$

(44)

$$\tau_{1xy} (x, - h) = 0\quad - \infty < x < \infty$$

(45)

$$\tau_{2xy} (x, - h) = 0\quad {\kern 1pt} - \infty < x < \infty$$

(46)

$$\sigma_{1y} (x,0) = \left\{ {\begin{array}{*{20}l} { - p(x)} \hfill & {a < x < b} \hfill \\ { - q(x)} \hfill & {c < x < d} \hfill \\ 0 \hfill & {b \le x \le c} \hfill \\ 0 \hfill & { - \infty < x \le a} \hfill \\ 0 \hfill & {d < x \le + \infty } \hfill \\ \end{array} } \right\}$$

(47)

$$\sigma_{{1y_{{}} }} (x, - h) = \sigma_{2y} (x, - h)\quad - \infty < x < \infty$$

(48)

$$\frac{\partial }{\partial x}{\kern 1pt} \left[ {v_{1} (x, - h) - v_{2} (x, - h)} \right]{\kern 1pt} = 0\quad - \infty < x < \infty$$

(49)

$$\frac{\partial }{\partial x}{\kern 1pt} \left[ {v_{1} (x,0)} \right]{\kern 1pt} = 0\quad a < x < b$$

(50)

$$\frac{\partial }{\partial x}{\kern 1pt} \left[ {v_{1} (x,0)} \right]{\kern 1pt} = 0\quad c < x < d$$

(51)

$M_{j} (j = 1, \ldots ,4)$ and $A_{j} (j = 3,4)$ constants are obtained by Eqs. (44–49) in terms of the unknown contact stresses under the rigid blocks.

Unknowns $p\left( x \right)$ and $q\left( x \right)$ will be obtained by solving the integral equation which will be found by using boundary conditions (50) and (51). Singular integral equations for $p\left( x \right)$ and $q\left( x \right)$ are obtained after some simple manipulations as follows;

$$\begin{aligned} & - \frac{1}{{\pi \,\mu_{0} }}\int\limits_{a}^{b} {p(t)dt\left[ {k_{1}^{*} (x,t) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{t - x}} \right]} \\ & \quad - \frac{1}{{\pi \,\mu_{0} }}\int\limits_{c}^{d} {q(t)dt\left[ {k_{1}^{*} (x,t) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{t - x}} \right]} = 0 \\ & \quad a < x < b \\ \end{aligned}$$

(52)

$$\begin{aligned} & - \frac{1}{{\pi \,\mu_{0} }}\int\limits_{a}^{b} {p(t)dt\left[ {k_{1}^{*} (x,t) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{t - x}} \right]} \\ & \quad - \frac{1}{{\pi \,\mu_{0} }}\int\limits_{c}^{d} {q(t)dt\left[ {k_{1}^{*} (x,t) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{t - x}} \right]} = 0 \\ & \quad c < x < d \\ \end{aligned}$$

(53)

The equilibrium conditions of the punches are

$$\int\limits_{a}^{b} {p\,(t)\,dt} = P$$

(54)

$$\int\limits_{c}^{d} {q\,(t)\,dt = Q}$$

(55)

The statement $k_{1}^{*} (x,t)$ in the above-given equations is defined as follows;

$$k_{1}^{*} (x,t) = \left( {k_{1} (x,t) - \left( {\frac{{\kappa_{1} + 1}}{4}} \right)} \right)\left[ {\sin \xi (t - x)d\xi } \right]$$

(56)

The stress statement given by (46) is written for the interface between FG layer and elastic semi-infinite plane is obtained to be

$$\begin{aligned} & \sigma_{{y_{1} }} (x, - h) = \frac{{\rho_{0} g\left( {e^{ - \gamma h} - 1} \right)}}{\gamma } - \frac{1}{\pi }\int\limits_{a}^{b} {k_{2} (x,t)p(t)dt} \\ & \quad - \frac{1}{\pi }\int\limits_{c}^{d} {k_{2} (x,t)q(t)dt} ,\quad - \infty < x < \infty . \\ \end{aligned}$$

(57)

where $k_{1} (x,t)$ and $k_{2} (x,t)$ are given in “Appendix”.

For the numerical solution of the integral Eqs. (52) and (53), the following dimensionless quantities are defined:

$$\begin{aligned} & x_{1} = \frac{b - a}{2}r_{1} + \frac{b + a}{2},\quad t_{1} = \frac{b - a}{2}s_{1} + \frac{b + a}{2} \\ & \quad x_{2} = \frac{d - c}{2}r_{2} + \frac{d + c}{2},\quad t_{2} = \frac{d - c}{2}s_{2} + \frac{d + c}{2} \\ & \quad g_{1} (s_{1} ) = {{p\left( {\frac{b - a}{2}s_{1} + \frac{b + a}{2}} \right)} \mathord{\left/ {\vphantom {{p\left( {\frac{b - a}{2}s_{1} + \frac{b + a}{2}} \right)} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}} \right. \kern-0pt} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}},\quad g_{2} (s_{2} ) = {{q\left( {\frac{d - c}{2}s_{2} + \frac{d + c}{2}} \right)} \mathord{\left/ {\vphantom {{q\left( {\frac{d - c}{2}s_{2} + \frac{d + c}{2}} \right)} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}} \right. \kern-0pt} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}} \\ \end{aligned}$$

(58a{-}f)

Substituting these quantities into Eqs. (54) and (55), the followings are obtained.

$$\int\limits_{ - 1}^{1} {g_{1} (s_{1} )\frac{b - a}{2h}ds_{1} = 1}$$

(59)

$$\int\limits_{ - 1}^{1} {g_{2} (s_{2} )\frac{d - c}{2h}ds_{2} = {Q \mathord{\left/ {\vphantom {Q P}} \right. \kern-0pt} P}}$$

(60)

Here $g(s)$ are the dimensionless contact stresses under the rigid blocks. These have singularity at the block corners. Therefore, the index of the integral equations is + 1. Thereby the solution can be assumed as follows [23];

$$g_{i} \left( {s_{i} } \right) = G_{i} \left( {s_{i} } \right)\left( {1 - s_{i}^{2} } \right)^{{ - \frac{1}{2}}} \quad - 1 \le s_{i} \le + 1\left( {i = 1,2} \right)\,$$

(61)

where $G_{i} \left[ { - 1, + 1} \right]$ is a closed function. Integral equations are obtained by using the appropriate Gauss–Chebyshev integration as follows:

• 1. Integral equation:

  $$\begin{aligned} - \sum\limits_{i = 1}^{n} {W_{i} } \,G_{1} \left( {s_{1i} } \right)\frac{b - a}{2h}\left[ {\varPhi_{1} (r_{1j} ,s_{1i} ) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{{\left( {\frac{b - a}{2}} \right)\left( {s_{1i} - r_{1j} } \right)}}} \right] - \sum\limits_{i = 1}^{n} {W_{i} } \,G_{2} \left( {s_{2i} } \right)\frac{d - c}{2h}\,\times \left[ {\varPhi_{2} (r_{1j} ,s_{2i} ) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{{\left( {\left( {\frac{d - c}{2}s_{2i} + \frac{d + c}{2}} \right) - \left( {\frac{b - a}{2}r_{1j} + \frac{b + a}{2}} \right)} \right)}}} \right] = 0 \hfill \\ \left( {j = 1, \ldots ,n - 1} \right) \hfill \\ \end{aligned}$$

  (62)

• 2. Integral equation:

  $$\begin{aligned} - \sum\limits_{i = 1}^{n} {W_{i} } \,G_{1} \left( {s_{1i} } \right)\frac{b - a}{2h}\times \left[ {\varPhi_{3} (r_{2j} ,s_{1i} ) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{{\left( {\left( {\frac{b - a}{2}s_{1i} + \frac{b + a}{2}} \right) - \left( {\frac{d - c}{2}r_{2j} + \frac{d + c}{2}} \right)} \right)}}} \right]\, - \sum\limits_{i = 1}^{n} {W_{i} } \,G_{2} \left( {s_{2i} } \right)\frac{d - c}{2h}\,\left[ {\varPhi_{4} (r_{2j} ,s_{2i} ) + \frac{{(1 + \kappa_{1} )}}{4}\frac{1}{{\left( {\frac{d - c}{2}} \right)\left( {s_{2i} - r_{2j} } \right)}}} \right] = 0 \hfill \\ \left( {j = 1, \ldots ,n - 1} \right) \hfill \\ \end{aligned}$$

  (63)

Dimensionless normal stress at the contact surface between the FG layer and the elastic semi-infinite plane is

$$\frac{{\sigma_{{1_{y} }} (x, - h)}}{P/h} = \frac{{\left( {e^{ - \gamma h} - 1} \right)}}{\gamma h}\frac{1}{\lambda } - \sum\limits_{i = 1}^{n} {W_{i} G_{1} } \left( {s_{1i} } \right)\frac{b - a}{2h}\varPhi_{5} \left( {r_{1j} ,s_{1i} } \right) - \sum\limits_{i = 1}^{n} {W_{i} G_{2} } \left( {s_{2i} } \right)\frac{d - c}{2h}\varPhi_{6} \left( {r_{2j} ,s_{2i} } \right)\quad - 1 < r_{1} ,r_{2} < + 1$$

(64)

where $W_{i} \,,\,r_{j} \,,\,\,s_{i\,}$ are given by

$$\begin{aligned} W_{1} = W_{n} = \frac{1}{2n - 2},\quad W_{i} = \frac{1}{n - 1},\quad \left( {i = 2, \ldots ,n - 1} \right) \hfill \\ s_{1i} = s_{2i} = \cos \left( {\frac{i - 1}{n - 1}\pi } \right)\quad \left( {i = 1, \ldots ,n} \right) \hfill \\ r_{1j} = r_{2j} = \cos \left( {\frac{2j - 1}{2n - 2}\pi } \right)\quad \left( {j = 1, \ldots ,n - 1} \right) \hfill \\ \end{aligned}$$

(65a{-}c)

$\lambda = {P \mathord{\left/ {\vphantom {P {\rho_{0} gh^{2} }}} \right. \kern-0pt} {\rho_{0} gh^{2} }}$ is the load factor. It should be compressive at every point along the contact surface $(\lambda_{cr} \le \lambda )$ for the continuous contact problem. Therefore, it is important to find the value of the critical load which will cause the separation. Equation (64) must be equal to zero in order to find the critical load. $x_{cr}$ value and corresponding $P_{cr}$ value providing this expression gives the point at which separation begins and the critical load, respectively. The 2n algebraic equations with 2n unknowns are obtained along with the integral equations and equilibrium equations. $G_{1} (s_{i} )$ and $G_{2} (s_{i} )$ $(i = 1, \ldots ,n)$ can be calculated by solving these equation systems. Thus, the contact stress values under the blocks are found as dimensionless.

3 Results and discussion

The effect of the distance variation ${{\left( {c - b} \right)} \mathord{\left/ {\vphantom {{\left( {c - b} \right)} h}} \right. \kern-0pt} h}$ between the blocks on stress distribution at contact surfaces is investigated. In addition, initial separation loads and distances between the layer and elastic plane are determined.

The variation of the rigidity and density parameters is defined as follows:

• If $\beta h > 0$ and $\gamma h > 0$, the rigidity and density of the upper surface of the FG layer are higher than lower surface.

• When $\beta h = 0.0001$ and $\gamma h = 0.00001$, the FG layer shows homogeneous behavior, and the study can be compared to the solution that was found according to the homogeneous layer.

• In case $\beta h < 0$ and $\gamma h < 0$, the rigidity and density of the lower surface of the FG layer is higher than the upper surface.

For the second case, the results of this study are compared with the homogeneous solution made by Özşahin [24] in Table 1. As seen, the results are in good agreement. 

Table 1 According to the distance variation between the blocks, the comparison of the initial separation loads and distances between FG layer and elastic semi-infinite plane (a/h = 3, (b − a)/h = 0.5, (d − c)/h = 1, μ0 = 1, μ2/μ_−h = 1, βh = 0.0001, γh = 0.0001, κ₁ = κ₂ = 2, y = − h, h = 1)

The dimensionless contact stresses under the blocks depending on the variation of rigidity parameter $\beta h$ are shown in Fig. 2. The (a) and (b) in the figure show the contact stresses under the 1st and 2nd block, respectively.

Fig. 2

The contact stress distribution under the blocks according to the variation of rigidity parameter ($\beta h$) (a/h = 3, (b − a)/h = 0.5, (c − b)/h = 1, (d − c)/h = 1, μ₀ = 1, κ₁ = κ₂ = 2, Q = 1.5P, y = 0, h = 1, μ₂/μ_−h = 1)

In case the rigidity of the upper surface of the FG layer is higher than the bottom surface of layer, while the contact stresses at the bottom of the blocks reduce, the stresses at the corners of the blocks increase. Since the 2nd block width is twice larger than the 1st block and the contact is spread over a larger area, the stress values are closer to each other, although Q = 1.5P.

The dimensionless contact stresses under the blocks are given in Fig. 3 according to the distance variation between the blocks. When the blocks are approached to each other, while the stress values are more at the far points of the blocks they decrease at the corners which are closer. It is also found that as the interaction between the blocks ended, the system behaved like two separate blocks and stress values are very close to each other.

Fig. 3

The distribution of the contact stresses under the blocks according to the distance variation between the blocks (a/h = 3, (b − a)/h = 0.5, (d − c)/h = 1, μ₀ = 1, βh = − 0.6931, κ₁ = κ₂ = 2, Q = 1.5P, y = 0, h = 1, μ₂/μ_−h = 1)

Initial separation loads and distances between the FG layer and the elastic semi-infinite plane according to the variation of distance between blocks for various values of $\beta h$ and $\gamma h$ are given in Table 2. As seen, the initial separation loads and the initial separation distances increase as the distance between the blocks increases. As the rigidity and density of the lower surface of the FG layer increase in comparison with the upper surface, it is seen that separation occurs at a closer point to the blocks, but it is harder to occur. Additionally, the results are found closer, because as the distance between the blocks increases, the interaction between them decreases.

Table 2 The examination of initial separation loads and distances between the FG layer and the elastic semi-infinite plane according to the variation of distance between blocks for various values of $\beta h$ and $\gamma h$ (a/h = 3, (b − a)/h = 0.5, (d − c)/h = 1, μ₀ = 1, μ₂/μ_−h = 1, κ₁ = κ₂ = 2, y = − h, h = 1, Q = 2P)

The dimensionless ${{\sigma_{y} \left( {x, - h} \right)} \mathord{\left/ {\vphantom {{\sigma_{y} \left( {x, - h} \right)} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}} \right. \kern-0pt} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}$ contact stress distribution according to various $\beta h$ values is given in Fig. 4. In case of the condition where 2nd block load is taken two times greater, when the rigidity of upper surface is more than the lower surface, the separation occurs at a further point, while the layer is separated from the plane with a less load. While the stress values under the blocks decrease, it increases between the two blocks.

Fig. 4

The dimensionless ${{\sigma_{y} \left( {x, - h} \right)} \mathord{\left/ {\vphantom {{\sigma_{y} \left( {x, - h} \right)} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}} \right. \kern-0pt} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}$ contact stress distribution between the FG layer and the elastic semi-infinite plane for various $\beta \,h$ values (a/h = 2, (b − a)/h = 1, (c − b)/h = 2, (d − c)/h = 1, μ₀ = 1, μ₂/μ_−h = 1, γh = − 0.6931, y = − h, h = 1, κ₁ = κ₂ = 2, Q = 2P)

The dimensionless ${{\sigma_{y} \left( {x, - h} \right)} \mathord{\left/ {\vphantom {{\sigma_{y} \left( {x, - h} \right)} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}} \right. \kern-0pt} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}$ contact stress distribution according to the distance between the blocks is given in Fig. 5. As the distance between the blocks increases, the initial separation distances and loads increase. In addition, the block interactions caused to increase in the stresses depending on the proximity of the blocks to each other.

Fig. 5

The dimensionless ${{\sigma_{y} \left( {x, - h} \right)} \mathord{\left/ {\vphantom {{\sigma_{y} \left( {x, - h} \right)} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}} \right. \kern-0pt} {{P \mathord{\left/ {\vphantom {P h}} \right. \kern-0pt} h}}}$ contact stress distribution between the FG layer and the elastic plane according to the distance variation between blocks (a/h = 3, (b − a)/h = 0.5, (d − c)/h = 1, μ₀ = 1, βh = − 0.6931, γh = − 0.6931, κ₁ = κ₂ = 2, Q = 1.5P, y = − h, h = 1, μ₂/μ_−h = 1)

The variation of $\sigma_{y}$ along the depth of the FG layer in the middle of two blocks with respect to the variation of the distance between the blocks is given in Fig. 6. Stress values increase considerably due to the interaction between the blocks when they are approaching to each other. However, the dimensionless stress values gradually decrease as the blocks are moved away. Furthermore, it is seen that the stress values on the upper surface of the layer are zero and fulfill the boundary conditions.

Fig. 6

Variation σ_y along the depth of the FG layer in the middle of two blocks with respect to the distance between blocks (a/h = 3, (b − a)/h = 0.5, (d − c)/h = 1, μ₀ = 1, βh = − 0.6931, γh = − 0.6931, κ1 = κ2 = 2, Q = 1.5P, h = 1, μ₂/μ_−h = 1)

4 Conclusion

A continuous contact problem of a functionally graded layer resting on an elastic semi-infinite plane loaded with through two different blocks is addressed in this study. The effect of the distance between the blocks on the stress values is examined depending on the variation of inhomogeneity parameters $\beta h$ and $\gamma h$ of the materials. When the distance between the blocks decrease, the interaction is formed and accordingly the initial separation distances decrease while the initial separation loads increase. When the blocks are approached to each other, the dimensionless contact stress values under the blocks are higher at the far points of the blocks, while they decrease at the corners. Similarly, as the blocks are approached to each other, the stresses along the layer depth increase due to the interaction. In case the rigidity and density of the lower surface of the FG layer is greater than upper surface of the layer, the contact stresses under the blocks increase. Additionally, while the FG layer separated from the elastic semi-infinite plane in a point which is closer to the blocks, the load causing the separation increases notably. Thus, the layer is separated from the elastic plane with more difficult.

Appendix

$$A1 = k_{1} (x,t) = \int\limits_{0}^{\infty } {\left\{ \begin{aligned} (\kappa_{2} + 1)\left[ \begin{aligned} e^{{h\left( {s_{1} + s_{2} } \right)}} \left( {D_{1} D_{3} E_{4} n_{2} - D_{1} D_{4} E_{3} n_{2} - D_{2} D_{3} E_{4} n_{1} + D_{2} D_{4} E_{3} n_{1} } \right) \hfill \\ + e^{{h\left( {s_{1} + s_{3} } \right)}} \left( { - D_{1} D_{2} E_{4} n_{3} + D_{1} D_{4} E_{2} n_{3} + D_{2} D_{3} E_{4} n_{1} - D_{3} D_{4} E_{2} n_{1} } \right) \hfill \\ + e^{{h\left( {s_{1} + s_{4} } \right)}} \left( {D_{1} D_{2} E_{3} n_{4} - D_{1} D_{3} E_{2} n_{4} - D_{2} D_{4} E_{3} n_{1} + D_{3} D_{4} E_{2} n_{1} } \right) \hfill \\ + e^{{h\left( {s_{2} + s_{3} } \right)}} \left( {D_{1} D_{2} E_{4} n_{3} - D_{1} D_{3} E_{4} n_{2} - D_{2} D_{4} E_{1} n_{3} + D_{3} D_{4} E_{1} n_{2} } \right) \hfill \\ + e^{{h\left( {s_{2} + s_{4} } \right)}} \left( { - D_{1} D_{2} E_{3} n_{4} + D_{1} D_{4} E_{3} n_{2} + D_{2} D_{3} E_{1} n_{4} - D_{3} D_{4} E_{1} n_{2} } \right) \hfill \\ + e^{{h\left( {s_{3} + s_{4} } \right)}} \left( {D_{1} D_{3} E_{2} n_{4} - D_{1} D_{4} E_{2} n_{3} - D_{2} D_{3} E_{1} n_{4} + D_{2} D_{4} E_{1} n_{3} } \right) \hfill \\ \end{aligned} \right] \hfill \\ \quad + 4\xi^{2} m\left[ \begin{aligned} e^{{h\left( {\beta + s_{1} + s_{2} } \right)}} \left( { - D_{1} D_{3} n_{2} n_{4} + D_{1} D_{4} n_{2} n_{3} + D_{2} D_{3} n_{1} n_{4} - D_{2} D_{4} n_{1} n_{3} } \right) \hfill \\ + e^{{h\left( {\beta + s_{1} + s_{3} } \right)}} \left( {D_{1} D_{2} n_{3} n_{4} - D_{1} D_{4} n_{2} n_{3} - D_{2} D_{3} n_{1} n_{4} + D_{3} D_{4} n_{1} n_{2} } \right) \hfill \\ + e^{{h\left( {\beta + s_{1} + s_{4} } \right)}} \left( { - D_{1} D_{2} n_{3} n_{4} + D_{1} D_{3} n_{2} n_{4} + D_{2} D_{4} n_{1} n_{3} - D_{3} D_{4} n_{1} n_{2} } \right) \hfill \\ + e^{{h\left( {\beta + s_{2} + s_{3} } \right)}} \left( { - D_{1} D_{2} n_{3} n_{4} + D_{1} D_{3} n_{2} n_{4} + D_{2} D_{4} n_{1} n_{3} - D_{3} D_{4} n_{1} n_{2} } \right) \hfill \\ + e^{{h\left( {\beta + s_{2} + s_{4} } \right)}} \left( {D_{1} D_{2} n_{3} n_{4} - D_{1} D_{4} n_{2} n_{3} - D_{2} D_{3} n_{1} n_{4} + D_{3} D_{4} n_{1} n_{2} } \right) \hfill \\ + e^{{h\left( {\beta + s_{3} + s_{4} } \right)}} \left( { - D_{1} D_{3} n_{2} n_{4} + D_{1} D_{4} n_{2} n_{3} {\kern 1pt} + D_{2} D_{3} n_{1} n_{4} - D_{2} D_{4} n_{1} n_{3} } \right) \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned} \right\}} /\Delta$$

$$\begin{aligned} A2 & = \Delta = ( - \xi e^{{ - h\left( {\beta + 2\xi + s_{1} + s_{2} + s_{3} + s_{4} } \right)}} {\kern 1pt} i((\kappa_{2} + 1)(e^{{h\left( {s_{1} + s_{2} } \right)}} (D_{1} D_{3} E_{2} E_{4} - D_{1} D_{4} E_{2} E_{3} - D_{2} D_{3} E_{1} E_{4} + D_{2} D_{4} E_{1} E_{3} ) \\ & \quad e^{{h\left( {s_{1} + s_{3} } \right)}} ( - D_{1} D_{2} E_{3} E_{4} + D_{1} D_{4} E_{2} E_{3} + D_{2} D_{3} E_{1} E_{4} - D_{3} D_{4} E_{1} E_{2} ) + e^{{h\left( {s_{1} + s_{4} } \right)}} (D_{1} D_{2} E_{3} E_{4} - D_{1} D_{3} E_{2} E_{4} \\ & \quad - \,D_{2} D_{4} E_{1} E_{3} + D_{3} D_{4} E_{1} E_{2} ) + e^{{h\left( {s_{2} + s_{3} } \right)}} (D_{1} D_{2} E_{3} E_{4} - D_{1} D_{3} E_{2} E_{4} - D_{2} D_{4} E_{1} E_{3} + D_{3} D_{4} E_{1} E_{2} ) \\ & \quad + \,e^{{h\left( {s_{2} + s_{4} } \right)}} ( - D_{1} D_{2} E_{3} E_{4} + D_{1} D_{4} E_{2} E_{3} + D_{2} D_{3} E_{1} E_{4} - D_{3} D_{4} E_{1} E_{2} ) + e^{{h\left( {s_{3} + s_{4} } \right)}} (D_{1} D_{3} E_{2} E_{4} - D_{1} D_{4} E_{2} E_{3} \\ & \quad - \,D_{2} D_{3} E_{1} E_{4} + D_{2} D_{4} E_{1} E_{3} )) + 4\xi m(e^{{h\left( {\beta + s_{1} + s_{2} } \right)}} ( - D_{1} D_{3} E_{2} n_{4} + D_{1} D_{4} E_{2} n_{3} + D_{2} D_{3} E_{1} n_{4} - D_{2} D_{4} E_{1} n_{3} ) \\ & \quad + \,e^{{h\left( {\beta + s_{1} + s_{3} } \right)}} (D_{1} D_{2} E_{3} n_{4} - D_{1} D_{4} E_{3} n_{2} - D_{2} D_{3} E_{1} n_{4} + D_{3} D_{4} E_{1} n_{2} ) + e^{{h\left( {\beta + s_{1} + s_{4} } \right)}} ( - D_{1} D_{2} E_{4} n_{3} + D_{1} D_{3} E_{4} n_{2} \\ & \quad + \,D_{2} D_{4} E_{1} n_{3} - D_{3} D_{4} E_{1} n_{2} ) + e^{{h\left( {\beta + s_{2} + s_{3} } \right)}} ( - D_{1} D_{2} E_{3} n_{4} + D_{1} D_{3} E_{2} n_{4} + D_{2} D_{4} E_{3} n_{1} - D_{3} D_{4} E_{2} n_{1} ) \\ & \quad + \,e^{{h\left( {\beta + s_{2} + s_{4} } \right)}} (D_{1} D_{2} E_{4} n_{3} - D_{1} D_{4} E_{2} n_{3} - D_{2} D_{3} E_{4} n_{1} + D_{3} D_{4} E_{2} n_{1} ) + e^{{h\left( {\beta + s_{3} + s_{4} } \right)}} ( - D_{1} D_{3} E_{4} n_{2} + D_{1} D_{4} E_{3} n_{2} \\ & \quad + \,D_{2} D_{3} E_{4} n_{1} - D_{2} D_{4} E_{3} n_{1} )))) \\ \end{aligned}$$

$$A3 = k_{2} (x,t) = \frac{{e^{\beta y} }}{{\kappa_{1} - 1}}\int\limits_{0}^{ + \infty } {\sum\limits_{j = 1}^{4} {\left[ {i\xi \left( {3 - \kappa_{1} } \right) + \left( {\kappa_{1} + 1} \right)n_{j} s_{j} } \right]M_{j} e^{{s_{j} y}} } } \left[ {\cos \xi \left( {t - x} \right)} \right]d\xi$$

$$\varPhi_{1} (r_{1} ,s_{1} ) = k_{1}^{*} (x_{1} ,t_{1} ),\quad \varPhi_{2} (r_{1} ,s_{2} ) = k_{1}^{*} (x_{1} ,t_{2} )$$

$$\varPhi_{3} (r_{2} ,s_{1} ) = k_{1}^{*} (x_{2} ,t_{1} ),\quad \varPhi_{4} (r_{2} ,s_{2} ) = k_{1}^{*} (x_{2} ,t_{2} )$$

$$\varPhi_{5} (r_{1} ,s_{1} ) = k_{2} (x_{1} ,t_{1} ),\quad \varPhi_{6} (r_{2} ,s_{2} ) = k_{2} (x_{2} ,t_{2} )$$