1 Introduction

Piezoelectric materials exhibit what is known as piezoelectric effect, which is an electric polarization induced in the material upon applying a mechanical load or vice-versa [1]. Thanks to this coupling phenomenon, piezoelectric materials have been exploited in the design of a wide range of engineering applications including transducers, actuators, and sensors [2].

Contact problems in homogeneous piezoelectric materials have attracted the attention of several researchers over the past twenty-five years primarily because these materials somewhat loose their serviceability performance when subjected to highly localized loading [3]. Matysiak [4] studied the contact problem between a rigid conducting punch and a piezoelectroelastic half-plane. Fan et al. [5] obtained the stress and electrical field distributions in a piezoelectric half-plane under a contact load using Stroh’s formalism. Giannakopoulos and Suresh [6] proposed a general theory for solving axisymmetric piezoelectric contact problems. Sridhar et al. [7] investigated analytically and experimentally the mechanical and electrical responses of piezoelectric solids to conical indentation. Ramirez and Heyliger [8] considered the contact of an arbitrarily multilayered piezoelectric half-plane indented by a rigid frictionless parabolic punch. Wang and Han [9] studied the axisymmetric contact of an insulating or conducting circular punch on a piezoelectric layer/half-plane. Ke et al. [10] investigated the frictionless contact between a rigid punch and a graded piezoelectric layer bonded to a homogeneous piezoelectric half-plane. Zhou and Lee [11] examined the thermal contact problem of a piezoelectric layer under a sliding flat punch. Liu and Yang [12] utilized finite element analysis (FEA) to study spherical indentation of transversely isotropic piezoelectric materials by a rigid spherical indenter. Wu et al. [13] investigated the indentation response of a piezoelectric layered half-space. Zhou and Lee [3] considered the frictional contact of anisotropic piezoelectric materials indented by flat and semi-parabolic stamps. Ma et al. [14] studied the sliding frictional contact of a piezoelectric half-plane under a rigid conducting punch. In a similar work, Li et al. [15] examined the frictional sliding contact of piezoelectric materials subjected to flat or parabolic indenters. Zhou and Zhong [16] investigated the interaction of two rigid semi-cylinders over anisotropic piezoelectric materials by the generalized Almansi theorem. Su et al. [17] examined the fretting contact of a graded piezoelectric layered half-plane subjected to a conducting punch.

Few investigators considered the continuous and discontinuous contact problems in homogeneous and graded materials. This paragraph summarizes few of these studies. Cakiroglu et al. [18] considered the contact problem for two elastic layers resting on an elastic half-plane. Birinci and Erdol [19] investigated the contact problem for a layered composite resting on simple supports. Ozsahin [20] studied the frictionless contact problem for a layer on an elastic half-plane loaded by means of two dissimilar rigid punches. Ozsahin and Taskiner [21] examined the continuous and discontinuous contact problems for an elastic layer on an elastic half-plane loaded by means of three rigid flat punches. Birinci et al. [22] investigated both analytically and numerically using the finite element method the continuous and discontinuous contact problems between two homogeneous layers resting on a Winkler-type foundation. Adıyaman et al. [23] considered the contact problem of a graded layer resting on a rigid foundation. Comez [24] investigated the contact of a graded layer pressed by a rigid cylindrical punch.

To the best of our knowledge, the problem involving continuous and discontinuous contact problems in a piezoelectric medium has not been investigated and reported in the published literature to date. To address this gap in the literature, this paper considers the frictionless continuous and discontinuous nonlinear contact problems between an electrically conducting rigid flat punch and a piezoelectric homogeneous layer, which is in turn resting on a rigid substrate. The mixed-boundary value problem is converted analytically to a coupled set of integral equations using suitable integral transforms which are in turn solved using appropriate numerical and iterative techniques.

The remainder of this paper is organized as follows: The description and formulation of the contact problem are provided in Sect. 2. The formulation of the continuous and discontinuous contact problems are, respectively, further detailed in Sects. 3 and 4 resulting in the derivation of a coupled set of singular integral equations (SIEs). In Sect. 5, the resulting SIEs are transformed into an equivalent system of algebraic equations using Gauss–Chebyshev integration formulas, which is in turn solved numerically. In Sect. 6, the obtained results are first validated based on published data, and then a parametric study is performed to investigate the influence of the various input parameters. Finally, a summary along with the key findings of this study is provided in Sect. 7.

2 Formulation of the problem

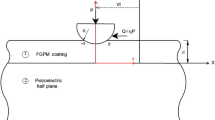
Consider the plane strain frictionless contact problem, illustrated in Fig. 1, between an electrically conducting rigid flat punch and a homogeneous piezoelectric layer, which is in turn resting on a rigid substrate. A Cartesian coordinate system (\(x,\,z\)) with the abscissa positioned at the contact zone between the piezoelectric layer and the rigid substrate is adopted as shown in Fig. 1. The layer of thickness h extends infinitely in the x direction. The equilibrium equations of elastostatic and Maxwell electrostatic equation can be written as

$$\begin{aligned}&\frac{\partial {{\sigma }_{x}}}{\partial x}+\frac{\partial {{\tau }_{xz}}}{\partial z}=0, \end{aligned}$$
(1.1)
$$\begin{aligned}&\frac{\partial {{\tau }_{xz}}}{\partial x}+\frac{\partial {{\sigma }_{z}}}{\partial z}-\rho g=0, \end{aligned}$$
(1.2)
$$\begin{aligned}&\frac{\partial {{D}_{x}}}{\partial X}+\frac{\partial {{D}_{z}}}{\partial Z}=0 \end{aligned}$$
(1.3)

where u and w are the x- and z-components of the displacement vector, \({{D}_{x}}\) and \({{D}_{z}}\) are the electric displacements, and \(\rho \) is the mass density. For the plane contact problem, the constitutive equations of linear piezoelectricity can be written as

$$\begin{aligned} {{\sigma }_{x}}= & {} {{c}_{11}}\frac{\partial u}{\partial x}+{{c}_{13}}\frac{\partial w}{\partial z}+{{e}_{31}}\frac{\partial \phi }{\partial z}, \end{aligned}$$
(2.1)
$$\begin{aligned} {{\sigma }_{z}}= & {} {{c}_{13}}\frac{\partial u}{\partial x}+{{c}_{33}}\frac{\partial w}{\partial z}+{{e}_{33}}\frac{\partial \phi }{\partial z}, \end{aligned}$$
(2.2)
$$\begin{aligned} {{\tau }_{xz}}= & {} {{c}_{44}}\left( \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right) +{{e}_{15}}\frac{\partial \phi }{\partial x}, \end{aligned}$$
(2.3)
$$\begin{aligned} {{D}_{x}}= & {} {{e}_{15}}\left( \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right) -{{\in }_{11}}\frac{\partial \phi }{\partial x}, \end{aligned}$$
(2.4)
$$\begin{aligned} {{D}_{z}}= & {} {{e}_{31}}\frac{\partial u}{\partial x}+{{e}_{33}}\frac{\partial w}{\partial z}-{{\in }_{33}}\frac{\partial \phi }{\partial z} \end{aligned}$$
(2.5)

where \(\phi \) is the electric potential and \({{c}_{ij}}\), \({{e}_{ij}}\), \({{\in }_{ij}}\) are the elastic, piezoelectric, and dielectric constants, respectively. Substituting Eq. (2) into Eq. (1), the following electro-elastic partial differential equations can be obtained:

$$\begin{aligned}&{{c}_{44}}\frac{{{\partial }^{2}}u}{\partial {{z}^{2}}}+{{c}_{11}}\frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+({{c}_{13}}+{{c}_{44}})\frac{{{\partial }^{2}}w}{\partial x\partial z}+({{e}_{15}}+{{e}_{31}})\frac{{{\partial }^{2}}\phi }{\partial x\partial z}=0, \end{aligned}$$
(3.1)
$$\begin{aligned}&({{c}_{13}}+{{c}_{44}})\frac{{{\partial }^{2}}u}{\partial x\partial z}+{{c}_{44}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+{{c}_{33}}\frac{{{\partial }^{2}}w}{\partial {{z}^{2}}}+{{e}_{33}}\frac{{{\partial }^{2}}\phi }{\partial {{z}^{2}}}+{{e}_{15}}\frac{{{\partial }^{2}}\phi }{\partial {{x}^{2}}}-\rho g=0, \end{aligned}$$
(3.2)
$$\begin{aligned}&({{e}_{15}}+{{e}_{31}})\frac{{{\partial }^{2}}u}{\partial x\partial z}+{{e}_{15}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+{{e}_{33}}\frac{{{\partial }^{2}}w}{\partial {{z}^{2}}}-{{\in }_{11}}\frac{{{\partial }^{2}}\phi }{\partial {{x}^{2}}}-{{\in }_{33}}\frac{{{\partial }^{2}}\phi }{\partial {{z}^{2}}}=0. \end{aligned}$$
(3.3)

Using the Fourier integral transform technique, partial differential equations (3) can be reduced to the ordinary differential equations. To use the Fourier transform, the following expressions may be written:

$$\begin{aligned} \{\ u(x,z),\,w(x,z),\phi (x,z)\ \}=\int \limits _{-\infty }^{\infty }{\{\ \tilde{u}(\xi ,z),\,\tilde{w}(\xi ,z),\tilde{\phi }(\xi ,z)\ \}}\,{{e}^{-I\xi x}}\hbox {d}\xi \end{aligned}$$
(4)

where \(\tilde{u}(\xi ,z)\), \(\tilde{w}(\xi ,z)\), and \(\tilde{\phi }(\xi ,z)\) are Fourier transforms of u(x, z), w(x, z), and \(\phi (x,z)\), respectively. \(\xi \) is the transform variable and \(I=\sqrt{-1}\). Substituting Eqs. (4) into (3) yields the following system of ordinary differential equations:

$$\begin{aligned}&-{{c}_{44}}\frac{{{\hbox {d}}^{2}}\tilde{u}}{\hbox {d}{{z}^{2}}}+{{\xi }^{2}}{{c}_{11}}\tilde{u}+I\xi ({{c}_{13}}+{{c}_{44}})\frac{{{\hbox {d}}^{2}}\tilde{w}}{\hbox {d}z}+I\xi ({{e}_{15}}+{{e}_{31}})\frac{\hbox {d}\tilde{\phi }}{\hbox {d}z}=0, \end{aligned}$$
(5.1)
$$\begin{aligned}&-I({{c}_{13}}+{{c}_{44}})\xi \frac{\hbox {d}\tilde{u}}{\hbox {d}z}-{{\xi }^{2}}{{c}_{44}}\tilde{w}+{{c}_{33}}\frac{{{\hbox {d}}^{2}}\tilde{w}}{\hbox {d}z}+{{e}_{33}}\frac{{{\hbox {d}}^{2}}\tilde{\phi }}{\hbox {d}{{z}^{2}}}-{{e}_{15}}{{\xi }^{2}}\tilde{\phi }-\rho g\delta (\xi )=0, \end{aligned}$$
(5.2)
$$\begin{aligned}&-I({{e}_{15}}+{{e}_{31}})\xi \frac{\hbox {d}\tilde{u}}{\hbox {d}z}-{{\xi }^{2}}{{e}_{15}}\tilde{w}+{{e}_{33}}\frac{{{\hbox {d}}^{2}}\tilde{w}}{\hbox {d}z}-{{\in }_{33}}\frac{{{\hbox {d}}^{2}}\tilde{\phi }}{\hbox {d}{{z}^{2}}}-{{\in }_{11}}{{\xi }^{2}}\tilde{\phi }=0 \end{aligned}$$
(5.3)

where \(\delta \) denotes the Dirac delta function.

The Fourier transform of the displacement field, \(\tilde{u}(\xi ,z)\), \(\tilde{w}(\xi ,z)\), and \(\tilde{\phi }(\xi ,z)\) can be obtained by solving the system of Eqs. (5). Taking the inverse Fourier transform using Eq. (4) results in the displacements and the electric potential that can be written as follows:

$$\begin{aligned} u(x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\left( \sum \limits _{j=1}^{6}{{{A}_{j}}}\,{{e}^{{{n}_{j}}\xi z}} \right) }{{e}^{-I\xi x}}\hbox {d}\xi , \end{aligned}$$
(6.1)
$$\begin{aligned} w(x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\left( \sum \limits _{j=1}^{6}{{{k}_{j}}{{A}_{j}}}\,{{e}^{{{n}_{j}}\xi z}}-\frac{\rho g{{\in }_{11}}}{{{c}_{44}}{{\xi }^{2}}(e_{15}^{2}+{{c}_{44}}{{\in }_{11}})}\delta (\xi ) \right) }{{e}^{-I\xi x}}\hbox {d}\xi , \end{aligned}$$
(6.2)
$$\begin{aligned} \phi (x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\left( \sum \limits _{j=1}^{6}{{{\lambda }_{j}}{{A}_{j}}}\,{{e}^{{{n}_{j}}\xi z}}-\frac{\rho g{{e}_{15}}}{{{c}_{44}}{{\xi }^{2}}(e_{15}^{2}+{{c}_{44}}{{\in }_{11}})}\delta (\xi ) \right) }{{e}^{-I\xi x}}\hbox {d}\xi \end{aligned}$$
(6.3)

where

$$\begin{aligned} {{\lambda }_{j}}= & {} \frac{-{{e}_{15}}{{k}_{j}}-I({{e}_{15}}+{{e}_{31}}){{n}_{j}}+{{e}_{33}}{{k}_{j}}n_{j}^{2}}{-{{\in }_{11}}+n_{j}^{2}{{\in }_{33}}} \quad j=1,2,\ldots \,6, \end{aligned}$$
(7.1)
$$\begin{aligned} {{k}_{j}}= & {} \frac{I{{n}_{j}}(-({{e}_{15}}+{{e}_{31}})({{e}_{15}}-{{e}_{33}}n_{j}^{2})-({{c}_{13}}+{{c}_{44}}){{\in }_{11}}+({{c}_{13}}+{{c}_{44}})n_{j}^{2}{{\in }_{33}}}{e_{15}^{2}-2{{e}_{15}}{{e}_{33}}n_{j}^{2}+e_{33}^{2}n_{j}^{4}+({{c}_{44}}-{{c}_{33}}n_{j}^{2})({{\in }_{11}}-n_{j}^{2}{{\in }_{33}})}. \end{aligned}$$
(7.2)

Note that \({{n}_{j}}\) are the roots of the following characteristic polynomials:

$$\begin{aligned} {{n}^{6}}+{{L}_{1}}{{n}^{4}}+{{L}_{2}}{{n}^{2}}+{{L}_{3}}=0 \end{aligned}$$
(8)

where \({{L}_{j}}\)\((j=1,2,3)\) can be expressed as follows:

$$\begin{aligned} {{L}_{1}}= & {} \frac{{{e}_{33}}(2{{c}_{44}}{{e}_{31}}+2{{c}_{13}}({{e}_{15}}+{{e}_{31}})-{{c}_{11}}{{e}_{33}})+{{c}_{13}}({{c}_{13}}+2{{c}_{44}}){{\in }_{33}}-{{c}_{33}}({{({{e}_{15}}+{{e}_{31}})}^{2}}+{{c}_{44}}{{\in }_{11}}+{{c}_{11}}{{\in }_{33}}))}{{{c}_{44}}(e_{33}^{2}+{{c}_{33}}{{\in }_{33}})}, \end{aligned}$$
(9.1)
$$\begin{aligned} {{L}_{2}}= & {} \frac{{{c}_{44}}e_{31}^{2}+2{{c}_{11}}{{e}_{15}}{{e}_{33}}-c_{13}^{2}{{\in }_{11}}+{{c}_{11}}{{c}_{33}}{{\in }_{11}}-2{{c}_{13}}({{e}_{15}}({{e}_{15}}+{{e}_{31}})+{{c}_{44}}{{\in }_{11}})+{{c}_{11}}{{c}_{44}}{{\in }_{33}}\quad }{{{c}_{44}}(e_{33}^{2}+{{c}_{33}}{{\in }_{33}})}, \end{aligned}$$
(9.2)
$$\begin{aligned} {{L}_{3}}= & {} \frac{{{c}_{11}}(e_{15}^{2}+{{c}_{44}}{{\in }_{11}})}{{{c}_{44}}(e_{33}^{2}+{{c}_{33}}{{\in }_{33}})}. \end{aligned}$$
(9.3)

Substituting Eqs. (6) into (1) gives the stress components and the electric displacements for the homogeneous piezoelectric layer that can be expressed as follows:

$$\begin{aligned} {{\sigma }_{x}}(x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\xi \left[ \sum \limits _{j=1}^{6}{{{A}_{j}}}(-I{{c}_{11}}+{{n}_{j}}({{c}_{13}}{{k}_{j}}+{{e}_{31}}{{\lambda }_{j}}))\,{{e}^{{{n}_{j}}\xi z}} \right] }{{e}^{-I\xi x}}\hbox {d}\xi , \end{aligned}$$
(10.1)
$$\begin{aligned} {{\sigma }_{z}}(x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\xi \left[ \sum \limits _{j=1}^{6}{{{A}_{j}}}(-I{{c}_{13}}+{{n}_{j}}({{c}_{33}}{{k}_{j}}+{{e}_{33}}{{\lambda }_{j}})\,){{e}^{{{n}_{j}}\xi z}} \right] }{{e}^{-I\xi x}}\hbox {d}\xi , \end{aligned}$$
(10.2)
$$\begin{aligned} {{\tau }_{xz}}(x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\xi \left[ \sum \limits _{j=1}^{6}{{{A}_{j}}}({{c}_{44}}(-I{{k}_{j}}+{{n}_{j}})-I{{e}_{15}}{{\lambda }_{j}})\,{{e}^{{{n}_{j}}\xi z}}+I\frac{\rho g}{{{\xi }^{2}}}\delta (\xi ) \right] }{{e}^{-I\xi x}}\hbox {d}\xi , \end{aligned}$$
(10.3)
$$\begin{aligned} {{D}_{x}}(x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\xi \left[ \sum \limits _{j=1}^{6}{{{A}_{j}}}({{e}_{15}}(-I{{k}_{j}}+{{n}_{j}})+I{{\in }_{11}}{{\lambda }_{j}})\,{{e}^{{{n}_{j}}\xi z}} \right] }{{e}^{-I\xi x}}\hbox {d}\xi , \end{aligned}$$
(10.4)
$$\begin{aligned} {{D}_{z}}(x,z)= & {} \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }{\xi \left[ \sum \limits _{j=1}^{6}{{{A}_{j}}}(-I{{e}_{31}}+{{n}_{j}}({{e}_{33}}{{k}_{j}}-{{\in }_{33}}{{\lambda }_{j}})\,){{e}^{{{n}_{j}}\xi z}} \right] }{{e}^{-I\xi x}}\hbox {d}\xi \end{aligned}$$
(10.5)

where \({{A}_{j}}\)\((j=1,2,\ldots ,6)\) are the unknowns, which will be determined from the mechanical and electrical boundary conditions of the moving contact problem.

3 Continuous contact problem

If the external load P is sufficiently small, then the contact along the layer-substrate interface will be continuous, and there is no separation between the layer and the substrate (see Fig. 1).

Fig. 1
figure 1

Geometry of the continuous contact problem

Full size image

3.1 The boundary conditions and the singular integral equations

In the Cartesian coordinate system (\(x,\,z\)), the governing equations of the continuous contact problem are subjected to the following boundary conditions:

$$\begin{aligned} {{\sigma }_{z}}(x,h)= & {} \left\{ \begin{array}{lll} -p(x)\quad \quad -a<x<a \\ \ 0\quad \quad \quad \quad |x|\ge a \\ \end{array} \right. , \end{aligned}$$
(11.1)
$$\begin{aligned} {{\tau }_{xz}}(x,h)= & {} 0\quad \quad \quad \,\quad \quad (-\infty< x<\infty ) \end{aligned}$$
(11.2)
$$\begin{aligned} {{\tau }_{xz}}(x,0)= & {} 0\quad \quad \quad \,\quad \quad (-\infty< x<\infty ) \end{aligned}$$
(11.3)
$$\begin{aligned} w(x,0)= & {} 0\quad \quad \quad \quad \ \quad (-\infty< x<\infty ), \end{aligned}$$
(11.4)
$$\begin{aligned} {{D}_{z}}(x,h)= & {} \left\{ \begin{array}{lll} -q(x)\quad \quad -a<x<a \\ \ 0\quad \quad \quad \quad |x|\ge a \\ \end{array} \right. \end{aligned}$$
(11.5)
$$\begin{aligned} \phi (x,0)= & {} 0\quad \quad \quad \quad \ \quad (-\infty< x<\infty ) \end{aligned}$$
(11.6)

where p(x) and q(x) are the unknown contact stress and the electric charge distributions on the contact area \((-a,a)\), respectively.

Using the boundary conditions given by Eq. (11), the unknowns \({{A}_{j}} \quad (j=1,2,\ldots ,6)\) can be determined depending on the unknown contact stress p(x) and the electric charge distributions q(x) in the following form:

$$\begin{aligned} A_{j}^{{}}=\int \limits _{-a}^{a}{\left[ A_{j}^{p}p(t)+\,A_{j}^{q}q(t)+{{\rho }_{0}}gA_{j}^{\rho } \right] }{{e}^{I\xi t}}\hbox {d}t. \end{aligned}$$
(12)

p(x) and q(x) can be found using the following boundary conditions:

$$\begin{aligned}&\frac{\partial w(x,h)}{\partial x}=0\quad -a<x<a, \end{aligned}$$
(13.1)
$$\begin{aligned}&\phi (x,h)={{\phi }_{0}}\quad \text {or} \quad \frac{\partial \phi (x,h)}{\partial x}=0\quad -a<x<a. \end{aligned}$$
(13.2)

Substituting the unknowns \({{A}_{j}}\) into the boundary conditions (13), the following system of singular integral equations may be obtained:

$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-a}^{a}{p(t)\hbox {d}t}\left[ \frac{{{\beta }_{11}}}{t-x}+{{k}_{11}}(x,t) \right] +\frac{1}{\pi }\int \limits _{-a}^{a}{q(t)\hbox {d}t}\left[ \frac{{{\beta }_{12}}}{t-x}+{{k}_{12}}(x,t) \right] =0\quad (-a<x<a), \end{aligned}$$
(14.1)
$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-a}^{a}{p(t)\hbox {d}t}\left[ \frac{{{\beta }_{21}}}{t-x}+{{k}_{21}}(x,t) \right] +\frac{1}{\pi }\int \limits _{-a}^{a}{q(t)\hbox {d}t}\left[ \frac{{{\beta }_{22}}}{t-x}+{{k}_{22}}(x,t) \right] =0 \quad (-a<x<a). \end{aligned}$$
(14.2)

The expressions of the Fredholm kernels, \({{k}_{11}}(x,t)\), \({{k}_{12}}(x,t)\), \({{k}_{21}}(x,t)\), \({{k}_{22}}(x,t)\), and the parameters \({{\beta }_{11}}\), \({{\beta }_{12}}\), \({{\beta }_{21}}\), and \({{\beta }_{22}}\) are given in “Appendix A.”

Note that the following equilibrium conditions should be satisfied for a complete solution:

$$\begin{aligned}&\int \limits _{-a}^{a}{p(t)\hbox {d}t}=P, \end{aligned}$$
(15.1)
$$\begin{aligned}&\int \limits _{-a}^{a}{q(t)\hbox {d}t}=T \end{aligned}$$
(15.2)

where P is the applied load in units of [N/m] and T is the electric charge in units of [C/m].

Note that when the value of external load exceeds \({{P}_\mathrm{cr}}\), the interface separation takes place between the layer and the substrate. The solution of the continuous contact problem is only valid if the external load is less than \({{P}_\mathrm{cr}}\) (\(0<P<{{P}_\mathrm{cr}}\)) which has not been determined yet. The contact stress on the interface \({{\sigma }_{z}}(x,0)\) should be evaluated first to find the value of separation load and separation distance. Substituting \({{A}_{j}}\) into (10.2), the contact stress between the layer and rigid substrate can be found as

$$\begin{aligned} {{\sigma }_{z}}(x,0)=\frac{1}{\pi }\int \limits _{-a}^{a}{p(t){{k}_{31}}(x,t)\hbox {d}t}+\frac{1}{\pi }\int \limits _{-a}^{a}{q(t){{k}_{32}}(x,t)\hbox {d}t}+\rho g\int \limits _{-\infty }^{\infty }{{{M}_{33}}(\xi )\delta (\xi ){{e}^{-I\xi x}}\hbox {d}x}. \end{aligned}$$
(16)

Knowing that

$$\begin{aligned} \underset{\alpha \rightarrow 0}{\mathop {\lim }}\,\ \int \limits _{-\infty }^{\infty }{{{M}_{33}}(\xi )}{{e}^{-I\xi x}}\hbox {d}\xi =-h, \end{aligned}$$
(17)

Eq. (16) becomes

$$\begin{aligned} {{\sigma }_{z}}(x,0)=\frac{1}{\pi }\int \limits _{-a}^{a}{p(t){{k}_{31}}(x,t)\hbox {d}t}+\frac{1}{\pi }\int \limits _{-a}^{a}{q(t){{k}_{32}}(x,t)\hbox {d}t}-\rho gh \end{aligned}$$
(18)

where

$$\begin{aligned} {{k}_{31}}(x,t)= & {} \int \limits _{0}^{\infty }{{{M}_{31}}}(\xi )\cos \xi (t-x)\hbox {d}\xi , \end{aligned}$$
(19.1)
$$\begin{aligned} {{k}_{32}}(x,t)= & {} \int \limits _{0}^{\infty }{{{M}_{32}}}(\xi )\cos \xi (t-x)\hbox {d}\xi , \end{aligned}$$
(19.2)
$$\begin{aligned} {{M}_{31}}(\xi )= & {} \xi \sum \limits _{j=1}^{6}{A_{j}^{p}}(-I{{c}_{13}}+{{n}_{j}}({{c}_{33}}{{k}_{j}}+{{e}_{33}}{{\lambda }_{j}})), \end{aligned}$$
(19.3)
$$\begin{aligned} {{M}_{32}}(\xi )= & {} \xi \sum \limits _{j=1}^{6}{A_{j}^{q}}(-I{{c}_{13}}+{{n}_{j}}({{c}_{33}}{{k}_{j}}+{{e}_{33}}{{\lambda }_{j}})), \end{aligned}$$
(19.4)
$$\begin{aligned} {{M}_{33}}(\xi )= & {} \xi \sum \limits _{j=1}^{6}{A_{j}^{\rho }}(-I{{c}_{13}}+{{n}_{j}}({{c}_{33}}{{k}_{j}}+{{e}_{33}}{{\lambda }_{j}})). \end{aligned}$$
(19.5)

3.2 On the solution of the singular integral equation

The singular integral equations (14) must be solved simultaneously to find the contact stress p(x) and the electric charge distributions q(x). Introducing the following normalization:

$$\begin{aligned} t=ar, \quad x=as \end{aligned}$$
(20)

the singular integral equations and \({{\sigma }_{z}}(x,0)\) may be expressed in the following form:

$$\begin{aligned}&\displaystyle \frac{1}{\pi }\int \limits _{-1}^{1}{p(r)\hbox {d}r}\left[ \frac{{{\beta }_{11}}}{r-s}+a{{k}_{11}}(s,r) \right] +\frac{1}{\pi }\int \limits _{-1}^{1}{q(r)\hbox {d}r}\left[ \frac{{{\beta }_{12}}}{r-s}+a{{k}_{12}}(s,r) \right] =0 \quad (-1<s<1), \end{aligned}$$
(21.1)
$$\begin{aligned}&\displaystyle \frac{1}{\pi }\int \limits _{-1}^{1}{p(r)\hbox {d}r}\left[ \frac{{{\beta }_{21}}}{r-s}+a{{k}_{21}}(s,r) \right] +\frac{1}{\pi }\int \limits _{-1}^{1}{q(r)\hbox {d}r}\left[ \frac{{{\beta }_{22}}}{r-s}+a{{k}_{22}}(s,r) \right] =0 \quad (-1<s<1), \end{aligned}$$
(21.2)
$$\begin{aligned}&\displaystyle {{\sigma }_{z}}(x,0)=\frac{1}{\pi }\int \limits _{-1}^{1}{p(t)a{{k}_{31}}(x,t)\hbox {d}t}+\frac{1}{\pi }\int \limits _{-1}^{1}{q(t)a{{k}_{32}}(x,t)\hbox {d}t}-\rho gh. \end{aligned}$$
(21.3)

Similarly, the equilibrium conditions (15) become

$$\begin{aligned}&a\int \limits _{-1}^{1}{p(r)\hbox {d}r}=P, \end{aligned}$$
(22.1)
$$\begin{aligned}&a\int \limits _{-1}^{1}{q(r)\hbox {d}r}=T. \end{aligned}$$
(22.2)

p(r) and q(r) have a square root singularity at both ends \(r=\pm 1\). Thus, both integral equations have the index “\(+1\).” The solution of the integral equations (21) may be expressed as

$$\begin{aligned}&p(r)={{g}_{1}}(r)/\sqrt{1-{{r}^{2}}}, \end{aligned}$$
(23.1)
$$\begin{aligned}&q(r)={{g}_{2}}(r)/\sqrt{1-{{r}^{2}}}. \end{aligned}$$
(23.2)

Using the Gauss–Chebyshev integration formulas [25], the integral equations (21) can be converted into a system of algebraic equations as follows:

$$\begin{aligned}&\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{i}})\left[ \frac{{{\beta }_{11}}}{{{r}_{i}}-{{s}_{k}}}+a{{k}_{11}}({{s}_{k}},{{r}_{i}}) \right] +\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{i}})\left[ \frac{{{\beta }_{12}}}{{{r}_{i}}-{{s}_{k}}}+a{{k}_{12}}({{s}_{k}},{{r}_{i}}) \right] =0 \quad k=1,2,\ldots ,N-1, \end{aligned}$$
(24.1)
$$\begin{aligned}&\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{i}})\left[ \frac{{{\beta }_{21}}}{{{r}_{i}}-{{s}_{k}}}+a{{k}_{21}}({{s}_{k}},{{r}_{i}}) \right] +\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{i}})\left[ \frac{{{\beta }_{22}}}{{{r}_{i}}-{{s}_{k}}}+a{{k}_{22}}({{s}_{k}},{{r}_{i}}) \right] =0 \quad k=1,2,\ldots ,N-1.\nonumber \\ \end{aligned}$$
(24.2)

Similarly, the equilibrium conditions (22.1) and (22.2) become

$$\begin{aligned}&a\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{i}})=\frac{1}{\pi }P, \end{aligned}$$
(25.1)
$$\begin{aligned}&a\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{i}})=\frac{1}{\pi }T \end{aligned}$$
(25.2)

where

$$\begin{aligned}&{{r}_{i}}=\cos \left( \frac{2i-1}{2N}\pi \right) \quad i=1,2,\ldots ,N, \end{aligned}$$
(26.1)
$$\begin{aligned}&{{s}_{k}}=\cos \left( \frac{k}{N}\pi \right) \quad k=1,2,\ldots ,N-1. \end{aligned}$$
(26.2)

In addition, Eq. (21.3) becomes

$$\begin{aligned} {{\sigma }_{z}}(x,0)=\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{i}})a{{k}_{31}}(x,{{r}_{i}})+\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{i}})a{{k}_{32}}(x,{{r}_{i}})-\rho gh. \end{aligned}$$
(27)

Equations (24) and (25) give 2N equations to determine 2N unknowns which are \({{g}_{1}}({{r}_{i}})\) and \({{g}_{2}}({{r}_{i}})\). Note that the solution must also ensure that the contact stress between the layer-substrate (27) is compressive everywhere, that is,

$$\begin{aligned} \hbox {Max}[{{\sigma }_{z}}(x,0)]\le 0. \end{aligned}$$
(28)

If condition (28) is satisfied, the continuous contact is ensured. It is clear that every load satisfying condition (28) is not critical. If the stress at the interface is equal to zero at a certain point \(x = x_\mathrm{cr}\), that is \(\sigma _z \left( {x_\mathrm{cr} ,0} \right) = 0\), the corresponding load is referred to as the critical load \(P_\mathrm{cr}\), and \(x_\mathrm{cr}\) is the critical separation point. The system of equations is linear in terms of \(g_1 \left( {r_i } \right) \) and \(g_2 \left( {r_2} \right) \) but highly nonlinear in terms of the variable P. Thus, an iteration procedure should be performed to obtain the critical load. In this method, the critical load is guessed at first, then \(g_1 \left( {r_i } \right) \) and \(g_2 \left( {r_2} \right) \) are computed from Eqs. (24) and (25). The condition (28) and \(\sigma _z \left( {x_\mathrm{cr} ,0} \right) = 0\) are checked by substituting \(g_1 \left( {r_i } \right) \) and \(g_2 \left( {r_2} \right) \) into them. The iterations are continued until an acceptable accuracy is achieved.

4 Discontinuous contact problem

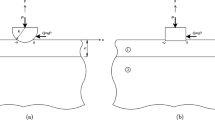
If the external load P exceeds the critical value \({{P}_\mathrm{cr}}\), then the contact along the layer–substrate interface will be discontinuous, and there occurs separation between the layer and substrate as shown in Fig. 2. The separation observed in this problem will be closed after the separation length reaches a critical value (\(|x|=c\)). This is due to the fact that when the body force is not neglected, the separation will be finite unlike the receding contact problems.

Fig. 2
figure 2

Geometry of the discontinuous contact problem

Full size image

4.1 The boundary conditions and the singular integral equations

The boundary conditions of the discontinuous contact problem can be written as follows:

$$\begin{aligned}&{{\sigma }_{z}}(x,h)=\left\{ \begin{array}{lll} -p(x)\quad \quad -a<x<a \\ \ 0\quad \quad \quad \quad |x| \ge a \\ \end{array} \right. , \end{aligned}$$
(29.1)
$$\begin{aligned}&{{\tau }_{xz}}(x,h)=0\quad \quad \quad \,\quad \quad (-\infty< x<\infty ), \end{aligned}$$
(29.2)
$$\begin{aligned}&{{\tau }_{xz}}(x,0)=0\quad \quad \quad \,\quad \quad (-\infty< x<\infty ), \end{aligned}$$
(29.3)
$$\begin{aligned}&\frac{\partial w(x,0)}{\partial x}=\left\{ \begin{array}{lll} &{}f(x)\quad \quad &{}(-c\le x<-b,\,\ b\le x<c) \\ &{}0\quad \quad &{}|x| \le b, |x| \ge c. \\ \end{array} \right. \end{aligned}$$
(29.4)
$$\begin{aligned}&{{D}_{z}}(x,h)=\left\{ \begin{array}{lll} &{}-q(x)\quad \quad &{}-a<x<a \\ &{}0\quad \quad &{}|x| \ge a. \\ \end{array} \right. \end{aligned}$$
(29.5)
$$\begin{aligned}&\phi (x,0)=0\quad \quad \quad \quad \ \quad (-\infty< x<\infty ) \end{aligned}$$
(29.6)

where p(x) and q(x) are the unknown contact stress and the electric charge distributions on the contact area \((-a,a)\), respectively. f(x) is the derivative of the interface displacement on the separation region \((-b,-c)\) and (b, c). Note that since the friction between the contacting components is ignored and they are not bonded to each other, the tangential tractions do not occur on the surfaces. Also, the vertical displacement outside the separation region will be zero since the substrate is rigid.

Applying the boundary conditions given by (29), the unknowns \({{A}_{j}} \quad (j=1,2,\ldots ,6)\) can be determined depending on the unknown contact stress p(x), the electric charge distributions q(x), and the derivative of the interface displacement f(x) as the following form:

$$\begin{aligned} A_{j}^{{}}=\int \limits _{-a}^{a}{\left[ \bar{A}_{j}^{p}p(t)+\,\bar{A}_{j}^{q}q(t)+\,\bar{A}_{j}^{f}f(t)+\rho g\bar{A}_{j}^{\rho } \right] }{{e}^{I\xi t}}\hbox {d}t. \end{aligned}$$
(30)

To find the p(x), q(x), and f(x), the following boundary conditions can be written:

$$\begin{aligned}&\displaystyle \frac{\partial w(x,h)}{\partial x}=0\quad -a<x<a, \end{aligned}$$
(31.1)
$$\begin{aligned}&\displaystyle \phi (x,h)={{\phi }_{0}}\quad \hbox {or} \quad \frac{\partial \phi (x,h)}{\partial x}=0\quad -a<x<a, \end{aligned}$$
(31.2)
$$\begin{aligned}&\displaystyle {{\sigma }_{z}}(x,0)=0\quad -c<x<-b,\quad b<x<c. \end{aligned}$$
(31.3)

Substituting the unknowns \({{A}_{j}}\) into the boundary condition (31), the following singular integral equations system may be obtained:

$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-a}^{a}{p({{t}_{1}})\hbox {d}{{t}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{11}}}{{{t}_{1}}-{{x}_{1}}}+{{{\bar{k}}}_{11}}({{x}_{1}},{{t}_{1}}) \right] +\frac{1}{\pi }\int \limits _{-a}^{a}{q({{t}_{1}})\hbox {d}{{t}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{12}}}{{{t}_{1}}-{{x}_{1}}}+{{{\bar{k}}}_{12}}({{x}_{1}},{{t}_{1}}) \right] \nonumber \\&\quad +\frac{1}{\pi }\int \limits _{b}^{c}{f({{t}_{2}})\hbox {d}{{t}_{2}}}\left[ {{{\bar{k}}}_{13}}({{x}_{1}},{{t}_{2}}) \right] =0\quad (-a<{{x}_{1}}<a), \end{aligned}$$
(32.1)
$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-a}^{a}{p({{t}_{1}})\hbox {d}{{t}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{21}}}{{{t}_{1}}-{{x}_{1}}}+{{{\bar{k}}}_{21}}({{x}_{1}},{{t}_{1}}) \right] +\frac{1}{\pi }\int \limits _{-a}^{a}{q({{t}_{1}})\hbox {d}{{t}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{22}}}{{{t}_{1}}-{{x}_{1}}}+{{{\bar{k}}}_{22}}({{x}_{1}},{{t}_{1}}) \right] \nonumber \\&\quad +\frac{1}{\pi }\int \limits _{b}^{c}{f({{t}_{2}})\hbox {d}{{t}_{2}}}\left[ {{{\bar{k}}}_{23}}({{x}_{1}},{{t}_{2}}) \right] =0\quad (-a<{{x}_{1}}<a), \end{aligned}$$
(32.2)
$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-a}^{a}{p({{t}_{1}})\hbox {d}{{t}_{1}}}\left[ {{{\bar{k}}}_{31}}({{x}_{2}},{{t}_{1}}) \right] +\frac{1}{\pi }\int \limits _{-a}^{a}{q({{t}_{1}})\hbox {d}{{t}_{1}}}\left[ {{{\bar{k}}}_{32}}({{x}_{2}},{{t}_{1}}) \right] \nonumber \\&\quad +\frac{1}{\pi }\int \limits _{b}^{c}{f({{t}_{2}})\hbox {d}{{t}_{2}}}\left[ \frac{{{{\bar{\beta }}}_{33}}}{2}\left( \frac{1}{{{t}_{2}}-{{x}_{2}}}+\frac{1}{{{t}_{2}}+{{x}_{2}}}\right) +{{{\bar{k}}}_{33}}({{x}_{2}},{{t}_{2}}) \right] =\rho gh\quad (b<{{x}_{2}}<c). \end{aligned}$$
(32.3)

The expressions of the \({{\bar{k}}_{11}}({{x}_{1}},{{t}_{1}})\), \({{\bar{k}}_{12}}({{x}_{1}},{{t}_{1}})\), \({{\bar{k}}_{13}}({{x}_{1}},{{t}_{2}})\), \({{\bar{k}}_{21}}({{x}_{1}},{{t}_{1}})\), \({{\bar{k}}_{22}}({{x}_{1}},{{t}_{1}})\), \({{\bar{k}}_{23}}({{x}_{1}},{{t}_{2}})\), \({{\bar{k}}_{31}}({{x}_{2}},{{t}_{1}})\), \({{\bar{k}}_{32}}({{x}_{2}},{{t}_{1}})\), \({{\bar{k}}_{33}}({{x}_{2}},{{t}_{2}})\) and the parameters \({{\bar{\beta }}_{11}}\), \({{\bar{\beta }}_{12}}\), \({{\bar{\beta }}_{21}}\), \({{\bar{\beta }}_{22}}\), and \({{\bar{\beta }}_{33}}\) are provided in “Appendix B.”

In the singular integral equations (32), the following equilibrium and single-value conditions must be satisfied:

$$\begin{aligned}&\int \limits _{-a}^{a}{p({{t}_{1}})\hbox {d}{{t}_{1}}}=P, \end{aligned}$$
(33.1)
$$\begin{aligned}&\int \limits _{-a}^{a}{q({{t}_{1}})\hbox {d}{{t}_{1}}}=T, \end{aligned}$$
(33.2)
$$\begin{aligned}&\int \limits _{b}^{c}{f({{t}_{2}})\hbox {d}{{t}_{2}}}=0. \end{aligned}$$
(33.3)

5 On the solution of the singular integral equations

Introducing the following normalizations:

$$\begin{aligned} {{t}_{1}}=a{{r}_{1}},\quad {{x}_{1}}=a{{s}_{1}},\quad {{t}_{2}}=\frac{b-c}{2}{{r}_{2}}+\frac{b+c}{2},\quad {{x}_{2}}=\frac{b-c}{2}{{s}_{2}}+\frac{b+c}{2}, \end{aligned}$$
(34)

the singular integral equations (32) may be expressed as follows:

$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-1}^{1}{p({{r}_{1}})\hbox {d}{{r}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{11}}}{{{r}_{1}}-{{s}_{1}}}+a{{{\bar{k}}}_{11}}({{s}_{1}},{{r}_{1}}) \right] +\frac{1}{\pi }\int \limits _{-1}^{1}{q({{r}_{1}})\hbox {d}{{r}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{12}}}{{{r}_{1}}-{{s}_{1}}}+{{{\bar{k}}}_{12}}({{s}_{1}},{{r}_{1}}) \right] \nonumber \\&\quad +\frac{1}{\pi }\int \limits _{-1}^{1}{f({{r}_{2}})\hbox {d}{{r}_{2}}}\left[ \frac{c-b}{2}{{{\bar{k}}}_{13}}({{s}_{1}},{{r}_{2}}) \right] =0 \quad (-1<{{s}_{1}}<1), \end{aligned}$$
(35.1)
$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-1}^{1}{p({{r}_{1}})\hbox {d}{{r}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{21}}}{{{r}_{1}}-{{s}_{1}}}+a{{{\bar{k}}}_{21}}({{s}_{1}},{{r}_{1}}) \right] +\frac{1}{\pi }\int \limits _{-1}^{1}{q({{r}_{1}})\hbox {d}{{r}_{1}}}\left[ \frac{{{{\bar{\beta }}}_{22}}}{{{r}_{1}}-{{s}_{1}}}+{{{\bar{k}}}_{22}}({{s}_{1}},{{r}_{1}}) \right] \nonumber \\&\quad +\frac{1}{\pi }\int \limits _{-1}^{1}{f({{r}_{2}})\hbox {d}{{r}_{2}}}\left[ \frac{c-b}{2}{{{\bar{k}}}_{23}}({{s}_{1}},{{r}_{2}}) \right] =0 \quad (-1<{{s}_{1}}<1), \end{aligned}$$
(35.2)
$$\begin{aligned}&\frac{1}{\pi }\int \limits _{-1}^{1}{p({{r}_{1}})\hbox {d}{{r}_{1}}}\left[ a{{{\bar{k}}}_{31}}({{s}_{2}},{{r}_{1}}) \right] +\frac{1}{\pi }\int \limits _{-1}^{1}{q({{r}_{1}})\hbox {d}{{r}_{1}}}\left[ a{{{\bar{k}}}_{32}}({{s}_{2}},{{r}_{1}}) \right] \nonumber \\&\quad +\frac{1}{\pi }\int \limits _{-1}^{1}{f({{r}_{2}})\hbox {d}{{r}_{2}}}\left[ \frac{{{{\bar{\beta }}}_{33}}}{2}\left( \frac{1}{{{r}_{2}}-{{s}_{2}}}+\frac{1}{{{r}_{2}}+{{s}_{2}}+2\frac{c+b}{c-b}}\right) +{{{\bar{k}}}_{33}}({{s}_{2}},{{r}_{2}}) \right] =\rho gh\nonumber \\&\quad (-1<{{s}_{2}}<1). \end{aligned}$$
(35.3)

The tractions p(r) and q(r) have a square root singularity at both ends of the contact \(r=\pm 1\). Thus, the index of the integral equations (32.1,2) is “\(+1\).” However, the contact stress between the layer and substrate vanishes at the ends of the contact region and the index of the integral equation (32.3) is “\(-1\).” Therefore, the solution of the integral equations may be expressed as

$$\begin{aligned} p({{r}_{1}})= & {} {{g}_{1}}({{r}_{1}})/\sqrt{1-r_{1}^{2}}, \end{aligned}$$
(36.1)
$$\begin{aligned} q({{r}_{1}})= & {} {{g}_{2}}({{r}_{1}})/\sqrt{1-r_{1}^{2}}, \end{aligned}$$
(36.2)
$$\begin{aligned} f({{r}_{2}})= & {} {{g}_{3}}({{r}_{2}})\sqrt{1-r_{2}^{2}}, \end{aligned}$$
(36.3)

Using the Gauss–Chebyshev integration formulas [25], the integral equations (35) can be converted into a system of algebraic equations as follows:

$$\begin{aligned}&\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{1i}})\left[ \frac{{{{\bar{\beta }}}_{11}}}{{{r}_{1i}}-{{s}_{1k}}}+a{{{\bar{k}}}_{11}}({{s}_{1k}},{{r}_{1i}}) \right] +\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{1i}})\left[ \frac{{{{\bar{\beta }}}_{12}}}{{{r}_{1i}}-{{s}_{1k}}}+a{{{\bar{k}}}_{12}}({{s}_{1k}},{{r}_{1i}}) \right] \nonumber \\&\quad +\sum \limits _{i=1}^{N}{\frac{1-r_{2i}^{2}}{N+1}}{{g}_{3}}({{r}_{2i}})\left[ \frac{c-b}{2}{{{\bar{k}}}_{13}}({{s}_{1k}},{{r}_{2i}}) \right] =0,\quad k=1,2,\ldots ,{N-1}, \end{aligned}$$
(37.1)
$$\begin{aligned}&\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{1i}})\left[ \frac{{{{\bar{\beta }}}_{21}}}{{{r}_{1i}}-{{s}_{1k}}}+a{{{\bar{k}}}_{21}}({{s}_{1k}},{{r}_{1i}}) \right] +\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{1i}})\left[ \frac{{{{\bar{\beta }}}_{22}}}{{{r}_{1i}}-{{s}_{1k}}}+a{{{\bar{k}}}_{22}}({{s}_{1k}},{{r}_{1i}}) \right] \nonumber \\&\quad +\sum \limits _{i=1}^{N}{\frac{1-r_{2i}^{2}}{N+1}}{{g}_{3}}({{r}_{2i}})\left[ \frac{c-b}{2}{{{\bar{k}}}_{23}}({{s}_{1k}},{{r}_{2i}}) \right] =0,\quad k=1,2,\ldots ,{N-1}, \end{aligned}$$
(37.2)
$$\begin{aligned}&\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{1i}})\left[ a{{{\bar{k}}}_{31}}({{s}_{2k}},{{r}_{1i}})\right] +\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{1i}})\left[ a{{{\bar{k}}}_{32}}({{s}_{2k}},{{r}_{1i}}) \right] +\sum \limits _{i=1}^{N}{\frac{1-r_{2i}^{2}}{N+1}}{{g}_{3}}({{r}_{2i}})\nonumber \\&\quad \times \left[ \frac{{{{\bar{\beta }}}_{33}}}{2}\left( \frac{1}{{{r}_{2i}}-{{s}_{2k}}}+\frac{1}{{{r}_{2i}}+{{s}_{2k}}+2\frac{c+b}{c-b}}\right) +{{{\bar{k}}}_{33}}({{s}_{2k}},{{r}_{2i}}) \right] =\rho gh,\quad k=1,2,\ldots ,{N+1}. \end{aligned}$$
(37.3)

Similarly, the equilibrium and single-value conditions (33) become

$$\begin{aligned}&\displaystyle a\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{1}}({{r}_{i}})=\frac{1}{\pi }P, \end{aligned}$$
(38.1)
$$\begin{aligned}&\displaystyle a\sum \limits _{i=1}^{N}{\frac{1}{N}}{{g}_{2}}({{r}_{i}})=\frac{1}{\pi }T, \end{aligned}$$
(38.2)
$$\begin{aligned}&\displaystyle \frac{c-b}{2}\sum \limits _{i=1}^{N}{\frac{1-r_{2i}^{2}}{N+1}}{{g}_{3}}({{r}_{2i}})=0 \end{aligned}$$
(38.3)

where

$$\begin{aligned} {{r}_{1i}}= & {} \cos \left( \frac{2i-1}{2N}\pi \right) ,\quad i=1,2,\ldots ,N, \end{aligned}$$
(39.1)
$$\begin{aligned} {{s}_{1k}}= & {} \cos \left( \frac{k}{N}\pi \right) ,\quad k=1,2,\ldots ,N-1, \end{aligned}$$
(39.2)
$$\begin{aligned} {{r}_{2i}}= & {} \cos \left[ \frac{i\pi }{N+1} \right] ,\quad i=1,2,\ldots ,N, \end{aligned}$$
(39.3)
$$\begin{aligned} {{s}_{2k}}= & {} \cos \left[ \frac{\pi (2k-1)}{2(N+1)} \right] ,\quad k=1,2,\ldots ,N+1. \end{aligned}$$
(39.4)

It is worth noting that Eqs. (37) and (38) provide \(3N+2\) equations to compute the \(3N+2\) unknowns, namely \(g_1 \left( {r_{1i} } \right) \), \(g_2 \left( {r_{1i} } \right) \), \(g_3 \left( {r_{2i} } \right) \), b, and c. Note that both in Eqs. (37.1) and (37.2), one equation is deficient, and the equilibrium conditions (38.1) and (38.2), respectively, must be added to Eqs. (37.1) and (37.2). Conversely, the additional equation in (37.3) is equivalent to the consistency condition and should be extracted from (37.3). The system of equations is linear in terms of \(g_1 \left( {r_{1i} } \right) \), \(g_2 \left( {r_{1i} } \right) \), \(g_3 \left( {r_{2i} } \right) \), but highly nonlinear in terms of the variables b and c. Thus, to solve this problem, an efficient iterative method should be used. In this study, an iterative method based on Newton–Raphson technique is performed with an acceptable accuracy of the order of \(10^{-10}\). The iterative method is started with an initial guess for b and c. With these values, \(g_1 \left( {r_{1i} } \right) \), \(g_2 \left( {r_{1i} } \right) \), and \(g_3 \left( {r_{2i} } \right) \) can be computed from Eqs. (37.1,2), (38.1), (37.2) and (37.3) with one extracted equation. The single-value condition (38.3) and the extracted equation from (37.3) are checked afterward by substituting \(g_1 \left( {r_{1i} } \right) \), \(g_2 \left( {r_{1i} } \right) \), and \(g_3 \left( {r_{2i} } \right) \) into them. Iterations are carried on until acceptable accuracy is obtained.

6 Validation of results and parametric study

Before going ahead with the results of this work, a validation study has been performed with Zhou and Lee [26]. These authors investigated the contact problem for magneto-electro-elastic materials under the action of a moving punch where the magneto-electro-elastic medium is assumed to be infinitely long. The compared quantities were the contact stress, p(x), and normal electric displacement, q(x), which were found to be in excellent agreement with the results of Zhou and Lee [26] (see Fig. 3). Additionally, Table 1 lists the critical load factor \(\lambda _\mathrm{cr}={P_\mathrm{cr}}/{\rho g h^2}\) by comparing the results of this study and those of Civelek et al. [27].

Fig. 3
figure 3

Comparison of the contact stress, p(x), and normal electric displacement, q(x), with [26] (\(h\rightarrow \infty \))

Full size image
Table 1 Comparison of the critical load factor, \(\lambda _\mathrm{cr}\), with those from Ref. [27]
Full size table
Table 2 Material parameters used in the parametric study
Full size table
Fig. 4
figure 4

Variations of the critical load, \(P_\mathrm{cr}\), and critical separation point, \(x_\mathrm{cr}\), with electric charge, T, and layer height, h (\(a=0.02\) m)

Full size image

For the parametric study, we used the material properties given in Table 2. Figure 4 shows the variations of the critical load \(P_\mathrm{cr}\) and critical separation point \(x_\mathrm{cr}\) with electric charge, T, and layer height, h. Note that punch half length is taken to be \(a=0.02\) m. The critical load, \(P_\mathrm{cr}\), and the critical separation point, \(x_\mathrm{cr}\), have almost linear relationship with the electric charge, T. As the electric charge increases, both critical load and the critical separation length decrease, which is expected. However, both critical load and the critical separation length increase when the layer height becomes higher. This result implies that, if the height of the layer is high enough, the layer turns to behave like a half-plane and the separation does not occur no matter how large the load is. Table 3 lists the critical load, \(P_\mathrm{cr}\), and critical separation point, \(x_\mathrm{cr}\), with respect to the half punch length, a, for a specific configuration of the parameters: \(T=1\times 10^{-4}\) C/m and \(h=0.5\) m. As the punch length increases, both critical load and critical separation length increase.

Table 3 Variations of the critical load \(P_\mathrm{cr}\) and critical separation point \(x_\mathrm{cr}\) with punch length a (\(T=1\times 10^{-4}\) C/m, \(h=0.5\) m)
Full size table
Fig. 5
figure 5

Variations of the contact stress, p(x), and normal electric displacement, q(x), on the top surface of the layer, contact stress between the layer and the substrate, \(\sigma _{z}(x,0)\), and derivative of the interface displacement, f(x), versus mechanical load, P. \(P_\mathrm{cr} =534.47\) kN/m (\(T=1\times 10^{-4}\) C/m, \(h=0.5\) m \(a=0.02\) m)

Full size image
Table 4 Variations of the critical load \(P_\mathrm{cr}\) and critical separation point \(x_\mathrm{cr}\) with electric charge T and layer height h (\(a= 0.02\) m)
Full size table
Table 5 Variation of the separation region with mechanical load P (\(T=1\times 10^{-4}\) C/m, \(h=0.5\) m \(a=0.02\) m)
Full size table
Fig. 6
figure 6

Variations of the contact stress, p(x), and normal electric displacement, q(x), on the top surface of the layer, contact stress between the layer and the substrate, \(\sigma _{z}(x,0)\), and derivative of the interface displacement, f(x), versus electric charge T (\(P = 2000\) kN/m, \(h=0.5\) m \(a=0.02\) m)

Full size image

The effect of the applied load on the behavior of the contact stress, p(x), and normal electric displacement, q(x), on the top surface of the layer, contact stress between the layer and the substrate, \(\sigma _{z}(x,0)\), and derivative of the interface displacement, f(x), was investigated next. As the load is increased, the magnitude of the contact pressure increases; however, there is no effect of the applied load on the electric displacement (see Fig. 5). As indicated in Ref. [26], the electric displacement is only affected by electrical properties. The interface contact stress, \(\sigma _{z}(x,0)\), is shown in Fig. 5c which clearly shows the discontinuous contact after increasing the load \(P>P_\mathrm{cr}\). At \(P=P_\mathrm{cr}\), \(b=c=0.91\) m (see Table 5), and the magnitude of the contact stress at that point is zero which means there is no separation. Note that for \(T = 0.0001\) C/m and \(h=0.5\) m the critical separation point is also \(x_\mathrm{cr}=0.91\) m (see Table 4) which agrees with the discontinuous contact result. After increasing the load above \(P_\mathrm{cr}\), the contact pressure becomes negative, indicating separation at the interface. As the load increases more, the separation length increases as shown in Fig. 5c. The derivative of the interface displacement f(x) is shown in Fig. 5d. Note that \(f(x) = 0\) at the critical load \(P=P_\mathrm{cr}\). As the applied load is increases, the derivative of the displacement becomes positive to the left and negative to the right. When separation occurs, there are two regions at the interface that looses contact between the substrate and the layer. These regions extend from \(-c\) to \(-b\) and from b to c, and they are symmetric due to the frictionless contact of the punch with the layer. As the applied load increased, the length of the separation region increases, i.e., c increases and b decreases as shown in Table 5. After certain values of \(x_\mathrm{cr}\), the effect of the applied load vanishes on the interface contact stress \(\sigma _{z} (x,0)\), and only the effect of body force remains as a constant, as expected

Figure 6 shows the variations of the contact stress, p(x), and normal electric displacement, q(x), on the top surface of the layer, contact stress between the layer and the substrate, \(\sigma _{z}(x,0)\), and derivative of the interface displacement, f(x), versus electric charge, T. For this Figure, the parameters are set such that \(P = 2000\) kN/m, \(h=0.5\) m, and \(a=0.02\) m. Since the parameter changed in this Figure is the electric charge T, the contact stress p(x) was not affected by the variation; however, as opposed to Fig. 5b, there is a considerable effect on the normal electric displacement field.

Fig. 7
figure 7

Variations of the contact stress, p(x), and normal electric displacement, q(x), on the top surface of the layer, contact stress between the layer and the substrate, \(\sigma _{z}(x,0)\) versus mechanical punch length a (\(P = 2000\) kN/m, \(T=1\times 10^{-4}\) C/m, \(h=0.5\) m)

Full size image

Figure 7 depicts the variations of the contact stress, p(x), and normal electric displacement, q(x), on the top surface of the layer, contact stress between the layer and the substrate, \(\sigma _{z}(x,0)\), versus punch length, a. This time the constant parameters are the load, electric charge, and the thickness of the layer, and they are set at \(P = 2000\) kN/m, \(T=1\times 10^{-4}\) C/m, \(h=0.5\) m), respectively.

Finally, to observe the effect of varying the layer thickness on p(x), q(x), and \(\sigma _{z}(x,0)\), the layer thickness was varied by setting \(P = 2000\) kN/m, \(T=1\times 10^{-4}\) C/m, \(a=0.02\) m (see Fig. 8). Since there is no change in both applied load and the electric charge, the contact stress and the electric displacement did not change; however, the interface contact stress changes dramatically as shown in Fig. 8c.

Fig. 8
figure 8

Variations of the contact stress, p(x), and normal electric displacement, q(x), on the top surface of the layer, contact stress between the layer and the substrate, \(\sigma _{z}(x,0)\), versus layer height, h (\(P = 2000\) kN/m, \(T=1\times 10^{-4}\) C/m, \(a=0.02\) m)

Full size image

7 Conclusions

The frictionless continuous and discontinuous contact problems between a rigid conducting flat punch and a piezoelectric homogeneous layer resting on a rigid substrate are considered in this study in the presence of the body force. The resulting mixed-boundary value problem is converted analytically using an appropriate integral transform to one of singular integral equations. The Gauss–Chebyshev integration formulas are utilized to convert the obtained integral equations into a set of nonlinear algebraic equations which are solved using an appropriate iterative algorithm to obtain the dimensions of the separation region and the associated contact pressure and normal electric displacement. Based on this investigation, the following conclusions can be drawn:

  • The critical load and critical separation point increase with increasing values of mechanical load, punch, length, and layer height. However, they decrease slightly when the electric charge increases.

  • The magnitude of the contact stress between the flat punch and the layer increases when the mechanical load increases and the punch length decreases. However, it is insensitive to the change in the electric charge and the layer height.

  • The electric displacement between the flat punch and the layer is not influenced by the mechanical load and the layer height. On the other hand, its magnitude increases when the electric charge is becoming bigger and punch length is becoming smaller.

  • Electric charge does not influence the separation region and the contact stress between the layer and the substrate.