Analysis of the Mechanical and Thermal Buckling of Laminated Beams by New Refined Shear Deformation Theory

Abstract

Thermo-mechanical buckling analysis of symmetric and antisymmetric laminated composite beams is performed based on a refined simple nth higher-order shear deformation theory. The theory accounts for the parabolic distribution of the transverse shear strains and satisfies the zero traction boundary conditions on the surfaces of the beam without using shear correction factors. The governing equations and corresponding simply boundary conditions are obtained with the aid of minimum total potential energy principle. The effects of temperatures on non-dimensional critical buckling loads are investigated. Numerical results due to present theory are compared with data available in the literature to show the accuracy and simplicity of the proposed theory in analyzing the thermo-mechanical buckling of laminated composite beams.

1 Introduction

The use of composite materials has been greatly increased in the weight-sensitive applications such as aerospace, marine, civil and mechanical engineering structures because of their superior mechanical properties such as high strength-to-weight ratio and high stiffness-to weight-ratio as well as their directionality property capable of providing the desired elastic couplings through the proper selection of the layup parameters. The laminated composite beams are basic structural components and are widely used in various structures. For the safe design of composite beams, accurate knowledge of their vibration characteristics and buckling behaviors are necessary. The wide use of laminated beams has stimulated considerable interest in their dynamic and buckling analyses. A lot of relevant papers have been published in recent decades, and many mathematical models and solution techniques have been developed, for example, Touratier (1991), Soldatos(1992), Khdeir and Reddy (1997), Khdeir (2001), Karama et al. (2003), Kapuria et al.(2004), Aydogdu (2006, 2009), Reddy (1997), Emam (2011), Xiaohui and Wanji (2009), Kim (2009), Della and Shu(2009), Akbas and Kocaturk (2012), Yu and Sun (2012), Mohri et al. (2012), Vo and Thai (2012a, b), Kim and Choi (2013), Huang et al. (2014), Aktaş and Balcıoğlu (2014).

Recently, Akgöz, and Civalek (2015) developed new non-classical sinusoidal plate model via modified strain gradient theory. This model takes into account the effects of shear deformation without any shear correction factors and also can capture the size effects due to additional material length-scale parameters. Li and Qiao (2015a, b) extended the Reddy’s high-order shear deformation beam theory with a von Karman type of kinematic nonlinearity for mechanical and thermal post-buckling analysis of anisotropic laminated beams with different boundary conditions. Kahya(2016) developed the multilayer beam finite element for vibration and buckling of laminated composite and sandwich beams via the first-order shear deformation theory. The multilayered beam element consists of N layers and includes totally 3N + 7 degrees of freedom (DOFs); in addition, slip and delamination between the layers are not allowed. Canales and Mantari (2016) derived the Ritz solution for vibration and buckling analysis of composite beams using a generalized higher-order shear deformation theory. Ergun et al. (2016) studied experimentally the free vibration and buckling behaviors of hybrid composite beams having different span lengths and orientation angles subjected to different impact energy levels.

The analytical solutions for simply supported and clamped boundary conditions of a post-buckling sandwich beam are obtained in the thermal environment presented by Li et al. (2018). The effect of the humidity conditions on thermal buckling analysis of grapheme system containing two layers under different boundary conditions is developed by Sobhy and Zenkour (2018); Dihaj et al.(2018) studied the free vibration analysis of chiral double-walled carbon nanotube embedded in an elastic medium using non-local elasticity theory and Euler–Bernoulli beam model. Akbaş (2018) presented a new method for post-buckling responses of a simply supported laminated composite beam subjected to a non-follower axially compression loads using nonlinear kinematic model of the laminated beam in conjunction with Timoshenko beam theory and total Lagrangian approach. The unified approach for compressive buckling analysis of stiffened composite plates, which takes into account the contribution of stringers’ rotational stiffness, achieves a closed-form solution presented by Feng (2018).

In the present paper, the authors combine the displacement field of theory developed by Xiang (2014) and the displacement field of refined shear deformation theory to develop a new refined simple nth higher-order shear deformation theory for thermo-mechanical buckling analysis of laminated beam. The theory satisfies that the transverse shear stresses should be vanished at the top and bottom surfaces of beam, and so there is no need for using a shear correction factor. That is because the present simplified refined nth-order theory is based on the assumption that the in-plane and transverse displacements consist of bending and shear components, in which the bending components do not contribute toward shear forces and, likewise, the shear components do not contribute toward bending moments. The governing differential equations and corresponding simply boundary conditions in buckling are derived with the aid of minimum total potential energy principle. The thermal effects on the critical buckling loads of simply supported laminate beams are investigated. The accuracy of this theory is demonstrated according to some numerical examples and comparisons with the corresponding data in the literature.

2 Theoretical Formulations

The displacement field of the conventional nth-order shear deformation theory is given by Xiang (2014):

$$\begin{aligned} & U\left( {x,y,z} \right) = u_{0}^{{}} \left( {x,y} \right) + z\varphi_{x}^{{}} \left( {x,y} \right) - \frac{1}{n}\left( {\frac{2}{h}} \right)_{{}}^{n - 1} z_{{}}^{n} \left( {\varphi_{x}^{{}} \left( {x,y} \right) + \frac{{{\partial }w\left( {x,y} \right)}}{{{\partial }x}}} \right) \\ & n = 3,5,7,9, \ldots \\ & W\left( {x,y,z} \right) = w_{0} \left( {x,y} \right) \\ \end{aligned}$$

(1)

where $w_{0}$ and ${\kern 1pt} \varphi_{x}^{{}}$ are two unknown displacement functions of the mid-plane of the beam; and h is the thickness of the beam. By dividing the transverse displacement into bending and shear parts (i.e., $w_{0}^{{}} = w_{b} + w_{s}$) and making further assumptions given by $\varphi_{x}^{{}} = - {{\partial w_{b} } \mathord{\left/ {\vphantom {{\partial w_{b} } {\partial x}}} \right. \kern-0pt} {\partial x}}$, the displacement field of the new refined theory can be rewritten in a simpler form as:

where

$$\begin{aligned} & U\left( {x,y,z} \right) = u_{0}^{{}} \left( {x,y} \right) - z\frac{{\partial w_{b} }}{\partial x} - \frac{1}{n}\left( {\frac{2}{h}} \right)_{{}}^{n - 1} z_{{}}^{n} \left( {\frac{{\partial w_{s}^{{}} }}{\partial x}} \right) \\ & n = 3,5,7,9, \ldots \\ & W\left( {x,y,z} \right) = w_{b} \left( {x,y} \right) + w_{s} \left( {x,y} \right) \\ \end{aligned}$$

(2)

Clearly, the displacement field in Eq. (2) contains only two unknowns, $w_{b}^{{}}$ and $w_{s}^{{}}$. The nonzero strains associated with the displacement field in Eq. (2) are:

$$\begin{aligned} & \varepsilon_{x} = \varepsilon_{x}^{0} + zk_{x}^{b} + f(z)k_{x}^{s} \\ & \gamma_{xz} = g(z)\gamma_{xz}^{s} \\ \end{aligned}$$

(3)

where

$$\begin{aligned} & \varepsilon_{x}^{0} = \frac{{\partial u_{0} }}{\partial x},\quad k_{x}^{b} = - \frac{{\partial^{2} w_{b} }}{{\partial x^{2} }}{\kern 1pt} ,\quad k_{x}^{s} = - \frac{{\partial^{2} w_{s} }}{{\partial x^{2} }},\quad {\kern 1pt} \gamma_{xz}^{s} = \frac{{\partial w_{s} }}{\partial x} \\ & g(z) = 1 - f^{{\prime }} (z){\kern 1pt} ,\quad f^{{\prime }} (z) = \frac{{{\text{d}}f(z)}}{{{\text{d}}z}},{\kern 1pt} \quad f(z) = {\kern 1pt} {\kern 1pt} \frac{1}{n}\left( {\frac{2}{h}} \right)_{{}}^{n - 1} z_{{}}^{n} {\kern 1pt} ,\quad g(z) = 1 - {\kern 1pt} \left( {\frac{2z}{h}} \right)_{{}}^{n - 1} {\kern 1pt} \\ \end{aligned}$$

(4)

Constitutive relation can be written in matrix form as follows:

$$\left\{ \begin{aligned} \sigma_{x} \hfill \\ \sigma_{xz} \hfill \\ \end{aligned} \right\}^{(k)} = \left[ {\begin{array}{*{20}c} {\bar{Q}_{11} } & 0 \\ 0 & {\bar{Q}_{55} } \\ \end{array} } \right]\left( {\left\{ \begin{aligned} \varepsilon_{x} \hfill \\ \gamma_{xz} \hfill \\ \end{aligned} \right\} - \alpha_{x}^{{}} \Delta T\left\{ \begin{aligned} 1 \hfill \\ 0 \hfill \\ \end{aligned} \right\}} \right)^{(k)}$$

(5)

where usual notations for normal and shear stress components are adopted. The relationship of the global reduced stiffness matrix $\bar{Q}_{ij}$ and transformed coefficient of thermal expansion can be referred to any standard texts such as (Reddy (1997)).

After substituting Eq. (3) in Eq. (5), the resulting equation is integrated through the thickness of the laminate. Then, the laminated constitutive equations take the form

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {M_{x}^{b} } \\ {M_{x}^{s} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {B_{11} } & {B_{11}^{s} } \\ {B_{11}^{{}} } & {D_{11}^{{}} } & {D_{11}^{s} } \\ {B_{11}^{s} } & {D_{11}^{s} } & {H_{11}^{s} } \\ \end{array} } \right]\left\{ \begin{aligned} \varepsilon_{x}^{0} \hfill \\ k_{x}^{b} \hfill \\ k_{x}^{s} \hfill \\ \end{aligned} \right\} - \left\{ \begin{aligned} N_{x}^{T} \hfill \\ M_{x}^{bT} \hfill \\ M_{x}^{sT} \hfill \\ \end{aligned} \right\} \\ & Q_{xz}^{{}} = A_{55}^{s} \frac{{\partial w_{s}^{{}} }}{\partial x} \\ \end{aligned}$$

(6)

where

$$\begin{aligned} & \left\{ {N_{x}^{{}} ,M_{x}^{b} ,M_{x}^{s} } \right\} = b\int\limits_{ - h/2}^{h/2} {\left( {1,z,f(z)} \right)\sigma_{x}^{{}} {\text{d}}z{\kern 1pt} } = b\sum\limits_{k = 1}^{N} {\int_{{Z_{k} }}^{{Z_{k + 1} }} {\left( {1,z,f(z){\kern 1pt} } \right)\sigma_{x}^{{}} {\text{d}}z} } \\ & Q_{xz}^{{}} = b\int_{ - h/2}^{h/2} {\sigma_{xz} g(z)} {\text{d}}z = b\sum\limits_{k = 1}^{N} {\int_{{Z_{k} }}^{{Z_{k + 1} }} {\sigma_{xz} g(z){\text{d}}z} } \\ & \left\{ {N_{x}^{T} ,M_{x}^{bT} ,M_{x}^{sT} } \right\} = b\sum\limits_{k = 1}^{N} {\int_{{Z_{k} }}^{{Z_{k + 1} }} {{\kern 1pt} \left( {1,z,f(z){\kern 1pt} } \right)\bar{Q}_{11}^{{}} \alpha_{x}^{{}} \Delta T{\text{d}}z} } \\ & (A_{11} ,{\kern 1pt} {\kern 1pt} B_{11} ,D_{11} ,B_{11}^{s} ,D_{11}^{s} ,H_{11}^{s} ) = b\sum\limits_{k = 1}^{N} {\int_{{Z_{k} }}^{{Z_{k + 1} }} {\bar{Q}_{11} (1,z,z^{2} ,f(z),zf(z),(f(z))_{{}}^{2} ){\text{d}}z} } \\ & A_{55}^{s} = b\sum\limits_{k = 1}^{N} {\int_{{Z_{k} }}^{{Z_{k + 1} }} {\bar{Q}_{55} (g(z))_{{}}^{2} {\text{d}}z} } \\ \end{aligned}$$

(7)

where $\bar{Q}_{11}^{{}}$ is the reduced stiffness matrix, $\alpha_{x}^{{}}$ the transformed thermal coefficient of expansion and $\Delta T$ the constant temperature rise or drop through the thickness.

The strain energy of the beam can be written as

$$U = \frac{1}{2}\int_{V} {\sigma_{ij} \varepsilon_{ij} {\text{d}}V = } \frac{1}{2}\int_{V} {\left( {\sigma_{x} \varepsilon_{x} + \sigma_{xz} \gamma_{xz} } \right){\text{d}}V}$$

(8)

Substituting Eqs. (3) and (5) into Eq. (8) and integrating through the thickness of the beam, the strain energy of the beam due to the normal force, shear force, bending moment and shear moment can be rewritten as

$$U = \frac{1}{2}\int\limits_{0}^{L} {\left[ {N_{x}^{{}} \delta \varepsilon_{x}^{0} + M_{x}^{b} \delta k_{x}^{b} + M_{x}^{s} k_{x}^{s} + Q_{xz}^{s} \gamma_{xz}^{s} } \right]{\text{d}}x}$$

(9)

The work of the beam done by applied forces (mechanical force and forces due to variation of temperature $\Delta T$) can be written as

$$V = \frac{1}{2}\int\limits_{0}^{L} {\left[ {\left( {P + N_{x}^{T} } \right)\frac{{\partial^{2} (w_{b}^{{}} + w_{s}^{{}} )}}{{\partial x^{2} }}} \right]} {\text{d}}x$$

(10)

where $P$ is a mechanical force and $N_{x}^{T}$ are applied forces due to variation of temperature.

The principle of minimum total potential energy (Reddy (1997)) is used here to derive the equations governing the displacement field and the constitutive equation. The principle can be stated in analytical form as

$$\delta (U + V) = 0$$

(11)

where $\delta$ indicates a variation in relation to x.

Substituting Eqs. (9) and (10) into Eq. (11) and integrating the equation by parts, collecting the coefficients of $\delta u_{0}^{{}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \delta w_{b}^{{}} {\kern 1pt} {\kern 1pt}$ and ${\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta w_{s}^{{}}$, the governing equations can be obtained as follows:

$$\frac{{\partial N_{x}^{{}} }}{\partial x} = 0$$

(12a)

$$\frac{{\partial^{2} M_{x}^{b} }}{{\partial x^{2} }} + \bar{N}\frac{{\partial^{2} (w_{b}^{{}} + w_{s}^{{}} )}}{{\partial x^{2} }} = 0$$

(12b)

$$\frac{{\partial^{2} M_{x}^{s} }}{{\partial x^{2} }} + \frac{{\partial Q_{xz}^{s} }}{\partial x} + \bar{N}\frac{{\partial^{2} (w_{b}^{{}} + w_{s}^{{}} )}}{{\partial x^{2} }} = 0$$

(12c)

where

$$\bar{N} = P + N_{x}^{T}$$

(13)

Equations (12a–12c) can be expressed in terms of displacements $\left( {u_{0}^{{}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} w_{b}^{{}} ,w_{s}^{{}} } \right){\kern 1pt}$ by substituting for the force and moment stress resultants from Eq. (7). For laminated beam, the governing Eqs. (12a–12c) take the form

$$A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} - B_{11} \frac{{\partial^{3} w_{b} }}{{\partial x^{3} }} - B_{11}^{s} \frac{{\partial^{3} w_{s} }}{{\partial x^{3} }} = 0$$

(14a)

$$B_{11} \frac{{\partial^{3} u}}{{\partial x^{3} }} - D_{11} \frac{{\partial^{4} w_{b} }}{{\partial x^{4} }} - D_{11}^{s} \frac{{\partial^{4} w_{s} }}{{\partial x^{4} }} + \bar{N}\frac{{\partial^{2} (w_{b}^{{}} + w_{s}^{{}} )}}{{\partial x^{2} }} = 0$$

(14b)

$$B_{11}^{s} \frac{{\partial^{3} u}}{{\partial x^{3} }} - D_{11}^{s} \frac{{\partial^{4} w_{b} }}{{\partial x^{4} }} - H_{11}^{s} \frac{{\partial^{4} w_{s} }}{{\partial x^{4} }} + A_{55}^{s} \frac{{\partial^{2} w_{s} }}{{\partial x^{2} }} + \bar{N}\frac{{\partial^{2} (w_{b}^{{}} + w_{s}^{{}} )}}{{\partial x^{2} }} = 0$$

(14c)

By following the Navier solution procedure, the solutions to the problem are assumed to take the following forms:

$$u(x) = \sum\limits_{m = 1}^{{\infty }} {U_{mn} \cos \lambda x}$$

(15a)

$$w_{b} (x,y) = \sum\limits_{m = 1}^{\infty } {W_{bmn} \sin \lambda x}$$

(15b)

$$w_{s}^{{}} (x,y) = \sum\limits_{m = 1}^{{\infty }} {W_{smn} \sin \lambda x}$$

(15c)

where$U_{mn}^{{}} ,{\kern 1pt} W_{bmn}^{{}} ,W_{smn}^{{}}$ are arbitrary parameters to be determined, $\lambda = {{m\pi } \mathord{\left/ {\vphantom {{m\pi } L}} \right. \kern-0pt} L}$.

Substituting the expansions of $\left( {u_{0}^{{}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} w_{b}^{{}} ,w_{s}^{{}} } \right){\kern 1pt}$ from Eqs. (15a)–(15c) into the stability Eqs. (14a)–(14c), the analytical solutions can be obtained from the following equations:

$$\left( {\left[ {\begin{array}{*{20}c} {k_{11}^{{}} } & {k_{12}^{{}} } & {k_{13}^{{}} } \\ {k_{12}^{{}} } & {k_{22}^{{}} } & {k_{23}^{{}} } \\ {k_{13}^{{}} } & {k_{23}^{{}} } & {k_{33}^{{}} } \\ \end{array} } \right] + \xi \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \\ \end{array} } \right]} \right)\left\{ {\begin{array}{*{20}c} {U_{mn}^{{}} } \\ {W_{bmn}^{{}} } \\ {W_{smn}^{{}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right\}$$

(16)

where

$$\begin{aligned} & k_{11}^{{}} = A_{11} \lambda_{{}}^{2} ,\quad k_{12}^{{}} = - B_{11} \lambda_{{}}^{3} ,\quad k_{13}^{{}} = - B_{11}^{s} \lambda_{{}}^{3} \\ & k_{22}^{{}} = D_{11} \lambda_{{}}^{4} ,\quad k_{23}^{{}} = D_{11}^{s} \lambda_{{}}^{4} ,\quad k_{33}^{{}} = H_{11}^{s} \lambda_{{}}^{4} + A_{55}^{s} \lambda_{{}}^{2} ,{\kern 1pt} \quad \xi = - \left( {P + N_{{}}^{T} } \right)\lambda_{{}}^{2} \\ \end{aligned}$$

(17)

For nontrivial solution, the determinant of the coefficient matrix in Eq. (16) must be zero. This gives the following expression for buckling load:

$$P = - N_{{}}^{T} + \frac{{\det \left[ {k_{ij} } \right]}}{{k_{11}^{{}} \lambda_{{}}^{2} \left( {k_{22}^{{}} + k_{33}^{{}} - 2k_{23}^{{}} } \right) - k_{12}^{{}} \lambda_{{}}^{2} \left( {k_{12}^{{}} - 2k_{13}^{{}} } \right) - k_{13}^{2} \lambda_{{}}^{2} }}$$

(18)

The equation below shows that temperature reduces the critical buckling load.

On the other hand, if the beam is subjected to temperature change only with no mechanical loads, it is possible to define the critical temperature change that causes buckling. In light of Eq. (16), the critical temperature change is given as follows:

$$\Delta T_{cr}^{{}} = \frac{1}{{T_{11}^{{}} }}\left\{ {\frac{{\det \left[ {k_{ij} } \right]}}{{k_{11}^{{}} \lambda_{{}}^{2} \left( {k_{22}^{{}} + k_{33}^{{}} - 2k_{23}^{{}} } \right) - k_{12}^{{}} \lambda_{{}}^{2} \left( {k_{12}^{{}} - 2k_{13}^{{}} } \right) - k_{13}^{2} \lambda_{{}}^{2} }}} \right\}$$

(19)

where

$${\kern 1pt} T_{11}^{{}} = \int\limits_{ - h/2}^{h/2} {\bar{Q}_{11} \alpha_{x}^{{}} {\text{d}}A}$$

(20)

3 Results and discussion

In this section, a number of numerical examples are presented and analyzed to verify the accuracy of the present theory and to investigate the critical buckling of symmetric and antisymmetric laminated simply supported shear-deformable composite beam. All laminates are of equal thickness and made of the same orthotropic material, whose properties are as follows (Khdeir and Reddy(1997), Khdeir(2001), Aydogdu(2006,009), Reddy (1997), Vo and Thai (2012a, 2012b), Li and Qiao(2015a, b), Kahya(2016), Canales and Mantari (2016)):

$$\begin{aligned} {\text{Material}}\;{\text{I:}}\;{{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = {\text{Open}},\quad G_{12} = G_{13} = 0.6E_{2} ,\quad G_{23} = 0.5E_{2} ,\quad v_{12} = 0.25{{,\quad \alpha_{1} } \mathord{\left/ {\vphantom {{,\quad \alpha_{1} } {\alpha_{2} }}} \right. \kern-0pt} {\alpha_{2} }} = {\text{Open}} \hfill \\ {\text{Material}}\;{\text{II:}}\;E_{1}^{{}} /E_{2}^{{}} = {\text{open}},\quad G_{12}^{{}} = G_{13}^{{}} = 0.5E_{2}^{{}} ,{\kern 1pt} \quad G_{23}^{{}} = 0.2E_{2}^{{}} ,\quad \nu_{12}^{{}} = 0.25 \hfill \\ \end{aligned}$$

We use the model developed in the present study to determine the non-dimensional first critical buckling load for laminated beams. The results are compared with those available in the literature. Firstly, mechanical buckling analysis of simply supported composite beams with symmetric cross-ply (0/90/0) is performed. Materials I and II with E₁/E₂ = 10 and 40 are used. The critical buckling loads for different length-to-thickness ratios are compared with analytical solutions (Khdeir and Reddy 1997; Aydogdu 2006) and the finite elements method (Vo and Thai 2012a; Kahya 2016) in Tables 1 and 2. The comparisons are well justified.

Table 1 Comparison of the non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ of symmetric cross-ply composite laminated beams (0/90/0) with simply supported boundary condition (Materials I and II with E₁/E₂ = 10)

Table 2 Comparison of the non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ of symmetric cross-ply composite laminated beams (0/90/0) with simply supported boundary condition (Materials I and II with E₁/E₂ = 40)

The second example concerns mechanical buckling behavior of simply supported cross-ply laminated beams. The non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ have been obtained for two-layer cross-ply beams with various values of length-to-thickness ratio L/h, which are presented in Table 3. The Material I is used with E₁/E₂ = 40. The present results are compared with those due to third-order beam theory (TOBT), the results given in Khdeir and Reddy (1997), the parabolic shear deformation beam theory (PSDBT) given in Aydogdu (2006), the refined shear deformation theory (RSDT) given in Vo and Thai (2012a, b), higher-order shear deformation beam theory (HOSDBT) given in Li and Qiao (2015a) and the finite element method (FEM) given in Kahya (2016). The differences between non-dimensional critical buckling loads obtained by the present formulation and those using different higher-order beam theories and the finite element method are very small.

Table 3 Comparison of the non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ of antisymmetric cross-ply composite laminated beams (0/90) with simply supported boundary condition (Material I E₁/E₂ = 40)

The next comparison example is presented in Table 4 that reports the non-dimensional critical buckling load for orthotropic the unidirectional composite beams (θ = 0 and 90) and symmetric cross-ply laminated beams four-layer (0/90)s a simply supported for different length-to-thickness ratios (L/h = 10, 20, 100). The Material II is used with E₁/E₂ = 25. The obtained are compared with those of Reddy (1997) based on the Timoshenko beam theory (TBT) and the results of Kahya (2016) based on finite elements methods via first-order shear deformation theory (FSDT). It is seen that the present results are in excellent agreement with the literature values using shear deformation theory as seen from the validation checks.

Table 4 Comparison of the non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ of composite laminated beams with simply supported boundary condition (Material II with E₁/E₂ = 25)

In order to discuss the applicability of the present refined simple nth higher-order shear deformation beam theory to other laminate schemes, the mechanical non-dimensional critical buckling load for laminated beams with a variety of stacking sequences, the results are reported in Table 5. The Material I is used with E₁/E₂ = 40. The present results have been compared with those reported in Mantari (2016). Once again, the present theory is in good agreement with the Ritz solution buckling analysis of composite beams via a generalized higher-order shear deformation theory given by Canales and Mantari (2016).

Table 5 Comparison of the non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ for simply supported composite laminated beams with a variety of stacking sequences (Material I with E₁/E₂ = 40)

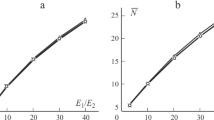
The effect of length-to-thickness ratios of the beam on non-dimensional critical buckling loads is shown in Fig. 1, for simply supported orthotropic composite beams and symmetric cross-ply laminated beams with four-layer (0/90)s and the material properties II used with E₁/E₂ = 25. The obtained results based on the refined simple nth higher-order shear deformation theory are compared with those of Reddy (1997) based on the Timoshenko beam theory. It can be seen that the results of the present theory are in excellent agreement with those of Timoshenko beam theory for all values of length-to-thickness ratios. Also, it can be seen that non-dimensional critical buckling load increases by the increase in length-to-thickness ratio.

Fig. 1

Effect of length-to-thickness ratio (a/h) on the non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$, with simply boundary conditions, (n = 3, Material II with E₁/E₂ = 25)

Finally, in this part, we still discuss the evaluation of the present refined simple nth higher-order shear deformation theory in the study of thermal buckling behavior. Tables 6, 7 and 8 present the non-dimensional critical temperature for different length-to-thickness ratios, different modulus ratios and different thermal expansions, respectively. The Material I is used. On the other hand, the critical buckling temperatures were compared with the theoretical results of the Euler–Bernoulli classical beam theory (CBT), the first-order beam theory (FOBT), the third-order beam theory (HOBT) developed by Khdeir (2001) and the higher-order shear deformation beam theory (HOSDBT) developed by Li and Qiao (2015a, b). The critical buckling temperature of the present theory is in excellent agreement with the results of the other theories of shear deformation. Also, it is observed that the Euler–Bernoulli classical beam theory overestimates the thermal critical buckling of laminated beams. Hence, in order to obtain accurate results for laminated beam, it is necessary to consider the transverse shear deformation effects by using shear deformation theories.

Table 6 Comparison of the non-dimensional critical temperature $\overline{T}_{\text{cr}} = T_{\text{cr}}^{{}} \alpha_{1}^{{}} \left( {{L \mathord{\left/ {\vphantom {L h}} \right. \kern-0pt} h}} \right)_{{}}^{2}$ results for a three layer (0/90/0) symmetric cross-ply beams, for different length-to-thickness ratios (Material I with ${{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 20{{,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha_{1} } \mathord{\left/ {\vphantom {{,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha_{1} } {\alpha_{2} }}} \right. \kern-0pt} {\alpha_{2} }} = 3\,$)

Table 7 Comparison of the non-dimensional critical temperature $\overline{T}_{\text{cr}} = T_{\text{cr}}^{{}} \alpha_{1}^{{}} \left( {{L \mathord{\left/ {\vphantom {L h}} \right. \kern-0pt} h}} \right)_{{}}^{2}$ results for three-layer (0/90/0) symmetric cross-ply beams, for different modulus ratios, (Material I, L/h = 10 ${{,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha_{1} } \mathord{\left/ {\vphantom {{,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha_{1} } {\alpha_{2} }}} \right. \kern-0pt} {\alpha_{2} }} = 3\,$)

Table 8 Comparison of the non-dimensional critical temperature $\overline{T}_{\text{cr}} = T_{\text{cr}}^{{}} \alpha_{1}^{{}} \left( {{L \mathord{\left/ {\vphantom {L h}} \right. \kern-0pt} h}} \right)_{{}}^{2}$ results for three-layer (0/90/0) symmetric cross-ply beams, for different thermal expansion coefficients ratio (Material I, with ${{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 20$, L/h = 10)

The effects of temperatures on non-dimensional critical buckling loads $\bar{P}$ are presented in Tables 9 and 10 for two types of stacking sequences of symmetric cross-ply laminated (0/90/0) and (0/90/90/0), respectively. The beams are subjected to the uniform temperature rises. The mechanical properties of each layer Shen (2001) are assumed to be.

$${{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 40,\quad G_{12} = G_{13} = 0.6E_{2} ,\quad G_{23} = 0.5E_{2} ,\quad v_{12} = 0.25,\quad \alpha_{1}^{{}} = 1.14 \times 10_{{}}^{ - 6} ,\quad \alpha_{2}^{{}} = 11.4 \times 10_{{}}^{ - 6}$$

Table 9 Effects of temperatures on-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ of simply supported symmetric (0/90/0) beam under three sets of thermal loading conditions

Table 10 Effects of temperatures on non-dimensional critical buckling loads $\left( {{{PL_{{}}^{2} } \mathord{\left/ {\vphantom {{PL_{{}}^{2} } {E_{2}^{{}} bh_{{}}^{3} }}} \right. \kern-0pt} {E_{2}^{{}} bh_{{}}^{3} }}} \right)$ of simply supported symmetric (0/90/90/0) beam under three sets of thermal loading conditions

It is seen from Tables 9 and 10 that difference between one-dimensional buckling loads evaluated by EBT and RPT is more considerable for lower slenderness ratios, while this difference almost disappears for higher slenderness ratios. In other words, an increase in slenderness ratio leads to a decline on effects of shear deformation and difference between the results of EBT and SBT. On the contrary, it can be emphasized that the thermal effects on dimensionless buckling loads become more significant for higher slenderness ratios. These numerical results are useful for numerical benchmarking by others.

4 Conclusion

Thermo-mechanical buckling response of simply supported laminated beams is investigated on the basis of a refined simple nth higher-order shear deformation beam theory. The governing differential equations are derived by implementing minimum total potential energy principle. Thermal effects on the critical buckling loads of simply supported laminated beams are investigated. The obtained results are compared with other available results in the published references. Significant observations from the results can be summarized as follows:

• 1. In the present paper, the authors combine the nth-order shear deformation theory developed by Xiang (2014) with the idea of the refined beam theory. The axial displacement field uses parabolic function in terms of thickness ordinate to include the effect of transverse shear deformation. The transverse displacement consists of bending and shear components. These ideas are used for developing the new nth-order shear deformation theory with modified displacement field to its optimization. Closed-form solutions for thermo-mechanical buckling behavior of composite beam are obtained.

• 2. This theory is seen to behave well, and the results of sample examples show good agreement with those in the literature as seen from the validation checks.

• 3. Effect of temperature change on buckling characteristic of laminated beams becomes more pronounced for larger values of length-to-thickness ratio.

• 4. The transverse shear deformation has the effect of decreasing both buckling loads. Thus, the classical laminate theory overpredicts buckling loads. This is primarily due to the assumed infinite rigidity of the transverse normals in the classical laminate theory. Note that the assumption does not yield a conservative result; i.e., if one designs a beam for buckling load based on the classical laminate theory and if no safety factor is used, it will fail for a working load smaller than the critical buckling load.

Appendix

(1) Consider a laminate beam made of n plies. Each ply has a thickness of $t_{k}^{{}}$. Then, the thickness of the laminate h is

$$h = \sum\limits_{k = 1}^{n} {t_{k}^{{}} }$$

Then, the location of the mid-plane is h/2 from the top or the bottom surface of the laminate. The z-coordinate of each ply k surface (top and bottom) is given by

Ply 1:

$$\begin{aligned} &h_{0}^{{}} = - \frac{h}{2}\quad \left( {{\text{top}}\;{\text{surface}}} \right) \hfill \\& h_{1}^{{}} = - \frac{h}{2} + t_{1}^{{}} \quad \left( {{\text{bottom}}\;{\text{surface}}} \right) \hfill \\ \end{aligned}$$

Ply k: $\left( {k = 2,3, \ldots n - 2,n - 1} \right)$

$$\begin{aligned} & h_{k - 1}^{{}} = - \frac{h}{2} + \sum\limits_{ = 1}^{k - 1} {t\quad \left( {{\text{top}}{\kern 1pt} \;{\text{surface}}} \right)} \\ & h_{k}^{{}} = - \frac{h}{2} + \sum\limits_{ = 1}^{k} {t{\kern 1pt} \quad {\kern 1pt} \left( {{\text{bottom}}\;{\text{surface}}} \right)} \\ \end{aligned}$$

(2) Find the value of the reduced stiffness matrix $[Q]$ for each ply using its six elastic moduli, $E_{1}^{{}} ,E_{2}^{{}} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} G_{12}^{{}} ,G_{13}^{{}} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} G_{23}^{{}} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} \nu_{12}^{{}}$ in constants $Q_{11} ,Q_{12} ,Q_{22} ,Q_{66} ,{\kern 1pt} Q_{44} {\kern 1pt}$ and $Q_{55}$.

(3) Find the value of the transformed reduced stiffness matrix for each ply using the $[\bar{Q}]$ matrix calculated in step 2, and the angle of the ply and transformed coefficient of thermal expansion can be referred to any standard texts such as (Reddy (1997)).

(4) Knowing the thickness, $t_{k}^{{}}$, of each ply, find the coordinate of the top and bottom surface, $h_{i}^{{}} ,\quad i = 1 \ldots ,n,$ of each ply, using the following equation:

Ply n:

$$\begin{aligned} & h_{n - 1}^{{}} = \frac{h}{2} - t_{n}^{{}} \left( {{\text{top}}{\kern 1pt} \;{\text{surface}}} \right) \\ & h_{n}^{{}} = \frac{h}{2}\left( {{\text{bottom}}\;{\text{surface}}} \right) \\ \end{aligned}$$

(5) Use the $[\bar{Q}]$ matrices from step 3 and the location of each ply from step 4 to find the six beam stiffness $(A_{11} ,{\kern 1pt} {\kern 1pt} B_{11} ,D_{11} ,B_{11}^{s} ,D_{11}^{s} ,H_{11}^{s}$ and $A_{55}^{s}$) from Eq. (7).

(6) Substitute the stiffness matrix values found in step 5 and the applied forces and moments in Eq. (6).

(7) Solve the three simultaneous Eqs. (14a–14c). Closed-form solutions are obtained using the Navier solution for simply supported laminated composite beams Eqs. (15a–15c), and the eigenvalue problem is solved to get the corresponding eigenvalues for buckling load equation with the effect temperature reduces the critical buckling load (18) and the critical temperature Eq. (19).