A dynamic stiffness method for analysis of thermal effect on vibration and buckling of a laminated composite beam

Abstract

Thermal effects on vibration and buckling behaviors of generally layered composite beams with arbitrary boundary conditions are dealt with in this paper. The composite beam is modeled using third-order shear deformation beam theory in which the Poisson effect is incorporated. A constant temperature change through the beam thickness is assumed. An exact dynamic stiffness matrix is formulated by directly solving the differential equations of motion governing the natural vibration of the composite beams subjected to uniform temperature changes along the beam thickness. Application of the derived dynamic stiffness matrix together with the Wittrick–Williams algorithm to compute the natural frequencies and buckling temperature changes of two particular composite beams is discussed. The correctness and accuracy of the derived dynamic stiffness matrix is evaluated by comparing the present results with the available solutions in literature. The influences of Poisson effect, boundary condition, temperature change, thermal expansion coefficient and material anisotropy on the natural frequencies of the composite beams are studied.

1 Introduction

Laminated composite beams are widely used in many engineering applications owing to many advantages that they can provide: high strength-to-weight ratio, high stiffness-to-weight ratio, superior fatigue characteristics, ability to be tailored to meet the design requirements by varying the fiber orientation, material and stacking pattern [1, 2]. Composite beams may be subjected to severe thermal environments, and their thermal stability is of paramount importance in specific cases [3,4,5,6,7,8,9,10,11,12, 12]. Geometrically perfect composite beams generally develop compressive axial stresses due to heating or cooling and buckle at a specific temperature.

A great deal of research is devoted to analyzing the vibration and mechanical buckling behaviors of laminated composite beams. However, the existing studies on the thermal buckling of composite beams are relatively few. Kapania and Raciti [1, 2] presented a review of the advances in the buckling and vibration analyses of laminated beams until 1989. Based on the first-order shear deformation theory, Mathew et al. [3] developed a one-dimensional beam finite element to investigate the thermal buckling of antisymmetric cross-ply composite beams. Lan et al. [4] developed a finite element model to explore the thermal buckling of three-layer sandwich beams with the effects of transverse shear deformation in the facings and the effects of stretching and bending deformations in the core considered. Abramovich [5] used the first-order deformation theory based on the Timoshenko-type equations to investigate the thermal buckling of cross-ply symmetric and non-symmetric laminated composite beams. Mannini [6] studied the thermal buckling of symmetric and antisymmetric cross-ply composite beams using the first-order shear deformation theory in conjunction with the Rayleigh–Ritz method. Suresh et al. [7] proposed a semi-analytical approach to determine the nonlinear dynamic stability characteristics of asymmetrically laminated composite beams based on the first-order shear deformation theory. Lee and Choi [8] studied the thermal buckling and postbuckling behaviors of a composite beam with embedded shape memory alloy wire actuators under a uniform temperature change on the basis of the classical lamination beam theory. Khdeir [9] adopted the state space concept in conjunction with Jordan canonical form to solve exactly the thermal buckling of cross-ply laminated composite beams. Aydogdu [10] presented the thermal buckling analysis of cross-ply laminated composite beams subjected to different sets of boundary conditions. The analysis was based on a three-degree-of-freedom shear deformable beam theory, and the numerical results were obtained by the Ritz method. Pradeep et al. [11] investigated the vibration and thermal buckling behaviors of sandwich beams with composite facings and viscoelastic core. Each composite laminate was modeled as an equivalent single layer, and the transverse shear deformation was neglected. Xiang and Yang [12] investigated the free and forced vibration behaviors of a three-layer laminated functionally graded beam subjected to one-dimensional steady heat conduction in the thickness direction based on the Timoshenko beam theory and differential quadrature method. Mahi et al. [13] used an analytical method to investigate the free vibration of symmetric functionally graded beams with general boundary conditions and subjected to initial thermal stresses on the basis of a unified higher-order shear deformation beam theory. Wattanasakulpongn et al. [14] adopted an improved third-order shear deformation beam theory and the Ritz method to study the thermal buckling and vibration of functionally graded beams with various immovable boundary conditions. Kiani et al. [15] studied the buckling behaviors of functionally graded material beams with surface-bonded piezoelectric layers subject to both the thermal loading and the constant voltage based on the Timoshenko beam theory. Based on the Euler–Bernoulli beam theory, Fu et al. [16] investigated the thermal buckling, nonlinear free vibration and dynamic stability of the clamped–clamped functionally graded material beam with surface-bonded piezoelectric actuators in thermal environment. Vosoughi et al. [17] presented the thermal buckling and postbuckling analysis of symmetric composite beams with temperature-dependent properties based on the first-order shear deformation beam theory and differential quadrature method. Anandrao et al. [18] used the finite element method to study the buckling and free vibration of functionally graded beams in thermal environment based on the Timoshenko beam formulation. Fu et al. [19] presented the analytical solutions of the thermal buckling and postbuckling of symmetrically laminated beams under the uniform temperature rise on the basis of the Timoshenko beam theory. Based on the Euler–Bernoulli beam theory and Reddy beam theory, Emam and Eltaher [20] studied the hygrothermal buckling and postbuckling behaviors of composite beams whose material properties are temperature- and moisture-dependent.

A literature survey indicates that almost all of the previous studies on the thermal buckling of composite beams are focused on the cross-ply laminated beams. To the best of authors’ knowledge, there is no investigation on the thermal buckling of general lay-up composite beams reported in literature. To achieve the maximum structural efficiency, it is often necessary to adopt the composite laminates with various stacking sequences. Therefore, there is a need to study the thermal buckling problem of generally layered composite beams. Furthermore, it seems that there is no work dealing with the effect of temperature change on the natural frequency of laminated composite beams.

In order to accurately and effectively predict the natural vibration and thermal buckling characteristics of generally laminated composite beams, a comprehensive structural model must be developed. It is well known that the classical beam theory with shear deformation and rotary inertia neglected overestimates the vibration frequency and buckling load of composite beams. Considering the fact that the transverse shear modulus of composite materials is much lower compared with the in-plane modulus, the shear deformation effect is taken into account in the present structural model. The material couplings among the extensional, bending and shear deformations, which are commonly present in the generally laminated composite beams, are also included in the present model. Furthermore, the Poisson effect which is often ignored in the analysis of cross-ply composite beams is incorporated in the present model for accurate prediction of the vibration and buckling characteristics of composite beams with arbitrary lay-ups.

In the present paper, the dynamic stiffness method is employed to investigate the natural vibration and thermal buckling of generally layered composite beams subjected to uniform temperature change along beam thickness for various classical boundary conditions. The third-order shear deformation beam theory [21] is used in the analysis, which assumes in-plane displacement as cubic function of thickness coordinate yielding parabolic transverse shear strain distribution through beam thickness and satisfying the strain-free conditions on the upper and lower surfaces of the beam. The coupled differential equations governing the natural vibration of generally laminated composite beams subject to uniform temperature changes are derived by use of the Hamilton’s principle. In the derivations, it is assumed that the material properties are independent of temperature, thus temperature enters the formulation only through constitutive equations. Also, the Poisson effect is accounted for in the one-dimensional beam constitutive equations. A dynamic stiffness matrix is established from the exact analytical solutions of the homogeneous differential equations of the general lay-up composite beams. Because of the use of the exact analytical solutions, the dynamic stiffness matrix describes the mass distribution within a composite beam element exactly. This property makes the dynamic stiffness method [22,23,24] very attractive to obtain the higher-order natural frequencies with better accuracy and reduce the computational cost when compared with the conventional finite element technique and other approximate approaches. The derived dynamic stiffness matrix in conjunction with the Wittrick–Williams algorithm [25] is used to accurately evaluate the natural frequency and critical temperature change of the composite beams. Comparisons between the present critical buckling temperatures and the available results in literature are given to demonstrate the correctness and accuracy of the proposed formulation. Natural frequencies for antisymmetric cross-ply and generally layered composite beams are also given for different boundary conditions, temperature changes, thermal expansion coefficients and material anisotropy.

2 Theoretical analysis

Consider a uniform straight laminated beam having length L, breadth b and thickness h as shown in Fig. 1. The laminated beam is made of linearly elastic orthotropic layers, and the principal material axes of each layer may be oriented at an arbitrary angle with respect to the x-axis. In the right-handed Cartesian coordinate system, the x-axis is coincident with the beam axis and the origin is in the middle plane of the beam. Only the deformation of the laminated beam in the $x{-}z$ plane is considered in the present work.

Fig. 1

Geometry of laminated beam and coordinate system

The assumed displacement field for the laminated composite beam on the basis of third-order shear deformation theory [21] can be written as

$$\begin{aligned}&\displaystyle u_1 (x,z,t)=u(x,t)+z\left[ {\phi -\frac{4}{3}\left( {\frac{z}{h}} \right) ^{2}\left( {\phi +\frac{\partial w}{\partial x}} \right) } \right] \end{aligned}$$

(1a)

$$\begin{aligned}&\displaystyle u_2 (x,z,t)=0 \end{aligned}$$

(1b)

$$\begin{aligned}&\displaystyle u_3 (x,z,t)=w(x,t) \end{aligned}$$

(1c)

where $u_1 (x,z,t)$, $u_2 (x,z,t)$ and $u_3 (x,z,t)$ denote the displacements of any point in the laminated beam domain along the x, y and z directions, respectively. u(x, t) and w(x, t) represent the displacements of a point in the beam mid-plane along the x and z directions, respectively. $\phi (x,t)$ is the rotation of the section normal to the mid-plane about the y-axis, t is time.

The strain–displacement relations are obtained from the displacement field given by Eqs. (1a)–(1c)

$$\begin{aligned} \varepsilon _x= & {} \varepsilon _x^0 +z\kappa _x^0 +z^{3}\kappa _x^2 \end{aligned}$$

(2a)

$$\begin{aligned} \gamma _{xz}= & {} \gamma _{xz}^0 +z^{2}\kappa _{xz}^2 \end{aligned}$$

(2b)

where

$$\begin{aligned} \varepsilon _x^0= & {} \frac{\partial u}{\partial x} \quad \kappa _x^0 =\frac{\partial \phi }{\partial x} \quad \kappa _x^2 =\,-\frac{4}{3h^{2}}\left( {\frac{\partial \phi }{\partial x}+\frac{\partial ^{2}w}{\partial x^{2}}} \right) \end{aligned}$$

(2c)

$$\begin{aligned} \gamma _{xz}^0= & {} \left( {\phi +\frac{\partial w}{\partial x}} \right) \quad \kappa _{xz}^2 =\,-\frac{4}{h^{2}}\left( {\phi +\frac{\partial w}{\partial x}} \right) \end{aligned}$$

(2d)

It can be seen from Eqs. (2b) and (2d) that the displacement field given by Eqs. (1a)–(1c) accommodates quadratic variation of transverse shear strain (and hence stress) and vanishing of transverse shear stress on the top and bottom surfaces of the laminated beam. Thus, there is no need to use the shear correction factor.

According to the third-order shear deformation laminate theory, when the thermal effect is present, the constitutive equations of the laminated composite plate can be written as

$$\begin{aligned} \left\{ {{\begin{array}{l} {N_x } \\ {N_y } \\ {N_{xy} } \\ {M_x } \\ {M_y } \\ {M_{xy} } \\ {P_x } \\ {P_y } \\ {P_{xy} } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{lllllllll} {A_{11} }&{} {A_{12} }&{} {A_{16} }&{} {B_{11} }&{} {B_{12} }&{} {B_{16} }&{} {E_{11} }&{} {E_{12} }&{} {E_{16} } \\ {A_{12} }&{} {A_{22} }&{} {A_{26} }&{} {B_{12} }&{} {B_{22} }&{} {B_{26} }&{} {E_{12} }&{} {E_{22} }&{} {E_{26} } \\ {A_{16} }&{} {A_{26} }&{} {A_{66} }&{} {B_{16} }&{} {B_{26} }&{} {B_{66} }&{} {E_{16} }&{} {E_{26} }&{} {E_{66} } \\ {B_{11} }&{} {B_{12} }&{} {B_{16} }&{} {D_{11} }&{} {D_{12} }&{} {D_{16} }&{} {F_{11} }&{} {F_{12} }&{} {F_{16} } \\ {B_{12} }&{} {B_{22} }&{} {B_{26} }&{} {D_{12} }&{} {D_{22} }&{} {D_{26} }&{} {F_{12} }&{} {F_{22} }&{} {F_{26} } \\ {B_{16} }&{} {B_{26} }&{} {B_{66} }&{} {D_{16} }&{} {D_{26} }&{} {D_{66} }&{} {F_{16} }&{} {F_{26} }&{} {F_{66} } \\ {E_{11} }&{} {E_{12} }&{} {E_{16} }&{} {F_{11} }&{} {F_{12} }&{} {F_{16} }&{} {H_{11} }&{} {H_{12} }&{} {H_{16} } \\ {E_{12} }&{} {E_{22} }&{} {E_{26} }&{} {F_{12} }&{} {F_{22} }&{} {F_{26} }&{} {H_{12} }&{} {H_{22} }&{} {H_{26} } \\ {E_{16} }&{} {E_{26} }&{} {E_{66} }&{} {F_{16} }&{} {F_{26} }&{} {F_{66} }&{} {H_{16} }&{} {H_{26} }&{} {H_{66} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\varepsilon _x^0 } \\ {\varepsilon _y^0 } \\ {\gamma _{xy}^0 } \\ {\kappa _x^0 } \\ {\kappa _y^0 } \\ {\kappa _{xy}^0 } \\ {\kappa _x^2 } \\ {\kappa _y^2 } \\ {\kappa _{xy}^2 } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {N_x^T } \\ {N_y^T } \\ {N_{xy}^T } \\ {M_x^T } \\ {M_y^T } \\ {M_{xy}^T } \\ {P_x^T } \\ {P_y^T } \\ {P_{xy}^T } \\ \end{array} }} \right\} \end{aligned}$$

(3a)

$$\begin{aligned} \left\{ {{\begin{array}{l} {Q_{yz} } \\ {Q_{xz} } \\ {R_{yz} } \\ {R_{xz} } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{llll} {A_{44} }&{} {A_{45} }&{} {D_{44} }&{} {D_{45} } \\ {A_{45} }&{} {A_{55} }&{} {D_{45} }&{} {D_{55} } \\ {D_{44} }&{} {D_{45} }&{} {F_{44} }&{} {F_{45} } \\ {D_{45} }&{} {D_{55} }&{} {F_{45} }&{} {F_{55} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\gamma _{yz}^0 } \\ {\gamma _{xz}^0 } \\ {\kappa _{yz}^2 } \\ {\kappa _{xz}^2 } \\ \end{array} }} \right\} \end{aligned}$$

(3b)

where $N_x$, $N_y$ and $N_{xy}$ denote the in-plane forces, $M_x$, $M_y$ and $M_{xy}$ the bending and twisting moments, $P_x$, $P_y$ and $P_{xy}$ the higher-order bending and twisting moments, $Q_{yz}$ and $Q_{xz}$ the shear forces, $R_{yz}$ and $R_{xz}$ the higher-order shear forces. $N_x^T$, $N_y^T$ and $N_{xy}^T$ denote the in-plane thermal forces, $M_x^T$, $M_y^T$ and $M_{xy}^T$ the thermal bending and twisting moments, $P_x^T$, $P_y^T$ and $P_{xy}^T$ the higher-order thermal bending and twisting moments. $\varepsilon _x^0$, $\varepsilon _y^0$, $\gamma _{xy}^0$, $\gamma _{yz}^0$ and $\gamma _{xz}^0$ represent the mid-plane strains, $\kappa _x^0$, $\kappa _y^0$ and $\kappa _{xy}^0$ the bending and twisting curvatures, $\kappa _x^2$, $\kappa _y^2$, $\kappa _{xy}^2$, $\kappa _{yz}^2$ and $\kappa _{xz}^2$ the higher-order bending and twisting curvatures. $A_{ij}$, $B_{ij}$, $D_{ij}$, $E_{ij}$, $F_{ij}$, $H_{ij} \quad (i,j=1,2,6)$ and $A_{ij}$, $D_{ij}$, $F_{ij} \quad (i,j=4,5)$ are the laminate stiffness coefficients.

For the case of the laminated beam under consideration, its width direction is free of stresses. Therefore, the in-plane forces $N_y$ and $N_{xy}$, the bending and twisting moments $M_y$ and $M_{xy}$, the higher-order bending and twisting moments $P_y$ and $P_{xy}$, and the shear forces $Q_{yz}$ and $R_{yz}$ are assumed to be equal to zero while the mid-plane strains $\varepsilon _y^0$, $\gamma _{xy}^0$ and $\gamma _{yz}^0$, the bending and twisting curvatures $\kappa _y^0$ and $\kappa _{xy}^0$, and the higher-order bending and twisting curvatures $\kappa _y^2$, $\kappa _{xy}^2$ and $\kappa _{yz}^2$ are assumed to be nonzero. The following constitutive equations for the laminated beam, in which the temperature effect and Poisson effect are taken into account, can be obtained from Eqs. (3a) and (3b)

$$\begin{aligned} \left\{ {{\begin{array}{l} {N_x } \\ {M_x } \\ {P_x } \\ \end{array} }} \right\}= & {} \left\{ {{\begin{array}{l} {\bar{{N}}_x } \\ {\bar{{M}}_x } \\ {\bar{{P}}_x } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {\bar{{N}}_x^T } \\ {\bar{{M}}_x^T } \\ {\bar{{P}}_x^T } \\ \end{array} }} \right\} \end{aligned}$$

(4a)

$$\begin{aligned} \left\{ {{\begin{array}{l} {Q_{xz} } \\ {R_{xz} } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{ll} {\bar{{A}}_{55} }&{} {\bar{{D}}_{55} } \\ {\bar{{D}}_{55} }&{} {\bar{{F}}_{55} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\gamma _{xz}^0 } \\ {\kappa _{xz}^2 } \\ \end{array} }} \right\} \end{aligned}$$

(4b)

where

$$\begin{aligned} \left\{ {{\begin{array}{l} {\bar{{N}}_x } \\ {\bar{{M}}_x } \\ {\bar{{P}}_x } \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{lll} {\bar{{A}}_{11} }&{} {\bar{{B}}_{11} }&{} {\bar{{E}}_{11} } \\ {\bar{{B}}_{11} }&{} {\bar{{D}}_{11} }&{} {\bar{{F}}_{11} } \\ {\bar{{E}}_{11} }&{} {\bar{{F}}_{11} }&{} {\bar{{H}}_{11} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\varepsilon _x^0 } \\ {\kappa _x^0 } \\ {\kappa _x^2 } \\ \end{array} }} \right\} \end{aligned}$$

(5a)

$$\begin{aligned}&\left[ {{\begin{array}{lll} {\bar{{A}}_{11} }&{} {\bar{{B}}_{11} }&{} {\bar{{E}}_{11} } \\ {\bar{{B}}_{11} }&{} {\bar{{D}}_{11} }&{} {\bar{{F}}_{11} } \\ {\bar{{E}}_{11} }&{} {\bar{{F}}_{11} }&{} {\bar{{H}}_{11} } \\ \end{array} }} \right] =\left[ {{\begin{array}{lll} {A_{11} }&{} {B_{11} }&{} {E_{11} } \\ {B_{11} }&{} {D_{11} }&{} {F_{11} } \\ {E_{11} }&{} {F_{11} }&{} {H_{11} } \\ \end{array} }} \right] \nonumber \\&-\,\left[ {{\begin{array}{llllll} {A_{12} }&{} {B_{12} }&{} {B_{16} }&{} {A_{16} }&{} {E_{12} }&{} {E_{16} } \\ {B_{12} }&{} {D_{12} }&{} {D_{16} }&{} {B_{16} }&{} {F_{12} }&{} {F_{16} } \\ {E_{12} }&{} {F_{12} }&{} {F_{16} }&{} {E_{16} }&{} {H_{12} }&{} {H_{16} } \\ \end{array} }} \right] \left[ {{\begin{array}{llllll} {A_{22} }&{} {B_{22} }&{} {B_{26} }&{} {A_{26} }&{} {E_{22} }&{} {E_{26} } \\ {B_{22} }&{} {D_{22} }&{} {D_{26} }&{} {B_{26} }&{} {F_{22} }&{} {F_{26} } \\ {B_{26} }&{} {D_{26} }&{} {D_{66} }&{} {B_{66} }&{} {F_{26} }&{} {F_{66} } \\ {A_{26} }&{} {B_{26} }&{} {B_{66} }&{} {A_{66} }&{} {E_{26} }&{} {E_{66} } \\ {E_{22} }&{} {F_{22} }&{} {F_{26} }&{} {E_{26} }&{} {H_{22} }&{} {H_{26} } \\ {E_{26} }&{} {F_{26} }&{} {F_{66} }&{} {E_{66} }&{} {H_{26} }&{} {H_{66} } \\ \end{array} }} \right] ^{-1}\left[ {{\begin{array}{lll} {A_{12} }&{} {B_{12} }&{} {E_{12} } \\ {B_{12} }&{} {D_{12} }&{} {F_{12} } \\ {B_{16} }&{} {D_{16} }&{} {F_{16} } \\ {A_{16} }&{} {B_{16} }&{} {E_{16} } \\ {E_{12} }&{} {F_{12} }&{} {H_{12} } \\ {E_{16} }&{} {F_{16} }&{} {H_{16} } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(5b)

$$\begin{aligned}&\left\{ {{\begin{array}{l} {\bar{{N}}_x^T } \\ {\bar{{M}}_x^T } \\ {\bar{{P}}_x^T } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {N_x^T } \\ {M_x^T } \\ {P_x^T } \\ \end{array} }} \right\} \nonumber \\&-\,\left[ {{\begin{array}{llllll} {A_{12} }&{} {B_{12} }&{} {B_{16} }&{} {A_{16} }&{} {E_{12} }&{} {E_{16} } \\ {B_{12} }&{} {D_{12} }&{} {D_{16} }&{} {B_{16} }&{} {F_{12} }&{} {F_{16} } \\ {E_{12} }&{} {F_{12} }&{} {F_{16} }&{} {E_{16} }&{} {H_{12} }&{} {H_{16} } \\ \end{array} }} \right] \left[ {{\begin{array}{llllll} {A_{22} }&{} {B_{22} }&{} {B_{26} }&{} {A_{26} }&{} {E_{22} }&{} {E_{26} } \\ {B_{22} }&{} {D_{22} }&{} {D_{26} }&{} {B_{26} }&{} {F_{22} }&{} {F_{26} } \\ {B_{26} }&{} {D_{26} }&{} {D_{66} }&{} {B_{66} }&{} {F_{26} }&{} {F_{66} } \\ {A_{26} }&{} {B_{26} }&{} {B_{66} }&{} {A_{66} }&{} {E_{26} }&{} {E_{66} } \\ {E_{22} }&{} {F_{22} }&{} {F_{26} }&{} {E_{26} }&{} {H_{22} }&{} {H_{26} } \\ {E_{26} }&{} {F_{26} }&{} {F_{66} }&{} {E_{66} }&{} {H_{26} }&{} {H_{66} } \\ \end{array} }} \right] ^{-1}\left\{ {{\begin{array}{l} {N_y^T } \\ {M_y^T } \\ {M_{xy}^T } \\ {N_{xy}^T } \\ {P_y^T } \\ {P_{xy}^T } \\ \end{array} }} \right\} \nonumber \\ \end{aligned}$$

(5c)

$$\begin{aligned}&\left[ {{\begin{array}{ll} {\bar{{A}}_{55} }&{} {\bar{{D}}_{55} } \\ {\bar{{D}}_{55} }&{} {\bar{{F}}_{55} } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {A_{55} }&{} {D_{55} } \\ {D_{55} }&{} {F_{55} } \\ \end{array} }} \right] -\left[ {{\begin{array}{ll} {D_{45} }&{} {A_{45} } \\ {F_{45} }&{} {D_{45} } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {F_{44} }&{} {D_{44} } \\ {D_{44} }&{} {A_{44} } \\ \end{array} }} \right] ^{-1}\left[ {{\begin{array}{ll} {D_{45} }&{} {F_{45} } \\ {A_{45} }&{} {D_{45} } \\ \end{array} }} \right] \end{aligned}$$

(5d)

The laminate stiffness coefficients $A_{ij}$, $B_{ij}$, $D_{ij}$, $E_{ij}$, $F_{ij}$, $H_{ij} \quad (i,j=1,2,6)$ and $A_{ij}$, $D_{ij}$, $F_{ij} \quad (i,j=4,5)$ appearing in Eqs. (3a) and (3b) are defined in terms of the transformed reduced stiffness constants $\bar{{Q}}_{ij}$ as follows

$$\begin{aligned} \left( {{\begin{array}{llllll} {A_{ij} }&{} {B_{ij} }&{} {D_{ij} }&{} {E_{ij} }&{} {F_{ij} }&{} {H_{ij} } \\ \end{array} }} \right)= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {\bar{{Q}}_{ij} \left( {{\begin{array}{llllll} 1&{} z&{} {z^{2}}&{} {z^{3}}&{} {z^{4}}&{} {z^{6}} \\ \end{array} }} \right) } {\hbox {d}}z \quad (i,j=1,2,6) \end{aligned}$$

(6a)

$$\begin{aligned} \left( {{\begin{array}{lll} {A_{ij} }&{} {D_{ij} }&{} {F_{ij} } \\ \end{array} }} \right)= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {\bar{{Q}}_{ij} \left( {{\begin{array}{lllll} 1&{} {z^{2}}&{} {z^{4}} \\ \end{array} }} \right) } {\hbox {d}}z \quad (i,j=4,5) \end{aligned}$$

(6b)

The thermal forces and moments appearing in Eq. (3a) can be expressed as

$$\begin{aligned} \left\{ {{\begin{array}{l} {N_x^T } \\ {N_y^T } \\ {N_{xy}^T } \\ \end{array} }} \right\}= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {\left[ {{\begin{array}{lll} {\bar{{Q}}_{11} }&{} {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{16} } \\ {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{22} }&{} {\bar{{Q}}_{26} } \\ {\bar{{Q}}_{16} }&{} {\bar{{Q}}_{26} }&{} {\bar{{Q}}_{66} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\alpha _x \Delta T} \\ {\alpha _y \Delta T} \\ {2\alpha _{xy} \Delta T} \\ \end{array} }} \right\} } {\hbox {d}}z \end{aligned}$$

(7a)

$$\begin{aligned} \left\{ {{\begin{array}{l} {M_x^T } \\ {M_y^T } \\ {M_{xy}^T } \\ \end{array} }} \right\}= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {\left[ {{\begin{array}{lll} {\bar{{Q}}_{11} }&{} {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{16} } \\ {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{22} }&{} {\bar{{Q}}_{26} } \\ {\bar{{Q}}_{16} }&{} {\bar{{Q}}_{26} }&{} {\bar{{Q}}_{66} } \\ \end{array} }} \right] z\left\{ {{\begin{array}{l} {\alpha _x \Delta T} \\ {\alpha _y \Delta T} \\ {2\alpha _{xy} \Delta T} \\ \end{array} }} \right\} } {\hbox {d}}z \end{aligned}$$

(7b)

$$\begin{aligned} \left\{ {{\begin{array}{l} {P_x^T } \\ {P_y^T } \\ {P_{xy}^T } \\ \end{array} }} \right\}= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {\left[ {{\begin{array}{llll} {\bar{{Q}}_{11} }&{} {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{16} } \\ {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{22} }&{} {\bar{{Q}}_{26} } \\ {\bar{{Q}}_{16} }&{} {\bar{{Q}}_{26} }&{} {\bar{{Q}}_{66} } \\ \end{array} }} \right] z^{3}\left\{ {{\begin{array}{l} {\alpha _x \Delta T} \\ {\alpha _y \Delta T} \\ {2\alpha _{xy} \Delta T} \\ \end{array} }} \right\} } {\hbox {d}}z \end{aligned}$$

(7c)

where $\alpha _x$, $\alpha _y$ and $\alpha _{xy}$ are the transformed thermal coefficients of the laminate, which are defined in the “Appendix.” $\Delta T$ is a constant temperature change from a reference state.

The transformed reduced stiffness constants $\bar{{Q}}_{ij} \quad (i,j=1,2,6)$ and $\bar{{Q}}_{ij} \quad (i,j=4,5)$ are given in the “Appendix.”

The strain energy of the laminated composite beam shown in Fig. 1 can be written as

$$\begin{aligned} V=\frac{1}{2}\int _0^L {\left( {\bar{{N}}_x \varepsilon _x^0 +\bar{{M}}_x \kappa _x^0 +\bar{{P}}_x \kappa _x^2 +Q_{xz} \gamma _{xz}^0 +R_{xz} \kappa _{xz}^2 } \right) b} {\hbox {d}}x \end{aligned}$$

(8a)

Substituting Eqs. (2c) and (2d) into Eq. (8a), one obtains

$$\begin{aligned} V=\frac{1}{2}\int _0^L {\left[ {\bar{{N}}_x \frac{\partial u}{\partial x}+\bar{{M}}_x \frac{\partial \phi }{\partial x}-\,\bar{{P}}_x \frac{4}{3h^{2}}\left( {\frac{\partial \phi }{\partial x}+\frac{\partial ^{2}w}{\partial x^{2}}} \right) +Q_{xz} \left( {\phi +\frac{\partial w}{\partial x}} \right) -R_{xz} \frac{4}{h^{2}}\left( {\phi +\frac{\partial w}{\partial x}} \right) } \right] b} {\hbox {d}}x\nonumber \\ \end{aligned}$$

(8b)

The kinetic energy of the laminated composite beam can be expressed as

$$\begin{aligned} T=\frac{1}{2}\int _0^L {\int _{-\frac{h}{2}}^{\frac{h}{2}} {\rho \left[ {\left( {\frac{\partial u_1 }{\partial t}} \right) ^{2}+\left( {\frac{\partial u_2 }{\partial t}} \right) ^{2}+\left( {\frac{\partial u_3 }{\partial t}} \right) ^{2}} \right] b} {\hbox {d}}z} {\hbox {d}}x \end{aligned}$$

(9a)

where $\rho$ is the mass density of the lamina material.

Introduction of Eqs. (1a)–(1c) into Eq. (9a) results in

$$\begin{aligned} T=\frac{1}{2}\int _0^L {\left[ {\begin{array}{l} I_1 \dot{u}^{2}+I_3 \dot{\phi }^{2}+\frac{16}{9h^{4}}I_7 \left( {\dot{\phi }+\frac{\partial \dot{w}}{\partial x}} \right) ^{2}+2I_2 \dot{u}\dot{\phi }-\frac{8}{3h^{2}}I_4 \dot{u}\left( {\dot{\phi }+\frac{\partial \dot{w}}{\partial x}} \right) \\ -\,\frac{8}{3h^{2}}I_5 \dot{\phi }\left( {\dot{\phi }+\frac{\partial \dot{w}}{\partial x}} \right) +I_1 \dot{w}^{2} \\ \end{array}} \right] b} {\hbox {d}}x \end{aligned}$$

(9b)

where the overdots represent the partial differentiation with respect to the time t, and

$$\begin{aligned} \left( {{\begin{array}{llllll} {I_1 }&{} {I_2 }&{} {I_3 }&{} {I_4 }&{} {I_5 }&{} {I_7 } \\ \end{array} }} \right) =\int _{-\frac{h}{2}}^{\frac{h}{2}} {\rho \left( {{\begin{array}{llllll} 1&{} z&{} {z^{2}}&{} {z^{3}}&{} {z^{4}}&{} {z^{6}} \\ \end{array} }} \right) } {\hbox {d}}z \end{aligned}$$

(9c)

The work $W_e$ done by the external load of the laminated composite beam is given by

$$\begin{aligned} W_e =\frac{1}{2}\int _0^L {\bar{{N}}_x^T \left( {\frac{\partial w}{\partial x}} \right) ^{2}b} {\hbox {d}}x \end{aligned}$$

(10)

The Hamilton’s principle is employed to derive the governing equations of motion and the related boundary conditions of the laminated composite beam:

$$\begin{aligned} \delta \int _{t_1 }^{t_2 } {\left( {T-V+W_e } \right) } {\hbox {d}}t=0 \end{aligned}$$

(11)

$\delta u=\delta w=\delta \phi =\delta w^{{\prime }}=0$ at $t=t_1 ,t_2$

where $\delta$ denotes the first variation, $t_1$ and $t_2$ are two arbitrary time instants, the superscript prime denotes the partial differentiation with the coordinate x.

Inserting Eqs. (8b), (9b) and (10) together with Eqs. (2c)–(2d), (4b) and (5a)–(5d) into Eq. (11), integrating by parts and noting that the variation must vanish leads the following governing equations of motion of the laminated composite beam

$$\begin{aligned}&-I_1 \ddot{u}+\frac{4}{3h^{2}}I_4 \ddot{w}^{{\prime }}-\left( {I_2 -\frac{4}{3h^{2}}I_4 } \right) \ddot{\phi }+\bar{{A}}_{11} u^{{\prime }{\prime }}+\left( {\bar{{B}}_{11} -\frac{4}{3h^{2}}\bar{{E}}_{11} } \right) \phi ^{{\prime }{\prime }}-\frac{4}{3h^{2}}\bar{{E}}_{11} w^{{\prime }{\prime }{\prime }}=0 \end{aligned}$$

(12a)

$$\begin{aligned}&-\,\frac{4}{3h^{2}}I_4 \ddot{u}^{{\prime }}+\frac{16}{9h^{4}}I_7 \ddot{w}^{{\prime }{\prime }}-I_1 \ddot{w}+\left( {\frac{16}{9h^{4}}I_7 -\frac{4}{3h^{2}}I_5 } \right) \ddot{\phi }^{{\prime }}+\frac{4}{3h^{2}}\bar{{E}}_{11} u^{{\prime }{\prime }{\prime }}-\frac{16}{9h^{4}}\bar{{H}}_{11} w^{{\prime }{\prime }{\prime }{\prime }} \nonumber \\&\quad +\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \phi ^{{\prime }{\prime }{\prime }}+\left( {\bar{{A}}_{55} -\frac{8}{h^{2}}\bar{{D}}_{55} +\frac{16}{h^{4}}\bar{{F}}_{55} } \right) \left( {\phi ^{{\prime }}+w^{{\prime }{\prime }}} \right) -\bar{{N}}_x^T w^{{\prime }{\prime }}=0 \end{aligned}$$

(12b)

$$\begin{aligned}&-\left( {I_2 -\frac{4}{3h^{2}}I_4 } \right) \ddot{u}-\left( {\frac{16}{9h^{4}}I_7 -\frac{4}{3h^{2}}I_5 } \right) \ddot{w}^{{\prime }}-\left( {I_3 +\frac{16}{9h^{4}}I_7 -\frac{8}{3h^{2}}I_5 } \right) \ddot{\phi } \nonumber \\&\quad +\left( {\bar{{B}}_{11} -\frac{4}{3h^{2}}\bar{{E}}_{11} } \right) u^{{\prime }{\prime }}+\left( {\bar{{D}}_{11} -\frac{8}{3h^{2}}\bar{{F}}_{11} +\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \phi ^{{\prime }{\prime }}-\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) w^{{\prime }{\prime }{\prime }} \nonumber \\&\quad -\left( {\bar{{A}}_{55} -\frac{8}{h^{2}}\bar{{D}}_{55} +\frac{16}{h^{4}}\bar{{F}}_{55} } \right) \left( {\phi +w^{{\prime }}} \right) =0 \end{aligned}$$

(12c)

and the appropriate boundary conditions at the laminated beam ends $(x=0,L)$ are

$$\begin{aligned} \left[ {\bar{{A}}_{11} u^{{\prime }}+\left( {\bar{{B}}_{11} -\frac{4}{3h^{2}}\bar{{E}}_{11} } \right) \phi ^{{\prime }}-\frac{4}{3h^{2}}\bar{{E}}_{11} w^{{\prime }{\prime }}} \right] \delta u=0 \end{aligned}$$

(13a)

$$\begin{aligned}&\left[ \frac{4}{3h^{2}}I_4 \ddot{u}-\frac{16}{9h^{4}}I_7 \ddot{w}^{{\prime }}-\left( {\frac{16}{9h^{4}}I_7 -\frac{4}{3h^{2}}I_5 } \right) \ddot{\phi }-\frac{4}{3h^{2}}\bar{{E}}_{11} u^{{\prime }{\prime }}+\frac{16}{9h^{4}}\bar{{H}}_{11} w^{{\prime }{\prime }{\prime }}\right. \nonumber \\&\left. \quad -\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \phi ^{{\prime }{\prime }}-\left( {\bar{{A}}_{55} -\frac{8}{h^{2}}\bar{{D}}_{55} +\frac{16}{h^{4}}\bar{{F}}_{55} } \right) \left( {\phi +w^{{\prime }}} \right) +\bar{{N}}_x^T w^{{\prime }} \right] \delta w=0 \end{aligned}$$

(13b)

$$\begin{aligned}&\left[ {-\left( {\bar{{B}}_{11} -\frac{4}{3h^{2}}\bar{{E}}_{11} } \right) u^{{\prime }}-\left( {\bar{{D}}_{11} -\frac{8}{3h^{2}}\bar{{F}}_{11} +\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \phi ^{{\prime }}+\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) w^{{\prime }{\prime }}} \right] \delta \phi =0\qquad \quad \end{aligned}$$

(13c)

$$\begin{aligned}&\left[ {\frac{4}{3h^{2}}\bar{{E}}_{11} u^{{\prime }}+\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \phi ^{{\prime }}-\frac{16}{9h^{4}}\bar{{H}}_{11} w^{{\prime }{\prime }}} \right] \delta w^{{\prime }}=0 \end{aligned}$$

(13d)

3 Dynamic stiffness method

For the case of undamped natural vibration, it can be seen that Eqs. (12a)–(12c) have solutions that are separable in time and space and that the time dependence is harmonic. Letting

$$\begin{aligned} \left\{ {{\begin{array}{lll} {u(x,t)}&{} {w(x,t)}&{} {\phi (x,t)} \\ \end{array} }} \right\} =\left\{ {{\begin{array}{lll} {U(x)}&{} {W(x)}&{} {\Phi (x)} \\ \end{array} }} \right\} {\hbox {e}}^{i\omega t} \end{aligned}$$

(14)

where $\omega$ is the circular frequency, U(x), W(x) and $\Phi (x)$ are the mode shapes of the harmonically varying axial displacement, bending displacement and normal rotation, respectively.

Substituting Eq. (14) into Eqs. (12a)–(12c) results in the following ordinary differential equations

$$\begin{aligned}&I_1 \omega ^{2}U-\left( {\frac{4}{3h^{2}}I_4 -I_2 } \right) \omega ^{2}\Phi -\frac{4}{3h^{2}}I_4 \omega ^{2}W^{{\prime }}+\bar{{A}}_{11} U^{{\prime }{\prime }}+\left( {\bar{{B}}_{11} -\frac{4}{3h^{2}}\bar{{E}}_{11} } \right) \Phi ^{{\prime }{\prime }}-\frac{4}{3h^{2}}\bar{{E}}_{11} W^{{\prime }{\prime }{\prime }}=0\nonumber \\ \end{aligned}$$

(15a)

$$\begin{aligned}&I_1 \omega ^{2}W+\frac{4}{3h^{2}}I_4 \omega ^{2}U^{{\prime }}-\left( {\frac{16}{9h^{4}}I_7 -\frac{4}{3h^{2}}I_5 } \right) \omega ^{2}\Phi ^{{\prime }}-\frac{16}{9h^{4}}I_7 \omega ^{2}W^{{\prime }{\prime }}+\frac{4}{3h^{2}}\bar{{E}}_{11} U^{{\prime }{\prime }{\prime }} \nonumber \\&\quad +\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \Phi ^{{\prime }{\prime }{\prime }}-\frac{16}{9h^{4}}\bar{{H}}_{11} W^{{\prime }{\prime }{\prime }{\prime }}+\left( {\bar{{A}}_{55} -\frac{8}{h^{2}}\bar{{D}}_{55} +\frac{16}{h^{4}}\bar{{F}}_{55} } \right) \left( {\Phi ^{{\prime }}+W^{{\prime }{\prime }}} \right) -\bar{{N}}_x^T W^{{\prime }{\prime }}=0\nonumber \\ \end{aligned}$$

(15b)

$$\begin{aligned}&\left( {I_2 -\frac{4}{3h^{2}}I_4 } \right) \omega ^{2}U+\left( {I_3 +\frac{16}{9h^{4}}I_7 -\frac{8}{3h^{2}}I_5 } \right) \omega ^{2}\Phi -\left( {\frac{4}{3h^{2}}I_5 -\frac{16}{9h^{4}}I_7 } \right) \omega ^{2}W^{{\prime }} \nonumber \\&\quad +\left( {\bar{{B}}_{11} -\frac{4}{3h^{2}}\bar{{E}}_{11} } \right) U^{{\prime }{\prime }}+\left( {\bar{{D}}_{11} -\frac{8}{3h^{2}}\bar{{F}}_{11} +\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \Phi ^{{\prime }{\prime }}\nonumber \\&\quad +\left( {\frac{16}{9h^{4}}\bar{{H}}_{11} -\frac{4}{3h^{2}}\bar{{F}}_{11} } \right) W^{{\prime }{\prime }{\prime }}+\left( {\frac{8}{h^{2}}\bar{{D}}_{55} -\bar{{A}}_{55} -\frac{16}{h^{4}}\bar{{F}}_{55} } \right) \left( {\Phi +W^{{\prime }}} \right) =0 \end{aligned}$$

(15c)

The solutions to Eqs. (15a)–(15c) can be expressed as

$$\begin{aligned} \left\{ {{\begin{array}{lll} {U(x)}&{} {W(x)}&{} {\Phi (x)} \\ \end{array} }} \right\} =\left\{ {{\begin{array}{lll} {\tilde{A}}&{} {\tilde{B}}&{} {\tilde{C}} \\ \end{array} }} \right\} {\hbox {e}}^{\kappa x} \end{aligned}$$

(16)

Introducing Eq. (16) into Eqs. (15a)–(15c) obtains a set of algebraic equations. Letting the determinant of the coefficient matrix of $\tilde{A}$, $\tilde{B}$ and $\tilde{C}$ equal to zero produces the characteristics equation, which is an eighth-order polynomial equation in $\kappa$:

$$\begin{aligned} \eta _4 \kappa ^{8}+\eta _3 \kappa ^{6}+\eta _2 \kappa ^{4}+\eta _1 \kappa ^{2}+\eta _0 =0 \end{aligned}$$

(17)

where the coefficients $\eta _k(k=0-4)$ are listed in the “Appendix.”

Equation (17) can be reduced to a fourth-order polynomial equation

$$\begin{aligned} \chi ^{4}+a_1 \chi ^{3}+a_2 \chi ^{2}+a_3 \chi +a_4 =0 \end{aligned}$$

(18a)

where

$$\begin{aligned} \chi =\kappa ^{2} \quad a_1 =\frac{\eta _3 }{\eta _4 } \quad a_2 =\frac{\eta _2 }{\eta _4 } \quad a_3 =\frac{\eta _1 }{\eta _4 } \quad a_4 =\frac{\eta _0 }{\eta _4 } \end{aligned}$$

(18b)

The solutions to Eq. (18a) can be found in closed-form [26].

Equations (15a)–(15c) are a set of linear homogeneous ordinary differential equations with constant coefficients, the general solutions to which can be written as

$$\begin{aligned} U(x)= & {} A_1 {\hbox {e}}^{\kappa _1 x}+A_2 {\hbox {e}}^{-\kappa _1 x}+A_3 {\hbox {e}}^{\kappa _2 x}+A_4 {\hbox {e}}^{-\kappa _2 x}+A_5 {\hbox {e}}^{\kappa _3 x}+A_6 {\hbox {e}}^{-\kappa _3 x}+A_7 {\hbox {e}}^{\kappa _4 x}+A_8 {\hbox {e}}^{-\kappa _4 x} \nonumber \\= & {} \sum _{j=1}^4 {\left( A_{2j-1} {\hbox {e}}^{\kappa _j x}+A_{2j} {\hbox {e}}^{-\kappa _j x}\right) } \end{aligned}$$

(19a)

$$\begin{aligned} W(x)= & {} B_1 {\hbox {e}}^{\kappa _1 x}+B_2 {\hbox {e}}^{-\kappa _1 x}+B_3 {\hbox {e}}^{\kappa _2 x}+B_4 {\hbox {e}}^{-\kappa _2 x}+B_5 {\hbox {e}}^{\kappa _3 x}+B_6 {\hbox {e}}^{-\kappa _3 x}+B_7 {\hbox {e}}^{\kappa _4 x}+B_8 {\hbox {e}}^{-\kappa _4 x} \nonumber \\= & {} \sum _{j=1}^4 {\left( B_{2j-1} {\hbox {e}}^{\kappa _j x}+B_{2j} {\hbox {e}}^{-\kappa _j x}\right) } \end{aligned}$$

(19b)

$$\begin{aligned} \Phi (x)= & {} C_1 {\hbox {e}}^{\kappa _1 x}+C_2 {\hbox {e}}^{-\kappa _1 x}+C_3 {\hbox {e}}^{\kappa _2 x}+C_4 {\hbox {e}}^{-\kappa _2 x}+C_5 {\hbox {e}}^{\kappa _3 x}+C_6 {\hbox {e}}^{-\kappa _3 x}+C_7 {\hbox {e}}^{\kappa _4 x}+C_8 {\hbox {e}}^{-\kappa _4 x} \nonumber \\= & {} \sum _{j=1}^4 {\left( C_{2j-1} {\hbox {e}}^{\kappa _j x}+C_{2j} {\hbox {e}}^{-\kappa _j x}\right) } \end{aligned}$$

(19c)

where $\kappa _j =\sqrt{\chi _j }(j=1-4)$. $A_1 -A_8$, $B_1 -B_8$ and $C_1 -C_8$ are three sets of eight constants, which are dependent. Substituting Eqs. (19a)–(19c) into Eqs. (15a) and (15b) obtains the following relations between the constants

$$\begin{aligned} A_{2j-1}= & {} t_j C_{2j-1} \quad A_{2j} =t_j C_{2j} \end{aligned}$$

(20a)

$$\begin{aligned} B_{2j-1}= & {} \bar{{t}}_j C_{2j-1} \quad B_{2j} =-\bar{{t}}_j C_{2j} \end{aligned}$$

(20b)

where

$$\begin{aligned} t_j= & {} \left( \left( -3\left( 3\bar{{B}}_{11} \left( 16\bar{{F}}_{55} -8\bar{{D}}_{55} h^{2}+h^{4}\left( \bar{{A}}_{55} -\bar{{N}}_x^T \right) \right) +4\bar{{E}}_{11} h^{2}\bar{{N}}_x^T \right) \kappa _j^4 \right. \right. \nonumber \\&-16\left( \bar{{E}}_{11} \bar{{F}}_{11} -\bar{{B}}_{11} \bar{{H}}_{11} \right) \kappa _j^6 +\kappa _j^2 \left( -144\bar{{F}}_{55} I_2 +3h^{2}\left( 4\bar{{E}}_{11} I_1 +24\bar{{D}}_{55} I_2 \right. \right. \nonumber \\&-\left. 3h^{2}\left( \bar{{B}}_{11} I_1 +\bar{{A}}_{55} I_2 \right) +\left( 3h^{2}I_2 -4I_4 \right) \bar{{N}}_x^T \right) +16\left( \bar{{H}}_{11} I_2 -\bar{{F}}_{11} I_4 \right. \nonumber \\&\left. \left. \left. -\left. \bar{{E}}_{11} I_5 +\bar{{B}}_{11} I_7 \right) \kappa _j^2 \right) \omega ^{2}-\left( 9h^{4}I_1 I_2 -12h^{2}I_1 I_4 +16\left( I_4 I_5 -I_2 I_7 \right) \kappa _j^2 \right) \omega ^{4}\right) \right) /{\Delta _j } \end{aligned}$$

(20c)

$$\begin{aligned} \bar{{t}}_j= & {} -\left( \kappa _j \left( 4\left( \bar{{E}}_{11} \kappa _j^2 +I_4 \omega ^{2}\right) \left( 4\bar{{E}}_{11} \kappa _j^2 -3\bar{{B}}_{11} h^{2}\kappa _j^2 +(-3h^{2}I_2 +4I_4 )\omega ^{2}\right) \right. \right. \nonumber \\&+\left( \bar{{A}}_{11} \kappa _j^2 +I_1 \omega ^{2}\right) \left( 144\bar{{F}}_{55} -72\bar{{D}}_{55} h^{2}+9\bar{{A}}_{55} h^{4}+4\left( 3\bar{{F}}_{11} h^{2}-4\bar{{H}}_{11} \right) \kappa _j^2 \right. \nonumber \\&\left. \left. +\left. 4\left( 3h^{2}I_5 -4I_7 \right) \omega ^{2}\right) \right) \right) /{\Delta _j } \end{aligned}$$

(20d)

$$\begin{aligned} \Delta _j= & {} \left( 16\left( \bar{{E}}_{11} \kappa _j^3 +I_4 \kappa _j \omega ^{2}\right) ^{2}+\left( \bar{{A}}_{11} \kappa _j^2 +I_1 \omega ^{2}\right) \left( 9\left( 16\bar{{F}}_{55} -8\bar{{D}}_{55} h^{2} \right. \right. \right. \nonumber \\&\left. \left. +\left. h^{4}\left( \bar{{A}}_{55} -\bar{{N}}_x^T \right) \right) \kappa _j^2 -16\bar{{H}}_{11} \kappa _j^4 +\left( 9h^{4}I_1 -16I_7 \kappa _j^2 \right) \omega ^{2}\right) \right) \end{aligned}$$

(20e)

It can be seen from Eqs. (20a) and (20b), only eight of the twenty-four constants are independent. It may be noted that if any of the $\chi _j$’s are zero or are repeated in the solution of Eq. (18a), Eqs. (19a)–(19c) must be modified according to the well-known technique of ordinary differential equations with constant coefficients, for those particular values of $\chi _j$.

Fig. 2

Sign convention for positive normal force N(x), shear force S(x), bending moment M(x) and higher-order bending moment P(x)

Following the sign convention established in Fig. 2, the expressions of normal force N(x), shear force S(x), bending moment M(x) and higher-order bending moment P(x) can be derived from Eqs. (13a)–(13d) and Eqs. (19a)–(19c) with the help of Eqs. (20a) and (20b)

$$\begin{aligned} N(x)= & {} \sum _{j=1}^4 {\left[ {\bar{{A}}_{11} \kappa _j t_j -\left( {\frac{4}{3h^{2}}\bar{{E}}_{11} -\bar{{B}}_{11} } \right) \kappa _j -\frac{4}{3h^{2}}\bar{{E}}_{11} \kappa _j^2 \bar{{t}}_j } \right] \left( {C_{2j-1} {\hbox {e}}^{\kappa _j x}-C_{2j} {\hbox {e}}^{-\kappa _j x}} \right) } \end{aligned}$$

(21a)

$$\begin{aligned} S(x)= & {} \sum _{j=1}^4 {\left[ {-\frac{4}{3h^{2}}I_4 \omega ^{2}t_j +\left( {-\frac{4}{3h^{2}}I_5 +\frac{16}{9h^{4}}I_7 } \right) \omega ^{2}+\frac{16}{9h^{4}}I_7 \omega ^{2}\kappa _j \bar{{t}}_j } \right. } \nonumber \\&-\frac{4}{3h^{2}}\bar{{E}}_{11} \kappa _j^2 t_j +\left( {\frac{16}{9h^{4}}\bar{{H}}_{11} -\frac{4}{3h^{2}}\bar{{F}}_{11} } \right) \kappa _j^2 +\frac{16}{9h^{4}}\bar{{H}}_{11} \kappa _j^3 \bar{{t}}_j \nonumber \\&\left. {+\left( {\frac{8}{h^{2}}\bar{{D}}_{55} -\bar{{A}}_{55} -\frac{16}{h^{4}}\bar{{F}}_{55} } \right) \left( {1+\kappa _j \bar{{t}}_j } \right) +\bar{{N}}_x^T \kappa _j \bar{{t}}_j } \right] \left( {C_{2j-1} {\hbox {e}}^{\kappa _j x}+C_{2j} {\hbox {e}}^{-\kappa _j x}} \right) \end{aligned}$$

(21b)

$$\begin{aligned} M(x)= & {} \sum _{j=1}^4 {\left[ {\left( {\frac{4}{3h^{2}}\bar{{E}}_{11} -\bar{{B}}_{11} } \right) \kappa _j t_j +\left( {\frac{8}{3h^{2}}\bar{{F}}_{11} -\bar{{D}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \kappa _j } \right. } \nonumber \\&\left. {+\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \kappa _j^2 \bar{{t}}_j } \right] \left( {C_{2j-1} {\hbox {e}}^{\kappa _j x}-C_{2j} {\hbox {e}}^{-\kappa _j x}} \right) \end{aligned}$$

(21c)

$$\begin{aligned} P(x)= & {} \sum _{j=1}^4 {\left[ {\frac{4}{3h^{2}}\bar{{E}}_{11} \kappa _j t_j +\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \kappa _j -\frac{16}{9h^{4}}\bar{{H}}_{11} \kappa _j^2 \bar{{t}}_j } \right] \left( {C_{2j-1} {\hbox {e}}^{\kappa _j x}-C_{2j} {\hbox {e}}^{-\kappa _j x}} \right) } \end{aligned}$$

(21d)

Fig. 3

Boundary conditions for generalized displacements and generalized forces of laminated beam

Referring to Fig. 3, the boundary conditions for the generalized displacements and generalized forces of the laminated composite beam can be written as

$$\begin{aligned} x= & {} 0: \quad U=U_1 \quad W=W_1 \quad \Phi =\Phi _1 \quad W^{{\prime }}=W_1^{\prime } \end{aligned}$$

(22a)

$$\begin{aligned} x= & {} L: \quad U=U_2 \quad W=W_2 \quad \Phi =\Phi _2 \quad W^{{\prime }}=W_2^{\prime } \end{aligned}$$

(22b)

$$\begin{aligned} x= & {} 0: \quad N=-N_1 \quad S=S_1 \quad M=M_1 \quad P=P_1 \end{aligned}$$

(22c)

$$\begin{aligned} x= & {} L: \quad N=N_2 \quad S=-S_2 \quad M=-M_2 \quad P=-P_2 \end{aligned}$$

(22d)

Introducing Eqs. (22a) and (22b) into Eqs. (19a)–(19c) and considering Eqs. (20a) and (20b), the nodal displacement vector $\{D\}$ can be expressed in terms of the constant vector $\{C\}$

$$\begin{aligned} \{D\}=[R]\{C\} \end{aligned}$$

(23)

where

$$\begin{aligned} \{D\}= & {} \left\{ {{\begin{array}{llllllll} {U_1 }&{} {W_1 }&{} {\Phi _1 }&{} {W_1^{\prime } }&{} {U_2 }&{} {W_2 }&{} {\Phi _2 }&{} {W_2^{\prime } } \\ \end{array} }} \right\} ^{T}\\ \{C\}= & {} \left\{ {{\begin{array}{lllllllll} {C_1 }&{} {C_3 }&{} {C_5 }&{} {C_7 }&{} {C_2 }&{} {C_4 }&{} {C_6 }&{} {C_8 } \\ \end{array} }} \right\} ^{T}\\ {[}R]= & {} \left[ {{\begin{array}{lllllllll} {t_1 }&{} {t_2 }&{} {t_3 }&{} {t_4 }&{} {t_1 }&{} {t_2 }&{} {t_3 }&{} {t_4 } \\ {\bar{{t}}_1 }&{} {\bar{{t}}_2 }&{} {\bar{{t}}_3 }&{} {\bar{{t}}_4 }&{} {-\bar{{t}}_1 }&{} {-\bar{{t}}_2 }&{} {-\bar{{t}}_3 }&{} {-\bar{{t}}_4 } \\ 1&{} 1&{} 1&{} 1&{} 1&{} 1&{} 1&{} 1 \\ {\kappa _1 \bar{{t}}_1 }&{} {\kappa _2 \bar{{t}}_2 }&{} {\kappa _3 \bar{{t}}_3 }&{} {\kappa _4 \bar{{t}}_4 }&{} {\kappa _1 \bar{{t}}_1 }&{} {\kappa _2 \bar{{t}}_2 }&{} {\kappa _3 \bar{{t}}_3 }&{} {\kappa _4 \bar{{t}}_4 } \\ {t_1 {\hbox {e}}^{\kappa _1 L}}&{} {t_2 {\hbox {e}}^{\kappa _2 L}}&{} {t_3 {\hbox {e}}^{\kappa _3 L}}&{} {t_4 {\hbox {e}}^{\kappa _4 L}}&{} {t_1 {\hbox {e}}^{-\kappa _1 L}}&{} {t_2 {\hbox {e}}^{-\kappa _2 L}}&{} {t_3 {\hbox {e}}^{-\kappa _3 L}}&{} {t_4 {\hbox {e}}^{-\kappa _4 L}} \\ {\bar{{t}}_1 {\hbox {e}}^{\kappa _1 L}}&{} {\bar{{t}}_2 {\hbox {e}}^{\kappa _2 L}}&{} {\bar{{t}}_3 {\hbox {e}}^{\kappa _3 L}}&{} {\bar{{t}}_4 {\hbox {e}}^{\kappa _4 L}}&{} {-\bar{{t}}_1 {\hbox {e}}^{-\kappa _1 L}}&{} {-\bar{{t}}_2 {\hbox {e}}^{-\kappa _2 L}}&{} {-\bar{{t}}_3 {\hbox {e}}^{-\kappa _3 L}}&{} {-\bar{{t}}_4 {\hbox {e}}^{-\kappa _4 L}} \\ {{\hbox {e}}^{\kappa _1 L}}&{} {{\hbox {e}}^{\kappa _2 L}}&{} {{\hbox {e}}^{\kappa _3 L}}&{} {{\hbox {e}}^{\kappa _4 L}}&{} {{\hbox {e}}^{-\kappa _1 L}}&{} {{\hbox {e}}^{-\kappa _2 L}}&{} {{\hbox {e}}^{-\kappa _3 L}}&{} {{\hbox {e}}^{-\kappa _4 L}} \\ {\kappa _1 \bar{{t}}_1 {\hbox {e}}^{\kappa _1 L}}&{} {\kappa _2 \bar{{t}}_2 {\hbox {e}}^{\kappa _2 L}}&{} {\kappa _3 \bar{{t}}_3 {\hbox {e}}^{\kappa _3 L}}&{} {\kappa _4 \bar{{t}}_4 {\hbox {e}}^{\kappa _4 L}}&{} {\kappa _1 \bar{{t}}_1 {\hbox {e}}^{-\kappa _1 L}}&{} {\kappa _2 \bar{{t}}_2 {\hbox {e}}^{-\kappa _2 L}}&{} {\kappa _3 \bar{{t}}_3 {\hbox {e}}^{-\kappa _3 L}}&{} {\kappa _4 \bar{{t}}_4 {\hbox {e}}^{-\kappa _4 L}} \\ \end{array} }} \right] \end{aligned}$$

Substituting Eqs. (22c) and (22d) into Eqs. (21a)–(21d), the nodal force vector $\{F\}$ corresponding to the nodal displacement vector $\{D\}$ can also be written in terms of the constant vector $\{C\}$

$$\begin{aligned} \{F\}=[H]\{C\} \end{aligned}$$

(24)

where

$$\begin{aligned} \{F\}= & {} \left\{ {{\begin{array}{lllllllll} {N_1 }&{} {S_1 }&{} {M_1 }&{} {P_1 }&{} {N_2 }&{} {S_2 }&{} {M_2 }&{} {P_2 } \\ \end{array} }} \right\} ^{T}\\ {[}H]= & {} \left[ {{\begin{array}{lllllllll} {-\hat{{t}}_1 }&{} {-\hat{{t}}_2 }&{} {-\hat{{t}}_3 }&{} {-\hat{{t}}_4 }&{} {\hat{{t}}_1 }&{} {\hat{{t}}_2 }&{} {\hat{{t}}_3 }&{} {\hat{{t}}_4 } \\ {\tilde{t}_1 }&{} {\tilde{t}_2 }&{} {\tilde{t}_3 }&{} {\tilde{t}_4 }&{} {\tilde{t}_1 }&{} {\tilde{t}_2 }&{} {\tilde{t}_3 }&{} {\tilde{t}_4 } \\ {\bar{{\bar{{t}}}}_1 }&{} {\bar{{\bar{{t}}}}_2 }&{} {\bar{{\bar{{t}}}}_3 }&{} {\bar{{\bar{{t}}}}_4 }&{} {-\bar{{\bar{{t}}}}_1 }&{} {-\bar{{\bar{{t}}}}_2 }&{} {-\bar{{\bar{{t}}}}_3 }&{} {-\bar{{\bar{{t}}}}_4 } \\ {\hat{{\hat{{t}}}}_1 }&{} {\hat{{\hat{{t}}}}_2 }&{} {\hat{{\hat{{t}}}}_3 }&{} {\hat{{\hat{{t}}}}_4 }&{} {-\hat{{\hat{{t}}}}_1 }&{} {-\hat{{\hat{{t}}}}_2 }&{} {-\hat{{\hat{{t}}}}_3 }&{} {-\hat{{\hat{{t}}}}_4 } \\ {\hat{{t}}_1 {\hbox {e}}^{\kappa _1 L}}&{} {\hat{{t}}_2 {\hbox {e}}^{\kappa _2 L}}&{} {\hat{{t}}_3 {\hbox {e}}^{\kappa _3 L}}&{} {\hat{{t}}_4 {\hbox {e}}^{\kappa _4 L}}&{} {-\hat{{t}}_1 {\hbox {e}}^{-\kappa _1 L}}&{} {-\hat{{t}}_2 {\hbox {e}}^{-\kappa _2 L}}&{} {-\hat{{t}}_3 {\hbox {e}}^{-\kappa _3 L}}&{} {-\hat{{t}}_4 {\hbox {e}}^{-\kappa _4 L}} \\ {-\tilde{t}_1 {\hbox {e}}^{\kappa _1 L}}&{} {-\tilde{t}_2 {\hbox {e}}^{\kappa _2 L}}&{} {-\tilde{t}_3 {\hbox {e}}^{\kappa _3 L}}&{} {-\tilde{t}_4 {\hbox {e}}^{\kappa _4 L}}&{} {-\tilde{t}_1 {\hbox {e}}^{-\kappa _1 L}}&{} {-\tilde{t}_2 {\hbox {e}}^{-\kappa _2 L}}&{} {-\tilde{t}_3 {\hbox {e}}^{-\kappa _3 L}}&{} {-\tilde{t}_4 {\hbox {e}}^{-\kappa _4 L}} \\ {-\bar{{\bar{{t}}}}_1 {\hbox {e}}^{\kappa _1 L}}&{} {-\bar{{\bar{{t}}}}_2 {\hbox {e}}^{\kappa _2 L}}&{} {-\bar{{\bar{{t}}}}_3 {\hbox {e}}^{\kappa _3 L}}&{} {-\bar{{\bar{{t}}}}_4 {\hbox {e}}^{\kappa _4 L}}&{} {\bar{{\bar{{t}}}}_1 {\hbox {e}}^{-\kappa _1 L}}&{} {\bar{{\bar{{t}}}}_2 {\hbox {e}}^{-\kappa _2 L}}&{} {\bar{{\bar{{t}}}}_3 {\hbox {e}}^{-\kappa _3 L}}&{} {\bar{{\bar{{t}}}}_4 {\hbox {e}}^{-\kappa _4 L}} \\ {-\hat{{\hat{{t}}}}_1 {\hbox {e}}^{\kappa _1 L}}&{} {-\hat{{\hat{{t}}}}_2 {\hbox {e}}^{\kappa _2 L}}&{} {-\hat{{\hat{{t}}}}_3 {\hbox {e}}^{\kappa _3 L}}&{} {-\hat{{\hat{{t}}}}_4 {\hbox {e}}^{\kappa _4 L}}&{} {\hat{{\hat{{t}}}}_1 {\hbox {e}}^{-\kappa _1 L}}&{} {\hat{{\hat{{t}}}}_2 {\hbox {e}}^{-\kappa _2 L}}&{} {\hat{{\hat{{t}}}}_3 {\hbox {e}}^{-\kappa _3 L}}&{} {\hat{{\hat{{t}}}}_4 {\hbox {e}}^{-\kappa _4 L}} \\ \end{array} }} \right] \end{aligned}$$

in which

$$\begin{aligned} \hat{{t}}_j= & {} \bar{{A}}_{11} \kappa _j t_j -\left( {\frac{4}{3h^{2}}\bar{{E}}_{11} -\bar{{B}}_{11} } \right) \kappa _j -\frac{4}{3h^{2}}\bar{{E}}_{11} \kappa _j^2 \bar{{t}}_j\\ \tilde{t}_j= & {} -\frac{4}{3h^{2}}I_4 \omega ^{2}t_j +\left( {-\frac{4}{3h^{2}}I_5 +\frac{16}{9h^{4}}I_7 } \right) \omega ^{2}+\frac{16}{9h^{4}}I_7 \omega ^{2}\kappa _j \bar{{t}}_j -\frac{4}{3h^{2}}\bar{{E}}_{11} \kappa _j^2 t_j +\bar{{N}}_x^T \kappa _j \bar{{t}}_j \\&+\left( {\frac{16}{9h^{4}}\bar{{H}}_{11} -\frac{4}{3h^{2}}\bar{{F}}_{11} } \right) \kappa _j^2 +\frac{16}{9h^{4}}\bar{{H}}_{11} \kappa _j^3 \bar{{t}}_j +\left( {\frac{8}{h^{2}}\bar{{D}}_{55} -\bar{{A}}_{55} -\frac{16}{h^{4}}\bar{{F}}_{55} } \right) \left( {1+\kappa _j \bar{{t}}_j } \right) \\ \bar{{\bar{{t}}}}_j= & {} \left( {\frac{4}{3h^{2}}\bar{{E}}_{11} -\bar{{B}}_{11} } \right) \kappa _j t_j +\left( {\frac{8}{3h^{2}}\bar{{F}}_{11} -\bar{{D}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \kappa _j +\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \kappa _j^2 \bar{{t}}_j\\ \hat{{\hat{{t}}}}_j= & {} \frac{4}{3h^{2}}\bar{{E}}_{11} \kappa _j t_j +\left( {\frac{4}{3h^{2}}\bar{{F}}_{11} -\frac{16}{9h^{4}}\bar{{H}}_{11} } \right) \kappa _j -\frac{16}{9h^{4}}\bar{{H}}_{11} \kappa _j^2 \bar{{t}}_j \qquad (j=1-4) \end{aligned}$$

The relationship between the nodal force vector $\{F\}$ and the nodal displacement vector $\{D\}$ can be obtained by eliminating the constant vector $\{C\}$ from Eqs. (23) and (24), which produces the dynamic stiffness equation

$$\begin{aligned} \{F\}=[K]\{D\} \end{aligned}$$

(25)

where $[K]=[H][R]^{-1}$ is the exact dynamic stiffness matrix, which is frequency-dependent. It should be mentioned that although the explicit analytical expressions for the elements of the dynamic stiffness matrix may be determined in partitioned form using the symbolic manipulator software such as Mathematica [27], they are too lengthy to list in the paper.

Having obtained the dynamic stiffness matrix, it can be directly applied to calculate the natural frequencies, thermal buckling loads and mode shapes of a laminated composite beam with various boundary conditions or a structure composed of such beams. An accurate, reliable and efficient method to obtain the natural frequencies and buckling loads of the laminated beam structure using the dynamic stiffness technique is to apply the Wittrick–Williams algorithm [25] which has been discussed and utilized in a number of papers [23] and is not reiterated here for brevity. The algorithm uses the Sturm sequence property of the dynamic stiffness matrix and ensures that there is no possibility of missing an eigenvalue (i.e., natural frequency in the natural vibration problem, or buckling load in the buckling problem) of the structure.

4 Numerical examples

In order to demonstrate the correctness and accuracy of the proposed dynamic stiffness formulation for the analysis of natural vibration and thermal buckling behaviors of laminated composite beams, two illustrative examples including a cross-ply composite beam and a generally laminated composite beam subjected to a constant temperature change through beam thickness are investigated.

Two classical boundary conditions at each end of the composite beams $(x=0,L)$ are considered, which are given as follows

For the clamped boundary (C): $U=W=\Phi =W^{{\prime }}=0$

For the hinged boundary (H): $U=W=M=P=0$

The first example is a two-layer antisymmetric cross-ply $[0^{\circ }/90^{\circ }]$ composite beam having a rectangular cross section. All the details about the geometric properties of the beam and the material properties of each lamina used here are given below

$$\begin{aligned} E_1= & {} 138\times 10^{9}\,\hbox {Pa}\quad E_2 =6.9\times 10^{9}\,\hbox {Pa} \quad G_{12} =G_{13} =4.14\times 10^{9} \,\hbox {Pa} \quad G_{23} =3.45\times 10^{9} \,\hbox {Pa}\\ \nu _{12}= & {} 0.25 \quad \rho =1550.1\hbox {kg/m}^{3} \quad L=0.381\hbox {m} \quad h=0.0381\hbox {m}\\ \alpha _1= & {} 6\times 10^{-6}1/\,^{\circ }\hbox {C} \quad \alpha _2 =18\times 10^{-6}1/\,^{\circ }\hbox {C} \end{aligned}$$

Numerical results are given for the cross-ply composite beam for different temperature changes, different boundary conditions and different thermal expansion coefficients. The Poisson effect is also discussed. This example is chosen because of some available results in the previous studies [9, 10].

In order to see the influences of temperature change and boundary condition on the natural frequencies of the cross-ply composite beam, three different temperature changes (i.e., $\Delta T=0\,^{\circ }\hbox {C}$, $\Delta T=100\,^{\circ }\hbox {C}$ and $\Delta T=-100\,^{\circ }\hbox {C})$ and three different boundary conditions (i.e., C–C, C–H and H–H) are considered in this example. For various boundary conditions, the first six natural frequencies of the cross-ply composite beam with no temperature change $(\Delta T=0\,^{\circ }\hbox {C})$, temperature rise $(\Delta T=100\,^{\circ }\hbox {C})$ and temperature fall $(\Delta T=-100\,^{\circ }\hbox {C})$ are shown in Tables 1 and 2. The natural frequencies are calculated by using the derived dynamic stiffness formulation and discretizing the whole beam with one element. In order to demonstrate the accuracy of the present formulation, the natural frequencies of the cross-ply composite beam with $\Delta T=0\,^{\circ }\hbox {C}$ are also calculated by the general purpose finite element code ANSYS. The element type selected in calculating the natural frequencies in ANSYS is a layered solid element SOLID191, which is defined by 20 nodes having three degrees of freedom per node. The element mesh used in the ANSYS model is 80 divisions along x direction, eight divisions along y direction and 1 division along z direction. For the clamped end, all degrees of freedom are constrained to zero at all nodes on the end surface. For the hinged end, all degrees of freedom are constrained to zero only at nodes on the line of intersection between beam mid-plane and end surface. The first six natural frequencies of the cross-ply composite beam vibrating in the oxz plane obtained by ANSYS are also given in Table 1. The ANSYS results are taken as a reference for the evaluation of the accuracy of the present formulation. The percentage errors, shown in Table 1, are calculated by using ANSYS results as baseline.

Table 1 Natural frequencies (in Hz) of cross-ply composite beam with $\Delta T=0\,^{\circ }\hbox {C}$

Table 2 Natural frequencies (in Hz) of cross-ply composite beam with $\Delta T=100\,^{\circ }\hbox {C}$ and $\Delta T=-100\,^{\circ }\hbox {C}$

Table 1 shows that the present results are in good agreement with the ANSYS results. The natural frequencies predicted by the present formulation are generally on the higher side of the ANSYS results. The maximum percentage differences in the first six natural frequencies obtained by the present formulation for the C–C, C–H and H–H boundary conditions are 7.4, 7.0 and 8.6%, respectively, as compared to the ANSYS results. It can also be found from Tables 1 and 2 that the temperature change has a significant effect on the lower natural frequencies of the cross-ply composite beam. Also, the effect of temperature change on the higher natural frequencies is marginal. The percentage differences between the fundamental frequencies of the cross-ply composite beam with temperature rise $(\Delta T=100\,^{\circ }\hbox {C})$ and the ones without temperature change for the C–C, C–H and H–H boundary conditions are $-3.2$, $-4.9$ and $-6.3$%, respectively. Similarly, the percentage differences between the fundamental frequencies of the cross-ply composite beam with temperature fall $(\Delta T=-100\,^{\circ }\hbox {C})$ and the ones without temperature change for the C–C, C–H and H–H boundary conditions are 3.0, 4.7 and 5.9%, respectively. For the cross-ply composite beam under study it is obvious that a temperature rise tends to decrease all of the natural frequencies, whereas a temperature fall increases them. Furthermore, a temperature rise has a more remarkable effect on the natural frequencies than the equal temperature fall. Tables 1 and 2 also show that among all of the boundary conditions the effect of temperature change on the natural frequencies is the most important for the H–H boundary condition and the least pronounced for the C–C boundary condition.

Next, the variation of the fundamental natural frequency of the cross-ply composite beam with the variation of the temperature rise is considered. Figure 4a–c shows the variation of the fundamental frequency with the temperature rise for the C–C, C–H and H–H boundary conditions, respectively.

Fig. 4

Variation of fundamental frequency of cross-ply composite beam with temperature rise for a C–C, b C–H, c H–H boundary conditions

It can be observed from Fig. 4 that the variation in the fundamental natural frequency due to the temperature rise is significant. The fundamental frequency decreases with the increase of the temperature rise, as expected. Finally at about $\Delta T=1530.1$, 1011.9 and $820.4\,^{\circ }\hbox {C}$ for the C–C, C–H and H–H boundary conditions, respectively, the fundamental frequency becomes zero which means that at this level of temperature rise, thermal buckling of the cross-ply composite beam occurs as a degenerate case of natural vibration at zero frequency.

Fig. 5

First six mode shapes of the H–H cross-ply composite beam with $\Delta T = 820\,^{\circ }\hbox {C}$: a mode 1; b mode 2; c mode 3; d mode 4; e mode 5; f mode 6

The first six mode shapes of the H–H cross-ply composite beam with $\Delta T=820\,^{\circ }\hbox {C}$, which is very close to the critical temperature change $\Delta T_\mathrm{cr} =820.4\,^{\circ }\hbox {C}$, are calculated by the present formulation and are illustrated in Fig. 5. It may be mentioned that the first six natural frequencies of the H–H cross-ply composite beam with $\Delta T=820\,^{\circ }\hbox {C}$ are 14.6, 1197.7, 3109.9, 4828.8, 7079.7 and 7112.4 Hz, respectively.

Figure 5 shows that the axial displacement and transverse displacement are coupled for all the six mode shapes. For the first mode, this coupling is rather weak. However, for the fifth mode, this coupling is rather strong.

To show the Poisson effect on the natural frequencies of the cross-ply composite beam, the first six natural frequencies of the same composite beam without the Poisson effect included are calculated and the results are displayed in Table 3. Again, three different temperature changes and three different boundary conditions are considered. It may be mentioned that if the Poisson effect is ignored, the quantities $\bar{{A}}_{11}$, $\bar{{B}}_{11}$, $\bar{{D}}_{11}$, $\bar{{E}}_{11}$, $\bar{{F}}_{11}$, $\bar{{H}}_{11}$, $\bar{{A}}_{55}$, $\bar{{D}}_{55}$, $\bar{{F}}_{55}$ and $\bar{{N}}_x^T$ appearing in the governing differential equations of motion and boundary conditions should be replaced by the quantities $A_{11}$, $B_{11}$, $D_{11}$, $E_{11}$, $F_{11}$, $H_{11}$, $A_{55}$, $D_{55}$, $F_{55}$ and $N_x^T$.

Table 3 Natural frequencies (in Hz) of cross-ply composite beam without Poisson effect

Tables 1, 2 and 3 show that all of the natural frequencies of the cross-ply composite beam with the Poisson effect ignored are almost the same as those with the Poisson effect considered, which implies that for the cross-ply composite beam the accuracy lost in the natural frequency obtained by excluding the Poisson effect is insignificant. However, this is not the case for the generally layered composite beam, as will be shown later.

To see the effect of thermal expansion coefficient on the natural frequency of the cross-ply composite beam, $\alpha _2$ varies from $\alpha _2 =18\times 10^{-6}1/\,^{\circ }\hbox {C}$ to $\alpha _2 =60\times 10^{-6}1/\,^{\circ }\hbox {C}$ while the other material properties keep the same. Three different temperature changes (namely, $\Delta T=0\,^{\circ }\hbox {C}$, $\Delta T=100\,^{\circ }\hbox {C}$ and $\Delta T=-100\,^{\circ }\hbox {C})$ and three different boundary conditions (namely, C–C, C–H and H–H) are considered. The first six natural frequencies of the cross-ply composite beam are shown in Table 4.

Table 4 Natural frequencies (in Hz) of cross-ply composite beam $(\alpha _2 =60\times 10^{-6}1/^{\circ }\hbox {C)}$

Tables 1, 2 and 4 clearly show that the variation of $\alpha _2$ has drastic effect on the natural frequencies of the cross-ply composite beam. In addition, Tables 1, 2 and 4 show clearly that when the temperature rises, the increase of $\alpha _2$ results in the decrease of the natural frequencies for all the boundary conditions. Also, Tables 1, 2 and 4 indicate that when the temperature falls, the larger the value of $\alpha _2$ is, the higher the natural frequencies will be.

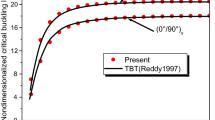
In order to validate the proposed dynamic stiffness formulation, it is used to evaluate the critical temperature change of the cross-ply composite beam with two different values of $\alpha _2$ (namely, $\alpha _2 =18\times 10^{-6}1/\,^{\circ }\hbox {C}$ and $\alpha _2 =60\times 10^{-6}1/\,^{\circ }\hbox {C})$. The critical temperature changes obtained by the present formulation are displayed in Table 5 and compared with some available results in the literature [9, 10].

Table 5 Buckling temperature changes $(^{\circ }\hbox {C)}$ of cross-ply composite beam

Table 6 frequencies (in Hz) of composite beam with $\Delta T=0\,^{\circ }\hbox {C}$

It can be found from Table 5 that the present results generally are in good agreement with the available results. The maximum percent differences between the present results and the available results in the literature [9, 10] are 3.7 and 6.3% for the cases of $\alpha _2 =18\times 10^{-6}1/\,^{\circ }\hbox {C}$ and $\alpha _2 =60\times 10^{-6}1/\,^{\circ }\hbox {C}$, respectively. The reasons for the differences are that different beam theories, constitutive equations, and solution methods are used in the present study and the literature [9, 10]. The first-order shear deformation beam theory (FOBT) and third-order shear deformation beam theory (HOBT) are used in the literature [9], in which the shear correction factor for the FOBT is set equal to 5/6. The exponential shear deformation beam theory (ESDBT) is used in the literature [10]. The beam theory adopted in the present study is the same as the third-order shear deformation beam theory in the literature [9]. The constitutive equations used in the literature [9, 10] do not consider the Poisson effect. However, the Poisson effect is considered in the present study. Although the Poisson effect may be ignored for the cross-ply composite beam, it does have minor influence on the critical buckling temperature. As for the solution method, the state space concept in conjunction with Jordan canonical form is used in the literature [9], and the Ritz method with algebraic polynomial trial functions, which is an approximate solution method, is used in the literature [10]. The exact dynamic stiffness method in conjunction with the Wittrick–Williams algorithm is used to evaluate the natural frequency and critical temperature change in the present study.

Table 5 shows that the critical temperature change obtained by the present formulation lies between the results obtained by the FOBT [9] and HOBT [9]. Also, the critical temperature changes predicted by the present formulation is on the higher side as compared to the results predicted by the ESDBT [10]. For the case of $\alpha _2 =18\times 10^{-6}1/\,^{\circ }\hbox {C}$ the present result is closer to the HOBT solution, while for the case of $\alpha _2 =60\times 10^{-6}1/\,^{\circ }\hbox {C}$ the present result is in excellent agreement with the FOBT solution. As stated previously, the effect of increasing the value of $\alpha _2$ is to decrease the critical temperature change of the cross-ply composite beam under considered. Increasing the value of $\alpha _2$ from $18\times 10^{-6}1/\,^{\circ }\hbox {C}$ to $60\times 10^{-6}1/\,^{\circ }\hbox {C}$ decreases the critical temperature change of the C–C cross-ply composite beam by approximately 25%.

Now, consider a generally layered composite beam. The ply-stacking sequence used is $[30^{\circ }\hbox {/50}^{\circ }/30^{\circ }\hbox {/50}^{\circ }]$. The following geometric properties of the beam and material properties of each layer are used in the analysis.

$$\begin{aligned} E_1= & {} 138\times 10^{9}\,\hbox {Pa} \quad E_2 =6.9\times 10^{9}\,\hbox {Pa} \quad G_{12} =G_{13} =4.14\times 10^{9}\,\hbox {Pa} \quad G_{23} =3.45\times 10^{9}\,\hbox {Pa}\\ \nu _{12}= & {} 0.25 \quad \rho =1550.1\,\hbox {kg/m}^{\hbox {3}} \quad L=0.381\,\hbox {m} \quad h=0.0381\,\hbox {m}\\ \alpha _1= & {} 6\times 10^{-6}1/\,^{\circ }\hbox {C} \quad \alpha _2 =18\times 10^{-6}1/\,^{\circ }\hbox {C} \end{aligned}$$

The first six natural frequencies of the composite beam with various boundary conditions are calculated using the proposed dynamic stiffness formulation, and the numerical results are presented in Tables 6 and 7, in which three different temperature changes (i.e., $\Delta T=0\,^{\circ }\hbox {C}$, $\Delta T=180\,^{\circ }\hbox {C}$ and $\Delta T=-180\,^{\circ }\hbox {C})$ are considered. The natural frequencies are obtained by idealizing the whole beam with single element. The natural frequencies of the composite beam with $\Delta T=0\,^{\circ }\hbox {C}$ are also calculated by the finite element software ANSYS. The element type and mesh division used in computing the natural frequencies in ANSYS are the same as those used in the cross-ply composite beam. The first five natural frequencies of the composite beam vibrating in the oxz plane obtained by ANSYS are also shown in Table 6. It should be noted that the fourth natural frequency obtained by the present formulation, which is a predominant longitudinal vibration frequency, is not captured by ANSYS solutions. The reason for this is perhaps that the longitudinal displacement and boundary condition of the beam are difficult to model using three-dimensional solid element. The ANSYS solutions are regarded as a reference for the evaluation of the accuracy of the present formulation. The percentage errors shown in Table 6 are calculated by using the ANSYS solutions as baseline.

Table 7 Natural frequencies (in Hz) of composite beam with $\Delta T=180\,^{\circ }\hbox {C}$ and $\Delta T=-180\,^{\circ }\hbox {C}$

Fig. 6

Variation of fundamental frequency of composite beam with temperature rise for a C–C, b C–H, c H–H boundary conditions

As can be observed from Table 6, the natural frequencies predicted by the present formulation are also found to be in good agreement with the ANSYS solutions. The natural frequencies produced by the present formulation are also on the higher side of the ANSYS solutions. Tables 6 and 7 clearly show that for the case of temperature rise, the lower natural frequencies decrease with fast rate and the higher natural frequencies decrease with slow rate. Similarly, for the case of temperature fall, the lower natural frequencies increase with fast rate and the higher natural frequencies increase with slow rate. The influence of temperature change on the much higher natural frequencies is practically negligible. In addition, Tables 6 and 7 show that the temperature change has virtually no influence on the fourth natural frequency of the C–C, C–H and H–H composite beam because these frequencies correspond to the modes with predominance of longitudinal vibrations. Moreover, Tables 6 and 7 clearly show that the H–H composite beam yields the lowest natural frequency and the C–C composite beam produces the highest one.

To demonstrate the effect of temperature change on the fundamental natural frequency of the composite beam, Fig. 6a–c illustrates the variation of the fundamental natural frequency of the composite beam with the temperature rise for the C–C, C–H and H–H boundary conditions, respectively.

It can be noted from Fig. 6 that the change in the fundamental frequency due to temperature rise is significant. The fundamental frequency monotonically reduces when the temperature rise increases. Finally, the fundamental frequency becomes zero at about $\Delta T=2752.6$, 1510.7 and $784.3\,^{\circ }\hbox {C}$ for the C–C, C–H and H–H boundary conditions, respectively. At this level of temperature rise, the thermal buckling of the composite beam appears.

Fig. 7

First six mode shapes of the H–H composite beam with $\Delta T=780\,^{\circ }\hbox {C}$: a mode 1; b mode 2; c mode 3; d mode 4; e mode 5; f mode 6

The first six mode shapes of the H–H composite beam with $\Delta T=780\,^{\circ }\hbox {C}$, which is very close to the critical temperature change $\Delta T_\mathrm{cr} =784.3\,^{\circ }\hbox {C}$, are plotted in Fig. 7. It may be noted that the first six natural frequencies of the H–H composite beam with $\Delta T=780\,^{\circ }\hbox {C}$ are 28.7, 1216.7, 2718.2, 4239.0, 4499.9, and 6365.0 Hz, respectively.

Figure 7 shows that the axial displacement is coupled with the transverse displacement except for the fundamental mode. The coupling between the axial displacement and the transverse displacement is rather weak for the second the third modes. However, this coupling is rather strong for the fourth mode.

To show the Poisson effect on the natural frequencies of the composite beam, the first six natural frequencies of the composite beam with the Poisson effect ignored for three boundary conditions and three temperature changes (i.e., $\Delta T=0\,^{\circ }\hbox {C}$, $\Delta T=180\,^{\circ }\hbox {C}$ and $\Delta T=-180\,^{\circ }\hbox {C})$ are computed and presented in Table 8.

Table 8 Natural frequencies (in Hz) of composite beam without Poisson effect

From Tables 6, 7 and 8, the influence of Poisson effect on the natural frequencies of the composite beam can be assessed. It is clear that the natural frequencies obtained with the Poisson effect excluded significantly deviate from the results predicted with the Poisson effect included. For the case of temperature rise $(\Delta T=180\,^{\circ }\hbox {C})$, it is worthwhile to observe that the maximum percentage differences between the first six natural frequencies obtained with and without the Poisson effect included are about 52.8, 59.3 and 70.2% for the C–C, C–H and H–H boundary conditions, respectively. Also the average differences are about 40.6, 44.9 and 50.2% for the C–C, C–H and H–H boundary conditions, respectively. The results presented in Tables 6, 7 and 8 indicate that the natural frequencies predicted with the Poisson effect ignored have large errors when compared to the results predicted with the Poisson effect included. Therefore, any one-dimensional laminated beam models with the Poisson effect neglected cannot be used to accurately estimate the natural frequency of the composite beams with general laminations.

The effect of material anisotropy on the first six natural frequencies of the composite beam with various boundary conditions is shown in Table 9. It is noted that the value of $E_1$ is varied from $138\times 10^{9}$ to $69\times 10^{9}\,\hbox {Pa}$, while the other material properties are kept the same.

Table 9 Natural frequencies (in Hz) of composite beam $(E_1 =69\times 10^{9}\hbox {Pa)}$

Tables 6, 7 and 9 show clearly that the smaller the value of $E_1$ is, the lower the natural frequency of the composite beam is. For the case of temperature rise $(\Delta T=180\,^{\circ }\hbox {C})$, altering the value of $E_1$ from $138\times 10^{9}$ to $69\times 10^{9}\,\hbox {Pa}$ decreases the fundamental frequencies of the composite beam by approximately 7.5, 8.1 and 8.8%, and decreases the sixth natural frequencies of the composite beam by approximately 4.1, 4.4 and 4.9% for the C–C, C–H and H–H boundary conditions, respectively. The natural frequencies of the composite beam for the fundamental modes decrease with faster rate than for the sixth modes.

5 Conclusions

Natural vibration and buckling behaviors of generally laminated composite beams subjected to uniform temperature changes along beam thickness are investigated. The third-order shear deformation beam theory is adopted and the Poisson effect is included in the one-dimensional beam constitutive equations. The coupled differential equations governing the natural vibration of generally laminated composite beams subject to uniform temperature changes are deduced using the Hamilton’s principle. The dynamic stiffness matrix is formulated from the exact analytical solutions of the homogeneous governing equations of motion of generally laminated composite beams. The dynamic stiffness method together with the Wittrick–Williams algorithm is successfully applied to calculate the natural frequencies and critical temperature changes of the composite beams. The proposed mathematical model and solution procedure gives good results for the prediction of critical temperature changes when compared with the available results in literature. A parametric study is presented to determine the influences of boundary conditions, Poisson effect, temperature change, thermal expansion coefficient and material anisotropy on the natural frequencies of the composite beams. This study is useful for the design engineers to choose the ply angle of laminated composite beams to shift the natural frequencies and critical temperature change as desired or to control the vibration and buckling level.

Appendix

The transformed thermal coefficients $\alpha _x$, $\alpha _y$ and $\alpha _{xy}$ are defined by [28]

$$\begin{aligned} \alpha _x= & {} \alpha _1 \cos ^{2}\vartheta +\alpha _2 \sin ^{2}\vartheta \end{aligned}$$

(26)

$$\begin{aligned} \alpha _y= & {} \alpha _2 \cos ^{2}\vartheta +\alpha _1 \sin ^{2}\vartheta \end{aligned}$$

(27)

$$\begin{aligned} \alpha _{xy}= & {} (\alpha _1 -\alpha _2 )\cos \vartheta \sin \vartheta \end{aligned}$$

(28)

where $\vartheta$ is the angle between the fiber direction and the beam axis, $\alpha _1$ and $\alpha _2$ are the thermal expansion coefficients along the fiber direction and normal to the fiber direction, respectively.

The transformed reduced stiffness constants $\bar{{Q}}_{ij} \quad (i,j=1,2,6)$ and $\bar{{Q}}_{ij} \quad (i,j=4,5)$ are defined by [28]

$$\begin{aligned} \bar{{Q}}_{11}= & {} Q_{11} \cos ^{4}\vartheta +2(Q_{12} +2Q_{66} )\sin ^{2}\vartheta \cos ^{2}\vartheta +Q_{22} \sin ^{4}\vartheta \end{aligned}$$

(29)

$$\begin{aligned} \bar{{Q}}_{12}= & {} (Q_{11} +Q_{22} -4Q_{66} )\sin ^{2}\vartheta \cos ^{2}\vartheta +Q_{12} (\sin ^{4}\vartheta +\cos ^{4}\vartheta ) \end{aligned}$$

(30)

$$\begin{aligned} \bar{{Q}}_{22}= & {} Q_{11} \sin ^{4}\vartheta +2(Q_{12} +2Q_{66} )\sin ^{2}\vartheta \cos ^{2}\vartheta +Q_{22} \cos ^{4}\vartheta \end{aligned}$$

(31)

$$\begin{aligned} \bar{{Q}}_{16}= & {} (Q_{11} -Q_{12} -2Q_{66} )\sin \vartheta \cos ^{3}\vartheta +(Q_{12} -Q_{22} +2Q_{66} )\sin ^{3}\vartheta \cos \vartheta \end{aligned}$$

(32)

$$\begin{aligned} \bar{{Q}}_{26}= & {} (Q_{11} -Q_{12} -2Q_{66} )\sin ^{3}\vartheta \cos \vartheta +(Q_{12} -Q_{22} +2Q_{66} )\sin \vartheta \cos ^{3}\vartheta \end{aligned}$$

(33)

$$\begin{aligned} \bar{{Q}}_{66}= & {} (Q_{11} +Q_{22} -2Q_{12} -2Q_{66} )\sin ^{2}\vartheta \cos ^{2}\vartheta +Q_{66} (\sin ^{4}\vartheta +\cos ^{4}\vartheta ) \end{aligned}$$

(34)

$$\begin{aligned} \bar{{Q}}_{44}= & {} Q_{44} \cos ^{2}\vartheta +Q_{55} \sin ^{2}\vartheta \end{aligned}$$

(35)

$$\begin{aligned} \bar{{Q}}_{45}= & {} (Q_{55} -Q_{44} )\cos \vartheta \sin \vartheta \end{aligned}$$

(36)

$$\begin{aligned} \bar{{Q}}_{55}= & {} Q_{55} \cos ^{2}\vartheta +Q_{44} \sin ^{2}\vartheta \end{aligned}$$

(37)

where the reduced stiffness constants $Q_{11}$, $Q_{12}$, $Q_{22}$, $Q_{66}$ and $Q_{44}$, $Q_{55}$ can be obtained in terms of the engineering constants [28]

$$\begin{aligned} Q_{11}= & {} \frac{E_1 }{1-\nu _{12} \nu _{21} } \end{aligned}$$

(38)

$$\begin{aligned} Q_{12}= & {} \frac{\nu _{12} E_2 }{1-\nu _{12} \nu _{21} }=\frac{\nu _{21} E_1 }{1-\nu _{12} \nu _{21} } \end{aligned}$$

(39)

$$\begin{aligned} Q_{22}= & {} \frac{E_2 }{1-\nu _{12} \nu _{21} } \end{aligned}$$

(40)

$$\begin{aligned} Q_{66}= & {} G_{12} \end{aligned}$$

(41)

$$\begin{aligned} Q_{44}= & {} G_{23} \end{aligned}$$

(42)

$$\begin{aligned} Q_{55}= & {} G_{13} \end{aligned}$$

(43)

The coefficients $\eta _k (k=0-4)$ appearing in Eq. (17) are

$$\begin{aligned} \eta _4= & {} {16\left( -2\bar{{B}}_{11} \bar{{E}}_{11} \bar{{F}}_{11} +\bar{{A}}_{11} \bar{{F}}_{11}^2 +\bar{{B}}_{11}^2 \bar{{H}}_{11} +\bar{{D}}_{11} \left( \bar{{E}}_{11}^2 -\bar{{A}}_{11} \bar{{H}}_{11} \right) \right) }/{\left( 9h^{4}\right) } \end{aligned}$$

(44)

$$\begin{aligned} \eta _3= & {} \left( 9\bar{{A}}_{11} \bar{{D}}_{11} \left( 16\bar{{F}}_{55} -8\bar{{D}}_{55} h^{2}+\bar{{A}}_{55} h^{4}\right) +16\bar{{E}}_{11}^2 \bar{{N}}_x^T -24\bar{{B}}_{11} \bar{{E}}_{11} h^{2}\bar{{N}}_x^T +\bar{{A}}_{11} \left( 24\bar{{F}}_{11} h^{2}\right. \right. \nonumber \\&\left. -9\,\bar{{D}}_{11} h^{4}-16\bar{{H}}_{11} \right) \bar{{N}}_x^T +32\bar{{B}}_{11} \left( \bar{{H}}_{11} I_2 -\bar{{F}}_{11} I_4 -\bar{{E}}_{11} I_5 \right) \omega ^{2}+16\left( \bar{{F}}_{11}^2 I_1 -\bar{{D}}_{11} \bar{{H}}_{11} I_1 \right. \nonumber \\&\left. -2\,\bar{{E}}_{11} \bar{{F}}_{11} I_2 +\bar{{E}}_{11}^2 I_3 -\bar{{A}}_{11} \bar{{H}}_{11} I_3 +2\bar{{D}}_{11} \bar{{E}}_{11} I_4 +2\bar{{A}}_{11} \bar{{F}}_{11} I_5 -\bar{{A}}_{11} \bar{{D}}_{11} I_7\right) \omega ^{2} \nonumber \\&\left. +\,\bar{{B}}_{11}^2 \left( -144\bar{{F}}_{55} +72\bar{{D}}_{55} h^{2}+9h^{4}\left( -\bar{{A}}_{55} +\bar{{N}}_x^T \right) +16I_7 \omega ^{2}\right) \right) /\left( 9h^{4}\right) \end{aligned}$$

(45)

$$\begin{aligned} \eta _2= & {} \left( 9\bar{{A}}_{11} \left( 16\bar{{F}}_{55} -8\,\bar{{D}}_{55} h^{2}+\bar{{A}}_{55} h^{4}\right) \bar{{N}}_x^T -16\,\bar{{E}}_{11}^2 I_1 \omega ^{2}+\left( -9\bar{{B}}_{11}^2 h^{4}I_1 \right. \right. \nonumber \\&-\,8\bar{{A}}_{11} \left( 3\bar{{F}}_{11} h^{2}-2\bar{{H}}_{11} \right) I_1 +\,9\bar{{A}}_{11} \left( 16\bar{{F}}_{55} -8\bar{{D}}_{55} h^{2}+\bar{{A}}_{55} h^{4}\right) I_3 +9\bar{{D}}_{11} I_1 \left( 16\bar{{F}}_{55} -8\bar{{D}}_{55} h^{2} \right. \nonumber \\&\left. +\,h^{4}\left( \bar{{A}}_{11} +\bar{{A}}_{55} -\bar{{N}}_x^T \right) \right) +(24\bar{{F}}_{11} h^{2}I_1 -16\bar{{H}}_{11} I_1 -24\bar{{E}}_{11} h^{2}I_2 -9\bar{{A}}_{11} h^{4}I_3 +32\bar{{E}}_{11} I_4 \nonumber \\&+24\bar{{A}}_{11} h^{2}I_5 -16\bar{{A}}_{11} I_7 )\bar{{N}}_x^T +6\bar{{B}}_{11} \left( -48\bar{{F}}_{55} I_2 +h^{2}\left( 4\bar{{E}}_{11} I_1 +24\bar{{D}}_{55} I_2 -3\bar{{A}}_{55} h^{2}I_2 \right. \right. \nonumber \\&\left. \left. \left. +\,3h^{2}I_2 \bar{{N}}_x^T -4I_4 \bar{{N}}_x^T \right) \right) \right) \omega ^{2}+16\left( \bar{{H}}_{11} \left( I_2^2 -I_1 I_3 \right) -2\bar{{F}}_{11} I_2 I_4 +2\bar{{E}}_{11} I_3 I_4 +\bar{{D}}_{11} I_4^2 \right. \nonumber \\&\left. \left. \left. \left. +\,2\bar{{F}}_{11} I_1 I_5 -2\bar{{E}}_{11} I_2 I_5 -2\bar{{B}}_{11} I_4 I_5 +\bar{{A}}_{11} I_5^2 -{\left( \bar{{D}}_{11} I_1 -2\bar{{B}}_{11} I_2 +\bar{{A}}_{11} I_3 \right) I_7} \right) \omega ^{4}\right) /{\left( 9h^{4}\right) } \right) \right) \end{aligned}$$

(46)

$$\begin{aligned} \eta _1= & {} \left( -9\left( 16\bar{{F}}_{55} -8\bar{{D}}_{55} h^{2}+\bar{{A}}_{55} h^{4}\right) I_1 \left( \bar{{A}}_{11} -\,\bar{{N}}_x^T \right) \omega ^{2}+\left( -24\bar{{F}}_{11} h^{2}I_1^2 +\,9\bar{{D}}_{11} h^{4}I_1^2 \right. \right. \nonumber \\&+\,16\bar{{H}}_{11} I_1^2 +24\bar{{E}}_{11} h^{2}I_1 I_2 -\,18\bar{{B}}_{11} h^{4}I_1 I_2 -144\bar{{F}}_{55} I_2^2 +\,72\bar{{D}}_{55} h^{2}I_2^2 -9\bar{{A}}_{55} h^{4}I_2^2 \nonumber \\&+\,144\bar{{F}}_{55} I_1 I_3 -72\bar{{D}}_{55} h^{2}I_1 I_3 +\,9\bar{{A}}_{11} h^{4}I_1 I_3 +9\bar{{A}}_{55} h^{4}I_1 I_3 -32\bar{{E}}_{11} I_1 I_4 +24\bar{{B}}_{11} h^{2}I_1 I_4 \nonumber \\&-\,24\bar{{A}}_{11} h^{2}I_1 I_5 +16\bar{{A}}_{11} I_1 I_7 +\,\left( 9h^{4}\left( I_2^2 -I_1 I_3 \right) -24h^{2}\left( I_2 I_4 -I_1 I_5 \right) \right. \nonumber \\&\left. \left. \left. +\,16\left( I_4^2 -I_1 I_7 \right) \right) \bar{{N}}_x^T \right) \omega ^{4}+16\left( -2I_2 I_4 I_5 +I_1 I_5^2 +I_2^2 I_7 +I_3 \left( I_4^2 -I_1 I_7\right) \right) \omega ^{6}\right) /{\left( 9h^{4}\right) } \end{aligned}$$

(47)

$$\begin{aligned} \eta _0= & {} \left( I_1 \omega ^{4}\left( -9\left( 16\bar{{F}}_{55} -\,8\bar{{D}}_{55} h^{2}+\bar{{A}}_{55} h^{4}\right) I_1 +\,\left( -9h^{4}\left( I_2^2 -I_1 I_3 \right) +24h^{2}\left( I_2 I_4 -I_1 I_5 \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +\,16\left( -I_4^2 +I_1 I_7 \right) \right) \omega ^{2}\right) \right) /\left( 9h^{4}\right) \end{aligned}$$

(48)