Holographic Dark Energy with Time Varying n ² Parameter in Non-Flat Universe

Abstract

We consider a holographic dark energy model, with a varying parameter, n, which evolves slowly with time. We obtain the differential equation describing evolution of the dark energy density parameter, Ω _d , for the flat and non-flat FRW universes. The equation of state parameter in this generalized version of holographic dark energy depends on n.

1 Introduction

The current observations [1–5] strongly support that our universe is in the accelerated expansion phase. In the standard cosmological structure, the existence of a component with antigravity effect is necessary for explaining this accelerated expansion. Using different approaches, many models have been suggested to explain the dark energy. One of them is the use of the Einstein cosmological constant, but it suffers from two problems (the “fine-tuning” and the “coincidence”) [6, 7]. The dynamical dark energy models with a variable equation of state have been investigated, scalar field models are one of these [8]. Another interesting approach for exploring the behavior of dark energy is through the use of the principles of quantum gravitation [9]. Proposal of holographic dark energy (HDE) is an example of such models [10–14]. The expression for energy density of HDE is:

$$ \rho_{d}=\frac{3n^{2}}{8\pi G L^{2}}, $$

(1)

where L is the infrared (IR) cut-off, n is a constant, and G is the Newton gravitational constant. The holographic dark energy scenario is one of the most widely studied model and there are many versions of this model in the literature [15–23].

If we take L as a Hubble horizon, it results in a wrong equation of state (EoS) and the accelerated expansion of the universe can not be obtained. However, this issue can be resolved in the case of interacting HDE. This model does not work with the particle horizon as well, but when L is chosen as future event horizon, the results favor the accelerated expansion.

There is no strong evidence for n to be taken a constant, so the HDE parameter, n ², has a vital role in characterizing the properties of the model. For example in future, the model could be like a phantom or quintessence dark energy model depends on whether the value of n ² is larger or smaller than 1 respectively. Model of HDE with variable n ² parameter for a flat universe has been studied in [29]. There are many models of HDE in literature with a variable gravitational constant, G. Following the approach adopted by Jamil et al. [24], here we investigate the HDE model with a variable n ² parameter, allowing the consequent modifications to the EoS parameter, w, of the dark energy. Plan of our work is as follows: In Section 2 we build the HDE model with a time varying n ²(z) and extract the evolution equations for the dark energy density parameter. In Section 3 we calculate the corrections to the parameter, w, at low redshifts. In Section 4 we demonstrate the numerical results and in Section 5 we summarize our results.

2 Holographic Dark Energy (HDE) with Variable n ² Parameter

2.1 Flat FRW Geometry

To construct the HDE model with a variable n ², we consider the flat Robertson-Walker geometry given as

$$ ds^{2}=-dt^{2}+a^{2}(t)\left(dr^{2}+r^{2}(d\theta^{2}+\sin^{2}\theta d\varphi^{2})\right), $$

(2)

where a(t) is the scale factor and t is the comoving time. The first Friedmann equation is given by

$$ H^{2}=\frac{8\pi G}{3}(\rho_{m}+\rho_{d}), $$

(3)

where H is the Hubble parameter, $\rho _{m}=\frac {\rho _{m0}}{a^{3}}$ denotes the matter density, and ρ _d is the dark energy density. The present value of a quantity is represented by index “0”. Using the density parameter, ${\Omega }_{d}\equiv \frac {8\pi G}{3H^{2}}\rho _{d}$, with (1) we get

$$ {\Omega}_{d}=\frac{n^{2}(z)}{H^{2}L^{2}}. $$

(4)

As discussed before, for flat universe, defining L as the future event horizon is the best option [13, 14, 25, 26], i.e. taking L ≡ R _h (a) as

$$ R_ h(a)=a{\int}_{t}^{\infty}\frac{dt}{a(t)}=a{\int}_{a}^{\infty}\frac{da}{Ha^{2}}~. $$

(5)

To denote the time derivative we use a dot, and prime is used for the differentiation with respect to the independent variable lna, i.e. we acquire $\dot {J}=J^{\prime }H$, for every quantity J. Differentiating (4), using (5), and $\dot {R}_{h}=HR_{h}-1$, we attain

$$ \frac{{\Omega}^{\prime}_{d}}{{{\Omega}^{2}_{d}}}=\frac{2}{{\Omega}_{d}}\left[\frac{n^{\prime}}{n}-1-\frac{\dot{H}}{H^{2}}+\frac{\sqrt{{\Omega}_{d}}}{n}\right]. $$

(6)

We can see that the varying behavior of n ² has become apparent. To eliminate $\dot {H}$ we differentiate the Friedman (3) and use the expression

$$ \rho^{\prime}_{d}=\rho_{d}\left(\frac{n^{\prime}}{n}-2+\frac{2\sqrt{{\Omega}_{d}}}{n}\right), $$

(7)

to get

$$ 2\frac{\dot{H}}{H^{2}}=-3+{\Omega}_{d}\left(1+\frac{2\sqrt{{\Omega}_{d}}}{n}\right)+\frac{2n^{\prime}}{n}{\Omega}_{d}, $$

(8)

where n is considered to be time dependent. Finally, using (8) in (6) we have

$$ {\Omega}_{d}^{\prime}={\Omega}_{d}(1-{\Omega}_{d})\left[1+\frac{2\sqrt{{\Omega}_{d}}}{n}\right]+2{\Omega}_{d}(1-{\Omega}_{d})\frac{n^{\prime}}{n}. $$

(9)

Note that the second term is the correction term appearing because of variable n, here n ^′/n is a dimensionless number.

2.2 Non-Flat FRW Geometry

Now we extend the work presented in the previous subsection for the FRW universe with metric

$$ ds^{2}=-dt^{2}+a^{2}(t)\left(\frac{dr^{2}}{1-kr^{2}}+r^{2}(d\theta^{2}+\sin^{2}\theta d\varphi^{2})\right), $$

(10)

where (t, r, θ, φ) are comoving coordinates and k represents the spacial curvature with k = − 1, 0, 1 respectively corresponding to the open, flat and the closed universes. In this geometry the first Friedmann equation becomes

$$ H^{2}+\frac{k}{a^{2}}=\frac{8\pi G}{3}(\rho_{m}+\rho_{d}). $$

(11)

In non-flat metric, the cosmological length, L, for the HDE model takes the following form [28]

$$ L\equiv\frac{a(t)}{\sqrt{|k|}}\,\text{sinn}\left(\frac{\sqrt{|k|}R_{h}}{a(t)}\right), $$

(12)

with

$$ \frac{{1}{\sqrt{|k|}}\text{sinn}(\sqrt{|k|}y)}= \left\{\begin{array}{llll} \sin y && \, \, k=+1,\\ y & &\, \, k=0,\\ \sinh y && \, \, k=-1.\\ \end{array}\right. $$

(13)

It is easy to find that

$$ \dot{L}=H L-\text{cosn}\left(\frac{\sqrt{|k|}R_{h}}{a}\right), $$

(14)

where

$$\text{cosn}(\sqrt{|k|}y)=\left\{\begin{array}{ll} \cos y & \, \, k=+1,\\ 1 & \, \, k=0,\\ \cosh y & \, \, k=-1.\\\end{array}\right. $$

(15)

Following the same steps as adopted in the previous subsection, differentiating (4) and using (12) and (14) we obtain

$$ \frac{{\Omega}^{\prime}_{d}}{{{\Omega}^{2}_{d}}}=\frac{2}{{\Omega}_{d}} \left(-1+\frac{n^{\prime}}{n}-\frac{\dot H}{H^{2}}+\frac{\sqrt{{\Omega}_{d}}}{n} \,\text{cosn}(\sqrt{|k|}y) \right). $$

(16)

From Friedmann (11) we get

$$ 2\frac{\dot H}{H^{2}}=-3-{\Omega}_{k}+{\Omega}_{d}+2\frac{{\Omega}_{d}^{3/2}}{n}\, \text{cosn}\left(\frac{\sqrt{|k|}R_{h}}{a}\right) +2{\Omega}_{d}\frac{n^{\prime}}{n}, $$

(17)

where ${\Omega }_{k}\equiv \frac {k}{(aH)^{2}}$ is the curvature density parameter. Using (17) into (16) we have

$$ {\Omega}_{d}^{\prime}={\Omega}_{d}\left[1+{\Omega}_{k}-{\Omega}_{d}+\frac{2\sqrt{{\Omega}_{d}}}{n}\, \text{cosn}\left(\frac{\sqrt{|k|}R_{h}}{a}\right)(1-{\Omega}_{d})\right] +2{\Omega}_{d}(1-{\Omega}_{d})\frac{n^{\prime}}{n}. $$

(18)

Here the correction made to the HDE differential equation in non-flat universe because of the variable n can be observed. Clearly, when k = 0 (and thus Ω _k = 0) we get (9).

3 Equation of State Parameter (w(z))

We find w(z) for small values of redshifts z. Since ρ _d ∼ a ^−3(1+w), taking the derivatives at the present time a ₀ = 1 (so ${\Omega }_{d}={{\Omega }_{d}^{0}}$) we get

$$ \ln\rho_{d} =\ln {\rho^{0}_{d}}+\frac{d\ln\rho_{d}}{d\ln a} \ln a +\frac{1}{2} \frac{d^{2}\ln\rho_{d}}{d(\ln a)^{2}}(\ln a)^{2}+\dots.... $$

(19)

Then, w(lna) up to second order is given by

$$ w(\ln a)=-1-\frac{1}{3}\left[\frac{d\ln\rho_{d}}{d\ln a} +\frac{1}{2} \frac{d^{2}\ln\rho_{d}}{d(\ln a)^{2}}\ln a\right]. $$

(20)

Using lna = − ln(1 + z) ≃ − z, which is applicable for small redshifts, one can easily compute w(z), as

$$ w(z)=-1-\frac{1}{3}\left(\frac{d\ln\rho_{d}}{d\ln a}\right)+ \frac{1}{6} \left[\frac{d^{2}\ln\rho_{d}}{d(\ln a)^{2}}\right]\,z\equiv w_{0}+w_{1}z. $$

(21)

3.1 Flat FRW Geometry

Using the expression for ${\Omega }_{d}^{\prime }$, given in (9) and aforementioned procedure leads to

$$\begin{array}{@{}rcl@{}} &&w_{0}=-\frac{1}{3}-\frac{2}{3n}\sqrt{{{\Omega}^{0}_{d}}} -\frac{2{\Delta}_{n}}{3}, \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} &&w_{1}=\frac{1}{6n}\sqrt{{{\Omega}^{0}_{d}}}(1-{{\Omega}^{0}_{d}})\left(1+\frac{2}{n}\sqrt{{{\Omega}^{0}_{d}}}\right)+2\frac{(1-{{\Omega}^{0}_{d}})\sqrt{{{\Omega}^{0}_{d}}}}{6n}{\Delta}_{n}. \end{array} $$

(23)

These w ₀ and w ₁ are for the HDE with varying n ², in a flat universe. It is clear that when n-variation Δ _n = 0, we obtain the results which are consistent with those of [14].

The best fit value for n obtained from supernovae type Ia observational data, within 1 − σ error range [19], is n = 0.21 and from the analysis of X−ray gas mass fraction of galaxy clusters it comes out as n = 0.61 [20]. While combing the results from different sources we have: the data obtained by the observations of type Ia supernovae, Cosmic Microwave Background (CMB) radiation and large scale structure gives n = 0.91 [21], whereas combining the observations of Baryon Acoustic Oscillation, X−ray gas and type Ia supernovae lead to n = 0.73 [22].

3.2 Non-Flat FRW Geometry

Using the expression of ${\Omega }_{d}^{\prime }$ for non-flat case, given in (18), we have

$$\begin{array}{@{}rcl@{}} &&w_{0}=-\frac{1}{3}-\frac{2}{3n}\sqrt{{{\Omega}^{0}_{d}}}\,\text{cosn}\frac{\sqrt{|k|}R_{h0}}{a_{0}} -\frac{2 {\Delta}_{n}}{3} \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} &&w_{1}=\frac{\sqrt{{{\Omega}^{0}_{d}}}}{6n}\left[1+{{\Omega}_{k}^{0}}-{{\Omega}^{0}_{d}}+\frac{2\sqrt{{{\Omega}^{0}_{d}}}}{n}\, \text{cosn}\left(\frac{\sqrt{|k|}R_{h0}}{a_{0}}\right)(1-{{\Omega}^{0}_{d}}) \right]\text{cosn}\left(\frac{\sqrt{|k|}R_{h0}}{a_{0}}\right)\\&& +\frac{{{\Omega}^{0}_{d}}}{3n^{2}}\,q\left(\frac{\sqrt{|k|}R_{h0}}{a_{0}}\right) +2\frac{\sqrt{{{\Omega}^{0}_{d}}}}{6n}(1-{{\Omega}^{0}_{d}})\text{cosn}\left(\frac{\sqrt{|k|}R_{h0}}{a_{0}}\right){\Delta}_{n}, \end{array} $$

(25)

where

$$q(\sqrt{|k|}y)=\left\{\begin{array}{ll} \sin^{2} y & {\kern1pc} \, \, k=+1,\\ 0 & \, \,{\kern1pc} k=0,\\ -\sinh^{2} y &{\kern1pc} \, \, k=-1.\end{array}\right. $$

(26)

Clearly, for k = 0, (24) and (25) reduce to (22) and (23) respectively.

The expressions given by (24) and (25) involve present values of the parameters ${{\Omega }_{d}^{0}}$, ${{\Omega }_{k}^{0}}$, a ₀, and R _h0. From (4) we obtain $L_{0}=n/(H_{0}\sqrt {{\Omega }_{\Lambda }^{0}})$. Also from (12), we get $R_{h0}/a_{0}=\frac {1}{\sqrt {|k|}}\text {sinn}^{-1}(\sqrt {|k|}L_{0}/a_{0})$. Hence,

$$\begin{array}{@{}rcl@{}} \frac{R_{h0}}{a_{0}}&=&\frac{1}{\sqrt{|k|}}\text{sinn}^{-1} \left(\frac{n\sqrt{|k|}}{a_{0}H_{0}\sqrt{{\Omega}_{\Lambda}^{0}}}\right), \\ &=& \frac{1}{\sqrt{|k|}}\text{sinn}^{-1}\left(\frac{n\sqrt{|{{\Omega}_{k}^{0}}|}}{\sqrt{{\Omega}_{\Lambda}^{0}}}\right).\end{array} $$

(27)

Substituting (27) in (24) and (25), we finally obtain

$$\begin{array}{@{}rcl@{}} w_{0}&=&-\frac{1}{3}-\frac{2}{3n}\sqrt{{{\Omega}^{0}_{d}}-n^{2}{{\Omega}^{0}_{k}}} -2\frac{{\Delta}_{n}}{3}, \end{array} $$

(28)

$$\begin{array}{@{}rcl@{}} w_{1}&=&\frac{{{\Omega}_{k}^{0}}}{3}+\frac{1}{6n}\sqrt{{{\Omega}^{0}_{d}}-n^{2}{{\Omega}_{k}^{0}}} \left[1+{{\Omega}_{k}^{0}}-{{\Omega}^{0}_{d}} + \frac{2}{n}(1-{{\Omega}^{0}_{d}})\sqrt{{{\Omega}^{0}_{d}}-n^{2}{{\Omega}_{k}^{0}}}\right]\\&& +\frac{1}{6n}\sqrt{{{\Omega}^{0}_{d}}-n^{2}{{\Omega}^{0}_{k}}} \left(1-{{\Omega}^{0}_{d}}\right){\Delta}_{n}. \end{array} $$

(29)

These w ₀ and w ₁ are for non-flat universe, depending only on ${{\Omega }_{d}^{0}}$, ${{\Omega }_{k}^{0}}$, n, and Δ _n .

4 Numerical Results

By solving the equations for EoS parameters we can give a numerical description of the evolution of GHDE model. For the choice of model parameter, n(z), we use the parameterization known as Chavallier-Polarski-Linder (CPL) [29] given as

$$ n(z)=n_{0}+n_{1}\frac{z}{1+z}. $$

(30)

When z → ∞ (in the early universe), we see that n → n ₀ + n ₁ and as z → 0 (at the present time), n → n ₀. Therefore, the value of n varies from n ₀ + n ₁ to n ₀ with passage of time. Also the positive energy condition of GHDE model requires that

$$ n_{0}>0,~~~~n_{0}+n_{1}>0. $$

(31)

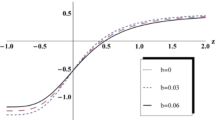
Since w(lna) ≡ w ₀ + w ₁ z, using (30) and solving w ₀ and w ₁ given in (22) and (23) we plot the evolutionary behavior of EoS parameter of GHDE model versus redshift variable Fig. 1. We choose the values for n ₀ and n ₁ such that they satisfy (31). Similarly we can draw the EoS parameter for non-flat case by solving (28) and (29) with (30). The behavior of curve is shown in Fig. 2. We see that the curve for EoS parameter enters from w _d > − 1 to w _d < − 1. So it crosses the phantom line, w _d = −1, without taking into account the interaction of dark energy and dark matter.

Fig. 1

Evolution of EoS parameter for flat universe versus redshift parameter z. Model parameters n ₀ and n ₁ are 0.75 and 0.1 respectively. The values for Ω _d and Ω _m are taken as 0.7 and 0.3 respectively

Fig. 2

Evolution of EoS parameter for non-flat universe versus redshift parameter z. Model parameters n ₀ and n ₁ are 0.5 and 0.1. The values for Ω _d , Ω _m and Ω _k are taken as 0.7, 0.285, and 0.015 respectively

5 Conclusions

In this paper, we have considered the generalized holographic dark energy model for spatially flat and non-flat universes with a future event horizon. Since the holographic parameter, n, is generally not constant and can be assumed as a function of cosmic redshift, we have provided the complete expressions for cosmological parameters, introducing the correction terms due to varying n. For GHDE with future event horizon, we have obtained the EoS parameter at small redshifts by performing the Taylor series expansion up to the first order i.e. w(z) ≡ w ₀ + w ₁ z. We have obtained w ₀ and w ₁ in terms of ${{\Omega }_{d}^{0}}$, ${{\Omega }_{k}^{0}}$ and n-variation Δn. The expressions for evolution of the dark energy density have an additional term depending on Δn.

For further exploration we have also considered the CPL parametrization in which $n(z)=n_{0}+n_{1}\frac {z}{1+z}$ . An investigation has been made for the effect of correction term on EoS parameters for flat and non-flat geometries. Obtaining numerical values of the cosmological parameters, we have plotted them against z(t). Graphical behavior of EoS parameters for our model shows that with a varying n a shifting from quintessence regime (w _d > − 1) to phantom regime (w _d < − 1) is possible, without taking into account the interaction of dark matter and dark energy. Hence the GHDE model has a correspondence with the observational data.