1 Introduction

The astronomical observations predict that the universe emerged from an inflationary universe in the past which is now not only expanding but accelerating [1, 2]. To accommodate accelerating universe the gravitational or matter sector needs to be modified. A number of modifications in the gravitational sector with theories of gravity namely, f(R), f(T), f(R, T), f(Q) and f(R, G) proposed in the literature [3,4,5,6,7,8]. It remains to be understood properly, consequently a modification of the matter sector with dark energy (DE) and dark matter (DM) originated. In this context holographic dark energy [9,10,11,12,13,14,15,16,17,18,19,20,21] is an interesting alternative for the quantitative description of the dark energy, that originated from the holographic principle [22,23,24,25,26]. It is known that the holographic principle in the cosmological framework is applicable assuming that the entropy of the universe is proportional to its area. The Bekenstein–Hawking entropy of a black-hole is proportional to the area. However, recently Barrow proposed a modified form of the black hole entropy that arises from the incorporation of quantum gravitational effects and considering an intricate idea i.e., fractal features of the black-hole structure.

In cosmology it is known that the universe on a sufficiently large scale is homogeneous and isotropic. However, on small scales it is neither homogeneous nor isotropic. The theoretical study that the universe was highly anisotropic in the past which is supported by cosmological observations [27, 28]. The Bianchi type-I space-time represents a universe which gives rise to a universe with anisotropic behaviour [29, 30]. In this paper, we consider Bianchi type-I universe with Barrow holographic dark energy principle to obtain cosmological model that describes the features of the observed universe with matter in the framework of Einstein gravity.

The holographic dark energy proposed by Barrow [31] has a complex structure that lead to a finite volume but with infinite (or finite) area, which is given by

$$\begin{aligned} S_{B} = \left( \frac{A}{A_{0}}\right) ^{1 + \frac{\varDelta }{2}} \end{aligned}$$
(1)

where A represents standard horizon area and \(A_{0}\) is the Planck area. The new form of the exponent \(\varDelta \) was introduced by Barrow, which lies in the range \(0 \le \varDelta \le 1\). For \(\varDelta = 0\), the expression reduces to the standard Bekenstein–Hawking entropy. It is interesting to look for a cosmological model with the above extended entropy relation which is the basis of holographic dark energy. The new functional form of the entropy improves the cosmological scenario compared to the standard scenarios of holographic dark energy [32,33,34,35]. The motivation of the paper is to investigate the evolution of an anisotropic universe with the Barrow Holographic dark energy [36] and to obtain an accelerated universe in the late epoch.

The paper is organized as follows: In Sect. 2 Bianchi type-I space-time and basic field equations in a four dimensional Einstein gravity are given. In Sect. 3 we discuss the isotropization of the Bianchi-I universe. The Barrow holographic dark energy and corresponding equations are discuss in Sect. 4. In Sect. 5, the evolution of dark energy density parameter and equation of state parameter are analyzed. Finally, in Sect. 6, we give brief discussions.

2 Einstein’s field equations

We consider anisotropic Bianchi I space-time metric given by

$$\begin{aligned} ds^2 = -dt^2+A^2(t)dx^2+B^2(t)dy^2+C^2(t)dz^2, \end{aligned}$$
(2)

where A, B and C are the directional scale factors, and are the functions of the cosmic time t. The Bianchi I space-time becomes isotropic if all the directional scale factor becomes same and we get usual FRW space-time. We assume that the cosmic matter is represented by the energy–momentum tensor as follows

$$\begin{aligned} T_{\mu \nu } = (\rho + p)u_{\mu }u_\nu +pg_{\mu \nu }, \end{aligned}$$
(3)

where \(\rho \) is the energy density of the cosmic matter, p is its pressure and \(u_\mu \) is the four velocity vector such that \(u_{\mu }u^{\mu } = 1.\)

The Einstein field equation is given by

$$\begin{aligned} R_{\mu \nu } - \frac{1}{2} Rg_{\mu \nu } = 8{\pi }GT_{\mu \nu }, \end{aligned}$$
(4)

where \(R_{\mu \nu }\), R and \(g_{\mu \nu }\) are the Ricci tensor, Ricci scalar and the metric tensor respectively with the Newton’s gravitational constant G. The non zero components of the field Eq. (4) for the metric (2) and the energy–momentum tensor (3), yield

$$\begin{aligned}&\frac{{\dot{A}}}{A}\frac{{\dot{B}}}{B} + \frac{{\dot{B}}}{B}\frac{{\dot{C}}}{C} + \frac{{\dot{A}}}{A}\frac{{\dot{C}}}{C} = 8{\pi }G\rho \end{aligned}$$
(5)
$$\begin{aligned}&\frac{{\ddot{B}}}{B} + \frac{{\ddot{C}}}{C} + \frac{{\dot{B}}}{B}\frac{{\dot{C}}}{C} = -8{\pi }Gp, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{{\ddot{A}}}{A} + \frac{{\ddot{C}}}{C} + \frac{{\dot{A}}}{A}\frac{{\dot{C}}}{C} = -8{\pi }Gp, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{{\ddot{A}}}{A} + \frac{{\ddot{B}}}{B} + \frac{{\dot{A}}}{A}\frac{{\dot{B}}}{B} = -8{\pi }Gp. \end{aligned}$$
(8)

The energy conservation equation \({T_{\mu }^{\nu }}_{;\nu } = 0,\) yields

$$\begin{aligned} {\dot{\rho }} + (\rho +p) \left( \frac{{\dot{A}}}{A} + \frac{{\dot{B}}}{B} + \frac{{\dot{C}}}{C} \right) = 0. \end{aligned}$$
(9)

We denote the average scale factor of the Bianchi-I universe by a(t) which is given by

$$\begin{aligned} a(t)=(ABC)^{\frac{1}{3}}. \end{aligned}$$
(10)

The Hubble parameters in different axial directions are \(H_{1} = \frac{{\dot{A}}}{A}\), \(H_{2} = \frac{{\dot{B}}}{B}\) and \(H_{3} = \frac{{\dot{C}}}{C}\), therefore, we define an average Hubble parameter H which is given by

$$\begin{aligned} H = \frac{{\dot{a}}}{a} = \frac{1}{3}\sum _{i = 1}^{3} H_{i}. \end{aligned}$$
(11)

In terms of the Hubble parameters in the axial directions the Eqs. (5)–(8) can be expressed as

$$\begin{aligned}&H_{1}H_{2} + H_{2}H_{3} + H_{3}H_{1} = 8\pi G\rho , \end{aligned}$$
(12)
$$\begin{aligned}&\dot{H_{2}} + \dot{H_{3}} + H_{2}^{2} + H_{3}^{2} + H_{2}H_{3} = - 8\pi G \,p, \end{aligned}$$
(13)
$$\begin{aligned}&\dot{H_{3}} + \dot{H_{1}} + H_{3}^{2} + H_{1}^{2} + H_{3}H_{1} = - 8\pi G \, p, \end{aligned}$$
(14)
$$\begin{aligned}&\dot{H_{1}} + \dot{H_{2}} + H_{1}^{2} + H_{2}^{2} + H_{1}H_{2} = - 8\pi G \, p, \end{aligned}$$
(15)

and the energy–momentum conservation Eq. (9) is given by

$$\begin{aligned} {\dot{\rho }} + 3H(\rho +p) = 0. \end{aligned}$$
(16)

Now the volume expansion (\(\varTheta \)), the average anisotropic expansion rate (A), shear (\(\sigma \)) and the deceleration parameter (q) are given by

$$\begin{aligned}&\varTheta = 3H, \end{aligned}$$
(17)
$$\begin{aligned}&A = \frac{1}{3}\sum _{i= 1}^{3}\left( \frac{\varDelta H_{i}}{H}\right) ^{2}, \end{aligned}$$
(18)
$$\begin{aligned}&\sigma ^{2} = \frac{1}{2}\sigma _{\mu \nu }\sigma ^{\mu \nu }, \end{aligned}$$
(19)
$$\begin{aligned}&q = - \frac{\ddot{a}}{aH^{2}} = - 1 - \frac{{\dot{H}}}{H^2}, \end{aligned}$$
(20)

where, \(\varDelta H_{i} = H_{i} - H\) and \(\sigma _{\mu \nu }\) is the sheer tensor.

For the Bianchi-I anisotropic metric given by Eq. (2) we express the shear tensor as

$$\begin{aligned} \sigma _{\mu \nu }\sigma ^{\mu \nu } = \sum _{i = 1}^{3}\left( H_{i} - H\right) ^{2} = H_{1}^{2} + H_{2}^{2} + H_{3}^{2} -3H^{2}. \end{aligned}$$
(21)

Using Eqs. (12), (19) and (21) we obtain the time-time component of the field equation as

$$\begin{aligned} 3M_{p}^{2}H^2 = \rho + M_{p}^{2}{\sigma }^2, \end{aligned}$$
(22)

where \(M_{p} = \frac{1}{\sqrt{8\pi {G}}}\) is the Plank mass.

Thereafter, using the Eqs. (12)–(15), (19) and (21), we obtain the following

$$\begin{aligned} 2\left( \dot{H_{1}} + \dot{H_{2}} + \dot{H_{3}}\right) + 9H^{2} + 3\sigma ^{2} = -24\pi G \,p. \end{aligned}$$
(23)

Now, differentiating Eq. (11) once with respect to t, it yields

$$\begin{aligned} \left( \frac{\ddot{a}}{a} - H^{2}\right) = \frac{1}{3}\left( \dot{H_{1}} + \dot{H_{2}} + \dot{H_{3}}\right) \end{aligned}$$
(24)

Eqs. (20), (23) and (24) leads to

$$\begin{aligned} M_{p}^{2}H^{2}(2q - 1) = p + M_{p}^{2}{\sigma }^2. \end{aligned}$$
(25)

To determine shear tensor we use Eqs. (13)–(15) and obtain

$$\begin{aligned} \frac{d (\dot{H_i}- \dot{H_j})}{H_i-H_j} = - \frac{dV}{V}, \end{aligned}$$

for \(i \ne j\) and \(i, j =1,\; 2, \;3 \) and \(V = a^{3} = ABC\). On integration we get the following

$$\begin{aligned} H_{i} - H_{j}= \frac{\sqrt{2}k_{j}}{V} \end{aligned}$$
(26)

where \(\sqrt{2}k_{1}\), \(\sqrt{2}k_{2}\) and \(\sqrt{2}k_{3}\) are the integration constant. The shear tensor is given by

$$\begin{aligned} \sigma _{\mu \nu }\sigma ^{\mu \nu }= & {} \sum _{i = 1}^{3}\left( H_{i} - H\right) ^{2} \nonumber \\= & {} \frac{1}{3}\left[ (H_{2} - H_{1})^{2} + (H_{3} - H_{2})^{2} \right. \nonumber \\&\quad \left. + (H_{1} - H_{3})^{2}\right] . \end{aligned}$$
(27)

Finally the sheer scalar (\(\sigma \)) can be expressed as

$$\begin{aligned} \sigma = \frac{k}{\sqrt{3}a^{3}}, \end{aligned}$$
(28)

where we denote \(k = \sqrt{k_{1}^{2} + k_{2}^{2} + k_{3}^{2}}\) in terms of the integration constant. It is important to mention here that although \(k^2= \sum _{i=1}^{3} \ne 0\) one gets \(\sum _{i=1}^{3}k_i=0\).

3 Isotropization of Bianchi-I universe

The present universe is isotropic and homogeneous which may have attained by an asymptotic situation emerged from an anisotropic universe, namely, Bianchi-I universe that formed at the phase transition of matter decoupling era. For this we define an isotropization criterion to distinguish anisotropic universe from an isotropic universe which however evolves in such a way that the effect of the anisotropic parameter is negligible at the present epoch \(z \rightarrow 0\). We study in this section the mean anisotropic parameter A and shear scalar \(\sigma \) in the anisotropic Bianchi-I universe as defined by the Eqs. (18) and (19) at the present epoch which are given by

$$\begin{aligned}&A = \frac{1}{3}\sum _{i =1}^{3}\left( \frac{\varDelta H_{i}}{H}\right) ^{2} \rightarrow 0 \end{aligned}$$
(29)
$$\begin{aligned}&\sigma ^{2} = \frac{1}{2}\sigma _{\mu \nu }\sigma ^{\mu \nu } = \frac{k^{2}}{3a^{6}} \rightarrow 0 \end{aligned}$$
(30)

for isotropization asymptotically. One obtains the above criterion if \(k \rightarrow 0\) 0r \(a \rightarrow \infty \) at late time.

Also, isotropization defined by the expansion factor of the Bianchi-I universe grows at the same rate at the late stage of evolution, when \(t \rightarrow t_{0}.\) The Bianchi-I universe becomes isotropic if the ratio of each of the directional scale factors A(t), B(t) and C(t) and the expansion factor a(t) follow

$$\begin{aligned} \frac{A}{a}, \frac{B}{a}, \frac{C}{a} \rightarrow constant \end{aligned}$$
(31)

when \(t \rightarrow \infty \).

The anisotropic Bianchi-I universe satisfying the above isotropization criterion becomes isotropic. In particular, its dynamics becomes FRW if the constant is unity.

4 Cosmological models with Barrow holographic dark energy

The standard holographic dark energy is given by the inequality \({\rho }_{DE}{L^4} {\le } S,\) where L is the horizon length, and imposing the inequalities \(S\propto {A}\propto {L^{2}}\). We consider here a modified form of density introduced by Barrow to define the entropy caused by quantum-gravitational effects, which yields

$$\begin{aligned} \rho _{DE } = CL^{\varDelta - 2}, \end{aligned}$$
(32)

with C is a parameter with dimension \([L]^{-2-\varDelta }.\) When \(\varDelta =0,\) the above expression provides the standard holographic dark energy \(\rho _{DE}=3M_{p}^{2}L^{-2}\) , where \(C=3M_{p}^{2}\) and setting c the velocity of light equal to unity. However in the case of the deformation effects introduced by \(\varDelta \) when non-zero, one gets the Barrow holographic dark energy which is distinguishable from the standard expression. The new formula for entropy introduced by Barrow may be important in understanding the evolution of the universe particularly, an anisotropic universe. This motivate us to take up Barrow’s formula in an anisotropic Bianchi-I universe for understanding the evolutionary behaviour. For a large horizon length L which occurs in the expression of holographic dark energy, although there are many possible choices, the most common in the literature is to use the future event horizon [11], which is given by

$$\begin{aligned} R_{h}\equiv {\int _{t}^{\infty }\frac{dt}{a}} = a\int _{a}^{\infty }\frac{da}{{a^2}H}. \end{aligned}$$
(33)

Substituting the expression for L in Eq. (32) with \(R_{h}\) we obtain the energy density due to the Barrow holographic dark energy,

$$\begin{aligned} \rho _{DE} = CR_{h}^{\varDelta -2}. \end{aligned}$$
(34)

We consider an anisotropic universe composed of matter describe by a linear EoS and a holographic dark energy. The total energy density \(\rho \) and pressure p are given by

$$\begin{aligned} \rho = \rho _{m} + \rho _{DE}, \end{aligned}$$

and

$$\begin{aligned} p = p_{m} + p_{DE}, \end{aligned}$$

where \(\rho _{m}\), \(p_{DE}\), \(p_{m}\) are the energy density, the pressure of the Barrow holographic dark energy and the pressure of matter respectively.

Now, the Eqs. (22) and (25) are expressed as

$$\begin{aligned}&3M_{p}^{2}H^2 = \rho _{m} + \rho _{DE} + M_{p}^{2}{\sigma }^2 \end{aligned}$$
(35)
$$\begin{aligned}&M_{p}^{2}H^{2}(2q - 1) = p_{m} + p_{DE} + M_{p}^{2}{\sigma }^2. \end{aligned}$$
(36)

We define the density parameters of matter (\(\varOmega _{m}\)), Barrow holographic dark energy (\(\varOmega _{DE}\)) and anisotropic energy (\(\varOmega _{\sigma }\)) as

$$\begin{aligned}&\varOmega _{m} = \frac{1}{3M_{p}^{2}H^{2}}\rho _{m}, \end{aligned}$$
(37)
$$\begin{aligned}&\varOmega _{DE} = \frac{1}{3M_{p}^{2}H^{2}}\rho _{DE}, \end{aligned}$$
(38)
$$\begin{aligned}&\varOmega _{\sigma } = \frac{\sigma ^{2}}{3H^{2}}. \end{aligned}$$
(39)

Using the above Eqs. (37)–(39) in Eq. (35) we get

$$\begin{aligned} \varOmega _{m} + \varOmega _{DE} + \varOmega _{\sigma } = 1. \end{aligned}$$
(40)

Using the density parameter \(\varOmega _{DE}\), we get from Eqs. (33) and (34),

$$\begin{aligned} \int _{x}^{\infty }\frac{dx}{aH} = \frac{1}{a}\left( \frac{C}{3M_{p}^{2}H^{2}\varOmega _{DE}}\right) ^{\frac{1}{2 - \varDelta }}, \end{aligned}$$
(41)

where \(x = \ln a\). Using the energy conservation equation of matter

$$\begin{aligned} {\dot{\rho }}_{m} + 3H(\rho _{m} + p_{m})=0, \end{aligned}$$

and integrating we get \(\rho _{m} = \frac{\rho _{m0}}{a^{3}},\) where \(\rho _{m0}\) the present matter energy density (setting the present size \(a_{0} = 1\)) as for matter \(p_m=0\). Substituting \(\rho _{m}\) into Eq. (37) we get

$$\begin{aligned} \varOmega _{m} = \frac{\varOmega _{m0}H_{0}^{2}}{a^{3}H^{2}}. \end{aligned}$$
(42)

Using Eqs. (39) and (42) with \(\sigma = \frac{k}{\sqrt{3}a^3}\) in the Eq. (40) we obtain

$$\begin{aligned} \frac{1}{aH} = 3\sqrt{\frac{a^{4}(1 - \varOmega _{DE})}{k^{2} + 9 \varOmega _{m0}H_{0}^{2}a^{3}}}. \end{aligned}$$
(43)

Now, making use of Eq. (43) in Eq. (41), we get the useful relation

$$\begin{aligned} \int _{x}^{\infty }3\sqrt{\frac{a^{4}(1 - \varOmega _{DE})}{k^{2} + 9\varOmega _{m0}H_{0}^{2}a^{3}}}dx = \frac{1}{a}\left( \frac{C}{3M_{p}^{2}H^{2}\varOmega _{DE}}\right) ^{\frac{1}{2 - \varDelta }}.\nonumber \\ \end{aligned}$$
(44)

Differentiating Eq. (44) once with respect to \(x = \ln a\), we get

$$\begin{aligned}&\frac{\varOmega _{DE}^{'}}{\varOmega {(1 - \varOmega _{DE})}} = 4 + \varDelta \nonumber \\&\ \ + \, \xi (1 - \varOmega _{DE})^{\frac{\varDelta }{2(\varDelta {-} 2)}}(\varOmega _{DE})^{\frac{1}{2 - \varDelta }}(k^2 {+} 9\varOmega _{m0}H_{0}^{2}e^{3x})e^{\frac{3\varDelta }{\varDelta - 2}x}\nonumber \\&\ \ - \, \frac{27\varOmega _{m0}H_{0}^{2}e^{3x}}{k^2 + 9\varOmega _{m0}H_{0}^{2}e^{3x}}, \end{aligned}$$
(45)

where \(\xi = (2 - \varDelta )3^{\frac{\varDelta }{\varDelta - 2}}\left( \frac{C}{3M_{p}^{2}}\right) ^{\frac{1}{\varDelta - 2}}\) is a dimensionless parameter and primes denote derivatives with respect to x. The above differential equation cannot be solved analytically. The numerical solutions determine the evolution of density parameter \(\varOmega _{DE}\) of Barrow holographic dark energy. Therefore, we obtain \(\varOmega _{m}\) and \(\varOmega _{\sigma }\) which are given in terms of dark energy density parameter as,

$$\begin{aligned}&\varOmega _{m} = (1 - \varOmega _{DE})\frac{9\varOmega _{m0}H_{0}^{2}a^{3}}{k^{2} + 9\varOmega _{m0}H_{0}^{2}a^{3}}, \end{aligned}$$
(46)
$$\begin{aligned}&\varOmega _{\sigma } = (1 - \varOmega _{DE})\frac{k^{2}}{k^{2} + 9\varOmega _{m0}H_{0}^{2}a^{3}}, \end{aligned}$$
(47)

where we set \(x = \ln a\). Using the above relations we can calculate the EoS parameter \(\omega _{DE} = \frac{p_{DE}}{\rho _{DE}}\) (we consider cosmic fluid obeying a linear EoS : \(p = \omega \rho \), \(\omega \) is the EoS parameter). Differentiation of Eq. (32) once gives \({\dot{\rho }}_{DE} = (\varDelta - 2)CR_{h}^{\varDelta - 3}{\dot{R}}_{h},\) with \({\dot{R}}_{h}\) calculated using Eq. (33) as \({\dot{R}}_{h} = HR_{h} - 1,\) and according to (32) \(R_{h}\) can be eliminated in terms of \(\rho _{DE}\) as \(R_{h} = (\rho _{DE}/C)^{\frac{1}{\varDelta - 2}}.\) Inserting this in the dark energy conservation equation given by

$$\begin{aligned} {\dot{\rho }}_{DE} + 3H\rho _{DE}(1 + \omega _{DE}) = 0, \end{aligned}$$

we get

$$\begin{aligned}&(\varDelta - 2)C\left( \frac{\rho _{DE}}{C}\right) ^{\frac{\varDelta - 3}{\varDelta - 2}}\left[ H\left( \frac{\rho _{DE}}{C}\right) ^{\frac{1}{\varDelta - 2}} - 1\right] \nonumber \\&\quad +3H\rho _{DE}(1 + \omega _{DE}) = 0. \end{aligned}$$
(48)

Inserting H from Eq. (43) and using (38) we finally obtain the EoS parameter of Barrow holographic dark energy as

$$\begin{aligned} \omega _{DE}= & {} -\frac{\varDelta + 1}{3} \nonumber \\&- \frac{\xi }{3}(\varOmega _{DE})^{\frac{1}{2 - \varDelta }}(1 - \varOmega _{DE})^{\frac{\varDelta }{2(\varDelta - 2)}}e^{\frac{3\varDelta }{\varDelta - 2}x} \nonumber \\&\qquad (k^{2} + 9\varOmega _{m0}H_{0}^{2}e^{3x})^{\frac{\varDelta }{2(2 - \varDelta )}}. \end{aligned}$$
(49)

Therefore, the evolution of \(\omega _{DE}\) in terms of \(x = \ln a\) can be determined as we find \(\varOmega _{DE}\) from the Eq. (45). For \(\varDelta = 0\) we obtain \(\omega _{DE}\vert _{\varDelta = 0} = -\frac{1}{3} - \frac{2}{3}\sqrt{\frac{3M^{2}_{p}\varOmega _{DE}}{C}},\) which reduces to the usual standard holographic dark energy. The present accelerating phase of the universe can be obtained in this case. But in the early epoch the universe was decelerating. Therefore, the transition from deceleration to present acceleration can be analyzed here plotting the variation of the deceleration parameter with redshift z. From Eq. (36), we get

$$\begin{aligned} q = \frac{1}{2} + \frac{3}{2}\omega _{DE} \varOmega _{DE} + \frac{3}{2}\frac{k^{2}(1 - \varOmega _{DE})}{k^{2} + 9\varOmega _{m0}H_{0}^{2}e^{3x}}, \end{aligned}$$
(50)

for dust (\(p_{m} = 0\)) dominated universe. In this model, we find the transition of the universe from deceleration to acceleration for different redshift parameter.

5 Evolution of \(\varOmega _{DE}\), \(\varOmega _{m}\), \(\omega _{DE}\) and q

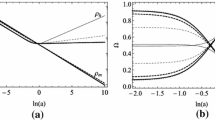
In this section we investigate the evolutionary behaviour of density parameter and EoS parameter in the framework of the Barrow holographic dark energy (HDE) in an anisotropic universe. For different values of \(\varDelta \) and k we plot the evolution of the density parameters and other cosmological parameters. The evolution of the dark energy density parameter \(\varOmega _{DE}\) is obtained from Eq. (45) by numerical integration making use of the initial conditions \(\varOmega _m \,(x = - ln \,(1+z) = 0) = \varOmega _{m0}\approx {0.3}\) and \(\varOmega _{DE} (x = - ln(1+z)=0) = \varOmega _{DE0}\approx {0.7}\) in agreement with observation. We now plot the different parameters with respect to redshift parameter z for \(k = 0.001, 0.01, 0.05\) and 0.1 for a given \(\varDelta = 0.2.\) In Figs. 1, 2, 3 and 4, we plot the evolution of the parameters \(\varOmega _{DE}\), \(\varOmega _{m}\), \(\omega _{DE}\) and q(z) with redshift (z) for \(\varDelta = 0.2\) and \(k = 0.001, 0.01, 0.05\) and 0.1. The plot in Fig. 1 shows that in an anisotropic universe the density parameter of DE, \(\varOmega _{DE}\) attains the present value \(\varOmega _{DE}=0.69\) independent of the anisotropy. It is evident that in a large anisotropic universe, the DE density was small in the early universe and a universe with small anisotropy the DE energy at an epoch was higher than that in a universe with large anisotropy for a given \(\varDelta \). The plot in Fig. 2 shows that the dark matter density with the usual matter decreases to 0.31 rapidly for a universe with lower anisotropic universe in the early era. However, a universe with large anisotropy the matter contribution increases as the universe evolves but in that case we do not find a universe with the observed predictions. In this case there exists a critical anisotropy below which it permits the observed universe otherwise the cosmological model fails to accommodate the present universe. This is a new result in an anisotropic universe when probed with the Barrow HDE. In Fig. 3 the evolution of DE EoS parameter is plotted, it is evident that the matter in the universe crosses phantom for lower anisotropy than a universe with higher anisotropy at the present epoch. In Fig. 4, the evolution of the deceleration parameter is plotted, it shows that for a fixed \(\varDelta \), an anisotropic decelerating universe in the past with small anisotropic parameter (say, \(k=0.001\)) transits to an accelerating universe before a universe with large initial anisotropy (say, \(k=0.1\)). The evolution of the density parameters drawn in Fig. 5 shows that \(\varOmega _{DE}\) increases and \(\varOmega _m\) decreases, it signals the existence of interaction in the early universe. It is also evident that for a given anisotropy as \(\varDelta \) is increased in the early universe the density parameter was small compared to lower \(\varDelta \) but the present value of \(\varOmega _{DE}\) is independent of the cosmological model parameters. It is also noted that the at the present epoch \(\varOmega _{\sigma } \rightarrow 0\), a homogeneous universe results.

Fig. 1
figure 1

Evolution of Barrow holographic dark energy density parameter, as a function of redshift z,  for \(\varDelta = 0.2\) and \(C = 3,\) in unit of \(M_{p}^{2} = 1\). The line corresponds: red: \(k = 0.001;\) blue: \(k = 0.01;\) green: \(k = 0.05;\) magenta: \(k = 0.1\)

Full size image
Fig. 2
figure 2

Evolution of matter density parameter, as a function of redshift z,  for \(\varDelta = 0.2\) and \(C = 3,\) in unit of \(M_{p}^{2} = 1.\) The line corresponds: red: \(k = 0.001;\) blue: \(k = 0.01;\) green: \(k = 0.05;\) magenta: \(k = 0.1\)

Full size image
Fig. 3
figure 3

Evolution DE EoS parameter, as a function of redshift z,  for \(\varDelta = 0.2\) and \(C = 3,\) in unit of \(M_{p}^{2} = 1\). The line corresponds: red: \(k = 0.001;\) blue: \(k = 0.01;\) green: \(k = 0.05;\) magenta: \(k = 0.1\)

Full size image
Fig. 4
figure 4

Evolution deacceleration parameter, as a function of redshift z,  for \(\varDelta = 0.2\) and \(C = 3,\) in unit of \(M_{p}^{2} = 1.\) The line corresponds: red: \(k = 0.001;\) blue: \(k = 0.01;\) green: \(k = 0.05;\) magenta: \(k = 0.1\)

Full size image

For others values of \(\varDelta \) and k, we also investigate the evolution of parameters to agree with the observation. Now we take (\(\varDelta \), k) \(=(0.3,0.01), (0.4,0.01), (0.4,0.05), (0.8,0.05)\). The results are shown in Figs. 5 and 6.

Fig. 5
figure 5

Evolution of density parameter of matter and Barrow holographic dark energy, as a function of redshift z,  for \(C = 3,\) in unit of \(M_{p}^{2} = 1\). The lines corresponds: red: \(\varDelta = 0.3\) and \(k = 0.01;\) blue: \(\varDelta = 0.4\) and \(k = 0.01;\) green: \(\varDelta = 0.4\) and \(k = 0.03;\) magenta: \(\varDelta = 0.5\) and \(k = 0.03\)

Full size image
Fig. 6
figure 6

Evolution of DE EoS parameter, as a function of redshift z,  for \(C = 3,\) in unit of \(M_{p}^{2} = 1\). The lines corresponds: red: \(\varDelta = 0.3\) and \(k = 0.01;\) blue: \(\varDelta = 0.4\) and \(k = 0.01;\) green: \(\varDelta = 0.4\) and \(k = 0.03;\) magenta: \(\varDelta = 0.5\) and \(k = 0.03\)

Full size image
Fig. 7
figure 7

Evolution of density parameter of matter and Barrow holographic dark energy, as a function of redshift z,  for \(C = 3,\) in unit of \(M_{p}^{2} = 1\). The lines corresponds: red: \(\varDelta = 0\) and \(k = 0.01;\) blue: \(\varDelta = 0.2\) and \(k = 0.01\)

Full size image
Fig. 8
figure 8

Evolution of DE EoS parameter, as a function of redshift z,  for \(C = 3,\) in unit of \(M_{p}^{2} = 1\). The lines corresponds: red: \(\varDelta = 0\) and \(k = 0.01;\) blue: \(\varDelta = 0.2\) and \(k = 0.01\)

Full size image

6 Discussion

In this paper, we present cosmological scenario in Bianchi type-I universe filled with Barrow holographic dark energy (HDE) and matter in the framework of Einstein’s general theory of relativity. We derive the field equations for the Bianchi-I universe and then construct Barrow HDE by applying the usual holographic principle at a cosmological framework, making use of the proposed Barrow entropy relation. We estimate different values of Barrow exponent \(\varDelta \) and anisotropy (k) which permits a realistic cosmology.

In Fig. 1, it is evident that in an anisotropic universe the evolution of density parameter (\(\varOmega _{DE}\)) is dependent on the anisotropy determined by k for a given Barrow’s exponent factor. Using the predictions of observational cosmology we set the boundary conditions and integrated the differential equation numerically setting \(\varDelta = 0.2\) with different values of k (0.1, 0.05, 0.01, 0.001). The dark energy which was lower in the early era is dominant and at the present epoch it attains \(\varOmega _{DE}=0.7\) which follows from PLANCK 2018 result [37]. It is evident that universe with a high anisotropy or low anisotropy which are prominently differentiated in the early era are insignificant at the present epoch. In Fig. 2 the evolution of the density parameter show that the matter density decreases and it gives the observed value which are same for \(k=0.01\) and \(k=0.001\) at the present epoch. But for higher k the present matter density are different. Thus our universe may not be highly anisotropic in the early universe. The evolution of the DE EoS parameter drawn in Fig. 3 shows that the universe always lies in the quintessence regime.

It is found from Fig. 4 that for a given Barrow’s exponent \(\varDelta =0.2\), the universe transits from decelerated phase to an accelerated phase at the red shift values \(z = 0.95\), \(z = 0.82\), \(z = 0.32\) and \(z = 0.14\) when \(k = 0.001, 0.01, 0.05, 0.1\) respectively. Thus we conclude that an anisotropic universe with lower anisotropy (determined by k) transits early from decelerating phase to an accelerating phase compared to that with higher anisotropy. It is evident from Fig. 5 that the cosmological parameters satisfy the present observed values although they are significantly different in the early universe for given values of k and \(\varDelta \). Thus Barrow’s exponent for \(0\le \varDelta \le 1\) leads to new cosmological scenario which is interesting. In Fig. 6, the evolution of the DE EoS parameter is plotted for a set of values of the following pairs (\(\varDelta \), k) to study the effect of the Barrow HDE in an anisotropic universe. It is found that DE EoS parameter \(\omega _{DE}\) is high for large anisotropic universe with the same \(\varDelta =0.4\). For a given anisotropic universe, \(\omega _{DE}\) is found lower as \(\varDelta \) is higher. We note that \(\omega _{DE}\) decreases then attains a minimum thereafter increases but does not cross the phantom limiting value at the present epoch. It is also evident from Fig. 7 that a universe with Barrow HDE the dark energy \(\omega _{DE}\) crosses the quintessence limit but it does not cross for \(\varDelta =0\) in an anisotropic universe with (\(k=0.01\)). The plot in Fig. 8 shows that in the case of an anisotropic universe the \(\omega _m\) is lower in the early universe and \(\omega _{DE}\) was higher which follows from the entropy proposed by Barrow compared to a universe described by Bekenstein and Hawking entropy though at the present epoch their values are same as predicted from observations. In an anisotropic universe the new exponent \(\varDelta \) changes with anisotropy where \(\omega _{DE0}\) lies in the phantom region but in an isotropic universe \(\omega _{DE0}\) lies in the quintessence region, the result obtained here is important to differentiate an isotropic universe from anisotropic universe. Thus \(\varDelta \) is playing an important role to identify the universe. It is necessary and interesting to study the effect of interaction among the fluids in anisotropic universes with Barrow HDE confronting the scenario with observational data in order to constrain the new exponent \(\varDelta \) which is beyond the scope of present work and left for future investigation.