1 Introduction

The mathematical description of a significant number of scientific and technological problems leads to nonlinear differential equations and most of them cannot be solved analytically using traditional methods. Therefore, these problems are often handled by the most common methods such as Adomian decomposition method, homotopy decomposition method, Taylor collocation method, differential transform method, homotopy perturbation method, variational iteration method (Adomian 1988; Atangana and Abdon 2012; Atangana et al. 2013; Bildik et al. 2006; Bulut et al. 2003; He 1999, 2005; Bayram et al. 2012; Bildik and Konuralp 2006; Bildik and Deniz 2015a, b; Öziş and Ağırseven 2008). These methods can deal with nonlinear problems, but they have also problems about the convergence region of their series solution. These regions are generally small according to the desired solution. In order to cope with this task, researchers have recently proposed some new methods.

In the presented study, we apply the perturbation-iteration method (PIM) and optimal homotopy asymptotic method (OHAM) to obtain an approximate solution of random nonlinear differential equations. Each method has its own characteristic and significance that shall be examined. PIM is constructed recently by Pakdemirli et al. They have modified well-known perturbation method to construct perturbation-iteration method. It has been efficiently applied to some strongly nonlinear systems and yields very approximate results (Aksoy and Pakdemirli 2010; Şenol and Mehmet 2013; Aksoy et al. 2012; Dolapçı et al. 2013). On the other hand, Vasile Marinca et al. have developed optimal homotopy asymptotic method for solving many different types of differential equations (Marinca and Herişanu 2008; Marinca et al. 2008, 2009). This method is straight forward and reliable for the approximate solution of many nonlinear problems (Gupta and Ray 2014a, b, 2015a; b; Iqbal et al. 2010; Ali et al. 2010). OHAM also provides us with a convenient way to control the convergence of approximation series and adjust convergence regions. Our purpose is to solve some nonlinear problems and test their convergence for these illustrations. Our results also prove one more time that both of these methods are very effective and powerful to solve nonlinear problems.

2 Perturbation-Iteration Method

In this section, we give some information about perturbation-iteration algorithms. They are classified with respect to the number of terms in the perturbation expansion (n) and with respect to the degrees of derivatives in the Taylor expansions (m). Briefly, this process has been represented as PIA (n, m) (Marinca and Herişanu 2008; Marinca et al. 2008, 2009).

2.1 PIA(1,1)

In order to illustrate the algorithm, consider a second-order differential equation in closed form:

$$F(y^{\prime\prime},y^{\prime},y,\varepsilon ) = 0 ,$$
(1)

where y = y(x) and ɛ is the perturbation parameter. For PIA(1,1), we take one correction term from the perturbation expansion:

$$y_{n + 1} = y_{n} + \varepsilon \left( {y_{c} } \right)_{n} .$$
(2)

Substituting (2) into (1) then expanding in a Taylor series gives

$$F(y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0) + F_{y} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c} )_{n} \varepsilon + F_{{y^{\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime } )_{n} \varepsilon + F_{{y^{\prime\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime \prime } )_{n} \varepsilon + F_{\varepsilon } \varepsilon = 0 .$$
(3)

Rearranging Eq. (3) yields a linear second-order differential equation as:

$$\left( {y_{c}^{\prime \prime } } \right)_{n} + \frac{{F_{{y^{\prime}}} }}{{F_{{y^{\prime\prime}}} }}\left( {y_{c}^{\prime } } \right)_{n} + \frac{{F_{y} }}{{F_{{y^{\prime\prime}}} }}\left( {y_{c} } \right)_{n} = - \frac{{\frac{F}{\varepsilon } + F_{\varepsilon } }}{{F_{{y^{\prime\prime}}} }} .$$
(4)

Note that all derivatives are computed at ɛ = 0. We can easily obtain (y c )0 from Eq. (4) by using an initial guess y 0. Then y 1 is determined by using this information. One can obtain satisfactory results for the considered equation by constructing an iterative scheme with the help of (2) and (4).

2.2 PIA(1,2)

As distinct from PIA(1,1), we need to take n = 1, m = 2 to obtain PIA(1,2). That is, we need to take also second-order derivatives:

$$\begin{aligned} F(y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0) + F_{y} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c} )_{n} \varepsilon + F_{{y^{\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime } )_{n} \varepsilon + F_{{y^{\prime\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime \prime } )_{n} \varepsilon + \hfill \\ F_{\varepsilon } \varepsilon + \frac{1}{2}\varepsilon^{2} F_{{y^{\prime\prime}y^{\prime\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime \prime } )_{n}^{2} + \frac{1}{2}\varepsilon^{2} F_{{y^{\prime}y^{\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime } )_{n}^{2} + \frac{1}{2}\varepsilon^{2} F_{yy} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c} )_{n}^{2} + \hfill \\ \varepsilon^{2} F_{{y^{\prime\prime}y^{\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)(y_{c}^{\prime \prime } )_{n} (y_{c}^{\prime } )_{n} + \varepsilon^{2} F_{{y^{\prime}y}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)(y_{c}^{\prime } )_{n} (y_{c} )_{n} + \varepsilon^{2} F_{{y^{\prime\prime}y}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime \prime } )_{n} (y_{c} )_{n} \hfill \\ + F_{{\varepsilon y^{\prime\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime \prime } )_{n} \varepsilon^{2} + F_{{\varepsilon y^{\prime}}} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c}^{\prime } )_{n} \varepsilon^{2} + F_{\varepsilon y} (y_{n}^{\prime \prime } ,y_{n}^{\prime } ,y_{n} ,0)\;(y_{c} )_{n} \varepsilon^{2} + \frac{1}{2}\varepsilon^{2} F_{\varepsilon \varepsilon } = 0 \hfill \\ \end{aligned}$$
(5)

or by rearranging

$$\begin{aligned} (y_{c}^{\prime \prime } )_{n} \left( {\varepsilon F_{{y^{\prime\prime}}} + \varepsilon^{2} F_{{\varepsilon y^{\prime\prime}}} } \right) + (y_{c}^{\prime } )_{n} \left( {\varepsilon F_{{y^{\prime}}} + \varepsilon^{2} F_{{\varepsilon y^{\prime}}} } \right) + (y_{c} )_{n} \left( {\varepsilon F_{y} + \varepsilon^{2} F_{\varepsilon y} } \right) + (y_{c}^{\prime \prime } )_{n}^{2} \left( {\frac{{\varepsilon^{2} }}{2}F_{{y^{\prime\prime}y^{\prime\prime}}} } \right) \hfill \\ + (y_{c}^{\prime } )_{n}^{2} \left( {\frac{{\varepsilon^{2} }}{2}F_{{y^{\prime}y^{\prime}}} } \right) + (y_{c} )_{n}^{2} \left( {\frac{{\varepsilon^{2} }}{2}F_{yy} } \right) + (y_{c} )_{n} (y_{c}^{\prime } )_{n} \left( {\varepsilon^{2} F_{{y^{\prime}y}} } \right) + (y_{c}^{\prime \prime } )_{n} (y_{c}^{\prime } )_{n} \left( {\varepsilon^{2} F_{{y^{\prime}y^{\prime\prime}}} } \right) + \hfill \\ (y_{c}^{\prime \prime } )_{n} (y_{c} )_{n} \left( {\varepsilon^{2} F_{{yy^{\prime\prime}}} } \right) = - F - F_{\varepsilon } \varepsilon - \frac{{\varepsilon^{2} F_{\varepsilon \varepsilon } }}{2} \hfill \\ \end{aligned}$$
(6)

Note again that all derivatives are calculated at ɛ = 0. By means of (2) and (6), iterative scheme is developed for the particular equation considered.

3 Optimal Homotopy Asymptotic Method

In order to review the basic principles of OHAM, let us consider the nonlinear differential equation:

$$F = L\left( {y(x)} \right) + g(x) + N\left( {y(x)} \right) = 0, \, B\left( {y,\frac{dy}{dx}} \right) = 0 ,$$
(7)

where g(x) is a source function, L, N and B are linear, nonlinear and boundary operators, respectively. First, we construct a homotopy h(ϕ i (x, p), p) which satisfies

$$\begin{aligned} (1 - p)\left[ {L\left( {\phi (x,p)} \right) + g(x)} \right] = H(p)\left[ {L\left( {\phi (x,p)} \right) + g(x) + N\left( {\phi (x,p)} \right)} \right], \, \hfill \\ B\left( {\phi (x,p),\frac{\partial \phi (x,p)}{\partial x}} \right) = 0, \, p \in [0,1], \, H(0) = 0, \hfill \\ \end{aligned}$$
(8)

where ϕ(x, p) is an unknown function, p is an embedding parameter, H(p) is a nonzero auxiliary function for p ≠ 0. Clearly, at p = 0 and p = 1, we have ϕ(x, 0) = y 0(x) and ϕ(x, 1) = y(x). So, as the embedding parameter p increases from 0 to 1, the solution ϕ(x, p) deforms from the initial guess y 0(x) to the exact solution y(x) of the original nonlinear differential equation. y 0(x) can be computed from (8) for p = 0:

$$L\left( {y_{0} (x)} \right) + g(x) = 0, \, B\left( {y_{0} ,\frac{{dy_{0} }}{dx}} \right) = 0 .$$
(9)

For this study, we choose the auxiliary function H(p) in the form:

$$H(p) = pC_{1} + p^{2} C_{2} + p^{3} C_{3} + \cdots$$
(10)

for the sake of simplicity. Here C 1, C 2,… are constants which are to be determined later. Most recently, Herişanu et al. have proposed a generalized auxiliary function:

$$H(t;p,C_{i} ) = pH_{1} (t,C_{i} ) + p^{2} H(t,C_{i} ) + \ldots ,$$

where H i (t, C i ), i = 1, 2,… are auxiliary functions. Some examples of such generalized auxiliary functions are presented in the papers (Herişanu et al. 2012, 2015). Let us consider the Taylor expansion of the solution of Eq. (8) about p:

$$\phi (x,p,C_{i} ) = y_{0} (x) + \sum\limits_{k = 1}^{\infty } {y_{k} (x,C_{i} )} p^{k} , \, i = 1,2, \ldots$$
(11)

Substituting (11) and (10) into (8) and equating the coefficients of the like powers of p equal to zero, we obtain the linear equations:

$$L\left( {y_{1} (x)} \right) = C_{1} N_{0} \left( {y_{0} (x)} \right), \, B\left( {y_{1} ,\frac{{dy_{1} }}{dx}} \right) = 0$$
(12)

and in general form

$$\begin{aligned} L\left( {y_{k} - y_{k - 1} } \right) = C_{k} N_{0} \left( {y_{0} } \right) + \sum\limits_{i = 1}^{k - 1} {C_{i} \left[ {L\left( {y_{k - i} } \right) + N_{k - i} \left( {y_{0} ,y_{1} , \ldots ,y_{k - 1} } \right)} \right]} \hfill \\ k = 2,3, \ldots , \, B\left( {y_{k} ,\frac{{dy_{k} }}{dx}} \right) = 0 \hfill \\ \end{aligned} ,$$
(13)

where N m (y 0, y 1, …, y m ) is the coefficient of p m in the expansion of about the embedding parameter p:

$$N\left( {\phi (x,p,C_{i} )} \right) = N_{0} \left( {y_{0} } \right) + \sum\limits_{m = 1}^{\infty } {N_{m} \left( {y_{0} ,y_{1} , \ldots ,y_{m} } \right)} p^{m} , \, i = 1,2, \ldots$$
(14)

Previous researches have showed that the convergence of the series (11) depends upon the constants C 1, C 2,…. If the series (11) is convergent at p = 1, one has

$$y(x,C_{i} ) = y_{0} (x) + \sum\limits_{k = 1}^{\infty } {y_{k} (x,C_{i} )} .$$
(15)

Generally speaking, the solution of Eq. (7) can be determined approximately in the form:

$$y^{(m)} (x,C_{i} ) = y_{0} (x) + \sum\limits_{k = 1}^{m} {y_{k} (x,C_{i} )} .$$
(16)

Substituting (16) into (8), the general problem results in the following residual:

$$R(x,C_{i} ) = L\left( {y^{(m)} (x,C_{i} )} \right) + g(x) + N\left( {y^{(m)} (x,C_{i} )} \right) .$$
(17)

Obviously, when R(x, C i ) = 0 then the approximation y (m)(x, C i ) will be the exact solution. For determining C 1, C 2,…, a and b are chosen such that the optimum values for C 1, C 2, … are obtained using the method of least squares:

$$J(C_{i} ) = \int\limits_{a}^{b} {R^{2} } (x,C_{i} )dx ,$$
(18)

where R = L(y (m)) + g(x) + N(y (m)) is the residual and

$$\frac{\partial J}{{\partial C_{1} }} = \frac{\partial J}{{\partial C_{2} }} = \cdots = \frac{\partial J}{{\partial C_{m} }} .$$
(19)

After finding constants, one can get the approximate solution of order m. The constants C 1, C 2, … can also be defined from

$$R(k_{1} ,C_{i} ) = R(k_{2} ,C_{i} ) = \cdots = R(k_{m} ,C_{i} ) = 0, \, i = 1,2, \ldots ,m ,$$
(20)

where k i  ∊ (a, b).

4 Numerical Examples

In this section, we will examine a few examples with a known analytic and numerical solution in order to compare the convergence of these two new methods. We wish to emphasize that the purpose of the comparisons is not definitive, but only to give the reader insight into the relative efficiencies of the two methods.

Example 1 Consider the following nonlinear differential equation (Fu 1989):

$$y^{\prime} = x^{2} + y^{2} , \, y(0) = 1$$
(21)

which has no exact solution.

4.1 PIA(1,1)

For the equation considered, an artificial perturbation parameter is inserted as follows:

$$F(y^{\prime},y,\varepsilon ) = y^{\prime} - x^{2} - \varepsilon y^{2} .$$
(22)

Performing the required calculations

$$F = y_{n}^{\prime } - x^{2} , \, F_{y} = 0,F_{{y^{\prime}}} = 1, \, F_{\varepsilon } = - (y_{n} )^{2}$$
(23)

for the formula (3) and setting ɛ = 1 yields

$$\left( {y_{c}^{\prime } } \right)_{n} = y_{n}^{2} - y_{n}^{\prime } + x^{2} .$$
(24)

We start the iteration by taking a trivial solution which satisfies the given initial conditions:

$$y_{0} = 1.$$
(25)

Substituting (25) into the iteration formula (24), we have

$$\left( {y_{c} } \right)_{0}\,= x + \frac{{x^{3} }}{3} + c_{1} .$$
(26)

Inserting Eq. (26) into Eq. (2) and applying the initial conditions we get

$$y_{1} = y_{0} + \varepsilon \left( {y_{c} } \right)_{0}\,= 1 + x + \frac{{x^{3} }}{3}.$$
(27)

We remind that y 1 does not represent the first correction term; rather it is the approximate solution after the first iteration. Following the same procedure, we obtain new and more approximate results:

$$y_{2} = 1 + x + x^{2} + \frac{{2x^{3} }}{3} + \frac{{x^{4} }}{6} + \frac{{2x^{5} }}{15} + \frac{{x^{7} }}{63}$$
(28)
$$\begin{aligned} y_{3} = 1 + x + x^{2} + \frac{{4x^{3} }}{3} + x^{4} + \frac{{2x^{5} }}{3} + \frac{{x^{7} }}{21} + \frac{{x^{8} }}{105} + \frac{{299x^{9} }}{11340} + \cdots \hfill \\ \, \vdots \hfill \\ \end{aligned}$$
(29)

4.2 PIA(1,2) Solution

As in the previous case, we construct a perturbation–iteration algorithm by taking one correction term in the perturbation expansion and two derivatives in the Taylor series. Then the algorithm takes the simplified form:

$$\left( {y_{c} '} \right)_{n} - 2\left( {y_{c} } \right)_{n} \left( {y_{n} } \right) = x^{ 2} + y_{n}^{ 2} - y_{n} ' .$$
(30)

Using the trivial solution y 0 = 1, we have

$$(y_{c}^{\prime } )_{0} - 2(y_{c} )_{0} = x^{2} + 1 .$$
(31)

Substituting the solution of (31) into (2) and applying the initial conditions yields

$$y_{1} = \frac{1}{4}(3e^{2x} - 2x^{2} - 2x + 1) .$$
(32)

Following the same procedure using (32), the second iteration is obtained as

$$y_{2} = \frac{1}{32}\left( { - 8x^{3} (e^{2x} + 2) - 4x^{2} (3e^{2x} + 14) + 50e^{2x} + 9e^{4x} - 4x(9e^{2x} + 17) - 4x^{4} - 27} \right) .$$
(33)

We do not give higher iterations here for brevity. One can easily realize that, we have functional expansion for PIA(1,2) instead of a polynomial expansion as obtained in PIA(1, 1).

4.3 OHAM Solution

We have

$$L\left( {y\left( x \right)} \right) = y', g\left( x \right) = - x^{ 2} , N\left( {y\left( x \right)} \right) = - y^{ 2} , y\left( 0 \right) = 1.$$
(34)

Problem of zero order is written as:

$$y_{0}^{\prime } (x) = x^{2} ,y_{0} (0) = 1,$$
(35)

from which we obtain

$$y_{0} = \frac{{x^{3} }}{3} + 1.$$
(36)

Substituting Eq. (36) into (12), we get first-order problem:

$$y_{1}^{\prime } (x) =C_{1} N_{0} = - C_{1} \left( {\frac{{x^{3} }}{3} + 1} \right)^{2} ,y_{1} (0) = 0$$
(37)

and its solution is

$$y_{1} = - C_{1} \left( {\frac{{x^{7} }}{63} + \frac{{x^{4} }}{6} + x} \right).$$
(38)

The problem of second order

$$y_{2}^{\prime } (x) = C_{1}^{2} \left( {\frac{{2x^{10} }}{189} + \frac{{x^{7} }}{7} - \frac{{x^{6} }}{9} + x^{4} - \frac{{2x^{3} }}{3} + 2x - 1} \right) - \frac{1}{9}(x^{3} + 3)^{2} (C_{1} + C_{2} ), \, y_{2} (0) = 0$$
(39)

with the solution

$$y_{2} (x) = \frac{{2C_{1}^{2} x^{11} }}{2079} + \frac{{C_{1}^{2} x^{8} }}{56} - \frac{{C_{1}^{2} x^{7} }}{63} + \frac{{C_{1}^{2} x^{5} }}{5} - \frac{{C_{1}^{2} x^{4} }}{6} + C_{1}^{2} x^{2} - C_{1}^{2} x - \frac{{C_{1} x^{7} }}{63} - \frac{{C_{1} x^{4} }}{6} - C_{1} x - \frac{{C_{2} x^{7} }}{63} - \frac{{C_{2} x^{4} }}{6} - C_{2} x$$
(40)

We can obtain the approximate solution of second order from Eqs. (36), (38), (40) and (16) for m = 2:

$$y^{(2)} (x,C_{1} ,C_{2} ) = y_{0} (x) + y_{1} (x,C_{1} ) + y_{2} (x,C_{1} ,C_{2} ) .$$
(41)

As we have mentioned in the previous section, one can find constants C 1 and C 2 by using Eq. (20) and

$$R(x,C_{i} ) = L\left( {y^{(2)} (x,C_{i} )} \right) + g(x) + N\left( {y^{(2)} (x,C_{i} )} \right)$$
(42)

Substituting \(x = \frac{1}{2},\frac{3}{4}\) into Eq. (42):

$$R(\frac{1}{2},C_{i} ) = R(\frac{3}{4},C_{i} ) = 0$$
(43)

and solving (43) we obtain

$$C_{1} = - 1.6494651884913274, \, C_{2} = 1.9241003665957586$$
(44)

and correspondingly the approximate solution of the second order takes the following form:

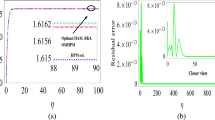
$$\begin{aligned} y^{(2)} (x) = 0.002617350x^{11} + 0.04858456x^{8} - 0.047545564x^{7} + 0.54414708x^{5} - 0.499228431x^{4} \hfill \\ \quad \quad \quad \quad + \frac{{x^{3} }}{3} + 2.72073540x^{2} + 1.64946518(\frac{{x^{7} }}{63} + \frac{{x^{4} }}{6} + x) - 2.9953705x + 1 \hfill \\ \end{aligned}$$
(45)

One can also compute more approximate results by following the same procedure with a computer program. We do not give higher iterations due to huge amount of calculations. Table 1 and Fig. 1 show the values of the PIM solutions, OHAM solution and solution by Runge–Kutta. It is clear that PIA(1,2) gives better results than OHAM even for m = 2. Table 2 demonstrates the absolute errors for different m.

Table 1 Comparison of numerical results with the Mathematica solution for different values of m
Full size table
Fig. 1
figure 1

Comparison of the solutions for Example 1

Full size image

Example 2 Consider the following nonlinear differential equation:

$$y^{\prime\prime} + (y^{\prime})^{2} + e^{y} = \cos x - 1, \, y(0) = y^{\prime}(0) = 0$$
(46)

with the exact solution \(y\left( x \right) = { \ln } \left( {{ \cos } x} \right)\).

4.4 PIA(1,1)

For the equation considered, an artificial perturbation parameter is inserted as follows:

$$F(y^{\prime\prime},y^{\prime},y,\varepsilon ) = y^{\prime\prime} + \varepsilon (y^{\prime})^{2} + e^{\varepsilon y} - \cos x + 1 .$$
(47)

Performing the required calculations for the formula (3) yields

$$F = y_{n}^{\prime \prime } - \cos x + 2, \, F_{y} = F_{{y^{\prime}}} = 0,F_{{y^{\prime\prime}}} = 1, \, F_{\varepsilon } = (y_{n}^{\prime } )^{2} + y_{n}$$
(48)

and setting ɛ = 1

$$\left( {y_{c}^{\prime \prime } } \right)_{n} = \cos x - \left( {y_{n}^{\prime \prime } + (y_{n}^{\prime } )^{2} + y_{n} + 2} \right).$$
(49)

We start the iteration by taking a trivial solution which satisfies the given initial conditions:

$$y_{0} = 0.$$
(50)

Substituting (50) into the iteration formula (49), we have

$$\left( {y_{c} } \right)_{0} = c_{1} + c_{2} x - \cos x - x^{2} .$$
(51)

Inserting Eq. (51) into Eq. (2) and applying the initial conditions we get

$$y_{1} = y_{0} + \varepsilon \left( {y_{c} } \right)_{0} = 1 - x^{2} - \cos x.$$
(52)

We remind that y 1 does not represent the first correction term; rather it is the approximate solution after the first iteration. Following the same procedure, we obtain new and more approximate result:

$$\begin{aligned} y_{2} = 1 - x^{2} - \cos x + \frac{1}{8}\left( { - 2x^{4} - 6x^{2} - 32x\sin (x) - 72\cos (x) - \cos (2x) + 73} \right) \hfill \\ \, \hfill \\ \end{aligned} .$$
(53)

4.5 PIA(1,2)

As in the previous case, we construct a perturbation–iteration algorithm by taking one correction term in the perturbation expansion and two derivatives in the Taylor series. Then Eq. (6) takes the simplified form:

$$(y_{c}^{\prime \prime } )_{n} + 2(y_{c}^{\prime } )_{n} (y_{n}^{\prime } ) + (y_{c} )_{n} = - y_{n}^{\prime \prime } - (y_{n}^{\prime } )^{2} - y_{n} - \frac{{y_{n}^{2} }}{2} + \cos x - 2 .$$
(54)

Using the trivial solution y 0 = 0 and Eq. (2) we get

$$y_{1} = - 2 + 2{\text{c}}osx + \frac{x\sin x}{2} .$$
(55)

Following the same procedure with Mathematica, we get

$$\begin{aligned} y_{2} = \frac{1}{432}\left( { - 3(27x^{2} - 324x\sin (x) + 20x\sin (2x) + 540) - 4(27x^{2} - 428)\cos (x) + (9x^{2} - 92)\cos (2x)} \right) \hfill \\ + \frac{1}{2}x\sin (x) + 2\cos (x) - 2 \hfill \\ \end{aligned}$$
(56)

Note that the function in the parentheses of the second term of Eq. (54) is approximated as 0 for simplicity.

4.6 OHAM

We have

$$L\left( {y\left( x \right)} \right) = y'', g\left( x \right) = { \cos } x - 1, N\left( {y\left( x \right)} \right) = \left( {y'} \right)^{ 2} + e^{y} , y\left( 0 \right) = y'\left( 0 \right) = 0 .$$
(57)

Problem of zero order is written as:

$$y_{0}^{\prime \prime } (x) = \cos x - 1,y_{0} (0) = y_{0}^{\prime } (0) = 0$$
(58)

from which we obtain

$$y_{0} = 1 - \frac{{x^{2} }}{2} - \cos x .$$
(59)

Substituting Eq. (59) into (12), we get first-order problem:

$$y_{1}^{\prime \prime } (x) = C_{1} \left( {2 - \cos x + \frac{{x^{2} }}{2} - 2x\sin x + \sin^{2} x} \right),y_{1} (0) = y_{1}^{\prime } (0) = 0$$
(60)

having solution

$$y_{1} = \frac{{C_{1} }}{24}\left( {x^{4} + 30x^{2} + 48x\sin (x) + 120\cos (x) + 3\cos (2x) - 123} \right) .$$
(61)

Second-order problem is

$$\begin{aligned} y_{2}^{\prime \prime } (x) = \frac{1}{48}\left[ \begin{aligned} - 3\cos (2x)\left\{ {C_{1}^{2} (x^{2} - 4) + 8C_{1} + 8C_{2} } \right\} - \cos (x)\left\{ {C_{1}^{2} (2x^{4} + 372x^{2} - 663) + 48C_{1} + 48C_{2} } \right\} \hfill \\ - C_{1}^{2} x^{6} - 42C_{1}^{2} x^{4} - 32C_{1}^{2} x^{3} \sin (x) + 27C_{1}^{2} x^{2} + 624C_{1}^{2} x\sin (x) + 72C_{1}^{2} x\sin (2x) + 120C_{2} \hfill \\ + 9C_{1}^{2} \cos (3x) - 636C_{1}^{2} + 24C_{1} x^{2} - 96C_{1} x\sin (x) + 120C_{1} + 24C_{2} x^{2} - 96C_{2} x\sin (x) \hfill \\ \end{aligned} \right] \hfill \\ y(0) = y^{\prime}(0) = 0 \hfill \\ \end{aligned}$$
(62)

The solution of Problem (62) is given by

$$\begin{aligned} y_{2} (x) = \frac{\cos (2x)}{128}\left\{ {C_{1}^{2} (2x^{2} - 59) + 16C_{1} + 16C_{2} } \right\} + \frac{\cos (x)}{48}\left\{ {C_{1}^{2} (2x^{4} + 492x^{2} - 4671) + 240C_{1} + 240C_{2} } \right\} - \hfill \\ \frac{{C_{1}^{2} x^{8} }}{2688} - \frac{{7C_{1}^{2} x^{6} }}{240} + \frac{{3C_{1}^{2} x^{4} }}{64} + \frac{1}{3}C_{1}^{2} x^{3} \sin (x) - \frac{{53C_{1}^{2} x^{2} }}{8} - 52C_{1}^{2} x\sin (x) - \frac{13}{32}C_{1}^{2} x\sin (2x) - \frac{1}{48}C_{1}^{2} \cos (3x) \hfill \\ + \frac{{37553C_{1}^{2} }}{384} + \frac{{C_{1} x^{4} }}{24} + \frac{{5C_{1} x^{2} }}{4} + 2C_{1} x\sin (x) - \frac{{41C_{1} }}{8} + \frac{{C_{2} x^{4} }}{24} + \frac{{5C_{2} x^{2} }}{4} + 2C_{2} x\sin (x) - \frac{{41C_{2} }}{8} \hfill \\ \end{aligned}$$
(63)

Following the procedure as in the previous example, we get

$$C_{1} = 0.905464108016448, \, C_{2} = - 0.099015663394332645 .$$
(64)

One can proceed to obtain higher iterations by using a computer program. Table 3 displays the approximate results of OHAM and PIM for m = 3. PIA(1,1) and PIA(1,2) gives better results than OHAM for this problem. Figure 2 also demonstrates the difference between OHAM solution and PIM solution. Table 4 shows the absolute errors of the proposed methods for m = 3.

Table 2 Absolute errors for OHAM, PIA(1, 1) and PIA(1, 2) for different values of m
Full size table
Fig. 2
figure 2

Comparison of the solutions for Example 2

Full size image

5 Conclusions

This paper applied the OHAM and PIM algorithms to solve random nonlinear differential equations. These two methods are very effective and accurate for solving nonlinear problems arising in many fields of science. In this work, we consider two examples which were selected to show the computational accuracy for illustration purposes. We have showed that OHAM has substantial computational requirements and more cumbersome to handle these chosen problems when compared with the PIM. Perturbation-iteration algorithms find more approximate results with less computational work. It is worth mentioning also that there might be some new developments about OHAM, but we just use the early stage of OHAM for our comparison for simplicity. For this study, it may be concluded that, the PIA(1,2) is more effective and powerful in obtaining approximate solutions for the selected problems.

Table 3 Comparison of numerical results with the Mathematica solution
Full size table
Table 4 Absolute errors for OHAM, PIA(1,1) and PIA(1,2) for m = 3
Full size table