1 Introduction

Partial differential equations (PDEs) are naturally encountered during the mathematical modeling of various physical phenomena and thus are of interest to several mathematicians and scientists [1]. These equations in general correspond to certain physical conservation laws (mass, energy) or balance of forces (momentum). Researchers always involve themselves in the development of mathematical theory and methods only for the treatment of PDEs, for instance, heat equation, Navier–Stokes equation, Schrodinger equation, Maxwell’s equation, etc. [2]. Our main aim is to explore GHPM to the different versions of PDEs.

Some of the well-known PDEs type wave equations are Klein–Gordon equation, Burger’s equation, Boussinesq equation, cubic Schrodinger equation, etc. [3]. Wave equations give the description for the propagation of the distinct kinds of waves like water waves, sound waves, light waves and typical example is tsunami propagation, acoustic, electrodynamics and traffic flow [4,5,6]. There is great need to thoroughly study these equations for the sake of their applications in the areas of engineering and other disciplines. Kaya and INC [7] found the solution of wave equations by decomposition method. Biazar and Islam have used ADM for the wave equation [8]. Further, Biazar and Ghazvini [9] investigated PDEs type wave equations by variational iteration method. Galerkin method has been used to study PDEs by using finite element in space and Crank-Nicolson algorithm [10].

In this article, we explore He’s homotopy theory with least square approximation to tackle PDEs especially wave equations and present the method as GHPM. Using GHPM, firstly, we construct reliable homotopy for the given problem along with homotopy parameter and receive a homotopy perturbated solution. After that linear combination of the terms appearing in homotopy solutions is assumed as approximate solution. Further, least square method is adopted to calculate the constants appearing in the involved solution. The interesting part of this procedure is that we need only initial approximation of HPM solution to achieve accurate result. The theoretical background has been built by [11]. Our results will fill the gap in the literature related to the exact solution of wave equations.

Rest part of the paper maintains following structure: In Sect. 2, the mathematical basis (algorithm) of GHPM has been discussed along with required definitions. In Sect. 3, the applications of GHPM have been demonstrated by presenting three examples whose exact solutions are already available. In the last section, we present our conclusion.

2 Foundation of GHPM for system of PDEs

Let us suppose following system of PDEs [12, 13]:

$$\begin{aligned} & L_{1} \left[ {Q\left( {\pi ,\tau } \right)} \right] + M\left[ {Q\left( {\pi ,\tau } \right), \;W\left( {\pi ,\tau } \right)} \right] - \upsilon_{1} \left( {\pi ,\tau } \right) = 0,\;\;\;\left( {\pi ,\tau } \right) \in \Omega = \left( {0,l} \right) \times \left( {0,t} \right), \\ & L_{2} \left[ {Q\left( {\pi ,\tau } \right)} \right] + N\left[ {Q\left( {\pi ,\tau } \right), \;W\left( {\pi ,\tau } \right)} \right] - \upsilon_{2} \left( {\pi ,\tau } \right) = 0,\;\;\;\left( {\pi ,\tau } \right) \in \Omega = \left( {0,l} \right) \times \left( {0,t} \right), \\ \end{aligned}$$
(1)

with

$$I_{1} \left( {Q,\frac{\partial Q}{{\partial n}}} \right) = 0,\;\;I_{2} \left( {W,\frac{\partial W}{{\partial n}}} \right) = 0, \left( {\pi ,\tau } \right) \in \partial \Omega.$$
(2)

Here \(L_{1}\) and \(L_{2}\) are linear differential operators, M, N are nonlinear differential operators, \(Q\left( {\pi ,\tau } \right), W\left( {\pi ,\tau } \right)\) are unknown functions, \(I_{1} , I_{2}\) are boundary operators, and \(\upsilon_{1} \left( {\pi ,\tau } \right),\) and \(\upsilon_{2} \left( {\pi ,\tau } \right)\) are known functions.

Let

\(\vartheta \left( {\pi ,\tau ;p} \right): \Omega \times \left[ {0,1} \right] \to {\mathbb{R}}, \omega \left( {\pi ,\tau ;p} \right): \Omega \times \left[ {0,1} \right] \to {\mathbb{R}}\),

which satisfy following homotopy equations (14–16):

$$\begin{aligned} & \left( {1 - p} \right)\left[ {L_{1} \left[ {\vartheta \left( {\pi ,\tau ;p} \right)} \right] - \upsilon_{1} \left( {\pi ,\tau } \right)} \right] + p[L_{1} \left[ {\vartheta \left( {\pi ,\tau ;p} \right) } \right] \\ & \quad + M\left[ {\vartheta \left( {\pi ,\tau ;p} \right),{ }\omega \left( {\pi ,\tau ;p} \right)} \right] - \upsilon_{1} \left( {\pi ,\tau } \right)] = 0, \\ \end{aligned}$$
(3)
$$\begin{aligned} & \left( {1 - p} \right)\left[ {L_{2} \left[ {{ }\omega \left( {\pi ,\tau ;p} \right)} \right] - \upsilon_{2} \left( {\pi ,\tau } \right)} \right] + p\left[ {{ }\omega \left( {\pi ,\tau ;p} \right)} \right] \\ & \quad + N\left[ {\vartheta \left( {\pi ,\tau ;p} \right),{ }\omega \left( {\pi ,\tau ;p} \right)} \right] - \upsilon_{2} \left( {\pi ,\tau } \right)] = 0. \\ \end{aligned}$$
(4)

Here, \({\Omega }\) is the simply connected domain under consideration, \(p \in \left[ {0,1} \right]\). \(p = 0\) gives

$$\vartheta \left( {\pi ,\tau ;0} \right) = Q_{0} \left( {\pi ,\tau } \right),\;\;{\text{and}}\;\;{ }\omega \left( {\pi ,\tau ;0} \right) = W_{0} \left( {\pi ,\tau } \right),$$

while initial guesses \(Q_{0} \left( {\pi ,\tau } \right)\) and \(W_{0} \left( {\pi ,\tau } \right)\) will be determined through

$$Q_{0} \left( {\pi ,\tau } \right) = L^{ - 1} \left( {\upsilon_{1} \left( {\pi ,\tau } \right)} \right)\;\;{\text{and}}\;\;W_{0} \left( {\pi ,\tau } \right) = L^{ - 1} \left( {\upsilon_{2} \left( {\pi ,\tau } \right)} \right),$$
(5)

Subjected to

$$I_{1} \left( {Q_{0} ,\frac{{\partial Q_{0} }}{\partial n}} \right) = 0,\;\;I_{2} \left( {W_{0} ,\frac{{\partial W_{0} }}{\partial n}} \right) = 0.$$

Further, \(p=1\), in equations (3) and (4) provides

$$\vartheta \left( {\pi ,\tau ;1} \right) = Q\left( {\pi ,\tau } \right),\;{ }\omega \left( {\pi ,\tau ;1} \right) = W\left( {\pi ,\tau } \right).$$

Following the classical procedure of ordinary homotopy perturbation, we assume that

$$\vartheta \left( {\pi ,\tau ;p} \right) = Q_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\gamma \ge 1} Q_{\gamma } \left( {\pi ,\tau } \right)p^{\gamma }.$$
(6)
$$\omega \left( {\pi ,\tau ;p} \right) = W_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\delta \ge 1} W_{\delta } \left( {\pi ,\tau } \right)p^{\delta }.$$
(7)

On substituting expansions (6) and (7) into (3) and (4), we have:

$$Q_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\gamma \ge 1} Q_{\gamma } \left( {\pi ,\tau } \right)p^{\gamma } = L_{1}^{ - 1} \left[ {\upsilon_{1} \left( {\pi ,\tau } \right) - M\left( {\left\{ {Q_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\gamma \ge 1} Q_{\gamma } \left( {\pi ,\tau } \right)p^{\gamma } } \right\},\left\{ {W_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\delta \ge 1} W_{\delta } \left( {\pi ,\tau } \right)p^{\delta } } \right\}} \right)} \right],$$
$$W_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\delta \ge 1} W_{\delta } \left( {\pi ,\tau } \right)p^{\delta } = L_{2}^{ - 1} \left[ {\upsilon_{2} \left( {\pi ,\tau } \right) - N\left( {\left\{ {Q_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\gamma \ge 1} Q_{\gamma } \left( {\pi ,\tau } \right)p^{\gamma } } \right\},\left\{ {W_{0} \left( {\pi ,\tau } \right) + \mathop \sum \limits_{\delta \ge 1} W_{\delta } \left( {\pi ,\tau } \right)p^{\delta } } \right\}} \right)} \right].$$

Solutions to set of above equations can be readily achieved in terms of \({Q}_{\kappa }\), \({W}_{i}\) for \(\kappa ,\iota = \mathrm{0,1},2,...,\infty .\) But here we proceed in a different way. So, we require only the initial iterations of homotopy perturbation method.

Remark 2.1

The zeroth-order solutions are similar to equation (5).

Let

$$\zeta_{\gamma } = Q_{0} + Q_{1} + \ldots + Q_{\gamma } ,\;\;{\text{and}}\;\;\xi_{\delta } = W_{0} + W_{1} + \ldots + W_{\delta } ,$$

are the HP-solution.

We prepare following two sets:

$$G_{\gamma } = \left\{ {\chi_{0} + \chi_{1} + \ldots + \chi_{\gamma } } \right\},\;\;{\text{and}}\;\;Z_{\delta } = \left\{ {\Theta_{0} + \Theta_{1} + \ldots + \Theta_{\delta } } \right\}\;\;{\text{where}}\;\;\gamma ,\;\delta = 0,1,2, \ldots ,$$
(8)

and \({\chi }_{0}={Q}_{0}\), \({\chi }_{1}={Q}_{1}\),…, \({\chi }_{\gamma }={Q}_{\gamma }\) and \({\Theta }_{0}={W}_{0}\), \({\Theta }_{1}={W}_{1}\),…, \({\Theta }_{\delta }={W}_{\delta }\). It can be easily verified here that \({G}_{\gamma -1}\subseteq {G}_{\gamma }\), \({Z}_{\delta -1}\subseteq {Z}_{\delta }\) and \({G}_{\gamma }\), \({Z}_{\delta }\) are L.I. in the vector space structure of continuous functions defined over \({\mathbb{R}}\).

Definition 2.1

Let [13]

$$\begin{aligned} R_{1} \left( {\pi ,\tau ,\overline{Q},\overline{W}} \right) = & L_{1} \left[ {\overline{Q}\left( {\pi ,\tau } \right)} \right] + M\left[ {\overline{Q}\left( {\pi ,\tau } \right), \overline{W}\left( {\pi ,\tau } \right)} \right] - \upsilon_{1} \left( {\pi ,\tau } \right) = 0, \\ \left( {\pi ,\tau } \right) \in {\Omega } = & \left( {0,l} \right) \times \left( {0,t} \right), \\ \end{aligned}$$
(9)
$$\begin{aligned} R_{2} \left( {\pi ,\tau ,\overline{Q},\overline{W}} \right) = & L_{2} \left[ {\overline{Q}\left( {\pi ,\tau } \right)} \right] + N\left[ {\overline{Q}\left( {\pi ,\tau } \right), \overline{W}\left( {\pi ,\tau } \right)} \right] - \upsilon_{2} \left( {\pi ,\tau } \right) = 0, \\ \left( {\pi ,\tau } \right) \in {\Omega } = & \left( {0,l} \right) \times \left( {0,t} \right), \\ \end{aligned}$$
(10)

be the residuals for the PDE (1), with

$$I_{1} \left( {\overline{Q},\frac{{\partial \overline{Q}}}{\partial n}} \right) = 0,\;\;I_{2} \left( {\overline{W},\frac{{\partial \overline{W}}}{\partial n}} \right) = 0,$$
(11)

where

$$\overline{Q} = \mathop \sum \limits_{l = 0}^{\gamma } {\Lambda }_{\gamma }^{l} \chi_{l} ,\;\;\overline{W} = \mathop \sum \limits_{h = 0}^{\delta } {\Delta }_{\delta }^{h} \Theta_{h} ,\;\;{\text{for}}\;\;\gamma ,\delta \ge 0,$$
(12)

are called as the approximate solution to (1).

Definition 2.2.

Let \({\left\{{S}_{\gamma }(\pi ,\tau )\right\}}_{\gamma \in {\mathbb{N}}}\) and \({\left\{{P}_{\delta }(\pi ,\tau )\right\}}_{\delta \in {\mathbb{N}}}\) are the two HP-sequences of HP-functions for equations (1), (2), then

$$S_{\gamma } \left( {\pi ,\tau } \right) = \mathop \sum \limits_{l = 0}^{\gamma } {\Lambda }_{\gamma }^{l} \chi_{l} ,\;P_{\delta } \left( {\pi ,\tau } \right) = \mathop \sum \limits_{h = 0}^{\delta } {\Delta }_{\delta }^{h} \Theta_{h} ,$$

where

$$\gamma ,\delta \in {\mathbb{N}}, \Lambda_{\gamma }^{l} , \Delta_{\delta }^{h} \in {\mathbb{R}} \left[ {13} \right].$$

Definition 2.3.

If

$$\mathop {\lim }\limits_{{\left( {\gamma ,\delta } \right) \to \left( {\infty ,\infty } \right)}} { }R_{1} \left( {\pi ,\tau ,{ }S_{\gamma } \left( {\pi ,\tau } \right),P_{\delta } \left( {\pi ,\tau } \right)} \right) = 0,$$

and

\(\mathop {\lim }\limits_{{\left( {\gamma ,\delta } \right) \to \left( {\infty ,\infty } \right)}} { }R_{2} \left( {\pi ,\tau ,{ }S_{\gamma } \left( {\pi ,\tau } \right),P_{\delta } \left( {\pi ,\tau } \right)} \right) = 0\).

Then \(\left\{{S}_{\gamma }\right\}\) and \(\left\{{P}_{\delta }\right\}\) converge to (1) and (2) [13].

Definition 2.4.

If

$$\left| {{ }R_{1} \left( {\pi ,\tau ,{ }\overline{Q},\overline{W}} \right)} \right| < \epsilon ,\;{\text{and}},\;\left| {{ }R_{2} \left( {\pi ,\tau ,{ }\overline{Q},\overline{W}} \right)} \right| < \epsilon ,$$

then \(\overline{Q },\overline{W }\) called as the \(\epsilon\)-approximate HP-solutions to the system (1), (2) on domain Ω along with (11) [13].

Definition 2.5.

If

$$\int {\int\limits_{0}^{\mathbb{R}} {R_{1}^{2} \left( {\pi ,\tau , \overline{Q},\overline{W}} \right){\text{d}}\pi {\text{d}}\tau \le \epsilon ,} } \;\;\int {\int\limits_{0}^{\mathbb{R}} {R_{2}^{2} \left( {\pi ,\tau , \overline{Q},\overline{W}} \right){\text{d}}\pi {\text{d}}\tau \le \epsilon } },$$

be the residual functions to the system (1), (2) [13].

Further, to calculate the scalars \({\Lambda }_{\gamma }^{l},\) and \({\Delta }_{\delta }^{h}\) (appearing in above linear combinations) accurately, we substitute the expression of \(\overline{Q },\overline{W }\) in (9) and (10) and achieve:

$$\Re_{1} \left( {\pi ,\tau , \Lambda_{\gamma }^{l} ,\Delta_{\delta }^{h} } \right) = R_{1} \left( {\pi ,\tau , \overline{Q},\overline{W}} \right),\;\;\Re_{2} \left( {\pi ,\tau , \Lambda_{\gamma }^{l} ,\Delta_{\delta }^{h} } \right) = R_{2} \left( {\pi ,\tau , \overline{Q},\overline{W}} \right).$$
(13)

Let \(J\left( { \Lambda_{\gamma }^{l} ,\;\Delta_{\delta }^{h} } \right)\) is defined as [13]

$$J\left( { \Lambda_{\gamma }^{l} ,\Delta_{\delta }^{h} } \right) = \int {\int\limits_{0}^{\mathbb{R}} {\left\{ { \Re_{1}^{2} \left( {\pi ,\tau , \Lambda_{\gamma }^{l} ,\Delta_{\delta }^{h} } \right) + \Re_{2}^{2} \left( {\pi ,\tau , \Lambda_{\gamma }^{l} ,\Delta_{\delta }^{h} } \right)} \right\}{\text{d}}\pi {\text{d}}\tau } },$$
(14)

real functional. Next, we minimize the functional (14) to determine the scalars.

Theorem 2.1.

If \(\left\{{S}_{\gamma }\left(\pi ,\tau \right)\right\}\), \(\left\{{P}_{\delta }\left(\pi ,\tau \right)\right\}\) are the HP-sequences (Definition (2.2)) then the following is true:

$$\mathop {\lim }\limits_{{\left( {\gamma ,\delta } \right) \to \left( {\infty ,\infty } \right)}} \int {\int\limits_{0}^{\mathbb{R}} {\left\{ { \Re_{1}^{2} \left( {\pi ,\tau ,S_{\gamma } \left( {\pi ,\tau } \right),P_{\delta } \left( {\pi ,\tau } \right)} \right) + \Re_{2}^{2} \left( {\pi ,\tau ,S_{\gamma } \left( {\pi ,\tau } \right),P_{\delta } \left( {\pi ,\tau } \right)} \right)} \right\}{\text{d}}\pi {\text{d}}\tau = 0.} }$$

Proof

The procedure for proof of this theorem is similar to [13].

3 Applications

Example 1.

Suppose a linear diffusion-wave equation as [17]:

$$\frac{{\partial^{2} Q}}{{\partial \pi^{2} }} - \frac{{\partial^{2} Q}}{{\partial \tau^{2} }} - \frac{\partial Q}{{\partial \tau }} + \left( {3\tau^{2} - \tau^{3} + 6\tau } \right)e^{\pi } = 0,$$
(15)

with

$$Q\left( {\pi ,0} \right) = \frac{\partial Q}{{\partial \tau }}\left( {\pi ,0} \right) = 0,\;\pi \in \left[ {0,1} \right],\,Q\left( {0,\tau } \right) = \tau^{3} ,\;Q\left( {1,\tau } \right) = e\tau^{3} ,\;\tau \in \left[ {0,1} \right].$$
(16)

The closed form solution given in [17] at \(\alpha\) = 2. Now continuing with GHPM procedure, let \(\gamma = 3\). Then

$$G_{3} = \left\{ {\tau \left( {e^{\pi } + \left( { - e + 1} \right)\pi - 1} \right),\tau^{2} \left( {e^{\pi } + \left( { - e + 1} \right)\pi - 1} \right),\tau^{3} \left( {\left( {e - 1} \right)\pi + 1} \right),\tau^{3} e^{\pi } } \right\}.$$

Applying the rest procedure, we will get same solution as given in [17]. In Table 1, we have presented the comparison of our results with OHAM [17].

Table 1 OHAM [17], GHPM and exact solutions for equation (16)
Full size table

Example 2.

Assume the nonlinear wave equation as considered in [18, 19]:

$$\frac{{\partial^{2} Q}}{{\partial \pi^{2} }} - Q\frac{{\partial^{2} Q}}{{\partial \tau^{2} }} = - \tau^{2} {\text{sin}}\left( {\uppi } \right) - 2\tau^{2} \sin^{2} \left( \pi \right), 0 \le \pi , \tau \le 1,$$
(17)

with

$$Q\left( {0,\tau } \right) = 0, \frac{\partial Q}{{\partial \pi }}\left( {0,\tau } \right) = \frac{{\tau^{2} }}{2}.$$
(18)

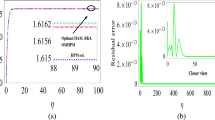
In this case let \(\gamma = 4\). For equation (18), surface and two-dimensional plots can be seen in Fig. 1. Table 2 is prepared for comparison.

Fig. 1
figure 1

Graphical presentation for equation (17)

Full size image
Table 2 LSM [19], HPM, GHPM and exact solutions of equation (17)
Full size table

Example 3

Let us suppose the two-dimensional system of partial differential equation [20]:

$$\frac{\partial Q}{{\partial \pi }} - W\frac{\partial Q}{{\partial \tau }} + Q\frac{\partial W}{{\partial \tau }} = - 1 + e^{\pi } \sin \left( \tau \right),$$
(19)
$$\frac{\partial W}{{\partial \pi }} + \frac{\partial Q}{{\partial \tau }}\frac{\partial W}{{\partial \pi }} + \frac{\partial W}{{\partial \tau }}\frac{\partial Q}{{\partial \pi }} = - 1 - e^{\pi } \cos \left( \tau \right),$$
(20)

and

$$Q\left( {0,\tau } \right) = \sin \left( \tau \right),\;\;W\left( {0,\tau } \right) = \cos \left( \tau \right).$$
(21)

Now apply the HPM procedure as described in section 2 we get:

$$Q_{0} = - \pi + e^{\pi } \sin \tau .$$
(22)
$$W_{0} = - \pi + e^{\pi } \cos \tau .$$
(23)

Consider \((\gamma ,\delta ) = (\mathrm{1,1})\), then set of functions as \({G}_{1}=\{\pi , {e }^{\pi }\mathrm{sin}\tau \}\) and \({Z}_{1}=\left\{\pi , {e }^{-\pi }\mathrm{cos}\tau \right\}.\)

Utilizing zeroth-order solutions of HPM to assume reliable approximate solutions for the system of Eq. (19), (20) as:

$$\overline{Q} = {\Lambda }_{0} \pi + {\Lambda }_{1} e^{\pi } \sin \tau ,$$
(24)
$$\overline{W} = {\Delta }_{0} \pi + {\Lambda }_{1} e^{ - \pi } \cos \tau .$$
(25)

Continuing with the procedure of GHPM, we obtain

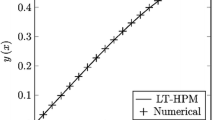
$$\overline{Q} = e^{\pi } \sin \left( \tau \right),\;\overline{W} = e^{ - \pi } \cos \left( \tau \right).$$
(26)

This solution matches with the exact solution [20]. The behavior of solutions attained by GHPM has been displayed in the form of Figs. 2, 3. The solutions presented by Biazar and Eslami in [20] used NHPM which depends upon traditional HPA. We can easily see that they found exact solutions for the same problem but they need higher-order approximation for this purpose. While in GHPM we manipulate only zeroth-order of HP-solutions and then apply LSA to get exact solutions.

Fig. 2
figure 2

GHPM solutions for equations (19) and (20) in terms of \(\overline{Q }(\pi ,\tau )\) and \(\overline{W }(\pi ,\tau )\)

Full size image
Fig. 3
figure 3

Plots for equations (19), (20)

Full size image

4 Conclusion

GHPM is explored to achieve the exact solutions for wave equations. The examples in the different forms of wave equations exactly validate the theory. The beauty of the method is its simplicity and accuracy and flexibility. Because of the flexibility of GHPM, it can be apply on both mixed type or Robin type boundary conditions particularly. The inclusion of these conditions might be a challenging task. But due to the homotopy parameter, GHPM can be handle the complexity of both types of the conditions in more easy way. This method will fill the gap in the literature by providing an alternating and simple way to obtain the solutions to PDEs, especially wave equations.