Abstract
We study several families of vertex operator superalgebras from a jet (super)scheme point of view. We provide new examples of vertex algebras which are “chiral-quantizations" of their \(C_{2}\)-algebras \(R_V\). Our examples come from affine \(C_\ell ^{(1)}\)-series vertex algebras, \(\ell \geqslant 1\), certain \(N=1\) superconformal vertex algebras, Feigin–Stoyanovsky principal subspaces, Feigin–Stoyanovsky type subspaces, graph vertex algebras \(W_{\Gamma }\), and extended Virasoro vertex algebras. We also give a counterexample to the chiral-quantization property for the \(N=2\) superconformal vertex algebra with central charge 1.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Beilinson, Feigin and Mazur in [18] introduced the notions of singular support and lisse representation in order to study Virasoro (vertex) algebras. Arakawa later extended these notions to any finitely strongly generated, non-negatively graded vertex algebra V. More precisely, via a canonical decreasing filtration \(\{F_{p}(V)\}\) introduced in [38], one can associate to V a positively graded vertex Possion algebra \(\mathrm{gr}^{F}(V)\). The spectrum of \(\mathrm{gr}^{F}(V)\) is called the singular support of V, and is denoted by  . With respect to this filtration, \(V/F_{1}(V)\) is the Zhu \(C_{2}\)-algebra \(R_V\). The reduced spectrum
. With respect to this filtration, \(V/F_{1}(V)\) is the Zhu \(C_{2}\)-algebra \(R_V\). The reduced spectrum  is a Poisson variety which is called the associated variety of V. A large body of work has been devoted to descriptions of associated varieties for various vertex operator algebras [5, 10, 12, 13]. Certainly the most prominent examples from this point of view are well-known lisse, or \(C_2\)-cofinite, vertex algebras characterized by
is a Poisson variety which is called the associated variety of V. A large body of work has been devoted to descriptions of associated varieties for various vertex operator algebras [5, 10, 12, 13]. Certainly the most prominent examples from this point of view are well-known lisse, or \(C_2\)-cofinite, vertex algebras characterized by  . Arakawa and Kawasetsu relaxed this condition to quasi-lisse in [7] which requires that \(X_{V}\) has finitely many symplectic leaves. Associated varieties are important in the geometry of Higgs branches in \(4\mathrm{d}/2\mathrm{d}\) dualities in physics [17].
. Arakawa and Kawasetsu relaxed this condition to quasi-lisse in [7] which requires that \(X_{V}\) has finitely many symplectic leaves. Associated varieties are important in the geometry of Higgs branches in \(4\mathrm{d}/2\mathrm{d}\) dualities in physics [17].
According to [5, Proposition 2.5.1], the embedding
can be extended to a surjective homomorphism of vertex Poisson algebras
where \(J_{\infty }(R_{V})\) is the (infinite) jet algebra of \(R_{V}\). The map \(\psi \) induces an injection from the singular support into the (infinite) jet scheme of the associated scheme of V,  , i.e.,
, i.e.,

In [11], authors showed that \(\phi \) is an isomorphism of varieties if V is quasi-lisse. It was shown in [52] that if the map \(\psi \) is an isomorphism, then one can compute Hochschild homology of the Zhu algebra via the chiral homology of elliptic curves. Proving that \(\psi \) is an isomorphsim or finding the kernel of \(\psi \) turns out to be subtle. In [9, 14, 52], authors provided examples for which \(\psi \) is not an isomorphism, including the \({\mathbb {Z}}_2\)-orbifold of the rank one Heisenberg algebra, affine vertex algebra \(L_{\widehat{\mathrm{sl}_{4}}}(-1,0)\), most Virasoro algebras, etc. However, a full description of the kernel, if non-trivial, of the map \(\psi \) is an interesting and difficult problem. Very recently, Andrews, van Ekeren and Heluani [4] found a remarkable q-series identity that allowed them to describe the kernel of \(\psi \) for the \(c=1/2\) Ising Virasoro vertex algebra.
For a vertex algebra V, where \(\psi \) is an isomorphism, one obtains a very interesting (and important) consequence

where the left-hand side is the character of V and the right-hand side is the Hilbert series of the jet algebra of \(R_{V}\). The left-hand side often has combinatorial interpretations which in turn can provide a non-trivial information about the jet scheme.
In Sects. 2–3, we recall some basics of vertex (super)algebras and generalize the notion of jet algebras to the super case. Then in Sect. 4 we investigate the map \(\psi \) in the cases of affine vertex algebras, rank one lattice vertex superalgebras including the simple \(N=2\) superconformal vertex algebra at level one. For the later case the map \(\psi \) is not an isomorphism, and we make a conjecture about its kernel. In Sect. 5 we analyze in great depth principal subspaces of lattice vertex algebras and affine vertex algebras, and show that the map \(\psi \) is an isomorphism for many examples. In particular, the principal subspaces are closely related to the jet algebras coming from graphs. Interestingly, in some examples their Hilbert series are (mixed) mock modular forms. In Sect. 6 we show that the map \(\psi \) is an isomorphism for the simple \(N=1\) vertex superalgebra associated with the \(N=1\) superconformal \((p,p')\)-minimal model if and only if \((p,p')=(2,4k)\), \(k\in {\mathbb {Z}}_{+}\). We also study extended Virasoro vertex algebras in Sect. 7.
2 Definitions and preliminary results
Definition 2.1
Let V be a superspace, i.e., a \({\mathbb {Z}}_{2}\)-graded vector space,  , where \(\{ {\overline{0}}, \overline{1} \}={\mathbb {Z}}_2\). If \(a\in V_{p(a)}\), we say that the element a has parity \(p(a)\in {\mathbb {Z}}_2\).
, where \(\{ {\overline{0}}, \overline{1} \}={\mathbb {Z}}_2\). If \(a\in V_{p(a)}\), we say that the element a has parity \(p(a)\in {\mathbb {Z}}_2\).
A field is a formal series of the form  where
where  and for each \(v\in V\) one has
and for each \(v\in V\) one has
We say that a field a(z) has parity \(p(a)\in {\mathbb {Z}}_2\) if
A vertex superalgebra contains the following data: a vector space of states V, the vacuum vector \(\mathbf{1 } \in V_{\overline{0}}\), derivation T, and state-field correspondence map

satisfying the following axioms:
-
(translation coinvariance): \([T,Y(a,z)]=\partial Y(a,z)\),
-
(vacuum): \(Y(\mathbf{1 } ,z)=\mathrm{Id}_{V}\),
 ,
, -
(locality):
 for \(N\gg 0\).
for \(N\gg 0\).
In particular, a vertex superalgebra V is called supercommutative if \(a_{(n)}=0\) for \(n\in {\mathbb {N}}\). It is well known that the category of commutative vertex superalgebras is equivalent with the category of unital commutative associative superalgebras equipped with an even derivation.
We say that a vertex superalgebra V is generated by a subset  if any element of V can be written as a finite linear combination of terms of the form
if any element of V can be written as a finite linear combination of terms of the form

for  , \(i_k \in {\mathbb {Z}}\), and \(n \in {\mathbb {N}}\). If every element of V can be written with \(i_k \in {\mathbb {Z}}_{-}\), we write
, \(i_k \in {\mathbb {Z}}\), and \(n \in {\mathbb {N}}\). If every element of V can be written with \(i_k \in {\mathbb {Z}}_{-}\), we write  , and say that V is strongly generated by
, and say that V is strongly generated by  .
.
Example 2.2
([53]) Let \({\mathfrak {g}}\) be a finite-dimensional Lie superalgebra with a non-degenerate even supersymmetric invariant bilinear form  . We can associate the affine Lie superalgebra \(\widehat{{\mathfrak {g}}}\) to the pair
. We can associate the affine Lie superalgebra \(\widehat{{\mathfrak {g}}}\) to the pair  .
.
Its universal vacuum representation of level k, \(V_{\hat{{\mathfrak {g}}}}(k,0)\), is a vertex superalgebra. In particular, when \({\mathfrak {g}}\) is a simple Lie superalgebra, \(V_{\hat{{\mathfrak {g}}}}(k,0)\) has a unique maximal ideal \(I_{\hat{{\mathfrak {g}}}}(k,0)\), and \(L_{\hat{{\mathfrak {g}}}}(k,0)=V_{\hat{{\mathfrak {g}}}}(k,0)/I_{\hat{{\mathfrak {g}}}}(k,0)\) is also a vertex superalgebra.
Example 2.3
([36]) To any n-dimensional superspace A with a non-degenerate anti-supersymmetric bilinear form  , we can associate a Lie superalgebra \(C_{A}\). If we fix a basis of A,
, we can associate a Lie superalgebra \(C_{A}\). If we fix a basis of A,

the free fermionic vertex algebra  associated to A is a vertex superalgebra strongly generated by \(\phi ^{i}_{(-{1}/{2})}\mathbf{1 }\), \(i=1,\dots ,n\), where \(Y(\phi ^{i}_{(-{1}/{2})}\mathbf{1 },z)= \sum _{n\in {1}/{2}+{\mathbb {Z}}}\phi _{(n)}^i z^{-n-{1}/{2}}\).
associated to A is a vertex superalgebra strongly generated by \(\phi ^{i}_{(-{1}/{2})}\mathbf{1 }\), \(i=1,\dots ,n\), where \(Y(\phi ^{i}_{(-{1}/{2})}\mathbf{1 },z)= \sum _{n\in {1}/{2}+{\mathbb {Z}}}\phi _{(n)}^i z^{-n-{1}/{2}}\).
Definition 2.4
A vertex superalgebra V is called a vertex operator superalgebra if it is \(\frac{1}{2} {\mathbb {Z}}\)-graded,

with a conformal vector \(\omega \) such that the set of operators \(\{L_{(n)}, \mathrm{id}_{V}\}_{n\in {\mathbb {Z}}}\) with \(L_{(n)}=\omega _{(n+1)}\) defines a representation of the Virasoro algebra on V; that is

We call \(c_{V}\) the central charge of V. We require that \(L_{(0)}\) is diagonalizible and it defines the \(\frac{1}{2} {\mathbb {Z}}\) grading — its eigenvalues are called (conformal) weights. In several examples we will encounter \(\frac{1}{2} {\mathbb {Z}}\)-graded vertex superalgebras without a conformal vector. For this reason, we define the character or graded dimension as

As we do not care about modularity here, we suppress the \(q^{-{c_{V}}/{24}}\) factor and also view q as a formal variable.
Example 2.5
([37]) Let \(\mathrm{Vir}\) denote the Virasoro Lie algebra. Then the universal \(\mathrm{Vir}\)-module \(V_{\mathrm{Vir}}(c,0)\) has a natural vertex operator algebra with central charge c.
Example 2.6
([36]) The universal vertex superalgebra associated with the \(N=1\) Neveu–Schwarz Lie superalgebra will be denoted by \(V_{c}^{N=1}\), where c is the central charge. It is a vertex operator superalgebra strongly generated by an odd vector \(G_{(-{3}/{2})}\mathbf{1 }\) and the conformal vector \(L_{(-2)}\mathbf{1 }\).
Example 2.7
([36]) The universal vertex superalgebra associated with the \(N=2\) superconformal Lie algebra will be denoted by \(V_{c}^{N=2}\). It is a vertex operator superalgebra strongly generated by two odd vectors \(G^{+}_{(-{3}/{2})}\mathbf{1 }\), \(G^{-}_{(-{3}/{2})}\mathbf{1 }\), and two even vectors \(L_{(-2)}\mathbf{1 }\), \(J_{(-1)}\mathbf{1 }\).
Definition 2.8
A commutative vertex superalgebra V is called a vertex Poisson superalgebra if it is equipped with a linear operation,

such that
-
\((Ta)_{n}={}-na_{(n-1)}\),
-
\(a_{(n)}b=\sum _{j\in {\mathbb {N}}} (-1)^{n+j+1}\,\frac{(-1)^{p(a)p(b)}}{j!}\, T^{j}(b_{(n+j)}a)\),
-
\([a_{(m)},b_{(n)}]=\sum _{j\in {\mathbb {N}}} \left( {\begin{array}{c}m\\ j\end{array}}\right) (a_{(j)}b)_{(m+n-j)}\),
-
 ,
,
for \(a,b,c\in V\) and \(n,m \in {\mathbb {N}}\).
A vertex Lie superalgebra structure on V is given by \((V,Y_{-},T)\). So one can also say that a vertex Poisson superalgebra is a commutative vertex superalgebra equipped with a vertex Lie superalgebra structure. In fact, one can obtain a vertex Poisson superalgebra from any vertex superalgebra through standard increasing filtration or Li’s filtration. Following [38], one can define a decreasing sequence of subspaces \(\{F_{n}(V)\}\) of the superalgebra V, where for \(n\in {\mathbb {Z}}\), \(F_{n}(V)\) is linearly spanned by the vectors
for \(r\in \mathbb {Z_{+}}\),  , \(k_{1},\dots ,k_{r}\in {\mathbb {N}}\) with \(k_{1}+\cdots +k_{r}\geqslant n\). Then Li’s filtration of V is given by
, \(k_{1},\dots ,k_{r}\in {\mathbb {N}}\) with \(k_{1}+\cdots +k_{r}\geqslant n\). Then Li’s filtration of V is given by
satisfying
The corresponding associated graded algebra \(\mathrm{gr}^{F}(V)=\coprod _{n\in {\mathbb {N}}} F_{n}(V)/F_{n+1}(V)\) is a vertex Poisson superalgebra. Its vertex Lie superalgebra structure is given by

for \(u\in F_{r}(z)\), \(v\in F_{s}(z)\) with \(r,s\in {\mathbb {N}}\). For the standard increasing filtration \(\{G_{n}(V)\}\), we also have the associated graded vertex superalgebra \(\mathrm{gr}^{G}(V)\). In [5, Proposition 2.6.1], it was shown that
as vertex Poisson superalgebras. Thus we sometimes drop the upper index F or G for brevity.
According to [38], we know that

In particular, \(F_{0}(V)/F_{1}(V)=V/C_{2}(V)=R_{V}\) is a Poisson superalgebra by [54]. Its Poisson structure is given by

for \(u,v\in V\) where \(\overline{u}=u+C_{2}(V)\). It was shown in [38, Corallary 4.3] that \(\mathrm{gr}^{F}(V)\) is generated by \(R_{V}\) as a differential algebra.
Next, let us compute the \(C_{2}\)-algebras for some simple examples.
Example 2.9
Following notations in Example 2.3, let  be a free fermionic vertex superalgebra associated with an n-dimensional superspace A. Clearly, the \(C_{2}\)-algebra of
be a free fermionic vertex superalgebra associated with an n-dimensional superspace A. Clearly, the \(C_{2}\)-algebra of  is
is

where \(\overline{\phi ^{i}_{(-{1}/{2})}\mathbf{1 }}\) is even (resp. odd) if \(\phi ^{i}\) is even (resp. odd) in A.
Example 2.10
According to [52, 16.16], for simple affine vertex algebras \(L_{\hat{{\mathfrak {g}}}}(k,0)\), \(k \in {\mathbb {N}}\), where \({\mathfrak {g}}\) is a simple Lie algebra, we have

where  is a basis of \({\mathfrak {g}}\), \(\theta \) is the highest root of \({\mathfrak {g}}\), and \(\circ \) represents the adjoint action. In particular, when \({\mathfrak {g}}=\mathrm{sl}_2\), we have
is a basis of \({\mathfrak {g}}\), \(\theta \) is the highest root of \({\mathfrak {g}}\), and \(\circ \) represents the adjoint action. In particular, when \({\mathfrak {g}}=\mathrm{sl}_2\), we have

where e, f, h correspond to \(e_{(-1)}\mathbf{1 }, f_{(-1)}\mathbf{1 }, h_{(-1)}\mathbf{1 }\).
Example 2.11
For any simple Virasoro algebras \(L_{\mathrm{Vir}}(c_{(p,p')},0)\), where \(c_{(p,p')}=1-{6(p-p')^{2}}/({p p'})\) with  and \(p,p'\) coprime, according to [18, 52] its \(C_{2}\)-algebra is isomorphic to \({\mathbb {C}}[x]/\langle x^{{(p-1)(p'-1)}/{2}}\rangle \), where x corresponds to \(\omega =L_{(-2)}\mathbf{1 }\).
and \(p,p'\) coprime, according to [18, 52] its \(C_{2}\)-algebra is isomorphic to \({\mathbb {C}}[x]/\langle x^{{(p-1)(p'-1)}/{2}}\rangle \), where x corresponds to \(\omega =L_{(-2)}\mathbf{1 }\).
Example 2.12
The \(C_{2}\)-algebra of \(V_{c}^{N=1}\) is \(R_{V_{c}^{N=1}}={\mathbb {C}}[x,\theta ]\), where x and \(\theta \) correspond to the even vector \(L_{(-2)}\mathbf{1 }\) and odd vector \(G_{(-{3}/{2})}\mathbf{1 }\), respectively.
Example 2.13
The \(C_{2}\)-algebra of \(V_{c}^{N=2}\) is \({\mathbb {C}}[x,y,\theta _{1},\theta _{2}]\) where \(x,y,\theta _{1},\theta _{2}\) correspond to \(L_{(-2)}\mathbf{1 }\), \(J_{(-1)}\mathbf{1 }\), \(G^{+}_{(-{3}/{2})} \mathbf{1 }\) and \(G^{-}_{(-{3}/{2})} \mathbf{1 }\), respectively. Here \(\theta _{1},\theta _{2}\) are odd variables.
3 Affine jet superalgebras
Inspired by the definition of a jet algebra, we may give an analogous definition of a jet superalgebra in the affine case. Here, we closely follow [5].
Let  be a polynomial superalgebra, where
be a polynomial superalgebra, where

are ordinary variables and

are odd variables, i.e., \((\theta ^{i})^{2}=0\) for \(1\leqslant i \leqslant m\). Let \(f_{1},f_{2}, \dots , f_{n}\) be \({\mathbb {Z}}_{2}\)-homogeneous elements in the polynomial superalgebra. We will define the jet superalgebra of the quotient superalgebra as

Firstly, let us introduce new even variables  and odd variables
and odd variables  for \(0\leqslant i\leqslant m\), where
for \(0\leqslant i\leqslant m\), where  and
and  are degrees of \(x^{j}\) and \(\theta ^{j'}\). In most cases, we will assume that the degree of each variable is 1, although in some cases the odd degree can be shifted by 1/2. We define an even derivation T on
are degrees of \(x^{j}\) and \(\theta ^{j'}\). In most cases, we will assume that the degree of each variable is 1, although in some cases the odd degree can be shifted by 1/2. We define an even derivation T on

as

and

Here we identify \(x^{j}\) and \(\theta ^{j'}\) with  and
and  , respectively. Set
, respectively. Set

Then the m-jet superscheme of  is defined as
is defined as  . The infinite jet superalgebra of \(R_{V}\) is defined as
. The infinite jet superalgebra of \(R_{V}\) is defined as

We often omit “infinite” and call it jet superalgebra for brevity. The jet superalgebra is a differential commutative superalgebra. We denote the ideal

by \(\langle f_{1},\dots ,f_n \rangle _{\partial }\). Later, we sometimes write \(x_{(j)}\) as x(j). The infinite jet superscheme, or arc space, of V is defined as

We define the degree of each variable \(u_{(-\Delta -j)}\) to be \(\Delta +j\), where \(u=x\) or \(\theta \). Then \(J_{\infty }(R)= \coprod _{m\in \frac{1}{2}{\mathbb {Z}}}(J_{\infty }(R))_{(m)}\), where \((J_{\infty }(R))_{(m)}\) is the set of all elements in the jet superalgebra with degree m. We define the Hilbert series of \(J_{\infty }(R)\) as

Following [5], \(J_{\infty }(R)\) has a unique vertex Poisson superalgebra structure such that
for \(u,v\in R\in J_{\infty }(R)\).
Furthermore, one can extend the embedding \(R_{V}\hookrightarrow \mathrm{gr}^{F}(V)\) to a surjective differential superalgebra homomorphism \(J_{\infty }(R_{V}) \twoheadrightarrow \mathrm{gr}^{F}(V)\). It is obvious that the map is a differential superalgebra homomorphism. It is surjective, since \(\mathrm{gr}^{F}(V)\) is generated by \(R_{V}\) as a differential algebra. Moreover, it was shown in [5] that this map is actually a vertex Poisson superalgebra epimorphism. From now on, we call this map \(\psi \). The map \(\psi \) is not necessarily injective, and it is an open problem to characterize rational vertex algebras for which \(\psi \) is injective.
3.1 Complete lexicographic ordering
Following [30], we define the complete lexicographic ordering on a basis or spanning set of the jet superalgebra. Given a jet superalgebra

where \(\Delta _{i}\) is the degree of \(y^{i}\), we can first define an ordering of all variables in the following way:
Definition 3.1
A monomial u of  is called an ordered monomial if it is of the form
is called an ordered monomial if it is of the form
where \(m\in {\mathbb {Z}}_{+}\) and  .
.
It should be clear that all ordered monomials form a spanning set of the jet superalgebra. Then let us define the multiplicity of an ordered monomial as
Given two arbitrary ordered monomials
we define a complete lexicographic ordering as follows. If \(\mu (u)<\mu (v)\), we say that \(u<v\). If \(\mu (u)=\mu (v)\), we compare exponents of
in this order. Namely, we say \(v<u\) if \(a^1_1<b^1_1\); if they are equal, we then compare \(a^{2}_{1}\) and \(b^2_1\), and so on. Given a polynomial f, we call the greatest monomial among all its terms with respect to the complete lexicographic ordering the leading term of f.
4 Affine and lattice vertex algebras
In this section we analyze the \(C_{2}\)-algebra \(R_V\) and the injectivity of the map \(\psi \) for some familiar examples of affine and lattice vertex algebras.
Example 4.1
It was shown in ([5, Proposition 2.7.1]) that for any simple Lie algebra \({\mathfrak {g}}\), we have \(J_{\infty }(R_{V_{\hat{{\mathfrak {g}}}(k,0)}})\cong \mathrm{gr}^{F}(V_{\hat{{\mathfrak {g}}}(k,0)})\).
Proposition 4.2
([6, Example 4.10]) For the free fermionic vertex superalgebra, we have  as vertex Poisson superalgebras.
as vertex Poisson superalgebras.
Proof
We use Arakawa’s argument in [5, Proposition 2.7.1]. We include the proof for completeness. Here we still follow the notations from Example 2.3. According to [36, Section 3.6], we can choose a conformal vector such that  is \(\frac{1}{2}{\mathbb {N}}\)-graded. We consider the standard filtration G on F. Firstly, we have
is \(\frac{1}{2}{\mathbb {N}}\)-graded. We consider the standard filtration G on F. Firstly, we have  as vector superspaces. Moreover,
as vector superspaces. Moreover,

where \(m\in \frac{1}{2}{\mathbb {N}}\) and  . So
. So  as vertex Poissson superalgebras. Therefore,
as vertex Poissson superalgebras. Therefore,  . \(\square \)
. \(\square \)
Similarly, we can show that \(\psi \) is an isomorphism for the vertex superalgebra \(V_{\hat{{{\mathfrak {g}}}}}(k,0)\), where \({\mathfrak {g}}\) is a Lie superalgebra satisfying conditions in Example 2.2, and for superconformal vertex algebras \(V_{c}^{N=1}\) and \(V_{c}^{N=2}\).
Let

be a rank one lattice vertex algebra (resp. superalgebra) constructed from an integral lattice \(L={\mathbb {Z}}\alpha \cong \sqrt{p}{\mathbb {Z}}\), where \(\langle \alpha ,\alpha \rangle =p\) is even (resp. odd). It has a conformal vector \(\omega =\frac{1}{2p}\alpha _{(-1)}^2 \mathbf{1 }\). As usual, we denote the extremal lattice vectors by \(e^{n \alpha }\), \(n \in {\mathbb {Z}}\).
Proposition 4.3
For the lattice vertex algebra  we have
we have

When p is odd, x and y are odd vectors.
Proof
According to the following calculations:

we know that all vectors except for \(\alpha _{(-1)}\mathbf{1 },\dots , \alpha _{(-1)}^{p}\mathbf{1 }\), \(e^{\alpha }\), \(e^{-\alpha }\) and \(\mathbf{1 }\) are zero in  .
.
We will show that all these vectors are indeed non-zero in  . Suppose there exist
. Suppose there exist  such that \(u_{(-2)}v= e^{\alpha }\). Then
such that \(u_{(-2)}v= e^{\alpha }\). Then  , which implies that \(u,v\in \pi _{{0}}\), where \(\pi _{0}\) is the Heisenberg subalgebra
, which implies that \(u,v\in \pi _{{0}}\), where \(\pi _{0}\) is the Heisenberg subalgebra  . This is a contradiction. So the equivalent class \(\overline{e^{\alpha }}\) is non-zero in
. This is a contradiction. So the equivalent class \(\overline{e^{\alpha }}\) is non-zero in  . Using a similar weight argument, we can show that equivalence classes
. Using a similar weight argument, we can show that equivalence classes
are all non-zero in  . Moreover, we have
. Moreover, we have

Then the map  , sending \(\overline{e^{\alpha }}\) to x, \(\overline{e^{-\alpha }}\) to y, \(\overline{\mathbf{1 }}\) to 1, and \(\root p \of {\frac{1}{p!}}\,\overline{\alpha _{(-1)}\mathbf{1 }}\) to z, is an isomorphism. \(\square \)
, sending \(\overline{e^{\alpha }}\) to x, \(\overline{e^{-\alpha }}\) to y, \(\overline{\mathbf{1 }}\) to 1, and \(\root p \of {\frac{1}{p!}}\,\overline{\alpha _{(-1)}\mathbf{1 }}\) to z, is an isomorphism. \(\square \)
Remark 4.4
By the Frenkel–Kac construction, we know that  . Following Proposition 4.3, we have
. Following Proposition 4.3, we have  . According to [52, 16.16], one can also compute \(R_{L_{\widehat{\mathrm{sl}_{2}}}(1,0)}\) directly.
. According to [52, 16.16], one can also compute \(R_{L_{\widehat{\mathrm{sl}_{2}}}(1,0)}\) directly.
Given a vertex superalgebra \(V=\coprod _{n\in \frac{1}{2}{\mathbb {Z}}}V_{(n)}\) where \(V_{\overline{0}}=\coprod _{n\in {\mathbb {Z}}}V_{(n)}\) and \(V_{\overline{1}}=\coprod _{n\in \frac{1}{2}+{\mathbb {Z}}}V_{(n)}\), there are two binary operations defined as follows: for homegeneous \(a,b\in V\),

and

Let O(V) be the linear span of elements of the form  in V. Then Zhu’s algebra A(V) is defined as the quotient space V/O(V) with the mutiplication from
in V. Then Zhu’s algebra A(V) is defined as the quotient space V/O(V) with the mutiplication from  . According to [54, Theorem 2.1.1], there is a filtration \(\{\overline{F}_{k}(A(V))\}\) on A(V), where \(\overline{F}_{k}(A(V)):=\bigl (\bigoplus _{i\in \frac{1}{2}{\mathbb {Z}}, i\leqslant k}V_{(i)}+O(V)\bigr )/O(V)\). Moreover, [54, Lemma 2.1.3] implies its associated graded algebra,
. According to [54, Theorem 2.1.1], there is a filtration \(\{\overline{F}_{k}(A(V))\}\) on A(V), where \(\overline{F}_{k}(A(V)):=\bigl (\bigoplus _{i\in \frac{1}{2}{\mathbb {Z}}, i\leqslant k}V_{(i)}+O(V)\bigr )/O(V)\). Moreover, [54, Lemma 2.1.3] implies its associated graded algebra,
is a commutative algebra with respect to the multiplication  and the commutation
and the commutation  . Note, by definition of Zhu’s algebra we have \(A(V)\cong V_{\overline{0}}/(V_{\overline{0}}\cap O(V))\). Following a similar argument to [25, Proposition 2.17 (c)] or [8, Propostion 3.3], we can define a surjective homomorphism of graded commutative Poisson algebras:
. Note, by definition of Zhu’s algebra we have \(A(V)\cong V_{\overline{0}}/(V_{\overline{0}}\cap O(V))\). Following a similar argument to [25, Proposition 2.17 (c)] or [8, Propostion 3.3], we can define a surjective homomorphism of graded commutative Poisson algebras:
given by  for \(a\in V_{(k)}\) and \(b\in V_{(l)}\). Now we can prove:
for \(a\in V_{(k)}\) and \(b\in V_{(l)}\). Now we can prove:
Corollary 4.5
Let p be a positive odd integer, then the even part of  , i.e.,
, i.e.,  , is isomorphic to the associated graded algebra
, is isomorphic to the associated graded algebra  .
.
Proof
According to [45, Theorem 3.3], we know that  , where \(F_{p}(x)=x(x+1)(x-1)\cdots (x+{(p-1)}/{2})(x-{(p-1)}/{2})\) in which x corresponds to \([\alpha _{(-1)}\mathbf{1 }]\) in
, where \(F_{p}(x)=x(x+1)(x-1)\cdots (x+{(p-1)}/{2})(x-{(p-1)}/{2})\) in which x corresponds to \([\alpha _{(-1)}\mathbf{1 }]\) in  . Then according to Proposition 4.3, we have
. Then according to Proposition 4.3, we have

via f. \(\square \)
Remark 4.6
If \(L=\sqrt{2k}{\mathbb {Z}}\), \(k\in {\mathbb {Z}}_{+}\), is an even lattice, the above result is true only for \(k=1\). Indeed, according to [26], \(z^{p-1}\) is a non-trivial element in the kernel of f in (1).
In [52], authors proved that the map \(\psi \) is an isomorphism for \(L_{\widehat{\mathrm{sl}_{2}}}(k,0)\) using a PBW-type basis of \(L_{\widehat{\mathrm{sl}_{2}}}(k,0)\) from [42] and Gröbner bases. In [32], the author essentially proved the same result using a technique called the “degeneration procedure". In the following, we briefly explain how his results imply the isomorphism.
Proposition 4.7
The map \(\psi :J_{\infty }(R_{L_{\widehat{\mathrm{sl}_{2}}}(k,0)})\cong \mathrm{gr}^{F}(L_{\widehat{\mathrm{sl}_{2}}}(k,0))\) is an isomorphism of vertex Poisson algebras.
Proof
According to Example 2.10, the \(C_{2}\)-algebra \(R_{L_{\widehat{\mathrm{sl}_{2}}}(k,0)}\) is isomorphic to

It is clear that \(\psi (u_{(-i)})=\overline{u_{(-i)}\mathbf{1 }}\) for \(u\in \{e,f,h\}\) and \(i\in {\mathbb {Z}}_{+}\). Let  where \(u\in \{e,f,h \}\). Now we consider \(e(z)^{k+1}\). The coefficient of \(z^{n}\) equals \(T^{n}(e_{(-1)}^{k+1})\) up to a scalar multiple for \(n\in {\mathbb {N}}\). We have similar results for
where \(u\in \{e,f,h \}\). Now we consider \(e(z)^{k+1}\). The coefficient of \(z^{n}\) equals \(T^{n}(e_{(-1)}^{k+1})\) up to a scalar multiple for \(n\in {\mathbb {N}}\). We have similar results for  . Thus
. Thus

where

stands for the ideal generated by the Fourier coefficients of

It is sufficient to show that

To this end, we use results from [32]. Feigin constructed the following three quotient polynomial algebras, \(B_{k},C_{k}\) and \(D_{k}\):
-
The quotient of the algebra \(B_{k}\) in variables \(e_{-1-i},h_{-1-i},f_{-1-i}\), \(i\in {\mathbb {N}} \), is generated by Fourier coefficients of the series:
$$\begin{aligned}e(z)^{i}h(z)^{k+1-i},\quad i=1,\dots ,k+1,\end{aligned}$$and

-
Let \(u^{[l]}(z)= \sum _{i\in {\mathbb {Z}}_{-}}z^{-1-l}u_{i}^{[l]}\), where \(u=e,h,f\) and \(u_{i}^{[l]}=0\) for \(i>-l\). Then the quotient of the polynomial algebra \(C_{k}\) in variables \(u_{i}^{[l]}\), \(l=1,\dots , k\), is generated by Fourier coefficients of the series:

-
Define a lattice Q generated by vectors \(p_{i},q_{i},r_{i}\in {\mathbb {R}}^{N}\), \(i=1,\dots ,k\), with scalar products:

The algebra \(D_{k}\) is generated from the highest weight vector with the Fourier coefficients of
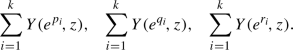
By using certain filtrations [32, Lemmas 3.2, 3.4], one gets
The “degenerate procedures” [32, Lemma 3.5, Proposition 3.1] give us

Combining (3), (4) and the fact that \(\psi \) is surjective, we get (2). \(\square \)
Before we prove the next result, let us fix some notations. Let \({\mathfrak {g}}\) be a finite-dimensional simple Lie algebra of type \(C_{n}, n\geqslant 2\). Here we assume that \({\mathfrak {g}}\) has a basis  . Let \(\theta \) be the maximal root of \({\mathfrak {g}}\), and \(x_{\theta }\) the corresponding maximal root vector. Let \(\widehat{{\mathfrak {g}}}\) be the affine Lie algebra associated with \({\mathfrak {g}}\) and its universal vacuum representation be \(V_{\hat{{\mathfrak {g}}}}(1,0)\) for \(k\in {\mathbb {Z}}_{+}\). Set
. Let \(\theta \) be the maximal root of \({\mathfrak {g}}\), and \(x_{\theta }\) the corresponding maximal root vector. Let \(\widehat{{\mathfrak {g}}}\) be the affine Lie algebra associated with \({\mathfrak {g}}\) and its universal vacuum representation be \(V_{\hat{{\mathfrak {g}}}}(1,0)\) for \(k\in {\mathbb {Z}}_{+}\). Set

where \(U({\mathfrak {g}})\) is the universal enveloping algebra of \({\mathfrak {g}}\), and \(\circ \) is the adjoint action. Then the \(\widehat{{\mathfrak {g}}}\)-module \(V_{\hat{{\mathfrak {g}}}}(1,0)\) has a maximal submodule \(I_{\hat{{\mathfrak {g}}}}(1,0)\) generated by  . Let \(L_{\hat{{\mathfrak {g}}}}(1,0)\) denote the simple quotient \(V_{\hat{{\mathfrak {g}}}}(1,0)/I_{\hat{{\mathfrak {g}}}}(1,0)\). Now we are ready to prove:
. Let \(L_{\hat{{\mathfrak {g}}}}(1,0)\) denote the simple quotient \(V_{\hat{{\mathfrak {g}}}}(1,0)/I_{\hat{{\mathfrak {g}}}}(1,0)\). Now we are ready to prove:
Theorem 4.8
The map \(\psi \) is an isomorphism for the affine vertex algebra \(L_{\hat{{\mathfrak {g}}}}(1,0)\).
Proof
It is clear that the \(C_{2}\)-algebra of \(L_{\hat{{\mathfrak {g}}}}(1,0)\) is  , where \(S({\mathfrak {g}})\) is the symmetric algebra of \({\mathfrak {g}}\). We denote the algebra
, where \(S({\mathfrak {g}})\) is the symmetric algebra of \({\mathfrak {g}}\). We denote the algebra

by Q, where  . Following a similar argument to Proposition 4.7, we see that \(J_{\infty }(R_{L_{\hat{{\mathfrak {g}}}}(1,0)})\cong Q\). In order to show that \(\psi \) is an isomorphism, it is enough to prove that \(\mathrm{gr}^{F}(L_{\hat{{\mathfrak {g}}}}(1,0))\) and Q have the same basis. Notice that
. Following a similar argument to Proposition 4.7, we see that \(J_{\infty }(R_{L_{\hat{{\mathfrak {g}}}}(1,0)})\cong Q\). In order to show that \(\psi \) is an isomorphism, it is enough to prove that \(\mathrm{gr}^{F}(L_{\hat{{\mathfrak {g}}}}(1,0))\) and Q have the same basis. Notice that

We can define an order on all monomials of \({\mathbb {C}}[x^{i}_{(-j)}\,{|}\,j\in {\mathbb {Z}}_{+}]\) in the sense of [49, Section 8]. From the same paper, we know that every non-zero homogeneous polynomial \({\mathbb {C}}[x^{i}_{(-j)}\,{|}\,j\in {\mathbb {Z}}_{+}]\) has a unique largest monomial. For an arbitrary non-zero polynomial u, we define the leading term \(\mathrm{lt}(u)\) as the largest monomial of the non-zero homogeneous component of the smallest degree, which is unique. We denote all monomials in \({\mathbb {C}}[x^{i}_{(-j)}\,{|}\,j\in {\mathbb {Z}}_{+}]\) by  . We clearly have
. We clearly have  as a spanning set of Q. Since \(u=0\) in Q if \(u\in I\), the leading term \(\mathrm{lt}(u)\) equals the linear combination of other terms. Therefore,
as a spanning set of Q. Since \(u=0\) in Q if \(u\in I\), the leading term \(\mathrm{lt}(u)\) equals the linear combination of other terms. Therefore,  is a smaller spanning set of Q. We denote it by
is a smaller spanning set of Q. We denote it by  . Meanwhile according to [49, Theorem 11.3], we know that
. Meanwhile according to [49, Theorem 11.3], we know that  is a basis of
is a basis of  . Together with the surjectivity of \(\psi \), we have that
. Together with the surjectivity of \(\psi \), we have that  is a basis of Q. So \(\psi \) is an isomorphism. \(\square \)
is a basis of Q. So \(\psi \) is an isomorphism. \(\square \)
4.1 \(N=2\) vertex superalgebra at \(c=1\)
In this section we study the simple \(N=2\) superconformal vertex algebra with central charge \(c=1\), denoted by \(L_{1}^{N=2}\). The odd lattice vertex algebra  is known to be isomorphic to \(L_{1}^{N=2}\). Here we identify \(\frac{1}{3}\alpha _{(-1)}\mathbf{1 } \) with \(J_{(-1)}\mathbf{1 }\), \(\frac{1}{\sqrt{3}}e^{\pm \alpha } \) with \(G_{(\pm {3}/{2})}\mathbf{1 }\), and \(\frac{1}{6}(\alpha _{(-1)}\alpha _{(-1)}\mathbf {1} )_{(-1)}\mathbf{1\mathbf } \) with \(L_{(-2)}\mathbf{1 }\).
is known to be isomorphic to \(L_{1}^{N=2}\). Here we identify \(\frac{1}{3}\alpha _{(-1)}\mathbf{1 } \) with \(J_{(-1)}\mathbf{1 }\), \(\frac{1}{\sqrt{3}}e^{\pm \alpha } \) with \(G_{(\pm {3}/{2})}\mathbf{1 }\), and \(\frac{1}{6}(\alpha _{(-1)}\alpha _{(-1)}\mathbf {1} )_{(-1)}\mathbf{1\mathbf } \) with \(L_{(-2)}\mathbf{1 }\).
According to [2, 3], the maximal submodule of \(V_1^{N=2}\) is generated by
Identifying \(G^{+}\) with \(G^{+}_{(-{3}/{2})}\mathbf{1 }\), \(G^{-}\) with \(G^{-}_{(-{3}/{2})}\mathbf{1 }\), and h with \(J_{(-1)}\mathbf{1 }\), we have

For \(J_{\infty }(R_{L^{N=2}_1})\) we identify  with \(G^{+}(-{3}/{2}),G^{-}(-{3}/{2}),h(-1)\). We have
with \(G^{+}(-{3}/{2}),G^{-}(-{3}/{2}),h(-1)\). We have

where  ,
,  . The map \(\psi \) is not an isomorphism in this case because the images of non-zero elements
. The map \(\psi \) is not an isomorphism in this case because the images of non-zero elements

in the jet superalgebra under \(\psi \), i.e., \(G^{+}_{(-{5}/{2})}G^{+}_{(-{3}/{2})}\mathbf{1 }\) and \(G^{-}_{(-{5}/{2})}G^{-}_{(-{3}/{2})}\mathbf{1 }\), are null vectors. Thus

where  and
and  . Let us consider
. Let us consider
We will write down a spanning set of \(J_{\infty }(R_{L^{N=2}_1})/\langle a,b\rangle _{\partial }\). We let the ordered monomial be a monomial of the form

Then we have a complete lexicographic ordering on the set of ordered monomials in the sense of Sect. 3.1. Now let us find the leading terms of the Fourier coefficients of

-
(a)
The leading term of
 :
:-
n is even, the leading term of the coefficient of \(z^{n}\) is

-
n is odd, the leading term of the coefficient of \(z^{n}\) is

-
-
(b)
The leading term of
 :
:-
n is even, the leading term of the coefficient of \(z^{n}\) is

-
n is odd, the leading term of the coefficient of \(z^{n}\) is

-
-
(c)
The leading term of
 :
:-
The leading term of the constant term is

-
n is even and not equal to 0, the leading term of the coefficient of \(z^{n}\) is

-
n is odd, the leading term of the coefficient of \(z^{n}\) is

-
-
(d)
The leading term of \(T^{n}(a)\) or \(T^{n}(b)\):
-
n is even, the leading term is

-
n is odd, the leading term is
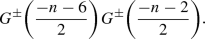
-
Clearly all ordered monomials constitute a spanning set of \(J_{\infty }(R_{L_{1}^{N=2}})/\langle a,b\rangle _{\partial }\). Since all polynomials we considered above equal zero in \(J_{\infty }(R_{L_{1}^{N=2}})/\langle a,b\rangle _{\partial }\), the leading term of each can be written as a linear combination of all other terms. Thus if we want to get a “smaller" spanning set, all above leading terms cannot appear as segments of an ordered monomial. Therefore, we can impose some difference conditions on ordered monomials using these leading terms to get a new spanning set.
Definition 4.9
We call an ordered monomial a Gh-monomial, if it satisfies the following conditions:
-
(i)
Either \(b_i\) or \(c_i\) is 0 and either \(b_i\) or \(c_{i+1}\) is 0,
-
(ii)
either \(a_{i}\) or \(b_{i}\) is 0 and either \(a_i\) or \(b_{i+1}\) is 0,
-
(iii)
\(b_{1}\leqslant 2\), \(a_{1}+c_{2}\leqslant 1\), and \(a_{i}+c_{i}+c_{i+1}\leqslant 1\) for \(i\geqslant 2\),
-
(iv)
\(c_{i}+c_{i+1}+c_{i+2}\leqslant 1\) and \(a_{i}+a_{i+1}+a_{i+2}\leqslant 1\).
Here constraints (i)–(iv) come from the leading terms in (a)–(d), respectively. Then we have the following:
Proposition 4.10
Gh-monomials form a spanning set of
Let us write down the first few terms of the Hilbert series of A.
Example 4.11
For \(i\leqslant 5\), Gh-monomials give us a basis of \(A_{i}\):

We have  . Meanwhile
. Meanwhile

Since in degree 9/2 the dimension of A is bigger than the dimension of  by 1, the induced map
by 1, the induced map

is not injective. It is not hard to see that the 1-dimensional kernel of \(\overline{\psi }\) in degree 9/2 is spanned by

We make the following conjecture:
Conjecture 4.12
The induced map  is an isomorphism.
is an isomorphism.
5 Principal subspaces
Principal subspaces of affine vertex algebras (at least in a special case) were introduced by Feigin and Stoyanovsky [31] and further studied by several people; see [21,22,23,24, 27] and references therein. In [47, 48], Primc studied Feigin–Stoyanovsky type subspaces which are analogs of principal subspaces but easier to analyze. They were further investigated for many integral levels and types [16, 35, 50, 51]. Here we follow notations from [44], where principal subspaces are defined for general integral lattices (not necessarily positive definite). As in [44], we let  denote a lattice vertex algebra. We fix a \({\mathbb {Z}}\)-basis
denote a lattice vertex algebra. We fix a \({\mathbb {Z}}\)-basis  of L. Let \(e^{\alpha _{i}}\) be an element in the group algebra \({\mathbb {C}}[L]\). Then the principal subspace associated to
of L. Let \(e^{\alpha _{i}}\) be an element in the group algebra \({\mathbb {C}}[L]\). Then the principal subspace associated to  and L is defined as
and L is defined as

that is the smallest vertex algebra that contains extremal vectors \(e^{\alpha _i}\). Once  is fixed, we shall drop
is fixed, we shall drop  in the parentheses and write \(W_{L}\) for convenience.
in the parentheses and write \(W_{L}\) for convenience.
Let \({\mathfrak {g}}\) be a simple finite-dimensional complex Lie algebra of type A, D or E, and \({\mathfrak {h}}\) be a Cartan subalgebra of \({\mathfrak {g}}\). We choose simple roots \(\{\alpha _{1},\dots ,\alpha _{n}\}\) of \(({\mathfrak {g}},{\mathfrak {h}})\), and let \(\Delta ^{+}\) denote the set of positive roots. Let  be a rescaled Killing form on \({\mathfrak {g}}\) such that \((\alpha _{i},\alpha _{i})=2\) for \(i=1,\dots ,n\) (as usual we identify \({\mathfrak {h}}\) and \({\mathfrak {h}}^{*}\) via the Killing form). Fundamental weights of \({\mathfrak {g}}\), \(\{\omega _{1},\dots , \omega _{n}\}\subset {\mathfrak {h}}^{*}\), are defined by
be a rescaled Killing form on \({\mathfrak {g}}\) such that \((\alpha _{i},\alpha _{i})=2\) for \(i=1,\dots ,n\) (as usual we identify \({\mathfrak {h}}\) and \({\mathfrak {h}}^{*}\) via the Killing form). Fundamental weights of \({\mathfrak {g}}\), \(\{\omega _{1},\dots , \omega _{n}\}\subset {\mathfrak {h}}^{*}\), are defined by  , \(1\leqslant i,j \leqslant n\).
, \(1\leqslant i,j \leqslant n\).
Let \({\mathfrak {n}}_+\) be \( \coprod _{\alpha \in \Delta ^{+}}{\mathbb {C}}x_{\alpha }\), where \(x_{\alpha }\) is a corresponding root vector, and  is its affinization. For an affine vertex algebra \(L_{\hat{{\mathfrak {g}}}}(k,0)\), \(k \ne -h^\vee \), which is isomorphic to \(L(k \Lambda _0)\) as \(\hat{{\mathfrak {g}}}\)-modules, we define the (FS)-principal subspace of the simple \(\widehat{{\mathfrak {g}}}\)-module \(L_{\hat{{\mathfrak {g}}}}(k,0)\) as
is its affinization. For an affine vertex algebra \(L_{\hat{{\mathfrak {g}}}}(k,0)\), \(k \ne -h^\vee \), which is isomorphic to \(L(k \Lambda _0)\) as \(\hat{{\mathfrak {g}}}\)-modules, we define the (FS)-principal subspace of the simple \(\widehat{{\mathfrak {g}}}\)-module \(L_{\hat{{\mathfrak {g}}}}(k,0)\) as

where \({\mathbb {1}}\) is the vacuum vector. It is easy to see that this is a vertex algebra (without conformal vector). For \(k=1\), we have \(W_L \cong W_{\Lambda _{1,0}}\), where L is the root lattice spanned by simple roots.
We fix a fundamental weight \(\omega =\omega _m\) and set

where \( \Delta \) is the root system of \({\mathfrak {g}}\), and \({\mathfrak {g}}_{1}:=\coprod _{\alpha \in \Gamma }\) \({\mathfrak {g}}_{\alpha }\), where \({\mathfrak {g}}_{\alpha }\) is the \(\alpha \)-root space. This Lie algebra is commutative. We let  be \(\widehat{{\mathfrak {g}}_{1}}\). Then we can define the so-called Feigin–Stoyanovsky type subspace of \(L_{\hat{{\mathfrak {g}}}}(k,0)\) as
be \(\widehat{{\mathfrak {g}}_{1}}\). Then we can define the so-called Feigin–Stoyanovsky type subspace of \(L_{\hat{{\mathfrak {g}}}}(k,0)\) as

Unlike the FS subspace, this vertex subalgebra is commutative. We denote

Notice that \(U(\widehat{{\mathfrak {g}}}_1)\cong {\mathbb {C}}[\widetilde{\Gamma }]\). Therefore, we can identify the elements in \(W'_{\Lambda _{k,0}}\) with the elements in \({\mathbb {C}}[\widetilde{\Gamma }^{-}]\). For any element in \(W'_{\Lambda _{k,0}}\),
we define the colored weight as

for the later use.
5.1 Root lattices of type A
Following the notations in [23], we can prove the following result.
Proposition 5.1
For \({\mathfrak {g}}=\mathrm{sl}_{2}\), we have  for \(k\in {\mathbb {Z}}_{+}\).
for \(k\in {\mathbb {Z}}_{+}\).
Proof
It is clear that  . The result follows from [23, Theorem 3.1]. \(\square \)
. The result follows from [23, Theorem 3.1]. \(\square \)
Remark 5.2
When \(k=1\), \(W_{\Lambda _{1,0}}\) of type A is isomorphic to \(J_{\infty }({\mathbb {C}}[x]/\langle x^{2}\rangle )\). Using different methods to calculate the Hilbert–Poincaré series, see [20] and [15], one can derive the famous Rogers–Ramanujan identities.
For the rest of this subsection, we let L be the \(A_{n-1}\) root lattice with the rescaled Killing form  such that \((\alpha ,\alpha )=2\) for any root and the standard \({\mathbb {Z}}\)-basis \(\alpha _1,\dots , \alpha _{n-1}\) of simple roots. We are going to prove that \(\psi \) is an isomorphism for the principal subspace \(W_{L}\) corresponding to this basis. In the following, we will identify \(W_{L}\) and \(W_{\Lambda _{1,0}}\).
such that \((\alpha ,\alpha )=2\) for any root and the standard \({\mathbb {Z}}\)-basis \(\alpha _1,\dots , \alpha _{n-1}\) of simple roots. We are going to prove that \(\psi \) is an isomorphism for the principal subspace \(W_{L}\) corresponding to this basis. In the following, we will identify \(W_{L}\) and \(W_{\Lambda _{1,0}}\).
Proposition 5.3
Given elements \(\alpha \), \(\beta \), \(\gamma \) and \(\tau \) in the lattice L, we have


Proof
From the definition of vertex operators in [36], we have

where \(\epsilon (\alpha ,\beta )\) is a 2-cocycle constant. We have

since the minimal power of z above is greater than 0. The coefficients of \(z^{0}\) of  and
and  are
are  and
and  . The identity (6) follows from this fact and the given condition. \(\square \)
. The identity (6) follows from this fact and the given condition. \(\square \)
It is clear that all quotient relations in \(R_{L_{\widehat{\mathrm{sl}_{n}}}(1,0)}\) come from (5) and (6). Thus \(R_{L_{\widehat{\mathrm{sl}_{n}}}}(1,0) \cap {\mathbb {C}}[E_{i,j}\,{|}\,1\leqslant i<j\leqslant n]=R_{W_{L}}\).
We let \(E_{i,j}\) be the (i, j)-th elementary matrix. Therefore, \(\{E_{i,j}\}_{1\leqslant i<j\leqslant n}\) is the set of all positive root vectors. It is not hard to see that the \(C_{2}\)-algebra \(R_{W_{L}}\) equals \({\mathbb {C}}[E_{i,j}\,{|}\,1\leqslant i<j\leqslant n]/I\), where we denote the equivalence class of \((E_{i,j})_{(-1)}\mathbf{1 }\) by \(E_{i,j}\). In [28, Corollary 2.7] (see also [31] for \({\mathfrak {g}}=\mathrm{sl}_{3}\)), authors wrote down the graded decomposition of \(R_{L_{\widehat{\mathrm{sl}_{n}}}(1,0)}\). By restricting it to its principal subspace, we have:
Proposition 5.4
The \(C_{2}\)-algebra of \(W_{L}\) equals

where \(1\leqslant i_{1}\leqslant i_{2}\leqslant n\) and \(1\leqslant j_{1}\leqslant j_{2}\leqslant n\).
Moreover, we have the following combinatorial q-identity which will be proven in a joint work with Milas [39], where we also establish more general identities.
Theorem 5.5
(Li–Milas) Let A be the Cartan matrix  of type \(A_{n-1}\), \(n \geqslant 2\), and
of type \(A_{n-1}\), \(n \geqslant 2\), and
Then we have

where

Example 5.6
For \(\mathrm{sl}_{4}\), we have the following q-series identity:

where we use multiindices \(\mathbf{n }=(n_{1},n_{2},\dots ,n_{6})\) and \(\mathbf{k }=(k_1,k_2,k_3)\). Upon the following replacement:
we recover the formula in Theorem 5.5.
Now we are ready to prove:
Theorem 5.7
The map \(\psi \) is an isomorphism between \(J_{\infty }(R_{W_{L}})\) and  .
.
Proof
From Proposition 5.4, we know that \(J_{\infty }(R_{W_{L}})\) is isomorphic to

where  and \(1\leqslant i_{1}\leqslant i_{2}\leqslant n\), \(1\leqslant j_{1}\leqslant j_{2}\leqslant n\). In order to simplify notation, we first order \(\{E_{i,j}\}_{1\leqslant i<j \leqslant n}\) as
and \(1\leqslant i_{1}\leqslant i_{2}\leqslant n\), \(1\leqslant j_{1}\leqslant j_{2}\leqslant n\). In order to simplify notation, we first order \(\{E_{i,j}\}_{1\leqslant i<j \leqslant n}\) as
and denote this sequence by \(\{E_{m}\}_{1\leqslant m \leqslant {n(n-1)}/{2}}\) (i.e., \(E_1=E_{1,2}\), \(E_2=E_{1,3}\) etc.). We then have a spanning set of jet algebras with each element of the form
where \(1\leqslant n_{m}^{k_{m}}\leqslant \cdots \leqslant n_{m}^{1}\) for \(1\leqslant m\leqslant {n(n-1)}/{2}\). Here \(k_{s}=0\) when we do not have terms involving \(E_{s}\). Now we can reduce this spanning set by using quotient relations as follows:
-
(difference two condition at distance 1) If we have \(E_{m}(z)^{2}=0\) in the quotient of the jet algebra, then we can impose the condition \(n_{m}^{p}\geqslant n_{m}^{p+1}+2\), \(1\leqslant p\leqslant k_{m}-1 \), on the above spanning set.
-
(boundary condition) If we have \(E_{s}(z)E_{t}(z)+\cdots =0\), \(s<t\), we can impose the condition \(n_{s}^{k_{s}}\geqslant k_{t}+1\).
Therefore, we have a reduced spanning set which implies

It is well known that

Surjectivity of \(\psi \) and identity (7) together imply that \(\psi \) is an isomorphism and the image of above spanning set under \(\psi \) is a basis of \(W_{L}\). \(\square \)
Remark 5.8
By a result in [44], we can write down a basis of \(W_{L}\) using \((e^{\alpha _{i}})_{(j)}\), where \(\alpha _{i}\) is a simple root of \(\mathrm{sl}_{n}\) and j can be greater than or equal to 0. If we want the subscript j to be always less than 0, we have to include \((e^{\beta })_{(j)}\), where \(\beta \) is a positive root. It is clear that \(E_{m}=E_{i_{m},j_{m}}\) is a root vector of a positive root

The above proposition gives us a new basis of \(W_{L}\):
where \(M={n(n-1)}/{2}\), \(n_{M}^{k_{M}}\in {\mathbb {Z}}_{+}\), \(n_{m}^{p}\geqslant n_{m}^{p+1}+2\), \(1\leqslant p\leqslant k_{m}-1\), and \(n_{s}^{k_{s}}\geqslant k_{t}+1\) if \(1\leqslant s<t\leqslant M\), \(i_t<j_{s}\leqslant j_{t}\).
5.2 Feigin–Stoyanovsky type subspaces
In this section, we consider Feigin–Stoyanovsky type subspaces of affine vertex algebras of type \(A_{n}\) at level 1. We first consider the special case when \(\omega =\omega _{1}\). For any element of the \(A_{n}\) root lattice, \(\alpha =m_{1}\alpha _1+m_{2}\alpha _2+\cdots +m_{n}\alpha _n\), we define a subspace of \(W'_{\Lambda _{1,0}}\) as  . It is not hard to see that \((W'_{\Lambda _{1,0}})^{\alpha }\) is non-trivial if and only if \(m_1 \geqslant m_2\geqslant \cdots \geqslant m_n\geqslant 0\). According to [51, (3.8)], we have
. It is not hard to see that \((W'_{\Lambda _{1,0}})^{\alpha }\) is non-trivial if and only if \(m_1 \geqslant m_2\geqslant \cdots \geqslant m_n\geqslant 0\). According to [51, (3.8)], we have

Then

Moreover, in this case,
Note that

is a lattice with basis \(\{\beta _1,\dots ,\beta _n\}\). Then we have
It is not hard to see that

According to Proposition 5.3, we have that the \(C_{2}\)-algebra of \(W_L\) is

By a similar argument as in the previous section, we get

which implies isomorphism between \(J_{\infty }(R_{W'_{\Lambda _{1,0}}})\) and  . Similarly we can prove isomorphism in cases where \(\omega =\omega _{i}\), \(2\leqslant i\leqslant n\), using [51, (3.21)].
. Similarly we can prove isomorphism in cases where \(\omega =\omega _{i}\), \(2\leqslant i\leqslant n\), using [51, (3.21)].
5.3 Principal subspaces and jet algebras from graphs
In this part we study principal subspaces and jet algebras coming from graphs. We begin from any graph G with k vertices and possibly with loops (and for simplicity we assume no double edges). We denote the vertices of G by \(\{v_1,v_2,\dots ,v_k\}\). We denote by \(\Gamma :=\Gamma (G)\) the (symmetric) incidence matrix of G and by  the rank k lattice with basis \(\alpha _1,\dots ,\alpha _k\) such that
the rank k lattice with basis \(\alpha _1,\dots ,\alpha _k\) such that  . The incidence matrix of the graph induces a quadratic form
. The incidence matrix of the graph induces a quadratic form

where we sum over all edges E(G). Out of monomials appearing in the sum we form the jet algebra \(J_\infty (R_\Gamma )\), where

We let \(W_{L(\Gamma )} \subset V_{L(\Gamma )}\) be the principal subspace corresponding to \(\{e^{\alpha _i} \}_{i=1}^k\) inside the lattice vertex algebra \(V_{L(\Gamma )}\). For simplicity we write \(W_\Gamma \) for \(W_{L(\Gamma )}\).
Example 5.9
Consider the graph \(\circ -\circ -\circ \). Then \(\Gamma =\left[ {\begin{matrix} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \end{matrix}}\right] \), and  where
where  with \(\langle \alpha _1,\alpha _2 \rangle =\langle \alpha _2,\alpha _3 \rangle =1\) (zero otherwise), \(R_\Gamma ={\mathbb {C}}[x_1,x_2,x_3]/(x_1 x_2, x_2 x_3)\), and \(Q(x_1,x_2,x_3)=x_1 x_2+x_2 x_3\).
with \(\langle \alpha _1,\alpha _2 \rangle =\langle \alpha _2,\alpha _3 \rangle =1\) (zero otherwise), \(R_\Gamma ={\mathbb {C}}[x_1,x_2,x_3]/(x_1 x_2, x_2 x_3)\), and \(Q(x_1,x_2,x_3)=x_1 x_2+x_2 x_3\).
Theorem 5.10
If the bilinear form associated with \(\Gamma \) is non-degenerate, that is \(\Gamma \) is invertible, then there exists a unique conformal vector in the lattice vertex algebra such that eigenvalue of \(L_{(0)}\) defines a grading such that

Moreover, the character is given by

Proof
Clearly, we have the standard conformal vector in the lattice vertex algebra given by \(\omega _{\mathrm{st}}=\frac{1}{2}\sum _{i=1}^{n}u^{(i)}_{(-1)}u^{(i)}_{(-1)}\mathbf{1 }\), where  is an orthonormal basis with respect to the bilinear form associated with \(\Gamma \). We know that
is an orthonormal basis with respect to the bilinear form associated with \(\Gamma \). We know that

It is clear that by adding a linear combination of \(\{(\alpha _{i})_{(-2)}\mathbf{1 }\}_{i=1}^{n}\), we will still get a conformal vector. Now assume that \(\omega _{\mathrm{st}}+\sum _{i=1}^{n}a_{i}(\alpha _{i})_{(-2)}\mathbf{1 }\), where \(a_{i}\in {\mathbb {C}}\), would give us expected weights. Then we have a system of linear equations. The non-degeneracy of the bilinear form implies that there is a unique solutions set. Thus we always have a conformal vector with the grading:

Applying [44, Corollary 4.14], we can write a combinatorial basis of \(W_{\Gamma }\). Now let us use this basis to write down the character. Firstly, the generating function of a colored partition into \((n_{1},n_{2},\dots ,n_{k})\) parts is \(\frac{1}{(q)_{n_{1}}\cdots (q)_{n_{k}}}\). It is clear that

where \(f_{(n_1,\dots ,n_k)}\) is the vector in \(W_{\Gamma }\) of charge \((n_{1},\dots ,n_{k})\) with the minimal weight. For the \(n_{i}\)-th part, there is a unique element \(u_{n_{i}}\) of the minimal weight which is

The weight of \(u_{n_{i}}\) is

Therefore,

Thus we proved the claimed identity. \(\square \)
Remark 5.11
If the lattice L is degenerate, then \(V_L\) has no conformal vector which can give us expected weights. But we can still view \(W_L\) as a graded vertex algebra, if we define the degree of \(e^{\alpha _{i}}\) as above. Then the character formula is still valid for singular \(\Gamma \).
Before we prove the next result, let us generalize [46, Theorem 4.3.1].
Proposition 5.12
We have an isomorphism

Proof
First, we define a map \(\pi \) from

to  by sending \(x_{i}(p)\) to \(e^{\alpha _{i}}_{(p)}\mathbf {1}\). We denote the ideal
by sending \(x_{i}(p)\) to \(e^{\alpha _{i}}_{(p)}\mathbf {1}\). We denote the ideal

by \(I_{\Gamma }\). We can use the same argument as in [46] to show that  .
.
We prove that  by contradiction. Suppose there exists an element \(a\in {\mathbb {C}}[x_{i}(p)\,{|}\,i=1,\dots ,k, p\in {\mathbb {Z}}_{-}]\) such that
by contradiction. Suppose there exists an element \(a\in {\mathbb {C}}[x_{i}(p)\,{|}\,i=1,\dots ,k, p\in {\mathbb {Z}}_{-}]\) such that  and \(a\notin I_{\Gamma }\). Suppose a is homogeneous with respect to weight and charge. Choose r such that a contains some element \(x_{r}(p)\) as a factor. We assume that a has the minimum weight among all elements that satisfy the above conditions. Again by the same argument as in [46], this a can be written as \(bx_{r}(-1) \), where \(b\in {\mathbb {C}}[x_{i}(p)\,{|}\,i=1,\dots ,k, p\in {\mathbb {Z}}_{-}]\). We shall prove the case when \(\langle \alpha _{r},\alpha _{r} \rangle =0\). For other cases, it is proved in [46]. Firstly we define a map \(\mathbf{e}^{\alpha _\mathbf{r}}:W_{\Gamma }\rightarrow W_{\Gamma }\) as
and \(a\notin I_{\Gamma }\). Suppose a is homogeneous with respect to weight and charge. Choose r such that a contains some element \(x_{r}(p)\) as a factor. We assume that a has the minimum weight among all elements that satisfy the above conditions. Again by the same argument as in [46], this a can be written as \(bx_{r}(-1) \), where \(b\in {\mathbb {C}}[x_{i}(p)\,{|}\,i=1,\dots ,k, p\in {\mathbb {Z}}_{-}]\). We shall prove the case when \(\langle \alpha _{r},\alpha _{r} \rangle =0\). For other cases, it is proved in [46]. Firstly we define a map \(\mathbf{e}^{\alpha _\mathbf{r}}:W_{\Gamma }\rightarrow W_{\Gamma }\) as

Then we lift this map to

which is defined as

Since  , \(\pi (a)=\pi (bx_{r}(-1))=0\). Then
, \(\pi (a)=\pi (bx_{r}(-1))=0\). Then
which implies that  . If \(b\in I_{\Gamma }\), then \(a=\mathbf{x_{r}}(b)\in \mathbf{x_{r}}I_{\Gamma }\in I_{\Gamma }\) which contradicts our assumption. If \(b\notin I_{\Gamma }\), then b is an element such that
. If \(b\in I_{\Gamma }\), then \(a=\mathbf{x_{r}}(b)\in \mathbf{x_{r}}I_{\Gamma }\in I_{\Gamma }\) which contradicts our assumption. If \(b\notin I_{\Gamma }\), then b is an element such that  and \(b\notin I_{\Gamma }\) but with the weight strictly less than the weight of a. This also contradicts our assumption. Thus we proved the claim. \(\square \)
and \(b\notin I_{\Gamma }\) but with the weight strictly less than the weight of a. This also contradicts our assumption. Thus we proved the claim. \(\square \)
Theorem 5.13
We have

Proof
From the definition of a jet superalgebra, we know that

where \(c_{m}^{l}\) is a constant coefficient. Therefore,

has quotient relation

Together with Proposition 5.12, we get an isomorphism of differential algebras induced from the map \(\psi :x_{i}(-1)\rightarrow y_{i}(-1)\). \(\square \)
When \(\langle \alpha _{i},\alpha _{i}\rangle =1\), we increase the degree of \(y_{i}(-1) \) by 1/2. Then clearly we have

5.4 Positive lattices
Given a lattice L of rank n with a \({\mathbb {Z}}\)-basis \(\{\alpha _i\}_{i=1}^{n}\), we say that the basis is positive if we have  for \(1\leqslant i\leqslant j\leqslant n\). In this part, we study principal subspaces associated with positive bases. The examples we studied in the previous two sections are such principal subspaces. Now let us prove a more general result about the map \(\psi \) and these principal subspaces.
for \(1\leqslant i\leqslant j\leqslant n\). In this part, we study principal subspaces associated with positive bases. The examples we studied in the previous two sections are such principal subspaces. Now let us prove a more general result about the map \(\psi \) and these principal subspaces.
Theorem 5.14
For a lattice L of rank n with a positive basis, the map \(\psi \) is an isomorphism for \(W_{L}\) if and only if its positive basis satisfies \(\langle \alpha _{i},\alpha _{i}\rangle =0\) or 1 or 2, and  or 1.
or 1.
Proof
First let us assume that the positive basis of the lattice L satisfies given conditions. According to Theorem 5.13, we know that when \(\langle \alpha _{i},\alpha _{i}\rangle =0\) or 1, and  or 1, the map \(\psi \) is an isomorphism for the principal subspace. Now the only case we need to consider is the positive basis for which
or 1, the map \(\psi \) is an isomorphism for the principal subspace. Now the only case we need to consider is the positive basis for which  . It is not hard to see that \(J_{\infty }({\mathbb {C}}[x]/\langle x^{2}\rangle )\) has a basis
. It is not hard to see that \(J_{\infty }({\mathbb {C}}[x]/\langle x^{2}\rangle )\) has a basis

Thus \(J_{\infty }({\mathbb {C}}[x_{1},x_{2}, \dots , x_{n}]/\langle x_{1}^{2},x_{2}^{2}, \dots , x_{n}^{2}\rangle )\) has a basis

Note that the \(C_{2}\)-algebra of \(W_{L}\) is
Now, the map \(\psi \) sends \((x_{i})_{(-1)}\) to \((e^{\alpha _i})_{(-1)}{} \mathbf{1}\). According to [44, Corollary 4.14], the image of the basis of \(J_{\infty }(R_{W_{L}})\) is a basis of  . Thus the map \(\psi \) is an isomorphism.
. Thus the map \(\psi \) is an isomorphism.
Next, let us prove that if a basis does not satisfy the given conditions, the map \(\psi \) is not an isomorphism. We will consider two cases:
-
Suppose that for one simple root \(\alpha _{i}\), we have \(\langle \alpha _{i},\alpha _{i}\rangle \geqslant 3\). Without loss generality, we prove that \(\psi \) is not an isomorphism when lattice \(L={\mathbb {Z}}\alpha _{i}\). In this case, from [44, Corollary 4.14], the basis of \(\mathrm{gr}^{F}(W_{L})\) is
 (8)
(8)It is clear that neither \(J_{\infty }({\mathbb {C}}[x]/(x^{2}))\) nor \(J_{\infty }(\bigwedge [x])\) has the same corresponding basis (here \(\bigwedge \) denotes the exterior algebra). Indeed, for the jet algebra \(J_{\infty }({\mathbb {C}}[x]/(x^{2}))\) we have two monomials of degree 4 with two variables, i.e., \(x_{(-1)}x_{(-3)}\) and \(x_{(-2)}x_{(-2)}\). But we only have one quotient relation of degree 4 involving these two monomials, i.e., \(x_{(-2)}x_{(-2)}+x_{(-1)}x_{(-3)}=0\). Therefore, either \(x_{(-1)}x_{(-4)}\) or \(x_{(-2)}x_{(-2)}\) should be a basis element. But we do not have such corresponding element in (8). A similar argument works for \(J_{\infty }(\bigwedge [x])\).
-
Suppose that there exist two distinct roots
 , \(i<j\), such that
, \(i<j\), such that  . Without loss of generality, we assume
. Without loss of generality, we assume  , then the basis of \(J_{\infty }(W_L)\) is
, then the basis of \(J_{\infty }(W_L)\) is 
Meanwhile, according to [44, Corollary 4.14], the image of this basis under \(\psi \) strictly contains the basis of \(W_{L}\). We do not have an isomorphism.
Thus we proved the statement. \(\square \)
5.5 New character formulas for 
If the graph \(\Gamma \) is a Dynkin diagram of type \(A_k\) or \(C_k\) (cycle of length k) we expect that the generating series \(\mathrm{HS}_{q}(J_{\infty }(R_{\Gamma }))\) has much better combinatorial behavior and perhaps even mock modular properties. We now present “sum of tails" formulas for \(\mathrm{HS}_{q}(J_{\infty }(R_{A_k}))\) for several low “rank" cases. To simplify notation we let
From Theorem 5.10 we have a fermionic formula

The next formulas have been established recently by Jennings-Shaffer and Milas [34].
Theorem 5.15
We have
-
\({A_2(q)= \frac{1}{(1-q)(q)_\infty }}\),
-
\({A_3(q)=q^{-1} \left( \frac{1}{(q)^2_\infty }- \frac{1}{(q)_\infty } \right) }\),
-
\({A_4(q)=\frac{q^{-1}}{(q)_\infty ^2}\sum _{n\geqslant 1}\frac{q^n}{1-q^n}}\),
-
\({A_5(q)=\frac{1}{(q)_\infty ^2}\sum _{n\in {\mathbb {N}}}\frac{q^n}{(q)_{n}(1-q^{n+1})^2}}\),
-
\({A_6(q)=\frac{1}{(q)_\infty ^2}\sum _{n,m\in {\mathbb {N}}}\frac{q^{n+m+nm}}{(q)_{n+1}(q)_{m+1}}}\).
Moreover, for cyclic \(C_k\)-graphs we have fermionic formulas for \(C_k(q):=\mathrm{HS}_{q}(J_{\infty }(R_{C_k}))\) valid for \(k \geqslant 3\),

Again we have partial results for “bosonic" representations for 3- and 5-cycle graphs [34].
Proposition 5.16
([34, Proposition 6.1 and Section 7]) We have

5.6 Combinatorial interpretation
Next we present combinatorial interpretations of formulas in Theorem 5.15 and Proposition 5.16. For simplicity, in several formulas we factored out a (power of) Euler factor which can be easily interpreted as the number of (colored) partitions.
Theorem 5.17
We have:
-
\(A_2(q)\) counts the number of partitions of 2n with all parts either even or equal to 1.
-
\(q A_3(q)\) counts the number of partitions of \(n+1\) into two kinds of parts with the first kind of parts used in each partition.
-
\(q (q)_\infty A_4(q)\) counts the total number of parts in all partitions of n, which is also the sum of largest parts of all partitions of n.
-
\((q)_\infty ^2 A_5(q)\) is the sum of the numbers of times that the largest part appears in each partition of n.
-
\(q (q)_\infty ^2 A_6(q)\) counts twice the total number of parts in all partitions of n minus the number of partitions of n.
-
\((q)_\infty C_3(q)\) counts the number of partitions of n such that twice the least part is bigger than the greatest part.
-
\(q (q)_\infty C_5(q)\) counts the sum of all parts of all partitions of n, also known as np(n).
Proof
For \(A_2(q)\), observe that \(\mathrm{Coeff}_{q^{n}}A_2(q)=p(1)+p(2)+\cdots + p(n)\), where p(i) is the number of partitions of i. The number of 1’s must be even, say 2k, so we have to compute the number of partitions of \(2n-2k\) where all parts are even. This is given by \(p(n-k)\). Then summing over k gives the claim.
The interpretation for the \(A_3(q)\) series is clear because we can also write
Extracting the coefficient on the right-hand side gives \(p_2(n)-p(n)\), where \(p_2(i)\) denotes the number of two colored partitions.
For \(A_4(q)\), this can be seen from the identity

which follows by taking the \(\bigl (x \frac{d}{d}\bigr )\) derivative of \(\frac{1}{(xq;q)_\infty }=\sum _{n \in {\mathbb {N}}} \frac{x^n q^n}{(q)_n}\). This clearly counts the total number of parts in all partitions of n.
The \((q)_\infty ^2 A_5(q)\) case has already been discussed in [34].
For \((q)_\infty ^2 A_6(q)\), this follows from another identity given in [34]:
together with a previous observation that \( \frac{\sum _{n \in {\mathbb {Z}}_{+}}\frac{q^n}{1-q^n}}{(q)_\infty }\) counts the total number of parts in all partitions of n.
For \((q)_\infty C_3(q)\) we use a well-known interpretation for the fifth order mock theta function, and finally for \((q)_\infty C_5(q)\) we observe the formula

as claimed. \(\square \)
Remark 5.18
It is interesting to observe that the numerators of \(C_3(q)\) and \(C_5(q)\) are mock modular forms, and thus \(C_3(q)\) and \(C_5(q)\) are mixed mock. Completion of the Ramanujan fifth order mock theta function \(\sum _{n \in {\mathbb {N}}} \frac{q^n}{ (q^{n+1})_{n+1}} \) is well-documented [19]. For \(\sum _{n \in {\mathbb {Z}}_{+}} \frac{nq^n}{1-q^n}\) we only have to observe that adding \(-{1}/{24}\) to the numerator gives \(E_2(\tau )\), the weight 2 quasimodular Eisenstein series, which is known to be mock.
6 \(N=1\) superconformal vertex algebras
In this section we consider rational \(N=1\) vertex superalgebras \(L_{c_{2,4k}}^{N=1}\), \(k\in {\mathbb {Z}}_{+}\), associated to \(N=1\) superconformal (2, 4k)-minimal models [1]. Here the central charge is \(c_{2,4k}=\frac{3}{2}\bigl (1-\frac{2(4k-1)^{2}}{8k}\bigr )\).
According to [41, 43], the normalized character of \(L_{c_{2,4k}}^{N=1}\) (without the \(q^{-c/24}\) factor) is

The fermionic character formula is the generating function (cf. [41])

of the number of partitions of \(D_{k,1}(n)\) of n/2 in the form \({n}/{2}=b_{1}+\cdots +b_{m}\),  , where \(b_{1},\dots , b_{m}\) satisfy the following conditions:
, where \(b_{1},\dots , b_{m}\) satisfy the following conditions:
-
no half-odd integer is repeated,
-
 , \(b_{m}\in \frac{3}{2}{\mathbb {Z}}_{+}\),
, \(b_{m}\in \frac{3}{2}{\mathbb {Z}}_{+}\), -
 if
if  ,
, -
 if
if  .
.
Since the \(N=1\) vertex superalgebra \(L_{c_{2,4}}^{N=1}\) is isomorphic to \({\mathbb {C}}\), we only need to consider \(L_{c_{2,4k}}^{N=1}\), where \(k>1\). First let us find the \(C_2\)-algebra of \(L_{c_{2,4k}}^{N=1}\). According to [43, Section 4], the null vector in the universal algebra which survives inside the \(C_{2}\)-algebra is \(L_{(-2)}^{k-1}G_{(-{3}/{2})}\mathbf{1 }\). Moreover, if we let \(G_{(-{1}/{2})}\) act on the null vector, we get another null vector which survives in the \(C_{2}\)-algebra, i.e., \(L_{(-2)}^{k}\mathbf{1 }\). These two null vectors in the vacuum algebra generate the whole quotient ideal of \(R_{L_{c_{2,4k}}^{N=1}}\). Thus \(R_{L_{c_{2,4k}}^{N=1}}\) is isomorphic to the superalgebra  , where g is an odd element.
, where g is an odd element.
We are going to prove that \(\psi \) is an isomorphism. We identify l, g with \(l(-2)\), \(g(-{3}/{2})\), respectively, inside the jet superalgebra.
It is clear that  is isomorphic to
is isomorphic to

 ,
,  and
and  is the ideal generated by the Fourier coefficients of
is the ideal generated by the Fourier coefficients of  . We define an ordered monomial in
. We define an ordered monomial in  to be a monomial of the form
to be a monomial of the form
where \(n\in {\mathbb {N}}\). Then we have a complete lexicographic ordering on all ordered monomials according to Sect. 3.1.
We know that all ordered monomials constitute a spanning set of the jet superalgebra. Following an argument similar to the one in Sect. 4.1, we can make use of the quotient relation to impose some conditions on the spanning set to get a smaller spanning set. Firstly, since all variables g(k)’s are odd, no two g(k) can appear in the ordered monomial. The leading term of any coefficient of \(z^{nk}\) in \(l(z)^{k}\) is \(l(-2-n)^{k}\). Thus \(l(-2-n)^{k}\) should not appear as a segment of any element in the spanning set. Similarly we can list further leading terms in the quotient:
-
The leading term of the coefficient of \(z^{nk}\) in \(l(z)^{k-1}g(z)\) is
$$\begin{aligned} l(-2-n)^{k-1}g\biggl (-\frac{3}{2}-n\biggr ). \end{aligned}$$ -
The leading term of the coefficient of \(z^{n(k-1-i)+(n-1)i+n}\) in \(l(z)^{k-1}g(z)\) is

Now we obtain a smaller spanning set, where the above three type leading terms cannot appear inside any ordered monomial. More precisely, any element in this spanning set is of the form
where \(b_{i}\geqslant b_{i+1}\), \(w(a)=l(a)\) if \(a\in {\mathbb {Z}}\) and \(w(a)=g(a)\) if \(a\in \frac{1}{2}{\mathbb {Z}}\). The fact that g(a) is odd implies that no half-odd-integer is repeated in \(\{b_{1},b_{2},\dots ,b_{m}\}\). Moreover, we have a condition

because

are leading terms of some elements in the quotient ideal. We also have a condition

because

is the leading term of some element in the quotient ideal. So we have

Meanwhile, the surjectivity of \(\psi \) implies that

Thus  , and \(\psi \) is an isomorphism. It implies that the above spanning set is a basis of the jet superalgebra. The image of the basis of jet superalgebra under the map \(\psi \) is a basis of
, and \(\psi \) is an isomorphism. It implies that the above spanning set is a basis of the jet superalgebra. The image of the basis of jet superalgebra under the map \(\psi \) is a basis of  [41].
[41].
We have following result which is a super-analog of [52, Theorem 16.13]:
Theorem 6.1
Let  satisfy that \(({p'-p})/{2}\) and p are coprime positive integers. Let \(L_{c_{p,p'}}^{N=1}\) be the simple \(N=1\) vertex superalgebra associated with the \(N=1\) superconformal \((p,p')\)-minimal model of central charge \(c_{p,p'}=\frac{3}{2}\bigl (1-\frac{2(p'-p)^{2}}{pp'}\bigr )\). Then the map \(\psi \) is an isomorphism if and only if \((p,p')=(2,4k)\), \(k\in {\mathbb {Z}}_{+}\).
satisfy that \(({p'-p})/{2}\) and p are coprime positive integers. Let \(L_{c_{p,p'}}^{N=1}\) be the simple \(N=1\) vertex superalgebra associated with the \(N=1\) superconformal \((p,p')\)-minimal model of central charge \(c_{p,p'}=\frac{3}{2}\bigl (1-\frac{2(p'-p)^{2}}{pp'}\bigr )\). Then the map \(\psi \) is an isomorphism if and only if \((p,p')=(2,4k)\), \(k\in {\mathbb {Z}}_{+}\).
Proof
We first consider the \(C_2\)-algebra of \(L_{c_{p,p'}}^{N=1}\). We let
When p and \(p'\) are both even, according to [43, Section 4], there are two null vectors which survive in \(R_{V_{c_{p,p'}}^{N=1}}\), i.e., \(L_{(-2)}^{|c_{p,p'}|}\mathbf{1 }\) and \(L_{(-2)}^{|c_{p,p'}|-1}G_{-{3}/{2}}\mathbf{1 }\). They generate the quotient ideal of \(R_{V_{c_{p,p'}}^{N=1}}\) in the vacuum algebra. In this case, the \(C_{2}\)-algebra \(R_{L_{c_{p,p'}}^{N=1}}\) is isomorphic to
When p and \(p'\) are both odd, again from [43, Section 4], the null vector \(L_{(-2)}^{|c_{p,p'}|}\mathbf {1}\) generates the quotient ideal of \(R_{L_{c_{p,p'}}^{N=1}}\). The \(C_{2}\)-algebra is isomorphic to
Suppose p and \(p'\) are both odd. Then

It is clear that \(\mathrm{HS}_{q}(J_{\infty }({\mathbb {C}}[g]))=\prod _{i \in {\mathbb {Z}}_{+}} (1+q^{i+1/2})\). According to [29], we get

where \(L_{\mathrm{Vir}}(c_{2,{(p-1)(p'-1)}/{2}+1},0)\) is the simple Virasoro vertex algebra coming from the \((2,{(p-1)(p'-1)}/{2}+1)\)-minimal model. Using the character formula of \(L_{\mathrm{Vir}}(c_{q,q'},0)\) from [29], the Hilbert series of \(J_{\infty }({\mathbb {C}}[l,g]/\langle l^{|c_{p,p'}|}\rangle )\) is
Meanwhile, by [41] the character of \(L_{c_{p,p'}}^{N=1}\) is

Comparing (9) and (10) we get that \(\psi \) is not an isomorphism in this case.
Let p and \(p'\) be both even. Suppose \((p,p')\notin \{(2,4k)\,{|}\,k\in {\mathbb {Z}}_{+}\}\) and \(\psi \) is an isomorphism for \(L_{c_{p,p'}}^{N=1}\). Then

On the other hand, we have shown that

Therefore, the character of \(L_{c_{p,p'}}^{N=1}\) must coincide with the character of \(L_{c_{2,4k}}^{N=1}\) for some k. Note, (10) is also true when p and \(p'\) are both even, and it is easy to verify from the numerator that no two \(N=1\) minimal vertex algebras have the same character. This is a contradiction. Thus the statement is proved. \(\square \)
7 Extended Virasoro vertex algebras
For a simple Virasoro vertex algebra \(L_{\mathrm{Vir}}(c_{2,2k+1},0)\) coming from the \((2,2k\,{+}\,1)\)-minimal model, according to [29], we know that \(R_{L_{\mathrm{Vir}}(c_{2,2k+1},0)}\cong {\mathbb {C}}[x]/(x^{k})\), and \(\psi \) is an isomorphism. Let p and \(p'\) be two positive coprime integers satisfying  . It is easy to see that \(\psi \) is an isomorphism if and only if \((p,p')=(2,2k\,{+}\,1)\) (see [52, Theorem 16.13]). Recently, the authors displayed the kernel of \(\psi \) [4, Theorem 1] for the \(c=1/2\) Ising model vertex algebra \(L_{\mathrm{Vir}}(c_{3,4},0)\), based on a new fermionic character formula for \(L_{\mathrm{Vir}}(c_{3,4},0)\).
. It is easy to see that \(\psi \) is an isomorphism if and only if \((p,p')=(2,2k\,{+}\,1)\) (see [52, Theorem 16.13]). Recently, the authors displayed the kernel of \(\psi \) [4, Theorem 1] for the \(c=1/2\) Ising model vertex algebra \(L_{\mathrm{Vir}}(c_{3,4},0)\), based on a new fermionic character formula for \(L_{\mathrm{Vir}}(c_{3,4},0)\).
If we consider extended Virasoro vertex algebras associated with minimal model which is not necessarily a \((2,2k\,{+}\,1)\)-minimal model, we might still have that \(\psi \) is an isomorphism. Our discussion is heavily motivated by [33], where the combinatorics of (super)extensions of (3, p)-minimal vertex algebras was discussed.
Example 7.1
For the free fermion model  , \(\psi \) is clearly an isomorphism as discussed in Proposition 4.2.
, \(\psi \) is clearly an isomorphism as discussed in Proposition 4.2.
Example 7.2
The \(L_{c_{2,8}}^{N=1}\) minimal vertex superalgebra has the following realization:

This realization is called the extended algebra, and it was studied in [33]. The map \(\psi \) is not an isomorphism in the case of \(L_{\mathrm{Vir}}(c_{(3,8)},0)\). But we have shown that for the extended algebra of \(L_{\mathrm{Vir}}(c_{(3,8)},0)\), the map \(\psi \) is an isomorphism. This model was analyzed from a different perspective in [40].
Example 7.3
Next, let us consider  . It is well known that
. It is well known that

We let \(\omega _1\) and \(\omega _2\) be conformal vectors of the first factor and the second factor of  . Then the isomorphism map f sends \(\omega _{1}+\omega _{2}\) to the conformal vector \(\omega \) of \(L_{\mathrm{Vir}}(c_{(3,10)},0)\), and \(\omega _{1}-\omega _{2}\) to the lowest weight vector \(\phi \) of \(L_{\mathrm{Vir}}(c_{(3,10)},2)\). Since we know that
. Then the isomorphism map f sends \(\omega _{1}+\omega _{2}\) to the conformal vector \(\omega \) of \(L_{\mathrm{Vir}}(c_{(3,10)},0)\), and \(\omega _{1}-\omega _{2}\) to the lowest weight vector \(\phi \) of \(L_{\mathrm{Vir}}(c_{(3,10)},2)\). Since we know that

the map \(\psi \) is an isomorphism for V, i.e.,

For  , its \(C_{2}\)-algebra is isomorphic to
, its \(C_{2}\)-algebra is isomorphic to

after we identify \(x+y\), \(x-y\) in  with u and v, respectively.
with u and v, respectively.
Remark 7.4
We also know from [33] that the normalized parafermionic character of  is given by
is given by

Next, let us consider the jet algebra

where degrees of u and v are both 2. Clearly, it has the following spanning set:
subject to constraints:
-
(a)
(difference two condition at distance 1) \(n_{i}\geqslant n_{i+1}+2 \),
-
(b)
(difference two condition at distance 2) \(m_{i}\geqslant m_{i+2}+2\),
-
(c)
(boundary condition) \(n_{N}\geqslant 2+M\),
where conditions (a), (b), (c) come from \((u^{2})_{\partial }\), \((v^{3})_{\partial }\), \((uv)_{\partial }\) in the quotient ideal of the jet algebra. Meanwhile, according to Proposition 5.1 and Theorem 5.13, we know that

where \(\Gamma \) is the graph \(\circ -\circ \). Using three realizations of jet algebras and the Gordon–Andrews character formulas from [23, 31], it is not hard to see that the above spanning set, subject to constraints (a)–(c), would produce a basis of the jet algebra  whose Hilbert series is given by
whose Hilbert series is given by

The normalized character formula for  is
is

Thus we have the following Hilbert series identities:

and

References
Adamović, D.: Rationality of Neveu–Schwarz vertex operator superalgebras. Int. Math. Res. Not. IMRN 1997(17), 865–874 (1997)
Adamović, D.: Rationality of unitary \(N= 2\) vertex operator superalgebras (1999). arXiv:math/9909055
Adamović, D.: Vertex algebra approach to fusion rules for \({N}= 2 \) superconformal minimal models. J. Algebra 239(2), 549–572 (2001)
Andrews, G.E., van Ekeren, J., Heluani, R.: The singular support of the Ising model (2020). arXiv:2005.10769
Arakawa, T.: A remark on the \(C_{2}\)-cofiniteness condition on vertex algebras. Math. Z. 270(1–2), 559–575 (2012)
Arakawa, T.: Introduction to \(W\)-algebras and their representation theory. In: Callegaro, F., et al. (eds.) Perspectives in Lie Theory. Springer INdAM Series, vol. 19, pp. 179–250. Springer, Cham (2017)
Arakawa, T., Kawasetsu, K.: Quasi-lisse vertex algebras and modular linear differential equations. In: Kac, V.G., Popov, V.L. (eds.) Lie Groups, Geometry, and Representation Theory. Progress in Mathematics, vol. 326, pp. 41–57. Springer, Cham (2018)
Arakawa, T., Lam, C.H., Yamada, H.: Zhu’s algebra, \(C_{2}\)-algebra and \(C_{2}\)-cofiniteness of parafermion vertex operator algebras. Adv. Math. 264, 261–295 (2014)
Arakawa, T., Linshaw, A.R.: Singular support of a vertex algebra and the arc space of its associated scheme. In: Gorelik, M., et al. (eds.) Representations and Nilpotent Orbits of Lie Algebraic Systems. Progress in Mathematics, vol. 330, pp. 1–17. Springer, Cham (2019)
Arakawa, T., Moreau, A.: Sheets and associated varieties of affine vertex algebras. Adv. Math. 320, 157–209 (2017)
Arakawa, T., Moreau, A.: Arc spaces and chiral symplectic cores (2018). arXiv:1802.06533
Arakawa, T., Moreau, A.: Joseph ideals and lisse minimal \( W \)-algebras. J. Inst. Math. Jussieu 17(2), 397–417 (2018)
Arakawa, T., Moreau, A.: On the irreducibility of associated varieties of \(W\)-algebras. J. Algebra 500, 542–568 (2018)
Arakawa, T., Moreau, A.: Corrigendum to “Sheets and associated varieties of affine vertex algebras" [Adv. Math. 320 (2017) 157–209]. Adv. Math. 372, Art. No. 107302 (2020)
Bai, Y., Gorsky, E., Kivinen, O.: Quadratic ideals and Rogers–Ramanujan recursions. Ramanujan J. 52(1), 67–89 (2020)
Baranović, I., Primc, M., Trupčević, G.: Bases of Feigin–Stoyanovsky’s type subspaces for \(C_{\ell }^{(1)}\). Ramanujan J. 45(1), 265–289 (2018)
Beem, C., Lemos, M., Liendo, P., Peelaers, W., Rastelli, L., van Rees, B.C.: Infinite chiral symmetry in four dimensions. Comm. Math. Phys. 336(3), 1359–1433 (2015)
Beilinson, A., Feigin, B., Mazur, B.: Introduction to Algebraic Field Theory on Curves. Unpublished manuscript
Bringmann, K., Folsom, A., Ono, K., Rolen, L.: Harmonic Maass Forms and Mock Modular Forms. American Mathematical Society Colloquium Publications, vol. 64. American Mathematical Society, Providence (2017)
Bruschek, C., Mourtada, H., Schepers, J.: Arc spaces and the Rogers–Ramanujan identities. Ramanujan J. 30(1), 9–38 (2013)
Butorac, M.: Combinatorial Bases of Principal Subspaces of Standard Modules for Affine Lie Algebra of Type \(B_{2}^{(1)}\). Ph.D. Thesis, Sveučilište u Zagrebu (2012)
Butorac, M., Kožić, S.: Principal subspaces for the affine Lie algebras in types \( D \), \( E \) and \( F\) (2019). arXiv:1902.10794
Calinescu, C., Lepowsky, J., Milas, A.: Vertex-algebraic structure of the principal subspaces of certain \(A_{1}^{(1)}\)-modules, II: Higher-level case. J. Pure Appl. Algebra 212(8), 1928–1950 (2008)
Capparelli, S., Lepowsky, J., Milas, A.: The Rogers–Selberg recursions, the Gordon–Andrews identities and intertwining operators. Ramanujan J. 12(3), 379–397 (2006)
De Sole, A., Kac, V.G.: Finite vs affine \(W\)-algebras. Jpn. J. Math. 1(1), 137–261 (2006)
Dong, C., Li, H., Mason, G.: Certain associative algebras similar to \(U({\rm sl}_2)\) and Zhu’s algebra \(A (V_{L})\). J. Algebra 196(2), 532–551 (1997)
Feigin, B., Feigin, E., Jimbo, M., Miwa, T., Mukhin, E., et al.: Principal \(\widehat{{\rm sl}}_3\) subspaces and quantum Toda Hamiltonian. In: Miwa, T., et al. (eds.) Algebraic Analysis and Around. Advanced Studies in Pure Mathematics, vol. 54, pp. 109–166. Mathematical Society of Japan, Tokyo (2009)
Feigin, B., Feigin, E., Littelmann, P.: Zhu’s algebras, \(C_{2}\)-algebras and abelian radicals. J. Algebra 329(1), 130–146 (2011)
Feigin, B., Frenkel, E.: Coinvariants of nilpotent subalgebras of the Virasoro algebra and partition identities. On: Gel’fand, S., Gindikin, S. (eds.) I.M. Gel’fand Seminar. Advances in Soviet Mathematics, vol. 16.1, pp. 139–148. American Mathematical Society, Providence (1993)
Feigin, B., Kedem, R., Loktev, S., Miwa, T., Mukhin, E.: Combinatorics of the \(\widehat{\rm sl}_2\) spaces of coinvariants. Transform. Groups 6(1), 25–52 (2001)
Feigin, B., Stoyanovsky, A.V.: Quasi-particles models for the representations of Lie algebras and geometry of flag manifold (1993). arXiv:hep-th/9308079
Feigin, E.: The PBW filtration. Represent. Theory 13, 165–181 (2009)
Jacob, P., Mathieu, P.: Embedding of bases: from the \({\mathscr {M}}(2, 2\kappa + 1)\) to the \({\mathscr {M}} (3, 4\kappa + 2- \delta )\) models. Phys. Lett. B 635(5–6), 350–354 (2006)
Jennings-Shaffer, C., Milas, A.: Further \( q \)-series identities and conjectures relating false theta functions and characters (2020). arXiv:2005.13620
Jerković, M.: Character formulas for Feigin–Stoyanovsky’s type subspaces of standard \({\mathfrak{ sl}(3,{\mathbb{C}})}^{\sim }\)-modules. Ramanujan J. 27(3), 357–376 (2012)
Kac, V.G.: Vertex Algebras for Beginners. University Lecture Series, 2nd edn, vol. 10. American Mathematical Society, Providence (1998)
Lepowsky, J., Li, H.: Introduction to Vertex Operator Algebras and Their Representations. Progress in Mathematics, vol. 227. Birkhäuser, Boston (2012)
Li, H.: Abelianizing vertex algebras. Comm. Math. Phys. 259(2), 391–411 (2005)
Li, H., Milas, A.: Quantum dilogarithm and characters of FS-principal subspaces. In preparation
Li, H., Milas, A., Wauchope, J.: \(S_{2}\)-orbifolds of \(N= 1\) and \(N= 2\) superconformal vertex algebras and \(W\)-algebras. Comm. Algebra 49(4), 1609–1638 (2020)
Melzer, E.: Supersymmetric analogs of the Gordon–Andrews identities, and related TBA systems (1994). arXiv:hep-th/9412154
Meurman, A., Primc, M.: Annihilating ideals of standard modules of \({sl(2, C)}^{\sim }\) and combinatorial identities. Adv. Math. 64(3), 177–240 (1987)
Milas, A.: Characters, supercharacters and Weber modular functions. J. Reine Angew. Math. 608, 35–64 (2007)
Milas, A., Penn, M.: Lattice vertex algebras and combinatorial bases: general case and \({W}\)-algebras. New York J. Math. 18, 621–650 (2012)
Ogawa, A.: Zhu’s algebra of rank one lattice vertex operator superalgebras. Osaka J. Math. 37(4), 811–822 (2000)
Penn, M.: Lattice vertex superalgebras, I: presentation of the principal subalgebra. Comm. Algebra 42(3), 933–961 (2014)
Primc, M.: Vertex operator construction of standard modules for \(A_{n}^{(1)}\). Pacific J. Math. 162(1), 143–187 (1994)
Primc, M.: Basic representations for classical affine Lie algebras. J. Algebra 228(1), 1–50 (2000)
Primc, M., Šikić, T.: Combinatorial bases of basic modules for affine Lie algebras \(C_{n}^{(1)}\). J. Math. Phys. 57(9), Art. No. 091701 (2016)
Trupčević, G.: Combinatorial bases of Feigin–Stoyanovsky’s type subspaces of higher-level standard \(\widetilde{\mathfrak{sl}}(\ell +1,{\mathbb{C}})\)-modules. J. Algebra 322(10), 3744–3774 (2009)
Trupčević, G.: Characters of Feigin–Stoyanovsky’s type subspaces of level one modules for affine Lie algebras of types \(A_\ell ^{(1)}\) and \(D_4^{(1)}\). Glas. Mat. Ser. III 46(1), 49–70 (2011)
van Ekeren, J., Heluani, R.: Chiral homology of elliptic curves and the Zhu algebra. Comm. Math. Phys. https://doi.org/10.1007/s00220-021-04026-w
Zheng, L.: Vertex operator superalgebras associated with affine Lie superalgebras. Comm. Algebra 45(6), 2417–2434 (2017)
Zhu, Y.: Modular invariance of characters of vertex operator algebras. J. Amer. Math. Soc. 9(1), 237–302 (1996)
Acknowledgements
The author would like to thank his supervisor, Antun Milas, for reading the manuscript, lots of advice and discussions. He is also grateful to anonymous referees for lots of suggestions on polishing this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author was supported by NSF grant NSF-DMS 1601070 of Antun Milas.
Rights and permissions
About this article
Cite this article
Li, H. Some remarks on associated varieties of vertex operator superalgebras. European Journal of Mathematics 7, 1689–1728 (2021). https://doi.org/10.1007/s40879-021-00477-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00477-6



 ,
, for
for  ,
,


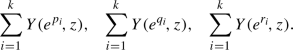
 :
:

 :
:

 :
:



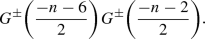

 ,
,  . Without loss of generality, we assume
. Without loss of generality, we assume  , then the basis of
, then the basis of 

 ,
,  if
if 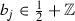 ,
, if
if  .
.