Bases of Feigin–Stoyanovsky’s type subspaces for $C_\ell ^{(1)}$

Abstract

In this paper, we construct combinatorial bases of Feigin–Stoyanovsky’s type subspaces of standard modules for level k affine Lie algebra $C_\ell ^{(1)}$. We prove spanning by using annihilating field $x_\theta (z)^{k+1}$ of standard modules. In the proof of linear independence, we use simple currents and intertwining operators whose existence is given by fusion rules.

1 Introduction

Let ${\mathfrak g}$ be a simple complex Lie algebra, ${\mathfrak h}\subset {\mathfrak g}$ its Cartan subalgebra, and R the corresponding root system. Let ${\mathfrak g}={\mathfrak h}+\sum _{\alpha \in R}{\mathfrak g}_\alpha$ be a root decomposition of ${\mathfrak g}$. Fix root vectors $x_\alpha \in {\mathfrak g}_\alpha$. Let

$$\begin{aligned} {\mathfrak g}={\mathfrak g}_{-1}\oplus {\mathfrak g}_0 \oplus {\mathfrak g}_1 \end{aligned}$$

(1)

be a ${\mathbb Z}$-gradation of ${\mathfrak g}$, where ${\mathfrak h}\subset {\mathfrak g}_0$. Such gradations correspond to a choice of a minuscule coweight $\omega \in {\mathfrak h}$. Denote by $\varGamma \subset R$ a set of roots such that ${\mathfrak g}_1=\sum _{\alpha \in \varGamma }{\mathfrak g}_\alpha =\sum _{\omega (\alpha )=1}{\mathfrak g}_\alpha$. We call $\varGamma$ the set of colors.

Affine Lie algebra associated with ${\mathfrak g}$ is $x={\mathfrak g}\otimes {\mathbb C}[t,t^{-1}]\oplus {\mathbb C}c \oplus {\mathbb C}d$, where c is the canonical central element and d is the degree operator. Elements $x_\alpha (n)=x_\alpha \otimes t^n$ are fixed real root vectors. The ${\mathbb Z}$-gradation of ${\mathfrak g}$ induces analogous gradation of $\tilde{\mathfrak {g}}$:

$$\begin{aligned} \tilde{\mathfrak {g}}=\tilde{\mathfrak {g}}_{-1}\oplus \tilde{\mathfrak {g}}_0 \oplus \tilde{\mathfrak {g}}_1, \end{aligned}$$

where $\tilde{\mathfrak {g}}_1={\mathfrak g}_1\otimes {\mathbb C}[t,t^{-1}]$ is a commutative Lie subalgebra with a basis

$$\begin{aligned} \tilde{{\varGamma }}=\{x_\gamma (n)\,|\,n\in {\mathbb Z},\gamma \in \varGamma \}. \end{aligned}$$

For a standard $\tilde{\mathfrak {g}}$-module $L(\varLambda )$ of level $k=\varLambda (c)$, define a Feigin–Stoyanovsky;s type subspace $W(\varLambda )$ as a $\tilde{\mathfrak {g}}_1$-submodule generated with a highest weight vector $v_\varLambda$,

$$\begin{aligned} W(\varLambda )=U(\tilde{\mathfrak {g}}_1)\cdot v_\varLambda \subset L(\varLambda ). \end{aligned}$$

In this paper, for a Lie algebra ${\mathfrak g}$ of type $C_\ell$, we construct a basis of $W(\varLambda )$ consisting of monomial vectors $x(\pi )v_\varLambda$, where $x(\pi )$ are monomials in $\tilde{{\varGamma }}$. Poincare–Birkhoff–Witt’s theorem gives a spanning set of $W(\varLambda )$

$$\begin{aligned} \{x_{\gamma _1}(-n_1) x_{\gamma _2}(-n_2)\cdots x_{\gamma _t}(-n_t) v_\varLambda \,|\, t\in {\mathbb Z}_+,\gamma _i\in \Gamma , n_i\in {\mathbb N}\}. \end{aligned}$$

(2)

In order to obtain a basis of $W(\varLambda )$, we find relations for standard modules upon which we reduce the spanning set. Finally, we prove linear independence by using intertwining operators.

The notion of Feigin–Stoyanovsky’s type subspaces is similar to a notion of principal subspaces that were introduced by Feigin and Stoyanovsky for ${\mathfrak sl}_2({\mathbb C})$ and ${\mathfrak sl}_3({\mathbb C})$ [31]. In this case, one looks at a triangular decomposition of ${\mathfrak g}$ instead of (1). Many different authors have studied these spaces, their bases, character formulas, exact sequences etc. [1, 4–9, 17, 29, 30].

Another type of principal subspaces, the so-called Feigin–Stoyanovsky’s type subspaces $W(\varLambda )$ defined above, was implicitly studied in [24] for ${\mathfrak sl}_{\ell +1}({\mathbb C})$. It turned out that in this case, bases are parameterized by $(k,\ell +1)$-admissible configurations, studied by Feigin et al. [12, 13]. The ${\mathbb Z}$-gradations (1) are closely related to simple current operators [11]. We hope that this kind of construction of combinatorial bases will be possible for all affine Lie algebras. Up to now, this was done for the type $A_\ell ^{(1)}$ in [26, 32, 33], for $B_2^{(1)}$ in [27], for $D_4^{(1)}$, levels 1 and 2, in [2], and for all classical types, level 1, in [25].

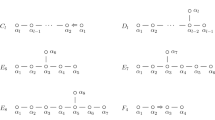
The first general case beyond admissible configurations was given in [32, 33] where a new kind of combinatorial conditions emerged. The minuscule coweight $\omega$ that was considered in these papers corresponds to a $\alpha _m$, $1\le m \le \ell$. If ${\mathfrak g}={\mathfrak sl}_{\ell +1}({\mathbb C})$ represents matrices of trace 0 then in the ${\mathbb Z}$-gradation (1) the subalgebra ${\mathfrak g}_0$ consists of block-diagonal matrices, while ${\mathfrak g}_1$ and ${\mathfrak g}_{-1}$ consist of matrices with nonzero entries only in the upper right or lower left block, respectively. This is illustrated on the Fig. 1.

Fig. 1

${\mathbb Z}$-gradation of ${\mathfrak sl}_{\ell +1}({\mathbb C})$

The set of colors $\varGamma$ corresponds to a rectangle with rows $1,\ldots ,m$ and columns $m,\ldots ,\ell$. Monomial basis of $W(\varLambda )$ is described in terms of difference and initial conditions.

In the level 1 case, a monomial vector (2) satisfies difference conditions for $W(\varLambda _r)$, if colors of elements of the same degree $-n$ lie on a diagonal path in $\varGamma$ as shown in Fig. 2. Furthermore, colors of elements of degree $-n-1$ lie on a diagonal path that lies below or to the left of the preceding path.

Fig. 2

Difference conditions for ${\mathfrak sl}_{\ell +1}({\mathbb C})$ level 1

A monomial vector (2) satisfies initial conditions for $W(\varLambda _r)$ if a diagonal path of colors of degree $-1$ lies either below the r-th row (if $1\le r \le m$) or on the left of the r-th column (if $m\le r \le \ell$).

In the case considered in this paper, when ${\mathfrak g}$ is a simple Lie algebra of type $C_\ell$, similar combinatorics appear. The set of colors $\varGamma$ can be represented as a triangle with rows and columns ranging from 1 to $\ell$ (cf. Fig. 4).

For a fundamental weight $\varLambda _r$, a monomial vector (2) satisfies difference conditions for $W(\varLambda _r)$, if colors of elements of two consecutive degrees lie on diagonal paths that are related in a way shown in Fig. 3, i.e., if $(-n)$-path ends in the ith column, then $(-n-1)$-path lies below the ith row. A monomial vector (2) satisfies initial conditions for $W(\varLambda _r)$ if a diagonal path of colors of degree $-1$ lies below the r-th row.

Fig. 3

Difference conditions for $C_\ell$ level 1

In the proof of linear independence, we follow ideas of Georgiev (cf. [17]), and of Caparelli, Lepowsky and Milas (cf. [8, 9]). Start from a relation of linear dependence

$$\begin{aligned} \sum c_{\pi }x(\pi ) v_\varLambda = 0, \end{aligned}$$

(3)

where $x(\pi )$ are some monomials that satisfy difference and initial conditions for $W(\varLambda )$ and $c_\pi \in {\mathbb C}$. The main idea is to use intertwining operators between standard modules (cf. [10, 15]) and simple current operators (cf. [11]) to reduce this relation to a relation of linear dependence on another standard module and proceed inductively.

More concretely, let $x(\mu )$ be, in some sense, the smallest monomial in (3). Then there is a coefficient of intertwining operator w that commutes with $\tilde{\mathfrak {g}}_1$ and which sends $v_\varLambda$ to a vector $v'$ from the top of a standard module $L(\varLambda ')$ that is annihilated by almost all monomials greater than $x(\mu )$. Furthermore, for the remaining monomials, the action of $x(\pi )$ on $v'$ yields $x(\pi _2) [\omega ] v_{\varLambda ''}$, where $[\omega ]$ is a simple current operator and $x(\pi _2)$ is a submonomial of $x(\pi )$. On the other side, commutation of a monomial with $[\omega ]$ raises degrees of factors by 1; thus we obtain

$$\begin{aligned} 0= \sum c_{\pi } [\omega ] x(\pi _2^+) v_{\varLambda ''}, \end{aligned}$$

(4)

where $x(\pi _2^+)$ is obtained from $x(\pi _2)$ by raising degrees of factors by 1. Finally, simple current operator $[\omega ]$ is a linear injection, hence

$$\begin{aligned} 0= \sum c_{\pi } x(\pi ^+) v_{\varLambda ''}. \end{aligned}$$

(5)

This is a relation of linear dependence on $L(\varLambda '')$ with monomials of higher degree than in (3). Since they are obtained from the ones from (3) by raising their degrees, it turns out that they also satisfy difference and initial conditions, this time for $W(\varLambda '')$. This enables us to use inductive argument to obtain $c_\mu =0$.

In the higher level case, difference and initial conditions are again given in terms of certain paths in $\varGamma$. Moreover, just like in the $A_\ell$ case considered in [32], in the $C_\ell$ case one can embed $L(\varLambda )$ into a tensor product of level 1 modules and factorize monomial vectors from the basis into a tensor product of level 1 monomial vectors from the corresponding bases (see Proposition 5 below). This fact is crucial for an easy transfer of the proof of linear independence from the level 1 case to higher levels. In this sense, this proof is different from the proof given in [27]. In the $D_4$-case (cf. [2]) it seems that this property does not hold and it remains to see what would be a good way to capture phenomenons that are happening there.

We give a brief outline of the paper. In Sects. 2 and 3, we introduce the setting and pose the main problem. In Sect. 4, we find relations between monomials and use them to reduce the spanning set in terms of difference and initial conditions. The existence and some properties of intertwining operators and a simple current operator are established in Sects. 5 and 6. In Sect. 7, we explore the action of monomials of higher degree on the vectors from the top of Feigin–Stoyanovsky’s type subspaces. This will enable us to find suitable coefficients of intertwining operators having properties that we have discussed above, and prove linear independence in the final section.

Fig. 4

The set of colors $\varGamma$

2 Affine Lie algebra $C_\ell ^{(1)}$

Let ${\mathfrak g}$ be a complex simple Lie algebra of type $C_\ell$ and let ${\mathfrak h}$ be a Cartan subalgebra of ${\mathfrak g}$. Let ${\mathfrak g}={\mathfrak h}+\sum {\mathfrak g}_\alpha$ be a root space decomposition of ${\mathfrak g}$. The corresponding root system R may be realized in $\mathbb R^\ell$ with the canonical basis $\epsilon _1,\ldots ,\epsilon _\ell$ as

$$\begin{aligned} R=\{\pm \epsilon _i\pm \epsilon _j\,|\, 1\le i\le j\le \ell \}\backslash \{0\}. \end{aligned}$$

We fix simple roots

$$\begin{aligned} \alpha _1=\epsilon _1-\epsilon _2,\ldots ,\alpha _{\ell -1}=\epsilon _{\ell -1}-\epsilon _\ell ,\quad \alpha _\ell =2\epsilon _\ell \end{aligned}$$

and let ${\mathfrak g}={\mathfrak n}_-+ {\mathfrak h}+ {\mathfrak n}_+$ be the corresponding triangular decomposition. Let $\theta =2\alpha _1+\cdots +2\alpha _{\ell -1}+\alpha _\ell =2\epsilon _1$ be the maximal root and

$$\begin{aligned} \omega _r= \epsilon _1+\cdots + \epsilon _r, \qquad r=1,\ldots ,\ell \end{aligned}$$

the fundamental weights. We fix root vectors $x_\alpha \in {\mathfrak g}_\alpha$ and denote by $\alpha ^\vee \in \mathfrak h$ dual roots. We identify $\mathfrak h$ and $\mathfrak h^*$ via the Killing form $\langle \,,\,\rangle$ normalized in such a way that $\langle \theta ,\theta \rangle =2$. We fix

$$\begin{aligned} \omega =\omega _\ell =\epsilon _1+\cdots +\epsilon _\ell \in {\mathfrak h}^*. \end{aligned}$$

This is the minuscule coweight, that is

$$\begin{aligned} \langle \omega ,\alpha \rangle \in \{-1,0,1\}\quad \text {for all}\quad \alpha \in R, \end{aligned}$$

and hence we have a $\mathbb Z$-gradation of ${\mathfrak g}$

$$\begin{aligned} \mathfrak g =\mathfrak g_{-1} + \mathfrak g_0 + \mathfrak g_1 , \qquad {\mathfrak g}_0 = {\mathfrak h} + \sum _{\langle \omega ,\alpha \rangle =0}\, {\mathfrak g}_\alpha , \qquad \displaystyle {\mathfrak g}_{\pm 1} = \sum _{\langle \omega ,\alpha \rangle = \pm 1}\, {\mathfrak g}_\alpha . \end{aligned}$$

Note that

$$\begin{aligned} \varGamma = \{\,\alpha \in R \mid \langle \omega ,\alpha \rangle = 1\} = \{\epsilon _i+\epsilon _j\,|\, 1\le i \le j\le \ell \}. \end{aligned}$$

(6)

We say that $\varGamma$ is the set of colors and we write

$$\begin{aligned} (ij)=\epsilon _i+\epsilon _j\in \varGamma \quad \text {and}\quad x_{ij}=x_{\epsilon _i+\epsilon _j} \end{aligned}$$

(7)

(see Fig. 4).

The subspaces ${\mathfrak g}_{\pm 1}\subset \mathfrak g$ are commutative subalgebras, ${\mathfrak g}_0$ is reductive, and $[{\mathfrak g}_0,{\mathfrak g}_0]$ is a simple algebra of type $A_{\ell -1}$ with root basis $\alpha _1,\ldots ,\alpha _{\ell -1}$. We identify $[{\mathfrak g}_0,{\mathfrak g}_0]$ with the Lie algebra $\mathfrak {sl}(\ell ,\mathbb C)$ acting on the canonical basis $e_1,\ldots ,e_\ell$ of the vector space ${\mathbb C}^\ell$ by the rule

$$\begin{aligned} e_i \xrightarrow {x_{-\alpha _i}} e_{i+1}. \end{aligned}$$

(8)

The subalgebra ${\mathfrak g}_0$ acts on ${\mathfrak g}_1$ by adjoint action. For a suitably chosen root vectors $x_{ij}$, this action is given by

$$\begin{aligned} x_{ij}&\xrightarrow {x_{-\alpha _i}}&x_{i+1,j}\quad \text {for}\ i<j, \end{aligned}$$

(9)

$$\begin{aligned} x_{ij}&\xrightarrow {x_{-\alpha _j}}&x_{i,j+1}\quad \text {for}\ i<j, \end{aligned}$$

(10)

$$\begin{aligned} x_{ii}&\xrightarrow {x_{-\alpha _i}}&2x_{i,i+1} \end{aligned}$$

(11)

(cf. [19]).

We identify the Weyl group ${\mathcal W}$ of $[{\mathfrak g}_0,{\mathfrak g}_0]$ with the group of permutations

$$\begin{aligned} \sigma :i \mapsto \sigma (i), \quad i=1,\ldots ,\ell , \end{aligned}$$

so that for $\alpha =\epsilon _{i}-\epsilon _{j}$, $i\ne j$, we have $\sigma \alpha =\epsilon _{\sigma (i)}-\epsilon _{\sigma (j)}$. For each $\sigma \in {\mathcal W}$, we have an automorphism $\sigma$ of ${\mathfrak g}_0$ and a linear map $\sigma$ on the vector representation $V_1={\mathbb C}^\ell$ of ${\mathfrak g}_0$,

$$\begin{aligned} \sigma :{\mathfrak g}_0\rightarrow {\mathfrak g}_0,\qquad \sigma :V_1\rightarrow V_1, \end{aligned}$$

(12)

such that

$$\begin{aligned} \sigma \,x_\alpha \in \mathbb C^\times x_{\sigma \alpha },\qquad \sigma \,e_i\in \mathbb C^\times e_{\sigma (i)} \end{aligned}$$

(13)

and

$$\begin{aligned} \sigma (xv)=(\sigma x)(\sigma v) \end{aligned}$$

(14)

for $x\in {\mathfrak g}_0$ and $v\in V_1$. For simple reflection $\sigma _i\in {\mathcal W}$, the linear map $\sigma _i$ is $(\exp x_{-\alpha _i})(\exp -x_{\alpha _i})(\exp x_{-\alpha _i})$ and formula (14) holds in general for integrable ${\mathfrak g}_0$-modules (cf. [20]). Since ${\mathfrak g}_1\cong S^2({\mathbb C}^\ell )$, we also have a linear map $\sigma$ on ${\mathfrak g}_1$ such that

$$\begin{aligned} \sigma \,x_{ij}\in \mathbb C^\times x_{\sigma (i)\sigma (j)}. \end{aligned}$$

(15)

To abbreviate expressions like the ones in (13) and (15), we introduce the following notation: for two vectors, monomials, etc., we write $x \sim y$ if the two are equal up to a nonzero scalar, i.e.,

$$\begin{aligned} x = Cy, \qquad \text {for some}\ C\in {\mathbb C}^\times . \end{aligned}$$

(16)

In this way, relations (13) and (15) can be rewritten in the following way:

$$\begin{aligned}&\sigma \,x_\alpha \sim x_{\sigma \alpha },\qquad \sigma \,e_i \sim e_{\sigma (i)},&\\&\sigma \,x_{ij} \sim x_{\sigma (i)\sigma (j)}.&\end{aligned}$$

Denote by $\tilde{\mathfrak g}$ the affine Lie algebra of type $C_\ell ^{(1)}$ associated to ${\mathfrak g}$,

$$\begin{aligned} \hat{\mathfrak g} = \mathfrak {g} \otimes \mathbb {C}[t,t^{-1}] + \mathbb {C}c, \qquad \tilde{\mathfrak g} = \hat{\mathfrak g} + \mathbb {C} d, \end{aligned}$$

with the canonical central element c and the degree element d . Set

$$\begin{aligned} x(n)=x\otimes t^{n} \end{aligned}$$

for $x\in {\mathfrak g}$ and $n\in \mathbb Z$ and denote by $x(z)=\sum _{n\in \mathbb Z} x(n) z^{-n-1}$ a formal Laurent series in formal variable z. The commutation relations in $\tilde{\mathfrak g}$ are

$$\begin{aligned}{}[x(i),y(j)]= [x,y](i+j)+ i\langle x,y\rangle \delta _{i+j,0}c,\qquad [c,\tilde{\mathfrak {g}}] = 0, \qquad [d,x(j)] = j x(j). \end{aligned}$$

We have a triangular decomposition

$$\begin{aligned} \tilde{\mathfrak {g}}=\tilde{{\mathfrak n}}_-+ \tilde{{\mathfrak h}} + \tilde{{\mathfrak n}}_+, \end{aligned}$$

where

$$\begin{aligned} \tilde{{\mathfrak n}}_-={\mathfrak n}_-+ {\mathfrak g}\otimes t^{-1}{\mathbb C}[t^{-1}],\qquad \tilde{{\mathfrak h}}={\mathfrak h}+ \mathbb {C}c + \mathbb {C} d,\qquad \tilde{{\mathfrak n}}_+={\mathfrak n}_++ {\mathfrak g}\otimes t{\mathbb C}[t]. \end{aligned}$$

We also have the induced ${\mathbb Z}$-gradation

$$\begin{aligned} \tilde{\mathfrak {g}}=\tilde{\mathfrak {g}}_{- 1}+\tilde{\mathfrak {g}}_{0}+\tilde{\mathfrak {g}}_{ 1} \end{aligned}$$

of affine Lie algebra $\tilde{\mathfrak {g}}$, where

$$\begin{aligned} \tilde{\mathfrak {g}}_0 = {\mathfrak g}_0\otimes {\mathbb C}[t,t^{-1}]\oplus {\mathbb C}c \oplus {\mathbb C}d,\qquad \tilde{\mathfrak {g}}_{\pm 1} = {\mathfrak g}_{\pm 1}\otimes {\mathbb C}[t,t^{-1}]. \end{aligned}$$

The subspace $\tilde{\mathfrak {g}}_1\subset \tilde{\mathfrak {g}}$ is a commutative subalgebra and ${\mathfrak g}_0$ acts on $\tilde{\mathfrak {g}}_1$ by adjoint action.

We denote by $\varLambda _0,\ldots ,\varLambda _\ell$ the fundamental weights of $\tilde{\mathfrak {g}}$,

$$\begin{aligned} \varLambda _r=\varLambda _0+\omega _r,\quad r=1,\ldots ,\ell . \end{aligned}$$

(17)

3 Feigin–Stoyanovsky’s type subspaces

Denote by $L(\varLambda )$ a standard (i.e., integrable highest weight) $\tilde{\mathfrak g}$-module with the highest weight

$$\begin{aligned} \varLambda =k_0 \varLambda _0+k_1 \varLambda _1+\cdots +k_\ell \varLambda _\ell , \end{aligned}$$

$k_i\in {\mathbb Z}_+$ for $i=0,\ldots ,\ell$. Throughout the paper, we denote by $k=\varLambda (c)$ the level of $\tilde{\mathfrak g}$-module $L(\varLambda )$,

$$\begin{aligned} k=k_0 +k_1 +\cdots +k_\ell , \end{aligned}$$

and by $v_\varLambda$ a fixed highest weight vector of $L(\varLambda )$.

For each integral dominant $\varLambda$, we have a Feigin–Stoyanovsky’s type subspace

$$\begin{aligned} W(\varLambda )=U(\widetilde{{\mathfrak g}}_1)v_\varLambda \subset L(\varLambda ). \end{aligned}$$

This space has a Poincare–Birkhoff–Witt spanning set

$$\begin{aligned} \{x_{\gamma _1}(-n_1) x_{\gamma _2}(-n_2)\cdots x_{\gamma _t}(-n_t) v_\varLambda \,|\, t\in {\mathbb Z}_+,\gamma _i\in \varGamma , n_i\in {\mathbb N}\}. \end{aligned}$$

(18)

The main problem considered in this paper is to reduce this PBW spanning set to a basis of $W(\varLambda )$. The main three steps in our construction are as follows:

• find relations for standard modules,

• reduce the spanning set, and

• prove linear independence by using intertwining operators.

4 Difference and initial conditions

Start from the vertex operator algebra relation on $L(\varLambda )$

$$\begin{aligned} x_\theta (z)^{k+1}=\sum _{N\in {\mathbb Z}}\left( \sum _{n_1+\cdots +n_{k+1}=N} x_{\theta }(-n_1)\cdots x_\theta (-n_{k+1})\right) z^{N-k-1}=0 \end{aligned}$$

(19)

(cf. [21–23]). Adjoint ${\mathfrak g}_0$-action on (19) gives us the space of relations $U({\mathfrak g}_0){\cdot }x_\theta (z)^{k+1}=0$. This is a finite-dimensional ${\mathfrak g}_0$-module with the highest weight $2(k+1)\omega _1$. Hence, as a vector space, it is isomorphic to $S^{2(k+1)}({\mathbb C}^\ell )$. The basis of $S^{2(k+1)}({\mathbb C}^\ell )$ is given by $e_1^{m_1}\cdots e_\ell ^{m_\ell }$, $m_1+\cdots +m_\ell =2(k+1)$, which we view as multisets $\{1^{m_1},\ldots ,\ell ^{m_\ell }\}$. Since relations (9)–(11) hold, one can easily see that the corresponding “basis” of the set of relations is given by the following proposition:

Proposition 1

On $L(\varLambda )$, the following relations hold

$$\begin{aligned} \sum _{\{i_1,\ldots ,i_{k+1}\}\cup \{ j_1,\ldots ,j_{k+1} \}=\{1^{m_1},\ldots ,\ell ^{m_\ell }\} } C_\mathbf{ij} x_{i_1 j_1}(z)x_{i_2 j_2}(z) \cdots x_{i_{k+1} j_{k+1}}(z)=0, \end{aligned}$$

(20)

for some $C_\mathbf{ij}\in {\mathbb C}^\times$, where the sum runs over all such partitions of the multiset $\{1^{m_1},\ldots ,\ell ^{m_\ell }\}$.

For each power of z from (20), we obtain a relation between monomials

$$\begin{aligned} \sum _{\begin{array}{c} n_1+\cdots +n_{k+1}=N\\ \{i_1,\ldots ,i_{k+1},j_1,\ldots ,j_{k+1} \}=\{1^{m_1},\ldots ,\ell ^{n_\ell }\} \end{array}} C_\mathbf{ij} x_{i_1 j_1}(-n_1)x_{i_2 j_2}(-n_2)\cdots x_{i_{k+1} j_{k+1}}(-n_{k+1})=0. \end{aligned}$$

(21)

We find the smallest monomials in these relation, the leading terms of relations. Since they can be expressed as a sum of higher terms, we can exclude them from the spanning set (18).

We introduce a linear order on monomials in the following way. First, define a linear order on the set of colors $\varGamma$: $(i'j')<(ij)$ if $i'>i$ or $i'=i,\, j'>j$. On the set of variables $\tilde{{\varGamma }}=\{x_\gamma (n) \,|\,\gamma \in \varGamma , n\in {\mathbb Z}\}$, define a linear order by $x_\alpha (n)<x_\beta (n')$ if $n<n'$ or $n=n',\, \alpha <\beta$. Assume that variables in monomials are sorted descendingly from right to left. The order < on the set of monomials is defined as a lexicographic order, where we compare variables from right to left (from the greatest to the lowest one).

Order < is compatible with multiplication (see [24, 33]):

$$\begin{aligned} \text {if} \quad x(\pi )<x(\pi ')\quad \text {then}\quad x(\pi )x(\pi _1)<x(\pi ')x(\pi _1)\quad \end{aligned}$$

(22)

for monomials $x(\pi ),x(\pi '),x(\pi _1)\in {\mathbb C}[\tilde{{\varGamma }}]$.

The leading terms can be most conveniently described in terms of exponents:

Proposition 2

A monomial

$$\begin{aligned} x(\pi ')&= x_{i_t j_t}(-n-1)^{b_{i_t j_t}}\cdots x_{i_1 j_1}(-n-1)^{b_{i_1 j_1}} \\&\quad \times x_{i_{s} j_{s}}(-n)^{a_{i_{s} j_{s}}}\cdots x_{i_{t+1} j_{t+1}}(-n)^{a_{i_{t+1} j_{t+1}}}, \end{aligned}$$

where $i_1 \le \cdots \le i_t \le j_t\le \cdots \le j_1 \le i_{t+1} \le \cdots \le i_{s} \le j_{s} \le \cdots \le j_{t+1}$, $(i_\nu ,j_\nu )\ne (i_{\nu +1},j_{\nu +1})$, and

$$\begin{aligned} b_{i_1 j_1}+\cdots +b_{i_t j_t}+a_{i_{t+1} j_{t+1}}+\cdots +a_{i_s j_s}=k+1, \end{aligned}$$

(23)

is a leading term of a relation (21) corresponding to the multiset

$$\begin{aligned}&\{{i_1}^{b_{i_1 j_1}},\ldots ,{i_t}^{b_{i_t j_t}},\ {j_t}^{b_{i_t j_t}} ,\ldots , {j_1}^{b_{i_1 j_1}},\\&\quad {i_{t+1}}^{a_{i_{t+1} j_{t+1}}},\ldots , {i_{s}}^{a_{i_{s} j_{s}}}, {j_{s}}^{a_{i_{s} j_{s}}},\ldots ,{j_{t+1}}^{a_{i_{t+1} j_{t+1}}}\} \end{aligned}$$

and a degree $N=(k+1)n + m$, where $m=b_{i_1 j_1}+\cdots +b_{i_t j_t}$.

The colors of leading terms lie on diagonal paths in $\varGamma$, see Fig. 5.

Fig. 5

Difference conditions for level k

Proof

Consider a relation (21) corresponding to a multiset $\{p_1\le \cdots \le p_{2k+2}\}$ and a total degree $-n_1-\cdots -n_{k+1}=-N\in -{\mathbb N}$.

First consider the case $N=(k+1)n$. In this case the leading term has all factors of the same degree $-n$ so we need to find minimal configuration of colors whose rows and columns joined give $\{p_1,\ldots ,p_{2k+2}\}$. It is clear that rows of the minimal configuration are $\{p_1,\ldots ,p_{k+1}\}$ and its columns are $\{p_{k+2},\ldots ,p_{2k+2}\}$. Otherwise there would exist a leading term $x(\pi )=x(\pi _1) x_{ij}(-n) x_{i'j'}(-n)$, $i\le j< i'\le j'$, and it is clear that a monomial $x(\pi ')=x(\pi _1)x_{ij'}(-n)x_{ji'}(-n)$ from the same relation is smaller than $x(\pi )$. By a similar argument we conclude that the minimal configuration is obtained by pairing maximal rows with minimal columns, i.e., it consists of colors $\{(p_1 p_{2k+2}), (p_2 p_{2k+1}), \ldots , (p_{k+1} p_{k+2})\}$ (if $x(\pi )=x(\pi _1)x_{ij}(-n)x_{i'j'}(-n)$, $i< i'< j < j'$, then $x(\pi ')=x(\pi _1)x_{ij'}(-n)x_{i'j}(-n)$ is smaller than $x(\pi )$). Hence it is a configuration whose colors lie on a diagonal path as shown in Fig. 5.

Next, consider the case $N=(k+1)n+m$. In this case, the leading term has m factors of degree $-n-1$ and $k+1-m$ factors of degree $-n$. The leading term is obtained first by choosing the minimal possible $(-n)$-part, and then the minimal possible $(-n-1)$-part. Hence $(-n)$-part corresponds to $\{p_{2m+1,\ldots ,p_{2k+2}}\}$, while $(-n-1)$-part corresponds to $\{p_1,\ldots , p_{2m}\}$, and colors of these parts lie on diagonal paths as shown in Fig. 5. $\square$

We say that a monomial $x(\pi )$ satisfies difference conditions, or shortly, that $x(\pi )$ satisfies DC, if it does not contain leading terms. More precisely, $x(\pi )$ satisfies difference conditions if for any $n\in {\mathbb N}$ and $i_1 \le \cdots \le i_t \le j_t\le \cdots \le j_1 \le i_{t+1} \le \cdots \le i_{s} \le j_{s} \le \cdots \le j_{t+1}$,

$$\begin{aligned} b_{i_1 j_1}+\cdots +b_{i_t j_t}+a_{i_{t+1} j_{t+1}}+\cdots +a_{i_s j_s}\le k, \end{aligned}$$

(24)

where $a_{ij}$’s and $b_{ij}$’s denote exponents of $x_{ij}(-n)$ and $x_{ij}(-n-1)$ in $x(\pi )$, respectively.

Note that in the case of level $k=1$, difference conditions imply that if $x(\pi )=x(\pi ') x_{ij}(-n)$ then $x(\pi ')$ does not contain factors $x_{i' j'}(-n)$, $i\le i'\le j'\le j$ or $i'\le i\le j\le j'$, nor it contains factors $x_{i' j'}(-n-1)$, $i'\le j' \le i$. Hence, $x(\pi )=\dots x_{i_s' j_s'}(-n-1)\cdots x_{i_1' j_1'}(-n-1) x_{i_{t} j_{t}}(-n) \cdots x_{i_1 j_1}(-n)\dots$ satisfies difference conditions for level $k=1$ if

$$\begin{aligned} i_1<\cdots<i_t,\quad j_1<\cdots<j_t,\quad i_1'<\cdots< i_s',\quad i_t<j_1'<\cdots <j_s'. \end{aligned}$$

(25)

Its colors lie on diagonal paths and a diagonal path of $(-n-1)$-part lies below $i_t$-th row, where $i_t$ is the column of the smallest color of the $(-n)$-part; see Fig. 3.

Remark 1

Similar difference conditions appear in another construction of combinatorial bases for $C_\ell ^{(1)}$ (cf. [28]).

Lemma 3

On $L(\varLambda _r)$

$$\begin{aligned} x_{ij}(-1)v_{\varLambda _r}=0,&\text {if} \ j\le r,\\ x_{ij}(-1)v_{\varLambda _r}\ne 0,&\text {if} \ j> r. \end{aligned}$$

Proof

For $\alpha \in R$ denote by ${\mathfrak sl}_2 (\alpha )\subset {\mathfrak g}$ a subalgebra generated by $x_{\alpha }$ and $x_{-\alpha }$, and let

$$\begin{aligned} \tilde{{\mathfrak sl}}_2(\alpha )={\mathfrak sl}_2 (\alpha )\otimes {\mathbb C}[t,t^{-1}]\oplus {\mathbb C}c \oplus {\mathbb C}d\subset \tilde{\mathfrak {g}}\end{aligned}$$

be the corresponding affine Lie algebra of type $A_1^{(1)}$. It has a canonical central element $c'=\langle x_{\alpha }, x_{-\alpha }\rangle c=2c/\langle \alpha ,\alpha \rangle$. Hence the restriction of $L(\varLambda _r)$ is a level 1 representation if $\alpha$ is a long root, and a level 2 representation if $\alpha$ is a short root.

Consider $\alpha =(jj)=2\epsilon _j$, $j\le r$. Then $(jj)^\vee =(jj)=2\epsilon _j$ and $\langle \omega _r,(jj)^\vee \rangle = \delta _{j>r}$. Hence, by (17), if $j\le r$, then $U(\tilde{{\mathfrak sl}}_2(\alpha ))v_{\varLambda _r}$ is a level 1 representation with 2-dimensional ${\mathfrak sl}_2(\alpha )$-module on top, and therefore it must be the standard $A_1^{(1)}$-module $L(\varLambda _1)$. If $j> r$, then the ${\mathfrak sl}_2(\alpha )$-module on top is 1-dimensional, hence $U(\tilde{{\mathfrak sl}}_2(\alpha ))v_{\varLambda _r}$ must be the standard $A_1^{(1)}$-module $L(\varLambda _0)$ (cf. [20]). Therefore

$$\begin{aligned} x_{jj}(-1)v_{\varLambda _r}=0,&\text {if} \ j\le r,\end{aligned}$$

(26)

$$\begin{aligned} x_{jj}(-1)v_{\varLambda _r}\ne 0,&\text {if} \ j> r, \end{aligned}$$

(27)

which proves the lemma for $i=j$. For $i<j$, action by $x_{\alpha _i}(0)\cdots x_{\alpha _{j-1}}(0)$ on (26) and (27) gives the claim. $\square$

A monomial $x(\pi )$ satisfies initial conditions for $W(\varLambda _r)$ if it does not contain a factor $x_{ij}(-1)$, $i\le j \le r$. Note that if a monomial $x(\pi )$ satisfies difference and initial conditions for $W(\varLambda _r)$, then the colors of $(-1)$-factors lie on a diagonal path below the r-th row (see Fig. 6).

Fig. 6

Initial conditions for $W(\varLambda _r)$

Generally, let $\varLambda =k_0\varLambda _0+\cdots +k_\ell \varLambda _\ell$. We say that $x(\pi )$ satisfies initial conditions for $W(\varLambda )$ if for every $i_1 \le \cdots \le i_t \le j_t\le \cdots \le j_1$,

$$\begin{aligned} a_{i_1 j_1}+\cdots +a_{i_t j_t}\le k_0+k_1+\cdots + k_{j_1-1}, \end{aligned}$$

(28)

where $a_{ij}$’s denote exponents of $x_{ij}(-1)$ in $x(\pi )$ (see Fig. 7). One immediately sees that for $\varLambda =\varLambda _r$ the two definitions of initial conditions are equivalent.

Fig. 7

Initial conditions for $\varLambda =k_0\varLambda _0+\cdots +k_\ell \varLambda _\ell$

Remark 2

Like in [2, 32], initial conditions can be expressed in terms of difference conditions by adding “imaginary” (0)-factors to $x(\pi )$. Let

$$\begin{aligned} x(\pi _0)=x_{1\ell }(0)^{k_1} x_{2\ell }(0)^{k_2}\cdots x_{\ell \ell }(0)^{k_\ell }. \end{aligned}$$

Note that colors of $x(\pi _0)$ lie on a diagonal path as shown in Fig. 5. Then $x(\pi )$ satisfies difference and initial conditions for $W(\varLambda )$ if and only if $x(\pi ')=x(\pi )x(\pi _0)$ satisfies difference conditions. In fact, initial conditions are defined in this way so that the property holds.

Proposition 4

The set of monomial vectors $x(\pi ) v_\varLambda$ satisfying difference conditions (24) and initial conditions (28) span $W(\varLambda )$.

Proof

By (21), if $x(\pi )$ does not satisfy difference condition (24), then $x(\pi )v_\varLambda$ can be expressed in terms of higher monomial vectors. Hence we can exclude $x(\pi )v_\varLambda$ from the spanning set (18).

By definition of level one initial conditions, if $x(\pi )$ does not satisfy initial conditions for $W(\varLambda _r)$, then $x(\pi )v_{\varLambda _r}=0$ and $x(\pi )v_{\varLambda _r}$ can be excluded from the spanning set (18). Assume $k>1$ and that $x(\pi )$ does not satisfy initial condition (28), and set $d=k_0+k_1+\cdots + k_{j_1-1}+1$. Factorize $x(\pi )=x(\pi '')x(\pi ')$, where $x(\pi ')$ consists only of $(-1)$-factors lying on a diagonal path from (28). Furthermore, one can assume that the length of $x(\pi ')$ is equal to d and that $d<k+1$ (otherwise (28) is equivalent to (24)).

Set $\varLambda ' = \sum _{r=0}^{j_1-1} k_r \varLambda _r$, $\varLambda '' = \sum _{r=j_1}^{\ell } k_r \varLambda _r=\varLambda - \varLambda '$. Denote by $v_{\varLambda '}$ and $v_{\varLambda ''}$ the highest weight vectors of standard modules $L(\varLambda ')$ and $L(\varLambda '')$. Then, by the complete reducibility, $L(\varLambda ) \subset L(\varLambda ')\otimes L(\varLambda '')$, $v_\varLambda = v_{\varLambda '}\otimes v_{\varLambda ''}$. Since, by Lemma 3, all factors of $x(\pi ')$ annihilate $v_{\varLambda ''}$, we have

$$\begin{aligned} x(\pi ')v_\varLambda =(x(\pi ')v_{\varLambda '})\otimes v_{\varLambda ''}. \end{aligned}$$

Note that $L(\varLambda ')$ is a module of level $d-1<k$. From relations (21) for the module $L(\varLambda ')$ we obtain monomials $x(\pi _1'),\ldots ,x(\pi _s')$ such that $x(\pi ')v_{\varLambda '}=C_1 x(\pi _1')v_{\varLambda '}+\cdots +C_s x(\pi _s')v_{\varLambda '}$, $C_t\in {\mathbb C}^\times$, and $x(\pi ')<x(\pi _t')$. Also from these relations, we see that colors of monomials $x(\pi _t')$ lie in the $j_1$-th row or above. By Lemma 3, all factors of $x(\pi _t')$ also act as 0 on $v_{\varLambda ''}$. Consequently,

$$\begin{aligned} x(\pi ')v_{\varLambda }=C_1 x(\pi _1')v_{\varLambda }+\cdots +C_s x(\pi _s')v_{\varLambda }, \end{aligned}$$

and $x(\pi )v_\varLambda$ can be expressed in terms of higher monomial vectors. Therefore, it can be excluded from the spanning set (18). $\square$

Like in the $A_\ell$-case [32], difference and initial conditions for level $k>1$ can be interpreted in terms of difference and initial conditions for level 1:

Proposition 5

Let $L(\varLambda )\subset L(\varLambda _{i_1})\otimes \cdots \otimes L(\varLambda _{i_k})$ be a standard module of level k. Monomial $x(\pi )$ satisfies difference and initial conditions for $W(\varLambda )$ if and only if there exists a factorization

$$\begin{aligned} x(\pi )=x(\pi ^{(1)})\cdots x(\pi ^{(k)}), \end{aligned}$$

such that $x(\pi ^{(j)})$ satisfies difference and initial conditions for $W(\varLambda _{i_j})$.

Proof

We follow the idea from [32]; here we give a sketch of the proof. First consider the case $\varLambda =k\varLambda _0$ for which initial conditions do not provide any additional relations and we only need to consider difference conditions.

Define another order on the set of variables: $x_{ij}(-n) \sqsubset x_{i'j'}(-n')$ if either $-n \le -n'-2$ or $-n=-n'-1,j>i'$ or $-n=-n',i>i', j>j'$. Equivalently, $x_{ij}(-n) \sqsubset x_{i'j'}(-n')$ if $x_{ij}(-n) < x_{i'j'}(-n')$ and a monomial $x_{ij}(-n) x_{i'j'}(-n')$ satisfies level 1 difference conditions. This is a strict partial order on $\tilde{{\varGamma }}$.

Consider monomials $x(\pi )\in {\mathbb C}[\tilde{{\varGamma }}]$ as multisets; then a monomial $x(\pi )$ satisfies level k difference conditions if and only if every subset of $x(\pi )$ in which there are no two elements comparable in the sense of $\sqsubset$, has at most k elements. To see this, let $x_{ij}(-n),x_{i'j'}(-n')\in \tilde{{\varGamma }}$, $x_{ij}(-n)< x_{i'j'}(-n')$. They are incomparable in the sense of $\sqsubset$ if and only if either $-n=-n'-1$ and $j\le i'$ or $-n=-n'$ and $i\ge i'$ or $j\ge j'$. It is clear that factors of leading terms (23) are mutually incomparable; consequently, if $x(\pi )$ does not satisfy difference conditions, then it has a subset of at least $k+1$ mutually incomparable elements. Conversely, consider a subset of $x(\pi )$ whose elements are mutually incomparable. By the observation above, degrees of its elements differ for at most 1. Moreover, elements of the same degree lie on a diagonal path and the two paths are related as shown in (23).

Note that if $x_{\gamma _1}(-n_1) \sqsubset \cdots \sqsubset x_{\gamma _t}(-n_t)$, then the corresponding monomial $x_{\gamma _1}(-n_1) \cdots x_{\gamma _t}(-n_t)$ satisfies level 1 difference conditions. Now, a combinatorial lemma from [32] implies that $x(\pi )$ can be partitioned into k linearly ordered subsets which proves proposition in the $\varLambda =k\varLambda _0$ case.

By Remark 2, in the general case $\varLambda =k_0\varLambda _0+\cdots +k_\ell \varLambda _\ell$, initial conditions can be regarded as difference conditions by considering monomials $x(\pi ')=x(\pi ) x(\pi _0)$ instead of $x(\pi )$, where $x(\pi _0)=x_{1\ell }(0)^{k_1} \cdots x_{\ell \ell }(0)^{k_\ell }$. By above arguments, we can partition $x(\pi ')$ into k linearly ordered subsets. Since $x_{i\ell }(0)$’s are mutually incomparable, they lie in different subsets. Moreover, a subset containing $x_{i\ell }(0)$ gives a monomial satisfying difference and initial conditions for $W(\varLambda _i)$, again by Remark 2. $\square$

5 Intertwining operators

Consider a ${\mathfrak g}_0$-module $V_i=U({\mathfrak g}_0)v_{\varLambda _i}\subset L(\varLambda _i)$ and ${\mathbb C}^\ell$ as the vector representation for ${\mathfrak g}_0$-action. Then

$$\begin{aligned} V_i=\bigwedge ^i {\mathbb C}^\ell , \end{aligned}$$

for $i=0,\ldots ,\ell$ (cf. [3, 19]). If $e_1,\ldots ,e_\ell$ is a basis for ${\mathbb C}^\ell$ with ${\mathfrak g}_0$-action defined by (8), then

$$\begin{aligned} v_{p_1 \cdots p_i}=e_{p_1}\wedge \cdots \wedge e_{p_i}, \qquad 1\le p_1<\cdots <p_i\le \ell \end{aligned}$$

(29)

is a basis for $V_i$. Moreover,

$$\begin{aligned} v_{\varLambda _i}=v_{1 2 \ldots i}. \end{aligned}$$

If $I=\{p_1,\ldots ,p_i\}$, $1\le p_1<\cdots <p_i\le \ell$, then denote by $v_I=v_{p_1 \ldots p_i}$. Note that for each $\sigma \in {\mathcal W}$ and each $i=1,\ldots ,\ell$ we have a linear map $\sigma$ on $V_i$ such that

$$\begin{aligned} \sigma v_{p_1 \ldots p_i} \sim v_{\sigma (p_1) \cdots \sigma (p_i)}, \end{aligned}$$

where we use the notation from (16). Later on we shall also use other consequences of the formula (14) for integrable ${\mathfrak g}_0$-modules, for example the formula

$$\begin{aligned} \sigma (x_{pq}(-1)v_{p_1 \ldots p_i})\sim x_{\sigma (p)\sigma (q)}(-1)v_{\sigma (p_1) \ldots \sigma (p_i)}. \end{aligned}$$

Lemma 6

Let $v\in V_i$. Then $x_\gamma (n)v=0$, for $\gamma \in \varGamma$, $n\ge 0$, and $x_\alpha (n)v=0$, for $\alpha \in R$, $n\ge 1$.

Proof

We only need to show $xv=0$ for all $x\in {\mathfrak g}_1, v\in V_i$; other relations are clear from the definition. Let $v'\in V_i$ be such that ${\mathfrak g}_1 v'=0$. Let $x\in {\mathfrak g}_1$ and $y\in {\mathfrak g}_0$. Then $x y v'=[xy]v'+yxv'=0$. Since ${\mathfrak g}_1 v_{\varLambda _i}=0$, the claim follows. $\square$

The standard $\tilde{\mathfrak g}$-module $L(\varLambda _0)$ is a vertex operator algebra and $L(\varLambda _1)$, ..., $L(\varLambda _\ell )$ are modules for vertex operator algebra $L(\varLambda _0)$ (cf. [16, 21]). By using Theorem 6.2 in [14], it is easy to see that the space of intertwining operators

$$\begin{aligned} {\mathcal Y}:L(\varLambda _1) \rightarrow \text {Hom}\,(L(\varLambda _i),L(\varLambda _{i+1}))\{\{z\}\}, \qquad {\mathcal Y}(w,z)u=\sum _{m\in \mathbb Q}w_m u\,z^{-m-1} \end{aligned}$$

is 1-dimensional for $i=0,\ldots ,\ell -1$.

By Lemma 6.1 in [27] for such nonzero $\mathcal Y$, there exists $m\in \mathbb Q$ such that

$$\begin{aligned} V_1\otimes V_i \rightarrow V_{i+1}, \qquad w\otimes u\mapsto w_m u \end{aligned}$$

(30)

is a nonzero homomorphism of ${\mathfrak g}_0$-modules. It is easy to see that the multiplicity of $V_{i+1}$ in $V_1\otimes V_i$ is 1—one way to see this is by using Parthasarathy–Ranga Rao–Varadarajan’s theorem 5.2 in [14]—hence we can normalize $\mathcal Y$ so that the map (30) is the homomorphism of ${\mathfrak g}_0$-modules

$$\begin{aligned} V_1\otimes V_i \rightarrow V_{i+1}, \qquad v_m u=v\wedge u. \end{aligned}$$

(31)

From the commutator formula for $\mathcal Y$ and Lemma 6, we have the following:

Proposition 7

For $v\in V_1={\mathbb C}^\ell$:

• ${\mathcal Y}(v,z)$ commutes with $\tilde{\mathfrak {g}}_1$

• for $u\in V_i$, the coefficient of $z^{-m-1}$ of ${\mathcal Y}(v,z)u$ is

  $$\begin{aligned} v_m u=v\wedge u. \end{aligned}$$

6 Simple current operator

Recall that we have fixed the minuscule coweight $\omega =\omega _\ell \in {\mathfrak h}^*$. We shall use simple current operators

$$\begin{aligned} L(\varLambda _i) \xrightarrow {[\omega ]} L(\varLambda _{\ell -i}) \xrightarrow {[\omega ]} L(\varLambda _i) \end{aligned}$$

such that simple current commutation relation

$$\begin{aligned} x_\alpha (n)[\omega ]=[\omega ] x_\alpha (n+\alpha (\omega )), \qquad \alpha \in R, \quad n\in \mathbb Z \end{aligned}$$

(32)

holds (see [11, 18], or Remark 5.1 in [27]). Then

$$\begin{aligned} x_\gamma (-n-1) [\omega ]= & {} [\omega ] x_\gamma (-n)\quad \text {for}\quad \gamma \in \varGamma \\ x(\mu )[\omega ]= & {} [\omega ]x(\mu ^+) \quad \text {for a monomial}\ x(\mu )\in U(\tilde{\mathfrak {g}}_1^-), \end{aligned}$$

where by $x(\mu ^+)$ we denote a monomial obtained by raising degrees in $x(\mu )$ by 1. Also,

$$\begin{aligned} x_\alpha (-n) [\omega ]= & {} [\omega ] x_\alpha (-n)\quad \text {for}\quad x_\alpha \in {\mathfrak g}_0,\\ \sigma [\omega ]= & {} [\omega ] \sigma \quad \text {for}\quad \sigma \in {\mathcal W}. \end{aligned}$$

In the level $k>1$ case, for $\varLambda = k_0\varLambda _0 + k_1\varLambda _1+ \cdots + k_\ell \varLambda _\ell$, we embed $L(\varLambda )$ in a tensor product of standard modules of level 1

$$\begin{aligned} L(\varLambda )\subset L(\varLambda _{0})^{k_0}\otimes L(\varLambda _{1})^{k_1}\otimes \cdots \otimes L(\varLambda _{\ell })^{k_\ell }, \end{aligned}$$

with a highest weight vector

$$\begin{aligned} v_\varLambda =v_{\varLambda _0}^{\otimes k_0}\otimes \cdots \otimes v_{\varLambda _\ell }^{\otimes k_\ell }, \end{aligned}$$

and we use the level k simple current operator $[\omega ]:L(\varLambda )\rightarrow L(\varLambda ')$,

$$\begin{aligned}{}[\omega ]=[\omega ]\otimes \cdots \otimes [\omega ]. \end{aligned}$$

7 Relations

From (21), we immediately obtain the following relations:

Lemma 8

On a level one module $L(\varLambda _r)$

$$\begin{aligned}&x_{ii}(-1) x_{ii}(-1) = 0, \end{aligned}$$

(33)

$$\begin{aligned}&x_{ij}(-1) x_{ii}(-1) = 0,\quad \text {for}\ i<j,\end{aligned}$$

(34)

$$\begin{aligned}&x_{jj}(-1) x_{ij}(-1) = 0,\quad \text {for}\ i<j,\end{aligned}$$

(35)

$$\begin{aligned}&x_{ij}(-1)x_{ij}(-1) \sim x_{ii}(-1)x_{jj}(-1), \quad \text {for} \ i<j,\end{aligned}$$

(36)

$$\begin{aligned}&x_{jk}(-1)x_{ii}(-1) \sim x_{ik}(-1)x_{ij}(-1) =0, \quad \text {for} \ i<j<k,\end{aligned}$$

(37)

$$\begin{aligned}&x_{jk}(-1)x_{ij}(-1) \sim x_{jj}(-1)x_{ik}(-1) =0, \quad \text {for} \ i<j<k,\end{aligned}$$

(38)

$$\begin{aligned}&x_{kk}(-1)x_{ij}(-1) \sim x_{jk}(-1)x_{ik}(-1) =0, \quad \text {for} \ i<j<k,\end{aligned}$$

(39)

$$\begin{aligned}&x_{jk}(-1)x_{il}(-1) \sim C_1 x_{jl}(-1)x_{ik}(-1) + C_2 x_{kl}(-1)x_{ij}(-1), \end{aligned}$$

(40)

for $i<j<k<l$ and some $C_1,C_2\in {\mathbb C}^\times$.

Lemma 9

If $i,j\in \{s_1,s_2,\ldots ,s_r\}$, where $1\le s_1,\ldots ,s_r \le \ell$, then

$$\begin{aligned} x_{i j}(-1) v_{s_1 s_2 \ldots s_r}=0. \end{aligned}$$

Proof

Let $i=s_p$, $j=s_q$, $p\le q\le r$. By Lemma 3, we have

$$\begin{aligned} x_{p q}(-1)v_{1 2 \ldots r}=0. \end{aligned}$$

(41)

Next, by acting on (41) with a linear map $\sigma$ corresponding to $\sigma \in {\mathcal W}$ such that $\sigma (t)=s_t$, $t=1,\ldots ,r$ (see (12)), we obtain the desired relation. $\square$

Lemma 10

If $i\notin \{s_1,s_2,\ldots ,s_r\}$, then

$$\begin{aligned} x_{i s_p}(-1) v_{s_1 s_2 \ldots s_r} \sim x_{s_p s_p}(-1)v_{s_1 \ldots i \ldots \underline{s_p} \ldots s_r}. \end{aligned}$$

(42)

We use underline to denote that the corresponding indices should be excluded.

Proof

Let $s_{q-1}<i<s_q$, $q\le p$. By Lemma 9, we have

$$\begin{aligned} x_{q+1, p+1}(-1)v_{1 \cdots q-1, q+1 \cdots r+1}=0. \end{aligned}$$

(43)

We act with $x_{\alpha _{q}}\in {\mathfrak g}_0$ and obtain

$$\begin{aligned} x_{q, p+1}(-1)v_{1 \cdots q-1, q+1 \cdots r+1} - C' x_{q+1, p+1}(-1)v_{1 \cdots q, q+2 \cdots r+1}=0, \end{aligned}$$

(44)

for some $C'\in {\mathbb C}^\times$. Hence

$$\begin{aligned} x_{q, p+1}(-1)v_{1 \cdots q-1, q+1 \cdots r+1} \sim x_{q+1, p+1}(-1)v_{1 \cdots q, q+2 \cdots r+1}. \end{aligned}$$

(45)

By induction, we obtain

$$\begin{aligned} x_{q, p+1}(-1)v_{1 \cdots q-1, q+1 \cdots r+1}\sim x_{p+1, p+1}(-1)v_{1 \cdots p, p+2 \cdots r+1}. \end{aligned}$$

(46)

By acting on (46) with a linear map $\sigma$ corresponding to $\sigma \in {\mathcal W}$ such that $\sigma (t)=s_t$, for $t\in \{1,\ldots ,q-1\}$, $\sigma (t)=s_{t-1}$, for $t\in \{q+1,\ldots ,r+1\}$, and $\sigma (q)=i$, we obtain (42). $\square$

Lemma 9 can be generalized in the following way:

Lemma 11

Let $x(\pi )=x_{i_m j_m}(-1) \cdots x_{i_1 j_1}(-1)$, $i_t\le j_t$, and assume $j_1<\cdots < j_m$. Let $I\subset \{1,\ldots ,\ell \}$ be such that $\{1,\ldots ,j_{m}\}\setminus \{j_1,\ldots ,j_{m}\}\subset I$. If $j_m\in I$, then

$$\begin{aligned} x(\pi ) v_I=0. \end{aligned}$$

Proof

If $m=1$ this is just Lemma 9 since $i_1,j_1\in I$. For $m>1$, we use induction. If $i_m\in I$, then Lemma 9 implies $x(\pi )v_I=0$. If $i_m\notin I$, then $i_m=j_r$, for some $r<m$. By Lemma 10

$$\begin{aligned} x_{j_r j_m} (-1) v_I= x_{j_m j_m} (-1) v_{I'}, \end{aligned}$$

where $I'=(I\setminus \{j_m\})\cup \{j_r\}$. By induction,

$$\begin{aligned} x_{i_r j_r}(-1) \cdots x_{i_1 j_1}(-1) v_{I'} = 0, \end{aligned}$$

which gives the claim.

Lemma 12

Let $x(\pi )=x_{i_m j_m}(-1) \cdots x_{i_1 j_1}(-1)$, $i_t\le j_t$, and assume $j_1< \cdots < j_{m-1} \le j_m$. Let $I\subset \{1,\ldots ,\ell \}$ be such that $\{1,\ldots ,j_{m}\}\setminus \{j_1,\ldots ,j_{m}\}\subset I$. If $j_{m-1}= j_m$, then

$$\begin{aligned} x(\pi ) v_I=0. \end{aligned}$$

Proof

For $m=2$, we have $x(\pi )v_I = x_{i_2 j_2}(-1) x_{i_1 j_2}(-1) v_I$. Assume $i_1\le i_2$. If $i_2=j_2$, then $x(\pi ) v_I=0$, by (35). Otherwise, $i_1,i_2\in I$ and $x(\pi ) v_I \sim x_{j_2 j_2}(-1) x_{i_1 i_2}(-1) v_I=0$, by (39), (36) and Lemma 9.

For $m>2$ we use induction. Assume $i_{m-1}\le i_m$. If $i_m=j_m$, then $x(\pi ) v_I=0$, by (35). Otherwise, by (39) and (36),

$$\begin{aligned} x(\pi )v_I \sim x_{j_m j_m}(-1) x_{i_{m-1} i_m}(-1) x_{i_{m-2} j_{m-2}} \cdots x_{i_1 j_1}(-1) v_I. \end{aligned}$$

If $i_m\in I$, then $x(\pi ) v_I=0$, by Lemma 11. If $i_m\notin I$, then $i_m=j_r$, for some $r<m-1$. By induction,

$$\begin{aligned} x_{i_{m-1} j_r}(-1) x_{i_{r} j_{r}} \cdots x_{i_1 j_1}(-1) v_I=0, \end{aligned}$$

from which the claim follows. $\square$

So far we have described conditions upon which a monomial of “small” degree will annihilate vectors from the top of a standard module. In the following two propositions, we describe in more detail the action of these monomials on vectors from the top.

Proposition 13

Let $x(\pi )=x_{i_m j_m}(-1)\cdots x_{i_2 j_2}(-1) x_{i_1 j_1}(-1)$ satisfy difference conditions, i.e., $i_1<\cdots < i_m$, $j_1<\cdots <j_m$ and $i_t\le j_t$. Set $I=\{1,\ldots ,\ell \}\setminus \{j_1,\ldots ,j_m\}$, $I'=\{i_1,\ldots ,i_m\}$. Then

$$\begin{aligned} x(\pi ) v_I \sim [\omega ] v_{I'}. \end{aligned}$$

(47)

Proof

We first show

$$\begin{aligned} x_{mm}(-1) x_{m-1,m-1}(-1)\cdots x_{22}(-1) x_{11}(-1) v_{m+1,\ldots ,\ell } \sim [\omega ] v_{1 2\cdots m}, \end{aligned}$$

(48)

i.e., we show that $[\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) v_{m+1,\ldots ,\ell }$ is a highest weight vector with the highest weight $\varLambda _m$. Like in the proof of lemma 3, one easily sees that $x_{mm}(-1) \cdots x_{11}(-1) v_{m+1,\ldots ,\ell }\ne 0$. By (32) and Lemma 6, we have

$$\begin{aligned}&x_{-\theta }(1)[\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) v_{m+1,\ldots ,\ell }\\&\quad = [\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) x_{-\theta } (2) v_{m+1,\ldots ,\ell } = 0. \end{aligned}$$

By (29) and (32) and

$$\begin{aligned}&x_{\alpha _i}(0) [\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) v_{m+1,\ldots ,\ell } \\&\quad = [\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) x_{\alpha _i}(0) v_{m+1,\ldots ,\ell } =0, \end{aligned}$$

for $i=m+1,\ldots ,\ell -1$. By (29), (32) and Lemma 9

$$\begin{aligned}&x_{\alpha _m}(0) [\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) v_{m+1,\ldots ,\ell } \\&\quad = [\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) v_{m,m+2,\ldots ,\ell } = 0, \end{aligned}$$

By (29), (32), and (34)

$$\begin{aligned}&x_{\alpha _i}(0) [\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) v_{m+1,\ldots ,\ell } = [\omega ]^{-1}x_{mm}(-1) \cdots x_{ii}(-1)\\&\quad \times x_{i+2,i+2}(-1) \cdots x_{11}(-1) (x_{i+1,i+1}(-1) x_{\alpha _i}(0) + x_{i,i+1}(-1))v_{m+1,\ldots ,\ell } = 0, \end{aligned}$$

for $i=1,\ldots ,m-1$. Since $\alpha _\ell =(\ell \ell )$, by (32) and Lemma 9

$$\begin{aligned}&x_{\alpha _\ell }(0) [\omega ]^{-1}x_{mm}(-1) \cdots x_{11}(-1) v_{m+1,\ldots ,\ell } \\&\quad = [\omega ]^{-1} x_{mm}(-1) \cdots x_{11}(-1) x_{\ell \ell }(-1) v_{m+1,\ldots ,\ell } = 0. \end{aligned}$$

Hence, (48) holds.

Next, ${\mathcal W}$-action on (48) gives

$$\begin{aligned} x_{j_m j_m}(-1)\cdots x_{j_2 j_2}(-1) x_{j_1 j_1}(-1)v_I \sim [\omega ] v_{j_1\cdots j_m}. \end{aligned}$$

(49)

Finally, ${\mathfrak g}_0$-action on (49) gives the claim. Assume that we have shown

$$\begin{aligned}&x_{j_m j_m}(-1)\cdots x_{j_{t+1} j_{t+1}}(-1) x_{n j_{t}}(-1) x_{i_{t-1} j_{t-1}}(-1) \cdots x_{i_1 j_1}(-1)v_I \\ \nonumber&\quad \sim [\omega ] v_{i_1\cdots i_{t-1} n j_{t+1}\cdots j_m}, \end{aligned}$$

(50)

where $i_t<n \le j_t$. Since $[x_{\alpha _{n-1}} (0),x_{n j_{t}}(-1)]=x_{n-1, j_{t}}(-1)$, we act on (50) with $x_{\alpha _{n-1}} (0)$. We claim that what we will get is

$$\begin{aligned}&x_{j_m j_m}(-1)\cdots x_{j_{t+1} j_{t+1}}(-1) x_{n-1, j_{t}}(-1) x_{i_{t-1} j_{t-1}}(-1) \cdots x_{i_1 j_1}(-1)v_I \\ \nonumber&\quad \sim [\omega ] v_{i_1\cdots i_{t-1}, n-1, j_{t+1}\cdots j_m}. \end{aligned}$$

(51)

Note that $[x_{\alpha _{n-1}} (0),x_{j_r j_{r}}(-1)]=0$, for $t<r\le m$.

First, consider the case when $n\in I$. In this case also $[x_{\alpha _{n-1}} (0),x_{i_r j_{r}}(-1)]=0$, for $1\le r< t$. If $n-1\in I$, then $x_{\alpha _{n-1}} (0) v_I=0$ and (51) follows. If $n-1\notin I$, then $x_{\alpha _{n-1}} (0) v_I=v_{I'}$, where $I'=(I\setminus \{n\})\cup \{n-1\}$. Since $n-1\notin I$, then $n-1=j_s$, for some $s<t$. By Lemma 11,

$$\begin{aligned} x_{i_{s} j_{s}}(-1) \cdots x_{i_1 j_1}(-1)v_{I'}=0, \end{aligned}$$

and (51) follows.

Now, consider the case when $n\notin I$. In this case $n=j_s$, for some $r<t$. Then $x_{\alpha _{n-1}} (0) v_I=0$, $[x_{\alpha _{n-1}} (0),x_{i_r j_{r}}(-1)]=0$, for $1\le r< t, r\ne s$, and $[x_{\alpha _{n-1}} (0),x_{i_s j_{s}}(-1)]=x_{i_s, n-1}(-1)$. If $n-1\in I$, then, by Lemma 11,

$$\begin{aligned} x_{i_{s}, n-1}(-1) x_{i_{s-1} j_{s-1}}(-1) \cdots x_{i_1 j_1}(-1)v_{I}=0. \end{aligned}$$

If $n-1\notin I$, then $n-1=j_{s-1}$ and

$$\begin{aligned} x_{i_{s} j_{s-1}}(-1) x_{i_{s-1} j_{s-1}}(-1) \cdots x_{i_1 j_1}(-1)v_{I}=0, \end{aligned}$$

by Lemma 12. In both cases, (51) follows.

After finitely many steps we will reach (47) $\square$

Proposition 14

Let $x(\pi )=x_{i_m j_m}(-1)\cdots x_{i_2 j_2}(-1) x_{i_1 j_1}(-1)$ be such that $j_1<\cdots < j_m$, $i_r\ne i_{t}$ for $r\ne t$, and $i_t\le j_t$. Set $I=\{1,\ldots ,\ell \}\setminus \{j_1,\ldots ,j_m\}$, $I'=\{i_1,\ldots ,i_m\}$. Then $x(\pi ) v_I \sim [\omega ] v_{I'}$.

Proof

Since $x(\pi )$ does not satisfy difference conditions, we can use relations (21) to express $x(\pi )$ in terms of monomials that satisfy difference conditions. We show that in each step of the reduction of $x(\pi )$, we will obtain another monomial $x(\pi ')$ such that $x(\pi )<x(\pi ')$, $x(\pi )v_I \sim x(\pi ')v_I$ and such that colors of factors of $x(\pi ')$ again lie in rows $j_1,\ldots ,j_m$ and columns $i_1,\ldots ,i_m$, as are the colors of $x(\pi )$. In the end we will obtain $x(\pi )v_I=x_{i_{s_m} j_m}(-1)\cdots x_{i_{s_1} j_1}(-1)v_I$, where $i_{s_1}<\cdots < i_{s_m}$, and proposition 13 gives the claim.

Let $x(\pi )=x(\pi _1)x(\pi _2)$, where $x(\pi _1)$ is a leading term of some relation (21). In fact, since colors of factors of $x(\pi )$ all lie in different rows and different columns, relations that we use are (38) and (40).

First, assume that the reduction is made upon relation (38). In this case $x(\pi _1)v_I \sim x(\pi _1')v_I$, with $x(\pi _1)<x(\pi _1')$, and after the reduction we obtain another monomial $x(\pi ')=x(\pi _1')x(\pi _2)$ whose colors lie in the same rows and columns as colors of $x(\pi )$ and $x(\pi _1)<x(\pi _1')$.

Next, assume that the reduction is made upon relation (40). Let $x(\pi _1)=x_{i_t j_t}(-1) x_{i_r j_r}(-1)$, for some $r<t$ and $i_t< i_r< j_r < j_t$. Let

$$\begin{aligned} x(\pi _1')=x_{i_r j_t}(-1)x_{i_t j_r}(-1), \quad x(\pi _1'')=x_{i_t i_r}(-1)x_{j_r j_t}(-1). \end{aligned}$$

Then, by (40),

$$\begin{aligned} x(\pi _1)v_I=C_1 x(\pi _1')v_I+ C_2 x(\pi _1'')v_I, \end{aligned}$$

for some $C_1,C_2\in {\mathbb C}^\times$ and $x(\pi _1)<x(\pi _1'),x(\pi _1'')$. Denote by $x(\pi ')=x(\pi _1')x(\pi _2)$ and $x(\pi '')=x(\pi _1'')x(\pi _2)$. Then

$$\begin{aligned} x(\pi )v_I=C_1 x(\pi ')v_I+ C_2 x(\pi '')v_I, \end{aligned}$$

and $x(\pi )<x(\pi '),x(\pi '')$. Note that colors of $x(\pi ')$ lie in the same rows and columns as colors of $x(\pi )$. We claim that $x(\pi '')v_I=0$. Let n be such that $j_{n}\le i_r < j_{n+1}$. If $i_r\in I$, then

$$\begin{aligned} x_{i_t i_r}(-1) x_{i_n j_n}(-1)\cdots x_{i_1 j_1}(-1)v_I=0, \end{aligned}$$

by Lemma 11. If $i_r\notin I$, then $j_{n}= i_r$ and

$$\begin{aligned} x_{i_t i_r}(-1) x_{i_n j_n}(-1)\cdots x_{i_1 j_1}(-1)v_I=0, \end{aligned}$$

by Lemma 12. In both cases, we get $x(\pi '')v_I=0$. $\square$

Remark 3

Let $x_{i_m j_m}(-1) \cdots x_{i_1 j_1}(-1)$ satisfy difference conditions. Assume

$$\begin{aligned} x_{i_m j_m}(-1) \cdots x_{i_1 j_1}(-1) v_{s_1 \cdots s_{\ell -m}}\ne 0. \end{aligned}$$

(52)

If $\{j_1,\ldots ,j_m\}\cap \{s_1,\ldots ,s_{\ell -m}\}=\emptyset$, then, by Proposition 13,

$$\begin{aligned} x_{i_m j_m}(-1) \cdots x_{i_1 j_1}(-1) v_{s_1 \cdots s_{\ell -m}} =[\omega ] v_{i_1\cdots i_m}. \end{aligned}$$

If $\{j_1,\ldots ,j_m\}\cap \{s_1,\ldots ,s_{\ell -m}\}\ne \emptyset$, we can use Lemma 10 to “switch” indices and reduce the expression (52) to the one appearing in Proposition 14. Concretely: Let t be the smallest possible so that $j_t \in \{s_1,\ldots ,s_{\ell -m}\}$. Then $i_t\notin \{s_1,\ldots ,s_{\ell -m}\}$, by (52) and Lemma 9, and

$$\begin{aligned} x_{i_t j_t}(-1) v_{s_1 s_2 \cdots s_{\ell -m}} \sim x_{j_t j_t}(-1) v_{s_1 \cdots i_t \cdots \underline{j_t} \cdots s_{\ell -m}}, \end{aligned}$$

by Lemma 10. Proceed inductively—reduce the expression

$$\begin{aligned} x_{i_m j_m}(-1) \cdots x_{j_t j_t}(-1) \cdots x_{i_1 j_1}(-1) v_{s_1 \cdots i_t \cdots \underline{j_t} \cdots s_{\ell -m}} \end{aligned}$$

to the one appearing in Proposition 14.

Hence, in this case, there is no index occurring more than twice in the sequence $i_1,\ldots ,i_m$,  $j_1,\ldots ,j_m$,  $s_1,\ldots ,s_{\ell -m}$, and

$$\begin{aligned} x_{i_m j_m}(-1) \cdots x_{i_1 j_1}(-1) v_{s_1 \cdots s_{\ell -m}} \sim [\omega ]v_{r_1 \cdots r_m}, \end{aligned}$$

where $r_1,\ldots ,r_m$ are exactly those indices appearing twice in the sequence.

8 Proof of linear independence

Let $x(\pi )=x_{i_m j_m}(-1)\cdots x_{i_2 j_2}(-1) x_{i_1 j_1}(-1)$ satisfy difference and initial conditions on $W(\varLambda _i)$. Set $J=\{1,\ldots ,\ell \}\setminus \{j_1,\ldots , j_m \}$, $I=\{i_1,\ldots ,i_m\}$. By Proposition 7 there are operators, denoted by $w_1, w_2$ that commute with $\tilde{\mathfrak {g}}_1$ and such that

$$\begin{aligned} w_1 v_{\varLambda _i}=v_J,\quad w_2 v_I= v_{\varLambda _{i_m}}. \end{aligned}$$

(53)

Moreover, operators $w_1$ and $w_2$ act on $V_{i}$ and $V_m$, correspondingly, as multiplication in the exterior algebra by suitable vectors. Let $w_2^{\omega } = [\omega ]w_2 [\omega ]^{-1}$; it also commutes with $\tilde{\mathfrak {g}}_1$. Then, by Proposition 13,

$$\begin{aligned} w_2^\omega w_1 x(\pi ) v_{\varLambda _i} \sim [\omega ] v_{\varLambda _{i_m}}. \end{aligned}$$

Let $x(\mu )=x_{r_{n} s_{n}}(-1)\cdots x_{r_2 s_2}(-1) x_{r_1 s_1}(-1)$ also satisfy difference and initial conditions on $W(\varLambda _i)$, and let $x(\mu )>x(\pi )$. We will show that

$$\begin{aligned} w_2^\omega w_1 x(\mu ) v_{\varLambda _i}=0. \end{aligned}$$

(54)

If $n>m$, then either

$$\begin{aligned} x_{r_{m} s_{m}}(-1)\cdots x_{r_1 s_1}(-1) v_J=0 \end{aligned}$$

or

$$\begin{aligned} x_{r_{m} s_{m}}(-1)\cdots x_{r_1 s_1}(-1) v_J \sim [\omega ] v', \end{aligned}$$

for some $v'\in V_m$ (cf. Remark 3). In the first case, Relation (54) directly follows. In the second case, we have

$$\begin{aligned} x(\mu )v_J \sim [\omega ]x_{r_{n} s_{n}}(0)\cdots x_{r_{m+1} s_{m+1}}(0) v'=0 \end{aligned}$$

by Lemma 6. Hence, (54) follows.

If $n=m$, then there exists t, $1\le t \le m$, such that $(r_1 s_1)=(i_1 j_1)$, $\ldots$, $(r_{t-1} s_{t-1})= (i_{t-1} j_{t-1})$ and $(r_{t} s_{t})> (i_{t} j_{t})$. Then either $r_t=i_t$ and $s_t<j_t$, or $r_t < i_t$.

Consider first the case when $r_t=i_t$ and $s_t<j_t$. Then $j_{t-1}=s_{t-1}<s_t<j_t$, hence $s_t\in J$. Then $x_{r_t s_t}(-1) \cdots x_{r_1 s_1}(-1) v_J=0$, by Lemma 11, and (54) follows.

Now, consider the case when $r_t < i_t$. If $x(\mu )v_J=0$, we are done. If $x(\mu )v_J\ne 0$, then, by Remark 3, in the multiset $\{r_1,\ldots ,r_m\}\cup \{s_1,\ldots ,s_m\}\cup J$ there is no index occurring more than twice. Furthermore, since $r_t<j_t$ and $s_p=j_p,$ for $p<t$, index $r_t$ appears twice in the aforementioned multiset. Hence $x(\mu )v_J \sim [\omega ] v_{I'}$ and $r_t\in I'$. Since $r_t\notin I$ and $r_t < i_t$, the action of $w_2$ will annihilate $v_{I'}$ (see (53) and Proposition 7), i.e., $w_2^\omega [\omega ] v_{I'}=0$.

Set $w=w_2^\omega w_1$. By the above considerations, we have the following.

Proposition 15

Let $x(\pi )$ satisfy difference and initial conditions for $L(\varLambda _i)$. Write $x(\pi )=x(\pi _1)x(\pi _2)$, where $x(\pi _1)$ is the $(-1)$-part of a monomial, and $x(\pi _2)$ the rest of the monomial. Then there exists an operator $w:L(\varLambda _i) \rightarrow L(\varLambda _{i'})$ such that

• w commutes with $\tilde{\mathfrak {g}}_1$,

• $w x(\pi _1) v_{\varLambda _i} \sim [\omega ] v_{\varLambda _{i'}},$

• $x(\pi _2^+)$ satisfies IC and DC for $L(\varLambda _{i'})$, and

• if $x(\pi ')$ has a $(-1)$-part $x(\pi _1')$ greater than $x(\pi _1)$, then $w x(\pi ') v_{\varLambda _i}=0$.

Proof

We have already shown the majority of the claims. It remains to see that $x(\pi _2^+)$ satisfies IC and DC for $L(\varLambda _{i'})$, but this is clear from the description of level 1 difference conditions in (25) and the definition of initial conditions (see also Remark 2). $\square$

Like in the $A_\ell ^{(1)}$-case, Proposition 5 enables us to straightforwardly generalize proposition 15 for higher levels (cf. [32]). Also, the proof of linear independence is the same as in the $A_\ell ^{(1)}$-case, hence we give here only the sketch of the proof.

Theorem 16

The set

$$\begin{aligned} \{x(\pi )v_\varLambda \,|\, x(\pi ) \ \text {satisfies DC and IC for}\ L(\varLambda )\} \end{aligned}$$

is a basis of $W(\varLambda )$.

Sketch of proof

Assume

$$\begin{aligned} \sum c_\pi x(\pi )v_\varLambda =0, \end{aligned}$$

(55)

where all monomials $x(\pi )$ satisfy difference and initial conditions for $W(\varLambda )$. Fix $x(\pi )$ in (55) and assume that $c_{\pi '}=0$ for $x(\pi ')<x(\pi )$. We show that $c_\pi =0$.

Choose an operator w from Proposition 15 and apply it on (55). By Proposition 15, we get

$$\begin{aligned} 0= & {} w \sum c_{\pi '}x(\pi ') v_\varLambda \\= & {} w \sum _{\pi _1'>\pi _1}c_{\pi '}x(\pi ') v_\varLambda + w \sum _{\pi _1'<\pi _1}c_{\pi '}x(\pi ') v_\varLambda + w \sum _{\pi _1'=\pi _1}c_{\pi '}x(\pi ') v_\varLambda \\= & {} w \sum _{\pi _1'=\pi _1}c_{\pi '}x(\pi ') v_\varLambda \sim \sum _{\pi _1'=\pi _1}c_{\pi '}x(\pi _2') [\omega ] v_{\varLambda '}\\= & {} [\omega ] \sum _{\pi _1'=\pi _1}c_{\pi '}x(\pi _2'^+) v_{\varLambda '}. \end{aligned}$$

Since $[\omega ]$ is injective, it follows that

$$\begin{aligned} \sum _{\pi _1'=\pi _1}c_{\pi '}x(\pi _2'^+) v_{\varLambda '}=0. \end{aligned}$$

This is a relation of linear dependence between monomial vectors satisfying difference and initial conditions for $W(\varLambda ')$ with all monomials of degree greater than the degree of $x(\pi )$. By the induction hypothesis, they are linearly independent, and, in particular, $c_\pi =0$.