On Flux-Difference Residual Distribution Methods

Abstract

In this paper, the properties of the newly developed flux-difference residual distribution methods will be analyzed. The focus would be on the order-of-accuracy and stability variations with respect to changes in grid skewness. Overall, the accuracy loss and the stability range of the new methods are comparable with the existing residual distribution methods. It will also be shown that new method has a general mathematical formulation which can easily recover the existing residual distribution methods.

1 Introduction

Although finite volume (FV) methods are widely used in many computational fluid dynamics (CFD) applications, but FV methods suffer from severe results degradation on skewed grids [9, 10, 13] which is unavoidable in industrial CFD. On the other hand, residual distribution (RD) methods are known to be less sensitive to mesh variations [4, 5, 9]. RD methods are also more compact which allows a more efficient parallel computation [15] and have a natural platform to incorporate multidimensional fluid physics [7].

However, there is still lot to be done for RD methods. Most RD methods are developed from mainly steady-state inviscid equations. Most of these methods will be at best first order accurate in space for unsteady calculations [2] even if they are high order accurate for steady-state problems unless there is a costly implicit sub-iterative process being applied at every time-step. To the authors’ best knowledge, there is only one type of explicit second-order RD scheme for unsteady calculations [3, 18]. In fact, most RD methods cannot even preserve second-order accuracy when solving steady-state scalar advection-diffusion problems which is the prerequisite of solving the steady-state Navier–Stokes equations [16]. One way to preserve second-order accuracy when solving advection-diffusion problems is the unified first-order hyperbolic systems approach [17].

Ismail and Chizari [11] have developed a new class of RD methods which ensures automatic conservation of the primary variables without any dependence on cell-averaging for any well-posed equations and preserves the spatial second-order accuracy on unsteady problems using any consistent explicit time integration scheme. The approach has also been extended to solve advection-diffusion problems with much success [19]. Since these flux-difference RD methods are new, very little has been done to understand the inherent properties of the scheme.

In this paper, our main intention is to provide a pure mathematical analysis to determine the mathematical properties of the newly developed flux-difference RD method on triangular grids when solving the two-dimensional linear advection equation. The analysis includes the determination of its positivity condition, stability analysis and the study of the order-of-accuracy variations as a function of grid skewness.

2 Residual Distribution Methods

Consider the two-dimensional scalar advection equation,

$$\begin{aligned} u_t+\mathbf {\nabla }\cdot \mathbf {F}=0, \end{aligned}$$

(1)

where u is the unknown quantity in temporal and two-dimensional space. The fluxes are $\mathbf {F}=(au)\hat{i}+(bu)\hat{j}=\mathbf {\lambda }{u}$. The $\hat{i}$ and $\hat{j}$ are the unique characteristic vector along x- and y-direction. $\mathbf {\lambda }$ is the wavespeed that defines the speed and direction of advection of u.

The main concept of the residual distribution method is finding the sub-residuals (or signals) for each point from the total residual of a cell (element) as shown in Fig. 1. By using Green’s theorem, the total cell residual ($\phi _{\mathrm{T}}$) of Eq. 1 would be

$$\begin{aligned} \phi _\mathrm{T}=\iint u_t \hbox {d}A=-\iint \mathbf {\nabla }\cdot \mathbf {F} \hbox {d}A=-\oint \mathbf {F}\cdot \hat{n} \hbox {d}S. \end{aligned}$$

(2)

In discrete form, the total residual over a triangular element using the trapezoidal rule by using the three nodes $p=(i,j,k)$ [11] is

$$\begin{aligned} \phi _\mathrm{T}=\frac{1}{2}\sum _{p}\mathbf {{F}_p}\cdot \mathbf {n_p}-\underbrace{\frac{1}{2}\sum _{p}\mathbf {{F}^*}\cdot \mathbf {n_p}}_{=0} =\frac{1}{2}\sum _{p}\left( \mathbf {{F}_p}-\mathbf {{F}^*}\right) \cdot \mathbf {n_p}, \end{aligned}$$

(3)

where $\mathbf {n_p}$ are the inward normal to the side opposite of node p and $\mathbf {F}^*$ is the degree of freedom for the flux-difference RD method. The way $\phi _\mathrm{T}$ is distributed locally to each node $\phi _i$ will define each type of RD method.

Fig. 1

Residual distributed over triangular mesh

2.1 Flux-Difference RD Methods

This newly developed RD method [11] has two components: isotropic signals and artificial signals.

2.1.1 Isotropic Signals

This isotropic signals ($\phi ^\text {iso}$) distribution is a central-type flux difference scheme of which the total residual of is equally distributed to each of the three nodes within an element. The $\phi ^\text {iso}$ also depends on $\mathbf {F}(u)$ rather than u, which is one of the key features of this alternative RD method that is quite different from the ones currently available in the literature. Similar to a FV approach, conservation of the primary variables (u) is automatic for the isotropic signals integrated over each local element since the summation of any $\mathbf {F}^*$ would be zero within each element. $\mathbf {F}^*$ is one of the degrees of freedom for which we could impose certain physical conditions. For the time being we choose an arithmetic average of three nodal values for $\mathbf {F}^*$ within the element. $\mathbf {F}^*$ will only affect the nodes of each element since overall update is on the nodes, where each node p would have an equal amount of sub-residuals.

$$\begin{aligned} \phi _p^{\text {iso}}&= \frac{1}{2}(\mathbf {F}_p-\mathbf {F}^*)\cdot \mathbf {n_p}, \quad p=i,j,k. \end{aligned}$$

(4)

2.1.2 Artificial Signals

Since the isotropic signals is pure central approach, it requires some form of artificial diffusion as an offset to achieve stability [11]. The idea is to add the artificial terms to the isotropic signals such that the primary variable u is discretely conserved over a local element (cell) but at the same time, will discretely augment u on each node.

Let us focus on a local element which has nodes i, j, k. Define

$$\begin{aligned} {[}\cdot ]_{ji}=(\cdot )_j-(\cdot )_i \end{aligned}$$

so for node i, the newly proposed sub-residuals are

$$\begin{aligned} \phi _i=\underbrace{\frac{1}{2}(\mathbf {F}_i-\mathbf {F}^*)\cdot \mathbf {n_i}}_{\phi ^{\text {iso}}_i} \underbrace{-\alpha [u]_{ji} -\beta [u]_{kj}-\gamma [u]_{ik}}_{\phi ^\text {art}_i}. \end{aligned}$$

(5)

Similarly, the sub-residuals to nodes j, k can also be determined as in [11]. $\alpha ,\beta ,\gamma$ are additional degrees of freedom for the new RD method. It will be shown in the next subsection that the flux-difference RD method can also be made upwind to account for physical wave propagation by controlling the artificial signals.

2.2 Recovery of Classic RD Methods

There will be a unique signal distribution ($\tilde{\phi _i}$) which will recover the classic RD methods by solving Eq. 5 for $\alpha ,\beta$ and $\gamma$. For each node i, j, k,

$$\begin{aligned} \left\{ \begin{array}{l} \phi ^{\text {iso}}_i -\alpha [u]_{ji}-\beta [u]_{kj}-\gamma [u]_{ik}=\tilde{\phi }_i\\ \phi ^{\text {iso}}_j -\alpha [u]_{kj}-\beta [u]_{ik}-\gamma [u]_{ji}=\tilde{\phi }_j\\ \phi ^{\text {iso}}_k -\alpha [u]_{ik}-\beta [u]_{ji}-\gamma [u]_{kj}=\tilde{\phi }_k. \end{array} \right. \end{aligned}$$

(6)

Equation 6 is linearly dependent for $\alpha ,\beta$ and $\gamma$, because the summation of both sides will be the total cell residual($\phi _\mathrm{T}$). This requires at least one parameter out of $\alpha ,\beta$ and $\gamma$ to be specified. From [11], one of the conditions for entropy-stability is that $\gamma =-\alpha$ and conservation requires that $\tilde{\phi }_i=-\tilde{\phi }_j-\tilde{\phi }_k$. Thus, the first equation of Eq. (6) is redundant since it can be rewritten in terms of $\tilde{\phi }_j, \tilde{\phi }_k$. Overall, we will now have two linearly independent equations that can be solved for $\alpha$ and $\beta$.

$$\begin{aligned} \left\{ \begin{array}{l} \phi ^{\text {iso}}_j-\alpha \left( [u]_{kj}-[u]_{ji}\right) -\beta [u]_{ik}=\tilde{\phi }_j\\ \phi ^{\text {iso}}_k-\alpha \left( [u]_{ik}-[u]_{kj}\right) -\beta [u]_{ji}=\tilde{\phi }_k. \end{array}\right. \end{aligned}$$

(7)

Therefore,

$$\begin{aligned} \begin{array}{l} \displaystyle \alpha =\frac{\left( \phi ^{\text {iso}}_j-\tilde{\phi }_j\right) [u]_{ij}+\left( \phi ^{\text {iso}}_k-\tilde{\phi }_k\right) [u]_{ik}}{\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }\\ \displaystyle \beta =\frac{\left( \phi ^{\text {iso}}_j-\tilde{\phi }_j\right) \left( [u]_{ik}-[u]_{kj}\right) -\left( \phi ^{\text {iso}}_k-\tilde{\phi }_k\right) \left( [u]_{ij}-[u]_{jk}\right) }{\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }. \end{array} \end{aligned}$$

(8)

Note that these $\alpha$ and $\beta$ are well-posed since the denominator will be always positive except for the trivial case for which the signals are all zero.

For the scalar linear advection, using $k_i=\frac{1}{2}\mathbf {\lambda }^*\cdot {\mathbf {n}_i}$ will yield

$$\begin{aligned} \begin{array}{l} {\phi }^{\text {iso}}_i=k_i(u_i-\bar{u})=\frac{1}{3}k_i([u]_{ij}-[u]_{ki}) \\ {\phi }^{\text {iso}}_j=k_j(u_j-\bar{u})=\frac{1}{3}k_j([u]_{jk}-[u]_{ij}) \\ {\phi }^{\text {iso}}_k=k_k(u_k-\bar{u})=\frac{1}{3}k_k([u]_{ki}-[u]_{jk}). \end{array} \end{aligned}$$

(9)

2.2.1 N-Scheme Recovery

The N-scheme is a classic first-order multidimensional upwind RD method. Essentially, it has two upwind conditions: one target and two target cells [1].

Recall that the signals (subresiduals) of classic N scheme are

$$\begin{aligned} \tilde{\phi _i^{N}}=k_i^+\left( u_i-\hat{u}\right) ,\quad \hat{u}=\left( \sum _pk_p^-\right) ^{-1}\sum _p k_p^-u_p,\quad p=i,j,k. \end{aligned}$$

(10)

$k_i$ is projection of the wavespeed $\mathbf {\lambda }$ onto the edge opposite node i within an element. $u_i$ refers to the values of node i opposite of the edge i. And, the upwind conditions are

$$\begin{aligned} k_i^+=\left\{ \begin{array}{ll} k_i&{}\quad k_i\ge 0\\ 0&{}\quad k_i<0 \end{array} \right. ,\quad k_i^-=\left\{ \begin{array}{ll} 0&{}\quad k_i\ge 0\\ k_i&{}\quad k_i<0. \end{array} \right. \end{aligned}$$

(11)

By choosing the following,

$$\begin{aligned} \begin{array}{l} \alpha ^\text {N}= \frac{([u]_{ji}+[u]_{ki})\phi _\mathrm{T}}{6\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }\\ \beta ^\text {N}= \frac{k_j-k_k}{6}+\frac{k_j[u]_{ik}^2-k_k[u]_{ij}^2}{[u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2}, \end{array} \end{aligned}$$

(12)

we shall recover the 2-target N-scheme as before.

For one-target cell,

$$\begin{aligned} \alpha ^\text {OneTarget}= & {} \frac{\phi _\mathrm{T}(4u_i+u_j+u_k)-3\left( k_iu_i^2+k_ju_j^2+k_ku_k^2\right) }{3\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }\nonumber \\ \beta ^\text {OneTarget}= & {} \left( \frac{k_j-k_k}{6}\right) \left( \frac{6[u]_{jk}^2}{[u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2}-1\right) . \end{aligned}$$

(13)

2.2.2 LDA Recovery

For two-target,

$$\begin{aligned} \begin{array}{l} \alpha ^\text {LDA}= -\frac{k_j+k_k}{6}+\frac{3\phi _{\mathrm{T}}^2+2(k_j+k_k)[k]_{jk}[u]_{jk}\left( [u]_{ij}+[u]_{ik}\right) }{6(k_j+k_k)\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }\\ \beta ^\text {LDA}= -\frac{k_j-k_k}{6}+\frac{\phi _{\mathrm{T}}\left( k_i[u]_{jk}+k_j[u]_{ki}+k_k[u]_{ij}\right) }{(k_j+k_k)\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) } +\frac{\left( k_j+k_k\right) [k]_{jk}[u]_{jk}^2}{(k_j+k_k)\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }. \end{array} \end{aligned}$$

(14)

Note that the one-target LDA is identical with one-target N scheme.

2.2.3 Lax–Friedrichs Method

The signal distribution for

Lax–Friedrichs using $\alpha$ and $\beta$,

$$\begin{aligned} \alpha ^\text {LxF}= & {} \frac{2|k|_\text {max}-k_j-k_k}{6}+\frac{\left( [u]_{ij}+[u]_{ik}\right) \left( k_j[u]_{ik}+k_k[u]_{ij}\right) }{3\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }\nonumber \\ \beta ^\text {LxF}= & {} \frac{k_k-k_j}{6}+\frac{[u]_{jk}\left( k_j[u]_{ik}+k_k[u]_{ij}\right) }{[u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2}. \end{aligned}$$

(15)

2.2.4 Lax–Wendroff Recovery

$$\begin{aligned} \alpha ^\text {LxW}= & {} -\frac{k_j+k_k}{6}+\frac{6\Delta t\phi _{\mathrm{T}}^2+2A\left( [u]_{ij}+[u]_{ik}\right) \left( 2[k]_{jk}[u]_{jk}-2\phi _{\mathrm{T}}\right) }{12A\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }\nonumber \\ \beta ^\text {LxW}= & {} -\frac{k_j-k_k}{6}+\frac{\Delta t\phi _{\mathrm{T}}\left( k_i[u]_{jk}+k_j[u]_{ki}+k_k[u]_{ij}\right) }{2A\left( [u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2\right) }\nonumber \\&+\frac{[u]_{jk}\left( [k]_{jk}[u]_{jk}-\phi _{\mathrm{T}}\right) }{[u]_{ij}^2+[u]_{jk}^2+[u]_{ki}^2}, \end{aligned}$$

(16)

where A is the cell area.

The specific $\alpha ,\beta ,\gamma$ formulation for the newly developed flux-difference RD method will be disclosed in the next section.

Fig. 2

Dual median area of a point ($A_p$ is the shaded area)

2.3 Time Integration Step

For each point, we could evaluate summation of the signals from neighboring cells as shown in Fig. 2. The time evolution of the solution is computed as

$$\begin{aligned} u^{m+1}_p=u^m_p-\frac{\Delta t}{A_p}\sum _j\phi _p^j, \end{aligned}$$

(17)

where j shows the neighboring cells to the main node (point) p.

3 Properties of the Flux-Difference RD Methods

3.1 Positivity Condition

Hyperbolic-type PDEs such as the scalar advection may contain discontinuities such as shockwaves. It is vital to capture a monotone shock profile, which can be mathematically presented as positivity. The constraints of positivity are defined as

$$\begin{aligned} \left( \frac{\partial u}{\partial t}\right) _i+\sum _ec_{ie}(u_i-u_e)=0 ,\quad c_{ie}\ge 0,\quad \forall {i,e},\quad i\ne e, \end{aligned}$$

(18)

which is identical to [12] LED (Local Extremum Diminishing) criterion. Recall that the signal distribution for a flux-differencing RD method is,

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{\phi }_i=\frac{1}{3}k_i\left( [u]_{ij}-[u]_{ki}\right) -\alpha [u]_{ji} -\beta [u]_{kj} -\gamma [u]_{ik} \\ \tilde{\phi }_j=\frac{1}{3}k_j\left( [u]_{jk}-[u]_{ij}\right) -\alpha [u]_{kj} -\beta [u]_{ik} -\gamma [u]_{ji} \\ \tilde{\phi }_k=\frac{1}{3}k_k\left( [u]_{ki}-[u]_{jk}\right) -\alpha [u]_{ik} -\beta [u]_{ji} -\gamma [u]_{kj}. \end{array} \right. \end{aligned}$$

(19)

Simplifying the previous equation will reduce to

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{\phi }_i =\left( \frac{2}{3}k_i+\alpha -\gamma \right) u_i +\left( -\frac{1}{3}k_i-\alpha +\beta \right) u_j +\left( -\frac{1}{3}k_i+\gamma -\beta \right) u_k \\ \tilde{\phi }_j =\left( -\frac{1}{3}k_j+\gamma -\beta \right) u_i +\left( \frac{2}{3}k_j+\alpha -\gamma \right) u_j +\left( -\frac{1}{3}k_j-\alpha +\beta \right) u_k \\ \tilde{\phi }_k =\left( -\frac{1}{3}k_j-\alpha +\beta \right) u_i +\left( -\frac{1}{3}k_j+\gamma -\beta \right) u_j +\left( \frac{2}{3}k_j+\alpha -\gamma \right) u_k. \end{array} \right. \end{aligned}$$

(20)

To achieve the mathematical positivity condition (Eq. (18)) requires that

$$\begin{aligned} \left\{ \begin{array}{l} \alpha -\gamma>-\frac{2}{3}k_i \\ \alpha -\gamma>-\frac{2}{3}k_j \\ \alpha -\gamma>-\frac{2}{3}k_k \end{array} \right. \Rightarrow \alpha -\gamma>\frac{2}{3}\max (-k_i,-k_j,-k_k) \Rightarrow \alpha -\gamma >-\frac{2}{3}k_\text {min}, \end{aligned}$$

(21)

with

$$\begin{aligned} \left\{ \begin{array}{l} \beta<\frac{1}{3}k_i+\alpha \\ \beta<\frac{1}{3}k_j+\alpha \\ \beta<\frac{1}{3}k_k+\alpha \end{array} \right. \Rightarrow \beta<\frac{1}{3}\min (k_i,k_j,k_k)+\alpha \Rightarrow \beta <\frac{1}{3}k_\text {min}+\alpha , \end{aligned}$$

(22)

and,

$$\begin{aligned} \left\{ \begin{array}{l} \beta>-\frac{1}{3}k_i+\gamma \\ \beta>-\frac{1}{3}k_j+\gamma \\ \beta>-\frac{1}{3}k_k+\gamma \end{array} \right. \Rightarrow \beta>\frac{1}{3}\max (-k_i,-k_j,-k_k)+\gamma \Rightarrow \beta >-\frac{1}{3}k_\text {min}+\gamma . \end{aligned}$$

(23)

Thus, the positivity condition will be

$$\begin{aligned} \alpha -\gamma >-\frac{2}{3}k_\text {min},\qquad \gamma -\frac{1}{3}k_\text {min}<\beta <\alpha +\frac{1}{3}k_\text {min}. \end{aligned}$$

(24)

Since $-\frac{2}{3}k_\text {min}$ is always positive then $\alpha >\gamma$ is a necessary condition to get positivity. Combining $\alpha >\gamma$ with the entropy-stability condition [11],

$$\begin{aligned} \gamma =-\alpha ,\quad \beta =0, \end{aligned}$$

(25)

therefore, the inequalities reduce into

$$\begin{aligned} \alpha >-\frac{1}{3}k_\text {min}. \end{aligned}$$

(26)

But $k_\text {min} \ge {0}$ and the fact that larger $\alpha$ corresponds to increasing entropy generation (hence increasing dissipation)[11], the best condition for positivity is

$$\begin{aligned} \alpha =-\frac{1}{3}k_\text {min}. \end{aligned}$$

(27)

To make the dimensions correct for the artificial signals in Eq. (5), we could select the following form for $\alpha$ based on the work of [11].

$$\begin{aligned} \alpha =\left( \frac{h}{L_\mathrm{r}}\right) ^q|\mathbf {\lambda }|h, \end{aligned}$$

(28)

where the $L_\mathrm{r}$ is a reference length and, $\mathbf {\lambda }$ is the cell characteristic vector.

Lemma 1

The local positivity is satisfied if and only if,

$$\begin{aligned} q\le \frac{\ln \left( -\frac{\min (\mathbf {d}\cdot \mathbf {n}_p)}{3h}\right) }{\ln \left( \frac{h}{L_\mathrm{r}}\right) }. \end{aligned}$$

(29)

Proof

The condition of Eq. (26) will be,

$$\begin{aligned} \left( \frac{h}{L_\mathrm{r}}\right) ^q|\mathbf {\lambda }|h\ge -\frac{1}{3}k_\text {min}, \end{aligned}$$

(30)

hence,

$$\begin{aligned} \left( \frac{h}{L_\mathrm{r}}\right) ^q\ge -\frac{\min (\mathbf {\lambda }\cdot \mathbf {n}_p)}{3|\mathbf {\lambda }|h}=-\frac{\min (\hat{d}\cdot \mathbf {n}_p)}{3h}, \end{aligned}$$

(31)

where $\hat{d}$ is the unique characteristic vector defined in [2]. Consequently,

$$\begin{aligned} q\le \frac{\ln \left( -\frac{\min (\hat{d}\cdot \mathbf {n}_p)}{3h}\right) }{\ln \left( \frac{h}{L_\mathrm{r}}\right) }, \end{aligned}$$

(32)

which is showing an approximation for q to satisfy local positivity. Note that $\ln \left( \frac{h}{L_\mathrm{r}}\right)$ is negative because $\frac{h}{L_\mathrm{r}}$ is considered very small therefore, the equality is reversed. $\square$

3.2 Truncation Error

Following the work of [4], the first step would be to determine general spatial update equation prior to the TE analysis. The equation could be discretely written in the following form.

$$\begin{aligned} u_i^{n+1}= u_i^{n}-\frac{\Delta t}{A_i}\left( w_iu_i+\sum _jw_ju_j\right) ^n. \end{aligned}$$

(33)

Note that $A_i$ is the median-dual cell area. Assume j denotes the neighboring nodes and $w_j$ is the coefficient distribution of the residual to that node. It is also assumed for this analysis that $(a,b)> 0$ and $\frac{b}{a} < \frac{h_2}{h}$. The analysis for $\frac{b}{a} > \frac{h_2}{h}$ follows the same steps and will not be shown here for conciseness.

In the limit of steady state, $u^{n+1}_i\rightarrow {u^{n}_i}$. Thus, the terms inside the parentheses in Eq. 33 will be the truncation error (TE).

$$\begin{aligned} \text {TE}=w_iu_i+\sum _jw_ju_j. \end{aligned}$$

(34)

Using the Taylor series expansion of the neighboring points about the main point of interest (node 0) as shown in Fig. 3, the TE will be determined. For a right running (RR) triangular grid, the Taylor series expansion of the neighboring points about the main node 0 is given as the following [4].

$$\begin{aligned} u_j = \sum _{d=0}^{\infty } \left( \frac{1}{d!} \sum _{k=0}^{d} \frac{d!}{(d-k)!k!} \frac{\partial ^d u}{\partial t^{d-k}\partial n^k} \left( l_t^j\right) ^{d-k}\left( l_n^j\right) ^k \right) , \end{aligned}$$

(35)

where $l_t^j$ and $l_n^j$ are the tangential to streamline and normal to streamline distances, respectively, for node j from the main node of interest i. The $\frac{\partial ^d u}{\partial t^{d-k}\partial n^k}$ is the $d^{th}$ order partial derivative with respect to tangential direction along the streamline, t and normal, n.

Fig. 3

Right-running grid topology. The characteristic line is $y=\frac{b}{a}x$

3.3 Formal Order-of-Accuracy on Structured Triangular Grids

To establish the order-of-accuracy for the “flux-difference” approach, first we need to determine its truncation error (TE) in general form with arbitrary $(\alpha ,\beta ,\gamma )$. For this case, $\left| \left| \mathbf {\lambda }\right| \right| =\sqrt{a^2+b^2}$.

The structured triangular grids would have uniform grid length and height with dimensions $(h_1,h_2)$. For conciseness, we rewrite the grid length in terms of h and the height in terms of a stretching factor (s) of the grid length.

$$\begin{aligned} h_1=h,\qquad h_2=hs. \end{aligned}$$

(36)

Note that the grid stretching parameter s is related to grid skewness by $s=2\tan \left( \frac{\pi }{2}Q\right)$ [4] for a right triangle. For $Q=1$, the stretching parameter is infinite.

Recall that the “flux-difference” signal distribution

$$\begin{aligned} \phi _i&=\underbrace{\frac{1}{2}(\mathbf {F}_i-\mathbf {F}^*)\cdot \mathbf {n_i}}_{\phi ^\text {iso}_i}\underbrace{-\alpha [u]_{ji}-\beta [u]_{kj}-\gamma [u]_{ik}\phantom {\frac{1}{2}}}_{\phi ^\text {art}_i}. \end{aligned}$$

(37)

As it was mentioned before, $(\alpha ,\beta ,\gamma )$ contain a length scale from the cell to ensure consistent units as in Eq. 28. Thus, we define the dimensionless parameters ($\tilde{\alpha }, \tilde{\beta }, \tilde{\gamma }$) as the following.

$$\begin{aligned} \alpha =\tilde{\alpha }\left| \left| \mathbf {\lambda }\right| \right| h,\quad \beta =\tilde{\beta }\left| \left| \mathbf {\lambda }\right| \right| h,\quad \gamma =\tilde{\gamma }\left| \left| \mathbf {\lambda }\right| \right| h. \end{aligned}$$

(38)

The TE analysis would depend on the isotropic and artificial signals about node 0 (Fig. 3).

3.3.1 Isotropic Signals

The isotropic signal truncation error is given as the following.

$$\begin{aligned} \text {TE}^\text {iso}=\frac{1}{A_i}\sum _e\phi _e^\text {iso}. \end{aligned}$$

(39)

We could expand the signals coming from each element in terms of u. For instance, the signals from elements 012, 023 and 032 are written as follows.

$$\begin{aligned} \phi _{012}^\text {iso}&=-\frac{ahs}{2}\left( u_0-\frac{1}{3}(u_0+u_1+u_2)\right) \end{aligned}$$

(40)

$$\begin{aligned} \phi _{023}^\text {iso}&=-\frac{bh}{2}\left( u_0-\frac{1}{3}(u_0+u_2+u_3)\right) \end{aligned}$$

(41)

$$\begin{aligned} \phi _{032}^\text {iso}&=\frac{ahs-bh}{2}\left( u_0-\frac{1}{3}(u_0+u_3+u_5)\right) . \end{aligned}$$

(42)

We could do a similar procedure for other signals coming from other elements, and thus, the TE reduces to the following.

$$\begin{aligned} \begin{array}{rl} \text {TE}^\text {iso}=&{}\displaystyle \frac{1}{6hs}\left( a s\left( 2 u_1+u_2-u_3-2u_5-u_6+u_7\right) \right. \\ &{}\displaystyle \quad \left. +\,b\left( -u_1+u_2+2u_3+u_5-u_6-2u_7\right) \right) . \end{array} \end{aligned}$$

(43)

By performing a Taylor series expansion about node 0, the overall truncation error of the isotropic signals can be written as below.

$$\begin{aligned} \begin{array}{rl} \text {TE}^\text {iso}=&{}\displaystyle \left( a^2 \left( u_\text {ttt}+s u_\text {ttn}+s^2 u_\text {tnn}\right) \right. \\ &{}\displaystyle +\,a b \left( s u_\text {ttt}+\left( 2 s^2-2\right) u_\text {ttn}-su_\text {tnn}\right) \\ &{}\displaystyle \left. +\,b^2 \left( s^2u_\text {ttt}-su_\text {ttn}+u_\text {tnn}\right) \right) \left( \frac{h^2}{6 \sqrt{a^2+b^2}}\right) +O\left( h^4\right) . \end{array} \end{aligned}$$

(44)

This implies that the isotropic signals are second-order accurate in general (even unsteady problems), unlike most RD methods. For inviscid steady-state conditions, we expect no changes in the derivatives tangential to the streamline, and thus the following is recovered.

$$\begin{aligned} \text {TE}^\text {iso}=\left( -\frac{a b \left( 2 a^4 s^4-5 a^3 b s^3+5 a b^3 s-2 b^4\right) }{360 \left( a^2+b^2\right) ^{5/2}}\right) u_\text {nnnnn}h^4+O\left( h^5\right) . \end{aligned}$$

(45)

The isotropic signals is fourth-order accurate for inviscid steady-state conditions.

3.3.2 Artificial Signals

Based on Eq. (38), the truncation error for the artificial terms of the signals could also be determined.

$$\begin{aligned} \text {TE}^\text {art}=\frac{1}{A_i}\sum _e\phi _e^\text {art}. \end{aligned}$$

(46)

By expanding each signal coming from the respective element,

$$\begin{aligned} \begin{array}{rl} \text {TE}^\text {art}=&{} \frac{\left| \left| \mathbf {\lambda }_\text {cell}\right| \right| }{h s}\left( \tilde{\alpha }_1\left( 3 u_0-u_1-u_3-u_6\right) +\tilde{\alpha }_2\left( 3 u_0-u_2-u_5-u_7\right) \right. \\ &{} +\,\tilde{\beta }_1 \left( u_1-u_2+u_3-u_5+u_6-u_7\right) \\ &{} -\,\tilde{\beta }_2 \left( u_1+u_2-u_3+u_5-u_6+u_7\right) \\ &{} \left. -3\tilde{\gamma }_1 \left( u_0+u_2+u_5+u_7\right) -\,3\tilde{\gamma }_2 \left( u_0+u_1+u_3+u_6\right) \right) . \end{array} \end{aligned}$$

(47)

The overall truncation error for the artificial signals is given as the following.

$$\begin{aligned} \begin{array}{rl} \text {TE}^\text {art}= &{}\displaystyle -\left( a^2 \left( s^2 u_\text {nn}+s u_\text {tn}+u_\text {tt}\right) +a b \left( 2 s^2 u_\text {tn}+s \left( u_\text {tt}-u_\text {nn}\right) -2 u_\text {tn}\right) \right. \\ &{}\displaystyle \qquad \left. +\,b^2 \left( s \left( s u_\text {tt}-u_\text {tn}\right) +u_\text {nn}\right) \right) \left( \frac{\tilde{\alpha }_\text {I}+\tilde{\alpha }_\text {II}-\tilde{\gamma }_\text {I}-\tilde{\gamma }_\text {II}}{s \left( a^2+b^2\right) }\right) \left| \left| \mathbf {\lambda }\right| \right| h +O\left( h^2 \right) . \end{array} \end{aligned}$$

(48)

From the previous equation, note that the artificial signals are second-order accurate when we select $\alpha =\gamma$, but this violates the entropy-stable condition of the method [11]. For the inviscid steady state case, the overall truncation error reduces to

$$\begin{aligned} \begin{array}{rl} \text {TE}^\text {art}= &{} -\left( \frac{(\tilde{\alpha }_\text {I}+\tilde{\alpha }_\text {II}-\tilde{\gamma }_\text {I}-\tilde{\gamma }_\text {II})(b^2-abs+a^2s^2)}{\left( a^2+b^2\right) s}\right) \left| \left| \mathbf {\lambda }\right| \right| u_\text {nn}h \\ &{} +\left( \frac{ab(\tilde{\alpha }_\text {I}-\tilde{\alpha }_\text {II}+\tilde{\gamma }_\text {I}-\tilde{\gamma }_\text {II}-2\tilde{\beta }_\text {I}+2\tilde{\beta }_\text {II})(b-as)}{2\left( a^2+b^2\right) ^{3/2}}\right) \left| \left| \mathbf {\lambda }\right| \right| u_\text {nnn}h^2 \\ &{} -\left( \frac{(\tilde{\alpha }_\text {I}+\tilde{\alpha }_\text {II}-\tilde{\gamma }_\text {I}-\tilde{\gamma }_\text {II})(b^2-abs+a^2s^2)^2}{12\left( a^2+b^2\right) ^{2}s}\right) \left| \left| \mathbf {\lambda }\right| \right| u_\text {nnnn}h^3 \\ &{} -\left( \frac{a b \left( a^3 s^3-2 a^2 b s^2+2 a b^2 s-b^3\right) \left( \tilde{\alpha }_\text {I}-\tilde{\alpha }_\text {II}-2 \tilde{\beta }_\text {I}+2 \tilde{\beta }_\text {II}+\tilde{\gamma }_\text {I}-\tilde{\gamma }_\text {II}\right) }{24 \left( a^2+b^2\right) ^{5/2}}\right) \left| \left| \mathbf {\lambda }\right| \right| u_\text {nnnnn}h^4 \\ &{} +O\left( h^5\right) . \end{array} \end{aligned}$$

(49)

It is clear that the obstacle to achieve high-order spatial accuracy in steady-state advection problems is due to the artificial signals. From [11], selecting $\beta =0$ and imposing $\alpha =-\gamma$ will yield the truncation error of the artificial signals in steady-state condition to be

$$\begin{aligned} \begin{array}{rl} \text {TE}^\text {art}= &{} -\left( \frac{(\tilde{\alpha }_\text {I}+\tilde{\alpha }_\text {II}-\tilde{\gamma }_\text {I}-\tilde{\gamma }_\text {II})(b^2-abs+a^2s^2)}{\left( a^2+b^2\right) s}\right) u_\text {nn}h \\ \displaystyle &{} -\left( \frac{(\tilde{\alpha }_\text {I}+\tilde{\alpha }_\text {II}-\tilde{\gamma }_\text {I}-\tilde{\gamma }_\text {II})(b^2-abs+a^2s^2)^2}{12\left( a^2+b^2\right) ^{2}s}\right) u_\text {nnnn}h^3 +O\left( h^4\right) . \end{array} \end{aligned}$$

(50)

The overall truncation error for the flux-difference approach is $\text {TE}^\text {iso} + \text {TE}^\text {art}$. TE equations for the classic RD methods are included in “Appendix A”.

3.4 First-Order Flux-Difference RD Method

To construct a baseline first-order entropy-stable method, we can just use the original $\phi ^{\mathrm{art}}$ with $\alpha =-\gamma$ and that $\beta =0$. In a more structured form, this can be viewed by choosing $\alpha$ such that

$$\begin{aligned} \alpha ^{1\mathrm{st}}=\left( \frac{h}{L_\mathrm{r}}\right) ^{q\mathrm{1st}}\left| \left| \mathbf {\lambda }\right| \right| h ,\quad q^{1{\mathrm{st}}}\rightarrow 0^+. \end{aligned}$$

(51)

A positive first-order method can be achieved if we select $\alpha$ based on Eq. (26), where the q can be determined by Eq. (32). Note that the positive first-order method is less diffusive than the baseline first-order method since it generates less entropy.

3.5 Second Order and Beyond

To develop a compact high-order (beyond first order) method, the main concept still remains the same. By controlling entropy generation produced by the artificial signals, one might be able to construct a high-order approach. Thus, we could achieve second order and third order by choosing

$$\begin{aligned} \alpha ^\text {high}=\left( \frac{h}{L_\mathrm{r}}\right) ^{q^\text {high}}\left| \left| \mathbf {\lambda }\right| \right| h, \end{aligned}$$

(52)

where $q^\text {high}\rightarrow 1^-$ for second order and $q^\text {high}\rightarrow 2^-$ for third order. Fourth-order accuracy can be theoretically achieved if $q^\text {high}\rightarrow 3^-$. The question remains on whether the high order-of-accuracy is preserved on distorted triangular grids. The following section will attempt to address this issue by examining the grid skewness effect on a specific test case in which the normal derivatives can be computed.

Fig. 4

Right-running grid terminology for stability analysis

3.6 von Neumann Stability Analysis

To assess the feasibility on the new flux difference RD method, the stability aspect is analyzed following the work of [8]. Only forward Euler time stepping scheme is considered in this study to maintain the explicit time feature of the new scheme while being consistent with the time integration step addressed in Sect. 2.3. The analysis is done again on the structured (right-running) grids as shown in Fig. 4. Hence, the Von Neumann analysis in this study starts with Eq. (17) as the general equation for RD method with forward Euler scheme and the sum of signals can be further categorized into isotropic and artificial signals. Collecting the isotropic and artificial terms from the neighboring cells and considering the entropy-stability condition [11] yields

$$\begin{aligned} u^{n+1}_{l,m}=u^n_{l,m}-\frac{\Delta t}{A_{l,m}}\left[ \left( \sum _j\phi _{l,m}^j\right) ^{\mathrm{iso}}+\left( \sum _j\phi _{l,m}^j\right) ^{\mathrm{art}}\right] , \end{aligned}$$

(53)

where

$$\begin{aligned} \begin{array}{rl} \left( \sum _j\phi _{l,m}^j\right) ^{\mathrm{iso}}=&{}\frac{1}{6}\left[ (-b h + 2 a k) u^n_{l+1,m} + (b h + a k) u^n_{l+1,m+1} + (2 b h + a k) u^n_{l,m+1}\right. \\ &{}+\,(b h {-} 2 a k) u^n_{l-1,m} - (b h + a k) u^n_{l-1,m-1} +\left. (-2 b h + a k) u^n_{l,m-1}\right] , \end{array} \end{aligned}$$

(54)

and

$$\begin{aligned} \begin{array}{rl} \left( \sum _j\phi _{l,m}^j\right) ^{\mathrm{art}}=&{} 2\alpha [6 u^n_{l,m} - u^n_{l+1,m} - u^n_{l+1,m+1} - u^n_{l,m+1}\\ &{}-\, u^n_{l-1,m} - u^n_{l-1,m-1} - u^n_{l,m-1}]. \end{array} \end{aligned}$$

(55)

Considering only the numerical errors, $\zeta ^m_{l,m}$, and casting the errors into Fourier forms, $\zeta ^n_{l,m} = \delta ^n \text {exp}^{i \theta (l x + m y)}$ and $i=\sqrt{-1}$, the numerical error equation is

$$\begin{aligned} \begin{array}{rl} \delta ^{n+1} \text {exp}^{i \theta (l x + m y)}=&{} \delta ^n \text {exp}^{i \theta (l x + m y)} -\frac{\Delta t}{A_{l,m}} \left( \frac{1}{6}\right) \left[ 72 \alpha \delta ^n \text {exp}^{i \theta (l x + m y)} \right. \\ &{}+\, (-12 \alpha - b h + 2 a k) \delta ^n \text {exp}^{i \theta ((l + 1) x + m y)} \\ &{}+\, (-12 \alpha + b h + a k) \delta ^n \text {exp}^{i \theta ((l+1) x + (m+1) y)} \\ &{}+\, (-12 \alpha + 2 b h + a k)\delta ^n \text {exp}^{i \theta (l x + (m+1) y)} \\ &{}+\, (-12 \alpha + b h - 2 a k) \delta ^n \text {exp}^{i \theta ((l-1) x + m y)} \\ &{}+\, (-12 \alpha - b h - a k) \delta ^n \text {exp}^{i \theta ((l-1) x + (m-1) y)} \\ &{}+\, \left. (-12 \alpha -2 b h + a k) \delta ^n \text {exp}^{i \theta (l x + (m-1) y)} \right] . \end{array} \end{aligned}$$

(56)

Dividing by $\delta ^n \text {exp}^{i \theta (l x + m y)}$ yields

$$\begin{aligned} \begin{array}{rl} \delta =&{} 1 - \frac{\Delta t}{A_{l,m}} \left( \frac{1}{6}\right) \left[ 72 \alpha \right. \\ &{}+\, (-12 \alpha - b h + 2 a k) \text {exp}^{i \theta (x)} \\ &{}+\, (-12 \alpha + b h + a k) \text {exp}^{i \theta (x + y)} \\ &{}+\, (-12 \alpha + 2 b h + a k) \text {exp}^{i \theta (y)} \\ &{}+\, (-12 \alpha + b h - 2 a k) \text {exp}^{i \theta (-x)} \\ &{}+\, (-12 \alpha - b h - a k) \text {exp}^{i \theta (-x-y)} \\ &{}+\, \left. (-12 \alpha -2 b h + a k) \text {exp}^{i \theta (-y)} \right] . \end{array} \end{aligned}$$

(57)

Using the identity of $\text {exp}^{i \theta } = \hbox {cos}\theta - i \hbox {sin}\theta$, we obtain

$$\begin{aligned} \begin{array}{rl} \delta =&{}1 + \frac{1}{3 s}\left( \alpha \frac{\Delta t}{h^2}\right) (-36 + 12\hbox {cos}(\theta x) + 12\hbox {cos}(\theta y) + 12\hbox {cos}(\theta x + \theta y)) \\ &{}+\, i \frac{1}{3 s} \left( a\frac{\Delta t}{h}\right) ((2 s -1)\hbox {sin}(\theta x) + (2-s)\hbox {sin}(\theta y) \\ &{}+\, (1+s) \hbox {sin}(\theta x + \theta y)), \end{array} \end{aligned}$$

(58)

where s is the stretching factor defined in Eq. 36. Since $\delta$ is the ratio of the numerical error at timestep n+1 to the error at timestep n, the magnitude, $|\delta |$, is the amplification factor which determines the stability of the numerical scheme. The stable condition is achieved if and only if $|\delta | \le 1$ $\forall \theta$, where

$$\begin{aligned} \begin{array}{rl} |\delta | =&{}\left\{ \left[ 1 + \frac{1}{3 s}\left( \alpha \frac{\Delta t}{h^2}\right) (-36 + 12cos(\theta x) + 12cos(\theta y) + 12cos(\theta x + \theta y))\right] ^2\right. \\ &{}+ \left[ i \frac{1}{3 s} \left( a\frac{\Delta t}{h}\right) ((2 s -1)sin(\theta x) + (2-s)sin(\theta y)\right. \\ &{}\left. \left. (1+s)sin(\theta x + \theta y))\right] ^2\right\} ^{\frac{1}{2}}. \end{array} \end{aligned}$$

(59)

A more generalized quantity is required to represent the stability condition of the schemes. We have employed the non-dimensional Courant–Friedrichs–Lewy (CFL) number for this purpose. Based on the CFL hypothesis [6], the characteristic vector should not exceed the element within one iteration as it might contradict with the characteristics in other elements which causes the solution to be unstable. The CFL condition for RD is demonstrated in Fig. 5 and the CFL number, $\nu$ is defined as

$$\begin{aligned} \nu = \frac{|\lambda |\Delta t}{\min d}, \end{aligned}$$

(60)

where d is the distance between the centroid to the edge of the cell along the direction of the characteristic vector. There are only two types of cell (type I and II from Fig. 3) for right running grid and their respective d ($d_{\text {I}}$ and $d_{\text {II}}$) is denoted in Fig. 4. $\min d$ is the minimum value of d among all the cells. Substituting $\Delta t$ into Eq. 59 results in

$$\begin{aligned} \begin{array}{rl} |\delta | =&{}\left\{ \left[ 1 + \nu \left( \frac{\alpha \min d}{3 s h^2 |\lambda |}\right) (-36 + 12\hbox {cos}(\theta x) + 12\hbox {cos}(\theta y) + 12\hbox {cos}(\theta x + \theta y))\right] ^2\right. \\ &{}+ \left[ i \nu \left( \frac{a \min d}{3 s h|\lambda |}\right) ((2 s -1)\hbox {sin}(\theta x) + (2-s)sin(\theta y)\right. \\ &{}\left. \left. (1+s)\hbox {sin}(\theta x + \theta y))\right] ^2\right\} ^{\frac{1}{2}}. \end{array} \end{aligned}$$

(61)

The stability equations for the classic RD methods are in “Appendix B”.

Fig. 5

The CFL condition for RD

3.6.1 CFL Number Range for Stable Condition

The stability of flux difference scheme is assessed based on the range of $\nu$ across different skewness. The amplification factor, $|\delta |$ (z-axis), is plotted against both normalized frequencies $\theta _x$ (x-axis) and $\theta _y$ (y-axis) in 3D graphs. Note that the ranges of the frequencies are $0 \le \theta _x \le \pi$ and $0 \le \theta _y \le \pi$ as the pattern repeats beyond this range. For conciseness, only selected plots with grid skewness, $Q = 0.3$ are shown. Unstable regions where $|\delta |> 1$ are shaded in grey, while the stable regions of $|\delta |\le 1$ are shaded in orange in Fig. 6. The lower limit of stable $\nu$ is always 0 as $\Delta t$ is also 0, and there is no time iteration.

Fig. 6

Amplification factor plots at stable (left)-unstable (right) CFL number, a N scheme, $\nu$ = 3.0, b N scheme, $\nu$ = 3.01, c LDA, $\nu$ = 3.0, d LDA, $\nu$ = 3.01, e Baseline 1st order, $\nu$ = 0.2, f Baseline 1st order, $\nu$ = 0.21, g Positive 1st order, $\nu$ = 2.0, h Positive 1st order, $\nu$ = 2.05, i 2nd order, $\nu$ = 0.3, j 2nd order, $\nu$ = 0.35

From Fig. 6, both N scheme and LDA have the highest maximum stable $\nu$ at 3.0. The positive first-order scheme performs very good in terms of stability $(\nu \le 2.0)$ compared to baseline ($q=0$) first order $(\nu \le 0.2)$. Hence, from this point onwards, the positive approach will be chosen as the first order scheme for the newly developed flux-difference method. Another point to note is the frequency regions where $|\delta |$ exceeds 1. Both the classic RD methods, together with the second-order approach, are unstable at low-frequency regions, while baseline and positive first order show instability at higher-frequency regions.

A summary of the maximum stable $\nu$ is shown in Table 1. The stability of higher-order schemes, i.e. third- and fourth-order schemes, was also analyzed and the excruciating limited ranges of $\nu$ have rendered these schemes to be too expensive to be used practically with explicit method. Hence, they are to be deemed unstable and will not be discussed further in the following sections. However, implicit solvers should be explored for these higher-order schemes in the future. The positive version will be used as our first-order method due to its larger stability range compared to the baseline first order approach.

Table 1 Upper limit of $\nu$ from Von Neumann analysis

Fig. 7

Analytical order of accuracy for various the skewness in right running grid. a $\omega _f=1$ b $\omega _f=4$ c $\omega _f=8$

4 Results on Variation of Grid Skewness

4.1 Order-of-Accuracy

The steady-state (linear advection) test case [14] has a square domain with an inlet boundary condition for left and bottom sides, and an outlet for the right and top sides. The inlet boundaries and the steady-state exact solution are determined as

$$\begin{aligned} u(x,y)=-\cos (2\pi \omega _f(bx-ay)), \end{aligned}$$

(62)

where a and b are the characteristic wave speeds in x and y direction and $\omega _f$ is the frequency of wave. For simplicity, all of the calculations below use $a=b=1$ but $\omega _f$ would vary and the square domain is one by one in lengths.

Using a right-running triangular grid shown in Fig. 3 and by controlling the length (h) an height (k) of the grid, analytical and numerical order of accuracy for different skewnesses (Q) could be determined. We denote the positive approach and $(q=1)$ to be first-order and second-order flux-difference RD methods, respectively. The range of skewness for the structured triangular grid is $0.3 \le {Q}\le {1}$ as done in [4]. From the truncation error equations in the previous section, each error term includes a coefficient and the normal derivative of the solution on a particular node. For this test case, the normal derivatives can be determined based on the repeating sine-cosine function of Eq. (62). The complete setup details of the truncation error (and consequently order-of-accuracy (OoA)) versus skewness variations can be obtained in [4]. Only the first six error terms in the TE equations are considered when performing the analysis. Note that the grid stretching parameter s is related to grid skewness by $s=2\tan \left( \frac{\pi }{2}Q\right)$ [4] for a right triangle. For the RD methods, the order of accuracy will be unbounded for $s=1$ due to perfect grid alignment with the characteristics $(a,b)=(1,1)$. However, the limit of $s\rightarrow 1^+$ still exists for most RD methods.

Fig. 8

Numerical order of accuracy for various the skewness in right running grid for $\omega _f=1$

Fig. 9

Analytical truncation error in logarithmic scale for all the skewness in right running grid. a $\omega _f=1$ b $\omega _f=4$ c $\omega _f=8$

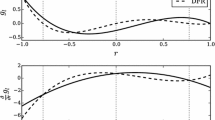
From Fig. 7, the asymptotic values for the analytical order-of-accuracy (OoA) when the stretching parameter is between $1< s <{\infty }$ . For all of the RD schemes reported herein, the magnitude of errors increases rapidly beyond certain skewness and reaches an asymptotic value when $Q=1.0$ (or $s\rightarrow {\infty }$) as shown in Fig. 9. However, the OoA of methods may increase (i.e Lax Wendroff, second FD), or decrease (LDA, N scheme) or even behave in an oscillatory fashion (highest frequency), depending on the respective TE equations. Of course numerically, we expect most schemes to have a drop in OoA as we increase the skewness (Fig. 8) but RD schemes are usually least affected relative to FV methods [4]. For brevity, we have only included the numerical OoA for low frequency since the methods have a similar pattern for higher frequencies but with more rapid deterioration at high skewness as shown in the analytical part. The $L_2$ errors for the numerical results are also similar to the truncation errors in Fig. 9 hence omitted for conciseness. Note that the Lax–Wendroff $L_2$ errors drop to round-off errors when $Q\rightarrow {0.3}$ due to the numerical solutions approach the exact solution at this configuration hence we could not compute its numerical OoA.

The order of accuracy for the first order scheme generally attains the desired accuracy and it is comparable to Lax–Friedrichs (LxF) which is also a central scheme. However, the first order positive scheme always has slightly lower L2 error compared to that of Lax–Friedrichs and the difference decreases when the grid is further skewed. The N-scheme is the best first order due to its narrowest stencil, which is least susceptible to grid changes.

The second order ($q=1$) version maintains its accuracy for the most part with varying skewness while the order of accuracy of classic second order LDA deteriorates at high skewness. The deterioration becomes more rapid as the frequency increases, although LDA achieves third order at $Q=0.5$ as the truncation error for LDA in steady state condition is given by

$$\begin{aligned} \text {TE}^\text {LDA} = \left( -\frac{a b \left( 2 a b^2 - 3 a b s + a^2 s^2\right) }{6 r^3}\right) u_\text {nnn}h^2+O\left( h^3\right) . \end{aligned}$$

(63)

With the condition of $a = b = 1$ and the identity of grid skewness of $s=2\tan \left( \frac{\pi }{2}Q\right)$, the TE for LDA at $Q=0.5$ becomes

$$\begin{aligned} \text {TE}^\text {LDA} = -\left( \frac{2 - 6\tan \left( \frac{\pi }{4}\right) + \left( 2\tan \left( \frac{\pi }{4}\right) \right) ^2}{6 r^3}\right) u_\text {nnn}h^2+O\left( h^3\right) . \end{aligned}$$

(64)

It can be seen that the second order term of the TE for LDA is cancelled perfectly at that specific skewness. The Lax–Wendroff (LxW) scheme is third order accurate for right-running grids since there the second order error terms drop out for this unique choice of structured (right running) grids. The Lax–Wendroff is generally a second order method as demonstrated in [5].

The sample of analytical OoA plot for one skewness value is shown in Fig. 10. The numerical OoA plot for a particular skewness has the same hierarchical pattern, therefore it is not included to maintain conciseness of the paper. The numerical velocity contours and the residual convergence history are shown in Figs. 11 and 12.

Fig. 10

Truncation error (analytical) verses the grid distance in logarithmic scale for the linear case $Q=0.7$ in the right running grid

Fig. 11

u velocity contours for steady state linear advection test case. a N, b 1st order, c LDA, d 2nd order

Fig. 12

L2 errors residual plots against number of iterations for different RD schemes for steady linear advection test case at $w_f=1$ and $Q = 0.4$

4.2 Shock-Tree Problem

This test case is to examine the ability of each method to capture a monotone shock profile on a discontinuous data. The shock-tree case is based on the Burgers’ equation, with the inflow boundary at the bottom, left and right of the domain.

$$\begin{aligned} u(x,0)=1.5-2 x. \end{aligned}$$

(65)

The steady state exact solution is,

$$ \begin{aligned} u(x,y)= {\left\{ \begin{array}{ll} -\,0.5 &{} y \le \frac{1}{2} \& \frac{x-\frac{3}{4}}{y-\frac{1}{2}} < \frac{1}{2}\\ 1.5 &{} y \le \frac{1}{2} \& \frac{x-\frac{3}{4}}{y-\frac{1}{2}} > \frac{1}{2}\\ \max \left( -\,0.5,\min \left( 1.5,\frac{x-\frac{3}{4}}{y-\frac{1}{2}}\right) \right) &{} \text {elsewhere}. \end{array}\right. } \end{aligned}$$

(66)

Fig. 13

Cross section of different schemes for shock tree problem

It is illustrated in Fig. 13 that both first order schemes preserve monotonicity in discontinuous domain and the positive approach performs exceptionally good as the diffusion is minimal. However, the second order approach is not monotone and oscillations occur near the shock region.

5 Conclusion

The flux-difference RD methods have a general mathematical form which can easily recover the classic central and upwind RD methods, hence all of their inherent properties as well. In addition, the new RD method can also be designed to have its own unique central-type methods with different order-of-accuracy by controlling the artificial signals. Overall, the flux-difference methods are minimally sensitive to grid skewness as much as the classic RD methods, which are known to be much less relative to finite volume methods.

Appendices

A Truncation Error (TE) of Classic RD Methods

The TE for different classic RD methods are determined with the assumption that $\frac{b}{a}<\frac{k}{h}$.

$$\begin{aligned} \text {TE}_\text {N}= & {} \left( -\frac{ab}{2r^2}(ak-bh)\right) u_{nn}\nonumber \\&+\,\left( \frac{ab}{6r^3}(ak-bh)(ak-2bh)\right) u_{nnn}\nonumber \\&+\,O(h^pk^q),\qquad p+q=3. \end{aligned}$$

(67)

$$\begin{aligned} \text {TE}_\text {LxF}= & {} \left( -\frac{\left( 4 a^3 k^3-3 a^2 b k^2h+4 a b^2 kh^2+b^3h^3\right) }{6kh\left( a^2+b^2\right) }\right) u_{nn}\nonumber \\&+\,\left( \frac{a b^2 (ak-bh)h}{12 \left( a^2+b^2\right) ^{3/2}}\right) u_{nnn}\nonumber \\&+\,O(h^pk^q),\qquad p+q=3. \end{aligned}$$

(68)

$$\begin{aligned} \text {TE}_\text {LDA}= & {} \left( \frac{ab(ak-bh)(ak-2bh)}{6r^3}\right) u_{nnn}\nonumber \\&+\,\left( -\frac{ab^2(ak-bh)^2h}{8r^4}\right) u_{nnnn}\nonumber \\&+\,O(h^pk^q),\qquad p+q=4. \end{aligned}$$

(69)

$$\begin{aligned} \text {TE}_\text {LxW}= & {} \left( -\frac{a b^2 (ak-bh)^2h}{12r^4}\right) u_{nnnn}\nonumber \\&+\,O(h^pk^q),\qquad p+q=4. \end{aligned}$$

(70)

B Stability Analysis on Classic RD Methods

With the same formulation in Sect. 3.6, the amplification factor, $\delta$ for N and LDA schemes are determined as the following.

$$\begin{aligned} |\delta |^{\mathrm{N}}= & {} \left\{ \left[ 1 + \frac{\nu }{3 s} \left( -s +(s-1) \hbox {cos}(\theta x) + \hbox {cos}(\theta x + \theta y)\right) \right] ^2\right. \nonumber \\&+ \left. \left[ i \frac{\nu }{3 s} \left( (s -1)\hbox {sin}(\theta x) + \hbox {sin}(\theta x + \theta y)\right) \right] ^2\right\} ^{\frac{1}{2}}. \end{aligned}$$

(71)

$$\begin{aligned} |\delta |^{\mathrm{LDA}}= & {} \left\{ \left[ 1 + \frac{\nu }{3 s^2} \left( -s^2+s-1+(s-1)s \hbox {cos}(\theta x)\right. \right. \right. \nonumber \\&\left. \left. +(1-s)\hbox {cos}(\theta y)+ s \hbox {cos}(\theta x + \theta y)\right) \right] ^2\nonumber \\&+ \left. \left[ i \frac{\nu }{3 s} \left( (s -1)\hbox {sin}(\theta x) + \hbox {sin}(\theta x + \theta y)\right) \right] ^2\right\} ^{\frac{1}{2}}. \end{aligned}$$

(72)