1 INTRODUCTION

Edge-based schemes represent a special class of finite-volume schemes for solving hyperbolic systems of equations on unstructured meshes. In these schemes, conservative variables are determined at mesh nodes, while flows used to approximate conservation laws are calculated in the middles of mesh edges or diagonals of elements. These schemes are first proposed in [1, 2]. The current state of them is represented mainly by schemes with the quasi-one-dimensional reconstruction of variables [3–6] and schemes based on the flux correction (FC) method [7–14].

The scheme of T. Barth [2] consists in the linear reconstruction of variables in the middle of an edge using gradients calculated at mesh nodes. The scheme has the first order of approximation and in practice demonstrates the order of accuracy from 3/2 to 2. At the same time, it is noted in [7] that if these gradients are calculated with the second order of approximation, then the entire scheme also has the second order of approximation. The order of accuracy of the obtained scheme on unsteady tasks remains equal to 2; however, on steady tasks the convergence order is often 3. Further development of these schemes is to transfer this superconvergence to unsteady tasks [8–12], but this is achieved at the cost of the significant complexity of the scheme and the loss of conservatism. Another approach uses the unsteady FC method [13, 14], which reduces the approximation order to 1, but in practice makes it possible to improve the accuracy of the steady method with negligible additional costs of the machine time.

A key place in FC-based schemes is occupied by the procedure for calculating gradients of physical variables at mesh nodes at least with the second order of approximation. This can be achieved, e.g., by calculating the gradient of an interpolation polynomial obtained by the least squares method (LSM). The problem is the possibility of degenerating the system of equations for finding coefficients of the polynomial. In addition, when using an anisotropy mesh in near-wall regions, the condition number of the system increases with the growth of the anisotropy and the curvature of a surface.

To avoid these problems, it is proposed to determine the gradients by spectral elements (see [8]). In this case, the calculation mesh should be the result of a single natural refinement (see Fig. 1) of another calculation mesh whose elements are called spectral. On each spectral element, the interpolant is defined unambiguously; after that, the gradient at a node is defined as the average gradient of such interpolants defined at this node. Here, on a uniform mesh, the scheme is heterogeneous: some of the mesh nodes are vertices of spectral elements, while some of the mesh nodes are not such vertices. Therefore, gradients in them are calculated differently. Currently, the method of calculating gradients by spectral elements seems to be optimal. However, as is shown below, the heterogeneity of a scheme can lead to a strange behavior of the solution.

Fig. 1.
figure 1

Natural refinement of mesh elements by factor of 2.

Full size image

In the three-dimensional case, in near-wall regions for viscid tasks, a calculation mesh has usually the strand type; i.e., its topology is the Cartesian product of a two-dimensional unstructured mesh and a one-dimensional mesh. In this case, another way of calculating gradients becomes possible. The gradient component along an edge coming into the boundary is calculated using a one-dimensional finite-difference scheme, and the tangential components, using only the value of the variables at the corresponding layer by one of two methods described above [10, 11]. We do not consider this type of mesh in the present paper and restrict the discussion to the inviscid case.

In this work, by the set of test tasks, we compare the FC-based schemes that are obtained using different gradient-computation procedures. Moreover, these schemes are related in accuracy to schemes with the quasi-one-dimensional reconstruction. In addition, a new slope limiter is proposed to deal with discontinuous problems using the FC method.

2 EDGE-BASED SCHEMES

In this paper, we consider the hyperbolic systems of equations

$$\frac{{\partial {\mathbf{Q}}}}{{\partial t}} + \nabla \cdot \mathcal{F}({\mathbf{Q}}) = 0,$$
(1)

where \(\mathcal{F} = ({{{\mathbf{F}}}_{x}},{{{\mathbf{F}}}_{y}},{{{\mathbf{F}}}_{z}})\). The hyperbolicity means that for any vector \({\mathbf{\tilde {n}}}\), the Jacobian of the vector of flows in this direction can be presented as

$$\frac{{d\mathcal{F}{\text{(}}{\mathbf{Q}}) \cdot {\mathbf{\tilde {n}}}}}{{d{\mathbf{Q}}}} = {\mathbf{S\Lambda }}{{{\mathbf{S}}}^{{ - 1}}},$$
(2)

where \({\mathbf{\Lambda }}\) is a diagonal matrix. In particular, such a form has the transfer equation for \({\mathbf{Q}} = u\) and \(\mathcal{F} = {\mathbf{a}}u\). Euler’s equations for an ideal gas have form (1) for \({\mathbf{Q}} = {{(\rho ,\rho {\mathbf{u}},E)}^{T}},\) and \(\mathcal{F} = {{(\rho {\mathbf{u}},\rho {\mathbf{u}} \otimes {\mathbf{u}} + {\kern 1pt} p\hat {I},(E + p){\mathbf{u}})}^{T}},\) where \(E = {{\rho {{{\mathbf{u}}}^{2}}} \mathord{\left/ {\vphantom {{\rho {{{\mathbf{u}}}^{2}}} 2}} \right. \kern-0em} 2} + \rho \varepsilon \) and \(\hat {I}\) is a unit matrix, and are closed by the state equation of an ideal gas p = \(\rho \varepsilon (\gamma - 1)\). Everywhere in this work we use the adiabatic index \(\gamma = 1.4\).

The construction of a finite-volume scheme involves dividing the computational domain into cells for which discrete conservation laws are formulated. For schemes that identify variables at mesh nodes, the role of cells is played by control volumes (each of which is built around its own mesh node). We describe their construction by the example of a triangular mesh.

Consider a triangle \(G{{K}_{1}}{{K}_{2}}\) shown in Fig. 2 at the right. The middles of the edges \(G{{K}_{1}}\), \(G{{K}_{2}}\), and \({{K}_{1}}{{K}_{2}}\) we denote by \({{M}_{1}},{{M}_{2}}\), and P12, respectively, and the center of the triangle we denote by O. The triangle \(G{{K}_{1}}{{K}_{2}}\) is divided into three quadrangles: \(G{{M}_{1}}O{{M}_{2}}\) (included in the control volume of the node G), \({{K}_{1}}{{M}_{1}}OP\) (included in the control volume of the node \({{K}_{1}}\)), and \({{K}_{2}}{{M}_{2}}OP\) (included in the control volume of the node \({{K}_{2}}\)). The control volume of the node G is an aggregate of such quadrangles, which is shown in Fig. 2 at the left. If as the center of a triangle is taken its center of mass, the resulting cells are called median or barycentric cells. The construction of analogous cells in the three-dimensional case is described in [15, 16].

Fig. 2.
figure 2

Two-dimensional median volume of node G (left) and part of triangular mesh element \(G{{K}_{1}}{{K}_{2}}\) related to it (right).

Full size image

The conservation law of form (1) for the cell G can be presented as

$$\frac{{d{{{\overline {\mathbf{Q}} }}_{G}}}}{{dt}} = - \frac{1}{{{{V}_{G}}}}\int\limits_{\partial {{C}_{G}}} {\mathcal{F} \cdot {\mathbf{n}}ds} ,$$
(3)

where \({{C}_{G}}\) is the control volume of the node G, \({{V}_{G}} = \left| {{{C}_{G}}} \right|\) is its value, \(\partial {{C}_{G}}\) is its boundary, n is an external unit normal to it, and \({{{\mathbf{\bar {Q}}}}_{G}}\) is the integral average of Q on the cell \({{C}_{G}}\).

The surface of the cell can be presented as \(\partial {{C}_{G}} = \bigcup\nolimits_{K \in {{N}_{1}}(G)} {\partial {{C}_{{GK}}}} \), where \({{N}_{1}}(G)\) is the set of nodes neighboring (i.e., connected by a common mesh element) the vertex G, and \(\partial {{C}_{{GK}}}\) is the total surface of cells G and K. Introduce the notation

$${{{\mathbf{n}}}_{{GK}}} = \int\limits_{\partial {{C}_{G}} \cap \partial {{C}_{K}}} {{\mathbf{n}}dS} ,\,\,\,\,{{{\mathbf{\tilde {n}}}}_{{GK}}} = {{{{{\mathbf{n}}}_{{GK}}}} \mathord{\left/ {\vphantom {{{{{\mathbf{n}}}_{{GK}}}} {\left| {{{{\mathbf{n}}}_{{GK}}}} \right|}}} \right. \kern-0em} {\left| {{{{\mathbf{n}}}_{{GK}}}} \right|}}.$$

For approximating (3), we substitute \({{{\mathbf{Q}}}_{G}}\) (the point value of \({\mathbf{Q}}\) at the mesh node G) instead of \({{\overline {\mathbf{Q}} }_{G}}\); in (4), we present the integral over \(\partial {{C}_{G}}\) as a sum of integrals over \(\partial {{C}_{{GK}}}\). In each such an integral we replace the flow \(\mathcal{F}\) with a certain value related to the middle of the edge. We have

$$\frac{{d{{{\mathbf{Q}}}_{G}}}}{{dt}} = - \frac{1}{{{{V}_{G}}}}\sum\limits_{K \in {{N}_{1}}(G)} {{{{\mathbf{h}}}_{{GK}}}} \left| {{{{\mathbf{n}}}_{{GK}}}} \right|,$$
(4)

where \({{{\mathbf{h}}}_{{GK}}}\) is a numerical flow, which not less than with the first order approximates \(\mathcal{F} \cdot {{{\mathbf{\tilde {n}}}}_{{GK}}}\) in the middle of the edge. Schemes of form (4) are called edge-based schemes. When using median cells on a simplicial mesh, edge-based schemes have the first approximation order at the inner nodes of the mesh [15]. This property follows from the accuracy of calculating the right side of (4) on the linear function if the flows \({{{\mathbf{h}}}_{{GK}}}\) are accurate on the linear function in the middles of edges.

On a hybrid mesh, we can build two types of control volumes: translucent [16] and direct [17, 16]. Translucent control volumes are a generalization of median volumes: they retain accuracy on a linear function on an arbitrary unstructured mesh (if flows are accurate on the linear function in the middles of edges), but the approximation error is proportional to the anisotropy factor. Direct control volumes do not retain the accuracy on the linear function. On a prismatic mesh in a near-wall region, the first approximation order usually is found due to the structuredness of the mesh in the normal direction, but is lost when coming to an unstructured mesh.

In order to ensure a sustainable calculation, flows are usually determined by some approximate solution of the Riemann problem; e.g., a scheme of the Courant–Isaacson–Rees type (see, e.g., [18])

$${{{\mathbf{h}}}_{{GK}}} = \frac{{\mathcal{F}({\mathbf{Q}}_{{GK}}^{ + }) + \mathcal{F}({\mathbf{Q}}_{{GK}}^{ - })}}{2} \cdot {{{\mathbf{\tilde {n}}}}_{{GK}}} - \frac{1}{2}{{{\mathbf{S}}}^{{ - 1}}}\left| {\mathbf{\Lambda }} \right|{\mathbf{S}}\frac{{{\mathbf{Q}}_{{GK}}^{ + } - {\mathbf{Q}}_{{GK}}^{ - }}}{2},$$

where the matrices S and \({\mathbf{\Lambda }}\) are determined by (2). A particular case of this scheme is the scheme of P.L. Roe [19]. In some cases, a more general kind of a flow is used:

$${{{\mathbf{h}}}_{{GK}}} = \frac{{{\mathbf{F}}_{{GK}}^{ + } + {\mathbf{F}}_{{GK}}^{ - }}}{2} - \frac{\delta }{2}{{{\mathbf{S}}}^{{ - 1}}}\left| {\mathbf{\Lambda }} \right|{\mathbf{S}}\frac{{{\mathbf{Q}}_{{GK}}^{ + } - {\mathbf{Q}}_{{GK}}^{ - }}}{2}.$$
(5)

Independently determining \({\mathbf{F}}_{{GK}}^{ \pm }\) allows gaining a greater order of accuracy on non-linear tasks on uniform meshes, although in practice this is usually not very noticeable. Determining a specific edge-based scheme is reduced to determining values of \({\mathbf{Q}}_{{GK}}^{ \pm }\) and \({\mathbf{F}}_{{GK}}^{ \pm }\). The simplest edge-based scheme is the Barth “linear” scheme [1]. It calculates pre-breakup values by the formulas

$${\mathbf{Q}}_{{GK}}^{ - } = {{{\mathbf{Q}}}_{G}} + {{\alpha }_{{GK}}}\frac{{{{{\mathbf{r}}}_{K}} - {{{\mathbf{r}}}_{G}}}}{2}\,\cdot{{(\nabla {\mathbf{Q}})}_{G}},\,\,\,\,{\mathbf{Q}}_{{GK}}^{ + } = {{{\mathbf{Q}}}_{K}} - {{\alpha }_{{KG}}}\frac{{{{{\mathbf{r}}}_{K}} - {{{\mathbf{r}}}_{G}}}}{2}\,\cdot{{(\nabla {\mathbf{Q}})}_{K}},$$
(6)

as an option for determining \({\mathbf{F}}_{{GK}}^{ \pm }\) proposes \({\mathbf{F}}_{{GK}}^{ \pm }\)\( = \mathcal{F}({\mathbf{Q}}_{{GK}}^{ \pm })\cdot\,{{{\mathbf{\tilde {n}}}}_{{GK}}}\), and calculates the function gradient at a mesh node by the Green–Gauss procedure

$${{\left( {\nabla {\mathbf{Q}}} \right)}_{G}} = \frac{1}{{{{V}_{G}}}}\sum\limits_{K \in {{N}_{1}}(G)} \frac{{{{{\mathbf{Q}}}_{G}} + {{{\mathbf{Q}}}_{K}}}}{2}{{{\mathbf{n}}}_{{GK}}}.$$
(7)

When solving problems with smooth solutions, the coefficients \(\alpha _{{GK}}^{{}}\) and \(\alpha _{{KG}}^{{}}\) are taken equal to 1. For calculations of discontinuous flows, they are taken independently for each component of the vector Q in such a way that the condition \(\min \{ {{{\mathbf{Q}}}_{G}},{{{\mathbf{Q}}}_{K}}\} \leqslant {\mathbf{Q}}_{{GK}}^{ \pm } \leqslant \max \{ {{{\mathbf{Q}}}_{G}},{{{\mathbf{Q}}}_{K}}\} \) is met [1].

Other examples of edge-based schemes are the scheme of H. Luo et al. [20], the scheme of P. Eliasson [21], and the FC method [7–14], together with the schemes of H. Nishikawa [22, 23], the mixed element-volume (MEV) schemes [3, 24, 25], and the edge-based reconstruction (EBR) schemes [3–6], which are based on the FC method.

3 FLUX CORRECTION METHOD

Consider scheme (6) for the transfer equation \({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial t}}} \right. \kern-0em} {\partial t}} + {\mathbf{a}} \cdot \nabla u = 0\). Suppose the gradient is calculated with the second order of approximation. We show that here the entire scheme (4)–(6) has also the second order of approximation at the internal nodes on the median cells of an unstructured mesh.

Since the accuracy on the linear function is found due to the properties of median cells, in order to show the second order of approximation, it is sufficient to consider the function of the form \(u({\mathbf{r}}) = {{(x - {{x}_{G}})}^{a}}{{(y - {{y}_{G}})}^{b}}{{(z - {{z}_{G}})}^{c}}\) for a + b + c = 2. The pre-breakup value from the side of the node G at the center of the edge GK is calculated by formula (6); here, this value is 0, because \(u({{{\mathbf{r}}}_{G}}) = \nabla u({{{\mathbf{r}}}_{G}}) = 0\). Consider the pre-breakup value from the side of the node K. We analyze its Taylor expansion in the neighborhood of the point rG. Denote by the stroke and by h the derivative in the direction of the edge and the length of the edge GK, respectively. We have

$$u_{{GK}}^{ + } = u({{{\mathbf{r}}}_{G}}) + u{\kern 1pt} '({{{\mathbf{r}}}_{G}})h + \frac{1}{2}u{\kern 1pt} ''({{x}_{G}})h_{{}}^{2} - \frac{1}{2}h(u{\kern 1pt} '({{x}_{G}}) + hu{\kern 1pt} ''({{x}_{G}})) = u({{x}_{G}}) + \frac{1}{2}u{\kern 1pt} '({{x}_{G}})h = 0.$$

Thus, on a quadratic function, the pre-breakup value from the K side is also zero. Consequently, the numerical flow (5) and the right side of the entire equality (4) are also zeros. For more details, see the proof in [7].

On nonuniform and unstructured meshes, schemes often ensure faster convergence than predicted by their approximation order (see, e.g., [26]). This phenomenon is sometimes called supra-convergence. For example, the Barth linear scheme (4)–(7) usually shows the second order of accuracy, although there is an example in which the solution by this scheme converges with the order of 3/2 [27]. For the FC scheme, the second order of approximation of the method provides the second order of accuracy (when the scheme is stable), but here the convergence order is also equal to 2; i.e., the effect of supra-convergence is absent. However, it is found that the supra-convergence of the FC scheme is observed in problems with steady solutions (see [7]). Therefore, provided that gradients with the second approximation order are calculated, scheme (4)–(6) is called the steady FC method.

Research in the field of the approximation of a source term (if the equation contains it) has resulted in the further development of FC-based schemes: A. Pincock and A. Katz, instead of (4), propose using the space-staggered approximation of the time derivative [8]:

$$\sum\limits_K {{{M}_{{GK}}}{{{\left( {\frac{{d{\mathbf{Q}}}}{{dt}}} \right)}}_{K}}} = - \frac{1}{{{{V}_{G}}}}\sum\limits_{K \in {{N}_{1}}(G)} {{{{\mathbf{h}}}_{{GK}}}} .$$

Here, hGK is a flow of type (5). The coefficients MGK are chosen in such a way that the second order of accuracy on an arbitrary unstructured mesh is retained and the third approximation order on translation-invariant meshes is ensured, but conservatism is lost. Translation-invariant meshes are called meshes in infinite space that pass into themselves during a spatial translation on the vector of any of their edges. Such meshes are uniform meshes of parallelepipeds or their homogeneous partitions into simplexes (see Fig. 3). The scheme obtained by the methodology described in Nishikawa’s work has the same properties [28]. The different variants of determining matrix M are summarized in [12].

Fig. 3.
figure 3

Triangular translation-invariant mesh (black lines) and median control volumes on it (gray lines).

Full size image

The author in [13] proposes the UFC scheme, which represents another algorithm for improving the accuracy of solving unsteady tasks. This scheme can be presented as

$${{\left( {\frac{{d{\mathbf{Q}}}}{{dt}}} \right)}_{G}} = - \frac{1}{{{{V}_{G}}}}\sum\limits_{K \in {{N}_{1}}(G)} {{{U}_{{GK}}}\sum\limits_{L \in {{N}_{1}}(K)} {{{{\mathbf{h}}}_{{KL}}}} } .$$

Coefficients of the matrix UGK are chosen in such a way as to preserve the conservatism of the original scheme and to ensure the third approximation order on translation-invariant meshes. However, here the second order of approximation on unstructured meshes is lost. The generalization of the UFC scheme for a hybrid mesh (which is, however, not applicable to tasks with an anisotropic mesh in a near-wall layer) is described in [13]. Note that if the FC method obtains a steady solution, then it represents a steady solution also for the UFC scheme.

In the nonlinear case, the determination \({\mathbf{F}}_{{GK}}^{ \pm } = \mathcal{F}({\mathbf{Q}}_{{GK}}^{ \pm })\,\cdot\,{{{\mathbf{\tilde {n}}}}_{{GK}}}\) limits the approximation order on uniform meshes by the second order. Instead of this, the present work uses the reconstruction of flow variables, which is analogous to the reconstruction of conservative variables:

$${\mathbf{F}}_{{GK}}^{ - } = {{{\mathbf{F}}}_{G}} + \frac{{{{{\mathbf{r}}}_{K}} - {{{\mathbf{r}}}_{G}}}}{2}\,\cdot\,{{(\nabla {\mathbf{F}})}_{G}},\,\,\,\,{\mathbf{F}}_{{GK}}^{ + } = {{{\mathbf{F}}}_{K}} - \frac{{{{{\mathbf{r}}}_{K}} - {{{\mathbf{r}}}_{G}}}}{2}\,\cdot\,{{(\nabla {\mathbf{F}})}_{K}},$$

where F is a flow in the direction of \({{{\mathbf{\tilde {n}}}}_{{GK}}}\). It should be noted that in [8] an alternative procedure is proposed,

$${\mathbf{F}}_{{GK}}^{ - } = {{{\mathbf{F}}}_{G}} + \frac{{{{{\mathbf{r}}}_{K}} - {{{\mathbf{r}}}_{G}}}}{2}\,\cdot\,{{\left( {\frac{{d{\mathbf{F}}}}{{d{\mathbf{Q}}}}} \right)}_{G}}{{(\nabla {\mathbf{Q}})}_{G}},\,\,\,\,{\mathbf{F}}_{{GK}}^{ + } = {{{\mathbf{F}}}_{K}} - \frac{{{{{\mathbf{r}}}_{K}} - {{{\mathbf{r}}}_{G}}}}{2}\,\cdot\,{{\left( {\frac{{d{\mathbf{F}}}}{{d{\mathbf{Q}}}}} \right)}_{K}}{{(\nabla {\mathbf{Q}})}_{K}},$$

which does not require the calculation of gradients of flow variables and thereby slightly reduces the computational cost.

4 CALCULATION OF GRADIENTS

A key place in FC-based schemes is occupied by the procedure for calculating gradients of physical variables at mesh nodes at least with the second order of approximation. Two procedures that meet this requirement are well known.

The easiest way to calculate a second-order node gradient is to calculate the gradient of an interpolation polynomial obtained by the LSM. Assume that it is necessary to calculate the gradient at node G. The pattern is chosen, e.g., by the set of nodes connected to node G by not more than two edges. This method has two critical disadvantages. First, the degeneration of the system of equations to finding coefficients of the polynomial is possible. It is easy to create such a mesh artificially; in practice, this sometimes happens at boundary or near-boundary nodes, where the number of neighbors of the second order is smaller than for internal nodes. Second, an anisotropic mesh is used in near-wall areas to model high-Reynolds flows. If the boundary of a region is curvilinear, then the construction of interpolation polynomials by the LSM is correct if the basic functions are polynomials of variables in a curvilinear coordinate system associated with the boundary. Using polynomials in the Cartesian coordinates can lead to a very large number of conditions of the system and, as a result, catastrophic errors.

To avoid these problems, it is suggested to calculate gradients by spectral elements [8]. In this case, the calculation mesh should be the result of a single natural (see Fig. 1) refinement of some other calculation mesh whose elements are called spectral. If the refinement is carried out k times on a linear size, then the spectral elements are called elements of the kth order. A spectral triangular element of the second order contains 6 nodes, and this allows unambiguously identifying on them a polynomial of the form \(a{{x}^{2}} + bxy + c{{y}^{2}} + dx + ey + f\) by the values of the variables at the nodes. A quadrangular second-order spectral element contains 9 nodes, and this allows unambiguously identifying a polynomial of the form \(a{{x}^{2}}{{y}^{2}} + b{{x}^{2}}y + c{{x}^{2}} + dx{{y}^{2}} + exy + fx + g{{y}^{2}} + hy + k\). Analogously, a spectral tetrahedral element of the second order contains 10 nodes, a pyramidal element contains 14 nodes, a prismatic element contains 18 nodes, and a hexahedral element contains 27 nodes, and this also allows unambiguously identifying a polynomial with the corresponding set of monomials [14]. After identifying a polynomial, we can also determine its gradient. Here, the gradient at a node is defined as the average of the gradients at this node for all spectral elements containing this node, with the weight equal to the volume of a spectral element. It is shown in [8] that the use of spectral elements of the third order leads to instability near the boundaries of the computational domain; therefore, it is necessary to use spectral elements just of the second order.

The method of calculating gradients using spectral elements has two drawbacks. First, the calculation mesh must be obtained by refining another, spectral, mesh. In a domain with a curvilinear boundary, the mesh-refining procedure involves technical difficulties due to the fact that the boundary nodes of the refined mesh must be displaced from the edges and faces of the spectral mesh to the boundary of the true computational domain. If an isotropic near-wall layer is available, such a displacement can lead to the rollout of the elements and therefore require a displacement also of a part of the internal nodes. Second, on a uniform mesh, the scheme is heterogeneous: some of the mesh nodes are vertices of spectral elements, while some of the mesh nodes are not such vertices; therefore, the gradients at these nodes are calculated differently.

Despite these drawbacks, the method of calculating gradients on spectral elements (perhaps, using the strand technology) appears to be optimal. However, as will be shown below, the scheme’s heterogeneity caused by the heterogeneous way of calculating gradients can lead to the partial disappearance of numerical dissipation and, as a result, the incorrect behavior of the solution.

5 TESTING: LINEAR PROBLEM WITH PERIODIC CONDITIONS

Consider a model task for the transfer equation \({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial t}}} \right. \kern-0em} {\partial t}} + {{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-0em} {\partial x}} = 0\) with the initial conditions \(u(0,x) = \exp ( - \alpha {{x}^{2}})\) for \(\alpha = {{\ln 2} \mathord{\left/ {\vphantom {{\ln 2} {{{{(0.03)}}^{2}}}}} \right. \kern-0em} {{{{(0.03)}}^{2}}}}\) and the periodic boundary conditions \(u(t, - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}) = u(t,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})\). As a measure of error, we take the maximum modulus of the difference of the numerical solution at the moment Tmax = 20 and the accurate solution at this moment.

We use the calculation mesh with the steps \({{h}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{h}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = {{h}_{{\min }}}\), \({{h}_{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}} = {{h}_{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}} = {{h}_{{\max }}}\), \({{h}_{{{9 \mathord{\left/ {\vphantom {9 2}} \right. \kern-0em} 2}}}} = {{h}_{{{{11} \mathord{\left/ {\vphantom {{11} 2}} \right. \kern-0em} 2}}}} = {{h}_{{\min }}}\), etc. (see Fig. 4). Introduce the notation \(K = {{{{h}_{{\max }}}} \mathord{\left/ {\vphantom {{{{h}_{{\max }}}} {{{h}_{{\min }}}}}} \right. \kern-0em} {{{h}_{{\min }}}}}\) and \(h = {{({{h}_{{\max }}} + {{h}_{{\min }}})} \mathord{\left/ {\vphantom {{({{h}_{{\max }}} + {{h}_{{\min }}})} 2}} \right. \kern-0em} 2}\).

Fig. 4.
figure 4

Calculation meshes for one-dimensional tests. Top down: K = 1, K = 1.2, and K = 2.

Full size image

To integrate over time, we use the Runge–Kutta method of the fifth order of accuracy with CFL = 0.5 (the Courant–Friedrichs–Lewy condition). We use the following FC-based schemes: (1) the steady FC scheme (the second order of accuracy), (2) the nonconservative modification of Nishikawa [26], (3) the nonconservative modification of Pincock [25], and (4) the UFC scheme. For the UFC scheme, two ways of calculating gradients are considered: first, by differentiating the Lagrange interpolation polynomial of the second order and, second, using spectral elements. For the rest of the schemes only the first way is used. The results are compared to the results obtained by the EBR3 and SEBR5 schemes [4].

The results of all calculations on the uniform meshes and the nonuniform meshes for K = 1.2 and K = 2 are presented in Fig. 5. On a uniform mesh, the UFC results are superimposed on the results of the Pincock method. Analyzing the results, we can draw the following conclusions.

Fig. 5.
figure 5

Accuracy of various FC and EBR schemes on one-dimensional transfer equation. (a) Uniform mesh, (b) nonuniform mesh with K = 1.2, and (c) nonuniform mesh with K = 2.

Full size image

1. On all meshes, including uniform meshes, the steady FC scheme shows the second order of accuracy. The use of nonconservative schemes with an unsteady term in the form of both Nishikawa [28] and Pincock [8], improves the accuracy to the third order; here, the use of an unsteady term in the form of Nishikawa ensures that the numerical errors are smaller by several factors.

2. On uniform meshes, as expected, the EBR3 and SEBR5 schemes show the third and fifth orders of accuracy, respectively. The UFC scheme with the three-point gradient approximation has the third order of accuracy. Using spectral elements to calculate gradients allows us to get the fourth order of accuracy. The explanation of this fact is not easy and will be studied in the future. The fourth order of accuracy on a uniform mesh, on the one hand, provides higher accuracy, but, on the other hand, raise concerns, because the leading term (the term of the fourth order) of the error accumulated over time is a phase (and not dissipative) term.

3. On nonuniform one-dimensional meshes, all versions of the UFC scheme, together with the EBR3 and SEBR5 schemes have the first order of approximation and the second order of accuracy. However, the numerical error here is significantly smaller than that of the steady FC scheme, which has the second order of approximation.

The results of testing on multidimensional linear tasks with periodic conditions can be found in [13]. On an unstructured mesh, both ways of calculating gradients (using spectral elements and using the LSM), as in the case of a one-dimensional nonuniform mesh, yield results that are close to each other. On the translation-invariant mesh, the use of spectral elements gives more accurate results, but, unlike the one-dimensional case, does not improve the accuracy to the fourth order.

6 TESTING: A POTENTIAL FLOW AROUND A SPHERE

Consider the problem of a potential flow past a sphere. The calculation is carried out within the Euler equations for an ideal gas at the Mach number of a background flow of M = 0.01. The calculation is carried out on the outside of a sphere of radius R = 0.5 with the center at the origin of coordinates; the outer boundaries of the computational domain should be sufficiently distant so as to not affect the solution. The no-fluid-loss conditions are imposed on the surface of the sphere. At the initial time, a homogeneous flow is assigned and it is kept on the external boundaries of the computational domain. The accurate solution of the problem when using the hydrodynamic nondimensionalization in neglecting terms of the order O(M4) has the form

$$\begin{gathered} u = 1 - {{{{R}^{3}}(3{{x}^{2}} - {{r}^{2}})} \mathord{\left/ {\vphantom {{{{R}^{3}}(3{{x}^{2}} - {{r}^{2}})} {{{r}^{5}},}}} \right. \kern-0em} {{{r}^{5}},}}\,\,\,\,{v} = {{ - 3{{R}^{3}}xy} \mathord{\left/ {\vphantom {{ - 3{{R}^{3}}xy} {(2{{r}^{5}})}}} \right. \kern-0em} {(2{{r}^{5}})}},\,\,\,\,w = {{ - 3{{R}^{3}}xz} \mathord{\left/ {\vphantom {{ - 3{{R}^{3}}xz} {(2{{r}^{5}}),}}} \right. \kern-0em} {(2{{r}^{5}}),}} \\ p = {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} \gamma }} \right. \kern-0em} \gamma } + p{\kern 1pt} ',\,\,\,\,p{\kern 1pt} ' = {{(1 - {{u}^{2}} - {{{v}}^{2}} - {{w}^{2}})} \mathord{\left/ {\vphantom {{(1 - {{u}^{2}} - {{{v}}^{2}} - {{w}^{2}})} 2}} \right. \kern-0em} 2},\,\,\,\,\rho = 1 + {{p{\kern 1pt} '} \mathord{\left/ {\vphantom {{p{\kern 1pt} '} {{{c}^{2}},}}} \right. \kern-0em} {{{c}^{2}},}} \\ \end{gathered} $$

where \({{r}^{2}} = {{x}^{2}} + {{y}^{2}} + {{z}^{2}}\) and \(c = \sqrt {{{\gamma \bar {p}} \mathord{\left/ {\vphantom {{\gamma \bar {p}} {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}} \) is the speed of sound in an unperturbed flow. It is well known that in the flow past a cylinder in the two-dimensional statement not only a noncirculating flow-past but also a circulating flow-past with any amount of circulation can be installed (see, e.g., [29]). An analogous effect is found in the flow past a sphere. To avoid this, the calculation mesh with the characteristic step h is constructed as follows. First, in the quarter of the computational domain (y > 0 and z > 0), we construct a mesh having the characteristic edge length 2h on the surface of the sphere and a runoff coefficient of 1.5. The mesh is then reflected against the planes y = 0 and z = 0. After that, the mesh is refined by a factor of 2 to have spectral elements and nodes that must lie on the surface of the sphere shifted on it. It can be considered that after the refinement, the runoff coefficient of the mesh from the boundary takes the value \(\sqrt {1.5} \). However, the calculations show that, despite the symmetry of the mesh, the arithmetic error accumulates over time and leads to a violation of the symmetry of the flow. Therefore, at every time step the flow was artificially symmetrized.

In order to improve the choice of the numerical dissipation, instead of solving the problem of breaking up a discontinuity by formula (5), the Roe scheme with the preconditioner of E. Turkel is used [30]; see also [6, 31].

The calculation data in the cross-section z = 0 when y > 0 on a mesh with h = 0.04 is presented in Fig. 6. The thin black and thick grey lines present the isolines of the exact and numerical solutions for p′, respectively. The flow is directed from left to right. Since the numerical solution is steady, the UFC calculations must produce exactly the same result as the steady FC scheme; therefore, such calculations were not carried out.

Fig. 6.
figure 6

Isolines of pressure pulsation in cross-section z = 0, y > 0 on mesh with h = 0.04, compared to exact solution. Top down: FC with polynomial gradients, FC with spectral-element gradients, and EBR5.

Full size image

It is seen that on the front side of the sphere, the isolines of the exact and numerical solutions are superimposed on one another, while on the back of the sphere, the numerical solution for pressure is somewhat less than the exact solution. This is the usual result of numerical dissipation. The author’s experience shows that dissipation in one or two layers of cells near a sphere plays a decisive role in this task. Figure 6 demonstrates that the SEBR5 scheme has less dissipation than the FC scheme with polynomial (FC-poly) gradients but more dissipation than the FC scheme with spectral-element (FC-SE) gradients. More detailed results of the calculations on the sequence of meshes are presented in Table 1.

Table 1.   Numerical error in solution of problem of flow past sphere
Full size table

Table 1 shows that the solution by the FC-poly gradients and by the SEBR5 scheme converges to the exact solution approximately at a rate of O(h). The first order of convergence on the maximums of the error is associated with the loss of accuracy of the edge schemes at the boundary. The faster convergence rate of the resistance is an unexpected result. However, when using spectral-element gradients, the solution near the back point of the sphere is incorrect. Since the underestimated pressure near the back point of the sphere is usually the result of excessive numerical viscosity, it can be assumed that the overestimated density is a consequence of the insufficient numerical viscosity.

7 TESTING: SMOOTH TWO-DIMENSIONAL VORTEX

Consider the problem of a two-dimensional steady vortex within the limits of the Euler equations. The azimuth speed profile is assigned as \({{u}_{\phi }}(r) = \frac{\Gamma }{{2\pi }}\frac{r}{{{{r}^{2}} + {{a}^{2}}}}\). Pressure and density are determined from the steadiness condition of the vortex \({{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial r}}} \right. \kern-0em} {\partial r}} = {{\rho u_{\phi }^{2}} \mathord{\left/ {\vphantom {{\rho u_{\phi }^{2}} r}} \right. \kern-0em} r}\) and the constancy of the entropy with allowance for the boundary conditions at infinity \({{\rho }_{\infty }} = 1,{{p}_{\infty }} = {1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }\). Since the circulation \(\Gamma (r) = 2\pi r{{u}_{\phi }}(r)\) = \({\kern 1pt} \Gamma (1 - {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {({{r}^{2}} + {{a}^{2}})}}} \right. \kern-0em} {({{r}^{2}} + {{a}^{2}})}})\) is a monotonically increasing function, according to the criterion of Rayleigh [32], this vortex is resistant to radial perturbations. Suppose the radius of the vortex is a = 0.001 and the circulation at infinity is Г = 0.0005; this corresponds to the maximum circular speed of the vortex of \({{u}_{{\phi ,\max }}}(r) \approx {\text{0}}{\text{.0398}}\).

The calculations are carried out on a sequence of five calculation meshes. A mesh is built using the mesh generator (GMSH) [33] as follows. In a circle of radius a, we build a quasi-uniform unstructured triangular mesh with the characteristic edge length of 2h, where h = a/N and N is the conditional number of nodes per vortex radius. In a circle of radius 10a, the mesh step increases with a factor of 1.05 and is limited by the size of 5h. Outside this circle, the step increases with a factor of 1.2 with no limit on the maximum step. The resulting mesh is naturally refined (each triangle is divided into four triangles).

The outer boundary of the computational domain (a cube with a side of 2) is far enough away from the domain of interest. All the physical variables were kept on this boundary according to the exact solution.

The results of the calculations at the time tmax = 0.02 are presented in Table 2; no data means that no calculation was performed.

Table 2.   Numerical error in solution of problem of steady vortex
Full size table

Analyzing the results of the calculations, we can draw the following conclusions. First, the results of the calculations obtained by the UFC scheme barely differ from the results obtained by the steady FC scheme when using the same gradients. This result is expected, because the exact solution of the problem is steady. Second, the order of accuracy of the FC scheme lies between 2 and 3. This is also expected, as the steady FC scheme has the second approximation order; the increased observed convergence rate (up to the third order) on steady tasks was also observed earlier [7–9]. Third, the FC scheme provides a smaller error (by factors of 1 to 4) when using spectral-based gradients than with polynomial gradients. This result is seen above in the one-dimensional transfer equation. Fourth, the EBR5 scheme on rough meshes is superior in accuracy not only to the EBR3 scheme but also to the FC scheme with polynomial gradients; however, on detailed meshes the results of the EBR3 and EBR5 schemes are close to each other and significantly worse than the results of the FC scheme. This effect is associated with a predominance for EBR schemes, of an error proportional to the second derivative of the solution; this component chaotically changes from node-to-node and is limited by a constant that does not grow over time. However, for small computation times it prevails and on unstructured meshes decreases the slowest when the mesh is refined. In the one-dimensional case, the analysis of the error’s structure is presented in [34].

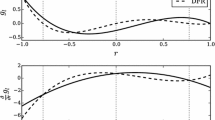
Eventually, in this test the FC scheme using spectral elements has the best result. However, the comparative characteristics of the schemes change if we increase the calculating time: instead of tmax = 0.02, we shall calculate up to tmax = 1. Testing in this formulation on a mesh sequence requires significant time; therefore, we limit ourselves to a mesh of 20 nodes per vortex radius. The results of calculations on the EBR and FC schemes with polynomial gradients show the smoothing of the profile of the azimuth velocity, i.e., the numerical dissipation of the vortex. This result is physically correct; here, if dissipation is excessive, it can be reduced by refining the mesh and, to some extent, by decreasing parameter δ in (5).

A different picture is obtained when calculating by the FC and UFC schemes with gradients on spectral elements. First, the radial instability arises: the profile of the azimuth velocity acquires parasitic oscillations exponentially increasing over time, and by t ~ 0.7 they become visible against the backdrop of the initial vortex (see Fig. 7). When t ~ 0.9, the violation of the axial symmetry of the flow becomes clearly visible, and by t ~ 1 the core of the vortex is completely destroyed. By t ~ 4, the solution almost completely “forgets” its initial state. On the whole, the results on the FC and UFC schemes coincide, only the moment of the vortex breakup changes slightly.

Fig. 7.
figure 7

Vortex breakup in calculation by FC scheme with spectral-element gradients. Top down and from left to right: t = 0.5, t = 0.7, t = 0.9, t = 0.95, t = 1.0, and t = 3.0. Color corresponds to velocity modulus.

Full size image

Thus, the specific nature of the dissipation of the fourth order (this nature is inherent in the UFC-SE scheme and is observed above on linear tasks), on the task of a vortex leads to the wrong solution, although it does not “fall apart” in the usual sense when the numerical oscillations grow without a limit. Since the additional dissipative terms inherent in the steady FC scheme are zeroed out on steady tasks, this scheme has the same disadvantage. This problem is apparently an irreparable flaw in the calculations of gradients based on second-order spectral elements. Using spectral elements of the third or higher order at internal nodes, this effect is not observed; however, as noted in [8], the boundary of the computational domain becomes instable.

8 PROBLEMS WITH DISCONTINUOUS SOLUTIONS

Since the main development of the FC scheme is aimed at creating a non-conservative scheme for smooth unsteady solutions that shows the third order of accuracy on unstructured meshes [8–12], little attention is paid to the question of the applicability of the FC scheme for solving problems with discontinuous solutions. Here, we can specify the work [11]; it considers steady tasks in which the FC scheme is a conservative method.

For solving problems with discontinuous solutions, in the FC scheme, as in other edge-based schemes, slope limiters are used. Their point is that values of \({{\alpha }_{{GK}}}\) and \({{\alpha }_{{KG}}}\) in (6) are taken smaller than 1. The paper [11] proposes the limiter

$${{\alpha }_{{GK}}} = 1 - {{\left| {\frac{{{{u}_{K}} - {{u}_{G}}}}{{\max \{ \left| {{{u}_{K}}} \right| + \left| {{{u}_{G}}} \right|{{{,10}}^{{ - 20}}}\} }}} \right|}^{3}},\,\,\,\,{{u}_{i}} = 2({{{\mathbf{r}}}_{K}} - {{{\mathbf{r}}}_{G}})\,\cdot\,{{(\nabla {\mathbf{Q}})}_{i}} - ({{{\mathbf{Q}}}_{K}} - {{{\mathbf{Q}}}_{G}}).$$
(8)

Consider also the other limiter

$${{\alpha }_{{GK}}} = 1 - {{\left| {\max \{ {{l}_{K}},{{l}_{G}}\} } \right|}^{3}},\,\,\,\,{{l}_{i}} = ~\frac{{({{u}_{K}} - {{u}_{G}}) - {{{({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial e}}} \right. \kern-0em} {\partial e}})}}_{G}}}}{{\max \{ \left| {{{u}_{K}} - {{u}_{G}}} \right| + \left| {{{{({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial e}}} \right. \kern-0em} {\partial e}})}}_{G}}} \right|{{{,10}}^{{ - 20}}}\} }},$$
(9)

where \({{({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial e}}} \right. \kern-0em} {\partial e}})}_{G}}\) is a derivative (along the GK edge) multiplied by the length of this edge and calculated using data at the G node and the value interpolated to the continuation of this edge analogously to the EBR3 scheme [4]. Although [11] proposes applying a limiter to conservative variables Q, we apply (8) and (9) to the characteristic variables SQ, where the matrix S is determined by (2). A detailed description of such a reconstruction of the characteristic variables is presented in [5].

In this section, we limit ourselves to two tests. As the first test, we take the task of a supersonic flow past a front step in a channel. The source data is the homogeneous flow with parameters ρ = 1.4, p = 1, u = 3, and v = 0. The calculations are conducted up to tmax = 4. We conduct the calculations of this task on a very detailed unstructured mesh, namely, with the characteristic step h = 1/320 in order that we can most clearly see the advantage of schemes with a greater degree of precision. The mesh is built by the GMSH generator [33].

Figure 8 shows the results of calculations on the EBR-minmod and FC schemes with limiters (8) and (9), as well as the EBR-WENO scheme. In all the calculations, to stabilize them, switching to Rusanov’s flow on the edges (when at least one edge node lies on the boundary) is used. For the EBR-WENO scheme, artificial viscosity with artificial thermal conductivity is included [36]. The figure shows that limiter (9) allows us to achieve less artificial dissipation on the contact discontinuity on the upper part of the computational domain than limiter (8).

Fig. 8.
figure 8

Solution of problem of flow over step in channel on unstructured mesh. Top down: EBR-minmod, FC with limiter (8), FC with limiter (9), and EBR-WENO5.

Full size image

Now consider a problem with an infinitely smooth solution to estimate the impact of the limiters. Choose a background field \(\bar {\rho } = 1,{\mathbf{\bar {u}}} = 0\,\,{\text{and}}\,\,\bar {p} = {1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }\) and place pulsations on it; at the initial instant, these pulsations are determined as follows:

$$\rho {\kern 1pt} '(0,{\mathbf{r}}) = p{\kern 1pt} '(0,{\mathbf{r}}) = {{10}^{{ - 4}}}\mathop \sum \limits_{i = - \infty }^\infty \mathop \sum \limits_{j = - \infty }^\infty \mathop \sum \limits_{k = - \infty }^\infty {{p}_{{ijk}}}\exp \left( { - \ln 2{{{\left( {\frac{{{\mathbf{r}} - 12.5(i{{{\mathbf{e}}}_{x}} + j{{{\mathbf{e}}}_{y}} + k{{{\mathbf{e}}}_{z}})}}{6}} \right)}}^{2}}} \right),$$

where ex, ey, and ez are unit vectors in the corresponding directions, while pijk = 1 if (i + j + k) is even, and 0 otherwise.

We conduct the calculation in a cube with the edge of 25 and periodic conditions in all directions up to tmax = 20. We limit ourselves to the case of the Cartesian mesh. The results are presented in Table 3. On average, the proposed limiter allows us to make an error that is 30–40% smaller than the error of limiter (8); however, the result remains significantly worse than the result obtained by the EBR-WENO5 scheme.

Table 3.   Numerical error in solution of acoustic problem on Cartesian mesh
Full size table

9 CONCLUSIONS

This paper considers various modifications of the FC method. Particular attention is paid to the way gradients are calculated at mesh nodes with the second order of approximation.

In linear tasks, we note that the unsteady FC scheme when using gradients calculated with the use of spectral elements gives a smaller numerical error compared to other modifications and other edge-based schemes. However, the apparent increase in accuracy is due to the loss of dissipation and, as a result, the error of the solution. In particular, on a vortex that should be resistant to radial perturbations, these perturbations increase and ultimately lead to the vortex breaking up.

If we use gradients from interpolation polynomials built by the LSM, then numerous experiments show that the unsteady FC method gives results very close to the results calculated by the EBR5 scheme. The computational cost of these schemes is also comparable: the time spent for one step in the FC method is from 0.85 to 1.5 times longer than that of EBR5. This value varies depending on modifications; measurements were taken when solving two-dimensional Euler equations.

The calculations presented above of the task of a flow over a forward step show that the FC method is fully compatible with the slopes’ limiters and through their use successfully copes with the tasks having discontinuous solutions. However, on smooth solutions, the use of these limiters affects the accuracy more than in schemes with a quasi-one-dimensional reconstruction. The numerical error of the FC method with different limiters is only slightly better than such an error of the MinMod limiter scheme. The EBR-WENO scheme is even more accurate. Thus, on tasks with discontinuous solutions, schemes with a quasi-one-dimensional reconstruction are preferable.

The main task of this work is to choose the main edge-based scheme used for calculations in the NOISEtte software code [37]. The calculations of the test tasks suggest that at present a scheme of the EBR family should be considered for such a scheme. Perhaps, the FC method has the potential for developing in the direction of nonconservative schemes. This issue is a topic of further investigations.