CODAS Method for Multi-Attribute Decision-Making Based on Some Novel Distance and Entropy Measures Under Probabilistic Dual Hesitant Fuzzy Sets

Abstract

Probabilistic dual hesitant fuzzy set (PDHFS) as an extension of the generalization of hesitant fuzzy set (HFS) and dual hesitant fuzzy set (DHFS). It not only reflects the hesitant attitude of decision-makers (DMs), but also reflects probabilistic information. It is a more powerful and important tool to express uncertain information. As we all know, the distance and entropy measures are very useful tool in the MADM problems. In many fuzzy environments, their distance and entropy measures are proposed, and the MADM methods depend on the distance and entropy measures are given. First, to overcome the disadvantages of destroying the original information caused by artificially adding elements, we defined the membership degree (MD) mean, non-membership degree (NMD) mean and standard deviation for PDHFE, based on above definitions, the mean and standard deviation distance were proposed. Secondly, without the aid of other auxiliary functions, we built some novel PDHF entropy measures. Third, depend on the distance and entropy measures built, we integrate the classical CODAS method with the PDHF setting, and build a novel MADM technique to solving the MADM problem. Finally, the built MADM technique is used to the evaluation of enterprise credit risk to testify the practicability and feasibility of the built MADM technique. Meanwhile, the MADM technique built in this study is compared with some existing methods, and the advantages of the MADM technique proposed in this study are put forward, which has a better effect in solving MADM problems.

1 Introduction

With the continuous development of people’s cognition, there were fewer and fewer cases of taking accurate data as the processing object in the past, and the uncertainty and fuzziness of things' cognition continued to appear. To better handle these situations, Zadeh [1] built the well-known fuzzy set (FS) in 1965. Since it was proposed, it was applied to many uncertain decision-making fields, such as concrete pavement construction and motion matching [2,3,4,5]. With the continuous development of science & technology, extended forms of FS have been put forward. In order to overcome the situation that FS can only deal with one-dimensional data, the multi-dimensional fuzzy sets are proposed and widely used in many fields, such as the reliability assessment, the energy policy problem, the distinguish of ORL face and the performance investigation [6,7,8]. In view of the disadvantage that FS only reflect approval but can’t reflect disapproval and hesitation, Atanassov [9] proposed the intuitionistic fuzzy set (IFS), Atanassov and Gargov [10] built the interval IFS (IVIFS). IFS better reflect people's intuitive cognition and better reflect the reality. Since IFS was proposed, it was widely used in the problems of supplier selection, dynamic air target threat assessment, technique evaluation and location selection [11,12,13]. The MD and NMD of IFS takes single value, it can’t reflect the hesitation of DM in multiple values. Torra [14] proposed the hesitant fuzzy set (HFS), which can better reflect the DM's hesitation in multiple values. Since HFS was proposed, it has also developed rapidly and has been applied to the offshore wind turbine technology selection [15]. The same problem exists, the HFS reflects the situation that the MD takes multiple values. Although HFS can reflect the situation of approval, it can’t reflect the situation of opposition. In view of this situation, Zhu, Xu and Xia [16] built the dual hesitant fuzzy set (DHFS), it solves the defect well and is widely used in the fields of new framework for FCMs and ancient Chinese character image retrieval [17, 18]. DHFS can reflect the DM's hesitation in multiple values, as well as the approval and disapproval, that is, considering the MD and NMD, but there are some new problems that when the DM gives the hesitation values of MD and NMD, it can’t reflect the probabilities of taking these values. For the problem, Hao, Xu, Zhao and Su [19] built the probabilistic dual hesitant fuzzy set (PDHFS), which well solves the problem, and gives the basic operation rules, at the same time, two PDHFEs are compared using the score and deviation degree of PDHFE. Since the PDHFS was put forward, there have been some studies on the PDHFS. Zhao, Ju and Pedrycz [20] gave the decision-making technique by PROMETHEE-II method to solve PDHF MCGDM problem. Garg and Kaur [21] presented a robust distance measure for PDHFS, and applied the decision method to project managers’ evaluation of a software company. Ren, Xu and Wang [22] extended TODIM method to PDHF environment and it was applied to enterprise strategic assessment. Zhang et al. [17] presented a MAGDM model under PDHF setting with MULTIMOORA and applied it to the evaluation of the P-J fit algorithm. Garg and Kaur [23] applied the MSM operator to PDHF environment to solve the medical diagnosis problem. Ning, Wei, Lin and Guo [24] defined a novel PDHF entropy to weight for decision attributes and some novel distance measures, PDHFEPGMSM and PDHFWEPGMSM operators were defined, and a fresh MADM approach was studied depend on the PDHFWEPGMSM operator and utilized to the evaluation of SSS. Although there have been some studies on the decision-making methods of PDHFS, on the whole, there are few studies on PDHFS.

Distance measure has always been a very concerned content in various fuzzy environments in the field of MADM, and there are many decision-making methods based on distance measure [25,26,27,28]. For instance, Liu [29] built the measures of distance, entropy and similarity of FS and studied the relationship between them. The distance measures of IFS and IVIFS [30,31,32,33,34], and some decision-making methods based on these distance measures were applied to the problems of pattern classification, house election, attractiveness of houses and human resource management. The distance measures of HFS [35,36,37], and these distance measures were applied to the evaluations of nutritive value of fruits and energy policy. The distance measures of DHFS [38,39,40,41], and applied to the evaluation problems of investment company, consumer’s buying behavior and pattern recognition. Ren, Xu and Wang [22] studied the equal probability distance of PDHFS, but it has some problems of complex calculation and inconsistency between calculated results and actual results. Garg and Kaur [42] also defined the distance between two PDHFEs, but from the definition of distance, the distance calculated according to this distance formula will be smaller than the real distance.

Entropy is an important concept in thermodynamics. Since it was proposed, it has been widely used in index weighting [43,44,45]. At the same time, many scholars also put forward the concept of fuzzy entropy, Rahimi, Kumar, Moomivand and Yari [46] and Xu and Tang [47] proposed the entropy measures of IFS and applied it to supplier selection and cold chain vulnerability assessment. Meng, Xu and Wang [48] and Thao and Smarandache [49] proposed the entropy measures for PFS and applied it to the evaluations of emerging technology enterprises and teaching management system. Anees, Zhang, Baig, Lougou and Bona [50] defined the hesitant fuzzy entropy measures and was applied to evaluation of heterogeneous wireless sensor networks. Zhang [51] proposed the entropy measure for DHFS and applied it to indexes weighting. There are many entropy measures for various fuzzy sets were proposed in the corresponding fuzzy environment. These entropy measures have been widely applied to their respective fuzzy environment and achieved good results. Hao, Xu, Zhao and Su [19] studied the PDHF entropy measure, which was defined on the basis of other auxiliary functions, and the calculation is relatively cumbersome. Meanwhile, it need add the new elements to the shorter PDHFS according to the pessimistic principle or optimistic principle, but such artificial addition of elements will change the original information of PDHFS, which has some disadvantages.

At present, there are many well-known methods for the research of MADM methods, and these decision-making techniques have been well applied in many fields. The study only lists some decision-making methods that are often used by scholars, these methods include TOPSIS method [52, 53], VIKOR method [54], ELECTRE method [55], PROMETHEE method [56], LINMAP method [57], QUALIFLEX method [58], TODIM method[59, 60], MULTIMOORA method [61], COPRAS method [62], EDAS method [63], GRA method[64], BWM method [65], ARAS method [66], WASPAS method [67]. By reviewing the original literature of each method, we find that each method has its own advantages and disadvantages.

The COmbinative Distance-based ASsessment (CODAS) method is a novel MADM method proposed by Keshavarz Ghorabaee, Zavadskas, Turskis and Antucheviciene [68], Keshavarz Ghorabaee, Zavadskas, Turskis and Antucheviciene [68] believes that the proposed CODAS method has some characteristics not considered in the above-mentioned methods, the advantages and disadvantages of the alternatives are measured according to the Euclidean distance and the taxicab distance with the negative ideal point. First, the alternatives are selected according to the Euclidean distance, if the Euclidean distance of the two alternatives is very close, then the taxicab distance is used to compare the two alternatives. The greater the distance, the better. In reference [68], CODAS method is used to compare with several methods such as WASPAS, COPRAS, TOPSIS, VIKOR and EDAS approaches to illustrate the advantages of CODAS method. Since it was built, it has been integrated into many fuzzy settings and worked some very pivotal roles in vehicle shredding facility location, assessment Urban transport service, investment project evaluation and appropriate system for cloud computing [69,70,71,72]. So far, CODAS method has been fused to many fuzzy settings, and has been continuously applied in practice, which has achieved good results. From the literature, it is feasible to integrate CODAS method with fuzzy environment.

In this study, the concepts of distance measure, entropy measure and CODAS in fuzzy environment are reviewed, but some problems are also found in the review process. The motivations of this study are put forward as follows:

• (1) In the increasingly complex decision-making environment, it is very important to obtain evaluation information effectively. PDHFS can more comprehensively and extensively express the preference information of DMs.

• (2) Ren, Xu and Wang [22] studied the equal probability distance of PDHFS, but it has some problems of complex calculation and inconsistency between calculated results and actual results. Garg and Kaur [42] also defined the distance between two PDHFEs, but from the definition of distance, the distance calculated according to this distance formula will be smaller than the real distance. Meanwhile, these distance measures don’t consider the psychological behavior of DMs. And we can find the famous Hamming distance, Euclidean distance have been successfully extended into many fuzzy setting and we extend the several famous distance measures to PDHF setting.

• (3) From the references review, only reference Hao, Xu, Zhao and Su [19] studied the PDHF entropy measure, which was defined on the basis of other auxiliary functions, and the calculation is relatively cumbersome. Meanwhile, it need add the new elements to the shorter PDHFS according to the pessimistic principle or optimistic principle, but such artificial addition of elements will change the original information of PDHFS, which has some disadvantages;

• (4) Because CODAS decision-making method has the advantages that other methods do not have, this method has been widely extended to other fuzzy environments, but there is no case about the application of codas method in PDHF environment;

• (5) Enterprise credit risk is a very important for an enterprise, scientific and reasonable evaluation methods are very important to the scientific management and development of enterprise, some novel enterprise credit risk evaluation methods are a very urgent task for us;

• (6) Finally, a numerical example of enterprise credit risk is built to illustrate the practicality of the proposed MADM technique. Comparative analysis attests the validity of the proposed MADM technique. The method presented in this paper can effectually solve the MADM problems which the decision-making information is expressed by PDHFEs and the attributes are interactive.

This study aims to propose a novel MADM method for MADM problems with PDHF information. Some main works of this study are as follows:

• (1) To solve the problem that the distance measures of PDHFSs have some problems of complex calculation and inconsistency between calculated results and actual results Ren, Xu and Wang [22], Garg and Kaur [42], famous Hamming distance and Euclidean distance are extended to PDHF setting, and some novel distance measures can consider the psychological behavior of DMs are built for PDHFSs which can reflect the reality better;

• (2) PDHF entropy in reference Ren, Xu and Wang [22] is defined on the basis of other auxiliary functions, and the calculation is relatively cumbersome. In this study, a novel probabilistic dual hesitation fuzzy entropy is proposed without the help of other auxiliary conditions and applied to weight for decision attributes;

• (3) In view of the successful application of CODAS method in other fuzzy environments, this study proposes to integrate CODAS method with PDHF environment, and a novel MADM technique based on the PDHF-CODAS approach in PDHF environment;

• (4) Finally, a numerical example of enterprise credit risk is built to illustrate the practicality of the proposed MADM technique. Further comparative analysis attests the validity of the proposed MADM technique. The method presented in this paper can effectually solve the MADM problems which the decision-making information is expressed by PDHFEs and the attributes are interactive.

In addition to the above parts, this study is mainly composed of the following parts: the second part reviewed some basic concepts of PDHFS, some classical distances and puts forward some new concepts about PDHFS; The third part puts forward the axiomatic definition of distance measures and some new distance measures and applies these distances to some cases; In the fourth part, some definitions of PDHF entropy measures are proposed, and some cases are given; In the fifth part, CODAS method and PDHFS are fused, and a MADM technique depend on the above distance measures and entropy measures is proposed; In the sixth part, the proposed new MADM technique is applied to the enterprise credit risk assessment and parameters analysis is performed; The seventh part gives the result analysis, compare analysis and comprehensive analysis; The eighth part gives some conclusions and prospects for future research.

2 Preliminaries

2.1 Probabilistic Dual Hesitant Fuzzy Sets

In such subsection, we will review the basic conception and aggregation operator for PDHFS.

Definition 1

[19] Let ${\mathbb{Z}}$ be a fixed set, a PDHFS on ${\mathbb{Z}}$ is built with mathematical equation:

$$\Im = \left\{ {\left\langle {\ell ,\left. {\hbar \left( \ell \right)} \right|\tau \left( \ell \right),\left. {\lambda\left( \ell \right)} \right|\upsilon \left( \ell \right)} \right\rangle ,\ell \in {\mathbb{Z}}|} \right\}$$

(1)

The components $\left. {\hbar \left( \ell \right)} \right|\tau \left( \ell \right)$ and $\left. {\lambda \left( \ell \right)} \right|\upsilon \left( \ell \right)$ are some possible elements of MD & NMD, where $\hbar \left( \ell \right)$ and $\lambda \left( \ell \right)$ are the MD & NMD of $\ell \in {\mathbb{Z}}$, respectively. $\tau \left( \ell \right)$ and $\upsilon \left( \ell \right)$ are the probabilistic information for $\hbar \left( \ell \right)$ & $\lambda \left( \ell \right)$. Meanwhile,

$$0 \le \gamma ,\eta \le 1,\;0 \le \gamma^{ + } + \eta^{ + } \le 1$$

(2)

and

$$\tau_{i} \in \left[ {0,1} \right],\;\upsilon_{j} \in \left[ {0,1} \right],\;\sum\limits_{i = 1}^{\# \hbar } {\tau_{i} } = 1,\;\sum\limits_{j = 1}^{\# \lambda } {\upsilon_{j} } = 1$$

(3)

where $\gamma \in \hbar \left( \ell \right)$, $\eta \in \lambda \left( \ell \right)$, $\gamma^{ + } \in \hbar^{ + } \left( \ell \right) = \cup_{\gamma \in \hbar \left( \ell \right)} \max \left\{ \gamma \right\}$, $\eta^{ + } \in \lambda^{ + } \left( \ell \right) = \cup_{\gamma \in \lambda \left( \ell \right)} \max \left\{ \eta \right\}$, $\tau_{i} \in \tau \left( \ell \right)$ and $\upsilon_{i} \in \upsilon \left( \ell \right)$. $\# \hbar$ is the number of elements in the components $\left. {\hbar \left( \ell \right)} \right|\tau \left( \ell \right)$, $\# \lambda$ is the number of elements in the components $\left. {\lambda \left( \ell \right)} \right|\upsilon \left( \ell \right)$.

To be more convenient in the process of use and calculation, the pair $\Im = \left\langle {\left. {\hbar \left( \ell \right)} \right|\tau \left( \ell \right),\left. {\lambda \left( \ell \right)} \right|\upsilon \left( \ell \right)} \right\rangle$ is called as the PDHFE, recorded as $\Im = \left\langle {\left. \hbar \right|\tau ,\left. \lambda \right|\upsilon } \right\rangle$ [19].

Under conditions $\sum\nolimits_{i = 1}^{\# \hbar } {\tau_{i} } < 1$ and $\lambda \sum\nolimits_{j = 1}^{\# \lambda } {\upsilon_{j} } < 1$, we need to normalize the PDHFS by the following formula:

$$\dot{\Im } = \left\{ {\left. {\left\langle {\ell ,\left. {\hbar \left( \ell \right)} \right|\tau \left( \ell \right),\left. {\lambda \left( \ell \right)} \right|\upsilon \left( \ell \right)} \right\rangle ,\ell \in {\mathbb{Z}}} \right|} \right\}$$

(4)

where the elements in $\tau \left( \ell \right)$ is computed by $\tau \left( \ell \right) = {{\tau_{i} } \mathord{\left/ {\vphantom {{\tau_{i} } {\sum\nolimits_{i = 1}^{\# \hbar } {\tau_{i} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{i = 1}^{\# \hbar } {\tau_{i} } }}$ and $\upsilon \left( \ell \right)$ is computed by $\upsilon \left( \ell \right) = {{\upsilon_{i} } \mathord{\left/ {\vphantom {{\upsilon_{i} } {\sum\nolimits_{i = 1}^{\# \lambda } {\upsilon_{i} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{i = 1}^{\# \lambda } {\upsilon_{i} } }}$.

Next, we gave some operation laws for PDHFEs.

Let $p$, $p_{1}$ and $p_{2}$ be three PDHFEs, $\Im = \left\langle {\left. \hbar \right|\tau ,\left. \lambda \right|\upsilon } \right\rangle$, $\Im_{1} = \left\langle {\left. {\hbar_{1} } \right|\tau_{{\hbar_{1} }} ,\left. {\lambda_{1} } \right|\upsilon_{{\lambda_{1} }} } \right\rangle$ and $\Im_{2} = \left\langle {\left. {\hbar_{2} } \right|\tau_{{\hbar_{2} }} ,\left. {\lambda_{2} } \right|\upsilon_{{\lambda_{2} }} } \right\rangle$, then some basic operation laws for PDHFEs were defined as [19]:

To compare the size of two PDHFEs, Hao et al. [19] defined the score function. Xu and Zhou [73] defined the accuracy function of PDHFEs.

Definition 2

[19] $\Im = \left\langle {\left. \hbar \right|\tau ,\left. \lambda \right|\upsilon } \right\rangle$ is a PDHFE, then the score function of the PDHFE are built as:

$$s\left( \Im \right) = \sum\limits_{i = 1\;\gamma \in \hbar }^{\# \hbar } {\hbar_{i} \cdot \tau_{i} } - \sum\limits_{j = 1\;\gamma \in \lambda }^{\# \lambda } {\lambda_{j} \cdot \upsilon_{j} }$$

(5)

Definition 3

[73] $\Im = \left\langle {\left. \hbar \right|\tau ,\left. \lambda \right|\upsilon } \right\rangle$ is a PDHFE, the accuracy function of the PDHFE is defined as:

$$h\left( \Im \right) = \sum\limits_{i = 1\;\gamma \in \hbar }^{\# \hbar } {\hbar_{i} \cdot \tau_{i} } + \sum\limits_{j = 1\;\gamma \in \lambda }^{\# \lambda } {\lambda_{j} \cdot \upsilon_{j} }$$

(6)

The size of two PDHFEs of comparing method is given as follows [73]:

If $s\left( {\Im_{1} } \right) > s\left( {\Im_{2} } \right)$, then the PDHFE $\Im_{1}$ is superior to $\Im_{2}$, recorded by $\Im_{1} > \Im_{2}$; On the contrary, there is $\Im_{1} < \Im_{2}$.

If $s\left( {\Im_{1} } \right) = s\left( {\Im_{2} } \right)$, then.

• (1) If $h\left( {\Im_{1} } \right) < h\left( {\Im_{2} } \right)$, the PDHFE $\Im_{1}$ is superior to $\Im_{2}$, denoted by $\Im_{1} < \Im_{2}$;

• (2) If $h\left( {\Im_{1} } \right) > h\left( {\Im_{2} } \right)$, the PDHFE $\Im_{1}$ is inferior to $\Im_{2}$, denoted by $\Im_{1} > \Im_{2}$;

• (3) If $h\left( {\Im_{1} } \right) = h\left( {\Im_{2} } \right)$, the PDHFE $\Im_{1}$ is equal to $\Im_{2}$, denoted by $\Im_{1} \sim \Im_{2}$.

How to use the information aggregation operator to effectively fuse the information provided by DMs for better decisions is very important, Hao, Xu, Zhao and Su [19] defined the PDHF weighted averaging (PDHFWA) operator.

Definition 4

[19] Let $\Im_{i} = \left\langle {\left. {\hbar_{i} } \right|\tau_{{h_{i} }} ,\left. {\lambda_{i} } \right|\upsilon_{{g_{i} }} } \right\rangle \left( {i = 1,2, \cdots ,n} \right)$ be $n$ PDHFEs and the weight be $\omega_{j} \left( {j = 1,2, \cdots ,n} \right)$ along with $\omega_{j} \in \left[ {0,1} \right]\left( {j = 1,2, \cdots ,n} \right)$ and $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$. Then the PDHFWA operator is given as:

$$\begin{gathered} PDHFWA\left( {\Im_{1} ,\Im_{2} , \cdots ,\Im_{n} ,} \right) = \mathop \oplus \limits_{j = 1}^{n} \omega_{j} \Im_{j} \hfill \\ = \mathop \cup \limits_{\begin{subarray}{l} \gamma_{1} \in \hbar_{1} ,\gamma_{2} \in \hbar_{2} , \cdots ,\gamma_{n} \in \hbar_{n} \\ \eta_{1} \in \lambda_{1} ,\eta_{2} \in \lambda_{2} , \cdots ,\eta_{n} \in \lambda_{n} \end{subarray} } \left\{ {\left\{ {\left. {\left( {1 - \mathop \Pi \limits_{j = 1}^{n} \left( {1 - \gamma_{j} } \right)^{{\omega_{j} }} } \right)} \right|\mathop \Pi \limits_{j = 1}^{n} p_{{\gamma_{j} }} } \right\},\left\{ {\left. {\left( {\mathop \Pi \limits_{j = 1}^{n} \eta_{j}^{{\omega_{j} }} } \right)} \right|\mathop \Pi \limits_{j = 1}^{n} q_{{\eta_{j} }} } \right\}} \right\} \hfill \\ \end{gathered}$$

(7)

2.2 Some Classical Distance Measures

Distance is a very important concept in the field of mathematics. If a measure $d$ is named as a distance measure, it should satisfy three properties in Theorem 1:

Theorem 1 [74] Let ${\mathbb{Z}}$ be a non-empty set. A metric $d\left( {\iota ,\kappa } \right)$ on ${\mathbb{Z}}$ is recorded as distance measure if for any $\iota ,\kappa ,\varsigma \in {\mathbb{Z}}$, the following three properties hold:

• (1) (Nonnegative) $d\left( {\iota ,\kappa } \right) \ge 0$ and $d\left( {\iota ,\kappa } \right){ = }0 \Leftrightarrow \iota = \kappa$;

• (2) (Symmetric) $d\left( {\iota ,\kappa } \right){ = }d\left( {\kappa ,\iota } \right)$;

• (3) (Triangle inequality) $d\left( {\iota ,\kappa } \right) \le d\left( {\iota ,\varsigma } \right){ + }d\left( {\varsigma ,\kappa } \right)$.

Distance measure is very important tools, which are widely used in important MADM and MAGDM issues, such as machine learning, pattern recognition, bilateral matching and so on. In most studies, the distance for ${\rm M}$ and ${\rm N}$ on ${\mathbb{Z}} = \left\{ {\ell_{1} ,\ell_{2} , \cdots ,\ell_{n} } \right\}$ mainly includes the following distances, here we give several distance measures [75,76,77].

• (1) The Hamming distance: $h\left( {{\rm M},{\rm N}} \right) = \sum\nolimits_{i = 1}^{n} {\left| {\zeta_{\rm M} \left( {\ell_{i} } \right) - \zeta_{\rm N} \left( {\ell_{i} } \right)} \right|}$

• (2) The normalized Hamming distance: $h_{n} \left( {{\rm M},{\rm N}} \right) = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left| {\zeta_{\rm M} \left( {\ell_{i} } \right) - \zeta_{\rm N} \left( {\ell_{i} } \right)} \right|}$

• (3) The Euclidean distance: $e\left( {{\rm M},{\rm N}} \right) = \left( {\sum\nolimits_{i = 1}^{n} {\left( {\zeta_{\rm M} \left( {\ell_{i} } \right) - \zeta_{\rm N} \left( {\ell_{i} } \right)} \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$

• (4) The normalized Euclidean distance: $e_{n} \left( {{\rm M},{\rm N}} \right) = \left( {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {\zeta_{\rm M} \left( {\ell_{i} } \right) - \zeta_{\rm N} \left( {\ell_{i} } \right)} \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$

• (5) The hausdorff metric: $h_{m} \left( {{\rm M},{\rm N}} \right) = \max \left| {\zeta_{\rm M} \left( {\ell_{i} } \right) - \zeta_{\rm N} \left( {\ell_{i} } \right)} \right|$

where $\zeta_{\rm M} \left( {\ell_{i} } \right)$ and $\zeta_{\rm N} \left( {\ell_{i} } \right)$ represent the membership degree of ${\rm M}$ and ${\rm N}$, and satisfy condition $0 \le \zeta_{\rm M} \left( {\ell_{i} } \right),\zeta_{\rm N} \left( {\ell_{i} } \right) \le 1$.

2.3 Some Novel Concepts for PDHFE

To overcome the defect of artificially adding elements to destroy the original information, this study gives some novel distance measures of PDHFS. These distance measures do not need to add elements and maintains the original information well, we first introduce some novel concepts as follows:

Let $d = \left( {\left. h \right|p,\left. g \right|q} \right)$ be any a PDHFE. Next, we give some notes for PDHFE as follows:

• (1) The mean of MD:

  $$\gamma \left( d \right){ = }\sum\nolimits_{j = 1}^{\# h} {h_{j} p_{j} }$$

  (8)

• (2) The mean of NMD:

  $$\eta \left( d \right){ = }\sum\nolimits_{j = 1}^{\# g} {g_{j} q_{j} }$$

  (9)

• (3) The standard deviation of MD:

  $$\Phi \left( d \right){ = }\sqrt {\sum\limits_{j = 1}^{\# h} {\left( {h_{j} p_{j} - \gamma \left( d \right)} \right)^{2} } }$$

  (10)

• (4) The standard deviation of NMD:

  $$\Psi \left( d \right){ = }\sqrt {\sum\limits_{j = 1}^{\# g} {\left( {g_{j} q_{j} - \eta \left( d \right)} \right)^{2} } }$$

  (11)

Let ${\rm M}$ and ${\rm N}$ be any two PDHFSs on ${\mathbb{Z}} = \left\{ {\ell_{1} ,\ell_{2} , \cdots ,\ell_{n} } \right\}$, meanwhile, we also give some notes for two PDHFEs in the two PDHFSs:

• (1) The mean distance of MD between ${\rm M}$ and ${\rm N}$:

  $$\gamma \left( {\ell_{i} } \right){ = }\left| {\gamma \left( {{\rm M}\left( {\ell_{i} } \right)} \right) - \gamma \left( {{\rm N}\left( {\ell_{i} } \right)} \right)} \right|$$

  (12)

• (2) The mean distance of NMD between ${\rm M}$ and ${\rm N}$:

  $$\eta \left( {\ell_{i} } \right){ = }\left| {\eta \left( {{\rm M}\left( {\ell_{i} } \right)} \right) - \eta \left( {{\rm N}\left( {\ell_{i} } \right)} \right)} \right|$$

  (13)

• (3) The standard deviation distance of MD between ${\rm M}$ and ${\rm N}$:

  $$\Phi \left( {\ell_{i} } \right){ = }\left| {\Phi \left( {{\rm M}\left( {\ell_{i} } \right)} \right) - \Phi \left( {{\rm N}\left( {\ell_{i} } \right)} \right)} \right|$$

  (14)

• (4) The standard deviation distance of NMD between ${\rm M}$ and ${\rm N}$:

  $$\psi \left( {\ell_{i} } \right){ = }\left| {\psi \left( {{\rm M}\left( {\ell_{i} } \right)} \right) - \psi \left( {{\rm N}\left( {\ell_{i} } \right)} \right)} \right|$$

  (15)

Next, we build some novel distance measures for PDHFS based on the above results.

3 Distance Measures for PDHFS

Before proposing the distance measures, we give an axiomatic concept of the distance measure of PDHFE.

Definition 5

Let $\Im_{1}$, $\Im_{2}$ and $\Im_{3}$ be three PDHFEs on ${\mathbb{Z}}$, then $d$ is named as a distance measure for PDHFE, if it satisfies the four properties:

• (A1) $0 \le d\left( {\Im_{1} ,\Im_{2} } \right) \le 1$;

• (A2) $d\left( {\Im_{1} ,\Im_{2} } \right) = 0$ if and only if $\Im_{1} = \Im_{2}$;

• (A3) $d\left( {\Im_{1} ,\Im_{2} } \right) = d\left( {\Im_{2} ,\Im_{1} } \right)$;

• (A4) $d\left( {\Im_{1} ,\Im_{2} } \right) \le d\left( {\Im_{1} ,\Im_{3} } \right) + d\left( {\Im_{3} ,\Im_{2} } \right)$.

Based on Eqs. (12–15) and Definition 5, we proposed some novel distance measures for PDHFS.

3.1 Some Distance Measures for PDHFS

Let ${\rm M}$ and ${\rm N}$ be any two PDHFSs on ${\mathbb{Z}} = \left\{ {\ell_{1} ,\ell_{2} , \cdots ,\ell_{n} } \right\}$, then the generalized normalized distance (GND) between ${\rm M}$ and ${\rm N}$ is defined as:

$$d_{gnd} \left( {{\rm M},{\rm N}} \right) = \left[ {\frac{1}{2n}\sum\limits_{i = 1}^{n} {\left( {\frac{{\gamma^{\lambda } \left( {\ell_{i} } \right) + \eta^{\lambda } \left( {\ell_{i} } \right)}}{2} + \frac{{\Phi^{\lambda } \left( {\ell_{i} } \right) + \Psi^{\lambda } \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

(16)

where $\lambda \in R$ and $\lambda \ge 1$.

If $\lambda { = 1}$, then the GND reduces to the normalized Hamming distance (NHD):

$$d_{nhd} \left( {{\rm M},{\rm N}} \right) = \frac{1}{2n}\sum\limits_{i = 1}^{n} {\left( {\frac{{\gamma \left( {\ell_{i} } \right) + \eta \left( {\ell_{i} } \right)}}{2} + \frac{{\Phi \left( {\ell_{i} } \right) + \Psi \left( {\ell_{i} } \right)}}{2}} \right)}$$

(17)

If $\lambda { = 2}$, then the GND reduces to the normalized Euclidean distance (NED):

$$d_{ned} \left( {{\rm M},{\rm N}} \right) = \left[ {\frac{1}{2n}\sum\limits_{i = 1}^{n} {\left( {\frac{{\gamma^{2} \left( {\ell_{i} } \right) + \eta^{2} \left( {\ell_{i} } \right)}}{2} + \frac{{\Phi^{2} \left( {\ell_{i} } \right) + \Psi^{2} \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$$

(18)

Next, let us take an example to show the calculation steps of these distances.

Example 1

Let ${\mathbb{Z}} = \left\{ {\ell_{1} ,\ell_{2} } \right\}$, ${\rm M}{ = }\left\{ {\left\langle {\ell_{1} ,\left\{ {\left. {0.1} \right|0.2,\left. {0.2} \right|0.8} \right\},\left\{ {\left. {0.4} \right|1} \right\}} \right\rangle ,\left\langle {\ell_{2} ,\left\{ {\left. {0.2} \right|0.6,\left. {0.3} \right|0.4} \right\},\left\{ {\left. {0.6} \right|1} \right\}} \right\rangle } \right\}$${\rm N}{ = }\left\{ {\left\langle {\ell_{1} ,\left\{ {\left. {0.4} \right|0.5,\left. {0.5} \right|0.5} \right\},\left\{ {\left. {0.2} \right|0.7,\left. {0.4} \right|0.3} \right\}} \right\rangle ,\left\langle {\ell_{2} ,\left\{ {\left. {0.5} \right|0.5,\left. {0.3} \right|0.5} \right\},\left\{ {\left. {0.2} \right|1} \right\}} \right\rangle } \right\}$. Then.

For ${\rm M}$, we have.

$\gamma \left( {{\rm M}\left( {\ell_{1} } \right)} \right){ = 0}{\text{.1}} \times 0.2{ + }0.2 \times 0.8{ = }0.18$, $\eta \left( {{\rm M}\left( {\ell_{1} } \right)} \right){ = }0.4$,

$\Phi \left( {{\rm M}\left( {\ell_{1} } \right)} \right){ = }\sqrt {\left( {0.1 \times 0.2 - 0.18} \right)^{2} + \left( {0.2 \times 0.8 - 0.18} \right)^{2} } = 0.1612$, $\Psi \left( {{\rm M}\left( {\ell_{1} } \right)} \right){ = }0$;

$\gamma \left( {{\rm M}\left( {\ell_{2} } \right)} \right){ = 0}{\text{.2}} \times 0.6{ + }0.3 \times 0.4{ = }0.24$, $\eta \left( {{\rm M}\left( {\ell_{2} } \right)} \right){ = 0}{\text{.6}}$,

$\Phi \left( {{\rm M}\left( {\ell_{2} } \right)} \right){ = }\sqrt {\left( {0.2 \times 0.6 - 0.24} \right)^{2} + \left( {0.3 \times 0.4 - 0.24} \right)^{2} } = 0.1697$, $\Psi \left( {{\rm M}\left( {\ell_{2} } \right)} \right){ = }0$.

For ${\rm N}$, we have.

$\gamma \left( {{\rm N}\left( {\ell_{1} } \right)} \right){ = 0}{\text{.4}} \times 0.5{ + }0.5 \times 0.5{ = }0.45$, $\eta \left( {{\rm N}\left( {\ell_{1} } \right)} \right){ = }0.2 \times 0.7 + 0.4 \times 0.3 = 0.26$,

$\Phi \left( {{\rm N}\left( {\ell_{1} } \right)} \right){ = }\sqrt {\left( {0.4 \times 0.5 - 0.45} \right)^{2} + \left( {0.5 \times 0.5 - 0.45} \right)^{2} } = 0.3202$, $\Psi \left( {{\rm N}\left( {\ell_{1} } \right)} \right){ = }\sqrt {\left( {0.2 \times 0.7 - 0.26} \right)^{2} + \left( {0.4 \times 0.3 - 0.26} \right)^{2} } = 0.1844$;

$\gamma \left( {{\rm N}\left( {\ell_{2} } \right)} \right){ = 0}{\text{.5}} \times 0.5{ + }0.3 \times 0.5{ = }0.4$, $\eta \left( {{\rm N}\left( {\ell_{2} } \right)} \right){ = 0}{\text{.2}}$,

$\Phi \left( {{\rm N}\left( {\ell_{2} } \right)} \right){ = }\sqrt {\left( {0.5 \times 0.5 - 0.4} \right)^{2} + \left( {0.3 \times 0.5 - 0.4} \right)^{2} } = 0.2915$, $\Psi \left( {{\rm N}\left( {\ell_{2} } \right)} \right){ = }0$.

Therefore,

$$\begin{gathered} d_{gnd} \left( {{\rm M},{\rm N}} \right) = \left[ {\frac{1}{2n}\sum\limits_{i = 1}^{n} {\left( {\frac{{\gamma^{\lambda } \left( {\ell_{i} } \right) + \eta^{\lambda } \left( {\ell_{i} } \right)}}{2} + \frac{{\Phi^{\lambda } \left( {\ell_{i} } \right) + \Psi^{\lambda } \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \hfill \\ { = }\left[ {\frac{1}{2 \times 2}\left( \begin{gathered} \frac{{\left| {0.18 - 0.45} \right|^{\lambda } + \left| {0.4 - 0.26} \right|^{\lambda } }}{2} + \frac{{\left| {0.1612 - 0.3202} \right|^{\lambda } + \left| {0 - 0.1844} \right|^{\lambda } }}{2} \hfill \\ { + }\frac{{\left| {0.24 - 0.4} \right|^{\lambda } + \left| {0.6 - 0.2} \right|^{\lambda } }}{2} + \frac{{\left| {0.1697 - 0.2915} \right|^{\lambda } + \left| {0 - 0} \right|^{\lambda } }}{2} \hfill \\ \end{gathered} \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \hfill \\ \end{gathered}$$

If $\lambda { = }1$, then the NHD $d_{nhd} \left( {{\rm M},{\rm N}} \right) = 0.1794$. If $\lambda { = 2}$, then the NED $d_{ned} \left( {{\rm M},{\rm N}} \right){ = 0}{\text{.022}}$.

3.2 Some Novel Distance Measures for PDHFS with Preference of DMs

If we consider the preferences influences of mean & standard deviation of PDHFE, then some novel distance measures with preference are defined as follows:

Let ${\rm M}$ and ${\rm N}$ be any two PDHFSs on ${\mathbb{Z}} = \left\{ {\ell_{1} ,\ell_{2} , \cdots ,\ell_{n} } \right\}$, $\gamma$ and $\varsigma$ are the weight of mean & standard deviation, respectively, then the generalized preference normalized distance (GPND) between ${\rm M}$ and ${\rm N}$ is built as:

$$d_{gpnd} \left( {{\rm M},{\rm N}} \right) = \left[ {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\tau \frac{{\gamma^{\lambda } \left( {\ell_{i} } \right) + \eta^{\lambda } \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi^{\lambda } \left( {\ell_{i} } \right) + \Psi^{\lambda } \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

(19)

where $\tau { + }\varsigma { = }1$ and $0 \le \tau {,}\varsigma \le 1$, $\lambda \in R$ and $\lambda \ge 1$.

If $\lambda { = 1}$, then the GPND reduces to the preference normalized Hamming distance (PNHD):

$$d_{pnhd} \left( {{\rm M},{\rm N}} \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\tau \frac{{\gamma \left( {\ell_{i} } \right) + \eta \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi \left( {x_{i} } \right) + \Psi \left( {\ell_{i} } \right)}}{2}} \right)}$$

(20)

If $\lambda { = 2}$, then the GPND reduces to the preference normalized Euclidean distance (PNED):

$$d_{pned} \left( {{\rm M},{\rm N}} \right) = \left[ {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\tau \frac{{\gamma^{2} \left( {\ell_{i} } \right) + \eta^{2} \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi^{2} \left( {\ell_{i} } \right) + \Psi^{2} \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$$

(21)

Example 2

We use the data in Example 1, where $\tau = 0.4$ and $\varsigma = 0.6$, then the GPND is.

$$\begin{gathered} d_{{gpnd}} \left( {{\rm M},{\rm N}} \right) = \left[ {\frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left( {\tau \frac{{\gamma ^{\lambda } \left( {\ell _{i} } \right) + \eta ^{\lambda } \left( {\ell _{i} } \right)}}{2} + \varsigma \frac{{\Phi ^{\lambda } \left( {\ell _{i} } \right) + \Psi ^{\lambda } \left( {\ell _{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \hfill \\ = \left[ {\frac{1}{2}\left( \begin{gathered} \left( {\tau \frac{{\left| {0.18 - 0.45} \right|^{\lambda } + \left| {0.4 - 0.26} \right|^{\lambda } }}{2} + \varsigma \frac{{\left| {0.1612 - 0.3202} \right|^{\lambda } + \left| {0 - 0.1844} \right|^{\lambda } }}{2}} \right) \hfill \\ {\text{ + }}\left( {\tau \frac{{\left| {0.24 - 0.4} \right|^{\lambda } + \left| {0.6 - 0.2} \right|^{\lambda } }}{2} + \varsigma \frac{{\left| {0.1697 - 0.2915} \right|^{\lambda } + \left| {0 - 0} \right|^{\lambda } }}{2}} \right) \hfill \\ \end{gathered} \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \hfill \\ \end{gathered}$$

If $\lambda { = }1$, then the PNHD $d_{pnhd} \left( {{\rm M},{\rm N}} \right) = 0.1668$. If $\lambda { = 2}$, then the PNED $d_{pned} \left( {{\rm M},{\rm N}} \right){ = 0}{\text{.0195}}$.

3.3 Some Novel Distance Measures for PDHFS with Preference of DM and Weight of Each Element

If we consider the influence of the preference of mean and standard deviation, we also consider the weight of each element $\ell_{i} \in {\mathbb{Z}}$, then the weighted normalized distances with preference are shown as follows:

Let ${\rm M}$ and ${\rm N}$ be any two PDHFSs on ${\mathbb{Z}} = \left\{ {\ell_{1} ,\ell_{2} , \cdots ,\ell_{n} } \right\}$, $\tau$ and $\varsigma$ are the weights of mean and standard deviation, respectively, $\omega_{i}$ is the weight of $x_{i} \in X$ with $0 \le \omega_{i} \le 1$ and $\sum\nolimits_{i = 1}^{n} {\omega_{i} } = 1$, then the generalized weighted preference normalized distance (GWPND) between ${\rm M}$ and ${\rm N}$ is defined as:

$$d_{g\omega pnd} \left( {{\rm M},{\rm N}} \right) = \left[ {\sum\limits_{i = 1}^{n} {\omega_{i} \left( {\tau \frac{{\gamma^{\lambda } \left( {\ell_{i} } \right) + \eta^{\lambda } \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi^{\lambda } \left( {\ell_{i} } \right) + \Psi^{\lambda } \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

(22)

where $\tau { + }\varsigma { = }1$ and $0 \le \tau {,}\varsigma \le 1$, $\lambda \in R$ and $\lambda \ge 1$, $\omega_{i}$ is the weight of $x_{i}$, $0 \le \omega_{i} \le 1$, $\sum\limits_{i = 1}^{n} {\omega_{i} } = 1$.

If $\lambda { = 1}$, then the GWPND reduces to the weighted preference normalized Hamming distance (PNHD):

$$d_{\omega pnhd} \left( {{\rm M},{\rm N}} \right) = \sum\limits_{i = 1}^{n} {\omega_{i} \left( {\tau \frac{{\gamma \left( {\ell_{i} } \right) + \eta \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi \left( {\ell_{i} } \right) + \Psi \left( {\ell_{i} } \right)}}{2}} \right)}$$

(23)

If $\lambda { = 2}$, then the GWPND reduces to the weighted preference normalized Euclidean distance (PNED):

$$d_{\omega pned} \left( {{\rm M},{\rm N}} \right) = \left[ {\sum\limits_{i = 1}^{n} {\omega_{i} \left( {\tau \frac{{\gamma^{2} \left( {\ell_{i} } \right) + \eta^{2} \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi^{2} \left( {\ell_{i} } \right) + \Psi^{2} \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$$

(24)

Example 3

We use the data in Example 1, where $\tau = 0.4$, $\varsigma = 0.6$ and $\omega = \left( {0.7,0.3} \right)$, then the generalized weighted preference normalized distance is.

$$\begin{gathered} d_{g\omega pnd} \left( {{\rm M},{\rm N}} \right) = \left[ {\sum\limits_{i = 1}^{n} {\omega_{i} \left( {\tau \frac{{\gamma^{\lambda } \left( {\ell_{i} } \right) + \eta^{\lambda } \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi^{\lambda } \left( {\ell_{i} } \right) + \Psi^{\lambda } \left( {\ell_{i} } \right)}}{2}} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \hfill \\ = \left( \begin{gathered} 0.7 \times \left( {0.4\frac{{\left| {0.18 - 0.45} \right|^{\lambda } + \left| {0.4 - 0.26} \right|^{\lambda } }}{2} + 0.6\frac{{\left| {0.1612 - 0.3202} \right|^{\lambda } + \left| {0 - 0.1844} \right|^{\lambda } }}{2}} \right) \hfill \\ { + 0}{\text{.3}} \times \left( {0.4\frac{{\left| {0.24 - 0.4} \right|^{\lambda } + \left| {0.6 - 0.2} \right|^{\lambda } }}{2} + 0.6\frac{{\left| {0.1697 - 0.2915} \right|^{\lambda } + \left| {0 - 0} \right|^{\lambda } }}{2}} \right) \hfill \\ \end{gathered} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \hfill \\ \end{gathered}$$

If $\lambda { = }1$, then the weighted PNHD $d_{\omega pnhd} \left( {{\rm M},{\rm N}} \right) = 0.194$. If $\lambda { = 2}$, then the PNED $d_{\omega pned} \left( {{\rm M},{\rm N}} \right){ = 0}{\text{.021}}$.

Theorem 2

If $\omega_{i} = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}\left( {i = 1,2, \cdots ,n} \right)$, then $d_{g\omega pnd}$, $d_{\omega pnhd}$ and $d_{\omega pned}$ are reduced to $d_{gpnd}$, $d_{pnhd}$, and $d_{pned}$, respectively. If $\tau = \varsigma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$, then $d_{gpnd}$, $d_{pnhd}$, and $d_{pned}$ are reduced to $d_{gnd}$, $d_{nhd}$ and $d_{ned}$, respectively.

Next, we prove the Theorem 2, Lemma 1 need to be given before proving the Theorem 2.

Lemma 1

[78] Let $\left( {\partial_{1} ,\partial_{2} , \cdots ,\partial_{n} } \right),\left( {\wp_{1} ,\wp_{2} , \cdots ,\wp_{n} } \right) \in R^{n}$, and $1 \le \lambda < + \infty$. Then.

$$\left( {\sum\limits_{i = 1}^{n} {\left| {\partial_{i} + \wp_{i} } \right|^{\lambda } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \le \left( {\sum\limits_{i = 1}^{n} {\left| {\partial_{i} } \right|^{\lambda } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} + \left( {\sum\limits_{i = 1}^{n} {\left| {\wp_{i} } \right|^{\lambda } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

(25)

According to Theorem 2, again, $d_{\omega pnhd}$ and $d_{\omega pned}$ are special cases of $d_{g\omega pnd}$, we only need to prove the $d_{g\omega pnd}$ satisfies the four properties in Definition 5.

Proof

The distance measures $d_{g\omega pnd}$ satisfies the properties (A1-A4) in Definition 5.

Assume that ${\rm T}$, $\Upsilon$ and $\Psi$ are three PDHFSs.

(A1) According to Eqs. (8–11), we can get $0 \le \gamma \left( d \right),\eta \left( d \right),\Phi \left( d \right),\Psi \left( d \right) \le 1$, then $0 \le \gamma \left( {\ell_{i} } \right),\eta \left( {\ell_{i} } \right),\Phi \left( {\ell_{i} } \right),\Psi \left( {\ell_{i} } \right) \le 1$. Hence, we have $0 \le \sum\limits_{i = 1}^{n} {\omega_{i} \left( {\tau \frac{{\gamma^{\lambda } \left( {\ell_{i} } \right) + \eta^{\lambda } \left( {\ell_{i} } \right)}}{2} + \varsigma \frac{{\Phi^{\lambda } \left( {\ell_{i} } \right) + \Psi^{\lambda } \left( {\ell_{i} } \right)}}{2}} \right)} \le 1$ for $\lambda \ge 1$ and $0 \le \omega_{i} \le 1$, $\sum\nolimits_{i = 1}^{n} {\omega_{i} } = 1$, so $0 \le d_{g\omega pnd} \le 1$.

(A2) If ${\rm T} = \Upsilon$, then $d_{g\omega pnd} \left( {{\rm T},\Upsilon } \right) = 0$.

On the other hand, if $d_{g\omega pnd} \left( {{\rm T},\Upsilon } \right) = 0$, for any $x_{i} \in X$, we have $\gamma \left( {x_{i} } \right) = 0$ and $\eta \left( {x_{i} } \right) = 0$, then for any $x_{i} \in X$, $\gamma \left( {{\rm T}\left( {x_{i} } \right)} \right) = \gamma \left( {\Upsilon \left( {x_{i} } \right)} \right)$ and $\eta \left( {{\rm T}\left( {x_{i} } \right)} \right) = \eta \left( {\Upsilon \left( {x_{i} } \right)} \right)$. Thus, $s\left( {{\rm T}\left( {x_{i} } \right)} \right) = \gamma \left( {{\rm T}\left( {x_{i} } \right)} \right) - \eta \left( {{\rm T}\left( {x_{i} } \right)} \right) = \gamma \left( {\Upsilon \left( {x_{i} } \right)} \right) - \eta \left( {\Upsilon \left( {x_{i} } \right)} \right) = s\left( {\Upsilon \left( {x_{i} } \right)} \right)$ and $h\left( {{\rm T}\left( {x_{i} } \right)} \right) = \gamma \left( {{\rm T}\left( {x_{i} } \right)} \right) + \eta \left( {{\rm T}\left( {x_{i} } \right)} \right) = \gamma \left( {\Upsilon \left( {x_{i} } \right)} \right) + \eta \left( {\Upsilon \left( {x_{i} } \right)} \right) = h\left( {\Upsilon \left( {x_{i} } \right)} \right)$ for any $x_{i} \in X$, from the Definitions 2, we get ${\rm T} = \Upsilon$.

(A3) From (12)-(15) and (22), we can easily get that $d_{g\omega pnd} \left( {{\rm T},\Upsilon } \right) = d_{g\omega pnd} \left( {\Upsilon ,{\rm T}} \right)$.

(A4) According to Lemma 1 and (22), we can get $d_{g\omega pnd} \left( {{\rm T},\Upsilon } \right) \le d_{g\omega pnd} \left( {{\rm T},\Psi } \right) + d_{g\omega pnd} \left( {\Psi ,\Upsilon } \right)$.

4 Entropy of PHDFS

Entropy is an important concept in the MADM fields. Since it was proposed, it has been widely used in index weighting.

Let $d = \left( {\left. h \right|p,\left. g \right|q} \right)$ be any a PDHFE. Next, we build the mean of hesitant degree for PDHFE according to Eqs. (8–9) as follows:

$$\pi \left( d \right){ = }1 - \gamma \left( d \right) - \eta \left( d \right){ = }1 - \sum\nolimits_{j = 1}^{\# h} {h_{j} p_{j} } - \sum\nolimits_{j = 1}^{\# g} {g_{j} q_{j} }$$

(26)

Definition 6

A mapping $E:P \to \left[ {0,1} \right]$ is named as entropy of PDHFE, if $E$ satisfy the following four conditions:

(E1) $E\left( d \right) = 0$ if and only if $d = \left( {\left\{ {\left. 0 \right|1} \right\},\left\{ {\left. 1 \right|1} \right\}} \right)$ or $d = \left( {\left\{ {\left. 1 \right|1} \right\},\left\{ {\left. 0 \right|1} \right\}} \right)$;

(E2) $E\left( d \right) = 1$ if and only if $\gamma \left( d \right){ = }\eta \left( d \right)$;

(E3) $E\left( {d_{1} } \right) \le E\left( {d_{2} } \right)$ when $\gamma \left( {d_{2} } \right) \ge \eta \left( {d_{2} } \right)$, there is $\gamma \left( {d_{1} } \right) \ge \gamma \left( {d_{2} } \right)$, $\eta \left( {d_{2} } \right) \ge \eta \left( {d_{1} } \right)$; or when $\gamma \left( {d_{2} } \right) \le \eta \left( {d_{2} } \right)$, there is $\gamma \left( {d_{1} } \right) \le \gamma \left( {d_{2} } \right)$, $\eta \left( {d_{2} } \right) \le \eta \left( {d_{1} } \right)$;

(E4) $E\left( d \right) = E\left( {d^{C} } \right)$.

The entropy of PDHFE is defined as follows:

Theorem 3

For any a PDHFE $d$, let.

$$E\left( d \right) = \frac{2\gamma \left( d \right)\eta \left( d \right) + \pi \left( d \right)}{{\gamma^{2} \left( d \right) + \eta^{2} \left( d \right) + \pi \left( d \right)}}$$

(27)

then $E\left( d \right)$ is called entropy of PDHFE.

Proof

If we want to prove that $E\left( d \right)$ is the entropy of PDHFE $d$, we only need to prove that the above formula satisfies the conditions (1)-(4) in Definition 6.

Since $0 \le h_{j} \le 1$, $0 \le p_{j} \le 1$, $0 \le g_{j} \le 1$, $0 \le q_{j} \le 1$ and $0 \le \gamma^{ + } + \eta^{ + } \le 1$, then $0 \le \gamma \left( d \right) \le 1$, $0 \le \eta \left( d \right) \le 1$, thus $0 \le \pi \left( d \right) \le 1$.

Again, $2\gamma \left( d \right)\eta \left( d \right) \le \gamma^{2} \left( d \right) + \eta^{2} \left( d \right)$, then $0 \le \frac{2\gamma \left( d \right)\eta \left( d \right) + \pi \left( d \right)}{{\gamma^{2} \left( d \right) + \eta^{2} \left( d \right) + \pi \left( d \right)}} \le 1$.

(E1) For condition (E1), $E\left( d \right) = 0$, then

$$\frac{2\gamma \left( d \right)\eta \left( d \right) + \pi \left( d \right)}{{\gamma^{2} \left( d \right) + \eta^{2} \left( d \right) + \pi \left( d \right)}} = 0 \Leftrightarrow 2\gamma \left( d \right)\eta \left( d \right) + \pi \left( d \right) = 0$$

Because $0 \le \gamma \left( d \right),\eta \left( d \right),\pi \left( d \right) \le 1$, if.

$2\gamma \left( d \right)\eta \left( d \right) + \pi \left( d \right) = 0 \Leftrightarrow 2\gamma \left( d \right)\eta \left( d \right) = 0$ and $\pi \left( d \right) = 0$.

then, we can get $\gamma \left( d \right) = 0$ and $\pi \left( d \right) = 0$, or $\eta \left( d \right) = 0$ and $\pi \left( d \right) = 0$.

Therefore, $E\left( d \right) = 0$ if and only if $d = \left( {\left\{ {\left. 0 \right|1} \right\},\left\{ {\left. 1 \right|1} \right\}} \right)$ or $d = \left( {\left\{ {\left. 1 \right|1} \right\},\left\{ {\left. 0 \right|1} \right\}} \right)$.

(E2) For condition (E2), $E\left( d \right) = 1$ then

$$\frac{2\gamma \left( d \right)\eta \left( d \right) + \pi \left( d \right)}{{\gamma^{2} \left( d \right) + \eta^{2} \left( d \right) + \pi \left( d \right)}} = 1 \Leftrightarrow 2\gamma \left( d \right)\eta \left( d \right) + \pi \left( d \right) = \gamma^{2} \left( d \right) + \eta^{2} \left( d \right) + \pi \left( d \right)$$

$\Leftrightarrow 2\gamma \left( d \right)\eta \left( d \right) = \gamma^{2} \left( d \right) + \eta^{2} \left( d \right)$,

so, $\gamma \left( d \right){ = }\eta \left( d \right)$.

(E3) For condition (E3), let $\gamma \left( d \right){ = }\gamma$, $\eta \left( d \right) = \eta$ then, $\pi \left( d \right){ = 1} - \gamma - \eta$, so

$$E\left( {\gamma ,\eta } \right) = \frac{2\gamma \eta + 1 - \gamma - \eta }{{\gamma^{2} + \eta^{2} + 1 - \gamma - \eta }}$$

if we want to prove that the above formula satisfies the condition (E3) in Definition 6, we only need to prove the following:

(3–1) When $\gamma \ge \eta$, $E\left( {\gamma ,\eta } \right)$ is monotonic decreasing for $\gamma$ and monotonic increasing for $\eta$;

(3–1) When $\gamma \le \eta$, $E\left( {\gamma ,\eta } \right)$ is monotonic increasing for $\gamma$ and monotonic decreasing for $\eta$;

Partial derivative of $E\left( {\gamma ,\eta } \right)$ with respect to $\gamma$:

$$\frac{{\partial E\left( {\gamma ,\eta } \right)}}{\partial \gamma } = \frac{{\left( {\eta - \gamma } \right)\left( {2\eta^{2} + 2 - \gamma - 3\eta + 2\gamma \eta } \right)}}{{\left( {\gamma^{2} + \eta^{2} + 1 - \gamma - \eta } \right)^{2} }}$$

(28)

Let $f\left( {\gamma ,\eta } \right) = 2\eta^{2} + 2 - \gamma - 3\eta + 2\gamma \eta$, partial derivative of $f\left( {\gamma ,\eta } \right)$ with respect to $\eta$:

$\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \eta } = 4\eta - 3 + 2\gamma$, let $\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \eta } = 0$, we get $\eta = \frac{3 - 2\gamma }{4}$, let $\eta^{ * } = \frac{3 - 2\gamma }{4}$.

When $\eta \le \eta^{ * }$, $\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \eta } \le 0$, then $f\left( {\gamma ,\eta } \right)$ is monotonic decreasing for $\eta$; when $\eta \ge \eta^{ * }$, $\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \eta } \ge 0$, then $f\left( {\gamma ,\eta } \right)$ is monotonic increasing for $\eta$.

We can easily obtain $f\left( {\gamma ,\eta^{ * } } \right) = \frac{{4\gamma \left( {1 - \gamma } \right) + 7}}{8} > 0$, then $f\left( {\gamma ,\eta } \right) > 0$ is constant.

For formula (28), $2\eta^{2} + 2 - \gamma - 3\eta + 2\gamma \eta \ge 0$ and $\left( {\gamma^{2} + \eta^{2} + 1 - \gamma - \eta } \right)^{2} > 0$, when $\gamma \ge \eta$, $\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \gamma } \le 0$, $E\left( {\gamma ,\eta } \right)$ is monotonic decreasing for $\gamma$; when $\gamma \le \eta$, $\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \gamma } \ge 0$, $E\left( {\gamma ,\eta } \right)$ is monotonic increasing for $\gamma$; Similarly, the following results can be obtained, when $\gamma \ge \eta$, $\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \eta } \ge 0$, $E\left( {\gamma ,\eta } \right)$ is monotonic increasing for $\eta$; when $\gamma \le \eta$, $\frac{{\partial f\left( {\gamma ,\eta } \right)}}{\partial \eta } \le 0$, $E\left( {\gamma ,\eta } \right)$ is monotonic decreasing for $\eta$. So, when $\gamma \left( {d_{2} } \right) \ge \eta \left( {d_{2} } \right)$, there is $\gamma \left( {d_{1} } \right) \ge \gamma \left( {d_{2} } \right)$, $\eta \left( {d_{2} } \right) \ge \eta \left( {d_{1} } \right)$, then $E\left( {d_{1} } \right) \le E\left( {d_{2} } \right)$; or when $\gamma \left( {d_{2} } \right) \le \eta \left( {d_{2} } \right)$, there is $\gamma \left( {d_{1} } \right) \le \gamma \left( {d_{2} } \right)$, $\eta \left( {d_{2} } \right) \le \eta \left( {d_{1} } \right)$, then $E\left( {d_{1} } \right) \le E\left( {d_{2} } \right)$;

(E4)The condition (E4) is very obvious, we omit it.

Combined with references [79,80,81], the entropy formulas of intuitionistic fuzzy sets and rough sets are summarized. Some entropy formulas can consider both the hesitation and intuition of intuitionistic fuzzy sets. These formulas are extended to PDHFS.

$$E_{1} \left( d \right) = \frac{{\pi \left( d \right) + 2 - \left| {\gamma \left( d \right) - \eta \left( d \right)} \right| - \left( {\gamma \left( d \right) + \eta \left( d \right)} \right)^{2} }}{{\pi \left( d \right) + 2 + \left| {\gamma \left( d \right) - \eta \left( d \right)} \right| - \left( {\gamma \left( d \right) + \eta \left( d \right)} \right)^{2} }}$$

(29)

$$E_{2} \left( d \right) = \frac{{1 - \left| {\gamma \left( d \right) - \eta \left( d \right)} \right| + \pi \left( d \right)}}{{1 + \left| {\gamma \left( d \right) - \eta \left( d \right)} \right| + \pi \left( d \right)}}$$

(30)

$$E_{3} \left( d \right) = \cos \frac{\gamma \left( d \right) - \eta \left( d \right)}{{2\left( {1 + \pi \left( d \right)} \right)}}\pi$$

(31)

$$E_{4} \left( d \right) = \frac{{2\gamma \left( d \right)\eta \left( d \right) + \pi^{2} \left( d \right)}}{{\gamma^{2} \left( d \right) + \eta^{2} \left( d \right) + \pi^{2} \left( d \right)}}$$

(32)

Example 4

$d_{1} = \left( {\left\{ {\left. {0.6} \right|0.2,\left. {0.2} \right|0.8} \right\},\left\{ {\left. {0.2} \right|0.5,\left. {0.4} \right|0.5} \right\}} \right)$, $d_{2} = \left( {\left\{ {\left. {0.3} \right|0.6,\left. {0.4} \right|0.4} \right\},\left\{ {\left. {0.2} \right|1} \right\}} \right)$, $d_{3} = \left( {\left\{ {\left. {0.2} \right|0.3,\left. {0.4} \right|0.7} \right\},\left\{ {\left. {0.4} \right|0.5,\left. {0.5} \right|0.5} \right\}} \right)$ and $d_{4} = \left( {\left\{ {\left. {0.4} \right|0.5,\left. {0.2} \right|0.5} \right\},\left\{ {\left. {0.5} \right|1} \right\}} \right)$ are four PDHFEs.

Next, we calculate the entropy measures of four PDHFEs by $E\left( d \right)$, $E_{1} \left( d \right)$, $E_{2} \left( d \right)$, $E_{3} \left( d \right)$ and $E_{4} \left( d \right)$, the entropy measures of four PDHFEs are listed as follows (Figs. 1 and 2).

Fig. 1

The entropy values obtained by several entropy measures

Fig. 2

The flowchart of the proposed MADM technique based on PDHF-CODAS

$E$	$E\left( d \right)$	$E_{1} \left( d \right)$	$E_{2} \left( d \right)$	$E_{3} \left( d \right)$	$E_{4} \left( d \right)$
$d_{1}$	0.5495	0.981	0.9722	0.9998	0.9988
$d_{2}$	0.5051	0.8787	0.825	0.9887	0.9446
$d_{3}$	0.4723	0.8703	0.8333	0.9898	0.9666
$d_{4}$	0.4762	0.7727	0.7143	0.9659	0.88947

Next, we give axiomatic definition for entropy of PDHFS.

Definition 7

A mapping $E:PDHFS\left( {\mathbb{Z}} \right) \to \left[ {0,1} \right]$ is called entropy of PDHFS, if $E$ satisfy the following conditions:

(E1) $E\left( A \right) = 0$ if and only if for any $i \in \left\{ {1,2, \cdots ,n} \right\}$, $d = \left( {\left\{ {\left. 0 \right|1} \right\},\left\{ {\left. 1 \right|1} \right\}} \right)$ or $d = \left( {\left\{ {\left. 1 \right|1} \right\},\left\{ {\left. 0 \right|1} \right\}} \right)$;

(E2) $E\left( A \right) = 1$ if and only if for any $i \in \left\{ {1,2, \cdots ,n} \right\}$, $\gamma \left( d \right){ = }\eta \left( d \right)$;

(E3) $E\left( A \right) \le E\left( B \right)$, if for any $x_{i} \in X$, when $\gamma \left( {d_{B} \left( {x_{i} } \right)} \right) \ge \eta \left( {d_{B} \left( {x_{i} } \right)} \right)$, there is $\gamma \left( {d_{A} \left( {x_{i} } \right)} \right) \ge \gamma \left( {d_{B} \left( {x_{i} } \right)} \right)$, $\eta \left( {d_{B} \left( {x_{i} } \right)} \right) \ge \eta \left( {d_{A} \left( {x_{i} } \right)} \right)$; or when $\gamma \left( {d_{B} \left( {x_{i} } \right)} \right) \le \eta \left( {d_{B} \left( {x_{i} } \right)} \right)$, there is $\gamma \left( {d_{A} \left( {x_{i} } \right)} \right) \le \gamma \left( {d_{B} \left( {x_{i} } \right)} \right)$, $\eta \left( {d_{B} \left( {x_{i} } \right)} \right) \le \eta \left( {d_{A} \left( {x_{i} } \right)} \right)$;

(E4) $E\left( A \right) = E\left( {A^{C} } \right)$.

A novel entropy of PDHFS is defined as follows:

Theorem 4

For any a PDHFS $A = \left\{ {\left. {\left\langle {x_{i} ,d_{A} \left( {x_{i} } \right)} \right\rangle } \right|x_{i} \in X} \right\}$, let.

$$E\left( A \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\frac{{2\gamma \left( {d_{A} \left( {x_{i} } \right)} \right)\eta \left( {d_{A} \left( {x_{i} } \right)} \right) + \pi \left( {d_{A} \left( {x_{i} } \right)} \right)}}{{\gamma^{2} \left( {d_{A} \left( {x_{i} } \right)} \right) + \eta^{2} \left( {d_{A} \left( {x_{i} } \right)} \right) + \pi \left( {d_{A} \left( {x_{i} } \right)} \right)}}}$$

(33)

then $E\left( A \right)$ is called entropy of PDHFS.

Proof

Next, we proof the entropy of PDHFS satisfy four axiomatic conditions in Definition 7.

Let $E_{i} \left( A \right) = \frac{{2\gamma \left( {d_{A} \left( {x_{i} } \right)} \right)\eta \left( {d_{A} \left( {x_{i} } \right)} \right) + \pi \left( {d_{A} \left( {x_{i} } \right)} \right)}}{{\gamma^{2} \left( {d_{A} \left( {x_{i} } \right)} \right) + \eta^{2} \left( {d_{A} \left( {x_{i} } \right)} \right) + \pi \left( {d_{A} \left( {x_{i} } \right)} \right)}}$.

Because $0 \le \gamma \left( {d_{A} \left( {x_{i} } \right)} \right) \le 1$, $0 \le \eta \left( {d_{A} \left( {x_{i} } \right)} \right) \le 1$ and $0 \le \pi \left( {d_{A} \left( {x_{i} } \right)} \right) \le 1$, we can get $0 \le E_{i} \left( A \right) \le 1$.

(E1) If $E\left( A \right) = 0$, due to $0 \le E_{i} \left( A \right) \le 1$ and $E\left( A \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {E_{i} \left( A \right)}$, then $E_{i} \left( A \right) = 0$. Hence, $2\gamma \left( {d_{A} \left( {x_{i} } \right)} \right)\eta \left( {d_{A} \left( {x_{i} } \right)} \right) + \pi \left( {d_{A} \left( {x_{i} } \right)} \right) = 0$.

Thus, we can get $\gamma \left( {d_{A} \left( {x_{i} } \right)} \right) = 0$, $\eta \left( {d_{A} \left( {x_{i} } \right)} \right) = 1$; or $\gamma \left( {d_{A} \left( {x_{i} } \right)} \right) = 1$, $\eta \left( {d_{A} \left( {x_{i} } \right)} \right) = 0$. Then $d = \left( {\left\{ {\left. 0 \right|1} \right\},\left\{ {\left. 1 \right|1} \right\}} \right)$ or $d = \left( {\left\{ {\left. 1 \right|1} \right\},\left\{ {\left. 0 \right|1} \right\}} \right)$, the reverse is true.

(E2) If $E\left( A \right) = 1$, due to $0 \le E_{i} \left( A \right) \le 1$ and $E\left( A \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {E_{i} \left( A \right)}$, then $E_{i} \left( A \right) = 1$. Hence, for $\forall x_{i} \in X$,

$2\gamma \left( {d_{A} \left( {x_{i} } \right)} \right)\eta \left( {d_{A} \left( {x_{i} } \right)} \right) + \pi \left( {d_{A} \left( {x_{i} } \right)} \right) = \gamma^{2} \left( {d_{A} \left( {x_{i} } \right)} \right) + \eta^{2} \left( {d_{A} \left( {x_{i} } \right)} \right) + \pi \left( {d_{A} \left( {x_{i} } \right)} \right)$.

Then, for $\forall x_{i} \in X$, $\gamma \left( {d_{A} \left( {x_{i} } \right)} \right) = \eta \left( {d_{A} \left( {x_{i} } \right)} \right)$, the reverse is true.

(E3) Let $f\left( {x,y} \right) = \frac{{2xy + \left( {1 - x - y} \right)}}{{x^{2} + y^{2} + \left( {1 - x - y} \right)}}$, where $x,y \in \left[ {0,1} \right]$ and $1 - x - y \in \left[ {0,1} \right]$. If we want to prove that the above formula satisfies the condition (E3) in Definition 7, we only need to prove the following:

• (1) When $x \ge y$, $f\left( {x,y} \right)$ is monotonic decreasing for $x$ and monotonic increasing for $y$;

• (2) When $x \le y$, $f\left( {x,y} \right)$ is monotonic increasing for $x$ and monotonic decreasing for $y$.

Calculate the partial derivative of $f\left( {x,y} \right)$ about $x$:

$$\frac{{\partial f\left( {x,y} \right)}}{\partial x} = \frac{{\left( {y - x} \right)\left( {2y^{2} + 2 - x - 3y + 2xy} \right)}}{{\left( {x^{2} + y^{2} + 1 - x - y} \right)^{2} }}$$

Let $g\left( {x,y} \right) = 2y^{2} + 2 - x - 3y + 2xy$, calculate the partial derivative of $g\left( {x,y} \right)$ about $y$:

$\frac{{\partial g\left( {x,y} \right)}}{\partial y} = 4y - 3 + 2x$, let $\frac{{\partial g\left( {x,y} \right)}}{\partial y} = 0$, we get $y = \frac{3 - 2x}{4}$, let $y^{ * } = \frac{3 - 2x}{4}$. when $y \le y^{ * }$, $\frac{{\partial g\left( {x,y} \right)}}{\partial y} \le 0$, then $g\left( {x,y} \right)$ is monotonic decreasing for $y$; when $y \ge y^{ * }$, $\frac{{\partial g\left( {x,y} \right)}}{\partial y} \ge 0$, then $f\left( {x,y} \right)$ is monotonic increasing for $y$, so, $g\left( {x,y} \right) \ge g\left( {x,y^{ * } } \right)$.

We can easily obtain $f\left( {x,y^{ * } } \right) = \frac{{4x\left( {1 - x} \right) + 7}}{8} > 0$ and $\left( {x^{2} + y^{2} + 1 - x - y} \right)^{2} > 0$, then when $x \ge y$, $\frac{{\partial f\left( {x,y} \right)}}{\partial x} \le 0$; when $x \le y$, $\frac{{\partial f\left( {x,y} \right)}}{\partial x} \ge 0$. Similarly, when $x \ge y$, $\frac{{\partial f\left( {x,y} \right)}}{\partial y} \ge 0$; when $x \le y$, $\frac{{\partial f\left( {x,y} \right)}}{\partial y} \le 0$.

Thus, for any $x_{i} \in X$, when $\gamma \left( {d_{B} \left( {x_{i} } \right)} \right) \ge \eta \left( {d_{B} \left( {x_{i} } \right)} \right)$, there is $\gamma \left( {d_{A} \left( {x_{i} } \right)} \right) \ge \gamma \left( {d_{B} \left( {x_{i} } \right)} \right)$ and $\eta \left( {d_{B} \left( {x_{i} } \right)} \right) \ge \eta \left( {d_{A} \left( {x_{i} } \right)} \right)$, then $E_{i} \left( A \right) \le E_{i} \left( B \right)$; or when $\gamma \left( {d_{B} \left( {x_{i} } \right)} \right) \le \eta \left( {d_{B} \left( {x_{i} } \right)} \right)$, there is $\gamma \left( {d_{A} \left( {x_{i} } \right)} \right) \le \gamma \left( {d_{B} \left( {x_{i} } \right)} \right)$, $\eta \left( {d_{B} \left( {x_{i} } \right)} \right) \le \eta \left( {d_{A} \left( {x_{i} } \right)} \right)$, then $E_{i} \left( A \right) \le E_{i} \left( B \right)$.

So, $E\left( A \right) \le E\left( B \right)$.

(E4) The condition (E4) is very obvious, we omit it.

Corollary 1

For any a PDHFS $A = \left\{ {\left. {\left\langle {x_{i} ,d_{A} \left( {x_{i} } \right)} \right\rangle } \right|x_{i} \in X} \right\}$, let.

$$\overline{\overline{E}} \left( A \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\overline{\overline{E}} \left( {d_{A} \left( {x_{i} } \right)} \right)}$$

(34)

where $\overline{\overline{E}} \left( {d_{A} \left( {x_{i} } \right)} \right)$ can be substituted by $E_{1} \left( d \right)$, $E_{2} \left( d \right)$, $E_{3} \left( d \right)$ and $E_{4} \left( d \right)$, then $\overline{\overline{E}} \left( {d_{A} \left( {x_{i} } \right)} \right)$ is called entropy of PDHFS.

Example 5

$A = \left\langle \begin{gathered} \left\{ {\left\{ {\left. {0.6} \right|0.2,\left. {0.2} \right|0.8} \right\},\left\{ {\left. {0.2} \right|0.5,\left. {0.4} \right|0.5} \right\}} \right\}, \hfill \\ \left\{ {\left\{ {\left. {0.2} \right|0.3,\left. {0.4} \right|0.7} \right\},\left\{ {\left. {0.4} \right|0.5,\left. {0.5} \right|0.5} \right\}} \right\}, \hfill \\ \left\{ {\left\{ {\left. {0.2} \right|0.3,\left. {0.4} \right|0.7} \right\},\left\{ {\left. {0.4} \right|0.5,\left. {0.5} \right|0.5} \right\}} \right\}, \hfill \\ \left\{ {\left\{ {\left. {0.4} \right|0.5,\left. {0.2} \right|0.5} \right\},\left\{ {\left. {0.5} \right|1} \right\}} \right\} \hfill \\ \end{gathered} \right\rangle$ is a PDHFS.

Next, we calculate the entropy measures of the PDHFE by $E\left( A \right)$, $E_{1} \left( A \right)$, $E_{2} \left( A \right)$, $E_{3} \left( A \right)$ and $E_{4} \left( A \right)$, the entropy measures of four PDHFEs are listed as follows.

$E$	$E\left( A \right)$	$E_{1} \left( A \right)$	$E_{2} \left( A \right)$	$E_{3} \left( A \right)$	$E_{4} \left( A \right)$
$A$	0.5008	0.8757	0.8362	0.986	0.9517

5 CODAS Technique for PDHF-MADM Problems

In the subsection, we will introduce the PDHF-CODAS technique. Let $X = \left\{ {X_{1} ,X_{2} , \cdots ,X_{m} } \right\}$ be a group of alternatives, and $C = \left\{ {C_{1} ,C_{2} , \cdots ,C_{n} } \right\}$ be decision attributes with the weight vector $\omega = \left\{ {\omega_{1} ,\omega_{2} , \cdots ,\omega_{n} } \right\}$, where $\omega_{j} \in \left[ {0,1} \right],j = 1,2, \cdots ,n$, $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$. Suppose a MADM problem has $n$ decision attributes $C = \left\{ {C_{1} ,C_{2} , \cdots ,C_{n} } \right\}$, furthermore, each expert gives the evaluation value as probabilistic dual hesitant fuzzy expressions $p_{ij}$.

Then, basic calculation steps of PDHF-CODAS technique are built as follows:

6 A Numerical Example and Parameters Analysis

6.1 A Numerical Example

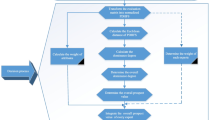
With the development of economy, people pay more and more attention to the enterprise credit risk assessment. Now, due to the needs of development, four green environmental protection enterprises have applied to the bank for loans, and the bank has organized experts to conduct corresponding credit risk assessment on the company's operation status and ability, the example (adapted from [19]). For the existing four green environmental protection enterprises $X_{i} \left( {i = 1,2, \cdots ,4} \right)$, the following four indicators are selected for assessment: $C_{1}$—risk compensation ability, $C_{2}$—operation efficiency ability, $C_{3}$—profitability ability and future growth ability, whose subjective weight is $w = \left( {0.3,0.3,0.4} \right)^{T}$. The expert made corresponding evaluation on the enterprise. Using the method given in the study, the four green environmental protection enterprises are ranked and optimized, and the enterprise with the best credit risk assessment value is selected to give loans. The assessments values are listed in Table 1.

Table 1 The PDHF decision information matrix

Next steps, the PDHF-CODAS technique is used to select the best green environmental protection enterprise.

Step 1: Because the decision attributes in this numerical example are benefit indexes, thus, normalized the decision attributes if not necessary through complement operation.

Step 2: Calculate the combined weight of every decision attribute by Eqs. (37–40) in Sect. 5, the entropy weight $\eta_{j}$, subject weight $w_{j}$ and combined weight $\omega_{j}$ are listed in the Table 3.

• (1) Calculate the information entropy for each element, all computing results are recorded in Table 2.

• (2) Calculate the entropy weights and combined weights for all decision attributes, all computing results are recorded in Table 3.

Table 2 The information entropy matrix

Table 3 The combined weights $\eta_{j}$, $w_{j}$ and $\omega_{j}$

Step 3: Obtain PDHF weighted normalized decision information matrix. The values $r_{ij}$ are derived by Eqs. (41–42) and all computing results are recorded in Table 4.

Table 4 The PDHF weighted normalized decision information matrix

Step 5: Determine the PDHF $NS$ by Eqs. (43–44) and all computing results are recorded in Table 5.

Table 5 The PDHF negative-ideal solution $NS$

Step 6: Obtain the weighted preference normalized $Ed_{i}$ and weighted preference normalized $Hd_{i}$ with $\tau = 0.5$ and $\zeta = 0.5$ by Eqs. (45–46) and all computing results are recorded in Table 6.

Table 6 The weighted preference normalized Euclidean distance $Ed_{i}$ and Hamming distance $Hd_{i}$

Step 7: Euclidean distance for alternative pairs matrix, Taxicab distances for alternative pairs matrix and threshold function matrix are calculated by Eqs. (47–48) according to the data in the Table 7, and all computing results are recorded in Tables 7, 8 and 9, respectively.

Table 7 The PDHF Euclidean distance for alternative pairs matrix

Table 8 The PDHF Hamming distance for alternative pairs matrix

Table 9 The PDHF threshold function matrix

Step 8: Derive relative assessment matrix $RA$ by Eqs. (47–48) according to the data in Tables 8, 9 and 10, and is listed in Table 10.

Table 10 The PDHF relative assessment matrix

Step 9: Compute the assessment score $AS_{i}$ of each given alternative by Eq. (50) and all results are listed in Table 11.

Table 11 The assessment score $AS_{i}$

Step 10: Rank the given alternatives depend on the decreasing values of $AS_{i}$. From the obtained $AS_{i}$ values of four alternatives, and the optimal enterprise is selected depend on the alternative with the maximum assessment score is the optimal alternative, From the values of $AS_{i} \left( {i = 1,2,3,4} \right)$ in Table 11, we can get the ranking of six alternatives is $X_{4} \succ X_{1} \succ X_{2} \succ X_{3}$(“$\succ$” means “super to”), the best alternative is $X_{4}$.

6.2 Parameters Analysis

Next, we analyze the influence of parameters $\tau$ and $\zeta$, subjective weight $w$ on the score values and ranking of four green environmental protection enterprises.

(a) we analyze the change of the ranking of the evaluated alternatives with the change of $\tau$ and $\zeta$ values with $w = \left( {0.3,0.3,0.4} \right)^{T}$, the ranking is listed in Table 12.

Table 12 The ranking for different values of $\tau$ and $\zeta$

According to the Table 12, Figs. 3 and 4, we can observe the change of the ranking of the evaluated green environmental protection enterprises with the change of values of parameters $\tau$ and $\zeta$. From the results, the ranking is relatively stable, and the best enterprise is always $X_{4}$, which also shows the superiority and effectiveness of the MADM technique built in this study.

Fig. 3

The score values with different parameters $\tau$ and $\zeta$

Fig. 4

The ranking with different parameters $\tau$ and $\zeta$

(b) we analyze the change of the ranking of the evaluated alternatives with the change of subjective weight $w$ when $\tau { = 0}{\text{.5}}$,$\zeta { = 0}{\text{.5}}$, the ranking is listed in Table 13.

Table 13 The ranking for different values of $w$

According to the Table 13, Figs. 5 and 6, we can observe the change of the ranking of the evaluated green environmental protection enterprises with the change of subjective weight $w$. From the results, the ranking is relatively stable, and the best enterprise is always $X_{4}$, which also shows the superiority and effectiveness of the MADM technique built in this study.

Fig. 5

The score values with different subjective weights $w$

Fig. 6

The ranking with different subjective weights $w$

7 Discussion

7.1 Results Analysis

In this section, the application process of the novel proposed MADM technique to the selection of green environmental protection enterprises is given in detail. As previously discussed in Sect. 3, some novel PDHF distance measures based on famous Hamming and Euclidean distances are introduced in the PDHF setting, these newly proposed distance measures don’t need to add new elements, which avoids the disadvantage of destroying the original information and better retains the original information, and the new distance fully considers the DM's preference for decision attributes, and some numerical examples are built to examine the validity of the built distance measures. In Sect. 4, a novel PDHF entropy is built, which not need to use other auxiliary functions, retains its most original information and has certain advantages, and enriches the basic theory of PDHF entropy, and some numerical examples are built to examine the validity of the built PDHF entropy. Through nine steps, the application of the newly proposed MADM technique in the process of green environmental protection enterprises selection is described and discussed in detail. Firstly, some basic assumptions are built and the decision information of four green environmental protection enterprises under three decision attributes in PDHF environment are given and shown in Table 1. In the second step, we use the Eqs. (35–36) to normalize the decision attributes, and convert the cost attributes into benefit decision attributes through complement operation. Because the three decision attributes in this numerical example are benefit decision attributes, this process is not required. The third step is to calculate the combined weight of the three decision attributes. Firstly, use Eq. (27) to calculate the information entropy of each decision attribute of each enterprise and shown in Table 2, and then use Eqs. (37–38) to calculate the entropy weight of the three decision attributes, meanwhile, the combined weights of three decision attributes are calculated according to Eqs. (39–40) by combining with the subjective weight of DM based on the principle of minimum information identification, and all calculation results are shown in Table 3. In the fourth step, use Eqs. (41–42) to calculate the PDHF weighted decision information matrix, the results are shown in Table 4. In the fifth step, we use Eqs. (43–44) to determine the fuzzy negative-ideal solution and shown in Table 5. In the sixth step, we calculate the PDHF Euclidean and Taxicab distances of given alternatives from the negative ideal solution by the weighted preference normalized Euclidean $Ed_{i}$ and weighted preference normalized Hamming $Hd_{i}$ distances as Eqs. (45–46), and the results are shown in Table 6. In the seventh step, we obtain relative PDHF assessment information matrix $RA$ by Eqs. (47–48) and shown in Tables 7, 8 and 9. In the eighth step, we calculate the assessment information score $AS_{i}$ of every given enterprise by Eq. (50) and the results are shown in Table 10. In the last step, we obtain the ranking of all alternatives is $X_{2} \succ X_{4} \succ X_{3} \succ X_{1}$, the alternative with the maximum assessment score value is $X_{2}$.

Through the example analysis of the above MADM technique in credit risk assessment, the ranking of four green environmental protection enterprises and the optimal enterprise are finally given, which shows that the MADM technique proposed in this study is practical.

We believe that the results of the new MADM technique on the green environmental protection enterprises will be affected by several parameters, such as the preference values $\tau$ and $\zeta$ in distance measures, subjective weight $w$ in the combined weight, therefore, we focus on the analysis of several parameters in the MADM technique, from the analysis results, the ranking of the four green environmental protection enterprises will indeed be affected by several parameters, on the whole, although the ranking will change, the optimal enterprise is $X_{4}$.

• (1) In Sect. 6.2, we assumed some specific values of other parameters in advance, and then we analyzed the impact of the change of parameter $\tau$ and $\zeta$ on the ranking of four green environmental protection enterprises in detail and shown in Table 12, Figs. 3 and 4. We can find that when $\rho$ changes, the scores of the four SSs also change, although the rankings of the four green environmental protection enterprises have slightly different, and the optimal enterprise is still the fourth enterprise $X_{4}$.

• (2) In Sect. 6.2, we assumed some specific values of other parameters in advance and then we analyzed the impact of the change of subjective weight $w$ on the ranking of four green environmental protection enterprises in detail and shown in Table 13, Figs. 5 and 6.

We can find that when $\tau { = 0}{\text{.5}}$,$\zeta { = 0}{\text{.5}}$ the scores and ranking of the four green environmental protection enterprises are changing with the change of $w$, but the optimal enterprise is always fourth enterprise $X_{4}$.

From the analysis of the above aspects, the MADM technique proposed in this study is more flexible than the existing methods. In practical application, DMs can choose a more practical MADM technique by adjusting the parameters in the MADM technique.

7.2 Comparative Analysis

In the section of comparative analysis, we compare the PDHF MADM technique built in such study with five aggregation operators WPDHFMSMA operator, WPDHFMSMG operator, PDHFWEA operator, PDHFWEG operator and PDHFWA operator proposed in the existing literatures [19, 23] and [39]. The study shows that the ranking of the four alternatives are basically consistent, moreover, the optimal alternative given by the research method proposed in such study and the optimal alternative given by five aggregation operators are $X_{4}$.

7.2.1 Comparative Analysis with Reference [23]

Here, we compare the method built in the study with by Garg and Kaur [23], let's bring the data into the WPDHFMSMA operator and WPDHFMSMG operator, according to the calculation formula of score function, we can get the score of $X_{i} \left( {i = 1,2,3,4} \right)$, all computing results are recorded in Table 14.

Table 14 The ranking of $X_{i}$ by the method [23]

From the result, the ranking of $X_{i} \left( {i = 1,2,3,4} \right)$ by the method built in the study is consistent with that by the method based on WPDHFMSMG operator in the reference [23].

From the result, the ranking of $X_{i} \left( {i = 1,2,3,4} \right)$ by the method built in the study is basically consistent with that by the method based on WPDHFMSMA operator in the reference [23].

Although the order of alternatives slightly different, the optimal enterprise is $X_{4}$.

7.2.2 Comparative Analysis with Reference [39]

Here, we compare the method built in the study with by Garg and Kumar [39], let's bring the data into the PDHFWEA operator and PDHFWEG operator, according to the calculation formula of score function, we can get the score of $X_{i} \left( {i = 1,2,3,4} \right)$, all computing results are recorded in Table 15.

Table 15 The ranking of $X_{i}$ by the method [39]

From the result, the ranking of $X_{i} \left( {i = 1,2,3,4} \right)$ by the method built in the study is consistent with that by the method based on PDHFWEG operator in the reference [39].

From the result, the ranking of $X_{i} \left( {i = 1,2,3,4} \right)$ by the method built in the study is basically consistent with that by the method based on PDHFWEA operator in the reference [39].

Although the order of alternatives slightly different, the optimal enterprise is $X_{4}$.

7.2.3 Comparative Analysis with Reference [19]

Here, we compare the method built in the study with the PDHFWA operator proposed by Hao, Xu, Zhao and Su [19], let's bring the data into the model, according to the calculation formula of score function, we can get the score of $X_{i} \left( {i = 1,2,3,4} \right)$, all computing results are recorded in Table 16.

Table 16 The ranking of $X_{i}$ by the method [19]

From the result, the ranking of $X_{i} \left( {i = 1,2,3,4} \right)$ by the method built in the study is basically consistent with that by the method based on PDHFWA operator in the reference [19].

Although the order of alternatives slightly different, the optimal enterprise is $X_{4}$.

7.3 Comprehensive Analysis

According to the ranking of four alternatives calculated by five decision-making methods in Table 17 and Figs. 7 and 8, although the ranking of the four alternatives is a little different, the optimal alternative is always $X_{2}$. Many MADM methods in the same fuzzy environment will have their own advantages. PDHFWEA, WPDHFMSMA and PDHFWA operators focus more on the overall balance, but PDHFWEG and WPDHFMSMG operators emphasize the importance of extreme data. However, compared with many existing decision-making methods, the PDHF MADM technique proposed in the study better handles the MADM problems with PDHF information and has more unique characteristics.

Table 17 The ranking of four alternatives by using different methods

Fig. 7

The score values of the four green environmental protection enterprises obtained by several methods

Fig. 8

The ranking of the four green environmental protection enterprises obtained by several methods

7.4 Sensitivity Analysis of Several Decision-Making Methods [82]

Because there is no unified dimension and contradiction between the evaluation indicators, there is generally no so-called “optimal solution” for multi-objective decision-making problems. The DM can only find the satisfactory solution that the DM is satisfied with all the target values, the DM evaluates and judges all the decision-making schemes through various decision-making models and algorithms, finding a satisfactory solution, this requires that the decision model and algorithm have enough sensitivity, so as to distinguish and sort the decision-making alternatives.

The final index used to evaluate and rank each scheme is defined as the decision coefficient. Using different decision-making methods to make decisions on the given practical problems, its main purpose is to distinguish the optimal alternative from other alternatives, if the decision coefficient $\delta_{\max }$ reflecting the optimal strategy is similar to the decision coefficient $\delta_{\sec }$ reflecting the suboptimal strategy and the discrimination is not high, so it is easy to get the wrong understanding of the two strategies. It is often considered that when there is a large difference between the coefficients of the optimal and suboptimal schemes, the difference between the two schemes is high enough, which can ensure better sensitivity of decision-making. The calculation formula of sensitivity of decision-making is defined as follows.

Let $\delta_{\max }$ be the decision coefficient of the optimal decision alternative obtained with $s{\text{th}}$ decision-making approach, $\delta_{\sec }$ be the decision coefficient of the suboptimal decision alternative with $s{\text{th}}$ decision-making approach, then sensitivity $\delta_{s} \left( {s = 1,2, \cdots ,6} \right)$ of with $s{\text{th}}$ decision-making approach is defined as:

$$\delta_{s} = \frac{{\delta_{\max }^{s} - \delta_{\sec }^{s} }}{{\left| {\delta_{\max }^{s} } \right|}} \times 100\%$$

The larger $\delta_{s}$, the better the $s{\text{th}}$ decision-making approach.

We use sensitivity to analyze the advantages and disadvantages of the six decision-making approaches in detail. The results are shown in Table 18.

Table 18 The sensitivity analysis of several decision-making approaches

According to the standards we put forward in this paper and $\delta_{s}$ in Table 18 and Fig. 9, we can get the optimal decision-making approach is the PDHF-CODAS approach built in the paper.

Fig. 9

The sensitivity analysis of several decision-making approaches

8 Conclusions

In the study, we systematically reviewed the researches on the decision-making methods of PDHFS. We found that there are still great deficiencies in the researches on the distance and entropy measures for PDHFS, especially the widely used CODAS method has no application in PDHF setting. As an extension of traditional FS, PDHFS can more comprehensively express the uncertainty and fuzzy information in MADM problems, through literatures review, PDHFS has not been fully developed. In this study, we study the distance and entropy measures in PDHF environment in detail. We extend the famous Hamming and Euclidean distances to the PDHF environment, and propose some novel distance measures that can reflect the psychological behavior of DMs and their weighting forms. In order to solve the weighting problem of decision attribute more scientifically and reasonably, a novel objective weighting method of decision attributes is proposed based on the PDHF entropy, the combined weight is calculated which combines the subjective weights of DMs by utilizing the principle of minimum information identification. Meanwhile, the CODAS method is fused with the PDHFS for the first time, and a novel PDHF MAGDM technique was proposed and applied to the evaluation of enterprise credit risk. Finally, we apply the novel MADM technique to the credit risk assessment problem where the decision attribute information is PDHFE, the novel MADM technique can solve the MADM problem in the PDHF setting from the decision-making process and results and the applicability of the novel MADM technique in solving MADM problems is explained. Then through parameter analysis and result analysis, we can see that our proposed MADM technique has more flexibility and can give DMs more choices by adjusting the parameters in the model, and better meet the needs of different practical problems. The MADM technique proposed in this study has proved to be effective through sufficient comparative analysis with PDHFWA, PDHFWEA, PDHFWEG, WPDHFMSMA, WPDHFMSMG operators. If HFS and DHFS are regarded as special cases of PDHFS, the distance and entropy measures proposed in this study can be used to solve those MADM problems in these three fuzzy environments.

In the future research, we will continue to focus on the research of decision-making methods and aggregation operators by fusing Dombi operator [83], Bonferroni mean operators [84], Muirhead mean (MM) operator [85] and Einstein operator [86] to PDHF environment and propose some new MADM methods. It is also committed to applying the decision-making method proposed in this study to uncertain MADM problems such as landfill site selection [87], offshore wind turbine selection [88], appropriate solar thermal technology selection [89], optimal configuration selection [90], emergency plan selection [91] and site selection [92], etc.