A Credibilistic Fuzzy DEA Approach for Portfolio Efficiency Evaluation and Rebalancing Toward Benchmark Portfolios Using Positive and Negative Returns

Abstract

This paper proposes a data envelopment analysis (DEA)-based portfolio efficiency evaluation approach integrated with a rebalancing method to help investors acquire efficient portfolios. Two fuzzy portfolio selection models with value at risk (VaR) and conditional value at risk (CVaR) as objectives are proposed under the credibilistic framework. The models are constrained by realistic constraints of short selling/no short selling, capital budget, bounds on investment in an asset, and minimum return desired by the investor. These models are used to compute the benchmark portfolios, which constitute the portfolio efficient frontier. Furthermore, random sample portfolios are generated individually for each model in compliance with their constraints. These random sample portfolios are evaluated in terms of their relative efficiency with risk (VaR or CVaR) as an input and return as an output using DEA. Bearing in mind the volatile nature of the investment market, negative returns are also considered for portfolio efficiency evaluation using the range directional model. Moreover, an efficiency frontier improvement algorithm is used to rebalance the inefficient random portfolios to make them efficient. The proposed approach provides an alternative to the investors to acquire benchmark portfolios using the traditional portfolio selection models. A detailed numerical illustration and an out of sample analysis with the Nifty 50 index from the National Stock Exchange, India, are presented to substantiate the proposed approach.

1 Introduction

The ground-breaking mean-variance (MV) model proposed by Markowitz [23] is considered as a giant leap in the development of modern portfolio theory. Since then, variance has been used as one of the popular tools to manage risk in a portfolio selection problem. However, variance is widely criticized in the literature because it endows equal weights to both positive and negative returns (irrespective of their desirability or undesirability). Also, it provides little information about how much loss investors may have to bear, while it is the loss that investors are primarily concerned about [15].

This has led researchers to explore risk measures that can be used to segregate desirable upside movements from undesirable downside movements. Amongst those risk measures, value at risk (VaR) is one such widely accepted popular risk measure. The VaR of an investment is the possibility of the utmost loss with a known confidence level. Not only VaR is more systematic, but it is also accepted by a host of investors. VaR enables the investors to adjust the robustness, as desired by the investors, using different confidence levels, thereby producing robust evaluations on risk. However, VaR does not provide any information regarding the losses exceeding it, and it also does not obey the coherence axioms of homogeneity, sub-additivity, monotonicity, and translational invariance. To resolve the inadequacies implicit in VaR, Rockafeller and Uryasev [29] proposed the conditional value at risk (CVaR), which is given as the weighted average of the VaR and the losses exceeding it. Consequently, CVaR has been widely utilized to manage risk in portfolio optimization problems [10, 35, 36].

All the aforementioned studies characterized security returns as random variables with known probability distributions. However, owing to the inherent complexity and volatile nature of the investment market, it is not possible to precisely predict the security returns using the available historical data. Since the introduction of the fuzzy set theory [37], the field of portfolio optimization has grown enormously with various risk measures being applied in the literature, see [7, 18, 25, 33, 34]. For detailed literature on fuzzy portfolio optimization, one can refer to the monograph by Gupta et al. [11].

Credibility theory has been extensively studied [19] and applied in the literature to study the behaviour of the fuzzy phenomenon, see [14, 38].

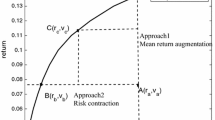
Due to the enormous advancements in the field of portfolio optimization, portfolio performance evaluation has become a significant field of study from the viewpoint of research and a necessary exercise for investors. A popular method to estimate a portfolio’s performance is the Sharpe ratio, which is the excess return per unit total risk [32]. Another extensively used method for estimating a portfolio’s efficiency is the real frontier approach (RFA) [26], which estimates a portfolio’s efficiency by calculating the relative distance of the asset under evaluation from the efficient frontier of the portfolio. However, Joro and Na [16] pointed out the difficulty in obtaining the portfolio efficient frontier owing to the high computation complexity involved in the RFA when applied to real-market applications. To tackle this issue, several researchers have forayed into frontier approaching methods for estimating a portfolio’s efficiency.

Data envelopment analysis (DEA) approach [5] can deal with multiple inputs and outputs. Therefore, it is being extensively used as a non-parametric approach for portfolio evaluation, see [16, 27]. Branda [3] used CVaR and return as input and output, respectively, for proposing new efficiency tests considering diversification. Ding et al. [8] presented a portfolio performance evaluation problem using margin constraints and demonstrated through simulation results that with an increase in sample size, the DEA frontier suitably approximates the portfolio frontier. Liu et al. [22] employed DEA to evaluate portfolio efficiency, and proved that when sample size approaches infinity, the DEA frontier effectively approximates the portfolio frontier. Zhou et al. [39] proposed a portfolio rebalancing approach using DEA frontier improvement under the MV framework. Chen et al. [6] proposed three DEA models using different risk measures for evaluation of portfolio efficiency under a possibilistic environment.

Conventionally, DEA models implicitly assume the input as well as the output values to be non-negative; however, in various situations, negative inputs or outputs can be encountered, e.g. the loss incurred w.r.t. net profit, negative net income when expenses are greater than the revenue, return rates for investment, etc. In recent literature, several approaches have been presented to deal with negative data, see [4, 9, 28, 30, 31].

1.1 Research Motivation

Although there are a handful of research works that deal with portfolio efficiency evaluation with different risk measures, to our knowledge, there are no research works on fuzzy portfolio efficiency evaluation using VaR and CVaR risk measures under the credibilistic environment. Further, the existing studies use randomly generated sample portfolios that are entirely random and compliant only with the capital budget constraint. However, to effectively mimic the behaviour of a real-market portfolio, it is customary for the randomly generated portfolios to comply with other realistic constraints of bounds on investment in an asset, short selling, or no short selling. Moreover, there are no studies on fuzzy portfolio efficiency evaluation using negative returns in the existing literature.

So, motivated to fill this void in the portfolio evaluation literature, in this paper, we propose two different fuzzy portfolio selection models using VaR and CVaR as objectives under a credibilistic framework. Several realistic constraints are used in both the models. A case of the proposed two models is also presented, where short selling is allowed. Further, random sample portfolios are generated specifically for each type of model by satisfying their respective constraints. Next, portfolio efficiency evaluation is carried out for these randomly generated portfolios using risk (VaR or CVaR) as input and expected return as output in the DEA models. Furthermore, a particular case of the portfolio efficiency evaluation is presented with negative returns using the range directional measure (RDM) model. The proposed approach enables the investors to conveniently acquire efficient portfolios using randomly generated portfolios, which closely approximate the benchmark portfolios on the portfolio efficient frontier.

1.2 Novelty of the Proposed Approach

• 1. In the existing literature on portfolio efficiency evaluation, there are no studies with VaR or CVaR employed as a risk measure under the credibilistic environment. Through this study, we contribute to the literature on portfolio efficiency evaluation by using VaR and CVaR as risk measures under a credibilistic environment.

• 2. We propose two fuzzy portfolio selection models with several realistic constraints to integrate the preferences of the investors into the models and generate random portfolios specifically for both of them by satisfying their respective constraints.

• 3. In the existing literature, studies on portfolio performance evaluation take into account only the positive returns of the assets or portfolios. Keeping in mind the volatile nature of the investment market and to present a more realistic account of how a portfolio performs, in this study, we have considered portfolios with both positive as well as negative returns, which are handled using the RDM model.

• 4. Furthermore, the proposed approach enables the investors to choose the confidence level ($\beta$) for VaR and CVaR and different transaction costs associated with each asset according to their preferences.

• 5. The proposed approach enables the investors to acquire efficient portfolios using randomly generated portfolios, which closely approximate the benchmark portfolios on the portfolio efficient frontier.

Table 1 Comparison with existing approaches

The novelty of the proposed approach is also highlighted through comparison with existing approaches in Table 1.

1.3 Organization of the Paper

The paper proceeds as follows. Section 2 revisits the basic definitions of fuzzy random variables and credibility theory. Further, formulas for credibilistic mean, variance, VaR, and CVaR are presented. Section 3 presents the proposed generalized Markowitz’s mean-VaR and mean-CVaR models, and DEA models for efficiency evaluation of the random sample portfolios. To validate the proposed approach, a detailed numerical illustration is presented in Sect. 4. Further, its subsequent subsections present the rebalancing of the inefficient portfolios, and an out of sample analysis. The paper concludes with Sect. 5.

2 Preliminaries

For various notations, terminologies and basics of fuzzy sets, fuzzy variables, and credibility theory, we shall refer to [20, 21], and [37].

Let $\tilde{\xi }$ be a fuzzy variable with possibility distribution $\mu{:}\; \mathbf {R}\rightarrow [0,1]$. A fuzzy variable is said to be normal if there exists a real number x such that $\mu _{\tilde{\xi }}(x) =1.$ In this paper, we assume that all the fuzzy variables are normal.

For a real number r, the possibility of the event $\{\tilde{\xi } \ge r \}$ is defined by

$$\begin{aligned} {\text{Pos}}\{\tilde{\xi } \ge r\} = \underset{x\ge r}{\text { sup }}\ \mu _{\tilde{\xi }}(x), \end{aligned}$$

and the necessity of the event $\{\tilde{\xi } \ge r \}$ is defined by

$$\begin{aligned} {\text{Nec}}\{\tilde{\xi } \ge r\} = 1-{\text{Pos}}\{\tilde{\xi }< r\} = 1 - \underset{x<r}{\sup \ } \mu _{\tilde{\xi }}(x). \end{aligned}$$

Definition 1

Let $\tilde{\xi }$ be a fuzzy variable. For any $r \in \mathbf {R}$, the credibility of the fuzzy event $\{\tilde{\xi } \ge r \}$ is defined as

$$\begin{aligned} {\text{Cr}}\{\tilde{\xi } \ge r \} = \displaystyle \frac{1}{2} \left( {\text{Pos}}\{\tilde{\xi } \ge r\} + {\text{Nec}}\{\tilde{\xi } \ge r\}\right) . \end{aligned}$$

Therefore, we have

$$\begin{aligned} {{\text{Cr}}\{\tilde{\xi } \ge r\} = \frac{1}{2}\left[ \sup _{x \ge r} \mu _{\tilde{\xi }}(x) + 1 - \sup _{x < r} \mu _{\tilde{\xi }}(x)\right] .} \end{aligned}$$

(1)

Similarly, we have

$$\begin{aligned} {{\text{Cr}}\{\tilde{\xi } \le r\} = \displaystyle \frac{1}{2}\left[ \underset{x \le r}{\sup \ } \mu _{\tilde{\xi }}(x) + 1 - \underset{x > r}{\sup \ } \mu _{\tilde{\xi }}(x)\right] .} \end{aligned}$$

(2)

Note that the credibility measure follows the five axioms of normality, monotonicity, self-duality, maximality, and sub-additivity.

Let $\tilde{\xi }$ be the fuzzy return of an asset, and ${\text{Cr}}\{\tilde{\xi } \ge 6\}$ = 0.75; then, it can be said that the credibility of the event of the future return not being less than 6 is 0.75.

Definition 2

Let $\tilde{\xi }$ be a fuzzy variable. Then, the expected value of $\tilde{\xi }$ is defined as

$$\begin{aligned} E[\tilde{\xi }] = \int _{0}^{\infty }{\text{Cr}}\{\tilde{\xi } \ge r\}{\text{d}}r - \int _{-\infty }^{0}{\text{Cr}}\{\tilde{\xi } \le r\}{\text{d}}r{,} \end{aligned}$$

provided that at least one of the two integrals is finite.

Definition 3

Let $\tilde{\xi }$ be a fuzzy variable with finite expected value e. Then, the variance of $\tilde{\xi }$ is defined as

$$\begin{aligned} V [\tilde{\xi }] = E[(\tilde{\xi } - e)^2] = \int _{0}^{\infty }{\text{Cr}}\{(\tilde{\xi }-e)^2 \ge r\}{\text{d}}r. \end{aligned}$$

Definition 4

Let $\tilde{L}$ be a fuzzy variable, denoting the fuzzy loss of an investment. The VaR of $\tilde{L}$ with a confidence level of $(1-\beta ); ~\beta \in (0, 1)$ is given by

$$\begin{aligned} \text{VaR}_{1-\beta }=\sup \ \{\lambda |{\text{Cr}}( \tilde{L} \ge \lambda )\ge \beta \}. \end{aligned}$$

(3)

The above equation states that the greatest loss $\tilde{L}$ associated with an investment with confidence level $(1-\beta )$ is $\lambda$.

Definition 5

Let $\tilde{\xi }$ be a fuzzy variable with finite expected value and credibility level $0<\beta <1$. Then the $\beta$-CVaR of $\tilde{\xi }$ is defined as

$$\begin{aligned} \text{CVaR}_{\beta } = \min _{x}\left [x+ \frac{1}{1- \beta }E\{\max (\tilde{\xi }-x, 0)\}\right ]. \end{aligned}$$

(4)

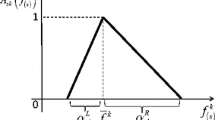
For a trapezoidal fuzzy number (TrFN) $\tilde{\xi } = (t_1, t_2, t_3, t_4)$ with possibility distribution

$$\begin{aligned} \mu _{\tilde{\xi }}(x)=\left\{ \begin{array}{lcl} 0, &{}\qquad &{} x<t_1, \\ \displaystyle \frac{x-t_1}{t_2 - t_1}, &{}\qquad &{} t_1\le x< t_2, \\ 1, &{}\qquad &{} t_2\le x \le t_3, \\ \displaystyle \frac{t_4 - x}{t_4-t_3}, &{}\qquad &{} t_3< x \le t_4, \\ 0, &{}\qquad &{} x>t_4, \end{array} \right. \end{aligned}$$

the expected value, variance, VaR, and CVaR are given as

$$\begin{aligned} E[\tilde{\xi }]&= (t_1+ t_2+ t_3+ t_4)/4, \end{aligned}$$

(5)

$$\begin{aligned} V[\tilde{\xi }]&= \displaystyle \frac{4l^2 + 3lv +v^2 +9lk+ 3vk + 6k^2}{48}\nonumber \\&\quad + \frac{[(l-v-2k)^+]^3}{384l}, \end{aligned}$$

(6)

$$\begin{aligned} \text{VaR}_{1-\beta }[\tilde{\xi }]&= \left\{ \begin{array}{ll} 2\beta t_2 + (1-2\beta )t_1, &{}\text{ if } 0< \beta \le 0.5, \\ (2\beta - 1)t_4 + (2-2\beta )t_3 , &{}\text{ if } 0.5 < \beta \le 1, \end{array}\right. \end{aligned}$$

(7)

$$\begin{aligned} \text{CVaR}_{\beta }[\tilde{\xi }]&= \left\{ \begin{array}{ll} \displaystyle \frac{(1-2\beta )^{2} t_1}{4(1-\beta )} + \displaystyle \frac{(1 + 2\beta )(1-2\beta )t_2}{4(1-\beta )}+\\ \displaystyle \frac{t_3}{4(1-\beta )}+ \displaystyle \frac{t_4}{4(1-\beta )}, ~\quad \text{ if } 0< \beta \le 0.5 \\ (1-\beta )t_3 + \beta t_4, ~\quad \text{ if } 0.5 < \beta \le 1, \end{array}\right. \end{aligned}$$

(8)

where $l = \max \{t_2 - t_1, t_4 -t_3\},\ v = \min \{t_2 - t_1, t_4 -t_3\},\ k = t_3-t_2$, and $(l-v-2k)^+ = \max \{l-v-2k, 0\}$.

3 Model Development

Assume there are n risky assets whose returns are TrFNs represented by $\tilde{\xi _i}=(t_1, t_2, t_3, t_4)_i,\ i = 1,2,\ldots ,n$ with investment proportions $w_i,\ i = 1,2,\ldots ,n$. Also, there is a fixed linear transaction cost $k_i$ associated with each asset. The expected net return, VaR, and CVaR of the portfolio are given as

$$\begin{aligned}&Re = \sum _{i=1}^{n}\tilde{\xi }w_i - \sum _{i=1}^{n}k_iw_i, \ \ \text{VaR} = \sum _{i=1}^{n}VaR_{1-\beta }[\tilde{\xi }]w_i, \\&\quad \text {and}\ \text{CVaR} = \sum _{i=1}^{n}\text{CVaR}_{\beta }[\tilde{\xi }] w_i,\ \text {respectively}. \end{aligned}$$

Using Eq. (5) and Eqs. (7–8), the credibilistic return, VaR, and CVaR of the portfolio are given as

$$\begin{aligned} \text{Re} &= {} \sum _{i=1}^{n}\frac{(t_1+ t_2+ t_3+ t_4)_i}{4}w_i - \sum _{i=1}^{n}k_iw_i,\\ \text{VaR} &= {} \small {{\left\{ \begin{array}{ll} \displaystyle \sum _{i=1}^{n}\left( 2\beta t_2 + (1-2\beta )t_1\right) _i w_i, ~ \text{ if } 0< \beta \le 0.5, \\ \displaystyle \sum _{i=1}^{n}\left( (2\beta - 1)t_4 + (2-2\beta )t_3\right) _i w_i, ~\text{ if } 0.5< \beta \le 1, \end{array}\right. }}\\ \text{CVaR} & = {} \small {{\left\{ \begin{array}{ll} \displaystyle \sum _{i=1}^{n}\left( \frac{(1-2\beta )^{2} t_1}{4(1-\beta )} + \frac{(1 + 2\beta )(1-2\beta )t_2}{4(1-\beta )} + \right. \\ \left. \displaystyle \frac{t_3}{4(1-\beta )}+ \frac{t_4}{4(1-\beta )}\right) _i w_i, ~\text{ if } 0< \beta \le 0.5, \\ \displaystyle \sum _{i=1}^{n}\left( (1-\beta )t_3 + \beta t_4\right) _i w_i,~ \text{ if } 0.5 < \beta \le 1. \end{array}\right. }} \end{aligned}$$

In accordance with the Markowitz’s [23] portfolio selection model, the generalized fuzzy mean-VaR and fuzzy mean-CVaR portfolio selection models under the credibilistic framework are presented as follows:

3.1 Credibilistic Mean-VaR and Mean-CVaR Portfolio Selection Models with Bounded Assets

$$\begin{aligned}&\mathbf{(Model\,1a) }\nonumber \\&\min \ \text{VaR} = {\left\{ \begin{array}{ll} \displaystyle \sum _{i=1}^{n}\left( 2\beta t_2 + (1-2\beta )t_1\right) _i w_i, ~\text{ if } 0< \beta \le 0.5, \\ \displaystyle \sum _{i=1}^{n}\left( (2\beta - 1)t_4 + (2-2\beta )t_3\right) _i w_i, ~\text{ if } 0.5 < \beta \le 1, \end{array}\right. }\nonumber \\&\text {subject\;to}\nonumber \\&\sum _{i=1}^{n}\frac{(t_1+ t_2+ t_3+ t_4)_i}{4}w_i - \sum _{i=1}^{n}k_iw_i \ge r, \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{i=1}^{n}w_i = 1, \end{aligned}$$

(10)

$$\begin{aligned}&w_i \ge 0, \ \ i = 1,2,\ldots ,n, \end{aligned}$$

(11)

$$\begin{aligned}&w_i \le 0.20, \ \ i = 1,2,\ldots ,n, \end{aligned}$$

(12)

where r is the minimum return desired by the investor.

$$\begin{aligned}&\mathbf{(Model\,1b) } \\&\min \text{CVaR} = {\left\{ \begin{array}{ll} \displaystyle \sum _{i=1}^{n}\left( \frac{(1-2\beta )^{2} t_1}{4(1-\beta )} + \frac{(1 + 2\beta )(1-2\beta )t_2}{4(1-\beta )} \right. + \\ \left. \displaystyle \frac{t_3}{4(1-\beta )} + \frac{t_4}{4(1-\beta )}\right) _i w_i, ~ \text{ if } 0< \beta \le 0.5, \\ \displaystyle \sum _{i=1}^{n}\left( (1-\beta )t_3 + \beta t_4\right) _i w_i, ~ \text{ if } 0.5 < \beta \le 1, \end{array}\right. } \\&\text {subject\;to\;Eqs.}\;(9{-}12). \end{aligned}$$

3.2 Credibilistic Mean-VaR and Mean-CVaR Portfolio Selection Models with Bounded Assets and Short Selling

$$\begin{aligned}& \mathbf{(Model\,2a) }\nonumber \\& \min \ \text{VaR} = {\left\{ \begin{array}{ll} \displaystyle \sum _{i=1}^{n}\left( 2\beta t_2 + (1-2\beta )t_1\right) _i w_i, ~ \text{ if } 0 < \beta \le 0.5, \\ \displaystyle \sum _{i=1}^{n}\left( (2\beta - 1)t_4 + (2-2\beta )t_3\right) _i w_i, ~ \text{ if } 0.5 < \beta \le 1, \end{array}\right. }\nonumber \\& \text {subject\;to\;Eqs.}\; (9{-}10) \;\text{and Eq.}\; (12),\nonumber \\& w_i \ge -0.25, \ \ i = 1,2,\ldots ,n. \end{aligned}$$

(13)

$$\begin{aligned}&\mathbf{(Model\,2b) }\nonumber \\& \min \text{CVaR} = {{\left\{ \begin{array}{ll} \displaystyle \sum _{i=1}^{n}\left( \frac{(1-2\beta )^{2} t_1}{4(1-\beta )} + \frac{(1 + 2\beta )(1-2\beta )t_2}{4(1-\beta )} + \right. \\ \left. \displaystyle \frac{t_3}{4(1-\beta )}+ \frac{t_4}{4(1-\beta )}\right) _i w_i, ~ \text{ if } 0 < \beta \le 0.5, \\ \displaystyle \sum _{i=1}^{n}\left( (1-\beta )t_3 + \beta t_4\right) _i w_i, ~ \text{ if } 0.5 < \beta \le 1, \end{array}\right. }} \nonumber \\& {\text{subject\;to\;Eqs.}} \;(9{-}10) \;\text{and Eqs.} \;(12{-}13).\nonumber \end{aligned}$$

Models (1a), 1(b) and (2a), (2b) are used to compute efficient portfolios, which are considered as benchmark portfolios. These benchmark portfolios constitute the portfolio efficient frontier. In the next subsection, we generate random sample portfolios and evaluate their efficiency using DEA for positive returns and RDM for negative returns.

Remark 1

The investor can choose the suitable risk measure (VaR or CVaR) and desired confidence level according to his/her preferences. If the investor chooses VaR as a risk measure, then for $0 < \beta \le 0.5$, $\text{VaR}_{1-\beta }(\tilde{\xi })= \sum _{i=1}^{n}\left( 2\beta t_2 + (1-2\beta )t_1\right) _i w_i$, and for $0.5 < \beta \le 1$, $\text{VaR}_{1-\beta }$$(\tilde{\xi }) = \sum _{i=1}^{n}\left( (2\beta - 1)t_4 + (2-2\beta )t_3\right) _i w_i$ (see Eq. (7)). If the investor chooses CVaR as a risk measure, then for $0< \beta \le 0.5$, $\text{CVaR}_{\beta }(\tilde{\xi })= \sum _{i=1}^{n}(\frac{(1-2\beta )^{2} t_1}{4(1-\beta )} + \frac{(1 + 2\beta )(1-2\beta )t_2}{4(1-\beta )}$$+ \frac{t_3}{4(1-\beta )}+ \frac{t_4}{4(1-\beta )})_i w_i$, and for $0.5 < \beta \le 1$, $\text{CVaR}_{\beta }(\tilde{\xi })= \sum _{i=1}^{n}\left( (1-\beta )t_3 + \beta t_4\right) _i w_i$ (see Eq. (8)).

Remark 2

For a trapezoidal return $\tilde{\xi } = (t_1, t_2, t_3, t_4)$, the VaR for $0 < \beta \le 0.5$ depends only on $t_1$ and $t_2$; however, the CVaR for $0 < \beta \le 0.5$ depends on all the values of $\tilde{\xi }$. This establishes the superiority of CVaR as a risk measure, viz., it accounts for losses exceeding VaR.

3.3 Efficiency Evaluation of Random Sample Portfolios Using DEA

Now, we generate m random sample portfolios with n risky assets $A_i$ having investment proportions $w_{i}, \ i=1,2,\ldots ,n$, which are considered as DMUs. These random sample portfolios are generated individually for Models (1a), (1b) and (2a), (2b) in compliance with their constraints (10–12), and (10, 12, 13), respectively. Let $\text{Re}_j=\sum _{i=1}^{n}w_{i}\xi _i$ be the expected return, $\text{VaR}_j = \sum _{i=1}^{n} \text{VaR}_{1-\beta }(\xi _i) w_i$ be the VaR, and $\text{CVaR}_j = \sum _{i=1}^{n} \text{CVaR}_{\beta }(\xi _i) w_i$ be the CVaR of the $j$th portfolio, $j= 1, 2, \ldots , m$, respectively. For evaluating the efficiency of m portfolios, the VaR or CVaR is considered as input while the expected return is considered as output. Let $\text{Re}_0$, $\text{VaR}_0,$ and $\text{CVaR}_0$ be the expected return, VaR, and CVaR of the $\text {DMU}_0$ being evaluated, respectively. Then, the efficiency of $\text {DMU}_0$ can be computed by using the following DEA models:

3.3.1 Risk-Oriented BCC-DEA Models with VaR and CVaR for Positive Returns

Following the BCC-DEA model’s framework [2], the risk-oriented DEA fuzzy portfolio efficiency evaluation models can be formulated as

$$\begin{aligned} & \mathbf{(Model\,3a) }\\& \min \ \theta _{0}^{\text{VaR}} \nonumber \\& \text {subject\;to} \nonumber \\& \sum _{j=1}^{m} \lambda _j \text{VaR}_{j} \le \theta _{0}^{\text{VaR}}\cdot \text{VaR}_0,\nonumber \\& \sum _{j=1}^{m} \lambda _j \text{Re}_j \ge \text{Re}_0, \end{aligned}$$

$$\sum _{j=1}^{m} \lambda _j = 1, $$

(14)

$$\begin{aligned}&\lambda _j \ge 0, \ j=1, 2, \ldots , m, \\& {0 \le \theta _0^{{\text{VaR}}} \le 1,} \end{aligned}$$

(15)

$$\begin{aligned}& \mathbf{(Model\,3b) }\\& \min \ \theta _{0}^{{\text{CVaR}}} \nonumber \\& \text {{subject}\;to\;Eqs.} (14){-}(15) \nonumber \\& \sum _{j=1}^{m} \lambda _j {\text{CVaR}}_{j} \le \theta _{0}^{{\text{CVaR}}} \cdot {\text{CVaR}}_0,\nonumber \\& \sum _{j=1}^{m} \lambda _j {\text{Re}}_j \ge {\text{Re}}_0, \nonumber \\& {0 \le \theta _0^{{\text{CVaR}}} \le 1,}\nonumber \end{aligned}$$

respectively. Here, $\theta _{0}^{{\text{VaR}}}$ and $\theta _{0}^{{\text{CVaR}}}$ represent the efficiency score of $\text {DMU}_0$, and $\theta _{0}^{{\text{VaR}}}$ or $\theta _{0}^{{\text{CVaR}}} = 1$ indicates that $\text{DMU}_0$ is efficient, the decision variable $\lambda _j \ge 0, \ j=1,2,\ldots ,m$, denotes the weight or intensity of $\text {DMU}_0$.

3.3.2 Range Directional Measure Model with VaR and CVaR for Negative Returns

In conventional DEA models, each DMU is specified by a pair of non-negative input and output vectors, in which inputs are utilized to produce outputs. These models cannot be used for the cases of DMUs having both positive and negative inputs and/or outputs. Portela et al. [28] introduced the RDM model, which can be applied in such cases. The RDM models with VaR or CVaR as input and return as output are presented as

$$\begin{aligned} &\mathbf{(Model\,4a) }\\& \max \ \eta _{0}^{{\text{VaR}}}\\& \text {subject\;to\;Eqs.}\; (14){-}(15), \\& \sum _{j=1}^{m} \lambda _j {\text{VaR}}_{j} \le {\text{VaR}}_0 - \eta _{0}^{{\text{VaR}}} \cdot d_1 ,\\& \sum _{j=1}^{m} \lambda _j {\text{Re}}_j \ge {\text{Re}}_0 + \eta _{0}^{{\text{VaR}}} \cdot d_2, \\& {0 \le \eta _0^{{\text{VaR}}} \le 1,}\\ &\mathbf{(Model\,4b) }\\& \max \ \eta _{0}^{{\text{CVaR}}}\\& \text {subject\;to\;Eqs.}\; (14){-}(15), \\& \sum _{j=1}^{m} \lambda _j {\text{CVaR}}_{j} \le {\text{CVaR}}_0 - \eta _{0}^{{\text{CVaR}}} \cdot d_3 ,\\& \sum _{j=1}^{m} \lambda _j {\text{Re}}_j \ge {\text{Re}}_0 + \eta _{0}^{{\text{CVaR}}} \cdot d_2, \\& {0 \le \eta _0^{{\text{CVaR}}} \le 1,} \end{aligned}$$

where $d_1={\text{VaR}}_0 - \displaystyle \min _{{1 \le j\le m}}^{}\{{\text{VaR}}_j\}$, $d_2 = \displaystyle \max _{{1 \le j\le m}}^{}\{{\text{Re}}_j\}$$- {\text{Re}}_0,$ and $d_3={\text{CVaR}}_0 - \displaystyle \min _{{1 \le j\le m}}^{}\{{\text{CVaR}}_j\}$ are the directional vectors. Here, $\eta _{0}^{{\text{VaR}}}$ and $\eta _{0}^{{\text{CVaR}}}$$(1 - \eta _{0}^{{\text{VaR}}}\ \text {and}\,1 - \eta _{0}^{{\text{CVaR}}})$ represent the inefficiency (efficiency) score of $\text {DMU}_0$, and $\eta _{0}^{{\text{VaR}}}$ or $\eta _{0}^{{\text{CVaR}}}$ = 0 indicates that $\text {DMU}_0$ is efficient.

3.4 Rebalancing of the Inefficient Portfolios

In order to offer the investors with more choices (options) of efficient portfolios, and to make the inefficient portfolios efficient, we employ the DEA frontier improvement algorithm given in [39]. This frontier improvement algorithm provides the investors with rebalanced portfolios, which are efficient. These rebalanced portfolios closely approximate the benchmark portfolios. The steps of the algorithm are as follows:

• Step 1. For $\text {DMU}_0$ being evaluated, compute the efficiency using the BCC-DEA (RDM) model as $\theta _{0}^{{\text{VaR}}}$ or $\theta _{0}^{{\text{CVaR}}}$ ($\eta _{0}^{{\text{VaR}}}$ or $\eta _{0}^{{\text{CVaR}}}$). If $\theta _{0}^{{\text{VaR}}}$ or $\theta _{0}^{{\text{CVaR}}}=1$ ($\eta _{0}^{{\text{VaR}}}$ or $\eta _{0}^{{\text{CVaR}}}=0$), and their corresponding virtual weight $\lambda _0^0=1, \ \lambda _j^0=0, \ j=1,2,\dots ,m, \ j\ne 0$, then $\text {DMU}_0$ is efficient and cannot be improved anymore; otherwise move to Step 2.

• Step 2. Initialize $\psi =1$. The inefficient $\text {DMU}_0$ is rebalanced by obtaining new weights as $w_{i}^{0(\psi )} = w_{i}^{0(1)}= \sum _{j=1}^{m}\lambda _{j}^{0}w_{i}^{j}, \ i = 1,2,\dots ,n.$ Then, the improved input (VaR or CVaR) and output (return) of the $\text {DMU}_0$ are obtained as ${\text{VaR}}_{0}= \sum _{i=1}^{n}{\text{VaR}}_{1-\beta }(\xi _i)w_{i}^{0(1)}$$\left( {\text{CVaR}}_{0} = \sum _{i=1}^{n}{\text{CVaR}}_{\beta }(\xi _i)w_{i}^{0(1)}\right)$, and ${\text{Re}}_{0}=$$\sum _{i=1}^{n}E(\xi _i)w_{i}^{0(1)}$, respectively.

• Step 3. Repeat Step 1.

The following algorithm sums up the whole portfolio efficiency evaluation and rebalancing process:

• Step 1. Consider n assets with trapezoidal fuzzy returns.

• Step 2. Compute the expected return, and VaR/CVaR using Eq. (5), and Eq. (7)/Eq. (8), respectively, for a given confidence level.

• Step 3. Choose the appropriate model according to the investor’s preferences.

• Step 4. Compute the portfolio efficient frontier for the chosen model by varying the return desirability.

• Step 5. Generate random sample portfolios for the chosen model by satisfying the capital budget and bounds constraints.

• Step 6. Compute the return for a given transaction cost and VaR/CVaR for these random sample portfolios.

• Step 7. Evaluate the efficiencies of the random sample portfolios using Model (3a)/Model (3b) for positive returns or Model (4a)/Model (4b) for negative returns.

• Step 8. Rebalance the inefficient portfolios using the rebalancing algorithm discussed in Sect. 3.4.

4 Numerical Illustration

In this section, we present numerical illustrations for portfolio efficiency evaluation using both BCC-DEA model and RDM model for assets/portfolios having only positive returns and assets/portfolios having positive as well as negative returns, respectively.

4.1 Portfolio Efficiency Evaluation for Positive Returns

To demonstrate the virtues of the proposed approach, we consider 20 risky assets with fuzzy trapezoidal returns from Mehlawat [24], presented in Table 2. The fixed linear transaction cost associated with each asset is assumed as 0.003, and the confidence level ($\beta$) for VaR and CVaR is taken as 0.1. The credibilistic expected return, VaR, and CVaR for each of the 20 risky assets are presented in Table 2.

The values from Table 2 are used to solve Models (1a), (2a) and Models (1b), (2b) to compute the VaR, CVaR, and respective returns to construct the portfolio efficient frontier for each model. Table 3 depicts the points at their respective efficient frontiers. Next, we generate 30 random sample portfolios composed of 20 assets, specifically for each model satisfying their respective constraints. For Models (1a) and (1b), the random sample portfolios satisfy the constraints (10–12), and for Models (2a) and (2b), the random sample portfolios satisfy the constraints (10) and (12, 13). These randomly generated sample portfolios are presented in Tables 4, 5, respectively, along with their return, VaR, and CVaR.

Table 2 Trapezoidal fuzzy returns of 20 risky assets with expected return, VaR, and CVaR for $\beta = 0.1$

Table 3 Portfolio efficient frontier values for Models (1a), (2a), and Models (1b), (2b)

Next, the VaR-return and CVaR-return values of the sample portfolios in Tables 4,  5 are used as input–output in Models (3a) and (3b), respectively, to compute the efficiencies $\theta _{0}^{{\text{VaR}}}$ and $\theta _{0}^{{\text{CVaR}}}$ (see Tables 4, 5) of each sample portfolio.

Results and Discussion

• VaR: The portfolio efficient frontiers obtained using Models (1a) and (2a) presented in Table 3, and the VaR-return DEA frontier of the sample portfolios from Tables 4, 5 are graphically represented in Figs. 1, 2, respectively. It is clear from Table 4 and Fig. 1 that only four DMUs P3, P13, P17, and P22 are efficient for the random sample portfolios generated for Model (1a). As seen in Table 5 and Fig. 2, only five DMUs P3, P14, P19, P27, and P29 are efficient for the random sample portfolios generated for Model (2a).

• CVaR: The portfolio efficient frontiers obtained using Models (1b) and (2b) presented in Table 3, and the CVaR-return DEA frontier of the sample portfolios from Tables 4, 5 are graphically represented in Figs. 3, 4, respectively. It is clear from Table 4 and Fig. 3 that DMUs P1, P3, P13, P17, P18, P19, and P22 are efficient for the random sample portfolios generated for Model (1b). As seen in Table 5 and Fig. 4, the DMUs P3, P8, P16, P19, P27, and P29 are efficient for the random sample portfolios generated for Model (2b).

4.2 Portfolio Efficiency Evaluation for Negative Returns

In this subsection, we deal with assets and portfolios that can have both positive as well as negative returns. Similar to Sect. 4.1, the values of fixed linear transaction cost associated with each asset, and the value of confidence level ($\beta$) for VaR and CVaR are assumed to be 0.003 and 0.1, respectively.

The fuzzy trapezoidal returns for the 20 risky assets having both positive and negative returns and their credibilistic expected return, VaR, and CVaR are presented in Table 6. Note that the VaR and CVaR values for some of the risky assets are negative. Since VaR and CVaR represent the loss of capital; therefore, the absolute values of VaR and CVaR have been used for further computation.

The results from Table 6 are used in the Models (1a), (2a) and Models (1b), (2b) to compute VaR, CVaR, and respective returns (see Table 7) to construct the portfolio efficient frontier for each model.

We use the results from Table 6 and the same random sample portfolios presented in Tables 4,  5 from the previous Sect. 4.1 to compute the VaR, CVaR, and returns of the sample portfolios, which are presented in Table 8. The VaR-return and CVaR-return values from Table 8 are used in Models (4a) and (4b), respectively, to compute the efficiency of each sample portfolio, presented in Table 8 as $\eta _{0}^{{\text{VaR}}}$ and $\eta _{0}^{{\text{CVaR}}}$.

Results and Discussion

• VaR: The portfolio efficient frontier obtained using Models (1a) and (2a) presented in Table 7, and VaR-return RDM frontier of the sample portfolios from Table 8 are graphically represented in Figs. 5, 6, respectively. It is clear from Table 8 and Fig. 5 that only two DMUs P9 and P21 are efficient for the random sample portfolios generated for Model (1a). From Table 8 and Fig. 6, only the DMUs P16 and P21 are efficient for the random sample portfolios generated for Model (2a).

• CVaR: The portfolio efficient frontier obtained using Models (1b) and (2b) presented in Table 7, and CVaR-return RDM frontier of the sample portfolios from Table 8 are graphically represented in Figs. 7, 8, respectively. It is clear from Table 8 and Fig. 7 that only four DMUs P9, P21, P24, and P25 are efficient for the random sample portfolios generated for Model (1b). From Table 8 and Fig. 8, only the DMUs P11, P16, and P21 are efficient for the random sample portfolios generated for Model (2b).

Table 4 Random sample portfolios for Models (1a) and (1b) with expected return, VaR, CVaR, efficiencies $\theta _{0}^{{\text{VaR}}}$ and $\theta _{0}^{{\text{CVaR}}}$ for $\beta =0.1$

Table 5 Random sample portfolios for Models (2a) and (2b) with expected return, VaR, CVaR, efficiencies $\theta _{0}^{{\text{VaR}}}$ and $\theta _{0}^{{\text{CVaR}}}$ for $\beta =0.1$

Table 6 Trapezoidal fuzzy returns of 20 risky assets and their expected return, VaR, and CVaR for $\beta = 0.1$

Table 7 Portfolio efficient frontier values for Models (1a), (2a) and Models (1b), (2b)

Table 8 Expected return, VaR, CVaR, $\eta _{0}^{{\text{VaR}}}$ and $\eta _{0}^{{\text{CVaR}}}$ for $\beta = 0.1$ for Models (1a), (1b) and (2a), (2b)

4.3 Rebalancing of the Inefficient Portfolios

Next, using the frontier improvement algorithm from Sect. 3.4, we rebalance the inefficient portfolios from Tables 4,  5, and  8 to make them efficient in order to offer the investors with more choices (options) of efficient portfolios.

4.3.1 Rebalanced Portfolios for Positive Returns

• VaR: The inefficient portfolios in Tables 4, 5 for Models (1a) and (2a) are rebalanced up to one iteration. These rebalanced portfolios are also presented graphically in Figs. 1, 2 as improved sample portfolios. For a coherent demonstration, we present these rebalanced portfolios in Table 9. On similar lines, inefficient portfolios for subsequent models can be rebalanced likewise. The remaining tables for rebalanced portfolios have been omitted owing to the space crunch.

• CVaR: The inefficient portfolios in Tables 4, 5 for Models (1b) and (2b) are rebalanced up to one iteration and are graphically represented in Figs. 3, 4 as improved sample portfolios, respectively.

Here, the DEA frontier constituted by the improved sample portfolios for CVaR (see Figs. 3 and 4) closely approximates the portfolio efficient frontier.

4.3.2 Rebalanced Portfolios for Negative Returns

• VaR: The inefficient portfolios in Table 8 for Models (1a) and (2a) are rebalanced up to one iteration and are graphically represented in Figs. 5, 6 as improved sample portfolios, respectively.

• CVaR: The inefficient portfolios in Table 8 for Models (1b) and (2b) are rebalanced up to one iteration and are graphically represented in Figs. 7, 8 as improved sample portfolios, respectively.

Here, the improved sample portfolios for CVaR (see Figs. 7, 8) constitute a DEA frontier that is closer to the portfolio efficient frontier in comparison to the DEA frontier for VaR.

4.4 Out of Sample Analysis

In this subsection, we perform an out of sample analysis to validate the proposed approach. For the purpose, we collect the monthly return data of all the firms listed in the Nifty 50 index of the National Stock Exchange (NSE), India from January 01, 2014 to December 31, 2018 (60 months). Using the ‘Delphi Method’ discussed in Gupta et al. [12], we convert these monthly returns into trapezoidal fuzzy returns, which are presented in Table 10. We employ the proposed approach on these trapezoidal fuzzy returns to compute the credibilistic expected return, VaR, CVaR, and variance (see Table 10) of the 50 risky assets.

The VaR and CVaR values are used to calculate the fuzzy VaR ratio ((Expected return − risk free return)/VaR) and fuzzy CVaR ratio ((Expected return − risk free return)/CVaR), respectively. To calculate the Sharpe ratio ((Expected return − risk free return)/S.D.), we have also taken into account the credibilistic variance as a risk measure, and a 5% annual return has been assumed from a risk-free asset. The results in Table 10 are used in the Models (1a) and (1b) to obtain the results presented in Table 11.

The fuzzy VaR ratio, fuzzy CVaR ratio, and Sharpe ratio depict that the performance of the proposed approach is better as compared to the actual Nifty 50 performance.

Remark 3

In this paper, we have used the risk-oriented BCC-DEA model to evaluate the efficiency of the random sample portfolios. However, any of the risk-oriented, return-oriented, or non-oriented BCC-DEA models can be used for the same. Also, the investors are free to choose any value of confidence level ($\beta$) and different transaction costs according to their preferences.

Remark 4

We abstain from performing simulation with a large number of sample portfolios as the literature is already replete with numerous research works with simulation studies which have proved that as the number of sample portfolios is increased sufficiently large (or to infinity), the DEA frontier approximates the portfolio efficient frontier irrespective of the risk measure being used, see [6, 22, 39].

Fig. 1

Efficient frontiers of sample portfolios for Models (1a) and (3a)

Fig. 2

Efficient frontiers of sample portfolios for Models (2a) and (3a)

Fig. 3

Efficient frontiers of sample portfolios for Models (1b) and (3b)

Fig. 4

Efficient frontiers of sample portfolios for Models (2b) and (3b)

Fig. 5

Efficient frontiers of sample portfolios for Models (1a) and (4a)

Fig. 6

Efficient frontiers of sample portfolios for Models (2a) and (4a)

Fig. 7

Efficient frontiers of sample portfolios for Models (1b) and (4b)

Fig. 8

Efficient frontiers of sample portfolios for Models (2b) and (4b)

Table 9 Rebalanced sample portfolios for Model (1a) with expected return, VaR, and efficiency $\theta _{0}^{{\text{VaR}}}$

Table 10 Trapezoidal fuzzy return of Nifty 50 stocks with expected return, VaR, and CVaR

5 Conclusions

This study proposed a portfolio efficiency evaluation approach using superior risk measures of VaR and CVaR under a credibilistic environment. The inherent uncertainty of the stock market was incorporated by assuming the return of the assets as TrFNs. Two fuzzy portfolio selection models with different constraints were proposed to integrate the preferences of the investors into the models, and random sample portfolios were generated specifically for each type of model by satisfying their respective constraints. These random sample portfolios were evaluated using the risk-oriented BCC-DEA model for positive returns and RDM model for negative returns to compute their efficiencies. The inefficient portfolios were then rebalanced using a frontier improvement technique to make them efficient to provide the investors with more choices (options) of efficient portfolios. A detailed numerical illustration with both positive and negative returns was presented to demonstrate the virtues of the proposed approach. Further, an out of sample analysis was performed with the Nifty 50 index from NSE, India to validate the proposed approach. The out of sample analysis revealed that the proposed approach overshadows the actual Nifty 50 performance.

The proposed approach in spite of its novelties is limited by its rather long and time-consuming evaluation and rebalancing process.

The present study can further be extended by using normally distributed fuzzy numbers instead of TrFNs. An integrated model for portfolio selection with both VaR and CVaR can also be constructed. Further, portfolio efficiency evaluation with multiple inputs and multiple outputs can be performed by using criteria such as higher moments, liquidity, or entropy.

Table 11 Out of sample analysis results