1 Introduction

Generalized linear discrete-time systems are commonly used in signal processing, electromechanical systems, and the aerospace industry, as well as other applications. The theory of generalized discrete-time systems, which was first proposed in the 1970s, has gradually developed into an independent branch of modern control theory. Research ranges from linear to nonlinear systems, continuous to discrete, and certainty to uncertainty. However, control systems have become more complex, therefore, the reliability of generalized linear discrete-time systems has been hindered by several issues. Nonetheless, faults within process control systems are inevitable, and can seriously affect the precision and reliability of generalized linear discrete-time systems. Thus, accurately estimating the system state and approximating fault information can improve the overall accuracy and reliability a system.

In recent years, fault-tolerant methods based on control models have advanced [1,2,3,4,5]. However, to allow previously proposed methods to provide fault tolerance, modern distributed storage systems must rely on specialized network topologies and consensus protocols that create high overheads. Moreover, efficient data placement schemes that take into account data locality are difficult to implement. As such, numerous fault detection and isolation methods have been proposed [6,7,8,9,10]. Typically, a filtering technique is used to estimate the system state and based on the error between the estimated system state and actual system state, faults are detected and isolated. One disadvantage of the filtering technique is that when a moving target is blocked for a long period of time, the target may be lost during tracking, which can seriously affect the precision of fault detection. As yet, no advanced method exists for simultaneously estimating the system state and fault function.

In [11], a neuro-fuzzy identification method based on parity equations was proposed to detect uncertain faults of a real nonlinear system—in this case, an industrial pilot plant—and demonstrated relatively good performance. In [12], an approach combining the Chi-squared test and fuzzy RTMAP neural network mapping was described for fault diagnosis of an integrated navigation system. With this method, the whole state vector was first tested using the Chi-squared test. Then, the pattern of the test results was used to isolate and identify faults using two separate Fuzzy-ARTMAP neural networks. Although faults can be detected, identified, and isolated using the previously proposed methods [11, 12], estimates of the system state are not always optimal and the accuracy of the control system is affected.

In [13], a linear descriptor stochastic system was established and a robust strategy was proposed to estimate the state and fault information of the above system. The proposed method was based on a robust two-stage Kalman filter and was applied to yield the optimal robust descriptor state and fault estimation. A model-based approach for fault detection of an electromagnetic actuator considering an observer has also been presented [14]. First, a segmented mathematical model was established based on clustering identification, then a Luenberger observer was created to simultaneously estimate the state of the segmented model. Finally, fault isolation was achieved by calculating the energy value of the estimated state.

Although the states and faults of control systems have been estimated and isolated [13, 14], the accuracy of the fault information was not considered. In practical engineering, systems often contain many uncertainties owing to faults that cannot be accurately described by mathematical models. The fuzzy system can effectively approximate these uncertainties, nonlinearities, and other complex problems of various control systems [15,16,17,18,19]. Furthermore, the approximation abilities of numerous proposed methods have been studied for variable control systems [20,21,22].

Many researchers have used fuzzy theory to study the fault information of control systems and numerous strategies have been proposed. A fault detection approach for unknown systems based on the fuzzy basis function network was presented in [23]. The unknown system was composed of a known part, unknown part, and fault information. The unknown part, which includes the model uncertainties and disturbances, was estimated using a fuzzy basis function network; however, the fault information was not obtained in the real sense. In [24], a fuzzy state observer was designed and an observer-based fault detection approach for a nonlinear networked control system was presented. The main idea behind the stagey was that states of the nonlinear control system could be observed in real time without changing the structure of the system. In [25], the Takagi–Sugeno (TS) fuzzy observer for disturbance rejection based on the \(H\infty\) optimization index was designed. When designing the observer, the proportion of unknown system variables owing to the perturbation residue was considered to improve the robustness of the observer and to reduce interference and sensitivity to failure. The fuzzy system was used to estimate the fault information and to effectively deal with the uncertainty of the control system [24, 25], but the structure of the fuzzy system cannot be adjusted online and does not have self-learning capabilities.

All of these factors affect the accuracy in approximating fault information and state estimation. Thus, to achieve accurate fault information, not only the state estimation but also the fault information estimation should be considered. This paper presents an optimal state estimation and fault information approximation method based on a self-constructing fuzzy unscented Kalman filter (UKF) for generalized linear discrete systems.

In comparison to existing schemes, the main contributions of this paper can be summarized as follows:

  1. I.

    Parameters of the control system can be adjusted in real time according to change in the system state and fault information.

  2. II.

    Accurate fault information can be obtained while the states of the control system with faults are simultaneously estimated.

  3. III.

    Fault diagnosis can be performed according to the fault information.

The rest of the paper is organized as follows: In Sect. 2, a generalized linear discrete-time system without faults is transformed into an equivalent standard state-space system with faults; A novel approach based on a self-constructing fuzzy UKF system is proposed in Sect. 3; Sect. 4 presents a method of fault diagnosis and isolation-based fuzzy clustering; Experimental results for a direct current (DC) motor are given as a DC motor was taken as an example in Sect. 5; Finally, conclusions are presented in Sect. 6.

2 Problem Statement

Consider a generalized linear discrete-time system of the following form:

$$x(k + 1) = Ax(k) + Bu(k) + w(k)$$
(1)
$$y(k) = Cx(k) + v(k),$$
(2)

where \(x\left( k \right)\) is the state vector,\(x\left( k \right) \in R^{n}\); \(u(k)\) is the known control input, \(u\left( k \right) \in R^{n}\); A, B, and C are known time-varying real matrices with appropriate dimensions; \(w(k)\) and \(v(k)\) are white noise Gaussian sequences of uncorrelated random vectors with zero means and covariance matrices \(Q\) and \(R\), respectively; \(y(k)\) is the output variable.

In the real world, if a control object fails in a control system, the control algorithm will also be seriously affected. Supposing the failure happens in a generalized linear discrete-time system, to accurately analyze the fault information of the control system, the \(i\)th input of the control system with the fault can be represented as

$$u_{F}^{i} (k) = u(k)(1 - \gamma_{k}^{i} ),$$
(3)

where \(\gamma_{k}^{i}\) is the loss of control effectiveness, if \(\gamma_{k}^{i} = 0\), the control input is fault-free; if \(\gamma_{k}^{i} = 1\), the control input is outage. The matrix of the loss of the control effectiveness can be defined as

$$\gamma_{k} = \left[ {\begin{array}{*{20}c} {\gamma_{k}^{1} } & {} & {} & {} & {} \\ {} & {\gamma_{k}^{2} } & {} & {} & {} \\ {} & {} & \cdots & {} & {} \\ {} & {} & {} & \vdots & {} \\ {} & {} & {} & {} & {\gamma_{k}^{n} } \\ \end{array} } \right]$$
(4)

Based on Eq. (4), the input of the control system with a fault can be further defined as

$$u_{F}^{{}} (k) = u(k)(I - \gamma_{k} )$$
(5)

Substituting Eq. (5) into Eq. (1), we obtain a generalized linear discrete-time system control model with faults, which can be defined as

$$x(k + 1) = Ax(k) + Bu(k)(I - \gamma_{k}^{{}} ) + w(k)$$
(6)
$$y_{d} (k) = Cx(k) + v(k)$$
(7)

Based on Eq. (6), we can derive

$$x(k + 1) = Ax(k) + Bu(k) - B\gamma_{k}^{{}} u(k) + w(k)$$
(8)

To facilitate the following discussion, \(\gamma_{k}\) can be defined in relation to the fault function. Thus, assuming \(f(k) = - B\gamma_{k} u(k)\), Eq. (8) can be rewritten as

$$x(k + 1) = Ax(k) + Bu(k) + f(k) + w(k),$$
(9)

where \(f(k)\) is the fault function of the uncertain generalized discrete-time linear system and can be described by

$$f(k) = [ - b_{1} \gamma_{k}^{1} \, - b_{2} \gamma_{k}^{2} \, - b_{3} \gamma_{k}^{3} \cdots - b_{n} \gamma_{k}^{n} ] \times \left[ {\begin{array}{*{20}c} {u_{k}^{1} } \\ {u_{k}^{2} } \\ \vdots \\ {u_{k}^{n} } \\ \end{array} } \right]$$
(10)

In the absence of the knowledge of \(w(k)\), \(f(k)\) can be modeled as follows:

$$f(k + 1) = f(k) + w(k)$$
(11)

A dedicated equivalent standard system with faults and unknown inputs can be expressed as follows:

$$x(k + 1) = Ax(k) + Bu(k) + f(k) + w(k)$$
(12)
$$y_{d} (k) = Cx(k) + v(k)$$
(13)
$$f(k + 1) = f(k) + w(k)$$
(14)

The aim of this paper is to present an optimal method for simultaneously estimating the state \(x(k)\) with a failure and the fault function \(f(k)\) of the generalized discrete-time linear system given by Eq. (12).

3 Design of Self-constructing Fuzzy UKF Controller

Since the fault characteristics are unknown, the self-constructing controller should be designed to take into account noise, interference, and dynamic performance changes. To achieve this, the self-constructing fuzzy UKF system was designed to control a system of unknown structure and unknown disturbances.

The self-constructing fuzzy UKF controller undergoes the following three phases:

  1. 1.

    During the first phase, consequences of the existing rules are adapted based on the plant’s output error.

  2. 2.

    In the second phase, a new membership function (MF) is added to controller inputs with faults, and as a result, new fuzzy rules are created. Then, consequences of all the rules must be adapted again.

  3. 3.

    For the third phase, the fault function and fault state are simultaneously estimated.

In this paper, the triangle membership function is introduced into the fuzzy inference system (FIS). Each fuzzy set contains three fuzzy subsets: fault, outage, and fault-free.

According to Eq. (11), since \(f\left( k \right)\) is a nonlinear function of arbitrary accuracy, the real matrix \(\theta \left( k \right)\) exists [26] and can be defined as

$$f(k) = \theta^{T} (k)\xi (k) + \varepsilon,$$
(15)

where \(\theta \left( k \right)\) is the consequence parameter matrix of the fuzzy rules; \(\varepsilon\) represents a nonnegative constant, \(1 > \varepsilon > 0\); \(\xi \left( k \right)\) is the fuzzy basis function.

Suppose the \(i\)th fuzzy rule is given as follows:

$$\begin{aligned} & {\text{if}}\;x_{1} (k)\;{\text{is}}\;A_{1}^{i} \;{\text{and }}x_{2} (k)\;{\text{is}}\;A_{2}^{i} \;{\text{and}} \ldots \;\,{\text{and}}\;x_{n} (k)\;{\text{is }}A_{n}^{i} \, \hfill \\ & {\text{then}}\;\;\hat{f}(k) = a_{1}^{i} (k) \hfill \\ \end{aligned},$$
(16)

where \(n\) is the number of inputs and \(A_{1}^{i}\) is the fuzzy set. In the FIS, multiplication reasoning and the weighted mean method can be used for fuzzy reasoning. Then, the output of the fuzzy system can be expressed as

$$\hat{f}(k) = \frac{{\sum\nolimits_{j = 1}^{r} {a_{1}^{i} (k)\prod\nolimits_{i = 1}^{n} {\mu_{{A_{j}^{i} }} (x_{j} (k))} } }}{{\sum\nolimits_{j = 1}^{r} {\prod\nolimits_{i = 1}^{n} {\mu_{{A_{j}^{i} }} (x_{j} (k))} } }},$$
(17)

where \(r\) is the number of fuzzy rules and \(\mu_{{A_{i}^{j} }}\) represents the membership function of the input variable.

According to Eqs. (15) and (17), the consequence parameter of fuzzy rule \(\theta \left( k \right)\) can be expressed as

$$\theta_{i} (k) = [a_{i}^{1} (k),a_{i}^{2} (k), \ldots ,a_{i}^{r} (k)]^{T}$$
(18)

The fuzzy basis function \(\xi \left( k \right)\) can be expressed as

$$\xi_{i} (k) = \frac{{\prod\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{j} }} (x_{i} (k)} )}}{{\sum\nolimits_{j = 1}^{r} {\prod\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{j} }} (x_{i} (k))} } }}$$
(19)

To improve the approximation accuracy of the self-constructing fuzzy system, the error between the output the control system with and without failure is considered as

$$e(k) = y(k) - y_{d} (k),$$
(20)

where \(e\left( k \right)\) is the error of the output state. According to Eq. (20) and supposing \(\varphi\) is the threshold of \(e\), \(\varphi = 10^{ - 5}\), if \(e > \varphi\), a new membership function will be added or not.

Assuming the number of the membership function is \(n\) in the self-constructing fuzzy system, in the case of \(e > \varphi\), a membership function of input variable \(x_{v}\) is added and the number of the membership functions will be \(n + 1\). Then, the number of fuzzy rules is added together, defined as

$$\sum\limits_{j = 1}^{N} {n_{i} } ,j \ne i$$
(21)

According to Eq. (16), the sum of the fuzzy rules can be expressed as

$$\begin{aligned} & {\text{if}}\;x_{1} (k)\;{\text{is}}\;A_{1}^{{i_{1} }} \;{\text{and}}\;x_{2} (k)\;{\text{is}}\;A_{2}^{{i_{2} }} \;{\text{and }} \ldots {\text{ and }}x_{v} (k)\;{\text{is}}\;A_{v}^{{i_{v} }} \, \hfill \\ & {\text{and}} \ldots {\text{and}}\;x_{n} (k)\;{\text{is}}\;A_{n}^{{i_{n} }} {\text{ then }}\hat{f}(k) = a_{{i_{1} i_{2} \ldots i_{N} }} \hfill \\ \end{aligned}$$
(22)

When a new fuzzy rule is added, the fuzzy consequence parameters should also be defined and initialized.

Assuming \(l\) fuzzy rules at time \({{t}}_{1}\), the fuzzy output can be expressed as

$$f(t) = \sum\limits_{i = 1}^{l} {a_{i} \xi_{i} }$$
(23)

At time \(t_{2}\), \(h\) fuzzy rules are added to the FIS, then the fuzzy output can be defined as

$$f(t_{1} + t_{2} ) = a_{{\text{new}}} \sum\limits_{i = l + 1}^{l + h} {\xi_{i} } + f(t),$$
(24)

where \(a_{{\text{new}}}\) is the new fuzzy consequence parameter.

Based on Eq. (23), the fuzzy output at time \(t_{1} + t_{2}\) can be expressed as

$$f(t_{1} + t_{2} ) = \sum\limits_{i = 1}^{l + h} {a_{i} \xi_{i} }$$
(25)

Substituting Eq. (25) into Eq. (24), we obtain

$$\sum\limits_{i = 1}^{l + h} {a_{i} \xi_{i} } = a_{{\text{new}}} \sum\limits_{i = l + 1}^{l + h} {\xi_{i} } + f(t)$$
(26)

Rearranging Eq. (26), we obtain

$$a_{{\text{new}}} = \frac{{f(t) - \sum\nolimits_{i = 1}^{l + h} {a_{i} \xi_{i} } }}{{\sum\nolimits_{i = l + 1}^{l + h} {\xi_{i} } }}$$
(27)

From Eq. (27), the consequence parameters of the fuzzy rules can be obtained. Since the self-constructing fuzzy system updates the fuzzy parameters in real time, a control law for the consequence parameters must be given. Furthermore, the control law of the consequence parameters can be defined as

$$\mathop a\limits^{.}_{i} = \left\{ {\begin{array}{ll} {\text{re}^{{\mathbf{T}}} \xi_{k} } &\;\; (u_{\text{L}} < a_{i} < u_{\text{U}} ) \ \text{or} \ (a_{i} = u_{\text{U}} \ \text{and} \ \text{re}^{T} \xi_{j} > 0) \\ {} & \;\; \text{or} \ (a_{i} = u_{\text{L}} \ \text{and} \ \text{re}^{T} \xi_{j} < 0) \\ 0 &\;\; {\text{others}} \\ \end{array} } \right. ,$$
(28)

where \(u_{\text{L}}\) and \(u_{\text{U}}\) are the lower and upper of self-constructing fuzzy system inputs, respectively; \(r\) is the control law parameter. Then, based on Eq. (12), (17), (22), and (23), the fuzzy output of the self-constructing system can be further expressed as

$$\begin{aligned} \hat{f}(k) &= \frac{{\sum\nolimits_{j = 1}^{R} {a_{1}^{i} (k)\prod\nolimits_{i = 1}^{n} {\mu_{{A_{j}^{i} }} (x_{j} (k))} } }}{{\sum\nolimits_{j = 1}^{r} {\prod\nolimits_{i = 1}^{n} {\mu_{{A_{j}^{i} }} (x_{j} (k))} } }} \hfill \\ & = \frac{{\sum\nolimits_{{j_{1} = 1}}^{{R_{1} }} {\sum\nolimits_{{j_{2 = 1} }}^{{R_{2} }} \cdots } \sum\nolimits_{{j_{N} = 1}}^{{R_{N} }} {a_{{i_{1} i_{2} \ldots i_{N} }} } \cdot \prod\nolimits_{m = 1}^{N} {\mu_{{A_{j}^{{i_{m} }} }} (x_{j} (k))} }}{{\sum\nolimits_{{i_{1} = 1}}^{{R_{1} }} {\sum\nolimits_{{i_{2 = 1} }}^{{R_{2} }} \cdots } \sum\nolimits_{{i_{N} = 1}}^{{R_{N} }} {\prod\nolimits_{m = 1}^{N} {\mu_{{A_{j}^{{i_{m} }} }} (x_{j} (k))} } }} \hfill \\ \end{aligned},$$
(29)

where \(R\) is the total number of fuzzy rules, \(\mu_{{A_{i}^{j} }}\) represents the membership functions of the input variables, and \(N\) is the number of the fuzzy input variables.

As seen from Eq. (29), the output of the self-constructing system depends not only on the fuzzy system parameters but also on the system inputs. From Eqs. (10), (11), and (12), it is clear that the fault function \(f(k)\) can only be estimated using one-step delayed estimation. More precisely, the estimation problem presented in this paper must focus on acquiring the state estimate \(\hat{x}_{k|k}\).

True values of the states can be estimated by applying the UKF, which is a nonlinear transformation-unscented transformation (UT) [27]. A set of weighted sigma points is chosen deterministically such that the sample mean and sample covariance of the points match those of the a priori distribution. The nonlinear function is applied to each point in turn to yield the transformed samples, and the predicted mean and covariance are calculated from the transformed samples.

Next, the procedure to estimate the state \(x_{k}\) using the UKF is described. According to Eq. (12), in the case of \(k = 0\), the mathematical expectation and the covariance of the system state \(x_{0}\) can be given, respectively, as follows:

$$\hat{x}_{0} = E[x_{0} ]$$
(30)
$$p_{0} = E[(x_{0} - \hat{x}_{0} ) \times (x_{0} - \hat{x}_{0} )^{T} ],$$
(31)

where \(E\left[ \,\right ]\) is the mathematical expectation of the state at time \(k\) and \(P_{0}\) is the covariance.

When \(k > 0\), sigma points are generated at time \(k\) as follows:

$$x_{k - 1} = [\hat{x}_{k - 1} \, \hat{x}_{k - 1} + \delta \sqrt {p_{k - 1} } \, \hat{x}_{k - 1} - \delta \sqrt {p_{k - 1} } ]$$
(32)
$$\delta = \sqrt {n + \lambda }$$
(33)
$$\lambda = \alpha^{2} (n + \beta ) - n,$$
(34)

where \(\delta\) and \(\lambda\) are proportional factors, \(n\) represents the dimension of the control system state, \(\alpha\) is the distribution of sigma points around \(\hat{x}\), \(0 \le \alpha \le 1\), and \(\beta > 0\).

The time update equations of the states, denoted by subscript \(t (k + 1|k)\), are used to obtain an a priori estimate by moving the state and error covariance one step forward in the time domain. According to Eqs. (12) and (13), the state estimator can be defined as

$$x_{k + 1|k} = Ax_{k|k} + Bu_{k} + f_{k|k} + w_{k}$$
(35)
$$\hat{x}_{k}^{ - } = \sum\limits_{i = 0}^{2L} {W_{m}^{(i)} x_{k + 1|k}^{(i)} }$$
(36)
$$P_{k}^{ - } = \sum\limits_{i = 0}^{2L} {W_{c}^{(i)} [x_{k + 1|k}^{(i)} - \hat{x}_{k}^{ - } ][x_{k + 1|k}^{(i)} - \hat{x}_{k}^{ - } ]^{T} + R^{w} }$$
(37)
$$(y_{d} )_{k + 1|k} = Cx_{k + 1|k} + v_{k}$$
(38)
$$(\hat{y}_{d} )_{k}^{ - } = \sum\limits_{i = 0}^{2L} {W_{m}^{(i)} (y_{d} )_{k + 1|k}^{(i)} }$$
(39)
$$W_{m}^{(0)} = \frac{\lambda }{n + \lambda }$$
(40)
$$W_{c}^{(0)} = \frac{\lambda }{n + \lambda } + 1 - \alpha^{2} + \beta$$
(41)
$$W_{c}^{(i)} = \frac{1}{2(n + \lambda )}$$
(42)
$$W_{m}^{(i)} = \frac{1}{2(n + \lambda )},$$
(43)

where \(W_{c}^{(i)}\) is the weight corresponding to each sigma point.

The measurement update equations of the states, denoted by subscript \((k + 1|k + 1)\), are used to obtain the a posteriori estimates based on feedback measurements into the a priori estimates.

The sigma points around state \(\hat{x}_{k}^{ - }\) and the covariance \(P_{k}^{ - }\), \(P_{{y_{d} }}\)\(P_{{xy_{d} }}\) at time k are updated using the following equations:

$$\hat{x}_{m}^{(i)} = \hat{x}_{m}^{ - } + \delta \sqrt {P_{k}^{ - } }$$
(44)
$$\hat{x}_{m}^{(i + L)} = \hat{x}_{m}^{ - } - \delta \sqrt {P_{k}^{ - } }$$
(45)
$$P_{{y_{d} }} = \sum\limits_{i = 0}^{2L} {W_{c}^{(i)} [(\hat{y}_{d} )_{k}^{(i)} - (\hat{y}_{d} )_{k} ][(\hat{y}_{d} )_{k}^{(i)} - (\hat{y}_{d} )_{k} ]^{T} + R^{v} }$$
(46)
$$P_{{xy_{d} }} = \sum\limits_{i = 0}^{2L} {W_{c}^{i} [\hat{x}_{k}^{(i)} - \hat{x}_{{_{k} }}^{ - } ][(\hat{y}_{d} )_{k}^{(i)} - (\hat{y}_{d} )_{k} ]^{T} + R^{v} },$$
(47)

where \(1 < i < L\).

The state estimation and error covariance estimation can be defined, respectively, as

$$\hat{x}_{k} = \hat{x}_{k}^{ - } + G_{k} ((y_{d} )_{k} - (\hat{y}_{d} )_{{_{k} }}^{ - } )$$
(48)
$$P_{k} = P_{k}^{ - } - G_{k} P_{{y_{d} }} G_{k}^{T},$$
(49)

where \(G_{k}\) is the Kalman gain matrix and \(G_{k} = P_{{xy_{d} }} P_{{y_{d} }}^{ - }\).

Based on this, the whole prediction–correction process is used to estimate the states as close as possible to their real values.

To more accurately estimate the fault information \(f\left( { k} \right)\) of the control system as Eq. (12), the fuzzy inputs of the membership function can be defined based on the error between the state estimation, using UKF \(\hat{x}_{k}\) and \(\tilde{x}_{k}\), as follows:

$$x_{e} (k) = \tilde{x}(k) - \hat{x}(k)$$
(50)

Substituting Eq. (50) into Eq. (29), we obtain the most accurate estimate of the fault function \(f\left( {k } \right)\), which can be further defined as follows:

$$\hat{f}(k) = \frac{{\sum\nolimits_{{j_{1} = 1}}^{{r_{1} }} {\sum\nolimits_{{j_{2 = 1} }}^{{r_{2} }} \ldots } \sum\nolimits_{{j_{N} = 1}}^{{r_{N} }} {f_{{i_{1} i_{2} \cdots i_{N} }} } \cdot \prod\nolimits_{m = 1}^{N} {\mu_{{A_{j}^{{i_{m} }} }} (x_{e}^{(j)} (k))} }}{{\sum\nolimits_{{i_{1} = 1}}^{{r_{1} }} {\sum\nolimits_{{i_{2 = 1} }}^{{r_{2} }} \ldots } \sum\nolimits_{{i_{N} = 1}}^{{r_{N} }} {\prod\nolimits_{m = 1}^{N} {\mu_{{A_{j}^{{i_{m} }} }} (x_{e}^{(j)} (k))} } }},$$
(51)

where \(\hat{f}(k) \in R^{n}\).

Thus, the fault function \(f(k)\) can be obtained as close as possible to its real values by using Eq. (51). Substituting Eq. (51) into Eq. (12), the generalized linear discrete-time system control model with faults and unknown inputs can be expressed as follows:

$$\tilde{x}(k + 1) = A\tilde{x}(k) + Bu(k) + \hat{f}(k) + w(k)$$
(52)
$$\tilde{y}_{d} (k) = C\tilde{x}(k) + v(k)$$
(53)
$$\hat{f}(k + 1) = \hat{f}(k) + w(k).$$
(54)

4 Fault Diagnosis Based on Fuzzy Clustering

In this section, the fault diagnosis is described in the case of the fault states of the self-constructing UKF control system.

Suppose set \(S\) can be defined as

$$S = \{ \hat{f}_{ik}^{{}} ,\hat{f}_{ik}^{{}} |\hat{f}_{ik}^{{}} \in \hat{f}(k))\},$$
(55)

where \(i = 1,2,3, \ldots ,m\); \(m\) is the dimension of the system state. Elements of set \(S\) are the fault information obtained in Sect. 3. The main purpose of fuzzy clustering is to divide similar data into groups. The optimization objective function can be defined as

$$J = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{k = 1}^{n} {u(f_{ik} )||\hat{f}_{ik} - c_{i} ||^{2} } } }}{{\sum\nolimits_{j = 1}^{n} {\mu (\hat{f}_{ik} )} }},$$
(56)

where \(c_{i}\) is a cluster center, and can be defined as

$$c_{i} = \frac{{\sum\nolimits_{k = 1}^{n} {(\hat{f}_{ik} u(\hat{f}_{ik} ))} }}{{\sum\nolimits_{k = 1}^{n} {u(\hat{f}_{ik} )} }},$$
(57)

where \(0 < u(\hat{f}_{ij} ) < 1\), and can be defined as

$$u(\hat{f}_{ij} ) = \frac{1}{{\sum\nolimits_{i = 1}^{m} {\left( {\frac{{||\hat{f}_{kj} - c_{kj} ||^{2} }}{{||\hat{f}_{ij} - c_{ij} ||^{2} }}} \right)} }}$$
(58)

The sum of the degrees of affiliation of a system state set is always equal to 1:

$$\sum\limits_{i = 1}^{m} {\mu (\hat{f}_{ik}^{{}} ) = 1},$$
(59)

where \(k = 1,2, \ldots ,n\).

Based on the above equations, fault diagnosis can be seen as a conditional minimization problem, given as

$${\text{find }}F_{ij} = \{ \hat{f}_{i1} ,\hat{f}_{i2} , \ldots ,\hat{f}_{ij} \}$$
(60)
$$\hbox{min} \, J = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {u_{ij} \left\|\hat{f}_{ij} - c_{i} \right\|^{2} } }$$
(61)
$${\text{S}}.{\text{T}}. \, \sum\limits_{i = 1}^{m} {\mu (f_{ij}^{{}} ) = 1},$$
(62)

where \(\hat{f}_{ij}\) is the real constant or vector and \(m\) is the dimension of the system state.

With these improvements, faults can be divided into three regions. According to the three regions, thresholds can be obtained, which are the parameters to diagnosis the faults. In the next section, a DC motor will be taken as an example to illustrate the usefulness of the self-constructing fuzzy UKF method.

5 Application of State Estimation and Fault Diagnosis to DC Motor

In this section, a DC motor was taken as an example to demonstrate the efficiency of the method.

5.1 Continuous-Time Model of DC Motor with Faults

The continuous-time model of a DC motor can be described by

$$J\frac{{{\text{d}}\omega (t)}}{{{\text{d}}t}} = - b\omega (t) + k_{i} i(t)$$
(63)
$$\frac{{{\text{d}}\theta (t)}}{{{\text{d}}t}} = \omega (t)$$
(64)
$$\frac{{{\text{d}}i(t)}}{{{\text{d}}t}} = - \frac{{R_\text{{a}} }}{{l_\text{{a}} }}i(t) - \frac{{k_{b} }}{{l_\text{{a}} }}\omega (t) + \frac{u(t)}{{l_\text{{a}} }}$$
(65)

The constraint equation is given by

$$R_\text{{a}} i(t) + k_{e} \omega (t) = au(t)$$
(66)

Variables in the above equations are defined as follows: \(l_\text{{a}}\) is the motor armature inductance, \(i\) is the current in the motor, \(u\) is the input voltage of the DC motor, \(\theta\) is the angular position, \(\omega\) is the motor speed, \(R_\text{{a}}\) is the motor armature resistance, \(b\) is the coefficient of viscous friction, \(J\) is the moment of inertia of the motor shaft, \(K_{e}\) is the back electromotive force constant, \(K_{i}\) is the back torque constant, \(a\) is the amplification constant.

Parameters of the DC motor used in the simulations are listed in Table 1.

Table 1 DC motor parameters
Full size table

In the simulations, disturbances from \(R_\text{{a}} , a, b\) were ignored and the armature inductance was assumed to be zero.

According to Eqs. (63)–(65), the continuous-time control model of the DC motor can be described as

$$\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & J & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{i}} \\ {\dot{\omega }} \\ {\dot{\theta }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_\text{{a}} }}{{l_\text{{a}} }}} & {\frac{{k_{e} }}{{l_\text{{a}} }}} & 0 \\ {k_{i} } & { - b} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} i \\ \omega \\ \theta \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{l_\text{{a}} }}} \\ 0 \\ 0 \\ \end{array} } \right]u(0)$$
(67)

The output current of the DC motor changes when there is a fault. Consequently, the motor’s fault information can be obtained via the output current. The output equation of the control system can be defined as

$$y = [1\, 0\, 0]\left[ {\begin{array}{*{20}c} i \\ \omega \\ \theta \\ \end{array} } \right]$$
(68)

By using the forward Euler method, the continuous-time DC motor model described by Eq. (67) can be simplified to yield a discrete-time descriptor system as follows:

$$\left[ {\begin{array}{*{20}c} {\frac{1}{T}} & 0 & 0 \\ 0 & {\frac{J}{T}} & 0 \\ 0 & 0 & {\frac{1}{T}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i(k + 1)} \\ {\omega (k + 1)} \\ {\theta (k + 1)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{1}{T} - \frac{{R_\text{{a}} }}{{l_\text{{a}} }}} & {\frac{{k_{e} }}{{l_\text{{a}} }}} & 0 \\ {k_{i} } & {\frac{1}{T} - b} & 0 \\ 0 & 0 & {\frac{1}{T}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i(k)} \\ {\omega (k)} \\ {\theta (k)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{l_\text{{a}} }}} \\ 0 \\ 0 \\ \end{array} } \right]u(0)$$
(69)
$$y(k) = [1\, 0\, 0]\left[ {\begin{array}{*{20}c} {i(k)} \\ {\omega (k)} \\ {\theta (k)} \\ \end{array} } \right],$$
(70)

where \(T = 1\) is the sampling time.

Here,

$$E = \left[ {\begin{array}{*{20}c} {\frac{1}{T}} & 0 & 0 \\ 0 & {\frac{J}{T}} & 0 \\ 0 & 0 & {\frac{1}{T}} \\ \end{array} } \right]\;\;\;\;\;A = \left[ {\begin{array}{*{20}c} {\frac{1}{T} - \frac{{R_\text{{a}} }}{{l_\text{{a}} }}} & {\frac{{k_{e} }}{{l_\text{{a}} }}} & 0 \\ {k_{i} } & {\frac{1}{T} - b} & 0 \\ 0 & 0 & {\frac{1}{T}} \\ \end{array} } \right]$$
$$B = \left[ {\begin{array}{*{20}c} {\frac{1}{{l_\text{{a}} }}} \\ 0 \\ 0 \\ \end{array} } \right]\;\;\;\;\;C = [1\, 0\, 0]$$
$$x(k) = [i(k) \, \omega (k) \, \theta (k)]^{T}$$

Then, the continuous-time DC motor model can be rewritten as

$$Ex(k + 1) = Ax(k) + Bu(k)$$
(71)
$$y(k) = Cx(k)$$
(72)

Since \(E\) is a full rank matrix, by multiplying both sides of Eq. (71) by \(E^{ - 1}\), the equation can be further simplified as

$$x(k + 1) = E^{ - 1} Ax(k) + E^{ - 1} Bu(k)$$
(73)

To monitor the fault, we assume the input is affected by additive faults. Based on Eq. (30), we can obtain the continuous-time model of a DC motor with fault as follows:

$$x(k + 1) = E^{ - 1} Ax(k) + E^{ - 1} Bu(k) + f(k),$$
(74)

where \(f(k) = - E^{ - 1} Bu(k)\gamma_{k} ,0 \le \gamma_{k} \le 1\).

5.2 Simulation Verification

According to Table 1, the system matrices of the DC motor model can be given as

$$E = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {0.01} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\;\;\;A = \left[ {\begin{array}{*{20}c} 0 & {0.125} & 0 \\ {0.25} & {0.95} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]$$
$$B = \left[ {\begin{array}{*{20}c} {0.5} \\ 0 \\ 0 \\ \end{array} } \right]\;\;\;u(0) = 220$$

Covariance matrices \(Q\) and \(R\) can be given as

$$Q = \left[ {\begin{array}{*{20}c} {1.440} & 0 & 0 \\ 0 & {1.440} & 0 \\ 0 & 0 & {1.440} \\ \end{array} } \right]\;\;\;R = 0.25$$

Parameters of the UKF can be given as

$$\alpha = 0.0001, \, \beta = 2.$$

The input of the system can be given as

$$x(0) = [9.432 \, - 0. 1 7 6 { } - 1. 2 4 0 ]$$
(75)

Substituting Eq. (75) into Eq. (16), the output of the self-constructing fuzzy system \(f(1)\) can be obtained. Then, based on Eqs. (30)–(32), the system state with fault \(\tilde{x}(1)\) and the output of control system \(\tilde{y}_{d} (1)\) can be obtained. Meanwhile, based on Eqs. (35)–(52), the state estimation \(\hat{x}(1)\) can also be obtained. Then, the error in estimated state \(x_{e} (1)\) can be further obtained based on Eq. (53).

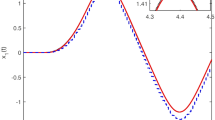
According to the principle of self-constructing fuzzy systems, \(x_{e} (1)\) will be the next input state. After repeating the fuzzy approach several times, the fault formation of current can be obtained according to the curve shown in Fig. 1.

Fig. 1
figure 1

The current fault curve

Full size image

As seen in Fig. 1, since faults are caused by many factors, the fault curve obtained using the proposed method is not a smooth curve but is irregular. At 180 steps, the fault curve shows excessive overshooting of the system, which suggests the state at step 180 is critical failure. Based on these results, the fault information of the system states can be obtained with high precision by adapting the self-constructing fuzzy UKF method, as illustrated in Fig. 1.

The current error of the system state is the error between the state estimation using UKF and the state estimated by the self-constructing method, presented in Fig. 2.

Fig. 2
figure 2

Current estimate error

Full size image

As shown in Fig. 2, large errors are present before 180 steps; however, after 180 steps, the error tends towards zero and is kept to within ± 0.02. The results suggest that the self-constructing fuzzy UKF method can be used to accurately estimate the system state. In the self-constructing fuzzy UKF system, the number of fuzzy rules changes along the curve is shown in Fig. 3.

Fig. 3
figure 3

Curve of fuzzy rule changes

Full size image

Figure 3 shows automatic changes in fuzzy rules within the fuzzy system. This suggests the structure of the self-constructing fuzzy UKF system is adaptively adjusted according to the fault information. As shown in Fig. 3, there are two fuzzy rules in the self-constructing fuzzy system before 360 step in the control system. When the system is stable, the number of the fuzzy rules is only 10.

5.3 Fault Diagnosis

According to the fault information presented in Fig. 1 and Eqs. (60)–(62), the fault information can be diagnosed, as presented in Fig. 4.

Fig. 4
figure 4

Fault regions

Full size image

As shown in Fig. 4, the fault information could be divided into three regions, corresponding to fault, outage, and fault-free. The fault information can be expressed as

$$F = \left\{ \begin{array}{ll} F < F_{1} & \quad {\text{fault-free}} \\ F_{1} \le F \le F_{2} & \quad {\text{fault }} \\ F > F_{2} & \quad {\text{outage}}\end{array} \right.,$$
(76)

where \(F_{1}\) and \(F_{2}\) are the parameters of the fault diagnosis. The parameters are positive constants when \(F_{1} < F_{2}\). Based on the simulation results, threshold values can be given as \(F_{1} = 0.3, \, F_{2} = 1\). Compared to the results presented in [14], parameters of the fault diagnosis in the present case were acquired by experiment and not expertise.

6 Conclusion

In this paper, a novel approach for integrated fault estimation, diagnosis, and state estimation was proposed for generalized linear discrete-time systems. First, parameters of the self-constructing fuzzy system, including the number of fuzzy rules and the fuzzy membership function, were adjusted in real time according to changes in the system state and fault information. Second, states with faults were approximated using either the self-constructing fuzzy system or UKF. Errors between the two estimated states were then obtained and used as fuzzy inputs for the self-constructing fuzzy system. Thus, the accuracy of approximating the fault information and estimation state was substantially improved substantially. Then, the fault information based on the self-constructing fuzzy UKF system was used to make the fault diagnosis. Finally, a DC motor was taken as an example to demonstrate the efficiency of the method. Compared to the preset work, the fault function and fault state were simultaneously estimated using the proposed method and the parameters of the fault diagnosis were acquired by experiment and not expertise.

Time-varying parameter perturbations corresponding to the nominal system matrices were not considered in this paper. Future research will investigate a self-constructing fuzzy system considering fault functions with parameter perturbations.