State and Fault Estimation for T–S Fuzzy Nonlinear Systems Using an Ensemble UKF

Abstract

This paper introduces a new filter based on a Takagi–Sugeno (T–S) fuzzy augmented ensemble unscented Kalman filter (FAEnUKF) for a class of nonlinear stochastic systems with multiplicative fault and noise. Multiplying a nonlinear term on the fault signal generates a non-Gaussian noise which cannot be optimally estimated by the Kalman filter. One way to resolve this problem is to transform the nonlinear system to several T–S fuzzy systems with Gaussian noise. Using the sector nonlinearity model, the nonlinear term can be derived as constant matrices for each fuzzy rule. Thus, fuzzy augmented UKFs (AUKFs) are designed for state and fault estimation. Using Lyapunov’s stability theory, the convergence conditions of the developed filter algorithm are presented as a theorem. In addition, the boundedness of the error covariance matrix of the proposed algorithm is discussed theoretically. Finally, selected illustrative examples to evaluate the effectiveness of the FAEnUKF are presented. Comparisons between the FAEnUKF and the augmented extended Kalman filter (AEKF) and the AUKF are made in a numerical example. The simulation results showed the robustness of the fuzzy ensemble UKF for modeling the non-Gaussian noise. Despite the increase in the number of calculations in this method, the root-mean-square error (RMSE) is less than other filters.

1 Introduction

Studies and developments, which have been made over the last few decades in the area of fault diagnosis, aim to improve the performance and reliability of industrial systems, and meet the environmental and safety requirements [6, 22, 54]. The fault is modeled as a signal or a function of system dynamics due to its effect on the system’s physics. If the fault is added to the system equations, it is called an additive fault [54, 55]. A multiplicative fault, which is usually a signal, is defined as a fault multiplied by a function of system dynamics [4, 22, 33, 57]. Fault estimation, which is used in the design of fault-tolerant control (FTC) systems and the course of maintenance for the equipment, is one of the crucial areas of studying the fault [22, 23, 25]. Fault estimation represents the value of the fault signal [6]. The dynamic model of the system, fault modeling, and system conditions have led to the introduction of various design methods for fault estimators. The estimators, which are divided into observer and filter, are designed in linear and nonlinear forms [9].

The most common observers for fault estimation include robust observers [15, 23, 54, 55], sliding mode observers (SMOs) [4, 25], adaptive observers [4, 23], and unknown input observers (UIOs) [52, 54, 57]. Robust observers have been used for systems with bounded parameters and functions where the optimization problem is solved by linear matrix inequalities (LMI) [54, 55]. Metaheuristic methods inspired by nature have been implemented as an auxiliary approach for optimizing and tuning the estimation methods. Some examples of such methods include ant colony, genetic algorithm (GA), bat algorithm, bee colony, levy flight, and whale optimization algorithm (WOA) [3, 16, 20, 30, 34]. The model-based method has been used for fault diagnosis in the electrohydraulic suspension system, which obtained the optimal point by the bat algorithm in the global system for the observer design [20]. The optimal Sugeno fuzzy controllers for wind turbine system with actuator fault using the WOA were presented in [30]. Also, the system parameters including time response, overshoot, and steady-state error were compared to those that have been achieved using the GA and gray wolf optimizer (GWO). Furthermore, the GA and the bee colony algorithms have also been employed to optimize the neural network coefficients in fault diagnosis [3]. The sliding mode has been implemented for uncertainty factors such as model, chaos, disturbance, and fault [4, 25, 44, 45]. SMO has been known as a robust observer approach for fault estimation [4, 25]. A robust adaptive SMO, which was used for the FTC of a single-link flexible joint robot system in [4], was presented based on the fuzzy model of the system with multiplicative fault. SMO was evaluated for the uncertain actuator and sensor faults in the active suspension systems for the design of the FTC [25]. The existence of disturbances and control delays in the wing flutter system was led to an adaptive observer for fault estimation and control design [23]. A UIO can be designed with algebraic and differential approaches for the system dynamic model [52, 54]. Unknown input can include disturbance, fault, or even noise. Also, a robust observer was designed for a system with unknown disturbance and additive fault using the ${H}_{\infty }$ performance [54]. In [57], a robust UIO was investigated in order to estimate multiplicative fault in a nonlinear system with unknown uncertainty and disturbance.

Stochastic systems use filters for fault estimation due to noise signals. The Kalman filter is a typical method in research and industrial applications [1, 5, 10, 17, 29]. The Kalman filter, which is optimal in the linear system with Gaussian noise, has been used for fault diagnosis [17]. A three-stage augmented Kalman filter was designed to estimate state, fault, and disturbance [5]. A two-stage exogenous Kalman filter was used to estimate the dynamics of an actuator time-varying fault in the attitude control system (ACS) [10]. A robust Kalman filter has been used for fault estimation when there is an uncertainty parameter in the stochastic system [29]. The EKF by Jacobian matrices estimates state variables of the nonlinear system where faults are modeled as additive and multiplicative [41]. The most useful Kalman filter for nonlinear systems is the UKF [11, 13, 31, 35, 48], and this filter and the EKF were compared to estimate the short-circuit fault in the permanent magnet synchronous generator (PMSG) [13]. One of the cases in which the UKF has been used is fault estimation in the ACS of satellite and spacecraft, which includes two-stage UKF [11] and adaptive UKF [31, 35, 48]. In [11], the two-stage UKF algorithm was presented to estimate the bias fault of the reaction wheel actuator. The adaptive UKF approach was introduced in [31] to improve the accuracy of the fault estimation performed on the reaction wheel. As noted earlier, the covariance matrix can be adapted to improve the estimation [35]. The adaptive UKF with the multiple-model adaptive estimation was performed for sensor fault estimation in a descriptor system [48]. The robust AUKF can be used to estimate unknown disturbances and faults [49]. A method based on the UKF was proposed to estimate the multiplicative fault in the nonlinear function of the system’s input and output. Using the Gaussian mixture model (GMM), the non-Gaussian noise was converted into several Gaussian noises [36].

The T–S fuzzy model has been used for fault estimation, developed based on fuzzy IF–THEN rules [4, 57]. A T–S locally linear model can be used for approximating nonlinear dynamics. A robust observer for the T–S systems has been introduced in [8, 12, 26, 27, 40, 56]. Based on the sensor and actuator faults estimation, the ${H}_{\infty }$ performance based on observer known as FTC has been designed [8, 12, 26, 40]. The design of the robust observer in the fuzzy dynamic system was performed due to disturbance [26] and unknown input [8]. In the permanent magnet DC motor [8], there is an uncertainty of the model and an unknown parameter in the system with noise and actuator fault. Fuzzy UIOs have been designed for a nonlinear system with an additive fault [27, 52, 56] and multiplicative fault [57]. The fault was modeled by the intermittent occurrence with the Bernoulli distribution in [37]. Since the norm of the fault signal was limited, an SMO was used for estimation. An adaptive observer was introduced to the design of the FTC, using the solution of Lyapunov inequality in a continuously stirred reactor system [47]. The idea of using Kalman filters in stochastic fuzzy systems for state and fault estimation was expressed in [38, 39, 42]. The T–S model described a nonlinear system using the Kalman filter for state and fault estimation in [39]. A descriptor Kalman filter was designed to estimate sensor and actuator multiplicative random faults for a nonlinear system with unknown dynamics [38].

Table 1 shows the system models and the performed fault estimation methods. This table shows the classification of references based on the system model (linear or nonlinear), the fault model (additive or multiplicative), the parameter multiplied by the fault, and the estimation method (observer or filter). In previous studies, a multiplicative fault was not fully discussed, and the fault was only multiplied by a function of state variables [4, 57]. On the other hand, in filter-based methods for fault estimation, the noise was assumed to be Gaussian, so the conventional Kalman filters have been used [5, 10, 11, 13, 17, 29, 31, 35, 41, 48, 49]. In closed-loop systems, the effect of the system output on the dynamic equations is related to the form of feedback. If the actuator fault appears due to a multiplicative fault, the fault signal is multiplied by a nonlinear function of the reference input and noise output. Thus, the non-Gaussian element is produced in the system model. In addition, the systems under study with fault are modeled using linear or nonlinear equations. In contrast, the T–S fuzzy method has been used to transform a nonlinear system into a linear model. This study introduces an estimator for a class of stochastic nonlinear systems with a multiplicative fault to eliminate non-Gaussian factors by T–S model and improve estimation. The main novelties and contributions of this work are as follows:

• 1. A class of nonlinear systems in which the fault is multiplied by a nonlinear function of the output has been considered.

• 2. An online fault estimator has been provided for T–S fuzzy model systems.

• 3. A Kalman filter has been introduced to estimate the state with a non-Gaussian process equation.

• 4. An ensemble fuzzy UKF whose stability has been proved is presented for fault estimation.

Table 1 Fault estimation methodologies

The structure of the paper is organized as follows. Section 2 introduces the system description with multiplicative faults. Section 3 describes the T–S fuzzy system and proposes a fuzzy UKF for fault estimation. In Sect. 3.1, the error dynamics and algorithm of the FAEnUKF are presented. Also, the computational load and complexity of the proposed algorithm are evaluated. The convergence proof of the error estimation is performed in Sect. 3.2, using the Lyapunov function. In Sect. 3.3, the fact that the covariance matrix as one of the parameters of filter performance has an upper bound is proved. Section 4 includes two numerical examples to demonstrate the effectiveness of the proposed estimator. In the first example, the performance of this method is evaluated by comparing against the AEKF and the AUKF. According to the simulation results of Example 1, the FAEnUKF method has been used as a filter for states and fault estimation in the inverted pendulum. Finally, the simulation results, discussion, and conclusions are presented in Sect. 5.

2 The Problem Statement and Preliminaries

Equation (1) represents a class of nonlinear time-varying discrete-time stochastic systems with multiplicative faults and additive noises, described as follows:

$$\begin{array}{c}{x}_{k+1}=f\left({x}_{k},{u}_{k}\right)+{F}_{1}\left({u}_{k},{y}_{k}\right){f}_{k}+{\omega }_{k}\\ {y}_{k+1}=h\left({x}_{k+1},{u}_{k+1}\right)+{F}_{2}\left({u}_{k+1},{x}_{k+1}\right){f}_{k+1}+{\vartheta }_{k+1}\end{array}$$

(1)

where ${x}_{k}\in {\mathbb{R}}^{n}$ is the state vector,${u}_{k}\in {\mathbb{R}}^{p}$ is the control input, and ${y}_{k}\in {\mathbb{R}}^{m}$ is the output vector at time $k$. $f\left({x}_{k},{u}_{k}\right)\in {\mathbb{R}}^{n}$ and $h\left({x}_{k},{u}_{k}\right)\in {\mathbb{R}}^{m}$ are nonlinear functions of the state variables and the control input and are differentiable concerning $x$ and $u$. ${f}_{k}$ is the multiplicative fault vector. The dynamic matrix ${F}_{1}\left({u}_{k},{y}_{k}\right){f}_{k}$ displays the actuator and component faults, and the matrix ${F}_{2}\left({u}_{k},{x}_{k}\right){f}_{k}$ displays the sensor fault. The fault dynamic is generated by [5, 49]:

$${f}_{k+1}={f}_{k}+{\epsilon }_{k}$$

(2)

The process noise ${\omega }_{k}$, the measurement noise ${\vartheta }_{k}$, and the noise ${\epsilon }_{k}$ are zero-mean white noises with covariance matrices ${Q}_{{\omega }_{k}}$, ${R}_{k}$, and ${Q}_{{\epsilon }_{k}}$. ${f}_{0}$ is uncorrelated with the system noises. Another assumption is that the noise signals referred to in these equations are independent.

The dynamic model (1) is more comprehensive than the models which are represented for fault estimation. For example, the multiplicative fault was employed as a parameter which was multiplied in the dynamic of the three-tank system [22] or as a multiplicative signal which was multiplied in the dynamic function of the state variables in the single-link flexible joint robot arm [4]. To achieve a physical model (1), we can allude to closed-loop systems with noisy output feedback.

Considering the system model (1) and inserting the measurement function into the process equation, the process equivalent noise will be a non-Gaussian noise as follows [36]:

$${\mathcal{W}}_{k}={F}_{1}\left({u}_{k},h\left({x}_{k},{u}_{k}\right)+{F}_{2}\left({u}_{k},{x}_{k}\right){f}_{k}+{\vartheta }_{k}\right){f}_{k}+{\omega }_{k}$$

This noise is a nonlinear function of the states, the fault, and the system noises. As mentioned, the UKF may not work correctly for this class of systems. The solution presented in the next section is to use a T–S fuzzy model to convert this non-Gaussian noise factor into Gaussian noise.

Remark 1

The nonlinear system (1) should satisfy the nonlinear observability rank condition.

3 State and Fault Estimator Design

According to the definition and hypothesis of the system model (1), we state the principles of the proposed filter design based on the UKF for the state variables and the multiplicative fault estimation. The augmented state vector is defined as ${X}_{k}=\left[\begin{array}{c}{{X}_{e1}}_{k}\\ {{X}_{e2}}_{k}\end{array}\right]=\left[\begin{array}{c}{x}_{k}\\ {f}_{k}\end{array}\right]$, and the dynamic system (1) can be rewritten as follows:

$$\begin{array}{c}{X}_{k+1}=\left[\begin{array}{c}f\left({{X}_{e1}}_{k},{u}_{k}\right)+{F}_{1}\left({u}_{k},{y}_{k}\right){{X}_{e2}}_{k}\\ {{X}_{e2}}_{k}\end{array}\right]+\left[\begin{array}{c}{\omega }_{k}\\ {\epsilon }_{k}\end{array}\right]\\ {y}_{k+1}=h\left({{X}_{e1}}_{k+1},{u}_{k+1}\right)+{F}_{2}\left({u}_{k+1},{{X}_{e1}}_{k+1}\right){{X}_{e2}}_{k+1}+{\vartheta }_{k+1}\end{array}$$

(3)

Now to use the UKF to estimation the system model (3), we convert the model into a usable model with Gaussian noise.

3.1 T–S Fuzzy Model

Using sector nonlinearity transformation, the nonlinear function ${F}_{1}\left({u}_{k},{y}_{k}\right)$ is converted into a constant matrix ${E}_{i}$ for each fuzzy set. A T–S fuzzy model for the process Eq. (3) can be obtained under the following condition [42, 57]:

$$\begin{array}{c}{R}^{i}:\mathrm{IF} {\theta }_{1}\left(u,y\right)\, \mathrm{is} \,{\mathcal{M}}_{1}^{i},\dots ,{\theta }_{m}\left(u,y\right)\, \mathrm{is} \,{\mathcal{M}}_{m}^{i} , \\ {\text {THEN}}\,{X}_{k+1}=\left[\begin{array}{c}f\left({{X}_{e1}}_{k},{u}_{k}\right)+{E}_{i}{{X}_{e2}}_{k}\\ {{X}_{e2}}_{k}\end{array}\right]+\left[\begin{array}{c}{\omega }_{k}\\ {\epsilon }_{k}\end{array}\right]\end{array}$$

where $i=1,\dots , r$ is the number of fuzzy rules, ${\mathcal{M}}_{m}^{i}$ is the fuzzy set, and ${\theta }_{m}\left(u,y\right)$ is the premise variable.

The final outputs of nonlinear T–S fuzzy systems are inferred as follows:

$$\begin{aligned} {X}_{k+1}=\sum_{i=1}^{r}{h}_{i}\left(\theta \left(u,y\right)\right)\left(\left[\begin{array}{c}f\left({{X}_{e1}}_{k},{u}_{k}\right)+{E}_{i}{{X}_{e2}}_{k}\\ {{X}_{e2}}_{k}\end{array}\right]+\left[\begin{array}{c}{\omega }_{k}\\ {\epsilon }_{k}\end{array}\right]\right)\\ {y}_{k+1}=h\left({{X}_{e1}}_{k+1},{u}_{k+1}\right)+{F}_{2}\left({u}_{k+1},{{X}_{e1}}_{k+1}\right){{X}_{e2}}_{k+1}+{\vartheta }_{k+1}\end{aligned}$$

(4)

where $\theta \left(u,y\right)=\left[{\theta }_{1}\left(u,y\right), {\theta }_{2}\left(u,y\right),\dots ,{\theta }_{m}\left(u,y\right)\right]$ is the premise variable vector and ${h}_{i}\left(\theta \left(u,y\right)\right)$ is the normalized membership function defined as

$$\begin{array}{c}\begin{array}{cc}\forall i\in \left\{1,\dots ,r\right\}& 0<{h}_{i}\left(\theta \left(u,y\right)\right)\le 1\end{array}\\ \sum_{i=1}^{r}{h}_{i}\left(\theta \left(u,y\right)\right)=1\end{array}$$

By simplifying (4), Eq. (5) will be obtained:

$$\begin{array}{c}{X}_{i,k+1}=\left[\begin{array}{c}f\left({{X}_{e1}}_{k},{u}_{k}\right)+{E}_{i}{{X}_{e2}}_{k}\\ {{X}_{e2}}_{k}\end{array}\right]+\left[\begin{array}{c}{\omega }_{k}\\ {\epsilon }_{k}\end{array}\right]={F}_{i}\left({X}_{k},{u}_{k}\right)+{{\omega }_{eq}}_{k}\\ {y}_{k+1}=H\left({X}_{k+1},{u}_{k+1}\right)+{\vartheta }_{k+1}\end{array}$$

(5)

The nonlinear function ${F}_{i}\left({X}_{k},{u}_{k}\right)$ states that for any fuzzy rule $i$, there is a nonlinear system. This method eliminates the dependence of the process noise on the state variables. The mean and covariance of ${{\omega }_{eq}}_{k}$ will be as follows:

$$\begin{array}{c}E\left\{{{\omega }_{eq}}_{k}\right\}=E\left\{\left[\begin{array}{c}{\omega }_{k}\\ {\epsilon }_{k}\end{array}\right]\right\}={\left[\begin{array}{c}0\\ 0\end{array}\right]}_{n+1\times 1}\\ cov\left({{\omega }_{eq}}_{k}\right)=E\left\{{{\omega }_{eq}}_{j}{{{\omega }_{eq}}_{l}}^{T}\right\}={\left[\begin{array}{cc}{Q}_{{\omega }_{k}}& 0\\ 0& {Q}_{{\upepsilon }_{\mathrm{k}}}\end{array}\right]}_{n+1\times n+1}={{Q}_{eq}}_{k}{\delta }_{j,l}\end{array}$$

(6)

where ${\delta }_{j,l}$ denotes the Kronecker delta function, and when $j=l$, ${\delta }_{j,l}=1$. The estimator for the nonlinear system (5) is considered as a UKF. With this proposed model, the ensemble UKF is designed for each fuzzy set, and when this method is integrated, it provides estimated states.

3.2 The FAEnUKF Algorithm

Considering the fuzzy form (5), for the augmented state estimation, the proposed fuzzy UKF algorithm is expressed as follows:

Step 1 The estimation initial values of the augmented system state and their covariance matrix are considered as $\hat{X}_{0} and \hat{P}_{{X_{0} }} .$

Step 2 The $(2(n+1)+1)$ sigma points ${\chi }_{k}$ are generated as follows [46]:

$$\begin{array}{c}{{\chi }_{k}}^{\left(0\right)}={\widehat{X}}_{k}\\ {{\chi }_{k}}^{\left(s\right)}={\widehat{X}}_{k}+{\left[\sqrt{\left(n+1+\lambda \right){\widehat{P}}_{k}}\right]}_{s}\\ {{\chi }_{k}}^{\left(s+n\right)}={\widehat{X}}_{k}-{\left[\sqrt{\left(n+1+\lambda \right){\widehat{P}}_{k}}\right]}_{s}\end{array}s=\mathrm{1,2},\dots ,n+1$$

(7)

Here, $n+1$ is the number of augmented state variables and ${[]}_{s}$ represents the $s$th real row of the matrix square root.

Step 3 The update sigma points ${\widehat{X}}_{i,\left.k+1\right|k}$ that are obtained for each fuzzy rule in the dynamic model (5) are as follows:

$${{\widehat{X}}_{i,\left.k+1\right|k}}^{(s)}={F}_{i}\left({{\chi }_{k}}^{(s)},{u}_{k}\right),s=\mathrm{0,1},\dots ,2(n+1)$$

(8)

The augmented state prediction and covariance matrix are calculated by the process noise:

$${\widehat{X}}_{i,\left.k+1\right|k}=\sum_{s=0}^{2(n+1)}{w}_{s}^{\left(m\right)}{{\widehat{X}}_{i,\left.k+1\right|k}}^{(s)}$$

(9)

$$ \hat{P}_{{X_{{i,\left. {k + 1} \right|k}} }} = \mathop \sum \limits_{s = 0}^{{2\left( {n + 1} \right)}} w_{s}^{\left( c \right)} \left( {\hat{X}_{{i,\left. {k + 1} \right|k}}^{\left( s \right)} - \hat{X}_{{i,\left. {k + 1} \right|k}} } \right)\left( {\hat{X}_{{i,\left. {k + 1} \right|k}}^{\left( s \right)} - \hat{X}_{{i,\left. {k + 1} \right|k}} } \right)^{T} + Q_{{eq_{k} }} $$

(10)

Step 4 The state estimation of the nonlinear system (2) by defuzzification (4) is as follows:

$$ \begin{array}{*{20}c} {\hat{X}_{{\left. {k + 1} \right|k}} = \mathop \sum \limits_{i = 1}^{r} h_{i} \left( {\theta \left( {u,y} \right)} \right)\hat{X}_{{i,\left. {k + 1} \right|k}} } \\ {\hat{P}_{{X_{{\left. {k + 1} \right|k}} }} = \mathop \sum \limits_{i = 1}^{r} h_{i} \left( {\theta \left( {u,y} \right)} \right)\hat{P}_{{X_{{\left. {k + 1} \right|k}} }} } \\ \end{array} $$

(11)

Step 5 The measurement estimation updates ${\widehat{y}}_{\left.k+1\right|k}$ that are obtained from the measurement Eq. (5) are as follows:

$${{\widehat{y}}_{\left.k+1\right|k}}^{\left(s\right)}=H\left({{\widehat{X}}_{\left.k+1\right|k}}^{\left(s\right)},{u}_{k+1}\right),s=\mathrm{0,1},\dots ,2\left(n+1\right)$$

(12)

The predicted mean and covariance of the measurement signal are obtained by the measurement noise:

$${\widehat{Y}}_{\left.k+1\right|k}=\sum_{s=0}^{2(n+1)}{w}_{s}^{\left(m\right)}{{\widehat{y}}_{\left.k+1\right|k}}^{(s)}$$

(13)

$$ \hat{P}_{{Y_{k + 1} }} = \mathop \sum \limits_{s = 0}^{{2\left( {n + 1} \right)}} w_{s}^{\left( c \right)} \left( {\hat{y}_{{\left. {k + 1} \right|k}}^{\left( s \right)} - \hat{Y}_{{\left. {k + 1} \right|k}} } \right)\left( {\hat{y}_{{\left. {k + 1} \right|k}}^{\left( s \right)} - \hat{Y}_{{\left. {k + 1} \right|k}} } \right)^{T} + R_{{\vartheta_{k} }} $$

(14)

There is no correlation between the process noise and the measurement noise at different times, so:

$$ \hat{P}_{{XY_{k + 1} }} = \mathop \sum \limits_{s = 0}^{{2\left( {n + 1} \right)}} w_{s}^{\left( c \right)} \left( {\hat{X}_{{\left. {k + 1} \right|k}}^{\left( s \right)} - \hat{X}_{{\left. {k + 1} \right|k}} } \right)\left( {\hat{y}_{{\left. {k + 1} \right|k}}^{\left( s \right)} - \hat{Y}_{{\left. {k + 1} \right|k}} } \right)^{T} $$

(15)

The weights in (9), (10), (13–15), and the scaling parameter of the UKF algorithm are derived from [46].

Step 6 The UKF gain ${K}_{k}$, the estimated augmented state, and covariance are calculated as follows:

$$ K_{k + 1} = \hat{P}_{{XY_{k + 1} }} \hat{P}_{{Y_{k + 1} }}^{ - 1} $$

(16)

$${\widehat{X}}_{k+1}={\widehat{X}}_{\left.k+1\right|k}+{K}_{k+1}({y}_{k+1}-{\widehat{Y}}_{\left.k+1\right|k})$$

(17)

$$ \hat{P}_{{X_{{\left. {k + 1} \right|k}} }} = \hat{P}_{{X_{{\left. {k + 1} \right|k}} }} - K_{k + 1} \hat{P}_{{Y_{k + 1} }} K_{k + 1}^{T} $$

(18)

Repeat steps 2–6 for the next sample.

Remark 2

Proper selection of the membership functions and convergence of UKFs are the main difficulties of using this method. The number of UKFs depends on the number of fuzzy rules, which also affects the computational volume. Another point that discusses the algorithm is the implementation of the method, which is examined from the computational complexity of the algorithm [2, 43]. The order of computational complexity of the FAEnUKF is $\mathcal{O}({{n}_{a}}^{3})$ (see Appendix A), which is equal to the order of the EKF and UKF methods [1, 2, 43].

3.3 Stability of the FAEnUKF

In this section, we want to prove the stability by defining Lyapunov’s function from the estimation error of the proposed algorithm.

First, define the estimation error for the fuzzy model (4):

$${\tilde{X }}_{k+1}={X}_{k+1}-{\widehat{X}}_{k+1}=\sum_{i=1}^{r}{h}_{i}\left(\theta \left(u,y\right)\right)\left({X}_{i,k+1}-{\widehat{X}}_{i,k+1}\right)=\sum_{i=1}^{r}{h}_{i}\left(\theta \left(u,y\right)\right){\tilde{X }}_{i,k+1}$$

(19)

The prediction error is defined as

$${\tilde{X }}_{\left.k+1\right|k}={X}_{k+1}-{\widehat{X}}_{\left.k+1\right|k}$$

(20)

Assuming that the functions ${F}_{i}\left(X,u\right)$ and $H\left(X,u\right)$ are differentiable at ${\widehat{X}}_{k}$, according to [7], the Taylor series expansion can be presented as

$${X}_{k+1}=\sum_{i=1}^{r}{h}_{i}\left(\theta \left(u,y\right)\right) \left({F}_{i}\left({\widehat{X}}_{k}\right)+\nabla {F}_{i}\left({\widehat{X}}_{k}\right){\tilde{X }}_{k}+\dots +{B}_{i}{u}_{k}+{{\omega }_{eq}}_{k}\right)$$

(21)

The Jacobian matrices are as follows:

$${F}_{i,k}={\left.\frac{\partial {F}_{i}\left(X,u\right)}{\partial X}\right|}_{X={\widehat{X}}_{k}} ,{{B}_{i,k}=\left.\frac{\partial {F}_{i}\left(X,u\right)}{\partial u}\right|}_{u=\overline{u} }, {H}_{k}={\left.\frac{\partial H\left(X,u\right)}{\partial X}\right|}_{X={\widehat{X}}_{k}},{D}_{k}={\left.\frac{\partial H\left(X,u\right)}{\partial u}\right|}_{u=\overline{u} }$$

The prediction error can eventually be obtained by using (20) and (21) as

$${\tilde{X }}_{\left.i,k+1\right|k}={\alpha }_{i,k}{F}_{i,k}{\tilde{X }}_{k}+{{\omega }_{eq}}_{k}$$

(22)

From (5), the measurement error is as follows:

$${\tilde{y }}_{k+1}={\beta }_{k+1}{H}_{k+1}{\tilde{X }}_{\left.k+1\right|k}+{\vartheta }_{k+1}$$

(23)

The unknown diagonal matrices ${\alpha }_{i,k}$ and ${\beta }_{k}$ complete the first-order linearization model in (22) and (23). By using (22), the real covariance matrix of the augmented state is written as follows:

$$ P_{{X_{{\left. {i,k + 1} \right|k}} }} = E\left\{ {\tilde{X}_{{\left. {i,k + 1} \right|k}} \tilde{X}_{{\left. {i,k + 1} \right|k}}^{T} } \right\} = \alpha_{i,k} F_{i,k} \hat{P}_{{X_{k} }} F_{i,k}^{T} \alpha_{i,k} + \Delta P_{{X_{{\left. {i,k + 1} \right|k}} }} + Q_{{eq_{k} }} $$

(24)

The matrix $\Delta {{P}_{X}}_{\left.k+1\right|k}$ is the calculated difference between $\alpha_{i,k} F_{i,k} \hat{P}_{{X_{k} }} F_{i,k}^{T} \alpha_{i,k}$ and$E\left\{{\alpha }_{i,k}{F}_{i,k}{\tilde{X }}_{k}{{\tilde{X }}_{k}}^{T}{{F}_{i,k}}^{T}{\alpha }_{i,k}\right\}$. The predicted covariance matrix calculated in (10) will be as

$$ \hat{P}_{{X_{{_{{\left. {i,k + 1} \right|k}} }} }} = \alpha_{i,k} F_{i,k} \hat{P}_{{X_{{_{k} }} }} F_{i,k}^{T} \alpha_{i,k} + \hat{Q}_{{eq_{{_{i,k} }} }} $$

(25)

where the covariance matrix of $\hat{Q}_{{eq_{ik} }}$ is defined as $\hat{Q}_{{eq_{ik} }} = Q_{{eq_{k} }} + \Delta Q_{k} + \Delta P_{{X_{{i,\left. {k + 1} \right|k}} }} + \delta P_{{X_{{i,\left. {k + 1} \right|k}} }}$ and $\delta P_{{X_{{\left. {i,k + 1} \right|k}} }}$ is the difference between $P_{{X_{{\left. {i,k + 1} \right|k}} }}$ and $\hat{P}_{{X_{{\left. {i,k + 1} \right|k}} }}$ in (10) and (24). For the matrix $\hat{Q}_{{eq_{k} }}$ to always be positive, the matrix $\Delta Q_{k}$ is added to (10), following [50]. Similarly, the covariance matrices $\hat{P}_{{XY_{k} }}$ and $\hat{P}_{{Y_{k} }}$ can be written as follows:

$$ \hat{P}_{{XY_{k + 1} }} = \hat{P}_{{X_{{\left. {k + 1} \right|k}} }} \left( {\beta_{k + 1} H_{k + 1} } \right)^{T} + \Delta P_{{XY_{k + 1} }} + \delta P_{{XY_{k + 1} }} $$

(26)

$$ \hat{P}_{{Y_{k + 1} }} = \beta_{k + 1} H_{k + 1} \hat{P}_{{X_{{\left. {k + 1} \right|k}} }} \left( {\beta_{k + 1} H_{k + 1} } \right)^{T} + \Delta P_{{Y_{k + 1} }} + \delta P_{{Y_{k + 1} }} + R_{{\vartheta_{k + 1} }} $$

(27)

From [24], by introducing the stochastic matrix ${\phi }_{k}$ and the matrix ${\Theta }_{k}={\beta }_{k}{H}_{k} {({\phi }_{k})}^{T}$ from (26), $\hat{P}_{{XY_{k + 1} }} = \hat{P}_{{X_{{\left. {k + 1} \right|k}} }} \Theta_{k}^{T}$. The covariance matrix (18) and the FAEnUKF gain matrix (16) are obtained as follows:

$$ \hat{P}_{{X_{k + 1} }} = \hat{P}_{{X_{{_{{\left. {k + 1} \right|k}} }} }} - K_{k + 1} \left( {\hat{P}_{{X_{{_{{\left. {k + 1} \right|k}} }} }} \Theta_{k + 1}^{T} } \right)^{T} $$

(28)

$$ K_{k + 1} = \hat{P}_{{X_{{_{{\left. {k + 1} \right|k}} }} }} \Theta_{k + 1}^{T} \left[ {\Theta_{k + 1} \hat{P}_{{X_{{_{{\left. {k + 1} \right|k}} }} }} \Theta_{k + 1}^{T} + \hat{R}_{k + 1} } \right]^{ - 1} = \hat{P}_{{X_{{_{k + 1} }} }} \Theta_{k + 1}^{T} \hat{R}_{k + 1}^{ - 1} $$

(29)

where

$$ \hat{R}_{k + 1} = \hat{P}_{{Y_{{_{k + 1} }} }} - \Theta_{k + 1} \hat{P}_{{X_{{_{{\left. {k + 1} \right|k}} }} }} \Theta_{k + 1}^{T} $$

(30)

From the inverse of (28) and using (29), (31) is obtained as

$$ \hat{P}_{{X_{{_{k + 1} }} }}^{ - 1} = \hat{P}_{{X_{{_{{\left. {k + 1} \right|k}} }} }}^{ - 1} + \Theta_{k + 1}^{T} \hat{R}_{k + 1}^{ - 1} \Theta_{k + 1} $$

(31)

Lemma 1

[51] According to the system (4), the parameters ${h}_{i}\left(\theta \right)$ and $r$ are defined. Also, the matrix $\hat{P}_{{X_{k} }} \in {\mathbb{R}}^{n \times n}$ is a positive definite matrix, and ${X}_{i,k}\in {\mathbb{R}}^{n\times m}$ is the state vector. It can be followed as

$$ \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)X_{i,k}^{T} \hat{P}_{{X_{{_{k} }} }} \mathop \sum \limits_{j = 1}^{r} h_{j} \left( \theta \right)X_{j,k} \le \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)X_{i,k}^{T} \hat{P}_{{X_{{_{k} }} }} X_{i,k} $$

(32)

Lemma 2

[21] Assuming that matrices $\Psi ,\Upsilon>0$, the matrix inversion lemma is ${\Psi }^{-1}>{(\Psi +\Upsilon)}^{-1}$.

Lemma 3

Reif et al. [32] said that if ${\xi }_{k}$ is the stochastic variable and there is a stochastic $V\left({\xi }_{k}\right)$ as well as real numbers,${\upsilon }_{max} , {\upsilon }_{min} ,\mu >0$, and $0<\lambda \le 1$ such that $\forall k$

$${\upsilon }_{min}{\Vert {\xi }_{k}\Vert }^{2}\le V({\xi }_{k})\le {\upsilon }_{max}{\Vert {\xi }_{k}\Vert }^{2}$$

(33)

$$E\left[\left.V\left({\xi }_{k}\right)\right|{\xi }_{k-1}\right]-V\left({\xi }_{k-1}\right)\le \mu -\lambda V\left({\xi }_{k-1}\right)$$

(34)

are fulfilled, then the $V\left({\xi }_{k}\right)$ is bounded in mean square, that is,

$$E\left\{{\Vert {\xi }_{k}\Vert }^{2}\right\}\le \frac{{\upsilon }_{max}}{{\upsilon }_{min}} E\left\{{\Vert {\xi }_{0}\Vert }^{2}\right\}{\left(1-\lambda \right)}^{k}+\frac{\mu }{{\upsilon }_{min}} \sum_{p=1}^{P}{(1-\lambda )}^{p}$$

(35)

According to Assumptions 1 and 2 in [50], the assumptions are developed to prove the stability of the FAEnUKF as follows:

Assumption 1

There exist real value constants ${\alpha }_{i,min},{\alpha }_{i,max},{f}_{i,min},{f}_{i,max},{\beta }_{min},{\beta }_{max},{h}_{min},$

${h}_{max},{\theta }_{min},{\theta }_{max}\ne 0$ such that the following bounds on various matrices are satisfied for every $k>0$:

$$\begin{array}{c}{{f}_{i,min}}^{2}I\le {F}_{i,k}{{F}_{i,k}}^{T}\le {{f}_{i,max}}^{2}I\\ \begin{array}{c}{{\alpha }_{i,min}}^{2}I\le {\alpha }_{i,k}{{\alpha }_{i,k}}^{T}\le {{\alpha }_{i,max}}^{2}I\\ {h}_{min}\le \Vert {H}_{k}\Vert \le {h}_{max}\\ \begin{array}{c}{\beta }_{min}\le \Vert {\beta }_{k}\Vert \le {\beta }_{max}\\ {\theta }_{min}\le \Vert {\Theta }_{k}\Vert \le {\theta }_{max}\end{array}\end{array}\end{array}$$

(36)

Assumption 2

There are real numbers ${p}_{i,min},{p}_{i,max},{p}_{min},{p}_{max},{q}_{min},{q}_{max},{\widehat{q}}_{i,min},{\widehat{q}}_{i,max},$

${r}_{max},{\widehat{r}}_{min},{\widehat{r}}_{max}>0$ such that the matrix is bounded via:

$$ \begin{aligned} p_{i,\min } I & \le \hat{P}_{{X_{i,k} }} \le p_{i,\max } I \\ q_{\min } I & \le Q_{{eq_{k} }} \le q_{\max } I \\ \hat{q}_{i,\min } I & \le \hat{Q}_{{eq_{i,k} }} \le \hat{q}_{\max } I \\ R_{k} & \le r_{\max } I \\ \hat{r}_{\min } I & \le \hat{R}_{k} \le \hat{r}_{\max } I \\ \end{aligned} $$

(37)

Theorem 1

Let Assumptions 1 and 2 for fuzzy subsystems are satisfied, then the estimation error ${\tilde{X }}_{k}$ is bounded in mean square.

Proof

Consider the Lyapunov function candidate as

$$ V_{k + 1} \left( {\tilde{X}_{k + 1} } \right) = \left( {\tilde{X}_{k + 1} } \right)^{T} \left( {\hat{P}_{{X_{{_{k + 1} }} }} } \right)^{ - 1} \left( {\tilde{X}_{k + 1} } \right) $$

(38)

According to Assumption 2 and (11), the matrix $\hat{P}_{{X_{k + 1} }}$ is limited. So, the Lyapunov function is limited:

$$\frac{{\Vert {\tilde{X }}_{k+1}\Vert }^{2}}{{p}_{max}}\le {V}_{k+1}\left({\tilde{X }}_{k+1}\right)\le \frac{{\Vert {\tilde{X }}_{k+1}\Vert }^{2}}{{p}_{min}}$$

(39)

From Lemma 1 and estimation errors (19), (22), and (23), the following equation will be derived:

$$ \begin{aligned} V_{k + 1} \left( {\tilde{X}_{k + 1} } \right) & = \left( {\tilde{X}_{{\left. {k + 1} \right|k}} - K_{k + 1} \tilde{y}_{k + 1} } \right)^{T} \left( {\hat{P}_{{X_{{_{k + 1} }} }} } \right)^{ - 1} \left( {\tilde{X}_{{\left. {k + 1} \right|k}} - K_{k + 1} \tilde{y}_{k + 1} } \right) \\ & \le \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)\left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{k} }} } \right)^{T} \left( {\hat{P}_{{X_{k + 1} }} } \right)^{ - 1} \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{{}} }} } \right) \\ & - \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)\left[ {\beta_{k + 1} H_{k + 1} \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{k} }} } \right) + \vartheta_{k + 1} } \right]^{T}\\ &\quad \times K_{k + 1}^{T} \left( {\hat{P}_{{X_{k + 1} }} } \right)^{ - 1} \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{k} }} } \right) \\ & - \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{k} }} } \right)^{T} \left( {\hat{P}_{{X_{k + 1} }} } \right)^{ - 1}\\ &\quad \times K_{k + 1} \left[ {\beta_{k + 1} H_{k + 1} \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{k} }} } \right) + \vartheta_{k + 1} } \right] \\ & + \left[ {\beta_{k + 1} H_{k + 1} \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{k} }} } \right) + \vartheta_{k + 1} } \right]^{T} K_{k + 1}^{T} \left( {\hat{P}_{{X_{k + 1} }} } \right)^{ - 1}\\ & K_{k + 1} \left[ { \beta_{k + 1} H_{k + 1} \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} + \omega_{{eq_{k} }} } \right) + \vartheta_{k + 1} } \right] \\ \end{aligned} $$

(40)

By taking a conditional expectation from (40), and using the conditional expectation properties where $\left. {E\{ \tilde{X}_{k} } \right|\tilde{X}_{k} \} = \tilde{X}_{k} { }$[28], it can be shown that

$$ \begin{gathered} E\left\{ {\left. {V_{{k + 1}} \left( {\tilde{X}_{{k + 1}} } \right)} \right|\tilde{X}_{k} } \right\} \hfill \\ \le E\left\{ \begin{gathered} \mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\left( {\alpha _{{i,k}} F_{{i,k}} \tilde{X}_{k} } \right)^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} \left( {\alpha _{{i,k}} F_{{i,k}} \tilde{X}_{k} } \right) \hfill \\ + \mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\left[ {\left( {\alpha _{{i,k}} F_{{i,k}} \tilde{X}_{k} } \right)^{T} \left[ \begin{gathered} \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{_{{k + 1}} }} }} } \right)^{{ - 1}} - \left( {\hat{P}_{{X_{{_{{k + 1}} }} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right]}\right. \hfill\\ \left.{\vphantom{\left[ \begin{gathered} \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{_{{k + 1}} }} }} } \right)^{{ - 1}} - \left( {\hat{P}_{{X_{{_{{k + 1}} }} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right]}\left( {\alpha _{{i,k}} F_{{i,k}} \tilde{X}_{k} } \right)\left| {\tilde{X}_{k} } \right.} \right] \hfill \\ \end{gathered} \right\} + \mu _{{k + 1}} \hfill \\ \end{gathered} $$

(41)

where ${\mu }_{k+1}$ is

$$\begin{gathered} \mu _{{k + 1}} \\ = E\left\{ {\omega _{{eq_{k} }} ^{T} \left[ \begin{gathered} \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} - \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ + \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} \hfill \\ \end{gathered} \right]\omega _{{eq_{k} }} }\right. \\ \quad \left.{ \vphantom{\left[ \begin{gathered} \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} - \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ + \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} \hfill \\ \end{gathered} \right]}+ \vartheta _{{k + 1}} ^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \vartheta _{{k + 1}} } \right\}\end{gathered} $$

(42)

Inserting (25) into (31), and using Lemma 2, for fuzzy sets with ${h}_{i}\left(\theta \right)\ne 0$, the first item in (40) may establish that

$$ \begin{gathered} \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)\left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} } \right)^{T} \left( {\hat{P}_{{X_{k + 1} }} } \right)^{ - 1} \left( {\alpha_{i,k} F_{i,k} \tilde{X}_{k} } \right) \hfill \\ = \tilde{X}_{k}^{T} \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)\left( {\alpha_{i,k} F_{i,k} } \right)^{T} \left( {\mathop \sum \limits_{i = 1}^{r} h_{j} \left( \theta \right)\hat{P}_{{X_{jk + 1} }} } \right)^{ - 1} \left( {\alpha_{i,k} F_{i,k} } \right)\tilde{X}_{k} \hfill \\ + \tilde{X}_{k}^{T} \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)\left( {\alpha_{i,k} F_{i,k} } \right)^{T} \Theta_{k + 1}^{T} \hat{R}_{k + 1}^{ - 1} \Theta_{k + 1} \left( {\alpha_{i,k} F_{i,k} } \right)\tilde{X}_{k} < rV_{k} \left( {\tilde{X}_{k} } \right) \hfill \\ + \tilde{X}_{k}^{T} \mathop \sum \limits_{i = 1}^{r} h_{i} \left( \theta \right)\left( {\alpha_{i,k} F_{i,k} } \right)^{T} \Theta_{k + 1}^{T} \hat{R}_{k + 1}^{ - 1} \Theta_{k + 1} \left( {\alpha_{i,k} F_{i,k} } \right)\tilde{X}_{k} \hfill \\ \end{gathered} $$

(43)

Focus on the second term in (41). Using (29) and Lemma 2, it can be shown that

$$ \begin{gathered} \tilde{X}_{k} ^{T} \mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\left\{ {\left( {\alpha _{{i,k}} F_{{i,k}} } \right)^{T} \left[ \begin{gathered} \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} K_{{k + 1}} ^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} \hfill \\ - \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} K_{{k + 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right]\left( {\alpha _{{i,k}} F_{{i,k}} } \right)} \right\} \hfill \\ \tilde{X}_{k} = \tilde{X}_{k} ^{T} \mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\left( {\alpha _{{i,k}} F_{{i,k}} } \right)^{T} \left[ \begin{gathered} - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \hfill \\ + \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right]\left( {\alpha _{{i,k}} F_{{i,k}} } \right)\tilde{X}_{k} \hfill \\ \end{gathered} $$

(44)

By inserting (43) and (44) into (41), (45) can be written as:

$$ \begin{gathered} \left\{ {\left. {V_{{k + 1}} \left( {\tilde{X}_{{k + 1}} } \right)} \right|\tilde{X}_{k} } \right\} - V_{k} \left( {\tilde{X}_{k} } \right) \hfill \\ \le \left( {r - 1} \right)\tilde{X}_{k} ^{T} \hat{P}_{{X_{k} }} ^{{ - 1}} \tilde{X}_{k} \hfill \\ + \tilde{X}_{k} ^{T} \mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\left( {\alpha _{{i,k}} F_{{i,k}} } \right)^{T} \left[ \begin{gathered} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hfill \\ + \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \hfill \\ - \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right] \hfill\\ \left( {\alpha _{{i,k}} F_{{i,k}} } \right)\tilde{X}_{k} + \mu _{{k + 1}} \hfill \\ \end{gathered} $$

(45)

Now, using ${\lambda }_{k+1}$ and ${\mu }_{max}$ that are introduced in Appendix B, the inequality (45) can be rewritten as follows:

$$E\left\{\left.{V}_{k+1}\left({\tilde{X }}_{k+1}\right)\right|{\tilde{X }}_{k}\right\}-{V}_{k}\left({\tilde{X }}_{k}\right)\le {\mu }_{max}-{\lambda }_{k+1}{V}_{k}\left({\tilde{X }}_{k}\right)$$

(46)

Therefore, Lemma 3 is applied and can be shown as

$$E\left\{{\Vert {\tilde{X }}_{k+1}\Vert }^{2}\right\}\le \frac{{p}_{max}}{{p}_{min}}E\left\{{\Vert {\tilde{X }}_{1}\Vert }^{2}\right\}{\left(1-{\lambda }_{min}\right)}^{k}+\frac{{\mu }_{max}}{{p}_{min}}\sum_{p=1}^{P}{(1-{\lambda }_{min})}^{p}$$

(47)

Finally, (47) is fulfilled to guarantee the boundedness of ${\tilde{X }}_{k+1}$.

Remark 3

The matrices ${F}_{i,k}$, ${\alpha }_{i,k}$, ${H}_{k}$, and ${\beta }_{k}$ in Assumption 1 are assumed to be bounded. These assumptions are also given in [24, 50]. This limitation is applied to estimate a finite physical system under (36) and (37) conditions. However, relatively significant changes in the diagonal matrices ${\alpha }_{i,k}$ and ${\beta }_{k}$ will affect the choice of ${\lambda }_{min}$, ${\mu }_{max}$ and the potential loss of stability.

Remark 4

The matrix $\hat{Q}_{{eq_{i,k} }}$ needs to be positively defined for the stability of the modified AUKF. The inequality (43) is obtained using Lemma 2 and knowing the positivity of the matrix $\hat{Q}_{{eq_{i,k} }}$. Also, the system noise covariance matrix $Q_{{eq_{k} }}$ and ${R}_{k}$ should be bounded.

Remark 5

To confirm the stability of Theorem 1, Assumptions 1 and 2 must be satisfied in that these inequalities depend on the number of fuzzy rules defined in (4).

3.4 Boundedness of the Error Covariance Matrix for the FAEnUKF

One of the performance criteria for filter design is the boundedness of the error covariance matrix [19, 28]. Based on Theorem 1, the estimation error of the proposed filter is bounded. This Sect. proves that the covariance matrix is bounded if the assumptions of Theorem 1, together with the condition of Theorem 2, are satisfied.

Lemma 4

[19] The matrices $\Psi ,\Upsilon\in {\mathbb{R}}^{n}$ and $\Psi ,\Upsilon>0$, then ${(\Psi +\Upsilon)}^{-1} >{\Psi }^{-1}-{\Psi }^{-1}\Upsilon{\Psi }^{-1}$.

Theorem 2

Suppose the linearized form of the nonlinear system (1), and there are real numbers in Assumptions 1 and 2, and real scalar ${\mathcal{P}}_{max}>0$ , also the matrix ${\Theta }_{k}$ are invertible, then the expectation of the covariance matrix will be bounded and $E\left\{ {\hat{P}_{{X_{k + 1} }} } \right\} \le {\mathcal{P}}_{\max } I$ .

The proof of Theorem 2 is given in Appendix C.

Remark 6

The matrix $E\left\{ {\hat{P}_{{X_{k} }} } \right\}$ is dependent on system dynamics and the covariance matrices $Q_{{eq_{k} }}$ and${R}_{k}$. According to Sect. 1, if the process noise is not converted to Gaussian noise, the upper bound of the covariance matrix is dependent on the state variables and fault signal and is not restricted.

4 Simulation Examples

Simulation examples are provided to verify the performance of the proposed fuzzy fault estimator scheme based on the UKF. In Example 1, the proposed scheme is evaluated using the EKF and the UKF. Also, in Example 2, the FAEnUKF method is implemented on the physical system of an inverted pendulum on a cart [14, 53], whose parameters are selected based on Reference [14]. To evaluate the effectiveness of the proposed method, MATLAB R2018b software and a computer with a CPU of 2.4 GHz and 8 GB installed memory (RAM) as the hardware have been used.

Example 1

Consider the following nonlinear discrete-time system with the multiplicative fault and additive Gaussian noises:

$$\begin{array}{c}{{x}_{1}}_{k+1}=\mathrm{sin}({{x}_{1}}_{k})\mathrm{cos}\left({{x}_{2}}_{k}\right)+{u}_{k}{f}_{k}+{{\omega }_{1}}_{k}\\ \begin{array}{c}{{x}_{2}}_{k+1}=\mathrm{cos}({{x}_{1}}_{k})\mathrm{cos}\left({{x}_{2}}_{k}\right)+{u}_{k}{{y}_{k}}^{2}{f}_{k}+{{\omega }_{2}}_{k}\\ {y}_{k+1}=\mathrm{sin}({{x}_{1}}_{k+1})\mathrm{sin}\left({{x}_{2}}_{k+1}\right)+{{x}_{1}}_{k+1}{f}_{k+1}+{\vartheta }_{k+1}\end{array}\end{array}$$

(48)

The nonlinear functions ${F}_{1}\left({u}_{k},{y}_{k}\right)=\left[\begin{array}{c}{u}_{k}\\ {u}_{k}{{y}_{k}}^{2}\end{array}\right]$ and ${F}_{2}\left({u}_{k},{x}_{k}\right)={{x}_{1}}_{k}$ are multiplied as matrix functions in the fault signal. By augmenting the fault as the state of the system, the following is obtained:

$$\begin{array}{c}{X}_{k+1}=\left[\begin{array}{c}\mathrm{sin}({{X}_{1}}_{k})\mathrm{cos}\left({{X}_{2}}_{k}\right)+{u}_{k}{{X}_{3}}_{k}\\ \mathrm{cos}({{X}_{1}}_{k})\mathrm{cos}\left({{X}_{2}}_{k}\right)+{u}_{k}{{y}_{k}}^{2}{{X}_{3}}_{k}\\ {{X}_{3}}_{k}\end{array}\right]+{{\varvec{\upomega}}}_{k}\\ {y}_{k+1}=\mathrm{sin}({{X}_{1}}_{k+1})\mathrm{sin}\left({{X}_{2}}_{k+1}\right)+{{X}_{1}}_{k+1}{{X}_{3}}_{k+1}+{\vartheta }_{k+1}\end{array}$$

(49)

${{\varvec{\upomega}}}_{k}=\left[\begin{array}{c}{{\omega }_{1}}_{k}\\ {{\omega }_{2}}_{k}\\ {\epsilon }_{k}\end{array}\right]$ and ${\vartheta }_{k}$ are zero-mean white noises with covariance matrices ${Q}_{{{\varvec{\upomega}}}_{k}}=0.01{I}_{3\times 3}$ and ${R}_{{\vartheta }_{k}}=0.01$. The input signal ${u}_{k}=5sin(0.05*pi*k/{T}_{s})$, and ${T}_{s}=0.5s$ is the sample time. The initial conditions are given by ${X}_{0}={\left[\begin{array}{ccc}1& 0.01& 2\end{array}\right]}^{T}$ and ${{P}_{X}}_{0}=0.1{I}_{3\times 3}$.

In Sect. 2, Eqs. (1) and (2) describe that the process equivalent noise ${\mathcal{W}}_{k}$ is non-Gaussian as can be seen in the distribution of the second element of this noise (${\mathcal{W}}_{2,k}$) in Fig. 1.

By defining the fuzzy sets (4) where $\theta \left(u,y\right)={u}_{k}{{y}_{k}}^{2}$ which is a premise variable, $\theta \left(u,y\right)$ is bounded to:

$$-5\le {u}_{k}\le 5,-24.37\le {y}_{k}\le 22.4$$

Using the polytopic transformation of the sector nonlinearity method and choosing the membership functions as ${h}_{1}\left(\theta \left(u,y\right)\right)=\overline{\theta }-\theta /\overline{\theta }-\underset{\_}{\theta }$ and ${h}_{2}\left(\theta \left(u,y\right)\right)=\theta -\underset{\_}{\theta }/\overline{\theta }-\underset{\_}{\theta }$, the premise variable will be $\theta \left(u,y\right)={h}_{1}(.)\underset{\_}{\theta }+{h}_{2}(.) \overline{\theta }$. Therefore, a local dynamic model as illustrated in (4) is established.

The proposed method FAEnUKF, the conventional EKF [18, 41], and the UKF [24, 46, 50] are simulated in Fig. 2. This figure shows the actual state vector ${{x}_{1}}_{k}$, ${{x}_{2}}_{k}$, and the fault ${f}_{k}$ and estimated values from each filter.

To evaluate the performance of the proposed method, compare the estimation error represented by the root-mean-square error (RMSE). The RMSE of the state vector with $N$ samples is calculated by

$$RMSE\left({X}_{k}\right)=\sqrt[2]{\frac{1}{N}\sum_{k=1}^{N}{({X}_{k}-{\widehat{X}}_{k})}^{2}}$$

(50)

The simulation results for the methods based on the Kalman filter are presented in Table 2. The estimation error depends on the system and noise model. The estimation error of the FAEnUKF and the AEKF is less than the AUKF, due to the presence of a conversion of the non-Gaussian noise ${\mathcal{W}}_{k}$ to Gaussian noise. The accuracy of the FAEnUKF is better than that of the AEKF method because it does not approximate the nonlinear system. The AEKF and the AUKF include non-Gaussian noise as a function of multiplying the states in the output noise, and in the AUKF, in addition to this noise, the second order of the output noise is multiplied by the states, which has negatively affected the estimation.

Table 2 Estimation error of the FAEnUKF, the AUKF, and the AEKF

Table 3 shows the mean and variance of the estimation error by performing 100 Monte Carlo simulations. The resulting high variance of the EKF is the derivative of the dynamic function. Also, the execution time of these filters can be seen in this table. As mentioned in Remark 2, the execution time of the FAEnUKF algorithm is longer due to the higher computational load. On the other hand, as presented in Table 4 the computational complexity of the FAEnUKF with two fuzzy rules is $\mathcal{O}(12{{n}_{a}}^{3})$.

Table 3 Performance benchmark of the FAEnUKF, the AUKF, and the AEKF

Table 4 Computational complexity for fuzzy UKF algorithm

In Fig. 3, the trace of the covariance matrix $\hat{P}_{{X_{k} }}$ for each method is shown. It is expected the Kalman filters will converge faster than the FAEnUKF, but due to the presence of nonlinear noise in the system model, the conventional Kalman filters converge less quickly and with more error.

Figure 4 shows the expectation of the covariance matrix $\hat{P}_{{X_{k} }}$ for the FAEnUKF. As presented in Theorem 2 and Remark 6, the covariance matrix is bounded. From (64), the upper bound is ${\mathcal{P}}_{max}=0.45$.

Example 2

In this example, the output feedback of the discrete-time inverted pendulum on a cart with the multiplicative actuator fault and additive sensor fault is considered:

$$\begin{array}{c}{{x}_{1}}_{k+1}={T}_{s}{{x}_{2}}_{k}+{{x}_{1}}_{k}+{{\omega }_{1}}_{k}\\ \begin{array}{c}{{x}_{2}}_{k+1}={T}_{s}\left(\frac{g\mathrm{sin}\left({x}_{1,k}\right)-\frac{aml{{x}_{2}}_{k}^{2}\mathrm{sin}\left(2{{x}_{1}}_{k}\right)}{2}-a\mathrm{cos}\left({{x}_{1}}_{k}\right){u}_{k}{f}_{k}}{\frac{4l}{3}-aml{\mathrm{cos}}^{2}({{x}_{1}}_{k})}\right)+{{x}_{2}}_{k}+{{\omega }_{2}}_{k}\\ {y}_{k+1}={{x}_{1}}_{k+1}+{f}_{k+1}+{\vartheta }_{k+1}\end{array}\end{array}$$

(51)

where ${{x}_{1}}_{k}$ is the angle of the pendulum from the vertical position and ${{x}_{2}}_{k}$ is the angular velocity. ${u}_{k}$ is the control signal, and the discrete-time PID controller gains are ${K}_{p}=200, {K}_{d}=20, {K}_{i}=50$, and filter time ${T}_{f}=0.002 s$. $g=9.8 m/{s}^{2}$ is the gravity acceleration, $m=2 kg$ is the pendulum mass, $M=8kg$ is the cart mass, $2l=1$ is the pendulum length, $a=1/(m + M)$, and ${T}_{s}=1ms$ is the sample time. The reference input is $y_{{rk}} = \frac{\pi }{2}$. The covariances of zero-mean noises are ${Q}_{{{\varvec{\upomega}}}_{k}}={10}^{-8}{I}_{3\times 3}$ and ${R}_{{\vartheta }_{k}}=0.0001$. The initial augmented state conditions are ${X}_{0}={\left[\begin{array}{ccc}1& 0& 0.5\end{array}\right]}^{T}$ and ${{P}_{X}}_{0}={10}^{3}{I}_{3\times 3}$.

Due to the presence of noise in the error signal and ${u}_{k}$, the non-Gaussian noise factor will be as follows:

$$\theta \left(u,y\right)=\frac{-a\mathit{cos}\left({{x}_{1}}_{k}\right){u}_{k}}{\frac{4l}{3}-aml{cos}^{2}\left({{x}_{1}}_{k}\right)}$$

where $\theta \left(u,y\right)\in [-\mathrm{0.06,0.01}]$ and the membership functions are chosen as ${h}_{1}\left(\theta \left(u,y\right)\right)=(0.01-\theta )/0.07$ and ${h}_{2}\left(\theta \left(u,y\right)\right)=\left(\theta +0.06\right)/0.07$. So, the T–S fuzzy model will be (4) and the system matrices are ${E}_{1}=\left[\begin{array}{c}0\\ -0.06\end{array}\right]$, ${E}_{2}=\left[\begin{array}{c}0\\ 0.01\end{array}\right]$.

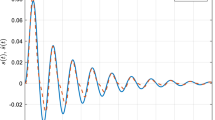
The reference and output signals in normal mode and faulty mode are shown in Fig. 5. The linear controller provides a stability in the system in the presence of a fault, but the steady-state error has increased. The control signal ${u}_{k}$ is shown in Fig. 6.

The actual states and fault and their estimates are shown in Fig. 7. The state estimation error is initially high due to sudden changes over time. Conversely, the estimation error also decreases as well. Figure 8 presents that the fuzzy filter estimates the actual fault signal ${f}_{k}$ with a small estimation error.

5 Conclusion

In this work, a novel optimal estimator was proposed for the state and fault estimation with a T–S fuzzy model based on the UKF for discrete-time nonlinear systems with a multiplicative fault. This method was investigated due to the influence of the non-Gaussian factor on the nonlinear system. The conventional UKF did not provide an appropriate estimator for the non-Gaussian system. However, the use of the UKF and the fuzzy model estimation for the state and fault improved the results. The Lyapunov function was employed to prove the stability of the proposed filter. The proof of the stability of this filter depends on the assumptions of the UKF and the number of fuzzy rules. Next, the covariance matrix was bounded in this method. The performance of the AEKF, the AUKF, and the FAEnUKF was demonstrated by numerical simulations. The AEKF and the AUKF showed a higher estimation error than the FAEnUKF due to the linearization of the nonlinear system model and non-Gaussian noise, respectively. The FAEnUKF was robust under the non-Gaussian noise changes. The fuzzy filter calculations were greater than the other two methods because this filter simultaneously calculated the ensemble UKFs and membership functions for each fuzzy set. The effects of this technique were illustrated for fault estimation in output feedback systems, e.g., the inverted pendulum system.

Fig. 1

The distribution of process equivalent noise (${\mathcal{W}}_{2,k}$)

Fig. 2

Augmented state estimation with the FAEnUKF, the AUKF, and the AEKF

Fig. 3

Convergence of the covariance matrix $\hat{P}_{{X_{k} }}$ with the FAEnUKF, the AUKF, and the AEKF

Fig. 4

Boundedness of the covariance matrix $\hat{P}_{{X_{k} }}$ with the FAEnUKF

Fig. 5

The reference and output signals in normal mode and faulty mode

Fig. 6

The control signal

Fig. 7

Augmented state estimation with the FAEnUKF

Fig. 8

The states and fault estimation error with the FAEnUKF

Appendices

Appendix A

According to [2, 43], the computational complexity for the proposed filter algorithm can be expressed in Table 4, where ${n}_{a}$, $p$, and $m$ are the sizes of the augmented state, input, and output. $r$ is the number of fuzzy rules.

Appendix B

In this Sect., ${\lambda }_{k}$ and ${\mu }_{max}$ are employed to get Lemma 3. Now, by definition ${\lambda }_{k}$ is given as follows:

$$ \begin{gathered} \lambda _{{k + 1}} = \tilde{X}_{k} ^{T} \\ \left[ \begin{gathered} \mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\left( {\alpha _{{i,k}} F_{{i,k}} } \right)^{T} \left[ \begin{gathered} \left( {\Theta _{{k + 1}} - \beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\left( {\Theta _{{k + 1}} - \beta _{{k + 1}} H_{{k + 1}} } \right) \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \left( {\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1,k}} }} \Theta _{{k + 1}} ^{T} + \hat{R}_{{k + 1}} } \right)^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right]\left( {\alpha _{{i,k}} F_{{i,k}} } \right) \hfill \\ + \left( {r - 1} \right)\hat{P}_{{X_{k} }} ^{{ - 1}} \hfill \\ \end{gathered} \right] \\ \tilde{X}_{k} /V_{k} \left( {\tilde{X}_{k} } \right) \end{gathered}$$

(52)

According to conditions (36) and (37), the following matrix inequality is obtained:

$$\sum_{i=1}^{r}{h}_{i}\left(\theta \right){\left({\alpha }_{i,k}{F}_{i,k}\right)}^{T}\left[{\left({\Theta }_{k+1}-{\beta }_{k+1}{H}_{k+1}\right)}^{T}{{\widehat{R}}_{k+1}}^{-1} \left({\Theta }_{k+1}-{\beta }_{k+1}{H}_{k+1}\right)\right]\left({\alpha }_{i,k}{F}_{i,k}\right)\ge 0$$

(53)

${\lambda }_{min}$ is chosen by Assumptions 1 and 2, and using (11) and (25):

$$ \begin{gathered} \lambda _{{k + 1}} V_{k} \left( {\tilde{X}_{k} } \right) \ge \lambda _{{\min }} V_{k} \left( {\tilde{X}_{k} } \right) \hfill \\ \triangleq \tilde{X}_{k} ^{T} \left[ \begin{gathered} \left( {r - 1} \right)p_{{\max }} ^{{ - 1}} \hfill \\ - \mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\alpha _{{i,\max }} ^{2} .f_{{i,\max }} ^{2} \beta _{{\max }} ^{2} .h_{{\max }} ^{2} \left( \begin{gathered} \mathop \sum \limits_{{j = 1}}^{r} h_{j} \left( \theta \right)\theta _{{\min }} ^{2} .p_{{\min }} .\alpha _{{j,\min }} ^{2} .f_{{j,\min }} ^{2} \hfill \\ + \theta _{{\min }} ^{2} .\hat{q}_{{j,\min }} + \hat{r}_{{\min }} \hfill \\ \end{gathered} \right)^{{ - 1}} \hfill \\ \end{gathered} \right]\tilde{X}_{k} \ge 0 \hfill \\ \end{gathered} $$

(54)

With respect to (34), the following condition must also be confirmed:

$${\lambda }_{k+1}{V}_{k}\left({\tilde{X }}_{k}\right)-{V}_{k}\left({\tilde{X }}_{k}\right)<0\to {\lambda }_{k+1}<1$$

(55)

Therefore,

$$ \begin{gathered} \lambda _{{k + 1}} V_{k} \left( {\tilde{X}_{k} } \right) - V_{k} \left( {\tilde{X}_{k} } \right) \hfill \\ = \tilde{X}_{k} ^{T} \left[ {\mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\left( {\alpha _{{i,k}} F_{{i,k}} } \right)^{T} \left[ \begin{gathered} \left( {\Theta _{{k + 1}} - \beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\left( {\Theta _{{k + 1}} - \beta _{{k + 1}} H_{{k + 1}} } \right) \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \left( {\Theta _{{k + 1}} \hat{P}_{{X_{{_{{k + 1\left| k \right.}} }} }} \Theta _{{k + 1}} ^{T} + \hat{R}_{{k + 1}} } \right)^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right]}\right. \\ \left.{\vphantom{\left[ \begin{gathered} \left( {\Theta _{{k + 1}} - \beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\left( {\Theta _{{k + 1}} - \beta _{{k + 1}} H_{{k + 1}} } \right) \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \left( {\Theta _{{k + 1}} \hat{P}_{{X_{{_{{k + 1\left| k \right.}} }} }} \Theta _{{k + 1}} ^{T} + \hat{R}_{{k + 1}} } \right)^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right]}\left( {\alpha _{{i,k}} F_{{i,k}} } \right) + \left( {r - 2} \right)\hat{P}_{{X_{{_{k} }} }} ^{{ - 1}} } \right]\tilde{X}_{k} \hfill \\ \end{gathered} $$

(56)

For (56), derived from conditions (36) and (37), we obtain

$$ \begin{gathered} \lambda _{{k + 1}} V_{k} \left( {\tilde{X}_{k} } \right) - V_{k} \left( {\tilde{X}_{k} } \right) \hfill \\ \le \tilde{X}_{k} ^{T} \left[ {\mathop \sum \limits_{{i = 1}}^{r} h_{i} \left( \theta \right)\alpha _{{i,\min }} ^{2} .f_{{i,\min }} ^{2} \left[ \begin{gathered} \left( {\theta _{{\max }} - \beta _{{\min }} .h_{{\min }} } \right)^{2} \hat{r}_{{\min }} ^{{ - 1}} \hfill \\ - \beta _{{\min }} ^{2} .h_{{\min }} ^{2} \left( {\mathop \sum \limits_{{j = 1}}^{r} h_{j} \left( \theta \right)\left( \begin{gathered} \theta _{{\max }} ^{2} .p_{{\max }} .\alpha _{{j,\max }} ^{2} .f_{{j,\max }} ^{2} \hfill \\ + \theta _{{\max }} ^{2} .\hat{q}_{{j,\max }} + \hat{r}_{{\max }} \hfill \\ \end{gathered} \right)} \right)^{{ - 1}} \hfill \\ \end{gathered} \right] + \left( {r - 2} \right)p_{{\min }} ^{{ - 1}} } \right]\tilde{X}_{k} < 0 \hfill \\ \end{gathered} $$

(57)

From (54) and (57), we get $0\le {\lambda }_{k+1}<1$.

Now, from (42), including noises ${{\omega }_{eq}}_{k}$ and ${\vartheta }_{k+1}$, and (29), ${\mu }_{k+1}$ will be:

$$ \begin{aligned} \mu _{{k + 1}} & = E\left\{ \begin{gathered} \omega _{{eq_{k} }} ^{T} \left[ \begin{gathered} \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ - \left( {\beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} - \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} + \hat{P}_{{X_{{k + 1}} }} ^{{ - 1}} \hfill \\ \end{gathered} \right]\omega _{{eq_{k} }} \hfill \\ + \vartheta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} ~\Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \vartheta _{{k + 1}} \hfill \\ \end{gathered} \right\} \\ & = E\left\{ \begin{gathered} \omega _{{eq_{k} }} ^{T} \left( {I - \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} ~\left( {I - \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} } \right)\omega _{{eq_{k} }} \hfill \\ + \vartheta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}} ^{T} \hat{R}_{{k + 1}} ^{{ - 1}} \vartheta _{{k + 1}} \hfill \\ \end{gathered} \right\} \\ \end{aligned} $$

(58)

Knowing that $tr\left(A+B\right)=tr\left(A\right)+tr(B)$ and Eq. (58) is scalar, traces are taken on both sides of (58)

$$ \begin{aligned} \mu _{{k + 1}} & = ~E\left\{ \begin{gathered} tr\left[ {\left( {I - \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}}^{T} \hat{R}_{{k + 1}}^{T} \beta _{{k + 1}} H_{{k + 1}} } \right)^{T} \left( {\hat{P}_{{X_{{k + 1}} }} } \right)^{{ - 1}} ~\left( \begin{gathered} I \hfill \\ - \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}}^{T} \hat{R}_{{k + 1}}^{{ - 1}} \beta _{{k + 1}} H_{{k + 1}} \hfill \\ \end{gathered} \right)} \right]Q_{{eq_{k} }} \hfill \\ + tr\left( {\hat{R}_{{k + 1}}^{{ - 1}} \Theta _{{k + 1}} \hat{P}_{{X_{{k + 1}} }} \Theta _{{k + 1}}^{T} \hat{R}_{{k + 1}}^{{ - 1}} } \right)R_{{k + 1}} \hfill \\ \end{gathered} \right\} \\ & \le \left\{ {\frac{{q_{{\max }} \left( {\hat{r}_{{\max }} - p_{{\min }} .\theta _{{\min }} .\beta _{{\min }} .h_{{\min }} } \right)^{2} }}{{p_{{\min }} .\hat{r}_{{\max }}^{2} }}L + \frac{{\theta _{{\max }} ^{2} .p_{{\max }} .r_{{\max }} }}{{\hat{r}_{{\min }}^{2} }}M} \right\} \\ \,\mathop = \limits^{\Delta } \mu _{{\max }} \\ \end{aligned} $$

(59)

Appendix C

This appendix presents the proof of Theorem 2.

Proof

For each fuzzy set, inserting (28) and (29) in (25) and rearranging the terms, we obtain

$$ \hat{P}_{{X_{{_{{\left. {i,k + 1} \right|k}} }} }} = \alpha_{i,k} F_{i,k} \left[ {\hat{P}_{{X_{{_{\left. k \right|k - 1} }} }} - \hat{P}_{{X_{{_{\left. k \right|k - 1} }} }} \Theta_{k}^{T} \left[ {\Theta_{k} \hat{P}_{{X_{{_{\left. k \right|k - 1} }} }} \Theta_{k}^{T} + \hat{R}_{k} } \right]^{ - 1} \Theta_{k} \hat{P}_{{X_{{_{\left. k \right|k - 1} }} }} } \right]F_{i,k}^{T} \alpha_{i,k} + \hat{Q}_{{eq_{{_{k} }} }} $$

(60)

By definition $\Psi = \Theta_{k} \hat{P}_{{X_{\left. k \right|k - 1} }} \Theta_{k}^{T}$ and$\Upsilon={\widehat{R}}_{k}$, and applying Lemma 4:

$$ \hat{P}_{{X_{{\left. {i,k + 1} \right|k}} }} \le \alpha_{i,k} F_{i,k} \left[ {\Theta_{k}^{ - 1} \hat{R}_{k} \Theta_{k}^{ - T} } \right]F_{i,k}^{T} \alpha_{i,k} + \hat{Q}_{{eq_{k} }} $$

(61)

Using Assumptions 1 and 2 for the upper bound (61), we obtain

$$ \hat{P}_{{X_{{_{{\left. {i,k + 1} \right|k}} }} }} \le \theta_{\min }^{ - 2} .\hat{r}_{\max } .\alpha_{i,\max }^{2} .f_{i,\max }^{2} + \hat{q}_{\max } I \triangleq \widehat{{p_{i} }}I $$

(62)

The upper bound of $\hat{P}_{{X_{{\left. {i,k + 1} \right|k}} }}$ is shown in (62). From (31) and Lemma 2, we obtain

$$ \hat{P}_{{X_{{_{k + 1} }} }} \le \hat{P}_{{X_{{_{{\left. {k + 1} \right|k}} }} }} \le \mathop \sum \limits_{i = 1}^{r} h_{i} \left( {\theta \left( {u,y} \right)} \right)\widehat{{p_{i} }}I $$

(63)

From ${h}_{i}\left(\theta \left(u,y\right)\right)\ge 0$, (18) and (63), the following is obtained:

$$ E\left\{ {\hat{P}_{{X_{{_{k + 1} }} }} } \right\} \le E\left\{ {\mathop \sum \limits_{i = 1}^{r} h_{i} \left( {\theta \left( {u,y} \right)} \right)\widehat{{p_{i} }}I} \right\} \triangleq {\mathcal{P}}_{\max } I $$

(64)

Thus, from Theorem 2, the upper bound ${\mathcal{P}}_{max}$ is obtained.