A Feasible Genetic Optimization Strategy for Parametric Interval Type-2 Fuzzy Logic Systems

Abstract

This paper presents an optimization strategy for interval type-2 fuzzy systems by using the conjunction operation called the (p)-monotone sum of t-norms. A direct-current servomotor control system is implemented to test the performance of the type-1, interval type-2 and interval type-2 fuzzy systems with parametric operations, under several noisy conditions. To rate them, a multi-objective fitness function, based on the main transient parameters, is proposed to ensure the genetic algorithm to find the best squared feedback signal, when a white noise signal with different amplitudes is added to the reference. In addition, the optimization strategy includes the parametric conjunction suppression to analyze how a rule-associated parametric conjunction directly influences on system performance. Such rule suppression can be used to reduce the number of parametric conjunction operations required to obtain an additional performance improvement. Experimental results of the servomotor control system show that parametric conjunctions used in the interval type-2 fuzzy logic system provide additional advantages over its nonparametric counterpart.

1 Introduction

The optimization of fuzzy systems with Mamdani-type rules is usually based on the tuning of membership functions of fuzzy sets. Several computing techniques have been used for that purpose, such as genetic algorithms (GA) [21, 40, 46], adaptive neural network-based fuzzy inference systems (ANFIS) [14, 25, 39], bee colony optimization (BCO) [3], ant colony optimization [35] and particle swarm optimization (PSO) [2].

In GA optimization of fuzzy systems, the fitness function definition is very important for success in search space. In the literature, several performance parameters are used to compute the fitness function. For instance, Park and Lee-Kwang [32] and Celikyilmaz and Turksen [13] use root-mean-square error to define the fitness function. Meanwhile, Hosseini et al. [21, 22] use the region of controllability and root-mean-square error.

Furthermore, a fitness function which considers the main transient parameters has not been widely evaluated in fuzzy systems optimization. However, in the proportional derivative and integrative control (PID control), this topic has been considered as a multi-objective fitness function (MOFF). For instance, in [6, 29] the authors use the integral of timed absolute error (ITAE) to rate the controller. In [16, 19, 47], the authors propose formulas that include overshoot, steady-state error, rise and settling times and other parameters.

The most important contribution that our proposal derives from is based on the advances of [37]. The multi-objective transient fitness function (MOTFF) provided is

$$\begin{aligned} f(\overrightarrow{k}) = \sum _{i = 1}^{J}w_{\mathrm{ci}}\left( \dfrac{f_i(\overrightarrow{k})}{\mu _i*\sum _{n = 1}^{J}(1/\mu _n)}\right) , \forall \sum _{i = 1}^{J}w_{\mathrm{ci}} = 1 \end{aligned}$$

(1)

where $w_{\mathrm{ci}}$ are the weights used to control the importance of all objective terms, $\dfrac{1}{\mu _i*\sum _{n = 1}^{J}(1/\mu _n)}$ is a compensated weighting factor and $f_i(\overrightarrow{k})$ is the ith objective function based on the PID constants vector $\overrightarrow{k}$ for tuning the controller. Here, the authors use the four main transient parameters to rate the controller performance. This means that there are four objectives $J = 4$ given in Eq. 1, where the maximum possible fitness value is 1 and the compensation factor $\dfrac{1}{\mu _i*\sum _{n = 1}^{J}(1/\mu _n)}$ depends on the variability of each transient parameter. In Sect. 5.1, our multi-objective transient fitness function is provided, based on Eq. 1.

Some optimization strategies can be found in the literature. For instance, Pelusi in [33] presents a genetic optimization strategy for a DC servomotor neuro-fuzzy system, claiming to reduce the rise and settling times by computing the error with the provided fitness function. A neural network is optimized, where every weight computes a rule and set distributions are also optimized with GA. Also, some other works provide in their strategy another single objective based on error measures, i.e., ITAE [29] for a type-1 fuzzy logic system (T1FLS) and for an interval type-2 fuzzy logic system (IT2FLS) [44].

The mutation probability, in any GA optimization strategy, may become the key for search success. Sometimes GA searches get stuck, and so the mutation probability is a solution for searching for other alternatives. Some authors [34, 42], provide some adaptive mutation rate function (AMRF) to change the mutation probability dynamically, i.e., during optimization process. Depending on the optimization constraints, the AMRF fulfills its main task: approximate to the global solution.

On the other hand, T1FLS optimization by using parametric conjunction operators (see Table 1) has been evaluated in some research [4, 5, 9]. Basically, in [9] a relatively simple parametric conjunction for controlling a vehicle with a neuro-fuzzy system, optimized by the gradient method, is proposed. Another study [1] tested three parametric conjunctions (Dubois, Dombi and Frank) in three different fuzzy systems.

The optimization of general type-2 fuzzy logic system (T2FLS) and IT2FLS represents a promise for constructing more robust controllers to operate in the presence of noise [7, 18, 28]. Although the fuzzy system optimization with parametric operations has been investigated, an influence analysis of the use of parametric conjunction operations in each rule has not been extensively explored [27]. Therefore, working in this direction, the main contributions of this paper are enlisted as follows:

• A genetic strategy is proposed for the IT2FLS optimization, containing parametric conjunction operations. This strategy let an expert design feasible fuzzy system, by reducing the search space to interval $\left[ -1, 1 \right]$, reducing the number of search parameters and reducing the parametric operations required to find the best performance.

• A multi-objective transient fitness function is proposed to rate the controller performance. This is based on the main transient performance parameters (Eq. 1).

• The use of a parametric conjunction called (p)-monotone sum of t-norms in the control of the DC servomotor system is presented as a complementary way to get additional performance improvement.

• Parametric conjunction suppression is proposed for reducing the number of parametric conjunctions required. An influence analysis for each rule is provided.

Table 1 Some classical parametric conjunction operations

2 Parametric Interval Type-2 Fuzzy Logic Systems

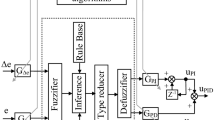
An IT2FLS, with parametric operators in its inference machine, differs from its nonparametric form, in the sense of having the ability of changing the way the decisions are taken [41]. To make difference between an IT2FLS with parametric conjunctions and a traditional IT2FLS, we will call it the parametric interval type-2 fuzzy logic system (PIT2FLS). A PIT2FLS structure is very similar to the general and IT2FLS (see Fig. 1).

Fig. 1

Parametric ITFLS structure

Let ${\mathbf{x }}$ be a set of p input variables and ${\mathbf{y }}$ be a set of q output variables in the fuzzy system. Also, for each $x_i \in {\mathbf{x }}$, $i=1, 2,\ldots , p$, there are $\delta _i$ premise sets denoted as $\left\{ {\tilde{A}}_i^1, {\tilde{A}}_i^2,\ldots , {\tilde{A}}_i^{\delta _i} \right\}$ and for each $y_j \in {\mathbf{y }}$, $j=1, 2,\ldots , q$, there are $\lambda _j$ consequent sets denoted as $\{ {\tilde{B}}_j^1, {\tilde{B}}_j^2,\ldots , {\tilde{B}}_j^{\lambda _j} \}$.

The system has L rules, where $l=1,2,\ldots ,L$ addresses each rule in the rule set. Now suppose that a fuzzy system is a MISO system (multiple input single output), where $(q=1)$ and in general there are consequent sets as much as the number of rules $\lambda = L$, which can be denoted as $\{ {\tilde{B}}^1, {\tilde{B}}^2,\ldots , {\tilde{B}}^L \}$. Therefore, each consequent set, due to each rule, resides in the same discourse universe (see Fig. 2).

Table 2 Complexity and operations of classical parametric conjunction operations

Fig. 2

Inference processes with parametric and nonparametric conjunction operations

Let $\mu _{{\tilde{I}}}(y)$ be the membership function that defines the resulting set called the inferred set (${\tilde{I}}$). This inferred MF can also be split into two membership functions: the upper membership function (UMF), ${\overline{\mu }}_{{\tilde{I}}}(y)$ and the lower membership function (LMF), ${\underline{\mu }}_{{\tilde{I}}}(y)$.

Equations 2 and 3 are the parametric versions of the IT2FLS inferred set. Notice that there are three arguments in the parametric conjunction operation represented with symbol T. First two arguments represent the membership values of the rule implied premise sets. Symbol ${\tilde{A}}_i^{k_1}$ represents the first operand in the parametric fuzzy conjunction, and symbol ${\tilde{A}}_h^{k_2}$ is the second operand, where $i,h \in [1, p] \in {\mathbb {N}}$; also $k_1 \in [1, \delta _i] \in {\mathbb {N}}$ and $k_2 \in [1, \delta _h] \in {\mathbb {N}}$. This means that a rule can pick up the first operand in the $k_1$th premise set from the ith input variable and pick up the second operand in the $k_2$th premise set from the hth input variable to perform the fuzzy operation. The third argument is the parameter $r_l$ which is associated with the lth rule in the rule set and therefore to the lth consequent set.

To this end, the inferred set FOU, i.e., $FOU({\tilde{I}})$, can be built from UMF and LMF functions defined in Eqs. 2 and 3.

$$\begin{aligned} {\overline{\mu }}_{{\tilde{I}}}(y)= & {} \bigvee _{l=1}^L {\overline{\mu }}_{{\tilde{B}}^l}(y) \wedge T \left( {\overline{\mu }}_{{\tilde{A}}_i^{k_1}}(x_i), {\overline{\mu }}_{{\tilde{A}}_h^{k_2}}(x_h), r_l \right) \end{aligned}$$

(2)

$$\begin{aligned} {\underline{\mu }}_{{\tilde{I}}}(y)= & {} \bigvee _{l=1}^L {\underline{\mu }}_{{\tilde{B}}^l}(y) \wedge T \left( {\underline{\mu }}_{{\tilde{A}}_i^{k_1}}(x_i), {\underline{\mu }}_{{\tilde{A}}_h^{k_2}}(x_h), r_l \right) \end{aligned}$$

(3)

where T in Eqs. 2 and 3 is the parametric firing strength of UMF and LMF, respectively. Assume that $\wedge$ is the minimum T-norm operation which is used to trim every consequent set in y and $\vee$ is the maximum S-norm operation which is used as the rule aggregation to complete the inference process.

This means that the resulting inferred set shape can be modified according to rule conjunction parameter values $r_l$, and consequently, the inferred crisp value can be modified according to expert needs.

This can be translated as a weighted action in the inference process, i.e., an expert system can modify the way premises are related to obtain a specific consequence (see Fig. 2, that the inferred set shape in PIT2FLS is different to the one in IT2FLS).

The following section explains the classical parametric conjunctions used in fuzzy systems and the advantages of the (p)-monotone sum conjunction proposed to tune the inference machine.

3 Parametric Conjunction Operations

A parametric inference machine is made of parametric operators. Each parametric operator receives in its input two operands and delivers a single output corresponding to the membership value obtained from the conjunction operation. Figure 2 shows that parameter r tunes the conjunction operator behavior.

The conjunction operation that can be used is the t-norm, and the disjunction can be the t-conorm (also called s-norm). Both are functions defined as $T,S:[0,1] \times [0,1] \rightarrow [0,1]$, which satisfy the axioms of commutativity, associativity, monotonicity and boundary conditions [26].

An interval type-2 inference machine is very similar to its corresponding type-1. The difference between T1 and T2 is that the T2 inference machine is comprised of two type-1 inference machines performing the same rule set, one for UMF and another for LMF. For instance, let ${\tilde{A}}_1^1$ and ${\tilde{A}}_2^3$ be the premise sets and ${\tilde{B}}_1^3$ their corresponding consequent set, as shown in Fig. 2. This means that,

$$\begin{aligned} \mu _{{\tilde{B}}_1^3}(y_1)=T\left( \mu _{{\tilde{A}}_1^1}, \mu _{{\tilde{A}}_2^3}, r \right) \forall r \in [0, 1] \end{aligned}$$

(4)

where T is a parametric conjunction with parameter r. As shown in Fig. 2, the parametric conjunction of Eq. 4 depends on r to control the way the relation is performed.

The computational complexity of classical parametric conjunctions have inspired several researchers to propose the use of simpler parametric conjunctions [8, 10, 36]. The following subsection provides information on the nonparametric conjunctions, classical parametric conjunctions and reduced in complexity parametric conjunctions used in this work, which involves the use of basic t-norms.

3.1 Nonparametric and Parametric Conjunctions

The following nonparametric t-norms [26] are the base of the parametric conjunction:

$$\begin{aligned} T_m(a,b)= {\mathrm{min}}(a, b) \end{aligned}$$

(5)

$$\begin{aligned} T_p(a,b)= ab \end{aligned}$$

(6)

$$\begin{aligned} T_b(a,b)= {\mathrm{max}}(0, a + b - 1) \end{aligned}$$

(7)

$$\begin{aligned} T_d(a,b)= \left\{ \begin{array}{ll} \textit{a}, &{} \textit{b} = 1 \\ \textit{b}, &{} \textit{a} = 1 \\ 0, &{} \hbox {else} \end{array} \right. \end{aligned}$$

(8)

where $T_m(a,b)> T_p(a,b)> T_b(a,b) > T_d(a,b) \forall a,b \in [0, 1]$. As is observed in Eqs. 5–8, the fuzzy membership degrees obtained from all these fuzzy intersection operators (minimum, product, bounded and drastic, respectively) depend only on the values of operands.

Until today, the most used t-norms in fuzzy control are $T_m$ and $T_p$, because they are simple and provide enough information to control a system adequately. However, this practice is not necessarily the best choice.

Other more complex operators have been studied and explored for their use in practical problems [23, 26]. In this case, a parameter has been added to intentionally change the system response. Unlike the nonparametric conjunctions, a parametric conjunction operation not only depends on the membership values of its operands, but also depends on one or more parameters that let an expert change the way the fuzzy intersection is going to be performed. All of them can be used in fuzzy control although its feasibility relies on its complexity. In fact, IT2FLS is complex for computation; so the integration of complex operators, like those in Table 1, would suppose an additional complexity increment.

These complex operators are obtained by specific functions called generators, which create different classes of operators, providing the possibility for designing rules based on parameterization.

Some of these are listed in Table 1, where a and b are the membership degrees of both operands, and r is the parameter that modifies the conjunction.

As shown in Tables 1 and 2, several parametric conjunctions involve the exponentiation operation of real numbers, having a complexity of up to $O(\log (\log n))$, which is computationally expensive when computing several rules. Although the rest of the parametric conjunction operators in Table 2 have a complexity of O(1) and a low number of arithmetic operations are required, these have involved the use of divisions and multiplications. As a consequence of this, a big rule set for a specific application may become impractical because its complexity can increase dramatically.

3.2 (p)-Monotone Sum

Before continuing, let us redefine p as the parameter of the (p)-monotone sum described in this subsection (as known in the literature). This parameter is referred to as the rule conjunction parameter r in the rest of this paper.

The (p)-monotone sum is defined in [11] as follows. Suppose we have four fuzzy conjunctions defined in [0, 1], such that $T_{11}(a,b) \le T_{12}(a,b) \le T_{22}(a,b)$, and $T_{11}(a,b) \le T_{21}(a,b) \le T_{22}(a,b)$ for all $a,b \in [0,1]$. Divide the domain $[0,1] \times [0,1]$ of the parametric conjunction T on four sections, as shown in Fig. 3, where p is a parameter, such that $0 \le p \le 1$. Assign to each $D_{ij}$, $i = 1,2$, the fuzzy conjunction $T_{ij}$.

Then, the (p)-monotone sum T is defined as follows:

$$\begin{aligned} T(a, b, p) = \left\{ \begin{array}{ll} T_{11}(a, b), &{} (a \le p) \wedge (b \le p) \\ T_{21}(a, b), &{} (a> p) \wedge (b \le p) \\ T_{12}(a, b), &{} (a \le p) \wedge (b> p) \\ T_{22}(a, b), &{} (a> p) \wedge (b > p) \\ \end{array} \right. \end{aligned}$$

(9)

Fig. 3

Partition of the domain of (p)-monotone sum on four sections

All four sections are defined by parameter p, so a monotone sum of conjunctions is able to behave in different ways, depending on this parameter (see Fig. 3). For instance, if $p = 0$, then its output will be $D_{22}$, or if $p = 1$ then its output will be $D_{11}$.

This means that each $T_{ij}$ in Eq. 9 may behave as a basic t-norm (Eqs. 5–8). This particularity makes the (p)-monotone sum a very practical parametric conjunction operator, for a big rule set or for hardware implementation. This is because the slowest operation involved, that could be computed, is a multiplication.

The following section describes the design of the fuzzy controller for a physical plant, which is going to be used to test the optimization strategy of this paper.

4 DC Servomotor Fuzzy Systems

The servomotor plant has been frequently used to test several control solutions [12, 24, 33]. Nguyen et al. describe in [30], an example of a physical plant of a direct-current servomotor (DC servo) and the corresponding fuzzy logic system that controls it.

According to Eq. 10, V(s) is the representation for the input voltage applied to servomotor terminals. The voltage magnitude is computed by a fuzzy logic system. Also, $\Theta (s)$ is the resulting rotor position in radians (rads) after applying a specific voltage to its input. This value is used as feedback, as can be seen in the closed loop in Fig. 4.

The servomotor laplace transfer function representation, that is going to be used in experiments by simulation in Sect. 6, is as follows:

$$\begin{aligned} G(s) = \frac{V(s)}{\Theta (s)}= \frac{0.5}{s^3 + 13.6667s^2 + 23.3487s} \end{aligned}$$

(10)

Table 3 The DC servomotor input and output variable ranges for the fuzzy systems evaluated in this work

Table 4 The DC servomotor PIT2FLS rule set

Fig. 4

A DC servomotor control system. A white noise generator is added to the signal reference to verify the performances of the T1, IT2 and IT2 fuzzy systems, under disturbances

In Fig. 4, the feedback of rotor position $\Theta$ is used to compute the multi-objective transient fitness function (MOTFF), as stated in Eq. 12, for each individual in the GA population.

PIT2FLS has two inputs: the error, e and the derivative of error or error change, c; also, it has a single output, i.e., the voltage, v applied to servomotor terminals.

Each variable has its own discourse universe range, as stated in Table 3, where there are only three sets.

Also, fuzzy system configuration is established in 9 rules, as shown in Table 3 and stated in [30]. Note the superscript number in each cell in Table  4 represents the rule number of each consequence.

Symbols NE, ZE, PE represent the linguistic terms “negative error,” “zero error” and “positive error,” respectively; NC, ZC, PC represent the “negative change,” “zero change” and “positive change,” respectively; also, the “negative voltage,” “zero voltage” and “positive voltage” is NV, ZV, PV, respectively.

The formula for the (p)-monotone sum of t-norms in Eq. 9 is initially used in all 9 rules, where every section is assigned the following t-norms: $D_{11}= T_d$ is the drastic t-norm, and $D_{12} = D_{21} = D_{22} = T_p$ is the product t-norm, as follows:

$$\begin{aligned} T_o(a, b, r) = \left\{ \begin{array}{ll} T_d(a, b), &{} (a \le r) \wedge (b \le r)\\ T_p(a, b), &{} \hbox {otherwise} \\ \end{array} \right. \end{aligned}$$

(11)

Assuming that maximal values of operands are normalized to 1, if parameter $r=0$, then the conjunction in Eq. 11 will behave as a product t-norm, but when parameter $r=1$, the drastic t-norm behavior will predominate.

The global behavior of this monotone sum helps to diminish the fuzzy implication between the two membership degrees of both premise.

This information is used to build the last part of the chromosome model (see Sect. 5.2), where every monotone sum parameter is produced by the GA and tested directly in the DC servomotor fuzzy controller.

Also, a detailed description about how our proposal plays an important role in GA is provided as follows.

5 Methodology

The optimization strategy presented in this paper provides a methodology for optimizing fuzzy systems, by using several resources that help an expert to reduce search space, to reduce the number of parameters to optimize, to rate the system response with a special multi-objective fitness function and to analyze how each rule parameter influences the system performance. This means that our methodology can be used with almost any genetic algorithm and fuzzy system that en expert prefers. Moreover, every optimization can be performed by using the entire chromosome information or by dividing the chromosome information in parts, i.e., by genotype.

First, we will present the methodology, with the following subsections providing more detailed information about it. In this sense, our optimization strategy is to:

• 1. Use the input scaling function (Eq. 14), to re-size the input variable discourse ranges, i.e., $[{\underline{R}}_{x_i}, {\overline{R}}_{x_i}] \rightarrow [-1, 1]$.

• 2. Create a normalized fuzzy system, where every input and output variable discourse range fits in interval $[-1,1]$ (see Fig. 6).

• 3. Use the output scaling function (Eq. 15), to re-size the output variable discourse ranges from the normalized fuzzy system, i.e., $[-1, 1] \rightarrow [{\underline{R}}_{y_j}, {\overline{R}}_{y_j}]$.

• 4. Define the number of sets of each variable and the number of rules in the normalized fuzzy system.

• 5. Define in each variable, the Symmetrical discourse universes and consequently, the symmetrical set distributions, if possible (see Sect. 5.2.3).

• 6. Bundle a chromosome with all set distributions, FOU widths and rule conjunction parameters, based on the chromosome model presented in Sect. 5.2.2.

• 7. Start genetic algorithm optimization.

  • (a) Generate randomly an initial population, computing the fitness value of every individual with Eq. 15 and sorting them in descending order according to their fitness values.

  • (b) Select the mating pool based on the crossover probability.

  • (c) Select two parents using the roulette method.

  • (d) Crossover two parents by the two-point method, where every parent must interchange their corresponding information about set distribution, FOU widths and rule conjunction parameters, according to the chromosome model in Figs. 10, 7 and Sect. 5.2.2. From this, two offsprings must be obtained with only one of them being selected randomly. If the optimization is performed by genotype, then the locus positions can be selected randomly.

  • (e) Apply the mutation operation in the selected offspring according to the mutation probability obtained with the adaptive mutation rate function in Eq. 17 (see Sect. 5.3).

  • (f) Calculate the fitness of final offspring with Eq.  12 unbundling its parameters. This way, the new individual can be evaluated in fuzzy system and the plant response be rated.

  • (g) If offspring fitness is better than the weakest individual fitness in population, then the new offspring will replace it. Otherwise, the algorithm must continue.

  • (h) This process must continue until 70$\%$ of population is very similar (in 90$\%$) to the best individual. If this occurs, then the population must be regenerated; otherwise it must continue.

  • (i) Insert the last best offspring in a new randomly generated population and repeat from a).

• 8. Once the best individual is found (the solution), every parameter must be unbundled, i.e., every parameter must be assigned to its corresponding set and rule, so the resulting fuzzy system must be evaluated in the plant with Eq. 10.

• 9. Perform the rule suppression and evaluate the system again with Eq. 12. Determine those rules with no influence in system performance and replace their corresponding parametric conjunctions with non- parametric conjunctions.

5.1 Multi-objective Transient Fitness Function

For comparison purposes, the optimization strategy of Sect. 5 is verified in the direct-current servomotor system by the plant function in Eq. 10. This fitness function must rate every new individual, aiming to reduce the following transient response parameters (see Fig. 5), in noisy and noise-free square references:

• Rise time ($t_{\mathrm{{r}}}$) This is a measure of how fast the rotor position reaches the reference. The timer starts counting when 10$\%$ of the reference is reached and stops when 90$\%$ is reached [31].

• Settling time ($t_{\mathrm{{s}}}$) This is a very important performance parameter, because it helps the GA to rate how long the signal reaches the steady state. Normally, this time is obtained when error amplitude is lower than 5$\%$.

• Steady-state error (SSE) This is computed as error average, after the steady state is reached, i.e., after the settling time.

• Overshoot Usually expressed as a percentage of errors compared with reference [31]. This performance parameter provides the GA information about how bad or good the reference is reached without peaks. Normally, this can be found after the rise time and before settling time.

Rise time is very important, when using the DC servomotor system of Sect. 4, to set the rotor in a desired position. According to application restrictions, it is desirable to get the best timing when setting the rotor in a specific position. The controller must do this as quickly and efficiently as possible.

Settling time is also important, because this is considered to be a measure of stability. This occurs, when controllers are able to sustain the desired position for a specific amount of time without ripple.

On the other hand, SSE and overshoot are very important because they measure how close the rotor is to the desired position. Therefore, the fewer errors that exist, the more precise the fuzzy system is.

Those four main objectives can be resumed in Eq. 12. If the optimization algorithm considers those measures, then it is able to know what to search for.

Fig. 5

Performance parameters involved in the fitness function calculation

Taking into account the research in [37], from Eq. 1, our purpose is derived. Now, consider only 4 objectives, i.e., $J=4$, then $f = \sum _{i=1}^Jw_if_i, \forall \sum _{i=1}^Jw_i=1$ $f = w_1f_1 + w_2f_2 + w_3f_3 + w_4f_4, \forall \sum _{i=1}^4w_i=1$ This can be described with the following equation, which represents our proposed multi-objective transient fitness function (MOTFF), applied to the ith individual in population:

$$\begin{aligned} \begin{aligned} f_i&= w_1 \left( \dfrac{1}{1 + |OS_i|} \right) + w_2 \left( \dfrac{1}{1 + |SSE_i|} \right) \\&\quad +w_3 \left( \dfrac{t_r^0}{\rho t_r^i} \right) + w_4 \left( \dfrac{t_s^0}{t_s^i} \right) \end{aligned} \end{aligned}$$

(12)

where $f_1=\dfrac{1}{1 + |OS_i|}$, $f_2=\dfrac{1}{1 + |SSE_i|}$, $f_3=\dfrac{t_r^0}{\rho t_r^i}$ and $f_4=\dfrac{t_s^0}{t_s^i}$, such $f_1, f_2, f_3, f_4 \in [0, 1] \subset {\mathbb {R}}$. Also, $t_r^0$ and $t_s^0$ in $f_3$ and $f_4$ are constants, which represent the best possible rise and settling times when the maximum absolute voltage (5 volts) is applied to servomotor terminals, respectively. Here, Greek letter $\rho$ is the rise time penalty factor when $[{\mathrm{min}}(\mathbf {\theta }). {\mathrm{max}}({\mathbf {\theta }})] \le [{\mathrm{min}}({\mathbf {\theta }}_0), {\mathrm{max}}({\mathbf {\theta }}_0)]$, where ${\mathbf {\theta }}$ is a collection of all the rotor position feedback and ${\mathbf {\theta }}_0$ is a collection of all the noise-free reference position signals, both during simulation time. This factor prevents rating with a good score all the very short and incorrect rise times, when the steady state is reached under the reference value. This can be represented as in Eq. 13.

$$\begin{aligned} \rho = \dfrac{\rho _0}{\rho _i}=\dfrac{\mathrm{max}(\mathbf {\theta }_0) - \mathrm{min}(\mathbf {\theta }_i)}{\mathrm{max}(\mathbf {\theta }) - \mathrm{min}(\mathbf {\theta })} \end{aligned}$$

(13)

Unlike the work in [33], our proposal not only considers error measures, such as SSE and overshoot, but also includes in the search the best settling and rise times in the evaluation of individuals, with our proposed fitness function.

Therefore, Eqs. 12 and 13 represent our proposed formulation to rate controller response, using these important performance parameters.

As stated in Eq. 1, each fitness function is weighted by $w_i$. To give those parameters the same importance, $w_1=w_2=w_3=w_4$. Also, in Eq. 12, any fitness values must be equal to one in the best cases, e.g., if settling time is equal to 13 s, then $f_4=\dfrac{t_s^0}{t_s^i}=1$, when $t_s^0=13$ s.

As stated in Eq. 12, the sum of all the factors is equal to one, so $w_i=0.25$ (which means that the four performance parameters, i.e., $J=4$, are evaluated and have the same importance). So, having a total fitness value equal to one means that the individual fits the entire search requirements at $100\%$.

On the other hand, this performance rating is only considered to get the best transient response when a positive step is supplied as reference. Now, if a square signal is supplied as reference, then the performance analysis must be considered in both the positive and negative steps of the square signal. Therefore, all factors can be considered as $w_i=0.125$, due to the fact that they are evaluated for each positive and negative part, i.e., $J=8$. In this case, the final fitness function must also be equal to one, in the best case.

5.2 The Chromosome Model

5.2.1 Normalized PIT2FLS

Fig. 6

Normalized fuzzy system and the use of scaling functions for the DC servomotor application

Let G be a normalized PIT2FLS, which has its input and output variable ranges and all its sets spread along interval $[-1,1]$. A normalized PIT2FLS (see Fig. 6) is an input/output normalized system, which can be used to represent proportionally an unnormalized PIT2FLS. Note in Fig. 6 that $F(x_i, \mathbf {r})$ is an unnormalized PIT2FLS, having $\mathbf {r}$ as a parameter set defined also in $[-1,1]$, $\underline{R_{x_i}}$ and $\overline{R_{x_i}}$ are the lower and upper ranges for the input variable i, respectively, and $\underline{R_{y_j}}$ and $\overline{R_{y_j}}$ for the output variable ranges for the output variable j, respectively. A normalized version of F can be found inside the unnormalized PIT2FLS, i.e., $G(x'_i, \mathbf {r})$.

For this purpose, scaling functions are required. With Eq. 14, i.e., the input scaling function, an unnormalized input variable value can pass from interval $[\underline{R_{x_i}}, \overline{R_{x_i}}]$ to interval $[-1,1]$. Also, with Eq. 15, i.e., the output scaling function, this process can be reversed. The normalized inferred value, obtained from the normalized PIT2FLS G, can pass from interval $[-1,1]$ to interval $[\underline{R_{y_j}}, \overline{R_{y_j}}]$.

$$\begin{aligned} x'_i= & {} \dfrac{2}{{\overline{R}}_{x_i} - {\underline{R}}_{x_i}}x_i - \dfrac{{\overline{R}}_{x_i} + {\underline{R}}_{x_i}}{{\overline{R}}_{x_i} - {\underline{R}}_{x_i}} \nonumber \\ \forall x_i\in & {} [{\underline{R}}_{x_i}, {\overline{R}}_{x_i}], x'_i \in [-1, 1], \mathbf {r} \in [0, 1] \end{aligned}$$

(14)

$$\begin{aligned} y_j= & {} \dfrac{{\overline{R}}_{y_j} - {\underline{R}}_{y_j}}{2}y'_j + \dfrac{{\overline{R}}_{y_j} + {\underline{R}}_{y_j}}{2} \nonumber \\ \forall y_j'\in & {} [-1, 1], y_j \in [{\underline{R}}_{x_i}, {\overline{R}}_{x_i}], \mathbf {r} \in [0, 1] \end{aligned}$$

(15)

A normalized PIT2FLS can be used for several purposes, because its output can fit the requirements of any application and GA search spaces can be bounded to interval $[-1,1]$.

5.2.2 The Chromosome Bundle

One of the benefits of using a normalized PIT2FLS is that each chromosome parameter (each gene) can be of fixed size. Therefore, each gene has the same data representation.

Each data is represented with a signed 10-bit fixed-point number. Also, the integer length is 1, one bit for signing and the remaining bits for the fractional part, as can be seen at the bottom of Fig. 7. This fixed-point data representation lets each gene in chromosome be concatenated one after another, letting the designer know the exact chromosome length used in each search.

Starting from a normalized PIT2FLS and the fixed-point data representation, every variable range must be defined in interval $[-1,1]$. This way, every parameter set $\mathbf {d} \in \mathbf {Q}$, as stated in Eq. 16, may also be defined in this interval and can be considered as part of the chromosome. Assume that all $\mathbf {d}$s in $\mathbf {Q}$ are previously ordered to fit the membership function parameters for correct set distribution, as shown in Fig. 8.

$$\begin{aligned} Q = \left\{ \begin{array}{l} \mathbf {d}_{{\tilde{A}}_1^1}, \mathbf {d}_{{\tilde{A}}_1^2},\ldots ,\mathbf {d}_{{\tilde{A}}_1^{\delta _1}}, \mathbf {d}_{{\tilde{A}}_2^1}, \mathbf {d}_{{\tilde{A}}_2^2},\ldots ,\mathbf {d}_{{\tilde{A}}_2^{\delta _2}},\ldots , \mathbf {d}_{{\tilde{A}}_p^1}, \mathbf {d}_{{\tilde{A}}_p^2},\ldots ,\mathbf {d}_{{\tilde{A}}_p^{\delta _p}}, \mathbf {d}_{{\tilde{B}}_1^1}, \mathbf {d}_{{\tilde{B}}_1^2},\ldots ,\mathbf {d}_{{\tilde{B}}_1^{\lambda _1}}, \mathbf {d}_{{\tilde{B}}_2^1}, \mathbf {d}_{{\tilde{B}}_2^2},\ldots ,\mathbf {d}_{{\tilde{B}}_2^{\lambda _2}},\ldots , \\ \mathbf {d}_{{\tilde{B}}_q^1}, \mathbf {d}_{{\tilde{B}}_q^2},\ldots ,\mathbf {d}_{{\tilde{B}}_q^{\lambda _q}}, \mathbf {\sigma }_{{\tilde{A}}_1^1}, \mathbf {\sigma }_{{\tilde{A}}_1^2},\ldots ,\mathbf {\sigma }_{{\tilde{A}}_1^{\delta _1}}, \mathbf {\sigma }_{{\tilde{A}}_2^1}, \mathbf {\sigma }_{{\tilde{A}}_2^2},\ldots ,\mathbf {\sigma }_{{\tilde{A}}_2^{\delta _2}},\ldots , \mathbf {\sigma }_{{\tilde{A}}_p^1}, \mathbf {\sigma }_{{\tilde{A}}_p^2},\ldots ,\mathbf {\sigma }_{{\tilde{A}}_p^{\delta _p}},\mathbf {\sigma }_{{\tilde{B}}_1^1}, \mathbf {\sigma }_{{\tilde{B}}_1^2},\ldots ,\mathbf {\sigma }_{{\tilde{B}}_1^{\lambda _1}},\ldots , \\ \mathbf {\sigma }_{{\tilde{B}}_2^1}, \mathbf {\sigma }_{{\tilde{B}}_2^2},\ldots ,\mathbf {\sigma }_{{\tilde{B}}_2^{\lambda _2}},\ldots , \mathbf {\sigma }_{{\tilde{B}}_q^1}, \mathbf {\sigma }_{{\tilde{B}}_q^2},\ldots ,\mathbf {\sigma }_{{\tilde{B}}_q^{\lambda _q}},r_1, r_2,\ldots ,r_L. \end{array} \right\} \end{aligned}$$

(16)

Therefore, consider Q in Eq. 16, the chromosome model used to build the GA population.

As an empirical design suggestion, consider delimiting the search space and redefining the FOU width ranges to $\mathbf {\sigma } \in [0, \dfrac{1}{5}] \subset [-1,1], \mathbf {r} \in [0,1] \subset [-1,1]$. This search restriction is due to the rule conjunction parameter values defined in interval $[0,1] \subset [-1,1]$, i.e., they cannot be negative. Also, the use of large FOU widths produces undesired effects in PIT2FLS output.

On the other hand, each parameter set $\mathbf {d}$, $\mathbf {\sigma }$ and $\mathbf {r}$ for the input variables in Eq. 16 is comprised of several parameters, i.e., $\mathbf {d} = \left\{ d_1,d_2,\ldots ,d_{\alpha } \right\}$; $\mathbf {\sigma } = \left\{ \sigma _1, \sigma _2,\ldots ,{\sigma _{\alpha }}\right\}$. Also for output variables $\mathbf {d} = \left\{ d_1,d_2,\ldots ,d_{\beta }\right\}$ and $\mathbf {\sigma } = \left\{ \sigma _1, \sigma _2,\ldots ,\sigma _{\beta }\right\}$. Symbols $\alpha$ and $\beta$ represent the number of parameters that describe a specific type-2 membership function (in Fig. 8, Z-function has an $\alpha = 2$, while for triangular function $\alpha = 3$ for input $x_1$).

Therefore, the chromosome model has the purpose of bounding the information that will be interchanged in the GA crossover operation. As shown in Eq. 16 and Fig. 7, three different genotypes are identified: the $\mathbf {d}$ distribution set parameters, the $\mathbf {\sigma }$ FOU width parameters and the rule conjunction parameter $\mathbf {r}$ (Fig. 9). Each one can be interchanged between parents when performing crossover operations, according to its fixed selected locus (see Fig. 10). For the DC servo problem of Sect. 4, 27 genes are required; so, for two-point crossovers, two locus positions will separate genes as follows: 1 to 9; 10 to 18; and 19 to 27. Then, every individual interchanges its set distribution with the set distribution of another individual during the crossover operation. Each interchange may produce a new offspring whose genotype may produce a different effect in PIT2FLS output.

Fig. 7

The PIT2FLS parameter set used to build the GA population. Signed fixed-point 10-bit value representation is used, for each parameter to fit in interval $[-1,1]$, in the PIT2FLS. This binary representation is used to encode the GA population, according to the chromosome model of Eq. 16

5.2.3 Symmetrical Discourses

A symmetrical variable is a variable whose range is defined in interval $[-z,z]$ such that $-z + z = 0$ and $z \in {\mathbb {R}}$. An example of a symmetrical variable is the error or error derivative specified in the PIT2FLS for DC servomotor application of Sect. 4.

The importance of a symmetrical variable is that an expert can distribute several sets to the positive part of the discourse universe and then reflect them all in the negative part. It is true that not all the applications can be addressed with symmetrical variables. For example, a real DC servomotor does not have an ideal response and may not have the same torque in one direction compared to the other; evidently, this may lead to an asymmetrical distribution of sets in a discourse universe. In spite of this, the reduction of the number of parameters in the GA search represents the real importance of the use of symmetrical variables.

The use of symmetrical variables is relevant to some applications, because it is desirable that every consequent action of the fuzzy system has the same magnitude in both positive or negative directions.

Fig. 8

Set generalization for variable $x_1$: e, position error. Symmetry in error variable is recommended to ensure an equivalent control action in both directions. When using symmetrical discourses, only the set parameters defined on the positive discourse are used to represent sets in both positive and negative parts

Fig. 9

Only 27 parameters are needed to optimize the PIT2FLS for controlling a servomotor. Each row represents a genotype

Fig. 10

Fixed-locus two-point crossover operation. A graphical representation of the three identified genotypes: set distributions, FOU widths and rule conjunction parameters. Here, locus positions of both crossover points are well defined

Therefore, assume that all the MFs of every set are symmetrical as shown in Fig. 8. So, the negative sets can be built with the positive set parameters.

In every symmetrical variable, there should be an odd number of sets, because the NULL or ZERO set is exactly in the middle of the discourse universe. This approach allows the number of parameters introduced in the GA search to be halved.

Specifically, for the servomotor application described in Sect. 4 and based on Eq. 16 and Fig. 7, the chromosome model for GA and set distribution can be reduced, as shown in Fig. 9. As can be seen, the number of parameters is reduced from 48 to 27 genes, when symmetrical discourses are considered.

The use of symmetrical variables and sets is not mandatory, because it will depend on the needs of the application. However, this must be considered as a good resource to decrease the number of parameters in the GA search.

5.3 Adaptive Mutation Rate Function

In GA, the mutation rate can be modified while the best individual evolves. This way, the mutation probability can be adjusted once the algorithm knows the best individual score with Eq. 12. The following equation is used to decrease the step size in search during optimization:

$$\begin{aligned} {\text pM} = \frac{k}{f_o} \exp {(-6f_o)} \end{aligned}$$

(17)

where $f_o$ is the fitness value of the best individual in population and k is a constant that expert propose to set the maximum mutation probability that will be applied to population.

This can be translated as a decreasing exponential selection of the number of individual bits that will be altered during the mutation operation. In other words, a low fitness value will produce a bigger mutation rate, and consequently, it will involve more bits (an aggressive step size).

With Eq. 17, an expert can start mutating the new population with an aggressive step and later, after fitness evaluation, determine the new reduced step size required to modify the next new individuals.

5.4 Rule Suppression

Rule suppression is an additional resource for identifying the useful conjunction parameters in our genetic optimization strategy. It consists of assigning a numerical value to each parameter that eliminates the conjunction effect during rule evaluation.

For instance, for our case study of DC servomotor in Sect. 4, we specified 9 parametric conjunctions, one for each rule. Also, we referred to Eq. 11 as a weighting action operator; if $r=1$, the parametric conjunction would behave as a drastic intersection t-norm, which is equivalent to eliminating the rule influence over the inferred set.

In this sense, the rule can be enabled or disabled. This way, we can inspect the output response and then deduce if that rule conjunction is useful for GA search. If there is no relation with the desired output, then it does not need to be parametric. The rule is very simple; if the lth rule is suppressed, then an expert system can discard the parametric conjunction and can replace it by a nonparametric conjunction operator, e.g., a basic t-norm.

The rule suppression scope aims to decrease the amount of parametric conjunction operators during inference stage computation; in other words, it aims to reduce the inference complexity.

6 Experimental Results

After experimentation, the following results can be summarized.

Table 5 Genotype: set distributions are defined in genes 1–9

Table 6 Genotype: footprints of uncertainty widths are defined in genes 10–18

Table 7 Rule conjunction parameter values are defined in genes 19–27

Table 8 Graphical representation of genotypes

Table 9 Final transient response

In Tables 5, 6 and 7, the best servomotor control performance results (optimal solutions) under several noise conditions are presented. As shown in Fig. 9, the chromosome is comprised of 27 genes for PIT2FLS, 18 genes for IT2FLS and 9 genes for T1FLS. Values from Tables 5, 6 and 7 represent the genotype of each optimal solution, and Table 8 provides its graphical representation; this shows the set distribution and FOU widths in T1FLS and PIT2FLS. Also, the final responses are shown in Table 9, which represent the resulting performance of each best genotype for each case of noise amplitude.

As shown in Tables 5 and 6, some of the corresponding rows for T1FLS are empty. This is evident, because the T1FLS has no information on FOU widths or rule parametric conjunction parameter values. Only set distribution parameters are shown for T1FLS.

Also, Table 10 shows the overall performance parameters for each system stimulated with its corresponding noise signal. Parameters such as rise and settling times, overshoot and steady-state error are used to establish a comparison between each system.

Observe that Table 13 provides a comparison between our proposed MOTFF against another two fitness functions that diminish the error measures, such as the RMSE [13, 21, 22, 32, 33] and the ITAE [29, 44] for T1FLS, IT2FLS and PIT2FLS, when simulating the most representative case of our experiments, i.e., when the noise percentage is 50$\%$. This can be performed by replacing our fitness function in (Sect. 5, step 7f and 9) by the RMSE or ITAE fitness functions. Note that the results in Table 13 were performed by modifying the set distributions for T1FLS [29], the set distributions and FOU widths for IT2FLS [7, 18, 28, 44] and the set distributions, FOU widths and rule parameters for PIT2FLS.

Table 11 is provided to show how rule conjunction parameters affect the transient response of a noisy square signal. In each transient parameter, there are two columns with symbols $+$ and −, which mean that such parameters affect the positive or the negative response of a square signal. Arrows $\uparrow$ and $\downarrow$ are used to show how that transient parameter is affected, when each rule is suppressed using the drastic conjunction operation, i.e., when the rule conjunction parameter value is set to one. Therefore, the rule set computation can be reduced as shown in Table 12, when replacing parametric conjunctions with nonparametric conjunctions.

Table 10 Overall performance and fitness function values

Table 11 Identifying the PIT2FLS rule conjunction parameter influence for suppressing rules when the noise amplitude is 50$\%$

Table 12 PIT2FLS parametric conjunction reduction for each rule, after suppression

Table 13 PIT2FLS, IT2FLS and T1FLS optimization, by using several fitness functions in our strategy after 11 runs, when noise percentage is 50$\%$

Fig. 11

Graphical representation of the transient parameters of Table 13 for T1FLS, IT2FLS and PIT2FLS, when using a our proposed MOTFF, b ITAE and c RMSE and noise percentage is 50$\%$

6.1 Transient Performance Parameters

The use of the main transient parameters in our optimization strategy is relevant to rate the fuzzy systems’ response, by using our proposed multi-objective transient fitness function (Eq. 12).

Analyzing the results of Table 10, the PIT2FLS is better than the T1FLS in any parameter, achieving the best error management and timing response, yet the error amplitude increases.

The reader must note that the more noise that exists, the more noise management disability will exist in both controllers (as shown in Table 9). This means that both controllers are affected by noise, but the advantage of IT2FLS over T1FLS is that those bad effects are minimized. This is evident when comparing the fitness values of Table 10, where noise amplitude increases.

Notice that the performance parameters in Tables 10 and 13 are different for PIT2FLS and T1FLS. This is because the data in Table 13 were obtained with a new set of experiments, described as follows. The experiment is comprised of: 3 fuzzy optimizations (with RMSE, ITAE and our MOTFF, a crossover probability of 65$\%$ and a mutation probability of 4.5$\%$) 11 times each. In every run, the best individual of the last run is reinserted in a new population to continue searching from it.

The results are the following: as shown in Table 13 and Fig. 11, both fitness functions RMSE and ITAE help to reach the reference, in both positive ($+$) and negative steps (−), though sometimes they are susceptible to getting stuck before the fuzzy systems settle on them, due to all the noise peaks. In some cases, the fuzzy system cannot reach the steady state. Observe that some cells in Table 13 have the value U, which means that the rise and settling times could not be found.

Observe that Figure 11 has two columns and three rows. Column 1 depicts the simulation of feedback during the entire simulation time. Column 2 depicts a scaled version of column 1, where the response of evaluated systems can be observed. Notice that some fuzzy systems get better rise time measures, and this is because the controller was not able to reach, in the first simulation seconds, the negative part of reference. This particularity (the fake rise time) would be penalized by our proposal with Eq. 13. Additionally, all settling times are the worst when using RMSE and ITAE, but they got the best error measures. Observe in Fig 11b, c that ITAE obtains better results than RMSE. In both cases, IT2FLS and PIT2FLS have the worst performance, compared to T1FLS. This is because T1FLS optimization could be performed in less time, because 9 parameters were tuned. This means that IT2FLS and PIT2FLS need more time to be completely optimized.

On the other hand, our MOTFF obtained the best transient parameters in both positive and negative steps. Figure 11a) and Table 13 show that PIT2FLS achieves better control than IT2FLS and T1FLS when the noise amplitude is 50$\%$. Although IT2FLS has a bigger SSE, it rises faster (rise time is very competitive) than T1FLS.

Also, a competitive performance improvement between IT2FLS and PIT2FLS can be observed. This means that PIT2FLS helps IT2FLS to achieve additional performance improvements, by integrating parametric conjunction operations, such as the (p)-monotone sum. Observe in Table 13 that PIT2FLS has the best timing performance and error management.

In general, the use of a single objective for a fitness function decreases the probability of finding the optimal individual in first generations. However, experts must analyze how many objectives should be pursued, because in the worst cases placing strict objectives can complicate and prolong the search.

6.2 Membership Function Parameters

The use of symmetrical discourses in Sect. 5.2.3 helps to decrease the amount of genes (the search space) required to compute the GA and impact on the final time required to get the optimal solution.

By observing Tables 5 and 8, set distributions present the following changes when noise amplitude increases:

• Error variable sets. From the system requirements established in Sects. 4, 5, the set distribution obtained from the experiments is symmetrical, where the left and right end sets are identically reflected. What can be observed here is, that sets NE and PE tend to be more drastic and distant from ZE, but ZE has no relevant change.

• Change variable sets. Although the experiment results do not provide clear evidence of noise amplitude increment effects over the set distributions in variable change, we can observe that sets NC and PC have no relevant changes, while set ZC becomes sharper.

• Voltage variable sets. In all case, NV, PV and ZV are almost completely separated, i.e., there are negligible overlapping FOU regions between sets.

However, by observing Tables 6 and 8, set FOU widths present the following characteristics:

• Error variable sets. In this case, all set FOU widths are preserved when noise amplitude increases.

• Change variable sets. In this variable, FOU widths of NC and PC become larger when noise amplitude increases, while the FOU width of ZC becomes smaller.

• Voltage variable sets. This last variable presents smaller FOU widths in every set when noise amplitude increases. This may lead to the idea of using singletons as consequent sets (such as the zero-order Takagi–Sugeno–Kang fuzzy system), which may also help to reduce the number of parameters in the GA search.

6.3 Parametric Conjunction Suppression

According to the results from Tables 7, 9 and 10, rule conjunction parameters present some changes, while noise amplitude increases.

This is given in Table 11, which provides additional information that may help to think about how a rule conjunction parameter can affect the transient response parameters. To get the best solution, the corresponding parameters are selected when noise amplitude is 50$\%$. When analyzing the data, the reader can infer the following:

• Rules 1–3 and 7–9 have no effect on PIT2FLS performance.

• Rule 4. This rule strongly affects some parameters of the negative feedback step. It decreases rise time but increases settling time.

• Rule 5. This is the most important rule, because all the transient parameters are strongly affected.

• Rule 6. This rule strongly affects some parameters of the positive feedback step. It decreases rise time but also increases settling time.

• The transient performance effects due to rule 4 and 6 are almost symmetrical.

Table 11 and the bullets points above show that some rules have no effect when optimizing. Therefore, those parametric conjunctions can be replaced by any nonparametric conjunction, e.g., the product t-norm $T_p$, because any change in fuzzy system output can be observed, when varying such rule conjunction parameters. This is particularly useful because it helps to reduce the PIT2FLS computation.

The rest rules can still be parametric, i.e., $T_0$ in Eq. 11. This is intuitive, because the most relevant information in the rule set is processed when the error is near to zero (i.e., in rules 4–6).

Consequently, the experiment results in Tables 11 and 12 provide relevant information about why parametric operations play an important role in the search for the best solution in adverse circumstances.

7 Conclusions

The methodology presented in this paper is a useful tool for improving, with genetic algorithms, the fuzzy system performance under the effects of large noise amplitudes in control applications, specifically the interval type-2 fuzzy systems with parametric operations. To this end, the methodology recommends the use of resources such as a chromosome model with fixed-point homogeneous genes (genes with the same length), normalized fuzzy systems, rule suppression, an adaptive mutation rate function and a multi-objective transient fitness function, as they are useful resources for designing feasible and optimal fuzzy systems for any application. In other words, the strategy proposed in this paper is feasible, as it helps an expert to use simple operations and basic concepts to keep complexity as low as possible.

To rate both T1FLS, IT2FLS and PIT2FLS performances, a multi-objective transient fitness function is proposed and used to select the best individual in the GA search. Moreover, in order to prevent searches getting stuck, an adaptive mutation rate function is provided.

Additionally, the use of simpler parametric conjunctions, such as the (p)-monotone sum instead of other more complex parametric conjunctions, helps the system to reduce the amount of operations required for the type-2 inference process, which is suitable for practical control applications. Experimental results found that not only system performance can be improved by optimizing the distributions and FOU widths, but also the rule conjunction parameters lead to improving performance even more.

Also, the use of parametric operations in IT2FLS can be reduced, when rule suppression is taken into account. Rule suppression lets an expert eliminate the parametric conjunctions with no influence during optimization.

As a future work, the chromosome model represented with genes of homogeneous data representation (signed 10-bit fixed point) should be extended to hardware control applications by using the optimization strategy presented in this paper. This means normalized fuzzy systems can help to improve the hardware utilization by using data registers and processing architectures of fixed length.

Another avenue of work will be considering the PIT2FLS for other motor control applications that require high-precision constraints. For instance, this work can be extended to the micro-CNC linear actuator control, where the benefits of using PIT2FLS would be greater. Here, a high-precision positioning requirement under disturbance represents a challenge. Likewise, the multi-objective transient fitness function proposed in this paper should be extended to include additional parameters, such as ITAE in steady state, to rate how noise is managed to obtain more precise positioning.