1 Introduction

Many control systems have the problem of time delay which are infinite dimensional in nature. No matter the presence of pure time delay in a control or/and state, it always leads to poor performance or instability. To solve the great challenge of its stability, time delays were paid full attention in academia [1–4]. In order to handle the nonlinear time delay systems, the Lyapunov theory of stability and the indirect adaptive fuzzy control have been used.

For the past few years, adaptive control for feedback linearization nonlinear systems has been discussed [5, 6]. There are two kind of adaptive control techniques, including direct adaptive control (DAC) and indirect adaptive control (IAC) [7–10, 28]. On the other hand, the FNN systems which were proven can precisely model any nonlinear system due to the ubiquitous approximation theorem [19–22]. For example, in [10, 11] it is shown that the FNN can model unknown functions in dynamic systems effectively. However, the nonlinear system and an approximate FNN exhibit an error which will degenerate the stability and control performance. Besides, the state which cannot be measured is another problem for nonlinear system. Therefore, an adaptive FNN control has been proposed to combine with the expert information systematically and the stability which is guaranteed by theoretical analysis [12–18, 29–31]. Adaptive fuzzy identification and combined backstepping and small-gain approach are introduced in [26, 27]. Also the concept of the state observer and constructor can solve the problem of the state which cannot be measured [23–25]. In [12], the unknown nonlinear dynamical system was successfully controlled by indirect adaptive control based on FNN with observer. Also, the concept of supervisory control which can be connected with FNN controller has been proposed [13]. Nevertheless, the indirect adaptive control based on FNN with observer combined with supervisory control for unknown nonlinear dynamical time delay system has never been shown in any publication.

In order to handle the instability resulting from time delay, to estimate the unknown system state and to force the state to be within the constraint set, in this paper, we propose an indirect adaptive control based on time delay FNN controller with state observer and supervisory controller for a class of uncertain nonlinear dynamic time delay systems. First, the unknown system functions are approximated by the adaptive time delay FNN. Next, a state observer is designed to estimate the unknown system states and the indirect adaptive fuzzy controller is constructed. Finally, the closed loop controller is obtained by incorporating the supervisory controller with the indirect adaptive fuzzy controller. The free parameters of the adaptive FNN controller can be tuned online by an observer-based output feedback control law and adaptive laws. Also a supervisory is observed from time to time by a human who, when deeming it necessary, intervenes to modify the control algorithm in some way. Therefore, if the system tends to be unstable, the supervisory controller will force the state to be stable. It is an economical design methodology in respect of control efforts.

The rest of the paper is organized as follows. The problem formulation is first presented in Sect. 2. The description of adaptive time delay FNN system presented in Sect. 3. Indirect adaptive control law design based on FNN controller with observer and supervisory controller is derived in Sect. 4. Section 5 shows the simulation examples and the performance of results. Conclusions are given in the last section, Sect. 6.

2 Problem Formulation

Consider the nth-order nonlinear dynamical system with time delays of the form:

$$ \begin{array}{l} {\dot{x}_{1} = x_{2} } \\ \vdots \\ {\dot{x}_{{n - 1}} = x_{n} } \\ {\dot{x}_{n} = f[x,x(t - \tau _{1} ), \ldots ,x(t - \tau _{r} )] + g[x,x(t - \tau _{1} ), \ldots ,x(t - \tau _{r} )]u + d} \\ {y = x_{1} } \\ {x_{i} \left( t \right) = \Xi \left( t \right),t \in \left[ { - \varsigma ,0} \right]} \\ \end{array} $$
(1)

where f and g are unknown but bounded functions and u ∊ R, y ∊ R are the control input and output of the system, respectively. d is the external bounded disturbance and τr denotes the time delays. Ξ(t) is the initial state of the system, ς = max {τ|1 ≤ r.} where r is the number of delay.

For simplicity, let f(x, τ) = f[x, x(t −τ1)···x(t − τr)] and g(x, τ) = g[x, x(t − τ1)···x(t − τr)], we can rewrite (1) in state-space representation form as

$$ \begin{aligned} \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } &= A\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} + B[f(x,\tau ) + g(x,\tau )u + d] \hfill \\ y &= C^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \hfill \\ \end{aligned}, $$
(2)

where

$$ A = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \begin{aligned} 0 \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} 0 \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} 0 \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} \cdots \hfill \\ \cdots \hfill \\ \end{aligned} & \begin{aligned} 1 \hfill \\ 0 \hfill \\ \end{aligned} \\ \end{array} } \right],\;B = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \vdots \\ 1 \\ \end{array} } \right],\;C = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right] $$

and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} = [x_{1} ,x_{2} , \ldots x_{n} ]^{T} = [x,\dot{x}, \ldots x^{(n - 1)} ]^{T} \in R^{n} \) is a state vector, but not all x are supposed to be available for measurement. Except for the system output, y is assumed to be measurable. Besides, it is required that g(x, τ) ≠ 0 for \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \) in a certain controllability region to make (2) controllable.

First of all, the desired signal vector \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y}_{d} \), the tracking error vector \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}, \) and the estimation error vector \( \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \) are defined as

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y}_{d} = \left[ {y_{d} ,\dot{y}_{d} , \ldots ,y_{d}^{(n - 1)} } \right]^{T} \in R^{n} $$
$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y}_{d} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} = \left[ {e,\dot{e}, \ldots ,e^{(n - 1)} } \right]^{T} \in R^{n} $$
$$ \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y}_{d} - \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } = \left[ {\hat{e},\dot{\hat{e}}, \ldots ,\hat{e}^{(n - 1)} } \right]^{T} \in R^{n}, $$

where \( \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \) and \( \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \) denote the estimates of \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} \), respectively.

If the functions f(x, τ) and g(x, τ) are known and the system is without the external disturbance d, then control law of the certainty equivalent controller [26, 27] is obtained as

$$ u^{*} = \frac{1}{g(x,\tau )}\left[ { - f(x,\tau ) + y_{r}^{(n)} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right], $$
(3)

where feedback gain vector \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k} = \left[ {k_{1} ,k_{2} , \ldots ,k_{n} } \right]^{T} \in R^{n} \) is chosen such that all roots of the characteristic equation are in the open left-half plane. However, f(x, τ) and g(x, τ) are unknown and not all system states x can be measured, hence we use time delay FNN system to model original system functions. The state observer is designed to estimate the state vector in the following context.

Let the control u is the sum of \( u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) \) and \( u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \) which are used to force the state to be within the constraint

$$ u = u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) + u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }), $$
(4)

where \( u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) \) is the indirect adaptive FNN controller with observer and \( u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \) is the supervisory controller (described in Sect. 4). Hence, the certainty equivalent controller (3) can be rewritten as

$$ u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) = \frac{1}{{g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )}}\left[ { - f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) + y_{r}^{(n)} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}_{{}}^{T} \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right]. $$
(5)

Using (4) and (5) in (2), we can obtain the error dynamic equation:

$$ \begin{aligned} \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } &= A\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} - B\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}_{{}}^{T} \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + B\left\{ {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right. \hfill \\ &\quad\left. { + \left[ {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\} - Bd - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \hfill \\ e_{1} &= C^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} \hfill \\ \end{aligned}.$$
(6)

From (6), the following observer that estimates the state error vector e in (6) is expressed as

$$ \begin{aligned} \dot{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} &= A\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } - B\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}_{{}}^{T} \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + L\left( {e_{1} - \hat{e}_{1} } \right) \hfill \\ \hat{e}_{1} &= C^{T} \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \hfill \\ \end{aligned}, $$
(7)

where L = [l1, l2,…, ln]T is the observer gain vector.

The observation errors are defined as \( \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} - \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } = \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \) and \( \tilde{e}_{1} = e_{1} - \hat{e}_{1} = \hat{x}_{1} - x_{1} \).

Subtracting (7) from (6), we can obtain the error dynamics

$$ \begin{aligned} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} &= \left( {A - LC^{T} } \right)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + B\left\{ {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right.\left. { + \left[ {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\} \hfill \\ &\quad - Bd - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \hfill \\ \tilde{e}_{1} &= C^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \hfill \\ \end{aligned}, $$
(8)

where

$$ A - LC^{T} = \left[ {\begin{array}{*{20}c} { - l_{1} } & 1 & 0 & 0 & \cdots & 0 & 0 \\ { - l_{2} } & 0 & 1 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ { - l_{{n - 1}} } & 0 & 0 & 0 & \cdots & 0 & 1 \\ { - l_{n} } & 0 & 0 & 0 & \cdots & 0 & 0 \\ \end{array} } \right]\;{\text{and}}\;B = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \\ \end{array} } \right] $$

where L is the observer gain vector which can be chosen such that the characteristic polynomial of (A − LCT)T is strictly Hurwitz (i.e., the roots of the closed loop system are all in the open left-half plane) and there exists a positive definite symmetric n × n matrix P which satisfies the Lyapunov equation.

$$ \left( {A - LC^{T} } \right)^{T} P + P\left( {A - LC^{T} } \right) = - Q, $$
(9)

where Q is an arbitrary positive definite matrix. To guarantee that our state observer can be implemented, let us rewrite (7) as

$$ \dot{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} = \hat{A}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + LC^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }, $$
(10)

where \( \hat{A} = A - B\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}_{{}}^{T} \) is a strictly Hurwitz matrix. Therefore, there exists a positive definite symmetric n × n matrix \( \hat{P} \) which satisfies the Lyapunov equation.

$$ \hat{A}^{T} \hat{P} + \hat{P}\hat{A} = - \hat{Q}, $$
(11)

where \( \hat{Q} \) is an arbitrary n × n positive definite matrix. Let \( V_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} = (1/2)\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} \hat{P}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }, \) then using (10) and (11) we get

$$ \begin{aligned} \dot{V}_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} & = \frac{1}{2}\dot{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}^{T} \hat{P}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \frac{1}{2}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} \hat{P}\dot{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \\ & = \frac{1}{2}\left( {\hat{A}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + LC^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right)^{T} \hat{P}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \frac{1}{2}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} \hat{P}\left( {\hat{A}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + LC^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right) \\ & = - \frac{1}{2}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} \hat{Q}\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} \hat{P}LC^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \\ \end{aligned}. $$

We can choose \( \hat{Q} \) and L, which are determined by the designer, such that \( \dot{V}_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} \le 0 \). Therefore, there exists a constant value \( \overline{V}_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} \) so that \( V_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} \) is a bounded function and satisfies \( V_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} \le \overline{V}_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} \).

3 Description of Adaptive Time Delay FNN System

Fuzzy logic system, which is proven to have the characteristic of approaching a definition of nonlinear function, has been widely utilized in control theme. The overall configuration of adaptive time delay FNN constructed to approach two time delay system functions f(x, τ) and g(x, τ) is shown in Fig. 1. Based on the Lyapunov approach, the adaptive laws can be developed to adjust the parameters of adaptive time delay FNN to attenuate the tracking error and external disturbance.

Fig. 1
figure 1

Configuration of adaptive time delay FNN

Full size image

The output of the adaptive time delay FNN system with central average defuzzifier can be expressed as

$$ y = \frac{{\sum\nolimits_{j = 1}^{p} {\theta_{j} \left[ {\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} )} } \right]} }}{{\sum\nolimits_{j = 1}^{p} {\left[ {\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} )} } \right]} }} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } ), $$
(12)

where \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } ) = \frac{{\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} )} }}{{\sum\nolimits_{j = 1}^{p} {\left[ {\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} )} } \right]} }} \) is the fuzzy basis function and \( \mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} ) = \mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} )\mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} (t - \tau ),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} ) \ldots \mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} (t - \tau_{r} ),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} ) \) with membership function \( \mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} ) \).

Therefore, by adjusting the adaption parameters \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} \) and incorporating with state observer, system functions f(x, τ) and g(x, τ) can be expressed in the form of (12) as

$$ \hat{f}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) $$
(13)
$$ \hat{g}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ), $$
(14)

where \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) \) are the fuzzy basis functions of \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{x},\hat{x}(t - \tau_{1} ) \cdots \hat{x}(t - \tau_{r} ),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{x},\hat{x}(t - \tau_{1} ) \cdots \hat{x}(t - \tau_{r} ),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) \), respectively.

4 Indirect Adaptive Control-Based FNN Controller With Observer and Supervisory Controller

To begin with, the Lyapunov function is defined as

$$ V_{{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} = \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }. $$
(15)

Taking the derivative of (15) with respect to time, we get

$$ \dot{V}_{{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} = \frac{1}{2}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} P\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}. $$
(16)

Using (9) and substituting the error dynamics (8) into (16), \( \dot{V}_{{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} \) can be rewritten as

$$ \begin{aligned} \dot{V}_{{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} &= \frac{1}{2}\left\{ {\left( {A - LC^{T} } \right)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + B\left\{ {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right.} \right. \hfill \\&\quad \left. { + \left[ {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\} - Bd\left. { - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\}P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \hfill \\ & \quad + \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} P\left\{ {\left( {A - LC^{T} } \right)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right. + B\left\{ {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right. \hfill \\ & \quad \left. { + \left[ {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\}\left. { - Bd - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} \left( {\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }} \right)} \right\} \hfill \\& = - \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} Q\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB\left\{ {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right.\left. { + \left[ {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\} \hfill \\ & \quad - \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PBd - \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PBg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \hfill \\& \le - \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} Q\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \left| {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB} \right|\left\{ {\left| {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )} \right| + \left| {f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right| + \left| {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right|} \right. \hfill \\ & \quad \left. { + \left| {g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| + \left| d \right|} \right\} - \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PBg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \hfill \\ \end{aligned}. $$
(17)

To derive the supervisory control us, the following assumption must be made such that \( \dot{V}_{{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} \le 0 \).

Assumption

We can determine the functions fU(x, τ), gU(x, τ), and gL(x, τ) such that

$$ \begin{aligned} & f^{U} (x,\,\tau ) \approx f^{U} (\hat{x},\,\tau ) < \infty ,\quad | {f(x,\,\tau )} | \le f^{U} (x,\,\tau ) \approx f^{U} (\hat{x},\,\tau ), \hfill \\ & g_{L} (\hat{x},\,\tau ) \approx g_{L} (x,\,\tau ) \le g(x,\,\tau ) \le g^{U} (x,\,\tau ) \approx g^{U} (\hat{x},\,\tau ),\quad g^{U} (x,\,\tau ) \approx g^{U} (\hat{x},\,\tau ) < \infty, \hfill \\ & g_{L} (\hat{x},\,\tau ) \approx g_{L} (x,\,\tau ) > 0 \hfill. \\ \end{aligned} $$

Based on the above hypothesis, the supervisory controller can be chosen as

$$ \begin{aligned} u_{s} (\hat{x}) & = \frac{{\left| {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB} \right|}}{{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB}}\frac{1}{{g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )}}\left\{ {\left| {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )} \right| + \left| {f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right| + \left| {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right|} \right. \\ & \left. {\quad + \left| {g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| + \left| d \right|} \right\} \\ & = \text{sgn} \left( {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB} \right)\frac{1}{{g_{L} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau )}}\left\{ {\left| {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )} \right| + f^{U} (\hat{x},\tau )} \right. + \left| {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| \\ & \left. {\quad + g^{U} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )\left| {u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| + d_{m} } \right\}. \\ \end{aligned} $$
(18)

Then inserting (18) into (17) we have

$$ \begin{aligned} \dot{V}_{{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}} & \le - \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} Q\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \left| {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB} \right|\left\{ {\left| {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )} \right| + \left| {f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right|} \right. + \left| {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| \\ &\quad \left. { \, + \left| {g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| + \left| d \right|} \right\} - \left| {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB} \right|\frac{{g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )}}{{g_{L} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau )}}\left\{ {\left| {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )} \right| + f^{U} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right. \\ & \quad \left. { + \left| {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| + g^{U} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )\left| {u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right| + d_{m} } \right\} \\ & \le - \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} Q\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \left| {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB} \right|\left\{ {\left[ {\left| {f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right| + \left| {g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right|} \right]} \right.\left. { - \frac{{g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )}}{{g_{L} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau )}}\left[ {f^{U} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ) + g^{U} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau )\left| {u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right|} \right]} \right\} \\ & \le - \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} Q\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \le 0 \\ \end{aligned}. $$

Next, based on the double Taylor series expansion at m = m* and σ = σ*, system functions (13) and (14) can be represented as

$$ \begin{aligned} &\hat{f}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} ) = \hfill \\ &\quad \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )} \right.\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} \left. { - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} } \right] \hfill \\& \quad + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f} } \right] \hfill \\& \quad + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} } \right] \hfill \\ \end{aligned} $$
(19)

and

$$ \begin{aligned} \hat{g}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} ) = \hfill \\ \quad \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )} \right.\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} \left. { - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} } \right] \hfill \\ \quad + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g} } \right] \hfill \\ \quad + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} } \right] \hfill \\ \end{aligned}, $$
(20)

where \( \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{*} ,\;\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} ,\;\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} \), \( \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{*} ,\;\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} ,\;\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} \) are presented as the approximation error of the parameters and the optimal parameter vectors are defined as

$$ \begin{aligned} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{*} = \arg \min_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} \in \varOmega_{{\theta_{f} }} }} \left[ {\mathop {\sup }\limits_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \in \varOmega_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }}} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \in \varOmega_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }} }} \left| {\hat{f}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right|} \right] \hfill \\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{*} = \arg \min_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} \in \varOmega_{{\theta_{g} }} }} \left[ {\mathop {\sup }\limits_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \in \varOmega_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }}} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \in \varOmega_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }} }} \left| {\hat{g}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right|} \right] \hfill \\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} = \arg \min_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} \in \varOmega_{{m_{f} }} }} \left[ {\mathop {\sup }\limits_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \in \varOmega_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }}} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \in \varOmega_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }} }} \left| {\hat{f}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right|} \right] \hfill \\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} = \arg \min_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} \in \varOmega_{{m_{g} }} }} \left[ {\mathop {\sup }\limits_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \in \varOmega_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }}} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \in \varOmega_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }} }} \left| {\hat{g}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right|} \right] \hfill \\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} = \arg \min_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} \in \varOmega_{{\sigma_{f} }} }} \left[ {\mathop {\sup }\limits_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \in \varOmega_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }}} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \in \varOmega_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }} }} \left| {\hat{f}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right|} \right] \hfill \\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} = \arg \min_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} \in \varOmega_{{\sigma_{g} }} }} \left[ {\mathop {\sup }\limits_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \in \varOmega_{{\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }}} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \in \varOmega_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }} }} \left| {\hat{g}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right|} \right] \hfill \\ \end{aligned}, $$

where \( \varOmega_{{\theta_{f} }} ,\;\varOmega_{{\theta_{f} }} ,\;\varOmega_{{m_{f} }} ,\;\varOmega_{{m_{g} }} ,\;\varOmega_{{\sigma_{f} }} ,\;\varOmega_{{\sigma_{g} }} ,\;\varOmega_{{\hat{x}}} ,\;\varOmega_{x} \) are the constraint sets of suitable bounds on \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{x}} ,\;{\text{and}}\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \), respectively, defined as follows:

$$ \begin{aligned} \varOmega_{{\theta_{f} }} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} } \right| \le M_{{\theta_{f} }} } \right\},\;\varOmega_{{\theta_{g} }} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} } \right| \le M_{{\theta_{g} }} } \right\},\;\varOmega_{{m_{f} }} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} } \right| \le M_{{m_{f} }} } \right\} \hfill \\ \varOmega_{{m_{g} }} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} } \right| \le M_{{m_{g} }} } \right\} \hfill \\ \end{aligned} $$
$$ \begin{aligned} \varOmega_{{\sigma_{f} }} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} } \right| \le M_{{\sigma_{f} }} } \right\},\varOmega_{{\sigma_{g} }} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} } \right| \le M_{{\sigma_{g} }} } \right\},\,\varOmega_{{\hat{x}}} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{x}} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{x}} } \right| \le M_{{\hat{x}}} } \right\} \hfill \\ \varOmega_{x} = \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} |\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} } \right| \le M_{x} } \right\} \hfill \\ \end{aligned}, $$

where \( M_{{\theta_{f} }} ,\;M_{{\theta_{g} }} ,\;M_{{m_{f} }} ,\;M_{{m_{g} }} ,\;M_{{\sigma_{f} }} ,\;M_{{\sigma_{G} }} ,\;M_{{\hat{x}}} \), and M x are positive constants.

In addition, \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) \) are partial derivatives of \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) \) with respect to \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} \) respectively; and so as \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) \) are partial derivatives of \( \, \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) \) with respect to \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}, \) respectively.

In order to simplify formula, we define the following notations:

$$ T_{f1} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} } \right.\left. { - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} } \right] $$
(21)
$$ T_{f2} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) = \left. {\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f} } \right. + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f} } \right] $$
(22)
$$ T_{g1} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )} \right.\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} \left. { - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} } \right] $$
(23)
$$ T_{g2} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g} } \right.\left. { + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g} } \right]. $$
(24)

Equation (8) can be rewritten as

$$ \begin{aligned} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} = \left( {A - LC^{T} } \right)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + B\left\{ {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) - f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} )} \right. + f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} ) \hfill \\ \quad - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )\left. {\left. { + \left[ {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} )} \right. - g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} ) + g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} ) - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\} \hfill \\ \quad - Bd - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \hfill \\ \end{aligned}. $$
(25)

The minimum approximation error is defined as

$$ \begin{aligned} \omega &= \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} } \right] + \left[ {f(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f}^{*} ) - f(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right] \hfill \\&\quad + {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} } \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} } \right.\left. { + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} } \right] \hfill \\ & \quad + \left[ {g(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g}^{*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g}^{*} )} \right.\left. { - g(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) - d \hfill \\ \end{aligned}. $$
(26)

Using (19–24) and (26) in (25), the error dynamics (25) can be expressed as

$$ \begin{aligned} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} = \left( {A - LC^{T} } \right)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + B\left\{ {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} T_{f1} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )} \right.\left. { + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{T} T_{f2} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) + \left[ {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} T_{g1} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )} \right.} \right\} \hfill \\ \left. {\left. { + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{T} T_{g2} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )} \right]u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\} + B\omega - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \hfill \\ \end{aligned} $$
(27)

In accordance with the preceding consideration, the following theorem is confirmed to show that the proposed overall control scheme is asymptotically stable.

Theorem 1

Considering the nth-order nonlinear dynamical time delay system in the form of (1) with the control law in (4), all the design parameters are adjusted by the adaptive laws (28)–(33):

$$ \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f} = - r_{f1} T_{f1} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right) $$
(28)
$$ \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g} = - r_{g1} T_{g1} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right)u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) $$
(29)
$$ \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f} = - r_{f2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{f} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right) $$
(30)
$$ \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g} = - r_{g2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{m_{g} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right)u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) $$
(31)
$$ \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f} = - r_{f3} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{f} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right) $$
(32)
$$ \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g} = - r_{g3} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{{\sigma_{g} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right)u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }), $$
(33)

where r f1 > 0, r f2 > 0, r f3 > 0, r g1 > 0, r g2 > 0, and r g3 > 0. Based on the Barbalat’s lemma [11], the tracking error e(t) will asymptotically approach zero, i.e., lim t → ∞e(t) = 0.

Proof

First of all, the Lyapunov function candidate is defined as

$$ \begin{aligned} V = \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \frac{1}{{2r_{f1} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f} + \frac{1}{{2r_{g1} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g} + \frac{1}{{2r_{f2} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f}^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f} + \frac{1}{{2r_{g2} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g}^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g} \hfill \\ + \frac{1}{{2r_{f3} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f}^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f} + \frac{1}{{2r_{g3} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g}^{T} \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g} + \frac{1}{2}\sum\limits_{i = 1}^{r} {\int_{{t - \tau_{i} }}^{t} {e^{T} (v)e(v)dv} } \hfill \\ \end{aligned} $$
(34)

Differentiating (34) with respect to time along the trajectory (27), we obtain

$$ \begin{aligned} \dot{V} = \frac{1}{2}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }}^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} P\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} + \frac{1}{{r_{f1} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{f} + \frac{1}{{r_{g1} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{g} + \frac{1}{{r_{f2} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{f} + \frac{1}{{r_{g2} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{g} \hfill \\ + \frac{1}{{r_{f3} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{f} + \frac{1}{{r_{g3} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{g} + \frac{1}{2}\sum\limits_{i = 1}^{r} {e^{T} (t)e(t)} - \frac{1}{2}\sum\limits_{i = 1}^{r} {e^{T} (t - \tau_{i} )e(t - \tau_{i} )} \hfill \\ \end{aligned}. $$
(35)

Substituting (27) into (35), \( \dot{V} \) can be rewritten as

$$ \begin{aligned} \dot{V} =& \frac{1}{2}\left\{ {\left( {A - LC^{T} } \right)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + B\left\{ {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} T_{{f1}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{f} ) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{f}^{T} T_{{f2}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{f} )} \right.} \right. \hfill \\ &\left. {\left. { + \left[ {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} T_{{g1}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{g} ) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{g}^{T} T_{{g2}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{g} )} \right]} \right\}u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) + B\omega - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\}^{T} \hfill \\ & \times P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} P\left\{ {\left( {A - LC^{T} } \right)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + B\left\{ {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} T_{{f1}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{f} ) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{f}^{T} T_{{f2}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{f} )} \right.} \right. \hfill \\ & \left. { + \,\left. {\left[ {\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} T_{{g1}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{g} ) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{g}^{T} T_{{g2}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{g} )u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right]} \right\} + B\omega - Bg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} })} \right\} \hfill \\ &+ \frac{1}{{r_{{f1}} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{f} + \frac{1}{{r_{{g1}} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{g} + \frac{1}{{r_{{f2}} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{f} + \frac{1}{{r_{{g2}} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{g} + \frac{1}{{r_{{f3}} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{f} + \frac{1}{{r_{{g3}} }}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g}^{T} \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{g} \hfill \\ &+ \frac{1}{2}\sum\limits_{{i = 1}}^{r} {e^{T} (t)e(t)} - \frac{1}{2}\sum\limits_{{i = 1}}^{r} {e^{T} (t - \tau _{i} )e(t - \tau _{i} )} \hfill \\ \le &\,\frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} (Q - rI)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \hfill \\ &+ \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f}^{T} \left[ {T_{{f1}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{f} )\left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right) + \frac{1}{{r_{{f1}} }}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{f} } \right] + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g}^{T} \left[ {T_{{g1}} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{g} )\left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right)u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) + \frac{1}{{r_{{g1}} }}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{g} } \right] \hfill \\ &+ \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } _{{m_{f} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{f} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right) + \frac{1}{{r_{{f2}} }}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{f} } \right] + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } _{{m_{g} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{g} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right)u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) + \frac{1}{{r_{{g2}} }}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{g} } \right] \hfill \\ &+ \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } _{{\sigma _{f} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{f} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{f} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right) + \frac{1}{{r_{{f3}} }}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{f} } \right] + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g}^{T} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } _{{\sigma _{g} }}^{T} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} _{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } _{g} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } _{g} \left( {B^{T} P\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }} \right)u_{I} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) + \frac{1}{{r_{{g3}} }}\dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{g} } \right] \hfill \\ & + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB\omega - \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PBg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \hfill \\ \end{aligned}, $$
(36)

where \( \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{f} = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{f} \), \( \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}_{g} = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }_{g} \), \( \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{f} = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{f} \), \( \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }}_{g} = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} }_{g} \),\( \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{f} = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{f}, \) and \( \dot{\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }}_{g} = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{g} \).

Substituting adaptive laws (28)–(33) into (36), we have

$$ \dot{V} = - \frac{1}{2}\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} (Q - rI)\tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } + \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PB\omega - \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PBg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }). $$
(37)

Because \( \tilde{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} }^{T} PBg(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ,\tau )u_{s} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }) \ge 0 \), and ω is very small, we can choose Q and r such that \( \dot{V} \le 0 \) is satisfied. Therefore, the tracking performance can be achieved. The proof is completed.

Summarizing the above analysis, the procedure of observer-based indirect adaptive fuzzy control with supervisory control can be presented as follows.

  • Step 1 The feedback and observer gain vector K and L are specified to obtain the strictly Hurwitz characteristic matrices A − LCT and \( A - B\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}_{{}}^{T} \).

  • Step 2 A positive definite n × n matrix Q is specified such that the Lyapunov Eq. (9) can be solved to obtain a positive definite n × n symmetric matrix P.

  • Step 3 The estimate state vector \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{x}} \) can be obtained by solving the state error in Eq. (7).

  • Step 4 A positive definite n × n matrix \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{Q}} \) is chosen to solve the Lyapunov Eq. (11) to obtain a positive definite n × n symmetric matrix \( \hat{P} \).

  • Step 5 The membership functions \( \mu_{{F_{i}^{j} }} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{j} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{j} ) \) for i = 1, 2,…,p are specified and the fuzzy basis functions \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) \) are computed. Then the outputs of the adaptive time delay FNN system are constructed as \( \hat{f}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{f} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ) \) and \( \hat{g}(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau |\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g}^{T} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi }_{g} (\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} },\tau ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} ) \).

  • Step 6 Obtain the control from Eq. (5) and apply to plant, then compute the adaptive laws (28)–(33) to adjust the parameters of weights \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }_{g} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m}_{g} \) and the width \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{f} ,\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{g} \).

5 Simulation Example

In this section, we will apply our observer-based indirect adaptive FNN controller to synchronize two different single-machine infinite-bus (SMIB) power systems described by delay differential equations (DDEs).

The dynamic equation of the SMIB power drive system is given by

$$ \begin{aligned} &\dot{x}_{1} = x_{2} \hfill \\ &\dot{x}_{2} = - 2x_{2} - 2\sin x_{1} + 3\sin 5t + 5\sin (5x_{1} (t - \tau )) \hfill \\ &y_{d} = x_{1} \hfill \\ \end{aligned}. $$

In a similar way, the response system is given by

$$ \begin{aligned}& \dot{y}_{1} = y_{2} \hfill \\ &\dot{y}_{2} = - 2.2y_{2} - 1.8\sin y_{1} + 3.3\sin 5t + 4.7\sin (5y_{1} (t - \tau )) + u + d \hfill \\& y_{r} = y_{1} \hfill \\ \end{aligned}, $$

where y d and y r are the outputs of the drive system and the response system, respectively. Also the external disturbance is assumed to be a sine wave with amplitude ±1, period 2π, and step size h = 0.001. According to the design procedure, the design is given in the following steps.

  • Step 1 The observer and feedback gain vectors are chosen as L = [89184] and K = [12], respectively.

  • Step 2 We select Q in (9) as \( \left[ {\begin{array}{cc} {10} & {13} \\ {13} & {28} \\ \end{array} } \right] \), then after solving (9), the positive definite symmetric 2 × 2 matrix P in (9) is \( \left[ {\begin{array}{cc} {29} & { - 14} \\ { - 14} & 7 \\ \end{array} } \right] \).

  • Step 3 Solve (7) to obtain \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{x}} \).

  • Step 4 We select \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{Q}} \) in (11) as \( \left[ {\begin{array}{cc} {40} & {25} \\ {25} & {30} \\ \end{array} } \right] \) and \( \hat{A} = \left[ {\begin{array}{*{20}c} 0 & { - 1} \\ { - 4} & { - 4} \\ \end{array} } \right] \) in (11). Therefore, the positive definite symmetric 2 × 2 matrix \( \hat{P} \) in (11) is \( \left[ {\begin{array}{cc} {15} & 5 \\ 5 & 5 \\ \end{array} } \right] \).

  • Step 5 The following membership functions for \( \hat{x}_{i} \, i = 1,2 \) are selected as

    $$ \begin{aligned} \mu F_{i}^{1} = \exp \left( - \left(\frac{{\hat{x}_{i} + 2.5}}{1.5}\right)^{2} \right),\;\mu F_{i}^{2} = \exp \left( - \left(\frac{{\hat{x}_{i} + 1.25}}{1.5}\right)^{2} \right),\;\mu F_{i}^{3} = \exp \left( - \left(\frac{{\hat{x}_{i} }}{1.5}\right)^{2} \right) \hfill \\ \mu F_{i}^{4} = \exp \left( - \left(\frac{{\hat{x}_{i} - .125}}{1.5}\right)^{2} \right),\;\mu F_{i}^{5} = \exp \left( - \left(\frac{{\hat{x}_{i} - 2.5}}{1.5}\right)^{2} \right) \hfill \\ \end{aligned}. $$

    To cover whole cases, we apply 25 fuzzy rules, and the initial values of \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} (0) \) and \( \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }(0) \) are given as [0.51]T and [0.150]T, respectively. Hence u i is constructed.

  • Step 6 Compute the adaptive laws (28)–(33).

The trajectories of the states x 1 and \( \hat{x}_{1} \) shown in Figs. 2 and 3 show that the estimation state \( \hat{x}_{1} \) takes very short time to catch up the system state x 1.

Fig. 2
figure 2

Trajectories of the states x 1 and \( \hat{x}_{1} \)

Full size image
Fig. 3
figure 3

Trajectories of the states x 1 and \( \hat{x}_{1} \) t = 0–0.08 s

Full size image

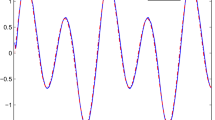
The tracking performance is also very good as shown in Fig. 4, in which y r is the reference output and y is the system output trajectory. Figure 5 shows the drive system and response trajectories x 2 and y 2.

Fig. 4
figure 4

Drive system output trajectory y d and the response output trajectory y r

Full size image
Fig. 5
figure 5

Drive system and response trajectories x 2 and y 2

Full size image

All the control inputs are shown in Fig. 6. Figure 7 shows the control input u I only. Figure 8 shows the supervisory control us and we can see that the supervisory control only works in the beginning period. Soon after, the FNN controller can stabilize the system and the supervisory control will be deactivated.

Fig. 6
figure 6

Trajectories of control input (u I  + u s )

Full size image
Fig. 7
figure 7

Trajectories of control input (u I only)

Full size image
Fig. 8
figure 8

Trajectories of the supervisory control u s

Full size image

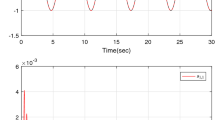
Figure 9 shows the values of \( \dot{V}(t) \). Because the maximum value of \( \dot{V}(t) \) is −9.9992e-013, consequently the stability is confirmed. The 3D phase portrait, i.e., synchronization performance, of the drive and response systems is shown in Fig. 10. We can see that drive system and response system can be synchronized instantly after the control input is applied.

Fig. 9
figure 9

Graph of \( \dot{V}(t) \)

Full size image
Fig. 10
figure 10

Three-dimensional phase portrait, i.e., synchronization performance, of the drive and response systems

Full size image

6 Conclusions

A novel IAC-based FNN controller appended with state observer and supervisory controller is proposed for a certain class of unknown nonlinear time delay systems. Simulation results confirm that the supervisory controller will be activated as long as the system tends to be unstable when it is controlled by FNN controller only. In other words, if the FNN controller works well, the supervisory controller will be deactivated. Meanwhile, the simulation results not only show that the adaptive control effort of the proposed control scheme is much less due to the assist of the supervisory controller, but also show how the supervisory control forces the state to be within the constraint set and how the adaptive FNN controller learned to regain control. In the future works, the results of this paper will be extended to the interval type-2 FNN, because type-1 fuzzy logic control cannot fully handle or accommodate the linguistic and numerical uncertainties associated with dynamic unstructured environments.