Composite adaptive fuzzy decentralized tracking control for pure-feedback interconnected large-scale nonlinear systems

Abstract

This paper focuses on a problem of composite adaptive fuzzy decentralized tracking control for a class of uncertain pure-feedback interconnected large-scale nonlinear systems with unmeasurable states. A fuzzy state observer is designed by using fuzzy logic systems; thus, the unmeasurable states of pure-feedback nonlinear systems are estimated based on the designed fuzzy state observer. A serial–parallel estimation model is designed by using the fuzzy state observer. To avoid the analytic computation, the command filters are employed to produce the command signals and their derivatives. The fuzzy adaptive laws are constructed by using prediction errors and compensating tracking errors. Finally, a controller is constructed by dynamic surface control technique. Through the proposed control method, all the signals in the closed-loop system are bounded, and the output of the system can track the given reference signal. The simulation studies verify the effectiveness of the proposed control method in this paper.

1 Introduction

In recent decades, adaptive control of practical industrial systems has always been a hot issue in the control field, but also a difficult problem, because almost all practical industrial systems have problems such as model uncertainties and unknown nonlinearities. A semi-global output-feedback adaptive tracking control for single-input single-output (SISO) nonlinear systems was considered in [1]. In [2], a global output-feedback adaptive tracking control method was considered for SISO nonlinear systems, where the constant parameter vector and input were linear. Similarly, based on Lyapunov principle, the adaptive control method of nonlinear systems was studied in [3, 4]. The control methods in [1,2,3,4] can be used to handle the control issues for nonlinear systems, but there were rigorous restrictions; that is, the system known functions must be linearly parameterizable. With unknown nonlinear functions and model uncertainties in the practical industrial systems, the aforementioned control methods are not feasible. With the rapid development of neural networks (NNs) [5,6,7,8,9,10,11,12] and fuzzy logic systems (FLSs) [13,14,15,16,17,18,19,20,21,22], the above problems were solved to a large extent. In [5], by using delay-dependent Lyapunov–Krasovskii functional and linear matrix inequalities, the stochastic sampled-data synchronization problem was considered for neural networks with generally incomplete transition rates. Combining the optimal control algorithm with the backstepping technique, the tracking control method of the surface vessel was proposed in [21]. In [22], based on event-trigger condition, a fuzzy adaptive distributed control method was discussed for nonlinear multi-agent systems. A lot of literature show that an unknown nonlinear function can be approximated by NNs or FLS with arbitrary precision; therefore, the problem of the model uncertainties and unknown nonlinear functions can be solved.

It is well known that the adaptive backstepping control technique is the main way to solve the control issues for strict-feedback nonlinear systems. Many mechanical systems can be modeled as strict feedback systems, such as robotic manipulators and inverted pendulum (see [23, 24]). Based on NN approximators, a backsetpping adaptive controller was designed for SISO nonlinear systems, and then the systems solution was bounded in [10]. In [25], under the condition of non-symmetric input constraints, an adaptive tracking control method was investigated for multi-input multi-output (MIMO) nonlinear systems. By using two-layer NN and backstepping approach, a robust control method was considered for motors, which can make the weight updates and tracking errors bounded in [11]. For the traditional backstepping control approach, the virtual controller design in each step needs to take the derivative of the previous controller in [10, 11, 25,26,27]. When the order of the system is higher, the complexity of the controller design increases exponentially. This is called “explosion of complexity” phenomenon. The “explosion of complexity” phenomenon can be resolved through the dynamic surface control (DSC), which introduces low-order filters in the traditional backstepping approach in [28,29,30,31]. In [28], a formation control of mutiple vehicles was considered by using hybrid systems and DSC technique. By designing a neural adaptive DSC for MIMO time-varying nonlinear systems with external disturbances and full-state constraint, the closed-loop system was made stable in [29]. In [30], by using the radial basis neural networks as approximator, a DSC method was studied for nonlinear systems with unknown disturbance and input saturation, and the disturbance observer was designed to estimate the unknown disturbance. But all above control methods require that all states of nonlinear systems are measurable.

For practical industrial systems, it is difficult to measure every signal in the systems due to the limitation of the existing technologies or complexity of work environments. And sometimes, the cost of measuring all the signals is huge. Then, state observer-based adaptive control methods are the main ways and effective to resolve the control issues of uncertain nonlinear systems with unmeasurable states. There are two ways to design a state observer for strict-feedback systems: one is a linear state observer [32, 33]. Another way is to design an intelligent state observer of strict-feedback systems by using fuzzy logic systems or neural networks as a approximator to identify of the unknown nonlinear functions [34,35,36,37,38]. The advantage of the intelligent state observer is that it can not only estimate the unmeasurable state, but also deal with the tracking control problem of strict-feedback systems. In [34], a fault-tolerant fuzzy adaptive control was considered for stochastic nonlinear systems with unmeasured states and input quantization. An adaptive output optimal control method was considered for SISO nonlinear strict-feedback systems with unmeasured states and unknown nonlinear functions in [36]. The state observer was used to estimate the unmeasurable states, and then the controller was designed through the use of observer information in [32,33,34,35,36,37,38]. But, from the control methods in [32,33,34,35,36,37,38], both the linear state observer and the intelligent state observer were designed for strict-feedback systems, which require virtual control gains and actual control gain are one.

Decentralized control of a large-scale system is a control way to decentralize control functions. Each control station receives only partial information, including feedback information of its subsystem and information transmitted by other subsystems. At the same time, the controller is only used in the subsystem itself, but it can indirectly affect other subsystems through the interconnection item. The control purpose is to stabilize the system and achieve the desired control performance. For example, some adaptive backstepping control methods were designed for nonlinear large-scale systems in [39,40,41,42,43]. In [39], a H-infinity adaptive decentralized was proposed for stochastic large-scale nonlinear systems by the backstepping control technique and neural networks. In [40], an adaptive decentralized control method was extended to large-scale nonlinear systems with unknown dead-zone inputs. Based on the state observer, some adaptive decentralized approaches with fault-tolerant control or event-triggered control were investigated for nonlinear large-scale systems in [41,42,43]. All nonlinear large-scale systems were required to be strict-feedback form in [39,40,41,42,43]. Some backstepping control methods were proposed for pure-feedback nonlinear systems in [44, 45], but the systems states must be required to be measurable. How to design a state observer for nonlinear pure-feedback systems is an open problem. But so far, there have been no results on the tracking control problem for uncertain large-scale pure-feedback interconnected nonlinear systems with unmeasurable states.

The motivation of proposed control in this paper is twofold. First, many practical systems can be described by nonlinear systems. Along this line, it is of practical significance to study nonlinear systems. Second, although many works have been focused on general pure-feedback nonlinear systems [15, 44, 45], it is assumed that all the system states are measurable. For practical industrial systems, it is difficult to measure every system state, which can make the control systems more complex. Along this line, we considered pure-feedback nonlinear systems with unmeasurable states. This paper is concerned with the composite adaptive fuzzy decentralized tracking control for uncertain pure-feedback large-scale nonlinear systems with unmeasurable states. By designing serial–parallel estimation model, a good control performance can be achieved. The main contributions are summarized in the following:

• 1. A fuzzy state observer is designed to estimate unmeasurable states of pure-feedback large-scale nonlinear systems, and then a controller is designed by using the fuzzy state observer information. Thus, the assumption that all states are measurable, which is required in [10], is not necessary. To the author’s best knowledge, it is the first time to design a fuzzy state observer for large-scale pure-feedback interconnected nonlinear systems.

• 2. Different from backstepping control methods in [44, 45], where pure-feedback systems must be transformed into strict-feedback systems, pure-feedback systems are converted into special pure-feedback systems which are composed of two terms: a virtual control variable and a nonlinear function of the virtual control variable and the state variables. The backstepping control is directly applied to deal with the tracking control problem of pure-feedback nonlinear systems.

• 3. The “explosion of complexity” phenomenon of the traditional backstepping control method is avoided by introducing first-order filters.

The paper is structured in the following. In Sect. 2, an uncertain pure-feedback large-scale nonlinear system and fuzzy logic systems are introduced. A fuzzy state observer and serial–parallel estimation model are designed in Sect. 3. Adaptive fuzzy control design and stability analysis are constructed in Sect. 4. Two examples simulation results are proved by the design control method in Sect. 5. The conclusion is shown in Sect. 6.

2 Problem description and preliminaries

2.1 Problem description

Consider an uncertain pure-feedback large-scale interconnected nonlinear system with N subsystems. The $\tau$-th $(\tau =1,2,\ldots ,N)$ subsystem is described as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_{\tau ,\xi } &=f_{\tau ,\xi }\left( \underline{x}_{\tau ,\xi },x_{\tau ,\xi +1}\right) +{g_{\tau ,\xi }\left( \underline{y}\right) +d_{\tau ,\xi }(t)}, \\ &\quad 1\le \xi \le m_{\tau }-1, \\ \dot{x}_{\tau ,m_{\tau }}&=f_{\tau ,m_{\tau }}\left( \underline{x}_{\tau ,m_{\tau }},u_{\tau }\right) +{g_{\tau ,m_{\tau }}\left( \underline{y}\right) +d_{\tau ,m_{\tau }}(t)}, \\ & \quad y_{\tau }=x_{\tau ,1}. \end{array}\right. } \end{aligned}$$

(1)

where $\underline{x}_{\tau ,\xi }=[x_{\tau ,1},x_{\tau ,2},\ldots ,x_{\tau ,\xi }]^{\mathrm{T}}\in R^{\xi }$, $\underline{x}_{\tau ,m_{\tau }}=[x_{\tau ,1},$ $x_{\tau ,2},\ldots ,x_{\tau ,m_{\tau }}]^{\mathrm{T}}\in R^{m_{\tau }}$ is the system state vector, $y_{\tau }$ and $u_{\tau }$ are the output and input of the $\tau$-th $(\tau =1,2,\ldots ,N)$ subsystem, respectively. $f_{\tau ,\xi }( \underline{x}_{\tau ,\xi })$ is an unknown smooth function, $g_{\tau ,\xi }( \underline{y})$ is an unknown smooth interconnection between the $\tau$-th subsystem and other subsystems. $d_{\tau ,\xi }(t)$ is a bounded external disturbance. The ideal signal $y_{\tau ,r}$ is a sufficiently smooth function, and $y_{\tau ,r}$, $\dot{y}_{\tau ,r}$ are all bounded. It is assumed that only the outputs of the subsystems are available.

Assumption 1

The unknown nonlinear function    $f_{\tau ,\xi }( \underline{x}_{\tau ,\xi },x_{\tau ,\xi +1})$ of the pure-feedback nonlinear system (1) satisfies $\frac{\partial f_{\tau ,\xi }(\underline{x} _{\tau ,\xi },x_{\tau ,\xi +1})}{\partial x_{\tau ,\xi +1}\ }\ne 0$ $(\xi =1,2,\ldots ,m_{\tau })$ for any $\underline{x}_{\tau ,\xi }$, $x_{\tau ,\xi +1}$, where $x_{\tau ,m_{\tau }+1}=u_{\tau }$.

Remark 1

Assumption 1 implies that $x_{\tau ,\xi +1}$ must be contained in the $\xi$-th differential equation, which means that the $\tau$-th subsystem is controllable by $x_{\tau ,\xi +1}$.

Assumption 2

The unknown smooth interconnection $g_{\tau ,\xi }(\underline{y})$and external disturbance $d_{\tau ,\xi }(t)$ of the pure-feedback nonlinear system (1) are bounded, that is, $\left| g_{\tau ,\xi }(\underline{y})+d_{\tau ,\xi }(t)\right| \le$ $p_{\tau ,\xi }^{*}$, where $p_{\tau ,\xi }^{*}$ is an unknown positive constant.

2.2 Fuzzy logic systems

Fuzzy logic systems are used to estimate the unknown nonlinear functions contained in (1). On the basis of [16, 37], the knowledge base for FLS is comprised of a collection of fuzzy If-then rules in the following form:

$R^l$: If $x_1$ is $F_l^l$ and $x_2$ is $F_2^l$ and $\ldots$ and $x_n$ is $F_n^l$,

then y is $G^l$, $l=1,2,\ldots ,N$,

where $x = (x_1,\ldots ,x_n)^{\mathrm{T}}$ and y are the FLS input and output, respectively. Fuzzy sets $F_i^l$ and $G^l$ are associated with the fuzzy membership functions $\mu _{F_i^l}(x)$ and $\mu _{G^l}(y)$, respectively. N is the rules number.

Through singleton fuzzifier, center average defuzzification and product inference, the FLS can be expressed as

$$\begin{aligned} y(x)=\frac{\sum _{l=1}^N\bar{y}_l\prod _{i=1}^n\mu _{F_i^l}\left( x_i\right) }{\sum _{l=1}^N\left[ \prod _{i=1}^n\mu _{F_i^l}\left( x_i\right) \right] } \end{aligned}$$

(2)

where $\bar{y}_l=\max _{y\in R}\mu _{G^l}(y)$.

Define the fuzzy basis functions as

$$\begin{aligned} {\varphi _l=\frac{\prod _{i=1}^n\mu _{F_i^l}(x_i)}{\sum _{l=1}^N\left( \prod _{i=1}^n\mu _{F_i^l}(x_i)\right) } } \end{aligned}$$

(3)

Denoting $\theta ^{\mathrm{T}}=[\bar{y}_1,\bar{y}_2,\ldots ,\bar{y}_N]=[\theta _1,\theta _2,\ldots ,\theta _N]$ and $\varphi (x)=[\varphi _1(x),\ldots ,\varphi _N(x)]^{\mathrm{T}}$, (3) can be rewritten as $y(x)=\theta ^{\mathrm{T}}\varphi (x)$. All the memberships are chosen as Gaussian functions; the lemma below holds.

Lemma 1

For any continuous function $f\left( x\right)$ defined on a compact set U , there exists an FLS $\theta ^{*T}\varphi \left( x\right)$ such that

$$\begin{aligned} \sup _{x\in U}\left| f\left( x\right) -\theta ^{*T}\varphi \left( x\right) \right| \le \varepsilon \end{aligned}$$

(4)

where $\theta ^{*T}=\left[ \theta _{1}^{*},\theta _{2}^{*},\ldots ,\theta _{N}^{*}\right]$ represents the optimal parameter vector, $\varepsilon$ is any given positive constant.

3 Design of the fuzzy state observer and serial–parallel estimation model

In order to design a state observer of the unmeasurable state, the system (1) is first transformed to the following special pure-feedback form

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_{\tau ,\xi }&=h_{\tau ,\xi }\left( \underline{x}_{\tau ,\xi },x_{\tau ,\xi +1}\right) +x_{\tau ,\xi +1}+p_{\tau ,\xi }, \\ &\quad 1\le \xi \le n_{\tau }-1, \\ \dot{x}_{\tau ,m_{\tau }}&=h_{\tau ,m_{\tau }}\left( \underline{x}_{\tau ,n_{\tau }},u_{\tau }\right) +u_{\tau }+p_{\tau ,m_{\tau }}, \\ &\quad y_{\tau }=x_{\tau ,1}. \end{array}\right. } \end{aligned}$$

(5)

where $h_{\tau ,\xi }(\underline{x}_{\tau ,\xi },x_{\tau ,\xi +1})=f_{\tau ,\xi }(\underline{x}_{\tau ,\xi },x_{\tau ,\xi +1})-x_{\tau ,\xi +1}$, $h_{\tau ,m_{\tau }}(\underline{x}_{\tau ,m_{\tau }},u_{\tau })=f_{\tau ,m_{\tau }}(\underline{x}_{\tau ,m_{\tau }},u_{\tau })-u_{\tau }$, $p_{\tau ,\xi }=g_{\tau ,\xi }(\underline{y})+d_{\tau ,\xi }(t)$ and $p_{\tau ,m_{\tau }}=g_{\tau ,m_{\tau }}(\underline{y})+d_{\tau ,m_{\tau }}(t)$.

Rewrite (5) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\underline{x}}_{\tau ,m_{\tau }}&= A_{\tau }\underline{x}_{\tau ,m_{\tau }}+\eta _{\tau }y_{\tau }+\sum _{\xi =1}^{m_{\tau }-1}B_{\tau ,\xi }h_{\tau ,\xi }\left( \underline{x}_{\tau ,\xi +1}\right) \\ &\quad +B_{\tau ,m_{\tau }}h_{\tau ,m_{\tau }}\left( \underline{x}_{\tau ,m_{\tau }},u_{\tau }\right) +B_{\tau ,m_{\tau }}u_{\tau }\\ &\quad +\sum _{\xi =1}^{m_{\tau }}B_{\tau ,\xi }p_{\tau ,\xi }, \\ y_{\tau }& = C_{\tau }\underline{x}_{\tau ,m_{\tau }}, \end{array}\right. } \end{aligned}$$

(6)

where $A_{\tau }=\left[ \begin{array}{cccc} -\eta _{\tau ,1} &{} &{} &{} \\ \vdots &{} &{} I &{} \\ -\eta _{\tau ,m_{\tau }} &{} 0 &{} \ldots &{} 0 \end{array} \right]$, $\eta _{\tau }=\left[ \begin{array}{c} \eta _{\tau ,1} \\ \vdots \\ \eta _{\tau ,m_{\tau }} \end{array} \right]$, $B_{\tau ,\xi }=[\mathop {\underbrace{0\cdots 0~1}}\limits _{\xi }\cdots 0]^{\mathrm{T}}$, $C_{\tau }=[1\cdots 0\cdots 0]$. Choose the vector $\eta _{\tau }$ to make matrix $A_{\tau }$ be a strict Hurwitz matrix. Therefore, given a matrix $Q_{\tau }=Q_{\tau }^{\mathrm{T}}>0$, there exists a matrix $P_{\tau }=P_{\tau }^{\mathrm{T}}>0$ such that

$$\begin{aligned} A_{\tau }^{\mathrm{T}}P_{\tau }+P_{\tau }A_{\tau }=-2Q_{\tau } \end{aligned}$$

(7)

According to Lemma 1, the unknown nonlinear functions $h_{\tau ,\xi }(\underline{x}_{\tau ,\xi +1})$ and $h_{\tau ,m_{\tau }}(\underline{x}_{\tau ,m_{\tau }},u_{\tau })$ can be approximated by FLSs $\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }(\underline{x}_{\tau ,\xi +1})$ and $\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}(\underline{x}_{\tau ,m_{\tau }},u_{\tau })$, that is to say, they can be expressed as $h_{\tau ,\xi }(\underline{x}_{\tau ,\xi +1})=\theta _{\tau ,\xi }^{*T}\varphi _{\tau ,\xi }(\underline{x}_{\tau ,\xi +1})+\varepsilon _{\tau ,\xi }$ and $h_{\tau ,m_{\tau }}(\underline{x}_{\tau ,m_{\tau }},u_{\tau })=\theta _{\tau ,m_{\tau }}^{*T}\varphi _{\tau ,m_{\tau }}$ $(\underline{x}_{\tau ,m_{\tau }},u_{\tau })+\varepsilon _{\tau ,m_{\tau }}$, where $\theta _{\tau ,\xi }^{*}$ is the ideal weight vector and $\theta _{\tau ,\xi }$ is the estimation of $\theta _{\tau ,\xi }^{*}$, $\varepsilon _{\tau ,\xi }$ represents a fuzzy approximated error. The fuzzy observer is designed in the following.

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\hat{x}}_{\tau ,\xi }=\hat{x}_{\tau ,\xi +1}+\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi +1}\right) +\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) , \\ \quad 1\le \xi \le m_{\tau }-1, \\ \dot{\hat{x}}_{\tau ,m_{\tau }}=u_{\tau }+\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) +\eta _{\tau ,m_{\tau }}\left( y_{\tau }-\hat{x}_{\tau ,1}\right) \\ \hat{y}_{\tau }=\hat{x}_{\tau ,1}. \end{array}\right. } \end{aligned}$$

(8)

Then, (8) can be further written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\hat{\underline{x}}}_{\tau ,m_{\tau }}&= A_{\tau }\hat{\underline{x}} _{\tau ,m_{\tau }}+\eta _{\tau }y_{\tau }+\sum _{\xi =1}^{m_{\tau }-1}B_{\tau ,\xi }\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}} _{\tau ,\xi +1}\right) \\ &\quad +B_{\tau ,m_{\tau }}\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) +B_{\tau ,m_{\tau }}u_{\tau }, \\ \hat{y}_{\tau }&= C_{\tau }\underline{\hat{x}}_{\tau ,m_{\tau }}. \end{array}\right. } \end{aligned}$$

(9)

Define the estimation error vector $e_{\tau }$ as

$$\begin{aligned} e_{\tau }=\left[ e_{\tau ,1},e_{\tau ,2},\ldots ,e_{\tau ,m_{\tau }}\right] ^{\mathrm{T}}= \underline{x}_{\tau ,m_{\tau }}-\hat{\underline{x}}_{\tau ,m_{\tau }}. \end{aligned}$$

(10)

It follows from (6) and (9) that

$$\begin{aligned} \dot{e}_{\tau }&= A_{\tau }e_{\tau }+\sum _{\xi =1}^{m_{\tau }-1}B_{\tau ,\xi }\left[ \theta _{\tau ,\xi }^{*T}\varphi _{\tau ,\xi }(\underline{x}_{\tau ,\xi +1})\right. \nonumber \\&\quad \left. -\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}} _{\tau ,\xi +1}\right) +\varepsilon _{\tau ,\xi }\right] +\sum _{\xi =1}^{m_{\tau }}B_{\tau ,\xi }p_{\tau ,\xi } \nonumber \\&\quad +B_{\tau ,m_{\tau }}\left[ \theta _{\tau ,m_{\tau }}^{*T}\varphi _{\tau ,m_{\tau }}\left( \underline{x}_{\tau ,m_{\tau }},u_{\tau }\right) \right. \nonumber \\&\quad \left. -\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{ \hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) +\varepsilon _{\tau ,m_{\tau }}\right] \nonumber \\&= A_{\tau }e_{\tau }+\sum _{\xi =1}^{m_{\tau }}B_{\tau ,\xi }\delta _{\tau ,\xi } \end{aligned}$$

(11)

where $\delta _{\tau ,\xi }=\theta _{\tau ,\xi }^{*T}\varphi _{\tau ,\xi }(\underline{x}_{\tau ,\xi +1})-\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }(\underline{\hat{x}}_{\tau ,\xi +1})+\varepsilon _{\tau ,\xi }+p_{\tau ,\xi }$, $\delta _{\tau ,m_{\tau }}=\theta _{\tau ,m_{\tau }}^{*T}\varphi _{\tau ,m_{\tau }}(\underline{x}_{\tau ,m_{\tau }},u_{\tau })-\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}$ $( \underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau })+\varepsilon _{\tau ,m_{\tau }}+p_{\tau ,m_{\tau }}$ and $\delta _{\tau }=[\delta _{\tau ,1},\delta _{\tau ,2},\ldots ,$ $\delta _{\tau ,m_{\tau }}]^{\mathrm{T}}$.

The Lyapunov function candidate of the state observer error is designed as

$$\begin{aligned} V_{\tau ,0}=\frac{1}{2}e_{\tau }^{\mathrm{T}}P_{\tau }e_{\tau } \end{aligned}$$

(12)

The derivative of $V_{\tau ,0}$ is obtained as

$$\begin{aligned} \dot{V}_{\tau ,0}&= \frac{1}{2}\dot{e}_{\tau }^{\mathrm{T}}P_{\tau }e_{\tau }+\frac{1}{2}e_{\tau }^{\mathrm{T}}P_{\tau }\dot{e}_{\tau } \nonumber \\&= \frac{1}{2}e_{\tau }^{\mathrm{T}}\left( A_{\tau }^{\mathrm{T}}P_{\tau }+P_{\tau }A_{\tau }\right) e_{\tau }+e_{\tau }^{\mathrm{T}}P_{\tau }\delta _{\tau } \end{aligned}$$

(13)

According to the definitions of $\delta _{\tau ,\xi }$ and $\delta _{\tau ,m_{\tau }}$ in [46], it is true that

$$\begin{aligned} \delta _{\tau ,\xi }&= \theta _{\tau ,\xi }^{*T}\left( \varphi _{\tau ,\xi }(\underline{x}_{\tau ,\xi +1})-\varphi _{\tau ,\xi }\left( \underline{\hat{x} }_{\tau ,\xi +1}\right) \right) \nonumber \\&\quad +\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}} _{\tau ,\xi +1}\right) +\varepsilon _{\tau ,\xi }+p_{\tau ,\xi } \end{aligned}$$

(14)

$$\begin{aligned} \delta _{\tau ,m_{\tau }}&= \theta _{\tau ,m_{\tau }}^{*T}\left( \varphi _{\tau ,m_{\tau }}\left( \underline{x}_{\tau ,m_{\tau }},u_{\tau }\right) -\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) \right) \nonumber \\&\quad +\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{ \hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) +\varepsilon _{\tau ,m_{\tau }}+p_{\tau ,m_{\tau }} \end{aligned}$$

(15)

From $0<\varphi _{\tau ,\xi }^{\mathrm{T}}\left( \cdot \right) \varphi _{\tau ,\xi }\left( \cdot \right) <1$ and Young’s inequality, it can be verified that

$$\begin{aligned} e_{\tau }^{\mathrm{T}}P_{\tau }\delta _{\tau }&\le \frac{\varrho _{\tau }\left\| P_{\tau }\right\| ^{2}}{2}\left\| e_{\tau }\right\| ^{2}+\sum _{\xi =1}^{m_{\tau }}\left[ \frac{\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2}}{\varrho _{\tau }}+\frac{8\left\| \theta _{\tau ,\xi }^{*}\right\| ^{2}}{\varrho _{\tau }}\right. \nonumber \\&\quad \left. +\frac{4\varepsilon _{\tau ,\xi }^{*2}}{\varrho _{\tau }}+\frac{ 4p_{\tau ,\xi }^{*2}}{\varrho _{\tau }}\right] \end{aligned}$$

(16)

According to (16), (13) can be rewritten as

$$\begin{aligned} \dot{V}_{\tau ,0}\leq-\mu _{\tau ,0}\left\| e_{\tau }\right\| ^{2}+\frac{1 }{\varrho _{\tau }}\sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2}+\varDelta _{\tau ,0} \end{aligned}$$

(17)

where $\mu _{\tau ,0}=\lambda _{\min }\left( Q_{\tau }\right) -\frac{\varrho _{\tau }\left\| P_{\tau }\right\| ^{2}}{2}$ and $\varDelta _{\tau ,0}=\sum _{\xi =1}^{m_{\tau }}\left[ \frac{8\left\| \theta _{\tau ,\xi }^{*}\right\| ^{2}}{\varrho _{\tau }}+\frac{4\varepsilon _{\tau ,\xi }^{*2}}{\varrho _{\tau }}+\frac{4p_{\tau ,\xi }^{*2}}{\varrho _{\tau }}\right]$.

Remark 2

So far, although there are many results on general pure-feedback nonlinear systems [15, 44, 45], it is assumed that all the system states are measurable. For practical industrial systems, it is difficult to measure every system state, which can make the control systems more complex. Therefore, the research on the control method of the pure-feedback nonlinear system with unmeasurable state is more meaningful and more challenging.

Design the serial–parallel estimation model as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\hat{\hat{x}}}_{\tau ,\xi }=\hat{x}_{\tau ,\xi +1}+\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi +1}\right) +\lambda _{\tau ,\xi }\left( \hat{x}_{\tau ,\xi }-\hat{\hat{x}}_{\tau ,\xi }\right) , \\ \quad \xi =1,2,\cdots ,m_{\tau }-1 \\ \dot{\hat{\hat{x}}}_{\tau ,m_{\tau }}=u_{\tau }+\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) \\ \quad +\lambda _{\tau ,m_{\tau }}\left( \hat{x}_{\tau ,m_{\tau }}-\hat{\hat{x}}_{\tau ,m_{\tau }}\right) \\ \hat{y}_{\tau }=\hat{x}_{\tau ,1}. \end{array}\right. } \end{aligned}$$

(18)

where $\hat{\hat{x}}_{\tau ,\xi }$ is the estimate of $\hat{x}_{\tau ,\xi }$ and $\lambda _{\tau ,\xi }$ is a positive design parameter.

The prediction error is defined as

$$\begin{aligned} q_{\tau ,\xi }=\hat{x}_{\tau ,\xi }-\hat{\hat{x}}_{\tau ,\xi } \end{aligned}$$

(19)

It follows from (8) and (18) that the derivative of $q_{\tau ,\xi }$ can be expressed as

$$\begin{aligned} \dot{q}_{\tau ,\xi }=\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) -\lambda _{\tau ,\xi }q_{\tau ,\xi } \end{aligned}$$

(20)

4 Adaptive fuzzy control design and stability analysis

A fuzzy adaptive tracking controller will be constructed through the backstepping control technique and FLSs in this section. For each subsystem, the virtual controllers are designed in the first $m_{\tau }-1$ steps, and the actual controller will be designed at the $m_{\tau }$-th step.

A coordinate transformation is introduced as follows:

$$\begin{aligned} s_{\tau ,1}&= x_{\tau ,1}-y_{\tau ,r} \end{aligned}$$

(21)

$$\begin{aligned} s_{\tau ,\xi }&= \hat{x}_{\tau ,\xi }-\bar{\alpha }_{\tau ,\xi },\quad \xi =2,3,\ldots ,m_{\tau } \end{aligned}$$

(22)

where $\bar{\alpha }_{\tau ,\xi }$ is the output of the following first-order filter

$$\begin{aligned} \pi _{\tau ,\xi }\dot{\bar{\alpha }}_{\tau ,\xi }+\bar{\alpha }_{\tau ,\xi }=\alpha _{\tau ,\xi },\quad \bar{\alpha }_{\tau ,\xi }(0)=\alpha _{\tau ,\xi }(0) \end{aligned}$$

(23)

with the backstepping virtual controller $\alpha _{\tau ,\xi }$ as a input, and $\pi _{\tau ,\xi }$ is a positive design parameter. The reason for introducing (23) is to avoid the repeated differentiation of the virtual controller $\alpha _{\tau ,\xi }$, which results in a differential explosion phenomenon.

Step 1 The time derivative of $s_{\tau ,1}$ is given by

$$\begin{aligned} \dot{s}_{\tau ,1}&= h_{\tau ,1}\left( \underline{x}_{\tau ,2}\right) +x_{\tau ,2}+p_{\tau ,1}-\dot{y}_{\tau ,r} \nonumber \\&= \theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \underline{x}_{\tau ,2}\right) +\varepsilon _{\tau ,1}+e_{\tau ,2}+s_{\tau ,2}+\bar{\alpha }_{\tau ,2} \nonumber \\&\quad +p_{\tau ,1}-\dot{y}_{\tau ,r}+\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) \nonumber \\&\quad -\theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) +\theta _{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) \end{aligned}$$

(24)

In order to compensate the impact of the error $\bar{\alpha }_{\tau ,2}-\alpha _{\tau ,2}$, the following compensating dynamics is introduced

$$\begin{aligned} \dot{z}_{\tau ,1}=-k_{\tau ,1}z_{\tau ,1}+z_{\tau ,2}+\left( \bar{\alpha } _{\tau ,2}-\alpha _{\tau ,2}\right) \end{aligned}$$

(25)

where $z_{\tau ,1}(0)=0$, $k_{\tau ,1}$ is a positive design parameter, and $z_{\tau ,2}$ will be defined later.

Define the compensated tracking error signals

$$\begin{aligned} v_{\tau ,1}=s_{\tau ,1}-z_{\tau ,1},\quad v_{\tau ,2}=s_{\tau ,2}-z_{\tau ,2} \end{aligned}$$

(26)

The derivative of $v_{\tau ,1}$ is obtained as

$$\begin{aligned} \dot{v}_{\tau ,1}&= \theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \underline{ x}_{\tau ,2}\right) +\varepsilon _{\tau ,1}+e_{\tau ,2}+v_{\tau ,2}+p_{\tau ,1} \nonumber \\&\quad -\dot{y}_{\tau ,r}+\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x} _{\tau ,1}\right) -\theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) \nonumber \\&\quad +\theta _{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) +k_{\tau ,1}z_{\tau ,1}+\alpha _{\tau ,2} \end{aligned}$$

(27)

The Lyapunov function candidate is considered in the following

$$\begin{aligned} V_{\tau ,1}&= V_{\tau ,0}+\frac{1}{2}\sum _{\xi =1}^{m_{\tau }}r_{\tau ,\xi }q_{\tau ,\xi }^{2}+\frac{1}{2}v_{\tau ,1}^{2}+\frac{1}{2c_{\tau ,1}}\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\tilde{\theta }_{\tau ,1} \nonumber \\&\quad +\frac{1}{2\bar{c}_{\tau ,1}}\tilde{\varTheta }_{\tau ,1}^{2} \end{aligned}$$

(28)

where $r_{\tau ,\xi }$, $c_{\tau ,1}$ and $\bar{c}_{\tau ,1}$ are positive design parameters, and $\tilde{\varTheta }_{\tau ,\xi}=\varTheta _{\tau ,\xi}^{*}-\varTheta _{\tau ,\xi}$ with $\varTheta _{\tau ,\xi}$ being the estimation of $\varTheta _{\tau ,\xi}^{*}=\left\| \theta _{\tau ,\xi}^{*}\right\| ^{2},\xi=1,2,\ldots,m_{\tau}$.

From (20) and (27), the derivative of $V_{\tau ,1}$ can be expressed as

$$\begin{aligned} \dot{V}_{\tau ,1}&= \dot{V}_{\tau ,0}+\sum _{\xi =1}^{m_{\tau }}r_{\tau ,\xi }q_{\tau ,\xi }\dot{q}_{\tau ,\xi }+v_{\tau ,1}\dot{v}_{\tau ,1}+\frac{1}{ c_{\tau ,1}}\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\dot{\tilde{\theta }}_{\tau ,1}\nonumber \\&\quad +\frac{1}{\bar{c}_{\tau ,1}}\tilde{\varTheta }_{\tau ,1}\dot{\tilde{\varTheta }} _{\tau ,1} \nonumber \\&= \dot{V}_{\tau ,0}+\sum _{\xi =1}^{m_{\tau }}r_{\tau ,\xi }q_{\tau ,\xi }\left( \eta _{\tau ,\xi }(y_{\tau }-\hat{x}_{\tau ,1})-\lambda _{\tau ,\xi }q_{\tau ,\xi }\right) \nonumber \\&\quad +v_{\tau ,1}\left( \theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \underline{ x}_{\tau ,2}\right) +\varepsilon _{\tau ,1}+e_{\tau ,2}+v_{\tau ,2}\right. \nonumber \\&\quad +p_{\tau ,1}-\dot{y}_{\tau ,r}+\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) -\theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) \nonumber \\&\quad \left. +\theta _{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) +k_{\tau ,1}z_{\tau ,1}+\alpha _{\tau ,2}\right) \nonumber \\&\quad +\frac{1}{c_{\tau ,1}}\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\dot{\tilde{\theta }} _{\tau ,1}+\frac{1}{\bar{c}_{\tau ,1}}\tilde{\varTheta }_{\tau ,1}\dot{\tilde{ \varTheta }}_{\tau ,1} \end{aligned}$$

(29)

It can be easily verified that the following inequalities hold

$$\begin{aligned}&\sum _{\xi =1}^{m_{\tau }}r_{\tau ,\xi }q_{\tau ,\xi }\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) \nonumber \\&\quad \le \sum _{\xi =1}^{m_{\tau }}\frac{r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}q_{\tau ,\xi }^{2}+m_{\tau }\Vert e_{\tau }\Vert ^{2} \end{aligned}$$

(30)

$$\begin{aligned}&v_{\tau ,1}\left( \varepsilon _{\tau ,1}+e_{\tau ,2}+p_{\tau ,1}\right) \nonumber \\&\quad \le v_{\tau ,1}^{2}+\frac{1}{2}\Vert e_{\tau }\Vert ^{2}+\varepsilon _{\tau ,1}^{*2}+p_{\tau ,1}^{*2} \end{aligned}$$

(31)

$$\begin{aligned}&v_{\tau ,1}\left( \theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \underline{x }_{\tau ,2}\right) -\theta _{\tau ,1}^{*T}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) \right) \nonumber \\&\quad \le \frac{\varGamma _{\tau ,1}}{2}v_{\tau ,1}^{2}\varTheta _{\tau ,1}^{*}+ \frac{2}{\varGamma _{\tau ,1}} \end{aligned}$$

(32)

with $\varGamma _{\tau ,1}$ being a positive design parameter. From (17) and (30)–32), $\dot{V}_{\tau ,1}$ can be rewritten as

$$\begin{aligned} \dot{V}_{\tau ,1}&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2}\right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }}\sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad +\varDelta _{\tau ,0}+\varepsilon _{\tau ,1}^{*2}-\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2} \nonumber \\&\quad +v_{\tau ,1}^{2}+p_{\tau ,1}^{*2}+\frac{2}{\varGamma _{\tau ,1}}+v_{\tau ,1}\left( v_{\tau ,2}-\dot{y}_{\tau ,r}+k_{\tau ,1}z_{\tau ,1}\right. \nonumber \\&\quad \left. +\theta _{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}(\hat{x}_{\tau ,1})+\alpha _{\tau ,2}+\frac{\varGamma _{\tau ,1}}{2}v_{\tau ,1}\varTheta _{\tau ,1}^{*}\right) \nonumber \\&\quad +\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\left( v_{\tau ,1}\varphi _{\tau ,1}(\hat{x}_{\tau ,1})-\frac{1}{c_{\tau ,1}}\dot{\theta }_{\tau ,1}\right) \nonumber \\&\quad -\frac{1}{\bar{c}_{\tau ,1}}\tilde{\varTheta }_{\tau ,1}\dot{\varTheta }_{\tau ,1} \end{aligned}$$

(33)

Choose the first virtual control $\alpha _{\tau ,2}$ and adaptive laws as

$$\begin{aligned} \alpha _{\tau ,2}&= -\theta _{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) +\dot{y}_{\tau ,r}-k_{\tau ,1}s_{\tau ,1}-\frac{\varGamma _{\tau ,1}}{2} v_{\tau ,1}\varTheta _{\tau ,1} \end{aligned}$$

(34)

$$\begin{aligned} \dot{\theta }_{\tau ,1}&= c_{\tau ,1}\left[ (v_{\tau ,1}+r_{\tau ,1}q_{\tau ,1})\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) -\beta _{\tau ,1}\theta _{\tau ,1}\right] \end{aligned}$$

(35)

$$\begin{aligned} \dot{\varTheta }_{\tau ,1}&= \bar{c}_{\tau ,1}\left[ \frac{\varGamma _{\tau ,1}}{2} v_{\tau ,1}^{2}+\delta _{\tau ,1}q_{\tau ,1}-\sigma _{\tau ,1}\varTheta _{\tau ,1}\right] \end{aligned}$$

(36)

where $\beta _{\tau ,1}$ and $\sigma _{\tau ,1}$ are positive design parameters.

From (34)–36), $\dot{V}_{\tau ,1}$ can be rewritten as

$$\begin{aligned} \dot{V}_{\tau ,1}&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2}\right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }}\sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{ r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2}-k_{\tau ,1}v_{\tau ,1}^{2} \nonumber \\&\quad+v_{\tau ,1}^{2}+v_{\tau ,1}v_{\tau ,2}+\varDelta _{\tau ,0}+\varepsilon _{\tau ,1}^{*2}+p_{\tau ,1}^{*2} \nonumber \\&\quad+\frac{2}{\varGamma _{\tau ,1}}+\beta _{\tau ,1}\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\theta _{\tau ,1}+\sigma _{\tau ,1}\tilde{\varTheta }_{\tau ,1}\varTheta _{\tau ,1} \nonumber \\&\quad-\delta _{\tau ,1}q_{\tau ,1}\tilde{\varTheta }_{\tau ,1}-r_{\tau ,1}q_{\tau ,1}\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right) \end{aligned}$$

(37)

It is true that

$$\begin{aligned} -\delta _{\tau ,1}q_{\tau ,1}\tilde{\varTheta }_{\tau ,1}&\le \frac{\delta _{\tau ,1}^{2}}{4}q_{\tau ,1}^{2}+\tilde{\varTheta }_{\tau ,1}^{2} \end{aligned}$$

(38)

$$\begin{aligned} -r_{\tau ,1}q_{\tau ,1}\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right)&\le \frac{r_{\tau ,1}^{2}}{4}q_{\tau ,1}^{2}+ \tilde{\theta }_{\tau ,1}^{\mathrm{T}}\tilde{\theta }_{\tau ,1} \end{aligned}$$

(39)

Then, the derivative of $V_{\tau ,1}$ can be rewritten as

$$\begin{aligned} \dot{V}_{\tau ,1}&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2}\right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }}\sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{ r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2}+\frac{ \delta _{\tau ,1}^{2}}{4}q_{\tau ,1}^{2}+ \nonumber \\&\quad\frac{r_{\tau ,1}^{2}}{4}q_{\tau ,1}^{2}-\left( k_{\tau ,1}-1\right) v_{\tau ,1}^{2}+v_{\tau ,1}v_{\tau ,2}+\beta _{\tau ,1}\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\theta _{\tau ,1} \nonumber \\&\quad +\sigma _{\tau ,1}\tilde{\varTheta }_{\tau ,1}\varTheta _{\tau ,1}+\tilde{\varTheta } _{\tau ,1}^{2}+\tilde{\theta }_{\tau ,1}^{\mathrm{T}}\tilde{\theta }_{\tau ,1}+\varDelta _{\tau ,1} \end{aligned}$$

(40)

where $\varDelta _{\tau ,1}=\varDelta _{\tau ,0}+\varepsilon _{\tau ,1}^{*2}+p_{\tau ,1}^{*2}+\frac{2}{\varGamma _{\tau ,1}}$.

Step $\xi$ ($2\le \xi \le m_{\tau }-1$): The derivative of $s_{\tau ,\xi }$ can be expressed as follows:

$$\begin{aligned} \dot{s}_{\tau ,\xi }&= s_{\tau ,\xi +1}+\bar{\alpha }_{\tau ,\xi +1}+\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi +1}\right) - \dot{\bar{\alpha }}_{\tau ,\xi } \nonumber \\&\quad+\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) +\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) \nonumber \\&\quad-\theta _{\tau ,\xi }^{*T}\varphi _{\tau ,\xi }\left( \underline{\hat{x}} _{\tau ,\xi }\right) +\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{ x}}_{\tau ,\xi }\right) \end{aligned}$$

(41)

In order to compensate the effect of the error $\bar{\alpha }_{\tau ,\xi }-\alpha _{\tau ,\xi }$, the following differential equation is employed.

$$\begin{aligned} \dot{z}_{\tau ,\xi }=-k_{\tau ,\xi }z_{\tau ,\xi }+z_{\tau ,\xi +1}-z_{\tau ,\xi -1}+\left( \bar{\alpha }_{\tau ,\xi +1}-\alpha _{\tau ,\xi +1}\right) \end{aligned}$$

(42)

where $z_{\tau ,\xi }(0)=0$, $k_{\tau ,\xi }$ is a positive design parameter, and $z_{\tau ,\xi +1}$ will be design later.

Define the compensated tracking error signal

$$\begin{aligned} v_{\tau ,\xi }=s_{\tau ,\xi }-z_{\tau ,\xi },v_{\tau ,\xi +1}=s_{\tau ,\xi +1}-z_{\tau ,\xi +1} \end{aligned}$$

(43)

From (41) and (42), $\dot{v}_{\tau ,\xi }$ becomes

$$\begin{aligned} \dot{v}_{\tau ,\xi }&= v_{\tau ,\xi +1}+\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi +1}\right) +\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) -\dot{\bar{\alpha }}_{\tau ,\xi } \nonumber \\&\quad +\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}} _{\tau ,\xi }\right) -\theta _{\tau ,\xi }^{*T}\varphi _{\tau ,\xi }\left( \underline{ \hat{x}}_{\tau ,\xi }\right) +\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) \nonumber \\&\quad +k_{\tau ,\xi }z_{\tau ,\xi }+z_{\tau ,\xi -1}+\alpha _{\tau ,\xi +1} \end{aligned}$$

(44)

The Lyapunov function candidate is considered in the following

$$\begin{aligned} V_{\tau ,\xi }=V_{\tau ,\xi -1}+\frac{1}{2}v_{\tau ,\xi }^{2}+\frac{1}{ 2c_{\tau ,\xi }}\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\tilde{\theta }_{\tau ,\xi }+ \frac{1}{2\bar{c}_{\tau ,\xi }}\tilde{\varTheta }_{\tau ,\xi }^{2} \end{aligned}$$

(45)

where $c_{\tau ,2}$ and $\bar{c}_{\tau ,2}$ are positive design parameters.

Differentiating $V_{\tau ,\xi }$ with respect to time yields

$$\begin{aligned} \dot{V}_{\tau ,\xi }&= \dot{V}_{\tau ,\xi -1}+v_{\tau ,\xi }\dot{v}_{\tau ,\xi }+\frac{1}{c_{\tau ,\xi }}\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\dot{\tilde{ \theta }}_{\tau ,\xi }+\frac{1}{\bar{c}_{\tau ,\xi }}\tilde{\varTheta }_{\tau ,\xi }\dot{\tilde{\varTheta }}_{\tau ,\xi } \nonumber \\&\quad \le \dot{V}_{\tau ,\xi -1}+v_{\tau ,\xi }\left( v_{\tau ,\xi +1}+\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi +1}\right) \right. \nonumber \\&\quad +\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) -\dot{\bar{\alpha }}_{\tau ,\xi }+\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x }}_{\tau ,\xi }\right) \nonumber \\&\quad -\theta _{\tau ,\xi }^{*T}\varphi _{\tau ,\xi }\left( \underline{\hat{x}} _{\tau ,\xi }\right) +\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{ x}}_{\tau ,\xi }\right) +k_{\tau ,\xi }z_{\tau ,\xi } \nonumber \\&\quad \left. +z_{\tau ,\xi -1}+\alpha _{\tau ,\xi +1}\right) - \frac{1}{c_{\tau ,\xi }}\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\dot{\theta }_{\tau ,\xi } \nonumber \\&\quad -\frac{1}{\bar{c}_{\tau ,\xi }}\tilde{\varTheta }_{\tau ,\xi }\dot{\varTheta } _{\tau ,\xi } \end{aligned}$$

(46)

By using the following inequalities

$$\begin{aligned}&v_{\tau ,\xi }\left( \theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi +1}\right) -\theta _{\tau ,\xi }^{*T}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) \right) \nonumber \\&\quad \le \frac{\varGamma _{\tau ,\xi }}{2}v_{\tau ,\xi }^{2}\varTheta _{\tau ,\xi }^{*}+\frac{2}{\varGamma _{\tau ,\xi }}+v_{\tau ,\xi }^{2}+\frac{1}{4} \tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\tilde{\theta }_{\tau ,\xi } \end{aligned}$$

(47)

with a positive design parameter $\varGamma _{\tau ,\xi }$, (46) becomes

$$\begin{aligned} \dot{V}_{\tau ,\xi }&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2} \right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }} \sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum \limits _{j=1}^{\xi -1}\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2}-\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }- \frac{r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2} \nonumber \\&\quad +\sum \limits _{j=1}^{\xi -1}\left( \frac{\delta _{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}+\frac{r_{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}\right) +v_{\tau ,\xi -1}v_{\tau ,\xi } \nonumber \\&\quad +\sum \limits _{j=1}^{\xi -1}\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j}+\sum \limits _{j=1}^{\xi -1}\sigma _{\tau ,j}\tilde{ \varTheta }_{\tau ,j}\varTheta _{\tau ,j}+\sum \limits _{j=1}^{\xi -1}\tilde{\varTheta } _{\tau ,j}^{2} \nonumber \\&\quad +v_{\tau ,\xi }^{2}+\sum \limits _{j=1}^{\xi -1}\frac{5}{4}\tilde{\theta } _{\tau ,j}^{\mathrm{T}}\tilde{\theta }_{\tau ,j}+\varDelta _{\tau ,\xi -1}+\frac{\varGamma _{\tau ,\xi }}{2}v_{\tau ,\xi }^{2}\varTheta _{\tau ,\xi }^{*} \nonumber \\&\quad +\frac{2}{\varGamma _{\tau ,\xi }}+\frac{1}{4}\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}} \tilde{\theta }_{\tau ,\xi }+v_{\tau ,\xi }\left( v_{\tau ,\xi +1}+\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) \right. \nonumber \\&\quad -\dot{\bar{\alpha }}_{\tau ,\xi }+\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) +\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) +k_{\tau ,\xi }z_{\tau ,\xi } \nonumber \\&\quad \left. +z_{\tau ,\xi -1}+\alpha _{\tau ,\xi +1}\right) - \frac{1}{c_{\tau ,\xi }}\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\dot{\theta }_{\tau ,\xi } -\frac{1}{\bar{c}_{\tau ,\xi }}\tilde{\varTheta }_{\tau ,\xi }\dot{\varTheta } _{\tau ,\xi } \end{aligned}$$

(48)

Design the virtual control $\alpha _{\tau ,\xi +1}$ and adaptive laws of the form

$$\begin{aligned} \alpha _{\tau ,\xi +1}&= -\theta _{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) -k_{\tau ,\xi }s_{\tau ,\xi }-s_{\tau ,\xi -1}+\dot{\bar{\alpha }}_{\tau ,\xi } \nonumber \\&\quad-\eta _{\tau ,\xi }\left( y_{\tau }-\hat{x}_{\tau ,1}\right) -\frac{\varGamma _{\tau ,\xi } }{2}v_{\tau ,\xi }\varTheta _{\tau ,\xi } \end{aligned}$$

(49)

$$\begin{aligned} \dot{\theta }_{\tau ,\xi }&= c_{\tau ,\xi }\left[ \left( v_{\tau ,\xi }+r_{\tau ,\xi }q_{\tau ,\xi }\right) \varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) -\beta _{\tau ,\xi }\theta _{\tau ,\xi }\right] \end{aligned}$$

(50)

$$\begin{aligned} \dot{\varTheta }_{\tau ,\xi }&= \bar{c}_{\tau ,\xi }\left[ \frac{\varGamma _{\tau ,\xi }}{2} v_{\tau ,\xi }^{2}+\delta _{\tau ,\xi }q_{\tau ,\xi }-\sigma _{\tau ,\xi }\varTheta _{\tau ,\xi }\right] \end{aligned}$$

(51)

where $\beta _{\tau ,\xi }$ and $\sigma _{\tau ,\xi }$ are positive design parameters.

Then, it can be shown that

$$\begin{aligned} \dot{V}_{\tau ,\xi }&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2} \right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }} \sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum \limits _{j=1}^{\xi }\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2}-\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }- \frac{r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2} \nonumber \\&\quad +\sum \limits _{j=1}^{\xi -1}\left( \frac{\delta _{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}+\frac{r_{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}\right) +v_{\tau ,\xi }v_{\tau ,\xi +1} \nonumber \\&\quad +\sum \limits _{j=1}^{\xi }\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j}+\sum \limits _{j=1}^{\xi }\sigma _{\tau ,j}\tilde{ \varTheta }_{\tau ,j}\varTheta _{\tau ,j}+\sum \limits _{j=1}^{\xi -1}\tilde{\varTheta } _{\tau ,j}^{2} \nonumber \\&\quad +\sum \limits _{j=1}^{\xi -1}\frac{5}{4}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\tilde{ \theta }_{\tau ,j}+\varDelta _{\tau ,\xi -1}+\frac{2}{\varGamma _{\tau ,\xi }}+ \frac{1}{4}\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\tilde{\theta }_{\tau ,\xi } \nonumber \\&\quad -\delta _{\tau ,\xi }q_{\tau ,\xi }\tilde{\varTheta }_{\tau ,\xi }-r_{\tau ,\xi }q_{\tau ,\xi }\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right) \end{aligned}$$

(52)

By using the following inequalities

$$\begin{aligned} -\delta _{\tau ,\xi }q_{\tau ,\xi }\tilde{\varTheta }_{\tau ,\xi }&\le \frac{ \delta _{\tau ,\xi }^{2}}{4}q_{\tau ,\xi }^{2}+\tilde{\varTheta }_{\tau ,\xi }^{2} \end{aligned}$$

(53)

$$\begin{aligned} -r_{\tau ,\xi }q_{\tau ,\xi }\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }\left( \underline{\hat{x}}_{\tau ,\xi }\right)&\le \frac{r_{\tau ,\xi }^{2}}{4}q_{\tau ,\xi }^{2}+\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\tilde{\theta } _{\tau ,\xi } \end{aligned}$$

(54)

(52) becomes

$$\begin{aligned} \dot{V}_{\tau ,\xi }&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2} \right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }} \sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{ r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2} \nonumber \\&\quad +\sum \limits _{j=1}^{\xi }\left( \frac{\delta _{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}+\frac{r_{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}\right) -\sum \limits _{j=1}^{\xi }\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2} \nonumber \\&\quad +v_{\tau ,\xi }v_{\tau ,\xi +1}+\sum \limits _{j=1}^{\xi }\beta _{\tau ,j} \tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j}+\sum \limits _{j=1}^{\xi }\sigma _{\tau ,j}\tilde{\varTheta }_{\tau ,j}\varTheta _{\tau ,j} \nonumber \\&\quad +\sum \limits _{j=1}^{\xi }\tilde{\varTheta }_{\tau ,j}^{2}+\sum \limits _{j=1}^{\xi }\frac{5}{4}\tilde{\theta }_{\tau ,j}^{\mathrm{T}} \tilde{\theta }_{\tau ,j}+\varDelta _{\tau ,\xi } \end{aligned}$$

(55)

where $\varDelta _{\tau ,\xi }=\varDelta _{\tau ,\xi -1}+\frac{2}{\varGamma _{\tau ,\xi }}$.

Step $m_{\tau }$: The derivative of $s_{\tau ,m_{\tau }}$ can be obtained as

$$\begin{aligned} \dot{s}_{\tau ,m_{\tau }}&= u_{\tau }+\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) +\eta _{\tau ,m_{\tau }}\left( y_{\tau }-\hat{x}_{\tau ,1}\right) \nonumber \\&\quad -\dot{\bar{\alpha }}_{\tau ,m_{\tau }}+\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau } }\left( \underline{\hat{x}}_{\tau ,m_{\tau }}\right) \nonumber \\&\quad -\theta _{\tau ,m_{\tau }}^{*T}\varphi _{\tau ,m_{\tau }}\left( \underline{ \hat{x}}_{\tau ,m_{\tau }}\right) +\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }}\right) \end{aligned}$$

(56)

The compensating signal is designed as

$$\begin{aligned} \dot{z}_{\tau ,m_{\tau }}=-k_{\tau ,m_{\tau }}z_{\tau ,m_{\tau }}-z_{\tau ,m_{\tau }-1} \end{aligned}$$

(57)

where $z_{\tau ,m_{\tau }}(0)=0$, $k_{\tau ,m_{\tau }}$ is a positive design parameter.

Define the compensated tracking error

$$\begin{aligned} v_{\tau ,m_{\tau }}=s_{\tau ,m_{\tau }}-z_{\tau ,m_{\tau }} \end{aligned}$$

(58)

By using (56) and (57), the derivative $\dot{v}_{\tau ,m_{\tau }}$ can be written as

$$\begin{aligned} \dot{v}_{\tau ,m_{\tau }}&= u_{\tau }+\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau }\right) +\eta _{\tau ,m_{\tau }}\left( y_{\tau }-\hat{x}_{\tau ,1}\right) \nonumber \\&\quad -\dot{\bar{\alpha }}_{\tau ,m_{\tau }}+\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }}\right) -\theta _{\tau ,m_{\tau }}^{*T}\varphi _{\tau ,m_{\tau }}\left( \underline{ \hat{x}}_{\tau ,m_{\tau }}\right) \nonumber \\&\quad+\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x} }_{\tau ,m_{\tau }}\right) +k_{\tau ,m_{\tau }}z_{\tau ,m_{\tau }}+z_{\tau ,m_{\tau }-1} \end{aligned}$$

(59)

The Lyapunov function candidate is considered as

$$\begin{aligned} V_{\tau ,m_{\tau }}&= V_{\tau ,m_{\tau }-1}+\frac{1}{2}v_{\tau ,m_{\tau }}^{2}+\frac{1}{2c_{\tau ,m_{\tau }}}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\tilde{\theta }_{\tau ,m_{\tau }} \nonumber \\&\quad+\frac{1}{2\bar{c}_{\tau ,m_{\tau }}}\tilde{\varTheta }_{\tau ,m_{\tau }}^{2} \end{aligned}$$

(60)

where $c_{\tau ,m_\tau }$ and $\bar{c}_{\tau ,m_\tau }$ are positive design parameters.

The time derivative of $V_{\tau ,m_{\tau }}$ becomes

$$\begin{aligned} \dot{V}_{\tau ,m_{\tau }}&= \dot{V}_{\tau ,m_{\tau }-1}+v_{\tau ,m_{\tau }} \dot{v}_{\tau ,m_{\tau }}-\frac{1}{c_{\tau ,m_{\tau }}}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\dot{\theta }_{\tau ,m_{\tau }} \nonumber \\&\quad -\frac{1}{\bar{c}_{\tau ,m_{\tau }}}\tilde{\varTheta }_{\tau ,m_{\tau }}\dot{ \varTheta }_{\tau ,m_{\tau }} \nonumber \\&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2}\right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }}\sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad+v_{\tau ,m_{\tau }-1}v_{\tau ,m_{\tau }}-\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\left( \frac{\delta _{\tau ,j}^{2}}{4} q_{\tau ,j}^{2}+\frac{r_{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}\right) -\sum \limits _{j=1}^{m_{\tau }-1}\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2}\nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j}+\sum \limits _{j=1}^{m_{\tau }-1}\sigma _{\tau ,j} \tilde{\varTheta }_{\tau ,j}\varTheta _{\tau ,j}+\varDelta _{\tau ,m_{\tau }-1} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\tilde{\varTheta }_{\tau ,j}^{2}+\sum \limits _{j=1}^{m_{\tau }-1}\frac{5}{4}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\tilde{\theta }_{\tau ,j}+v_{\tau ,m_{\tau }}\left( u_{\tau }\right. \nonumber \\&\quad +\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x} }_{\tau ,m_{\tau }},u_{\tau }\right) +\eta _{\tau ,m_{\tau }}\left( y_{\tau }-\hat{x} _{\tau ,1}\right) \nonumber \\&\quad -\dot{\bar{\alpha }}_{\tau ,m_{\tau }}+\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }}\right) -\theta _{\tau ,m_{\tau }}^{*T}\varphi _{\tau ,m_{\tau }}\left( \underline{ \hat{x}}_{\tau ,m_{\tau }}\right) \nonumber \\&\quad +\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x} }_{\tau ,m_{\tau }}\right) \left. +k_{\tau ,m_{\tau }}z_{\tau ,m_{\tau }}+z_{\tau ,m_{\tau }-1}\right) \nonumber \\&\quad -\frac{1}{c_{\tau ,m_{\tau }}}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\dot{ \theta }_{\tau ,m_{\tau }}-\frac{1}{\bar{c}_{\tau ,m_{\tau }}}\tilde{\varTheta } _{\tau ,m_{\tau }}\dot{\varTheta }_{\tau ,m_{\tau }} \end{aligned}$$

(61)

From the fact

$$\begin{aligned}&v_{\tau ,m_{\tau }}\left( \theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}(\underline{\hat{x}}_{\tau ,m_{\tau }},u_{\tau })-\theta _{\tau ,m_{\tau }}^{*T}\varphi _{\tau ,m_{\tau }}(\underline{\hat{x}}_{\tau ,m_{\tau }})\right) \nonumber \\&\quad \le \frac{\varGamma _{\tau ,m_{\tau }}}{2}v_{\tau ,m_{\tau }}^{2}\varTheta _{\tau ,m_{\tau }}^{*}+\frac{2}{\varGamma _{\tau ,m_{\tau }}}+v_{\tau ,m_{\tau }}^{2}+\frac{1}{4}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\tilde{\theta } _{\tau ,m_{\tau }} \end{aligned}$$

(62)

with a positive design parameter $\varGamma _{\tau ,m_\tau }$, it is easily verified that $\dot{V}_{\tau ,m_{\tau }}$ can be further written as

$$\begin{aligned} \dot{V}_{\tau ,m_{\tau }}&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2} \right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }} \sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{ r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2}\nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\left( \frac{\delta _{\tau ,j}^{2}}{4} q_{\tau ,j}^{2}+\frac{r_{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}\right) \nonumber \\&\quad -\sum \limits _{j=1}^{m_{\tau }-1}\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2}+v_{\tau ,m_{\tau }-1}v_{\tau ,m_{\tau }} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j}+\sum \limits _{j=1}^{m_{\tau }-1}\sigma _{\tau ,j} \tilde{\varTheta }_{\tau ,j}\varTheta _{\tau ,j} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\tilde{\varTheta }_{\tau ,j}^{2}+\sum \limits _{j=1}^{m_{\tau }-1}\frac{5}{4}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\tilde{\theta }_{\tau ,j}+\varDelta _{\tau ,m_{\tau }-1} \nonumber \\&\quad +\frac{\varGamma _{\tau ,m_{\tau }}}{2}v_{\tau ,m_{\tau }}^{2}\varTheta _{\tau ,m_{\tau }}^{*}+\frac{2}{\varGamma _{\tau ,m_{\tau }}}+v_{\tau ,m_{\tau }}^{2} \nonumber \\&\quad +\frac{1}{4}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\tilde{\theta }_{\tau ,m_{\tau }}+v_{\tau ,m_{\tau }}\left( u_{\tau }+\eta _{\tau ,m_{\tau }}\left( y_{\tau }-\hat{x}_{\tau ,1}\right) \right. \nonumber \\&\quad-\dot{\bar{\alpha }}_{\tau ,m_{\tau }}+\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }}\right) \nonumber \\&\quad\left. +\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{ \hat{x}}_{\tau ,m_{\tau }}\right) +k_{\tau ,m_{\tau }}z_{\tau ,m_{\tau }}+z_{\tau ,m_{\tau }-1}\right) \nonumber \\&\quad-\frac{1}{c_{\tau ,m_{\tau }}}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\dot{ \theta }_{\tau ,m_{\tau }}-\frac{1}{\bar{c}_{\tau ,m_{\tau }}}\tilde{\varTheta } _{\tau ,m_{\tau }}\dot{\varTheta }_{\tau ,m_{\tau }} \end{aligned}$$

(63)

Design an actual controller $u_{\tau }$ and adaptive laws as

$$\begin{aligned} u_{\tau }&= -\theta _{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}\left( \underline{\hat{x}}_{\tau ,m_{\tau }}\right) -k_{\tau ,m_{\tau }}s_{\tau ,m_{\tau }}-s_{\tau ,m_{\tau }-1}+\dot{\bar{\alpha }}_{\tau ,m_{\tau }} \nonumber \\&\quad -\eta _{\tau ,m_{\tau }}\left( y_{\tau }-\hat{x}_{\tau ,1}\right) -\frac{\varGamma _{\tau ,m_{\tau }}}{2}v_{\tau ,m_{\tau }}\varTheta _{\tau ,m_{\tau }} \end{aligned}$$

(64)

$$\begin{aligned} \dot{\theta }_{\tau ,m_{\tau }}&= c_{\tau ,m_{\tau }}\left[ \left( v_{\tau ,m_{\tau }}+r_{\tau ,m_{\tau }}q_{\tau ,m_{\tau }}\right) \varphi _{\tau ,m_{\tau }}-\beta _{\tau ,m_{\tau }}\theta _{\tau ,m_{\tau }}\right] \end{aligned}$$

(65)

$$\begin{aligned} \dot{\varTheta }_{\tau ,m_{\tau }}&= \bar{c}_{\tau ,m_{\tau }}\left[ \frac{\varGamma _{\tau ,m_{\tau }}}{2}v_{\tau ,m_{\tau }}^{2}+\delta _{\tau ,m_{\tau }}q_{\tau ,m_{\tau }}-\sigma _{\tau ,m_{\tau }}\varTheta _{\tau ,m_{\tau }}\right] \end{aligned}$$

(66)

where $\beta _{\tau ,m_{\tau }}$ and $\sigma _{\tau ,m_{\tau }}$ are positive design parameters.

Substituting (64)–(66) into (63) gives

$$\begin{aligned} \dot{V}_{\tau ,m_{\tau }}&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2} \right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }} \sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{ r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2}\nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\left( \frac{\delta _{\tau ,j}^{2}}{4} q_{\tau ,j}^{2}+\frac{r_{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}\right) \nonumber \\&\quad -\sum \limits _{j=1}^{m_{\tau }-1}\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2}+\sum \limits _{j=1}^{m_{\tau }}\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }}\sigma _{\tau ,j}\tilde{\varTheta }_{\tau ,j}\varTheta _{\tau ,j}+\sum \limits _{j=1}^{m_{\tau }-1}\frac{5}{4}\tilde{\theta } _{\tau ,j}^{\mathrm{T}}\tilde{\theta }_{\tau ,j} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }-1}\tilde{\varTheta }_{\tau ,j}^{2}+\varDelta _{\tau ,m_{\tau }-1}+\frac{2}{\varGamma _{\tau ,m_{\tau }}}+v_{\tau ,m_{\tau }}^{2}\nonumber \\&\quad +\frac{1}{4}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\tilde{\theta }_{\tau ,m_{\tau }}-\delta _{\tau ,m_{\tau }}q_{\tau ,m_{\tau }}\tilde{\varTheta }_{\tau ,m_{\tau }} \nonumber \\&\quad -k_{\tau ,m_{\tau }}v_{\tau ,m_{\tau }}^{2}-r_{\tau ,m_{\tau }}q_{\tau ,m_{\tau }}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }} \end{aligned}$$

(67)

By using the following inequalities

$$\begin{aligned} -\delta _{\tau ,m_{\tau }}q_{\tau ,m_{\tau }}\tilde{\varTheta }_{\tau ,m_{\tau }}&\le \frac{\delta _{\tau ,m_{\tau }}^{2}}{4}q_{\tau ,m_{\tau }}^{2}+\tilde{ \varTheta }_{\tau ,m_{\tau }}^{2} \end{aligned}$$

(68)

$$\begin{aligned} -r_{\tau ,m_{\tau }}q_{\tau ,m_{\tau }}\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\varphi _{\tau ,m_{\tau }}&\le \frac{r_{\tau ,m_{\tau }}^{2}}{4} q_{\tau ,m_{\tau }}^{2}+\tilde{\theta }_{\tau ,m_{\tau }}^{\mathrm{T}}\tilde{\theta } _{\tau ,m_{\tau }} \end{aligned}$$

(69)

(67) becomes

$$\begin{aligned} \dot{V}_{\tau ,m_{\tau }}&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2} \right) \left\| e_{\tau }\right\| ^{2}+\frac{1}{\varrho _{\tau }} \sum _{\xi =1}^{m_{\tau }}\left\| \tilde{\theta }_{\tau ,\xi }\right\| ^{2} \nonumber \\&\quad -\sum _{\xi =1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{ r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}\right) q_{\tau ,\xi }^{2}\nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }}\left( \frac{\delta _{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}+\frac{r_{\tau ,j}^{2}}{4}q_{\tau ,j}^{2}\right) \nonumber \\&\quad -\sum \limits _{j=1}^{m_{\tau }}\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2}+\sum \limits _{j=1}^{m_{\tau }}\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }}\sigma _{\tau ,j}\tilde{\varTheta }_{\tau ,j}\varTheta _{\tau ,j}+\sum \limits _{j=1}^{m_{\tau }}\tilde{\varTheta }_{\tau ,j}^{2} \nonumber \\&\quad +\sum \limits _{j=1}^{m_{\tau }}\frac{5}{4}\tilde{\theta }_{\tau ,j}^{\mathrm{T}} \tilde{\theta }_{\tau ,j}+\varDelta _{\tau ,m_{\tau }-1}+\frac{2}{\varGamma _{\tau ,m_{\tau }}} \end{aligned}$$

(70)

It follows from Young inequality that

$$\begin{aligned} \sum \limits _{j=1}^{m_{\tau }}\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}}\theta _{\tau ,j}&\le \frac{1}{2}\sum \limits _{j=1}^{m_{\tau }}\beta _{\tau ,j}\theta _{\tau ,j}^{*T}\theta _{\tau ,j}^{*}-\frac{1}{2} \sum \limits _{j=1}^{m_{\tau }}\beta _{\tau ,j}\tilde{\theta }_{\tau ,j}^{\mathrm{T}} \tilde{\theta }_{\tau ,j} \end{aligned}$$

(71)

$$\begin{aligned} \sum \limits _{j=1}^{m_{\tau }}\sigma _{\tau ,j}\tilde{\varTheta }_{\tau ,j}\varTheta _{\tau ,j}&\le \frac{1}{2}\sum \limits _{j=1}^{m_{\tau }}\sigma _{\tau ,j}^{*T}\varTheta _{\tau ,j}^{*}\varTheta _{\tau ,j}^{*}-\frac{1}{2} \sum \limits _{j=1}^{m_{\tau }}\sigma _{\tau ,j}\tilde{\varTheta }_{\tau ,j}^{2} \end{aligned}$$

(72)

Then, $\dot{V}_{\tau ,m_{\tau }}$ satisfies

$$\begin{aligned} \dot{V}_{\tau ,m_{\tau }}&\le -\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2} \right) \left\| e_{\tau }\right\| ^{2}-\sum \limits _{j=1}^{m_{\tau }}\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2} \nonumber \\&\quad -\sum _{j=1}^{m_{\tau }}\left( r_{\tau ,\xi }\lambda _{\tau ,\xi }-\frac{ r_{\tau ,\xi }^{2}\eta _{\tau ,\xi }^{2}}{4}-\frac{\delta _{\tau ,j}^{2}}{4}- \frac{r_{\tau ,j}^{2}}{4}\right) q_{\tau ,\xi }^{2} \nonumber \\&\quad -\sum \limits _{j=1}^{m_{\tau }}\left( \frac{\beta _{\tau ,j}}{2}-\frac{5}{4} -\frac{1}{\varrho _{\tau }}\right) \tilde{\theta }_{\tau ,j}^{\mathrm{T}}\tilde{\theta } _{\tau ,j} \nonumber \\&\quad -\sum \limits _{j=1}^{m_{\tau }}\left( \frac{\sigma _{\tau ,j}}{2}-1\right) \tilde{\varTheta }_{\tau ,j}^{2}+\varDelta _{\tau ,m_{\tau }} \end{aligned}$$

(73)

where $\varDelta _{\tau ,m_{\tau }}=\varDelta _{\tau ,m_{\tau }-1}+\frac{2}{\varGamma _{\tau ,m_{\tau }}}+\frac{1}{2}\sum \limits _{j=1}^{m_{\tau }}\beta _{\tau ,j}\theta _{\tau ,j}^{*T}\theta _{\tau ,j}^{*}+\frac{1}{2} \sum \limits _{j=1}^{m_{\tau }}\sigma _{\tau ,j}^{*T}\varTheta _{\tau ,j}^{*}\varTheta _{\tau ,j}^{*}$.

Consider a whole Lyapunov function candidate as

$$\begin{aligned} V&= \sum _{\tau =1}^{N}\frac{1}{2}e_{\tau }^{\mathrm{T}}P_{\tau }e_{\tau }+\sum _{\tau =1}^{N}\sum _{j=1}^{m_{\tau }}\frac{1}{2}r_{\tau ,j}q_{\tau ,j}^{2}+\sum _{\tau =1}^{N}\sum _{j=1}^{m_{\tau }}\frac{1}{2}v_{\tau ,j}^{2} \nonumber \\&\quad +\sum _{\tau =1}^{N}\sum _{j=1}^{m_{\tau }}\frac{1}{2c_{\tau ,j}}\tilde{ \theta }_{\tau ,j}^{\mathrm{T}}\tilde{\theta }_{\tau ,j}+\sum _{\tau =1}^{N}\sum _{j=1}^{m_{\tau }}\frac{1}{2\bar{c}_{\tau ,j}}\tilde{\varTheta } _{\tau ,j}^{2} \end{aligned}$$

(74)

Then, $\dot{V}$ becomes

$$\begin{aligned} \dot{V}&\le -\sum _{\tau =1}^{N}\left( \mu _{\tau ,0}-m_{\tau }-\frac{1}{2}\right) \left\| e_{\tau }\right\| ^{2} \nonumber \\&-\sum _{\tau =1}^{N}\sum \limits _{j=1}^{m_{\tau }}\left( k_{\tau ,j}-1\right) v_{\tau ,j}^{2} \nonumber \\&\quad -\sum _{\tau =1}^{N}\sum _{j=1}^{m_{\tau }}\left( r_{\tau ,j}\lambda _{\tau ,j}-\frac{r_{\tau ,j}^{2}\eta _{\tau ,j}^{2}}{4}-\frac{\delta _{\tau ,j}^{2}}{4}-\frac{r_{\tau ,j}^{2}}{4}\right) q_{\tau ,j}^{2} \nonumber \\&\quad -\sum _{\tau =1}^{N}\sum \limits _{j=1}^{m_{\tau }}\left( \frac{\beta _{\tau ,j}}{2}-\frac{5}{4}-\frac{1}{\varrho _{\tau }}\right) \tilde{\theta }_{\tau ,j}^{\mathrm{T}}\tilde{\theta }_{\tau ,j} \nonumber \\&\quad -\sum _{\tau =1}^{N}\sum \limits _{j=1}^{m_{\tau }}\left( \frac{\sigma _{\tau ,j}}{2}-1\right) \tilde{\varTheta }_{\tau ,j}^{2}+\varDelta \end{aligned}$$

(75)

where $\varDelta =\sum _{\tau =1}^{N}\varDelta _{\tau ,m_{\tau }}$.

Remark 3

Traditional backstepping control method cannot directly solve the control problem of pure-feedback nonlinear systems [44, 45], where the pure-feedback systems must be transformed into strict-feedback systems. Because the system states $x_{\tau ,\xi +1},\ldots ,x_{\tau ,m_\tau }$ are not available for the $\xi$-th backstepping controller design. In this paper, by adding and subtracting $\tilde{\theta }_{\tau ,\xi }^{\mathrm{T}}\varphi _{\tau ,\xi }(\underline{\hat{x}}_{\tau ,\xi })$ and inequalities scaling (47), the backstepping control is directly applied to deal with the tracking control problem of pure-feedback nonlinear systems.

So far, the adaptive fuzzy decentralized tracking control design has been completed by using the state observer, the serial–parallel estimation model, backstepping technique and the compensated tracking error. Then, the main result of the proposed control method in this paper can be summarized as a theorem in the following.

Theorem 1

Based on Assumptions 1–2, with the fuzzy adaptive controller, which is composed of the state observer (8), the serial–parallel estimation model (18), the compensating signals (25), (42) and (57), the virtual controllers (34) and (49), the actual controller (64), and adaptive laws (35), (36), (50), (51), (65) and (66), if there exist the positive design parameters $r_{\tau ,\xi }$, $\lambda _{\tau ,\xi }$, $\eta _{\tau ,\xi }$, $\delta _{\tau ,j}$, $k_{\tau ,\xi }$, $\beta _{\tau ,\xi }$, $\varrho _{\tau }$ and $\sigma _{\tau ,j}$ such that $r_{\tau ,j}\lambda _{\tau ,j}-\frac{ r_{\tau ,j}^{2}\eta _{\tau ,j}^{2}}{4}-\frac{\delta _{\tau ,j}^{2}}{4}-\frac{ r_{\tau ,j}^{2}}{4}>0$, $k_{\tau ,j}-1>0$, $\frac{\beta _{\tau ,j}}{2}-\frac{ 5}{4}-\frac{1}{\varrho _{\tau }}>0$ and $\frac{\sigma _{\tau ,j}}{2}-1>0$, then all the signals in the closed-loop system are bounded and the output can track the given reference signal.

Proof

Define $c_{\tau }=\min _{\xi =1,\ldots ,m_{\tau }}\{\frac{\mu _{\tau ,0}-m_{\tau }-\frac{1}{2}}{\lambda _{\max }(P_{\tau })},(2\lambda _{\tau ,j}-\frac{r_{\tau ,j}\eta _{\tau ,j}^{2}}{2}-\frac{\delta _{\tau ,j}^{2}}{2r_{\tau ,j}}-\frac{r_{\tau ,j}}{2}),2(k_{\tau ,\xi }-1)$, $2c_{\tau ,j}(\frac{\beta _{\tau ,j}}{2}-\frac{5}{4}-\frac{1}{\varrho _{\tau }}),2 \bar{c}_{\tau ,j}( \frac{\sigma _{\tau ,j}}{2}-1)\}$ and $c=\min \{c_{1},\ldots ,c_{N}\}$. It follows from (75) that

$$\begin{aligned} \dot{V}\le -cV+\varDelta , \end{aligned}$$

(76)

which has a solution of the form

$$\begin{aligned} V(t)\le V(0){\mathrm{e}}^{-ct}+\frac{\varDelta }{c}. \end{aligned}$$

(77)

The proof is completed. $\square$

Remark 4

It is worth noting that the above parameters only guarantee the stability of the nonlinear systems (1). The parameters selection of the above controller design process directly affects the control performance. The control performance can be improved by increasing the design parameters $k_{\tau ,\xi }$, $c_{\tau ,\xi }$, $\bar{c}_{\tau ,\xi }$, $\varGamma _{\tau ,\xi }$, or decreasing $r_{\tau ,\xi }$ ($\tau =1,\ldots ,N$, $\xi =1,\ldots ,m_\tau$).

5 Simulation example

In this part, numerical as well a practical examples are presented in order to illustrate the effectiveness of the proposed composite adaptive fuzzy decentralized tracking control method.

Example 1

The uncertain large-scale pure-feedback nonlinear system is considered as follows:

$$\begin{aligned}&{\left\{ \begin{array}{ll} \dot{x}_{1,1}={\mathrm{e}}^{0.5x_{1,1}^{2}}x_{1,2}+0.1\cos \left( y_{1}y_{2}\right) +0.02\cos (0.5t) \\ \dot{x}_{1,2}=x_{1,1}x_{1,2}+u_{1}+2\sin \left( 0.1y_{1}y_{2}\right) +0.01sin(t) \\ y_{1}=x_{1,1} \end{array}\right. } \end{aligned}$$

(78)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \dot{x}_{2,1}&={\mathrm{e}}^{0.5x_{2,1}^{2}}x_{2,2}+\sin \left( x_{2,1}^{2}\right) x_{2,2}+0.1\sin \left( 3y_{1}\right) \\ &\quad+0.01\sin (0.2t) \\ \dot{x}_{2,2}&=x_{2,1}x_{2,2}\sin \left( x_{2,1}\right) +u_{2}+\cos \left( 0.5y_{1}y_{2}\right) \\ &\quad +0.02\cos (0.5t) \\ y_{2}&=x_{2,1} \end{array}\right. } \end{aligned}$$

(79)

where $f_{1,1}\left( x_{1,1},x_{1,2}\right) ={\mathrm{e}}^{0.5x_{1,1}^{2}}x_{1,2}$, $f_{1,2}\left( x_{1,1},x_{1,2},u_{1}\right) =x_{1,1}x_{1,2}+u_{1}$, $f_{2,1}\left( x_{2,1},x_{2,2}\right) ={\mathrm{e}}^{0.5x_{2,1}^{2}}x_{2,2}+\sin (x_{2,1}^{2})x_{2,2}$, $f_{2,2}\left( x_{2,1},x_{2,2}\right) =x_{2,1}x_{2,2}\sin (x_{2,1})+u_{2}$, $g_{1,1}\left( y_{1},y_{2}\right) =0.1\cos (y_{1}y_{2})$, $g_{1,2}\left( y_{1},y_{2}\right) =2\sin (0.1y_{1}y_{2})$, $g_{2,1}\left( y_{1},y_{2}\right) =0.1\sin (3y_{1})$, $g_{2,2}\left( y_{1},y_{2}\right) =\cos (0.5y_{1}y_{2})$, $d_{1,1}(t)=0.02\cos (0.5t)$, $d_{1,2}(t)=0.01sin(t)$, $d_{2,1}(t)=0.01\sin (0.2t)$ and $d_{2,2}(t)=0.02\cos (0.5t)$. The reference signals are given as $y_{1,r}=\sin (t)$ and $y_{2,r}=\cos (t)$.

Choose the fuzzy membership functions as

$$\begin{aligned} \mu _{F_{\tau ,1}^{l}}\left( \hat{x}_{\tau ,1}\right) &=\exp \left( \frac{-\left( \hat{x}_{\tau ,1}+2-0.5l\right) ^{2}}{2}\right) \\ \mu _{F_{\tau ,2}^{l}}\left( \hat{x}_{\tau ,1},\hat{x}_{\tau ,2}\right) &=\exp \left( \frac{-(\hat{x}_{\tau ,1}+2-0.5l)^{2}}{2}\right) \\&\quad \times \exp \left( \frac{-(\hat{x}_{\tau ,2}+2-0.5l)^{2}}{2}\right) \end{aligned}$$

where $l=1,\ldots ,7$. Design the fuzzy basis functions as

$$\begin{aligned} \varphi _{\tau ,1}\left( \hat{x}_{\tau ,1}\right)&= \left[ \varphi _{\tau 11}\left( \hat{x}_{\tau ,1}\right) ,\ldots ,\varphi _{\tau 17}\left( \hat{x}_{\tau ,1}\right) \right] ^{\mathrm{T}}\\ \varphi _{\tau ,2}\left( \hat{x}_{\tau ,1},\hat{x}_{\tau ,2}\right)&= \left[ \varphi _{\tau 21}\left( \hat{x}_{\tau ,1},\hat{x}_{\tau ,2}\right) ,\ldots ,\varphi _{\tau 27}(\hat{x} _{\tau ,1},\hat{x}_{\tau ,2})\right] ^{\mathrm{T}} \end{aligned}$$

where

$$\begin{aligned} \varphi _{\tau 1l}\left( \hat{x}_{\tau ,1}\right)&= \frac{\mu _{F_{\tau ,1}^{l}}\left( \hat{x} _{\tau ,1}\right) }{\sum _{l=1}^{7}\mu _{F_{\tau ,1}^{l}}\left( \hat{x}_{\tau ,1}\right) }\\ \varphi _{\tau 2l}\left( \hat{x}_{\tau ,1},\hat{x}_{\tau ,2}\right)&= \frac{\mu _{F_{\tau ,2}^{l}}\left( \hat{x}_{\tau ,1},\hat{x}_{\tau ,2}\right) }{\sum _{l=1}^{7}\mu _{F_{\tau ,2}^{l}}\left( \hat{x}_{\tau ,1},\hat{x}_{\tau ,2}\right) } \end{aligned}$$

with $\tau =1,2$, $l=1,2,\ldots ,7$.

Remark 5

According to Lemma 1, an unknown nonlinear function can be approximated by a FLS. For each input variable x of the FLS, Gaussian-type functions $\mu _{F_i}(x_i)=\exp [-(x-\mu _i)^2/\sigma _i]$ are chosen as fuzzy membership functions, where $i=1,\ldots ,n$, $\mu _i$ is the center point, and $\sigma _i$ is the width. The whole sequence of fuzzy membership functions is required to cover the universe of discourse of the variable x.

In this paper, the universes of discourse for $\hat{x}_{\tau ,1}$ and $\hat{x}_{\tau ,2}$ are chosen as $[-1.5,1.5]$. The center points of seven Gaussian-type membership function $\mu _{F_{\tau ,\xi }^l}$ are chosen as $-1.5, -1, -0.5, 0, 0.5, 1, 1.5$. And the widths of all fuzzy membership functions are chosen as 2.

The initial values of all the variables and adaptation laws are chosen as zero. The design parameters are chosen as $k_{1,1}=18$, $k_{1,2}=18$, $k_{2,1}=18$, $k_{2,2}=18$, $\alpha _{1,2}=\alpha _{2,2}=0.01$, $\beta _{1,1}=\beta _{1,2}=\beta _{2,1}=\beta _{2,2}=120$, $c_{1,1}=0.02$, $c_{1,2}=0.03$, $c_{2,1}=0.02$, $c_{2,2}=0.03$, $\bar{c}_{1,1}=\bar{c}_{1,2}=\bar{c}_{2,1}= \bar{c}_{2,2}=3$.

Fig. 1

The system tracking performance

Fig. 2

The system tracking performance

Fig. 3

Curves of $x_{1,\xi }$ and $\hat{x}_{1,\xi }$ for the first subsystem ($\xi =1,2$)

Fig. 4

Curves of $x_{2,\xi }$ and $\hat{x}_{2,\xi }$ for the second subsystem ($\xi =1,2$)

Fig. 5

The control input $u_1$ of the first subsystem

Fig. 6

The control input $u_2$ of the second subsystem

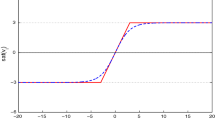
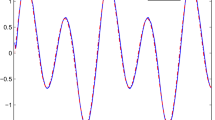
Through the proposed controller, the simulation results are given in Figs. 1, 2, 3, 4, 5 and 6. Figures 1 and 2 show the good tracking performance of the proposed control method. Figures 3 and 4 are the curves of the system states and state observer. The controllers $u_{1}$ and $u_{2}$ of the pure-feedback nonlinear system are shown in Figs. 5 and 6.

Example 2

In order to illustrate the practicality of the proposed control method in this paper, an interconnected system composed of coupled inverted double pendulums [17] and [24] is considered by denoting $x_{1,1}=\theta _1$ (angular position), $x_{1,2}=\dot{\theta _1}$ (angular rate), $x_{2,1}=\theta _2$ and $x_{2,2}=\dot{\theta _2}$ as

$$\begin{aligned}&{\left\{ \begin{array}{ll} \dot{x}_{1,1}&=x_{1,2},\\ \dot{x}_{1,2}&=\left( \frac{M_1gr}{J_1}-\frac{kr^2}{4J_1}\right) \sin \left( x_{1,1}\right) +\frac{kr}{2J_1}(l-b)\\ &\quad +\frac{u_1}{J_1}+\frac{kr^2}{4J_1}\sin \left( x_{2,1}\right) ,\\ y_1&=x_{1,1} \end{array}\right. }\\&{\left\{ \begin{array}{ll} \dot{x}_{2,1}&=x_{2,2},\\ \dot{x}_{2,2}&=\left( \frac{M_2gr}{J_2}-\frac{kr^2}{4J_2}\right) \sin \left( x_{2,1}\right) +\frac{kr}{2J_2}(l-b)\\ &\quad +\frac{u_2}{J_2}+\frac{kr^2}{4J_2}\sin \left( x_{1,2}\right) \\ y_2&=x_{2,1} \end{array}\right. } \end{aligned}$$

where $M_1=M_2=2$ kg are the pendulum end masses, $J_1=J_2=1$ kg are the moments of inertia, $k=10$ N/m is the spring constant of the connecting spring, $r=0.1$ m is the pendulum height, $l=0.5$ m is the natural length of the spring, and $g=9.81 m/s^2$ is gravitational acceleration. The distance between the pendulum hinges is defined as $b=0.4$ m.

Denote $f_{1,1}(x_{1,1})=x_{1,2}$, $f_{1,2}(\underline{x}_{1,2})=(\frac{m_1gr}{J_1}-\frac{kr^2}{4J_1})\sin (x_{1,1})+\frac{u_1}{J_1}$, $f_{2,1}(x_{2,1})=x_{2,2}$, $f_{2,2}(\underline{x}_{2,2})=(\frac{m_2gr}{J_2}-\frac{kr^2}{4J_2})\sin (x_{2,1})+\frac{u_2}{J_2}$, $g_{1,1}(t)=0$, $g_{1,2}=\frac{kr^2}{4J_1}\sin (x_{2,1})$, $g_{2,1}(t)=0$, $g_{2,2}(t)=0$, $d_{1,1}(t)=0$, $d_{1,2}(t)=\frac{kr}{2J_1}(l-b)$, $d_{2,1}(t)=0$, $d_{2,2}(t)=\frac{kr^2}{4J_2}\sin (x_{1,2})+\frac{kr}{2J_2}(l-b)$.

The initial values of all the variables and adaptation laws are chosen as zero. The design parameters are chosen as $k_{1,1}=278$, $k_{1,2}=k_{2,1}k_{2,2}=178$, $\alpha _{1,2}=\alpha _{2,2}=0.01$, $\beta _{1,1}=\beta _{1,2}=\beta _{2,1}=\beta _{2,2}=120$, $c_{1,1}=0.02$, $c_{1,2}=0.03$, $c_{2,1}=0.02$, $c_{2,2}=0.03$, $\bar{c}_{1,1}=\bar{c}_{1,2}=\bar{c}_{2,1}= \bar{c}_{2,2}=3$.

Fig. 7

The system tracking performance

Fig. 8

The system tracking performance

Fig. 9

Curves of $x_{1,\xi }$ and $\hat{x}_{1,\xi }$ for the first subsystem ($\xi =1,2$)

Fig. 10

Curves of $x_{2,\xi }$ and $\hat{x}_{2,\xi }$ for the second subsystem ($\xi =1,2$)

Fig. 11

The control input $u_1$ of the first subsystem

Fig. 12

The control input $u_2$ of the second subsystem

The simulation results are given in Figs. 7, 8, 9, 10, 11 and 12. Figures 7 and 8 display the curves of the ideal signal $y_{\tau ,r}$ and the output $y_\tau$ of the $\tau$-th subsystem $(\tau =1,2)$. In order to illustrate the advantages of the proposed observer-based composite adaptive tracking control method (OB-CATC), we have added a comparison with the adaptive tracking control method (ATC) in [17]. The comparison results are shown in Figs. 7 and 8. Compared with the ATC method in [17], the proposed control method in this paper has better tracking accuracy and faster tracking speed. Meanwhile, the proposed adaptive tracking control method in [17] cannot solve the control problem for the nonlinear systems with unmeasurable states. Figures 9 and 10 are the curves of the system states and state observer. The controllers $u_{1}$ and $u_{2}$ of the coupled inverted double pendulums are shown in Figs. 11 and 12.

6 Conclusion

A composite adaptive fuzzy decentralized tracking control method has been proposed for a class of uncertain pure-feedback large-scale nonlinear systems with unmeasurable states and interconnection items. The fuzzy state observer has been designed to solve the unmeasurable state problem. The serial–parallel estimation model and compensating signals were used to construct the system controller. In addition, with the proposed controller, all the signals in the closed-loop system are bounded, and the tracking error and the state observer error converge to a compact neighborhood around zero. For each step of traditional backstepping control, only one adaptive law needs to be designed. But for the proposed control method in this paper, two adaptive laws need to be designed in each step, which leads to relatively complicated controller design. In the future, our research scope will be extended to reduce the complexity of the controller design of uncertain pure-feedback nonlinear systems.