Introduction

Measles, a highly contagious disease caused by the measles virus, is spread by coughing and sneezing via close interpersonal contact or direct contact with secretions. It is one of the leading causes of death among young children globally, despite the availability of a safe and effective vaccine. Approximately 134,200 people died from measles in 2015, mostly children under the age of 5. Since there is no specific treatment for measles, routine measles vaccination for children is the key public health strategy to prevent the disease (WHO 2017).

Measles virus continues to circulate and cause significant morbidity in China which accounts for a large proportion of the measles cases reported in the Western Pacific Region (WHO 2009). In 1978, China established the national Expanded Programme on Immunization and began to implement a standard schedule for routine immunization that included a dose of measles vaccine administered at 8 months of age. In 1986, a second routine dose of measles vaccine, at 7 years of age, was recommended (Ma et al. 2011). The mean annual measles incidence reported in China was 572.0/100,000 population in the 1960s, 355.3/100,000 population in the 1970s, 52.9/100,000 population in the 1980s, and 7.6/100,000 population in the 1990s (Wang et al. 2003). A nationwide measles supplementary immunization activity was conducted in 2010, and the incidence of measles in mainland China subsequently reached its lowest reported level in 2012 (6,183 cases, 0.46/100,000 population). However, in 2013, a nationwide resurgence of measles occurred primarily among young, unvaccinated children with 27,647 cases and an incidence rate 2.05/100,000 population, and in 2014, there were 52,628 cases and the incidence reached 3.88/100,000 population (National Health and Family Planning Commission of PRC 2017; Ma et al. 2014) (see Fig. 1). This outbreak was believed to be a result of measles vaccination coverage gaps among young children and adults, and insufficient hospital isolation of cases (Zheng et al. 2016).

Fig. 1
figure 1

Reported human measles a annual data and b monthly data in mainland China from January 2004 to December 2016 (National Health and Family Planning Commission of PRC 2017)

Full size image

The transmission dynamics of measles epidemics have been extensively modeled and studied (measles is probably the first and the most studied infectious disease using mathematical models). Hamer (1906) studied the regular occurrence of measles in London. Soper (1929) was the first to propose a mathematical model to explain the periodic occurrence of measles. Bartlett (1957) observed that the number of localized extinctions of measles was related to the population size of the community. Later, Bartlett (1960) and Bolker and Grenfell (1996) observed that in small communities epidemics are often followed by extinction of disease as the chain of transmission breaks down by mass vaccination. Bolker and Grenfell (1993) and Keeling and Grenfell (1997) found that the critical community size above which measles can persist may depend on the spatial structure and connectedness of the regional population. Many researchers have studied the periodic reoccurrence of measles which is believed to be strongly related to the seasonal forcing (Bartlett 1957; London and Yorke 1973; Yorke and London 1973; Anderson and May 1983, 1991; Hethcote 1983; Conlan and Grenfell 2007). In fact, sinusoidal functions have been extensively used to describe the seasonal factor in modeling measles (Dietz 1976; Schenzle 1984; Earn et al. 2000). Various mathematical models have also been developed to study the transmission dynamics of measles in different countries and regions (Bartlett 1960; Bolker and Grenfell 1996; Earn et al. 2000; Ferrari et al. 2008; McLean and Anderson 1988; Pang et al. 2015).

Though measles is a serious public health problem, there are very few studies on modeling the transmission dynamics of measles in China (Bai and Liu 2015). Since the monthly measles data from China exhibit periodic pattern, in this paper, we adapt the periodic measles model from Earn et al. (2000) to study the effect of vaccination and seasonality on the transmission dynamics of measles and use the model to simulate the monthly data in China from January 2004 to December 2016.

The paper is organized as follows. In “Mathematical modeling” section, the periodic measles model will be introduced. Mathematical analysis, including the boundedness of solutions, calculation of the basic reproduction number, global stability of the disease-free equilibrium, and existence of positive periodic solutions, is carried out in “Mathematical analysis” section. Sensitivity analysis of the basic reproduction number and simulation of the measles data from China are given in “Simulations and sensitivity analysis” section. A brief discussion is presented in “Discussion” section.

Mathematical modeling

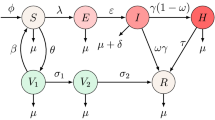
We denote the total numbers of humans by N(t) and classify the human population into four subclasses: susceptible, exposed, infections, and removed, with the numbers denoted by S(t), E(t), I(t), and R(t) at time t,  respectively. The transmission dynamics associated with these subpopulations are illustrated in Fig. 2.

Fig. 2
figure 2

Flowchart of measles transmission in a population

Full size image

The transmission rate between S(t) and I(t) is described \(\beta (t)\). Since the monthly measles data in China exhibit seasonal pattern, we use the periodic function \(\beta (t)=a[1+b \sin \left( \frac{\pi }{6}t+8 \right) ]\) to describe the transmission rate, where a is the baseline contact rate and b is the magnitude of forcing (Dietz 1976; Zhang et al. 2012). The birth numbers of humans per unit time are constant. Natural death rate is \(\mu\). Based on the model in Earn et al. (2000) with periodic transmission rate, we consider the following periodic measles model:

$$\begin{aligned} \frac{{\mathrm{d}}S}{{\mathrm{d}}t} &=A(1-\rho )- \beta (t)IS- \mu S, \\ \frac{{\mathrm{d}}E}{{\mathrm{d}}t} &=\beta (t)IS-(\sigma +\mu )E, \\ \frac{{\mathrm{d}}I}{{\mathrm{d}}t}&=\sigma E-(\gamma +\mu )I, \\ \frac{{\mathrm{d}}R}{{\mathrm{d}}t}&=A\rho +\gamma I-\mu R, \end{aligned}$$
(1)

where all parameters are positive constants and the interpretations and values are described in Table 1.

Table 1 Parameters in model (1)
Full size table

Mathematical analysis

Extinction and persistence of the disease

Notice that from the equations in model (1), we have

$$\frac{{\mathrm{d}}N}{{\mathrm{d}}t}=A-\mu N.$$
(2)

Letting \(\Lambda =\left\{ \left( S,E,I,R \right) \mid S>0, E\ge 0, I \ge 0, R>0, 0<S+E+I+R< \frac{A}{\mu } \right\}\), we have the following results.

Theorem 3.1

The region \(\Lambda\) is positively invariant with respect to system (1). In particular, (S(t), E(t), I(t), R(t)) is positive for all \(t>0\) if the initial values \(S(0)=S_0>0, E(0)=E_0>0, I(0)=I_0>0, R(0)=R_0>0\) at \(t=0\).

Proof

On the nonnegativity of solutions of system (1) with nonnegative initial conditions, by the continuous dependence of solutions with respect to initial values, we only need to show that when \(S_{0}>0, E_{0}>0, I_{0}>0\) and \(R_{0}>0, \left( S(t),E(t),I(t),R(t) \right)\) is positive for all \(t>0\). Let

$$n(t)=\min \left\{ S(t),E(t),I(t),R(t) \right\} , \; \forall t>0.$$

Clearly, \(n(0)>0\). Assuming that there exists a \(t_{1}>0\) such that \(n(t_{1})=0\) and \(n(t)>0,\forall t \in \left[ 0,t_{1} \right) .\)

If \(n(t_{1})=S(t_{1})\), from the first equation of system (1), we have

$$\frac{{\mathrm{d}}S}{{\mathrm{d}}t} \geqslant -(\beta (t)I+\mu )S, \quad \forall t>[0,t_1].$$

Thus,

$$0=S(t_1) \geqslant S_{0}{\mathrm{e}}^{-\int _{0}^{t_{1}} (\beta (t)I+\mu ) {\mathrm{d}}s}>0,$$

which leads to a contradiction.

If \(n(t_{1})=E(t_{1})\), since \(I(t)\ge 0\) and \(S(t)\ge 0\) for all \(t \in \left[ 0,t_{1} \right]\), from the second equation of system (1), it follows that

$$\frac{{\mathrm{d}}E}{{\mathrm{d}}t} \geqslant -(\sigma +\mu )E, \quad \forall t>[0,t_1].$$

Hence,

$$0=E(t_1) \geqslant E_{0}{\mathrm{e}}^{-(\sigma +\mu )t_{1}}>0,$$

which also leads to a contradiction.

Similar contradictions can be deduced in the cases of \(n(t_{1})=I(t_{1})\) and \(n(t_{1})=R(t_{1})\). Therefore, \(S(t)>0,E(t)>0,I(t)>0\) and \(R(t)>0\) for all \(t>0\).

Concerning (2), we have \(N(t) = \frac{A}{\mu }+N_{0}{\mathrm{e}}^{-\mu t},\) where \(N_{0}=S(0)+E(0)+I(0)+R(0)\). Hence, N(t) is bounded for all \(t \geqslant 0\) and

$$\limsup _{t \rightarrow \infty }N(t) = \frac{A}{\mu },$$

which implies S(t), E(t), I(t), and R(t) are also bounded for all \(t>0\). This completes the proof. \(\square\)

It is easy to see that system (1) has one disease-free equilibrium

$$P_{0}=\left( {\hat{S}},0,0,{\hat{R}} \right) ,$$

where \({\hat{S}}=\frac{A\left( 1-\rho \right) }{\mu },{\hat{R}}=\frac{A\rho }{\mu }\). Now, we deduce the basic reproduction number \({\mathcal {R}}_{0}\) for model (1) following the definition of Bacaër and Guernaoui (2006) and the general calculation procedure in Wang and Zhao (2008). Firstly, we can verify that model (1) satisfies the conditions \(\left( A{1}\right) -\left( A{7}\right)\) given in Wang and Zhao (2008).

Denote

$$F(t)=\left( \begin{array}{cc} 0 &\quad\beta (t){\hat{S}} \\ 0&\quad 0 \end{array}\right) , \;\; V(t)=\left( \begin{array}{cc} \sigma +\mu &\quad0 \\ -\sigma &\quad \gamma +\mu \end{array}\right) .$$

Let Y(t, s) be the \(2\times 2\) matrix solution of the following initial value problem

$$\left\{ \begin{array}{l} \frac{{\mathrm{d}}Y(t,s)}{{\mathrm{d}}t}=-V(t)Y(t,s),\\ Y(s,s)=I.\\ \end{array} \right.$$

Further, let \(\omega =12\) and \(C_{\omega }\) be the ordered Banach space of all \(\omega -\)periodic continuous functions from \({\mathbb {R}}\) to \({\mathbb {R}}^{2}\) with maximum norm \(\left\| \cdot \right\|\) and positive cone \(C^+_{\omega }:=\left\{ \varphi \in C_{\omega }: \varphi (t)\geqslant 0,\forall t \in {\mathbb {R}} \right\}\). Suppose \(\varphi \in C^+_{\omega }\) is the initial distribution of infections individuals, then \(F(s)\varphi (s)\) is the rate of new infection produced by the infectious individuals who were introduced at time s, and \(Y(t,s)F(s)\varphi (s)\) represents the distributions of those infection individuals who were newly infected at time s and remain in the infected compartments at time t for \(t \geqslant s\). Naturally,

$$\int _{-\infty }^{t}Y(t,s)F(s)\varphi (s){\mathrm{d}}s=\int _{0}^{+\infty }Y(t,t-a)F(t-a)\varphi (t-a)da$$
(3)

is the distribution of accumulative new infections at times t produced by all those infected individuals \(\varphi (s)\) introduced at times previous to t. Then, we define a linear operator \(L:C_{\omega } \rightarrow C_{\omega }\) as follows

$$\left( L\varphi \right) =\int _{0}^{+\infty }Y(t,t-a)F(t-a)\varphi (t-a)da,\forall t \in {\mathbb {R}},\varphi \in C_{\omega }.$$
(4)

L is called the next infection operator.

By the definition of Bacaër and Guernaoui (2006) and the general calculation procedure in Wang and Zhao (2008), the basic reproduction number \({\mathcal {R}}_{0}\) for the model (1) is defined as the spectral radius \(\rho (L)\) of operator L, that is,

$${\mathcal {R}}_{0}=\rho (L).$$
(5)

Employing Theorem 2.1 and Theorem 2.2 given in Wang and Zhao (2008), we can deduce the following results with respect to \({\mathcal {R}}_{0}\) and the locally asymptotical stability of the disease-free equilibrium \(P_{0}\) for model (1).

Theorem 3.2

On the basic reproduction number \({\mathcal {R}}_{0}\) of model (1), we have

  1. (i)

    \({\mathcal {R}}_{0}<1\) if and only if \(\rho (\Phi _{F-V}(\omega ))<1\);

  2. (ii)

    \({\mathcal {R}}_{0}=1\) if and only if \(\rho (\Phi _{F-V}(\omega ))=1\);

  3. (iii)

    \({\mathcal {R}}_{0}>1\) if and only if \(\rho (\Phi _{F-V}(\omega ))>1\).

Moreover, \(P_{0}\) is locally asymptotically stable if \({\mathcal {R}}_{0}<1\) and unstable if \({\mathcal {R}}_{0}>1\), where \(\Phi _{F-V}(t)\) is the monodromy matrix of the linear \(\omega\)-periodic system \(\frac{du}{{\mathrm{d}}t}=[F(t)-V(t)]u\).

Lemma 3.3

For an arbitrary positive number \(\theta\), there exists \(t_{1}>0\) such that for all \(t> t_{1}, S(t)\le {\hat{S}}+\theta\).

Proof

From the first two equations of system (1), we have

$$\begin{aligned}\frac{d(S+E)}{{\mathrm{d}}t}&= A(1-\rho )-\mu S-(\sigma +\mu )E \\ &\le A(1-\rho )-\mu S-\mu E \\ &=A(1-\rho )-\mu (S+E) \end{aligned}$$

which implies that

$$\limsup _{t\rightarrow \infty } (S(t)+E(t))\le \frac{A(1-\rho )}{\mu }.$$

Because \(E\ge 0\), it follows that

$$\limsup _{t\rightarrow \infty } S(t) \le \frac{A(1-\rho )}{\mu }={\hat{S}}.$$

Thus, there is \(t_{1}> 0\), such that for all \(t> t_{1}, S(t) \le {\hat{S}}+\theta\) for arbitrary positive number \(\theta\). \(\square\)

Theorem 3.4

The disease-free equilibrium \(P_{0}\) is globally asymptotically stable when \({\mathcal {R}}_{0}<1\).

Proof

If \({\mathcal {R}}_{0}<1\), we know that \(\rho (\Phi _{F-V}(\omega ))<1\) and \(P_{0}\) is locally asymptotically stable by Theorem 3.2. We can choose \(\theta >0\) small enough such that \(\rho (\Phi _{F-V+M_{\theta }}(\omega ))<1\), where

$$M_{\theta }=\left( \begin{array}{cc} 0 &{} \theta \\ 0 &{} 0 \end{array}\right) .$$

Considering the region X and using Lemma 3.3, when \(t> t_{1}\), we have

$$\left\{ \begin{array}{lr} \frac{{\mathrm{d}}E}{{\mathrm{d}}t}\le \beta (t)({\hat{S}}+\theta )I-\left( \sigma +\mu \right) E, &{} \\ \frac{{\mathrm{d}}I}{{\mathrm{d}}t}=\sigma E-\left( \gamma +\mu \right) I. &{} \end{array} \right.$$
(6)

with the following comparison system

$$\left\{ \begin{array}{lr} \frac{{\mathrm{d}}E}{{\mathrm{d}}t}=\beta (t)({\hat{S}}+\theta )I-\left( \sigma +\mu \right) E, &{} \\ \frac{{\mathrm{d}}I}{{\mathrm{d}}t}=\sigma E-\left( \gamma +\mu \right) I, &{} \end{array} \right.$$
(7)

that is,

$$\frac{{\mathrm{d}}h}{{\mathrm{d}}t}=(F(t)-V(t)+M_{\theta })h(t),\ h(t)=(E(t),I(t))^{\mathrm{T}}.$$
(8)

By Lemma 2.1 in Zhang and Zhao (2007), it follows that there exists a positive \(\omega -\)periodic functions \({\hat{h}}(t)\) such that \(h(t)={\mathrm{e}}^{pt}{\hat{h}}(t)\) is a solution of system (8), where \(p=\frac{1}{\omega } \ln \rho (\Phi _{F-V+M_{\theta }}(\omega ))\). We know that \(\rho (\Phi _{F-V+M_{\theta }}(\omega ))<1\) when \({\mathcal {R}}_{0}<1\). Therefore, we have \(h(t)\rightarrow 0\) as \(t\rightarrow \infty\), which implies that the zero solution of system (7) is globally asymptotically stable. Applying the comparison principle (Smith and Waltman 1995), we know that for system (1), \(E(t)\rightarrow 0\) and \(I(t)\rightarrow 0\) as \(t\rightarrow \infty\). By the theory of asymptotic autonomous systems (Thieme 1992), it is also known that \(S(t)\rightarrow {\hat{S}}\) and \(R(t)\rightarrow {\hat{R}}\) as \(t\rightarrow \infty\). So \(P_{0}\) is globally attractive when \({\mathcal {R}}_{0}<1\). It follows that \(P_{0}\) is globally asymptotically stable when \({\mathcal {R}}_{0}<1\). \(\square\)

Existence of positive periodic solutions

Define

$$\begin{aligned}X:&=\left\{ (S,E,I,R)\in X: S>0, E\ge 0, I\ge 0, R>0 \right\} ,\\ X_{0}:&=\left\{ (S,E,I,R)\in X: E> 0, I> 0 \right\} , \\ \partial X_{0}&=X\setminus X_{0}=\left\{ (S,E,I,R)\in X: E=I=0 \right\} . \end{aligned}$$

Let \(u(t,x_{0})\) be the unique solution of system (1) with the initial value \(x_{0}=(S_{0},E_{0},I_{0},R_{0})\). Let \(P:X\rightarrow X\) be the \(\hbox {Pincar}\acute{e}\) map associated with system (1), i.e.,

$$P(x_{0})=u(\omega ,x_{0}), \; \forall x_{0}\in X,$$

where \(\omega =12\) is the period. Applying the existence-uniqueness theorem (Perko 2001), we know that \(u(t,x_{0})\) is the unique solution of system (1) with \(u(0,x_{0})=x_{0}\). From Theorem 3.1, we know the X is positively invariant and P is point dissipative.

Lemma 3.5

When \({\mathcal {R}}_{0}>1\), then there exist a \(\delta >0\) such that when

$$\left\| (S_{0},E_{0},I_{0},R_{0}) -P_{0}\right\| \le \delta$$

for any \((S_{0},E_{0},I_{0},R_{0})\in X_{0}\), we have

$$\limsup _{m\rightarrow \infty }d\left[ P^{m}(S_{0},E_{0},I_{0},R_{0}),P_{0} \right] \ge \delta ,$$

where \(P_{0}=({\hat{S}},0,0,{\hat{R}})\).

Proof

If \({\mathcal {R}}_{0}>1\), we obtain \(\rho (\Phi _{F-V}(\omega ))>1\) by Theorem 2.2 in Wang and Zhao (2008). Choose \(\epsilon >0\) small enough such that \(\rho (\Phi _{F-V+M_{\epsilon }}(\omega ))>1\), where

$$M_{\epsilon }=\left( \begin{array}{cc} 0 &\quad \epsilon \\ 0 &\quad 0 \end{array}\right) .$$

Now, we proceed by contradiction to prove that

$$\limsup _{m\rightarrow \infty }d\left[ P^{m}(S_{0},E_{0},I_{0},R_{0}),P_{0} \right] \ge \delta .$$

If not, then

$$\limsup _{m\rightarrow \infty }d\left[ P^{m}(S_{0},E_{0},I_{0},R_{0}),P_{0} \right] < \delta$$

for some \(\left( S_{0},E_{0},I_{0},R_{0} \right) \in X_{0}\). Without loss of generality, we assume that \(d\left[ P^{m}(S_{0},E_{0},I_{0},R_{0}),P_{0} \right] < \delta\) for all \(m\ge 0\). By the continuity of the solutions with respect to the initial values, we obtain

$$\left\| u\left( t_1,P^{m}(S_{0},E_{0},I_{0},R_{0}) \right) -u(t_1,P_{0}) \right\| \le \epsilon , \quad \forall m\ge 0,\forall t_{1}\in \left[ 0,\omega \right] .$$

For any \(t\ge 0\), let \(t=m\omega +t_{1}\), where \(t_{1}\in \left[ 0,\omega \right]\) and \(m=\left[ \frac{t}{\omega } \right]\), which is the greatest integer less than or equal to \(\frac{t}{\omega }\). Then, we have

$$\left\| u(t,(S_{0},E_{0},I_{0},R_{0})) -u(t,P_{0})\right\| = \left\| u\left( t_{1},P^{m}(S_{0},E_{0},I_{0},R_{0}) \right) -u(t_{1},P_{0}) \right\| \le \epsilon$$

for any \(t>0\), which implies that when \(t\ge 0\), we have \({\hat{S}}-\epsilon \le S(t)\le {\hat{S}}+\epsilon , 0\le E(t)\le \epsilon , 0\le I(t)\le \epsilon\). Then, for \(\left\| (S_{0}, E_{0}, I_{0}, R_{0}) -P_{0}\right\| \le \delta\), we have

$$\left\{ \begin{array}{lr} \frac{{\mathrm{d}}E}{{\mathrm{d}}t}\ge \beta (t)({\hat{S}}-\epsilon )I-\left( \sigma +\mu \right) E, &{} \\ \frac{{\mathrm{d}}I}{{\mathrm{d}}t}=\sigma E-\left( \gamma +\mu \right) I. &{} \end{array} \right.$$
(9)

Next, we consider the linear system

$$\left\{ \begin{array}{lr} \frac{{\mathrm{d}}E}{{\mathrm{d}}t}=\beta (t)({\hat{S}}-\epsilon )I-\left( \sigma +\mu \right) E, &{} \\ \frac{{\mathrm{d}}I}{{\mathrm{d}}t}=\sigma E-\left( \gamma +\mu \right) I. &{} \end{array} \right.$$
(10)

Once again by Lemma 2.1 in Zhang and Zhao (2007), it follows that there exists a positive \(\omega -\)periodic function \({\hat{g}}(t)\) such that \(g(t)=(E(t), I(t))={\mathrm{e}}^{pt}{\hat{g}}(t)\) is a solution of system (10), where \(p=\frac{1}{\omega } \ln \rho (\Phi _{F-V+M_{\epsilon }}(\omega ))\). Because \({\mathcal {R}}_{0}>1\) and \(\rho (\Phi _{F-V+M_{\epsilon }}(\omega ))>1\), when \(g(0)>0\), \(g(t)\rightarrow \infty\) as \(t\rightarrow \infty\). Applying the comparison principle (Smith and Waltman 1995), we know that when \(E(0)>0, I(0)>0, E(t)\rightarrow \infty\) and \(I(t)\rightarrow \infty\) as \(t\rightarrow \infty\). This is a contradiction. The proof of the lemma is complete. \(\square\)

Theorem 3.6

If \({\mathcal {R}}_{0}>1\), then system (1) admits at least one positive periodic solution.

Proof

We need to prove that P is uniformly persistent with respect to \((X_{0},\partial X_{0})\). First of all, we claim that \(X_{0}\) and \(\partial X_{0}\) are positively invariant with respect to system (1). In fact, for any \((S_{0},E_{0},I_{0},R_{0})\in X_{0}\), solving the equations of system (1), we have

$$\begin{aligned}S(t)&= {\mathrm{e}}^{-\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t}\left[ S_{0}+\int _{0}^{t}A(1-\rho ){\mathrm{e}}^{\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t}{\mathrm{d}}t \right] \nonumber \\ &> A(1-\rho ){\mathrm{e}}^{-\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t}\int _{0}^{t}{\mathrm{e}}^{\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t}{\mathrm{d}}t>0, \quad \forall t> 0,\end{aligned}$$
(11)
$$\begin{aligned} R(t) &= {\mathrm{e}}^{-\mu t}\left[ R_{0}+\int _{0}^{t}(A\rho +\gamma I(t)) {\mathrm{e}}^{\mu t}{\mathrm{d}}t \right] \nonumber \\ &> {\mathrm{e}}^{-\mu t}\int _{0}^{t}(A\rho +\gamma I(t)) {\mathrm{e}}^{\mu t}{\mathrm{d}}t>0,\quad \forall t> 0, \end{aligned}$$
(12)
$$\begin{aligned} E(t) &= {\mathrm{e}}^{-(\sigma +\mu ) t}\left[ E_{0}+\int _{0}^{t}\beta (t)S(t)I(t){\mathrm{e}}^{(\sigma +\mu ) t}{\mathrm{d}}t \right] \nonumber \\ &> {\mathrm{e}}^{-(\sigma +\mu ) t}\left[ \int _{0}^{t}\beta (t)S(t)I(t){\mathrm{e}}^{(\sigma +\mu ) t} {\mathrm{d}}t \right] \ge 0,\quad \forall t> 0,\end{aligned}$$
(13)
$$\begin{aligned} I(t) &= {\mathrm{e}}^{-(\gamma +\mu ) t}\left[ I_{0}+\int _{0}^{t}\sigma E(t){\mathrm{e}}^{(\gamma +\mu ) t} {\mathrm{d}}t \right] \nonumber \\ &> {\mathrm{e}}^{-(\gamma +\mu ) t} \int _{0}^{t}\sigma E(t){\mathrm{e}}^{(\gamma +\mu ) t}{\mathrm{d}}t> 0,\quad \forall t> 0.\end{aligned}$$
(14)

So \(X_{0}\) is positively invariant. Clearly, \(\partial X_{0}\) is relatively closed in X. Set

$$M_{\partial }=\left\{ (S_{0},E_{0},I_{0},R_{0})\in \partial X_{0}: P^{m}(S_{0},E_{0},I_{0},R_{0})\in \partial X_{0},\ \forall m\ge 0\right\} .$$

We firstly show that

$$M_{\partial }=\left\{ (S,0,0,R)\in X:S>0, R>0\right\} .$$
(15)

Note that \(\left\{ (S,0,0,R)\in X :S>0, R>0\right\} \subseteq M_{\partial }\) is obvious, we only need to prove that

$$M_{\partial }\subseteq \left\{ (S,0,0,R)\in X :S>0, R>0 \right\} .$$

Otherwise, if \(M_{\partial }\backslash \left\{ (S,0,0,R)\in X :S>0, R>0\right\} \ne \emptyset\), then there exists at least a point \((S_{0},E_{0},I_{0},R_{0})\in M_{\partial }\) satisfying \(E_{0}>0\) or \(I_{0}>0\).

If \(E_{0}>0\), from the second equation of model (1) and Theorem 3.1, we have that for all \(t>0\)

$$E(t)\ge E_{0}\exp ^{-(\sigma +\mu )t}>0.$$

Thus, from the third equation of model (1) and inequality (14), we also have \(I(t)>0\) for all \(t>0\). From \(S_{0}>0\) and inequality (11), we have \(S(t)>0\) for all \(t>0\). Similarly, From \(R_{0}>0\) and inequality (12), we have \(R(t)>0\) for all \(t>0\). Thus, with initial value \((S_{0},E_{0},I_{0},R_{0})\), we finally obtain that \((S(t), E(t), I(t), R(t))>(0,0,0,0)\) for all \(t>0\), which contradicts that \((S_{0},E_{0},I_{0},R_{0}) \in M_{\partial }\) that requires \(P^{m}(S_{0},E_{0},I_{0},R_{0})\in \partial X_{0}, \forall m\ge 0\).

If \(I_{0}>0\), similarly, we can also prove that \((S(t), E(t), I(t), R(t))>(0,0,0,0)\) for all \(t>0\), which leads to a contradiction. Therefore, we finally have \(M_{\partial }\subseteq \left\{ (S,0,0,R)\in X :S>0, R>0 \right\}\). So the claim (15) holds, which implies \(E_{0}(S,0,0,R)\) is the only fixed point of P in \(M_{\partial }\).

Moreover, Lemma 3.5 implies that \(P_{0}=({\hat{S}},0,0,{\hat{R}})\) is an isolated invariant set in X and \(W^{S}(P_{0})\cap X_{0}=\emptyset\). By the acyclicity theorem on uniform persistence for maps (Theorem 1.3.1 and Remark 1.3.1 in Zhao (2007)), it follows that P is uniformly persistent with respect to \((X_{0}, \partial X_{0} )\).

Now, Theorem 1.3.6 in Zhao (2007) implies that P has a fixed point

$$(S^{*}(0),E^{*}(0),I^{*}(0),R^{*}(0))\in X_{0}.$$

From the first equation of system (1), we have

$$\begin{aligned}S^{*}(t)&= {\mathrm{e}}^{-\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t}\left[ S^{*}(0)+\int _{0}^{t}A(1-\rho ){\mathrm{e}}^{\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t}{\mathrm{d}}t \right] \\&> A(1-\rho ){\mathrm{e}}^{-\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t}\int _{0}^{t}{\mathrm{e}}^{\int _{0}^{t}(\beta (t)I+\mu ){\mathrm{d}}t} {\mathrm{d}}t \\&> 0,\quad \forall t\in \left[ 0,\omega \right] .\end{aligned}$$

The periodicity of \(S^{*}(t)\) implies that \(S^{*}(t)>0\) for all \(t> 0\). Following the processes as in inequalities (11)–(14), we have \(E^{*}(t)>0, I^{*}(t)>0, R^{*}(t)>0\) for all \(t> 0\). Therefore, \((S^{*}(t), E^{*}(t), I^{*}(t), R^{*}(t))\) is a positive \(\omega -\)periodic solution of system (1). \(\square\)

Simulations and sensitivity analysis

In this section, we firstly use the model (1) to simulate the reported measles data of China from January 2004 to December 2016, predict the trend of the disease, and seek for some control and prevention measures. To do so, we need to estimate the parameter values. We obtain the annual number of human population using the annual birth and death data from the National Bureau of Statistics of China 2016. Then, we calculate the average and divide it by 12 to derive the monthly human birth population \(A=1340000\). For \(\beta (t), \rho\) and \(\mu\) by using the least square fitting of I(t) through discretizing the ordinary differential system (1) as follows:

$$I(t_{i}+\bigtriangleup t)=(\sigma E-(\gamma +\mu )I)\bigtriangleup t+I(t_{i}).$$

The least square fitting is to minimize the objective function

$$J(\theta )=\frac{1}{n}\sum _{i=1}^{n}(I(t_{i}-{\hat{I}}(t_{i})),$$

which is implemented by the instruction lsqnonlin, a part of the optimization toolbox in MATLAB. By the least square method, we obtain \(a=1.2527\times 10^{-9}, b=0.3346,\) and \(\rho =0.8216\). The parameter values are listed in Table 1.

We need the initial values to perform the numerical simulations of the model. The number of the initial susceptible population, S(0), is obtained from the China Statistical Yearbook. However, the numbers of the initial exposed population E(0) and the recovered population R(0) cannot be obtained. According to the least square method, We estimate E(0) and R(0), respectively. The comparison between the reported measles data in mainland China from January 2004 to December 2016 and the simulation of I(t) from model (1) is given in Fig. 3.

Fig. 3
figure 3

Comparison between the reported human measles data in mainland China from January 2004 to December 2016 and the simulation of I(t) from model (1). The dashed curve represents the monthly measles data, while the solid curve is simulated by using our model. The values of parameters are given in Table 1. The initial values used in the simulations were \(S(0)=1.29\times 10^9, E(0)=18527, I(0)=1754, R(0)=640000\)

Full size image

Moreover, with these parameter values, we can roughly estimate that the basic reproduction number \({\mathcal {R}}_{0}=0.4663\) under the current circumstances in China. From Fig. 4, we can see that when \({\mathcal {R}}_{0}<1\), the number of infected humans I(t) tends to 0. On the contrary, when \({\mathcal {R}}_{0}>1, I(t)\) tends to a stable periodic solution. We can also predict the general tendency of the epidemic in a long term according to the current situation in China, which is presented in Fig. 5, where the basic reproduction number is \({\mathcal {R}}_{0}=0.4663\). From these figures, we can see that the epidemic of measles can be relieved in a short time and eradicated by strengthening the current prevention and control measures.

Fig. 4
figure 4

Tendency of the human measles cases I(t) in a long term with different values of \({\mathcal {R}}_{0}\). \(A=1900000\) in the upper curve with \({\mathcal {R}}_{0}=1.3614\) and \(A=1300000\) in the lower curve with \({\mathcal {R}}_{0}=0.4663\), respectively, and the other parameter values are in Table 1

Full size image
Fig. 5
figure 5

Tendency of the human measles cases I(t) in a short and b long terms, where the basic reproduction number is \({\mathcal {R}}_{0}=0.4663\)

Full size image

Next, we perform some sensitivity analysis to determine the influence of parameters \(\rho\) (vaccination rate) and a (the contact rate) on \({\mathcal {R}}_{0}\). From Fig. 6a, we observe that \(\rho\) has an obvious effect on \({\mathcal {R}}_{0}\) which indicates that immunization is an effective measure to control measles. Next, we consider the effect of a on \({\mathcal {R}}_{0}\), which is depicted in Fig. 6b. Although they are linear, a is very small and a slight change of a can lead to large variations of \({\mathcal {R}}_{0}\). So reducing the contact between susceptible and infective individuals is important to control measles.

Fig. 6
figure 6

Influence of parameters on \({\mathcal {R}}_0\) a versus \(\rho\) and b versus a

Full size image

Finally, we consider the combined influence of \(\rho\) and a on \({\mathcal {R}}_{0}\) in Fig. 7. From the contour surface, we can see that when the increasing of vaccination and the reduction of contact are combined, controlling measles will be more effective.

Fig. 7
figure 7

Graph of \({\mathcal {R}}_0\) in the terms of a and \(\rho\)

Full size image

Discussion

Measles virus causes significant morbidity in China which accounts for a large proportion of the measles cases reported in the Western Pacific Region (WHO 2009). Thanks to the national Expanded Programme on Immunization established in 1978 and a national plan of action for accelerated measles control (vaccine coverage of at least 90%) in 1997 (Ma et al. 2011). China made significant progress in controlling measles and the mean annual measles incidence decreased dramatically from 355.3/100,000 population in the 1970s to 7.6/100,000 population in the 1990s (Wang et al. 2003).

In 2005, the Regional Committee of WHO Western Pacific Region established 2012 as the target date for the complete regional elimination of measles (WHO 2009; Perry et al. 2014). In 2006, the Chinese Ministry of Health initiated mandatory measles vaccination and set a goal of accelerating the progress of eliminating measles by 2012 (Ma et al. 2011). In 2010, a nationwide measles supplementary immunization activity was conducted, and in 2012, the incidence of measles in China reached its lowest reported level (6,183 cases, 0.46/100,000 population). However, in 2013–2015, a nationwide resurgence of measles occurred in China (27,647 cases, 2.05/100,000 population; 52,628 cases, 3.88/100,000 population; 42,361 cases, 3.11 /100,000 population) (National Health and Family Planning Commission of PRC 2017). Some believed that this outbreak was a result of measles vaccination coverage gaps among young children and adults, and insufficient hospital isolation of cases (Zheng et al. 2016). Other researchers suggested that multiple highly connected foci of measles transmission coexist in China and that migrant workers likely facilitate the transmission of measles across regions (Yang et al. 2017).

The data of human measles cases reported in China exhibit seasonal characteristics. In order to study the transmission dynamics of measles in China, vaccination and seasonality of the spreading of the measles were incorporated into a SEIR epidemic model with periodic transmission rate. Firstly, we calculated the basic reproduction number \({\mathcal {R}}_{0}\) and analyzed the dynamics of the model including the global stability of the disease-free equilibrium and the existence of periodic solutions. The analytical results demonstrate that seasonality plays a key in the persistence of the disease in terms of periodic solutions. Then, we used the periodic model to simulate the monthly data on the number of measles cases from January 2004 to December 2016 in China and predicted the general tendency of disease in China. It was estimated that the basic reproduction number \({\mathcal {R}}_{0}=0.4663\) under the current circumstances in China. This indicates that the epidemic of measles in China can be relieved in a short time, but extra efforts are needed in order to eradicate the disease. Moreover, we carried out some sensitivity analysis of parameters on \({\mathcal {R}}_{0}\) to test some control measures and found that the vaccination rate \(\rho\) has an obvious effect on \({\mathcal {R}}_{0}\) which indicates that immunization is an effective measure to control measles. We also observed that a slight change of the contact rate a can lead to large variations of \({\mathcal {R}}_{0}\), so reducing the contact between susceptible and infective individuals is also important to control measles. Our study shows that measles in China can be controlled and eventually eradicated by increasing the immunization rate, improving the effective vaccine management, and enhancing the awareness of people about measles.

Since one of the main issues in controlling and eliminating measles is the optimal age to vaccinate children in order to have the maximum impact on the incidence of measles-related morbidity and mortality for a given rate of vaccination coverage, age-structured epidemic models have been extensively used to study the transmission dynamics and control of measles (Schenzle 1984; Tudor 1985; Greenhalgh 1988; Hethcote 1988; McLean and Anderson 1988; Ferguson et al. 1996). Taking the periodic and age-dependent transmission rate into consideration, it will be interesting to study the following age-structured periodic measles model:

$$\begin{aligned} \frac{\partial S}{\partial t} + \frac{\partial S}{\partial a}&= - S(t, a) \int ^{\infty }_0 \beta (t; a, a') I(t, a')da' - \left( \mu (a) + \rho (a) \right) S(t, a), \\ \frac{\partial E}{\partial t} + \frac{\partial E}{\partial a}&=S(t, a) \int ^{\infty }_0 \beta (t; a, a') I(t, a')da' - (\sigma (a)+\mu (a))E(t, a), \\ \frac{\partial I}{\partial t} + \frac{\partial I}{\partial a}&=\sigma (a) E(t, a)-(\gamma (a) +\mu (a) )I(t, a), \\ \frac{\partial R}{\partial t} + \frac{\partial R}{\partial a}&=\rho (a) S(t, a) +\gamma (a) I(t,a)-\mu (a) R(t,a) \end{aligned}$$
(16)

with boundary conditions

$$S(t, 0)=A, \;\; E(t, 0)=0, \;\; I(t, 0)=0, \;\; R(t, 0)=0$$
(17)

and initial conditions

$$S(0, a)=S_0(a), \;\; E(0, a)=E_0(a), \;\; I(0, a)=I_0(a), \;\; R(0, a)=R_0(a),$$
(18)

where \(\beta (t; a, a')\) is the rate at which susceptible individuals of age a are infected by infectious individuals of age \(a'\) and is a time periodic function (Schenzle 1984). Interesting properties of the model such as existence and stability of periodic solutions, optimal age vaccinations, and so on deserve further consideration.