Keywords

1 Introduction

By some estimates, as many as two thirds of American adults currently suffer from some type of math phobia due to bad educational experiences with mathematics [1]. Our work with students performing in the bottom quartile in mathematics tests has demonstrated some ways that adding technologies like mobile apps with a particular pedagogical approach can help. Many studies have shown that targeted use of multimedia technologies can make a significant impact on a student’s sense of ownership and engagement [2,3,4,5,6], and yet the lowest-performing students are often the most disengaged, while they are often in a resource-poor environment, with less frequent access to rich interactive technologies. The low cost, the prevalence, and the social appeal of tablets in the classroom can help.

In four schools in Atlanta where our research was conducted, more than 95% of the students are eligible for free and reduced cost lunch, and they only had access to computer labs on the average of once a week, instead of the daily access that is available in more affluent schools. And yet, most of the students we worked with either owned or had some type of access to cellphones. With this in mind, we applied for and received an NSF Early-Concept Grant for Exploratory Research (EAGER) in which we examined the feasibility of combining mathematics curricula with simple mobile app development [7].

Throughout the fall of 2016, and the spring and summer of 2017, we have undertaken to develop a new approach to using mobile apps for introducing educational mathematics simulations in a set of middle-school math classes in a way that blends computing ideas with math instruction. The curricular material involved was developed specifically for students in the lower quartile by the Algebra Project, to further enhance these students’ conceptual and procedural knowledge of mathematics content and to strengthen students’ mathematical practices. The Algebra Project curriculum is based on an experiential mathematics pedagogy and a curricular process with extensive past documentation and research and evidence that it assists the low-performing students that we were targeting [8,9,10,11,12,13].

2 Study Design

The experientially based curriculum of the Algebra Project engages students in concrete events and activities that are then examined reflectively to analyze them mathematically. This reflection and exploration happens during the following five-step curricular process that occurs during the many different units of the Algebra Project curriculum:

  • Step 1: Experience a physical event as a group.

  • Step 2: Represent that event through drawings or by creating models.

  • Step 3: Describe the event informally and intuitively, using natural and idiomatic language.

  • Step 4: Translate the idiomatic description into a structured, formal, feature-rich description.

  • Step 5: Create a symbolic representation of the event using mathematical formalisms.

For our EAGER grant, we proposed integrating basic programming experiences involved in developing mobile apps into these five steps in the following way:

  • Step 1: Experience a simulation of the physical event.

  • Step 2: Represent that simulation through drawings or by creating models.

  • Step 3: Describe the simulation informally and intuitively, using natural and idiomatic language.

  • Step 4: Translate the idiomatic description into a structured set of visual program blocks that represent functional units.

  • Step 5: Connect the functional programming units to recreate the simulated experience as a mobile app.

Two units of the Algebra Project curriculum were chosen for this intervention: the Road Coloring module and the Race Against Time module.

3 The Curricular Units

The first unit of study in this research was the Road Coloring module. In this unit, functions are modeled as simultaneous physical movements by groups of students, and students use ordered pairs and point on a coordinate plane and arrow diagrams to represent the functional transitions. The notions of domain and range are developed and have easily accessible, concrete interpretations.

Along with the conceptual underpinning of the function concept, students are introduced to the Road Coloring challenge based on a famous problem in theoretical computer science first stated in a paper by Adler, Goodwyn, and Weiss [14] that remained unsolved for over 30 years. The original problem asks if all strongly connected, aperiodic, directed graphs have an edge labeling for which a synchronizing instruction exists. In this unit, the directed graphs become “cities” that students represent with the points on the floor (the vertices) serving as “buildings” with numbered “addresses” (building 1, building 2, etc.). And the paths between the points serve as the edges and as one-way roads. The students then attempt to find a set of directions that will get everyone from their different vertices to the same building at the same time.

Once the students physically experience the concept of functions in this manner, multiple representations are introduced. As an example, below are arrow diagrams the students produce of a city with three buildings, with one red road and one blue road leading away from each building (this representation constitutes an edge-colored directed graph with three vertices) (Fig. 1).

Fig. 1
figure 1

Road Coloring task

Full size image

Other standard representations are also introduced to the students, and included are representations of 0–1 stochastic matrices (such as permutation matrices) and one-out directed graphs. The last two representations represent important innovations for function representations in the high school curriculum and were particularly important in the mathematics research that led to the eventual solution of the original Road Coloring problem [15,16,17].

The second unit of study in this research was the Race Against Time module. This module uses relay races as the shared concrete event, and through this event, students are introduced to the concept of linear equations that ultimately lead to the form ax + b = c. Linear equations are developed within the context of “detective work” to determine the locations a team has visited in the course of a race. The concept of slope is introduced and analyzed, as students graph relay race trajectories as “distance traveled” versus time elapsed. The “average velocity” of a relay race leg allows the natural introduction of slope.

The relay races are not outdoor foot races. Students race by stacking plastic cubes on top of one another in a fixed amount of time. The cubes are then laid out in a direction determined by a flip of a coin from a starting point, or from the last endpoint achieved by a previous student racing for the same team. As each team member adds a new displacement during the race to a set of previous displacements, a new distance from the origin is produced. Students produce tables, arrow diagrams, graphs, and equations of the resulting displacements and use these to explore various linear transformations involved in their analyses (Fig. 2):

Fig. 2
figure 2

Various Race Against Time representations

Full size image

This specific development of linear equations makes direct contact with the more general development of the concept of function in the Algebra Project Road Coloring module. The two approaches, from Road Coloring to Race Against Time, provide students with a binocular and complementary perspective on these central concepts of early algebra.

3.1 Developing the Simulated Units: Road Coloring

The Road Coloring mobile app was designed in the fall semester of the 2016–2017 school year to simulate the creation of Road Coloring “cities” made up of a directed graph of vertices called “buildings” connected with edges called red and blue “roads.” The app was originally developed using MIT App Inventor and its Visual Blocks system, and it was tested in Algebra Project classrooms in San Francisco in the fall of 2016, and then it was further developed and tested in the four Algebra Project classrooms in Atlanta in the spring and summer of 2017.

Without the app, constructing cities of more than four buildings (vertices) was very difficult for the students, but with the app, students were able to come up with synchronizing instructions for cities of more than ten buildings. The following shows cities of three buildings, four buildings, and ten buildings, respectively (Fig. 3):

Fig. 3
figure 3

Road Coloring cities and synchronizing instructions

Full size image

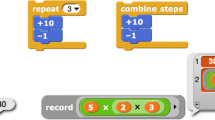
Initially the students used the visual programming block system from MIT App Inventor, to create the apps, but it ran much too slowly when a class of 20+ students were using the web-based program at the same time. Because of this, we developed a scaled down version of the same visual programming block system that worked with blocks that were specific to only the Road Coloring and the Race Against Time units, unlike App Inventor which allows students to create blocks for more general purposes. The blocks for a three-building city appeared as follows (Fig. 4):

Fig. 4
figure 4

Road Coloring program blocks

Full size image

3.2 Developing the Simulated Units: Race Against Time

The Race Against Time app was designed in the spring semester of the 2016–2017 school year to simulate the relay races that make up the Algebra Project’s Race Against Time unit. The app is also an Android app, and it was tested in Algebra Project classrooms in Atlanta in the spring and summer of 2017.

The Relay Race simulation consisted of students dragging cubes that were scrolling along in a box at the top of the screen and stacking them in vertical line. The challenge had different levels of difficulty because of different time constraints placed on them that the students were able to control programmatically (Fig. 5):

Fig. 5
figure 5

Race Against Time simulation

Full size image

After finishing the race, the arrow diagrams produced by the app look the same as the textbook arrow diagrams that the students are familiar with in the classroom. Yet in the app, the students can modify the magnitude and direction of the vectors in real time. In the following diagram is a set of visual programming blocks the students could have constructed to create the simulation shown above (Fig. 6):

Fig. 6
figure 6

Race Against Time programming blocks

Full size image

Using the app, students determine how many legs they will have in their race, which can be any number from 2 to 10, and they also determine how many seconds they will have to stack cubes during each leg, which can be some number from 2 to 25. The students run a simulation where a group of cubes moves along the top of the screen horizontally, and the students must drag them one by one down onto a stack that they are creating. When a leg ends, their stack has a certain amount of cubes which represents a magnitude. And the students press a button that randomly assigns a left or right direction for their stack, which gives it both a magnitude and a direction, making it a vector.

Once a student has finished all of their legs, they have a set of consecutive vectors that have a total set of magnitudes (called the “total distance”) and a resulting displacement from the origin (called the “total displacement”). The total distance concept involves adding the absolute value of the distance traveled during each leg, but it also just represents how many cubes the students stacked during all of the legs combined. The total displacement represents the final distance and direction from the origin, so it represents a new vector that is the result of adding up all of the vectors from each leg of the race.

After finishing all of the legs, students calculate the total distance and the total displacement, and then the students examine tables and arrow diagrams representing the details of their race in different ways. Then the students use the app to solve linear equations that involve the resulting displacements that occur when legs of their race are modified using various linear transformations.

4 Theoretical Underpinnings

The five-step curricular process that we have adapted for this research exploits an experiential learning cycle that begins with the students working through a concrete event and moving progressively to an abstract symbolic and mathematical representation of that event. During this process, the students reflect upon the event by identifying important features captured in informal language (called people-talk) and formal representations (called feature-talk) of the event to figure out how the features are related with symbolic representations (Fig. 7).

Fig. 7
figure 7

Experiential learning cycle

Full size image

The multiple representations of the event that are constructed as students move through the experiential learning cycle are described by W. V. Quine’s notion of the language foundations of mathematics as a circular curricular process [18]. Quine saw mathematics as a conceptual language that has its beginnings in the structuring and regimentation of ordinary discourse. In the curricular process, this structuring occurs with the students in their discussions about their exploration of the important features of the event. In this discourse, students try to make sense of abstract symbolic representations of conventional mathematics. Students work to gain the ability to read algebraic sentences in a meaningful and interpretive fashion. This ability to interpret the symbols of mathematics enables students to affect a shift from algorithms and computation to logic and reasoning as the basis for problem-solving in mathematics.

Our research has allowed us to extend that process of reflection through the interaction with simulations and computing. By developing apps which produce simulations of the concrete experiences being used in the Algebra Project curriculum, students acquire an additional dimension to the experiential learning process they are engaged in. There are both cognitive and affective dimensions to the use of app-based simulations.

The work of Jerome Bruner is particularly relevant here. Bruner has asserted the importance of representation in the learning of knowledge domains in general and of mathematics in particular. In this work, Toward a Theory of Instruction [19], Bruner describes the structure of a knowledge domain in terms of the representations that are used to capture its content. This representational view captures the structure in terms of the modes of representation (enactive, iconic/graphic, or symbolic), the economy of the representation (the cognitive load that students are required to carry), and the power of the representation (descriptive, explanatory, and predictive), and we would add to Bruner’s list the scope of the representation (the degree to which it facilitates near transfer to problems/questions within its defining context or far transfer to problems/questions outside of its original/defining context).

For example, students only used the Road Coloring app simulation after they had built a model city in their classroom. The app’s simulation was always a representation for the students of the real event. The app’s simulation also introduced a hybridization of Bruner’s modes of representations. In traditional mathematics, classroom students typically use enactive representations of mathematical concepts. We call them manipulatives. And students construct iconic representations of mathematics concepts: pictures, graphs, and diagrams. The app simulations provided students with enactive-iconic representations of the mathematical concepts they were engaged with. This type of enactive-iconic representation created a space of possibilities for different types of student engagement and understanding in the classroom. The enactive-iconic representation gave students capability to rapidly construct and manipulate cities of greater complexity than could easily be made of real materials or from paper and pencil.

We also note that in the case of the Relay Race app simulation, the enactive-iconic representation provided by the app gave students the cognitive space to apply visual reasoning and logic to the solution of linear equations. This suggests that the traditional learning progression that takes students through one-step, two-step, to multi-step linear equations may be more a consequence of a didactic choice than a requirement of the cognitive stages that students must go through to achieve mastery of the subject.

One final point is worth making. The concrete events of the Algebra Project’s Curricular Process are in stark contrast to the “hands-on” paradigm employed in many math curricula. In many of these curricula, every lesson can have its own hands-on component, each one separate and distinct, characterizing the particular lesson. Over the years, the Algebra Project has targeted what they consider to be a few foundational events/experiences which meet the representational criteria given above of having broad scope. These experiences embody representations of concepts that apply to broad swaths of the mathematical landscape primarily at the level of introductory algebra. These events and their representations thus act as grounding metaphors for the construction of the foundational concepts of algebra.

Our work with app simulations for two of these grounding metaphors suggests that by providing students, particularly “low-performing” students, with enactive-iconic representations, we create a space for them to apply cognitive abilities that do not normally present in the traditional mathematics classroom. We have yet to see, given the time and the affordances which this technology provides, if the traditional learning progressions will need to be re-written especially for what are now considered “low-performing” students.

These considerations are what lead us to develop our app simulations according to a three-dimensional approach. We sought to design them to include (1) a physical experience that could be shared as a social activity with mathematical implications; (2) enactive-iconic representational objects that can connect naturally to a discourse about the experience and activity; and (3) mathematics knowledge and computational logic that is involved in specific learning unit/learning progression currently in the classroom. Our design goals for app simulations of this nature are thus given by the following image (Fig. 8):

Fig. 8
figure 8

Three-dimensional design of app simulations

Full size image

5 Initial Results

Over 200 students participated in some aspect of this intervention. Initially, we had intended to focus on just four schools in the Atlanta area (Brown, Bunche, Harper Archer, and Long), but due to administrative problems, we were not able to begin the work in the Atlanta schools until the spring of 2017. So in the fall of 2016, we worked with approximately 50 students from the June Jordan School for Equity in San Francisco. During the spring of 2017, we finally began work with about 140 students from the four Atlanta schools. And during the summer of 2017, we worked with about 15 more students as part of a summer school program at the Harper Archer Middle School in Atlanta.

In our work during the fall and spring, our instructional material and our modified visual programming block system were going through an incremental development process, whereby we would try a particular version of the material and then make modifications based on student and teacher feedback or our own analysis. This led to our having a well-defined set of materials and a working version of our own modified visual programming block system by the summer of 2017.

The difference between the work in the summer and the work in that occurred earlier in the fall and spring was that during the fall and spring, our materials were going through constant revision, making it difficult to evaluate formally the impact of any one set of materials. In the summer, however, our materials development process was finished, and so we worked with a stable set of materials during the entire 4 weeks of the summer school. It was during this time that we were able to implement a set of pre- and post-test to begin to evaluate how the work we did contributed to a sense of ownership, engagement, and comprehension within the students.

Our students who participated in the work and the pre- and post-tests over the summer were a very small sample, only 15 students. But all 15 of the students said in one-on-one interviews we conducted that they enjoyed working with the apps, and some explained that they thought of it as a “hands-on” way of doing math. Some went on to say that they felt a true sense of accomplishment when they were able to solve difficult problems using the simulations that would have been much more difficult with only pencil and paper. In many cases, we recorded students showing other students the solutions they came up with displaying a sense of accomplishment in their work, and one student said he was doing this to prove to the other students how “smart” he was.

The summer students were all rising sixth graders, entering the seventh grade, and none of them had been in an algebra class yet. Therefore, on the pre- and post-test, we had the students work on algebraic problems before and after they worked on the curricular material involving the apps. The students spent 2 weeks working on the Road Coloring unit and 2 weeks working on the Race Against Time unit.

The Road Coloring unit dealt with how Red and Blue functions (enactively and iconically represented by the roads) which take inputs and produce an output, and how a sequence of those functions, which is function composition, can be used to produce a particular output. In the pre- and post-tests, students were asked to analyze a set of connected cell towers and how phone calls are routed between them to get to a particular target. Before the unit, only 1 of the 15 could correctly draw composed sequence of routes and solve problems to achieve a correct route for certain calls. After the unit, eight students could accomplish the same tasks.

The Race Against Time unit dealt with representing vectors with arrow diagrams and using the arrow diagrams to solve linear equations. In the pre- and post-tests, students were asked to represent trips on the Marta (Atlanta’s tramline) using arrow diagrams and, when given a sequence of trips, to determine the total distance traveled and the ultimate displacement (the final distance from the beginning of the trip to the end of the trip). On these tasks, only three students could draw an accurate arrow diagram representing a complex trip, only seven students could calculate the correct total distance traveled, and only two calculated the correct displacement. After the unit, 11 students were able to draw an accurate arrow diagram, ten were able to calculate the correct distance, and eight were able to calculate the correct displacement.

Our tests were designed to show increases in conceptual understanding, visual reasoning, and representational logic, not just the ability to manipulating math symbols when solving linear equations. And the majority of the students in both units did improve in these areas. However, we also did do some tests of the ability of students to manipulate mathematical symbols as well after the second unit. Students were shown the following arrow diagram, which was similar to the ones they dealt with in the app simulation (Fig. 9):

Fig. 9
figure 9

Displacement arrow diagram

Full size image

And without any instruction in algebra, students were then shown the following equation and asked to solve for X:

$$ 4+X+4=13 $$

Fourteen of the students were able to answer the question correctly. Then a diagram was shown for the equation 4 + X + 4 = −13, and only ten of the students were still able to solve for X. Then the following was shown with the equation 4 + 2X + 4 = −2, and still ten students (67%) solved this expression for X, again using non-algebraic processes (Fig. 10).

Fig. 10
figure 10

Another displacement arrow diagram

Full size image

This indicated that for those ten students, the conceptual understanding of what that equation represents was grounded in visual reasoning and representational logic. From many indicators, we saw obvious improvements in ownership, engagement, and increased comprehension.

6 Conclusion and Future Directions

Because our research was part of an EAGER grant, which involves early-concept exploratory research, our work was primarily focused on demonstrating that a fuller study is warranted. Although about 200 students participated in some aspect of the research, only 15 students in the summer were part of the sample that dealt with the actual pre- and post-test. The others helped in our exploratory and developmental effort that the EAGER grant is designed for. However, the summer students didn’t have a traditional math class context where we could spend more time with them and see how they performed on traditional mathematics materials before and after our intervention. We see this as the logical next step for our research, as well as to expand on the number of curricular units that we develop simulations for using our three-dimensional design criteria.

And finally, we also see the potential for expanding this intervention into science curricula as well. The Algebra Project was a great fit for this intervention because simulations and experiential learning can be aligned by identifying an appropriate simulation for the concrete experiences in their curriculum. Other math curricula may not always have easily identified concrete experiences that are enactive-iconic and reasonable to simulate. However, we believe that science classes are often focused on physical phenomena that would satisfy this criterion and be reasonable to simulate, and therefore this presents us with another area for future research.