Perhaps the most extensively researched behavioral model of complex behavior is found in stimulus equivalence theory (Sidman, 1994, 2000; Sidman & Tailby, 1982), which posits that unique conditional discriminations can emerge in the absence of direct reinforcement when prerequisite conditional discriminations are directly trained. For example, if a person is taught to match a stimulus A to a stimulus B (A = B), and the same stimulus A to a stimulus C (A = C), the person will most likely also match the stimulus B to the stimulus C (C = B) and vice versa (B = C) without being taught to do so. This derived relation contains the mathematical properties of symmetry and transitivity, both of which are necessary for equivalence (Sidman & Tailby, 1982).Footnote 1 Critchfield, Barnes-Holmes, and Dougher (2018), in a prior issue of Perspective on Behavior Science, discussed how stimulus equivalence represented a marked advance in behavior science, providing lawful descriptions of emergent language learning in humans. Indeed, as the authors claimed, deriving equivalence relations may be a human-specific behavior (see Galizio & Bruce, same issue, for an in-depth review of current animal models of derived relational responding) that opens the door to new areas of research on human language and cognition.

This basic model has been extensively evaluated in human subjects by basic experimental researchers (e.g., Arntzen, Grondahl, & Eilifsen, 2010; Dougher, Augustson, Markham, Greenway, & Wulfert, 1994), and increasingly is the basis of applied technologies for, among other things, teaching language skills to children both with and without disabilities (e.g., LeBlanc, Miguel, Cummings, Goldsmith, & Carr, 2003; Rose, Souza, & Hanna, 1996). Despite vast empirical advances stemming from equivalence theory (McLay, Sutherland, Church, & Tyler-Merrick, 2013; Zentall, Galizio, & Critchfield, 2002), there are disagreements about the fundamental processes that govern the emergence of equivalence responding (Barnes, 1994; Clayton & Hayes, 1999; Hayes & Barnes-Holmes, 2004; Hayes, Barnes-Holmes, & Roche, 2001; Horne & Lowe, 1996, 1997; McIlvane, 2003; Palmer, 2004; Sidman, 1994, 2000).

In an attempt to expand the scope of theoretical accounts of stimulus equivalence, in this article we propose relational density theory as a quantitative metaphor adapted from Newtonian classical mechanics in physics. The theory is an extension of behavioral momentum theory as proposed by Nevin and colleagues (Nevin, 2002; Nevin & Grace, 2000; Nevin & Shahan, 2011). In this article, we introduce the theory, offer a reinterpretation of some existing findings in the basic experimental equivalence literature, and provide recommendations for potential translational application and experimental research needed to validate and extend core assumptions. Our purpose in this article is not to provide an exhaustive account of the theory. Rather, the goal is to lay out the precepts and structure of the theory and relate these to enough experimental findings to demonstrate plausibility. As we will discuss toward the end of the article, an exhaustive evaluation of the ideas proposed here will require both additional theoretical work and new experiments.

The Basic Theory

Quantitatively described models of behavior may hold utility over narratively described theories by allowing for (1) parsimonious descriptions of how selected features operate on a continuum to influence a behavior outcome, and (2) descriptions of higher-order relations (interactions among variables) that are not easily communicated using narratively described models (e.g., Critchfield & Reed, 2009). For example, the matching law (Herrnstein, 1961, 1970; Poling, Edwards, Weeden, & Foster, 2011) describes the relationship between relative rates of behavior and relative rates of reinforcement, expressed in the standard equation: B1/(B1+B2) = r1/(r1+r2) (Herrnstein, 1961). This equation provides a quantitative account of central tenants of Skinner’s (1938, 1953) narrative operant theory, and its extensions (Baum, 1979; Davison & McCarthy, 1988; Herrnstein, 1974) that employ fitted parameters to describe higher-order relations (bias and sensitivity) in choice behavior.

Of primary interest to the present discussion is behavioral momentum theory (BMT; Nevin, 1992; Nevin & Grace, 2000; Nevin & Shahan, 2011). BMT, utilizing Newton’s second law of thermodynamics as a metaphor, describes a change in behavior as a function of two factors: momentary force applied to the behavior system (e.g., present levels of reinforcement or punishment), and the higher-order variable of behavioral mass, or the resistance of behavior to the application of force (also called resistance to change). Mass is usually taken to result from a history of reinforcement and modulates the effects of contemporary contingencies. The BMT equation originally introduced by Nevin and colleagues has been refined to allow for direct computation and prediction of behavior (Nevin & Shahan, 2011; Shahan & Sweeney, 2011), and accounts well for data obtained from both animal models (Nevin & Shahan, 2011; Podlesnik & Shahan, 2009) and clinical interventions (e.g., Mace et al., 1990, 2010).

From the perspective of research on derived stimulus relations, which reveals a number of indirect influences over behavior (Greer & Keohane, 2005; Hayes et al., 2001; Horne & Lowe, 1996, 1997; Sidman & Tailby, 1982), a potential limitation of models like the matching law and BMT is the assumption that behavior is necessarily under direct contingency control. An extensive literature on derived stimulus relations reveals effects that are more extended than those usually addressed by invoking immediate and historical contingencies of reinforcement.

Relational density theory is an attempt to provide a unifying, quantitativeFootnote 2 account of relational responding that integrates stimulus equivalence and relational frame theory, and potentially extends BMT into the realm of human language and cognitive behavior, which is usually thought of within the province of behavior science. Our purpose in developing this account, consistent with the breakdown provided by Critchfield and Reed (2009), is to parsimoniously describe how relational networks interact as a function of the higher-order properties of relational volume, mass, and density. Decades of research focusing on stimulus equivalence and relational frame theory have shown that the stimuli that comprise relational networks rarely are “equivalent” (Fields, Verhave, & Fath, 1984; Sidman, 2000; Saunders & Green, 1999) in the strict sense of being functionally substitutable (Spencer & Chase, 1996). Rather, the responding that normally is taken to suggest “substitutability” appears to be influenced by a variety of factors, including but not limited to degree of derivation (Pilgrim & Galizio, 1990), stimulus complexity (Stromer, McIlvane, & Serna, 1993), the number of relations between equivalent stimuli (nodal distance; Fields, Adams, Verhave, & Newman, 1990), and stimulus familiarity (Holth & Arntzen, 1998). These factors create degrees of nonequivalence, or nonlinearity, that is not accounted for in the basic narrative of equivalence theory or in subsequent theoretical extensions (e.g., naming theory and RFT). To be clear, we define nonlinearity in equivalence classes, or networks, as occurring when (1) inequalities exist between stimulus relations within the network, and (2) the addition or subtraction of some variable leads to an unequal change in dependent network properties. For example, Arntzen and Holth (2000) demonstrated that although the probability of demonstrating a derived relation decreases from a three-nodeFootnote 3 network to a four-node network, a much greater decrease in the probability of a correct response is seen when moving from a four-node network to a five-node network. Nonlinearity of relational responses is problematic to traditional explanations of equivalence like that of Sidman (Sidman, 1994; see Pilgrim & Galizio, 1995, for an explanation), but may be parsimoniously predicted by quantifying the relationship between higher-order network properties described in the theory.

Relational density theory posits that the nonlinearity of relational responding, like operant responding in BMT, can be described and modeled using Newton’s second law in classical mechanics as a metaphor.Footnote 4 The theory’s bedrock assumption is that the historical influence of prior relational learning can be understood in terms of the classical mechanical properties of volume, density, and mass. Experiments have not yet been conducted to prospectively test theory predictions, but several findings in basic experimental research, which we will describe in the following section, are consistent with theory predictions and therefore suggest that experimental tests will in fact be productive to conduct.

We begin with an equation derived from the standard model of BMT put forward by Nevin and colleagues, but expressed in terms of relational or equivalence responding:

$$ \Delta R=\frac{-x}{Rm} $$
(1)

Here a change in relational responding (∆R) is equal to counterforce (-x) against relational mass (Rm). Mass, like in BMT, refers to the resistance of a network to change when counterforce is applied to contained relations. Thus, mass is an inferred property that can be experimentally demonstrated by applying equal counterforce to two networks and evaluating relative degrees of change in relational responding. Counterforce can be created by conditioning competing relations, punishing existing relations, or introducing rules or distractions; we will refer to the processes that produce counterforce as counterconditioning. These yield nonlinear changes in relational responding in proportion to the mass of the relational network. For example, if we take two relational networks, one involving DOG and one involving VALLHUND (a Swedish breed of dog), and apply the same counterforce, such as in the statement “X does not bark,” where X is either DOG or VALLHUND, the probability of a change in the DOG relation is low, because, based on a history of relational responding, a person is unlikely to believe that a dog does not bark. However, if a person is unfamiliar with a vallhund, the probability of a change in the relational response is significantly higher, in that the person may readily repeat that “a vallhund does not bark.” Thus, we can say that DOG participates in a network with greater mass than does VALLHUND (i.e., is more resistant to change).

An assumption in BMT is that behavioral mass, or resistance to change, emerges through historical participation of behavior in contingencies of reinforcement (Nevin & Grace, 2000). The theory proposed here, however, assumes that relational nonlinearity is the result of a history of relational learning, which can include but is not limited to the effects of direct acting contingencies. As we discuss in detail below, it is common to find that derived relations are nonequivalent (i.e., nonlinear), both in terms of response strength and resistance to change. Newton’s volumetric-mass-density formula may appropriately describe relational factors that contribute to relational mass, or the resistance to change of relational networks, expressed in the equationFootnote 5:

$$ Rm= Rp\ast Rv $$
(2)

Here relational mass (Rm) is a function of relational density (Rp) and relational volume (Rv). Relational mass refers to the resistance to change of a relational network. Density refers to the strength of the various relations contained in a network, as measured through such variables as response latency, probability, and rate. Relational volume refers to the number of relations contained in the network. For example, DOG participates in a high-mass network. It is related to barking, is contained in the class animal, is the opposite of CAT, and is a best friend and loyal companion (among many other densely established relations). It is not surprising, therefore, that most people will quickly match the printed word “dog” to a picture of a dog and other related stimuli. Because of high relational mass DOG is resistant to change, hence the unlikelihood of incorporating "does not park" into its relational network. For the typical English-speaking American the same may not be true for VALLHUND.

Density and volume are higher-order properties, because many complex and likely dynamical factors can contribute to the density and volume of a network as well as to potentially self-organizational factors that we describe below. Figure 1 shows high- and low-density networks in terms of geometric space, where the distance between any two nodes is inversely proportional to the strength of the relation; thus, strongly related nodes are shown as close together, and weakly related ones are shown as farther apart. As noted above, relation strength can be measured in several ways, but in the equivalence literature it has been operationalized primarily in terms of either response latency (e.g., Spencer & Chase, 1996) or relative probability of a particular relational response given a particular stimulus context (e.g., Arntzen & Holth, 2000). Thus, for instance, in Figure 1 space could represent response latency, in which case the faster the response the smaller the distance between two nodes and thus the greater the relational density. Or it could represent the reciprocal of the relative probability of a given relational response, in which case the more probable a criterion response the smaller the distance between nodes and thus the higher the relational density. The figure also shows volume in terms of the number of stimuli contained in the network, where the high-volume networks contain more stimuli and therefore more relations. Networks therefore can differ simultaneously in terms of volume and density.

Fig. 1.
figure 1

Graphic display of four equivalence networks differing along the higher-order properties of density and volume. The space between relata (letters) represent the strength of the relation (i.e., smaller space = stronger relation).

Full size image

Based on Equation 1, we can solve for density using the equation:

$$ Rp=\frac{Rm}{Rv} $$
(3)

as well as for volume using the equation:

$$ Rv=\frac{Rm}{Rp} $$
(4)

Figure 2 shows the effect of these higher-order properties on relational mass. It can be inferred from Equations 3 and 4 that density and volume do not necessarily operate in the same direction in terms of their effects on mass, but may instead operate as opposing properties where increases in one property (e.g., volume) will likely lead to decreases in the other property (e.g., density). For example, for a person you’ve only just met, it may be easy to “recall” (i.e., respond in terms of) simple relations involving isolated facts such as the person’s report that he enjoys maple syrup on his eggs at breakfast. In this instance, relational volume is low and relational density is high. By contrast, once the person becomes “familiar” (more is learned about him), relational volume increases and overall mass increases as a result, yet the probability of recalling the relatively trivial facts becomes diminished because relative relational density involving such facts decreases (see Figure 2).

Fig. 2.
figure 2

Matrix of relative expected relational mass given known high and low density and volume values. Upward facing arrows indicate a high value, downward facing arrow represent a low value, and dashes indicate neither a high nor low value.

Full size image

At the same time, important facts about a person that are regularly repeated, such as the person’s name or the fact that he regularly exhibits kindness toward others, retain or increase in density and, along with increases in relational volume, participate in a network that is resistant to counterforce. Such an effect may be captured when, upon hearing something incongruous (e.g., the person was reportedly cruel to someone), we say “that doesn’t sound like him!” or “I cannot believe he would do that!” Such reactions indicate resistance to change of a well-established network, one that does not readily admit incongruent new nodes. Research has in fact established that networks can be resistant to class mergers (the absorption of new stimuli) when the networks involve incompatible stimuli, such as in a study conducted by Watt and colleagues in which Northern Irish and English participants’ preexperimental religious beliefs influenced the emergence of transitive relations between Protestant and Catholic symbols (Watt, Keenan, Barnes, & Cairns, 1991).

Combining Equations 1 through 3 yields a complete standard equation for relational density theory, expressed as:

$$ \Delta R=\frac{-x}{Rp\ast Rv} $$
(5)

A change in relational responding is equal to counterforce over mass as in Equation 1, where relational mass is the product of competing properties of network density and volume. As explored in the following section, we propose that this standard equation may account for some of the nonlinearity observed in equivalence relational networks by introducing volumetric-mass-density as higher-order properties, allowing for greater prediction and influence of relational responding in humans.

Reinterpreting Nonlinearity using Relational Density Theory

As noted by Hursh (1984), the value of theoretical extensions is always measured in terms of data: either validity when directly tested under laboratory conditions, or utility when compared to existing models in interpreting existing experimental findings. In the present section, we take up the latter challenge by interpreting results from several basic experimental equivalence studies that have all demonstrated nonlinearity and nonequivalence of emergent relations. When interpreted in terms of the present equations, these studies speak to the potential utility of the theory in explaining and predicting human behavior in equivalence tasks.

Traditional equivalence-based accounts assume that stimuli contained in an equivalence class are functionally substitutable, that is, equivalent (Barnes & Holmes, 1991; Sidman, 2000; Sidman & Tailby, 1982). As such, the strength of one conditional discrimination in a network should be the same as any other, and an intentional reconditioning of one relation within the network should, via the phenomenon of transformation of function (Dymond & Rehfeldt, 2000) be accompanied by parallel changes in other related nodes. For example, if A1 = B1 and B1 = C1, then the directly trained (A1–B1, B1–C1), symmetrical (B1–A1, C1–B1), and transitive (A1–C1, C1–A1) relations should occur at the same strength. Thus, changes in relational responding should be linearly equal to the force applied to the network by adding new relations (e.g., if an A1 = D1 and A1 = E1 relation are reinforced), such that the new relations are as strong as the old relations and equally related to already established relations (e.g., the strength of A1–E1 = the strength of A1–B1 = the strength of D1–C1). Basic research in equivalence has shown that this is not the case, as the strength of network relations appear to erode as the derived response becomes more complex (i.e., response strength for symmetrical responses > response strength for transitive responses; Spencer & Chase, 1996) and as more nodes are added to the network (i.e., response strength for five class members < response strength for three members; Arntzen & Holth, 2000).

Continuing with the above example if one of the relations (e.g., A1–B1) is suddenly put on a continuous punishment schedule, and a new A1–B2 relation is continuously reinforced (i.e., reconditioning), then the C1–B2 and B2–C1 relational responses should also emerge because the C1 stimulus was transitively related to the A1 stimulus. Moreover, if reconditioning a relation leads to changes in the remaining network relations, the change should be equal whether the network contains 3 class members or 300 class members. Again, basic research in stimulus equivalence does not support this prediction, because equivalence networks appear to be highly resistant to reconditioning (Pilgrim, Chambers, & Galizio, 1995; Pilgrim & Galizio, 1995). As noted by Pilgrim and Galizio (1995), this outcome “may have important implications because it is not easily accounted for by current models of equivalence phenomena” (p. 225). Those models make no special provision for resistance to change, and therefore default apparently assume equivalence networks to be nonresistant. relational density theory, by contrast, anticipates the aforementioned findings of nonlinearity as interactions of the higher-order properties of volume, mass, and density. Below we describe three additional predictions that derive from relational density equations and are imminently testable.

Prediction 1: Density and Volume are Inversely Related Properties

As seen in Equations 2 through 4, nonlinearity of equivalence responding can be predicted in terms of the interacting higher-order properties of volume (i.e., the number of relations or relata), density (i.e., the strength of contained relations), and mass (i.e., the resistance to change of the network). When solving for Rp, Rv necessarily serves as the denominator on the right side of the equation, meaning that an increase in Rv will lead to a corresponding decrease in Rp when mass is held constant. The same is true when solving for Rv, where increase in Rp will decrease Rv. Thus, a first source of nonlinearity of equivalence responding may be imposed by the competing properties of volume and density, where greater volume may detract from overall network density, and low network density may be predictive of high network volume.

Such nonlinearity can be captured using response time as a measure of response strength or density (Spencer & Chase, 1996). In a traditional equivalence account, one would expect the response time of any relational response within a network to be equal. Results obtained by Spencer and Chase (1996), contrary to this prediction, demonstrated that not only were response times not equal for all relational responses within an equivalence network, but that the number of nodes, or volume, was predictive of a nonlinear decay in response strength, or density. Throughout six training stages with college participants, three 7-member classes were established (directly reinforced relations: A–B, B–C, C–D, D–E, E–F, F–G). The training stages were conducted in a linear order, where the A–B relation was trained to mastery, and subsequent relations were added to the network in each successive phase (B–C, C–D . . . F–G). Thus, at each step the volume of the network was expanded by one relation, and the nodal distanceFootnote 6 between A and subsequent relations was also increased by 1. Symmetrical and transitive relations across nodal distances up to 5 were tested in a combined testing phase, where greater nodal distance is indicative of greater relational volume.

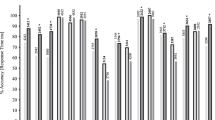
To repeat a point, if the concept of equivalence is interpreted traditionally, with no provision for nonlinearity (e.g., as per Sidman, 1994), differences in response density or strength would not be expected at greater nodal distance (i.e., with volumetric increases). However, relational density theory, using Equation 3 (Rp = Rm/Rv) in fact predicts nonlinearity. We assume that relational mass is held constant across nodal distance such that Rm1 node = Rm2 node = Rm3 node… = Rm5 node. We know that adding nodes increases the volume of the network, therefore Rv1 node < Rv2 node < Rv3 node… < Rv5 node. Because an increase in the denominator (Rv) on the right side of the equation will lead to a decrease in the left side of the equation (Rp), assuming mass is held constant, we would predict that Rp1 node > Rp2 node > Rp3 node… > Rp5 node. As shown in Figure 3, for three of the four participants in from Spencer and Chase (1996), response strength was inversely related to nodal distance as predicted by the model. As more relations were added to the network, the speed of the transitive relational responses decreased, and this effect was replicated across the six of the remaining eight participants under different testing conditions. Therefore, 9 of 12 participants demonstrated nonlinear equivalence responding that would be predicted by Equation 3.

Fig. 3.
figure 3

Response strength (speed = 1/latency in seconds) as a function of the number of relations contained in a coordinated network. Each set of bar graphs represent one participant. From Spencer and Chase (1996). Reproduced by permission

Full size image

A limitation of the Spencer and Chase (1996) study, with respect to relational density theory, is that the number of class members was not manipulated across classes, so we cannot compare relational density across networks differing in volume and established under the same overall rates of reinforcement. Data from Arntzen and Holth (2000) allow for such a comparison as relations were manipulated in terms of both the number of class members within a given class and the number of established classes. In the first of two studies, the authors recruited 50 college student participants and assigned the participants to 10 experimental groups. The groups differed in terms of both the number of relations directly reinforced (i.e., nodal distance or network volume) and the number of classes established, in both cases ranging from three to six. In this study response strength was described as probability of occurrence of an expected relational response, rather than in terms of response latency, with probability defined by the authors as the percentage of participants in each group that demonstrated all transitive responses. The same general predictions would be made for this study as for Spencer and Chase (1996). Figure 4 shows that as the number of class members increased from three to six, the percentage of participants that demonstrated the transitive responses decreased, and this was evident when three, four, or five classes were established. On the other hand, response strength appeared relatively unaffected by the number of classes, and especially when those classes operated at low volume (i.e., Rv = three members). Therefore, this finding, and when interpreted in the context of results reported by Spencer and Chase (1996), support the prediction that when volume is added to a relational network the strength of the established network relations is weakened.

Fig. 4.
figure 4

Percentage of participants who responded consistent with established equivalence classes as a function of (a) the number of class members (volume) and (b) the number of classes. See text for further explanation. From Arntzen and Holth (2000). Reproduced by permission.

Full size image

Prediction 2: High-Volume and High-Density Networks are Highly Resistant

One limitation of the relational density model as we have described it so far is that, if relational density and volume are inversely related, relational mass would almost necessarily become equal across networks. For example, if volume increases, and therefore overall network density decreases, then network mass remains unaffected (assuming Rm is equal to Rv * Rp). If so, there would be no utility in incorporating mass into the model. However, research (Bortoloti, Rodrigues, Cortez, Pimentel, & de Rose, 2013) indicates that overtraining of directly taught relations increases relational response strength without altering the volume or number of relations contained in the network. The result should be that networks that are high in volume, but also contain dense relations, may exhibit higher order properties consistent with relational mass as predicted in Equation 4.

Some empirical evidence exists that suggests that volume and density may both participate in relational network resistance to counterconditioning as a source of counterforce. Pilgrim and Galizio (1995), extending prior work (Pilgrim & Galizio, 1990; Saunders, Saunders, Kirby, & Spradlin, 1988), evaluated several outcomes of equivalence class resistance when counterconditioning was applied to baseline equivalence networks. Upon reversingFootnote 7 contingencies for a single relation in four-member classes, the authors assessed the degree to which responding in terms of symmetrical and transitive responses in the network would also be influenced. Then, upon training additional relations following the contingency reversal, they assessed the degree to which the new relations cohered with the baseline class or with the reversed contingencies. For five student participants, baseline A–B, A–C, and A–D relations were established, and several transitive relations were tested. Then, contingencies for the A–D relations were reversed (i.e., reinforcement was provided when participants selected a stimulus other than the original D stimulus), followed by a probe of the transitive C–D and D–C relations. D–E training was then conducted to establish a fifth class member, along with symmetry and transitivity test probes. Finally, a B–C reversal was conducted along with test probes, followed by a return to baseline contingency conditions (i.e., consistent with the first noncounterconditioned networks).

Framed using Equation 1, the same counterforce was applied to the A–D and B–C relations through counterconditioning (-x), or −xA − D =  − xB − C. We know that no direct counterforce was applied to either the symmetrical or transitive relations, therefore −xsymmetry =  − xtransitivity. The difference in the symmetrical and transitive networks is in terms of volume, where Rvsymmetry < Rvtransitivity, and assuming density is the same (because the authors did not measure response time), given Equation 5, we can also say that Rmsymmetry < Rmtransitivity. The theory predicts that greater changes (∆R) should be observed in terms of the symmetrical relations that operate at lower mass (i.e., less resistance) than the transitive network relations. The results of the study are shown in Figures 5 (symmetrical relations) and 6 (transitive relations). Results for both symmetrical and transitive relational responses show that, although the counterconditioning was effective in influencing the directly targeted relations (A–D and B–C counterconditioning), the other symmetrical relations and the transitive relations were relatively unaffected. Although not shown in the figure, emergent symmetrical and transitive relations following the introduction of the D–E relation also were consistent with the original networks. Traditional theories would posit that changes in responding to subsets of relations, assuming the relations are equivalent, should result in corresponding changes in related network stimulus relations.

Fig. 5.
figure 5

The effect of punishing subsets of derived relations on emergent symmetrical relations across four subjects. See text for further explanation. From Pilgrim and Galizio (1995). Reproduced by permission

Full size image
Fig. 6.
figure 6

The effect of punishing subsets of derived relations on emergent symmetrical relations. See text for further explanation. From Pilgrim and Galizio (1995). Reproduced by permission

Full size image

These results suggest that the transitive relations consistent with the theory are highly resistant to counterconditioning. Results from Pilgrim and Galizio (1990), Pilgrim & Galizio, 1995, Pilgrim et al., 1995) suggest that contingency reversals only influence directly retrained relations and their symmetrical counterparts. Based on this we may reasonably assume that the impact of counterconditioning is inversely related to network size. If a network contains three class members (i.e., Rv = 3), then two of six possible relations (33%) may be influenced by counterconditioning, or counterforce (i.e., the counterconditioned relation and the derived symmetrical relation). If a network contains six class members (e.g., Rv = 6), then 2 of 30 possible relations (6.7%) may be influenced by counterconditioning.

Another study involving counterconditioning was described by Dixon, Rehfeldt, Zlomke, and Robinson (2006). They employed familiar stimuli, some of which were related to the concept of “terrorist” whereas some were not. Shortly after the terrorist attack on September 11, 2001, the authors attempted to determine if college participants could be taught to match nonterrorist stimuli to traditionally American images and traditionally Middle Eastern images. The nonterrorist-to-American relations and terrorist-to-Middle Eastern relations were considered to be culturally established, that is, conditioned prior to the experiment. In the first study, eight participants demonstrated a high probability of matching terrorist–terrorist stimuli during a pretest phase, suggesting that these relations were, as assumed, culturally established prior to the study. Participants were then taught to match nonterrorist stimuli to both American and Middle Eastern images, and the result was that the participants demonstrated fewer culturally established relations following counterconditioning. Direct support for greater resistance to counterconditioning via network density and volume was provided in the second study, during which the researchers compared resistance to counterconditioning of the terrorist–terrorist relations to two other stimulus sets, one involving mixed terrorist/American stimuli, and one involving neutral images. Because terrorist stimuli are culturally established, we can reasonably assume that the “terrorist” network contains greater volume and density than the nonassociated mixed and neutral networks (i.e., prior to baseline conditioning, the mixed and neutral networks are not related to one another, and “terrorist” is likely related to much more than the stimuli used in the study). Therefore, we can assume that Rmterrorist > Rmmixed/neutral.Because equal counterconditioning was applied to all networks, −xterrorist =  − xmixed/neutral, then according to Equations 1 and 5, we therefore predict that ∆Rterrorist < ∆Rmixed/neutral. Consistent with this prediction, five of seven participants (71.4%) demonstrated less change in responding (greater resistance to change) for culturally established terrorist-terrorist relations compared to the mixed and neutral classes.

Another source of resistance to change resulting from relational mass may be suggested by relapse models developed from BMT (Podlesnik & Shahan, 2009, 2010). As a preliminary point, relational networks can show resurgence, as Wilson and Hayes (1996) demonstrated for baseline equivalence relations with college student participants. Three, four-member equivalence class were established using several baseline conditioning experimental phases (e.g., A1–B1–C1–D1, A2–B2–C2–D2). Following the development of the baseline relations, in which three new classes were established by rearranging the stimuli from baseline conditioning (e.g., A1–B3–C2–D3, A2–B1–C3–D2). As they were taught to do, participants demonstrated responding consistent with the reconditioned class arrangement, but when responses consistent with these alternative classes subsequently were punished, responding consistent with the baseline classes reemerged for 16 of 23 participants. Therefore, these results suggest that equivalence relations may demonstrate resistance to counterconditioning through resurgence, similar to resistance of operant behaviors observed in research on BMT.

The Wilson and Hayes (1996) study is not a direct test of the combined influence of volume and density on network mass, or resistance, because neither network volume nor density was manipulated. The study simply demonstrated that relational networks can show resurgence. More recent research, however, has shown that increasing density, or response strength, can make resurgence more likely. Doughty, Cash, Finch, Holloway, and Wallington (2010) established classes that differed in the frequency of reinforcement to which baseline relations were exposed. Thus, some classes received more extensive conditioning than other classes, and prior research has demonstrated that overtraining specific relations can increase the response strength, or density, of the relations within a class while overall class volume is held constant (Bortoloti et al., 2013). Therefore, we know that volume (Rv) was held constant across classes, and that density (Rp) was likely greater for the overtrained class; or that Rmovertrained > Rmundertrained.We also know that equal counterforce through counterconditioning was applied to both networks, or −xovertrained =  − xundertrained. Therefore, according to Equation 1 and 5, we predict less change in responding, or greater resistance predicted by resurgence models, for the network with greater mass (i.e., the overtrained network); or, ∆Rovertrained < ∆Rundertrained. Two of three participants indeed showed greater resurgence of relations for the classes with a lengthier baseline relation reinforcement history (2 out of 3; 66%). Therefore, the overall probability of the baseline conditioned responses occurring following the application of counterforce through reconditioning was greater for more-dense baseline relations.Footnote 8

Summary of Support for Predictions 1 and 2

In examining research in which nonlinearity of equivalence relations was apparent, but not readily interpretable using existing accounts (Pilgrim & Galizio, 1995), relational density theory anticipates the obtained results in most cases. Four studies employing within-subject designs have arranged appropriate conditions and measured response strength in terms of either reaction time or probability. Figure 7 summarizes the outcomes from these studies. All told, 21 of 27 participants (78%) demonstrated responding consistent with the theory (Dixon et al., 2006; Doughty et al., 2010; Pilgrim & Galizio, 1995; Spencer & Chase, 1996). In studies employing between-group analyses, networks with greater volume also have shown lower response strength (Arntzen & Holth, 2000). That is, when response strength and volume both were high, the networks appeared to be resistant to counterforce (Arntzen & Vie, 2013). Of course, the present account is not an exhaustive literature review. We have merely sought to show how results obtained by independent research laboratories and framed in different theoretical orientations (e.g., RFT, equivalence, naming), speak to the interrelatedness of volume, mass, and density as higher order properties.

Fig. 7.
figure 7

Percentage of participants from four studies that demonstrated relational responding, or changes in relational responding, consistent with Relational Density Theory. The dashed line shows chance responding. Sample sizes are presented above each bar. See text for additional explanation

Full size image

Prediction 3: High-Mass Networks Demonstrate the Emergent Properties of Acceleration and Gravity

A major advance of BMT was the use of Newton’s second law to model behavioral mass as resistance to counterforce, where mass was described as the aggregate outcome of a dense history of reinforcement for an operant response (Nevin & Grace, 2000). In classical mechanics, an important implication is that force is provided, not only by external events, but also within a system through acceleration and gravity. In the present article we have proposed, and provided preliminary support for, the notion that relational mass can be modeled via Newton’s volumetric-mass-density formula, in terms of the volume and density of equivalence networks of verbally sophisticated humans. We now turn our attention to how the concepts of acceleration and gravity might inform an analysis of derived stimulus relations. Available data, though limited, suggest promise for these concepts.

We first suggest that relational acceleration may be defined as a positive relationship between network mass and rate of acquisition of new relations into the network. For example, if a person is taught a new equation that predicts the movement of orbiting planets, the person is more likely to restate the new equation if they are already familiar with planetary movement and equations. Familiar, understood in the context of relational density theory, would mean that the related networks operate at high mass and high volume. Therefore, the already established mass of networks involving “planetary movement” and “mathematical properties” may accelerate the establishment of new relations that correspond to these networks. On the other hand, if a person is familiar with neither planetary movement nor mathematical equations, the person may be less likely to restate the new equation, let alone to use the equation in any meaningful way.

A few studies have attempted to evaluate how stimulus familiarity can influence the development of new relations. Arntzen (2004) examined the influence of familiar stimuli contained in established equivalence networks on derived responding. Fifty college student participants took part in the study, in which 3 five-member equivalence classes (A–B–C–D–E) were established, where either the A stimuli or the E stimuli were familiar pictures for two groups and three additional groups had different arrangements of all abstract stimuli. All stimuli were trained to the B stimulus in the following order: A–B, C–B, D–B, E–B. Thus, for the picture (A) group, the familiar stimuli were involved in the first relational training, and for the picture (E) group, the familiar stimuli were involved in the final relational training. Figure 8 shows the results. The probability of participants demonstrating derived relational responses was enhanced when familiar stimuli participated in the network. Thus, relational responding appeared to be accelerated by the inclusion of stimuli that already participated in high mass networks. Greater acceleration was also observed when the familiar stimuli were involved in the initial stages of training. Interpreted in the context of the theory, if the inclusion of a familiar stimulus accelerates learning, then the A–B relation would be established quickly, leading to the inclusion of the B stimulus in the high-mass network of the A stimulus (i.e., Rm-combined = Rm-familiarA + B). Therefore, when all other stimuli (C, D, and E) were trained to B, the mass of Rm-combined accelerated the acquisition of the new relations. By contrast, when the other stimuli were trained to B, but B was not yet trained to A, the substantially lower mass of Rm-B only failed to accelerate the acquisition of the new relations.

Fig. 8.
figure 8

Number of participants who demonstrated correct equivalence-responding as a function of the familiarity of network stimuli and location in the training arrangement. From Arntzen (2004). Reproduced by permission

Full size image

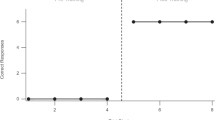
Directly related to Newton’s model of acceleration and mass is force resultant from gravity. In physics, two systems that contain mass are attracted to one another as a function of the relative mass of the two systems (greater mass = greater attraction or force) and the distance between them (greater distance = lesser attraction or force). Framed in this way, we expect that high-mass relational networks will strongly attract new relations or networks. That is, when a new stimulus could be related to either a high-mass network or a low-mass network, it will more likely be incorporated into the high mass network, even in the absence of direct instruction or reinforcement. Consider as a point of departure a study conducted by Saunders et al. (1988). In a series of three experiments conducted with individuals with intellectual disabilities, the authors evaluated: (1) the likelihood that participants with a history of equivalence class formation would respond consistently to new discriminations in the absence of any sort of feedback or reinforcement; and (2) if once the new discriminations were established, participants would respond in terms of already established equivalence relations that were indirectly related to the new discrimination. Figure 9 (left panel) shows the breakdown of training in Experiment 1, in which four baseline equivalence classes were established (i.e., A1, A2–H1, H2 and I1, I2–L1, L2). Participants were then presented with A–I conditional discriminations, and were tested, in the absence of any reinforcement or feedback, until they achieved consistent responding in the form of either A1–I1/A2–I2 or A1–I2/A2–I1 relations. Participants consistently arrived at one of the two possible sets of conditional discriminations (they did not respond randomly).

Fig. 9.
figure 9

Procedure summary of Saunders et al. (1988). Left: The actual procedure; reproduced by permission. Right: Modified procedure showing a hypothetical difference in the probability of ambiguous equivalence responding as a function of network volume.

Full size image

The question raised by relational density theory is whether the mass of baseline classes in a study like that of Saunders et al. (1988) would influence the relative probability of participants arriving at one set of class-consistent conditional discriminations versus another. In the right panel of Figure 9, we altered the diagram of the Saunders et al. procedure to show what such an arrangement might look like along with expected results. In the actual study, classes had equal numbers of class members (equal volume) and, presumably, equal density (i.e., all relations had equal exposure to the same schedule of reinforcement). We have modified the hypothetical arrangement such that Class 1 contains eight members and Class 2 contains three members.Footnote 9 Given this arrangement, if the predictions made in the theory hold true, participants will be significantly more likely to relate the I stimuli to the Class 1 network if network mass exerts gravitational attraction to the I-L network. As well, given findings reported by Saunders et al., we would expect the derived equivalence relations to be consistent with the probabilistic conditional discrimination in terms of network mass. Research by Quinones and Hayes (2014) suggests that this sort of “self-organization” may be likely when stimulus relations are ambiguous. When a stimulus could be related to two competing networks, the network containing a greater historical density of reinforcement and established relational exemplars will be more likely to acquire the ambiguous relational stimulus.

Fields and Arntzen (2018) described how the prior meaningfulness of stimuli can enhance the formation of equivalence classes. The author’s detailed review of the extant literature supports the assumption that the multitude of relations and functions contained within already meaningful stimulus relations can affect how new classes develop, or self-organize, within conditional discrimination arrangements. Two points raised by the authors are most relevant in developing relational density theory. First, research by Nartey, Arntzen, and Fields (2014, 2015) suggested that if meaningful stimuli were introduced at the beginning of a linear training arrangement (i.e., as the A stimulus), greater enhancement was observed than when the stimuli were introduced at the end. More research is needed to quantitatively evaluate the influence of nodal location of meaningful stimuli, but the relationship does appear to be nonlinear. Introducing high-mass stimuli initially in training may accelerate the formation of equivalence classes. Second, the authors cite several studies showing that when classes contained meaningful stimuli with preexperimental conflicting valence, yields were lower than when valence was nonconflicting. In physical models of gravity, distance serves as the denominator term, wherein objects that are closer are more likely to attract. The research reviewed by these authors may suggest that preexperimental relational properties such as valence, and we argue coherence, may be useful in modelling the preexperimental distance between two classes and predicting the probability that the two classes will merge under training and testing conditions.

Although limited data are available through which to evaluate the concepts of relational acceleration and gravity, we advance them here in part because of their potential to aid in the understanding of phenomena that often are labeled as “cognitive.” A key tenet of many cognitive theories is that such phenomena are self-organizing. Examples include cognitive schemas, mental maps, and perhaps even the development of correlated behaviors that comprise personalities or a transcendent self. Marr (1992, 1996) has argued that behavior science is obliged to account for self-organization and, in a more general sense, dynamical system evolution. Proponents of stimulus equivalence and relational frame theories clearly agree (Barnes & Holmes, 1991; Cassidy, Roche, & O’Hora, 2010; Dymond & Rehfeldt, 2000; Hayes et al., 2001; Zentall et al., 2002), and they have offered narrative interpretations inspired by our understanding of stimulus relations (Barnes-Holmes, Hayes, & Dymond, 2002; Dougher, 1998; Weinstein, Wilson, Drake, & Kellum, 2008). Our current point is that relational density theory offers a means of better operationalizing relevant variables. The theory’s key premise is that although reinforcement (of directly trained relations) undoubtedly exerts force and is necessary for the initial development of subsets of relations, relational networks may generate their own force, that (1) interacts with reinforcement to accelerate the acquisition and strengthening of new relations, and (2) establishes new relations under novel or ambiguous situations that may not involve direct reinforcement. In this sense relational density theory complements previous narrative interpretations by proposing a well-defined self-organizing property of relational behavior that may help to account for the development of so-called “cognitive” phenomena.

Translational Implications and Avenues for Future Research

As discussed by Critchfield et al. (2018), one of the greatest achievements of stimulus equivalence theory is its potential to mend bridges with other approaches to behavior science. Finally, we can develop models of meaning and complex cognition that do not require mediational accounts as have emerged within other literatures. Relational density theory is an attempt to continue this tradition in a conceptually systematic way while accounting for nonlinearity and self-organization evident within derived relational responding. The present account of relational density theory, though preliminary and not fully vetted by experimental findings, is sufficient to support predictions for real-world phenomena that can be tested in translational research. Below we describe three potentially valuable lines of research suggested by the theory.

First, if high mass networks can accelerate learning when force instead of counterforce is applied, by understanding the current state of important relational networks we can best choose which force to apply to achieve desired changes in relational behavior. For example, when teaching a new concept, using an already established network as a relational metaphor or analogy could accelerate learning, such as by saying “planets are to solar systems as neutrons and protons are to atoms” (Stewart, 2004). The basic experimental research findings reported by Arntzen (2004) suggests that this may be the case, and research on utilizing analogical reasoning to teach new concepts to children support that this strategy could be effective (Stewart, Barnes-Holmes, Roche, & Smeets, 2001). Likewise, in treating challenging behavior that operates at high mass, fewer resources may be required to apply force that moves with the network rather than high-dose counterforce. This difference may be seen in cognitive-therapy strategies that emphasize “acceptance,” rather than attempting to decondition erroneous beliefs (Hayes, 2004).

Second, if we can estimate the relative resistance to change of relational responses given knowledge of the volume and density of a given network,Footnote 10 it should be possible to predict the counterforce needed to change the desired relational response. Behavior analysts have an ethical obligation to use least restrictive procedures (Bailey & Burch, 2016; Johnston & Sherman, 1993), therefore “least-restrictive” could become a quantifiable reality. For example, if densely established rules participate in the challenging behavior exhibited by an adolescent (see Vahey, Boles, & Barnes-Holmes, 2010, for a study on relations that may contribute to youth smoking), several intervention components may be required to reduce the influence of high mass rules, perhaps including regular therapeutic exercises and strict contingency-management approaches. On the other hand, if the same rule operates at low mass for another adolescent, simply “discussing” the problem may be a sufficient intervention. This conditional prescribing of an intervention mirrors the “tiered” approach employed in Positive Behavior Intervention and Support (PBIS; Sugai et al., 2000) and the AIM Curriculum (Dixon & Paliliunas, 2018) that directly targets verbal relations that contribute to challenging behavior of children in schools.Footnote 11 Another ready example can be seen in conditioning against racist belief structures, which are highly resistant to change (Campbell & Deacon, 2006; Guerin, 2006). Intervening at a younger age, when networks operate at a lower mass, may be pivotal in decreasing racist beliefs and human suffering resultant from it.

Third, if we know that adding volume to a network can decrease density, and vice versa, then we can use this information to optimize educational strategies both in schools and in the workforce. For example, undertraining several concepts may lead to a loose understanding of new concepts that contain adequate volume but insufficient density. On the other hand, although overtraining only a few relations will result in dense relational responses, because the responses operate at low volume the relations will be highly susceptible to change. It is interesting to note that recent changes in the Common Core State Standards of the United States (e.g., Porter, McMaken, Hwang, & Yang, 2011) emphasize teaching the same information in a number of different ways (i.e., differentiated instruction), potentially simultaneously increasing volume and density to produce high mass learning.

Limitations and Conclusions

We readily acknowledge that much more basic experimental research is needed to validate and expand relational density theory before its translational implications can be properly examined. Each of the three predictions offered above needs to be directly evaluated across several dimensions. For example, although some evidence suggests that increases in volume will correspond with decreases in density, we do not know if increasing density of certain relations will reduce volume or the probability of demonstrating other relations in the network, and we do not know how mass enters into the system as the numerator when isolating for either density or volume. As well, although the standard equation assumes that resistance is equal to density times volume, basic research may show that this is an oversimplification, such as would occur if increases in density have a disproportionate influence on resistance than do increases in volume, requiring more precise equations that provide an appropriate curve fit to this relationship (Critchfield & Reed, 2009).

It is also important to acknowledge that stimulus relations are far more diverse than simply equivalence. Research inspired by relational frame theory has established that relata can also be framed in terms of opposition, comparison, deictically, among other contextual cues. There is already some evidence suggesting that reaction times, or density, may be influenced by the type of relations (e.g., “same,” “opposite,” “different”) comprising a network (O'Hora, Roche, Barnes-Holmes, & Smeets, 2002). In the present article we restricted our focus to equivalence relations because relevant data were more readily available for them. Studies will need to be designed that specifically test predictions made by entering nonequivalence relations into the model. For now, little can be assumed about how volume, mass, and density interact with such relations, or if the model is even applicable to nonequivalence relations.

Another limitation of the theory as described here is that it does not directly address transformation of function, which both stimulus equivalence and relational frame theories consider to be a central phenomenon. It is well known that stimulus functions can be transformed through class memberships (Hayes et al., 2001). For example, Dougher, Hamilton, Fink, and Harrington (2007) demonstrated that when human participants were shocked prior to the presentation of an arbitrary stimulus, and taught that other stimuli are “more” or “less” than the initial stimulus, that the physiological reaction to the “more” and “less” stimuli were transformed consistent with class participation. An important focus for future research is on the relationship between transformation of function and the higher-order properties of volume, mass, and density in basic research. We suggest as a starting point that experiences that directly establish various psychological functions of stimuli be thought of in terms of force and counterforce.

Although our primary goal is to recruit the assistance of other researchers in exploring the implications of relational density concepts for the broad spectrum of stimulus relations phenomena, and equally intriguing direction for future research is to explore the implications of relational density theory for the model that inspired it (BMT). For instance, can the theory shed light on resistance to change of responding to a single stimulus? Nevin and Grace (2000) implied that such resistance is the result of a history of direct reinforcement, but training multiple exemplars of a stimulus (i.e., increasing volume) or overtraining several exemplars of a stimulus (i.e., increasing volume and density) may contribute to mass in a nonlinear way that is not currently accounted for in BMT. This may then circle back to relational cues as a single relational response, where multiple exemplar training of the various cues (e.g., same, opposite, different) could contribute to greater resistance, and potentially to a higher probability of interpreting novel events in terms of a given cue through acceleration and gravity as a product of “cue mass.” We look forward to new research exploring these avenues.

In summary, quantitative approaches to understanding human behavior confer the benefits of speaking parsimoniously and describing higher-order relations (Critchfield & Reed, 2009). We have proposed that complex models of human behavior consistent with stimulus equivalence and related theories can be modeled in terms of the higher order properties of volume, mass, and density, consistent with Newtonian classical mechanics, and may explain part of the nonlinearity of equivalence relations observed in basic experimental research with humans. We have shown how selected predictions derived from the theory square with existing experimental data that are difficult to account with traditional accounts of stimulus equivalence. We have also illustrated the theory’s heuristic value by showing that (1) it makes testable predictions for which new basic research studies are needed and (2) it offers potentially valuable guidance to application. We now invite other researchers to help refine the theory and evaluate its utility.