1 Introduction

The Euclidean ball has been extensively studied for a long time. Since it is a geometric object rich in interesting properties, several characterizations of the ball have appeared in the literature. We are especially interested in characterizations that are related to properties of circumscribed polytopes. We must recall that a polytope is the convex hull of a finite set of points, for instance, the convex hull of a finite set of points in the plane is a polygon. We say that a convex set \(K\subset {\mathbb {R}}^n\), \(n\ge 2\), is a convex body if it is compact and with non-empty interior. A polytope \({\mathcal {P}}\) is circumscribed to a convex body K if \(K\subset {\mathcal {P}}\) and every \(n-1\)-dimensional face of \({\mathcal {P}}\) is tangent to K. We have the following: Let \(K\subset {\mathbb {R}}^n\) be a convex body and let \({\mathcal {P}}\) be any rectangular parallelepiped circumscribed to K. If the centers of all the \((n-1)\)-dimensional faces of \({\mathcal {P}}\) are in the boundary of K, then K is a ball. This characterization was posed as a problem in 1926 by Blaschke (see [4]) and was solved by Kneser (see for instance [5]). The two dimensional analogue of this result was proved by Green [7], Khassa [10], and Groemer [8]. In [2], Bezdek and Connelly proved a similar result that considers equilateral circumscribed triangles instead of rectangles.

A convex polygon, all of whose internal angles have the same measure is called an equiangular polygon. In the case of three and four sides the corresponding equiangular polygons are the equilateral triangles and the rectangles. Inspired by the two results mentioned above and looking for another proof of a Gutkin’s theorem on caustics of constant angle (see [9]), the following was conjectured in [1]:

Conjecture 1

Let \(n\ge 3\) be a fixed integer number and let \(K\subset {\mathbb {R}}^2\) be a convex body such that for every equiangular circumscribed n-gon, the midpoints of its sides belong to K. Then K is a disc.

In this note, we provide a proof for this conjecture and a characterization of the 3-dimensional ball in the sense of the Blaschke–Kneser’s result mentioned at the beginning. More precisely, we prove the following two results.

Theorem 1

Let \(n\ge 3\) be a fixed integer and let \(K\subset {\mathbb {R}}^2\) be a convex body. Suppose that for every equiangular circumscribed n-gon, the midpoints of its sides belong to K. Then K is a disc.

Theorem 2

Let \(K\subset {\mathbb {R}}^3\) be a convex body. Suppose that for every circumscribed regular tetrahedra the centers of its faces belong to K. Then K is a ball.

2 Auxiliary results on isoptic curves

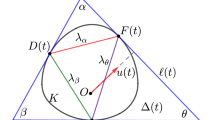
The proof of Theorem 1 relies in some results related to some especial curves known as isoptic curves. Let K be a strictly convex body (without segments in its boundary) in the plane with differentiable boundary. For any \(\alpha \in (0,\pi )\), the \(\alpha\)-isoptic \(K_{\alpha }\) of K is defined as the locus of points from which K is seen under an angle \(\alpha\), i.e., \(K_{\alpha }\) is the set of points where two tangent lines of K intersect at an angle \(\alpha\) (see Fig. 1).

Fig. 1
figure 1

The \(\pi /2\)-isoptic of an ellipse is a circle

Full size image

Isoptic curves were first studied by La Hire in 1704 and Chasles in 1837, and have important applications in Kinematic Geometry, cam mechanisms, architecture, and there is an extensive bibliography dealing with isoptic curves and their properties [3, 5, 11].

Let \(p:{\mathbb {R}}\rightarrow {\mathbb {R}}\) denote the support function of K, i.e., the value p(t) is defined as \(\max \nolimits _{z\in K}\langle z,(\cos t, \sin t) \rangle\). In particular, if O is in the interior of K and using complex notation, we have that p(t) is the positive number such that \(p(t)e^{it}\) lies on one of the two tangent lines of K that are orthogonal to \(e^{it}\). It is well known that the boundary of K can be parametrized by (see [11] and Fig. 2)

$$\begin{aligned} z(t)=p(t)e^{it}+p'(t)ie^{it}, \end{aligned}$$
(1)

while \(K_{\alpha }\) can be parametrized as (see [6])

$$\begin{aligned} z_{\alpha }(t)=p(t)e^{it}+\left[ p(t)\cot \alpha +\frac{1}{\sin \alpha }p(t+\pi -\alpha )\right] ie^{it}. \end{aligned}$$
(2)

For any \(t\in {\mathbb {R}}\), we denote (see Fig. 3)

$$\begin{aligned} a(t)&=|z_{\alpha }(t)-z(t)|, \end{aligned}$$
(3)
$$\begin{aligned} b(t)&=|z_{\alpha }(t)-z(t+\pi -\alpha )|. \end{aligned}$$
(4)
Fig. 2
figure 2

Parametrization of the boundary of K

Full size image
Fig. 3
figure 3

Parameters of the isoptic curve

Full size image

After some simple computations, we have (see Fig. 4)

$$\begin{aligned} a(t)&=\frac{1}{\sin \alpha }[p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha ], \end{aligned}$$
(5)
$$\begin{aligned} b(t)&=\frac{1}{\sin \alpha }[p(t+\pi -\alpha )\cos \alpha +p'(t+\pi -\alpha )\sin \alpha +p(t)]. \end{aligned}$$
(6)
Fig. 4
figure 4

\(a(t)= \frac{1}{\sin \alpha }\left[ p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha \right]\)

Full size image

3 Proof of Theorem 1

We need the following lemmas.

Lemma 1

Let \(\alpha \in (0,\pi )\). For any natural number \(n\ge 2\), the following inequality is satisfied:

$$\begin{aligned} |\sin n\alpha |<n\sin \alpha . \end{aligned}$$

Proof

Notice that

$$\begin{aligned} |\sin 2\alpha |=|2\cos \alpha \sin \alpha |<2|\sin \alpha |=2\sin \alpha . \end{aligned}$$

Assume that \(|\sin n\alpha |<n\sin \alpha\), for every \(n\le k\), where k is a natural number. Then, for \(n=k+1\), we have that

$$\begin{aligned} |\sin (k+1)\alpha |&=|\sin k\alpha \cos \alpha +\sin \alpha \cos k\alpha |\\&\le |\sin k\alpha \cos \alpha |+\sin \alpha |\cos k\alpha |\\&<k\sin \alpha +\sin \alpha =(k+1)\sin \alpha . \end{aligned}$$

Thus, the result follows by induction. \(\square\)

To prove that the only convex body such that its circumscribed rectangles are touched at the midpoints of their sides must be a disc, Green arrives in [7] to the equation \(2 p'(t)=p(t+\pi /2)-p(t-\pi /2)\) whose solution is of the form \(p(t)=c+a\sin t+b\cos t\), which corresponds to the support function of a disc (see Fig. 5). The following lemma shows that when we replace the angle \(\pi /2\) by the angle \(\pi -\alpha\), in Green’s equation, the solution is also of the same form.

Fig. 5
figure 5

Support function of a disc with center (a, b) and radius c

Full size image

Lemma 2

Let \(\alpha\) be a fixed number in the interval \((0,\pi )\) and let \(p:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a differentiable periodic function with period \(2\pi\) that satisfies the differential equation

$$\begin{aligned} 2\sin \alpha \, p'(t)=p(t+\pi -\alpha )-p(t-\pi +\alpha ). \end{aligned}$$
(7)

Then p is of the form \(p(t)=c+a\sin t+b\cos t\), where a, b and c are real constants.

Proof

Since p is a periodic function with period \(2\pi\), we may consider its Fourier series, i.e.,

$$\begin{aligned} p(t)=\frac{a_0}{2}+\sum _{n=1}^\infty \left( a_n\cos nt+b_n\sin nt\right) . \end{aligned}$$

On the other side, the Fourier series of \(p'\) is given by (see for instance [8])

$$\begin{aligned} p'(t)=-\sum _{n=1}^\infty \left( na_n\sin nt-nb_n\cos nt\right) . \end{aligned}$$

Substituting the Fourier series representation of p and \(p'\) into (7) gives

$$\begin{aligned}&-2\sin \alpha \sum _{n=1}^\infty \left( na_n\sin nt-nb_n\cos nt\right) \\&=\frac{a_0}{2}+\sum _{n=1}^\infty \left[ a_n\cos n(t+\pi -\alpha )+b_n\sin n(t+\pi -\alpha )\right] \\&-\frac{a_0}{2}-\sum _{n=1}^\infty \left[ a_n\cos n(t-\pi +\alpha )+b_n\sin n(t-\pi +\alpha )\right] . \end{aligned}$$

Simplifying the previous equation using trigonometrical identities yields

$$\begin{aligned}&\sin \alpha \sum _{n=1}^\infty \left[ na_n\sin nt-nb_n\cos nt\right] =\sum _{n=1}^\infty \sin n(\pi -\alpha )\left[ a_n\sin nt-b_n\cos nt\right] . \end{aligned}$$

For \(n=1\), we have

$$\begin{aligned} (a_1\sin t-b_1\cos t)\sin \alpha =(a_1\sin t-b_1\cos t)\sin (\pi -\alpha ). \end{aligned}$$

Since \(\sin \alpha = \sin (\pi -\alpha )\), the previous equality holds for any real numbers \(a_1\) and \(b_1\).

Now, for any \(n>1\), we have

$$\begin{aligned} (a_n\sin nt-b_n\cos nt)n\sin \alpha =(a_n\sin nt-b_n\cos nt)\sin n(\pi -\alpha ). \end{aligned}$$

By Lemma 1, we know that \(n\sin \alpha \ne \sin n(\pi -\alpha )\) for \(\alpha \in (0,\pi )\), it follows that \(a_n\sin nt-b_n\cos nt=0,\) for every \(t\in [0,2\pi ).\) Hence, we have that \(a_n=b_n=0\) for every \(n>1\). Therefore,

$$\begin{aligned} p(t)=\frac{a_0}{2}+a_1\cos t+b_1\sin t. \end{aligned}$$

\(\square\)

We have the following result.

Theorem 3

Let K be a strictly convex body with differentiable boundary. If there exists an \(\alpha \in (0,\pi )\) such that \(b(t)=a(t+\pi -\alpha )\) for every \(t\in {\mathbb {R}}\), then K is a disc.

Proof

Using the hypothesis \(b(t)=a(t+\pi -\alpha )\) and Eqs. (5) and (6), we have

$$\begin{aligned} 2\sin \alpha \, p'(t+\pi -\alpha )=p(t+2\pi -2\alpha )-p(t). \end{aligned}$$

Letting \(\theta =t+\pi -\alpha\), we obtain the differential equation

$$\begin{aligned} 2\sin \alpha \, p'(\theta )=p(\theta +\pi -\alpha )-p(\theta -\pi +\alpha ). \end{aligned}$$

It follows from Lemma 2 that p is of the form \(p(\theta )=c+a\sin \theta +b\cos \theta\), i.e., p is the support function of a disc with center (a, b) and radius \(r=c\). \(\square\)

Proof of Theorem 1

Let n be any integer greater than or equal to 3. It is not difficult to see that a convex body with the property that all the sides of the circumscribed equiangular n-gons are touched at their midpoints must be strictly convex and with differentiable boundary. Since the circumscribed n-gons are equiangular, we have that all its vertices are in the isoptic curve \(K_{\alpha }\), for \(\alpha =\frac{(n-2)\pi }{n}.\) The hypothesis of the theorem means that \(a(t+\pi -\alpha )=b(t)\) for every \(t\in {\mathbb {R}}\), so we apply Theorem 3 and conclude that K must be a disc. \(\square\)

4 Proof of the 3-dimensional characterization of the ball

Before proving Theorem 2, we show an easy consequence of Theorem 1 which contains as a particular case the Blaschke–Kneser’s theorem. We say that a prism is an n-equiangular prism if its base is an equiangular polygon with n sides.

Proposition 1

Let \(K\subset {\mathbb {R}}^3\) be a convex body and let \(n\ge 3\) be a fixed integer number. If all the lateral faces of every circumscribed n-equiangular prism are touched at their centers, then K is a ball.

Proof

Let \(u\in {\mathbb {S}}^2\) be a fixed direction. Consider all the n-equiangular prisms circumscribed to K and whose base is orthogonal to u. Since the lateral faces of any circumscribed prism are touched at their centers, we have that the orthogonal projection of K in direction u, denoted by \(\pi _u(K)\), is a planar convex body with the property that the sides of every circumscribed equiangular n-gon are touched at their midpoints. We apply Theorem 1 and obtain that \(\pi _u(K)\) is a disc. Since this is true for every vector \(u\in {\mathbb {S}}^2\), we have that all the 2-dimensional projections of K are discs, therefore, K is a ball. \(\square\)

Proof of Theorem 2

Let \(u\in {\mathbb {S}}^2\) be an arbitrary unit vector and let H(u) be the support plane of K which has u as outward normal vector. Consider an arbitrary regular simplex circumscribed to K with one face on the plane H(u). The envelope of the sides of the faces contained in H(u), of all such simplexes, is a convex curve \(\gamma (u)\). To see that \(\gamma (u)\) is the boundary of a convex set just notice the following: if \(\ell \subset H(u)\) is the line that contains one side of a simplex (among the simplexes with one face in H(u)), then \(\gamma (u)\) is contained in a half-plane in H(u) with boundary \(\ell\). This means that through every point of \(\gamma (u)\) there exists a support line and hence \(\gamma (u)\) is the boundary of a convex planar body (see for instance [11]).

By hypothesis, we have that \(\gamma (u)\) has the property that the sides of every circumscribed equilateral triangle are touched at their midpoints. By Theorem 1, we have that \(\gamma (u)\) is a circle. Every tangent line of the circle \(\gamma (u)\) is obtained as intersection between H(u) and a support plane of K which has outward normal vector forming an angle \(\beta =\pi -2\arcsin (\frac{1}{\sqrt{3}})\) with respect to u. It follows that all the support planes of K with outward normal vector forming an angle \(\beta\) with respect to u, concur at a point \(x_u.\) Note that the central projection of K over the plane H(u) from the point \(x_u\) is precisely the disc with boundary \(\gamma (u)\). If we consider all the unit vectors \(u\in {\mathbb {S}}^2\), the points \(x_u\) comprise a closed surface \(\Omega\) which encloses K and such that from every point \(z\in \Omega\), K looks circular. It was proved by Bianchi and Gruber [3], that a convex body under these conditions must be a ball. Therefore, the proof is complete. \(\square\)