1 Introduction

Let K be a strictly convex body in the plane, i.e., a compact and convex set with non-empty interior and without segments in its boundary. Denote by \(\ell (t)\) the support line of K with outward normal vector \(u(t)=(\cos t, \sin t)\), for every real number t. Consider now a triangle \(\Delta =\triangle ABC\) with given angles \(\alpha \), \(\beta \), and \(\theta \). For every \(t\in [0,2\pi ]\) there exists exactly one triangle similar to \(\Delta \) circumscribed to K, with its side A(t)C(t) over the line \(\ell (t)\), and with the angles \(\alpha \), \(\beta \), and \(\theta \) in the counter clockwise sense as shown in Fig. 1. We denote such a triangle by \(\Delta (t)=A(t)B(t)C(t)\) and name it \((\alpha ,\beta ,\theta )\)-triangle. Let D(t), E(t), and F(t) be the contact points between K and the sides of \(\Delta (t)\). When K is a disc, the following conditions hold:

  1. (1)

    \(\overline{A(t)D(t)}=\overline{A(t)F(t)}\), \(\overline{B(t)D(t)}=\overline{B(t)E(t)}\), \(\overline{C(t)E(t)}=\overline{C(t)F(t)}\),

  2. (2)

    \(\frac{\overline{A(t)D(t)}}{\overline{D(t)B(t)}}=\lambda _1\), \(\frac{\overline{B(t)E(t)}}{\overline{E(t)C(t)}}=\lambda _2\), \(\frac{\overline{C(t)F(t)}}{\overline{F(t)A(t)}}=\lambda _3\), for three fixed numbers \(\lambda _1\), \(\lambda _2\), \(\lambda _3\),

  3. (3)

    \(\overline{D(t)F(t)}=\lambda _{\alpha }\), \(\overline{D(t)E(t)}=\lambda _{\beta }\), \(\overline{E(t)F(t)}=\lambda _{\theta }\), for some fixed numbers \(\lambda _{\alpha },\) \(\lambda _{\beta }\), \(\lambda _{\theta }\),

for every \(t\in [0,2\pi ]\).

Fig. 1
figure 1

A triangle similar to \(\Delta \) circumscribed to K

Full size image

However, what happens if for a convex body K, any one of conditions (1), (2) or (3) holds for every \(t\in [0,2\pi ]\)? Is K a disc?

As we will see in the following sections, the answer is positive and it relies on results about isoptic curves. We may think that if the size of \(\Delta (t)\) is independent of t, i.e., it always has the same size, then it is sufficient to ensure that K must be a disc. However, this is not true: Let K be a convex body in the plane and let \({\mathcal {P}}\) be a convex polygon. It is said that K is a rotor in \({\mathcal {P}}\) if for every rotation \(\rho \), there is a translate of \({\mathcal {P}}\) that contains \(\rho (K)\) and all sides of \({\mathcal {P}}\) are tangent to K. In the case where the polygon \({\mathcal {P}}\) is a triangle with angles \(\alpha ,\) \(\beta \), \(\theta \), it is known that there exist rotors different from discs if \(\frac{\alpha }{\pi }\), \(\frac{\beta }{\pi }\), and \(\frac{\theta }{\pi }\) are all rational numbers, see for instance [3], and for the particular case of rotors in equilateral triangles see [11].

Similar problems were recently studied: a convex body K is a disc if for some angles \(\alpha \in (0,\pi )\) and \(\beta =\alpha \), it holds that \(\overline{A(t)D(t)}=\overline{D(t)B(t)}\), for every \(t\in [0,2\pi ]\) (see [9]). If for some \(\alpha \in (0,\pi )\) it holds that \(\overline{B(t)D(t)}\) has a constant value for every \(t\in [0,2\pi ]\), K is a disc (see [4]). If \(D(t)F(t)=\lambda _{\alpha }\), for every \(t\in [0,2\pi ]\) and for a constant number \(\lambda _{\alpha }\), and K has constant width or has rotational symmetry of angle \(\pi -\alpha \), then K is a disc (see [7]). We can see that condition (1) implies that K must be a disc: just notice that the points D(t), E(t), F(t), are points of contact between the incircle of \(\triangle A(t)B(t)C(t)\) and its sides. Now we use Lemma 3.3 in [6] and conclude that K is a disc. However, there are convex bodies different from discs, for which \(\overline{A(t)D(t)}=\overline{A(t)F(t)}\) for every \(t\in [0,2\pi ]\) (see [8]). Indeed, there are convex bodies, different from discs, for which this condition holds for three (or more) different angles \(\alpha , \beta , \theta \in (0,\pi )\), but in this case the condition \(\alpha +\beta +\theta =\pi \) does not hold.

The main purpose of this paper is to prove that a convex body for which condition (3) holds, must be a disc.

2 Basic concepts of isoptic curves

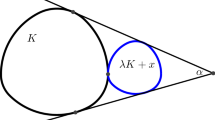
The function \(p:{\mathbb {R}}\longrightarrow {\mathbb {R}}\), defined as \(p(t)=\max _{x\in K} \langle u(t), x\rangle \), is known by the name of support function of K. When the origin O is contained in K, p(t) is nothing else but the distance from O to the support line \(\ell (t).\) The distance between the support lines \(\ell (t)\) and \(\ell (t+\pi )\) is called the width of K in direction u(t) and it is denoted by w(t), in other words, \(w(t)=p(t)+p(t+\pi )\). If w(t) is constant, independently of t, we say that K is a body of constant width. For any \(\alpha \in (0,\pi )\), the \(\alpha \)-isoptic \(K_{\alpha }\) of K is defined as the locus of points at which two tangent lines to K intersect at an angle \(\alpha \). Using the support function, \(\partial K\) is parameterized (see for instance [10]) by

$$\begin{aligned}{} \gamma (t)=p(t)u(t)+ p'(t) u'(t), \ \text {for} \ t\in [0,2\pi ]. \end{aligned}$$

The isoptic curve \(K_{\alpha }\) can be parameterized by the same angle by the formula (see [2] or [8])

$$\begin{aligned}{} \gamma _{\alpha }(t)=p(t)u(t)+\left[ p(t)\cot \alpha +\frac{1}{\sin \alpha }p(t+\pi -\alpha )\right] u'(t). \end{aligned}$$

By Cauchy’s formula, the perimeter of K can be obtained by (see [10])

$$\begin{aligned} L(K)=\int _0^{2\pi }p(t)dt. \end{aligned}$$
(1)

For any \(t\in {\mathbb {R}}\) we define (see Fig. 2)

$$\begin{aligned} a_{\alpha }(t)&=|\gamma _{\alpha }(t)-\gamma (t)|,\\ b_{\alpha }(t)&=|\gamma _{\alpha }(t)-\gamma (t+\pi -\alpha )|,\\ q_{\alpha }(t)&=|\gamma (t)-\gamma (t+\pi -\alpha )|. \end{aligned}$$
Fig. 2
figure 2

Parameters of the isoptic curve

Full size image

By some simple calculations we can express the lengths a(t) and b(t) in terms of the support function of K:

$$\begin{aligned} a_{\alpha }(t)&=\frac{1}{\sin \alpha }[p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha ], \end{aligned}$$
(2)
$$\begin{aligned} b_{\alpha }(t)&=\frac{1}{\sin \alpha }[p(t+\pi -\alpha )\cos \alpha +p'(t+\pi -\alpha )\sin \alpha +p(t)]. \end{aligned}$$
(3)

3 Some useful lemmas about isoptic curves

Lemma 1

Let K be a strictly convex body in the plane and let \(\alpha ,\theta \in (0,\pi )\) be angles such that \(a_{\alpha }(t)=a_{\alpha }(t+\theta )\), for every \(t\in [0,2\pi ]\). Then, K has rotational symmetry of angle \(\theta \).

Proof

Recall that \(a_{\alpha }(t)=\frac{1}{\sin \alpha }[p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha ]\). The hypothesis \(a_{\alpha }(t)=a_{\alpha }(t+\theta )\) implies that

$$\begin{aligned} p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha&=p(t+\theta +\pi -\alpha )\\&\quad +p(t+\theta )\cos \alpha -p'(t+\theta )\sin \alpha , \end{aligned}$$

which is equivalent to

$$\begin{aligned}{}[p'(t+\theta )-p'(t)]\sin \alpha =[p(t+\theta )-p(t)]\cos \alpha + p(t+\theta +\pi -\alpha )-p(t+\pi -\alpha ). \end{aligned}$$

Let \(y(t)=p(t+\theta )-p(t)\). Using the previous equality we obtain the following differential equation

$$\begin{aligned} y'(t)\sin \alpha =y(t)\cos \alpha +y(t+\pi -\alpha ). \end{aligned}$$
(4)

We express y and \(y'\) in terms of their Fourier Series:

$$\begin{aligned} y(t)= & {} \sum _{n=-\infty }^{\infty }c_ne^{int}, \\ y'(t)= & {} \sum _{n=-\infty }^{\infty }nic_ne^{int}. \end{aligned}$$

Then,

$$\begin{aligned} \sum _{n=-\infty }^{\infty }ni\sin \alpha c_ne^{int}=\sum _{n=-\infty }^{\infty }\cos \alpha c_ne^{int}+\sum _{n=-\infty }^{\infty }(-1)^ne^{-in\alpha }c_ne^{int} \end{aligned}$$

and we have

$$\begin{aligned} ni\sin \alpha c_n=\cos \alpha +(-1)^ne^{-in\alpha }c_n. \end{aligned}$$

We claim that \(c_n=0\) for every n not equal to 1 or \(-1\). Suppose this is not the case. Then,

$$\begin{aligned} ni\sin \alpha =\cos \alpha +(-1)^n\cos n\alpha -(-1)^ni\sin (n\alpha ). \end{aligned}$$

Equivalently

$$\begin{aligned} n\sin \alpha =-(-1)^n\sin (n\alpha )\text { and }\cos \alpha +(-1)^n\cos n\alpha =0. \end{aligned}$$

Notice that the first equation is not satisfied when \(n\ne 0,1,-1\) while the second is false for \(n=0\). The claim now follows and we conclude that

$$\begin{aligned} p(t+\theta )-p(t)=y(t)=c_{-1}e^{-it}+c_1e^{it}=a_1\cos t+b_1\sin t, \end{aligned}$$

where \(c_1=a_1-b_1i=\overline{c_{-1}}\). Using vector notation we obtain

$$\begin{aligned} p(t+\theta )=p(t)+\langle (a_1,b_1), u(t)\rangle . \end{aligned}$$

Let \(t_0\) be such that \(u(t_0+\theta )\) is parallel to \((a_1,b_1)\). Notice that

$$\begin{aligned} p(t_0+2\theta )&=p(t_0+\theta )+\langle (a_1,b_1), u(t_0+\theta )\rangle =p(t_0+\theta )+||(a_1,b_1)||,\\ p(t_0+3\theta )&=p(t_0+2\theta )+||(a_1,b_1)||=p(t_0+\theta )+2||(a_1,b_1)||,\\ \vdots \\ p(t_0+n\theta )&=p(t_0+\theta )+(n-1)||(a_1,b_1)||. \end{aligned}$$

Since the support function is bounded, we must have \((a_1,b_1)=(0,0)\). We conclude that \(p(t+\theta )=p(t)\) for every t, which implies that K has rotational symmetry of angle \(\theta \). \(\square \)

As an application of Lemma 1, we have the following characterization of the disc, which we will prove for every kind of triangles in the following section.

Proposition 1

Let K be a convex body and \(\alpha ,\beta \in (0,\pi )\) such that \(2\alpha +\beta =\pi \). Suppose that \(q_{\alpha }(t)=\lambda _{\alpha }\) and \(q_{\beta }(t)=\lambda _{\beta }\), for every \(t\in [0,2\pi ]\) and for some positive numbers \(\lambda _{\alpha }\) and \(\lambda _{\beta }\). Then K is a disc.

Fig. 3
figure 3

An isosceles circumscribed triangle

Full size image

Proof

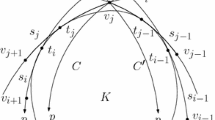
Let \(\measuredangle \gamma (t)\gamma (t+\pi -\alpha )\gamma (t-2\alpha )=\phi \) and \(\measuredangle \gamma (t)\gamma (t+\pi -\alpha )\gamma _{\alpha }(t)=\alpha _1(t)\), for every \(t\in [0,2\pi ]\), as shown in Fig. 3. Notice that \(\alpha _1(t+\pi -\alpha )=\alpha _1(t)+\phi -\alpha \), for every t. Let \(t_1,t_2\in [0,2\pi ]\) be such that \(\alpha (t_1)\le \alpha (t)\le \alpha (t_2)\) for every \(t\in [0,2\pi ]\). Since \(\alpha _1(t_1+\pi -\alpha )=\alpha _1(t_1)+\phi -\alpha \), we must have that \(\phi -\alpha \ge 0\). Similarly, \(\alpha (t_2+\pi -\alpha )=\alpha _1(t_2)+\phi -\alpha \) implies that \(\phi -\alpha \le 0\). We conclude that \(\alpha =\phi \) and \(\alpha _1(t+\pi -\alpha )=\alpha _1(t)\) for every \(t\in [0,2\pi ]\). Using the previous equality and the Law of sines for the triangles \(\Delta \gamma _{\alpha }(t+\pi -\alpha )\gamma (t-2\alpha )\gamma (t+\pi -\alpha )\) and \(\Delta \gamma _{\alpha }(t)\gamma (t+\pi -\alpha )\gamma (t)\) we conclude that for every t the following equalities hold

$$\begin{aligned} \frac{a_{\alpha }(t)}{\sin \alpha _1(t)}=\frac{\lambda _{\alpha }}{\sin \alpha }=\frac{a_{\alpha }(t+\pi -\alpha )}{\sin \alpha _1(t)}. \end{aligned}$$

It follows that \(a_{\alpha }(t)=a_{\alpha }(t+\pi -\alpha )\) for every t. By Lemma 1, K has rotational symmetry of angle \(\alpha \). The result now follows from Theorem 2 in [7]. \(\square \)

Lemma 2

Let K be a strictly convex body in the plane and let \(\alpha \in (0,\pi )\) be a given angle. Then there exist two real numbers \(t_0,t_1\in [0,2\pi ]\) such that \(a_{\alpha }(t_0)=b_{\alpha }(t_0)\) and \(a_{\alpha }(t_1+\pi -\alpha )=b_{\alpha }(t_1)\).

Proof

From (2) and (3) we have that

$$\begin{aligned}{} & {} \sin \alpha [a_{\alpha }(t)-b_{\alpha }(t)]\\{} & {} \quad =p(t+\pi -\alpha )(1- \cos \alpha )-p(t)(1- \cos \alpha )-p'(t)\sin \alpha -p'(t+\pi -\alpha )\sin \alpha . \end{aligned}$$

By Cauchy’s formula for the perimeter and since p is a periodic function with period equal to \(2\pi \), we have that

$$\begin{aligned}{} & {} \int \limits _0 ^{2\pi } \sin \alpha [a_{\alpha }(t)-b_{\alpha }(t)] dt\\{} & {} \quad = L(K)(1-\cos \alpha )-L(K)(1-\cos \alpha )-p(t)\sin \alpha |_0 ^{2\pi }-p(t+\pi -\alpha )\sin \alpha |_0 ^{2\pi }, \end{aligned}$$

hence

$$\begin{aligned} \int \limits _0 ^{2\pi } \sin \alpha [a_{\alpha }(t)-b_{\alpha }(t)] dt=0. \end{aligned}$$

Since a and b are continuous functions, we have that there exists a number \(t_0\) such that \(a_{\alpha }(t_0)=b_{\alpha }(t_0)\).

The proof of the existence of \(t_1\) such that \(a_{\alpha }(t_1+\pi -\alpha )=b_{\alpha }(t_1)\) is completely analogous. \(\square \)

The following lemma gives another characterization of the disc.

Lemma 3

Let K be a strictly convex body in the plane and let \(\alpha \in (0,\pi /2)\) be a given angle. Suppose \(a_{\alpha }(t)=\lambda a_{\pi -\alpha }(t)\), for every \(t\in [0,2\pi ]\) and for \(\lambda >1\). Then K is a disc.

Proof

We know that

$$\begin{aligned} a_{\alpha }(t)=\frac{1}{\sin \alpha }[p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha ] \end{aligned}$$

and

$$\begin{aligned} \lambda a_{\pi -\alpha }(t)=\frac{\lambda }{\sin \alpha }[p(t+\alpha )-p(t)\cos \alpha -p'(t)\sin \alpha ]. \end{aligned}$$

Then,

$$\begin{aligned} p(t+\pi -\alpha )+p(t)\cos \alpha -p'(t)\sin \alpha =\lambda p(t+\alpha )-\lambda p(t)\cos \alpha -\lambda p'(t)\sin \alpha , \end{aligned}$$

or

$$\begin{aligned} (\lambda -1) p'(t)\sin \alpha +p(t+\pi -\alpha )-\lambda p(t+\alpha )+(\lambda +1) p(t) \cos \alpha =0. \end{aligned}$$
(5)

Let the Fourier series of p be given by

$$\begin{aligned} p(t)=\sum _{n=-\infty }^{\infty }c_ne^{int}. \end{aligned}$$

By equation (5) we have

$$\begin{aligned}{} & {} \sum _{n=-\infty }^{\infty }i(\lambda -1)n\sin \alpha c_ne^{int}+\sum _{-\infty }^{\infty }(-1)^nc_ne^{-in\alpha }e^{int}-\sum _{n=-\infty }^{\infty }\lambda c_ne^{in\alpha }e^{int}\\{} & {} \quad +\sum _{n=-\infty }^{\infty }i(\lambda +1)\cos \alpha c_ne^{int}=0. \end{aligned}$$

We conclude that

$$\begin{aligned}{}[i(\lambda -1)n\sin \alpha +(-1)^ne^{-in\alpha }-\lambda e^{in\alpha }+(\lambda +1)\cos \alpha ]c_n=0, \end{aligned}$$

i.e.,

$$\begin{aligned}{} & {} [i(\lambda -1)n\sin \alpha +(-1)^n\cos n\alpha -(-1)^n i\sin n\alpha -\lambda \cos n\alpha -i\lambda \sin n\alpha \\{} & {} \quad +(\lambda +1)\cos \alpha ]c_n=0. \end{aligned}$$

For \(n=0\) we obtain

$$\begin{aligned} 1-\lambda +(\lambda +1)\cos \alpha =0, \end{aligned}$$

which implies

$$\begin{aligned} \lambda =\frac{1+\cos \alpha }{1-\cos \alpha }. \end{aligned}$$
(6)

Notice that if \(c_n\ne 0\) we must have

$$\begin{aligned} (\lambda -1)n\sin \alpha -(\lambda +(-1)^n)\sin n\alpha =0\text { and }((-1)^n-\lambda )\cos n\alpha +(\lambda +1)\cos \alpha =0. \end{aligned}$$

Now, if \(n\ne 1\) is an odd natural number, the first equation simplifies to

$$\begin{aligned} n\sin \alpha +\sin n\alpha =0, \end{aligned}$$

which is never satisfied. It follows that \(c_n=0\) for every odd natural number \(n\ne 1\). On the other hand, for every natural even number \(n\ne 0\), we have

$$\begin{aligned} (1-\lambda )\cos n\alpha +(\lambda +1)\cos \alpha =0. \end{aligned}$$

Using equation (6) we conclude that

$$\begin{aligned} \cos n\alpha =-1, \end{aligned}$$

which is impossible, since \(0<\alpha <\pi /2\). It follows that \(c_n=0\) for every even number \(n>0\) and that \(p(t)=c_0+ce^{it}\). Thus, K is a disc. \(\square \)

4 Main results

The first result we prove here is concerns property (2) mentioned in the introduction.

Theorem 1

Let \(K\subset {\mathbb {R}}^2\) be a strictly convex body and let \(\alpha , \beta , \theta \in (0,\pi )\) be three angles such that \(\alpha +\beta +\theta =\pi \). Suppose that for every \(t\in [0,2\pi ]\)

$$\begin{aligned} \frac{b_{\alpha }(t)}{a_{\beta }(t+\pi -\alpha )}=\lambda _1, \ \ \frac{b_{\beta }(t+\pi -\alpha )}{a_{\theta }(t-\pi +\theta )}=\lambda _2, \ \ \frac{b_{\theta }(t-\pi +\theta )}{a_{\alpha }(t)}=\lambda _3, \end{aligned}$$

for some constants \(\lambda _1\), \(\lambda _2\), and \(\lambda _3\). Then K is a disc.

Fig. 4
figure 4

\(\gamma (t+\pi -\alpha )\), \(\gamma (t-\pi +\theta )\), \(\gamma (t)\), divide the corresponding sides in the given ratios

Full size image

Proof

Since all \((\alpha ,\beta ,\theta )\)-triangles are similar and the points \(\gamma (t+\pi -\alpha )\), \(\gamma (t-\pi +\theta )\), \(\gamma (t)\), divide the corresponding sides in the given ratios \(\lambda _1\), \(\lambda _2,\) \(\lambda _3\), we have that

$$\begin{aligned} \frac{a_{\alpha }(t)}{b_{\alpha }(t)}, \ \ \frac{a_{\beta }(t+\pi -\alpha )}{b_{\beta }(t+\pi -\alpha )}, \ \ \text {and} \ \ \frac{a_{\theta }(t-\pi +\theta )}{b_{\theta }(t-\pi +\theta )} \end{aligned}$$

are also constant. Now, by Lemma 2 we have that \(a_{\alpha }(t)=b_{\alpha }(t)\), \(a_{\beta }(t)=b_{\beta }(t)\), \(a_{\theta }(t)=b_{\theta }(t)\) for every \(t\in [0,2\pi ]\). It follows that the points \(\gamma (t+\pi -\alpha )\), \(\gamma (t-\pi +\theta )\), \(\gamma (t)\) are the contact points between the incircle of the triangle \(\triangle \gamma _{\alpha }(t)\gamma _{\beta }(t+\pi -\alpha )\gamma _{\theta }(t-\pi +\theta )\) and its sides, for every \(t\in [0,2\pi ]\). Now, the hypothesis of Lemma 3.3 in [6] holds, and so we conclude that K is a disc. \(\square \)

Now we present the main result of this work.

Theorem 2

Let \(K\subset {\mathbb {R}}^2\) be a regular convex body and let \(\alpha , \beta , \theta \in (0,\pi )\) be three angles such that \(\alpha +\beta +\theta =\pi \). Suppose that for every \(t\in [0,2\pi ]\), \(q_{\alpha }(t)=\lambda _{\alpha }\), \(q_{\beta }(t)=\lambda _{\beta }\), \(q_{\theta }(t)=\lambda _{\theta }\), for some constants \(\lambda _{\alpha }\), \(\lambda _{\beta }\), and \(\lambda _{\theta }\). Then K is a disc.

In the proof of Theorem 2 we will use the following lemma (see [11]). For the sake of completeness we give a proof here.

Lemma 4

Let C be one of the points of intersection between two circles \(\Gamma _1\) and \(\Gamma _2\) with centres \(O_1\) and \(O_2\), respectively. The unique chord AB, with \(A\in \Gamma _1\), \(B\in \Gamma _2\), through C and with maximum length is obtained when AB is orthogonal to the common chord between \(\Gamma _1\) and \(\Gamma _2\), i.e., when AB is parallel to \(O_1O_2\).

Proof

Let AB be any chord through C, as shown in Fig. 5. Let \(M_1\) and \(M_2\) be the orthogonal projections of \(O_1\) and \(O_2\) onto AB. We know that the length of \(M_1M_2\) is half the length of AB. Suppose the orthogonal projection, T, of \(O_1\) onto the line \(O_2M_2\) lies in the segment \(O_2M_2\). Since \(O_1M_1M_2T\) is a rectangle, we have that the lengths of \(O_1T\) and \(M_1M_2\) are equal. From here we see that the maximum length of \(M_1M_2\) and hence of AB is when AB is parallel to \(O_1O_2\). The case when the orthogonal projection of \(O_2\) onto the line \(O_1M_1\) lies in the segment \(O_1M_1\), is completely analogous. \(\square \)

Fig. 5
figure 5

Maximum chord AB is when AB is parallel to \(O_1O_2\)

Full size image
Fig. 6
figure 6

All circumscribed \((\alpha ,\beta ,\theta )\)-triangles are maximal

Full size image

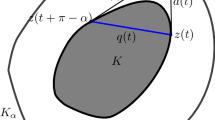
Proof of Theorem 2

Let \(t\in [0,2\pi ]\) be any angle and let \(\Delta (t)=\triangle \gamma _{\alpha }(t)\gamma _{\beta }(t+\pi -\alpha )\gamma _{\theta }(t-\pi +\theta )\) be the corresponding circumscribed \((\alpha ,\beta ,\theta )\)-triangle. The contact points between the sides of \(\Delta (t)\) and the boundary of K are \(\gamma (t)\), \(\gamma (t+\pi -\alpha )\), and \(\gamma (t-\pi +\theta )\), respectively. By Miquel’s theorem we know that there exists a point m(t) in common to the circumcircles of triangles \(\triangle \gamma _{\alpha }(t)\gamma (t+\pi -\alpha )\gamma (t)\), \(\triangle \gamma _{\beta }(t+\pi -\alpha )\gamma (t-\pi +\theta )\gamma (t+\pi -\alpha )\), and \(\triangle \gamma _{\theta }(t-\pi +\theta )\gamma (t)\gamma (t-\pi +\theta )\). By Lemma 4 we obtain that the maximum \((\alpha ,\beta ,\theta )\)-triangle circumscribed to \(\triangle \gamma (t)\gamma (t+\pi -\alpha )\gamma (t-\pi +\theta )\) is obtained when \([m(t),\gamma (t)]\), \([m(t),\gamma (t+\pi -\alpha )]\), \([m(t),\gamma (t-\pi +\theta )]\) are orthogonal to the corresponding sides of \(\Delta (t)\). Suppose that this is not the case and let \(\triangle z_{\alpha }z_{\beta }z_{\theta }\) be the maximum \(((\alpha ,\beta ,\theta )\)-triangle circumscribed to \(\triangle \gamma (t)\gamma (t+\pi -\alpha )\gamma (t-\pi +\theta )\), as shown in Fig. 6. Since the boundary of K is regular, the sides of \(\triangle z_{\alpha }z_{\beta }z_{\theta }\) intersect the interior of K. If we consider the corresponding support lines of K, parallel to the sides of \(\triangle z_{\alpha }z_{\beta }z_{\theta }\), we obtain an \((\alpha ,\beta ,\theta )\)-triangle circumscribed to K with size bigger than the size of \(\triangle z_{\alpha }z_{\beta }z_{\theta }\). This is a contradiction since such a triangle must touch the boundary of K in three points which are vertices of a triangle congruent to \(\Delta (t)\). It follows that the triangle \(\Delta (t)\), for every \(t\in [0,2\pi ]\), is maximal. In particular, we have that the length of \(a_{\alpha }(t)\) is constant for every \(t\in [0,2\pi ]\). We apply Lemma 2 in [4] and conclude that K is a disc. \(\square \)

Remark 1

Indeed, we have that the points \(\gamma (t)\), \(\gamma (t+\pi -\alpha )\), and \(\gamma (t-\pi +\theta )\) are the contact points between the incircle of \(\Delta (t)\) and the sides of \(\Delta (t)\). We can also conclude the proof of the theorem using Lemma 3.3 in [6].