Bifurcation trees of periodic motions to chaos in a parametric Duffing oscillator

Abstract

In this paper, bifurcation trees of periodic motions to chaos in a damped, parametric Duffing oscillator are investigated. From the semi-analytic method, differential equations of nonlinear dynamical systems are discretized first to obtain implicit mappings. Following the implicit mapping structures, periodic nodes of periodic motions are computed. The bifurcation trees of period-1 to period-4 motions are presented to demonstrate the routes of period-1 motions to chaos, and the corresponding stability and bifurcation are determined by eigenvalue analysis. For a better understanding of nonlinear behaviors of periodic motions in a parametric Duffing oscillator, harmonic frequency–amplitude characteristics of periodic motions are presented. From the analytical predictions, numerical simulations are performed. The trajectory, time-histories of displacement and velocity, harmonic amplitudes and phases of period-1 to period-4 motions are presented. Based on comparison of numerical and analytical results, determined is how many harmonic terms should be included in finite Fourier series, which help one select harmonic terms in analytical solutions and engineering application.

1 Introduction

Nonlinear oscillators extensively exist in engineering. An important issue is how to achieve accurate approximate solutions of nonlinear oscillators with strong nonlinearity. For recent hundreds years, several analytic methods have been developed for periodic motions of nonlinear oscillators, such as the method of averaging, perturbation methods, harmonic balance method, generalized harmonic balance method. In this paper, a semi-analytic method will be applied to determine the route of period-1 motion to chaos in a parametric Duffing oscillator.

In 1788, Lagrange [1] studied the three-body problem as a perturbation of two-body problem by using the method of averaging. The basic idea of this method is the original dynamical system can be approximated by an averaged system. In 1899, Poincare [2] used the perturbation method for analyzing the periodic motion of celestial mechanics. In 1920, van der Pol [3] built the oscillator by circuits and the periodic motions were determined by the method of averaging. In 1935, Krylov and Bogoliubov [4] continued developing the method of averaging in nonlinear dynamical systems. In 1964, Hayashi [5] used several analytic methods to determine the periodic solutions and the stability of nonlinear systems. In 1973, Nayfeh [6] introduced the perturbation method systematically and used multi-scale perturbation method to approximate the periodic motions of Duffing oscillator. 1976, Holmes and Rand [7] investigated the existence and stability of periodic solutions of the Duffing oscillator. The catastrophe theory was used for the stability and bifurcations of Duffing equation. In 1979, Nayfeh and Mook [8] employed the perturbation method for periodic motions of the Duffing oscillators in structural vibrations. In 1980, Ueda [9] numerically simulated chaos of the Duffing oscillator by numerical simulation. In 1987, Garcia-Margallo and Bejarano [10] employed a generalized harmonic balance method to determine the approximate solutions of periodic motions in dynamical systems with strong nonlinearity. In 1990, Coppola and Rand [11] discussed the approximation of limit cycle determined by averaging method with elliptic functions.

In 1868, the linear Mathieu equation was first investigated by Mathieu [12]. In 1913, Whittaker [13] introduced a method to find the general solution of the Mathieu equation. In 1961, Sevin [14] studied a pendulum-type vibration absorber with parametric excitation. In 1965, Tso and Caughey [15] investigated the stability of nonlinear systems with parametric excitation. In 1993, Mond [16] discussed the stability of nonlinear Mathieu equation. In 1997, Luo and Han [17] studied the stability and bifurcations of periodic motions in the generalized Duffing oscillator. In 1999, Luo and Han [18] gave the analytical prediction of chaos in a nonlinear rod, and the chaos and periodic motions were simulated by Poincare mapping. In 2004, Luo [19] developed the analytical conditions for chaotic motions in the resonant separatrix bands of a Mathieu-Duffing oscillator. The numerical prediction of chaotic motion in the resonant bands was also completed through the energy increment spectrum method. In 2008, Peng et al. [20] used the harmonic balance method with three harmonic terms to approximate the periodic motions in the Duffing oscillator.

In 2012, Luo [21] developed a generalized harmonic balance method for the approximation of analytic solutions, and the finite Fourier series was used to approximate the analytical solution of periodic motions. Luo and Huang [22] employed such an analytical method for the approximate analytical solutions of periodic motions in a periodically forced Duffing oscillator. Analytical period-1 motions were obtained. From the analytical solutions, the initial conditions can be computed and numerical solutions of periodic motion were computed. Luo and Huang [23] used the generalized harmonic balance method for the analytical solutions of period-m motions in such a nonlinear dynamical system, and the bifurcation trees of period-1 to period-8 motions were obtained. In 2013, Luo and Yu [24] presented the bifurcation trees of period-1 motions to chaos in a quadratic nonlinear oscillator. In 2013, Luo and Laken [24] investigated the analytical solutions of periodic motions in van der Pol oscillator. In 2013, Luo and Dennis [25] presented the asymmetric period-1 and symmetric period-2 motions in a parametric Duffing oscillator.

In this paper, the routes of period-1 motion to chaos in a parametric Duffing oscillator will be developed by a semi-analytic method. From the semi-analytical method, the corresponding differential equations of nonlinear dynamical systems will be discretized to obtain implicit discrete mappings. From the appropriate mapping structures, the periodic motions on the bifurcation trees will be computed, and the corresponding stability and bifurcation will be carried out through eigenvalue analysis. Harmonic frequency–amplitude characteristics will be presented for a better understanding of bifurcations of periodic motions. To verify the analytic prediction of periodic motions, comparison of analytic and numerical results will be completed, and harmonic amplitude and phase distributions of periodic motions will be presented for the harmonic effects on the periodic motions in the parametric Duffing oscillator.

2 Methods

From Luo [26], periodic motions can be presented by implicit mappings. If a nonlinear system possesses a period-m flow, the solution of period-m flows can be represented by discrete nodes of the continuous system.

Theorem 1

Consider a nonlinear dynamical system as

$$\begin{aligned} {\dot{\mathbf{x}}}=\mathbf{f}(\mathbf{x},t,\mathbf{p})\in {{\mathbf {\mathsf{{R}}}}}^{n} \end{aligned}$$

(1)

where $\mathbf{f}(\mathbf{x},t,\mathbf{p})$ is a $C^{r}$-continuous nonlinear vector function ($r\ge 1$). If such a dynamical system has a period-m flow $\mathbf{x}^{(m)}(t)$ with finite norm $||\mathbf{x}^{(m)}||$ and period $mT (T={2\pi }/\Omega$), there is a set of discrete time $t_k (k=0,1,\ldots ,mN$) with ($N\rightarrow \infty$) during m-periods (mT), and the corresponding solution $\mathbf{x}^{(m)}(t_k )$ and vector field $\mathbf{f}(\mathbf{x}^{(m)}(t_k ),t_k ,\mathbf{p})$ are exact. Suppose a discrete node $\mathbf{x}_k^{(m)}$ is on the approximate solutions of the periodic flow under $||\mathbf{x}^{(m)}(t_k )-\mathbf{x}_k^{(m)} ||\le \varepsilon _k$ with a small $\varepsilon _k \ge 0$ and

$$\begin{aligned} ||\mathbf{f}(\mathbf{x}^{(m)}(t_k ),t_k ,\mathbf{p})-\mathbf{f}(\mathbf{x}_k^{(m)} ,t_k ,\mathbf{p})||\le \delta _k \end{aligned}$$

(2)

with a small $\delta _k \ge 0$. During a time interval $t\in [t_{k-1} ,t_k ]$, there is a mapping $P_k :\mathbf{x}_{k-1}^{(m)} \rightarrow \mathbf{x}_k^{(m)} (k=1,2,\ldots ,mN)$, i.e.,

$$\begin{aligned}&{} \mathbf{x}_k^{(m)} =P_k \mathbf{x}_{k-1}^{(m)} \hbox { with }{} \mathbf{g}_k (\mathbf{x}_{k-1}^{(m)} ,\mathbf{x}_k^{(m)} ,\mathbf{p})=\mathbf{0}, \nonumber \\&k=1,2,\ldots ,mN \end{aligned}$$

(3)

where $\mathbf{g}_k$ is an implicit vector function. Consider a mapping structure as

$$\begin{aligned}&P=P_{mN} \circ P_{mN-1} \circ \cdots \circ P_1 :\mathbf{x}_0^{(m)} \rightarrow \mathbf{x}_{mN}^{(m)} ; \nonumber \\&\hbox {with }P_k :\mathbf{x}_{k-1}^{(m)} \rightarrow \mathbf{x}_k^{(m)} \quad (k=1,2,\ldots ,mN). \end{aligned}$$

(4)

For $\mathbf{x}_{mN}^{(m)} =P\mathbf{x}_0^{(m)}$, if there is a set of points $\mathbf{x}_k^{(m){*}} (k=0,1,\ldots ,mN$ ) computed by

$$\begin{aligned}&{} \mathbf{g}_k (\mathbf{x}_{k-1}^{(m){*}} ,\mathbf{x}_k^{(m){*}} ,\mathbf{p})=\mathbf{0},\quad (k=1,2,\ldots ,mN) \nonumber \\&{} \mathbf{x}_0^{(m){*}} =\mathbf{x}_{mN}^{(m){*}} , \end{aligned}$$

(5)

then the points $\mathbf{x}_k^{(m){*}} (k=0,1,\ldots ,mN$) are approximations of points $\mathbf{x}^{(m)}(t_k )$ of the periodic solution. In the neighborhood of $\mathbf{x}_k^{(m){*}}$, with $\mathbf{x}_k^{(m)} =\mathbf{x}_k^{(m){*}} +\Delta \mathbf{x}_k^{(m)}$, the linearized equation is given by

$$\begin{aligned}&\Delta \mathbf{x}_k^{(m)} =\hbox {D}P_k \cdot \Delta \mathbf{x}_{k-1}^{(m)} \nonumber \\&\hbox {with }{} \mathbf{g}_k (\mathbf{x}_{k-1}^{(m){*}}+\Delta \mathbf{x}_{k-1}^{(m)} ,\mathbf{x}_k^{(m){*}} +\Delta \mathbf{x}_k^{(m)} ,\mathbf{p})=\mathbf{0} \nonumber \\&(k=1,2,\ldots ,mN). \end{aligned}$$

(6)

The resultant Jacobian matrices of the periodic flow are

$$\begin{aligned}&DP_{k(k-1)\cdots 1} =DP_k \cdot DP_{k-1} \cdot \cdots \cdot DP_1 ,\nonumber \\&\quad (k=1,2,\ldots ,mN); \nonumber \\&DP\equiv DP_{mN(mN-1)\cdots 1} \nonumber \\&\quad =DP_{mN} \cdot DP_{mN-1} \cdot \cdots \cdot DP_1 \end{aligned}$$

(7)

where

$$\begin{aligned} DP_k= & {} \left[ {\frac{\partial \mathbf{x}_k^{(m)} }{\partial \mathbf{x}_{k-1}^{(m)} }} \right] _{(\mathbf{x}_{k-1}^{(m){*}} ,\mathbf{x}_k^{(m){*}} )} \nonumber \\= & {} -\left. {\left[ {\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_k^{(m)} }} \right] ^{-1}\left[ {\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_{k-1}^{(m)} }} \right] } \right| _{(\mathbf{x}_{k-1}^{(m){*}} ,\mathbf{x}_k^{(m){*}} )} . \end{aligned}$$

(8)

The eigenvalues of $DP(\mathbf{x}_0^{(m){*}} )$ and $DP_{k(k-1)\cdots 1}$ for such a periodic flow are determined by

$$\begin{aligned}&|DP_{k(k-1)\cdots 1} -\bar{{\lambda }}{} \mathbf{I}_{n\times n} |=0, \quad (k=1,2,\ldots ,mN); \nonumber \\&|DP-\lambda \mathbf{I}_{n\times n} |=0. \end{aligned}$$

(9)

Thus, the eigenvalues of $DP_{k(k-1)\cdots 1}$ gives the properties of $\mathbf{x}_k$ varying with $\mathbf{x}_0$. The stability and bifurcation of the periodic flow can be classified by the eigenvalues of $DP(\mathbf{x}_0^{(m){*}} )$ with

$$\begin{aligned} ([n_1^m ,n_1^o ]:[n_2^m ,n_2^o ]:[n_3 ,\kappa _3 ]:[n_4 ,\kappa _4 ]|n_5 :n_6 :[n_7 ,l,\kappa _7 ]).\nonumber \\ \end{aligned}$$

(10)

• I. If the magnitudes of all eigenvalues of DP are less than one (i.e., $|\lambda _i \hbox {|}<1, i=1,2,\ldots ,n$), the approximate period-m solution is stable.

• II. If at least the magnitude of one eigenvalue of DP is greater than one (i.e., $|\lambda _i \hbox {|}>1, i\in \{1,2,\ldots ,n\}$), the approximate period-m solution is unstable.

• III. The boundaries between stable and unstable period-m flow with higher order singularity give bifurcation and stability conditions.

3 Parametric Duffing oscillator

3.1 Discretization

Consider a parametric Duffing oscillator as

$$\begin{aligned} {\ddot{x}}+\delta {\dot{x}}+(\alpha +Q_0 \cos \Omega t)x+\beta x^{3}=0 \end{aligned}$$

(11)

where $\alpha$ and $\beta$ are positive constants. $\delta$ is damping coefficient. $Q_0$ and $\Omega$ are excitation amplitude and frequency, respectively. The foregoing equation can be rewritten in a state space form as

$$\begin{aligned} {\dot{x}}= & {} y \nonumber \\ {\dot{y}}= & {} -\delta y-(\alpha +Q_0 \cos \Omega t)x-\beta x^{3} \end{aligned}$$

(12)

In a time interval $t\in (t_{k-1} ,t_k )$, the discretization of the foregoing differential equations is obtained by a midpoint scheme to form the map $P_k (k=1,2,\ldots )$:

$$\begin{aligned}&P_k :(\mathbf{x}_{k-1} ,\mathbf{y}_{k-1} )\rightarrow (\mathbf{x}_k ,\mathbf{y}_k )\nonumber \\&\quad \Rightarrow (\mathbf{x}_k ,\mathbf{y}_k ) =P_k (\mathbf{x}_{k-1} ,\mathbf{y}_{k-1} ) \end{aligned}$$

(13)

The implicit relations of mapping are

$$\begin{aligned} x_k= & {} x_{k-1} +\frac{1}{2}h(y_{k-1} +y_k ), \nonumber \\ y_k= & {} y_{k-1} +h\Big \{-\frac{1}{2}\delta (y_{k-1} +y_k )\nonumber \\&-\frac{1}{2}\Big [\alpha +Q_0 \cos \Omega (t_{k-1}+\frac{1}{2}h)\Big ](x_{k-1} +x_k )\nonumber \\&-\frac{1}{8}\beta (x_{k-1} +x_k)^{3}\Big \}. \end{aligned}$$

(14)

3.2 Period-m motions

Consider the mapping structure for a period-1 motion as

$$\begin{aligned} P=\underbrace{P_N \circ P_{N-1} \circ \cdot \cdot \cdot \circ P_2 \circ P_1 :}_{{\textit{N-actions}}}(\mathbf{x}_0 ,\mathbf{y}_0 )\rightarrow (\mathbf{x}_N ,\mathbf{y}_N )\nonumber \\ \end{aligned}$$

(15)

The corresponding algebraic equations are

$$\begin{aligned} x_1= & {} x_0 +\frac{1}{2}h(y_0 +y_1 ), \nonumber \\ y_1= & {} y_0 +h\Big \{-\frac{1}{2}\delta (y_0 +y_1 )\nonumber \\&-\frac{1}{2}\left[ \alpha +Q_0 \cos \Omega \Big (t_0 +\frac{1}{2}h\Big )\right] (x_0 +x_1 )\nonumber \\&-\frac{1}{8}\beta (x_0 +x_1 )^{3}\Big \}; \nonumber \\&\vdots&\nonumber \\ x_k= & {} x_{k-1} +\frac{1}{2}h(y_{k-1} +y_k ), \nonumber \\ y_k= & {} y_{k-1} +h\Big \{-\frac{1}{2}\delta (y_{k-1} +y_k )\nonumber \\&-\frac{1}{2}\Big [\alpha +Q_0 \cos \Omega \Big (t_{k-1} +\frac{1}{2}h\Big )\Big ](x_{k-1} +x_k )\nonumber \\&-\frac{1}{8}\beta (x_{k-1} +x_k )^{3}\Big \}; \nonumber \\&\vdots&\nonumber \\ x_N= & {} x_{N-1} +\frac{1}{2}h(y_{N-1} +y_N ), \nonumber \\ y_N= & {} y_{N-1} +h\Big \{-\frac{1}{2}\delta (y_{N-1} +y_N )\nonumber \\&-\frac{1}{2}\Big [\alpha +Q_0 \cos \Omega \Big (t_{N-1} +\frac{1}{2}h\Big )\Big ](x_{N-1} +x_N )\nonumber \\&-\frac{1}{8}\beta (x_{N-1} +x_N )^{3}\Big \} \nonumber \\&(k=1,2,3,\ldots ,N) \end{aligned}$$

(16)

The corresponding periodicity condition is $(\mathbf{x}_N ,\mathbf{y}_N )=(\mathbf{x}_0 ,\mathbf{y}_0 )$. Once the discrete nodes of period-1 motions are attained by $2(N+1)$ algebraic equations, the corresponding stability analysis can be carried out by eigenvalues analysis. In the neighborhood of $\mathbf{x}_k^*,\mathbf{x}_k =\mathbf{x}_k^*+\Delta \mathbf{x}_k , (k=1,2,\ldots ,N)$, the linearization of the foregoing equation gives

$$\begin{aligned} \Delta \mathbf{x}_N= & {} DP\Delta \mathbf{x}_0 \nonumber \\= & {} \mathop {\underbrace{DP_N \cdot DP _{N-1} \cdot \cdots \cdot DP_2 \cdot D{P}_1 }}\limits _{{\textit{N-mutiplication}}}\Delta \mathbf{x}_0 \end{aligned}$$

(17)

with

$$\begin{aligned} \Delta \mathbf{x}_k =DP_k \Delta \mathbf{x}_{k-1} \equiv \left[ {\frac{\partial \mathbf{x}_k }{\partial \mathbf{x}_{k-1} }} \right] _{(\mathbf{x}_k^*,\mathbf{x}_{k-1}^*)} \Delta \mathbf{x}_{k-1} \end{aligned}$$

(18)

where

$$\begin{aligned} DP_k= & {} \left[ {\frac{\partial \mathbf{x}_k }{\partial \mathbf{x}_{k-1} }} \right] _{(\mathbf{x}_k^*,\mathbf{x}_{k-1}^*)} \nonumber \\= & {} \left[ {\begin{array}{ll} {\frac{\partial \mathbf{x}_k }{\partial \mathbf{x}_{k-1} }}&{}{\frac{\partial \mathbf{x}_k }{\partial \mathbf{y}_{k-1} }} \\ {\frac{\partial \mathbf{y}_k }{\partial \mathbf{x}_{k-1} }}&{}{\frac{\partial \mathbf{y}_k }{\partial \mathbf{y}_{k-1} }} \\ \end{array}} \right] _{\left( {\mathbf{x}_k^*,\mathbf{x}_{k-1}^*} \right) }\nonumber \\&k=1,2,\ldots ,N \end{aligned}$$

(19)

Four elements of the foregoing matrix are

$$\begin{aligned} \frac{\partial \mathbf{x}_k}{\partial \mathbf{x}_{k-1} }= & {} 1+\frac{1}{2}h\frac{\partial y_k }{\partial {x}_{k-1} },\quad \nonumber \\ \frac{\partial \mathbf{x}_k }{\partial \mathbf{y}_{k-1} }= & {} \frac{1}{2}h\left( 1+\frac{\partial y_k }{\partial y_{k-1} }\right) , \nonumber \\ \frac{\partial \mathbf{y}_k }{\partial \mathbf{x}_{k-1} }= & {} \frac{-2\Delta }{1+\frac{1}{2}h\delta +\frac{1}{2}h\Delta },\quad \nonumber \\ \frac{\partial \mathbf{y}_k }{\partial \mathbf{y}_{k-1} }= & {} \frac{1-\frac{1}{2}h\delta -\frac{1}{2}h\Delta }{1+\frac{1}{2}h\delta +\frac{1}{2}h\Delta }; \end{aligned}$$

(20)

with $\Delta =\frac{1}{2}h[\alpha +Q_0 \cos \Omega (t_{k-1} +\frac{1}{2}h)]+\frac{3}{8}h\beta (x_{k-1} +x_k )^{2}.$

To determine the stability and bifurcation conditions of the period-1 motion, the eigenvalues can be computed by

$$\begin{aligned} \left| {DP-\lambda \mathbf{I}} \right| =0 \end{aligned}$$

(21)

where

$$\begin{aligned} DP= & {} \left[ {\frac{\partial \mathbf{x}_N }{\partial \mathbf{x}_0 }} \right] _{\left( {\mathbf{x}_N^*,\mathbf{x}_{N-1}^*,\ldots ,\mathbf{x}_0^*} \right) }=\prod _{k=N}^1 {\left[ {\frac{\partial \mathbf{x}_k }{\partial \mathbf{x}_{k-1} }} \right] _{(\mathbf{x}_k^*,\mathbf{x}_{k-1}^*)} } \nonumber \\= & {} DP_N \cdot DP_{N-1} \cdot \cdots \cdot DP_2 \cdot DP_1 \end{aligned}$$

(22)

From Luo [26], the eigenvalues of the DP matrix are denoted by $\lambda _i (i=1,2)$,

• (i) If $\left| {\lambda _i } \right| <1(i=1,2)$, the periodic solution is stable.

• (ii) If $\left| {\lambda _i } \right| >1(i\in \{1,2\})$, the periodic solution is unstable.

The bifurcation conditions of periodic motions are

• (i) If $\lambda _i =1,i\in \{1,2\}$ and $|\lambda _j |<1,j\in \{1,2\},j\ne i$, the saddle-node (SN) bifurcation occurs.

• (ii) If $\lambda _i =-1,i\in \{1,2\}$ and $|\lambda _j |<1,j\in \{1,2\},j\ne i$, the period-doubling (PD) bifurcation occurs.

• (iii) If $|\lambda _{1,2} |=1$ and $\lambda _{1,2} =\alpha \pm \beta i$, the Neimark bifurcation occurs.

Consider the mapping structure of period-m motion as

$$\begin{aligned}&P=\underbrace{P_{mN} \circ P_{mN-1} \circ \cdot \cdot \cdot \circ P_2 \circ P_1 :}_{{\textit{mN-actions}}}\nonumber \\&(\mathbf{x}_0^{(m)} ,\mathbf{y}_0^{(m)} )\rightarrow (\mathbf{x}_{mN}^{(m)} ,\mathbf{y}_{mN}^{(m)} ) \end{aligned}$$

(23)

The corresponding algebraic equations are as follows,

$$\begin{aligned} x_k^{(m)}= & {} x_{k-1}^{(m)} +\frac{1}{2}h\big (y_{k-1}^{(m)} +y_k^{(m)} \big ), \nonumber \\ y_k^{(m)}= & {} y_{k-1}^{(m)} +h\Big \{-\frac{1}{2}\delta \big (y_{k-1}^{(m)} +y_k^{(m)} \big )\nonumber \\&\left. -\frac{1}{2}\Big [\alpha +Q_0 \cos \Omega (t_{k-1} +\frac{1}{2}h)\Big ]\big (x_{k-1}^{(m)} +x_k^{(m)} \big ) \right. \nonumber \\&-\frac{1}{8}\beta \big (x_{k-1}^{(m)} +x_k^{(m)} \big )^{3}\Big \} \nonumber \\&(k=1,2,\ldots ,mN) \end{aligned}$$

(24)

The periodicity condition is

$$\begin{aligned} \left( \mathbf{x}_{mN}^{(m)} ,\mathbf{y}_{mN}^{(m)} \right) = \left( \mathbf{x}_0^{(m)} ,\mathbf{y}_0^{(m)} \right) \end{aligned}$$

(25)

For period-m motions, the discrete nodes can be computed by $2(mN+1)$ equations. The corresponding stability and bifurcation conditions of period-m motion can be carried out by the eigenvalue analysis. Once the periodic nodes are obtained, in the vicinity of $\mathbf{x}_k^{(m)*} , \mathbf{x}_k^{(m)} =\mathbf{x}_k^{(m)*} +\Delta \mathbf{x}_k^{(m)} , (k=0,1,2,\ldots ,mN)$, the linearization of the equation gives

$$\begin{aligned} \Delta \mathbf{x}_{mN}= & {} DP\Delta \mathbf{x}_0^{(m)} \nonumber \\= & {} \underbrace{DP_{mN} \cdot DP_{mN-1} \cdot \cdots \cdot DP_2 \cdot DP_1 }_{{ mN-multiplication}}\Delta \mathbf{x}_0^{(m)} , \end{aligned}$$

(26)

with

$$\begin{aligned} \Delta \mathbf{x}_k^{(m)}= & {} DP_k \Delta \mathbf{x}_{k-1}^{(m)} \nonumber \\\equiv & {} \left[ {\frac{\partial \mathbf{x}_k^{(m)} }{\partial \mathbf{x}_{k-1}^{(m)} }} \right] _{\left( \mathbf{x}_k^{(m)*} ,\mathbf{x}_{k-1}^{(m)*}\right) } \Delta \mathbf{x}_{k-1}^{(m)} , \end{aligned}$$

(27)

where

$$\begin{aligned} DP_k= & {} \left[ {\frac{\partial \mathbf{x}_k^{(m)} }{\partial \mathbf{x}_{k-1}^{(m)} }} \right] _{(\mathbf{x}_k^{(m)*} ,\mathbf{x}_{k-1}^{(m)*} )}\nonumber \\= & {} \left[ {\begin{array}{ll} {\frac{\partial \mathbf{x}_k^{(m)} }{\partial \mathbf{x}_{k-1}^{(m)} }}&{}{\frac{\partial \mathbf{x}_k^{(m)} }{\partial \mathbf{y}_{k-1}^{(m)} }} \\ {\frac{\partial \mathbf{y}_k^{(m)} }{\partial \mathbf{x}_{k-1}^{(m)} }}&{}{\frac{\partial \mathbf{y}_k^{(m)} }{\partial \mathbf{y}_{k-1}^{(m)} }} \\ \end{array}} \right] _{\left( {\mathbf{x}_k^{(m)*} ,\mathbf{x}_{k-1}^{(m)*} } \right) } , \quad k=1,2,\ldots mN\nonumber \\ \end{aligned}$$

(28)

To determine the stability and bifurcation conditions of period-m motion, the eigenvalues can be computed by

$$\begin{aligned} \left| {DP-\lambda \mathbf{I}} \right| =0 \end{aligned}$$

(29)

where

$$\begin{aligned} DP= & {} \left[ {\frac{\partial \mathbf{x}_{mN}^{(m)} }{\partial \mathbf{x}_0^{(m)} }} \right] _{\left( {\mathbf{x}_{mN}^{(m)*} ,\mathbf{x}_{mN-1}^{(m)*} ,\ldots ,\mathbf{x}_0^{(m)*} } \right) } \nonumber \\= & {} \prod _{k=mN}^1 {\left[ {\frac{\partial \mathbf{x}_k^{(m)} }{\partial \mathbf{x}_k^{(m)} }} \right] _{(\mathbf{x}_k^{(m)*} ,\mathbf{x}_{k-1}^{(m)*} )} } \nonumber \\= & {} DP_{mN} \cdot DP_{mN-1} \cdot \cdots \cdot DP_2 \cdot DP_1 . \end{aligned}$$

(30)

The period-m motions possess the same criterion for stability and bifurcation conditions with period-1 motions.

3.3 Finite Fourier series formulation

From Luo [26], once the node points of period-m motions are obtained, the node points $x_k^{(m)} =(x_k^{(m)} ,y_k^{(m)} )^{T}(k=0,1,2,\ldots ,mN)$ of parametric Duffing oscillator can be expressed by the finite Fourier series as

$$\begin{aligned} \mathbf{x}^{(m)}(t)\approx & {} \mathbf{a}_0^{(m)} +\sum _{j=1}^M \mathbf{b}_{j/m} \cos \Big (\frac{j}{m}\Omega t\Big )\nonumber \\&+\,\mathbf{c}_{j/m} \sin \Big (\frac{j}{m}\Omega t\Big ) . \end{aligned}$$

(31)

For $M=mN/2,$ the expression of the node points $\mathbf{x}_k^{(m)}$ by the finite Fourier series for $t\in [0,mT]$ is

$$\begin{aligned} \mathbf{x}_k^{(m)}\approx & {} \mathbf{x}^{(m)}(t_k ) \nonumber \\\approx & {} \mathbf{a}_0^{(m)}+\sum _{j=1}^{mN/2} {\mathbf{b}_{j/m} } \cos \left( \frac{j}{m}\Omega t_k \right) \nonumber \\&+\,\mathbf{c}_{j/m} \sin \left( \frac{j}{m}\Omega t_k \right) \nonumber \\= & {} \mathbf{a}_0^{(m)} +\sum _{j=1}^{mN/2} \mathbf{b}_{j/m} \cos \Big (\frac{j}{m}\frac{2k\pi }{N}\Big )\nonumber \\&+\,\mathbf{c}_{j/m} \sin \Big (\frac{j}{m}\frac{2k\pi }{N}\Big ) \nonumber \\&(k=0,1,\ldots ,mN-1) \end{aligned}$$

(32)

where

$$\begin{aligned}&T=\frac{2\pi }{\Omega }=N\Delta t,\\&\Omega t_k =\Omega k\Delta t=\frac{2k\pi }{N}, \end{aligned}$$

$$\begin{aligned} \mathbf{a}_0^{(m)}= & {} \frac{1}{mN}\sum _{k=0}^{mN-1} {\mathbf{x}_k^{(m)} } , \nonumber \\ \mathbf{b}_{j/m}= & {} \frac{2}{mN}\sum _{k=1}^{mN-1} {\mathbf{x}_k^{(m)} \cos \Big (k\frac{2j\pi }{mN}\Big )} , \nonumber \\ \mathbf{c}_{j/m}= & {} \frac{2}{mN}\sum _{k=1}^{mN-1} {\mathbf{x}_k^{(m)} \sin \Big (k\frac{2j\pi }{mN}\Big )} . \nonumber \\&(j=1,2,\ldots ,mN/2) \end{aligned}$$

(33)

and

$$\begin{aligned} \mathbf{a}_0^{(m)}= & {} (a_{01} ^{(m)},a_{02} ^{(m)})^{\mathrm{T}}, \nonumber \\ \mathbf{b}_{j/m}= & {} (b_{j/m1} ,b_{j/m2} )^{\mathrm{T}}, \nonumber \\ \mathbf{c}_{j/m}= & {} (c_{j/m1} ,c_{j/m2} )^{\mathrm{T}}. \end{aligned}$$

(34)

The harmonic amplitude and phase for both displacement and velocity of the period-m motions are

$$\begin{aligned}&A_{j/m1} =\sqrt{b^{2}_{j/m1} +c^{2}_{j/m1} },\nonumber \\&\varphi _{j/m1} =\arctan \frac{c_{j/m1} }{b_{j/m1} }, \nonumber \\&A_{j/m2} =\sqrt{b^{2}_{j/m2} +c^{2}_{j/m2} },\nonumber \\&\varphi _{j/m2} =\arctan \frac{c_{j/m2} }{b_{j/m2} }. \end{aligned}$$

(35)

The approximate expression can be written as

$$\begin{aligned} \mathbf{x}^{(m)}(t)\approx & {} \mathbf{a}_0^{(m)}+\sum _{j=1}^{mN/2} {\mathbf{b}_{j/m} \cos \Big ( {\frac{k}{m}\Omega t} \Big )} \nonumber \\&+\,\mathbf{c}_{j/m} \sin \Big ( {\frac{k}{m}\Omega t} \Big ) \end{aligned}$$

(36)

4 Bifurcation trees

The bifurcation trees of period-1 motion to chaos for the parametric Duffing oscillator are predicted analytically in this section. Two branches of bifurcation trees of asymmetric period-1 to period-4 motions and one branch of symmetric period-2 motions are illustrated. In all illustrations, the black-solid and red-dash curves represent stable and unstable solutions, respectively. The acronyms ‘PD’ and ‘SN’ represent period-doubling and saddle node bifurcations, respectively. The ‘S’ and ‘A’ denote symmetric and asymmetric solutions, respectively. The period-1, period-2 and period-4 motions are labeled as P-1, P-2 and P-4.

Fig. 1

The global view of the first branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\bmod (k,N)}$, ii periodic node velocity $y_{\bmod (k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

4.1 The first bifurcation tree

The first branch of bifurcation trees of period-1 to period-4 motions for the parametric Duffing oscillator is illustrated in Figs. 1–6. The parameters are chosen as

$$\begin{aligned} Q_0 =30,\quad \delta =0.1,\quad \alpha =5,\quad \beta =30 \end{aligned}$$

(37)

The global view of bifurcation trees for displacement and velocity of periodic nodes are plotted in Fig. 1 through $x_k$ and $y_k$ for $\bmod (k,N)=0.$ For a better view of the bifurcation tree, the zoomed view of bifurcation trees of period-2 and period-4 motions are illustrated in Figs. 2–6. The corresponding bifurcation points for period-1 to period-4 motions are presented in Tables 1–3.

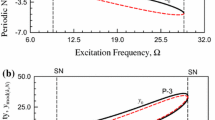
In Fig. 1, the horizontal axis is for the excitation frequency and the vertical axes are for the displacement and velocity of periodic nodes with $\bmod (k,N)=0$, respectively. The solution of period-1 to period-4 motions are asymmetric for the first branch of bifurcation trees. Two SN and four PD bifurcation points of period-1 motion have been observed. The stable period-1 motions lie in ranges of $\Omega \in (1.9947,1.99595), (3.262,3.989)$, (4.946, 11.8164). For the unstable period-1 motion, the ranges of excitation frequency are $\Omega \in (1.99595,3.262), (3.989,4.946), (3.3272,11.8164)$. Once the period-doubling bifurcations of period-1 motion occur, the period-2 motions will appear from the period-1 motions and the stable period-1 motions become unstable. The period-doubling bifurcation points of period-1 motions are the saddle-node bifurcation points of the period-2 motions. The bifurcation points of asymmetric period-1 motions are listed in Table 1. Similarly, once the period-doubling bifurcation points of period-2 motion occur, the period-4 motions will appear, and the stable period-2 motions become unstable. Once again, the period-doubling bifurcation points of period-2 motions are the saddle-node bifurcation points of the period-4 motions.

Fig. 2

The first zoomed view of first branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\bmod (k,N)}$, ii periodic node velocity $y_{\bmod (k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 3

The second zoomed view of first branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\bmod (k,N)}$, ii periodic node velocity $y_{\bmod (k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 4

The third zoomed view of first branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 5

The fourth zoomed view of first branch of bifurcation trees of period-2 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 6

The fifth zoomed view of first branch of bifurcation trees of period-2 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

For a better view of bifurcation trees, the period-1 to period-4 motions are presented in the zoomed view of bifurcation trees in Figs. 2 and 3. There are two period-2 motions exist in the range of frequency $\Omega \in (1.99595,4.946)$ and (3.262, 3.989). The period-2 motions possess four period-doubling bifurcation points at 1.99611, 4.578, 2.91837 and 3.24085. The saddle-node bifurcation points of period-2 motions are $\Omega =1.99595, 4.946, 3.989,4.07176, 2.91570$ and 3.262. The onsets of period-4 motions are at the period-doubling bifurcations of period-2 motions where the stable period-2 motions become unstable. The ranges of stable period-2 motions are $\Omega \in$ (1.99595,1.99611), (4.578,4.946), (3.989,4.07176), (2.91537,2.91570) and (3.24085, 3.262). The three ranges of unstable period-2 motions are in the intervals of $\Omega \in (1.99611,4.578), (4.0176,2.91570)$ and (2.91537, 3.24085). The bifurcation points are listed in Table 2.

In Figs. 4–6, the zoomed view of bifurcation tress from period-1 to period-4 motions is presented. The onsets of period-8 motions occur at the period-doubling bifurcations of period-4 motions where the stable period-4 motions become unstable. Such period-doubling bifurcations are also the saddle-node bifurcations of period-8 motions. The period-4 motions possess six saddle-node and six period-doubling bifurcations, respectively. The saddle-node bifurcations of period-4 motions are $\Omega$ =1.99611, 3.558458, 3.609964, 4.578, 3.24085 and 2.915837. The period-doubling bifurcations are $\Omega =$ 1.996126, 3.558465, 3.609961, 4.52,3.23885 and 2.915872. The ranges of stable period-4 motions are $\Omega \in$ (1.99611, 1.996126), (3.558458, 3.558465), (3.609961, 3.609964), (4.52, 4.578), (3.23885, 3.24085) and (2.915837, 2.915872). The unstable period-4 motions are in $\Omega \in$ (1.996126, 3.558465), (3.558458, 3.609964), (3.609961, 4.52) and (2.915872, 3.23885). The bifurcations are tabulated in Table 3.

4.2 The second bifurcation tree

The second branch of bifurcation trees of period-1 to period-4 motions are illustrated in Figs. 7–12. The parameters are same as the first branch of bifurcation trees. The global view of bifurcation tree is presented in Fig. 7 and other zoomed views are presented in Figs. 8–12.

Bifurcation trees of period-1 to period-4 motions are illustrated by the displacement and velocity of periodic nodes with $\bmod (k,N)=0$ in Fig. 7. Four branches of period-2 and period-4 motions have been observed. The solutions of the second bifurcation trees are asymmetric. There are four saddle-node and four period-doubling bifurcations of period-1 motions. The four saddle-node bifurcations are at $\Omega =1.102954$ ,1.90124, 1.4207, 2.9127. The four period-doubling bifurcations are at $\Omega =1.102957$, 1.87395 and 1.4350, 2.520. The stable period-1 motions are in $\Omega \in$ (1.102954, 1.102957), (1.87395,1.90124), (1.4207,1.4350) and (2.52, 2.9127). The bifurcation trees possess the unstable period-1 motions in the range of frequency $\Omega \in$ (1.102957, 1.87395), (1.4207, 1.90124), (1.4350, 2.520) and (1.4190, 2.9127). The onsets of period-2 motions are at the period-doubling bifurcations of period-1 motions. The stable period-1 motions become unstable at the period-doubling bifurcations of period-1 motions, which are also the saddle-node bifurcation points of period-2 motions. The bifurcation points of asymmetric period-1 motions are tabulated in Table 4. The second branch of bifurcation trees possesses four branches of period-2 motions. The eight saddle-node bifurcations are $\Omega =$ 1.102957, 2.109832, 1.552185, 2.520, 1.87395, 1.134039, 2.163203 and 1.4350. The eight period-doubling bifurcations are $\Omega =$ 1.102958, 2.108141, 1.552186, 2.4823, 1.87005, 1.134040, 2.155383 and 1.44518. The stable period-2 motions lie in the ranges of frequency $\Omega \in$ (1.102957, 1.102958), (2.108141, 2.109832), (1.552185, 1.552186), (2.4823, 2.520), (1.87005, 1.87395), (1.134039, 1.134040), (2.155383, 2.163203) and (1.4350, 1.44518) The unstable period-2 motions are in $\Omega \in$ (1.102958, 2.108141), (1.552185, 2.109832), (1.552186, 2.4823), (1.134039, 2.163203), (1.87005, 1.134040), (2.155383, 1.44518). The bifurcation points are listed in Table 5.

Table 1 Bifurcations for asymmetric period-1 motions $(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)$

Table 2 Bifurcations for asymmetric period-2 motions $(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)$

Table 3 Bifurcations for asymmetric period-4 motions $(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)$

Fig. 7

The global view of second branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod \!(k,N)=0$

Fig. 8

The first zoomed view of second branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 9

The second zoomed view of second branch of bifurcation trees of period-2 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\bmod (k,N)}$. ii periodic node velocity $y_{\bmod (k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 10

The third zoomed view of second branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\bmod (k,N)}$, ii periodic node velocity $y_{\bmod (k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 11

The fourth zoomed view of second branch of bifurcation trees of period-2 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 12

The fifth zoomed view of second branch of bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

If the period-doubling bifurcation points of period-2 motions are observed, the period- 4 motions appear. The stable period-2 motions became unstable at the period-doubling bifurcation points, which are the saddle-node bifurcation points of the corresponding period-4 motions. For the second branch of bifurcation trees, there are four branches of period-4 motions. Similarly, period-8 motions can be observed at the period-doubling bifurcation points of period-4 motions. The saddle-node bifurcation points of period-4 motions are at $\Omega =$ 1.102958, 2.108141, 1.44518, 2.155383, 1.134040, 1.87005, 1.552186 and 2.4823. The period-doubling bifurcation points are $\Omega =$ 1.102959, 2.107731,1.445337, 2.153383, 1.134041, 1.869552, 1.552187 and 2.4783. The stable period-4 motions are in the ranges of frequency $\Omega \in$ (1.102958, 1.102959), (2.107731, 2.108141), (1.552186, 1.552187), (2.4783, 2.4823), (1.445180, 1.448337), (2.153383, 2.155383), (1.134040, 1.134041) and (1.869552, 1.87005). The unstable ranges of period-4 motions are $\Omega \in$ (1.102959, 2.107731), (1.552186, 2.108141), (1.552187, 2.4783), (1.445337, 2.153383), (1.134040, 2.155383), (1.134041, 1.869552). The bifurcation points of period-4 motions are listed in Table 6. Through the zoomed views in Figs. 7–11, the bifurcation trees are clearly presented.

4.3 Symmetric period-2 motions

The symmetric period-2 motion is presented in Fig. 13. This branch of solution is pure symmetric. The symmetric period-2 motion only possesses a single saddle-node bifurcation point. The saddle-node of symmetric period-2 motion is $\Omega =7.840.$ The stable period-2 motion lies in the interval of frequency $\Omega \in (7.840,\infty ).$ The unstable range of period-2 motion is $\Omega \in (3.393,7.840)$.

5 Frequency–amplitude responses

Once discrete nodes of periodic motions are obtained by the implicit discrete mappings structures, the harmonic amplitude can be computed by application of the finite Fourier series. To avoid abundant illustration, only selected harmonic amplitude curves of displacement are presented. The picked harmonic amplitude is constant term $a_0^{(m)} ,(m=1,2,3,4)$ and $A_{k/m} (m=4,k=1,2,3,4,\ldots ).$ The harmonic amplitude for symmetric period-2 motion will not presented because it is very simple in this paper.

The global view of constant terms versus excitation frequency for the first branch of bifurcation trees is presented in Fig. 14(i). For asymmetric period-1 to period-4 motions, $a_0^{(m)} \ne 0.$The maximum value of constant term is $a_0^{(m)} \approx 0.77.$ For $\Omega >5,$ the bifurcation trees are simple. The bifurcation points mainly occur in the range of frequency $\Omega \in (1.9,5).$ The excitation frequency varies from the approximate range of $\Omega \in (1.9,11.7).$ Asymmetric period-1 to period-4 motions are clearly observed from the bifurcation trees. For a better illustration of bifurcation trees, the zoomed view of constant terms versus excitation frequency is presented in Fig. 14(ii)–(iv). The period-1 to period-2 motions and period-2 to period-4 motions are observed.

Harmonic amplitude $A_{1/4}$ versus excitation frequency is presented in Fig. 14(v). For period-1 and period-2 motions, we have $A_{1/4} =0.$ For period-4 motions, $A_{1/4} \ne 0.$ The maximum value of the harmonic amplitude is about $A_{1/4} \approx 0.16.$ The period-4 motions exist in the approximate range of frequency $\Omega \in (1.9,4.6).$ Harmonic amplitude $A_{1/2}$ versus excitation frequency is presented in Fig. 14(vi). For period-1 motions, we have $A_{1/2} =0.$ For period-2 and period-4 motions, $A_{1/2} \ne 0.$ The maximum value is about $A_{1/2} \approx 1.88.$ Two branches of period-2 motions are presented in Fig. 14(vi). The period-2 motions lie in the approximate range of frequency $\Omega \in (1.9,5).$ Harmonic amplitude $A_{3/4}$ versus excitation frequency is presented in Fig. 14(vii). Such a harmonic amplitude is similar to the harmonic amplitude $A_{1/4}$. The maximum value is about $A_{3/4} \approx 0.14.$ Fig. 14(viii) shows the harmonic amplitude $A_1$ versus excitation frequency. Such a harmonic amplitude is for all period-1, period-2, and period-4 motions. The maximum value is about $A_1 \approx 2.4.$ The zoomed views of harmonic amplitude $A_1$ are presented in Fig. 14(ix)–(xi). The detailed bifurcation tree is observed clearly.

To avoid abundant illustrations, only a few primary harmonic amplitudes are presented to show the harmonic amplitude variations. Harmonic amplitude $A_2$ is presented in Fig. 14(xii). The maximum value for this harmonic amplitude is about $A_2 \approx 0.51.$ Harmonic amplitude $A_3$ versus excitation frequency is presented in Fig. 14(xiii). The maximum values for this harmonic amplitude is about $A_3 {\approx } 0.14.$

Table 4 Bifurcations for asymmetric period-1 motions $(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)$

Table 5 Bifurcations for asymmetric period-2 motions $(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)$

Table 6 Bifurcations for asymmetric period-4 motions $(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)$

To avoid abundant illustration, harmonic amplitudes $A_4$ to $A_{16}$ is not presented herein. In Fig. 14(xiv), the harmonic amplitude $A_{17}$ versus excitation frequency curve is presented. The harmonic amplitude drops dramatically at the onset of the bifurcation trees, which is in the approximate range of excitation frequency $\Omega \in (1.9,2.0)$ . Harmonic amplitude $A_{69/4}$ versus excitation frequency is presented in Fig. 14(xv). The quantity levels for the two branches of period-4 motions are approximate to $A_{69/4} \sim 9.0\times 10^{-9}$ and $1.4\times 10^{-8}$ at excitation frequency $\Omega \approx 3.0$, respectively. Harmonic amplitude $A_{35/2}$ versus excitation frequency is presented in Fig. 14(xvi). Two bifurcation trees from period-2 to period-4 motions are showed in Fig. 14(xvii). The quantity levels of harmonic amplitude for the two branches of bifurcation trees are different. For the excitation frequency $\Omega \approx 3.0,$ the quantity levels for the two bifurcation trees are $A_{35/2} \sim 8.0\times 10^{-9}$ and $1.6\times 10^{-8}$, respectively. Harmonic amplitude $A_{71/4}$ versus excitation frequency is presented in Fig. 14(xviii). For the excitation frequency $\Omega \approx 3.0,$ the quantity levels for the two bifurcation trees are $A_{71/4} \sim 4.3\times 10^{-9}$ and $6.4\times 10^{-9}$, respectively. In Fig. 14(xvi), the harmonic amplitude $A_{18}$ versus excitation frequency is presented. The harmonic amplitude drops exponentially at the onset of the bifurcation trees. For the range of $\Omega \in (1.99,1.996)$ and $\Omega \in (3.3,3.7),$ the harmonic amplitude $A_{18} <1\times 10^{-15}.$

Fig. 13

The global view of bifurcation trees of symmetric period-1 to period-4 motions varying with excitation frequency. i Periodic node displacement $x_{\!\!\bmod \!\!(k,N)}$, ii periodic node velocity $y_{\!\!\bmod \!\!(k,N)} , (Q_0 =30,\delta =0.1,\alpha =5,\beta =30), \bmod (k,N)=0$

Fig. 14

The frequency–amplitude characteristics of first bifurcation trees of period-1 to period-4 motions varying with excitation frequency. i $a_0^{(m)} (m=4)$, ii–xiv $A_{k/m}$ ($k=1,2,3,4,8,68,\ldots ,71,72)(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)\bmod \!(k,N)=0$

The harmonic frequency–amplitude characteristics of the second bifurcation trees varying with excitation will be presented in Fig. 15. Constant terms for such bifurcation trees versus is presented in Fig. 15(i). The second bifurcation trees are more complicated than the first one. For asymmetric period-1 to period-4 motions, $a_0^{(m)} \ne 0.$The second bifurcation tree experiences two branches of period-2 and four branches of period-4 motions, respectively. The maximum value of constant term is about $a_0^{(m)} \approx 0.53.$ The excitation frequency is in the approximate range of $\Omega \in (1.1,2.9).$ For a better illustration of bifurcation trees, the zoomed view of constant terms versus excitation frequency is presented in Fig. 15(ii). One branch of bifurcation trees of period-2 to period-4 motions is observed in the range of frequency $\Omega \in (2.10,2.18)$.

Harmonic amplitude $A_{1/4}$ versus excitation frequency is presented in Fig. 15(iii). For period-1 and period-2 motions, $A_{1/4} =0.$ The maximum value of the harmonic amplitude is about $A_{1/4} \approx 0.15$. The period-4 motions exist in the range of $\Omega \in (1.1,2.48).$ Harmonic amplitude $A_{1/2}$ versus excitation frequency is presented in Fig. 15(iv). For the period-1 motion, $A_{1/2} =0.$ The maximum value is about $A_{1/2} \approx 0.24$ for period-2 and period-4 motions. Two branches of period-2 motions are presented in Fig. 15(v). The period-2 motions lie in the approximate range of frequency $\Omega \in (1.1,2.5).$ Harmonic amplitude $A_{3/4}$ versus excitation frequency is presented in Fig. 15(v). The maximum value is about $A_{3/4} \approx 0.15$ for period-4 motion. In Fig. 15(vi), shown is the harmonic amplitude $A_1$ varying with excitation frequency. The maximum value is about $A_1 \approx 0.5$ for period-1, period-2 and period-4 motions. The zoomed view of the harmonic amplitude in the second bifurcation tree is in Fig. 15(vii). Harmonic amplitude $A_2$ varying with excitation frequency is presented in Fig. 15(viii). The maximum value for this harmonic amplitude is about $A_2 \sim 1.0.$ Harmonic amplitude $A_3$ versus excitation frequency is presented in Fig. 15(ix). The maximum values for such a harmonic amplitude is about $A_3 \approx 0.64.$

To avoid abundant illustration, harmonic amplitudes of $A_4$ to $A_{23}$ are not presented herein In Fig. 15(x), harmonic amplitude $A_{24}$ versus excitation frequency is presented. The harmonic amplitude decreases at the onsets of the bifurcation trees in the range of $\Omega \in (1.1,1.15)$. Harmonic amplitude $A_{97/4}$ versus excitation frequency is presented in Fig. 15(xi). The maximum quantity level for the four branches of period-4 motions is about $A_{97/4} \sim 1.7\times 10^{-5}$. Harmonic amplitude $A_{49/2}$ varying with excitation frequency is presented in Fig. 15(xii). The maximum quantity level for the two branches of period-2 motions is about $A_{49/2} \sim 3.2\times 10^{-5}$. Harmonic amplitude $A_{99/4}$ versus excitation frequency is presented in Fig. 15(xiii). The maximum quantity level of $A_{99/4} \sim 1.4\times 10^{-5}$ is for the four branches of period-4 motions. In Fig. 15(xiv), harmonic amplitude $A_{25}$ versus excitation frequency is presented. The harmonic amplitude drops at the onset of the bifurcation trees. For the range of $\Omega \in (1.10,1.11)$ and $\Omega \in (1.40,1.42),$ the harmonic amplitude of $A_{25} <1\times 10^{-15}$ is observed. For more accuracy, the more harmonic terms in the expression of periodic motions should be included.

Fig. 15

The frequency–amplitude characteristics of second bifurcation tree of period-1 to period-4 motions varying with excitation frequency. i $a_0^{(m)} (m=4)$, ii–xiii $A_{k/m}$ ($k=1,2,3,4,8,96,\ldots ,99,100)(Q_0 =30,\delta =0.1,\alpha =5,\beta =30)\bmod \!(k,N)=0$

Fig. 16

Stable symmetric period-2 motion ($\Omega =8.5)$. i Trajectory, ii displacement, iii velocity, iv harmonic amplitudes, v harmonic phases. Initial conditions ($x_0 \approx -0.010513, {\dot{x}}_0 \approx 5.536104)$. ($Q_0 =30, \delta =0.1, \alpha =5, \beta =30)$

6 Sampled illustrations

In this section, comparison of numerical and analytical solutions of periodic motions for a parametric Duffing oscillator is presented. The initial conditions for numerical simulation are obtained from analytical predictions. The black solid curves represent numerical simulation result while white hollow symbols are analytical results. The initial conditions are represented by green circular symbols. To show effects of harmonic amplitudes of periodic motions, harmonic amplitudes versus harmonic orders are presented herein. For a pair of asymmetric periodic motions, harmonic phases for left asymmetric periodic motions are represented by gray circles while the right asymmetric periodic motions are red circles.

6.1 Symmetric period-2 motion

For $\Omega =8.5,$ the trajectory for a symmetric period-2 motion is showed in Fig. 16(i). The time histories of displacement and velocity are presented in Fig. 16(ii), (iii), respectively. Harmonic amplitude is presented in Fig. 16(iv). The initial conditions ($x_0 \approx -0.010513, {\dot{x}}_0 \approx 5.536104)$ are obtained from analytical prediction. The constant term is for $A_0 =a_0^{(2)} =0.$ The selected harmonic amplitudes are $A_{1/2} \approx 1.1279,A_{3/2} \approx 0.0617,A_{5/2} \approx \hbox {1.9123e-}3,A_{7/2} \approx \hbox {9.3468e-}5, A_{9/2} \approx \hbox {3.7946e-}6, A_{11/2} \approx \hbox {1.5804e-}7, A_{13/2} \approx \hbox {6.6735e-}9, A_{15/2} \approx \hbox {2.7338e-}10, A_{17/2} \approx \hbox {1.1673e-}11,A_{19/2} \approx \hbox {4.7600e-}13,A_{21/2} \approx \hbox {2.0472e-}14.$ Other harmonic amplitudes are $A_{2l/2} =A_l =0$ ($l=1,2,3,\ldots )$. The harmonic amplitude decreases with increasing harmonic order. In Fig. 16(v), harmonic phases are presented. $\upvarphi _{1/2} \approx \hbox {1.5824},\upvarphi _{3/2} \approx \hbox {1.5290},\upvarphi _{5/2} \approx \hbox {4.7275},\upvarphi _{7/2} \approx \hbox {4.5935}, \upvarphi _{9/2} \approx \hbox {1.5856}, \upvarphi _{11/2} \approx \hbox {1.3786}, \upvarphi _{13/2} \approx \hbox {4.7310}, \upvarphi _{15/2} \approx \hbox {4.4494}, \upvarphi _{17/2} \approx \hbox {1.5929}, \upvarphi _{19/2} \approx \hbox {1.2379},$ and $\upvarphi _{21/2} \approx \hbox {4.7372}.$ The symmetric period-2 motion needs about 21 terms to get an approximate analytical expression by the finite Fourier series. This is a traditional (1:2) periodic motion through perturbation method with one harmonic term. The rough analytical solution can use two harmonic terms to express the period-2 motion.

6.2 Asymmetric periodic motion on the first bifurcation trees

For $\Omega =5.265,$ the trajectory of a pair of asymmetric period-1 motions are presented in Fig. 17(i), (ii), respectively. The two asymmetric period-1 motions experience one cycle for the two trajectories. To reduce abundant illustrations, the time-histories of displacement and velocity will not be presented hereafter. Harmonic amplitudes and phases are presented in Fig. 17(iii), (iv), respectively. From the analytical prediction, the initial condition ($x_0 \approx 0.781730, {\dot{x}}_0 \approx 0.194175)$ for the left asymmetric period-1 motion is obtained. Similarly, the initial condition ($x_0 \approx -0.781730, {\dot{x}}_0 \approx -0.194175)$ is for the right asymmetric period-1 motion. The paired asymmetric period-1 motions have the same magnitudes. The constant term is $A_0 =a_0^R =-a_0^L \approx 0.5867.$ The main harmonic amplitudes are $A_1 \approx 1.0104,A_2 \approx 0.0269, A_3 \approx 0.0393,A_4 \approx \hbox {9.0195e-}4.$ Other harmonic amplitudes are in $A_l \in (10^{-15},10^{-4}) (l=5,6,\ldots ,22)$ with $A_{22} \approx \hbox {1.1917e-}15.$ The first harmonic term of $A_1$ is very important for such period-1 motion. The asymmetric period-1 motion needs about 22 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of the pair of asymmetric period-1 motions are $\varphi _k^{L} =\bmod (\varphi _k^{R} +\pi ,2\pi )$. Three harmonic terms in the Fourier series can give an acceptable analytical solution of such asymmetric period-1 motions.

Fig. 17

Stable asymmetric period-1 motion ($\Omega =5.265)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions $x_0 \approx 0.781730, {\dot{x}}_0 \approx 0.194175$ and $x_0 \approx -0.781730,, {\dot{x}}_0 \approx -0.194175$ ($Q_0 =30, \delta =0.1, \alpha =5, \beta =30)$

On the same bifurcation tree, after period-doubling bifurcation, the asymmetric period-2 motion will be obtained. For $\Omega =4.60,$ the trajectories of the paired left and right asymmetric period-2 motions are presented in Fig. 18(i), (ii), respectively. In Fig. 18(iii), (iv), harmonic amplitude and phase distributions are presented. The initial conditions ($x_0 \approx 0.908633, \dot{x}_0 \approx 0.347649)$ and ($x_0 \approx -0.908633, {\dot{x}}_0 \approx -0.347649)$ are obtained from analytical prediction. The constant term is $A_0 =a_0^{(2)R} =-a_0^{(2)L} \approx 0.5941.$ The main harmonic amplitudes are $A_{1/2} \approx {0.0791}, A_1 \approx {0.7720}, A_{3/2} \approx {0.3522}, A_2 \approx {0.1403}, A_{5/2} \approx {0.0193}, A_3 \approx \hbox {1.8867e-}3.$ Other harmonic amplitudes are in the interval of $A_{l/2} \in (10^{-14},10^{-3}) (l=7,8,\ldots ,48)$ with $A_{24} \approx \hbox {2.4033e-}14.$ The harmonic terms of $A_{l/2}$ ($l=2,3,4)$ play important roles in two asymmetric period-2 motions. The relations of harmonic phase of this pair of period-2 motions are $\varphi _{k/2}^{L} =\bmod (\varphi _{k/2}^{R} +\pi ,2\pi )$. The asymmetric period-2 motion needs about 48 terms to get an approximate analytical expression by finite Fourier series. The rough analytical solutions of the period-2 motions can use 5 harmonic terms plus a constant to express.

On the same bifurcation tree. A pair of asymmetric period-4 motions for $\Omega =4.576$, are presented in Fig. 19. In Fig. 19(i), (ii), the trajectories of the left and right asymmetric period-4 motion are presented. Harmonic amplitude and phase distributions are presented in Fig. 19(iii), (iv), respectively. The initial conditions ($x_0 \approx 0.918978, {\dot{x}}_0 \approx 0.471648)$ and ($x_0 \approx -0.918978, {\dot{x}}_0 \approx -0.471648)$ are obtained from analytical prediction. The constant term is $A_0 =a_0^{(4)R} =-a_0^{(4)L} \approx 0.5922.$ The main harmonic amplitudes are $A_{1/4} \approx \hbox {5.5231e-}3, A_{1/2} \approx {0.0813}, A_{3/4} \approx {0.0149},A_1 \approx {0.7611},A_{5/4} \approx {0.0122},A_{3/2} \approx {0.3593}, A_{7/4} \approx \hbox {7.4385e-}3, A_2 \approx {0.1462}, A_{9/4} \approx \hbox {4.3680e-}3,A_{5/2} \approx {0.0177}, A_{11/4} \approx \hbox {1.5081e-}3,A_3 \approx \hbox {2.0663e-}3.$ Other harmonic amplitudes are in $A_{l/4} \in (10^{-14},10^{-3})(l=13,14,\ldots ,96)$ with $A_{24} \approx \hbox {3.0248e-}14.$ The harmonic terms of $A_{l/2}$ ($l=2,3,4)$ still play important roles in two asymmetric period-4 motions. The relations of harmonic phase of this pair of period-4 motions are $\varphi _{k/4}^{L} =\bmod (\varphi _{k/4}^{R} +\pi ,2\pi )$. The analytical expression of the two asymmetric period-4 motions can use 96 harmonic terms to express. The approximate expression of such periodic motions can use 12 harmonic terms in the finite Fourier series.

Fig. 18

Stable asymmetric period-2 motion ($\Omega =4.60)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ( $x_0 \approx 0.908633, {\dot{x}}_0 \approx 0.347649)$ and ($x_0 \approx -0.908633, {\dot{x}}_0 \approx -0.347649)$ ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

Fig. 19

Stable asymmetric period-4 motion ($\Omega =4.576)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ( $x_0 \approx 0.918978, {\dot{x}}_0 \approx 0.471648)$ and ($x_0 \approx -0.918978, {\dot{x}}_0 \approx -0.471648)$ ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

On the first bifurcation tree, there are multiple bifurcation branches. The trajectories of a pair of asymmetric period-1 motions for $\Omega =1.99595$ are presented in Fig. 20(i), (ii), respectively. Harmonic amplitude and phase distributions are presented in Fig. 20(iii), (iv), respectively. The initial conditions ($x_0 \approx 0.025705,{\dot{x}}_0 \approx -\hbox {1.248546e-}3)$ and ($x_0 \approx -0.025705, {\dot{x}}_0 \approx \hbox {1.248546e-}3)$ for the two asymmetric period-1 motions are obtained from analytical prediction. The trajectories of asymmetric period-1 motions have two cycles, compared with the one cycle period-1 motions. The asymmetry of the paired period-1 motions can be observed. The constant term is $A_0 =a_0^R =-a_0^L \approx \hbox {0.0186}.$ The main harmonic amplitudes are $A_1 \approx \hbox {3.1997e-}3, A_2 \approx \hbox {0.0184},A_3 \approx \hbox {0.0103}$ and $A_4 \approx \hbox {2.7366e-}3.$ Other harmonic amplitudes are in $A_l \in (10^{-15},10^{-4}) (l=5,6,\ldots 20)$ with $A_{20} \approx \hbox {2.3436e-}15$. The harmonic terms of $A_l$ ($l=2,3)$ play important roles in two asymmetric period-1 motions. The asymmetric period-1 motion needs about 20 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of this pair of period-1 motions are $\varphi _k^{L} =\bmod (\varphi _k^{R} +\pi ,2\pi )$. The four harmonic terms can be used to determine the analytical expression of asymmetric period-1 motions.

On the same sub-branch of bifurcation tree, the period-1 motion with $\Omega =1.99609$ is considered, and the trajectories of a pair of asymmetric period-2 motions are presented in Fig. 21(i), (ii). The corresponding harmonic amplitude and phase distributions are presented in Fig. 21(iii), (iv). The initial conditions ($x_0 \approx 0.030354, {\dot{x}}_0 \approx -\hbox {1.5026e-}3)$ and ($x_0 \approx -0.030354, {\dot{x}}_0 \approx \hbox {1.5026e-}3)$ for the paired asymmetric period-2 motions are analytical predicted. The four cycles of trajectories of the paired period-2 motions are observed, which are doubled from the two cycles of the trajectories of period-1 motion. The constant term is $A_0 =a_0^{(2)R} =-a_0^{(2)L} \approx 0.0189.$ The main harmonic amplitudes are $A_{1/2} \approx \hbox {1.9132e-}3, A_1 \approx \hbox {3.2548e-}3,A_{3/2} \approx \hbox {2.4284e-}3,A_2 \approx \hbox {0.0187}, A_{5/2} \approx \hbox {2.5442e-}3, A_3 \approx \hbox {0.0104.}$ Other harmonic amplitudes are in the interval of $A_{l/2} \in (10^{-15},10^{-3})(l=7,8,\ldots 40)$ with $A_{20} \approx \hbox {3.2308e-}15.$ The asymmetric period-2 motion needs about 40 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of this pair of period-2 motions are $\varphi _k^{L} =\bmod (\varphi _k^{R} +\pi ,2\pi )$ .

Fig. 20

Stable asymmetric period-1 motion ($\Omega =1.99595)$: i trajectory (left), ii trajectory (right), iii harmonic amplitude, iv harmonic phase. Initial conditions ($x_0 \approx 0.025705, {\dot{x}}_0 \approx -\hbox {1.248546e}{-}3)$ and ($x_0 \approx -0.025705, {\dot{x}}_0 \approx \hbox {1.248546e}{-}3)$. ($Q_0 =30,\delta =0.1, \alpha =5, \beta =30)$

Fig. 21

Stable asymmetric period-2 motion ($\Omega =1.99609)$: i trajectory (left), ii trajectory (right), iii harmonic amplitude, iv harmonic phase. Initial conditions ( $x_0 \approx 0.030354, {\dot{x}}_0 \approx -\hbox {1.502572e-}3)$ and ($x_0 \approx -0.030354, {\dot{x}}_0 \approx \hbox {1.502572e-}3)$. ($Q_0 =30,\delta =0.1, \alpha =5, \beta =30)$

Fig. 22

Stable asymmetric period-4 motion ($\Omega =1.996104)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx 0.030609, {\dot{x}}_0 \approx -\hbox {4.810879e}{-}3)$ and ($x_0 \approx -0.030609, {\dot{x}}_0 \approx \hbox {4.810879e}{-}3)$. ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

On the same bifurcation tree, the trajectories of left and right asymmetric period-4 motions are presented for $\Omega =1.996104$ in Fig. 22(i), (ii), respectively. The initial conditions from the analytical prediction are ($x_0 \approx 0.030609, {\dot{x}}_0 \approx -\hbox {4.810879e-}3)$ and ($x_0 \approx -0.030609, \dot{x}_0 \approx \hbox {4.810879e-}3)$. Harmonic amplitude and phase distributions are presented in Fig. 22(iii), (iv). The constant term is $a_0 \approx \hbox {0.0189}.$ Only the four cycles for the trajectories of period-4 motions are observed. The main harmonic amplitudes are $A_{1/4} \approx \hbox {3.9723e-}9, A_{1/2} \approx \hbox {2.0122e-}3, A_{3/4} \approx \hbox {1.0844e-}9,A_1 \approx \hbox {3.2595e-}3, A_{5/4} \approx \hbox {2.3410e-}9, A_{3/2} \approx \hbox {2.5540e-}3,A_{7/4} \approx \hbox {4.1711e-}9, A_2 \approx \hbox {0.0187}, A_{5/4} \approx \hbox {4.1573e-}9, A_{5/2} \approx \hbox {2.6759e-}3, A_{7/4} \approx \hbox {3.0619e-}9, A_3 \approx \hbox {0.0105.}$ Other harmonic amplitudes are in the interval of $A_{l/4} \in (10^{-15},10^{-3}) (l=13,14,\ldots ,80)$ . Harmonic amplitude $A_{20} \approx \hbox {3.3245e-}15.$ Since the effects of harmonic amplitude $A_{l/4} ,(l=1,5,7,\ldots )$ are very small, the trajectory of this asymmetric period-4 motion and the corresponding period-2 motion are very close to each other. The relations of harmonic phase are $\varphi _{k/4}^{L} =\bmod (\varphi _{k/4}^{R} +\pi ,2\pi )$. The 12 harmonic terms can be used for the approximate analytical expressions of such paired period-4 motions.

On the such bifurcation tree, there are two period-2 motion bifurcation trees without period-1 motions. Consider the complex asymmetric period-2 motion at $\Omega =2.9158,$ the trajectories of a pair of asymmetric period-2 motions are presented in Fig. 23(i), (ii). Harmonic amplitude and phase distributions are presented in Fig. 23(iii), (iv). The trajectories of the paired period-2 motions have three cycles rather than two cycles and four cycles. The constant term is $A_0 =a_0^{(2)R} =-a_0^{(2)L} \approx \hbox {0.5394}.$ The main harmonic amplitudes are $A_{1/2} \approx \hbox {0.1797}, A_1 \approx \hbox {0.3937}, A_{3/2} \approx \hbox {0.3315}, A_2 \approx \hbox {0.1568}, A_{5/2} \approx \hbox {0.0716}, A_3 \approx \hbox {0.0542}, A_{7/2} \approx \hbox {0.0115}, A_4 \approx \hbox {5.2709e-}3.$ Other harmonic amplitudes are in $A_{l/2} \in (10^{-15},10^{-3}) (l=9,10,\ldots , 56)$ with $A_{28} \approx \hbox {1.3600e-}15.$ The harmonic terms of $A_1 \hbox { and }A_{3/2}$ play the most important role on the two asymmetric period-2 motions. In addition, the harmonic terms of $A_{1/2} \hbox { and }A_2$ are also important to change the trajectories. The asymmetric period-2 motion needs about 56 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of this pair of period-2 motions are $\varphi _{k/2}^{L} =\bmod (\varphi _{k/2}^{R} +\pi ,2\pi )$.

Fig. 23

Stable asymmetric period-2 motion ($\Omega =2.9158)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.348140}, {\dot{x}}_0 \approx \hbox {1.841828})$ and ($x_0 \approx -\hbox {0.348140}, {\dot{x}}_0 \approx -\hbox {1.841828})$. ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

Fig. 24

Stable asymmetric period-4 motion ($\Omega =2.91587)$. i Trajectory (left). ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions( $x_0 \approx \hbox {0.346939}, {\dot{x}}_0 \approx \hbox {1.842291})$ and ($x_0 \approx -\hbox {0.346939}, {\dot{x}}_0 \approx -\hbox {1.842291})$. ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

On the sub-bifurcation tree with period-1 motion, $\Omega =2.91587$ is considered, and the corresponding trajectories of a pair of asymmetric period-4 motions are presented in Fig. 24(i), (ii). Harmonic amplitude and phase distributions are presented in Fig. 24(iii), (iv). The initial conditions ($x_0 \approx \hbox {0.346939}, {\dot{x}}_0 \approx \hbox {1.842291})$ and ($x_0 \approx -\hbox {0.346939}, {\dot{x}}_0 \approx -\hbox {1.842291})$ are obtained from analytical prediction. The constant term is $A_0 =a_0^{(4)R} =-a_0^{(4)L} \approx \hbox {0.5397}.$ The main harmonic amplitudes are $A_{1/4} \approx \hbox {6.1734e-}4,A_{1/2} \approx \hbox {0.1797},A_{3/4} \approx \hbox {7.7205e-}6,A_1 \approx \hbox {0.3938}, A_{5/4} \approx \hbox {3.3498e-}4, A_{3/2} \approx \hbox {0.3314},A_{7/4} \approx \hbox {1.3875e-}3, A_2 \approx \hbox {0.1573},A_{9/4} \approx \hbox {1.1294e-}3, A_{5/2} \approx \hbox {0.0717}, A_{11/4} \approx \hbox {3.4317e-}{5}, A_3 \approx \hbox {0.0542}, A_{9/4} \approx \hbox {1.2517e-}{4}, A_{5/2} \approx \hbox {0.0115}, A_{11/4} \approx \hbox {1.7765e-}{4}$, and $A_4 \approx \hbox {5.3041e-}{3},$ Other harmonic amplitudes are in the interval of $A_{l/4} \in (10^{-15},10^{-3})(l=13,14,\ldots , 56)$ with $A_{14} \approx \hbox {1.3620e-}{15}.$ The asymmetric period-4 motion needs about 112 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of this pair of period-4 motions are $\varphi _{k/4}^{L} =\bmod (\varphi _{k/4}^{R} +\pi ,2\pi )$. The harmonic terms of $A_{k/4}$ with $\bmod (k,2)\ne 0$ and $\bmod (k,4){\ne }0$ have very small effects on the period-4 motions.

6.3 Asymmetric motions on the second bifurcation tree

The second branch of bifurcation tree possesses asymmetric period-1 to period-4 motions in the interval of $\Omega \in (1.1,2.9)$. Two branches of period-2 and four branches of period-4 motions have been observed in the second branch of bifurcation trees. Compared with the first branch of bifurcation trees, the second branch of bifurcation trees possesses more complicated periodic motions. The initial points are represented by green solid circle and I.C. represents initial conditions.

Consider a pair of asymmetric period-1 motions at $\Omega =2.7,$ the trajectories for two paired trajectories are presented in Fig. 25(i), (ii). Harmonic amplitude and phase distributions are presented in Fig. 25(iii), (iv), respectively. The initial conditions ($x_0 \approx \hbox {0.610248}, {\dot{x}}_0 \approx -\hbox {2.607625})$ and ($x_0 \approx -\hbox {0.610248}, {\dot{x}}_0 \approx \hbox {2.607625})$ for the two paired asymmetric period-1 motions are obtained from analytical prediction. Such asymmetric period-1 motions have two large cycles. The second harmonic term plays important role in such periodic motions. The two paired asymmetric period-1 motions have the same harmonic amplitude. The constant term is $A_0 =a_0 \approx \hbox {0.1527}.$ The main harmonic amplitudes are $A_1 \approx \hbox {0.4053}, A_2 \approx \hbox {0.9126}, A_3 \approx \hbox {0.2101}, A_4 \approx \hbox {0.0923}, A_5 \approx \hbox {0.0450}, A_6 \approx \hbox {0.0171.}$ Other harmonic amplitudes are in the interval of $A_l \in (10^{-15},10^{-2}) (l=7,8,\ldots ,45)$ with $A_{45} \approx \hbox {1.9000e-}{15}.$ The asymmetric period-1 motion needs about 45 terms to get an approximate analytical expression by finite Fourier series. The main effects on the period-1 motions are from the harmonic terms of $A_2 ,A_1 \hbox { and }A_3$. The relations of harmonic phase of the paired asymmetric period-1 motions are given by $\varphi _k^{L} =\bmod (\varphi _k^{R} +\pi ,2\pi )$ .

Consider a pair of asymmetric period-2 motions at $\Omega =2.516,$ the trajectories for two paired trajectories of the asymmetric period-2 motions are presented in Fig. 26(i), (ii). The corresponding harmonic amplitudes and phases are presented in Fig. 26(iii), (iv), respectively. The initial conditions ($x_0 \approx \hbox {0.723750}, {\dot{x}}_0 \approx \hbox {0.530036})$ and ($x_0 \approx -\hbox {0.723750}, {\dot{x}}_0 \approx -\hbox {0.530036})$ for two paired asymmetric period-2 motions are also obtained from the analytical prediction. Such asymmetric period-2 motions have two large cycles. The two paired asymmetric period-1 motions have the same harmonic amplitude. The constant term is $A_0 =a_0^{(2)R} =-a_0^{(2)L} \approx \hbox {0.1861}.$ The main harmonic amplitudes are $A_{1/2} \approx \hbox {0.0169}, A_1 \approx \hbox {0.4166}, A_{3/2} \approx \hbox {0.0507}, A_2 \approx \hbox {0.8117}, A_{5/2} \approx \hbox {0.0639},A_3 \approx \hbox {0.1859},A_{7/2} \approx \hbox {0.0153}, A_4 \approx \hbox {0.1023}, A_{9/2} \approx \hbox {0.0189}, A_5 \approx \hbox {0.0381}, A_{11/2} \approx \hbox {0.0189},$ and $A_6 \approx \hbox {0.0117.}$ Other harmonic amplitudes are in the interval of $A_{l/2} \in (10^{-15},10^{-2}) (l=13,14,\ldots ,90)$ with $A_{45} \approx \hbox {2.3000e-}{15}.$ The main effects on the period-2 motions are also from the harmonic terms of $A_2 ,A_1 \hbox { and }A_3$. The asymmetric period-2 motion needs about 90 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of the paired asymmetric period-1 motions are given by $\varphi _{k/2}^{L} =\bmod (\varphi _{k/2}^{R} +\pi ,2\pi )$ .

Fig. 25

Stable asymmetric period-1 motion ($\Omega =2.7)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.837291}, {\dot{x}}_0 \approx \hbox {1.541319})$ and ($x_0 \approx -\hbox {0.837291}, {\dot{x}}_0 \approx -\hbox {1.541319})$. ($Q_0 =30,\delta =0.1, \alpha =5, \beta =30)$

Fig. 26

Stable asymmetric period-1 motion ($\Omega =2.516)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.723750}, {\dot{x}}_0 \approx \hbox {0.530036})$ and ($x_0 \approx -\hbox {0.723750}, {\dot{x}}_0 \approx -\hbox {0.530036})$. ($Q_0 =30,\delta =0.1, \alpha =5, \beta =30)$

Fig. 27

Stable asymmetric period-1 motion ($\Omega =2.4803)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitude, iv harmonic phase. Initial conditions ($x_0 \approx \hbox {0.658462}, {\dot{x}}_0 \approx \hbox {0.527202})$ and ($x_0 \approx -\hbox {0.658462}, {\dot{x}}_0 \approx -\hbox {0.527202})$. ($Q_0 =30,\delta =0.1, \alpha =5, \beta =30)$

Consider a pair of asymmetric period-4 motions at $\Omega =2.4803,$ and the trajectories for two paired trajectories of the asymmetric period-4 motions are presented in Fig. 27(i), (ii). The corresponding harmonic amplitudes and phases are presented in Fig. 27(iii), (iv), respectively. The initial conditions ($x_0 \approx \hbox {0.658462}, {\dot{x}}_0 \approx \hbox {0.527202})$ and ($x_0 \approx -\hbox {0.658462}, {\dot{x}}_0 \approx -\hbox {0.527202})$ for two paired asymmetric period-4 motions are obtained from the analytical prediction. Such asymmetric period-4 motions have eight large cycles. The second harmonic term plays important role in such periodic motions. The two paired asymmetric period-1 motion have the same harmonic amplitude. The constant term is $A_0 =a_0^{(4)R} =-a_0^{(4)L} \approx \hbox {0.1851}.$ The main harmonic amplitudes are $A_{1/4} \approx \hbox {1.7731e-}{3}, A_{1/2} \approx \hbox {0.0473},A_{3/4} \approx \hbox {9.7882e-}{3}, A_1 \approx \hbox {0.4061}, A_{5/4} \approx \hbox {9.0097e-}{3}, A_{3/2} \approx \hbox {0.1397},A_{7/4} \approx \hbox {0.0187}, A_2 \approx \hbox {0.7611},A_{9/4} \approx \hbox {0.0167},A_{5/2} \approx \hbox {0.1735},A_{11/4} \approx \hbox {0.0144}, A_3 \approx \hbox {0.2152}, A_{13/4} \approx \hbox {7.9782e-}{3},A_{7/2} \approx \hbox {0.0353},A_{15/4} \approx \hbox {5.8061e-}{3}, A_4 \approx \hbox {0.0834},A_{17/4} \approx \hbox {2.5797e-}{3}, A_{9/2} \approx \hbox {0.0456},A_{19/4} \approx \hbox {5.1039e-}{3},A_5 \approx \hbox {0.0181},A_{21/4} \approx \hbox {2.0830e-}{3},A_{11/2} \approx \hbox {0.0255}, A_{23/4} \approx \hbox {2.9280e-}{3}, A_6 \approx \hbox {3.1804e-}{4},A_{25/4} \approx \hbox {1.7848e-}{3},A_{13/2} \approx \hbox {0.0100.}$ Other harmonic amplitudes are in the interval of $A_{l/4} \in (10^{-15},10^{-2}) (l=27,28,\ldots ,220)$ with $A_{45} \approx \hbox {1.8000e-}{15}.$ Because the main effects on the period-2 motions are also from the harmonic terms of $A_2 ,A_1 \hbox { and }A_3$, the period-4 motions are similar to the period-2 and period-1 motions on the same bifurcation trees. The asymmetric period-1 motion needs about 220 terms to get an approximate analytical expression by finite Fourier series. However, the harmonic phases are different. The relations of harmonic phase of the paired asymmetric period-1 motions are given by $\varphi _{k/4}^{L} =\bmod (\varphi _{k/4}^{R} +\pi ,2\pi )$.

Consider another pair of asymmetric period-1 motions with smaller $\Omega =1.90122,$ and the corresponding trajectories for the paired asymmetric period-1 motions are presented in Fig. 28(i), (ii). Harmonic amplitude and phase are presented in Fig. 28(iii), (iv), respectively. The initial conditions ($x_0 \approx \hbox {0.610248}, {\dot{x}}_0 \approx -\hbox {2.607625})$ and ($x_0 \approx -\hbox {0.610248}, {\dot{x}}_0 \approx \hbox {2.607625})$ for this pair of asymmetric period-1 motions are obtained from analytical prediction. The trajectories of the two paired asymmetric periodic motions experience two large cycles and one small cycles. The constant term is $A_0 =a_0^R =-a_0^L \approx \hbox {0.5184}.$ The main harmonic amplitudes are $A_1 \approx \hbox {0.4786}, A_2 \approx \hbox {0.1470},A_3 \approx \hbox {0.6217},A_4 \approx \hbox {0.1325},A_5 \approx \hbox {0.0456},A_6 \approx \hbox {0.0286}$ and $A_7 \approx \hbox {0.0197}.$ Other harmonic amplitudes are in $A_l \in (10^{-14},10^{-3}) (l=8,9,\ldots ,50)$ with $A_{50} \approx \hbox {1.1810e-}{14}.$ The asymmetric period-1 motions are mainly determined by the harmonic terms of $A_3 ,A_1 ,A_2 \hbox { and }A_4 .$ The asymmetric period-1 motion needs about 50 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phases of this pair of period-1 motions are $\varphi _k^{L} =\bmod (\varphi _k^{R} +\pi ,2\pi )$.

Fig. 28

Stable asymmetric period-1 motion ($\Omega =1.90122)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.610248}, {\dot{x}}_0 \approx -\hbox {2.607625})$ and ($x_0 \approx -\hbox {0.610248}, {\dot{x}}_0 \approx \hbox {2.607625})$. ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

For $\Omega =1.873052,$ the trajectories, harmonic amplitudes and phase of a pair of asymmetric period-2 motions are presented in Fig. 29. The initial conditions ($x_0 \approx \hbox {0.681983}, \dot{x}_0 \approx -\hbox {2.031983})$ and ($x_0 \approx -\hbox {0.681983}, {\dot{x}}_0 \approx \hbox {2.031983})$ for the paired asymmetric period-2 motions are obtained from analytical prediction. The trajectories of the paired period-2 motions have the six cycles. The constant term is $A_0 =a_0^{(2)R} =-a_0^{(2)L} \approx \hbox {0.4936}.$ The main harmonic amplitudes are $A_{1/2} \approx \hbox {6.9424e-}{3}, A_1 \approx \hbox {0.4286}, A_{3/2} \approx \hbox {0.0197}, A_2 \approx \hbox {0.0727},A_{5/2} \approx \hbox {0.0227}, A_3 \approx \hbox {0.6383}, A_{7/2} \approx \hbox {0.0280}, A_4 \approx \hbox {0.1872}, A_{9/2} \approx \hbox {1.4866e-}{3}, A_5 \approx \hbox {0.0324}, A_{11/2} \approx \hbox {3.7601e-}{3}, A_6 \approx \hbox {0.0343}, A_{13/2} \approx \hbox {2.6339e-}{3},$ and $A_7 \approx \hbox {0.0132}.$ Other harmonic amplitudes are in $A_{l/2} \in (10^{-14},10^{-3}) (l=15,16,\ldots ,100)$ with $A_{50} \approx \hbox {1.8888e-}{14}.$ The asymmetric period-2 motions are still mainly determined by the harmonic terms of $A_3 ,A_1 ,A_4 \hbox { and} A_2$. The asymmetric period-2 motion needs about 100 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of this pair of period-2 motions are $\varphi _k^{L} =\bmod (\varphi _k^{R} +\pi ,2\pi )$.

For $\Omega =1.873052,$ The trajectories, harmonic amplitudes and phases for a pair of asymmetric period-4 motions are presented in Fig. 30 with initial conditions ($x_0 \approx \hbox {0.693702}, \dot{x}_0 \approx -\hbox {1.839290})$ and ($x_0 \approx -\hbox {0.693702}, {\dot{x}}_0 \approx \hbox {1.839290})$. The paired period-4 motions have 12 cycles for phase trajectory. The constant term is $A_0 =a_0^{(4)R} =-a_0^{(4)L} \approx \hbox {0.4925}.$ The main harmonic amplitudes are $A_{1/4} \approx \hbox {1.3062e-}{3}, A_{1/2} \approx \hbox {0.0141}, A_{3/4} \approx \hbox {1.3826e-}{3}, A_1 \approx \hbox {0.4269}, A_{5/4} \approx \hbox {3.5668e-}{3}, A_{3/2} \approx \hbox {0.0399},A_{7/4} \approx \hbox {4.7811e-}{3}, A_2 \approx \hbox {0.0717}, A_{9/4} \approx \hbox {3.5498e-}{3}, A_{5/2} \approx \hbox {0.0456}, A_{11/4} \approx \hbox {7.1946e-}{3}, A_3 \approx \hbox {0.6328}, A_{13/4} \approx \hbox {5.0205e-}{3}, A_{7/2} \approx \hbox {0.0565}, A_{15/4} \approx \hbox {5.6333e-}{3}, A_4 \approx \hbox {0.1870}, A_{17/4} \approx \hbox {4.0999e-}{4}, A_{9/2} \approx \hbox {2.8431e-}{3}, A_{19/4} \approx \hbox {8.9165e-}{4}, A_5 \approx \hbox {0.0326}, A_{21/4} \approx \hbox {7.8678e-}{4}, A_{11/2} \approx \hbox {7.5104e-}{3}, A_{23/4} \approx \hbox {1.2025e-}{3}, A_6 \approx \hbox {0.0332}, A_{25/4} \approx \hbox {4.7468e-}{4}, A_{13/2} \approx \hbox {5.2392e-}{3}, A_{27/4} \approx \hbox {5.3030e-}{4}, A_7\approx \hbox {0.0125}.$ Other harmonic amplitudes are in $A_{l/4} \in (10^{-14},10^{-3}) (l=29,30,\ldots 200)$ with $A_{50} \approx \hbox {1.3299e-}{14}.$ The asymmetric period-4 motions are also mainly determined by the harmonic terms of $A_3 ,A_1 ,A_4 \hbox { and }A_2 .$ The asymmetric period-4 motion needs about 200 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of this pair of period-4 motions are $\varphi _{k/4}^{L} =\bmod (\varphi _{k/4}^{R} +\pi ,2\pi )$ .

Fig. 29

Stable asymmetric period-2 motion ($\Omega =1.873052)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.681983}, {\dot{x}}_0 \approx -\hbox {2.031983})$ and ($x_0 \approx -\hbox {0.681983}, {\dot{x}}_0 \approx \hbox {2.031983})$ ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

Fig. 30

Stable asymmetric period-4 motion ($\Omega =1.869652)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.693702}, {\dot{x}}_0 \approx -\hbox {1.839290})$ and ($x_0 \approx -\hbox {0.693702}, {\dot{x}}_0 \approx \hbox {1.839290})$. ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

Consider a pair of asymmetric period-1 motions at $\Omega =1.4208,$ and the corresponding trajectories and harmonic amplitudes and phases are presented in Fig. 31. The initial conditions ($x_0 \approx \hbox {0.059049}, {\dot{x}}_0 \approx -\hbox {0.069673})$ and ($x_0 \approx -\hbox {0.059049}, {\dot{x}}_0 \approx \hbox {0.069673})$ for the right and left asymmetric period-1 motions are obtained from analytical prediction. The two paired period-1 motions are very asymmetric. The constant term is $A_0 =a_0^R =-a_0^L \approx \hbox {0.4120}.$ The main harmonic amplitudes are $A_1 \approx \hbox {0.3682}, A_2 \approx \hbox {0.2451}, A_3 \approx \hbox {0.1235}, A_4 \approx \hbox {0.1265}, A_5 \approx \hbox {0.0563}, A_6 \approx \hbox {0.0423}, A_7 \approx \hbox {0.0248},A_8 \approx \hbox {0.0156}.$ Other harmonic amplitudes are in the interval of $A_l \in (10^{-15},10^{-3}) (l=9,10,\ldots ,68)$ with $A_{68} \approx \hbox {4.4420e-}{15}.$ The most contributions of harmonic terms on the period-1 motions are the first, second, third and fourth harmonic terms. The two paired asymmetric period-1 motions need about 68 terms to get an approximate analytical expression by finite Fourier series. The relations of harmonic phase of this pair of period-1 motions are $\varphi _k^{L} =\bmod (\varphi _k^{R} +\pi ,2\pi )$.

On the same bifurcation trees, $\Omega =1.443083$ is considered for a pair of asymmetric period-2 motions. The corresponding trajectories, harmonic amplitudes and phases are presented in Fig. 32. The initial conditions ($x_0 \approx \hbox {0.064165}, \dot{x}_0 \approx \hbox {0.391496})$ and ($x_0 \approx -\hbox {0.064165}, {\dot{x}}_0 \approx -\hbox {0.391496})$ for the paired asymmetric period-2 motions are obtained from the analytical prediction. The doubled trajectory of the period-1 motion become the trajectory of the asymmetric period-2 motion. The constant term is $A_0 =a_0^{(2)R} =-a_0^{(2)L} \approx \hbox {0.4177}.$ The main harmonic amplitudes are $A_{1/2} \approx \hbox {0.0347},A_1 \approx \hbox {0.3742},A_{3/2} \approx \hbox {0.0222},A_2 \approx \hbox {0.2476}, A_{5/2} \approx \hbox {0.0369}, A_3 \approx \hbox {0.1172},A_{7/2} \approx \hbox {0.0373},A_4 \approx \hbox {0.1263},A_{9/2} \approx \hbox {0.0188},A_5 \approx \hbox {0.0539},A_{11/2} \approx \hbox {4.2620e-}{3}, A_6 \approx \hbox {0.0407}, A_{13/2} \approx \hbox {1.7209e-}{3}, A_7 \approx \hbox {0.0236},A_{15/2} \approx \hbox {7.2592e-}{4}$ and $A_7 \approx \hbox {0.0147.}$ Other harmonic amplitudes are in $A_{l/2} \in (10^{-15},10^{-3})(l=17,18,\ldots ,136)$ with $A_{68} \approx \hbox {2.3866e-}{15}.$ The most contributions of harmonic terms on the period-2 motions are also the first, second, third and fourth harmonic terms. The contributions of $A_l$ ($\bmod (l,2)\ne 0)$ on the period-2 motion are not very small. So the trajectory difference between period-1 and period-2 motions can be observed clearly. The asymmetric period-2 motion needs about 136 terms to get an approximate analytical expression. The harmonic phases of the two period-2 motions satisfy $\varphi _{k/2}^{L} =\bmod (\varphi _{k/2}^{R} +\pi ,2\pi )$.

Fig. 31

Stable asymmetric period-1 motion ($\Omega =1.4208)$. i Trajectory (left), ii trajectory (right, iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.059049}, {\dot{x}}_0 \approx -\hbox {0.069673})$ and ($x_0 \approx -\hbox {0.059049}, {\dot{x}}_0 \approx \hbox {0.069673})$. ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

Fig. 32

Stable asymmetric period-2 motion ($\Omega =1.443083)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.064165}, {\dot{x}}_0 \approx \hbox {0.391496})$ and ($x_0 \approx -\hbox {0.064165}, {\dot{x}}_0 \approx -\hbox {0.391496})$. ($Q_0 =30,\delta =0.1, \alpha =5,\beta =30)$

Fig. 33

Stable asymmetric period-4 motion ($\Omega =1.445237)$. i Trajectory (left), ii trajectory (right), iii harmonic amplitudes, iv harmonic phases. Initial conditions ($x_0 \approx \hbox {0.064293}, {\dot{x}}_0 \approx \hbox {0.364504})$ and ($x_0 \approx -\hbox {0.064293}, {\dot{x}}_0 \approx -\hbox {0.364504})$. ($Q_0 =30,\delta =0.1,\alpha =5,\beta =30)$

On the same bifurcation tree, $\Omega =1.445237$ is considered for a pair of asymmetric period-4 motions are presented. The corresponding trajectories, harmonic amplitudes and phases are presented in Fig. 33. The initial conditions ($x_0 \approx \hbox {0.064293}, \dot{x}_0 \approx \hbox {0.364504})$ and ($x_0 \approx -\hbox {0.064293}, {\dot{x}}_0 \approx -\hbox {0.364504})$ for the paired two asymmetric period-4 motions are obtained from the analytical prediction. The constant term is $A_0 =a_0^{(4)R} =-a_0^{(4)L} \approx \hbox {0.4178}.$ The main harmonic amplitudes are $A_{1/4} \approx \hbox {4.0681e-}{4},A_{1/2} \approx \hbox {0.0374},A_{3/4} \approx \hbox {7.7298e-}{4},A_1 \approx \hbox {0.3746}, A_{5/4} \approx \hbox {5.8643e-}{4}, A_{3/2} \approx \hbox {0.0239},A_{7/4} \approx \hbox {2.4921e-}{4},A_2 \approx \hbox {0.2480},A_{9/4} \approx \hbox {3.6485e-}{4}, A_{5/2} \approx \hbox {0.0398}, A_{11/4} \approx \hbox {9.8609e-}{4}, A_3 \approx \hbox {0.1181},A_{13/4} \approx \hbox {9.3527e-}{4},A_{7/2} \approx \hbox {0.0402},A_{15/4} \approx \hbox {5.4981e-}{4}, A_4 \approx \hbox {0.1258}, A_{17/4} \approx \hbox {3.6439e-}{4}, A_{9/2} \approx \hbox {0.0203}, A_{19/4} \approx \hbox {3.6759e-}{4}, A_5 \approx \hbox {0.0542}, A_{21/4} \approx \hbox {1.9883e-}{4}, A_{11/2} \approx \hbox {4.5420e-}{3}, A_{23/4} \approx \hbox {3.2059e-}{5}, A_6 \approx \hbox {0.0404}, A_{25/4} \approx \hbox {2.0653e-}{5}, A_{13/2} \approx \hbox {1.8217e-}{3}, A_{27/4} \approx \hbox {6.8546e-}{5}, A_7 \approx \hbox {0.0235}, A_{29/4} \approx \hbox {3.8022e-}{5}, A_{15/2} \approx \hbox {7.4559e-}{4}, A_{31/4} \approx \hbox {4.0792e-}{5}, A_8 \approx \hbox {0.0147}.$ Other harmonic amplitudes are in $A_{l/4} \in (10^{-15},10^{-3}) (l=33,34,\ldots ,272)$ with $A_{68} \approx \hbox {2.2652e-}{15}.$ The asymmetric period-4 motion needs about 272 terms to get an approximate analytical expression by finite Fourier series. Because of small $A_{m/4} (m=1,5,9,\ldots ),$ the trajectories of period-2 and period-4 motions are very close to each other. The relations of harmonic phase of this pair of period-4 motions are $\varphi _{k/4}^{L} =\bmod (\varphi _{k/4}^{R} +\pi ,2\pi )$.

7 Conclusions

In this paper, bifurcation trees of period-1 motion to chaos in a parametric Duffing oscillator were obtained by a semi-analytic method. The semi-analytic method can be directly employed for such a nonlinear dynamical system. The bifurcation trees of period-1 to period-4 motions were presented to demonstrate the bifurcation tree of period-1 motions to chaos. Through the discretization of differential equations, the mapping structure of periodic motions was constructed. The periodic motions were analytically predicted by the implicit mapping structure and the corresponding stability and bifurcation analysis were carried out by eigenvalue analysis. The harmonic frequency–amplitude characteristic was discussed for a better understanding of the complexity of periodic motions. Using the analytical prediction from periodic motions, the numerical simulations for period-1 to period-4 motions were completed. Through the numerical simulations, analytical and numerical results of periodic motions on the bifurcation trees matched each other very well. The complexity and asymmetry of periodic motions were strongly dependent on the contributions of harmonic amplitudes of periodic motions.