Bifurcation Trees of Period-3 Motions to Chaos in a Time-Delayed Duffing Oscillator

Abstract

The time-delayed Duffing oscillator is extensively applied in engineering and particle physics. Determination of periodic motions in such a system is significant. Thus, here in, period motions in the time-delayed Duffing oscillator are discussed through a semi-analytical method. The semi-analytical method is based on the implicit mappings constructed by discretization of the corresponding differential equation. Complex period-3 motions are predicted, and the corresponding stability and bifurcation analysis are completed.

The time-delayed Duffing oscillator is extensively applied in engineering and particle physics. Determination of periodic motions in such a system is significant. Thus, here in, period-1 motions in the time-delayed Duffing oscillator are discussed through a semi-analytical method. The semi-analytical method is based on the implicit mappings constructed by discretization of the corresponding differential equation. Complex period-3 motions are predicted, and the corresponding stability and bifurcation analysis are completed. From predictions, complex periodic motions are simulated numerically, and the harmonic amplitudes and phases are presented. Through this study, the complexity of periodic motions in the time-delayed Duffing oscillator can be better understood. This chapter is dedicated to Professor Valentin Afraimoich’s 70$^\mathrm{{th}}$ birthday.

10.1 Introduction

In recent decades, time-delay nonlinear systems have received great attentions. Periodic solutions in nonlinear dynamical systems have been of great interest for a long time. However, one still cannot obtain adequate solutions of periodic motions to chaos in nonlinear dynamical systems.

In 1788, Lagrange [1] investigated periodic motions of three-body problem through a perturbation of the two-body problem with the method of averaging. In the end of 19th century, Poincare [2] developed the perturbation theory for periodic motions of celestial bodies. In 1920, van der Pol [3] employed the method of averaging for the periodic solutions of oscillation systems in circuits. Until 1928, the asymptotic validity of the method of averaging was not proved. Fatou [4] gave the proof of the asymptotic validity through the solution existence theorems of differential equations. In 1935, Krylov and Bogoliubov [5] further developed the method of averaging for nonlinear oscillations in nonlinear vibration systems. Since then, one extensively used the perturbation method to investigate periodic solutions in nonlinear dynamical systems. In 2012, Luo [6] developed an analytical method for analytical solutions of periodic motions in nonlinear dynamical systems. Luo and Huang [7] applied such a method to the Duffing oscillator for approximate solutions of periodic motions, and Luo and Huang [8] gave the analytical bifurcation trees of period-m motions to chaos in the Duffing oscillator (also see, Luo and Huang [9, 10]).

The approximate solutions of periodic motion in the time-delayed nonlinear oscillators were investigated by the method of multiple scales (e.g., Hu et al. [11], Wang and Hu [12]). The harmonic balance method was also employed for approximate solutions of periodic motions in time-delayed nonlinear oscillators (e.g., MacDonald [13]; Liu and Kalmar-Nagy [14]; Lueng and Guo [15]). However, these methods are not accurate enough to give reliable results. For instance, the multiple scale method can only be applied to dynamical systems with weak nonlinear terms. The harmonic balance method is based on one or two harmonic terms. In 2013, Luo [16] systematically presented an analytical method for periodic motions in time-delayed, nonlinear dynamical systems. Luo and Jin [17] applied such an analytical method to the time-delayed, quadratic nonlinear oscillator, and the analytical bifurcation trees of period-1 motions to chaos were obtained. In Luo and Jin [18], complex period-1 motions of the periodically forced Duffing oscillator with a time-delayed displacement were investigated, which cannot be obtained from the traditional harmonic balance and perturbation methods. In Luo and Jin [19], the period-m motions of the time-delayed Duffing oscillator were investigated analytically, and complex period-m motions were observed in such a time-delayed Duffing oscillator . The bifurcation trees of period-1 motion to chaos were also discussed.

To determine stability of time-varying coefficient systems with time-delay, Insperger and Sepan [20] developed the semi-discretization method, and the detailed description of such a method can be found in Insperger and Sepan [21]. In 2011, based on the ideas of finite element method, Khasawneh and Mann [22] developed the spectral element approach for stability of delayed systems. In 2016, Lehotzsky, Insperger, and Stepan [23] extended this idea for time-periodic delayed, differential equations with multiple and distributed delay. Such a method cannot be applied to periodic motions in nonlinear time-delay systems. In 2015, Luo [24] developed a semi-analytical method to determine periodic motions in nonlinear dynamical systems with/without time-delay through discrete implicit maps. Luo [25] systematically discussed the discretization methods of continuous dynamical systems with/ without time-delay. Luo and Guo [26] applied such an approach to investigate bifurcation trees of the Duffing oscillator, and nonlinear frequency-amplitude characteristics of periodic motion to chaos.

This semi-analytical method for time-delayed, nonlinear dynamical systems is different from the aforementioned semi-analytical method for non-time-delayed nonlinear dynamical systems. Thus, for a periodically forced, time-delayed, hardening Duffing nonlinear oscillator, the different semi-analytical method was adopted in Luo and Xing [27] for determining complex symmetric and asymmetric period-1 motions. With decreasing excitation frequency, symmetric and asymmetric period-1 motions become very complicated. From the asymmetric period-1 motions, the corresponding period-doubling bifurcations were observed. Thus, period-2 motions should be discovered. If the period-doubling bifurcations of period-2 motions exist, the period-4 motions will be discovered. In Luo and Xing [28], the bifurcation trees of periodic motions to chaos in the hardening Duffing oscillator were discussed. The double-well Duffing oscillators extensively exist in engineering and physical systems, and one often used displacement feedback to control periodic motions in such a twin-well Duffing oscillator. Thus, the bifurcation trees of periodic motions to chaos in such a time-delayed Duffing oscillator are of great interest for a better understanding of global pictures of periodic motions switching and complexity. Before determining bifurcation trees, period-3 motions should be determined first.

In this chapter, the semi-analytical method will be used to investigate period-3 motions in a periodically forced Duffing oscillator with time-delay. This time-delay is caused by the displacement feedback. The analytical predictions of period-3 motions will be completed, and the corresponding stability and bifurcation will be carried out through the eigenvalue analysis. To understand the motion complexity, the numerical simulations will be completed and harmonic amplitudes and phases will be presented.

10.2 Discrete Mappings

Consider a time-delayed, Duffing oscillator

$$\begin{aligned} \ddot{x}+\delta \dot{x}+\alpha _1 x-\alpha _2 x^{\tau }+\beta x^{3}=Q_0 \cos \Omega t \end{aligned}$$

(10.1)

where $x=x(t)$ and $x^{\tau }=x(t-\tau )$. In state space, the above equation becomes

$$\begin{aligned} \begin{array}{l} \dot{x}=y, \\ \dot{y}=Q_0 \cos \Omega t-\delta y-\alpha _1 x+\alpha _2 x^{\tau }-\beta x^{3}. \\ \end{array} \end{aligned}$$

(10.2)

Let $\mathbf{x}=(x,y)^{\text {T}}$ and $\mathbf{x}^{\tau }=(x^{\tau },y^{\tau })^{\text {T}}$. For discrete time $t_k =kh$ ($k=0,1,2,\ldots )$, $\mathbf{x}_k =(x_k ,y_k )^{\text {T}}$ and $\mathbf{x}_k^\tau =(x_k^\tau ,y_k^\tau )^{\text {T}}$. Using a midpoint scheme for the time interval $t\in [t_{k-1} ,t_k ]$ ($k=1,2,\ldots )$, the foregoing differential equation is discretized to form an implicit map$P_k$:

$$\begin{aligned} \begin{array}{l} P_k :(\mathbf{x}_{k-1}^{(m)} ,\mathbf{x}_{k-1}^{\tau (m)} )\rightarrow (\mathbf{x}_k^{(m)} ,\mathbf{x}_k^{\tau (m)} ) \\ \Rightarrow (\mathbf{x}_k^{(m)} ,\mathbf{x}_k^{\tau (m)} )=P_k (\mathbf{x}_{k-1}^{(m)} ,\mathbf{x}_{k-1}^{\tau (m)} ) \\ \end{array} \end{aligned}$$

(10.3)

The corresponding implicit relations for the implicit map are

$$\begin{aligned} \begin{array}{l} x_k =x_{k-1} +\frac{1}{2}h(y_k +y_{k-1} ), \\ y_k =y_{k-1} +h[Q_0 \cos \Omega (t_{k-1} +\frac{h}{2})-\frac{1}{2}\delta (y_k +y_{k-1} ) \\ \;\;\;\;-\frac{1}{2}\alpha _1 (x_k +x_{k-1} )+\frac{1}{2}\alpha _2 (x_k^\tau +x_{k-1}^\tau )-\frac{1}{8}\beta (x_k +x_{k-1} )^{3}]. \\ \end{array} \end{aligned}$$

(10.4)

The time-delay node $\mathbf{x}_k^\tau \approx \mathbf{x}(t_{k-\tau })$ of $\mathbf{x}_k \approx \mathbf{x}(t_k )$ lies between $\mathbf{x}_{k-l_k }$and $\mathbf{x}_{k-l_k -1}$ ($l_k =\mathrm{int}(\tau /h))$. The time-delay nodes can be expressed by an interpolation function of two points $\mathbf{x}_{k-l_k }$and $\mathbf{x}_{k-l_k -1}$. For a time-delay node $\mathbf{x}_j^\tau$ ($j=k-1,k$), we have

$$\begin{aligned} \mathbf{x}_j^\tau =\mathbf{h}_j (\mathbf{x}_{r_j -1} ,\mathbf{x}_{r_j } ,\theta _{r_j } )\hbox { for }r_j =j-l_j . \end{aligned}$$

(10.5)

For instance, the time-delay discrete node $\mathbf{x}_j^\tau$ is determined by the simple Lagrange interpolation, i.e.,

$$\begin{aligned} \begin{array}{l} x_j^\tau =x_{j-l_j -1} +(1-\frac{\tau }{h}+l_j )(x_{j-l_j } -x_{j-l_j -1} ), \\ y_j^\tau =y_{j-l_j -1} +(1-\frac{\tau }{h}+l_j )(y_{j-l_j } -y_{j-l_j -1} ). \\ \end{array} \end{aligned}$$

(10.6)

Thus, the time-delay nodes are expressed by non-time-delay nodes. The discretization of differential equation for the time-delayed Duffing oscillator is completed. In the next section, the discrete mapping will be used to determine period-3 motions in the time-delayed Duffing oscillator .

10.3 Period-m Motions and Stability

To represent the period-m motion in such a Duffing oscillator, a discrete mapping structure, presented in Luo [20], is constructed as

$$\begin{aligned} P=\underbrace{P_{mN} \circ P_{mN-1} \circ \cdots \circ P_2 \circ P_1 }_{mN-\hbox {actions}}:(\mathbf{x}_0^{(m)} ,\mathbf{x}_0^{\tau (m)} )\rightarrow (\mathbf{x}_N^{(m)} ,\mathbf{x}_N^{\tau (m)} ) \end{aligned}$$

(10.7)

with

$$\begin{aligned} \begin{array}{l} P_k :(\mathbf{x}_{k-1}^{(m)} ,\mathbf{x}_{k-1}^{\tau (m)} )\rightarrow (\mathbf{x}_k^{(m)} ,\mathbf{x}_k^{\tau (m)} ) \\ (k=1,2,\cdots ,mN). \end{array} \end{aligned}$$

(10.8)

By applying a midpoint scheme discretization, the corresponding algebraic equations of $P_k$ are obtained as follows:

$$\begin{aligned} P_k :\left\{ {\begin{array}{rl} x_k^{(m)} &{}=x_{k-1}^{(m)} +\frac{1}{2}h(y_k^{(m)} +y_{k-1}^{(m)} ), \\ y_k^{(m)} &{}=y_{k-1}^{(m)} +h[Q_0 cos\omega (t+\frac{1}{2}h)-\frac{1}{2}\delta (y_k^{(m)} +y_{k-1}^{(m)} ) \\ &{}\,-\frac{1}{2}\alpha _1 (x_k^{(m)} +x_{k-1}^{(m)} )+\frac{1}{2}\alpha _2 (x_k^{\tau (m)} +x_{k-1}^{\tau (m)} )\; \\ &{}\,-\frac{1}{8}\beta (x_k^{(m)} +x_{k-1}^{(m)} )^{3}] \\ (k&{}=1,2,\cdots ,mN). \\ \end{array}} \right. \end{aligned}$$

(10.9)

Application of the simple Lagrange interpolation, the time-delay node $\mathbf{x}_j^\tau ={} \mathbf{h}_j (\mathbf{x}_{r_j -1} ,\mathbf{x}_{r_j } ,\theta _{rj} )$ is expressed as

$$\begin{aligned} \begin{array}{l} x_k^{\tau (m)} =x_{k-l_k -1}^{(m)} +(1-\frac{\tau }{h}+l_k )(x_{k-l_k }^{(m)} -x_{k-l_k -1}^{(m)} ), \\ y_k^{\tau (m)} =y_{k-l_k -1}^{(m)} +(1-\frac{\tau }{h}+l_k )(y_{k-l_k }^{(m)} -y_{k-l_k -1}^{(m)} ). \\ \end{array} \end{aligned}$$

(10.10)

Then, the set of points on the periodic motion are computed by

$$\begin{aligned} \begin{array}{l} \left. {\begin{array}{l} \mathbf{g}_k (\mathbf{x}_{k-1}^{(m)*} ,\mathbf{x}_k^{(m)*} ;\mathbf{x}_{k-1}^{\tau (m){*}} ,\mathbf{x}_k^{\tau (m){*}} ,\mathbf{p})=\mathbf{0} \\ \mathbf{x}_j^{\tau (m){*}} =\mathbf{h}_j (\mathbf{x}_{r_j -1}^{(m)*} ,\mathbf{x}_{r_j }^{(m)*} ,\theta _{rj} ),j=k,k-1 \\ \end{array}} \right\} (k=1,2,\cdots ,mN) \\ \mathbf{x}_0^{(m)*} =\mathbf{x}_{mN}^{(m)*} \;and\;\mathbf{x}_0^{\tau (m)*} =\mathbf{x}_{mN}^{\tau (m)*} \; \\ \end{array} \end{aligned}$$

(10.11)

Once the node points $\mathbf{x}_k^{(m){*}}$ ($k=1,2,\cdots ,mN)$ of the period-m motion are obtained, the stability of period-m motion can be discussed through the eigenvalue analysis of the corresponding Jacobian matrix.

$$\begin{aligned} \begin{array}{l} \displaystyle \sum _{j=k-1}^k {\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_j^{(m)} }\Delta \mathbf{x}_j^{(m)} +\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_j^{\tau (m)} }(\frac{\partial \mathbf{x}_j^{\tau (m)} }{\partial \mathbf{x}_{r_j }^{\tau (m)} }\Delta \mathbf{x}_{r_j }^{\tau (m)} +\frac{\partial \mathbf{x}_j^{\tau (m)} }{\partial \mathbf{x}_{r_j -1}^{\tau (m)} }\Delta \mathbf{x}_{r_j -1}^{\tau (m)} )} =\mathbf{0} \\ \hbox {with }r_j =j-l_j ,j=k-1,k;(k=1,2,\cdots ,mN). \\ \end{array} \end{aligned}$$

(10.12)

As in Luo [20], new vectors are introduced as

$$\begin{aligned} \begin{array}{l} \mathbf{y}_k^{(m)} =(\mathbf{x}_k^{(m)} ,\mathbf{x}_{k-1}^{(m)} ,\cdots ,\mathbf{x}_{r_{k-1} }^{(m)} )^{\text {T}}, \\ \mathbf{y}_{k-1}^{(m)} =(\mathbf{x}_{k-1}^{(m)} ,\mathbf{x}_{k-2}^{(m)} ,\cdots ,\mathbf{x}_{r_{k-1} -1}^{(m)} )^{\text {T}}, \\ \Delta \mathbf{y}_k^{(m)} =(\Delta \mathbf{x}_k^{(m)} ,\Delta \mathbf{x}_{k-1}^{(m)} ,\cdots ,\Delta \mathbf{x}_{r_{k-1} }^{(m)} )^{\text {T}}, \\ \Delta \mathbf{y}_{k-1}^{(m)} =(\Delta \mathbf{x}_{k-1}^{(m)} ,\Delta \mathbf{x}_{k-2}^{(m)} ,\cdots ,\Delta \mathbf{x}_{r_{k-1} -1}^{(m)} )^{\text {T}}. \\ \end{array} \end{aligned}$$

(10.13)

The resultant Jacobian matrices of the periodic motions are

$$\begin{aligned} DP=DP_{mN(mN-1)\cdots 1} =\left[ {\frac{\partial \mathbf{y}_{mN}^{(m)} }{\partial \mathbf{y}_0^{(m)} }} \right] =\mathbf{A}_{mN} \mathbf{A}_{mN-1} \cdots \mathbf{A}_1 \end{aligned}$$

(10.14)

with

$$\begin{aligned} \Delta \mathbf{y}_k^{(m)} =\mathbf{A}_k^{(m)} \Delta \mathbf{y}_{k-1}^{(m)} ,\,\mathbf{A}_k^{(m)} \equiv \left[ {\frac{\partial \mathbf{y}_k^{(m)} }{\partial \mathbf{y}_{k-1}^{(m)} }} \right] _{(\mathbf{y}_{k-1}^{(m){*}} ,\mathbf{y}_k^{(m){*}} )} \end{aligned}$$

(10.15)

and

$$\begin{aligned} \begin{array}{l} \mathbf{A}_k^{(m)} =\left[ {{\begin{array}{ll} {\mathbf{B}_k^{(m)} }&{} {(\mathbf{a}_{k(r_{k-1} -1)}^{(m)} )_{2\times 2} } \\ {\mathbf{I}_k^{(m)} }&{} {\mathbf{0}_k^{(m)} } \\ \end{array} }} \right] _{2(s+1)\times 2(s+1)} ,s=1+l_{k-1} \\ \mathbf{B}_k^{(m)} =[(\mathbf{a}_{k(k-1)}^{(m)} )_{2\times 2} ,\mathbf{0}_{2\times 2} ,\cdots ,(\mathbf{a}_{k(r_k -1)}^{(m)} )_{2\times 2} ], \\ \mathbf{I}_k^{(m)} =diag(\mathbf{I}_{2\times 2} ,\mathbf{I}_{2\times 2} ,\cdots ,\mathbf{I}_{2\times 2} )_{2s\times 2s} , \\ \mathbf{0}_k^{(m)} =(\underbrace{\mathbf{0}_{2\times 2} ,\mathbf{0}_{2\times 2} ,\cdots ,\mathbf{0}_{2\times 2} }_s)^{\hbox {T}}; \\ \end{array} \end{aligned}$$

(10.16)

$$\begin{aligned} \begin{array}{l} \mathbf{a}_{kj}^{(m)} =[\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_k^{(m)} }]^{-1}\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_j^{(m)} }, \\ \mathbf{a}_{kr_j }^{(m)} =[\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_k^{(m)} }]^{-1}\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_j^{(m)\tau } }\frac{\partial \mathbf{x}_j^{(m)\tau } }{\partial \mathbf{x}_{r_j }^{(m)\tau } }, \\ \mathbf{a}_{k(r_j -1)}^{(m)} =[\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_k^{(m)} }]^{-1}\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_j^{(m)\tau } }\frac{\partial \mathbf{x}_j^{(m)\tau } }{\partial \mathbf{x}_{r_j -1}^{(m)\tau } } \\ \hbox {with }r_j =j-l_j ,j=k-1,k; \\ \end{array} \end{aligned}$$

(10.17)

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_{k-1}^{(m)} }=\left[ {{\begin{array}{ll} {-1}&{} {-\frac{1}{2}h} \\ \Delta &{} {\frac{1}{2}\delta h-1} \\ \end{array} }} \right] ,\;\frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_{k1}^{(m)} }=\left[ {{\begin{array}{ll} 1&{} {-\frac{1}{2}h} \\ \Delta &{} {\frac{1}{2}\delta h+1} \\ \end{array} }} \right] , \\ \displaystyle \frac{\partial \mathbf{g}_j^{\tau (m)} }{\partial \mathbf{x}_{r_j -1}^{(m)} }=\left[ {{\begin{array}{ll} 0&{} 0 \\ {\frac{\tau }{h}-l_j }&{} 0 \\ \end{array} }} \right] ,\;\frac{\partial \mathbf{g}_j^{\tau (m)} }{\partial \mathbf{x}_{r_j }^{(m)} }=\left[ {{\begin{array}{ll} 0&{} 0 \\ {1-\frac{\tau }{h}+l_j }&{} 0 \\ \end{array} }} \right] , \\ \displaystyle \frac{\partial \mathbf{g}_k }{\partial \mathbf{x}_j^{\tau (m)} }=\left[ {{\begin{array}{ll} 0&{} 0 \\ 0&{} {-\frac{1}{2}h\alpha _2 } \\ \end{array} }} \right] , \\ \Delta =\frac{1}{2}h[\alpha _1 +\beta (x_k +x_{k-1} )]. \\ \end{array} \end{aligned}$$

(10.18)

The eigenvalues of DP for such periodic flow are determined by

$$\begin{aligned} \hbox {|}DP-\lambda \mathbf{I}_{2(s+1)\times 2(s+1)} \hbox {|}=0. \end{aligned}$$

(10.19)

• (i) If the magnitudes of all eigenvalues of DP are less than one (i.e., $|\lambda _i \hbox {|}<1, i, 1,2,\cdots ,2(s+1))$, the approximate periodic solution is stable.

• (ii) If at least the magnitude of one eigenvalue of DP is greater than one (i.e., $|\lambda _i \hbox {|}>1$, $i\in \{1,2,\cdots ,n(s+1)\})$, the approximate periodic solution is unstable.

• (iii) The boundaries between stable and unstable periodic flow with higher-order singularity give bifurcation and stability conditions with higher-order singularity.

The bifurcation conditions are given as follows.

• (1) If $\lambda _i =1$ with $|\lambda _j \hbox {|}<1(i,j\in \{1,2,\cdots ,2(s+1)\}$ and $i\ne j$), the saddle-node bifurcation (SN) occurs.

• (2) If $\lambda _i =-1$ with $|\lambda _j \hbox {|}<1(i,j\in \{1,2,\cdots ,2(s+1)\}$ and $i\ne j$), the period-doubling bifurcation (PD) occurs.

• (3) If $|\lambda _{i,j} |=1$ with $|\lambda _l \hbox {|}<1(i,j,l\in \{1,2,\cdots ,2(s+1)\}$ and $\lambda _i =\bar{{\lambda }}_j \quad l\ne i,j)$, Neimark bifurcation (NB) occurs.

10.4 Frequency-Amplitude Analysis

From the node points of period-m motions in the time-delayed Duffing oscillator, $\mathbf{x}_k^{(m)} =(x_k^{(m)} ,y_k^{(m)} )^{\text {T}}$ ($k=0,1,2,\cdots ,mN)$, the period-m motions can be approximately expressed by the Fourier series, i.e.,

$$\begin{aligned} \mathbf{x}^{(m)}(t)\approx \mathbf{a}_0^{(m)} +\sum _{j=1}^M {\mathbf{b}_{j/m} } \cos (\frac{k}{m}\Omega t)+\mathbf{c}_{j/m} \sin (\frac{k}{m}\Omega t) \end{aligned}$$

(10.20)

The $(2M+1)$ unknown vector coefficients of $\mathbf{a}_0^{(m)} ,\mathbf{b}_{j/m} ,\mathbf{c}_{j/m}$ should be determined from discrete nodes $\mathbf{x}_k^{(m)} (k=0,1,2,\cdots ,mN)$ with $mN+1 \ge 2M+1.$ For $M=mN/2$, the node points $\mathbf{x}_k^{(m)}$ on the period-m motion can be expressed for $t_k \in [0,mT]$

$$\begin{aligned} \mathbf{x}^{(m)}(t_k )\equiv \mathbf{x}_k^{(m)}&=\mathbf{a}_0^{(m)} +\sum _{j=1}^{mN/2} {\mathbf{b}_{j/m} } \cos (\frac{j}{m}\Omega t_k )+\mathbf{c}_{j/m} \sin (\frac{j}{m}\Omega t_k ) \nonumber \\&=\mathbf{a}_0^{(m)} +\sum _{j=1}^{mN/2} {\mathbf{b}_{j/m} } \cos (\frac{j}{m}\frac{2k\pi }{N})+\mathbf{c}_{j/m} \sin (\frac{j}{m}\frac{2k\pi }{N}) \\ (k&=0,1,\cdots ,mN-1) \nonumber \end{aligned}$$

(10.21)

where

$$\begin{aligned} \begin{array}{l} T=\frac{2\pi }{\Omega }=N\Delta t;\Omega t_k =\Omega k\Delta t=\frac{2k\pi }{N} \\ \mathbf{a}_0^{(m)} =\frac{1}{N}\sum _{k=0}^{mN-1} {\mathbf{x}_k^{(m)} } , \\ \left. {\begin{array}{l} \displaystyle \mathbf{b}_{j/m} =\frac{2}{mN}\sum _{k=1}^{mN-1} {\mathbf{x}_k^{(m)} \cos (k\frac{2j\pi }{mN})} , \\ \displaystyle \mathbf{c}_{j/m} =\frac{2}{mN}\sum _{k=1}^{mN-1} {\mathbf{x}_k^{(m)} \sin (k\frac{2j\pi }{mN})} \\ \end{array}} \right\} (j=1,2,\cdots ,mN/2) \\ \end{array} \end{aligned}$$

(10.22)

and

$$\begin{aligned} \mathbf{a}_0^{(m)} =(a_{01}^{(m)} ,a_{02}^{(m)} )^{\text {T}},\mathbf{b}_{j/m} =(b_{j/m1} ,b_{j/m2} )^{\text {T}}\hbox {, }{} \mathbf{c}_{j/m} =(c_{j/m1} ,c_{j/m2} )^{\text {T}}. \end{aligned}$$

(10.23)

The harmonic amplitudes and phases for the period-m motions are expressed by

$$\begin{aligned} \begin{array}{l} A_{j/m1} =\sqrt{b_{j/m1}^2 +c_{j/m1}^2 }\hbox {, }\varphi _{j/m1} =\arctan \frac{c_{j/m1} }{b_{j/m1} }, \\ A_{j/m2} =\sqrt{b_{j/m2}^2 +c_{j/m2}^2 }\hbox {, }\varphi _{j/m2} =\arctan \frac{c_{j/m2} }{b_{j/m2} }. \\ \end{array} \end{aligned}$$

(10.24)

Thus, the approximate expression of period-m motions in Eq. (10.20) can be given as

$$\begin{aligned} \mathbf{x}^{(m)}(t)\approx \mathbf{a}_0^{(m)} +\sum _{j=1}^{mN/2} {\mathbf{b}_{j/m} } \cos (\frac{k}{m}\Omega t)+\mathbf{c}_{j/m} \sin (\frac{k}{m}\Omega t). \end{aligned}$$

(10.25)

For the time-delayed Duffing oscillator ,

$$\begin{aligned} \left\{ {\begin{array}{l} x^{(m)}(t) \\ y^{(m)}(t) \\ \end{array}} \right\} \equiv \left\{ {\begin{array}{l} x_1^{(m)} (t) \\ x_2^{(m)} (t) \\ \end{array}} \right\} \approx \left\{ {\begin{array}{l} a_{01}^{(m)} \\ a_{02}^{(m)} \\ \end{array}} \right\} +\sum _{j=1}^{mN/2} {\left\{ {\begin{array}{l} A_{j/m1} \cos (\frac{k}{m}\Omega t-\varphi _{j/m1} ) \\ A_{j/m1} \cos (\frac{k{}}{m}\Omega t-\varphi _{j/m2} ) \\ \end{array}} \right\} } . \end{aligned}$$

(10.26)

To reduce illustrations, only frequency-amplitude curves of displacement $x^{(m)}(t)$ for period-m motions are presented. However, the frequency-amplitudes for velocity $y^{(m)}(t)$ can also be done in a similar fashion. Thus, the displacement for period-m motion is given by

$$\begin{aligned} x^{(m)}(t)\approx a_0^{(m)} +\sum _{j=1}^{mN/2} {b_{j/m} } \cos (\frac{k}{m}\Omega t)+c_{j/m} \sin (\frac{k}{m}\Omega t) \end{aligned}$$

(10.27)

or

$$\begin{aligned} x^{(m)}(t)\approx a_0^{(m)} +\sum _{j=1}^{mN/2} {A_{j/m} \cos (\frac{k}{m}\Omega t-\varphi _{j/m} )} \end{aligned}$$

(10.28)

where

$$\begin{aligned} A_{j/m} =\sqrt{b_{j/m}^2 +c_{j/m}^2 }\hbox {, }\varphi _{j/m} =\arctan \frac{c_{j/m} }{b_{j/m} }. \end{aligned}$$

(10.29)

10.5 Bifurcation Trees of Period-3 to Period-6 Motions

In this section, a complete picture of P-3 motions and bifurcation trees of P-3 to P-6 motions will be presented. The corresponding stability and bifurcation will be investigated through eigenvalue analysis. Consider a set of parameters under strong excitation as

$$\begin{aligned} \alpha _1 =2.0,\alpha _2 =1.0,\;\beta =4.0,\delta =0.2,\;Q_0 =100.0 \end{aligned}$$

(10.30)

and the time-delay term $\tau =T/4$ where $T=2\pi /\Omega .$

Fig. 10.1

Period-3 motions a displacement, b velocity for $\Omega \in (9.385, 28.943)$, c displacement, d velocity for $\Omega \in (4.987, 5.425)$

Fig. 10.2

Bifurcation trees of period-3 to period-6 motions a displacement, b velocity for $\Omega \in (2.812, 3.352)$; c displacement, d velocity for $\Omega \in (2.277, 2.762)$

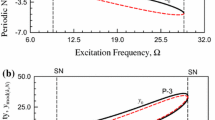
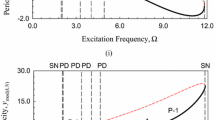
Two branches of simple symmetric period-3 motions and another two branches of period-3 to period-6 motions are presented in Figs. 10.1 and 10.2, respectively. For each branch of periodic motions, the displacement and velocity of periodic nodes $x_{mod(x,N)}$ and $y_{mod(x,N)}$ for $\bmod (x,N)=0$ are presented. Two simple symmetric period-3 motions exist in $\Omega \in (9.385, 28.943)$ and $\Omega \in (4.987, 5.425)$, while two period-3 to period-6 motions exist in $\Omega \in (2.812, 3.352)$ and $\Omega \in (2.277, 2.762)$. The acronyms ‘SN’ and ‘PD’ denote saddle-node bifurcation and period-doubling bifurcation, respectively. The letters ‘A’ and ‘S’ are for asymmetric and symmetric motions, respectively. The black solid curve is for the stable periodic motions while the red-curve for the unstable periodic motions. For the first branch of period-3 motion, two saddle-node bifurcations are observed at $\Omega \approx 9.385$ and $\Omega \approx 28.943$. For the second branch of period-3 motion, four saddle-node bifurcations are observed at $\Omega \approx 4.987, \Omega \approx \hbox {4.943}, \Omega \approx \hbox {5.143}$, and $\Omega \approx 5.452$, respectively. Two of them where $\Omega \approx 4.987$ and $\Omega \approx \hbox {5.143}$ are for jump phenomena. No period-doubling bifurcation is observed in these two branches of period-3 motions. Thus, no higher periodic motions appear. For the first period-3 to period-6 motions, two saddle-node bifurcations for jump phenomena are observed at $\Omega \approx \hbox {3.352}\, and\, \Omega \approx \hbox {3.289}$. Two saddle-node bifurcations for symmetric to asymmetric period-3 motions occur at $\Omega \approx \hbox {2.880}$ and $\Omega \approx 3.180$. Two period-doubling bifurcations for period-3 to period-6 motions appear at $\Omega \approx \hbox {2.916}$ and $\Omega \approx \hbox {3.106}$. Two period-doubling bifurcations for period-6 to period-12 motions emerge at $\Omega \approx \hbox {3.097}$ and $\Omega \approx 2.920$. For the second period-3 to period-6 motions, no saddle-node bifurcations for jump phenomena are observed. Saddle-node bifurcations for symmetric to asymmetric period-3 motions appear at $\Omega \approx \hbox {2.287}$ and $\Omega \approx \hbox {2.714}$. Period-doubling bifurcations occur at $\Omega \approx \hbox {2.289}$ and $\Omega \approx 2.701$ for period-3 to period-6 motions and at $\Omega \approx \hbox {2.290}$ and $\Omega \approx \hbox {2.699}$ for period-6 to period-12 motions.

10.6 Numerical Illustrations

The analytical prediction of period-3 to period-6 motions was predicted analytically for the bifurcation trees of period-3 to period-6 motions. To illustrate complexity of periodic motions in the time-delayed Duffing oscillator , initial conditions from the analytical prediction will be used for numerical simulations of period-3 to period-6 motions in the bifurcation trees, and the corresponding harmonic amplitudes of periodic motions will be presented to show harmonic terms effects on periodic motions. The system parameters in Eq. (10.30) are used. Numerical and analytical results are presented by solid curves and symbols, respectively. The initial time-delay is presented through blue circular symbols. The delay-initial starting and delay-initial finishing points are ‘D.I.S’ and ‘D.I.F,’ respectively.

Fig. 10.3

A stable symmetric period-3 motion for $\Omega =3.3.$ a trajectory, b displacement versus time, c harmonic amplitude spectrum, d harmonic phase spectrum with initial conditions $(x_0 ,\dot{x}_0 )\approx \left( {2.714985, -14.294936} \right) (\alpha _1 = -10.0, \alpha _2 = 5.0, \beta = 10.0, \delta = 0.5, Q_0 = 100.0, \tau = T/4)$

Fig. 10.4

A pair of stable asymmetric period-3 motion for $\Omega =3.15.$ a, b trajectory, c harmonic amplitude spectrum, d harmonic phase spectrum with initial conditions a $(x_0 ,\dot{x}_0 )\approx \left( {3.567230,-10.284055} \right)$ and b $(x_0 ,\dot{x}_0 )\approx \left( {2.899588,9.507185}\right)$ $(\alpha _1 =-10.0, \alpha _2 =5.0, \beta =10.0, \delta =0.5, Q_0 =100.0, \tau =T/4)$

Fig. 10.5

A pair of stable asymmetric period-6 motion for $\Omega =3.10$. a, b trajectory, c harmonic amplitude spectrum, d) harmonic phase spectrum with initial 0 conditions a $(x_0 ,\dot{x}_0 )\approx \left( {4.039509, 19.992432} \right)$ and b $(x_0 ,\dot{x}_0 )~\approx ~(4.044199,-6.483031)$ $(\alpha _1 = -10.0,\alpha _2 = 5.0, \beta =10.0, \delta =0.5, Q_0 =100.0, \tau =T/4)$

Consider a stable symmetric period-3 motion of $\Omega = 3.3$, and the initial condition $(x_0 ,\dot{x}_0 )\approx \left( {2.714985, -14.294936}\right)$ is computed from the analytical prediction. Trajectory and displacement for such a simple symmetric period-3 motion are presented in Fig. 10.3a, b, respectively. The initial time-delay is presented by green symbols. The numerical solution of the stable period-3 motion is presented by solid curves, and the analytical prediction is depicted by red symbols. The corresponding harmonic amplitudes and phases are presented in Fig. 10.3c, d, respectively. The harmonic terms $A_{n/3} = 0 (n = 0,2,4,6,\ldots )$. The main harmonic amplitudes are $A_{1/3} = 1.1264, A_1 = 2.7333, A_{5/3} = 0.4010, A_{7/3} = 2.0006, A_3 = 0.3755, A_{11/3} {=} 0.0621, A_{13/3} {=} {0.2879}, A_5 {=} {0.0300}, A_{17/3} {=} {0.1362}, A_{19/3} {=}{0.0607}, A_7 = {0.0288}, A_{23/3} = {0.0288}, A_{25/3} = \hbox {8.3549e-3}$, and $A_9 = {0.0119}$. Other harmonic amplitudes lie in $A_{(2l-1)/3} \in (10^{-15}, 10^{-3})$ ($l = 15, 16,\cdots , 80)$, and $\hbox {6.2469e-15}$. For such a period-3 motion, one can use 150 harmonic terms to approximate exact solution.

Consider a pair of asymmetric period-1 motions at $\Omega = 3.15$, as shown in Fig. 10.4. The initial conditions are obtained from the analytical prediction. $x_0 \approx 3.567230$ and $\dot{x}_0 \approx -10.284055$ are for the asymmetric period-3 motion in Fig. 10.4a and $x_0 \approx 2.899588$ and $\dot{x}_0 \approx 9.507185$ are for the asymmetric period-3 motion in Fig. 10.4b. The harmonic amplitudes and phases are presented in Fig. 10.3c, d, respectively. The center of the trajectory is far away from the origin compared to the previous symmetric period-3 motion. That is, $a_0^{black} = -a_0^{blue} = A_0 =0.0220$.

The main harmonic amplitudes for the two asymmetric period-3 motions are $A_{1/3} \approx 1.1178, A_{2/3} \approx 0.0161, A_1 \approx 2.7884, A_{4/3} \approx 0.0625, A_{5/3} \approx 0.3811, A_2 \approx 0.1265, A_{7/3} {\approx } 1.5774, A_{8/3} {\approx } 0.4019, A_3 \approx 0.6085, A_{10/3} \approx 0.0360, A_{11/3} \approx 0.0561, A_4 \approx 0.0560, A_{13/3} \approx 0.2871, A_{14/3} {\approx } 0.0725, A_5 {\approx } 0.0738, A_{16/3} {\approx } 0.0131, A_{17/3} \approx 0.0820, A_6 {\approx } 0.0542, A_{19/3} {\approx } 0.0737, A_{20/3} {\approx } 0.0253, A_7 \approx 0.0185, A_{22/3} \approx 0.0149, A_{23/3} \approx 0.0241, A_8 \approx 0.0164, A_{25/3} \approx 0.0120$. Other harmonic amplitudes lie in $A_{l/3} \in (10^{-14}, 10^{-3})$ ($l=26,27,\cdots , 150)$ and $A_{50} \approx \hbox {7.2626e-14}$. The two asymmetric period-3 motions need about 150 harmonic terms in the finite Fourier series for an approximate analytical expression. The first and third harmonic terms play very important roles on such symmetric period-3 motions. Because harmonic amplitude of even terms is relatively small, such harmonic terms make the two asymmetric period-3 motions be close to asymmetric period-3 motions. In addition, harmonic phase distribution varying with harmonic orders is clearly presented. The gray circular symbols are for the harmonic phases of the upper asymmetric period-3 motion and the red symbols are for the harmonic phases of the lower asymmetric period-3 motion. The harmonic phase relations between the two asymmetric period-3 motions are $\varphi _{k/(2^{l}m)}^{black} =\bmod (\varphi _{k/(2^{l}m)}^{blue} +((m+2r)k/(2^{l}m)+1))\pi ,2\pi )$ for $l = 0, m = 3, r = 1$ and $t_0 = rT$ with $r\in \{0, 1,\cdots , 2^{l}m-1\}.$

Consider a pair of asymmetric period-6 motions at $\Omega =3.10$, as shown in Fig. 10.5. The initial conditions are obtained from the analytical prediction. $x_0 \approx {\begin{array}{l} {4.039509} \end{array} }$and $\dot{x}_0 \approx 19.992432$ are for the asymmetric period-6 motion in Fig. 10.5a and $x_0 \approx 4.044199$ and $\dot{x}_0 \approx -6.483031$ are for the asymmetric period-6 motion in Fig. 10.5b. The harmonic amplitudes and phases are presented in Fig. 10.5c, d, respectively. The center of the trajectory is far away from the origin compared to the previous asymmetric period-3 motion. That is, $a_0^{black} =-a_0^{blue} =A_0 =0.0319$. The main harmonic amplitudes for the two asymmetric period-1 motions are $A_{1/6} \approx {0.0131,}\, A_{1/3} \approx {1.0622,}\, A_{1/2} \approx {0.0160,}\, A_{2/3} \approx {0.0646,}\,A_{5/6} \approx \hbox {3.7917e-3},\, A_1 {\approx } {2.6545,}\, A_{7/6} {\approx } \hbox {6.2608e-4,}\, A_{4/3} {\approx } {0.0345,}\, A_{3/2} \approx \hbox {1.8623e-3,}\, A_{5/3} \approx {0.3432,}\, A_{11/6} \approx \hbox {7.8357e-3,}\,\, A_2 \approx {0.0910,}\, A_{13/6} \approx {0.0139,}\, A_{7/3} \,{\approx }\, {1.2285,}\,\, A_{5/2}\approx {0.0305,}\, A_{8/3} \approx {0.2763,}\, A_{17/6} \approx {0.0124,}\, A_3 \approx {1.0138,}\, A_{19/6} \approx \hbox {7.2666e-3,}\, A_{10/3} \approx {0.0509,}\, A_{7/2} \approx \hbox {3.1323e-4,}\,\, A_{11/3} \approx {0.0866,}\,\, A_{23/6} \approx \hbox {1.6868e-3,}\, A_4 \approx {0.0.0280,} \text {and}\, A_{25/6} \approx \hbox {3.7414e-3},\, A_{13/3} \approx {0.0.2680},\,\, A_{9/2} \approx \hbox {6.9915e-3},\,\, A_{14/3} \approx {0.0667},\, A_{29/6} \approx \text{2.9448e-3, }\, A_{5} \approx {0.1699},\, A_{31/6} \approx \text{8.1422e-4, }\, A_{16/3} \approx {0.0.2680},\, A_{11/2} \approx \text{7.9530e-4, }\, A_{17/3} \approx {0.0433},\, A_{35/6} \approx \text{2.6005e-3, }\, A_{6} \approx {0.0306}, A_{37/6} \approx \text{2.8367e-3, } A_{19/3} \approx {0.1016},\, A_{13/2} \approx \text{3.0073e-3, } A_{20/3} \approx {0.0285},\, A_{41/6} \approx \text{9.4470e-4, }\,A_{7} \approx 0.0398,\, A_{43/6} \approx \text{1.0742e-3, } A_{22/3} \approx \text{9.9107e-3 }, A_{15/2} \approx \text{5.8637e-3, } A_{23/3} \approx 0.0217, A_{47/6} \approx \text{1.3083e-3, }\, A_{8} \approx {0.0139},\, A_{49/6} \approx \text{8.0876e-4, }\, A_{25/3} \approx {0.0264}$. Other harmonic amplitudes lie in $A_{l/6} \in (10^{-14},10^{-3})$ ($l=51, 52, \cdots ,300)$, and $A_{50} \approx \hbox {2.4131e-13.}$ The two asymmetric period-6 motions need about 300 harmonic terms in the finite Fourier series for an approximate analytical expression. The first and third harmonic terms play very important roles on such asymmetric period-6 motions. Because harmonic amplitude of even terms is relatively small, such harmonic terms make the two asymmetric period-6 motions be close to asymmetric period-3 motions. In addition, harmonic phase distribution varying with harmonic orders is clearly presented. The gray circular symbols are for the harmonic phases of the upper asymmetric period-6 motion, and the blue symbols are for the harmonic phases of the lower asymmetric period-6 motion. The harmonic phase relations between the two asymmetric period-6 motions are for $\varphi _{k/(2^{l}m)}^{blue} =\bmod (\varphi _{k/(2^{l}m)}^{black} +((m+2r)k/(2^{l}m) (2^{l}m)+1))\pi ,2\pi )$ for $l=1, m=3, r=5$ and $t_0 =rT$ with $r\in \{0, 1, \cdots , 2^{l}m-1\}$.

10.7 Conclusions

The symmetric and asymmetric period-3 motions in the time-delayed, double-well Duffing oscillator were predicted through the semi-analytical method. The semi-analytical method is based on the implicit mappings constructed by discretization of the corresponding differential equation. The corresponding stability and bifurcation analysis were studied. From the analytical predictions, numerical simulations of complex periodic motions were presented, and the harmonic amplitudes and phases were presented. The harmonic effects on period-3 motions can be clearly observed.