1 Introduction

A multi-stage gear system is used in a variety of applications in vehicles, ships, aerospace, etc. The vibration and noise generated during the gear operation process can cause mechanical failure, shorten the life of devices and cause damage or injury to personnel [1]. Therefore, the mechanism of vibration and noise during the gear system needs to be analyzed. The time-varying mesh stiffness is one of the main causes of vibration and noise. The stiffness of the different stages of the multi-stage gear system interacts with each other through the phase angle and the tooth number ratio of the intermediate shaft, which are influencing factors that cannot be ignored. To differentiate from gear ratios, this paper uses coaxial teeth ratio to represent the tooth number ratios of the two gears on the intermediate shaft between the different stages.

The mesh phasing as an influencing factor is often achieved by affecting the mesh stiffness in a gear system. For the study of the mesh phasing, Kahraman [2] established a dynamic model of a multi-mesh gear system containing idlers and found that there was a suppression effect on the vibration of the system at specific frequencies at different mesh phasing. Lin [3] derived the range of stable and unstable domains for a two-stage gear system and considered the effect of mesh phasing and contact ratio on the mesh stiffness by means of the Fourier series. Parker [4] found that mesh phasing suppresses harmonics at specific mesh frequencies for a planetary gear system, which lead to a series of studies on mesh phasing in a planetary gear system. Parker [5] next derived the mesh phasing difference for a planetary gear system, laying the foundation for the study of mesh phasing for a planetary gear system. Al-shyyab [6, 7] analyzed the nonlinear vibration characteristics of a two-stage gear system based on the harmonic balance method, simply considering the effect of the mesh phasing on the period-one motion, but with coaxial teeth ratio 1 which corresponds to an idler system. Gill-Jeong [8] used the mesh phasing in a single-stage gear pair to smooth out the time-varying mesh stiffness by adding another pair of gears with half-pitch phasing, thus achieving vibration and noise reduction. Guo [9] studied the mesh phasing relationship for general compound planetary gears, extending on the mesh phasing relationship. Wang [10] found that the factors influencing the mesh phasing are the number of teeth, the number of planets, and their greatest common divisor of a planetary gear system, and mainly found that the mesh phasing changes the vibration mode of the system. Kang [11] developed a test rig for a double-helical gear, based on experimental data showing that the mesh phasing is the most key parameter impacting the dynamic response. Vavuz [12] analyzed the nonlinear characteristics of the two-stage gear system based on the harmonic balance method, where the effect of the mesh phasing was considered. Brecher [13] tested a two-stage gearbox for dynamic noise and confirmed that the effect of the mesh phasing angle of the intermediate shaft could not be ignored. Peng [14, 15] proposed a fault diagnosis method for a planetary gear system, which focuses on distinguishing the type of fault and identifying the faulty gear by transmission error and mesh phasing. Wang [16] established a dynamical model of a planetary gear system and proposed a spectral analysis method based on the mesh phasing. Sanchez-Espiga [17, 18] considered the influence of the mesh phasing of a planetary gear system and made the system load balance by adjusting the mesh phasing. Wang [19, 20] obtained the rule that the mesh phasing affects the vibration of a planetary gear system, and the number of teeth and the mesh phasing can be used to determine the vibration mode of the system.

Through the study of mesh phasing in a gear system, mesh phasing is used predominantly in a single-stage gear pair, a planetary gear system, and a multi-stage gear system. The single-stage gear pair achieves control of the mesh phasing by means of a double-row gear. Theoretical and experimental studies have confirmed the effectiveness of mesh phasing on vibration suppression. Due to the complex structure of planetary gear trains, the process has evolved from the discovery of the effects of mesh phasing to the derivation of mesh phasing relationships and ultimately to the development of rules for the effects of mesh phasing and their application in fault diagnosis [21, 22]. Most scholars in the study of multi-stage gear system will assume an intermediate shaft teeth ratio 1, which is consistent with idler system and reduces the complexity of the mesh phasing. In terms of experimentation, it was demonstrated that the influence of the intermediate shaft mesh phasing could not be ignored. The coupling mesh stiffness of the multi-stage gear system is importantly related to the mesh phasing and coaxial teeth ratio. Thus, the dynamic model of multi-stage gear that considers mesh phasing and coaxial teeth ratio needs to be studied.

Vinayak [23] developed the dynamic model of multi-mesh gear based on the concentrated mass method, and this model framework has been universally valid. Eritenel [24] considered the multi-degree-of-freedom, multi-mesh gear transmission model in which three vibration directions were added in addition to the mesh line direction, allowing for a more detailed analysis of the vibration characteristics. Wang [25] established the dynamic model of the multi-stage system with crack fault, whose crack stiffness was calculated using the potential energy method. Li [26] established the dynamic model of a two-stage parallel shaft transmission system and analyzed the system dynamic in terms of speed, damping, and accuracy, but did not consider the effect of its nonlinear behavior and mesh phasing. He [27] investigated the effect of gear eccentricity on the time-varying mesh stiffness and dynamic behavior of the two-stage gear system. Lu [28] established a coupled dynamic model of a multi-stage gear with a box and explored the effect of mesh frequency. The multi-stage gear system models are all based on a concentrated mass model [29], focusing on the calculation of its time-varying mesh stiffness and the factors which considers in the model.

The time-varying mesh stiffness is related to the mesh phasing, contact ratio, speed, and coaxial teeth ratio, and it is particularly essential to develop a suitable time-varying mesh stiffness model to include these parameters [30]. The stiffness can be approximated in the form of a Fourier series [31], which can simply reflect the nonlinear characteristics of the system. The potential energy method has recently been modified and improved to use in calculating time-varying stiffnesses [32, 33]. With the development of science and technology, the use of the finite element method to calculate stiffness is considered accurate and thus used for the verification of the analytical method [34]. In order to calculate quickly and to take into account the influence parameters, the potential energy method is chosen to solve the time-varying mesh stiffness and is verified using finite element method.

In summary, mesh phasing has been studied more in single-stage gear pairs and a planetary gear system. In a multi-stage gearing system, only the case of the intermediate shaft teeth ratio 1 is considered, ignoring the coupling effect of different intermediate shaft teeth ratios. However, the coaxial teeth ratio not equal to 1 is more widely used in applications. In the current work, the time-varying mesh stiffness model considering the mesh phasing is established by Lagrange equation and derived by dimensionless method. Based on the theory of periodic function and the meshing principle of multistage gear transmission system, the relationship between the mesh phasing and the coaxial teeth ratio is derived. It is found that the coaxial teeth ratio reduces the periodic variation range of mesh phasing. Furthermore, the phase relationship is verified using the rigid-flexible coupling model. A two-stage gear dynamic model based on the concentrated mass method is used to study the effects of mesh phasing and coaxial teeth ratio on the vibration characteristics. The nonlinear frequency response is analyzed in terms of the mesh phasing. The mesh phasing characteristics of the chaotic and stable motion zones are compared. Based on the relationship between the mesh phasing and the coaxial teeth ratio, the variation law of the system vibration characteristics with the mesh phasing and the coaxial teeth ratio is revealed, which provides a reliable basis for the dynamic design of a multi-stage gear system.

Based on the theory of periodic function and the meshing principle of multistage gear transmission system, the coupling relationship between the mesh phasing angle and the coaxial teeth ratio is derived. A dynamic model of a two-stage parallel gear train with time-varying meshing stiffness is established.

2 Dynamic model of two-stage gear system considering coupling relationship between mesh phasing angle and coaxial teeth ratio

The mesh phasing relationship in the multi-stage gear system is generally represented by the two mesh phasing angles of the intermediate shaft. Adjustment is carried out in the actual reducer by the position of the key or spline in the gear connection. In previous studies [3, 6], no attention has been paid to the relationship between the mesh phasing angle and the coaxial teeth ratio. This section derives the relationship between the mesh phasing angle and the coaxial teeth ratio, and develops a dynamic model of a two-stage gear transmission system.

2.1 The coupling relationship between the mesh phasing angle and coaxial teeth ratio

In multi-stage gear system, the mesh stiffness of each stage is essentially similar to that of a gear pair. In the two-stage parallel shaft spur gearing system, the coupling stiffness of the first and second stages is the system stiffness. The mesh stiffness of each phase is approximated by a periodic rectangular wave. Figure 1 shows the shape of the mesh stiffness for two different periods. The mesh stiffness of the first-stage gear has a period of \(T_{1}\), and the mesh stiffness of the second-stage gear has a period of \(T_{2}\). The alternating single and double pairs of the spur gear mesh stiffness can be clearly seen in Fig. 1a. From Fig. 1b, the quantitative relationship between the contact ratio \(\varepsilon\) and the mesh period \(T_{2}\) can be found. Since the number of teeth is a positive integer, according to Fig. 1c, the system stiffness period \(T_{12}\) can be obtained as the least common multiple of the relationship between \(T_{1}\) and \(T_{2}\). There is a time-independent phase difference between the two mesh stiffnesses, and different phase differences correspond to different coupling stiffnesses of the system. The phase difference between \(k_{12} (t)\) and \(k_{12}^{\prime } (t)\) is \(\varphi_{2} T_{2}\)

Fig. 1
figure 1

Mesh phasing relationship of mesh stiffness. a Mesh stiffness of the first stage, b Mesh stiffness of the second stage, c Coupling stiffness at mesh phasing \(\varphi_{2} = 0\), d Coupling stiffness at mesh phasing \(\varphi_{2} = 0.2\)

Full size image

The mesh phasing (\(\varphi_{1}\) and \(\varphi_{2}\)) of the two-stage gear transmission is defined as the phase angle of the initial meshing position of the first stage and the second stage. According to the meshing principle, the mesh phasing changes in the period of 0–1. When \(\varphi_{2} = 0\) and \(\varphi_{2} = 1\), it means that the initial meshing positions of the second stage are one tooth different. So, they're the same. According to the circles in Fig. 1c and d, although there is a certain time difference, the coupling stiffnesses \(k_{12} (t)\) and \(k_{12}^{\prime } (t)\) are revealed to be the same. Although mesh phasing \(\varphi_{2}\) is less than 1, the two coupling stiffnesses \(k_{12} (t)\) and \(k_{12}^{\prime } (t)\) correspond to the same mesh state of system. In view of this phenomenon, it is found that when the coaxial teeth ratio is not equal to 1, the periodic range of mesh phasing will be reduced.

According to [31], the time-varying mesh stiffness is approximated by the Fourier series based on a two-stage parallel shaft gearing system as follows.

$$ \begin{aligned} k_{1} (t) & = k_{1}^{(0)} + \sum\limits_{s = 1}^{S} {k_{1}^{(s)} \cos (2\pi s\Omega_{1} t - 2\pi \varphi_{1s} )} \\ k_{2} (t) & = k_{2}^{(0)} + \sum\limits_{s = 1}^{S} {k_{2}^{(s)} \cos (2\pi s\Omega_{2} t - 2\pi \varphi_{2s} )} \\ \end{aligned} $$
(1)

where \(\Omega_{1} ,\Omega_{2}\) is the mesh frequency of the first and second stages \(\Omega_{1} = R\Omega_{2}\), \(R = {{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }}\).\(\varphi_{1} ,\varphi_{2}\) is the mathematical representation of the mesh phasing, and the range is from 0 to 1.

System stiffness is regarded as the whole of first-stage stiffness and second-stage stiffness. The system stiffness (\(\varphi_{1} = 0\), \(\varphi_{2} = 0\)) corresponds to Fig. 1c and the system stiffness (\(\varphi_{1} = 0\), \(\varphi_{2} = 0.2\)) corresponds to Fig. 1d, where there is a phase difference \(\varphi_{2} T_{2}\). According to the circles in Fig. 1c and d, the two stiffness curves in Fig. 1c and the two stiffness curves in Fig. 1d are in the same state at the circle. Since the steady state of gear operation is periodic, it indicates that the stiffness states represented by the stiffness curves of Fig. 1c and d are the same. This means that there is a quantitative relationship between the coaxial teeth ratio and the mesh phasing.

The mesh period of the first and second stages is obtained from the speed of the intermediate shaft.

$$ \left\{ {\begin{array}{*{20}l} {T_{1} = \frac{60}{{n_{2} z_{2} }}} \hfill \\ {T_{2} = \frac{60}{{n_{3} z_{3} }}} \hfill \\ \end{array} } \right. $$
(2)

where \(n_{2} ,n_{3}\) represents the speed of the gear 2 and gear 3 and \(n_{2} = n_{3}\), \(z_{2} ,z_{3}\) represents the number of teeth of gear 2 and gear 3. Since the speed of the two intermediate gears is the same, the mesh period is related to the teeth number of the two gears. Total period of the two-stage gear system.

$$ T_{12} = \frac{{\left[ {z_{2} ,z_{3} } \right]}}{{n_{2} z_{2} z_{3} }} $$
(3)

where \(\left[ , \right]\) is the symbol for solving the lowest common multiple of two integers. As the number of teeth is a positive integer, different mesh phasing angles correspond to different mesh states when mesh stiffness of two stages are coupled. Based on Eqs. (1)–(3), it is deduced that:

$$ \Phi_{12} = \frac{{(z_{2} ,z_{3} )}}{{z_{2} z_{3} }} $$
(4)

where \((,)\) is the symbol for solving the greatest common divisor of two integers. In this paper, \(\Phi_{12}\) is defined as a characteristic quantity of the relationship between the coaxial teeth ratio and the mesh phasing of the two-stage gear system. The periodic range \(\Phi_{1} ,\Phi_{2}\) of \(\varphi_{1} ,\varphi_{2}\) can be given by Eq. (4). For the mesh stiffness \(k_{1} (t),k_{2} (t)\) of a two-stage gear train, \(\varphi_{1} = 0,\varphi_{2} \in (0,\Phi_{2} )\) or \(\varphi_{1} \in (0,\Phi_{1} ) = 0,\varphi_{2} = 0\) describes the coupling state of all mesh phasing to the stiffness. All calculations in this paper are in the form of \(\varphi_{1} = 0,\varphi_{2} \in (0,\Phi_{2} )\).

$$ \begin{array}{*{20}c} {\Phi_{1} = \Phi_{12} z_{2} } & {\Phi_{2} = \Phi_{12} z_{3} } \\ \end{array} $$
(5)

In order to verify the correctness of Eq. (4), the dynamic equations were solved using ode45, and the coaxial teeth ratio and mesh phasing relationships are shown in Table 1. In order to compare their mesh state are the same, the root mean square (RMS) values of the first and second stage DTE \(q_{1}^{(\text{rms})}\) and \(q_{2}^{(\text{rms})}\) are chosen as the results shown in Fig. 2.

Table 1 Coupling relationship between mesh phasing angle and different coaxial teeth ratios
Full size table
Fig. 2
figure 2

Effect of mesh phasing on the vibration in different coaxial teeth ratios. a \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = 1\), b \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = 2\), c \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = 3\)

Full size image

When \(R = {{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = }}} \right. \kern-0pt} {z_{3} = }}{{20} \mathord{\left/ {\vphantom {{20} {20}}} \right. \kern-0pt} {20}}\) and \(\Phi_{2} = 1\), \(q_{1}^{(\text{rms})}\) and \(q_{2}^{(\text{rms})}\) change in \(\varphi_{2} \in (0,1.0)\). when \(R = {{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = }}} \right. \kern-0pt} {z_{3} = }}{{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}\) and \(\Phi_{2} = 0.5\), \(q_{1}^{(\text{rms})}\) and \(q_{2}^{(\text{rms})}\) change in \(\varphi_{2} \in (0,0.5)\) the same as in \(\varphi_{2} \in (0.5,1)\). When \(R = {{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = }}} \right. \kern-0pt} {z_{3} = }}{{60} \mathord{\left/ {\vphantom {{60} {20}}} \right. \kern-0pt} {20}}\) and \(\Phi_{2} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}\), \(q_{1}^{(\text{rms})}\) and \(q_{2}^{(\text{rms})}\) change in \(\varphi_{2} \in (0,{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3})\) the same as in \(\varphi_{2} \in ({1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3},{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3})\) and \(\varphi_{2} \in ({2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3},1)\). Thus, the paper finds that the coaxial teeth ratio will affect the periodic range of the mesh phasing, which is smaller when the numbers of teeth of the intermediate shaft are coprime. Meanwhile, the relationship (Eq. (4)) between the coaxial tooth ratio and the mesh phasing angle is verified.

2.2 Establishment of dynamic model

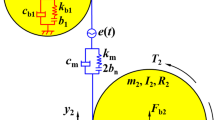
The gear ratio of each stage, coaxial teeth ratio, and their mesh phasing angle led to differences in vibration characteristics in the multi-stage gear system. In order to describe the nonlinear dynamic behavior in the two-stage gear system, its dynamic model is shown in Fig. 3. This includes the basic parameters of the gear system. For example, the inertia of the four gears \(J_{i}\) (i = 1,2,3,4), number of teeth \(z_{i}\) (i = 1,2,3,4), Input and output torque \(To_{1}\), \(To_{2}\) for stable system operation. The dynamic parameters of the gear are mainly considered in terms of the time-varying mesh stiffness \(k_{1} (t)\) and \(k_{2} (t)\), the mesh damping \(c_{1}\) and \(c_{2}\), the nonlinear backlash \(2b_{1}\) and \(2b_{2}\). In the two-stage gear transmission system, the intermediate shaft plays the role of connecting the first and second stage, so this paper considers the torsional stiffness \(k_{n}\) and torsional damping \(c_{n}\) of the intermediate shaft. The equations of motion for this 4-degree-of-freedom (4-DOF) system are shown in Eq. (6).

$$ \left\{ {\begin{array}{*{20}l} {J_{1} \ddot{\theta }_{1} + r_{{b1}} [c_{1} (r_{{b1}} \dot{\theta }_{1} - r_{{b2}} \dot{\theta }_{2} + \dot{\tilde{e}}_{1} ) + k_{1} (t)f_{1} (r_{{b1}} \theta _{1} - r_{{b2}} \theta _{2} + \tilde{e}_{1} )] = To_{1} } \hfill \\ {J_{2} \ddot{\theta }_{2} - r_{{b2}} [c_{1} (r_{{b1}} \dot{\theta }_{1} - r_{{b2}} \dot{\theta }_{2} + \dot{\tilde{e}}_{1} ) + k_{1} (t)f_{1} (r_{{b1}} \theta _{1} - r_{{b2}} \theta _{2} + \tilde{e}_{1} )] + c_{n} (\dot{\theta }_{2} - \dot{\theta }_{3} ) + k_{n} (\theta _{2} - \theta _{3} ) = 0} \hfill \\ {J_{3} \ddot{\theta }_{3} + r_{{b3}} [c_{2} (r_{{b3}} \dot{\theta }_{3} - r_{{b4}} \dot{\theta }_{4} + \dot{\tilde{e}}_{2} ) + k_{2} (t)f_{2} (r_{{b3}} \theta _{3} - r_{{b4}} \theta _{4} + \tilde{e}_{2} )] - c_{n} (\dot{\theta }_{2} - \dot{\theta }_{3} ) - k_{n} (\theta _{2} - \theta _{3} ) = 0} \hfill \\ {J_{4} \ddot{\theta }_{4} - r_{{b4}} [c_{2} (r_{{b3}} \dot{\theta }_{3} - r_{{b4}} \dot{\theta }_{4} + \dot{\tilde{e}}_{2} ) + k_{2} (t)f_{2} (r_{{b3}} \theta _{3} - r_{{b4}} \theta _{4} + \tilde{e}_{2} )] = - To_{2} } \hfill \\ \end{array} } \right.$$
(6)
Fig. 3
figure 3

Dynamic model of a two-stage gear system

Full size image

To reduce computational complexity and accurately reflect model characteristics, Eq. (6) is converted to a 3-DOF equation using Eq. (7).

$$ \left\{ \begin{gathered} u_{1} = r_{b1} \theta_{1} - r_{b2} \theta_{2} - \tilde{e}_{1} (t) \hfill \\ u_{2} = r_{b3} \theta_{3} - r_{b4} \theta_{4} - \tilde{e}_{2} (t) \hfill \\ u_{3} = {\raise0.5ex\hbox{$\scriptstyle {(r_{b2} + r_{b3} )}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}} \cdot (\theta_{2} - \theta_{3} ) \hfill \\ \end{gathered} \right. $$
(7)

\(u_{1}\) and \(u_{2}\) is generally defined as transmission error. \(u_{3}\) is defined in this paper as the vibration displacement of intermediate shaft. The derived equation is as in Eq. (8).

$$ \left\{ \begin{gathered} m_{1} \ddot{u}_{1} + c_{1} \dot{u}_{1} + k_{1} (t)f_{1} (u_{1} ) = \tilde{F}_{1} + m_{1} \frac{{r_{b2} r}}{{J_{2} }}(c_{3} \dot{u}_{3} + k_{3} u_{3} ) + m_{1} \ddot{\tilde{e}}_{1} (t) \hfill \\ m_{2} \ddot{u}_{2} + c_{2} \dot{u}_{2} + k_{2} (t)f_{2} (u_{2} ) = \tilde{F}_{2} + m_{2} \frac{{r_{b3} r}}{{J_{3} }}(c_{3} \dot{u}_{3} + k_{3} u_{3} ) + m_{2} \ddot{\tilde{e}}_{2} (t) \hfill \\ m_{3} \ddot{u}_{3} + c_{3} \dot{u}_{3} + k_{3} u_{3} = m_{3} \frac{{r_{b2} r}}{{J_{2} }}(c_{1} \dot{u}_{1} + k_{1} (t)f_{1} (u_{1} )) + m_{3} \frac{{r_{b3} r}}{{J_{3} }}(c_{2} \dot{u}_{2} + k_{2} (t)f_{2} (u_{2} )) \hfill \\ \end{gathered} \right. $$
(8)

where \(m_{1} = \frac{{J_{1} J_{23} }}{{J_{1} r_{b2}^{2} + J_{23} r_{b1}^{2} }}\), \(m_{2} = \frac{{J_{23} J_{4} }}{{J_{23} r_{b4}^{2} + J_{4} r_{b3}^{2} }}\), \(m_{3} = \frac{{J_{2} J_{3} }}{{(J_{2} + J_{3} )r^{2} }}\), \(c_{3} = \frac{{c_{n} }}{{r^{2} }}\), \(k_{3} = \frac{{k_{n} }}{{r^{2} }}\),\(\tilde{F}_{1} = m_{1} \frac{{r_{rb1} }}{{J_{1} }}To_{1}\), \(\tilde{F}_{2} = m_{2} \frac{{r_{rb4} }}{{J_{4} }}To_{2}\), \(r = \frac{{(r_{b2} + r_{b3} )}}{2}\), \(m_{13} = \frac{{J_{2} }}{{r_{b2} r}}\), \(m_{23} = \frac{{J_{3} }}{{r_{b3} r}}\).

\(f_{1} ,f_{2}\) is a non-linear gear clearance function, which is mathematically defined as:

$$ f_{i} = \left\{ \begin{gathered} \begin{array}{*{20}c} {u_{i} - b_{i} } & {u_{i} > b_{i} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} 0 & { - b_{i} \le u_{i} \le b_{i} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {u_{i} + b_{i} } & {u_{i} < - b_{i} } \\ \end{array} \hfill \\ \end{gathered} \right. $$
(9)

Defining:

$$ \kappa_{1} = \frac{{k_{1} (t)}}{{k_{1m} }}\,\kappa_{2} = \frac{{k_{2} (t)}}{{k_{2m} }}\,\kappa_{3} = \frac{{k_{3} }}{{k_{3} }} $$
$$ \varpi_{11}^{2} = \frac{{k_{1m} }}{{m_{1} }}\,\varpi_{22}^{2} = \frac{{k_{2m} }}{{m_{2} }}\,\varpi_{33}^{2} = \frac{{k_{3} }}{{m_{3} }}\,\varpi_{13}^{2} = \frac{{k_{3} }}{{m_{13} }}\,\varpi_{23}^{2} = \frac{{k_{3} }}{{m_{23} }}\,\varpi_{31}^{2} = \frac{{k_{1m} }}{{m_{13} }}\,\varpi_{32}^{2} = \frac{{k_{2m} }}{{m_{23} }} $$
$$ \zeta_{11} = \frac{{c_{1} }}{{2m_{1} \varpi_{11} }}\,\zeta_{22} = \frac{{c_{2} }}{{2m_{2} \varpi_{22} }}\,\zeta_{33} = \frac{{c_{3} }}{{2m_{3} \varpi_{33} }}\,\zeta_{13} = \frac{{c_{3} }}{{2m_{13} \varpi_{13} }} $$
$$ \zeta_{23} = \frac{{c_{3} }}{{2m_{23} \varpi_{23} }}\,\zeta_{31} = \frac{{c_{1} }}{{2m_{13} \varpi_{31} }}\,\zeta_{32} = \frac{{c_{2} }}{{2m_{23} \varpi_{32} }} $$

In order to obtain a dimensionless equation, it is necessary to define: \(q_{i} = u_{i} /b_{i}\) (i = 1,2,3), \(\tau = \omega_{n} t\), \(\omega_{ij} = {{\varpi_{ij} } \mathord{\left/ {\vphantom {{\varpi_{ij} } {\omega_{n} }}} \right. \kern-0pt} {\omega_{n} }}\), \(F_{i} = {{\tilde{F}_{i} } \mathord{\left/ {\vphantom {{\tilde{F}_{i} } {b_{n} \omega_{n}^{2} }}} \right. \kern-0pt} {b_{n} \omega_{n}^{2} }}\), \(e_{i} = {{\tilde{e}_{i} } \mathord{\left/ {\vphantom {{\tilde{e}_{i} } {b_{n} \omega_{n}^{2} }}} \right. \kern-0pt} {b_{n} \omega_{n}^{2} }}\).Where \(b_{n}\) is the system characteristic length and \(\omega_{n}\) is the system characteristic frequency. The dimensionless equation is shown in Eq. (10).

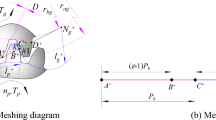
$$ \left\{ {\begin{array}{*{20}l} {\ddot{q}_{1} + 2\zeta _{{11}} \omega _{{11}} \dot{q}_{1} + \omega _{{11}}^{2} \kappa _{1} (\tau )f_{1} (q_{1} ) = F_{1} + 2\zeta _{{13}} \omega _{{13}} \dot{q}_{3} + \omega _{{13}}^{2} \kappa _{3} q_{3} + \ddot{e}_{1} (\tau )} \hfill \\ {\ddot{q}_{2} + 2\zeta _{{22}} \omega _{{22}} \dot{q}_{2} + \omega _{{22}}^{2} \kappa _{2} (\tau )f_{2} (q_{2} ) = F_{2} + 2\zeta _{{23}} \omega _{{23}} \dot{q}_{3} + \omega _{{23}}^{2} \kappa _{3} q_{3} + \ddot{e}_{2} (\tau )} \hfill \\ {\ddot{q}_{3} + 2\zeta _{{33}} \omega _{{33}} \dot{q}_{3} + \omega _{{33}}^{2} \kappa _{3} q_{3} = 2\zeta _{{31}} \omega _{{31}} \dot{q}_{1} + \omega _{{31}}^{2} \kappa _{1} (\tau )f_{1} (q_{1} ) + 2\zeta _{{32}} \omega _{{32}} \dot{q}_{2} + \omega _{{32}}^{2} \kappa _{2} (\tau )f_{2} (q_{2} )} \hfill \\ \end{array} } \right. $$
(10)

The most widely used method for calculating the mesh stiffness of single tooth in previous studies is the potential energy method [33], the geometric model which is shown in Fig. 4. The potential energy method considers four components of energy in a mesh gear pair, Hertzian contact potential energy, bending energy, shear energy and axial compressive energy. According to contact theory [32], the contact stiffness is:

$$ k_{h} = \frac{\pi EL}{{2(1 - \upsilon^{2} )}}\left[ {\ln \frac{{2R_{1} }}{a} + \ln \frac{{2R_{1} }}{a} + \frac{\upsilon }{1 - \upsilon }a\left( {\ln \frac{{2R_{1} }}{a} + \ln \frac{{2R_{2} }}{a}} \right)} \right]^{ - 1} $$
(11)

where \(a = \sqrt {{{4PR} \mathord{\left/ {\vphantom {{4PR} {\pi E}}} \right. \kern-0pt} {\pi E}}}\), P is the load per unit length \({F \mathord{\left/ {\vphantom {F L}} \right. \kern-0pt} L}\). The bending, shear and axial compression stiffnesses can be obtained by derivation [35].

$$ \frac{1}{{k_{b} }} = \int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}}^{\alpha } {\frac{{[\cos \beta (y_{\beta } - y_{1} ) - x_{\beta } \sin \beta ]^{2} }}{{EI_{y1} }}\frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma } + \int\limits_{{\tau_{c} }}^{\beta } {\frac{{[\cos \beta (y_{\beta } - y_{2} ) - x_{\beta } \sin \beta ]^{2} }}{{EI_{y2} }}\frac{{{\text{d}}y_{2} }}{{{\text{d}}\phi }}{\text{d}}\phi } $$
(12)
$$ \frac{1}{{k_{s} }} = \int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}}^{\alpha } {\frac{{1.2\cos^{2} \beta }}{{GA_{y1} }}\frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma } + \int\limits_{{\tau_{c} }}^{\beta } {\frac{{1.2\cos^{2} \beta }}{{GA_{y2} }}\frac{{{\text{d}}y_{2} }}{{{\text{d}}\phi }}{\text{d}}\phi } $$
(13)
$$ \frac{1}{{k_{a} }} = \int\limits_{\pi /2}^{\alpha } {\frac{{\sin n^{2} \beta }}{{EA_{y1} }}\frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma } + \int\limits_{{\tau_{c} }}^{\beta } {\frac{{\sin^{2} \beta }}{{EA_{y2} }}\frac{{{\text{d}}y_{2} }}{{{\text{d}}\phi }}{\text{d}}\phi } $$
(14)
Fig. 4
figure 4

Geometric model of the single tooth stiffness

Full size image

When calculating the stiffness, it is necessary to consider the influence of the fillet-foundation, in which the radius of the inner hole plays an important role. According to the fillet-foundation stiffness calculation method [36], the interaction between the two tooth regions is taken into account. The fillet-foundation stiffness of a single tooth and the mutual influence stiffness of two tooth regions are as follows:

$$ \frac{1}{{k_{f11} }} = \frac{{\cos^{2} \beta_{1} }}{EL}\left[ {L_{1}^{*} \left( {\frac{{u_{f1} }}{{S_{f} }}} \right)^{2} + M_{1}^{*} \left( {\frac{{u_{f1} }}{{S_{f} }}} \right) + P_{1}^{*} (1 + Q_{1}^{*} \tan^{2} \beta_{1} )} \right] $$
(15)
$$ \frac{1}{{k_{f21} }} = \frac{{\cos \beta_{1} \cos \beta_{2} }}{EL}\left[ \begin{gathered} L_{2}^{*} \left( {\frac{{u_{f1} u_{f1} }}{{S_{f}^{2} }}} \right) + (\tan \beta_{2} M_{2}^{*} + P_{2}^{*} )\left( {\frac{{u_{f1} }}{{S_{f} }}} \right) + (\tan \beta_{1} Q_{2}^{*} + R_{2}^{*} )\left( {\frac{{u_{f2} }}{{S_{f} }}} \right) + \hfill \\ (\tan \beta_{1} S_{2}^{*} + T_{2}^{*} )\tan \beta_{2} + U_{2}^{*} \tan \beta_{1} + V_{2}^{*} \hfill \\ \end{gathered} \right] $$
(16)
$$ \frac{1}{{k_{f12} }} = \frac{{\cos \beta_{1} \cos \beta_{2} }}{EL}\left[ \begin{gathered} L_{3}^{*} \left( {\frac{{u_{f1} u_{f2} }}{{S_{f}^{2} }}} \right) + (\tan \beta_{1} M_{3}^{*} + P_{3}^{*} )\left( {\frac{{u_{f2} }}{{S_{f} }}} \right) + (\tan \beta_{2} Q_{3}^{*} + R_{3}^{*} )\left( {\frac{{u_{f1} }}{{S_{f} }}} \right) + \hfill \\ (\tan \beta_{2} S_{3}^{*} + T_{3}^{*} )\tan \beta_{1} + U_{3}^{*} \tan \beta_{2} + V_{3}^{*} \hfill \\ \end{gathered} \right] $$
(17)

\(k_{f11}\) represents fillet-foundation stiffness of gear tooth 1. \(k_{fij}\) represents the equivalent stiffness in gear tooth i due to the load on gear tooth j. \(k_{fi}\) represents the total fillet foundation stiffness the of gear tooth i considering the stiffness of neighboring teeth.

$$ \left\{ {\begin{array}{*{20}l} {\frac{1}{{k_{f1} }} = \frac{1}{{k_{f11} }} + \frac{1}{{k_{f12} }}} \hfill \\ {\frac{1}{{k_{f2} }} = \frac{1}{{k_{f22} }} + \frac{1}{{k_{f21} }}} \hfill \\ \end{array} } \right. $$
(18)

Finally, the mesh stiffness of the gear pair is calculated as:

$$ \frac{1}{{k_{e} }} = \frac{1}{{k_{h} }} + \frac{1}{{k_{b}^{p} }} + \frac{1}{{k_{s}^{p} }} + \frac{1}{{k_{a}^{p} }} + \frac{1}{{k_{f}^{p} }} + \frac{1}{{k_{b}^{w} }} + \frac{1}{{k_{s}^{w} }} + \frac{1}{{k_{a}^{w} }} + \frac{1}{{k_{f}^{w} }} $$
(19)

where the superscript p and w represent a pair of pinion and wheel. From Eqs. (12) to (19), the value of the mesh stiffness depends on the mesh position parameter \(\phi\), which can correspond to the rotation angle of the gear 1, ultimately transforming the mesh stiffness into a function of time.

3 Validation

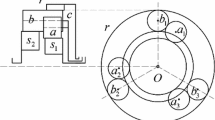
In order to verify the coupling relationship between the coaxial teeth ratio and the mesh phasing angle, this paper uses a simulation test model based on Adams software to carry out a dynamic analysis. The two-stage parallel shaft gear train of \(R = {{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = }}} \right. \kern-0pt} {z_{3} = }}{{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}\) was selected for simulation and the simulation test model is shown in Fig. 5.

Fig. 5
figure 5

Simulation test model of a two-stage gear system

Full size image

In the Adams software, the mesh phasing \(\varphi_{2}\) is adjusted by changing the initial meshing positions of gear 3 and gear 4 while not changing the gear 1 and gear 2 (\(\varphi_{1} = 0\)). It can be clearly seen in Fig. 5 that the meshing positions of gear 3 and gear 4 are different for \(\varphi_{2} = 0\) and \(\varphi_{2} = 0.25\). The results of the simulation test model are shown in Fig. 6. Under different mesh phasing \(\varphi_{2} = 0\),\(\varphi_{2} = 0.25\), and \(\varphi_{2} = 0.5\), the amplitude of the first stage mesh force \(F_{{\text{m}}1}\) is different. Since the mesh phasing \(\varphi_{2}\) of the second stage is changed, the amplitude and phase of the second stage mesh force \(F_{{\text{m}}2}\) change and offset in the time domain. Using mesh phasing step size of 0.05 and mesh phasing range \(\varphi_{2} \in [0,1][0,1]\), the meshing force \(F_{{\rm m}1}^{(\text{rms})}\) and \(F_{{\rm m}2}^{(\text{rms})}\) were obtained by solving the simulation test model (Fig. 5), the results of which are shown in Fig. 7. According to Eqs. (4) and (5), when \(R = {{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = }}} \right. \kern-0pt} {z_{3} = }}{{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}\), \(\Phi_{2} = 0.5\). From the periodic range in Fig. 6, it is possible to obtain that \(F_{{\rm m}1}^{(\text{rms})}\) and \(F_{{\rm m}2}^{(\text{rms})}\) change in \(\varphi_{2} \in (0,0.5)\) the same as in \(\varphi_{2} \in (0.5,1)\). Thus, the coaxial teeth ratio (\(R = {{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = }}} \right. \kern-0pt} {z_{3} = }}{{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}\)) reduces the periodic variation range of the mesh phasing from \((0,1)\) to \((0,0.5)\). Ultimately the relationship of Sect. 3 is verified.

Fig. 6
figure 6

Time history of mesh force under different mesh phasing based on simulation test model

Full size image
Fig. 7
figure 7

The influence of different mesh phasing on mesh force based on simulation test model

Full size image

4 Results and discussions

The above validation shows the validity and correctness of the modelling process. On this basis, the effect of the mesh phasing on the nonlinear response characteristics of the two-stage spur gear pair is first investigated in detail. Next, the effect of mesh phasing in the chaotic motion region is explored. Finally, the comprehensive variation law of coaxial teeth ratio and mesh phasing on vibration characteristics is revealed. The basic parameters of the two-stage gear pair are shown in Table 2. The characteristic frequency of the gear pair is \(\omega_{n} = 8380.8\;{\text{Hz}}\).

Table 2 Parameters of gear pairs in the two-stage system
Full size table

4.1 Frequency response considering mesh phasing angle

In order to investigate the nonlinear characteristics of the two-stage gear system, numerical simulations were carried out using the Runge–Kutta method based on the parameters in Table 2. The integration time step is \({{T_{p} } \mathord{\left/ {\vphantom {{T_{p} } {200}}} \right. \kern-0pt} {200}}\), \(T_{p} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\Omega_{1} }}} \right. \kern-0pt} {\Omega_{1} }}\), and to obtain a stable vibration response, the total integration time is \(200T_{p}\). According to the relationship between the mesh phasing and the coaxial teeth ratio, the mesh phasing is taken as \(\varphi_{2} = 0\sim 0.5\), and the mesh frequency is taken as \(\Omega_{1} = 0.2\sim 2.2\). The RMS (\(\dot{q}_{1}^{(\text{rms})}\), \(\dot{q}_{2}^{(\text{rms})}\), and \(\dot{q}_{3}^{(\text{rms})}\)) of the velocities of the DTE of the first and second stages and vibration displacement of intermediate shaft are chosen to characterize their vibration and the results are shown in Fig. 8.

Fig. 8
figure 8

Effect of mesh phasing and mesh frequency on the system in \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}} \right. \kern-0pt} {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}\), \(\zeta = 0.08\), \(\omega_{11} = 1\), \(\omega_{22} = 1.5\). a \(\dot{q}_{1}^{(\text{rms})}\), b \(\dot{q}_{2}^{(\text{rms})}\), c \(\dot{q}_{3}^{(\text{rms})}\)

Full size image

The nonlinear characteristics of the system such as the nonlinear softening curve of the stiffness, coexistence solutions, super-harmonic resonances, subharmonic resonances and nonlinear jumps can be clearly observed. In Fig. 8a the main resonance frequency \(\omega_{11}\), the super-harmonic resonance frequency \({{\omega_{11} } \mathord{\left/ {\vphantom {{\omega_{11} } 2}} \right. \kern-0pt} 2}\), the subharmonic resonance frequency \(2\omega_{11}\) and the coexisting solution represented by the transparent surface are clearly evident, and there is a second stage to first stage influence \({{\omega_{22} } \mathord{\left/ {\vphantom {{\omega_{22} } 2}} \right. \kern-0pt} 2}\). The mesh phasing has a suppressive effect for \(\dot{q}_{1}^{(\text{rms})}\) in the \(\omega_{11}\), \({{\omega_{11} } \mathord{\left/ {\vphantom {{\omega_{11} } 2}} \right. \kern-0pt} 2}\) and \({{\omega_{11} } \mathord{\left/ {\vphantom {{\omega_{11} } 3}} \right. \kern-0pt} 3}\). In addition, there is a significant suppression of sub-harmonic resonances by the mesh phasing. It is clear from Fig. 8 that the mesh phasing has a small effect in the stable zone and a significant effect for \(\dot{q}_{1}^{(\text{rms})}\) in \({{\omega_{11} } \mathord{\left/ {\vphantom {{\omega_{11} } 2}} \right. \kern-0pt} 2}\) and \({{\omega_{11} } \mathord{\left/ {\vphantom {{\omega_{11} } 3}} \right. \kern-0pt} 3}\). the position of the nonlinear jumps in the system is changed and the generation of sub-harmonic resonances is suppressed in \(\omega_{11}\) and \(2\omega_{11}\). The time history in Fig. 10 shows that the mesh phasing reduces the amplitude of the system vibration by changing the phase angle of the mesh stiffness so that the peaks of the first-stage and second-stage waves are staggered.

The essence of adjusting the mesh phasing is to change the phase difference by adjusting the keyway or spline position between the first and second gears. The two waveforms are coupled with each other through the phase difference, which can play a role in controlling the harmonic amplitude. Specifically, when one wave is at the peak and the other wave is at the trough at the same time, the coupled waveform is smaller than when both waves are at the peak. The harmonic amplitude in the linear region is controlled by changing mesh phasing. However, the control principle of mesh phasing is not obvious in the nonlinear region because the gear teeth will be separated. The meshing frequency (Rotational speed) has a great influence on the coupling of the waveform. The phenomenon of subharmonic resonance has a great relationship with the parameters, which can be observed only by controlling the parameters [37]. The mesh phasing is to change the amplitude of the specific order harmonics of the system so that there is no subharmonic resonance phenomenon.

The intermediate shaft is affected not only by the vibration response of the first and second stage, but also by its own natural frequency response. As shown in Fig. 8c, the influence curve of mesh phasing on the vibration of intermediate shaft appears multi-peak curve, and the number of peaks decreases with the increase of rotational speed. At the same time, from the linear region of Fig. 8a and b, it can also be seen that the number of peaks decreases with the increase of rotational speed. The reason for this is due to the relationship between the excitation frequency and the natural frequency of the system. In the two-stage gear transmission system, the excitation frequency is controlled by the rotational speed, and the natural frequency of the system is related to the meshing natural frequency or torsional natural frequency under this degree of freedom. When the excitation frequency is lower than the natural frequency of the system, the mesh phasing affects the amplitude of higher harmonics for many times in the range of change, which results in a multi-peak curve. But the curve is not necessarily periodic.

The two-stage gear system is an integration and the vibration characteristics of the second stage need to be taken into account when looking at the vibration characteristics of the first stage. Through Fig. 8b, it is evident that the primary resonance frequency \(\omega_{22}\), the super-harmonic resonance frequency \({{\omega_{22} } \mathord{\left/ {\vphantom {{\omega_{22} } 2}} \right. \kern-0pt} 2}\) and \({{\omega_{22} } \mathord{\left/ {\vphantom {{\omega_{22} } 3}} \right. \kern-0pt} 3}\), the subharmonic resonance frequency \(2\omega_{11}\) of the second stage, verifying the influence of the first stage on the second stage. Combined with the \(\dot{q}_{2}^{(\text{rms})}\) in Fig. 9b, it can be seen that the nonlinear characteristics (nonlinear jumps and co-existence of solutions) of the first stage in \(\omega_{11}\) and \(2\omega_{11}\) have a clear impact, while the impact at the corresponding mesh frequencies of \({{\omega_{11} } \mathord{\left/ {\vphantom {{\omega_{11} } 2}} \right. \kern-0pt} 2}\) and \({{\omega_{11} } \mathord{\left/ {\vphantom {{\omega_{11} } 3}} \right. \kern-0pt} 3}\) is smaller. Figure 10 shows the time histories of the first and second stages. The phase changes of \(q_{2}\) and \(\dot{q}_{2}\) of the second stage can be clearly seen. By the variation of their maximum vibration amplitude, it can be found that there is a controlling effect of the mesh phasing on the vibration amplitude.

Fig. 9
figure 9

RMS variation in \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}} \right. \kern-0pt} {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}\), \(\zeta = 0.08\), \(\omega_{11} = 1\),\(\omega_{22} = 1.5\). a \(\dot{q}_{1}^{(\text{rms})}\), b \(\dot{q}_{2}^{(\text{rms})}\)

Full size image
Fig. 10
figure 10

Time history at different mesh phasing in \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}} \right. \kern-0pt} {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}\), \(\Omega_{1} = 0.5\), \(\zeta = 0.08\), \(\omega_{11} = 1\), \(\omega_{22} = 1.5\). a \(q_{1}\), b \(\dot{q}_{1}\), c \(q_{2}\), d \(\dot{q}_{2}\)

Full size image

In order to further analyze the effect of mesh phasing on vibration intensity control. The percentage decline of \(\dot{q}_{1}^{(\text{rms})}\) (\(i = 1,2,3\)) at the optimal mesh phasing compared to the worst mesh phasing under different mesh frequencies is calculated and shown in Fig. 11. The percentage decline curve of \(\dot{q}_{1}\) is more consistent with the curve change of \(\dot{q}_{1}^{(\text{rms})}\) in Fig. 9a. For example, the vibration reduction effect of mesh phasing at the main resonance point, super-harmonic resonance point, and sub-harmonic resonance point of the first stage gear is better. Among them, the percentage decline reaches more than 60% at the main resonance frequency, and more than 80% at the sub-harmonic resonance frequency. The curve of the percentage decline of \(\dot{q}_{2}\) is similar to that of \(\dot{q}_{2}^{(\text{rms})}\) (Fig. 9b), but it is more similar to the percentage decline curve of \(\dot{q}_{1}\).The percentage decline curve of \(\dot{q}_{3}\) is basically the collection of characteristics of \(\dot{q}_{1}\) and \(\dot{q}_{2}\), because the torsion of the intermediate shaft is directly affected by the first-stage and second-stage meshing forces. In general, the vibration reduction effect of the mesh phasing is about 20% on average, and can reach more than 60% at special frequency.

Fig. 11
figure 11

Percentage decline in vibration of the optimal mesh phasing

Full size image

4.2 Effect of mesh phasing angle on chaotic motion

In order to further explore the effect of mesh phasing on the nonlinear characteristics of gear, this section explores the effect of mesh phasing on the chaotic motion of a two-stage gear system. Gear system with strong nonlinear characteristics can have chaotic motion at high speeds and light loads [38]. Chaotic motion in gear trains generally occurs in the resonance and subharmonic resonance regions, in the low damping region, in the light load region and in the large tooth profile error excitation region. Since \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}} \right. \kern-0pt} {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}\), the DTE of the second stage affects the period of the DTE of the first stage, the interval of the time section should be \(T_{o} = 2T_{p}\) when performing the Poincaré mapping of the system. Choosing \(\Omega_{1} = 1.8\) and \(e = 0.3\), the bifurcation diagrams and largest Lyapunov exponent (LLE) for the \(q_{1}\) and \(q_{2}\) with different damping are shown in Fig. 12.

Fig. 12
figure 12

Bifurcation diagrams and LLE diagram of \(q_{1}\) and \(q_{2}\) with mesh phasing in \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}} \right. \kern-0pt} {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}\), \(\omega_{11} = 1\), \(\omega_{22} = 1.5\), \(\Omega_{1} = 1.8\), \(e = 0.3\). a \(\zeta = 0.02\), b \(\zeta = 0.03\), c \(\zeta = 0.04\)

Full size image

Due to the interaction between \(q_{1}\) and \(q_{2}\) of a two-stage gear system, the bifurcation diagrams of \(q_{1}\) and \(q_{2}\) are consistent with the variation of the mesh phasing, e.g. they have the same range of chaotic motion and location of the bifurcation points. As the mesh frequency is chosen in the \(2\omega_{11}\) subharmonic resonance region of the first stage gear, the system has strong nonlinear characteristics here according to Fig. 12, so it can be judged that the chaotic motion is mainly generated by the first stage gear. A comparison of the bifurcation diagrams for different damping ratios \(\zeta\) shows that the smaller the damping ratio, the more likely chaotic motion is to occur in the system. In Fig. 12c, the LLE is always negative, which means that the system is always in periodic motion when the damping = 0.04. In Fig. 12a, when the mesh phasing is less than 0.03, the system is in 2T-periodic motion, and LLE is negative. When the mesh phasing ranges from 0.03 to 0.48, the system is in chaotic motion and LLE is positive. When the mesh phasing is greater than 0.8, the system is in 1T-periodic motion and LLE is negative. Under \(\zeta = 0.02\), the proportion of chaotic motion is large, and it is difficult to determine how the gear system transfers into chaotic motion. From Fig. 12b, it can be seen that the system seems to have a period-doubling bifurcation, but it cannot be determined from the LLE diagram. When the mesh phasing is greater than 1.4, the system is in 1T-periodic motion and LLE is negative. In order to further judge the bifurcation characteristics of the system when the mesh phasing is less than 0.14, the phase diagram under different mesh phasing is drawn (Fig. 13).

Fig. 13
figure 13

Phase portrait of different mesh phasing in \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}} \right. \kern-0pt} {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}\), \(\omega_{11} = 1\), \(\omega_{22} = 1.5\), \(\Omega_{1} = 1.8\), \(e = 0.3\) \(\zeta = 0.03\)

Full size image

As can be seen from Fig. 13, when the mesh phasing is 0.02, the system is in 4T-periodic motion and the LLE is negative (Fig. 12b). With the increase of mesh phasing, when it is equal to 0.03, the system is in a chaotic motion state, and the LLE is positive. When the mesh phasing is 0.04, the system returns to 4T-periodic motion. When it continues to increase to 0.05, the system is in 2T-periodic motion. A period-doubling bifurcation occurs between 0.04 and 0.05, and the presence of 0 values can also be seen from the LLE diagram. Then, when the mesh phasing is 0.75, the system is in a chaotic motion state, but when the mesh phasing is 0.8, a 2T-periodic motion point appears, and it can be found in the LLE is negative. Then the system is in chaotic motion again at mesh phasing 0.85. When mesh phasing is 0.1, the system returns to 2T-periodic motion and LLE is negative. When the mesh phasing is between 0.1 and 0.12, the system is in chaotic motion. At the mesh phasing 0.125, it goes to 4T-periodic state. The period-doubling bifurcation occurs when the mesh phasing is 0.135, and LLE is 0. When the mesh phasing is greater than equal 0.14, the system is in 1T-period state, and LLE is always negative. Through the above analysis, it is obvious that the mesh phasing enters the chaotic motion through period-doubling bifurcation (Fig. 13).

Fig. 14
figure 14

Bifurcation diagrams and LLE diagram of \(q_{1}\) and \(q_{2}\) with mesh phasing in \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}} \right. \kern-0pt} {z_{3} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}}}\), \(\omega_{11} = 1\), \(\omega_{22} = 1.5\), \(\Omega_{1} = 0.9\), \(e = 0.3\). a \(\zeta = 0.01\), b \(\zeta = 0.015\), c \(\zeta = 0.02\)

Full size image

Next, the analysis is carried out in the primary resonance area of the first stage gear. The Poincaré mapping of the system using time sections \(T_{o} = 2T_{p}\), choosing \(\Omega_{1} = 0.9\) and \(e = 0.3\), and the bifurcation diagrams for \(q_{1}\) and \(q_{2}\) at different damping ratios \(\zeta\) are shown in Fig. 14. According to Fig. 14a and b, chaotic motion occurs on both sides of the mesh phasing, and near the mesh phasing \(\varphi = 0.25\), the mesh phasing has a significant suppression effect on chaotic motion. This is not consistent with the results in Fig. 12 and illustrates the other parameters that play a controlling role. Comparing Sects. 4.1, it can be seen that the control laws of the mesh phasing in steady and chaotic motion are not the same and need to be discussed separately in calculations for the design of an actual gear system.

The results indicate that the mesh phasing has a rich influence on the nonlinear dynamic characteristics of the two-stage gear system. As the mesh phasing changes, the system presents a variety of response states such as 1T-periodic, 2T-periodic, 4T-periodic, and chaotic motion. There are also period-doubling bifurcations and period windows. When the system is in chaotic motion, it means that the movement is irregular and the stability is poor. For the gear system, the phenomenon of tooth separation and tooth collision may occur, which greatly increases the possibility of gear failure. Therefore, chaos control can be carried out through mesh phasing to avoid the chaotic motion region reasonably and improve the stability of the system.

4.3 Effect of the coaxial teeth ratio on the vibration characteristics

According to the relationship between the mesh phasing and the coaxial teeth ratio, the coaxial teeth ratio has a direct influence on the range of the mesh phasing, so it is necessary to investigate the influence of the mesh phasing on the vibration characteristics of the system at different coaxial teeth ratios. Five different coaxial teeth ratios were selected for comparison and the relationship between coaxial teeth ratio and mesh phasing is shown in Table 3, the range of mesh phasing can be obtained by Eqs. (4)–(5). Taking into account the influence of coaxial teeth ratios on the DTE of the system, different integration steps are used for different coaxial teeth ratios as shown in Table 3. Selecting \(\zeta = 0.1\) and \(\Omega = 0.32\), the variation curves of \(\dot{q}_{1}^{(\text{rms})}\) and \(\dot{q}_{2}^{(\text{rms})}\) with the mesh phasing for different coaxial teeth ratios are shown in Fig. 15.

Table 3 Relationship between mesh phasing and different coaxial teeth ratios
Full size table
Fig. 15
figure 15

Effect of mesh phasing on system vibration for different coaxial teeth ratios at \(\omega_{11} = 1\), \(\Omega = 0.32\) a \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}\), b \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {24}}} \right. \kern-0pt} {24}}\), c \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {25}}} \right. \kern-0pt} {25}}\), d \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {22}}} \right. \kern-0pt} {22}}\), e \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {21}}} \right. \kern-0pt} {21}}\)

Full size image

In Fig. 15a, the change in mesh phasing is a three-peaked curve. Comparing the variation curves of different coaxial teeth ratios, it is found that the variation curves of \(\dot{q}_{1}^{(\text{rms})}\) are single-peak at different coaxial teeth ratios \(R_{2}\), \(R_{3}\), \(R_{4}\) and \(R_{5}\), but the locations of the extreme points are different. The change curve of \(\dot{q}_{2}^{(\text{rms})}\) is a double-peak curve at coaxial teeth ratio \(R_{1}\)\(R_{3}\)\(R_{5}\), while it is a single-peak curve at coaxial teeth ratio \(R_{2}\)\(R_{4}\). It can be seen that the multi-peaked curves of \(\dot{q}_{1}^{(\text{rms})}\) and \(\dot{q}_{2}^{(\text{rms})}\) are not so obvious for different coaxial teeth ratios. The difference between the maximum and minimum \(\dot{q}_{1}^{(\text{rms})}\) and \(\dot{q}_{2}^{(\text{rms})}\) for different coaxial teeth ratios was calculated to investigate the effect of mesh phasing and coaxial teeth ratio on the suppression of vibration amplitude, and the results are shown in Table 3. To facilitate comparative ordering, the difference between the maximum and minimum of \(\dot{q}_{1}^{(\text{rms})}\) and \(\dot{q}_{2}^{(\text{rms})}\) for different coaxial teeth ratios is defined as \(\Delta R_{i1} = \Delta \dot{q}_{1}^{(\text{rms})}\) and \(\Delta R_{i2} = \Delta \dot{q}_{2}^{(\text{rms})}\). According on the y-coordinate in Fig. 15 and the data in Table 3, \(\Delta R_{11} > \Delta R_{21} > \Delta R_{31} > \Delta R_{41} > \Delta R_{51}\) is obtained, which corresponds to the magnitude of the mesh phasing for different coaxial teeth ratios. However, \(\Delta R_{12} > \Delta R_{32} > \Delta R_{22} > \Delta R_{42} > \Delta R_{52}\), the difference in the relationship between the coaxial teeth ratio \(R_{2}\) and \(R_{3}\) is due to the fact that the effect of changes in geometric parameters caused by the number of teeth \(z_{3}\) exceeds the effect of the mesh phasing. Thus, the relationship between the magnitude of \(\Delta \dot{q}_{2}^{(\text{rms})}\) and the range of mesh phasing \(\varphi_{2}\) for different coaxial teeth ratios is roughly the same.

In order to further explore the vibration reduction effect of the mesh phasing of the coaxial tooth ratio, based on Fig. 15 and Table 3, the percentage decline of the mesh phasing on the vibration intensity under different coaxial tooth ratio is plotted, as shown in Fig. 16. Combined with Sect. 4.1, when the coaxial tooth ratio is \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {24}}} \right. \kern-0pt} {24}}\), the average percentage decline of vibration is 20%, which is consistent with the results in Fig. 16, and the periodic range of the mesh phasing is 0.5 at this time. According to the coupling relationship between the mesh phasing and the coaxial teeth ratio, the larger the minimum common multiple of the number of coaxial teeth, the smaller the periodic range of the mesh phasing. It can be concluded from Fig. 16 that as the periodic range of mesh phasing decreases, the influence of mesh phasing on vibration will also decrease. When the periodic range of mesh phasing is less than 0.05, the vibration reduction effect of mesh phasing will be completely less than 1%, which means that the influence of mesh phasing on vibration can be ignored. However, when the mesh phasing variation range is greater than 0.2, the percentage decline of mesh phasing can reach 7.57%. At this time, the purpose of reducing vibration and noise can be achieved by adjusting the mesh phasing angle.

Fig. 16
figure 16

Percentage decline in vibration of the optimal mesh phasing under different coaxial teeth ratios

Full size image

In order to eliminate the contingency of the mesh phasing and the coaxial teeth ratio on the vibration characteristics, mesh frequency \(\Omega = 0.6\) are selected and the curves of \(\dot{q}_{1}^{(\text{rms})}\) and \(\dot{q}_{2}^{{({\text{rms}})}}\) with the mesh phasing for different coaxial teeth ratios are solved as shown in Fig. 17. The variation with mesh phasing in Fig. 17a is a double-peak curve, which is consistent with previous results. Comparing the relationship between \(\Delta R_{i1} = \Delta \dot{q}_{1}^{{({\text{rms}})}}\) and \(\Delta R_{i2} = \Delta \dot{q}_{2}^{{({\text{rms}})}}\) at different coaxial teeth ratios according to Fig. 14 those magnitude of the relationship is consistent with the mesh frequency \(\Omega = 0.32\), thus verifying the effect law of the mesh phasing and coaxial teeth ratio on the vibration characteristics. According to the magnitude relationship between \(\Delta R_{i1} = \Delta \dot{q}_{1}^{{({\text{rms}})}}\) and \(\Delta R_{i2} = \Delta \dot{q}_{2}^{{({\text{rms}})}}\) as well as the variation law of the mesh phasing range, it can be obtained that the mesh phasing range is small when the number of teeth of the intermediate shaft is coprime. The smaller the range of mesh phasing, the smaller the effect of mesh phasing on \(\dot{q}_{1}^{{({\text{rms}})}}\) and \(\dot{q}_{2}^{{({\text{rms}})}}\). The law is found to hold for steady motion by numerical calculations. In the design of a two-stage gear system, it is possible to choose the prime number of teeth of the intermediate shaft, and thus ignore the effect of the mesh phasing on the vibration characteristics of the system, which has some engineering significance.

Fig. 17
figure 17

Effect of mesh phasing on system vibration for different coaxial teeth ratios at \(\omega_{11} = 1\), \(\Omega = 0.6\) a \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {20}}} \right. \kern-0pt} {20}}\), b \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {24}}} \right. \kern-0pt} {24}}\), c \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {25}}} \right. \kern-0pt} {25}}\), d \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {22}}} \right. \kern-0pt} {22}}\), e \({{z_{2} } \mathord{\left/ {\vphantom {{z_{2} } {z_{3} }}} \right. \kern-0pt} {z_{3} }} = {{40} \mathord{\left/ {\vphantom {{40} {21}}} \right. \kern-0pt} {21}}\)

Full size image

Other gear systems have different results for the mesh phasing. In the planetary gear transmission system [19], the mesh phasing is determined by adjusting the number of planets and the number of teeth of the sun wheel, so as to achieve different vibration reduction effects. However, in idler system, only adjusting gear train layout can reduce the amplitude of the meshing force through the mesh phasing [39]. The results obtained in this paper are obtained by adjusting the number of coaxial teeth and the mesh phasing to suppress the vibration. The result forms of different gear transmission systems are different, the influence law of the mesh phasing is also very different, so this paper fills the gap of the mesh phasing in the multi-stage gear system.

5 Conclusion

In the current work, the time-varying mesh stiffness taking into account the mesh phasing and the coaxial teeth ratio is developed based on the potential energy method. The dynamic model for a two-stage gear system is established. The coupling relationship between the mesh phasing and the coaxial teeth ratio is derived. The nonlinear vibration characteristics with mesh phasing and coaxial teeth ratio are analyzed. The effect of these factors on the system vibration response is revealed. The main conclusions reached in this paper are as follows:

  • (1) The coupling relationship between the mesh phasing and the coaxial teeth ratio is derived and validated by the simulation test model at different coaxial teeth ratios. It is found that the coaxial teeth ratio reduces the periodic variation range of mesh phasing. Due to the periodic rotation of the gear, the larger the minimum common multiple of the number of coaxial teeth, the smaller the range of mesh phasing.

  • (2) The nonlinear characteristics of the two-stage gear system (softening curve, super-harmonic resonance, subharmonic resonance, and co-existence solutions) are obtained based on numerical calculations. The influence of mesh phasing at different mesh frequencies is analyzed. The mesh phasing will suppress the super-harmonic resonance. The vibration intensity changes with the mesh phasing are a multi-peak curve, and the number of peaks decreases with the increase of rotational speed. When the coaxial tooth number ratio is 40/20, the vibration reduction effect of the mesh phasing is about 20% on average, and can reach more than 60% at special speed.

  • (3) At different speeds, the mesh phasing and damping coefficient have different effects on the chaotic motion of the system. Therefore, by matching mesh phasing, damping coefficient and speed reasonably, the gear system can achieve the purpose of controlling chaotic motion. Compared with mesh phasing, the damping system has more obvious suppression of chaotic motion. But the mesh phasing as a design parameter needs to be designed in advance.

  • (4) the larger the lowest common multiple of the coaxial teeth number, the smaller the range of mesh phasing, and the smaller the effect of the mesh phasing on the vibration amplitude. When the range of mesh phasing is less than 0.125, the effect of mesh phasing on vibration is less than 1%, which can be ignored. When the range of mesh phasing is 0.5, the corresponding percentage decline of vibration intensity is about 20%, and the effect of vibration reduction can be achieved by adjusting the mesh phasing. In actual gear design, the range of mesh phasing change can be calculated by the number of coaxial teeth ratio to determine whether the effect of mesh phasing should be considered.

The relationship between the mesh phasing and the coaxial teeth ratio is derived and its influence on the vibration of multi-stage gear system is obtained. However, the actual damping effect and the optimal value of mesh phasing can be calculated only with given parameters in engineering practice. The effect of mesh phasing relationship on the vibration characteristics of multi-stage and multi-degree-of-freedom gear transmission system can be further studied. For example, the vibration effect of mesh phasing on axial and translational degree-of-freedom of gear is considered. The method of finding the optimal parameters for mesh phasing damping under given parameters is also a valuable topic.