Numerical modeling of elastohydrodynamic lubrication of line contact lubricated with micropolar fluid

Abstract

This paper presents numerical investigation on elastohydrodynamic lubrication (EHL) of line contacts lubricated with micropolar fluids. Numerical model of EHL line contact has been developed by coupled solution of Reynolds equation, elastic deformation equation, load balance equation and fluid rheology equation from inlet to the outlet region. This system of equations has been solved using finite element method techniques. The influence of micropolar fluid parameters and operating parameter on the performances EHL line contacts has been investigated. Further, a comparative assessment on the micropolar and Newtonian fluid-lubricated contact has been presented. It has been observed that the use of micropolar fluid parameters enhances the values of minimum and central fluid film thickness and contact pressure within the EHL line contacts. The empirical formulae for minimum $\left( {\bar{H}_{\hbox{min} } } \right)$ and central $\left( {\bar{H}_{\text{cent}} } \right)$ fluid film thickness are formulated based on the numerically simulated results. The study reveals that overall performances of EHL line contacts increases significantly with micropolar fluid parameter. Further, it has been observed due to micropolar lubricant in EHL line contacts, chances of metal-to-metal contact reduces.

1 Introduction

The tribo-elements such as gears, cams, roller bearings, etc., form an integral part of all machines involving the transmission of power and/or motion. Owing to the non-conformal contacts involved, these elements operate under elastohydrodynamic lubrication (EHL) regime. EHL is a complex mode of hydrodynamic lubrication phenomenon in which sufficiently thick fluid film is generated due to elastic deformation of surfaces and pressure dependence of viscosity. In order to prevent premature failure, it is very important to make certain complete separation of the interacting surfaces along with sufficiently low friction coefficients under the operating conditions [1, 2]. The EHL of line contacts have been widely used in various engineering applications. The line contacts are formed, when the contacting surfaces meet along a line prior to any deformation, specifically between the races and the rollers in a cylindrical roller bearing, between a disk cam and its roller follower and in the contact between pair of involute gear teeth. The developments in EHL theory are relatively recent with major developments being postulated in the 20th century. Grubin made the notable breakthrough by incorporating both the elastic deformation of solids and pressure–viscosity behavior of lubricants to analyze the lubricated non-conformal [3]. They presented the solution for hydrodynamic lubricated heavily loaded elastic cylinder under isothermal conditions. Xu and Smith [4] formulated a finite element method-based model for simulating the EHL performance. The influence of mesh and time step sizes upon the solution accuracy was extensively studied. Wang et al. [5] developed an EHL model based on simplified multigrid method. The algorithm can be used in both steady-state and transient isothermal line contact EHL analysis. Lee et al. [6] proposed an inverse approach-based model that can generate a smooth pressure distribution with small number of measuring points of the film thickness and overcomes the problems of pressure fluctuations. Jolkin and Larsson [7] studied the lubricant film thickness in an EHL conjunction under mixed sliding and rolling conditions using optical interferometry. Bovington and LA Fountain [8] adopted the optical interferometry method of measuring film thickness under EHL conditions to facilitate the study of lubricant behavior at contact pressure of 100 MPa.

Due to the recent technological advancements, use of complex fluids as lubricants is getting more attention. In order to estimate the performance of EHL contacts lubricated with such complex fluids, the fluid film thickness distribution needs to be established. Shimpi [9] and Moldovanu [10] presented the influence of lubricant mixture and roughness effect in hydrodynamic lubrication. The lubricant effectiveness can be enhanced by including little quantities of long-chain polymer additives into Newtonian lubricant. Further, during machine operation the lubricant becomes heavily adulterates with metal particles or dirt in suspension form, thus rendering non-Newtonian behavior to the lubricant. The investigators namely Oliver [11], Scott and Suntiwattana [12] have shown that behavior of fluids changes predominantly with the blending of additives. They also described that there is substantial change in the characteristics of lubricant due to blending of additives.

Over the last few decades, the studies pertaining to the experimental and theoretical studies on influence of non-Newtonian lubricants on elastohydrodynamic (EHD)-lubricated contacts have gained significance [13,14,15,16,17,18,19]. Jacobson and Hamrock [14], Bell [15], Tsann-rong et al. [16], Gecim and Winer [17], Iivonen and Hamrock [18] and Wang and Zhang [18], Thakre et al. [19], Kumar et al. [20, 21] studied different fluid models such as Ree-Eyring model, pseudo-plastic fluids, dilatant fluids, Power law fluid model, etc., to investigate the effect of non-Newtonian lubricants on pressure distribution, load carrying capacity and fluid film distribution in lubricated contacts.

Numerous theories have been developed to understand the behavior of non-Newtonian fluids. The microcontinuum theory which takes into account translation as well as rotation of additives in lubricant can be precisely used to prognosticate their behavior [22]. The micropolar fluid theory precisely describes the non-Newtonian behavior of lubricants blended with polymer additives and/or blended/adulterated with solid particles, where classical theory of Newtonian fluid cannot be applied [23]. The micropolar fluid theory has been successfully applied by various investigators to study the bearing systems of the type squeeze film bearings [24,25,26], porous bearings [27] and multirecess journal bearing [28, 29]. It has been observed from the above literature that the behavior of micropolar lubricants significantly alters the performance characteristics of the bearings. Micropolar fluids have also been studied in the field of biomechanics for the applications of knee cap mechanics, synovial lubrication, cardio-vascular flows and arterial blood flows [30]. In the engineering domain, micropolar fluids have been studied for a different manufacturing processes that occur in the industries for example solidification of liquid crystal, extrusion of polymer fluids, exotic lubricants, colloidal and suspension, cooling of metallic plate in a bath, etc. [31]. However, very few studies are available on elastohydrodynamically lubricated line contacts using micropolar lubricants. Prakash and Christensen [32] investigated the influence of micropolar lubricants in EHL line contact. The authors have investigated the fluid film thickness for EHL line contacts at inlet zone, operating with micropolar lubricants. The study reports collective influence of speed parameter on performance of EHL line contact.

A thorough scan of available literature reported that scant studies are available in the open literature on the EHL line contacts dealing with micropolar lubricants. To the best of author knowledge, only Prakash and Christensen [32] have investigated the influence of micropolar fluid in EHL line contact. This study, however, is not a comprehensive one as it only investigates effect of micropolar lubricant on the fluid film thickness, with pressure profile and pressure spike neglected altogether. Moreover, it is only confined to inlet zone of EHL line contact. Furthermore, almost no information is provided on iterative solution procedure and convergence criteria used for computing the numerically simulated results. These key issues necessitate re-investigation of EHL line contacts lubricated with micropolar lubricant. Therefore, this study is planned to comprehensively investigate the effect of micropolar lubricant on the fluid film thickness, pressure profile and pressure spike in the entire domain of fluid film. In contrast to reference study and to have better understanding on the effect of speed, load and material parameters on the aforesaid performance parameters is presented both individually and collectively. The study is expected to be useful to the design engineers.

2 Mathematical model

The governing equation namely the modified Reynolds equation, fluid film thickness equation, viscosity–pressure relationship, density–pressure relationship and load balance equation followed by their finite element analysis formulation are discussed in succeeding subsections.

2.1 Reynolds equation

The analysis includes the solution of the modified Reynolds equation governing the flow of micropolar lubricant in the EHL line contacts. The micropolar function in this equation has been derived from the Eringen’s micropolar lubrication theory [23]. Couples and forces are assumed to be zero. The governing equations for micropolar fluids are expressed in vectorial form as [24, 33, 34]:

$$\frac{\partial \rho }{\partial t} + {\nabla } \cdot \left( {\rho V} \right) = 0$$

(1)

$$\rho \frac{{{\text{D}}V}}{{{\text{D}}t}} = \left( {\eta + 2\mu } \right){\nabla \nabla } \cdot V - \frac{1}{2}\left( {2\mu + \chi } \right){\nabla } \times {\nabla } \times V + \chi {\nabla } \times v - {\nabla }\pi + \rho F$$

(2)

$$\rho j\frac{{{\text{D}}v}}{{{\text{D}}t}} = \left( {\phi_{1} + \phi_{2} + \phi_{3} } \right){\nabla \nabla } \cdot v - \phi_{3} {\nabla } \times {\nabla } \times v + \chi {\nabla } \times V - 2\chi v + \rho L$$

(3)

Above equations are based on the principle of the conservation of mass, linear and angular momentum, respectively, where the component of velocity, microrotation velocity and pressure are given by [34],

$$V = \left( {u\left( {x,y} \right),v\left( {x,y} \right),0} \right)$$

(4a)

$$v = \left( {0,0,v\left( {x,y} \right)} \right)$$

(4b)

$$p = p\left( {x,y} \right)$$

(4c)

After replacing the value of $V$, $\nu$ and $p$ in Eqs. (1–3), we get following expression

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(4d)

$$\frac{1}{2}\left( {2\mu + \chi } \right)\left[ {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right] + \chi \frac{\partial v}{\partial y} - \frac{\partial p}{\partial x} = \rho \left[ {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right]$$

(4e)

$$\frac{1}{2}\left( {2\mu + \chi } \right)\left[ {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right] - \chi \frac{\partial v}{\partial x} - \frac{\partial p}{\partial y} = \rho \left[ {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right]$$

(4f)

$$\phi_{3} \left[ {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right] + \chi \left( {\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}} \right) - 2\chi v = \rho j\left[ {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right]$$

(4g)

These equations can be simplified by making the usual lubrication assumptions and making an order of magnitude study [33]. Thus, the following system of coupled equations to determine the velocity and the microrotation velocity is obtained.

$$\frac{\partial p}{\partial x} = \frac{1}{2}\left( {2\mu + \chi } \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + \chi \frac{\partial v}{\partial y}$$

(4h)

$$\phi_{3} \frac{{\partial^{2} v}}{{\partial y^{2} }} - 2\chi v - \chi \frac{\partial u}{\partial y} = 0$$

(4i)

For one-directional flow, the components of microrotation velocity, pressure, velocity are only in one direction, i.e., x-direction, the necessary boundary conditions are [34, 35]

$$v = 0,u = - U\,{\text{at}}\,y = 0$$

(4j)

$$v = 0,u = - U\,{\text{at}}\,y = h$$

(4k)

Incorporating the boundary conditions from Eqs. (4j) and (4k) in Eqs. (4e), (4g), (4h) and (4i), we get the following solution:

$$\begin{aligned} u & = U + \frac{1}{2\mu }\frac{\partial p}{\partial x}y^{2} - \frac{h}{\mu }\frac{\partial p}{\partial x}\frac{{N^{2} }}{m}\frac{{\left\{ {\text{Cosh} \left( {my} \right) - 1} \right\}}}{{\sinh \left( {mh} \right)}} \\ & \quad - \left[ {\frac{{U \sinh \left( {mh} \right)}}{{R^{*} }} + \frac{h}{2\mu }\frac{\partial p}{\partial x}} \right]\left[ {y - \frac{{N^{2} }}{m}\left[ {\text{Sinh} \left( {my} \right) - \frac{{\left\{ {\text{Cosh} \left( {mh} \right) - 1} \right\}\left\{ {\text{Cosh} \left( {my} \right) - 1} \right\}}}{{\sinh \left( {mh} \right)}}} \right]} \right] \\ \end{aligned}$$

(5)

Velocity in the $\left( y \right)$ direction for one-dimensional equation is zero.

$$v = 0$$

(6)

where $N = \left( {\frac{\chi }{2\mu + \chi }} \right)^{1/2} ; \,l = \left( {\frac{{\phi_{3} }}{4\mu }} \right)^{1/2} ;\,m = \frac{N}{l};\,R^{*} = \left[ {h\sinh \left( {mh} \right) - \frac{{2N^{2} }}{m}\left\{ {\cosh \left( {mh} \right) - 1} \right\}} \right]$

The volume flow rate $\left( {q_{x} } \right)$ along the $x$ direction is expressed as:

$$q_{x} = \mathop \int \limits_{0}^{h} u{\text{d}}y$$

(7a)

The volume flow rate $\left( {q_{y} } \right)$ along the $y$ direction is zero.After integrating Eq. (7a) the following expressions is obtained as

$$q_{x} = \frac{Uh}{2} - \frac{{h^{3} }}{12\mu }\xi_{\text{M}} \left( {N,l,h} \right)\frac{\partial p}{\partial x}$$

(7b)

$$\xi_{\text{M}} \left( {N,l,h} \right) = 1 + \frac{{12l^{2} }}{{h^{2} }} - \frac{6Nl}{h}\text{Coth} \left( {\frac{Nh}{2l}} \right)$$

(8)

Thereafter, the principle of continuity of flow is applied on the control volume and Eq. (7b) is used to yield the continuity equation. The pressure gradient acting in $y$-direction is negligibly small compared to that in $x$-direction. Therefore, it is assumed that the pressure gradient acting in $y$-direction is zero, i.e., $\frac{\partial p}{\partial y} = 0$. This assumption reduces the Reynolds equation to one-dimensional form. Thus, the modified Reynolds equation with micropolar lubricant in EHL line contact [33, 36] is obtained as:

$$\frac{\partial }{\partial x}\left[ {\frac{{h^{3} }}{12\mu }\xi_{\text{M}} \left( {N,l,h} \right)\frac{\partial p}{\partial x}} \right] = \frac{\varOmega }{2}\frac{\partial h}{\partial x}$$

(9)

where

$$\xi_{\text{M}} \left( {N,l,h} \right) = 1 + \frac{{12l^{2} }}{{h^{2} }} - \frac{6Nl}{h}\text{Coth} \left( {\frac{Nh}{2l}} \right),\varOmega = \frac{{6 \eta_{0} u_{\text{a }} R^{2} }}{{b^{3} p_{\text{h}} }}$$

Utilizing the non-dimensional parameters given in nomenclature, modified Reynolds equation in dimensionless form is given by,

$$\frac{\text{d}}{{{\text{d}}X}}\left( {\frac{{\bar{\rho }H^{3} }}{{\bar{\eta }}}\bar{\xi }_{M} \left( {N,l_{\text{m}} ,\bar{h}} \right) = \frac{{{\text{d}}P}}{{{\text{d}}X}}} \right) = \varOmega \frac{{{\text{d}}\left( {\bar{\rho }H} \right)}}{{{\text{d}}X}}$$

(10)

where $\bar{\xi }_{\text{M}} \left( {N,l_{\text{m}} ,\bar{h}} \right) = 1 + \frac{12}{{\bar{h}^{2} l_{\text{m}}^{2} }} - \frac{6N}{{\bar{h}l_{\text{m}} }}\coth \left( {\frac{{N\bar{h}l_{\text{m}} }}{2}} \right)$, $N = \left( {\frac{\chi }{2\mu + \chi }} \right)^{1/2}$, $\varOmega = \frac{{3U\pi^{2} }}{{4W^{2} }}$

The fluid pressure at the inlet as well as the outlet of an EHL conjunction is assumed to be equal to the ambient pressure. Therefore, the Reynolds equation is solved for the pressure subjected to the following boundary condition.

Inlet boundary condition

$$P = 0 \,{\text{at}}\,P = X_{\text{in}}$$

(11)

Outlet boundary condition

$$P = \frac{{{\text{d}}P}}{{{\text{d}}X}} \,{\text{at}}\,X = X_{\text{o}}$$

(12)

2.2 Fluid film thickness equation

The shape of the lubricant film is determined by fluid film thickness equation, which includes the elastic deformation for a given pressure distribution [37]. Dimensionless fluid film thickness equation is expressed as:

$$H = H_{0} + \frac{{X^{2} }}{2} - \frac{1}{\pi }\mathop \int \limits_{{X_{\text{in}} }}^{{X_{\text{o}} }} \ln \left| {X - X^{{\prime }} } \right|P\left( {X^{{\prime }} } \right){\text{d}}X^{{\prime }}$$

(13)

Here, integral term describes the elastic deformation.

2.3 Density–pressure relation

Density–pressure relation [38] in the dimensionless form is expressed as:

$$\bar{\rho } = \left( {1 + \frac{{0.6 \times 10^{ - 6} P \cdot P_{\text{h}} }}{{1 + 1.7 \times 10^{ - 9} P \cdot P_{\text{h}} }}} \right)$$

(14)

2.4 Viscosity–pressure relation

Viscosity–pressure relation [38] in the non-dimensional form is given by

$$\bar{\eta } = \exp \left( {\left( {\ln \eta_{0} + 9.67} \right)\left\{ { - 1 + \left( {1 + 5.1 \times 10^{ - 9} P \cdot P_{\text{h}} } \right)^{z} } \right\}} \right)$$

(15)

2.5 Load balance equation

The pressure developed in the lubricant supports the lubricant, the fluid film pressure distribution obtained from the Reynolds equation, should satisfy the load balance condition [1].

$$\mathop \int \limits_{{x_{i} }}^{{x_{o} }} p{\text{d}}x = w$$

(16)

where w represents external load for width of one unit. Non-dimensionalization of the above expression results in:

$$\mathop \int \limits_{{x_{i} }}^{{x_{o} }} P{\text{d}}X = \frac{\pi }{2}$$

(17)

2.6 Finite element analysis formulation

In the present work, the EHL line contact problem has been modeled considering a cylinder on flat surface with lubricating oil in between them as depicted in Fig. 1. The standard Galerkin’s formulation has been applied to the modified Reynold’s equation, fluid film thickness equation and load balance equation. The fluid flow field (of one-dimensional EHL line contact problem) is discretized utilizing two-noded linear isoparametric elements. The domain of interest has been meshed from $X_{\text{in}} = - 5$ to $X_{\text{o}} = 2.5$ with uniform optimize grid size of 450 elements in the lubricant flow field which is taken from the grid converging study. The Lagrangian interpolation function has been applied to the two-noded linear isoparametric elements.

Fig. 1

Geometrical representation of EHL line contact

The residue from Eq. (10) is expressed as:

$$R^{e} = \frac{\partial }{{\partial \bar{x}}}\left[ {\frac{{\bar{\rho }\bar{h}^{3} }}{{\bar{\eta }}}\xi_{\text{M}} \frac{{\partial \bar{p}}}{{\partial \bar{x}}}} \right] - \varOmega \frac{{\partial \left( {\bar{\rho }\bar{h}} \right)}}{{\partial \bar{x}}}$$

(18)

The Galerkin’s technique is used to minimize the residue by multiplying weighting function and equating its integral to zero.

$$\mathop \int \limits_{{\varOmega^{e} }} WR_{i}^{e} {\text{d}}x = 0$$

(19)

$$\int\limits_{{\varOmega^{e} }} {W\frac{\partial }{{\partial \bar{x}}}\left[ {\frac{{\bar{\rho }\bar{h}^{3} }}{{\bar{\eta }}}\xi_{\text{M}} \frac{{\partial \bar{p}}}{{\partial \bar{x}}}} \right]{\text{d}}x - W\varOmega \frac{{\partial \left( {\bar{\rho } \bar{h}} \right)}}{{\partial \bar{x}}}{\text{d}}x = 0}$$

(20)

Differentiation of any two functions $\left( {f_{1} ,f_{2} } \right)$ is

$$\frac{{{\text{d}}\left( {f_{1} f_{2} } \right)}}{{{\text{d}}x}} = f_{1} \frac{{{\text{d}}f_{2} }}{{{\text{d}}x}} + f_{2} \frac{{{\text{d}}f_{1} }}{{{\text{d}}x}}$$

(21)

Using Eq. (21), Eq. (20) is transformed to,

$$\mathop \sum \limits_{\varGamma } \left( {\frac{{W\bar{\rho }\bar{h}^{3} }}{{\bar{\eta }}}\xi_{M} \frac{{\partial \bar{p}}}{{\partial \bar{x}}}} \right) - \mathop \int \limits_{{\varOmega^{e} }} \frac{{\rho \bar{h}^{3} }}{{\bar{\eta }}}\xi_{\text{M}} \frac{{\partial \bar{p}}}{{\partial \bar{x}}}\frac{\partial W}{{\partial \bar{x}}}{\text{d}}\bar{x} - \varOmega \mathop \sum \limits_{\varGamma } \left( {W\bar{\rho } \bar{h}} \right) + \varOmega \mathop \int \limits_{{\varOmega^{e} }} \frac{{\bar{\rho } \bar{h}\partial \left( W \right)}}{{\partial \bar{x}}}{\text{d}}\bar{x} = 0$$

(22)

In this technique, weighted function $W$ is replaced by the shape function of primary variable, i.e., Pressure. The solution is therefore approximated as:

$$\bar{p} = \mathop \sum \limits_{i = 1}^{{p^{e + 1} }} N_{i} \bar{p}_{i}$$

(23)

$$N_{1} \left( \xi \right) = \frac{1 - \xi }{2}\quad {\text{and}}\quad N_{2} \left( \xi \right) = \frac{1 + \xi }{2}$$

(24)

$$\mathop \sum \limits_{j = 1}^{2} \left[ {\mathop \int \limits_{{\varOmega^{e} }} \left[ {\frac{{\bar{\rho }\bar{h}^{3} }}{{12\bar{\eta }}}\xi_{\text{M}} \frac{{\partial N_{i} }}{{\partial \bar{x}}}\frac{{\partial N_{j} }}{{\partial \bar{x}}}{\text{d}}x} \right]\bar{p}_{j} } \right] = \frac{\varOmega }{2}\mathop \int \limits_{{\varOmega^{e} }} \left( {\bar{\rho } \bar{h}} \right)\frac{{\partial N_{i} }}{{\partial \bar{x}}}dx + \mathop \sum \limits_{\varGamma } \frac{{W\bar{\rho }\bar{h}^{3} }}{{12\bar{\eta }}}\xi_{M} \frac{{\partial N_{j} }}{{\partial \bar{x}}}\bar{p}_{j} - \frac{\varOmega }{2}\mathop \sum \limits_{\varGamma } \left( {N_{i} \bar{\rho }\bar{h}} \right)$$

(25)

Considering the boundary condition and continuity condition of pressure $\left( {\bar{p}} \right)$ over inter-element boundaries, Eq. (25) becomes.

$$\left[ {F_{ij}^{e} } \right]\left\{ {\bar{p}_{j}^{e} } \right\} = \varOmega \left\{ {R_{i}^{e} } \right\}$$

(26)

where

$$\left[ {F_{ij}^{e} } \right] = \mathop \int \limits_{{\varOmega^{e} }} \left[ {\frac{{\bar{\rho }\bar{h}^{3} }}{{12\bar{\eta }}}\xi_{M} \frac{{\partial N_{i} }}{{\partial \bar{x}}}\frac{{\partial N_{j} }}{{\partial \bar{x}}}{\text{d}}x} \right]$$

(27)

$$\left\{ {R_{i}^{e} } \right\} = \mathop \int \limits_{{\varOmega^{e} }} \left( {\bar{\rho }\bar{h}} \right)\frac{{\partial N_{i} }}{{\partial \bar{x}}}{\text{d}}x$$

(28)

Film thickness equation is computed introducing a new kernel [39, 40] for elastic deformation as follows.

$$H\left( X \right) = H_{0} + \frac{{X^{2} }}{2} - \frac{1}{\pi }\mathop \sum \limits_{e = 1}^{N} \int \ln \left| {X - X^{{\prime }} } \right|\mathop \sum \limits_{i = 1}^{{p^{e} + 1}} N_{i} \bar{p}_{i} \left( {X^{{\prime }} } \right){\text{d}}X^{{\prime }}$$

(29)

$$H\left( X \right) = H_{0} + \frac{{X^{2} }}{2} - \frac{1}{\pi }\mathop \sum \limits_{e = 1}^{N} \mathop \sum \limits_{i = 1}^{{p^{e} + 1}} K_{i}^{e} \left( X \right)\bar{p}_{1}^{e}$$

(30)

where $K_{i}^{e} \left( X \right)$ is the kernel expressed as:

$$K_{i}^{e} \left( X \right) = \int \ln \left| {X - X^{{\prime }} } \right|N_{1}^{e} \left( {X^{{\prime }} } \right){\text{d}}X^{{\prime }}$$

(31)

$$= \frac{{h^{e} }}{2}\mathop \sum \limits_{i = 1}^{m} (\ln \left| {X - X^{{\prime }} \left( {\xi_{i} } \right)} \right|N_{i}^{e} \left( {\xi_{i} } \right))w_{i}$$

(32)

$K_{i}^{e} \left( X \right)$ computed numerically, when $X$ is outside of $e$ elsewhere Gaussian quadrature can be used.

The load equilibrium equation is discretized according to [41, 42]:

$$\mathop \sum \limits_{e = 1}^{N} \mathop \sum \limits_{i = 1}^{{p^{e} + 1}} p_{i}^{e} N_{i}^{e} \left( X \right){\text{d}}X - \frac{\pi }{2} = 0$$

(33)

Using Gaussian quadrature, load balance equation takes form,

$$\mathop \sum \limits_{e = 1}^{N} \mathop \sum \limits_{i = 1}^{{p^{e} + 1}} p_{i}^{e} N_{i}^{e} \left| J \right|w - \frac{\pi }{2} = 0$$

(34)

3 Solution procedure

In the preceding section, modified Reynolds equation, fluid film thickness equation and load balance equation were formulated using finite element equations. The solution procedure adopted in the present case is shown in Fig. 2. However, the major steps followed for the development of an efficient and stable numerical FEM solver based on the analysis and formulation discussed in the previous section are given below,

Fig. 2

Solution scheme of EHL contact

• 1. Discretization of solution domain using the two-noded linear isoparametric elements.

• 2. Initialization of fluid film pressure using Hertzian pressure distribution.

• 3. Computation of density and viscosity (from initial guess of pressure, i.e., Hertzian pressure) are done by using Eqs. (14) and (15).

• 4. Computation of fluid film thickness by considering elastic deformation and offset film thickness.

• 5. Computation of elemental fluidity matrices and vector by using Gaussian quadrature numerical integration technique.

• 6. Assembly of elemental fluidity matrices and vector into global fluidity matrix and vector.

• 7. Application boundary conditions to the global fluidity matrices.

• 8. Computation of linearized system of equation for the fluid film pressure distribution using sparse generalized minimal residual (GMRES) algorithm.

• 9. Repetition of steps 3–8 until the convergence criteria for pressure is satisfied.

  Pressure convergence

  $${\text{conv}}_{p} = \frac{{[\sum p_{i} ]_{n + 1} - [\sum p_{i} ]_{n} }}{{[\sum p_{i} ]_{n} }} \le 1.0 \times 10^{ - 5}$$

  (35)

• 10. Computation of the residual of load balance equation and central offset fluid film thickness

• 11. Repetition of steps 3–10 until the convergence criteria for load balance is satisfied.

  Load convergence

  $${\text{conv}}_{w} = \frac{{\sum {\text{Load}} - {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}{{\sum {\text{Load}}^{n} - \sum {\text{Load}}^{n - 1} }} \le 1.0 \times 10^{ - 5}$$

  (36)

• 12. Computation of fluid film distribution and fluid film pressure using the expressions described in earlier sections, once the convergence criteria is satisfied.

4 Numerical model validation

A MATLAB source code has been developed for obtaining the nodal fluid film pressure and elastic deformation. The finite element analysis technique has been successfully implemented for the solution of the EHL line contact. However, it is essential to validate the program thoroughly so as to rely on the accuracy of simulated results. Therefore, the values of minimum fluid film thickness computed from the developed code have been compared with results of Hamrock et al. [42] and [43], which is also 1D numerical model for EHL line contact. Table 1 presents the computed results from the present analytical model showing good agreement with published results of Hamrock et al. [42] and [43]. The small deviation in the results is less than 5% which is due to different solution scheme adopted in two studies. However, the variation is very minor and hence is acceptable to compute the results. Thus, on the basis of the comparative assessment it can be concluded that the model developed in the present study stands validated.

Table 1 Influence of dimensionless load, speed and material parameters on minimum fluid film thickness of elastohydrodynamic lubrication line contact

5 Results and discussion

A parametric study has been undertaken to investigate influences of each of the dimensionless design variable, i.e., micropolar lubricant parameters, speed parameter, load parameter and material parameter on the fluid film thickness (i.e., minimum and central fluid film thickness) and the contact pressure of the EHL line contact. The coupling number $N^{2}$ is defined as the parameter which couples the linear and the angular momentum equations. The larger value of $N^{2}$ indicates that the individuality of the substructure becomes significant. Another parameter $l_{\text{m}}$ is the characterization of the interaction of lubricant with the contact surfaces. The smaller value of $l_{\text{m}}$ indicates that characteristic length of the substructure is larger than that of the clearance dimension, and therefore, the effect of microstructure is more pronounced. In the limiting case, as the value of $N^{2}$ approaches zero or the value of $l_{\text{m}}$ approaches infinity, the micropolarity is lost and then the lubricant is considered to behave as Newtonian lubricant. In the present study, operating variables have been chosen from available literature [42, 44,45,46] and presented in Table 2. A steady-state pressure distribution is obtained by coupled solution of Reynolds Eq. (10), film thickness Eq. (13), load balance Eq. (17) and the fluid rheology Eqs. (14, 15), satisfying the boundary condition and using finite element analysis technique.

Table 2 Dimensionless parameters selected for present numerical analysis [38,39,40,41]

5.1 Effect of micropolar lubricant parameters on variation of fluid film thickness

This section considers the effect of micropolar lubricant parameters, i.e., coupling number $\left( {N^{2} } \right)$ and characteristics length $(l_{\text{m}} )$ to study the lubricant behavior of micropolar fluid in EHL line contact. The lubricant behaves like Newtonian fluid when $(l_{\text{m}} )$ approaches zero and $\left( {N^{2} } \right)$ to zero. The physical interpretation of these parameters is that a higher value of $\left( {N^{2} } \right)$ implies high microrotation and a smaller value of $(l_{\text{m}} )$ implies big suspended particle size in the micropolar lubricant. The values of micropolar parameters $\left( {N^{2} } \right)$ and $(l_{\text{m}} )$ have been chosen from the published literature [44,45,46]. Figures 3 and 4 illustrate that the fluid film thickness $\left( {\bar{H}} \right)$ increases with increase in the characteristics length $(\bar{l}_{\text{m}} )$ and coupling number $\left( {N^{2} } \right)$ of micropolar lubricant. However, due to brevity of space, in the present study the values of characteristics length $(\bar{l}_{\text{m}} = 2 \times 10^{ - 5} ,6 \times 10^{ - 5} )$ and coupling number $(N^{2} = 0.3,0.7)$ are considered for further simulation.

Fig. 3

Variation of fluid film thickness $\left( {\bar{H}} \right)$ with characteristics length of micropolar fluid $\left( {\bar{l}_{\text{m}} } \right)$

Fig. 4

Variation of fluid film thickness $\left( {\bar{H}} \right)$ with coupling number of micropolar fluid $\left( {N^{2} } \right)$

5.2 Effect of micropolar lubricant parameters on fluid film thickness distribution

Figure 5 shows the fluid film distribution as a function of micropolar fluid parameters, i.e., coupling number $\left( {N^{2} } \right)$ and characteristics length $\left( {\bar{l}_{\text{m}} } \right)$ for different material parameter values (i.e., for soft and hard material). Result presented in Fig. 5 indicate that the values of minimum and central fluid film thickness are higher in case of non-Newtonian fluid due to the presence of micropolar additives in it. It is also observed that a maximum increment of 109.875% $(\bar{l}_{\text{m}} = 6 \times 10^{ - 05} ;N^{2} = 0.7)$ and 109.568% $(\bar{l}_{\text{m}} = 6 \times 10^{ - 05} ;N^{2} = 0.7)$) in minimum and central fluid film thickness, respectively, is achieved owing to the use of micropolar lubricant vis-a-vis to Newtonian lubricant. This is due to fact that blending of additives increases the apparent viscosity of lubricant; this in turn increases the fluid film thickness between the contacting surfaces. Material parameter G is a function of α and E′. In a physical system, there is increase in the viscosity with increase in the value of α which leads to higher value of fluid film thickness; whereas the contact area decreases with increase in the value of E′ which represents the case of hard EHL and vice versa. Hence, to carry the same load, the contact pressure increases which is responsible for higher value of fluid film thickness when flow is not restricted. A detailed comparison along with percentage increase in fluid film thickness, under variable operating conditions for soft and hard materials, is depicted in Tables 3 and 4.

Fig. 5

Fluid film thickness distribution for $\bar{W} = 3 \times 10^{ - 5} \,,\,\,\bar{U} = 1 \times 10^{ - 11}$

Table 3 Percentage (%) variation in central fluid film thickness $\left( {\bar{H}_{cent} } \right)$ of elastohydrodynamic lubrication line contact due to use of micropolar lubricant

Table 4 Percentage (%) variation in central fluid film thickness $\left( {\bar{H}_{\hbox{min} } } \right)$ of elastohydrodynamic lubrication line contact due to use of micropolar lubricant

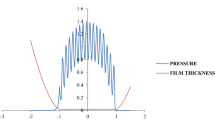
5.3 Effect of micropolar fluid parameter on fluid film pressure distribution

Figure 6 depicts the contact pressure profile for micropolar and Newtonian fluid-lubricated EHL contacts formed between soft and hard materials. It is clearly observed from the results that micropolar lubricants have positive influence on the pressure distribution. The presence of micropolar additives bounds to increase the pressure spike compared to the Newtonian fluid. Furthermore, the influence of additives is more pronounced for hard bearing materials (G = 5000) in comparison with that of soft materials (G = 3591.1). Use of harder bearing material in conjunction with micropolar lubricants results into maximum of 33% increase in peak pressure compared to soft bearing materials lubricated with Newtonian lubricants. Pressure spike is associated with the presence of the film thickness constriction and its inherent localized and abrupt variation in velocity flow component, both in terms of magnitude and direction. After the spike, pressure falls rapidly toward the ambient level, leading to cavitation and film breakup. Finally, the outlet zone and the lubricant properties in that region influence the minimum film thickness. Or, to be more precise, it influences the extent of deviation between the central and minimum film thickness that is the depth of the film thickness constriction. Figure 6 shows that the pressure profile increases with increase in the value of micropolar lubricant parameter. This can be attributed to the larger values of micropolar lubricant parameter, having more prominent polar effects, resulting in increased value of effective viscosity of lubricant which leads to rise in pressure. Under similar operating condition, it is obvious that there is significant rise in the fluid film thickness with the increase in micropolar lubricant parameter. The higher pressure can be accounted for increase in apparent viscosity of lubricant by blending traces of micropolar additives with the base fluid.

Fig. 6

Fluid film pressure distribution for $\bar{W} = 3 \times 10^{ - 5} \,,\,\,\bar{U} = 1 \times 10^{ - 11}$

5.4 Effect of operating parameters on fluid film thickness

In this section, the influence of operating (i.e., load, speed and material) parameters on fluid film thinness of EHL contacts lubricated with different micropolar fluids (represented by different micropolar parameters) is discussed. Relation between dimensionless load parameter and central/minimum fluid film thickness is plotted as shown in Figs. 7 and 8. A parametric study is performed with different range of dimensional load parameter and micropolar lubricant parameters, i.e., $(\bar{l}_{\text{m}} )$ and $(N^{2} )$. These plots reveal drop in minimum and central film thickness, irrespective of lubricant used in EHL line contacts. However, use of micropolar lubricant show a tendency of increasing the minimum and central fluid film thickness. Thus, application of micropolar lubricant tends to provide higher fluid film thickness for contacts operating at higher loads vis-à-vis Newtonian lubricants. The maximum increase in values of central and minimum fluid film thickness on account of use of micropolar lubricants is 106% and 109%, respectively. This is achieved owing to the use of micropolar lubricants when compared with the Newtonian fluid. Blending of polymer additive molecule helps in thickening the fluid film and also in maintaining constant film thickness at varying dimensionless load parameter.

Fig. 7

Variation of central fluid film thickness $\left( {\bar{H}_{cent} } \right)$ with load parameter $\bar{W}\,\left( {10^{ - 5} } \right)$

Fig. 8

Variation of minimum fluid film thickness $\left( {\bar{H}_{\hbox{min} } } \right)$ with load parameter $\bar{W}\,\left( {10^{ - 5} } \right)$

Figures 9 and 10 depict the variation of non-dimensional central and minimum fluid film thickness under varying speed and micropolar lubricant parameters, i.e., $(\bar{l}_{\text{m}} )$ and $(N^{2} )$. As expected, the increase in central and minimum fluid film thickness with micropolar lubricant parameters, i.e., $(\bar{l}_{\text{m}} )$ and $(N^{2} )$ is consistent throughout the range of dimensionless speed parameter. A common observation is that minimum and central film thickness increases continuously as speed parameter increases for both micropolar and Newtonian lubricant. The increase is more profound for higher values of micropolar parameters. Use of soft material (G = 3591.1) in EHL yields a 24–110% increase in both the minimum and central film thickness due to use of micropolar fluid $(\bar{l}_{\text{m}} = 6 \times 10^{ - 05} ;N^{2} = 0.7)$) as compared to Newtonian fluid. For hard EHL contacts, the corresponding increase in minimum and central film thickness is 24–109 and 24–106%, respectively.

Fig. 9

Variation of central fluid film thickness $\left( {\bar{H}_{\text{cent}} } \right)$ with load parameter $\bar{U}\,\left( {10^{ - 11} } \right)$

Fig. 10

Variation of minimum fluid film thickness $\left( {\bar{H}_{\hbox{min} } } \right)$ with load parameter $\bar{U}\,\left( {10^{ - 11} } \right)$

Tables 3 and 4 present the simulation results with detailed comparison along with percentage change in fluid film thickness, under different operating condition for soft and hard EHL contacts. The results present in aforementioned table’s report that the performance of EHL line contact is significantly affected by selection of type of lubricant, operating condition and material of contacting surfaces. The results presented herein are expected to be useful for design engineers dealing with EHL problems in applications such as cams, rolling element bearings, gears, etc.

5.5 Empirical relations for minimum fluid film thickness $(H_{\hbox{min} } )$ and central fluid film thickness $(H_{\text{cent}} )$

The EHL numerical simulations are carried out for different combinations of the operating parameters, for Newtonian and micropolar fluids. The numerical values of non-dimensional minimum $(H_{\hbox{min} } )$ and central $(H_{\text{cent}} )$ fluid film thickness are subjected to nonlinear regression analysis to yield the following empirical expressions for $H_{\hbox{min} }$ and $H_{\text{cent}}$

$$\bar{H}_{\hbox{min} } = \gamma *a_{1} *W^{{a_{2} }} U^{{a_{3} }} G^{{a_{4} }} \exp \left( {a_{5} *lc + N*a_{6} } \right) + \left( {1 - \gamma } \right)*a_{7} *W^{{a_{8} }} *U^{{a_{9} }} *G^{{a_{10 } }}$$

(37)

where a₁ = 0.051239987; a₂ = − 1.08863022; a₃ = 0.552911372; a₄ = 0.441622566; a₅ = 7823.22614; a₆ = 0.97889577; a₇ = 1.3671; a₈ = − 1.08962; a₉ = 0.66320; a₁₀ = 0.44047.

$$\bar{H}_{\text{cent}} = \gamma *b_{1} *W^{{b_{2} }} U^{{b_{3} }} G^{{b_{4} }} \exp \left( {b_{5} *lc + N*b_{6} } \right) + \left( {1 - \gamma } \right)*b_{7} *W^{{b_{8} }} *U^{{b_{9} }} *G^{{b_{10 } }}$$

(38)

where b₁ = 0.0400; b₂ = − 1.103808355; b₃ = 0.508548718; b₄ = 0.366667828; b₅ = 8083.522048; b₆ = 0.923798807; b₇ = 0.7126; b₈ = − 1.109158302; b₉ = 0.63110973; b₁₀= 0.425542075.

Here $\gamma$ denotes switch function which will reduces above equation for Newtonian fluid $\left( {\gamma = 0} \right)$ and micropolar fluid $\left( {\gamma = 1} \right)$ in EHL line contact. From Tables 5 and 6, it can be noticed that there is good agreement between the results obtained using new derived empirical formula (for the $H_{\hbox{min} }$ and $H_{\text{cent}}$) and result of Hamrock and Dowson curve fit formula [38]. In addition to operating conditions, i.e., load, speed, etc., above expressions have been developed to describe the effect of characteristic length and coupling number of micropolar fluid on fluid film thickness. Therefore, under given operating conditions these formulated equation yields the value of minimum fluid film thickness $(H_{\hbox{min} } )$ and central fluid film thickness $(H_{\text{cent}} )$ for EHL line contact problems under micropolar and Newtonian fluid lubrication.

Table 5 Comparison of minimum fluid film thickness and central fluid film thickness from the developed empirical relation for Newtonian lubricant

Table 6 Comparison of minimum fluid film thickness and central fluid film thickness from the developed empirical relation for non-Newtonian lubricant

6 Conclusion

On the basis of Erigen microcontinuum theory [22], the effect of micropolar lubricant on steady-state characteristics of EHL line contacts is presented in this study. The numerically simulated results from the present work can be summarized as follows:

• 1. It has been observed that a maximum increment of 109.875% $(\bar{l}_{\text{m}} = 6 \times 10^{ - 05} ;N^{2} = 0.7)$ and 109.568% $(\bar{l}_{\text{m}} = 6 \times 10^{ - 05} ;N^{2} = 0.7)$ in minimum and central fluid film thickness, respectively, is achieved owing to the use of micropolar fluid vis-a-vis to Newtonian fluid.

• 2. Use of harder bearing material in conjunction with micropolar lubricants results into maximum of 33% increase in peak pressure compared to soft bearing materials lubricated with Newtonian lubricants.

• 3. Application of micropolar lubricant tends to provide higher fluid film thickness for contacts operating at higher loads compared to Newtonian lubricants. The maximum increase in values of central and minimum fluid film thickness on account of use of micropolar lubricants are 106 and 109%, respectively.

• 4. Minimum and central film thickness increases continuously as speed parameter increases for both micropolar and Newtonian lubricant. The increase is more profound for higher values of micropolar parameters.

• 5. Use of soft material in EHL line contacts yields a 24–110% increase in both the minimum and central film thickness due to use of micropolar fluid $(\bar{l}_{\text{m}} = 6 \times 10^{ - 05} ;N^{2} = 0.7)$) as compared to Newtonian fluid. For hard EHL contacts, the corresponding increase in minimum and central film thicknesses is 24–109 and 24–106%, respectively.

• 6. New empirical relation have been developed for the computation of non-dimensional minimum fluid film thickness $(H_{\hbox{min} } )$ and central fluid film thickness $(H_{\text{cent}} )$, based on heavy and moderate different operating parameters condition, applicable to both Newtonian lubricant and micropolar lubricant, expected to be used by the practicing engineer