Effects of Heterogeneous Particle Parameters on Micro-EHL Lubrication on Composite Surface in Line Contact

Abstract

In this paper, a numerical model of elastohydrodynamic lubrication (EHL) in the line contact which happens on the surface of particle-reinforced composites is given. The influence of the particle size and burial depth on the EHL is studied. According to the influence of the structural parameters on the friction coefficient of the EHL contact, the structural parameters of the particles in the composites are optimized and the proper region of the parameters is obtained. The displacement and stress in elastic field caused by the uniform eigenstrains in the particles are described in terms of Galerkin vectors with the interactions between the particles are ignored. A coupling method of particle reinforced composites problem and EHL problem is presented, a new film thickness function is given considered the uneven elastic deformation caused by the presence of the particles. Finally, the presentation of film thickness and fluid pressure of the EHL explains that appropriate particle size, particle burial depth and particle distance can effectively reduce the friction coefficient. The lubrication behavior between the contacted surfaces can be improved under the heavy load.

1 Introduction

Under the heavy load conditions, friction and wear between the contact surfaces are extremely serious, and the higher load capacity and smaller friction is in great demand to improve the mechanical efficiency. Elastohydrodynamic lubrication (EHL)as a special form of hydrodynamic lubrication often appears in the high-stress contact friction pairs [1,2,3,4], it can be used to describe the lubrication mechanism of the point and line contact friction pairs. The micro-EHL behavior is sensitive to the contact surface topography, because of the thin oil film between the contact pairs. Surface roughness [1, 5,6,7] have a large effect on the friction coefficient, as a consequence, the friction force in the EHL can be greatly changed. Micro-textures are found favorable due to an additional hydrodynamic pressure, a local lubricant gap enlargement as well as reduced solid–solid contact, which can improve the load capacity and reduce the friction force [8,9,10,11]. Textures usually contribute to develop the lubricating interface under the initial point contact [12, 13].

The particles or inclusions [14] which are distributed under the surface of the half-space regularly and designated as cube regions that is subject to eigenstrains [15,16,17], the eigenstrains are often used to express the non-elastic strains such as plastic deformation, thermal expansion, residual strains, phase transformation. The existing particles as a heterogeneous material in the matrix can effectively hinder or promote the migration of matrix material under the external force, thus affecting the internal stress field of the composites, as a result, the micromechanics properties of the matrix will become discontinuous. Then, a kind of texture-like 3D topology structure is formed on the surface of this composite under the help of the particles [18,19,20,21]. The same as texture, lubricating fluid will be accumulated in the 3D topology structure to reduce the friction. In addition, the size of surface topology structure can be adjusted automatically according to the contact load in the EHL.

In current study, a model of a half space which contains inclusions contacts with a semi-cylinder is built. The contact bodies as mentioned above are separated by a thin oil film, the semi-cylinder only do the sliding movement on the surface of the half space as Fig. 1 shows. Under the heavy contact stress, a texture similar structure will be formed on the surface of the half-space S, it can have an effect on the behavior of EHL. To study the specific impact of the inclusions on the EHL, an approach is put forward to calculate the inclusion-EHL (I-EHL) problems.

Fig. 1

A half-cylinder EHL contact with a half-space contains inclusions

2 Governing Equation for the Inclusion Problem

2.1 Inclusion Contact Problems Description

Consider a half-space S which contains n arbitrarily-shaped inhomogeneous domains $\Omega_{\psi } \left( {\psi = 1,2, \ldots ,n} \right)$ under its surface $x_{3} = 0$ and the model is described in the coordinate system $Ox_{1} x_{2} x_{3}$, as show in Fig. 2. The inclusion domain $\Omega_{\psi }$ which can be defined as a region contains eigenstrains e_ij (i, j = 1, 2, 3) is distributed under the surface of the half-space S, and the eigenstrains in each inclusion are uniform. The material properties of matrix S and the inclusions domain $\Omega_{\psi }$ are respectively given by Lame’s constant, $\lambda$ and $\mu$, Possion’s ratio $v_{1}$, Young’s modulus $E_{1}$, as presented in the nomenclature.

Fig. 2

Half-space S with n arbitrary shaped inclusion domains $\Omega_{\psi }$$\left( {\psi = 1,2, \ldots ,n} \right)$

2.2 Governing Equation for the Inclusion Problem

Assuming the distance between adjacent particles is large enough that the interaction between them can be ignored. Three identical cubic inclusions are equidistant distributed in the matrix, the burial depth is 0.1 mm and particle side length is 0.04 mm, the effect of different distance values on the surface displacement of the composite under the uniform load is analyzed.

Figure 3 studies the effect of different cubic particles distance on the surface displacement of particle reinforced composites. It shows when the distance of two adjacent particles is 2 or 4 times the length of the particle side length, the deviation of surface displacement is larger than that only one particle is included in the matrix. But when the particle spacing is 6 times longer than the side length of particles, the surface displacement of the composites with a plurality of particles is almost the same as that of only one particle, that is, when the spacing of the cubic particles is more than six times the particle size, the interaction between particles can be neglected.

Fig. 3

surface displacement with different particle distances $H_{s} = 2L,4L,8L,10L,15L$

The elastic field u_ij caused by the eigenstrains e_ij is expressed in terms of Galerkin vectors, F (Yu and Sanday, 1991a) [22]:

$$ 2\mu \mathop {u_{e} }\nolimits_{i} (x_{1} ,x_{2} ,x_{3} ) = 2GF_{i,ij} - F_{k,ki} , $$

(1)

The calculative process has been conducted in the early work of Zeng’s research group [2, 23, 24], the result is as follow:

$$ u_{ei} = - \frac{1}{2\pi }\int\limits_{\Omega } {\mathbf{u}}_{{\mathbf{e}}i} {\mathbf{e}}d{\mathbf{x}}^{\mathbf{{\prime}}}\quad \left( {i = 1,2,3} \right) $$

(2)

With this method, the result of surface displacement component u_e3 in the elastic field caused by the eigenstrains which produced by the inclusions is same as that put forward by Eshelby [14].

3 Inclusion Elastohydrodynamic Lubrication (I-EHL) Problem

For convenience, the inclusion-EHL contact problem is decomposed into two parts: the first part is inhomogeneous inclusion problem and the second part is elastohydrodynamic lubrication (EHL) problem. The inhomogeneous inclusion problem solves the total surface displacement u_e of the half-space S which is caused by the inhomogeneous inclusions. Then the EHL film thickness equation is changed because of the inclusions, and the pressure generated in the fluid film must balance the external application load. The two processes interact with each other, a method is adopted to accelerate the convergence of the fluid film thickness.

3.1 Elastic Deformation Caused by the Inclusions

Elastohydrodynamic lubrication takes the elastic deformation of the contact surfaces into account. According to the Eq. (2), the surface elastic deformation in the I-EHL caused by the inclusions is defined as

$$ u_{{\text{I}}} = - \frac{1}{2\pi }\int\limits_{\Omega } {{\mathbf{u}}_{{\text{I}}} } {\mathbf{e}}dx^{\prime}_{1} dx^{\prime}_{2} dx^{\prime}_{3} $$

(3)

where

$$ {\mathbf{u}}_{{\text{I}}} = \left( {\begin{array}{*{20}l} {x_{3}^{\prime } \left[ {R^{2} - 3\left( {x_{1} - x_{1}^{\prime } } \right)^{2} } \right]/R^{5} - 2\nu \phi _{{,3}} + C\psi _{{,11}} } \hfill \\ {x_{3}^{\prime } \left[ {R^{2} - 3\left( {x_{2} - x_{2}^{\prime } } \right)^{2} } \right]/R^{5} - 2\nu \phi _{{,3}} + C\psi _{{,22}} } \hfill \\ {3x_{3}^{\prime } \left[ {R^{2} - 3x^{{\prime _{3}^{2} }} } \right]/R^{5} - 3\phi _{{,3}} } \hfill \\ { - x_{3}^{\prime } \left( {x_{1} - x_{1}^{\prime } } \right)\left( {x_{2} - x_{2}^{\prime } } \right)/R^{5} + C\psi _{{,12}} } \hfill \\ {\left( {x_{1} - x_{1}^{\prime } } \right)\left[ {R^{2} - 3x^{{\prime _{3}^{2} }} } \right]/R^{5} + \phi _{{,1}} } \hfill \\ {\left( {x_{2} - x_{2}^{\prime } } \right)\left[ {R^{2} - 3x^{{\prime _{3}^{2} }} } \right]{\text{ }}R^{5} + \phi _{{,2}} } \hfill \\ \end{array} } \right)^{T} $$

(4)

3.2 Governing Equations for the I-EHL Problem

Considering that a series of inclusions distribute under the surface of the half-space, an infinite-long semi-cylinder sliding on the surface of half-space, the elastohydrodynamic lubrication occurs in the contact area of them.

3.2.1 Reynolds Equation of EHL

The Reynolds Equation is usually used in describing the question of fluid flow in the narrow gap. Among all kinds of lubrication problems, the Reynolds Equation of steady-state isothermal EHL in line contact is

$$ \frac{d}{dx}\left( {\frac{{\rho h^{3} }}{\eta }\frac{dp}{{dx_{1} }}} \right) = 12u_{s} \frac{{d\left( {\rho h} \right)}}{{dx_{1} }} $$

(5)

where η is viscosity, u_S is the average velocities respectively to the up and down surface along x₁ direction.

The left side term in the Reynolds Eq. (5) indicates that the variety of lubrication film pressure with x₁ and the term on the right hand represents the dynamic pressure effect in lubrication film.

The Reynolds Eq. (5) is expressed in dimensionless form as

$$ \frac{d}{{dX_{1} }}\left( {\varepsilon \frac{dP}{{dX_{1} }}} \right) - \frac{{d\left( {\rho^{*} H} \right)}}{{dX_{1} }} = 0 $$

(6)

where $\varepsilon = {{\rho^{*} H^{3} } \mathord{\left/ {\vphantom {{\rho^{*} H^{3} } {\eta^{*} }}} \right. \kern-\nulldelimiterspace} {\eta^{*} }}$, ρ^* is the dimensionless form of density, η^* is the dimensionless form of the viscosity, their expressions are listed below.

3.2.2 Boundary Conditions

Reynolds boundary conditions is adopted to limit the inlet and outlet pressure of the contact area, Inlet boundary condition $P(X_{1 - in} ) = 0$; Outlet boundary condition $P(X_{1 - out} ) = 0$, $\frac{{dP(X_{1 - out} )}}{{dX_{1} }} = 0$

3.2.3 Fluid Film Thickness

Assumed that the semi-cylinder has Young’s modulus E₁and Possion’s ratio ν₁, the half–space surface will be deformed under the contact pressure. The model is cut by the particle symmetry plane which is perpendicular to the x₂-axis, then the fluid film thickness equation in EHL line contact problem on x₁ direction can be written as,

$$ h\left( {x_{1} } \right) = h_{0} + \frac{{x_{1}^{2} }}{2R} - \frac{2}{{\pi E^{\prime}}}\int_{{x_{1 - in} }}^{{x_{1 - out} }} {\ln \left| {\frac{{x_{1} - s}}{{x_{0} }}} \right|} p\left( s \right)ds + u_{I} \left( {x_{1} } \right) $$

(7)

where the third term is the elastic deformation equation of the EHL in line contact, Eq. (7) in non-dimensional form is given by,

$$ H\left( {X_{1} } \right) = H_{0} + \frac{{X_{1i}^{2} }}{2} - \frac{2}{{\pi E^{\prime}}}\int_{{X_{1 - in} }}^{{X_{1 - out} }} {\ln \left| {X_{1i} - S} \right|} P\left( S \right){\text{d}}S + U_{I} \left( {X_{1} } \right) $$

(8)

where $U_{I} \left( {X_{I} } \right) = {{u_{I} \left( {x_{I} } \right)} \mathord{\left/ {\vphantom {{u_{I} \left( {x_{I} } \right)} L}} \right. \kern-\nulldelimiterspace} L}$, E′ is the equivalent elastic modulus, L is the side length of the particle.

3.2.4 Viscosity-Pressure Equation

The viscosity-pressure equation of EHL in line contact ignored the influence of the temperature is

$$ \eta = \eta_{0} \exp \left\{ {\left( {\ln \eta_{0} + 9.67} \right)\left[ {\left( {1 + \frac{{p\left( {x_{1} } \right)}}{{p_{0} }}} \right)^{2} - 1} \right]} \right\} $$

(9)

The Eq. (9) in dimensionless form is

$$ \eta^{*} = \exp \left\{ {\left( {\ln \eta_{0} + 9.67} \right)\left[ {\left( {1 + \frac{{p_{H} P(X_{1} )}}{{p_{0} }}} \right)^{z} - 1} \right]} \right\} $$

(10)

where z is experimental constant, it can be solved by the following formula:

$$ z = \frac{\alpha }{{5.1 \times 10^{ - 9} \left( {\ln \eta_{0} + 9.67} \right)}} $$

(11)

where α is the viscosity-pressure coefficient which is put forward by Barus.

3.2.5 Density-Pressure Equation

Density–pressure equation is used to described the density change with the fluid film pressure, it is written as

$$ \rho = \rho_{0} \left( {1 + \frac{{0.6p\left( {x_{1} } \right)}}{{1 + 1.7p\left( {x_{1} } \right)}}} \right) $$

(12)

The Eq. (12) in dimensionless form is

$$ \rho^{*} = 1 + \frac{{0.6p\left( {x_{1} } \right)}}{{1 + 1.7p\left( {x_{1} } \right)}} $$

(13)

3.2.6 Load Balance Equation

The hydrodynamic load should balance the total load which acts on the contact process, the non-dimensional load balance equation given as,

$$ w - \int\limits_{{x_{1 - in} }}^{{x_{1 - out} }} {p(x_{1} )} dx_{1} = 0 $$

(14)

The Eq. (14) in dimensionless form is as follow, the details of the dimensionless process can be referenced in [25],

$$ W = \int_{{x_{1 - in} }}^{{x_{1 - out} }} {P\left( {X_{1} } \right)} dX_{1} = \frac{\pi }{2} $$

(15)

3.2.7 Coefficient of Friction in the EHL Contact

Two components have relative sliding under the EHL contact, the friction force F_x1 between them is the sum of the shear stress which comes from the fluid film and the contact surface. The coefficient of friction cof in the EHL contact can be considered as the ratio of the friction force F_x1 and the normal force W which is perpendicular to the x₁-axis,

$$ cof = \frac{{F_{{x_{1} }} }}{W} $$

(16)

According to Wen et al. [25], the equation of friction force for Newtonian fluid,

$$ F_{{x_{1} }} = \iint_{\Omega } {\frac{\partial p}{{\partial x_{1} }}}\left( {h - \mathop z\limits^{ \wedge } } \right)dx_{1} dx_{2} + \iint_{\Omega } {\frac{{u_{{rx_{1} }} }}{{F_{0} }}}dx_{1} dx_{2} $$

(17)

where urx1 is the relative speed in x1 direction, urx1 = u2 − u1, and u1 and u2 are respectively the velocity of half-space and semi-cylinder in x1 direction, the integral term $\hat{z} = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}$.

In Eq. (17) the first part is rolling friction force, and the second is sliding friction force. Considering that the viscosity of the fluid does not change along the film thickness direction, the integral coefficient F0 in Eq. (17) can be written as F0 = h/η. Then, the friction coefficient is solved by substituting Eq. (17) into Eq. (16).

4 Solution Scheme

The solution system is operated with the problem of inclusions and the problem of EHL are coupled and solved. The elastic deformation of the half-space surface caused by the eigenstrains is expressed in terms of Galerkin vectors. The EHL process is solved by the Newton-Rapshon method. The elastic deformation of the contact body in the EHL is considered in the film thickness of the EHL, and the pressure of the EHL is worked out through the iteration, the whole process of calculation shows in Fig. 4.

Fig. 4

Flow chart for solving the problem of I-EHL

In the calculation interval, the region is subdivided into a series of cube elements, the surface is also divided into $n_{1} \times n_{2}$ units ( n1 = n2 = 125).

The effect of each element in the inclusion domain on the surface element is calculated in the solution system. According to the Eq. (12), the side lengths of the element in the inclusion domain are respectively $2\Delta x^{\prime}_{1}$,$2\Delta x^{\prime}_{2}$$2\Delta x^{\prime}_{3}$ in the direction of $x_{1}$, $x_{2}$, $x_{3}$, the equation for the displacement of any element on the surface can be written as,

$$ u_{I} \left( {x,y} \right) = \sum\limits_{n = 1}^{{n_{5} }} {\sum\limits_{m = 1}^{{n_{4} }} {\sum\limits_{l = 1}^{{n_{3} }} {{\mathbf{U}}_{{\mathbf{I}}} {\mathbf{e}}} } } $$

(18)

where,

$$ {\mathbf{U}}_{{\mathbf{I}}} (x_{1} ,x_{2} ) = \int_{{x^{\prime}_{3} - \Delta x^{\prime}_{3} }}^{{x^{\prime}_{3} + \Delta x^{\prime}_{3} }} {\int_{{x^{\prime}_{2} - \Delta x^{\prime}_{2} }}^{{x^{\prime}_{2} + \Delta x^{\prime}_{2} }} {\int_{{x^{\prime}_{1} - \Delta x^{\prime}_{1} }}^{{x^{\prime}_{1} + \Delta x^{\prime}_{1} }} {{\mathbf{u}}_{{\text{I}}} } } } dx^{\prime}_{1} dx^{\prime}_{2} dx^{\prime}_{3} $$

(19)

The equations of EHL are solved with Newton–Raphson method, at the same time the Newton down-hill method is used to ensure that the results decline steadily, and it also can assist in speeding up the convergence rate of the solving process.

5 Results and Discussions

The results of the simulation of the EHL which occur on the surface of the particle reinforced composite are presented. The effects of different values of particle size and burial depth on EHL are studied. The parameters of particle reinforced composites are shown in Table 1. The whole problem is solved by using Matlab code on a personal computer and the calculation flow chart is given in Fig. 4.

Table 1 Input parameters used in analysis

5.1 The Effects of Particle Size on Film Thickness

Three cubic inclusions are buried at a certain depth under the surface of composite, take the depth value as $D = 0.1$, the distance between the particles is equal and the eigenstrains e in inclusion domain is uniform. Because of the existence of particles, the surface displacement of the composites will be inhomogeneous and the surface deformation will vary with the particle size. In Fig. 5, the film thickness of EHL in line contact on the surface of the composites with different particle size values is compared. In order to ignore the interaction between particles, $H_{s} = 0.7$, L = 0.04, $H_{s}$ is 17.5 times that of the side length of the cubic particles. $D$ and $H_{s}$ are presented in Fig. 6.

Fig. 5

Non-dimensional film thickness of EHL with different particle sizes. $L$ = 0.04 mm, $L$ = 0.06 mm, $L$ = 0.08 mm, $L$ = 0.1 mm and the matrix without inclusions

Fig. 6

The burial depth D, the distance between the adjacent particles H_s and particle size L

Figure 5 shows the effects of different particle sizes on film thickness of EHL. As cubic particles side length $L = 0.08,0.1$, the equivalent film thickness is bigger than the film thickness of same material without inclusions $H_{n}$. This is different from $L$ = 0.04 and 0.06, the trough of film thickness curve at the points which are located at the particle area is smaller than $H_{n}$, while the film thickness of the area where there are no particles is bigger than $H_{n}$. It is obvious that the peaks of the different film thickness curves are almost equal, while the trough gradually rising when the value of particle size increases. It is worth concerning that the minimum film thickness is reduced with the particle size, which can easily cause the damage of the lubrication film and the dry friction contact of the two contact bodies. As a consequence, the adverse effect is the wear of the composite surface. However, the increase of the distance between the peak and the trough of the surface topological structure is conducive to the accumulation of the lubricant. That means the increase of particle side length helps to elastic deformation on surface. And the lubrication film thickness increases and the coefficient of friction decreases, which are benefit to a better lubrication performance. While, the ability of the friction surface to accumulate lubricating fluid will be decreased as the particles sizes is too big, and the function of reducing friction is no longer obvious. Therefore, the film thickness can be controlled in a proper range by taking the appropriate particle size, so that the material with this structure can play a more effective role in the process of reducing friction.

5.2 The Effects of Particle Burial Depth on Film Thickness

Three particles have the same size, with the side length $L = 0.04$, the distance between particles $H_{s}$ and the eigenstrains of the particle ${\mathbf{e}}$ as described in chapter 5.1. The film thickness has changed due to the presence of particles. Figure 7 shows the effects of different particle burial depths on film thickness of EHL. When the burial depth $D = 0.15,0.2$, the equivalent film thickness values are bigger than the film thickness $H_{n}$, but the trough values is smaller than $H_{n}$ at the particle located position.

Fig. 7

Non-dimensional film thickness of EHL with different particle burial depths, D = 0.05 mm, 0.1 mm, 0.15 mm, 0.2 mm, and the matrix without inclusions

With the decrease of D the fluctuation margin of the film thickness increases gradually. The effect of particle on the surface structure of the half-space is weakened, as the burial depth D is too deep, and the presence of the particles will be meaningless. The film thickness in the particle located area is decreased drastically by the decrease of the burial depth D, at the same time the possibility of the lubrication film being damaged is increased. The critical burial depth D which generates a thinner film thickness is about 0.15 mm. To put it in a nutshell, the decrease of burial depth D would increase solid–solid contact and thus lead to surface wear. Compared with the effects of the particle size on film thickness, it can be seen that the film thickness is more sensitive to the particle burial depth. On the other hand, the effect of particle size on the wave length of the film thickness is also remarkable. The distance between the adjacent troughs is increased for the reason of the influence basin of the individual particles is expanded by the increase of the particle size.

5.3 The Effects of Particle Size on Film Pressure

Figure 8 shows the effects of different particle sizes on film pressure of EHL. The values of burial depth $D$, eigenstrains ${\mathbf{e}}$ and particles distance $H_{s}$ are the same as in chapter 5.1. The dynamic pressure of EHL in particle located position increases obviously, because the existence of the particles causes stress concentration in the particle located area. The finer particles mean that the area where the particles are used to block the material transition is getting smaller, this will result in tighter stress concentration, so the pressure peaks will increase with the decrease of particle size. What’s more, the existence of heterogeneous particles helps to reduce the outlet pressure peak. This may regard the material fatigue and wear [26].

Fig. 8

Non-dimensional pressure of EHL with different particle sizes L. $L$ = 0.04 mm, $L$ = 0.06 mm, $L$ = 0.08 mm, $L$ = 0.1 mm and the matrix without inclusions

5.4 The Effects of Particle Burial Depth on Film Pressure

Figure 9 shows the effects of different particle burial depths on film pressure of EHL. The values of particle size $L$, eigenstrains ${\mathbf{e}}$, particles distance $H_{s}$ as described in Sect. 5.2. Contrary to the effects of burial depth $D$ on film thickness, the pressure of the film gradually increases as the burial depth decreases, this is because when the particles get closer to the surface of the half-space, the stress concentration at the particle located area will be more obvious. As the distance between the particle and the surface is far enough, the influence effect of the stress concentration on the surface becomes weak, this is a good explanation for the high consistence between the pressure curve as $D = 0.2$ and the curve as there are no inclusions. The same circumstance occurs for the outlet pressure peak: all the cases for composite surface shows the lower pressure peaks than surface with no inclusions. Combined the case of 5.2, the elastic deformations caused by particles in different burial depths are similar to surface textures with different depth/width ratios. The deeper burial depth $D$, liked shallower texture depth, may generate thick film and reduce solid–solid contact [10, 13, 26, 27].

Fig. 9

Non-dimensional pressure of EHL with different particle burial depths, D = 0.05 mm, 0.1 mm, 0.15 mm, 0.2 mm, and the matrix without inclusions

5.5 The Coefficient in the Condition of Different Particle Sizes and Burial Depths

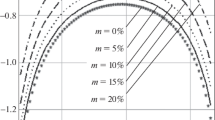
The friction coefficient of the EHL is carried out and presented in Figs. 10, 11 and 12, the effects of different particle side length L, burial depths D and particle distances H_s on the coefficient are investigated. When the burial depth D = 0.3 mm and the particle distance H_s = 0.7 mm, the variation law of the friction coefficient caused by the particle side length is shown in Fig. 10. Compared with the friction coefficient of the case of no inclusions, the percentage reduction of the friction coefficient cof to the order of 4.8% is observed in the case of L = 0.04 mm. What’s more, when the particle length L exceeds a certain value (0.40 mm in this study), the friction coefficient doesn’t increase. This trend is similar to the case of texture depth in the literature [8, 12].

Fig. 10

The coefficient in the condition of different particle sizes

Fig. 11

The coefficient in the condition of different burial depths

Fig. 12

The coefficient in the condition of different distance $H_{s}$

When the particle side length L = 0.04 mm and particle distance H_s = 0.7 mm, the particles are buried at different depths, the changing trend of the friction coefficient cof as shown in Fig. 11. The coefficient becomes much bigger as D = 0.1 mm, while it is minimized when D = 0.2 mm and the percentage reduction to the order of 4.91%. When the burial depth D > 0.7 mm, the friction coefficient cof is almost equal to the friction coefficient of the case of no inclusions.

Figure 12 shows the variation law of the friction coefficient caused by the different particle distance H_s as the particle side length L = 0.04 mm and the burial depth D = 0.3 mm. When the distance between the adjacent two particles H_s < 0.9 mm, the friction coefficient is less than that of the case of no inclusions. The friction coefficient is minimized at H_s = 0.6 mm, the percentage reduction of the friction coefficient cof to the order of 4.95%. At last, the friction coefficient is obtained by choosing L = 0.04 mm, D = 0.2 mm, H_s = 0.6 mm, the percentage reduction to the order of 5.3%. In general, the particle reinforced composite improves the micro-EHL performance in the way that facilitates elastic deformation on the surface, increases locally lubricant film and builds up hydrodynamic lift force. As side length, burial depth and particle distance have strongly effect on friction behavior, which are equal to texture parameters, the proper values of above three need to rationally design for improving the friction environment.

6 Conclusions

The problem of elastohydrodynamic lubrication (EHL) in line contact at steady state occurs on the surface of the particle reinforced composites is investigated by theoretical means in this paper. The influences of different particle size and burial depths on the film thickness and pressure are analyzed. The salient conclusions that can be drawn from the study are:

• 1. The variation law of the film thickness of the EHL in the given condition under the different particle side length is investigated, the particles are buried at the same depth $D = 0.3{\text{mm}}$, the film thickness follows the trend of $H_{\min } \left( {L = 0.04} \right) < H_{\min } \left( {L = 0.06} \right) < H_{\min } \left( {{\text{No}}\,{\text{inclusions}}} \right) < H_{\min } \left( {L = 0.08} \right) < H_{\min } \left( {L = 0.1} \right)$.

• 2. When the particles have the same side length $L = 0.04({\text{mm}})$, the film thickness of the EHL is observed follow the regular of $H_{\min } \left( {D = 0.05} \right) < H_{\min } \left( {D = 0.1} \right) < H_{\min } \left( {{\text{No}}\,{\text{inclusions}}} \right) < H_{\min } \left( {D = 0.15} \right) < H_{\min } \left( {D = 0.2} \right)$.

• 3. The maximum film pressure of the EHL reduces in case of the side length and burial depth of the particle increase, and the maximum pressure of EHL which happens on the surface of the particle reinforced composites is always bigger than the normal situation. The existence of heterogeneous particles helps to reduce the outlet pressure peak and thus may lead to lower surface wear.

• 4. The friction coefficient of the EHL contact is obtained, as the burial depth $D = 0.3\,{\text{mm}}$ and the distance between the particles $H_{s} = 0.7\,{\text{mm}}$, the friction coefficient increases as the particle side length increases, when $L > 0.2\,{\text{mm}}$ the friction coefficient is greater than the situation of no inclusions under the contact surface.

• 5. When the burial depth of the particles is too small, the friction coefficient will increase significantly. As $D > 0.7\,{\text{mm}}$, the friction coefficient approaches the case of no inclusions.

• 6. When the burial depth $D = 0.3\,{\text{mm}}$ and the side length $L = 0.04\,{\text{mm}}$, the friction coefficient is minimized at the particle distance $H_{s} = 0.6\,{\text{mm}}$. As $H_{s} > 0.9\,{\text{mm}}$, the friction coefficient will exceed the case of no inclusions.

• 7. In order to get an optimum performance of the EHL contact, a proper selection of particle side length, burial depth and the particle distance mentioned above is quite essential.

• 8. This study establishes the numerical model of micro- EHL lubrication on composite surface in line contact on the steady state. However, in order to reach an even more practical related description and a more accurate physical numerical model, further progress in simulation approaches is indeed necessary. The issues includes transient effects, thermal effects and cavitation effects needs to be taken into account, which are evolved in our follow-on research work.