1 Introduction

In modern society, with the increasing height of buildings, the proportion of high-speed elevator (speed ≥ 2.5 m/s) has gradually increased to ensure efficiency. With the increase of the elevator running speed and attention to the ride comfort and safety, effectively reducing the vibration generated by the high-speed operation of the elevator has become a key issue.

In recent years, many scholars have studied transverse vibration of elevator cars. Feng et al. [1] established a dynamic model of the transverse vibration of an elevator car based on the rigid body dynamics theory, and they derived differential equations based on Newton’s laws of motion and the Euler equations. Bao et al. [2] used the finite element method to establish the car frame model, and revealed the acceleration responses on the condition of dynamic loads from the perspective of transient dynamics. Chang et al. [3] established a four-degree-of-freedom elevator system to study the excitation characteristics and the car dynamic response, and developed an active mass driver based on the H∞ direct output feedback control algorithm. Herrera et al. [4] considered the behavior of passengers in the car and established a model to analyze the influence of the car’s dynamic characteristics under different loading conditions. Because the rolling guide shoe liners are made of rubber materials, its material properties give guide shoes nonlinear characteristics. For this problem, these literatures simplified guide shoes as a linear spring-damper system. The rolling guide shoes are key components that directly contact the guide rails, and the nonlinear function relationship between the amounts of deformation and restoring force is bound to have an effect on the vibration responses. Thus, it is necessary to further explore the nonlinear characteristics of rolling guide shoes and apply them to the car vibration response analysis.

In addition, there are many random factors in the car system, including the randomness of the parameters and the randomness of the excitation. In the product design stage, all of the parameters are definite. However, due to the influence of actual installation circumstance, live debugging, manufacturing errors, installation errors, the influence of temperature and uncertainty of physical parameters of materials, etc., the parameters of the same batch of elevator products are different. For an actual product, its parameters are uncertain, and they present some randomness. Therefore, the actual parameters of the same specification’s elevators are slightly different. The randomness of these parameters can make the vibration responses of different elevators produce variability under the same condition. The randomness of excitations is caused by the irregularity of the guide rails. To distinguish them from the time-invariant property of parameters, the excitations are time-varying, and they can affect the vibration of the car at different times. To make a more accurate vibration response analysis of a car system, the above factors must be comprehensively considered.

For the random factors that exist in the car system, the dynamic response analysis of an uncertain structure is involved. Currently, this response analysis is mainly used in the structure of building and a small number of mechanical structures, and is seldom used in the car system of high-speed elevators. Xu et al. [5] analyzed the stochastic dynamic characteristics of beams under the stochastic material properties by the random factor method. However, the authors did not combine this research with random excitation. Marcin et al. [6] solved the dynamic response of the truss structure using the Taylor expansion stochastic finite element method. The stochastic finite element method needs to set up all kinds of random parameters corresponding to the stochastic finite element characteristic matrix, and it causes much inconvenience to its computer program design. Szafran [7] analyzed the horizontal vibration responses of cable structures under the influence of a random elastic modulus and random loads by the stochastic perturbation method, and further analyzed the reliability. Although the stochastic perturbation method can quickly and easily calculate the mean and variance of the responses, it only applies to small parameter perturbation, and this method inevitably exists in secular term. That is, this method only applies to the beginning of a short period of time, and the accuracy of results quickly deteriorates with time.

For a series of problems related to the analysis of horizontal vibration responses of a high-speed elevator car system, first, the nonlinear model of rolling guide shoes was established, and then the acceleration responses of the composite random vibration of the car system were determined by the orthogonal polynomial approximation method, and the responses’ standard deviations were determined by the complex Cotes precise integration method provided by Song [8]. This set of analytical methods not only avoids the secular term problem of the stochastic perturbation method but also obtains more accurate results by combining with the rolling guide shoe nonlinear model.

2 The rolling guide shoe nonlinear model

The schematic diagram of the structure of rolling guide shoe is shown in Fig. 1. The guide shoe has two elastic elements. One is the rubber lining of the roller, and the other is the spring. In the process of the traditional vibration responses analysis of a high-speed elevator car system, as an important dynamic component, the guide shoe is usually simplified as the spring-damper model. However, related research has shown that nonlinear behavior exists in the rolling guide shoe [9]. Under the effect of guide rail irregularity, the nonlinear characteristics of the guide shoes are bound to have an impact on the horizontal vibration of the car. Solving the vibration responses of the car with the spring-damping model reduces the accuracy of the solution. Taking into account the nonlinear behavior of the rolling guide shoes, in this section, the functional relationship between the amount of deformation of rolling guide shoes and the restoring force are derived by the Hertz contact theory of the elastic solid contact area [10,11,12,13].

Fig. 1
figure 1

The schematic diagram of the structure of rolling guide shoe

Full size image

The guide wheel and guide rail contact area are shown in Fig. 2. R is the radius of the guide wheel, L is the width of the guide wheel, F k is the normal force of impact on the guide wheel, p is the contact stress, and a is the half-width of the contact line.

Fig. 2
figure 2

The guide wheel and guide rail contact area

Full size image

On the basis of the Hertz contact theory, the stress on the contact surface is elliptical. The stress of the contact center is the largest, marked as p0. The stress distribution of the remaining points is:

$$p = p_{0} \sqrt {1 - \frac{{x^{2} }}{{a^{2} }}}$$
(1)

The volume of a semi-elliptical cylinder of stress distribution is equal to total pressure F k , that is:

$$F_{k} = \frac{\pi a}{2}Lp_{0}$$
(2)

The maximum contact stress is:

$$p_{0} = \sigma_{H} = \frac{2F}{\pi aL}$$
(3)

The half-width a derived from the Hertz formula is:

$$a = \sqrt {\frac{4F}{\pi L} \times \frac{{\frac{{1 - \mu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \mu_{2}^{2} }}{{E_{2} }}}}{{\frac{1}{{R_{1} }} + \frac{1}{{R_{2} }}}}}$$
(4)

In which, μ1 and μ2 are Poisson’s ratio of guide wheel and guide rail, respectively, E1 and E2 are the elastic modulus of the guide wheel and guide rail, respectively, and R1 and R2 are the radius of curvature of guide wheel and guide rail, respectively. When the material of the guide wheel is rubber and the material of guide rail is steel, E2 is much greater than E1 and R2 tends to infinity, thus Eq. (2) can be simplified as:

$$a = \sqrt {\frac{4F}{\pi L} \times \frac{{R\left( {1 - \mu_{1}^{2} } \right)}}{{E_{1} }}}$$
(5)

Substituting Eq. (5) into Eq. (3), and the following equation is obtained:

$$\sigma_{H} = \sqrt {\frac{F}{\pi L} \times \frac{{E_{1} }}{{R\left( {1 - \mu_{1}^{2} } \right)}}}$$
(6)

Thus, the functional relationship between rubber’s deformation z1 and pressure F is:

$$F = \left( {\frac{{z_{1} }}{d}} \right)^{2} \pi LR\left( {1 - \mu_{1}^{2} } \right)E$$
(7)

In which, d is the rubber’s thickness of guide wheel. \(A = {{\pi LR\left( {1 - \mu_{1}^{2} } \right)E} \mathord{\left/ {\vphantom {{\pi LR\left( {1 - \mu_{1}^{2} } \right)E} {d^{2} }}} \right. \kern-0pt} {d^{2} }}\) is set and the elastic coefficient of the spring in the guide shoe is k, so the functional relationship between the total deformation of the guide shoe and pressure F is:

$$F = kz - \left( {\frac{{k^{3} z}}{A} + \frac{{k^{4} }}{{4A^{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} + \frac{{k^{2} }}{2A}$$
(8)

To verify the accuracy of the Eq. (7), the finite element model of guide wheel’s rubber is built. The required parameters are L = 0.05 m, R = 0.1 m, d = 0.04 m, μ1 = 0.47, E = 2.5e+07 pa, and k = 1.2e+06 N/m. The finite element calculation result is shown in Fig. 3 and the curves of pressure change with deformation of guide wheel’s rubber are shown in Fig. 4. The two curves shown in Fig. 4 are basically identical, and the accuracy of the Eq. (7) in rolling guide shoe nonlinear model. The curve of the pressure change with total deformation of the guide shoe is shown in Fig. 5. In the early part of the deformation, the main variable is the rubber of the guide shoe, thus showing the strong nonlinear characteristics. With an increase of z, the deformation of the spring on the guide shoe is dominant, the slope of the curve slowly increases, and shows near linear characteristics. Overall, the slope of the curve increases with the increase of z, which indicates that the nonlinearity of the guide shoe has a tendency to increase the vibration.

Fig. 3
figure 3

The finite element calculation result (equivalent stress)

Full size image
Fig. 4
figure 4

The curves of pressure change with deformation of guide wheel’s rubber

Full size image
Fig. 5
figure 5

Curve of the stress change with total deformation of the guide shoe

Full size image

To simulate the guide rail irregularities, random excitations were constructed by superimposing Gauss white noises on deterministic pulse excitations, as shown in Fig. 6. The S is the vertical displacement of the elevator. The d0 represents the horizontal deviation between the actual guide rail and the ideal guide rail. Because of the pretightening force in the rolling guide shoe, the roller of the guide shoe is always in contact with the guide rail, so the d0 is equivalent to z. The pulse excitations were caused by common guide rail joint irregularities, and the length of a single guide rail was 5 m. The Gauss white noises were caused by small fluctuations of the guide rail surface and guide wheel surface, and the standard deviation was 0.05. Figures 8 and 9 show the random waveform established by the nonlinear guide shoes and the traditional linear guide shoes, in which, the stiffness of linear guide shoes is fitted by the curve of Fig. 5 (The comparison between nonlinear and linear guide shoe model is shown in Fig. 7). Comparing with Figs 8 and 9, in the larger amplitude pulse points, the exciting forces are larger than that of the linear model, and this is bound to aggravate the vibration responses of the car. Between the two joints of the guide rail, the surface is relatively smooth. Because the initial slope of the F-z curve of the nonlinear guide shoe model is smaller than that of the linear model, the amplitude of the former is smaller than that of the latter. But the differences can be ignored because they are very small.

Fig. 6
figure 6

Guide rail irregularity curve

Full size image
Fig. 7
figure 7

The comparison between nonlinear and linear guide shoe model

Full size image
Fig. 8
figure 8

Guide rail excitations by the nonlinear model

Full size image
Fig. 9
figure 9

Guide rail excitations by the linear model

Full size image

3 The dynamic analysis of a car system based on the orthogonal polynomial approximation method

This section uses the orthogonal polynomial approximation method dealing with the randomness of parameters in a car system [14,15,16]. This method can solve problems according to the following. In random function space, first, the responses are expanded into the generalized Fourier series according to a standard orthogonal basis. Then, the random system is converted into the equivalent determinacy system by utilizing the inner product properties of standard orthogonal basis functions. This method is not affected by large parameter perturbations and can avoid the adverse effects of the secular terms of the stochastic perturbation method.

3.1 Orthogonal decomposition of the random function

Let {H i (ξ), i = 1, 2, 3…} be a cluster of the orthogonal function system. For random variables with a normal distribution, the Hermite polynomials can be functions of the orthogonal system. For random variables with a uniform distribution, the Legendre polynomials can be functions of the orthogonal system [17]. For random variables with an exponential distribution [18], the Laguerre polynomials can be functions of the orthogonal system [19]. p(ξ) as a probability density distribution function of ξ, together with H i (ξ) satisfies the following equation:

$$\int_{\varOmega } {p\left( \xi \right)} H_{m} \left( \xi \right)H_{n} \left( \xi \right) = \delta_{mn} h_{m}$$
(9)

In which, Ω is the definitional domain of the real variable ξ and δ mn is the Kronecker delta.

Equation (9) is the weighted orthogonal relation of the orthogonal functions system. In addition, the orthogonal function system also has the following recurrence relation:

$$\xi H_{n} \left( \xi \right) = \alpha_{n} H_{n - 1} \left( \xi \right) + \beta_{n} H_{n} \left( \xi \right) + \gamma_{n} H_{n + 1} \left( \xi \right)$$
(10)

If all the Cauchy sequence of points in the random function space are convergent, any function in this space can be expanded into the following series:

$$f\left( \xi \right) = \sum\limits_{i = 0}^{\infty } {a_{i} H_{i} \left( \xi \right)}$$
(11)

In which

$$a_{i} = \int_{\varOmega } {p\left( \xi \right)f\left( \xi \right)H_{i} \left( \xi \right){\text{d}}x}$$
(12)

Equation (11) is the orthogonal expansion of the random function f(ξ) and it is the basis of the orthogonal polynomial approximation method.

3.2 Analysis of horizontal vibration responses of a high-speed elevator

For a high-speed elevator system with random parameters under random excitations, its dynamic differential equations can be expressed as:

$$\varvec{M}{\ddot{\varvec{X}}} + \varvec{C}{\dot{\varvec{X}}} + \varvec{KX} = \varvec{F}\left( t \right)$$
(13)

In which, M, C, and K are the mass matrix, damping matrix, and stiffness matrix respectively, F(t) is the external excitation vector, and X is the displacement response. When the M, C, K, and F(t) are random parameters, this system becomes a composite random system. Then, converting Eq. (13) into the expression of the collection of independent random variables:

$$\left( {\varvec{M}_{0} + \sum\limits_{i = 1}^{{N_{m} }} {\varvec{M}_{i} \xi_{i} } } \right)\ddot{\varvec{X}} + \left( {\varvec{C}_{0} + \sum\limits_{i = 1}^{{N_{c} }} {\varvec{C}_{i} \xi_{i} } } \right)\dot{\varvec{X}} + \left( {\varvec{K}_{0} + \sum\limits_{i = 1}^{{N_{k} }} {\varvec{K}_{i} \xi_{i} } } \right)\varvec{X} = \varvec{F}\left( t \right)$$
(14)

In which, N m , N c , and N k are the number of independent random variables of the mass matrix, damping matrix, and stiffness matrix, respectively. The total number of random variables is:

$$R = N_{m} + N_{c} + N_{k} .$$
(15)

The subscript 0 indicates the mean of M, C, and K. The subscript i indicates the corresponding standard deviation coefficient matrix. \(\xi_{i}\) is a random variable which obeys arbitrary distribution. According to the orthogonal decomposition, the responses \(X\), \(\dot{X}\), and \(\ddot{X}\) are expanded to the series of the orthogonal basic functions:

$$\varvec{X}\left( \xi \right) = \sum\limits_{{n_{1} = 0}}^{{N_{1} - 1}} { \ldots \sum\limits_{{n_{R} = 0}}^{{N_{R} - 1}} {Y_{{n_{1} n_{2} \ldots n_{R} }} H_{{n_{1} }} \left( {\xi_{1} } \right) \ldots H_{{n_{R} }} \left( {\xi_{R} } \right)} }$$
(16)
$$\dot{\varvec{X}}\left( \xi \right) = \sum\limits_{{n_{1} = 0}}^{{N_{1} - 1}} { \ldots \sum\limits_{{n_{R} = 0}}^{{N_{R} - 1}} {\dot{Y}_{{n_{1} n_{2} \ldots n_{R} }} H_{{n_{1} }} \left( {\xi_{1} } \right) \ldots H_{{n_{R} }} \left( {\xi_{R} } \right)} }$$
(17)
$$\ddot{\varvec{X}}\left( \xi \right) = \sum\limits_{{n_{1} = 0}}^{{N_{1} - 1}} { \ldots \sum\limits_{{n_{R} = 0}}^{{N_{R} - 1}} {\ddot{Y}_{{n_{1} n_{2} \ldots n_{R} }} H_{{n_{1} }} \left( {\xi_{1} } \right) \ldots H_{{n_{R} }} \left( {\xi_{R} } \right)} }$$
(18)

Equations (16–18) are substituted into Eq. (14), and the following formula is obtained by utilizing Eq. (10).

$$\begin{aligned} \left( {\varvec{M}_{0} \frac{{d^{2} }}{{dt^{2} }} + \varvec{C}_{0} \frac{d}{dt} + \varvec{K}_{0} } \right)\sum\limits_{{n_{1} = 0}}^{{N_{1} - 1}} { \ldots \sum\limits_{{n_{R} = 0}}^{{N_{R} - 1}} {\varvec{Y}_{{N_{1} N_{2} \ldots N_{R} }} H_{{n_{1} }} \left( {\xi_{1} } \right) \ldots H_{{n_{R} }} \left( {\xi_{R} } \right)} } \hfill \\ + \sum\limits_{i = 1}^{{N_{m} }} {\varvec{M}_{i} } \sum\limits_{{n_{1} = 0}}^{{N_{1} - 1}} { \ldots \sum\limits_{{n_{R} = 0}}^{{N_{R} - 1}} {\varvec{\ddot{Y}}_{{N_{1} N_{2} \ldots N_{R} }} H_{{n_{1} }} \left( {\xi_{1} } \right) \ldots H_{{n_{i - 1} }} \left( {\xi_{i - 1} } \right)\left[ {\alpha_{{n_{i} }} H_{{n_{i - 1} }} \left( {\xi_{i} } \right) + \beta_{{n_{i} }} H_{{n_{i} }} \left( {\xi_{i} } \right) + \gamma_{{n_{i + 1} }} H_{{n_{i + 1} }} \left( {\xi_{i} } \right)} \right]H_{{n_{i + 1} }} \left( {\xi_{i + 1} } \right) \ldots H_{{n_{R} }} \left( {\xi_{R} } \right)} } \hfill \\ + \sum\limits_{i = 1}^{{N_{c} }} {\varvec{C}_{i} } \sum\limits_{{n_{1} = 0}}^{{N_{1} - 1}} { \ldots \sum\limits_{{n_{R} = 0}}^{{N_{R} - 1}} {\dot{\varvec{Y}}_{{N_{1} N_{2} \ldots N_{R} }} H_{{n_{1} }} \left( {\xi_{1} } \right) \ldots H_{{n_{i - 1} }} \left( {\xi_{i - 1} } \right)\left[ {\alpha_{{n_{i} }} H_{{n_{i - 1} }} \left( {\xi_{i} } \right) + \beta_{{n_{i} }} H_{{n_{i} }} \left( {\xi_{i} } \right) + \gamma_{{n_{i + 1} }} H_{{n_{i + 1} }} \left( {\xi_{i} } \right)} \right]H_{{n_{i + 1} }} \left( {\xi_{i + 1} } \right) \ldots H_{{n_{R} }} \left( {\xi_{R} } \right)} } \hfill \\ + \sum\limits_{i = 1}^{{N_{k} }} {\varvec{K}_{i} } \sum\limits_{{n_{1} = 0}}^{{N_{1} - 1}} { \ldots \sum\limits_{{n_{R} = 0}}^{{N_{R} - 1}} {\varvec{Y}_{{N_{1} N_{2} \ldots N_{R} }} H_{{n_{1} }} \left( {\xi_{1} } \right) \ldots H_{{n_{i - 1} }} \left( {\xi_{i - 1} } \right)\left[ {\alpha_{{n_{i} }} H_{{n_{i - 1} }} \left( {\xi_{i} } \right) + \beta_{{n_{i} }} H_{{n_{i} }} \left( {\xi_{i} } \right) + \gamma_{{n_{i + 1} }} H_{{n_{i + 1} }} \left( {\xi_{i} } \right)} \right]H_{{n_{i + 1} }} \left( {\xi_{i + 1} } \right) \ldots H_{{n_{R} }} \left( {\xi_{R} } \right)} } \hfill \\ = \varvec{F}\left( t \right) \hfill \\ \end{aligned}$$
(19)

Both ends of Eq. (19) are multiplied by \(H_{{r_{1} }} \left( {\xi_{1} } \right) \ldots H_{{r_{R} }} \left( {\xi_{R} } \right)\), and the following formula is obtained by utilizing the weighted orthogonal relation Eq. (9).

$$\begin{aligned} \left( {\varvec{M}_{0} \frac{{d^{2} }}{{dt^{2} }} + \varvec{C}_{0} \frac{d}{dt} + \varvec{K}_{0} } \right)\varvec{Y}_{{r_{1} r_{2} \cdots r_{R} }} + \sum\limits_{i = 1}^{R} {\varvec{M}_{i} \left[ {\alpha_{{r_{i + 1} }} \varvec{\ddot{Y}}_{{r_{1} r_{2} \cdots r_{i - 1} r_{i + 1} r_{i + 1} \cdots r_{R} }} + \beta_{{r_{i} }} \varvec{\ddot{Y}}_{{r_{1} r_{2} \cdots r_{R} }} + \gamma_{{r_{i - 1} }} \varvec{\ddot{Y}}_{{r_{1} r_{2} \cdots r_{i - 1} r_{i - 1} r_{i + 1} \cdots r_{R} }} } \right]} \hfill \\ + \sum\limits_{i = 1}^{R} {\varvec{C}_{i} \left[ {\alpha_{{r_{i + 1} }} \dot{\varvec{Y}}_{{r_{1} r_{2} \cdots r_{i - 1} r_{i + 1} r_{i + 1} \cdots r_{R} }} + \beta_{{r_{i} }} \dot{\varvec{Y}}_{{r_{1} r_{2} \cdots r_{R} }} + \gamma_{{r_{i - 1} }} \dot{\varvec{Y}}_{{r_{1} r_{2} \cdots r_{i - 1} r_{i - 1} r_{i + 1} \cdots r_{R} }} } \right]} \hfill \\ + \sum\limits_{i = 1}^{R} {\varvec{K}_{i} \left[ {\alpha_{{r_{i + 1} }} \varvec{Y}_{{r_{1} r_{2} \cdots r_{i - 1} r_{i + 1} r_{i + 1} \cdots r_{R} }} + \beta_{{r_{i} }} \varvec{Y}_{{r_{1} r_{2} \cdots r_{R} }} + \gamma_{{r_{i - 1} }} \varvec{Y}_{{r_{1} r_{2} \cdots r_{i - 1} r_{i - 1} r_{i + 1} \cdots r_{R} }} } \right]} \hfill \\ = \varvec{F}\left( t \right)\delta_{{0r_{1} }} \delta_{{0r_{2} }} \cdots \delta_{{0r_{R} }} \hfill \\ \end{aligned}$$
(20)

After every \(r_{i} \left( {i = 1,2, \ldots R} \right)\) of \(H_{{r_{1} }} \left( {\xi_{1} } \right) \ldots H_{{r_{R} }} \left( {\xi_{R} } \right)\) is taken over all \(r_{i} = 0,1, \ldots N_{i} - 1\), \(\prod\nolimits_{{i = 1}}^{R} {N_{i} }\) deterministic equations of responses \(\varvec{Y} = \left[ {\varvec{Y}_{00 \ldots 0} \varvec{Y}_{00 \ldots 1} \ldots \varvec{Y}_{{N_{1} - 1N_{2} - 1 \ldots N_{R - 1} }} } \right]^{T}\) are obtained. At this point, a random dynamic equation with n degrees of freedom is converted into an equivalent extended-order deterministic system dynamic equation with \(\prod\nolimits_{{i = 1}}^{R} {N_{i} }\) degrees of freedom. To obtain the response of the original system, the components of Y are substituted into Eqs. (16–18).

The standard deviations of the extended-order system dynamic responses under the random excitation F(t) are obtained by the complex Cotes integration method suggested by [8].

4 Example analysis

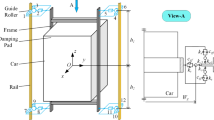
In this section, a two-degree-of-freedom high-speed elevator car system vibration model was used as an example (refer to [20]), and the vibration responses of the car and the numerical characteristics of responses were analyzed. As shown in Fig. 10, a rectangular coordinate system was established. The elevator car’s centroid o is the origin, and the horizontal direction and the plumb direction are the x axis and y axis, respectively. The elevator car has two degrees of freedom, and they are the translation of the horizontal direction and the rotation around the centroid on the oxy surface. The mass of the elevator car is m, the moment of inertia is J, the stiffness of the spring in the guide shoes is k, and the damping of the guide shoes is c. The distance from the upper guide shoes to the mass is l1 and the distance from the lower guide shoes to the mass is l2. For the values of the car’s parameters refer to [20]. The calculation results of [20] showed that the sensitivity of geometric parameters l1 and l2 were much greater than that of the quality parameters m and J and kinetic parameters k and c. That is, under the same coefficient of variation, the influences of the randomness of parameters l1 and l2 on the responses are much larger than the other parameters. Therefore, the car mass m, the moment of inertia J, the stiffness of the spring k, and the damping of guide shoes c are considered as deterministic parameters. Their values are m = 1000 kg, J = 1500 kg m2, k = 7500 N/m and c = 120 N/(m/s). The geometric parameters are considered as random parameters. The mean values of l1 and l2 are \(\bar{l}_{1} = 1.6\;{\text{m}}\) and \(\bar{l}_{2} = 1.4\;{\text{m}}\). In this case, the coefficient of variation is 0.05, the standard deviations \(\sigma_{{l_{1} }} = 0.08\;\text{m}\), and \(\sigma_{{l_{2} }} = 0.07\;\text{m}\).

Fig. 10
figure 10

Vibration model of the two-degrees-of-freedom car system

Full size image

The dynamical differential equations of this system are shown below

$$\varvec{M}{\ddot{\varvec{X}}} + \varvec{C}{\dot{\varvec{X}}} + \varvec{KX} = \varvec{F}\left( t \right)$$
(21)

In which

$$\varvec{M} = \left( {\begin{array}{*{20}c} m 0 \\ 0 J \\ \end{array} } \right),\quad\varvec{C} = \left( {\begin{array}{*{20}c} {4c} { - \;2c\left( {l_{1} - l_{2} } \right)} \\ { - \;2c\left( {l_{1} - l_{2} } \right)} {2c\left( {l_{1}^{2} + l_{2}^{2} } \right)} \\ \end{array} } \right),\,\varvec{K} = \left[ {\begin{array}{*{20}c} {4k} { - \;2k\left( {l_{1} - l_{2} } \right)} \\ { - \;2k\left( {l_{1} - l_{2} } \right)} {2k\left( {l_{1}^{2} + l_{2}^{2} } \right)} \\ \end{array} } \right]\,\varvec{X} = \left( {\begin{array}{*{20}c} x \\ \theta \\ \end{array} } \right)$$

F (t) is the external excitation vector caused by the irregularity of the guide rails in the car system shown in Fig. 8.

The stiffness matrix and damping matrix of the differential equation of the car vibration system can be written as the following equations:

$$\varvec{K} = \varvec{K}_{0} + \varvec{K}_{1} \xi_{1} + \varvec{K}_{2} \xi_{2}$$
(22)
$$\varvec{C} = \varvec{C}_{0} + \varvec{C}_{1} \xi_{1} + \varvec{C}_{2} \xi_{2}$$
(23)

In which\(\varvec{K}_{0} = \left[ {\begin{array}{ll} {4k} &\quad { - 2k\left( {\bar{l}_{1} - \bar{l}_{2} } \right)} \\ { - 2k\left( {\bar{l}_{1} - \bar{l}_{2} } \right)}& \quad {2k\left( {\bar{l}_{1}^{2} + \bar{l}_{2}^{2} } \right)} \\ \end{array} } \right], \quad \varvec{K}_{1} = \left[ {\begin{array}{ll} 0 &\quad { - 2k} \\ { - 2k} &\quad {4k\bar{l}_{1} } \\ \end{array} } \right]\sigma_{{l_{1} }}, \quad \varvec{K}_{2} = \left[ {\begin{array}{ll} 0 &\quad {2k} \\ {2k}&\quad {4k\bar{l}_{2} } \\ \end{array} } \right]\sigma_{{l_{2} }}, \quad \varvec{C}_{0} = \left[ {\begin{array}{ll} {4c} &\quad { - 2c\left( {\bar{l}_{1} - \bar{l}_{2} } \right)} \\ { - 2c\left( {\bar{l}_{1} - \bar{l}_{2} } \right)} &\quad {2c\left( {\bar{l}_{1}^{2} + \bar{l}_{2}^{2} } \right)} \\ \end{array} } \right], \quad \varvec{C}_{1} = \left[ {\begin{array}{ll} 0 &\quad{ - 2c} \\ { - 2c} &\quad{4c\bar{l}_{1} } \\ \end{array} } \right]\sigma_{{l_{1} }}, \quad \varvec{C}_{1} = \left[ {\begin{array}{ll} 0 &\quad{ - 2c} \\ { - 2c}&\quad {4c\bar{l}_{1} } \\ \end{array} } \right]\sigma_{{l_{1} }}, \quad \varvec{C}_{2} = \left[ {\begin{array}{ll} 0 &\quad {2c} \\ {2c} &\quad {4c\bar{l}_{2} } \\ \end{array} } \right]\sigma_{{l_{2} }}.\)The \(\xi_{1}\) and \(\xi_{2}\) obey the standard normal distribution. Equation (21) can be written as:

$$\varvec{M}{\ddot{\varvec{X}}} + \left( {\varvec{C}_{0} + \varvec{C}_{1} \xi_{1} + \varvec{C}_{2} \xi_{2} } \right)\dot{\varvec{X}} + \left( {\varvec{K}_{0} + \varvec{K}_{1} \xi_{1} + \varvec{K}_{2} \xi_{2} } \right)\varvec{X} = \varvec{F}\left( t \right).$$
(24)

According to the orthogonal polynomial approximation method, the responses of a system are decomposed in accordance with three-order Hermite polynomials.

$$\varvec{X}\left( \xi \right) = \sum\limits_{{n_{1} = 0}}^{3} { \ldots \sum\limits_{{n_{R} = 0}}^{3} {\varvec{Y}_{{n_{1} n_{2} }} H_{{n_{1} }} \left( {\xi_{1} } \right)H_{{n_{2} }} \left( {\xi_{2} } \right)} }$$
(25)
$$\dot{\varvec{X}}\left( \xi \right) = \sum\limits_{{n_{1} = 0}}^{3} { \ldots \sum\limits_{{n_{R} = 0}}^{3} {\dot{\varvec{Y}}_{{n_{1} n_{2} }} H_{{n_{1} }} \left( {\xi_{1} } \right)H_{{n_{2} }} \left( {\xi_{2} } \right)} }$$
(26)
$$\ddot{\varvec{X}}\left( \xi \right) = \sum\limits_{{n_{1} = 0}}^{3} { \ldots \sum\limits_{{n_{R} = 0}}^{3} {\ddot{\varvec{Y}}_{{n_{1} n_{2} }} H_{{n_{1} }} \left( {\xi_{1} } \right)H_{{n_{2} }} \left( {\xi_{2} } \right)} }$$
(27)

where \(H_{{n_{1} }} \left( {\xi_{1} } \right)\) and \(H_{{n_{2} }} \left( {\xi_{2} } \right)\) are the corresponding order Hermite polynomials.Substituting Eqs. (25–27) into Eq. (24) and utilizing the weighted orthogonal relation to rearrange it, a 32-order deterministic vibration differential equation can be obtained

$$\varvec{M}_{{\left( {32 \times 32} \right)}} \ddot{\varvec{Y}} + \varvec{C}_{{\left( {32 \times 32} \right)}} \dot{\varvec{Y}} + \varvec{K}_{{\left( {32 \times 32} \right)}} \varvec{Y} = \varvec{F}_{{\left( {32 \times 1} \right)}} \left( t \right)$$
(28)

Equation (28) can be solved by the Wilson-θ numerical integration method. The responses of the original system can be obtained by substituting the responses of the extended-order system into Eqs. (25–27). In this paper, the center point of car bottom is regarded as observation point \(o'\). The acceleration mean responses of the observation point were calculated in the case of the irregularity of the guide rails as shown in Fig. 6, and compared with the results obtained by Monte Carlo method, as shown in Fig. 11.

Fig. 11
figure 11

Mean horizontal vibration acceleration responses of the observation point

Full size image

As can be seen from Fig. 11, the curve obtained by this method is in good agreement with the Monte Carlo method. It suggests that this method has high precision. On the graph, the point of the sharp change of acceleration is located at the junctions of the guide rail, and the direction of acceleration is the same as the deviation direction of the guide rail junctions, which is in accordance with the actual situation. After removing the points of guide rail joints, the car is similar to a harmonic vibration, and the non-smooth shape of the wave is caused by the irregularity of the guide rails’ surface.

The mean responses of the horizontal acceleration at the observation point of the car were calculated by the random excitations of Figs. 8 and 9, respectively, and the resulting contrast images are shown in Fig. 12. The random excitations of the former were produced in the nonlinear guide shoe model, and the random excitations of the latter were produced in traditional linear guide shoe model. It can be seen that the mean responses of the former are generally greater than the latter. This is especially evident in the guide rail junctions. This is further verified by the result obtained from the analysis of Fig. 5 in Sect. 2: the nonlinearity of the guide shoes will aggravate the vibration of the car.

Fig. 12
figure 12

Mean acceleration responses obtained by the nonlinear guide shoe model and linear guide shoe model

Full size image

To study the influence of different Cv (coefficient of variation) of parameters on the mean horizontal acceleration responses of the observation point, the mean responses of acceleration were calculated in the case of the Cv of the car parameters equal to 0.05 and 0.005, respectively, and the resulting image is shown in Fig. 13. Comparing the two curves of Fig. 13, under the low coefficient of variation, the acceleration response amplitudes of the observation point are slightly lower than those under the high coefficient of variation. This shows that reducing only the variability of random parameters has little effect on reducing the horizontal vibration acceleration of the car. The standard deviations of the acceleration responses were calculated, and the results are shown in Table 1. Ten equally spaced time points are chosen as the object of inspection. The coefficient of variation of responses are obtained by calculating means and standard deviations of the responses. After calculation, the difference of their means is small, but the values of standard deviations of the latter are on average 8.1 times that of the former, and the coefficient of variation of the latter are on average 3 times that of the former. This shows that reducing the variability of random parameters has a great effect on reducing the degree of dispersion of acceleration responses.

Fig. 13
figure 13

Mean horizontal vibration acceleration responses of the observation point at different coefficients of variation

Full size image
Table 1 Numerical characteristics of responses in the case of the same random excitation and different parameters’ Cv
Full size table

When the irregularity of the guide rails was lowered, the acceleration responses at the observation point were calculated, and compared with the original acceleration responses. The results are shown in Fig. 14. The irregularity of the guide rail was reduced to 0.5 times the original, and the vibration acceleration response amplitudes of the observation point were obviously smaller than the amplitudes of the original vibration responses. This shows that improving the straightness and flatness of the guide rails can effectively reduce the horizontal vibration of the car.

Fig. 14
figure 14

Mean vibration acceleration responses at the original and 0.5 times the original irregularity of the guide rails

Full size image

5 Conclusions

  1. (1.)

    To make the model closer to the actual situation, in this paper, the shortcomings of the linear guide shoe model were avoided in the analysis of the horizontal vibration of a traditional high-speed elevator car. The functional relationship between the amount of deformation of the rolling guide shoes and the restoring force were derived by the Hertz contact theory, and the nonlinear guide shoe model was established. Under the same random irregularity of the guide rails, random guide rail excitations generated by these two models were compared and analyzed. It was concluded that the nonlinearity of the rolling guide shoes can aggravate the vibration of the car.

  2. (2.)

    The response analysis method of composite random vibration of a high-speed elevator was established by the orthogonal polynomial approximation method, and the horizontal vibration acceleration responses of a two-degree-freedom car model were analyzed and calculated. The acceleration diagram obtained by this method can well fit the acceleration diagram obtained by Monte Carlo method, and the accuracy of the method used in this paper is verified.

  3. (3.)

    Under the different parameters’ coefficients of variation and different irregularities of the guide rails, the horizontal vibration acceleration responses of high-speed elevator car system were compared and analyzed. The results showed that reducing the random parameters’ coefficient of variation can greatly reduce the dispersion degree in the mean of responses, but it can not effectively reduce the amplitude of the mean vibration acceleration responses, but reducing the irregularity of the guide rails (increasing the flatness and straightness of the guide rail) can greatly reduce the vibration acceleration of the car.