Time-varying characteristics of guide roller-rail contact stiffness of super high-speed elevator under aerodynamic load

Abstract

The super high-speed operation of the elevator will inevitably make the elevator bear significant aerodynamic load. Under the action of the aerodynamic load, the rubber on the outer ring of the guide roller will produce a certain deformation, which will cause the contact stiffness between the guide roller and the rail to change. Moreover, because the aerodynamic load is time-varying, the guide roller-rail contact stiffness will also show the time-varying characteristics. In view of this, considering the time-varying characteristics of the contact stiffness, a 17 degrees-of-freedom (DOF) dynamic model of the horizontal vibration of the super high-speed elevator is established in this paper; the Gaussian white noise is employed to simulate the excitations of guide, and the Savitzky–Golay filter is used to filter the excitations; based on Hertz elastic contact theory, the guide roller-rail contact stiffness model is established under the action of preload and aerodynamic loads; for the calculation of aerodynamic load, a user-defined file is compiled according to the actual running curve of the elevator to set the velocity inlet boundary condition, and CFD numerical simulation is used to obtain the aerodynamic load data of the whole running process of the elevator; finally, using Newmark-β method, the time-varying characteristics of the contact stiffness under the action of aerodynamic load are analyzed, so as to influence the horizontal vibration of the elevator. The results show that, under the action of aerodynamic load, the maximum change rate of contact stiffness is 5.2%, which has a significant impact on the horizontal vibration of the elevator, among which the vibration acceleration of the elevator in the X-direction increases by 16.97%. Therefore, the effect of aerodynamic load should be considered in the study of the dynamic response of the super high-speed elevator.

1 Introduction

The vibration is one of the important indexes to evaluate the ride comfort of an elevator. The amplitude, the frequency, and the direction of vibration can all affect passengers' perception of vibration. Compared with vertical vibration, human body is more sensitive to horizontal vibration [1]. There are many excitation sources that cause the horizontal vibration of elevator, such as guide rail defect, air disturbance in hoistway, swing of traction rope, shaking of building caused by strong wind or earthquake [2]. Among all these excitation sources, guide rail excitation plays a major role, and it exists in the whole process of elevator operation.

In view of the influence of rail excitation on elevator horizontal vibration, many scholars have done a lot of useful exploration. In order to analyze the dynamic characteristics of the elevator, Li et al. [3] proposed a model construction method suitable for analyzing the horizontal vibration of the elevator; up to now, this method has been widely used; guide rail excitation was one of the important factors that affect the horizontal vibration of elevator; Feng et al. [4] constructed the horizontal vibration model of elevator, calculated the acceleration of elevator horizontal vibration with the rail excitation measured by experiment as input, and verified its correctness by experiment;

Song [5] used the sinusoidal signal to approximate the fluctuation of the guide rail, the step signal to the gap excitation at the connection of the guide rail, and the random signal to the rail surface roughness; on this basis, the 1/4 model of the elevator was established. Du et al. [6] introduced wavelet de-noising method to improve the effectiveness of elevator guide rail irregularity identification; the results show that discrete wavelet change can be used as a tool for elevator horizontal vibration signal de-noising and rail fault diagnosis; the coupling vibration between the elevator components also affected the horizontal vibration of the elevator. Xia et al. [7] constructed the elevator dynamic model in the horizontal direction, including the guide roller-rail interface contact stiffness, and by considering the guide rail excitation, the horizontal vibration law of the elevator was analyzed; Zhang et al. [8] considered the coupling effect of various parts in the elevator system, established the coupling dynamic model of guide rail, guide shoes, and car, and analyzed the influence of structural parameters of guide rail (the length, the weight of rail per unit length, and bending stiffness) on the dynamic characteristics of rail; Cao et al. [9] considered the influence of the forced vibration of the rail on the vibration of the elevator, and the coupling between the various system components, established the dynamic model of the coupling of the car-rail-guide shoe, and studied the influence of the rail parameters on the horizontal vibration of the super high-speed elevator car.

With the increase in elevator operation speed, the influence of air disturbance on the horizontal vibration becomes more and more significant. Mao [10] studied the air flow disturbance characteristics in the working process of the mining elevator and obtained the total lateral vibration displacement of the elevator by considering the aerodynamic load and the eccentric load during the operation of the elevator; Liu et al. [11] comprehensively considered the common excitation effect of shaft air flow and guiding system, proposed a gas structure coupling vibration analysis method for high-speed elevator, and analyzed the influence of shaft air flow on the horizontal vibration of car under different operating speeds.

As we all know, in the process of elevator operation, the contact between the guide rollers and the rails ensures that the elevator runs along the fixed direction. In order to reduce the vibration of elevator, the outer ring of guide roller is usually made of rubber, which can absorb vibration [12]. Moreover, the preload is applied to ensure that the two are in contact all the time [13]. For the guide roller-rail contact stiffness, according to Kalker’s three-dimensional Hertz rolling contact simplification theory, Mei et al. [14] established the three-dimensional rolling contact model of guide roller-rail and deduced the normal, longitudinal, and transverse contact stiffness coefficients; based on the contact stiffness model established by Mei et al. [14], Wang et al. [15] established the dynamic model of car-roller-rail coupling vibration and calculated the horizontal vibration response of the elevator system under the multi-point excitation of guide rail bracket; Zhu et al. [16] calculated the contact force between the guide roller and the rail by the proposed judgment algorithm of the contact state, and then constructed the coupled vibration dynamic model of the car-frame-rail, and analyzed the seismic response of the coupling system under the seismic excitation; according to Hertz contact theory, Zhang et al. [17] derived the function expression of the relationship between the roller deformation and the guide roller-rail contact force and established the nonlinear model of the guide roller.

Although the existing research has done some research on the guide roller-rail contact stiffness of elevator, to our best knowledge, the influence of aerodynamic load on the wheel rail contact stiffness has not been considered. In the actual operation of the elevator, especially for the high-speed (2 m/s < $v_{{{\text{elevator}}}}$ ≤ 5 m/s)/super high-speed ($v_{{{\text{elevator}}}}$ > 5 m/s) elevator, the aerodynamic loads are relatively significant, which will inevitably change the resulting preload between the roller and the rail. Therefore, under the constant change of contact force, the roller will produce different degrees of deformation, which makes the contact stiffness show the "time-varying characteristics" and ultimately affect the dynamic behavior of the elevator. To solve this problem, a time-varying model of guide roller-rail contact stiffness under the action of aerodynamic load is established in this paper. Based on this model, a 17-DOF dynamic model of elevator horizontal vibration is constructed, and the impact of aerodynamic loads on the wheel rail contact stiffness and the dynamic response of elevator are analyzed.

2 Dynamic model construction of super high-speed elevator

2.1 17-DOF dynamic model of elevator horizontal vibration

The purpose of this paper is to study the influence of aerodynamic force (moment) on guide roller-rail contact stiffness, and the change of elevator vibration acceleration caused by it, and it was necessary to consider the influence of the excitation disturbance at each guide boot. Meanwhile, the car and the frame are regarded as one [18] for a more obvious influence law in this paper. Referring to above work and the assumptions, the dynamic model constructed has 17 degrees of freedom (DOFs), the translation of car system along X-axis and Y-axis, the rotation around X-, Y-, and Z-axis, and the translation of 12 rollers, as shown in Fig. 1, where O is the centroid of the car system; $h_{1}$ is the vertical distance from the centroid of car top guide roller to O; $h_{2}$ is the vertical distance from the centroid of car bottom guide roller to O; $W_{g}$ is the horizontal distance from the centroid of roller to O in Y-direction. The differential equation of the horizontal vibration of the super high-speed elevator is,

$${\mathbf{M\ddot{X}}} + {\mathbf{C\dot{X}}} + {\mathbf{KX}} = {\mathbf{F}}$$

(1)

where

$$X = [x_{cf} ,y_{cf} ,\theta_{x} ,\theta_{y} ,\theta_{z} ,x_{1} ,y_{2} ,x_{3} ,x_{4} ,y_{5} ,x_{6} ,x_{7} ,y_{8} ,x_{9} ,x_{10} ,y_{11} ,x_{12} ]^{T}$$

(A1)

$$M = diag\left( {m_{cf} ,m_{cf} ,J_{x} ,J_{y} ,J_{z} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} } \right)$$

(A2)

$${\mathbf{K}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{11} } & {{\mathbf{K}}_{12} } \\ {{\mathbf{K}}_{21} } & {{\mathbf{K}}_{22} } \\ \end{array} } \right],$$

$${\mathbf{K}}_{11} = \left[ {\begin{array}{*{20}l} {8k_{s} } \hfill & 0 \hfill & 0 \hfill & {4k_{s} \left( {h_{1} - h_{2} } \right)} \hfill & 0 \hfill \\ 0 \hfill & {4k_{s} } \hfill & {2k_{s} \left( {h_{1} - h_{2} } \right)} \hfill & 0 \hfill & { - k_{s} } \hfill \\ 0 \hfill & {2k_{s} \left( {h_{1} - h_{2} } \right)} \hfill & {2k_{s} \left( {h_{1}^{2} + h_{2}^{2} } \right)} \hfill & 0 \hfill & 0 \hfill \\ {4k_{s} \left( {h_{1} - h_{2} } \right)} \hfill & 0 \hfill & 0 \hfill & {4k_{s} \left( {h_{1}^{2} + h_{2}^{2} } \right)} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {8k_{s} w_{g} } \hfill \\ \end{array} } \right],$$

$$\begin{gathered} {\mathbf{K}}_{12} = {\mathbf{K}}_{21}^{T} \hfill \\ = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ { - k_{s} h_{1} } \\ { - k_{s} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - k_{s} } \\ \end{array} } \\ { - k_{s} h_{1} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ { - k_{s} h_{1} } \\ { - k_{s} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ { - k_{s} h_{1} } \\ {k_{s} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - k_{s} } \\ \end{array} } \\ { - k_{s} h_{1} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ { - k_{s} h_{1} } \\ {k_{s} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ {k_{s} h_{2} } \\ { - k_{s} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - k_{s} } \\ \end{array} } \\ {k_{s} h_{2} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ {k_{s} h_{2} } \\ { - k_{s} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ {k_{s} h_{2} } \\ {k_{s} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - k_{s} } \\ \end{array} } \\ {k_{s} h_{2} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{s} } \\ 0 \\ \end{array} } \\ 0 \\ {k_{s} h_{2} } \\ {k_{s} w_{g} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$

$${\mathbf{K}}_{22} = k_{s} {\mathbf{I}}_{12 \times 12} + {\text{diag}}\left( {k_{c1} ,k_{c2} ,k_{c3} ,k_{c4} ,k_{c5} ,k_{c6} ,k_{c7} ,k_{c8} ,k_{c9} ,k_{c10} ,k_{c11} ,k_{c12} } \right),$$

$${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{11} } & {{\mathbf{C}}_{12} } \\ {{\mathbf{C}}_{21} } & {{\mathbf{C}}_{22} } \\ \end{array} } \right],$$

$${\mathbf{C}}_{11} { = }\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {8c_{g} } \\ 0 \\ \end{array} } \\ 0 \\ {4c_{gf} \left( {h_{1} - h_{2} } \right)} \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {4c_{gf} } \\ \end{array} } \\ {{2}c_{gf} \left( {h_{1} - h_{2} } \right)} \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {2c_{gf} \left( {h_{1} - h_{2} } \right)} \\ \end{array} } \\ {2c_{gf} \left( {h_{1}^{2} + h_{2}^{2} } \right)} \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {4c_{g} \left( {h_{1} - h_{2} } \right)} \\ 0 \\ \end{array} } \\ 0 \\ {4c_{gf} \left( {h_{1}^{2} + h_{2}^{2} } \right)} \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ {{8}c_{gf} w_{g} } \\ \end{array} } \\ \end{array} } \right],$$

$$\begin{gathered} {\mathbf{C}}_{12} = {\mathbf{C}}_{21}^{T} = \hfill \\ \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ { - c_{gf} h_{1} } \\ { - c_{gf} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - c_{gf} } \\ \end{array} } \\ { - c_{gf} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ { - c_{gf} h_{1} } \\ { - c_{gf} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ { - c_{gf} h_{1} } \\ {c_{gf} w_{g} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - c_{gf} } \\ \end{array} } \\ { - c_{gf} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ { - c_{gf} h_{1} } \\ {c_{gf} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ {c_{gf} h_{2} } \\ { - c_{gf} w_{g} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - c_{gf} } \\ \end{array} } \\ { - c_{gf} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ {c_{gf} h_{2} } \\ { - c_{gf} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ {c_{gf} h_{2} } \\ {c_{gf} w_{g} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - c_{gf} } \\ \end{array} } \\ { - c_{gf} } \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - c_{gf} } \\ 0 \\ \end{array} } \\ 0 \\ {c_{gf} h_{2} } \\ { - c_{gf} w_{g} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$

$${\mathbf{C}}_{22} = c_{gf} {\mathbf{I}}_{12 \times 12} ,{\mathbf{F}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{O}}_{1 \times 5} } & {{\mathbf{F}}_{12} } \\ \end{array} } \right]^{T} ,$$

$$\begin{gathered} {\mathbf{F}}_{12} = [\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{c1} e_{1} \left( t \right)} & {k_{c2} e_{2} \left( t \right)} & { - k_{c3} e_{3} \left( t \right)} \\ \end{array} } & {k_{c4} e_{4} \left( t \right)} & { - k_{c5} e_{5} \left( t \right)} & {_{6} - k_{c6} e_{6} \left( t \right)} \\ \end{array} \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {k_{c7} e_{1} \left( t \right)} & {k_{c8} e_{2} \left( t \right)} & { - k_{c9} e_{3} \left( t \right)} \\ \end{array} } & {k_{c10} e_{4} \left( t \right)} & { - k_{c11} e_{5} \left( t \right)} & { - k_{c12} e_{6} \left( t \right)} \\ \end{array} ]^{T} \\ \end{gathered}$$

where $M$ is mass matrix, ${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{11} } & {{\mathbf{C}}_{12} } \\ {{\mathbf{C}}_{21} } & {{\mathbf{C}}_{22} } \\ \end{array} } \right]$ is damping matrix, ${\mathbf{K}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{11} } & {{\mathbf{K}}_{12} } \\ {{\mathbf{K}}_{21} } & {{\mathbf{K}}_{22} } \\ \end{array} } \right]$ is stiffness matrix, ${\mathbf{F}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{O}}_{1 \times 5} } & {{\mathbf{F}}_{12} } \\ \end{array} } \right]^{T}$ is external force matrix of lift car, ${\mathbf{O}}_{1 \times 5}$ is zero matrix, ${\mathbf{I}}_{12 \times 12}$ is identity matrix, and $e_{i} \left( t \right)(i = 1,2, \ldots \ldots ,6)$ is displacement excitation of “T” guide rail.

Fig. 1

17-DOF dynamic model of elevator horizontal vibration

2.2 The contact stiffness between the guide roller and the rail

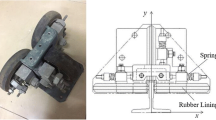
As shown in Fig. 2, it is the structure diagram of guide roller, a guide roller contains three rollers, and the outer ring of roller is made of rubber. The guide roller replaces the sliding friction with the rolling friction to reduce the friction loss, so it is usually installed on the elevator with a running speed of more than 2 m/s [19]. The connection between guide roller and frame can be regarded as spring-damping structure, because the stiffness of rail is much greater than that of the rubber, so the rail is regarded as a rigid rail.

Fig. 2

The structure diagram of guide roller

Furthermore, compared with the normal contact force, the creep force in the contact area is very small, so the effect of creep force is ignored in this paper. And the single guide roller-rail contact model constructed is shown in Fig. 3, where $k_{s}$ and $c_{gf}$ are the equivalent stiffness and damping of connecting structure between guide roller and frame; $F_{{\text{l}}}$ is the total load on each roller; $k_{c}$ is the contact stiffness between guide roller and rail; $e\left( z \right)$ is the surface roughness of guide rail.

Fig. 3

The single guide roller-rail contact model

To ensure that the guide roller and rail are in contact at all times during the operation of the elevator, a preload $F_{pre}$ is usually applied during installation. Under the action of preload, the rubber will have some elastic deformation $\delta_{0} \left( {F_{pre} } \right)$. In addition to the preload, the super high-speed elevator will be subjected to a large aerodynamic force (moment) in the horizontal direction during its operation [20]. And with the increase in the speed of the elevator, the horizontal aerodynamic force (moment) of the elevator will increase substantially, because of this the rubber deformation changes during the motion, and lead to the change of the guide roller-rail contact stiffness. Therefore, in the dynamic model construction of the super high-speed elevator, considering the time-varying characteristics of the contact stiffness between the rolling guide shoe and the guide rail, under the aerodynamic load, is more reasonable.

According to Hertz contact theory [21], under the action of normal loads such as preload and aerodynamic force, the contact between guide roller and rail can be regarded as two cylinders with parallel axes, the section radius of one cylinder (roller) is the roller radius $R_{g}$, and the another (rail) is $\infty$. The radial width of the contact area is,

$$a = \sqrt {\frac{{4PR_{g} }}{{\pi E^{*} }}}$$

(2)

The approximate analytical expression [22] of the elastic deformation $\delta \left( F \right)$ of roller is,

$$\delta { = }\frac{P}{{\pi E^{*} }}\left[ {1 + \ln \left( {\frac{{\pi E^{*} l^{3} }}{{FR_{g} }}} \right)} \right]$$

(3)

where P is the load distribution on roller, $P = F/l$, F is the total load on roller, l is the axial width of roller; $E^{*}$ is the plane strain modulus of elasticity, $\frac{1}{{E^{*} }}{ = }\frac{{1 - \nu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu_{2}^{2} }}{{E_{2} }}$, $\nu_{1}$ and $\nu_{2}$ are the Poisson’s ratio of roller rubber and rail, $E_{1}$ and $E_{2}$ are the elastic modulus of roller rubber and rail. Because the elastic model of the rail is much larger than the elastic modulus of the rubber on the outer ring of the roller, the influence of the guide rail is ignored, namely, $E^{*} { = }\frac{{E_{1} }}{{1 - \nu_{1}^{2} }}$.

According to Eq. (3), the contact stiffness between guide roller and rail is,

$$k_{c} \left( t \right){ = }\frac{F\left( t \right)}{\delta }{ = }\left( {\pi E^{*} l} \right){/}\left[ {\ln \left( {\frac{{\pi E^{*} l^{3} }}{{F\left( t \right)R_{g} }}} \right) + 1} \right]$$

(4)

2.3 The irregularity excitation of rail

According to previous study [23,24,25], in this paper, the Gaussian white noise is employed to simulate the excitation of rail, its mean value is $\mu_{g} = 0$, and standard deviation is $\sigma_{g} = 0.6\,{\text{mm}}$. Because the actual contact between the guide roller and the rail is face contact, not point contact, so the Savitzky–Golay filter is used to filter the rail excitation [26], as shown in Fig. 4.

Fig. 4

The rail excitation after filtering

3 Numerical calculation of aerodynamic load

3.1 Computational model and operating conditions

The hoistway section and geometric details used in the simulations are shown in Fig. 5. It is obtained by simplifying an elevator experimental tower, which is equipped with a 7-m/s super high-speed elevator. Considering that the actual elevator shape modeling will make the calculation results not representative, so, in this paper, some small parts in the elevator system, such as guide shoes, safety gear, were ignored. In the calculation model built in this paper, the height of hoistway in elevator tower is 27 m, and the section size of hoistway is $2.55\,{\text{m}} \times 2.5\,{\text{m}}$. The height of car is 3 m, and the section size is $1.9\,{\text{m}} \times 2.0\,{\text{m}}$, the car is placed symmetrically in Y-direction, and the distance between the door of car and the wall of hoistway is 0.13 m. When the elevator is in the initial position, the distance between its centroid and the nearer end of the hoistway is 10.5 m.

Fig. 5

Simplified geometric model of elevator experimental tower

The running speed curve of the super high-speed elevator is shown in Fig. 6. It can be divided into three phase: $t \le 7s$, the elevator is in variable acceleration phase; $7s < t \le 9s$, the elevator runs at a constant speed, 6.3 m/s; $9s < t \le 22s$, the elevator is in variable deceleration phase.

Fig. 6

The running speed curve of the super high-speed elevator

3.2 Simulation details

The simulation of this study used the ANSYS-FLUENT® CFD software. As for the boundary conditions, the upper-end face of hoistway is set as velocity inlet, and the setting of velocity is defined by user-defined function (UDF), which is written according to the actual running speed of the super high-speed elevator. The lower-end face of hoistway is set as zero pressure outlet. The hoistway wall was set as a nonslip moving wall with the same velocity as the inlet. The elevator car wall was set as a nonslip stationary wall.

As for the setting of solver, the standard $k - \varepsilon$ model [27,28,29] is used, the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) [30, 31] is used to solve the pressure and velocity coupling equation, and the second-order upwind scheme is used to solve the momentum equation. The time step $\Delta t = 1 \times 10^{ - 2} {\text{s}}$, which is less than $1.8 \times 10^{ - 2} {\text{s}}$ [32].

3.3 Data processing

For the convenience of data analysis and comparison [33, 34], the aerodynamic forces and the aerodynamic moments can be defined as follows:

$$\left\{ \begin{gathered} \begin{array}{*{20}c} {F_{hx} = \frac{1}{2}C_{hx} \rho v^{2} A} & {F_{hy} = \frac{1}{2}C_{hy} \rho v^{2} A} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {M_{pm} = \frac{1}{2}C_{pm} \rho v^{2} Al} & {M_{ym} = \frac{1}{2}C_{ym} \rho v^{2} Al} & {M_{rm} = \frac{1}{2}C_{rm} \rho v^{2} Al} \\ \end{array} \hfill \\ \end{gathered} \right.$$

(5)

where $F_{hx}$, $F_{hy}$, $M_{pm}$, $M_{ym}$, and $M_{rm}$ denote the horizontal force in X-direction, the horizontal force in Y-direction, the pitching moment, the yawing moment, and the rolling moment, respectively; $C_{hx}$, $C_{hy}$, $C_{pm}$, $C_{ym}$, and $C_{rm}$ denote the coefficient of horizontal force in X-direction, the coefficient of horizontal force in Y-direction, the pitching moment coefficient, the yawing moment coefficient, and the rolling moment coefficient, respectively; $\rho$ is the air density, $\rho = 1.225\,{\text{kg/m}}^{3}$; v is the operation speed of elevator, $v = 7\,{\text{m/s}}$; A is the cross-sectional area of elevator car, $A = 3.8\,{\text{m}}^{2}$; l is the reference length, $l = 2.525\,{\text{m}}$.

3.4 Mesh convergence analysis

In order to ensure that the selected mesh meets the calculation requirements, in this paper, three different densities, “coarse,” “medium,” “fine,” are used to determine the most suitable mesh density, and all meshes are hexahedral. Besides, the boundary layer is set to ensure the correctness of the velocity gradient near the car wall and obtain more accurate aerodynamic load data on the elevator car. In this convergence analysis, the minimum thickness of the first boundary layer is 1.53 mm, the maximum number of boundary layer is 15, and the total number of meshes is $1.29 \sim {2}{\text{.36}} \times 10^{6}$. The detail parameters of different density meshes are shown in Table 1, and the mesh division of elevator and the boundary layer under different density mesh are shown in Fig. 7.

Table 1 The detail parameters of different mesh

Fig. 7

The mesh around car with different mesh densities

The simulation results show that, except for the horizontal force in X-direction $F_{hx}$, all aerodynamic loads are small [20], so only $F_{hx}$ is considered.

Figure 8 and Table 2 are the numerical simulation results of three sets of different density meshes. It can be seen that the maximum error of the mean value, maximum value, and root-mean-squares (RMSs) between the "medium" and the "fine" is 1.59%, while the maximum error of the mean value, maximum value, and RMSs between the "coarse" and the "medium" is 2.17%. Therefore, the aerodynamic load data are gradually converging from "coarse" to "fine" with the increase in mesh density; therefore, the aerodynamic load data calculated under "fine" density are selected in this paper.

Fig. 8

The aerodynamic coefficients in X-direction under three mesh densities

Table 2 The mean value, the maximum value, and the RMSs of aerodynamic coefficients in X-direction under different mesh densities

4 Results and discussion

In this paper, a 7-m/s super high-speed elevator is selected as an example, to analyze the influence rule of the time-varying characteristics of the contact stiffness of guide roller and rail, under the aerodynamic action. The detailed structural parameters of the selected super high-speed elevator are shown in Table 3.

Table 3 The detailed structural parameters of the selected 7-m/s super high-speed elevator

In this paper, MATLAB is used to solve the change rule of guide roller-rail contact force and contact stiffness under the action of aerodynamic load, and Newmark-β method is used to solve the dynamic response of elevator vibration acceleration considering the influence of aerodynamic load and no aerodynamic load.

4.1 Guide roller-rail contact force

In the super high-speed elevator system, the guide roller-rail contact force is mainly composed of two parts, namely the preload of guide shoe and the aerodynamic load. Figure 8 shows the relation between the contact force of each roller and the time. It can be seen from Fig. 9 that the influence of other aerodynamic forces is ignored. Except the rollers 2/5 (f_c2 = f_c5 = F_pre = 40 N) and rollers 8/11 (f_c8 = f_c11 = − F_pre = − 40 N), keep the original contact force unchanged, the wheel rail contact force changes at all other rollers, and the change trend is the same as that of the aerodynamic force in X-direction. When the elevator speed reaches the maximum, each contact force also reaches its own extreme value. Due to the aerodynamic force in the positive direction of X, the rollers 3/6/7/10 reach the maximum value of the absolute value of the wheel rail contact force. Relatively, the rollers 1/4/9/12 also reach their minimum value.

Fig. 9

The change of guider roller-rail contact force on each roller

4.2 Guide roller-rail contact stiffness

Although the force direction is opposite, the force on rollers 1/4 and rollers 9/12 is the same. Therefore, the change law of contact stiffness on these four rollers is the same. Similarly, the stiffness change of roller 3/6/7/10 is the same. The blue lines in Fig. 10 show the guide roller-rail contact stiffness at the rollers 2/5/8/11. Because the unexpected aerodynamic loads in the X-direction are ignored, there is no change in the contact stiffness at the four rollers. In addition, it can be seen from the figure that the contact stiffness fluctuates in the range of $1.277\sim 1.404\times {10}^{5}\mathrm{N}\bullet \mathrm{m}$ under the action of aerodynamic force. Compared with that without considering the aerodynamic force, the contact stiffness at 3/6/7/10 of the roller increases by 5.2%, while that at 2/5/8/11 increases by 4.23%, which is quite significant. According to the previous research, with the increase in the elevator speed, the aerodynamic load of the elevator will increase sharply, and the elevator operation condition simulated in this paper is relatively ideal. In the actual installation process, the elevator will inevitably have some position deviation, and the car surface is not completely flat, which will increase the aerodynamic load of the elevator in all directions, resulting in a more significant change in contact stiffness. Therefore, it is necessary to consider the influence of the time-varying characteristics of the upper wheel rail contact stiffness in the dynamic modeling of ultra-high-speed elevator.

Fig. 10

Variation of the guide roller-rail contact stiffness under aerodynamic load

4.3 Dynamic response analysis of super high-speed elevator

This section mainly discusses the influence of the fixed wheel rail contact stiffness and time-varying conditions on the X- and Y-direction vibration characteristics (including vibration acceleration (time domain) and vibration amplitude (frequency domain)) of the super high-speed elevator under aerodynamic load. The linear scale of vibration amplitude in low-frequency domain (0–5 Hz) was transformed into log10 scale. This is shown in Figs. 12, 14, 16, and 18, the embedded figure of Figs. 12, 14, 16, and 18. Additionally, the typical digital characteristics of the vibration acceleration in the time domain (RMS, mean, and maximum) were compared and analyzed, as shown in Table 4.

Table 4 Comparison of means, maximums, and RMSs of time domain signals

Figures 11, 12, 13, and 14 show the vibration acceleration of the elevator (time domain) and the vibration amplitude (frequency domain) in X- and Y-directions. It can be seen from the figures that the horizontal vibration acceleration and the vibration amplitude of the elevator increase after considering the aerodynamic force, that is, after the change of contact stiffness.

Fig. 11

X-direction vibration acceleration under fixed contact stiffness and time-varying conditions (time domain)

Fig. 12

X-direction vibration amplitude under fixed contact stiffness and time-varying conditions (frequency domain)

Fig. 13

Y-direction vibration acceleration under fixed contact stiffness and time-varying conditions (time domain)

Fig. 14

Y-direction vibration amplitude under fixed contact stiffness and time-varying conditions (frequency domain)

Figures 15, 16, 17, and 18 show the vibration angular acceleration (time domain) and the angular amplitude of vibration (frequency domain) signals of the elevator around the Y-axis and Z-axis. Since the aerodynamic load except for the aerodynamic force in X-direction is ignored, the contact stiffness in Y-direction has no change, which is not compared here. It can be seen from the figure that the angular acceleration and the angular amplitude of vibration increase after considering the time-varying effect of contact stiffness.

Fig. 15

Angular acceleration of vibration around Y-axis under fixed contact stiffness and time-varying conditions (time domain)

Fig. 16

Angular amplitude of vibration around Y-axis under fixed contact stiffness and time-varying conditions (frequency domain)

Fig. 17

Angular acceleration of vibration around Z-axis under fixed contact stiffness and time-varying conditions (time domain)

Fig. 18

Angular amplitude of vibration around Z-axis under fixed contact stiffness and time-varying conditions (frequency domain)

It can be found from Table 4 that the change of contact stiffness has a significant impact on elevator dynamics. In addition to the angular acceleration around Z-axis, the most significant change is the maximum value of each response. Considering the contact stiffness of $a_{cx}$, $a_{cy}$, and $\alpha_{y}$ after considering aerodynamic force, it increases 16.97%, 8.04%, and 15.13%, respectively. Among the four accelerations studied, the angular acceleration around Y-axis is the most significant one. This is because, among the aerodynamic loads on the elevator, the aerodynamic load in the X-direction is the most significant, so the stiffness change of the rollers in the X-direction is the biggest, which results in the vibration acceleration in the X-direction and the angular acceleration around the Y-axis of the elevator. To sum up, it is necessary to consider the influence of contact stiffness change on elevator vibration when the elevator is running at a speed of 7 m/s.

5 Conclusion

In this paper, the influence of aerodynamic load on the guide roller-rail contact stiffness is considered. A 17 degree-of-freedom dynamic model of elevator horizontal vibration including time-varying contact stiffness is proposed, and the influence of time-varying contact stiffness on the dynamic response of elevator is further analyzed. This not only improves the existing dynamic model of super high-speed elevator, but also has a certain guiding significance for the selection of roller rubber stiffness. The main conclusions of this chapter are as follows:

• (1) When the elevator is running at super high speed, the aerodynamic load on the elevator has obvious influence on the guide roller-rail contact force in the horizontal direction, and the aerodynamic force in the X-direction has the most significant effect;

• (2) Under the action of aerodynamic force, the guide roller-rail contact stiffness fluctuates in the range of $1.277\sim 1.404\times {10}^{5}\mathrm{N}\bullet \mathrm{m}$. Compared with the effect of aerodynamic force, the contact stiffness at rollers 3/6/7/10 increases by 5.2%, while that of rollers 2/5/8/11 increases by 4.23%;

• (3) In addition to the angular acceleration around Z-axis, the most significant change is the maximum value of each response. Considering the contact stiffness after aerodynamic effect, $a_{cx}$, $a_{cy}$, and $\alpha_{y}$ increase by 16.97%, 8.04%, and 15.13%, respectively, and the influence of aerodynamic load on the angular acceleration around Y-axis and vibration acceleration in X-direction is the most obvious.

Appendix

According to the D'Alembert's principle, the 17 degree-of-freedom dynamic model was constructed and deduced as follows:

$$X = [x_{cf} ,y_{cf} ,\theta_{x} ,\theta_{y} ,\theta_{z} ,x_{1} ,y_{2} ,x_{3} ,x_{4} ,y_{5} ,x_{6} ,x_{7} ,y_{8} ,x_{9} ,x_{10} ,y_{11} ,x_{12} ]^{T}$$

(A1)

$$M = diag\left( {m_{cf} ,m_{cf} ,J_{x} ,J_{y} ,J_{z} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} ,m_{g} } \right)$$

(A2)

$$\begin{aligned} T & { = }\frac{{1}}{{2}}m_{cf} \left( {\dot{x}_{cf}^{2} + \dot{y}_{cf}^{2} } \right) + \frac{{1}}{{2}}J_{x} \dot{\theta }_{x}^{2} + \frac{{1}}{{2}}J_{y} \dot{\theta }_{y}^{2} + \frac{{1}}{{2}}J_{z} \dot{\theta }_{z}^{2} + \frac{{1}}{{2}}m_{g} \\ & \quad \left( \begin{gathered} \dot{x}_{1}^{2} + \dot{y}_{2}^{2} + \dot{x}_{3}^{2} + \dot{x}_{4}^{2} + \dot{y}_{5}^{2} + \dot{x}_{6}^{2} \hfill \\ + \dot{x}_{7}^{2} + \dot{y}_{8}^{2} + \dot{x}_{9}^{2} + \dot{x}_{10}^{2} + \dot{y}_{11}^{2} + \dot{x}_{12}^{2} \hfill \\ \end{gathered} \right) \\ \end{aligned}$$

(A3)

$$\begin{gathered} V{ = }\frac{{1}}{{2}}k_{c1} \left[ {x_{1} - e_{1} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} + \theta_{y} h_{1} + \theta_{z} w_{g} - x_{1} } \right)^{2} + \frac{{1}}{{2}}k_{c2} \left[ {y_{2} - e_{2} \left( t \right)} \right]^{2} \\ + \frac{{1}}{{2}}k_{s} \left( {y_{cf} + \theta_{x} h_{1} - y_{2} } \right)^{2} + \frac{{1}}{{2}}k_{c3} \left[ {x_{3} - e_{3} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} + \theta_{y} h_{1} + \theta_{z} w_{g} - x_{3} } \right)^{2} \\ + \frac{{1}}{{2}}k_{c4} \left[ {x_{4} - e_{4} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} + \theta_{y} h_{1} - \theta_{z} w_{g} - x_{4} } \right)^{2} + \frac{{1}}{{2}}k_{c5} \left[ {y_{5} - e_{5} \left( t \right)} \right]^{2} \\ + \frac{{1}}{{2}}k_{s} \left( {y_{cf} + \theta_{x} h_{1} - y_{5} } \right)^{2} + \frac{{1}}{{2}}k_{c6} \left[ {x_{6} - e_{6} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} + \theta_{y} h_{1} - \theta_{z} w_{g} - x_{6} } \right)^{2} \\ + \frac{{1}}{{2}}k_{c7} \left[ {x_{7} - e_{1} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} - \theta_{y} h_{2} + \theta_{z} w_{g} - x_{7} } \right)^{2} + \frac{{1}}{{2}}k_{c8} \left[ {y_{8} - e_{2} \left( t \right)} \right]^{2} \\ + \frac{{1}}{{2}}k_{s} \left( {y_{cf} - \theta_{x} h_{2} - y_{8} } \right)^{2} + \frac{{1}}{{2}}k_{c9} \left[ {y_{9} - e_{3} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} - \theta_{y} h_{2} + \theta_{z} w_{g} - x_{9} } \right)^{2} \\ + \frac{{1}}{{2}}k_{c10} \left[ {y_{10} - e_{4} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} - \theta_{y} h_{2} - \theta_{z} w_{g} - x_{10} } \right)^{2} + \frac{{1}}{{2}}k_{c11} \left[ {y_{11} - e_{5} \left( t \right)} \right]^{2} \\ + \frac{{1}}{{2}}k_{s} \left( {y_{cf} - \theta_{x} h_{2} - y_{11} } \right)^{2} + \frac{{1}}{{2}}k_{c12} \left[ {y_{12} - e_{6} \left( t \right)} \right]^{2} + \frac{{1}}{{2}}k_{s} \left( {x_{cf} - \theta_{y} h_{2} - \theta_{z} w_{g} - x_{12} } \right)^{2} \\ \end{gathered}$$

(A4)

$$\begin{gathered} \Psi_{d} { = }\frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} + \dot{\theta }_{y} h_{1} + \dot{\theta }_{z} w_{g} - \dot{x}_{1} } \right)^{2} + \frac{{1}}{{2}}c_{gf} \left( {\dot{y}_{cf} + \dot{\theta }_{x} h_{1} - \dot{y}_{2} } \right)^{2} \\ + \frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} + \dot{\theta }_{y} h_{1} + \dot{\theta }_{z} w_{g} - \dot{x}_{3} } \right)^{2} + \frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} + \dot{\theta }_{y} h_{1} - \dot{\theta }_{z} w_{g} - \dot{x}_{4} } \right)^{2} \\ + \frac{{1}}{{2}}c_{gf} \left( {\dot{y}_{cf} + \dot{\theta }_{x} h_{1} - \dot{y}_{5} } \right)^{2} + \frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} + \dot{\theta }_{y} h_{1} - \dot{\theta }_{z} w_{g} - \dot{x}_{6} } \right)^{2} \\ + \frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} - \dot{\theta }_{y} h_{2} + \dot{\theta }_{z} w_{g} - \dot{x}_{7} } \right)^{2} + \frac{{1}}{{2}}c_{gf} \left( {\dot{y}_{cf} - \dot{\theta }_{x} h_{2} - \dot{y}_{8} } \right)^{2} \\ + \frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} - \dot{\theta }_{y} h_{2} + \dot{\theta }_{z} w_{g} - \dot{x}_{9} } \right)^{2} + \frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} - \dot{\theta }_{y} h_{2} - \dot{\theta }_{z} w_{g} - \dot{x}_{10} } \right)^{2} \\ + \frac{{1}}{{2}}c_{gf} \left( {\dot{y}_{cf} - \dot{\theta }_{x} h_{2} - \dot{y}_{11} } \right)^{2} + \frac{{1}}{{2}}c_{gf} \left( {\dot{x}_{cf} - \dot{\theta }_{y} h_{2} - \dot{\theta }_{z} w_{g} - \dot{x}_{12} } \right)^{2} \\ \end{gathered}$$

(A5)

It is decided by $L = T - V$.

The solution of vibration response under the force ($\begin{gathered} F_{pre} :\,A\,preload \hfill \\ F_{air} :\,The\,aerodynamic \, force \, \left( {moment} \right) \hfill \\ \end{gathered}$) of X and Y-direction of car:

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{x}_{cf} }}} \right) + \frac{\partial V}{{\partial x_{cf} }} + \frac{{\partial \Psi_{d} }}{{\partial \dot{x}_{cf} }} = F_{x}$$

(A6)

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{y}_{cf} }}} \right) + \frac{\partial V}{{\partial y_{cf} }} + \frac{{\partial \Psi_{d} }}{{\partial \dot{y}_{cf} }} = F_{y}$$

(A7)

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{\theta }_{x} }}} \right) + \frac{\partial V}{{\partial \theta_{x} }} + \frac{{\partial \Psi_{d} }}{{\partial \dot{\theta }_{x} }} = M_{x}$$

(A8)

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{\theta }_{y} }}} \right) + \frac{\partial V}{{\partial \theta_{y} }} + \frac{{\partial \Psi_{d} }}{{\partial \dot{\theta }_{y} }} = M_{y}$$

(A9)

According to the research content of this paper, $M_{z}$ has little influence on the calculation results and can be ignored.

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{\theta }_{z} }}} \right) + \frac{\partial V}{{\partial \theta_{z} }} + \frac{{\partial \Psi_{d} }}{{\partial \dot{\theta }_{z} }} = 0$$

(A10)

The actual contact force between each roller and guide rail under pneumatic action is solved:

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{x}_{i} }}} \right) + \frac{\partial V}{{\partial x_{i} }} + \frac{{\partial \Psi_{d} }}{{\partial \dot{x}_{i} }} = f_{pre} \quad i = (1,3,4,6,7,9,10,12)$$

(A11)

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{y}_{i} }}} \right) + \frac{\partial V}{{\partial y_{i} }} + \frac{{\partial \Psi_{d} }}{{\partial \dot{y}_{i} }} = f_{pre} \quad i = (2,5,8,11)$$

(A12)