Impinging of metallic nanoparticles along with the slip effects through a porous medium with MHD

Abstract

The considered analysis comprises the effects of nanoparticles on the characteristics of the peristaltic flow through a homogeneous porous medium under the impact of magnetic field and slip effects by considering an appropriate mathematical model. Analysis is introduced by considering blood as the base fluid and metals such as copper and silver as the nanoparticles in the existence of the thermal and velocity slip effects. Lubrication approach is used to simplify the problem. Impact of related parameters on temperature, pressure rise, pressure gradient, velocity and streamlines are interpreted graphically. Comparison of the pure blood, silver blood and copper blood is presented and analyzed. It is also revealed that inclusion of nanoparticles scales down the velocity and temperature of fluid. Another valuable finding of the present investigation is that the silver nanoparticles enhance the pressure gradient when compared with the copper nanoparticles. Therefore, the current investigation is capable to achieve some essential and interesting characteristics in few biomedical applications.

1 Introduction

Flows in a tube or channel caused by sinusoidal waves generated along the channel walls are defined as peristaltic flows. It has abundant applications in physiology such as transport of bile, urine, chyme, food, male and female breeding cells through their specific tracks. Dialysis, heart–lung machines, roller, finger pumps and hose pumps are the engineering applications of peristalsis. Transit of sensitive and corrosive fluids is transported by means of peristalsis to prevent the direct influence towards the outer environment. Due to specific usefulness and immense continuation of peristaltic flows, various analyses are introduced to examine the peristalsis by considering distinct flow configurations [1,2,3,4,5,6]. Impact of external magnetic field is more useful, for instance, hyperthermia, reduction of bleeding during surgeries, drug carriers, advancement of magnetic devices utilizing magnetic particles and many others. Such biomedical applications motivate the researchers and, therefore, many theoretical investigations have been tackled to see the impact of magnetic field on peristaltic flows [7,8,9,10].

Beach sand, rye bread, human lung, wood and filter paper are the examples of naturally existing porous media. A superb biological illustration of a porous medium is the pharmaceutical position of gallstones when they decline into bile ducts and partially or completely close them. In recent years, many researchers have described the influence of porous medium on the flow by employing the Darcy’s law [11,12,13,14]. Fluid bounded by vertical infinite plate and passing through the porous media has been investigated by Rapits et al. [15]. Varshney [16] has also considered the porous media with horizontal surface. Nonlinear peristaltic flow passing through porous inclined channel has been examined by Mekheimer [17]. Vasudev et al. [18] has considered the vertical tube to discuss the impact of magnetic field and porous media.

Nanoparticle investigation is an area of impressive scientific interest in view of extensive range of promising utilization in biomedical, optical and electronic field. In the field of nanotechnology, a particle describes a small object which behaves like an individual in terms of its characteristic and transport. Nanotechnology introduced the creation and uses of different materials having the nanoscale levels of 1–100 nm to make products that exhibit peculiar properties. Implementation of nanotechnology in biomedical applications giving exclusive physical and chemical property has the capability to give strongly improved distinguishing methods and efficient mechanism for molecular liability [19,20,21,22,23]. This new kind of nanotechnology was first introduced by Choi and Eastman [24]. Buongiorno [25] showed that Brownian motion and thermophoresis effects are significant in the dynamics of nanofluids. Later on, Akbar [26] investigated the impact of nanoparticles on incompressible viscous fluid by considering asymmetric channel. Nadeem and Shahzadi [27] analyzed the two-phase nanofluid in a curved channel. Nanoparticles with exclusive properties has earned much consideration from researchers and extensive studies investigate the influence of nanotechnology in various applications available in the literature such as [28,29,30,31,32].

The mechanics of peristaltic flow through different configuration with no slip condition have been elaborated by various researchers in which they stimulate that the fluid film moves with closest to the boundary surface [33, 34]. It is now acceptable fact that the fluid flow through all tubular organs in human body are inwardly laminated with secretion layers and mucus. These layers consecutively avoid the fluid from sticking to the tube walls. In this aspect no slip condition is valid between the solid boundary and fluid. The important applications of boundary slip conditions are in polishing valves of fabricated hearts and internal cavities. With such motivation, some researchers investigated the slip effects on the peristaltic flow of commonly used fluids [35, 36]. Yıldırım and Sezer [37] examined the influence of partial slip condition on MHD viscous fluid by assuming asymmetric channel.

The aspiration of present analysis is to investigate the impinging of metallic nanoparticles on magneto hydrodynamic flow through a uniform porous medium with slip effects. Indeed, the magnetic nanofluid has both the prospects of liquid and magnetic field. Such fluids have beneficial applications related to modulators, adjustable optical fiber filters, optical gratings and switches. Magnetic nanoparticles have significant importance in cancer therapy, medicine and to instruct the particles to move along the blood stream towards the tumor with magnets. In hyperthermia, contrast improvement in magnetic resonance and drug delivery, the magneto nanofluids have significant importance. The influence of magnetic nanoparticles on the tumor cells has been found in more adhesive than invigorating cells. Here, for the present analysis we have used copper (Cu) and silver (Ag) nanoparticles. Magnetic properties of nanoparticles add a new extent where they can enhance the application of an external magnetic field. Thermophysical properties of the nanofluids such as effective viscosity, density, electric conductivity and thermal conductivity are taken into account. By employing the approximation of long wavelength and low Reynolds number, the mathematical model is presented. Resulting equations are solved exactly. Physical clarification of results is interpreted by means of graphs and tables.

2 Formulation of the problem

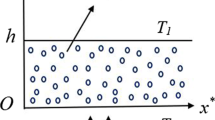
We have considered the vertical tube of width 2a for peristaltic flow of nanofluid through a homogenous porous medium under velocity and thermal slip effects. A nanofluid flow phenomenon is consisting of blood with copper/silver as the nanoparticles. An external magnetic field of strength $B_{0}$ is applied and effects of induced magnetic field are neglected for low magnetic Reynolds number condition. It is supposed that the thermal equilibrium is maintained between the base fluid and the nanoparticles. The coordinates (R,  Z) are elected in such a way that R-axis is along the radial direction and Z-axis lies along the length of the tube. Furthermore, walls of tube are preserved at a constant temperature of $T_{0}.$ A sinusoidal wave of small amplitude b and wavelength moves down the walls with constant speed c. Flow in the tube is generated by these waves. Schematic geometrical sketch is represented in Fig. 1.

Fig. 1

Geometrical sketch

The shape of traveling waves is represented as:

$$\begin{aligned} \bar{H}(\bar{t}, \bar{Z})=b\sin \left[ \left( \bar{Z}-c\bar{t}\right) \frac{2\pi }{\lambda }\right] +a, \end{aligned}$$

(1)

In Eq. (1), amplitude of the wave is expressed by b,  width of the tube is expressed by a, wave speed is expressed by c and wavelength is expressed by $\lambda$.

The two-dimensional continuity equation for incompressible fluid is defined below

$$\begin{aligned} \frac{\bar{U}}{\bar{R}}+\frac{\partial \bar{U}}{\partial \bar{R}}+\frac{ \partial \bar{W}}{\partial \bar{Z}}=0, \end{aligned}$$

(2)

in which $\bar{W}$ and $\bar{U}$ represent the transverse and longitudinal components of velocity in the laboratory frame. The $\bar{R}$ and $\bar{Z}$ components of momentum equation in the presence of mixed convection are [5,6,7,8,9,10,11]

$$\begin{aligned} \rho _{\rm nf}\left( \frac{\partial \bar{U}}{\partial \bar{R}}\bar{U}+\frac{ \partial \bar{U}}{\partial \bar{Z}}\bar{W}+\frac{\partial \bar{U}}{\partial \bar{t}}\right) &= \mu _{\rm nf}\left( \frac{\partial ^{2}\bar{U}}{\partial \bar{ Z}^{2}}+\frac{1}{\bar{R}}\frac{\partial \bar{U}}{\partial \bar{R}}+\frac{ \partial ^{2}\bar{U}}{\partial \bar{R}^{2}}-\frac{\bar{U}}{\bar{R}^{2}} \right) -\frac{\mu _{\rm nf}}{K_{1}}\bar{U} \nonumber \\ & \quad +(\rho \alpha )_{\rm nf}g(\bar{T}-T_{0})-\frac{\partial \bar{P}}{\partial \bar{ R}}, \end{aligned}$$

(3)

$$\begin{aligned} \rho _{\rm nf}\left( \frac{\partial \bar{W}}{\partial \bar{R}}\bar{U}+\frac{ \partial \bar{W}}{\partial \bar{t}}+\frac{\partial \bar{W}}{\partial \bar{Z}} \bar{W}\right) &= \mu _{\rm nf}\left( \frac{\partial ^{2}\bar{W}}{\partial \bar{Z }^{2}}+\frac{1}{\bar{R}}\frac{\partial \bar{W}}{\partial \bar{R}}+\frac{ \partial ^{2}\bar{W}}{\partial \bar{R}^{2}}\right) -\sigma _{\rm nf}B_{0}^{2} \bar{W} \nonumber \\ & \quad -\frac{\mu _{\rm nf}}{K_{1}}\bar{W}+(\rho \alpha )_{\rm nf}g(\bar{T}-T_{0})-\frac{ \partial \bar{P}}{\partial \bar{Z}}. \end{aligned}$$

(4)

Energy equation in the presence of heat generation is defined by

$$\begin{aligned} (\rho C_{p})_{\rm nf}\left( \frac{\partial \bar{T}}{\partial \bar{R}}\bar{U}+ \frac{\partial \bar{T}}{\partial \bar{Z}}\bar{W}+\frac{\partial \bar{T}}{ \partial \bar{t}}\right) =K_{\rm nf}\left( \frac{\partial ^{2}\bar{T}}{\partial \bar{Z}^{2}}+\frac{\partial ^{2}\bar{T}}{\partial \bar{R}^{2}}+\frac{1}{\bar{ R}}\frac{\partial \bar{T}}{\partial \bar{R}}\right) +Q_{0}. \end{aligned}$$

(5)

In the above equations, $\bar{T}$ is the temperature of the fluid, $K_{1}$ is the permeability of the porous medium, $\bar{P}$ is the pressure, $B_{0}$ is the magnetic field strength, $Q_{0}$ is the constant heat absorption and generation. For the proposed nanofluid model, $\rho _{\rm nf}$ is the density of the nanofluid, $\mu _{\rm nf}$ is the variable nanofuid viscosity, $\alpha _{\rm nf}$ is the thermal expansion coefficient, $\sigma _{\rm nf}$ is the electrical conductivity of the nanofluid, $K_{\rm nf}$ is the thermal conductivity of the nanofluid and $(\rho C_{p})_{\rm nf}$ is the nanofluid heat capacitance.

In this investigation, we have utilized the relation given by Brinkman [22] as,

$$\begin{aligned} \mu _{\rm nf}=\frac{\mu _{\rm f}}{(1-\varphi )^{2.5}}. \end{aligned}$$

(6)

The effective density, electrical conductivity, thermal conductivity and specific heat of nanofluid are defined as [23],

$$\begin{aligned} (\rho c_{p})_{\rm nf}=\phi (\rho c_{p})_{\rm s}+\left( 1-\phi \right) (\rho c_{p})_{\rm f}, \alpha _{\rm nf}=\frac{K_{\rm nf}}{(\rho C_{p})_{\rm nf}}, \end{aligned}$$

(7)

$$\begin{aligned} (\rho \alpha )_{\rm nf} &= \phi (\rho \alpha )_{\rm s}+( 1-\phi ) (\rho \alpha )_{\rm f}, \quad \frac{\sigma _{\rm nf}}{\sigma _{\rm f}}=1+\frac{3\left( \frac{\sigma _{\rm s}}{\sigma _{\rm f}}-1\right) \phi }{\left( \frac{\sigma _{\rm s}}{\sigma _{\rm f}}+2\right) -\left( \frac{ \sigma _{\rm s}}{\sigma _{\rm f}}-1\right) \phi }, \nonumber \\ \frac{K_{\rm nf}}{K_{\rm f}} &= \frac{2k_{\rm f}+k_{\rm s}+2\phi (k_{\rm s}-k_{\rm f})}{ 2k_{\rm f}+k_{\rm s}+\phi (k_{\rm f}-k_{\rm s})}, \quad \rho _{\rm nf}=\phi \rho _{\rm s}+ ( 1-\phi) \rho _{\rm f}, \end{aligned}$$

(8)

Here effective thermal conductivity of the nanofluid is given by Maxwell–Gamett’s (MG-model). For the base fluid $\rho _{\rm f}$ is the density, $\alpha _{\rm f}$ is thermal expansion coefficient, $\mu _{\rm f}$ is the viscosity, $K_{\rm f}$ is the thermal conductivity and $(\rho c_{p})_{\rm f}$ is heat capacitance for the base fluid while $\rho _{\rm s}$ is the density, $(\rho c_{p})_{\rm s}$ is heat capacitance, $k_{\rm s}$ is thermal conductivity, $\alpha _{\rm s}$ is thermal expansion coefficient and $\phi$ is the volume fraction of nanoparticles. The experimental values of these physical parameters are presented in Table 1.

Table 1 Thermophysical parameters of blood, silver and copper [31]

In the fixed frame the velocity and the thermal slip conditions are defined as [35,36,37]

$$\begin{aligned} \frac{\partial \bar{W}}{\partial \bar{R}} &= 0, \quad \bar{T}=\bar{T}_{0},\quad \text { at } \ \bar{R}=0, \end{aligned}$$

(9)

$$\begin{aligned} \bar{W}-\bar{W}_{w} &= -\delta _{1}\tau _{\bar{R}\bar{Z}}, \quad \bar{T}- \bar{T}_{w}=-\beta _{1}\frac{\partial \bar{T}}{\partial \bar{R}},\quad \text { at } \ \bar{R}=\bar{H}(\bar{Z},t), \end{aligned}$$

(10)

where $\tau _{\bar{R}\bar{Z}}$ is the extra stress tensor, $\bar{T}_{w}$ is the temperature which is equal to $\bar{T}_{0},$ $\alpha _{1}$ is the velocity slip and $\beta _{1}$ is the thermal slip parameter.

The following transformation is used to swap from fixed frame $(\bar{R},\bar{ Z},\bar{t})$ to wave frame $(\bar{r},\bar{z})$,

$$\begin{aligned} \bar{Z}=\bar{z}+c\bar{t}, \quad \bar{p}(\bar{z},\quad \bar{r})=\bar{P}(\bar{Z}, \bar{R},\bar{t}),\quad \bar{w}=\bar{W}-c, \quad \bar{R}=\bar{r},\quad \bar{u}=\bar{U}, \end{aligned}$$

(11)

in which $\bar{p}$ is the pressure and $\bar{u}$ and $\bar{w}$ are the velocity components. Equations (2)–(5) through Eqs. (6)–(11) give,

$$\begin{aligned} \frac{\partial \bar{w}}{\partial \bar{z}}+\frac{\partial \bar{u}}{\partial \bar{r}}+\frac{\bar{u}}{\bar{r}}=0, \end{aligned}$$

(12)

$$\begin{aligned} \left. (( 1-\phi ) \rho _\mathrm{f}+\varphi \rho _\mathrm{s})\left( \frac{ \partial \bar{u}}{\partial \bar{r}}\bar{u}-\frac{\partial \bar{u}}{\partial \bar{z}}c+\frac{\partial \bar{u}}{\partial \bar{z}}(\bar{w}+c)\right) \right. &= \left. \frac{\mu _\mathrm{f}}{(1-\phi )^{2.5}}\left( \frac{1}{\bar{r}} \frac{\partial \bar{u}}{\partial \bar{r}}+\frac{\partial ^{2}\bar{u}}{ \partial \bar{r}^{2}}-\frac{\bar{u}}{\bar{r}^{2}}+\frac{\partial ^{2}\bar{u} }{\partial \bar{z}^{2}}\right) \right. \nonumber \\ & \quad \left. +\left( 1-\phi \right) (\rho \alpha )_\mathrm{f}+\phi (\rho \alpha )_\mathrm{s}g(T-T_{0})\right. \nonumber \\&\left. -\frac{\mu _\mathrm{nf}}{K_{1}}(\bar{u}+c)-\frac{\partial \bar{p}}{ \partial \bar{r}},\right. \end{aligned}$$

(13)

$$\begin{aligned} \left. (( 1-\phi ) \rho _\mathrm{f}+\phi \rho _\mathrm{s})\left( \frac{\partial \bar{w}}{\partial \bar{r}}\bar{u}-\frac{\partial \bar{w}}{\partial \bar{z}}c+ \frac{\partial \bar{w}}{\partial \bar{z}}(\bar{w}+c)\right) \right. &= \left. \frac{\mu _\mathrm{f}}{(1-\phi )^{2.5}}\left( \frac{1}{\bar{r}}\frac{ \partial \bar{w}}{\partial \bar{r}}+\frac{\partial ^{2}\bar{w}}{\partial \bar{r}^{2}}+\frac{\partial ^{2}\bar{w}}{\partial \bar{z}^{2}}\right) \right. \nonumber \\&\left. +\left( 1-\phi \right) (\rho \alpha )_\mathrm{f}+\phi (\rho \alpha )_\mathrm{s}g(T-T_{0})\right. \nonumber \\& \quad \left. -\sigma _\mathrm{nf}B_{0}^{2}(\bar{w}+c)-\frac{\mu _\mathrm{nf}}{K_{1}}(\bar{w} +c)\right. \nonumber \\&\left. -\frac{\partial \bar{p}}{\partial \bar{z}},\right. \end{aligned}$$

(14)

$$\begin{aligned} \left( \frac{\partial \bar{T}}{\partial \bar{r}}\bar{u}-\frac{\partial \bar{T }}{\partial \bar{z}}c+\frac{\partial \bar{T}}{\partial \bar{z}}(\bar{w} +c)\right) =\frac{Q_{0}}{( 1-\phi ) (\rho c_{p})_{\rm f}+\phi (\rho c_{p})_{\rm s}}+\alpha _{\rm nf}\left( \frac{\partial ^{2}\bar{T}}{\partial \bar{r} ^{2}}+\frac{1}{\bar{r}}\frac{\partial \bar{T}}{\partial \bar{r}}+\frac{ \partial ^{2}\bar{T}}{\partial \bar{z}^{2}}\right) . \end{aligned}$$

(15)

Dimensionless quantities that are used in the above equations are

$$\begin{aligned} w &= \frac{\bar{w}}{c}, \ \zeta _{1}=\frac{a}{\lambda }, \ r=\frac{ \bar{r}}{a}, \ z=\frac{\bar{z}}{\lambda }, \ \varepsilon =\frac{b}{ a}, \ t=\frac{c\bar{t}}{\lambda }, \ h=\frac{\bar{h}}{a} =1+\varepsilon \sin (2\pi z), \nonumber \\ u &= \frac{\lambda \bar{u}}{ac}, \ \bar{\theta }=\frac{\bar{T}-T_{0}}{ T_{0}}, \ \gamma =\frac{a^{2}Q_{0}}{T_{0}k_{\rm f}}, \ R_{en}=\frac{ ac\rho _{\rm f}}{\mu _{\rm f}}, \ G_{r}=\frac{a^{2}T_{0}\rho _{\rm f}\alpha _{\rm f}g}{ c\mu _{\rm f}}, \nonumber \\ p &= \frac{a^{2}\bar{p}}{c\lambda \mu _{\rm f}}, \ M^{2}=\frac{\sigma _{\rm f}}{ \mu _{\rm f}}B_{0}^{2}a^{2}, \ D_{a}=\frac{K_{1}}{a^{2}}, \ u=-\frac{1 }{r}\frac{\partial \psi }{\partial z}, \ w=\frac{1}{r}\frac{\partial \psi }{\partial r}. \end{aligned}$$

(16)

In the above expressions $G_{r}$, $\bar{\theta },$ $R_{en},$ $\gamma ,$ $\zeta _{1},$ M,  $D_{a}$ represents the Grashof number, dimensionless temperature, Reynolds number, dimensionless heat source parameter, wave number, Hartmann number and Darcy number, respectively. After using the lubrication approach, the continuity equation is exactly satisfied and Eqs. (13)–(15) take the form:

$$\begin{aligned} \frac{\partial p}{\partial r}=0, \end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial p}{\partial z}\frac{\mu _{\rm f}}{\mu _{\rm nf}} &= \frac{\partial ^{2}w}{\partial r^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}+G_{r}(1-\phi +\phi \frac{(\rho \alpha )_{\rm s}}{(\rho \alpha )_{\rm f}})(1-\phi )^{2.5}\theta - \frac{w+1}{D_{a}} \nonumber \\ & \quad -M^{2}\left( 1+\frac{3\phi (\frac{\sigma _{\rm s}}{\sigma _{\rm f}}-1)}{(\frac{ \sigma _{\rm s}}{\sigma _{\rm f}}+2)-\phi (\frac{\sigma _{\rm s}}{\sigma _{\rm f}}-1)} \right) (1-\phi )^{2.5}(w+1), \end{aligned}$$

(18)

$$\begin{aligned} \frac{\partial ^{2}\bar{\theta }}{\partial r^{2}}+\frac{1}{r}\frac{\partial \bar{\theta }}{\partial r}+\gamma \left( \frac{2k_{\rm f}+k_{\rm s}+(k_{\rm f}-k_{\rm s})\phi }{2k_{\rm f}+k_{\rm s}-(k_{\rm f}-k_{\rm s})2\phi }\right) =0. \end{aligned}$$

(19)

The suitable boundary conditions in the wave frame are given as

$$\begin{aligned}& \left. \bar{\theta }+\beta \frac{\partial \bar{\theta }}{\partial r}=0, \quad w+\delta \frac{\mu _{\rm nf}}{\mu _{\rm f}}\frac{\partial w}{\partial r}=-1, \quad \text { at } \ r=h(z),\right. \nonumber \\ &\left. \frac{\partial \bar{\theta }}{\partial r}=0, \quad \frac{\partial w }{\partial r}=0, \quad \text { at } \ r=0,\right. \end{aligned}$$

(20)

where $\delta =\frac{\mu _{\rm f}\delta _{1}}{a}$, $\beta =\frac{\beta _{1}}{a}$ are defined as the dimensionless velocity and thermal slip parameters. Dimensionless flow rate F in the laboratory frame is associated with the dimensionless flow rate q in the wave frame and defined as

$$\begin{aligned} F &= q+\frac{1}{2}\left( 1+\frac{\varepsilon ^{2}}{2}\right) , \end{aligned}$$

(21)

$$\begin{aligned} q &= \int _{0}^{h}rw {\rm d}r \end{aligned}$$

(22)

3 Solution of the problem

Equations (18) and (19) are solved exactly by utilizing the boundary conditions given in Eq. (20). The solutions for temperature and velocity profile are as follows

$$\begin{aligned} \bar{\theta }=\gamma \left( \frac{k_{\rm s}+2k_{\rm f}+\phi (k_{\rm f}-k_{\rm s})}{ k_{\rm s}+2k_{\rm f}-2\phi (k_{\rm f}-k_{\rm s})}\right) \left( \frac{h^{2}-r^{2}+2h\beta }{4 }\right) , \end{aligned}$$

(23)

$$\begin{aligned} w &= \left( \frac{D_{1}h^{2}}{S^{2}(I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}} I_{1}(Sh))}+\frac{4D_{1}}{S^{4}(I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}} I_{1}(Sh))}+\frac{2D_{1}h}{S^{2}(I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}} I_{1}(Sh))}\right. \nonumber \\ & \quad \left. -\frac{1}{I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}}I_{1}(Sh)}\right) I_{0}(Sr)+\frac{\mu _{\rm f}}{\mu _{\rm nf}}\frac{1}{S^{2}(I_{0}(Sh)+S\frac{\mu _{\rm f} }{\mu _{\rm nf}}I_{1}(Sh))}\frac{{\rm d}p}{{\rm d}z}I_{0}(Sr) \nonumber \\ & \quad +\frac{(-D_{1}h^{2}-2D_{1}h\beta +S^{2})}{S^{2}(I_{0}(Sh)+S\frac{\mu _{\rm f}}{ \mu _{\rm nf}}I_{1}(Sh))}I_{0}(Sr)-\frac{D_{1}}{S^{2}}r^{2}-\frac{4D_{1}}{S^{4}} +D_{1}h^{2}+2D_{1}h\beta -1-\frac{1}{S^{2}}\frac{\mu _{\rm f}}{\mu _{\rm nf}}\frac{{\rm d}p }{{\rm d}z}, \end{aligned}$$

(24)

where

$$\begin{aligned} D_{1} &= (1-\phi +\varphi \frac{(\rho \alpha )_{\rm s}}{(\rho \alpha )_{\rm f}} )(1-\phi )^{2.5}\frac{\gamma }{4}\frac{K_{\rm f}}{K_{\rm nf}}, \nonumber \\ S &= \sqrt{M^{2}\left( 1+\frac{3(\frac{\sigma _{\rm s}}{\sigma _{\rm f}}-1)\phi }{( \frac{\sigma _{\rm s}}{\sigma _{\rm f}}+2)-(\frac{\sigma _{\rm s}}{\sigma _{\rm f}}-1)\phi } \right) (1-\phi )^{2.5}+\frac{1}{D_{a}}} \end{aligned}$$

(25)

Flow rate is given as

$$\begin{aligned} q=\int _{0}^{h}rw {\rm d}r \end{aligned}$$

(26)

By substituting Eq. (24) into Eq. (26), we obtain the pressure gradient as defined below (Table 2),

$$\begin{aligned} \frac{{\rm d}p}{{\rm d}z}=\frac{q-l_{1}}{l_{2}} \end{aligned}$$

(27)

where

$$\begin{aligned} l_{1} &= \frac{\left( \frac{D_{1}h^{2}}{S^{2}(I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}}I_{1}(Sh))}+\frac{4D_{1}}{S^{4}(I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}} I_{1}(Sh))}+\frac{2D_{1}h}{S^{2}(I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}} I_{1}(Sh))}-\frac{1}{I_{0}(Sh)+S\frac{\mu _{\rm f}}{\mu _{\rm nf}}I_{1}(Sh)}\right) hI_{1}(Sh)}{S} \nonumber \\ &\quad +\frac{(-D_{1}h^{2}-2D_{1}h\beta +S^{2})hI_{1}(Sh)}{S^{3}(I_{0}(Sh)+S\frac{ \mu _{\rm f}}{\mu _{\rm nf}}I_{1}(Sh))}+\left( -\frac{D_{1}h^{4}}{4S^{2}}+-\frac{4D_{1}}{ S^{4}}+D_{1}h^{2}+2D_{1}h\beta -1\right) \frac{h^{2}}{2}, \nonumber \\ l_{2} &= \frac{\mu _{\rm f}}{\mu _{\rm nf}}\frac{hI_{1}(Sh)}{S^{3}(I_{0}(Sh)+S\frac{ \mu _{\rm f}}{\mu _{\rm nf}}I_{1}(Sh))}-\frac{1}{S^{2}}\frac{\mu _{\rm f}}{\mu _{\rm nf}} \frac{h^{2}}{2}. \end{aligned}$$

(28)

Table 2 Comparison of temperature profile for different values of slip parameter $\beta$

4 Graphical results and discussion

Impact of silver and copper nanoparticles with the aid of embedded parameters on the characteristics of peristaltic flow is presented in this section through the graphs of temperature, axial velocity, pressure gradient, pressure rise and stream lines. These graphs are prepared by controlling the parameters restricted such as $\phi =0.0-0.2,$ $\gamma =0.1-0.3,$ $D_{a}=0.1-0.2,$ $M=0.1-1.5$, $\delta =0.00-0.09,$ $\beta =0.0-0.2,$ $G_{r}=0.5-1.5.$ Influence of different embedded parameters such as heat source $(\gamma )$, and nanoparticle volume fraction $( \phi )$ on temperature profile is shown in Figs. 2 and 6. Significant growth in temperature is shown in Fig. 2 with increasing values of heat source parameter $\gamma$. Temperature profile decreases when the volume fraction $\phi$ is increased. It is depicted that the heat being gained by the heat source is rapidly transferred to the walls (due to the inclusion of nanoparticles) and thus the fluid temperature decreases (Fig. 3). Effective thermal conductivity of nanoparticles plays a key role in the quick decrease of the fluid temperature. This supports the inclusion of nanoparticles in peculiar situation such as coolants. We primarily focus to inspect the behaviors of various embedded parameters like Darcy number $(D_{a}),$ Hartmann number $\left( M\right) ,$ Velocity slip parameter $\left( \delta \right) ,$ Thermal slip parameter $(\beta ) ,$ Heat source/sink parameter $( \gamma )$ and Grashof number $(G_{r})$ on velocity profile as shown in Figs. 4, 5, 6, 7, 8 and 9. All these figures illustrated that the velocity profile attains maximum value at the center and traces a trajectory like parabolic curve. Furthermore, maximum value of velocity is greater for pure blood when compared with copper blood and silver blood. It is also seen from these figures that the maximum velocity of base fluid reduces due to the accession of nanoparticles. Velocity profile for distinct values of Darcy number $(D_{a})$ is plotted in Fig. 4. We examine that the significance of velocity increases with the increase of the values of $D_{a}.$ The effect is of sublime importance in blood capillaries where pores in walls allow exchange of water, oxygen and many other nutrients between the blood and the tissues. Figure 5 depicts that an increase in the value of Hartmann number $\left( M\right)$ decreases the velocity around the center of the tube. Moreover, this figure also described that the significantly strong magnetic field reduces the velocity profile of vertical tube. The mitigating aspect of MHD aids in curing and treatment of arthritis, cancer and migraine without effecting blood flow stream. Figures 6 and 7 shows the behavior for different values of the velocity slip parameter $\left( \delta \right)$ and thermal slip parameter $( \beta )$. It is elucidated that the velocity profiles give higher altitude for copper when compared to silver nanoparticles and reduce by increasing velocity and thermal slip parameters. We depicted from Fig. 8 that variation in heat source parameter $( \gamma )$ decreases the velocity of the nanofluid. Further, it is delineated that the incorporation of silver nanoparticles decreases the velocity profile minimal higher than that of copper nanoparticles. It is analyzed that the velocity profile decreases with an increase in the values of Grashof number $(G_{r}).$ Change in pressure gradient for Darcy number, Hartmann number, velocity slip parameter, thermal slip parameter, heat source/sink parameter and Grashof number is observed from Figs. 10, 11, 12, 13, 14, 15 and 16. Common observation from these figures is that the pressure gradient shows oscillatory behavior which is the truth be told because of peristalsis. The graph for the variation in Darcy number is described in Fig. 10 and shows that the pressure gradient enhances with the larger values of Darcy number. Note that the addition of silver nanoparticles enhances the pressure gradient slightly more than for the copper nanoparticles. Figure 11 is plotted to discuss the effects of Hartmann number M and analyze that the magnetic field decreases the pressure gradient with increasing values of Hartmann number because magnetic field becomes stronger for higher values of Hartmann number. Figures 12 and 13 describe the effects of velocity slip parameter $\delta$ and thermal slip parameter $\beta$ on the pressure gradient. It is investigated form these figures that the pressure gradient in vertical tube gives higher height for silver nanoparticles and improves on increasing thermal and velocity slip parameters. It is obtained from these figures that both the slip parameters are directly related to pressure gradient. Figure 14 depicts that the increase in heat source parameter increases the pressure gradient since more heat is generated inside the considered base fluid. The effect of Grashof number $G_{r}$ on the pressure gradient is discussed in Fig. 15 and noticed that with the growth of the viscous forces the pressure gradient increases. The pressure rise per wavelength is important to explain the pumping properly and sketched here from Figs. 16, 17, 18, 19, 20 and 21. One regular observation from these figures is that the pressure rise per wavelength diminishes with the expansion in flow rate. Figures 16 and 17 describe the effect of Darcy number $D_{a}$ and Hartmann number M on the pressure rise. It is declared from these figures that the pressure rise per wavelength is inversely related to the Darcy number $D_{a}$ and directly related to the Hartmann number M. Figures 16 and 17 enclose that inclusion of nanoparticles reduces the free pumping flux (value of q for $\Delta p=0$). Furthermore, pressure rise upgraded in the retrograde pumping region $(q<0,$ $\Delta p>0)$ with the increase of nanoparticle volume fraction. Figure 18 is plotted for different values of velocity slip parameter like $(\delta =0, 0.05, 0.09)$ cross ponds to no slip and slip effects, respectively. It is depicted that pressure rise declines when we consider the slip effects. The fluctuation of pressure rise versus q for different values of thermal slip parameter is given in Fig. 19 and observed that the pressure rise for the vertical tube enhances when thermal slip effects are taken into account. Figures 20 and 21 show the behavior for various values of heat source parameter and Grashof number. It is depicted from Fig. 20 that the pressure starts increasing for larger values of heat source parameter. Figure 21 shows that the pressure rise increases with an increase in the viscous forces for distinct values of Grashof number. A stream line describes a fascinating phenomenon for fluid flow of an inside flowing bolus and has been plotted here in Figs. 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34 and 35 for copper and silver nanoparticles. It is analyzed that the number of trapping bolus increases by increasing Darcy number for both cases by the closed stream lines as shown in Figs. 22 and 23. The influence of Hartmann number $H_{a}$ is given in Figs. 24 and 25. It is seen that the expanding values of Hartmann number reduce the size of trapped bolus for the silver nanoparticles and enhances the trapping. The trapping phenomena for the velocity $\delta$ and thermal $\beta$ slip parameters are examined through Figs. 26, 27, 28 and 29. It is inspected that more bolus appears for larger values of slip parameters when compared with no slip effects $(\delta =0,$ $\beta =0)$. These stream lines additionally pronounce that the number of trapped bolus increases with the growth of thermal slip parameter while decreases for velocity slip parameter. The trapping phenomenon for the heat source parameter $\gamma$ is given in Figs. 30 and 31. The number of the bolus increases by increasing $\gamma$ for both the cases. Figures 32 and 33 are for distant values of Grashof number. We can watch from these streamlines pattern that number of bolus decreases for silver nanoparticles and size of the bolus decreases for copper nanoparticles. From Figs. 34 and 35, it is inspected that the number of trapping bolus increases when we increase the concentration of nanoparticles as contrast to pure blood case.

Fig. 2

Temperature profile for various values of the heat source parameter $\gamma$

Fig. 3

Temperature profile for various values of the nanoparticle volume fraction $\phi$

Fig. 4

Variation of velocity profile for particular values of the Darcy number $D_{a}$

Fig. 5

Variation of velocity profile for particular values of the Hartmann number M

Fig. 6

Variation of velocity profile for particular values of the velocity slip parameter $\delta$

Fig. 7

Variation of velocity profile for particular values of the thermal slip parameter $\beta$

Fig. 8

Variation of velocity profile for particular values of the heat source/sink parameter $\gamma$

Fig. 9

Variation of velocity profile for particular values of the Grashof number $G_{r}$

Fig. 10

Change in pressure gradient for distant values of the Darcy number $D_{a}$

Fig. 11

Change in pressure gradient for distant values of the Hartmann number M

Fig. 12

Change in pressure gradient for distant values of the velocity slip parameter $\delta$

Fig. 13

Change in pressure gradient for distant values of the thermal slip parameter $\beta$

Fig. 14

Change in pressure gradient for distant values of the heat source/sink parameter $\gamma$

Fig. 15

Change in pressure gradient for distant values of the Grashof parameter $G_{r}$

Fig. 16

Variation of pressure rise for distinct values of the Darcy number $D_{a}$

Fig. 17

Variation of pressure rise for distinct values of the Hartmann number M

Fig. 18

Variation of pressure rise for distinct values of the velocity slip parameter $\delta$

Fig. 19

Variation of pressure rise for distinct values of the thermal slip parameter $\beta$

Fig. 20

Variation of pressure rise for distinct values of the heat source/sink parameter $\gamma$

5 Conclusions

In this investigation, we have analyzed the impinging of silver and copper nanoparticles on MHD flow along slip effects through a porous medium. The impact of different rheological parameters on the important flow quantities is described via graphs. Some crucial observations of the present analysis are mentioned as,

• It is noted that the temperature inside the vertical tube increases for heat source parameter ($\gamma >0$). This result is obtained due to increase in internal heat source of the fluid, i.e., through metabolic process.

• With the increase of nanoparticle volume fraction, temperature of the nanofluid decreases with an increase in the nanoparticle volume fraction because high thermal conductivity of nanoparticles plays a key role in quick dissipation of the temperature. This observation justifies the use of nanoparticles as coolants in several engineering applications

• Velocity profiles exhibit higher results for pure blood than for the copper blood and silver blood.

• It is observed with an increase in the intensity of magnetic field velocity profile decreases. This result is concluded from the fact that the external magnetic field slows down the random motion of nanoparticles and hence also tends down the blood movement.

• It is elucidated that the velocity increases for velocity and thermal slip parameters which is physically true because slip effects reduce the drag force between the boundary and fluid and hence velocity increases.

• Pressure gradient increases with increasing nanoparticle volume fraction. It is due to the fact that the inclusion of nanoparticles allows the quick passage of fluid through vertical tube.

• Pressure rise enhances due to the impulsion of metallic nanoparticles when compared to that of the pure blood $(\phi =0.00).$

• The number of bolus increases throughout the vertical tube with the addition of silver and copper nanoparticles in the presence of slip effects when compare with $( \beta =0, \delta =0) .$

• The trapping bolus phenomenon shows that the number of the bolus increases with an increase in the concentration of nanoparticles as compared to the pure blood case $(\phi =0)$.

Fig. 21

Variation of pressure rise for distinct values of the Grashof number $G_{r}$

Fig. 22

Streamlines (copper nanoparticles) for different values of the a $D_{a}=0.1,$ b $D_{a}=0.15,$ c $D_{a}=0.2$

Fig. 23

Streamlines (silver nanoparticles) for different values of the a $D_{a}=0.1,$ b $D_{a}=0.15,$ c $D_{a}=0.2$

Fig. 24

Streamlines (copper nanoparticles) for different values of the a $M=0.05,$ b $M=0.1,$ c $M=0.2$

Fig. 25

Streamlines (silver nanoparticles) for different values of the a $M=0.05,$ b $M=0.1,$ c $M=0.2$

Fig. 26

Streamlines (copper nanoparticles) for different values of the a $\delta =0.00,$ b $\delta =0.05,$ c $\delta =0.09$

Fig. 27

Streamlines (silver nanoparticles) for different values of the a $\delta =0.00,$ b $\delta =0.05,$ c $\delta =0.09$

Fig. 28

Streamlines (copper nanoparticles) for different values of the a $\beta =0.00,$ b $\beta =0.05,$ c $\beta =0.09$

Fig. 29

Streamlines (silver nanoparticles) for different values of the a $\beta =0.00,$ b $\beta =0.05,$ c $\beta =0.09$

Fig. 30

Streamlines (copper nanoparticles) for different values of the a $\gamma =0.1,$ b $\gamma =0.2,$ c $\gamma =0.3$

Fig. 31

Streamlines (silver nanoparticles) for different values of the a $\gamma =0.1,$ b $\gamma =0.2,$ c $\gamma =0.3$

Fig. 32

Streamlines (copper nanoparticles) for different values of the a $G_{r}=1,$ b $G_{r}=1.3,$ c $G_{r}=1.6$

Fig. 33

Streamlines (silver nanoparticles) for different values of the a $G_{r}=1,$ b $G_{r}=1.3,$ c $G_{r}=1.6$

Fig. 34

Streamlines (copper nanoparticles) for different values of the a $\phi =0.00$ (pure blood),  b $\phi =0.05,$ c $\phi =0.09$

Fig. 35

Streamlines (silver nanoparticles) for different values of the a $\phi =0.00$ (pure blood),  b $\phi =0.05,$ c $\phi =0.09$