1 Introduction

The study related to pulsatile flow has gained special attention because of its applications in the natural and engineering systems. For example, the respiratory system, circulatory systems, vascular diseases, reciprocating pumps, pulse combustors, microelectromechanical systems (MEMS), and IC engines [1,2,3,4,5,6]. Particularly, in the procedure of dialysis of blood in an artificial kidney, the pulsatile flow is playing a very important role [6]. The pulsatile flow of viscous fluid in a permeable channel with heat transfer was investigated by Radhakrishnamacharya and Maiti [6]. Malathy and Srinivas [7] studied analytically, the MHD pulsating flow between two permeable beds using the perturbation method. Srinivas et al. [8] investigated the problem of hydromagnetic pulsatile flow of non-Newtonian fluid in porous a channel with the Joule heating and thermal radiation effects. Recently, Pan et al. [9] examined the behavior reverse flow of pulsatile flow and heat transfer in a grooved channel.

Many materials like biological products (Vaccines, blood, syrups, synovial fluids, and so on), foodstuffs (ketchup, yogurt, ice creams, sauce, and so on), and chemical products (saints, toothpastes, shampoos, cosmetics, and so on) do not obey Newton law of viscosity which are named as non-Newtonian fluids. These are classified into three types such as the differential, integral and rate types. One of the important cases of non-Newtonian fluids is viscoelastic fluids. The study related to hydromagnetic viscoelastic fluids is very important in many industrial and scientific applications like MHD pumps, MHD generators, transpiration cooling, food processing, and biomechanics. The Oldroyd-B model belongs to non-Newtonian fluids has attracted much attention of researchers [10,11,12,13,14,15,16,17,18] several references therein. Srinivas et al. [19] developed analytical solutions for the pulsatile flow of Oldroyd-B fluid in a channel with a magnetic field and heat transfer using the perturbation technique. Zheng et al. [20] obtained exact solutions for generalized Oldroyd-B fluid flow over an infinite accelerated plate with an applied magnetic field. Gosh et al. [21] made an initial value investigation to study the MHD flow of Oldroyd-B between two infinite rigid non-conducting plates. Sandeep and Reddy [22] examined the Oldroyd-B fluid flow across a melting surface with a magnetic effect. An analytical treatment for an electrically conducting mixed convective flow of Oldroyd-B fluid over a stretchable surface was made by Mustafa [23]. Malathy et al. [24] computed analytical solutions for chemically reacted pulsating flow of Oldroyd-B fluid in a channel with thermal radiation and applied magnetic field using perturbation method.

Nowadays, the study of nanofluid is very important due to their significant applications in biomedical, optical and electronic fields [25,26,27,28,29,30,31,32,33,34]. The term nanofluid was first used by Choi [25]. Nanofluid is a combination of base fluid and nano-sized particles. Agarwal and Rana [35] examined the nonlinear convective analysis of a rotating Oldroyd-B Al\(_2\)O\(_3\)-EG nanofluid fluid layer under the thermal non-equilibrium. Ifran et al. [36] discussed the problem of Oldroyd-B nanofluid flow with variable thermal conductivity in the presence of thermal and solutal stratification. Hayat et al. [37] obtained series solutions for the two-dimensional flow of Oldroyd-B nanofluid over a stretching sheet. Hatami et al. [38] have analyzed analytically and numerically, the third-grade nanofluid flow in a hollow vessel in the presence of a magnetic field and porous medium. Akbar [39] investigated the impact of a magnetic effect on carbon nanotubes-blood flow in stenosed arteries. Vijayalakshmi and Srinivas [40] examined the pulsatile flow of nanofluid between two permeable walls with magnetic and radiation effects. The transport of Au-blood nanofluid between two permeable moving/stationary walls was examined by Srinivas et al. [41]. Kumar et al. [42] have made a study of the pulsatile flow of Casson nanofluid in a vertical porous space in the presence of radiation, magnetic field, and chemical reaction. Ijaz and Nadeem [43] modelled a problem to study the impact of blood-mediated nanoparticle (Ag-Al\(_2\)O\(_3\)/blood) non-hemodynamics of overlapped stenotic artery. Elgazery [44] examined the flow of non-Newtonian fluid through non-Darcian porous medium with gold and alumina nanoparticles by considering blood as base fluid. Ijaz and Nadeem [45] studied the consequences of blood mediated Al\(_2\)O\(_3\) nanoparticle transportation as drug agent to attenuate atherosclerotic lesions with permeability impact.

Though the combined effects of viscous dissipation and Joule heating are ignored in the above studies. The effects bear great importance on heat transfer which is a viscous dissipation. The dissipation becomes significant when the viscosity of the fluid is high. Viscous dissipation occurs in geological processes, stronger gravitational fields, and polymers [42, 46]. Cotrtell [47] analysed viscous dissipation and radiation effects on the thermal boundary layer over a nonlinearly stretching sheet using the \(4\mathrm{th}\)-order Runge–Kutta method with shooting method. Ahmed et al. [48] explored the influence of viscous dissipation and thermal radiation on CNT-water nanofluid between Riga plates. Salawu et al. [49] made a theoretical study on double exothermic combustible reaction and thermal ignition of viscous dissipative Oldroyd 8-constant fluid in a channel. Hashmi et al. [50] have investigated the heat and mass transfer characteristics of Oldroyd-B fluid between two exponentially stretching disks with viscous dissipation and Joule heating effects.

The impact of Joule heat and thermal radiation in the study of non-Newtonian fluids is an important factor for researchers due to their vital uses in micro-fluidic devices, miniaturized chemical reactors, aerospace, heat transfer increases, and micro-electromechanical systems, etc. [51,52,53,54,55]. Hayat et al. [56] studied the combined effects of Joule heating viscous dissipation on MHD radiative flow due to a rotating disk using the homotopy analysis method. Khan et al. [57] examined the thermal analysis and entropy generation for the swirling motion of Casson nanofluid past a rotating cylinder with the impact of Joule heating. Shamshuddin et al. [58] made an analytical investigation on MHD squeezing flow, heat and mass transfer of viscous fluid between two Riga plates by considering the impacts of Joule heating and viscous dissipation. Aly and Pop [59] investigated the study of MHD stagnation point of hybrid nanofluid over a stretching/shrinking surface with viscous dissipation and Joule heating effects.

A careful literature survey reveals that no study is available which considers the pulsating flow of Oldroyd-B nanofluid in a channel with Joule heating and viscous dissipation effects. Keeping in view the wide range of applications in engineering and biological models and motivated by previous studies [24, 48, 56], we made an attempt to fill up this gap with an analytical study to analyze the flow of the Oldroyd-B nanofluid in a channel in the presence of thermal radiation, viscous dissipation and Joule heating. The flow analysis is carried out after reducing the equations governing the flow into a set of ordinary differential equations. The solution to the problem is obtained analytically using the perturbation method. The graphs are plotted to highlight the effects of various emerging parameters. A comprehensive discussion over those graphs is also presented. Owing to the importance of this kind of problems, the present analysis aims to manifest answers to the following research questions: (1) what are the impacts of frequency parameter and heat source on the temperature distribution of nanofluid? (2) What is the influence of viscous dissipation and Joule heating on pulsatile flow of nanofluid? (3) What is the significance of magnetic field on temperature and heat transfer rate of Oldroyd-B nanofluid?

2 Formulation

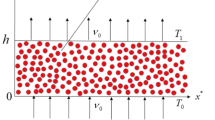
Consider an electrically conducting pulsatile flow of a non-Newtonian nanofluid in a channel which is laminar, incompressible. \(\hbox {Al}_2\hbox {O}_3\) is chosen as nanoparticle and blood is taken as Oldroyd-B fluid. Thermal radiation, viscous dissipation and Joule heating are taken into account. As presented in Fig. 1, the \(x^*\)-axis is taken along the lower wall and the \(y^*\)-axis as perpendicular to the walls. A magnetic field of strength \(B_0\) is applied uniformly opposite to the flow direction. The top and bottom walls are at the temperatures \(T_1\) and \(T_0\), respectively.

Fig. 1
figure 1

Coordinate system of the geometry

Full size image

Since the present analysis is based on the Oldroyd-B model of a viscoelastic fluid, the constitutive equation for Oldroyd-B fluid model is [10, 24]

$$\begin{aligned} \tau =-PI+S, \ \ \left( 1+\lambda _1\frac{\partial }{\partial t}\right) S=\mu \left( 1+\lambda _2\frac{\partial }{\partial t}\right) D_1,\nonumber \\ \end{aligned}$$
(1)

where \(\tau \) is Cauchy stress tensor, P is pressure, I is identity tensor, S is an extra tensor, \(\mu \) is the dynamic viscosity, \(\lambda _1\) and \(\lambda _2\) are relaxation and retardation times, respectively, and \(D_1\) is the first Rivlin–Ericksen tensor. All physical quantities excepting pressure are functions of \(y^*\) and \(t^*\) only because the walls are infinitely extend. The pulsatile flow is driven by the pressure gradient of the form [6]

$$\begin{aligned} -\frac{1}{\rho _{\mathrm{nf}}}\frac{\partial P^*}{\partial x^*}=A\left( 1+\epsilon e^{i \omega t^*}\right) , \end{aligned}$$
(2)

here A is a constant, \(\epsilon (<<1)\) is a positive quantity, \(\omega \) is frequency, and \(t^*\) is time. We assumed that the fluid velocity, and temperature are parallel to the \(x^*\)-axes. So that only \(x^*\)-component of \(u^*\) of the velocity does not vanish. The condition of fully developed flow implies that \(\dfrac{\partial u^*}{\partial x^*}=0\). Since the velocity is solenoidal, we obtain \(\dfrac{\partial v^*}{\partial y^*}=0\). As a consequence, the velocity component \(v^*\) is constant in any channel section and is equal to zero at the channel walls, so \(v^*\) must be vanishing at any position. The \(y^*\)-momentum balance equation can be expressed as \(\dfrac{\partial P^*}{\partial y^*}=0\) (see Ref. [41, 42]). Under these assumptions, the governing equations are

$$\begin{aligned}&\left( 1+\lambda _1\frac{\partial }{\partial t^*}\right) \frac{\partial u^*}{\partial t^*}\nonumber \\&\quad =-\frac{1}{\rho _{\mathrm{nf}}}\left( 1+\lambda _1\frac{\partial }{\partial t^*}\right) \frac{\partial P^*}{\partial x^*}+\frac{\mu _{\mathrm{nf}}}{\rho _{\mathrm{nf}}}\left( 1+\lambda _2\frac{\partial }{\partial t^*}\right) \frac{\partial ^2 u^*}{\partial y^{*2}}\nonumber \\&\qquad -\left( 1+\lambda _1\frac{\partial }{\partial t^*}\right) \frac{\sigma _{\mathrm{nf}}}{\rho _{\mathrm{nf}}}B_0^2u^* \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial T^*}{\partial t^*}&=\frac{k_{\mathrm{nf}}}{(\rho C_p)_{\mathrm{nf}}}\frac{\partial ^2 T^*}{\partial y^{*2}}+\frac{\mu _{\mathrm{nf}}}{(\rho C_p)_{\mathrm{nf}}}\left( \frac{\partial u^*}{\partial y^*}\right) ^2\nonumber \\&\quad +\frac{16\sigma ^*T_1^3}{3k^*(\rho C_p)_{nf}}\frac{\partial ^2 T^*}{\partial y^{*2}}+\frac{\sigma _{nf}}{(\rho C_p)_{\mathrm{nf}}}B_0^2u^{*2}\nonumber \\&\quad +\frac{Q_0}{(\rho C_p)_{\mathrm{nf}}}(T^*-T_0), \end{aligned}$$
(4)

where \(u^*\) is velocity component in \(x^*\)- direction, \(\rho _{\mathrm{nf}}\) is density of nanofluid, \(P^*\) is the pressure, \(\mu _{\mathrm{nf}}\) is dynamic viscosity of the nanofluid, \(\sigma _{\mathrm{nf}}\) is the electrical conductivity of the nanofluid, \((\rho C_p)_{\mathrm{nf}}\) is effective specific heat of nanofluid, \(k_{\mathrm{nf}}\) thermal conductivity of nanofluid, \(T^*\) is the temperature of the nanofluid, \(\sigma ^*=5.6697 \times 10^{-8}\,\, \mathrm{Wm}^{-2}\mathrm{K}^{-4}\) is the Stefan–Boltzmann constant and \(k^*\) is the Rosseland mean absorption coefficient and h is the distance between the walls.

Table 1 The thermophysical properties of blood and Al\(_2\)O\(_3\) nanoparticles
Full size table

The appropriate boundary conditions (B.Cs) are

$$\begin{aligned}&u^*(0)=0, \quad T^*(0)=T_0 \end{aligned}$$
(5)
$$\begin{aligned}&u^*(h)=0, \quad T^*(h)=T_1 . \end{aligned}$$
(6)

The thermophysical properties of base fluid (blood) and nanoparticle (Al\(_2\)O\(_3\)) are given in Table 1 and the properties of nanofluid such as \(\rho _{\mathrm{nf}}\), \(\mu _{\mathrm{nf}}\), \((\rho C_\mathrm{p})_{\mathrm{nf}}\) and \(k_{\mathrm{nf}}\) are defined as [27, 40, 41]

$$\begin{aligned} \left. \begin{aligned} \mu _{\mathrm{nf}}&=\frac{\mu _f}{(1-\phi )^{2.5}}; \ \rho _{\mathrm{nf}}=(1-\phi )\rho _f+\phi \rho _\mathrm{s}; \ (\rho C_\mathrm{p})_{\mathrm{nf}}&=(1-\phi )(\rho C_\mathrm{p})_f+\phi (\rho C_\mathrm{p})_\mathrm{s};\\ \frac{k_{\mathrm{nf}}}{k_\mathrm{f}}&=\frac{k_\mathrm{s}+2k_\mathrm{f}-2\phi (k_\mathrm{f}-k_\mathrm{s})}{k_\mathrm{s}+2k_\mathrm{f}+\phi (k_\mathrm{f}-k_\mathrm{s})}; \ \frac{\sigma _{\mathrm{nf}}}{\sigma _\mathrm{f}}\\&=1+\dfrac{3(\frac{\sigma _\mathrm{s}}{\sigma _\mathrm{f}}-1)\phi }{(\frac{\sigma _\mathrm{s}}{\sigma _\mathrm{f}}+2)-\left( \frac{\sigma _\mathrm{s}}{\sigma _\mathrm{f}}-1\right) \phi }. \end{aligned} \right\} \end{aligned}$$
(7)

Using Eqs. (7), (3) and (4) become

$$\begin{aligned}&\left( 1+\lambda _1\frac{\partial }{\partial t^*}\right) \frac{\partial u^*}{\partial t^*} =-\frac{1}{\rho _{f}A_1}\left( 1+\lambda _1\frac{\partial }{\partial t^*}\right) \frac{\partial P^*}{\partial x^*}\nonumber \\&\qquad +\frac{\mu _{f}}{\rho _{f}}\frac{A_2}{A_1}\left( 1+\lambda _2\frac{\partial }{\partial t^*}\right) \frac{\partial ^2 u^*}{\partial y^{*2}}\qquad \qquad \nonumber \\&\qquad -\left( 1+\lambda _1\frac{\partial }{\partial t^*}\right) \frac{\sigma _{\mathrm{f}}}{\rho _{\mathrm{f}}}\frac{A_5}{A_1}B_0^2u^* \end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial T^*}{\partial t^*}&=\frac{k_{f}}{(\rho C_\mathrm{p})_{f}}\frac{A_4}{A_3}\frac{\partial ^2 T^*}{\partial y^{*2}}\nonumber \\&\qquad +\frac{\mu _{f}}{(\rho C_\mathrm{p})_{f}}\frac{A_2}{A_3}\left( \frac{\partial u^*}{\partial y^*}\right) ^2+\frac{16\sigma ^* T_1^3}{3k^*(\rho C_\mathrm{p})_{f}}\frac{1}{A_3}\frac{\partial ^2 T^*}{\partial y^{*2}}\nonumber \\&\qquad +\frac{\sigma _{f}}{(\rho C_\mathrm{p})_{f}}\frac{A_5}{A_3}B_0^2u^{*2}+\frac{Q_0}{(\rho C_\mathrm{p})_{\mathrm{nf}}}(T^*-T_0), \end{aligned}$$
(9)

here \(A_1=(1-\phi )+\phi \frac{\rho _\mathrm{s}}{\rho _\mathrm{f}}\), \(A_2=\frac{1}{(1-\phi )^{2.5}}\), \(A_3=(1-\phi )+\phi \frac{(\rho C_\mathrm{p})_\mathrm{s}}{(\rho C_\mathrm{p})_\mathrm{f}}\), \(A_4=\frac{k_\mathrm{s}+2k_\mathrm{f}-2\phi (k_\mathrm{f}-k_\mathrm{s})}{k_\mathrm{s}+2k_\mathrm{f}+\phi (k_\mathrm{f}-k_\mathrm{s})}\), \(A_5=1+\dfrac{3(\frac{\sigma _\mathrm{s}}{\sigma _\mathrm{f}}-1)\phi }{(\frac{\sigma _\mathrm{s}}{\sigma _\mathrm{f}}+2)-(\frac{\sigma _\mathrm{s}}{\sigma _\mathrm{f}}-1)\phi }\).

Now, using the following dimensionless variables and parameters,

$$\begin{aligned} x= & {} \frac{x^*}{h}, \ y=\frac{y^*}{h}, \ t=t^*\omega , \ u=\frac{u^* \omega }{A}, \ P=\frac{P^*}{\rho Ah},\nonumber \\ \theta= & {} \frac{T^*-T_0}{T_1-T_0}, \end{aligned}$$
(10)

Equations (2), (8) and (9) become

$$\begin{aligned}&-\frac{\partial P}{\partial x}=1+\epsilon e^{it} \end{aligned}$$
(11)
$$\begin{aligned}&\left( 1+\lambda _1\omega \frac{\partial }{\partial t}\right) \frac{\partial u}{\partial t}\nonumber \\&\quad =-\frac{1}{A_1}\left( 1+\lambda _1 \omega \frac{\partial }{\partial t}\right) \frac{\partial P}{\partial x}+\frac{A_2}{A_1}\frac{1}{H^2}\left( 1+\lambda _2\omega \frac{\partial }{\partial t}\right) \frac{\partial ^2 u}{\partial y^{2}}\qquad \qquad \nonumber \\&\qquad -\frac{A_5}{A_1}\frac{M^2}{H^2}\left( 1+\lambda _1\omega \frac{\partial }{\partial t}\right) u \end{aligned}$$
(12)
$$\begin{aligned} H^2\frac{\partial \theta }{\partial t}&=\frac{A_4}{A_3}\frac{1}{Pr}\frac{\partial ^2 \theta }{\partial y^{2}}+\frac{A_2}{A_3}\mathrm{Ec}\left( \frac{\partial u}{\partial y}\right) ^2\nonumber \\&\qquad +\frac{1}{A_3}\frac{4}{3}\frac{\mathrm{Rd}}{\mathrm{Pr}}\frac{\partial ^2 \theta }{\partial y^{2}}+\frac{A_5}{A_3}\mathrm{Ec}M^2u^{2}+\frac{Q}{A_3}\theta , \end{aligned}$$
(13)

where \(H=h\sqrt{\frac{\omega }{\nu _\mathrm{f}}}\) is the frequency parameter, \(M=B_0h\sqrt{\frac{\sigma _f}{\mu _\mathrm{f}}}\) is the Hartmann number, \(\Pr =\frac{\nu _\mathrm{f}(\rho C_\mathrm{P})_\mathrm{f}}{k_\mathrm{f}}\) is the Prandtl number, \(\mathrm{Ec}=\dfrac{(\frac{A}{\omega })^2}{(\rho C_\mathrm{P})_f(T_1-T_0)}\) is the Eckert number, \(\mathrm{Rd}=\frac{4\sigma ^*T_1^3}{k^*k_\mathrm{f}}\) is the radiation parameter, \(Q=\frac{Q_0h^2}{(\rho C_\mathrm{p} \nu )_{f}}\) is heat source/sink parameter.

The appropriate B.Cs are

$$\begin{aligned}&u(0)=0, \quad \theta (0)=0 \end{aligned}$$
(14)
$$\begin{aligned}&u(1)=0, \quad \theta (1)=1 . \end{aligned}$$
(15)
Fig. 2
figure 2

Temperature distribution a impact of Ec, b impact of H, c impact of Q

Full size image
Fig. 3
figure 3

Temperature distribution a combine impact of M and Ec, b combine impact of Ec and Rd

Full size image
Fig. 4
figure 4

Unsteady temperature distribution a impact of Ec, b impact of \(\lambda _1\), c impact of \(\lambda _2\), d impact of M, e impact of Rd, f impact of t

Full size image
Fig. 5
figure 5

Nu at the lower wall a impact of \(\phi \), b impact of Ec, c impact of Q

Full size image
Fig. 6
figure 6

Nu at the lower wall a combine impact of Ec and M, b combine impact of Ec and Rd

Full size image
Fig. 7
figure 7

Nu at the lower wall. a Effect of Ec, b impact of \(\lambda _1\), c impact of \(\lambda _2\), d impact of Q, e impact of H, f impact of M, g impact of Rd

Full size image
Fig. 8
figure 8

Nu at the lower wall a impact of \(\phi \), b impact of Ec, c impact of \(\lambda _1\), d impact of \(\lambda _2\), e impact of Q, f impact of H, g impact of Rd, h impact of M

Full size image

3 Analytical solution

In view of (11), the velocity u and temperature \(\theta \) are taken as

$$\begin{aligned} u(y)&=u_0(y)+\epsilon u_1(y)e^{it} \end{aligned}$$
(16)
$$\begin{aligned} \theta (y)&=\theta _0(y)+\epsilon \theta _1 (y)e^{it}. \end{aligned}$$
(17)

On substituting Eqs. (16) and (17) into (12) and (13), and by equating the coefficients of different powers of \(\epsilon \), we obtain

$$\begin{aligned}&\frac{A_2}{A_1}u_0''-\frac{A_5}{A_1}M^2u_0=-\frac{H^2}{A_1} \end{aligned}$$
(18)
$$\begin{aligned}&\frac{A_2}{A_1}u_1''-\left( \frac{A_5}{A_1}M^2+iH^2\right) \beta ^2u_1=-\frac{H^2}{A_1}\beta ^2 \end{aligned}$$
(19)
$$\begin{aligned}&\left( \frac{A_4}{A_3}+\frac{1}{A_3}\frac{4}{3}\mathrm{Rd}\right) \theta _0''+\frac{Q\Pr }{A_3}\theta _0\nonumber \\&\quad =-\,\frac{A_2}{A_3}\mathrm{EcPr}(u_0')^2-\frac{A_5}{A_3}M^2\mathrm{EcPr} u_0^2 \end{aligned}$$
(20)
$$\begin{aligned}&\left( \frac{A_4}{A_3}+\frac{1}{A_3}\frac{4}{3}\mathrm{Rd}\right) \theta _1''-\left( i\mathrm{Pr}H^2-\frac{Q\Pr }{A_3} \right) \theta _1\nonumber \\&\quad =-\frac{A_2}{A_3}2\mathrm{EcPr}u_0'u_1'-\frac{A_5}{A_3}2M^2\mathrm{EcPr} u_0u_1, \end{aligned}$$
(21)

where primes denote differentiation with respect to y. The related B.Cs are

$$\begin{aligned}&u_0(0)=0, \quad u_0(1)=0, \quad u_1(0)=0, \quad u_1(1)=0\end{aligned}$$
(22)
$$\begin{aligned}&\theta _0(0)=0, \quad \theta _0(1)=1, \quad \theta _1(0)=0, \quad \theta _1(1)=0. \end{aligned}$$
(23)

Now, by solving equations (18)–(21) with the corresponding B.Cs (22) and (23), we get

$$\begin{aligned} u_0(y)=&B_5 e^{-\sqrt{B_3}y}+B_6 e^{\sqrt{B_3}y} -\frac{B_4}{B_3} \end{aligned}$$
(24)
$$\begin{aligned} u_1(y)=\,\,&B_{10} e^{-\sqrt{B_8}y}+B_{11} e^{\sqrt{B_8}y} -\frac{B_9}{B_8} \end{aligned}$$
(25)
$$\begin{aligned} \theta _0(y)=\,\,&C_{11}e^{-\sqrt{C_3}y} + C_{12}e^{\sqrt{C_3}y} + C_{13} e^{ - 2\sqrt{B_3 } y }\nonumber \\&+ C_{14} e^{2\sqrt{B_3 } y } + C_{15} e^{ - \sqrt{B_3 } y }\nonumber \\&+ C_{16} e^{\sqrt{B_3 } y } + C_{17} \end{aligned}$$
(26)
$$\begin{aligned} \theta _1(y)=\,\,&C_{33} e^{-\sqrt{C_{19}}y} + C_{34} e^{\sqrt{C_{19}}y} + C_{35} e^{ - (\sqrt{B_3 } + \sqrt{B8} )y } \nonumber \\&+ C_{36} e^{ - (\sqrt{B_3 } - \sqrt{B8} )y } \nonumber \\&+ C_{37} e^{(\sqrt{B_3 } - \sqrt{B8} )y } \nonumber \\&+ C_{38} e^{(\sqrt{B_3 } + \sqrt{B8} )y } \nonumber \\&+ C_{39} e^{ - \sqrt{B_3 } y } + C_{40} e^{\sqrt{B_3 } y } \nonumber \\&+ C_{41} e^{ - \sqrt{B_8 } y } + C_{42} e^{\sqrt{B_8 } y } + C_{43}. \end{aligned}$$
(27)

Here, the coefficients Bs and Cs are given in Appendix.

Further, the physical quantity rate of heat transfer (Nusselt number) at the walls is defined as [6]

$$\begin{aligned} \mathrm{Nu}=A_4\left( \frac{\partial \theta }{\partial y}\right) _{y=0,1}. \end{aligned}$$
(28)

4 Results and discussion

In the present section, results are sketched through graphs by taking set of parameters \(H=2, \ M=2,\ \mathrm{Pr}=21,\ \mathrm{Ec}=1,\ \mathrm{Rd}=1,\ \lambda _1=0.2,\ \lambda _2=0.8,\ Q=0.5\). In this study, \(\theta _t\) and \(\mathrm{Nu}_t\) represent the unsteady temperature and Nusselt number respectively. The impact of physical parameters on temperature and heat transfer rate are presented. Figure 2a–c depicts the impact of \(\mathrm{Ec},\ H,\ Q\). Figure 2a depicts that there is an enhancement in the temperature of nanofluid by rising Ec. This is due to the friction between the molecules, the energy generated because of the collision of the molecules, is retained in the fluid, which higher the temperature. Similar behavior can be found by increasing the frequency parameter H and heat source parameter Q (see Fig. 2b and c). From Fig. 2c, it is clear that increasing the heat source produces heat.

The influence of \(\mathrm{Ec}, M, \mathrm{Rd}\) on temperature distribution is shown in Fig. 3a and b. The combined effect of the magnetic field (Lorentz force) and viscous dissipations is presented in Fig. 3a. It reveals that enhancing the viscous dissipation (Ec) enhances the temperature of nanofluid. This is due to the fact that inside friction of molecules the conversion of mechanical energy to thermal energy is the reason for temperature enhancement. Also noticed that there is a fall in temperature in with increasing Hartmann number. From Fig. 3b, one can see that increasing radiation parameter decreases the temperature of nanofluid. This decrease may be to the physical fact that increasing the radiation parameter decreases the thermal boundary layer thickness. From Fig. 3a and b, it is relevant to mention here that for all the cases involved, the temperature is on a higher with increasing Ec.

Figure 4a–f is plotted to see the influence of \(\mathrm{Ec}, \ \lambda _1, \ \lambda _2, M, \ \mathrm{Rd} \) and t on \(\theta _t\). From these figures, it is presented that the profiles of \(\theta _t\) are oscillating and the maximum is towards the walls. Figure 4a presents that there is an enhancement in \(\theta _t\) with an increase in Ec. The temperature profile exhibits an oscillating character. The effect of \(\lambda _1\) on \(\theta _t\) is shown in Fig. 4b. It is depicted that temperature profile exhibits oscillating nature and also noticed that \(\theta _t\) is an increasing function of \(\lambda _1\). From Fig. 4c, it is found out that \(\theta _t\) is a decreasing function of \(\lambda _2\). From Fig. 4d–f, it observed that the unsteady temperature profiles display oscillating character by varying \(M,\ \mathrm{Rd}\) and t.

To see the impact of physical parameters on the rate of heat transfer, 2D and 3D graphs are given in Figs. 5, 6, 7 and 8. The rate of heat transfer at the wall \(y=0\) against the frequency parameter H is presented in Fig. 5a–c. From these figures it is shown that Nu enhances with enhancing H. Figure 5a depicts an increase in \(\phi \) accelerates the heat transfer rate. From Fig. 5b and c, one can see that Nu is an increasing function of Ec and Q. Figure 6a and b elucidates the effect of Ec, M, Rd on Nusselet number distribution. These figures show that there is a decrease in heat transfer rate for a given increase in M and Rd, while there is an enhancement in heat transfer rate with increasing Ec. The total and unsteady Nusselt numbers are plotted in 3-D graphs which are presented in Figs. 7 and 8 respectively. From Fig. 7a–g, it is observed that the total Nusselt number Nu is a rising function of \(\mathrm{Ec}, \ \lambda _1, \ \lambda _2, \ Q\) and H where as it is decreasing function of M and Rd. The unsteady Nusselt number \(\mathrm{Nu}_t\) is presented in 3-D graphs against t for different values of the parameters in Fig. 8a–h. It is concluded that the unsteady Nusselt number profiles exhibit oscillating by varying \(\phi \), Ec,\(\ \lambda _1, \ \lambda _2, \ Q,\ H,\) Rd and M.

5 Conclusion

In this study, analytical solutions for MHD pulsating flow of Al\(_2\)O\(_3\)-blood nanofluid in a channel in the presence of viscous dissipation, Joule heating, thermal radiation and heat source/sink had been carried out. The base fluid is blood which is taken as Oldroyd-B fluid and Al\(_2\)O\(_3\) as nanoparticle. Brinkman and Maxwell Garnett models are considered. Special emphasis has been given to the effects of viscous dissipation and Joule heating and the following conclusions have been drawn from the obtained results:

  • The temperature of nanofluid enhances with increasing viscous dissipation.

  • Nanofluid temperature is a rising function of heat source while it is a decreasing function of radiation parameter.

  • A rise in frequency parameter raises the temperature of the nanofluid.

  • Increase in the Lorentz force decreases the heat transfer rate.

  • The unsteady temperature profiles show oscillating character which may be due to unsteady pressure gradient. The unsteady temperature is maximum near the walls.

  • There is an enhancement in Nu at \(y=0\) with enhancing volume fraction of nanoparticles.

  • Nusselt number (Nu) increases for a given increase in Ec and Q.