Influence of viscous dissipation on MHD flow of micropolar fluid over a slendering stretching surface with modified heat flux model

Abstract

The current research article delivers a numerical study of an electrically conducting magnetohydrodynamic nonlinear convection flow of micropolar fluid over a slendering stretching surface. The flow is laminar and time independent. The influence of viscous dissipation, Joule heating, non-uniform heat source or sink, temperature-dependent thermal conductivity and thermal radiation is deemed. Heat-transfer characteristics are scrutinized with the aid of modified Fourier’s law. We presented simultaneous solutions for a flat surface and variable thickened surface. At first, appropriate similarity transformations are considered to convert the basic partial differential equations as ordinary ones and then solved by the successive application of numerical procedures such as shooting and fourth-order Runge–Kutta method. Graphs are delineated to observe the influence of diverse nondimensional parameters on the flow fields. Along with the skin friction coefficient, couple stress coefficient and local Nusselt number are also discussed and bestowed with the support of the table. Results stipulate that the distribution of temperature increases with thermal relaxation and radiation parameters, but a contradictory outcome is spotted for Prandtl number. Also, the microrotation velocity is suppressed with an enhancement in magnetic field parameter, but an opposite trend is observed for buoyancy force.

Introduction

Newly, combining dynamic fluids with thermal transport has been an exclusive, worthy concern due to its abundant mechanical and industrial significances. Some of such noteworthy applications of the heat-transfer phenomenon are the rate of cooling, polymer indulgence, ornament evolving, sanitize-care of dissolved metals, painting material and coating of threads. It is well known that the phenomenon of heat exchange happens when there is a temperature difference between objects or within various portions of the object. This process has ample significances in thermal transmission in muscles, power regiment, an amalgamation of nuclear energy and many engineering fields. To describe the heat transport mechanism, Fourier’s heat conduction law is strongly accomplished by the previous investigators. In 1948, Cattaneo [1] wished for a new model to accomplish effective thermal transfer rate with the addition of relaxation time to Fourier’s model. Later, Christov [2] wished for the time derivative model to Cattaneo’s model, and it is entitled as Cattaneo–Christov heat flux model. Some significant applications of improved heat flux model are pasteurization of toned milk, making of microchips and automatic devices. Hayat et al. [3] reported the thermal characteristics of an incompressible free convective boundary layer flow of non-Newtonian fluid over a slendering stretching surface. This investigation is carried out under the attendance of improved Fourier’s model. Analytical solutions are presented with the assistance of homotopic convergent series. The authors [4,5,6] considered a model to scrutinize the heat-transfer behavior of MHD flows under sundry geometries. The solutions to the problems are obtained with a joint application of R.K. and shooting methods. Recently, Nadeem et al. [7] presented an analytical treatment for MHD non-Newtonian nanoliquid due to stretching of a plate in the presence of Brownian motion and concluded that the thermal relaxation parameter has a propensity to enhance the fluid temperature.

The fluid flow due to stretching of a slendering surface with heat transfer has an extensive collection of solicitations in geophysics, biotechnological process and aeronautical engineering. Also, it has massive prominence in the fabrication of rubber mugs and sheets, space vehicles, glass gusting, polymer physics, whirling of fiber and so on. Crane [8] initiated an incompressible flow over a stretching plate. Further, Anderson [9] extended this with Lorentz force and presented an analytical solution. The inspiration of temperature-reliant thermal conductivity on non-Newtonian fluids over a slendering surface was inspected by Hayat et al. [10] in the attendance of improved Fourier’s model. A few weeks ago, Anantha Kumar et al. [11] scrutinized the inspiration of drag force on non-Newtonian fluid over a stretching sheet with the attendance of melting heat transfer and concluded that the magnetic parameter has a tendency to reduce the velocity distribution.

The exploration of non-Newtonian liquid flows due to stretching of surfaces has countless applications in biomechanics, aeronautical and mechanical engineering and in some manufacturing procedures such as thermal isolation, the invention of paper, biological material developments, plastic sheets extrusion, crystal expansion, purification of milk, food dispensation, hot rolling and glass fiber. Non-Newtonian fluids are the fluids which do not monitor Newton’s law of viscosity. The micropolar liquid is one of a special kind and the most familiar non-Newtonian liquid. The micropolar liquids are liquids with microstructure. Some oils, honey, mango juice, mud, toothpaste, some ointments and emulsions are some notable non-Newtonian liquids in our daily life handling. Owing to this, they have massive solicitations in industries such as constructing of semiconductor tools, geothermal salvage and freezing of magma. Initially, Chiam [12] scrutinized the heat-transfer features of non-Newtonian fluid flows across a permeable stretching sheet and obtained a numerical solution by the consecutive implication of Newton’s and R.K. methods. The characteristics of shear-thickening stagnation point flow due to stretching of a surface were discussed by Nazar et al. [13] by the aid of Keller-box numerical scheme. Further, the work of Nazar et al. [13] is extended by Ishak et al. [14] with the flow across a shrinking sheet. Gupta et al. [15] deliberated the impact of buoyancy and suction parameters on an electrically conducting liquid subject to shrinking surface. They bestowed a numerical treatment for the problem with the finite element method. Recently, the authors [16, 17] examined the flow and heat-transfer features of non-Newtonian nanofluids across a permeable stretching surface in the attendance of drag force.

Viscous dissipation is an irretrievable procedure, in which heat is converted to the motion when liquid is stimulated along the surface. This happens due to the stroke of shear powers nearby the sheet. This phenomenon shows a vital role in enormous industrialized and industrial solicitations such as cuisine food, rock hard, electronic coffee makers and purification. Motivated by this, Cortell [18] discussed the influence of Eckert number on magnetohydrodynamic flow of non-Newtonian fluid due to a shrinking sheet. Further, Chen [19] discussed the combined influence of dissipation generated by viscosity on MHD flow over a stretching sheet in the attendance of thermal radiation. They bestowed a numerical solution with the aid of Keller-Box scheme and clinched that the rate of thermal transport reduced with an enhancement in the Eckert number. The influence of velocity slip on MHD flow due to stretching of a permeable sheet was studied by Anantha Kumar et al. [20]. Novickij et al. [21] conducted an experimental study to discuss the influence of Eckert number on the flow fields in the presence of magnetic field. Recently, Sulochana et al. [22] discussed the characteristics of heat transfer on convective non-Newtonian liquids across a stretching surface in the attendance of Joule heating and attained the results with the implication of R.K. and shooting techniques.

The process of non-uniform heat source or sink has widespread solicitations in paramedical and many technological undertakings such as radiated diffusers and crude oil retrieval . Hayat et al. [23] deliberated the effect of irregular heat parameters on the radiative flow due to the stretched cylinder by accounting Rosseland approximation. They presented an exact solution with the aid of HAM. Further, the researchers [24,25,26] deliberated the features of thermal transport on non-Newtonian fluids across a stretching sheet under the influence of irregular heat source or sink parameters and concluded that the heat transport performance can be controlled by the variable heat sink/source parameters.

Presently, many researchers have examined the effect of thermal radiation on the heat-transfer features of fluids done by a solid surface. Some illustrations of this situation are space technology, the invention of glass and polymer dispensation, etc. Bhattacharyya et al. [27] reported the heat-transfer characteristics of micropolar liquid due to the permeable shrinking surface with suction and thermal radiation. Also, they bestowed simultaneous consequences. The heat-transfer characteristic on MHD stagnation point flow over a porous stretching sheet was discussed by Ahmad et al. [28], Gupta et al. [29] and Kundu et al. [30] with the attendance of linear radiative heat flux. Haq et al. [31] discussed the effect of slip on electrically conducting MHD non-Newtonian fluid flow past a stretching surface in the attendance of radiation. It was found that the distribution of temperature was enhanced by the radiation parameter. Ramadevi et al. [32] reported a numerical solution for the magnetohydrodynamic radiative flow of shear-thickening liquids across a coagulated surface in the presence of thermo-diffusion and diffusion-thermo impacts. A new heat flux model is considered to analyze the heat-transfer phenomenon. The natural convective flow and heat-transfer characteristics in a square enclosure in the attendance of Lorentz force were examined by Doganchi et al. [33,34,35,36,37], and it was found that the magnetic field parameter has a propensity to enhance the local Nusselt number. Kumar et al. [38] considered a problem to study the flow and heat-transfer features of hybrid ferrofluid due to stretching of an unsteady surface under the influence of irregular heat source/sink. Simultaneous solutions are presented for ferrofluid and hybrid ferrofluids.

From the earlier literature, it is evident that very limited effort has been carried out for the magnetohydrodynamic stagnation point flow of micropolar fluid across a slendering stretching surface. Thus, in the present article, we are interested to examine the flow and heat-transfer features of a time-independent stagnation point flow of an electrically conducting magnetohydrodynamic micropolar fluid over a variable thickness surface. Suitable similarity transformations are used to transform the initial partial differential equations into ordinary ones and then solved numerically by using the fourth-order Runge–Kutta and shooting methods. Results are revealed graphically and bestowed numerical values for various physical parameters.

Mathematical formulation

Consider a steady two-dimensional incompressible stagnation point flow of an electrically conducting micropolar fluid past a stretching sheet with variable thickness. The fluid flow is considered in the $x$ way. Let us assume that the variable thickness of the surface is $y = L_{1} \left( {x + p} \right)^{{\frac{1 - {\text n}}{2}}}$; here $L_{1}$, $p$ are positive quantities and ($n \ne 1$, $n = 1$), respectively, the flow past a slendering stretching surface and flat surface. The fluid flow is occupied in the region $y \ge 0$. The $y -$ axis is taken perpendicular to the flow direction. We assume the stretching and ambient velocities of the surface are $u_{\text{s}} = a\left( {x + p} \right)^{{\text n}} ,$ and $u_{\text{e}} = b\left( {x + p} \right)^{{\text n}}$, respectively, where $a \;{\text{and}}\; b$ are nonnegative constants. Varying magnetic force $B\left( x \right) = B_{0 } \left( {x + p} \right)^{{\frac{{\text n} - 1}{2}}}$ is applied in the route of $y -$ as portrayed in Fig. 1.

Fig. 1

Flow geometry

The assumptions of the problem are:

• 1. Micropolar liquid model.

• 2. Stagnation point flow.

• 3. Modified heat flux model is considered.

• 4. Frictional heating, Joule heating, variable heat sink/source and thermal radiation impacts are deemed.

• 5. The partial slip boundary condition is applied to the boundary.

The governing equations are

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$

(1)

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = u_{\text{e}} \frac{{{\text{d}}u_{\text{e}} }}{{{\text{d}}x}} + \left( {\upsilon + \frac{\kappa }{\rho }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\kappa }{\rho }\frac{\partial N}{\partial y} + g\left( {\beta_{1} (T - T_{\infty } ) + \beta_{2} (T - T_{\infty } )^{2} } \right) - \frac{{\sigma B(x)^{2} u}}{\rho },$$

(2)

$$u\frac{\partial N}{\partial x} + v\frac{\partial N}{\partial y} = \frac{\Gamma }{\rho j}\frac{{\partial^{2} N}}{{\partial y^{2} }} - \frac{\kappa }{\rho j}\left( {2N + \frac{\partial u}{\partial y}} \right),$$

(3)

$$\begin{aligned} & (\rho C_{\text{P}} )\left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) + \gamma^{*} (\rho C_{\text{P}} )\left( \begin{aligned} u\frac{\partial u}{\partial x}\frac{\partial T}{\partial x} + v\frac{\partial v}{\partial y}\frac{\partial T}{\partial y} + u\frac{\partial v}{\partial x}\frac{\partial T}{\partial y} + \hfill \\ v\frac{\partial u}{\partial y}\frac{\partial T}{\partial x} + 2uv\frac{{\partial^{2} T}}{\partial x\partial y} + u^{2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} T}}{{\partial y^{2} }} \hfill \\ \end{aligned} \right) = \frac{\partial }{\partial y}\left( {K\left( T \right)\frac{\partial T}{\partial y}} \right) \\ & \quad + \left( {\mu + \kappa } \right)\left( {\frac{\partial u}{\partial y}} \right)^{2} + \sigma B(x)^{2} u^{2} + \frac{{K\left( T \right)u_{\text{s}} (x)(T_{\text{s}} - T_{\infty } )}}{(x + p)\upsilon }\left( {A^{ * } f^{\prime} + B^{ * } \frac{{(T - T_{\infty } )}}{{(T_{s} - T_{\infty } )}}} \right) + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}, \\ \end{aligned}$$

(4)

Here, $\left( {u,v} \right)$ are, respectively, the components of velocity, $\rho$ is the density, $\nu$ is the kinematic viscosity, $N$ is the microrotation (dimensional), $\left( {\beta_{1} ,\;\beta_{2} } \right)$ volumetric thermal expansion, $g$ is acceleration owing to gravity, $\sigma$ is the electrical conductivity, j is the density of the microinertia, $\kappa$ is the vortex viscosity, $T$ is temperature, $C_{\text{p}}$ is specific heat, $\gamma^{*}$ is the relaxation time, $\mu$ is dynamic viscosity, $\left( {A^{*} ,B^{*} } \right)$ are irregular heat generation or absorption parameters ($A^{*} ,\;B^{*} > 0$ and $A^{*} ,B^{*} < 0$) correspondingly, internal heat source or sink, $T_{\infty }$ is the ambient temperature, $\left( {k^{*} ,\sigma^{*} } \right)$ are, respectively, mean absorption coefficient and Stefan Boltzmann constant.

$\left( {\Gamma , K\left( T \right)} \right)$ are, respectively, the spin gradient viscosity and temperature-dependent thermal conductivity. These are well defined as

$$\begin{aligned} &\Gamma = \left( {\mu + \frac{\kappa }{2}} \right)j = \mu j\left( {1 + \frac{\alpha }{2}} \right) \\ & K\left( T \right) = k_{\infty } \left( {1 + \varepsilon \left( {\frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}} \right)} \right) \\ \end{aligned}$$

(5)

Here, $k_{\infty }$ is thermal conductivity and $\alpha = \frac{\kappa }{\mu }$ is the micropolar constant.

The boundary conditions are

$$\left. {\begin{array}{*{20}l} { u = u_{\text{s}} \left( x \right) + L\frac{\partial u}{\partial y}, \;v = 0, \;N = - M_{\text{r}} \frac{\partial u}{\partial y},\; T = T_{\text{w}} \;{\text{at}}\;y = L_{1} \left( {x + p} \right)^{{\frac{1 - {\text n}}{2}}} ,} \hfill \\ {u \to u_{\text{e}} \left( x \right), \;N \to 0,\; T \to T_{\infty } \;{\text{as}}\;y \to \infty ,} \hfill \\ \end{array} } \right\}$$

(6)

Consider the velocity, temperature and microrotation in terms of similarity variables

$$\left. {\begin{array}{*{20}l} {\chi = \sqrt {\frac{2\,\upsilon a}{n + 1}} (x + p)^{{{\raise0.7ex\hbox{${{\text n} - 1}$} \!\mathord{\left/ {\vphantom {{{\text n} - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} F(\zeta ),\;\zeta = y\sqrt {\frac{(n + 1)a}{2\upsilon }} (x + p)^{{{\raise0.7ex\hbox{${{\text n} - 1}$} \!\mathord{\left/ {\vphantom {{{\text n} - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} ,} \hfill \\ {u = \frac{\partial \chi }{\partial y} = a(x + p)^{{\text n}} F^{\prime}(\zeta ),\;N = \sqrt {\frac{{(x + p)^{{\text n} - 1} (n + 1)a}}{2\upsilon }} a(x + p)^{{\text n}} G(\zeta ),} \hfill \\ { - v = \frac{\partial \chi }{\partial x} = \sqrt {\frac{(n + 1)a\upsilon }{2}} (x + p)^{{{\raise0.7ex\hbox{${{\text n} - 1}$} \!\mathord{\left/ {\vphantom {{{\text n} - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {F(\zeta ) + \zeta \left( {\frac{n - 1}{n + 1}} \right)F^{\prime}(\zeta )} \right),\Theta (\zeta ) = \frac{{T - T_{\infty } }}{{T_{\text{s}} - T_{\infty } }},} \hfill \\ \end{array} } \right\}$$

(7)

Here, $(\zeta ,\chi )$, correspondingly, are the similarity variable and stream function, $F^{\prime}, G,\Theta$ (functions of $\zeta$) designate the velocity, microrotation and temperature correspondingly with $[\beta ,\infty )$.

By invoking similarity transformations, Eqs. (2)–(4) are transmuted as

$$\left( {1 + \alpha } \right)\frac{{{\text{d}}^{3} F}}{{{\text{d}}\zeta^{3} }} + F\frac{{{\text{d}}^{2} F}}{{{\text{d}}\zeta^{2} }} - \frac{2n}{n + 1}\left( {\frac{{{\text{d}}F}}{{{\text{d}}\zeta }}} \right)^{2} + \alpha \frac{{{\text{d}}G}}{{{\text{d}}\zeta }} + \frac{2}{n + 1}\left( {\lambda \left( {1 + \delta \,\Theta } \right)\Theta - M\frac{{{\text{d}}F}}{{{\text{d}}\zeta }}} \right) + \frac{2n}{n + 1}A^{2} = 0,$$

(8)

$$\left( {1 + \frac{\alpha }{2}} \right)\frac{{{\text{d}}^{2} G}}{{{\text{d}}\zeta^{2} }} - \frac{3n - 1}{n + 1}\frac{{{\text{d}}F}}{{{\text{d}}\zeta }}G + \frac{{{\text{d}}G}}{{{\text{d}}\zeta }}F - \frac{2}{n + 1}\alpha \left( {2G + \frac{{{\text{d}}^{2} F}}{{{\text{d}}\zeta^{2} }}} \right) = 0,$$

(9)

$$\begin{aligned} & \left( {\varepsilon \,\Theta + 1} \right)\frac{{{\text{d}}^{2}\Theta }}{{{\text{d}}\zeta^{2} }} + \varepsilon \left( {\frac{{{\text{d}}\Theta }}{{{\text{d}}\zeta }}} \right)^{2} + FPr\frac{{{\text{d}}\Theta }}{{{\text{d}}\zeta }} + \frac{2}{n + 1}PrM\,Ec\left( {\frac{{{\text{d}}F}}{{{\text{d}}\zeta }}} \right)^{2} + (1 + \alpha )PrEc\left( {\frac{{{\text{d}}^{2} F}}{{{\text{d}}\zeta^{2} }}} \right)^{2} \\ & + Rd\frac{{{\text{d}}^{2}\Theta }}{{{\text{d}}\zeta^{2} }} + Pr\gamma \left( {\frac{n - 3}{2}F\frac{{{\text{d}}F}}{{{\text{d}}\zeta }}\frac{{{\text{d}}\Theta }}{{{\text{d}}\zeta }} - \frac{n + 1}{2}F^{2} \frac{{{\text{d}}^{2}\Theta }}{{{\text{d}}\zeta^{2} }}} \right) + \frac{2}{n + 1}\left( {1 + \varepsilon \,\Theta } \right)\left( {A^{*} \frac{{{\text{d}}F}}{{{\text{d}}\zeta }} + B^{*}\Theta } \right) = 0, \\ \end{aligned}$$

(10)

Here, $\lambda$ is the convection parameter, $\delta$ is the nonlinear convection parameter, $M$ is the magnetic field parameter, $A$ is the stretching ratio parameter, Pr is the Prandtl number, $Ec$ is the Eckert numbers and $\gamma$ is the thermal relaxation parameter. These are defined as

$$\left. {\begin{array}{*{20}l} {\lambda = \frac{{Gr_{\text{x}} }}{{Re_{\text{x}}^{2} }},Gr_{\text{x}} = \frac{{g\beta_{1} (T_{\text{s}} - T_{\infty } )(x + p)^{3} }}{{\upsilon^{2} }},\;Re_{\text{x}} = \frac{{u_{\text{s}} (x)(x + p)}}{\upsilon },\delta = \frac{{\beta_{2} (T_{\text{s}} - T_{\infty } )}}{{\beta_{1} }},} \hfill \\ {M = \frac{{\sigma B_{0}^{2} }}{a\,\rho },Rd = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k_{\infty } k^{*} }},Pr = \frac{{\mu C_{\text{p}} }}{{k_{\infty } }},\gamma = \gamma^{*} a(x + p)^{{\text n} - 1} ,A = \frac{b}{a},Ec = \frac{{u_{\text{s}}^{2} }}{{C_{\text{p}} (T_{\text{s}} - T_{\infty } )}},} \hfill \\ \end{array} } \right\}$$

(11)

The transformed boundary conditions are

$$\left. {\begin{array}{*{20}l} {\,F = \left( {\frac{1 - n}{1 + n}} \right)\beta ,\;\frac{{{\text{d}}F}}{{{\text{d}}\zeta }} = 1,\,G = - M_{\text{r}} \frac{{{\text{d}}^{2} F}}{{{\text{d}}\zeta^{2} }},\;\Theta = 1,\;{\text{at}}\;\beta = L_{1} \sqrt {\frac{(n + 1)p}{2\upsilon }} } \hfill \\ {\frac{{{\text{d}}F}}{{{\text{d}}\zeta }} \to A,\;G \to 0,\Theta \to 0\,,\quad {\text{as}}\;\;\beta \to \infty } \hfill \\ \end{array} } \right\}$$

(12)

Here, $\beta = L_{1} \sqrt {\frac{(n + 1)p}{2\upsilon }}$ is the wall thickness parameter.

Equations (8)–(10) are nonlinear ODEs with the domain $[\beta ,\infty )$. In order to facilitate the computation, we change it into $[0,\infty )$ using the following transformations.

$$f(\eta ) = f(\zeta - \beta ) = F(\zeta ),g(\eta ) = g(\zeta - \beta ) = G(\zeta ),\theta (\eta ) = \theta (\zeta - \beta ) =\Theta (\zeta ),$$

(13)

Here, $\eta$ is the new similarity variable.

Making use of Eq. (13), Eqs. (8)–(10) and (12) become

$$\frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta^{3} }}\left( {1 + \alpha } \right) + \frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }}f - \frac{2n}{n + 1}\left( {\frac{{{\text{d}}f}}{{{\text{d}}\eta }}} \right)^{2} + \alpha \frac{{{\text{d}}g}}{{{\text{d}}\eta }} + \frac{2}{n + 1}\left( {\lambda \left( {1 + \delta \,\theta } \right)\theta - M\frac{{{\text{d}}f}}{{{\text{d}}\eta }}} \right) - \frac{2n}{n + 1}A^{2} = 0$$

(14)

$$\left( {1 + \frac{\alpha }{2}} \right)\frac{{{\text{d}}^{2} g}}{{{\text{d}}\eta^{2} }} + f\frac{{{\text{d}}g}}{{{\text{d}}\eta }} - \frac{3n - 1}{n + 1}g\frac{{{\text{d}}f}}{{{\text{d}}\eta }} - \frac{2}{n + 1}\alpha \left( {2g + \frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }}} \right) = 0,$$

(15)

$$\begin{aligned} & \left( {\varepsilon \,\theta + 1} \right)\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} + \varepsilon \left( {\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }}} \right)^{2} + fPr\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} + \frac{2}{n + 1}PrM\,Ec\left( {\frac{{{\text{d}}f}}{{{\text{d}}\eta }}} \right)^{2} + (1 + \alpha )PrEc\left( {\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }}} \right)^{2} \\ & + Rd\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} + Pr\gamma \left( {\frac{n - 3}{2}f\frac{{{\text{d}}f}}{{{\text{d}}\eta }}\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} - f^{2} \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }}\frac{n + 1}{2}} \right) + \frac{2}{n + 1}\left( {1 + \varepsilon \,\theta } \right)\left( {A^{*} \frac{{{\text{d}}f}}{{{\text{d}}\eta }} + B^{*} \theta } \right) = 0, \\ \end{aligned}$$

(16)

$$\left. {\begin{array}{*{20}l} {f = \left( {\frac{1 - n}{1 + n}} \right)\beta ,\;\frac{{{\text{d}}f}}{{{\text{d}}\eta }} = 1,\,g = - M_{\text{r}} \frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }},\;\theta = 1,\;{\text{at}}\;\eta = 0} \hfill \\ {\frac{{{\text{d}}f}}{{{\text{d}}\eta }} \to A,\,g \to 0,\;\theta \to 0,\quad {\text{as}}\;\eta \to \infty } \hfill \\ \end{array} } \right\},$$

(17)

The mathematical expressions for the physical quantities (friction factor, couple stress coefficient and local Nusselt number) are

$$C_{\text{f}} = \frac{{\tau_{\text{s}} }}{{\tfrac{1}{2}\rho (u_{\text{s}} )^{2} }},C_{\text{S}} = \frac{{M_{\text{w}} }}{{\mu \,u_{\text{s}} }},Nu = \frac{{xq_{\text{s}} }}{{k_{\infty } (T_{\text{w}} - T_{\infty } )}},$$

(18)

Here, the surface shear stress, couple stress and heat flux ($\tau_{\text{s}} ,M_{\text{w}} ,q_{\text{s}}$) can be defined as

$$\tau_{\text{s}} = \left( {(\mu + \kappa )\frac{\partial u}{\partial y} + \kappa N} \right)_{{{\text{y}} = 0}} ,\;M_{\text{w}} = \left( {\mu + \frac{\kappa }{2}} \right)j\left( {\frac{\partial N}{\partial y}} \right)_{{{\text{y}} = 0}} ,\;q_{\text{s}} = - \left( {K(T) + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{*} }}} \right)\left( {\frac{\partial T}{\partial y}} \right)_{{{\text{y}} = 0}} ,$$

(19)

Making use of Eq. (7) in Eqs. (19) and (18), it becomes

$$Re_{x}^{{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} C_{\text{F}} = 2\left( {1 + \alpha (1 - M_{\text{r}} )} \right)\left( {\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }}} \right)_{{\upeta = 0}} ,\;C_{\text{S}} = \left( {1 + \frac{\alpha }{2}} \right)\left( {\frac{{{\text{d}}g}}{{{\text{d}}\eta }}} \right)_{{\upeta = 0}} ,\;Re_{x}^{{{\raise0.5ex\hbox{$\scriptstyle { - 1}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} Nu = - \frac{(1 + \varepsilon \theta )}{{\left( {1 + Rd} \right)^{ - 1} }}\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }}} \right)_{{\upeta = 0}} ,$$

(20)

where $Re_{\text{x}} = \frac{{u_{\text{s}} (x)(x + p)}}{\upsilon }$ is the local Reynolds number.

Results and discussion

The coupled and nonlinear system of ordinary differential Eqs. (14)–(16) with the corresponding boundary conditions (17) is solved numerically with the shooting and the fourth-order Runge–Kutta methods. The influence of various dimensionless parameters on the fluid velocity, temperature and microrotation is exposed via plots. Further, we scrutinize the influence of the same parameters on the physical quantities and the results are presented in the table. Results are attained by allocating the values of physical parameters as $\alpha = 0.2$, $A = 0.05$, $M = 0.5$, $Ec = 0.3$, $Rd = A^{*} = B^{*} = 0.1$, $Pr = 7$, $\lambda = 0.1$, $\in = 0.5$, $\eta = 0.1$, $\delta = 0.3$, $\gamma = 0.5$ and $M_{\text{r}} = 0.5$. We have chosen these values as common for the whole study of results unless otherwise specified in graphs and tables. In all the figures, $f^{\prime}\left( \eta \right)$, $g\left( \eta \right)$ and $\theta (\eta )$ symbolize the distributions of velocity, microrotation and temperature. In diagrams, solid lines signify the curves for the flow over a flat sheet ($\beta = 0$) and dashed lines signify the curves for the flow due to stretching of a variable thickness sheet ($\beta = 0.5$).

In Figs. 2–4, we plot the influence of magnetic field parameter ($M$) on the flow fields such as velocity, microrotation and temperature ($f^{\prime}\left( \eta \right)$, $g\left( \eta \right)$ and $\theta (\eta )$). Figure 2 displays that the distribution of velocity and its boundary layer thickness get suppressed as the values of magnetic field parameter increase. This contests the physical interpretation on applying the magnetic force to an electrically conducting fluid, and this provides an elevation in the drag force, which results in decreasing strength on the distribution of velocity. Due to this, a reduction in the distribution of velocity is noticed. But in the cases of microrotation and temperature fields, it is quite reverse to fluid velocity as shown in Figs. 3 and 4. Due to the Lorentz force, some additional heat energy will be produced in the flow, which causes an enhancement in the distributions of microrotation and temperature. Here, it is evident that maximum temperature is attained in the case of slendering stretching surface when compared to the flat surface.

Fig. 2

Impact of magnetic field parameter (M) on fluid velocity

Fig. 3

Impact of magnetic field parameter (M) on fluid microrotation

Fig. 4

Impact of magnetic field parameter (M) on fluid temperature

The impact of buoyancy parameter ($\lambda$) on the velocity, microrotation and temperature ($f^{\prime}\left( \eta \right)$, $g\left( \eta \right)$ and $\theta (\eta )$) is portrayed in Figs. 5–7. As likely, for enhancing values of convection parameter the profiles of velocity increase, but an opposite result is perceived for the distributions of temperature and microrotation field. Due to high buoyancy forces, we noticed a decrement in the thickness of thermal and microrotation fields and an enhancement in the momentum boundary layer thickness.

Fig. 5

Impact of buoyancy parameter (λ) on fluid velocity

Fig. 6

Impact of buoyancy parameter (λ) on fluid microrotation

Fig. 7

Impact of buoyancy parameter (λ) on fluid temperature

Figures 8–10 are outlined to see the impression of the material parameter on velocity, microrotation and temperature ($f^{\prime}\left( \eta \right)$, $g\left( \eta \right)$ and $\theta (\eta )$), respectively. It is fascinating to notice that all the distributions are escalating factors of material parameters. It is worth mentioning that the maximum velocity and temperature are noticed in the case of flow past a slendering surface when compared to the other.

Fig. 8

Impact of material parameter (α) on fluid velocity

Fig. 9

Impact of material parameter (α) on fluid microrotation

Fig. 10

Impact of material parameter (α) on fluid temperature

Influence of stretching ratio parameter ($A$) on velocity, microrotation and temperature is portrayed in Figs. 11–13. From Fig. 11, we observe that the distribution of velocity is overshot by an escalation in values of stretching ratio parameter. But the microrotation and temperature distributions are reduced with larger $A$.

Fig. 11

Impact of stretching ratio parameter (A) on fluid velocity

Fig. 12

Impact of stretching ratio parameter (A) on fluid microrotation

Fig. 13

Impact of stretching ratio parameter (A) on fluid temperature

Figure 14 is plotted to discuss the influence of thermal radiation ($Rd$) on the distribution of temperature. From the figure, it is noticed that the effect of radiation parameter on $\theta (\eta )$ is increasing. It is familiar that the mechanism of radiation is the heat transference phenomenon which releases the energy via liquid grains such that some additional heat is produced in the flow. Hence, we detected an enhancement in the thickness of thermal boundary layer for larger $Rd$. We witnessed a motivating result that the curves of temperature ($\theta (\eta )$) are more affected for $\beta = 0.5$ when compared to that of $\beta = 0$.

Fig. 14

Impact of thermal parameter (Rd) on fluid temperature

Figure 15 is sketched to examine the influence of Prandtl number ($Pr$) on the distribution of temperature. As expected, for increasing values of Prandtl number the fluid temperature reduces. The reason behind this is that the momentum diffusivity dominates with larger Prandtl number. Moreover, the thermal diffusivity is lesser. Hence, the distribution of temperature and the corresponding boundary layer thickness reduces with larger Prandtl number.

Fig. 15

Impact of Prandtl number (Pr) on fluid temperature

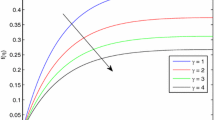
The influence of thermal relaxation parameter (γ) on temperature is portrayed in Fig. 16. By the strengthening of relaxation parameter, the fluid temperature enhances. Physically, for higher thermal relaxation time, the fluid particles unveil non-conducting performance. Due to this, the particles oblige more time to fetch temperature to their corresponding particles. It is also observed that the profiles of temperature are more affected for $\beta = 0.5$ than that of $\beta = 0$.

Fig. 16

Impact of thermal relaxation parameter (γ) on fluid temperature

Figures 17 and 18 unveil the influence of irregular heat source or sink parameters ($A^{*}$, $B^{*}$) on the distribution of temperature. It was detected that increasing values of $A^{*}$ and $B^{*}$ result in the enrichment in the profiles of temperature. Physically, increasing values of irregular heat source/sink parameters assist as an agent to spawn temperature in the flow. Due to this, we observed a rise in the fluid temperature for swelling values of $A^{*}$ and $B^{*}$. It is noticeable that the maximum temperature is achieved in the case of flow past a slendering surface when compared to the other.

Fig. 17

Impact of irregular heat source/sink parameter (A^*) on fluid temperature

Fig. 18

Impact of irregular heat source/sink parameter (B^*) on fluid temperature

In Fig. 19, the graph for dissimilar values of Eckert number ($Ec$) against the fluid temperature is sketchily revealed. As expected, for rising values of Eckert number the profiles of temperature are enhanced. The ratio between kinetic energy and enthalpy change is the so-called Eckert number. Therefore, kinetic energy boosts with Eckert number. Ergo, the distribution of temperature and the corresponding thermal boundary layer thickness are raising functions of Eckert number.

Fig. 19

Impact of Eckert number (Ec) on fluid temperature

Influence of $n$ on the distributions of velocity and temperature is portrayed in Figs. 20 and 21 correspondingly. An increment in the values of $n$ results in an increase in the fields of $f^{\prime}\left( \eta \right)$ and $\theta (\eta )$. Figures 22 and 23 render the impact of $\delta$ on $f^{\prime}\left( \eta \right)$ and $\theta (\eta )$. As expected, for growing values of nonlinear convection parameter both the distributions (velocity and temperatures) are enhanced. Also, it is fascinating to perceive that high temperature and velocity are accomplished in the case of flow past a slendering surface when compared to the other.

Fig. 20

Impact of power index parameter (n) on fluid velocity

Fig. 21

Impact of power index parameter (n) on fluid temperature

Fig. 22

Impact of nonlinear convection parameter (δ) on fluid velocity

Fig. 23

Impact of nonlinear convection parameter (δ) on fluid temperature

Figures 24 and 25 are plotted to examine the effect of microrotation parameter ($y$) on the distributions of velocity and temperature. An escalating value of microrotation parameter results in a hike in the distribution of temperature and a fall in the fluid velocity. Impact of wall thickness parameter (β) on the distribution of velocity and temperature is illustrated in Figs. 26 and 27 disparately. As likely, for increasing values of β enhances both the velocity and temperatre fields. It is easy to see that an enhancement in the wall thickness parameter causes a hike in the fluid velocity. Originally, an increment in the values of $\beta$ barricades the flow motion and hence improves the fluid velocity. Hence, the results of that kind are noticed.

Fig. 24

Impact of microrotation parameter (M_r) on fluid velocity

Fig. 25

Impact of microrotation parameter (M_r) on fluid temperature

Fig. 26

Impact of wall thickness parameter (β) on fluid velocity

Fig. 27

Impact of wall thickness parameter (β) on fluid temperature

In Table 1, geometrically $\beta = 0$ symbolizes the flow over a flat surface and $\beta \ne 0$ denotes the variable thickened surface. The impacts of all sundry parameters are alike in both cases except the Prandtl number and power-law index parameter. The higher values of buoyancy and nonlinear convection parameters enhance the friction factor, couple stress and heat transfer rate, but a contrary movement is noticed due to the Lorentz force. The swelling values of uneven heat source/sink and Eckert number inflate the couple stress and skin friction coefficients but suppress the local Nusselt number. Shear and couple stresses are improved, and the rate of thermal transport lessens with an intensification in the radiation parameter. The boosting values of microrotation parameter dwindle the Nusselt number and friction factor and enhance the coefficient of couple stress. In both $\beta = 0$ and $\beta \ne 0$ cases, the higher values of Pr enhance the couple stress and local Nusselt number but the coefficient of skin friction increases in the case of $\beta = 0$, while it decreases in the $\beta \ne 0$ case. The swelling values of power-law index parameter suppress the couple stress coefficient in both the cases. The local Nusselt number enhances if $\beta = 0$ and dwindles if $\beta \ne 0$ with an increase in n. An incompatible result is noticed in friction factor when compared in both cases.

Table 1 Effect of the different flow regulating parameters on $C_{\text{f}}$, $C_{\text{S}}$ and $Nu$ for the flow past a variable thickness surface and flat surface

Conclusions

This research article explains the MHD nonlinear convective stagnation point flow and heat-transfer characteristics of micropolar fluid across a slendering stretching surface. Simultaneous solutions were bestowed for the flow past a flat surface and slendering surface. The impacts of thermal radiation, temperature-dependent thermal conductivity, frictional heat and variable heat sink/source are examined. The principal consequences are listed as follows

• The distribution of temperature and the boundary layer thickness reduces with an enhancement in the buoyancy ratio parameter.

• It is noticed that high temperature is accomplished in the case of flow past a variable thickness surface than that of the other (flat surface).

• An increase in nonlinear convection parameter enhances the friction factor, couple stress and heat transfer rate, but an opposite result is noticed due to the Lorentz force.

• Microrotation parameter has a propensity to enhance the couple stress coefficient.

• Eckert number and thermal radiation parameter have a tendency to enhance the fluid temperature.

• An enhancement in the local Nusselt number is observed for increasing values of thermal relaxation parameter.