1 Introduction

In an effort to develop super heat-resistant materials, Japanese material scientists proposed the concept of FGM in the early 1980s. These materials, which are microscopically heterogeneous and are typically made from isotropic components, such as metals and ceramics, were initially designed as thermal barrier materials for aerospace structures and fusion reactors [3]. FGMs are composite materials with inhomogeneous micromechanical structure and are generally composed of two different parts such as ceramic and metal, in which the material properties change smoothly between two surfaces. This kind of material as a novel generation of composites of microscopical heterogeneity is achieved by controlling the volume fractions, microstructure, porosity, etc. of the material constituents during manufacturing, resulting in spatial gradient of macroscopic material properties of mechanical strength and thermal conductivity. As a result, in comparison with traditional composites, FGMs possess various advantages, for instance, ensuring smooth transition of stress distributions, minimization or elimination of stress concentration, and increased bonding strength along the interface of two dissimilar materials. Therefore, FGMs have received wide applications in modern industries including aerospace, mechanical, electronics, optics, chemical, biomedical, nuclear, and civil engineering to name a few during the past two decades. Moreover, porous FGMs have some other specific applications, as thermal barrier coatings and filtration and also in biomaterial usages such as dental implants and bone replacements. Motivated by these engineering applications, FGMs have also attracted intensive research interests, which were mainly focused on their static, dynamic, and vibration characteristics of FG structures [4, 5]. Rotating FG beams attached to a rigid hub occur in different engineering applications such as wind turbines, gas turbines, ship propellers, helicopter rotor blades, robot manipulators, and spinning space structures. To control the vibration behavior of these bodies it is important to find natural frequencies.

Further, the increasing use of beams as structural components in various fields such as marine, civil, and aerospace engineering has necessitated the study of their vibration behavior and a large number of studies can be found in literature about transverse vibration of uniform isotropic beams. In this study, a relatively new approach called differential transformation method (DTM) is applied in analyzing vibration analysis of rotating FG beams. The concept of DTM was first proposed by Zhou [12] in solving linear and non-linear initial value problems in electrical circuit analysis. The superiority of the DTM is its simplicity and good precision and depends on Taylor series expansion, while it takes less time to solve polynomial series. It is different from the traditional high-order Taylor’s series method, which requires symbolic competition of the necessary derivatives of the data functions. The Taylor series method computationally takes a long time for large orders. With this method, it is possible to obtain highly accurate results or exact solutions for differential equations. With this technique, the given partial differential equation and related initial conditions are transformed into a recurrence equation that finally leads to the solution of a system of algebraic equations as coefficients of a power series solution. This method is useful for obtaining exact and approximate solutions for both linear and nonlinear ordinary and partial differential equations, and there is no need for linearization or perturbations, and large computational work and round-off errors are avoided. It is a proper method to analyze beam vibrations. A study on rotating Timoshenko beams by differential transform method has been presented by some researchers [6, 8].

Due to porosities occurring inside FGMs during fabrication, it is therefore necessary to consider the vibration behavior of beams having porosities in this investigation. The porous materials are composed of two elements, one of which is solid (body) and the other element is either liquid or gas that is frequently found in nature, such as wood, stone, and layers of dust. For many years, porous material structures, such as beams, plates, and shells, have been widely discussed in structural design problems. The problem of vibration of the porous structures has been studied by some authors. For example, Wattanasakulpong et al. [11] analyzed free vibration of layered functionally graded beams and validated their results with experimental results; they concluded that discrepancies between theoretical and experimental results could arise from porosities due to imperfect infiltration and from approximation in material profile in calculation. Wattanasakulpong and Ungbhakorn [10] studied linear and nonlinear vibration analysis of elastically restrained end FGM beams. They used a modified form of rule of mixture to describe the material properties of the FG beam with porosities. But in all of these articles, the FG beam is not rotating and thus the need for investigation of vibration characteristics of the rotating porous FG beams is very much felt, but it has not been found in the literature. Consequently, in this study, the semi-analytical DTM method is applied for studying the vibration characteristics of rotating thick porous FG beam considering the effects of shear deformation and rotatory inertia within the context of Timoshenko beam theory. The gradation of material properties is assumed to be along the thickness of the beam. Comparisons with the results from the existing literature are provided for validation in special cases. Numerical results are presented to examine the effect of several beam parameters such as constituent volume fractions, slenderness ratios, rotational speed, and hub radius on vibration behavior of the rotating porous FG beam.

2 Theory and formulation

2.1 Functionally graded porous material

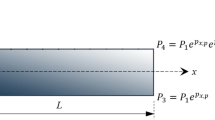
One of the most favorable models for FGMs is the power-law model, in which the material properties of FGMs are assumed to vary according to a power law about spatial coordinates. The coordinate system for FGM rotating beam is shown in Fig. 1. The length of the beam is L and thickness is h. The FG beam is attached to the periphery of a rigid hub of radius R and the hub rotates about the z-axis at a constant angular speed Ω. A Cartesian coordinate system O(x, y, z) is defined on the central axis of the beam where the x axis is taken along the central axis, the y-axis in the width direction, and the z-axis in the depth direction. The FG beam is assumed to be composed of ceramic and metal, and the effective material properties (P f) of the FG beam such as Young’s modulus E f, shear modulus G f, and mass density ρ f are assumed to vary continuously in the thickness direction (z-axis direction) according to a power function of the volume fractions of the constituents, while the Poisson’s ratio is assumed to be constant in the thickness direction.

Fig. 1
figure 1

Typical functionally graded beam with Cartesian coordinates

Full size image

V m and V c are the material properties and the volume fractions of the metal and the ceramic constituents related by:

$$V_{\text{c}} + V_{\text{m}} = 1 .$$
(1a)

The volume fraction of the metal constituent of the beam is assumed to be given by:

$$V_{\text{c}} = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{P}$$
(1b)

Here, P is the non-negative variable parameter (power-law exponent) which determines the material distribution through the thickness of the beam. The modified rule of mixture to find the effective material properties of porous beam (P) can be expressed as follows [10]

$$P_{\text{f}} \left( z \right) = \left( {P_{\text{c}} - P_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + P_{\text{m}} - \left( {P_{\text{c}} + P_{\text{m}} } \right)\frac{\alpha }{2} \quad\alpha \ll 1$$
(2)
$$E_{\text{f}} \left( z \right) = \left( {E_{\text{c}} - E_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + E_{\text{m}} - \left( {E_{\text{c}} + E_{\text{m}} } \right)\frac{\alpha }{2}$$
(3)
$$\rho_{\text{f}} \left( z \right) = \left( {\rho_{\text{c}} - \rho_{\text{m}} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + \rho_{\text{m}} - \left( {\rho_{\text{c}} + \rho_{\text{m}} } \right)\frac{\alpha }{2}.$$
(4)

Here, α is the volume fraction of porosity. According to this distribution, the bottom surface (z = −h/2) of functionally graded beam is pure metal, whereas the top surface (z = h/2) is pure ceramics.

2.2 Formulation of porous FGM beam using Timoshenko beam theory

In a Cartesian coordinate system, x is the distance of the point from the hub edge parallel to the beam length, u 0 is the axial displacement due to the centrifugal force, z is the vertical distance of the point from the middle plane, w is the transverse displacement of any point on the neutral axis, and θ is the rotation due to bending. Displacement field components are considered based on Timoshenko beam theory. Considering [7] assumption and neglecting terms which are greater than ε 2, the strain–displacement and strain energy simplified relations are calculated as follows:

$$\varepsilon_{xx} = u_{0}^{{\prime }} - z\theta^{{\prime }} + \frac{{(w^{{\prime }} )^{2} }}{2}$$
(5)
$$\gamma_{xz} = w^{{\prime }} - \theta$$
(6)
$$\gamma_{xy} = 0.$$
(7)

Bending strain energy U b and shear strain energy U s are given, respectively, by:

$$U_{\text{b}} = \int\int\int_{V} \frac{{E(z)\varepsilon^{2} }}{2} {\text{d}}V$$
(8)
$$U_{\text{s}} = \int\int\int_{V} \frac{{G(z)\gamma^{2} }}{2} {\text{d}}V.$$
(9)

Substituting Eqs. (5–7) into Eqs. (8–9) leads to

$$U_{\text{b}} = \frac{1}{2}\int_{A} \int_{0}^{L} {E(z)\left\{ {u_{0}^{{\prime }} - z\theta^{{\prime }} + \frac{{(w^{{\prime }} )^{2} }}{2}} \right\}^{2} } \;{\text{d}}A{\text{d}}x$$
(10)
$$U_{\text{s}} = \int\int\int_{V} \frac{{G(z)(\gamma_{xy}^{2} + \gamma_{xz}^{2} )}}{2} {\text{d}}V.$$
(11)

Further, the total strain energy is given by:

$$U = U_{\text{s}} + U_{\text{b}} \infty .$$
(12)

Here, A 1 and A 2 are bending rigidity and axial rigidity of the beam cross section, respectively, and are defined as:

$$\left( {A_{1 } ,\,A_{2} \,} \right) = \int_{ - h/2}^{h/2} {E\left( z \right)(1,z^{2} ){\text{d}}A.}$$
(13)

B 1 and B 2 are normal and rotary inertia terms, respectively, and C is the shear rigidity factor which are as follows:

$$(B_{1} ,B_{2} ) = \int_{ - h/2}^{h/2} {\rho (z)(1,z^{2} ){\text{d}}A} \,$$
(14)
$$C = \mathop \int \nolimits kG(z){\text{d}}A,$$
(15)

where A, ρ, and E are the area of cross section, the mass density, and modulus of elasticity of the beam, respectively; G is the shear modulus and k is the Timoshenko shear correction factor which has been assumed equal to the isotropic case, i.e., k = 5/6. The axial displacement \(u_{0}^{{\prime }} (x)\), which is uniform across the cross section, is related to strain ε 0 (x) by:

$$u_{0}^{{\prime }} \left( x \right) = \varepsilon_{0} \left( x \right) = \frac{T(x)}{{A_{1} }}.$$
(16)

The centrifugal force T(x) is defined as:

$$T\left( x \right) = \int_{x}^{L} {B_{1} \Omega^{2} \left( {R + x} \right){\text{d}}x} .$$
(17)

According to Eqs. (13–17) bending and shear strain energy are obtained, respectively, as follows:

$$U_{\text{b}} = \frac{1}{2}\int_{0}^{L} {\left( {A_{2} (\theta^{{\prime }} )^{2} + T(w^{{\prime }} )^{2} } \right){\text{d}}x + {\text{const}}}$$
(18)
$$U_{\text{s}} = \frac{1}{2} \int_{0}^{L} {C(w^{{\prime }} - \theta ){\text{d}}x} .$$
(19)

Further, substituting Eqs. (18–19) into Eq. (12) one gets the total strain energy of the beam in the following form:

$$U = \frac{1}{2}\int_{0}^{L} {A_{2} (\theta^{'} )^{2} + T(w^{'} )^{2} + C\left( {w^{'} - \theta } \right) {\text{d}}x} .$$
(20)

Also the kinetic energy expression is given as:

$$\tau = \frac{1}{2}\int_{A} \int_{0}^{L} {\left( {V_{x}^{2} + V_{y}^{2} + V_{z}^{2} } \right)\rho \;{\text{d}}A\; {\text{d}}x}$$
(21)

The total velocity \(\vec{V}\) can be expressed in terms of deformed positions as:

$$\vec{V} = (\dot{x}_{1} - \Omega y_{1} )\vec{i} + (\dot{y}_{1} + \Omega yx_{1} )\vec{j} + \dot{z}_{1} \vec{k}$$
(22)
$$V_{x } = - \xi \dot{\theta } - \eta \Omega$$
(23)
$$V_{y} = (R + x + u_{0} - \xi \theta )\Omega$$
(24)
$$V_{z} = \dot{\omega }.$$
(25)

Now, substituting Eqs. (22–24) into Eq. (20) kinetic energy is obtained as follows:

$$\tau = \frac{1}{2} \int_{0}^{L} {[B_{1} \dot{\omega } ^{2} + A_{2} \dot{\theta }^{2} + A_{2} \Omega^{2} \theta^{2} ]{\text{d}}x} .$$
(26)

2.3 Deriving governing equations for rotating FG beam

Hamilton’s principle is used herein to derive the equations of motion. The principle can be stated in analytical form as:

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta U + \delta V - \delta \tau } \right) = 0} ,$$
(27)

where t 1 and t 2 are the initial and end time, respectively; δU is the virtual variation of the strain energy; δV is the virtual variation of the potential energy; and δτ is the virtual variation of the kinetic energy. According to Hamilton’s principle, the equations of motion can be obtained as:

$$- B_{2 } \ddot{\theta } + B_{2} \Omega^{2} \,\theta + A_{2} \theta^{{\prime \prime }} + kC\left( {W^{{\prime }} - \theta } \right) = 0$$
(28)
$$- B_{1} \textit{\"{W}} + (TW^{{\prime }} )^{{\prime }} + kC\left( {W^{{\prime \prime }} - \theta^{{\prime }} } \right) = 0.$$
(29)

Further, the two ends of the Timoshenko cantilever beam (x = 0 and x = L) are subjected to the following boundary conditions:

$$\begin{array}{*{20}c} {{\text{at}}\,x = 0:} \quad & {W\left( 0 \right) = 0\,,\theta \left( 0 \right) = 0} \\ \end{array}$$
(30)
$$\begin{array}{*{20}c} {{\text{at }}x = L:} & \quad{{\theta^{{\prime }} \left( 1 \right) = 0,\,W^{{\prime }} \left( 1 \right) - \theta \left( 1 \right) = 0}} \\ \end{array}.$$
(31)

Assuming simple harmonic oscillation, w and θ can be written as:

$$W\left( {x,t} \right) = \bar{W}(x){\text{e}}^{i\omega t}$$
(32)
$$\theta \left( {x,t} \right) = \bar{\theta }(x){\text{e}}^{i\omega t} .$$
(33)

Substituting Eqs. (32) and (33) into Eqs. (28) and (29), the governing equations are as follows:

$$B_{2 } \omega^{2 } \bar{\theta } + B_{2} \Omega^{2} \bar{\theta } + A_{2} \bar{\theta }^{{\prime \prime }} + A_{2} \bar{\theta }^{{\prime \prime }} + kC\left( {\bar{W}^{{\prime }} - \bar{\theta } } \right) = 0$$
(34)
$$B_{1} \omega^{2} \bar{W} + (T\bar{W}^{{\prime }} )^{{\prime }} + kC\left( {\bar{W}^{{\prime \prime }} - \bar{\theta }^{{\prime }} } \right) = 0.$$
(35)

The dimensionless parameters which were found according to FGM characteristics are used to simplify the equations and to make comparisons with the studies in literature such as that by Banerjee [2]. These are given as follows:

$$\eta^{2} = \frac{{B_{1} L^{4} \Omega^{2} }}{{A_{2} }},\quad r^{2} = \frac{{B_{2} }}{{A_{1} L^{2} }}, \quad \delta = \frac{R}{L}, \quad \xi = \frac{x}{L}, \quad W(\xi ) = \frac{{\bar{W}}}{L}$$
$$\mu^{2} = \frac{{B_{1} L^{4} \omega^{2} }}{{A_{2} }}\quad{s^{2} = \frac{{A_{2} }}{{kCL^{2} }}}.$$
(36)

Then dimensionless expressions for centrifugal force and governing equations are obtained as follows:

$$T\left( \xi \right) = B_{1} \Omega^{2} L^{2} \left[ {\delta \left( {1 - \xi } \right) + \frac{{(1 - \xi^{2} )}}{2}} \right]$$
(37)
$$\bar{\theta }^{{\prime \prime }} + \eta^{2} r^{2} \left( {1 + \frac{{\omega^{2} }}{{\Omega^{2} }}} \right)\bar{\theta } + \frac{1}{{s^{2} }}\left( {\bar{W}^{{\prime }} - \bar{\theta }} \right) = 0.$$
(38)
$$\left\{ {\left[ {\delta \left( {1 - \xi } \right) + \frac{{\left( {1 - \xi^{2} } \right)}}{2}} \right]\bar{W}^{{\prime }} } \right\}^{{\prime }} + \left( {\frac{{\omega^{2} }}{{\Omega^{2} }}} \right)\bar{W} + \frac{1}{{s^{2} \eta^{2} }}\left( {\bar{W}^{{\prime \prime }} - \bar{\theta }^{{\prime }} } \right) = 0 .$$
(39)

2.4 Implementation of differential transform method

Generally, it is rather difficult to derive an analytical solution for Eqs. (38–39) due to the nature of non-homogeneity. In this circumstance, the DTM is employed to translate Eqs. (34–35) into a set of ordinary equations. First, the procedure of differential transform method is briefly reviewed. Differential transformation of function y(x) according to [1] is defined as follows:

$$Y\left( k \right) = \frac{1}{k!}\left[ {\frac{{{\text{d}}^{k} }}{{{\text{d}}x^{k} }}y\left( x \right)} \right]_{x = 0} ,$$
(40)

in which y(x) is the original function and Y(k) is the transformed function. Also, the differential inverse transformation of Y(k) can be obtained as follows:

$$y\left( x \right) = \sum\nolimits_{n + 1}^{\infty } {x^{k} Y(k)} .$$
(41)

Consequently from Eqs. (40–41), we obtain:

$$y\left( x \right) = \sum\nolimits_{k = 0}^{n} {\frac{{x^{k} }}{k!}\left[ {\frac{{{\text{d}}^{k} }}{{{\text{d}}x^{k} }}y\left( x \right)} \right]_{x = 0} } .$$
(42)

Equation (42) reveals that the concept of the differential transformation is derived from Taylor’s series expansion. In real applications, the function y(x) in Eq. (41) can be written in a finite form as:

$$y\left( x \right) = \sum\nolimits_{k = 0}^{n} {x^{k} Y(k)} .$$
(43)

In these calculations \(y\left( x \right) = \sum\nolimits_{n + 1}^{\infty } {x^{k} Y\left( k \right)}\) is small enough to be neglected, and n is determined by the convergence of the eigenvalues. In Table 1, the basic theorem of DTM is stated, while Table 2 presents the differential transformation of conventional boundary conditions. Applying the DTM rule on the equations of motion (38–39) and boundary conditions (30–31), the next four equations are obtained as:

$$\begin{gathered} \left( {\delta + 0.5 + \frac{1}{{s^{2} \eta^{2} }}} \right)\left( {k + 1} \right)\left( {k + 2} \right)W\left( {k + 2} \right) - \delta \left( {k + 1} \right)^{2} W\left( {k + 1} \right) + \left( {\frac{{\omega^{2} }}{{\Omega^{2} }} - \frac{{k\left( {k + 1} \right)}}{2}} \right)W\left( k \right) - \hfill \\ \frac{1}{{s^{2} \eta^{2} }}(k + 1)\theta \left( {k + 1} \right) = 0 \hfill \\ \end{gathered}$$
(44)
$$\left( {k + 1} \right)\left( {k + 2} \right)\theta \left( {k + 2} \right) + \left[ {\eta^{2} r^{2} \left( {1 + \frac{{\omega^{2} }}{{\Omega^{2} }}} \right) - \frac{1}{{s^{2} }}} \right]\theta \left( k \right) + \frac{1}{{s^{2} }}\left( {k + 1} \right)W\left( {k + 1} \right) = 0$$
(45)
$$\sum\nolimits_{i = 0}^{n} {k*\varTheta \left( k \right) = 0}$$
(46)
$$\sum\nolimits_{i = 0}^{n} {k*w(k) - \varTheta \left( k \right) = 0} ,$$
(47)
Table 1 Some of the transformation rules of the one-dimensional DTM
Full size table
Table 2 Transformed boundary conditions (B.C.) based on DTM
Full size table

where W(k) and θ(k) are the differential transforms of w(ξ) and θ(ξ), respectively. Substituting W(k) and θ(k) in Eqs. (46–47), we have:

$$M_{j1}^{(n)} c_{1} + M_{j2}^{(n)} c_{2} = 0 , \quad j = 1,2,3, \ldots ,n,$$
(48)

in which M ij are polynomials in terms of ω corresponding to the nth term. The matrix form of Eq. (48) can be prescribed as:

$$\left[ {\begin{array}{*{20}c} {\varvec{M}_{{{\mathbf{11}}}}^{{(\varvec{n})}} } & {\varvec{M}_{12}^{{(\varvec{n})}} } \\ {\varvec{M}_{{{\mathbf{21}}}}^{{(\varvec{n})}} } & {\varvec{M}_{{{\mathbf{22}}}}^{{(\varvec{n})}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varvec{c}_{{\mathbf{1}}} } \\ {\varvec{c}_{{\mathbf{2}}} } \\ \end{array} } \right\} = 0.$$
(49)

Further, studying the existence condition of the non-trivial solutions yields the following characteristic determinant:

$$\left| {\begin{array}{*{20}c} {M_{11}^{(n)} } & {M_{12}^{(n)} } \\ {M_{21}^{(n)} } & {M_{22}^{(n)} } \\ \end{array} } \right| = 0.$$
(50)

Solving Eq. (50), the ith estimated eigenvalue for the nth iteration (ω = ω (n) i ) may be obtained and the total number of iterations is related to the accuracy of calculations which can be determined by the following equation:

$$\left| {\omega_{i}^{(n)} - \omega_{i}^{(n - 1)} } \right| < \varepsilon .$$
(51)

In this study, ε = 0.0001 is considered in the procedure of finding eigenvalues which results in four-digit precision in the estimated eigenvalues. Further a Matlab program has been developed according to the DTM rule as stated before, to find eigenvalues.

3 Results and discussion

In the present section, a numerical testing of the procedure as well as parametric studies is performed to establish the validity and usefulness of the DTM approach and the influence of different beam parameters such as constituent volume fractions, slenderness ratios, rotational speed, and hub radius on the natural frequencies and mode shapes of the rotating beam. The material properties of the power-law FG constituents are presented in Table 3. Relations described in Eq. (52) are performed to calculate the non-dimensional natural frequencies

Table 3 Material properties of the FGM constituents [9]
Full size table
$$\lambda = \frac{{\omega L^{2} }}{h}\sqrt {\frac{{\rho_{\text{m}} }}{{E_{\text{m}} }}} .$$
(52)

Table 4 shows the convergence study of the DTM method for first three frequencies. It is found that in the DTM method after a certain number of iterations, the eigenvalues converged to a value with good precision, so the number of iterations is important in DTM method convergence. From the results of Table 4, high convergence rate of the method may be easily observed. For better observations, Figs. 2 and 3 show the convergence trend of DTM for the first and second frequencies. As seen in Fig. 2, the first natural frequency converged after 27 iterations with four-digit precision, while according to Fig. 3 the second natural frequency converged after 29 iterations.

Table 4 Convergence study of the first three frequencies, L/h = 20, P = 2, and η = 4
Full size table
Fig. 2
figure 2

Convergence study of first frequency, L/h = 20, P = 2

Full size image
Fig. 3
figure 3

Convergence study of second frequency, L/h = 20, P = 2

Full size image

After looking into the satisfactory results for the convergence of frequencies, to demonstrate the correctness of the present study, the results for FG rotating beam are compared with the results of FG rotating beams presented by Şimşek [9]. Table 5 compares the results of the present study and the results presented by Şimşek [9], which has been obtained by using Lagrange’s equations for non-porous FG beam with different slenderness ratios. One may clearly notice here that the fundamental frequency parameters obtained in the present investigation are approximately close enough to the results provided in these studies that are used for comparison and validate the proposed method of solution. Frequency parameters of power-law FG porous beam affected by various porosity parameters are studied in Table 6. Inspection of this table reveals that an increase in the value of the power-law exponent leads to a decrease in the fundamental frequencies. The lowest frequency values are obtained for a full metal beam (P → ∞).

Table 5 Comparison of fundamental frequencies for different power-law indices and slenderness ratio parameter, α = 0
Full size table
Table 6 Variation of the first five natural frequencies of FG rotating beam with power-law exponent, L/h = 10, η = 4
Full size table

This is due to the fact that an increase in the value of the power-law exponent results in a decrease in the value of elasticity modulus and the value of bending rigidity. In other words, the beam becomes flexible as the power-law exponent increases. Therefore, as also known from mechanical vibrations, natural frequencies decrease as the stiffness of a structure decreases. It is also interesting to note that the decrease in the frequency values due to the increase in the power-law exponent is almost the same for higher mode frequencies. It is also observed that an increase in the volume fraction of porosity (α) leads to a slight increase in the fundamental frequencies. Also, the effect of power-law exponent on the first five natural frequencies of the FG rotating beam has been illustrated in Figs. 4 and 5 for two cases of P < 10 and P > 10, respectively. It is observed that an increase in the value of the power-law exponent leads to a decrease in the fundamental frequencies. Besides, linear reduction occurs when P is increased from 2 to 10. It is shown that the decrease in frequency parameters due to the increase in power-law exponent is also correct for higher mode frequencies.

Fig. 4
figure 4

Effect of power-law indices on the first five natural frequencies of FG rotating beam, L/h = 10, η = 4, α = 0.1

Full size image
Fig. 5
figure 5

Effect of power-law indices on the first five natural frequencies of FG rotating beam, L/h = 10, η = 4, α = 0.1

Full size image

The other important parameter in vibration behavior of rotating FG beam is its rotational speed parameter. Table 7 presents the variation of the first five natural frequencies of FG porous rotating beam for different rotational speed parameters (η = 0, 2, 4, 6, 8) with different power-law exponents. It is observed that increasing the rotational speed increases the first five natural frequencies and, as seen in Fig. 7, an ascending pattern is more sensitive for the fifth natural frequency. For instance for FG beam with power-law exponent defined as P = 2, increasing normal rotational speed from 2 to 4 leads to 34.9, 7.4,2.8,1.5, and 1.04 % increase in the first five natural frequencies, respectively, and on increasing the normal rotational speed from 4 to 8, the first five natural frequencies increase by about 65.6, 23.8, 10.3, 6 and 4 %, respectively.

Table 7 The effect of rotational speed parameter on natural frequencies of FG rotating beam with different porosities for the case: L/h = 20, P = 2
Full size table

Also in different rotational speeds when volume fraction of porosities increases, the natural frequencies decrease, while the rate of descent in the first five natural frequencies is not similar. Three lines in Figs. 6 and 7 are plotted for three different values of volume fraction of porosities. Figure 6 and 7 illustrate the effect of rotational speed and volume fraction of porosity on the first and fifth natural frequencies. In fact, this figure can be regarded as the visual representation of Table 7. It is obvious that the rate of changes in the fifth natural frequency is higher and the volume fraction of porosity has significant effect on higher mode numbers as depicted in Fig. 7.

Fig. 6
figure 6

Effect of hub normal rotational speed and porosity volume fraction on first natural frequency, L/h = 20, P = 2

Full size image
Fig. 7
figure 7

Effect of hub normal rotational speed and porosity volume fraction on the fifth natural frequency, L/h = 20, P = 2

Full size image

Also, the effect of slenderness ratio (L/h) on the first five natural frequencies for different power-law exponents is presented in Table 8. As would be expected, the frequencies are increased when the value of L/h is increased and this effect become less dominant in higher slenderness ratios. Also, the effect of slenderness ratio on the first five natural frequencies of FG rotating beam is plotted in Fig. 8. It can be concluded that by increasing the L/h ratio, the natural frequency parameters increase, while the L/h ratio has more dominant effects on higher mode natural frequencies compared with the lower ones. It is noteworthy that the effect of slenderness ratio on the frequencies is negligible for long FG beams (i.e., L/h ≥ 20); in other words, the fundamental frequency of the FG rotating beam is saturated after the value of L/h = 20.

Table 8 Variation of the first five natural frequencies of FG rotating beam with L/h ratio for various values of the power-law exponent, η = 2, α = 0.1
Full size table
Fig. 8
figure 8

Effect of slenderness ratio of FG rotating beam on the first five natural frequencies, η = 2, P = 5

Full size image

The next set of results was obtained to demonstrate the effect of hub radius parameter on the non-dimensional natural frequencies of the rotating FG beam. Variations of the first five natural frequencies of rotating FG beam with various hub radius parameters are tabulated in Table 9. Figure 9 illustrates this effect for the first natural frequency when L/h = 10, P = 4, η = 6, α = 0.1. It is observed that the non-dimensional natural frequencies increase with the increase in hub radius parameter as expected because of the increase in centrifugal stiffening of the beam.

Table 9 Effect of hub radius parameter on the first five natural frequencies of an FG rotating beam, P = 4, η = 6, and α = 0.1
Full size table
Fig. 9
figure 9

Effect of hub radius on the first natural frequency of an FG rotating beam, P = 4, η = 6, α = 0.1

Full size image

4 Conclusion

In this paper a new semi-analytical model for the vibration analysis of a rotating functionally graded beam made of porous materials was introduced based on Timoshenko beam theory. The differential transform method as an efficient and accurate numerical tool was applied to solve the governing differential equations derived through Hamilton’s principle. The good agreement between the results of this article and those available in literature validated the presented approach. After demonstrating the fast rate of convergence and accuracy of the approaches, emphasis is placed on investigating the influences of the several parameters such as volume fraction of porosity, mode number, constituent volume fractions, slenderness ratio, rotational speed, and hub radius on the natural frequencies of the rotating porous FG beam. Based on the presented results, one can conclude that rotational speed has a significant influence on natural frequency parameter. Also, it is observed that increasing the porosity and the power-law index has an important effect on the vibration responses of porous FG beam, and the dynamic behavior can be enhanced by selecting appropriate values of the power-law index while the slenderness ratio has negligible effect for long FG beams. Moreover in comparison with other parameters, hub radius has slight effect on natural frequency and increasing hub radius increases natural frequency with low gradient. Numerical results are presented to serve as benchmarks for future analyses of FG porous structures.