A generalized Shapley index-based interval-valued Pythagorean fuzzy PROMETHEE method for group decision-making

Abstract

Multi-criteria group decision-making (MCGDM) problems, where correlations commonly exist among input arguments, are becoming increasingly complex. However, most of the existing consensus-reaching methods for MCGDM problems fail to adequately consider the effects of these interactions among criteria and experts, which may bring about inaccurate results. Therefore, this paper establishes a novel MCGDM framework based on the generalized Shapley value to solve the consensus-reaching problem with interval-valued Pythagorean fuzzy sets (IVPFS). First, experts’ evaluations are collected using IVPFS, which offers a more flexible way to express this vague information. Second, the interval-valued Pythagorean fuzzy Choquet integral operator and the interval-valued Pythagorean fuzzy Shapley aggregation operator are developed to fuse the decision information with complementary, redundant, or independent characteristics. Third, an integrated consensus-reaching algorithm is established to improve group consensus by iteratively updating the evaluations until the group consensus level reaches the preset threshold. Then, the classical PROMETHEE method is extended using the generalized Shapley value within an IVPFS context to derive a more scientific ranking result. Finally, a case study for a sustainable supplier evaluation problem is presented to validate the proposed method. The results and comparative analysis show that the proposed method can represent experts’ evaluations more flexibly, integrate inputs with interrelationships more effectively, and improve group consensus more efficiently.

1 Introduction

With continuous economic and technological development, the associated decision-making problems are becoming increasingly complex (Yan and Pei 2022; Şerif Özlü 2022). Therefore, multi-criteria group decision-making (MCGDM) has recently emerged as a research hotspot and has been widely applied in multiple fields, such as scenic spots recommendation (Ma et al. 2023) and risk management problems (Hua et al. 2023). MCGDM involves a series of techniques to effectively support experts in obtaining the optimal solution within a set of alternatives. This process generally involves the following three aspects: (i) information expression and aggregation; (ii) consensus-reaching process (CRP); (iii) ranking method of alternatives.

In a practical MCGDM problem, the conventional representation structure (e.g., crisp values) is incapable of depicting the situation with strong uncertainty and ambiguity (Khan et al. 2022). To better handle such circumstances, various information expression structures have been investigated. Zadeh reported his pioneering work regarding fuzzy set theory (FST) in 1965 (Zadeh 1965); however, the fuzzy set could not adequately reflect the degree of hesitancy in human perception. Then, Atanassov (1986) extended the FST to intuitionistic fuzzy sets (IFS). However, the sum of membership and nonmembership degrees of IFS is restrained within the range of [0,1], which is unrealistic because human conception cannot perfectly fit within this constraint. To address this concern, Yager (2014) further extended the IFS to Pythagorean fuzzy sets (PFS). More recently, Zhang (2016) extended the PFS to interval-valued Pythagorean fuzzy sets (IVPFS), wherein the membership, nonmembership, and indeterminacy degrees are characterized as interval numbers, rather than crisp numbers. Given the capacity of IVPFS to model the actual MCGDM process with strong fuzziness, it is employed in this work to represent the uncertain information given by the decision-makers (DMs).

Another fundamental issue in MCGDM involves how to integrate the decision evaluations in a reasonable and structured manner. Although the existing interval-valued Pythagorean fuzzy weighted average (IVPFWA) and the interval-valued Pythagorean fuzzy weighted geometric (IVPF-WG) operators can successfully aggregate interval-valued Pythagorean fuzzy numbers (IVPFN) from multiple sources (Peng and Yang 2016), these additive measures fail to reflect the correlations among input arguments. However, interaction phenomena commonly exist among criteria and DMs, ranging from redundancies to synergies (Teng and Liu 2021). Investigating the effects of the interactions inherent to the MCGDM process provides an opportunity to comprehensively analyze the importance of each element. The fuzzy measure and Choquet integral can overcome the deficiency of additive measures and have been explored in various fuzzy environments. However, the Choquet integral only takes the interactions between the adjacent coalitions of elements into account (Chen et al. 2020). To overcome this limitation, the generalized Shapley index can be introduced to reflect the overall importance of each element and the global correlations among them. This motivates us to investigate the generalized Shapley function under an IVPFS environment and develop the interval-valued Pythagorean fuzzy Choquet integration (IVPFCI) and interval-valued Pythagorean fuzzy Shapley aggregation (IVPFSA) operators to fuse the information from correlated criteria and interrelated DMs.

At the beginning of an MCGDM problem, the experts’ opinions may vary considerably. Therefore, it is necessary to reach a designated level of consensus to ensure the group evaluation is satisfactory to most DMs, which could further benefit the implementation of the decision result (Hua et al. 2022; Hua and Xue 2022). Various consensus models have been proposed, and they can generally be divided into two categories. The first is an iterative model based on identification and direction rules (IDR). Individual evaluations that deviate far from the group are first identified and then modified based on a specific recommendation rule until the group consensus reaches a preset threshold. The second category is the optimization-based model. Optimization algorithms are utilized to find the best available solution under the given constraints and have been widely applied in different fields (Agushaka et al. 2022; Abualigah et al. 2021, 2022). The mathematical and metaheuristic approaches are two well-known strategies for tackling optimization problems (Oyelade et al. 2022; Abualigah et al. 2021, 2021). Inspired by optimization methods, the optimization-based consensus-reaching model has been proposed. Although the optimization-based CRP models can significantly improve consensus efficiency, the results derived only from a mathematical model cannot ensure individual participation. To overcome this limitation, this study develops an integrated model that combines the advantages of IDR-based methods and optimization models to maximize the improvement in group consensus.

Once a group evaluation with adequate consensus has been obtained, the MCGDM proceeds to the ranking process. To date, various methods have been explored to facilitate MCGDM, including Techniques for Order Preferences by Similarity to Ideal Solution (TOPSIS) (Wang et al. 2022), ELimination and Choice Translating REality (ELECTRE) (Chen 2020), Preference Ranking Organization METHod for Enrichment Evaluations (PROMETHEE) (Wang et al. 2022), and Vlsekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) (Raj Mishra et al. 2022), among others. In particular, PROMETHEE is one of the most effective outranking techniques based on dominance relations between alternatives. However, the classical PROMETHEE method has difficulty dealing with highly uncertain information. Additionally, the heterogeneous correlations among criteria and DMs are neglected, which could reduce the rationality of the decision result. Considering this limitation, we aim to extend the traditional PROMETHEE into the IVPFS context to propose IVPF-PROMETHEE. Then, the generalized Shapley value is introduced into the IVPF-PROMETHEE method to analyze the correlative characteristic in MCGDM problems. The main contributions of this study are outlined as follows:

• (1) The decision information is represented by IVPFS, which offers a flexible way to assess the MCGDM problem from both positive and negative perspectives with indeterminacy. More importantly, the generalized Shapley value is integrated into the IVPFS to handle the correlation between variables and their combinations.

• (2) An optimization model is constructed based on TOPSIS to derive the fuzzy measures on the criteria set, and $\lambda$-fuzzy measure is applied to reduce the computational complexity when the number of input arguments becomes relatively large.

• (3) The interval-valued Pythagorean fuzzy Choquet integral and the interval-valued Pythagorean fuzzy Shapley aggregation operators are developed to aggregate the decision information with complementary, redundant, or independent characteristics.

• (4) To resolve conflicts among DMs, an integrated consensus-reaching model is constructed, which can simultaneously ensure expert participation and maximize consensus enhancement.

• (5) The classical PROMETHEE method is extended to the IVPFS for the first time to our knowledge, and the generalized Shapley index is incorporated into the IVPF-PROMETHEE; these processes make the ranking result more scientific.

The remainder of this paper is structured as follows: Sect. 2 reviews the representation of fuzzy information, consensus-reaching strategies, and alternative ranking methods. A brief introduction to PFS, IVPFS, fuzzy measures, and the PROMETHEE method is presented in Sect. 3. In Sect. 4, the extended IVPF-PROMETHEE method based on the generalized Shapley value with CRP is described. A case study and comparative analysis are presented in Sect. 5, and in Sect. 6, the conclusions are summarized.

2 Literature review

2.1 Representation of fuzzy information

Considering the inherent ambiguity in human cognition, various fuzzy set theories have been introduced to better express experts’ evaluations in MCGDM problems. Liu et al. (2022) used intuitionistic fuzzy values to model the opinions from DMs with particle swarm optimization. Ke et al. (2022) proposed an MCGDM framework for photovoltaic poverty alleviation project site selection under an intuitionistic fuzzy environment. Given that the traditional intuitionistic fuzzy aggregation operators cannot reflect the correlative relationships of criteria, Jia and Wang (2022) proposed the Choquet integral-based intuitionistic fuzzy arithmetic aggregation operator to support MCGDM. However, the sum of membership and nonmembership degrees of intuitionistic fuzzy numbers is constrained within 0 and 1. Additionally, the Choquet integral only considers the correlation between adjacent coalitions of the elements, ignoring the global interactions between them.

To overcome the limitation of IFS, Pythagorean fuzzy sets (PFS) were proposed and applied to MCGDM problems. For example, Zhang and Chen (2022) employed Pythagorean fuzzy preference relations in group decision-making to select excellent doctors for international exchange. Zhou et al. (2022) developed a statistical estimation method for handling Pythagorean fuzzy information in a green credit problem. Recently, Zhang (2016) extended PFS to IVPFS to better describe the uncertainty in membership, nonmembership, and indeterminacy degrees. Mohagheghi et al. (2020) used IVPFS to evaluate high-technology project portfolios in port operations. Fu et al. (2020) established a new product ranking method combining the opinions represented with IVPFS. However, the existing IVPF operators cannot consider the relationship among input arguments. Therefore, to take advantage of IVPFS’s ability to express uncertain information and overcome the shortcomings of the existing operators, we introduce the generalized Shapley index into IVPF operators to reflect the overall importance of elements and their global correlations in information fusion.

2.2 Consensus-reaching strategies

Consensus-reaching is essential in MCGDM since a consensual decision outcome can benefit its further implementation. The consensus-reaching strategies can mainly be categorized into two types. The first one is the IDR-based consensus model. Liu et al. (2022) proposed an IDR-based model to determine the DMs with inadequate consensus and to generate the modified evaluations. Liao et al. (2021) addressed the large-scale GDM problems considering local and global consensus with an IDR-based model. In Liu et al. (2022), the DM whose evaluations deviate most from the group is first identified and then modified toward those they trust in the social network.

The second one is the optimization-based method. Wu et al. (2022) developed a two-fold personalized feedback approach by minimizing the adjustment cost of the consensus-reaching process. Yuan et al. (2021) proposed a minimum adjustment consensus method to obtain the updated evaluations with incomplete decision information. Wang et al. (2022) extended the traditional minimum adjustment model to handle large-scale MCGDM issues with a two-stage consensus feedback mechanism. Recently, Yuan et al. (2022) established a minimum conflict model with a limited budget to improve group consensus in a pollution remediation assessment problem.

The traditional IDR-based models often involve updating evaluations for iterations to improve the group consensus, which reduces the efficiency of the consensus-reaching process. Though optimization-based methods can greatly enhance consensus efficiency, the results obtained from mathematical models cannot reflect experts’ participation. To take advantage of both IDR-based models and optimization-based methods, we proposed an integrated consensus-reaching strategy to maximize the consensus improvement at each modification, which can ensure both expert participation and consensus efficiency.

2.3 Alternative ranking methods

Based on the achieved consensual group evaluation, the optimal solution can be obtained with alternative ranking methods. Corrente and Tasiou (2023) utilized the TOPSIS method for MCGDM problems with hierarchical and non-monotonic criteria. Kumar and Chen (2022) extended the traditional TOPSIS with the weighted distance measure of linguistic intuitionistic fuzzy sets to prioritize the alternatives. In terms of the outranking methods, Kirişci et al. (2022) proposed the Fermatean fuzzy ELECTRE method for biomedical material selection problems. Zahid et al. (2022) extended the ELECTRE method to complex spherical fuzzy sets to rank water treatment technologies. Raj Mishra et al. (2022) modified the traditional VIKOR method based on Fermatean hesitant fuzzy sets and proposed the remoteness index for alternative ranking. Wang et al. (2022) used the PROMETHEE method to assist with nested information representation of multi-dimensional decision problems.

Among these ranking methods, PROMETHEE stands out as the most effective outranking technique since it can obtain the ranking of alternatives with their dominance relations. PROMETHEE method is characterized by the elimination of scale effects between criteria and managing incomparability with comprehensive rankings. However, the classical PROMETHEE cannot handle uncertain information and does not consider the correlations between input arguments. To address this issue, we first extend the traditional PROMETHEE into the IVPFS environment to propose IVPF-PROMETHEE. Then, we introduce the generalized Shapley value into IVPF-PROMETHEE to investigate the correlated property in MCGDM problems.

3 Preliminaries

In this section, some important fundamental concepts are reviewed, including IVPFS, the generalized Shapley index, and the PROMETHEE method.

3.1 Interval-valued Pythagorean fuzzy set

Definition 1

(Zhang 2016). X is a universe of discourse, then the IVPFS H on X is given as:

$$\begin{aligned} H = \left\{ {\left\langle {x,\left[ {\mu _H^L(x),\mu _H^U(x)} \right] ,\left[ {\upsilon _H^L(x),\upsilon _H^U(x)} \right] } \right\rangle \left| {x \in X} \right. } \right\} \end{aligned}$$

(1)

where $\mu _H^L(x),\mu _H^U(x),\upsilon _H^L(x),\upsilon _H^U(x) \in [0,1]$, $0 \le {(\mu _H^U(x))^2} + {(\upsilon _H^U(x))^2} \le 1$. The indeterminacy degree of $x \in X$ to H is defined as ${\pi _H}(x) = \left[ {\pi _H^L(x),\pi _H^U(x)} \right]$, with $\pi _H^L(x) = \sqrt{1 - {{(\mu _H^U(x))}^2} - {{(\upsilon _H^U(x))}^2}}$ and $\pi _H^U(x) = \sqrt{1 - {{(\mu _H^L(x))}^2} - {{(\upsilon _H^L(x))}^2}}$. For brevity, we define $h = \left( {\left[ {\mu _H^L(x),\mu _H^U(x)} \right] ,\left[ {\upsilon _H^L(x),\upsilon _H^U(x)} \right] } \right)$ as an IVPFN. If $\mu _H^L(x) = \mu _H^U(x)$ and $\upsilon _H^L(x) = \upsilon _H^U(x)$, the IVPFS is reduced to a PFS. If $\mu _H^U(x) + \upsilon _H^U(x) \le 1$, then the IVPFS is reduced to an IVIFS. Thus, the IVPFS can be considered as a generalization of PFS and IVIFS.

The fundamental operations of IVPFN are presented as follows.

Definition 2

(Peng and Yang 2016). Let $\widetilde{{p_1}} = \left( \left[ {\mu _1^L,\mu _1^U} \right] ,\left[ {\upsilon _1^L,\upsilon _1^U} \right] \right)$, $\widetilde{{p_2}} = \left( {\left[ {\mu _2^L,\mu _2^U} \right] ,\left[ {\upsilon _2^L,\upsilon _2^U} \right] } \right)$, and ${{\widetilde{p}}} = \left( {\left[ {{\mu ^L},{\mu ^U}} \right] ,} \right.$ $\left. {\left[ {{\upsilon ^L},\upsilon {}^U} \right] } \right)$ be three IVPFNs where $\lambda > 0$, then their operations are defined as follows:

$$\begin{aligned}{} & {} \widetilde{{p_1}} \oplus \widetilde{{p_2}} = \left( \left[ \sqrt{{{(\mu _1^L)}^2} + {{(\mu _2^L)}^2} - {{(\mu _1^L)}^2}{{(\mu _2^L)}^2}} ,\right. \right. \nonumber \\{} & {} \qquad \left. \left. \sqrt{{{(\mu _1^U)}^2} + {{(\mu _2^U)}^2} - {{(\mu _1^U)}^2}{{(\mu _2^U)}^2}} \right] , \right. \nonumber \\{} & {} \quad \left. {\left[ {\upsilon _1^L\upsilon _2^L,\upsilon _1^U\upsilon _2^U} \right] } \right) \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \widetilde{{p_1}} \otimes \widetilde{{p_2}} = \left( \left[ {\mu _1^L\mu _2^L,\mu _1^U\mu _2^U} \right] ,\right. \nonumber \\{} & {} \quad \left. \left[ \sqrt{{{(\upsilon _1^L)}^2} + {{(\upsilon _2^L)}^2} - {{(\upsilon _1^L)}^2}{{(\upsilon _2^L)}^2}} ,\right. \right. \nonumber \\{} & {} \qquad \left. \left. \sqrt{{{(\upsilon _1^U)}^2} + {{(\upsilon _2^U)}^2} - {{(\upsilon _1^U)}^2}{{(\upsilon _2^U)}^2}} \right] \right) \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \lambda {{\widetilde{p}}} = \left( \left[ {\sqrt{1 - {{(1 - {{({\mu ^L})}^2})}^\lambda }} ,\sqrt{1 - {{(1 - {{({\mu ^U})}^2})}^\lambda }} } \right] ,\right. \nonumber \\{} & {} \quad \left. \left[ {{{\left( {{\upsilon ^L}} \right) }^\lambda },{{\left( {{\upsilon ^U}} \right) }^\lambda }} \right] \right) \end{aligned}$$

(4)

$$\begin{aligned}{} & {} {\left( {{{\widetilde{p}}}} \right) ^c} = \left( {\left[ {{\upsilon ^L},\upsilon {}^U} \right] ,\left[ {{\mu ^L},{\mu ^U}} \right] } \right) \end{aligned}$$

(5)

Definition 3

(Peng and Yang 2016). Let ${{\widetilde{p}}} = \left( \left[ {{\mu ^L},{\mu ^U}} \right] ,\left[ {{\upsilon ^L},\upsilon {}^U} \right] \right)$ be an IVPFS, then its score function and accuracy function are calculated as:

$$\begin{aligned} S\left( {{{\widetilde{p}}}} \right) = \frac{1}{2}\left[ {{{\left( {{\mu ^L}} \right) }^2} + {{\left( {{\mu ^U}} \right) }^2} - {{\left( {{\upsilon ^L}} \right) }^2} - {{\left( {\upsilon {}^U} \right) }^2}} \right] \end{aligned}$$

(6)

$$\begin{aligned} A\left( {{{\widetilde{p}}}} \right) = \frac{1}{2}\left[ {{{\left( {{\mu ^L}} \right) }^2} + {{\left( {{\mu ^U}} \right) }^2} + {{\left( {{\upsilon ^L}} \right) }^2} + {{\left( {\upsilon {}^U} \right) }^2}} \right] \end{aligned}$$

(7)

where $S\left( {{{\widetilde{p}}}} \right) \in [ - 1,1],A\left( {{{\widetilde{p}}}} \right) \in [0,1]$.

Then, for any two IVPFNs $\widetilde{{p_1}}$ and $\widetilde{{p_2}}$, the comparison rules are given as:

• (1) If $S\left( {\widetilde{{p_1}}} \right) > S\left( {\widetilde{{p_2}}} \right)$, then $\widetilde{{p_1}} \succ \widetilde{{p_2}}$;

• (2) If $S\left( {\widetilde{{p_1}}} \right) = S\left( {\widetilde{{p_2}}} \right)$, then

  • (a) If $A\left( {\widetilde{{p_1}}} \right) > A\left( {\widetilde{{p_2}}} \right)$, then $\widetilde{{p_1}} \succ \widetilde{{p_2}}$,

  • (b) If $A\left( {\widetilde{{p_1}}} \right) = A\left( {\widetilde{{p_2}}} \right)$, then $\widetilde{{p_1}} = \widetilde{{p_2}}$.

Definition 4

(Peng and Yang 2016). Let $\widetilde{{p_1}} = \left( \left[ {\mu _1^L,\mu _1^U} \right] ,\left[ {\upsilon _1^L,\upsilon _1^U} \right] \right)$ and $\widetilde{{p_2}} = \left( {\left[ {\mu _2^L,\mu _2^U} \right] ,\left[ {\upsilon _2^L,\upsilon _2^U} \right] } \right)$ be two IVPFNs, then the distance between them is calculated as:

$$\begin{aligned} d\left( {\widetilde{{p_1}},\widetilde{{p_2}}} \right)= & {} \frac{1}{4}\left( \left| {{{\left( {\mu _1^L} \right) }^2} - {{\left( {\mu _2^L} \right) }^2}} \right| + \left| {{{\left( {\mu _1^U} \right) }^2} - {{\left( {\mu _2^U} \right) }^2}} \right| \right. \nonumber \\{} & {} + \left| {{{\left( {\upsilon _1^L} \right) }^2} - {{\left( {\upsilon _2^L} \right) }^2}} \right| + \left| {{\left( {\upsilon _1^U} \right) }^2} {-} {{\left( {\upsilon _2^U} \right) }^2} \right| \nonumber \\{} & {} \left. {+} \left| {{{\left( {\pi _1^L} \right) }^2} {-} {{\left( {\pi _2^L} \right) }^2}} \right| {+} \left| {{{\left( {\pi _1^U} \right) }^2} {-} {{\left( {\pi _2^U} \right) }^2}} \right| \right) \nonumber \\ \end{aligned}$$

(8)

3.2 Fuzzy measure and the generalized Shapley index

The fuzzy measure, introduced by Sugeno (1974), is a powerful tool to determine the correlations among input arguments. It replaces additivity with monotonicity and has been widely employed in different fields.

Definition 5

(Michio 1974). Suppose $X = \left\{ {{x_1},{x_2},...,{x_n}} \right\}$ denotes a universe of discourse and P(X) is the power set of X, then $\xi$ is a fuzzy measure on X that satisfies certain boundary conditions (i.e.,$\xi (\phi ) = 0$ and $\xi (X) = 1$) and monotonicity (i.e., if $A,B \in P(X)$ and $A \subseteq B$, then $\xi (A) \le \xi (B)$).

Considering the difficulty in calculating the fuzzy measure when large numbers of elements are involved, Sugeno proposed the $\lambda$-fuzzy measure.

Definition 6

(Michio 1974). Suppose $X = \left\{ {{x_1},{x_2},...,{x_n}} \right\}$ denotes a universe of discourse. If the fuzzy measure $\xi$ on X meets Eq. (9),

$$\begin{aligned} \xi (A \cup B) = \xi (A) + \xi (B) + \lambda \xi (A)\xi (B) \end{aligned}$$

(9)

where $A \cap B = \phi$ and $\lambda$ represents the interaction between A and B, with $\lambda \in [ - 1, + \infty ]$, then it is $\lambda$-fuzzy measure. Specifically, $\lambda > 0$ indicates a positive interrelation between A and B, whereas $\lambda < 0$ indicates a negative interaction, and $\lambda =0$ denotes that A and B are mutually independent.

Given a finite set X, the $\lambda$ -fuzzy measure is denoted as:

$$\begin{aligned} \xi (X) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{\lambda }\left[ {\prod \limits _{i = 1}^n {(1 + \lambda \xi ({x_i})) - 1} } \right] }&{}{\lambda \ne 0}\\ {\sum \limits _{i = 1}^n {\xi ({x_i})} }&{}{\lambda = 0} \end{array}} \right. \end{aligned}$$

(10)

With $\xi (X) = 1$, Eq. (10) can be rewritten as:

$$\begin{aligned} \lambda + 1 = \prod \limits _{i = 1}^n {(1 + \lambda \xi ({x_i}))} \end{aligned}$$

(11)

Then, $\lambda$ can be uniquely derived.

Definition 7

(Choquet 1955). Suppose f is a positive real-valued mapping on $X = \left\{ {{x_1},{x_2},...,{x_n}} \right\}$ and $\xi$ is a fuzzy measure. The Choquet integral regarding $\xi$ can be given as:

$$\begin{aligned}{} & {} {C_\xi }(f({x_1}),f({x_2}),...,f({x_n}))\nonumber \\{} & {} \quad = \sum \limits _{i = 1}^n {(\xi ({A_{(i)}}) - \xi ({A_{(i + 1)}}))} f({x_{(i)}}) \end{aligned}$$

(12)

where $( \cdot )$ denotes a permutation on X, such that $f({x_{(1)}}) \le f({x_{(2)}}) \le ... \le f({x_{(n)}})$ and ${A_{(i)}} = \left\{ {{x_{(i)}},{x_{(i + 1)}},...,{x_{(n)}}} \right\}$ with ${A_{(n + 1)}} = \phi$.

To evaluate the importance of each coalition rather than each element, Marichal (2000) introduced the concept of the Shapley index to the game theory.

Definition 8

(Marichal 2000). Let $\xi$ be a fuzzy measure on $X = \left\{ {{x_1},{x_2},...,{x_n}} \right\}$, then the generalized Shapley value for $\forall S \subseteq X$ can be determined as:

$$\begin{aligned} {\varphi _S}(\xi ,X)= & {} \sum \limits _{T \subseteq X\backslash S} {\frac{{(\left| X \right| - \left| S \right| - \left| T \right| )!\left| T \right| !}}{{(\left| X \right| - \left| S \right| + 1)!}}} \nonumber \\{} & {} (\xi (S \cup T) - \xi (T)) \end{aligned}$$

(13)

where $\left| X \right| ,\left| S \right|$, and $\left| T \right|$ denote the number of elements in the subsets. ${\varphi _S}(\xi ,X)$ is an expected value that reflects the global correlation between set S and each set in $N\backslash S$. If $S = \left\{ i \right\}$ for $\forall i \in X$, then Eq. (13) is reduced to the Shapley function (Shapley 1953):

$$\begin{aligned} {\varphi _i}(\xi ,X)= & {} \sum \limits _{T \subseteq X\backslash \left\{ i \right\} } {\frac{{(\left| X \right| - \left| T \right| - 1)!\left| T \right| !}}{{\left| X \right| !}}} (\xi (i \cup T) - \xi (T)) \nonumber \\ \end{aligned}$$

(14)

3.3 The classical PROMETHEE method

The PROMETHEE method, initially proposed by Brans et al. (1986), is an effective outranking technique based on pairwise comparisons and preference functions. The fundamental principle of PROMETHEE is to obtain the net outranking flow of alternatives. Its basic processes are described as follows:

Let ${\left[ {{x_{ij}}} \right] _{m \times n}}$ denote the decision information, where ${x_{ij}}$ indicates the evaluation of the alternatives ${{a}_i}(i = 1,2,...,m)$ over criteria ${{c}_j}(j = 1,2,...,n)$, and let ${w_j}(j = 1,2,...,n)$ represent the weight of ${c}_j$, with ${w_j} \in [0,1]$ and $\sum \limits _{j = 1}^n {{w_j}} = 1$.

Step 1: Normalize the decision information ${\left[ {{x_{ij}}} \right] _{m \times n}}$ into ${\left[ {\widetilde{{x_{ij}}}} \right] _{m \times n}}$.

Step 2: Calculate the divergence between each pair of ${{a}_t}$ and ${{a}_s}(t,s = 1,2,...,m)$ over each criterion ${{c}_j}(j = 1,2,...,n)$:

$$\begin{aligned} {d_j}({{a}_t},{{a}_s}) = \widetilde{{x_{tj}}} - \widetilde{{x_{sj}}} \end{aligned}$$

(15)

Step 3: Obtain the preference value of ${{a}_t}$ over ${{a}_s}$ on ${{c}_j}$:

$$\begin{aligned} P{V_j}({{a}_t},{{a}_s}) = P{V_j}({d_j}({{a}_t},{{a}_s})) \end{aligned}$$

(16)

where $P{V_j}( \cdot )$ denotes the preference function governing the mapping of the divergence of different alternative to a preference value.

Step 4: Determine the overall preference value of ${{a}_t}$ over ${{a}_s}$:

$$\begin{aligned} \tau ({{a}_t},{{a}_s}) = \sum \limits _{j = 1}^n {P{V_j}({{a}_t},{{a}_s}){w_j}} \end{aligned}$$

(17)

Step 5: Obtain the positive and negative outranking flow of alternatives ${{a}_t}$:

$$\begin{aligned} {\delta ^ + }({{a}_t}) = \frac{1}{{m - 1}}\sum \limits _{x \in A} {\tau ({{a}_t},x)} \end{aligned}$$

(18)

$$\begin{aligned} {\delta ^ - }({{a}_t}) = \frac{1}{{m - 1}}\sum \limits _{x \in A} {\tau (x,{{a}_t})} \end{aligned}$$

(19)

Step 6: Obtain the alternative ranking by computing the net outranking index:

$$\begin{aligned} \delta ({{a}_t}) = {\delta ^ + }({{a}_t}) - {\delta ^ - }({{a}_t}) \end{aligned}$$

(20)

4 The extended IVPF-PROMETHEE method based on the Shapley value with CRP

The proposed MCGDM framework includes four main steps: (i) Establish and standardize the decision matrix; (ii) Develop the generalized Shapley interval-valued Pythagorean fuzzy aggregation operator; (iii) Implement the consensus-reaching process; (iv) Rank the alternatives. The general procedures of the proposed method are illustrated in Fig. 1.

Fig. 1

General procedures the proposed method

4.1 Determination of fuzzy measures on the criteria set and the expert set

Suppose there is a MCGDM problem where m alternatives $A = ({{a}_1},{{a}_2},...,{{a}_m})$ are evaluated by K experts $E = ({e_1},{e_2},...,{e_K})$ on n criteria $C = ({{c}_1},{{c}_2},...,{{c}_n})$ to form an interval-valued Pythagorean fuzzy decision matrix as:

$$\begin{aligned} P = {\left[ {p_{ij}^k} \right] _{m \times n}} = \left[ {\begin{array}{*{20}{c}} {p_{11}^1}&{}{p_{12}^2}&{} \cdots &{}{p_{1n}^K}\\ {p_{21}^1}&{}{p_{22}^2}&{} \cdots &{}{p_{2n}^K}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {p_{m1}^1}&{}{p_{m2}^2}&{} \cdots &{}{p_{mn}^K} \end{array}} \right] \end{aligned}$$

(21)

where $p_{ij}^k = \left( {\left[ {\mu _{ij}^{kL},\mu _{ij}^{kU}} \right] ,\left[ {\upsilon _{ij}^{kL},\upsilon _{ij}^{kU}} \right] } \right)$ is an IVPFN representing ${e_k}(k = 1,2,...,K)$ ’s assessment of ${{a}_i}(i = 1,2,...,m)$ on ${{c}_j}(j = 1,2,...,n)$.

Afterward, ${\left[ {p_{ij}^k} \right] _{m \times n}}$ is standardized into ${\left[ {\widetilde{p_{ij}^k}} \right] _{m \times n}}$ by converting cost-type attributes into benefit-type attributes.

$$\begin{aligned} \widetilde{p_{ij}^k} = \left\{ {\begin{array}{*{20}{c}}{p_{ij}^k}&{}{\mathrm{{for\ benefit\ criterion}}}\\ {{{(p_{ij}^k)}^c}}&{}{\mathrm{{for\ cost\ criterion}}}\end{array}}\right. \end{aligned}$$

(22)

Most existing studies assume that criteria and DMs are independent. However, this premise is rarely true in practical MCGDM problems, where correlative effects commonly exist among criteria and DMs. Thus, the generalization of additive measures, namely non-additive measures, should be implemented to reflect the mutual influences between input arguments.

Based on the principle of TOPSIS, the best option should be the furthest from the negative ideal solution (NIS) and the nearest to the positive ideal solution (PIS). To maximize the performance of alternatives, we construct an optimization model to derive the fuzzy measure on the criteria set as follows:

$$\begin{aligned} \begin{array}{l} \max \sum \limits _{i = 1}^m {\sum \limits _{j = 1}^n {C{C_{ij}}} } (\widetilde{{p_{ij}}},{{{\widetilde{p}}}^ - }){\varphi _{{{c}_j}}}(\xi ,C)\\ s.t.\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\xi (\phi ) = 0,\xi (C) = 1,}\\ {\xi ({{c}_j}) \in {W_j},\xi ({{c}_j}) \ge 0,}\\ {\xi (S) \le \xi (T),\forall S,T \in C,S \subseteq T,}\\ {{\varphi _{{{c}_j}}}(\xi ,C) = \sum \limits _{T \subseteq C\backslash {{c}_j}} {\frac{{(n - \left| T \right| - 1)!\left| T \right| !}}{{n!}}} (\xi ({{c}_j} \cup T) - \xi (T)),} \end{array}}\\ {C{C_{ij}}(\widetilde{{p_{ij}}},{{{{\widetilde{p}}}}^ - }) = \frac{{{d_{ij}}(\widetilde{{p_{ij}}},{{{{\widetilde{p}}}}^ - })}}{{{d_{ij}}(\widetilde{{p_{ij}}},{{{{\widetilde{p}}}}^ + }) + {d_{ij}}(\widetilde{{p_{ij}}},{{{{\widetilde{p}}}}^ - })}}.} \end{array}} \right. \end{array}\nonumber \\ \end{aligned}$$

(23)

where $\widetilde{{p_{ij}}}$ denotes the group decision matrix; ${{{\widetilde{p}}}^ + } = ([\mathop {\max }\limits _{} (\mu _{ij}^L),\mathop {\max }\limits _{} (\mu _{ij}^U)],[\mathop {\min }\limits _{} (\upsilon _{ij}^L),\mathop {\min }\limits _{} (\upsilon _{ij}^U)])$ and ${{{\widetilde{p}}}^ - } = ([\mathop {\min }\limits _{} (\mu _{ij}^L),\mathop {\min }\limits _{} (\mu _{ij}^U)],[\mathop {\max }\limits _{} (\upsilon _{ij}^L),\mathop {\max }\limits _{} (\upsilon _{ij}^U)])$ indicate the PIS and NIS, respectively; $C{C_{ij}}(\widetilde{{p_{ij}}},{{{\widetilde{p}}}^ - })$ is the closeness coefficient of evaluation $\widetilde{{p_{ij}}}$ from the NIS, where ${d_{ij}}(\widetilde{{p_{ij}}},{{{\widetilde{p}}}^ + })$ is the distance measure from $\widetilde{{p_{ij}}}$ to ${{{\widetilde{p}}}^ + }$; ${\varphi _{{C_j}}}(\xi ,C)$ is the generalized Shapley value of ${{c}_j}$ on fuzzy measure $\xi$; ${W_j}$ denotes the known weight information.

Then, with the optimal fuzzy measure $\xi$, the generalized Shapley indices of the criteria and their combinations can be calculated using Eq. (13).

Next, the fuzzy measure of expert ${e_k}(k = 1,2,...,K)$ is discussed. Practical MCGDM problems typically involve a series of correlated DMs. Because $\xi$ is given on the power set, this computation would become exponentially complex if a large number of factors is involved. To address this issue, the $\lambda$-fuzzy measure is introduced.

Given an expert set E, the $\lambda$-fuzzy measure satisfies

$$\begin{aligned} \xi (E)= & {} \sum \limits _{k = 1}^K {\xi ({e_k})} + \lambda \sum \limits _{{k_1} = 1}^{K - 1} \sum \limits _{{k_2} = {k_1} + 1}^K \nonumber \\{} & {} {(\xi ({e_{{k_1}}})\xi ({e_{{k_2}}}) + \cdots + {\lambda ^{n - 1}}\xi ({e_1}) \cdots \xi ({e_K}))} \nonumber \\= & {} \frac{1}{\lambda }\left( \prod \limits _{k = 1}^K {(1 + \lambda \xi ({e_k})) - 1} \right) \end{aligned}$$

(24)

Since $\xi (E) = 1$, $\lambda = \prod \limits _{k = 1}^K {(1 + \lambda \xi ({e_k})) - 1}$. Then, based on the importance of single experts $\xi ({e_k})$ and Eq. (9), the fuzzy measure of the subsets of E, namely $\xi ({E_{(k)}})$, can be easily obtained.

4.2 The generalized Shapley interval-valued Pythagorean fuzzy aggregation operator

When correlations exist, aggregating the individual evaluations without considering the interaction effects would lead to unreliable results. Therefore, to derive more accurate importance values, all subsets including the specific element must be considered apart from their individual importance. The prominent advantage of the Shapley value is that the correlations between elements can be characterized by fuzzy measures, which ensures the weight can be allocated to elements and their coalitions simultaneously. Thus, the generalized Shapley value is introduced to represent each element’s average contribution value in all coalitions.

This subsection develops the interval-valued Pythagorean fuzzy Choquet integral and the interval-valued Pythagorean fuzzy Shapley aggregation operators and briefly describes their basic properties and some special cases.

4.2.1 Interval-valued Pythagorean fuzzy Choquet integral operator

Definition 9

Suppose $\widetilde{{p_j}} = \left( {\left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] } \right) \left( {j = 1,2,...,n} \right)$ is a set of IVPFNs and $\xi$ be a fuzzy measure on $P = \left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, then the IVPFCA operator is defined as:

$$\begin{aligned}{} & {} IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) = \mathop \oplus \limits _{j = 1}^n (\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widetilde{{p_{(j)}}} \nonumber \\{} & {} \quad = \left( {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\mu _{(j)}^L,\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\mu _{(j)}^U} } \right] ,} \right. \nonumber \\{} & {} \quad \left. {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\upsilon _{(j)}^L,\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{(j)}^U} } \right] } \right) \nonumber \\ \end{aligned}$$

(25)

where $( \cdot )$ represents a permutation on $\left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, satisfying $\widetilde{{p_{(1)}}} \le \widetilde{{p_{(2)}}} \le ... \le \widetilde{{p_{(n)}}}$ and ${P_{(j)}} = \left\{ {\widetilde{{p_{(j)}}},\widetilde{{p_{(j + 1)}}},...,\widetilde{{p_{(n)}}}} \right\}$, with ${P_{(n + 1)}} = \phi$, and $(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))$ is the weight vector with $\sum \limits _{j = 1}^n (\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})) = 1$.

Theorem 1

Given a collection of $\widetilde{{p_j}} = \left( \left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] \right) \left( {j = 1,2,...,n} \right)$. $\xi$ is a fuzzy measure on $P = \left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$. Then, the aggregated value by IVPFCA operator is still an IVPFN.

Some properties of the IVPFCA operator are discussed below, including idempotency, commutativity, monotonicity, and boundedness.

Property 1

(Idempotency) Let $\widetilde{{p_j}} = \left( \left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] \right) \left( {j = 1,2,...,n} \right)$ be a set of IVPFNs. If $\widetilde{{p_j}} = {{\widetilde{p}}}$ for all j, then $IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) = {{\widetilde{p}}}$.

Proof

Since $\left( {\left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] } \right) = \left( {\left[ {\mu _{}^L,\mu _{}^U} \right] ,\left[ {\upsilon _{}^L,{\upsilon ^U}} \right] } \right)$ for all j, $\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}) \ge 0$ and $\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))} = 1$.

Thus, $IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) = \mathop \oplus \limits _{j = 1}^n (\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})){{\widetilde{p}}}$

$\begin{array}{l} = \left( {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\mu _{}^L,\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\mu _{}^U} } \right] ,} \right. \\ \left. {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\upsilon _{}^L,\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{}^U} } \right] } \right) \end{array}$

$\begin{array}{l} = \left( {\left[ {\mu _{}^L\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} ),\mu _{}^U\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))} } \right] ,} \right. \\ \left. {\left[ {\upsilon _{}^L\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} ),\upsilon _{}^U\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))} } \right] } \right) \\ = \left( {\left[ {\mu _{}^L,\mu _{}^U} \right] ,\left[ {\upsilon _{}^L,{\upsilon ^U}} \right] } \right) \end{array}$

$\square$

Property 2

(Commutativity) Let $\widetilde{{p_j}} = \left( \left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] \right) \left( {j = 1,2,...,n} \right)$ be a set of IVPFNs and $\left\{ {{{\widetilde{{p_1}}}^\prime },{{\widetilde{{p_2}}}^\prime },...,{{\widetilde{{p_n}}}^\prime }} \right\}$ be any permutation of $\left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, then $IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}})=IVPF$ $CA({\widetilde{{p_1}}^\prime },{\widetilde{{p_2}}^\prime },...,{\widetilde{{p_n}}^\prime })$ .

Proof

Since $\left\{ {{{\widetilde{{p_1}}}^\prime },{{\widetilde{{p_2}}}^\prime },...,{{\widetilde{{p_n}}}^\prime }} \right\}$ denotes any permutation of $\left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, based on Definition 7, it is straightforward to obtain this property. $\square$

Property 3

(Monotonicity) Let $\left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$ and $\left\{ {\widehat{{p_1}},\widehat{{p_2}},...,\widehat{{p_n}}} \right\}$ be two sets of IVPFNs, where $\widetilde{{p_j}} = \left( {\left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] } \right)$, $\widehat{{p_j}} = \left( {\left[ {\widehat{\mu _j^L},\widehat{\mu _j^U}} \right] ,\left[ {\widehat{\upsilon _j^L},\widehat{\upsilon _j^U}} \right] } \right)$ , and $\widetilde{{p_j}} \succ \widehat{{p_j}}(j = 1,2,...,n)$ , then $IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) > IVPFCA(\widehat{{p_1}},\widehat{{p_2}},...,\widehat{{p_n}})$.

Proof

$IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}})$

$= \left( {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\mu _{(j)}^L,\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\mu _{(j)}^U} } \right] ,} \right.$

$\left. {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\upsilon _{(j)}^L,\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{(j)}^U} } \right] } \right)$

$IVPFCA(\widehat{{p_1}},\widehat{{p_2}},...,\widehat{{p_n}})$

$= \left( {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\widehat{\mu _{(j)}^L},\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\mu _{(j)}^U}} } \right] ,} \right.$

$\left. {\left[ {\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\widehat{\upsilon _{(j)}^L},\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\upsilon _{(j)}^U}} } \right] } \right)$

According to Definition 3, the score value of these two sets of IVPFNs can be derived as:

$\begin{array}{lll} S(IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}})) \\ = \frac{1}{2}\left[ (\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\mu _{(j)}^L{)^2} + {{(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\mu _{(j)}^U} )}^2} \right. \\ - \left. {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\upsilon _{(j)}^L{)^2} - {{(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{(j)}^U} )}^2}} \right] \end{array}$

$\begin{array}{l} S(IVPFCA(\widehat{{p_1}},\widehat{{p_2}},...,\widehat{{p_n}}))\\ = \frac{1}{2}\left[ {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\widehat{\mu _{(j)}^L}{)^2} + } \right. {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\mu _{(j)}^U}} )^2}\\ - \left. {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}})} )\widehat{\upsilon _{(j)}^L}{)^2} - {{(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\upsilon _{(j)}^U}} )}^2}} \right] \end{array}$

Since $\widetilde{{p_j}} \succ \widehat{{p_j}}$, then ${\left( {\mu _j^L} \right) ^2} + {\left( {\mu _j^U} \right) ^2} - {\left( {\upsilon _j^L} \right) ^2} - {\left( {\upsilon _j^U} \right) ^2} > {\left( {\widehat{\mu _j^L}} \right) ^2} + {\left( {\widehat{\mu _j^U}} \right) ^2} - {\left( {\widehat{\upsilon _j^L}} \right) ^2} - {\left( {\widehat{\upsilon _j^U}} \right) ^2}$.

Thus, ${((\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\mu _{(j)}^L)^2} + ((\xi ({P_{(j)}})$ $- \xi ({P_{(j + 1)}}))\mu _{(j)}^U)^2 - {((\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{(j)}^L)^2}$

$- {((\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{(j)}^U)^2} > ((\xi ({P_{(j)}})$ $- \xi ({P_{(j + 1)}}))\widehat{\mu _{(j)}^L})^2 + {((\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\mu _{(j)}^U})^2}$

$- {((\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\upsilon _{(j)}^L})^2}$ $- {((\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\upsilon _{(j)}^U})^2}$

Then, ${(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\mu _{(j)}^L} )^2}+ (\sum \limits _{j = 1}^n (\xi ({P_{(j)}})$ $- \xi ({P_{(j + 1)}}))\mu _{(j)}^U )^2 - {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{(j)}^L} )^2}$

$- {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\upsilon _{(j)}^U} )^2} > (\sum \limits _{j = 1}^n (\xi ({P_{(j)}})$ $- \xi ({P_{(j + 1)}}))\widehat{\mu _{(j)}^L} )^2 + (\sum \limits _{j = 1}^n (\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\mu _{(j)}^U} )^2$

$- {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\upsilon _{(j)}^L}} )^2} - {(\sum \limits _{j = 1}^n {(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widehat{\upsilon _{(j)}^U}} )^2}$

Thus, $S(IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}})) > S(IVPFCA(\widehat{{p_1}},\widehat{{p_2}},...,\widehat{{p_n}}))$, and $IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) > IVPFCA(\widehat{{p_1}},\widehat{{p_2}},...,\widehat{{p_n}})$ is obtained. $\square$

Property 4

(Boundedness) Let $\widetilde{{p_j}} = \left( \left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] \right) \left( {j = 1,2,...,n} \right)$ be a set of IVPFNs. Let NIS be ${{{\widetilde{p}}}^ - } = \left( {\left[ {\mathop {\min }\limits _{} (\mu _j^L),\mathop {\min }\limits _{} (\mu _j^U)} \right] ,\left[ {\mathop {\max }\limits _{} (\upsilon _j^L),\mathop {\max }\limits _{} (\upsilon _j^U)} \right] } \right)$ and PIS be ${{{\widetilde{p}}}^ + } {=} \left( {\left[ {\mathop {\max }\limits _{} (\mu _j^L),\mathop {\max }\limits _{} (\mu _j^U)} \right] } \right.$, $\left. {\left[ {\mathop {\min }\limits _{} (\upsilon _j^L),\mathop {\min }\limits _{} (\upsilon _j^U)} \right] } \right)$, then ${{{\widetilde{p}}}^ - } \le IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) \le {{{\widetilde{p}}}^ + }$.

Proof

Since $\mu _j^L \ge \min (\mu _j^L)$, $\mu _j^U \ge \mathop {\min }\limits _{} (\mu _j^U)$, $\mathop {\upsilon _j^L \le \max }\limits _{} (\upsilon _j^L)$ and $\upsilon _j^U \le \mathop {\max }\limits _{} (\upsilon _j^U)$, based on Property 1 and Property 3, we can obtain ${{{\widetilde{p}}}^ - } = IVPFCA({{{\widetilde{p}}}^ - },{{{\widetilde{p}}}^ - },...,{{{\widetilde{p}}}^ - }) \le IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}})$. Similarly, this proves that $IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) \le IVPFCA({{{\widetilde{p}}}^ + },{{{\widetilde{p}}}^ + },...,{{{\widetilde{p}}}^ + }) = {{{\widetilde{p}}}^ + }$. Thus, ${{{\widetilde{p}}}^ - } \le IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) \le {{{\widetilde{p}}}^ + }$. $\square$

Remark 1

If the fuzzy measure $\xi$ degenerates to an additive measure, i.e., $\xi ({P_{(j)}}) = \sum \limits _{\widetilde{{p_{(j)}}} \in {P_{(j)}}}^{} {\xi (\widetilde{{p_{(j)}}})} ,$ $\forall {P_{(j)}} \subseteq P$, then the IVPFCA operator will be degenerated into IVPFWA operator.

Proof

Since $\xi$ is an additive measure, $\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}) = \xi (\widetilde{{p_{(j)}}})$. Then, $IVPFCA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}})$

$= \mathop \oplus \limits _{j = 1}^n (\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))\widetilde{{p_{(j)}}} = \mathop \oplus \limits _{j = 1}^n \xi (\widetilde{{p_{(j)}}})\widetilde{{p_{(j)}}} = \mathop \oplus \limits _{j = 1}^n \xi (\widetilde{{p_j}})\widetilde{{p_j}}$ $= \left( {\left[ {\sum \limits _{j = 1}^n {\xi (\widetilde{{p_j}})} \mu _j^L,\sum \limits _{j = 1}^n {\xi (\widetilde{{p_j}})\mu _j^U} } \right] ,} \right.$ $\left. {\left[ {\sum \limits _{j = 1}^n {\xi (\widetilde{{p_j}})} \upsilon _j^L,\sum \limits _{j = 1}^n {\xi (\widetilde{{p_j}})\upsilon _j^U} } \right] } \right)$, where $\xi (\widetilde{{p_{(j)}}})$ represents the weight of IVPFN $\widetilde{{p_{(j)}}}$. $\square$

Definition 10

Let $\widetilde{{p_j}} = \left( {\left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] } \right) \left( {j = 1,2,...,n} \right)$ be a set of IVPFNs and $\xi$ be a fuzzy measure on $P = \left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, then the IVPFCG operator is defined as:

$$\begin{aligned}{} & {} IVPFCG(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) = \mathop \otimes \limits _{j = 1}^n {(\widetilde{{p_{(j)}}})^{(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))}}\nonumber \\{} & {} \quad = \left( {\left[ {\prod \limits _{j = 1}^n {{{(\mu _{(j)}^L)}^{(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))}}} ,\prod \limits _{j = 1}^n {{{(\mu _{(j)}^U)}^{(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))}}} } \right] } \right. ,\nonumber \\{} & {} \quad \left. {\left[ {\prod \limits _{j = 1}^n {{{(\upsilon _{(j)}^L)}^{(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))}}} ,\prod \limits _{j = 1}^n {{{(\upsilon _{(j)}^U)}^{(\xi ({P_{(j)}}) - \xi ({P_{(j + 1)}}))}}} } \right] } \right) \nonumber \\ \end{aligned}$$

(26)

where $( \cdot )$ represents a permutation on $\left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, such that $\widetilde{{p_{(1)}}} \le \widetilde{{p_{(2)}}} \le ... \le \widetilde{{p_{(n)}}}$ and ${P_{(j)}} = \left\{ {\widetilde{{p_{(j)}}},\widetilde{{p_{(j + 1)}}},...,\widetilde{{p_{(n)}}}} \right\}$, with ${P_{(n + 1)}} = \phi$.

Remark 2

When the fuzzy measure $\xi$ reduces to an additive measure, i.e., $\xi ({P_{(j)}}) = \sum \limits _{\widetilde{{p_{(j)}}} \in {P_{(j)}}}^{} {\xi (\widetilde{{p_{(j)}}})} ,$ $\forall {P_{(j)}} \subseteq P$, then the IVPFCG operator will be degenerated into IVPFWG operator. For brevity, the proof is omitted here.

4.2.2 Interval-valued Pythagorean fuzzy Shapley aggregation operator

The developed IVPFCA and IVPFCG operators can elucidate the correlation between two adjacent coalitions, namely ${P_{(j)}}$ and ${P_{(j+1)}}$ for $j = 1,2,...,n$. To further characterize the overall interactions among various combinations of input arguments, the IVPFSA operator is proposed.

Definition 11

Given a collection of IVPFNs $\widetilde{{p_j}} = \left( {\left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] } \right) \left( {j = 1,2,...,n} \right)$ and defining $\xi$ as a fuzzy measure on $P = \left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, then the IVPFSA operator is defined as:

$$\begin{aligned} \begin{array}{lll} IVPFSA(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) = \mathop \oplus \limits _{j = 1}^n \left[ {{\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P)} \right] \widetilde{{p_{(j)}}}\\ \qquad = \left( {\left[ {\sum \limits _{j = 1}^n {({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P)} )\mu _{(j)}^L,\sum \limits _{j = 1}^n {({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P))\mu _{(j)}^U} } \right] ,} \right. \\ \qquad \left. {\left[ {\sum \limits _{j = 1}^n {({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P)} )\upsilon _{(j)}^L,\sum \limits _{j = 1}^n {({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P))\upsilon _{(j)}^U} } \right] } \right) \end{array} \end{aligned}$$

(27)

where $( \cdot )$ represents a permutation on $\left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, satisfying $\widetilde{{p_{(1)}}} \le \widetilde{{p_{(2)}}} \le ... \le \widetilde{{p_{(n)}}}$ and ${P_{(j)}} = \left\{ {\widetilde{{p_{(j)}}},\widetilde{{p_{(j + 1)}}},...,\widetilde{{p_{(n)}}}} \right\}$, with ${P_{(n + 1)}} = \phi$, and ${\varphi _{{P_{(j)}}}}(\xi ,P)$ is the generalized Shapley index of ${P_{(j)}}$ with respect to fuzzy measure $\xi$ on P.

Theorem 2

Given a set of $\widetilde{{p_j}} = \left( {\left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] } \right) \left( {j = 1,2,...,n} \right)$. $\xi$ is a fuzzy measure on $P = \left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$. Then, the aggregated value by IVPFSA operator is still an IVPFN.

The IVPFSA operator also has the properties discussed above, and since the proofs are similar to those already presented in subsection 3.2.1, the detailed process is omitted here.

Remark 3

When the fuzzy measure $\xi$ reduces to an additive measure, the IVPFSA operator will be degraded to the IVPFWA operator.

Definition 12

Let $\widetilde{{p_j}} = \left( {\left[ {\mu _j^L,\mu _j^U} \right] ,\left[ {\upsilon _j^L,\upsilon _j^U} \right] } \right) \left( {j = 1,2,...,n} \right)$ be a set of IVPFNs. $\xi$ is a fuzzy measure on $P = \left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$. Then, the interval-valued Pythagorean fuzzy Shapley geometric (IVPFSG) operator is defined as:

$$\begin{aligned} \begin{array}{ll} IVPFSG(\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}) = \mathop \otimes \limits _{j = 1}^n {(\widetilde{{p_{(j)}}})^{({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P))}}\\ \qquad = \left( {\left[ {\prod \limits _{j = 1}^n {{{(\mu _{(j)}^L)}^{({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P))}}} ,\prod \limits _{j = 1}^n {{{(\mu _{(j)}^U)}^{({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P))}}} } \right] } \right. ,\\ \qquad \left. {\left[ {\prod \limits _{j = 1}^n {{{(\upsilon _{(j)}^L)}^{({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P))}}} ,\prod \limits _{j = 1}^n {{{(\upsilon _{(j)}^U)}^{({\varphi _{{P_{(j)}}}}(\xi ,P) - {\varphi _{{P_{(j + 1)}}}}(\xi ,P))}}} } \right] } \right) \end{array} \end{aligned}$$

(28)

where $( \cdot )$ represents a permutation on $\left\{ {\widetilde{{p_1}},\widetilde{{p_2}},...,\widetilde{{p_n}}} \right\}$, satisfying $\widetilde{{p_{(1)}}} \le \widetilde{{p_{(2)}}} \le ... \le \widetilde{{p_{(n)}}}$ and ${P_{(j)}} = \left\{ {\widetilde{{p_{(j)}}},\widetilde{{p_{(j + 1)}}},...,\widetilde{{p_{(n)}}}} \right\}$, with ${P_{(n + 1)}} = \phi$.

Remark 4

If no interaction exists among elements and their combinations, $\xi$ is reduced to an additive measure. Then the IVPFSG operator is degenerated to the IVPFWG operator.

4.3 Consensus reaching based on the generalized Shapley index with IVPFS

Before arriving at a decision, it is necessary to ensure that the group consensus has reached a certain level. In this subsection, the generalized Shapley value is first introduced into the CRP, and a novel feedback strategy is proposed to guide the CRP with effective modification suggestions.

4.3.1 Consensus measurements

In this study, we measure the consensus according to the deviation between individual opinions and the collective opinion.

With the developed IVPFSA operator (subsection 3.2.2), the group evaluation can be derived as:

$$\begin{aligned} \begin{array}{lll} \widetilde{p_{ij}^{}} = \mathop \oplus \limits _{k = 1}^K ({\varphi _{{E_{(k)}}}}(\xi ,E) - {\varphi _{{E_{(k + 1)}}}}(\xi ,E))\widetilde{p_{ij}^{(k)}}\\ \qquad = \left( {\left[ {\sum \limits _{k = 1}^K {({\varphi _{{E_{(k)}}}}(\xi ,E) - {\varphi _{{E_{(k + 1)}}}}(\xi ,E))\mu _{ij}^{(k)L}} ,\sum \limits _{k = 1}^K {({\varphi _{{E_{(k)}}}}(\xi ,E) - {\varphi _{{E_{(k + 1)}}}}(\xi ,E))\mu _{ij}^{(k)U}} } \right] ,} \right. \\ \qquad \left. {\left[ {\sum \limits _{k = 1}^K {({\varphi _{{E_{(k)}}}}(\xi ,E) - {\varphi _{{E_{(k + 1)}}}}(\xi ,E))\upsilon _{ij}^{(k)L}} ,\sum \limits _{k = 1}^K {({\varphi _{{E_{(k)}}}}(\xi ,E) - {\varphi _{{E_{(k + 1)}}}}(\xi ,E))\upsilon _{ij}^{(k)U}} } \right] } \right) \end{array} \end{aligned}$$

(29)

where $\widetilde{p_{ij}^{(k)}} = \left( {\left[ {\mu _{ij}^{(k)L},\mu _{ij}^{(k)U}} \right] ,\left[ {\upsilon _{ij}^{(k)L},\upsilon _{ij}^{(k)U}} \right] } \right)$ represents the decision information from ${e_k}$ on ${{a}_i}$ over ${{c}_j}$, and $( \cdot )$ is a permutation on $\left\{ {\widetilde{p_{ij}^1},\widetilde{p_{ij}^2},...,\widetilde{p_{ij}^K}} \right\}$, such that $\widetilde{p_{ij}^{(1)}} \le \widetilde{p_{ij}^{(2)}} \le ... \le \widetilde{p_{ij}^{(K)}}$ and ${E_{(k)}} = \left\{ {\widetilde{p_{ij}^{(k)}},\widetilde{p_{ij}^{(k + 1)}},...,\widetilde{p_{ij}^{(K)}}} \right\}$, with ${E_{(K + 1)}} = \phi$, and ${\varphi _{{E_{(k)}}}}(\xi ,E)$ is the generalized Shapley index of ${E_{(k)}}$ regarding fuzzy measure $\xi$ on E.

Definition 13

(Consensus at the evaluation level) Let $\widetilde{p_{ij}^k}$ be the evaluation from ${e_k}(k = 1,2,...,K)$ to ${{a}_i}(i = 1,2,...,m)$ over ${{c}_j}(j = 1,2,...,n)$ and $\widetilde{p_{ij}^{}}$ denotes the group opinion, then the consensus at ${e_k}$’s evaluation level is defined as:

$$\begin{aligned} CL_{ij}^k = 1 - \left| {\widetilde{p_{ij}^k} - \widetilde{p_{ij}^{}}} \right| \end{aligned}$$

(30)

where $CL_{ij}^k \in [0,1]$.

Definition 14

(Consensus at the alternative level) ${e_k}$’s consensus degree $CL_i^k$ at the alternative level can be calculated as:

$$\begin{aligned} CL_i^k = \frac{1}{n}\sum \limits _{j = 1}^n {CL_{ij}^k} \end{aligned}$$

(31)

where $CL_i^k \in [0,1]$.

Definition 15

(Consensus at the expert level) ${e_k}$’s consensus degree $C{L^k}$ at the expert level can be obtained as:

$$\begin{aligned} C{L^k} = \frac{1}{m}\sum \limits _{i = 1}^m {CL_i^k} \end{aligned}$$

(32)

where $C{L^k} \in [0,1]$. A smaller divergence between ${e_k}$’s assessment and the collective opinion means a larger consensus degree.

Definition 16

(Consensus at the group level) The group consensus level GCL is then computed as:

$$\begin{aligned} GCL = \mathop \oplus \limits _{k = 1}^K ({\varphi _{{M_{(k)}}}}(\xi ,M) - {\varphi _{{M_{(k + 1)}}}}(\xi ,M))C{L^{(k)}} \end{aligned}$$

(33)

where ${\varphi _{{M_{(k)}}}}(\xi ,M)=\sum \limits _{T \subseteq M\backslash {M_{(k)}}} {\frac{{(K - \left| {{M_{(k)}}} \right| - \left| T \right| )!\left| T \right| !}}{{(K - \left| {{M_{(k)}}} \right| + 1)!}}} (\xi ({M_{(k)}} \cup T) - \xi (T))$ is the generalized Shapley index of ${M_{(k)}}$ regarding fuzzy measure $\xi$ on set M, and $( \cdot )$ is a permutation on $\left\{ {C{L^1},C{L^2},...,C{L^K}} \right\}$, such that $C{L^{(1)}} \le C{L^{(2)}} \le ... \le C{L^{(K)}}$ and ${M_{(k)}} = \left\{ {C{L^{(k)}},C{L^{(k + 1)}},...,C{L^{(K)}}} \right\}$, with ${M_{(K + 1)}} = \phi$. Therefore, it is clear that $GCL \in [0,1]$.

Next, GCL is compared with a predefined parameter $\eta$ to test whether the consensus level meets the requirements. If $GCL \ge \eta$, then the extended PROMETHEE method can be employed to rank alternatives; otherwise, the feedback strategy should be implemented to improve group consensus.

4.3.2 Feedback mechanism with maximum consensus improvement

The feedback strategy includes two steps: first, the IVPFNs that must be adjusted are identified, and second, we develop an optimization model to maximize GCL improvement.

First, the assessments that need to be modified are selected according to three consensus levels.

• (1) First, the DMs that contribute less to a sufficient GCL are identified:

  $$\begin{aligned} \textrm{EXPS} = \left\{ {k\left| {C{L^k} < \eta } \right. } \right\} \end{aligned}$$

  (34)

• (2) Then, for the DMs in EXPS , the alternatives whose consensus levels are below the threshold are identified:

  $$\begin{aligned} \textrm{ALS} = \left\{ {(k,i)\left| {k \in \textrm{EXPS} \wedge CL_i^k < \eta } \right. } \right\} \end{aligned}$$

  (35)

• (3) For the alternatives in ALS, the specific evaluations that must be modified are identified:

  $$\begin{aligned} \textrm{EVS} = \left\{ {(k,i,j)\left| {(k,i) \in \textrm{ALS} \wedge CL_{ij}^k < \eta } \right. } \right\} \end{aligned}$$

  (36)

Suppose $\widetilde{p_{ij}^k}$ is one of the identified IVPFNs and group evaluation $\widetilde{{p_{ij}}}$ is used to guide the adjustment to promote consensus, then the updated $\overline{p_{ij}^k}$ can be derived as:

$$\begin{aligned} \overline{p_{ij}^k} = \theta \widetilde{p_{ij}^k} + (1 - \theta )\widetilde{{p_{ij}}},(i,j,k \in EVS) \end{aligned}$$

(37)

where $\theta \in (0,1)$ is an adjustment parameter indicating the degree of modification.

In contrast with the traditional IDR-based model, which randomly selects the adjustment parameters, this study establishes an optimization model to determine $\theta$, which could maximize GCL improvement. The integrated CRP model is given as follows:

$$\begin{aligned} \begin{array}{l} \max :\Delta GCL = {\overline{GCL}} - GCL\\ s.t.\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \overline{p_{ij}^k} = \theta \widetilde{p_{ij}^k} + (1 - \theta )\widetilde{{p_{ij}}},i,j,k \in EVS,\\ \theta \in (0,1), \end{array}\\ {\widetilde{{p_{ij}}} = \mathop \oplus \limits _{k = 1}^K ({\varphi _{{E_{(k)}}}}(\xi ,E) - {\varphi _{{E_{(k + 1)}}}}(\xi ,E))\widetilde{p_{ij}^{(k)}},}\\ {\overline{{p_{ij}}} = \mathop \oplus \limits _{k = 1}^K ({\varphi _{{E_{(k)}}}}(\xi ,E) - {\varphi _{{E_{(k + 1)}}}}(\xi ,E))\overline{p_{ij}^{(k)}} ,}\\ {C{L^k} = \frac{1}{{mn}}\sum \limits _{i = 1}^m {\sum \limits _{j = 1}^n {\left[ {1 - \left| {\widetilde{p_{ij}^k} - \widetilde{{p_{ij}}}} \right| } \right] } ,} }\\ {\overline{C{L^k}} = \frac{1}{{mn}}\sum \limits _{i = 1}^m {\sum \limits _{j = 1}^n {\left[ {1 - \left| {\overline{p_{ij}^k} - \overline{{p_{ij}}} } \right| } \right] } ,} }\\ {GCL = \mathop \oplus \limits _{k = 1}^K ({\varphi _{{M_{(k)}}}}(\xi ,M) - {\varphi _{{M_{(k + 1)}}}}(\xi ,M))C{L^{(k)}},}\\ {{\overline{GCL}} = \mathop \oplus \limits _{k = 1}^K ({\varphi _{{M_{(k)}}}}(\xi ,M) - {\varphi _{{M_{(k + 1)}}}}(\xi ,M))\overline{C{L^{(k)}}} .} \end{array}} \right. \end{array} \end{aligned}$$

(38)

where $\overline{C{L^k}}$ and ${\overline{GCL}}$ denote the updated consensus at the expert and group levels, respectively.

Using the optimal $\theta$ determined by Lingo 17.0, the adjusted IVPFNs can be obtained. These procedures should be conducted iteratively until $GCL \ge \eta$. Then, the decision information can be reaggregated based on the IVPFSA operator to obtain the final group evaluation for the ranking process.

4.4 The extended IVPF-PROMETHEE method with the Shapley value

In the classical PROMETHEE method, the crisp number is utilized to represent the preference value between alternatives. However, the inevitable uncertainty of MCGDM problems is not well reflected and cannot be properly handled with crisp values. Additionally, the traditional method fails to adequately consider criteria interactions. To fill this gap, we incorporate the generalized Shapley index into the classical PROMETHEE method with IVPFS to improve the ranking process.

The key aim of the PROMETHEE method is to determine the preference value from the divergence between alternatives using Eq. (16). In this study, the preference values are represented with IVPFN to better reflect the inherent ambiguity in MCGDM problems.

Let $\alpha _{ts}^j = \left( {\left[ {{{\widetilde{\mu }}} (d_{ts}^{jL}),{{\widetilde{\mu }}} (d_{ts}^{jU})} \right] ,\left[ {{{\widetilde{\upsilon }}} (d_{ts}^{jL}),{{\widetilde{\upsilon }}} (d_{ts}^{jU})} \right] } \right)$ denote the IVPF preference value of alternative ${{a}_t}$ over ${{a}_s}(t,s = 1,2,...,m)$ on criteria ${{c}_j}(j = 1,2,...,n)$, where $\left[ {{{\widetilde{\mu }}} (d_{ts}^{jL}),{{\widetilde{\mu }}} (d_{ts}^{jU})} \right]$ indicates the preference degree of ${{a}_t}$ over ${{a}_s}$ and $\left[ {{{\widetilde{\upsilon }}} (d_{ts}^{jL}),{{\widetilde{\upsilon }}} (d_{ts}^{jU})} \right]$ is the degree to which ${{a}_t}$ is not preferred over ${{a}_s}$. A qualified IVPF preference value should meet the following requirements (Chen 2019):

• (1) ${{\widetilde{\mu }}} (d_{ts}^{jL}),{{\widetilde{\mu }}} (d_{ts}^{jU}),{{\widetilde{\upsilon }}} (d_{ts}^{jU}),{{\widetilde{\upsilon }}} (d_{ts}^{jL}) \in [0,1]$, $0 \le {({{\widetilde{\mu }}} (d_{ts}^{jU}))^2} + {({{\widetilde{\upsilon }}} (d_{ts}^{jU}))^2} \le 1$, $\forall d \in R$;

• (2) $d_{ts}^j \buildrel \Delta \over = \widetilde{{p_{tj}}} - \widetilde{{p_{sj}}}$, then ${{\widetilde{\upsilon }}} (d_{ts}^{jL}) = {{\widetilde{\mu }}} (d_{st}^{jL})$ and ${{\widetilde{\upsilon }}} (d_{ts}^{jU}) = {{\widetilde{\mu }}} (d_{st}^{jU})$;

• (3) When $0 \le d_{ts}^j \le q$, ${{\widetilde{\mu }}} (d_{ts}^{jL}) = {{\widetilde{\upsilon }}} (d_{ts}^{jL}) = {{\widetilde{\mu }}} (d_{ts}^{jU}) = {{\widetilde{\upsilon }}} (d_{ts}^{jU}) = r$;

• (4) When $d_{ts}^j \ge p \ge 0$, ${{\widetilde{\mu }}} (d_{ts}^{jL}) = {{\widetilde{\mu }}} (d_{ts}^{jU}) = 1$ and ${{\widetilde{\upsilon }}} (d_{ts}^{jL}) = {{\widetilde{\upsilon }}} (d_{ts}^{jU}) = 0$;

• (5) ${{\widetilde{\mu }}} (d_{ts}^{jL})$ and ${{\widetilde{\mu }}} (d_{ts}^{jU})$ increase monotonically, whereas ${{\widetilde{\upsilon }}} (d_{ts}^{jL})$ and ${{\widetilde{\upsilon }}} (d_{ts}^{jU})$ decrease monotonically as $d_{ts}^j$ increases.

Property (1) guarantees the preference degree is an IVPFN. Property (2) is reasonable because $\left[ {{{\widetilde{\mu }}} (d_{st}^{jL}),{{\widetilde{\mu }}} (d_{st}^{jU})} \right]$ indicates the preference degree of ${{a}_s}$ over ${{a}_t}$, so it must be equal to $\left[ {{{\widetilde{\upsilon }}} (d_{ts}^{jL}),{{\widetilde{\upsilon }}} (d_{ts}^{jU})} \right]$. Property (3) corresponds to the situation where the divergence between ${a}_t$ and ${a}_s$ is below the indifference threshold q, which implies the deviation is too small to show any preference to any single alternative. Additionally, r is a “blind” confidence parameter, which can be obtained based on how certain the DM is in a given situation. Property (4) indicates that when the divergence between ${{a}_t}$ and ${{a}_s}$ is above the strict preference threshold p, the DM should have an absolute preference of ${{a}_t}$ over ${{a}_s}$. Property (5) indicates that the DM’s preference would gradually increase as the divergence between ${{a}_t}$ and ${{a}_s}$ increases from q to p.

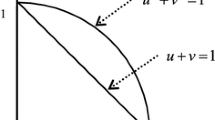
In general, there are five kinds of preference functions in PROMETHEE method: (i) the usual preference function, (ii) the quasi-preference function, (iii) the linear preference function, (iv) the linear preference function with indifference area, and (v) the Gaussian preference function (Brans et al. 1986). In this paper, (iv) is selected to obtain the preference index, which is shown in Fig. 2.

Fig. 2

Linear preference function with indifference area. a and b denote the preference and nonpreference degrees of the preference function, respectively

The IVPF-PROMETHEE method that considers the global interactions among criteria is developed as follows:

Step 1. Let ${\left[ {\widetilde{{p_{ij}}}} \right] _{m \times n}}$ be the final group decision matrix, where $\widetilde{{p_{ij}}} = \left( {\left[ {\mu _{ij}^L,\mu _{ij}^U} \right] ,\left[ {\upsilon _{ij}^L,\upsilon _{ij}^U} \right] } \right)$ is the evaluation of ${{a}_i}(i = 1,2,...,m)$ regarding ${{c}_j}(j = 1,2,...,n)$.

Step 2. The deviation between ${{a}_t}$ and ${{a}_s}(t,s = 1,2,...,m)$ over ${{c}_j}$ can be obtained as:

$$\begin{aligned} d_{ts}^{jL} = h_{tj}^L - h_{sj}^L \end{aligned}$$

(39)

$$\begin{aligned} d_{ts}^{jU} = h_{tj}^U - h_{sj}^U \end{aligned}$$

(40)

where $h_{tj}^L = \left( {\mu _{tj}^L,\upsilon _{tj}^L} \right)$, $h_{tj}^U = \left( {\mu _{tj}^U,\upsilon _{tj}^U} \right)$, and $h_{sj}^L = \left( {\mu _{sj}^L,\upsilon _{sj}^L} \right)$, $h_{sj}^U = \left( {\mu _{sj}^U,\upsilon _{sj}^U} \right)$.

Step 3. Based on the linear preference function with indifference area, the deviation is mapped into an IVPF preference value as:

$$\begin{aligned} {{\widetilde{\mu }}} (d_{ts}^{jL}) = \left\{ {\begin{array}{*{20}{l}} r&{}{0 \le d_{ts}^{jL} \le q}\\ {\frac{{(1 - r)(d_{ts}^{jL} - q)}}{{p - q}} + r}&{}{q < d_{ts}^{jL} \le p}\\ 1&{}{d_{ts}^{jL} > p} \end{array}} \right. \end{aligned}$$

(41)

$$\begin{aligned} {{\widetilde{\upsilon }}} (d_{ts}^{jL}) = \left\{ {\begin{array}{*{20}{l}} r&{}{0 \le d_{ts}^{jL} \le q}\\ {\frac{{r(p - d_{ts}^{jL})}}{{p - q}}}&{}{q < d_{ts}^{jL} \le p}\\ 0&{}{d_{ts}^{jL} > p} \end{array}} \right. \end{aligned}$$

(42)

${{\widetilde{\mu }}} (d_{ts}^{jU})$ and ${{\widetilde{\upsilon }}} (d_{ts}^{jU})$ can be determined in the same way. Since ${({{\widetilde{\mu }}} (d_{ts}^{jU}))^2} + {({{\widetilde{\upsilon }}} (d_{ts}^{jL}))^2} \le 1$, $2{(1 - r)^2}{d{_{ts}^{jU}}^2} + 2{r^2}{p^2} \le 2{(1 - r)^2}{p^2} + 2{r^2}{p^2} \le 1$. Thus, $r \in [0,\frac{1}{2}]$.

Step 4. The IVPF preference value of ${{a}_t}$ over ${{a}_s}(t,s = 1,2,...,m)$ on ${{c}_j}(j = 1,2,...,n)$ can be represented as:

$$\begin{aligned} \alpha _{ts}^j = \left( {\left[ {{{\widetilde{\mu }}} (d_{ts}^{jL}),{{\widetilde{\mu }}} (d_{ts}^{jU})} \right] ,\left[ {{{\widetilde{\upsilon }}} (d_{ts}^{jU}),{{\widetilde{\upsilon }}} (d_{ts}^{jL})} \right] } \right) \end{aligned}$$

(43)

Step 5. Considering the correlations among criteria, the overall IVPF preference value of ${{a}_t}$ over ${{a}_s}$ can be aggregated based on the developed IVPFSA operator.

$$\begin{aligned} \begin{array}{lll} \alpha _{ts}^{} = \left( {\left[ {\mu _{ts}^L,\mu _{ts}^U} \right] ,\left[ {\upsilon _{ts}^U,\upsilon _{ts}^L} \right] } \right) = \textrm{IVPFSA}(\alpha _{ts}^1,\alpha _{ts}^2,...,\alpha _{ts}^n) = \mathop \oplus \limits _{j = 1}^n \left[ {{\varphi _{{C_{(j)}}}}(\xi ,C) - {\varphi _{{C_{(j + 1)}}}}(\xi ,C)} \right] \alpha _{ts}^{(j)}\\ \qquad = \left( {\left[ {\sum \limits _{j = 1}^n {({\varphi _{{C_{(j)}}}}(\xi ,C) - {\varphi _{{C_{(j + 1)}}}}(\xi ,C)){{\widetilde{\mu }}} (d_{ts}^{(j)L})} ,\sum \limits _{j = 1}^n {({\varphi _{{C_{(j)}}}}(\xi ,C) - {\varphi _{{C_{(j + 1)}}}}(\xi ,C)){{\widetilde{\mu }}} (d_{ts}^{(j)U})} } \right] ,} \right. \\ \qquad \left. {\left[ {\sum \limits _{j = 1}^n {({\varphi _{{C_{(j)}}}}(\xi ,C) - {\varphi _{{C_{(j + 1)}}}}(\xi ,C)){{\widetilde{\upsilon }}} (d_{ts}^{(j)U})} ,\sum \limits _{j = 1}^n {({\varphi _{{C_{(j)}}}}(\xi ,C) - {\varphi _{{C_{(j + 1)}}}}(\xi ,C)){{\widetilde{\upsilon }}} (d_{ts}^{(j)L})} } \right] } \right) \end{array} \end{aligned}$$

(44)

where $( \cdot )$ is a permutation on $\left\{ {\alpha _{ts}^1,\alpha _{ts}^2,...,\alpha _{ts}^n} \right\}$, such that $\alpha _{ts}^{(1)} \le \alpha _{ts}^{(2)} \le ... \le \alpha _{ts}^{(n)}$ and ${C_{(j)}} = \left\{ {\alpha _{ts}^{(j)},\alpha _{ts}^{(j + 1)},...,\alpha _{ts}^{(n)}} \right\}$, with ${C_{(n + 1)}} = \phi$, and ${\varphi _{{C_{j}}}}(\xi ,C)$ is the generalized Shapley index of ${C_{(j)}}$ regarding fuzzy measure $\xi$ on C.

Then, the IVPF preference relation matrix R can be established as:

$$\begin{aligned} R={\left[ {\begin{array}{*{20}{c}} - &{}{\left( {\left[ {\mu _{12}^L,\mu _{12}^U} \right] ,\left[ {\upsilon _{12}^U,\upsilon _{12}^L} \right] } \right) }&{} \cdots &{}{\left( {\left[ {\mu _{1m}^L,\mu _{1m}^U} \right] ,\left[ {\upsilon _{1m}^U,\upsilon _{1m}^L} \right] } \right) }\\ {\left( {\left[ {\mu _{21}^L,\mu _{21}^U} \right] ,\left[ {\upsilon _{21}^U,\upsilon _{21}^L} \right] } \right) }&{} - &{} \cdots &{}{\left( {\left[ {\mu _{2m}^L,\mu _{2m}^U} \right] ,\left[ {\upsilon _{2m}^U,\upsilon _{2m}^L} \right] } \right) }\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\left( {\left[ {\mu _{m1}^L,\mu _{m1}^U} \right] ,\left[ {\upsilon _{m1}^U,\upsilon _{m1}^L} \right] } \right) }&{}{\left( {\left[ {\mu _{m2}^L,\mu _{m2}^U} \right] ,\left[ {\upsilon _{m2}^U,\upsilon _{m2}^L} \right] } \right) }&{} \cdots &{} - \end{array}} \right] _{m \times m}} \end{aligned}$$

(45)

Step 6. The IVPF positive and negative outranking flow of ${{a}_t}$ can be calculated as:

$$\begin{aligned} {\delta ^ + }({{a}_t})= & {} \frac{1}{{m - 1}}\mathop \oplus \limits _{s = 1,s \ne t}^m \nonumber \\ {\alpha _{ts}}= & {} \frac{1}{{m - 1}}\mathop \oplus \limits _{s = 1,s \ne t}^m \left( {\left[ {\mu _{ts}^L,\mu _{ts}^U} \right] ,\left[ {\upsilon _{ts}^U,\upsilon _{ts}^L} \right] } \right) \end{aligned}$$

(46)

$$\begin{aligned} {\delta ^ - }({{a}_t})= & {} \frac{1}{{m - 1}}\mathop \oplus \limits _{s = 1,s \ne t}^m\nonumber \\ {\alpha _{st}}= & {} \frac{1}{{m - 1}}\mathop \oplus \limits _{s = 1,s \ne t}^m \left( {\left[ {\mu _{st}^L,\mu _{st}^U} \right] ,\left[ {\upsilon _{st}^U,\upsilon _{st}^L} \right] } \right) \end{aligned}$$

(47)

Step 7. Thus, the final ranking result is obtained according to the net outranking flow, which is calculated as:

$$\begin{aligned} \delta ({{a}_t}) = S({\delta ^ + }({{a}_t})) - S({\delta ^ - }({{a}_t})) \end{aligned}$$

(48)

4.5 Flowchart and algorithm of the proposed MCGDM method

The detailed steps of the proposed method are shown in Fig. 3 and Algorithm 1 to illustrate our method more clearly.

Fig. 3

Detailed steps of the proposed MCGDM method

5 Case study

To illustrate the superiority of the proposed method, a practical problem concerning sustainable supplier evaluation is given.

5.1 Problem description

The increasing scientific and public awareness about climate change and ecological challenges has driven organizations to implement sustainable production processes. Thus, sustainable supplier selection and performance evaluations have become key components in supply chain management. This section works through a supplier evaluation problem involving a company located in Beijing, China. To achieve the sustainable development goals, this company must select the most suitable supplier from the social, economic, and environmental perspectives.

Following preliminary analyses, four suppliers comprise the alternative set $A = \left\{ {{{a}_1},{{a}_2},{{a}_3},{{a}_4}} \right\}$. A group of five experts $E = \left\{ {{e_1},{e_2},...,{e_5}} \right\}$ of the company are gathered to address the MCGDM problem. After a careful discussion, three attributes are selected to assess these suppliers: ${{c}_1}$-social responsibility; ${{c}_2}$-research and development capacity; ${{c}_3}$-green manufacturing.

5.2 Specific procedures of the proposed MCGDM method for sustainable supplier selection

Phase 1: Establish and standardize the decision matrix

Step 1. The performance of four alternatives ${{a}_i}(i = 1,2,3,4)$ are assessed by each expert ${e_k}(k = 1,2,...,5)$ considering three criteria ${{c}_j}(j = 1,2,3)$ with IVPFN $p_{ij}^k$, which is presented in Table 1.

Table 1 Original decision information from the experts

Step 2. All criteria belong to benefit type. Therefore, we do not need to normalize the decision information. Thus, ${\left[ {\widetilde{p_{ij}^k}} \right] _{4 \times 3}} = {\left[ {p_{ij}^k} \right] _{4 \times 3}}$.

Phase 2: Develop the generalized Shapley IVPF aggregation operator

Step 3. The importance of DMs is given in advance: ${\xi _1} = 0.4$, ${\xi _2} = 0.2$, ${\xi _3} = 0.3$, and ${\xi _4} = 0.4$. According to Eq. (11), $\lambda$ is obtained as -0.41. Subsequently, the $\lambda$-fuzzy measures on the expert set is computed by Eq. (10), which are given in Table 2.

Table 2 $\lambda$-fuzzy measure on the expert set E

Step 4. Then, the generalized Shapley values of the DMs are determined using Eq. (13), which gives the results in Table 3.

Table 3 Generalized Shapley values of the DMs

Step 5. Based on the developed IVPFSA operator, the initial group opinion ${\left[ {\widetilde{p_{ij}^{(0)}}} \right] _{4 \times 3}}$ can be obtained as:

$$\begin{aligned} {\left[ {\widetilde{p_{ij}^{(0)}}} \right] _{4 \times 3}} = \left[ {\begin{array}{*{20}{c}} {([0.748,0.840],[0.275,0.380])}&{}{([0.697,0.829],[0.331,0.458])}&{}{([0.429,0.566],[0.638,0.729])}\\ {([0.697,0.829],[0.331,0.458])}&{}{([0.573,0.706],[0.449,0.578])}&{}{([0.709,0.809],[0.322,0.411])}\\ {([0.453,0.595],[0.553,0.654])}&{}{([0.568,0.702],[0.483,0.607])}&{}{([0.729,0.836],[0.284,0.394])}\\ {([0.827,0.913],[0.177,0.285])}&{}{([0.541,0.694],[0.475,0.575])}&{}{([0.530,0.679],[0.535,0.629])} \end{array}} \right] \end{aligned}$$

(49)

Phase 3: Consensus-reaching process

Step 6. Let $\varepsilon = 0$, then the initial consensus at the evaluation level $CL_{ij}^{k(0)}$, at the alternative level $CL_i^{k(0)}$, and at the expert level $C{L^{k(0)}}$ can be obtained using Eqs. (30)–(32), respectively; the outcomes are compiled in Table 4 and Table 5

Then, the temporary GCL is determined using Eq. (33) as: $GC{L^{(0)}} = 0.801$.

Step 7. We set the consensus parameter as $\eta = 0.85$; therefore, the feedback strategy should be activated to promote group consensus.

Step 8. According to the identification rule, the IVPFNs need to be adjusted are determined through three levels. From Table 5, we can obtain $\textrm{EXPS} = \left\{ {1,2,3,4} \right\}$, and from Table 4, we can determine that

$$\begin{aligned}{} & {} \textrm{ALS} =\\{} & {} \left\{ {(1,2),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(4,1),(4,3)} \right\} \end{aligned}$$

$$\begin{aligned}{} & {} \textrm{EVS} =\\{} & {} \left\{ \begin{array}{llll} (1,2,1),(1,2,2),(1,2,3),(2,1,1),(2,1,2),(2,1,3),(2,2,1),\\ (2,3,2),(2,3,3),(2,4,1),(2,4,3),(3,1,1),(3,1,3),(3,2,2),\\ (3,2,3),(3,3,2),(3,3,3),(4,1,1),(4,1,3),(4,3,2),(4,3,3) \end{array} \right\} \end{aligned}$$

Table 4 The initial consensus at the evaluation level $CL_{ij}^{k(0)}$

Step 9. Based on Model (38), the optimal adjustment parameter ${\theta ^{(0)}}$ can be generated by maximizing the improvement in GCL, as ${\theta ^{(0)}} = 0.381$. Table 6 shows the adjusted IVPFNs.

Table 5 Initial consensus at the alternative level $CL_i^{k(0)}$ and at the expert level $C{L^{k(0)}}$

Step 10. The group opinion is reaggregated using the IVPFSA operator to obtain the following matrix:

$$\begin{aligned} {\left[ {\widetilde{p_{ij}^{(1)}}} \right] _{4 \times 3}} = \left[ {\begin{array}{*{20}{c}} {([0.741,0.839],[0.280,0.398])}&{}{([0.705,0.838],[0.320,0.448])}&{}{([0.426,0.540],[0.653,0.745])}\\ {([0.631,0.776],[0.417,0.526])}&{}{([0.553,0.692],[0.464,0.584])}&{}{([0.768,0.860],[0.252,0.333])}\\ {([0.453,0.595],[0.553,0.654])}&{}{([0.583,0.722],[0.468,0.587])}&{}{([0.742,0.849],[0.269,0.387])}\\ {([0.833,0.916],[0.169,0.276])}&{}{([0.541,0.694],[0.475,0.575])}&{}{([0.544,0.695],[0.522,0.615])} \end{array}} \right] \end{aligned}$$

Step 11. Based on the current group opinion ${\left[ {\widetilde{p_{ij}^{(1)}}} \right] _{4 \times 3}}$, the updated consensus levels are presented in Table 7 and Table 8.

Table 6 The modified decision information in the first iteration

Then, the group consensus is recalculated as: $GC{L^{(1)}} = 0.896 > 0.85$. Figure 4 and Fig. 5 show the improvement in consensus at the evaluation and the alternative levels, respectively. It is clear that the consensus has been improved significantly after one iteration, which indicates the effectiveness of the proposed method.

Phase 4: Rank the alternatives based on the IVPF-PROMETHEE method

Step 12. From the final group evaluation, the PIS is ${{{\widetilde{p}}}^ + } = \left( {\left[ {0.833,0.916} \right] ,\left[ {0.169,0.276} \right] } \right)$, and the NIS is ${{{\widetilde{p}}}^ - } = \left( \left[ {0.426,0.540} \right] ,\left[ {0.653,0.745} \right] \right)$. Then, the optimization model is established to derive the optimal fuzzy measures on the criteria set with incomplete weight information:

$\begin{array}{l} \max 0.205\xi ({C_1}) - 0.121\xi ({C_2}) - 0.084\xi ({C_3}) + 0.084\xi ({C_1},{C_2}) \\ \quad + 0.121\xi ({C_1},{C_3}) - 0.205\xi ({C_2},{C_3}) + 2.044\\ s.t.\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\xi (\phi ) = 0,\xi ({C_1},{C_2},{C_3}) = 1}\\ {\xi (S) \le \xi (T),\forall S,T \in \left\{ {{C_1},{C_2},{C_3}} \right\} ,S \subseteq T}\\ {\xi ({C_1}) \in [0.25,0.35]}\\ {\xi ({C_2}) \in [0.30,0.40]} \end{array}}\\ {\xi ({C_3}) \in [0.30,0.35]} \end{array}} \right. \end{array}$

Thus, we obtain $\xi \left( {{C_1}} \right) = 0.35$, $\xi \left( {{C_2}} \right) = 0.3$, $\xi \left( {{C_3}} \right) = 0.3$, $\xi \left( {{C_1},{C_2}} \right) = 1$, $\xi \left( {{C_1},{C_3}} \right) = 1$, $\xi \left( {{C_2},{C_3}} \right) = 0.3$, and $\xi \left( {{C_1},{C_2},{C_3}} \right) = 1$. For example, the sum of $\xi \left( {{C_1}} \right)$ and $\xi \left( {{C_2}} \right)$ is less than $\xi \left( {{C_1},{C_2}} \right)$, which implies that a positive synergistic interaction exists between ${C_1}$ and ${C_2}$. On the other hand, the sum of $\xi \left( {{C_2}} \right)$ and $\xi \left( {{C_3}} \right)$ is larger than $\xi \left( {{C_2},{C_3}} \right)$, which indicates that a negative synergistic interaction exists between ${C_2}$ and ${C_3}$.

Step 13. Using Eq. (13), the generalized Shapley values of $C_j$ is determined as: ${\varphi _{\left\{ {{C_1}} \right\} }}(\xi ,C) = 0.583$, ${\varphi _{\left\{ {{C_2}} \right\} }}(\xi ,C) = 0.208$, ${\varphi _{\left\{ {{C_3}} \right\} }}(\xi ,C) = 0.208$, ${\varphi _{\left\{ {{C_1},{C_2}} \right\} }}(\xi ,C) = 0.85$, ${\varphi _{\left\{ {{C_1},{C_3}} \right\} }}(\xi ,C) = 0.85$, ${\varphi _{\left\{ {{C_2},{C_3}} \right\} }}(\xi ,C) = 0.475$, and ${\varphi _{\left\{ {{C_1},{C_2},{C_3}} \right\} }}(\xi ,C) = 1$.

Step 14. The deviation between alternatives ${{a}_t}$ and ${{a}_s}(t,s = 1,2,3,4)$ over each criterion can be calculated using Eqs. (39)–(40). The linear preference function with indifference area is adopted, in which the preference values increase proportional to the divergence from indifference to strict preference. In this study, the strict preference threshold is set as $p = 0.4$, the indifference threshold is $q=0$, and the “blind” confidence parameter is $r=0.5$. Then, the IVPF preference relation of alternatives over each criterion $\alpha _{ts}^j(t,s = 1,2,3,4,j = 1,2,3)$ can be obtained via Eqs. (41)–(43), which are shown in Table 9.

Table 7 The updated consensus at the evaluation level $CL_{ij}^{k(1)}$

Step 15. Based on the developed IVPFSA operator, the overall IVPF preference relation of alternatives can be established as:

$$\begin{aligned} R = \left[ {\begin{array}{*{20}{c}} - &{}{\left( {\left[ {1,1} \right] ,\left[ {0,0} \right] } \right) }&{}{\left( {\left[ {1,1} \right] ,\left[ {0,0} \right] } \right) }&{}{\left( {\left[ {0.668,0.689} \right] ,\left[ {0.311,0.332} \right] } \right) }\\ {\left( {\left[ {0.263,0.282} \right] ,\left[ {0.716,0.753} \right] } \right) }&{} - &{}{\left( {\left[ {0.677,0.735} \right] ,\left[ {0.271,0.327} \right] } \right) }&{}{\left( {\left[ {0.780,0.844} \right] ,\left[ {0.159,0.222} \right] } \right) }\\ {\left( {\left[ {0.136,0.152} \right] ,\left[ {0.885,0.898} \right] } \right) }&{}{\left( {\left[ {0.343,0.368} \right] ,\left[ {0.642,0.676} \right] } \right) }&{} - &{}{\left( {\left[ {1,1} \right] ,\left[ {0,0} \right] } \right) }\\ {\left( {\left[ {0.321,0.337} \right] ,\left[ {0.664,0.680} \right] } \right) }&{}{\left( {\left[ {0.259,0.287} \right] ,\left[ {0.736,0.780} \right] } \right) }&{}{\left( {\left[ {0.226,0.234} \right] ,\left[ {0.835,0.843} \right] } \right) }&{} - \end{array}} \right] \end{aligned}$$

Step 16. The IVPF positive and negative outranking flow of ${{a}_i}(i = 1,2,3,4)$ is computed using Eqs. (46)–(47), and the results are presented in Table 10.

Step 17. Based on the net outranking flow, the final ranking of alternatives can be acquired as: ${{a}_1} \succ {{a}_2} \succ {{a}_3} \succ {{a}_4}$. In other words, ${{a}_1}$ is selected as the most suitable supplier.

5.3 Comparison and discussions

To further demonstrate the effectiveness of the proposed method, a comprehensive comparison with several studies is conducted. First, qualitative comparisons are made from the following aspects: (i) the representation and fusion of decision information, (ii) the correlation among criteria and DMs, (iii) the consensus-reaching strategy, (iv) and the ranking method. The details are presented in Table 11.

Few studies on CRP for MCGDM have considered various correlations among criteria (Long et al. 2021; Du et al. 2021; Cheng et al. 2018), which could lead to inaccurate results, while in our method, a novel IVPFSA operator is defined based on the generalized Shapley value to capture the global relationships among input arguments, thereby comprehensively representing vague information. When the criteria or DMs are independent, the IVPFSG operator can reduce to the IVPFWG operator (Haktanır and Kahraman 2019), which verifies that this method can handle MCGDM problems more flexibly.

Additionally, unlike studies that used IDR-based methods (Du et al. 2021) or the optimization models (e.g., minimum cost model (Cheng et al. 2018), minimum adjustment model (Long et al. 2021)) as consensus-reaching strategies, an integrated approach has been proposed herein. Specifically, the adjustment parameter in the direction rule (Eq. (37)) is obtained by maximizing the improvement in group consensus, which could significantly enhance the consensus efficiency.

Compared with utility theory-based approaches, the PROMETHEE method considers dominance relations to determine how much an alternative is preferred over the others, which could retain the original information to a larger extent. The proposed method extends the classical PROMETHEE into the IVPF context to better model the uncertainty inherent to the MCGDM problem. Furthermore, the preference function and the positive and negative outranking flows are all characterized by IVPFNs. To our knowledge, our work is the first to incorporate the generalized Shapley value into the PROMETHEE method to address MCGDM problems with IVPFS.

Following qualitative comparisons from multiple aspects, a quantitative comparison is also conducted with the same example. Since the evaluation structure varies among different methods, some transformation should be made to suit different conditions. The IVPFN can be converted into different evaluation structures as follows: (i) PFS—given the IVPFN $\widetilde{p_{ij}^k} = \left( {\left[ {\mu _{ij}^{kL},\mu _{ij}^{kU}} \right] ,\left[ {\upsilon _{ij}^{kL},\upsilon _{ij}^{kU}} \right] } \right)$, the converted PFN can be obtained as $\widetilde{\alpha _{ij}^k} = \left( {\frac{{\mu _{ij}^{kL} + \mu _{ij}^{kU}}}{2},\frac{{\upsilon _{ij}^{kL} + \upsilon _{ij}^{kU}}}{2}} \right)$; (ii) numerical values—this transformation can be achieved by applying the score function given in Eq. (6); (iii) BPA—the closeness index of IVPFN $\widetilde{p_{ij}^k}$ can be denoted as $\kappa (\widetilde{p_{ij}^k}) = \frac{{d(\widetilde{p_{ij}^k},{{{{\widetilde{p}}}}^ - })}}{{d(\widetilde{p_{ij}^k},{{{{\widetilde{p}}}}^ - }) + d(\widetilde{p_{ij}^k},{{{{\widetilde{p}}}}^ + })}}$, then the converted BPA can be derived as $m_j^k({A_i}) = \frac{{\kappa (\widetilde{p_{ij}^k})}}{{\sum \limits _{i = 1}^m {\kappa (\widetilde{p_{ij}^k})} }}$. First, three typical methods with CRP (Long et al. 2021; Du et al. 2021; Cheng et al. 2018) are selected to compare the information deviation with the proposed method and it can be determined as:

$$\begin{aligned} InD{e^k} = \frac{1}{{mn}}\sum \limits _{i = 1}^m {\sum \limits _{j = 1}^n {\left| {\widetilde{p_{ij}^k} - \widetilde{{p_{ij}}}} \right| } } \end{aligned}$$

(50)

where $\widetilde{p_{ij}^k}(k = 1,2,3,4)$ and $\widetilde{{p_{ij}}}$ denote the initial individual evaluation and the adjusted group assessment, respectively. Figure 6 shows that our approach has the ability to retain the individual decision information to the greatest extent in consensus-reaching process, which reduces the loss of information. Therefore, our approach can more effectively preserve the initial decision information.

Table 8 Updated consensus at the alternative level $CL_i^{k(1)}$ and at the expert level $C{L^{k(1)}}$

Fig. 4

Improvements in $CL_{ij}^k(i = 1,2,3,4,j = 1,2,3)$ regarding each expert ${e_k}(k = 1,2,3,4)$ are shown in (a–d), respectively

Fig. 5

Improvement in consensus at the alternative level $CL_i^k(i,k = 1,2,3,4)$

Table 9 IVPF preference relation of alternatives over each criterion

Table 10 Positive, negative, and net outranking flow of alternatives

Table 11 Qualitative comparisons of various published methods

Fig. 6

Information deviation of different methods regarding each DM

Table 12 Quantitative comparison of this work with previously published methods

Then, the overall ranking results of different methods are presented in Table 12. It is clear that the same best and worst alternatives are generated, which supports the effectiveness of the proposed method. However, there are some differences in the ranking order. The main reason is that previous methods (Chen 2019; Haktanır and Kahraman 2019) ignore the correlative characteristics among criteria and DMs, whereas the proposed method considers the positive or negative influences contained in the fuzzy measure. It can be concluded that our method is more reasonable and effective.

However, it is not convincing enough to demonstrate the effectiveness of our method with a single calculation. Therefore, we conduct the following simulation experiment with the same case in Section 5. MATLAB is used to generate 10000 sets of criteria weights randomly. Afterward, these six methods in Table 12 are applied to determine the alternative ranking. Then, we analyze the proportion of each alternative in the final ranking under these methods, which is shown in Fig. 7.

Fig. 7

a, b, c, d, e, and f represent the percentages of alternatives in the highest rank in Chen (2019), Fei and Feng (2021), Long et al. (2021), Bakioglu and Atahan (2021), Haktanır and Kahraman (2019), and the proposed method, respectively

We can observe from Fig. 7 that the largest proportion of alternatives with the highest ranking determined by each method is $a_1$, which further illustrates the effectiveness of our method. Besides, we also found that in the proposed method, the alternative with the largest percentage has an obvious advantage: the percentage of $a_1$ in the highest rank in our method is 89%, which is larger than the percentages obtained with other methods (i.e., 78% in Chen (2019), 73% in Fei and Feng (2021), 81% in Long et al. (2021), 77% in Bakioglu and Atahan (2021), and 68% in Haktanır and Kahraman (2019)). As a result, compared with other methods, our approach can better distinguish the ranking of alternatives.

6 Conclusion

This paper develops an extended IVPF-PROMETHEE method based on the generalized Shapley value with a consensus-reaching process for MCGDM problems. The novelty and implications of this work are summarized as follows:

• (1) IVPFS is utilized to handle vague and uncertain decision information. The generalized Shapley value is firstly extended into the IVPF environment, which can comprehensively reflect the importance of input arguments and globally depict the mutual influences among them.

• (2) The weights of criteria and DMs are determined using the generalized Shapley value by simultaneously considering the importance of the element itself and the overall influence from the other elements; this allows flexible characterization of realistic MCGDM situations.

• (3) The classical operators of IVPFS are built on the principle of nonnegative additive set function. However, ignoring the interaction effect in the aggregation process may lead to confusing results. Thus, IVPFCA and IVPFSA operators are developed to reflect the global importance of the factors and the interactions among them.

• (4) We establish an integrated consensus-reaching model by integrating the IDR-based approach and the optimization model. Ultimately, the maximum consensus improvement can be achieved to reduce the conflicts within the group.

• (5) For the first time, the generalized Shapley index and IVPFS are introduced into the classical PROME-THEE method to overcome the limitations of additive measures and to better handle imprecise decision information.

This paper describes the construction of a comprehensive framework on CRP for MCGDM problems. The proposed method could be tuned further to address problems in more complex situations, such as large-scale MCGDM problems. Furthermore, owing to the diverse backgrounds of the experts, they tend to utilize different evaluation structures to represent their opinions. Therefore, it would be interesting to study heterogeneous MCGDM problems in subsequent research.