1 Introduction

Mixed convection boundary layer flow and heat transfer have attracted much attention in the literature due to their wide applications in many industrial engineering (Ahmad et al. 2009; Rosali et al. 2016), such as solar central receivers, heat exchangers, geothermal systems, drying processes and food industries, etc. Rashad et al. (2013) studied steady mixed convection boundary-layer flow past a horizontal circular cylinder embedded in a porous medium filled with a nanofluid. Mustafa (2017) provided an analytical treatment for mixed convection flow of an electrically conducting Oldroyd-B fluid adjacent to a vertical stretchable surface. Othman et al. (2017) investigated mixed convection boundary layer flow near stagnation point on impermeable vertical stretching/shrinking surface in nanofluid. Ghalambaz et al. (2019) discussed mixed convection boundary layer flow and thermal behavior of nano-encapsulated phase change materials dispersed in a liquid over a vertical flat plate. Singh et al. (2019) analyzed the mixed convection water boundary layer flows over moving vertical plate with variable viscosity and Prandtl number.

In recent years, the spatial fractional derivative has been frequently applied to describe the mechanism of deformation and characterize nonlocal continua. Lazopoulos (2006) introduced fractional calculus into the continuum mechanics area describing nonlocal constitutive relations. Carpinteri et al. (2011) provided a mechanical interpretation to nonlocal fractional elastic model and applied it to study the strain field in a finite bar. Pan et al. (2016a, 2018) studied the convective flow and heat transfer of nanofluids with spatial fractional derivatives in disordered porous media. Yang et al. (2018, 2020) proposed fractional seepage model and spatiotemporal imbibition model for non-Newtonian fluid via spatial fractional derivative. Belevtsov and Lukashchuk (2018) studied the symmetry properties of the space-fractional filtration equation with the Riesz potential through a naturally fractured porous medium. Liu et al. (2019a, b) investigated the space-fractional anomalous advection–diffusion through a porous medium. Chang et al. (2019) proposed and evaluated a spatial fractional Darcy’s law model for the flow rate of fluids in natural heterogeneous oil/gas reservoirs. Płociniczak (2019) considered a nonlinear and spatially nonlocal PDE modeling moisture evolution in a porous medium. Li and Liu (2020) investigated viscoelastic fluid over a non-uniform permeable surface employing a fractional derivative model. Moreover, finite volume method has been employed to deal with space fractional derivative problem in many fluid fields, such as fractional diffusion equations (Liu et al. 2014; Fu et al. 2019a, b) and fractional advection–dispersion equation (Hejazi et al. 2014; Li et al. 2017).

Thus far, there are no researches related to investigating mixed convection boundary layer flow and heat transfer of viscoelastic fluid by fractional finite volume method. The mixed convection boundary layer flow has nonlinear convection terms, flow instability in the inlet boundary and coupled transport characteristic with heat transfer. This work purposes to develop the fractional finite volume method to solve these problems. Spatial fractional derivatives are employed in the constitutive relation and modified Fourier’s law. Nonlinear and coupled boundary layer governing equations are formulated and solved by fractional finite volume method, which are discretized by the shifted Grünwald-Letnikov formula and linear processing. The stability and convergence of the numerical scheme are proved, further the numerical results are validated by comparison with exact solutions of a special case. Effects of fractional derivative parameters and other involved parameters on velocity and temperature fields are presented graphically and discussed in detail.

2 Mathematical formulation

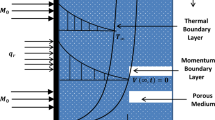
Consider unsteady mixed convection flow of an incompressible viscoelastic fluid over a flat plate. The x-coordinate is measured along the surface of the plate, and y-coordinate is normal to the surface, which is shown in Fig. 1. The fluid and plate are at the same temperature \(T_{\infty }\) initially. After a time \(t > 0\), the surface of the plate is maintained at a constant temperature \(T_{w}\). The velocity of the uniform free stream flowing vertically upwards over the plate is \(U_{\infty }\). It is assumed that the Boussinesq approximation is valid and thermal dispersion effect is neglected. Under these assumptions, the boundary layer governing equations are:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$
(1)
$$ \frac{\partial u}{{\partial t}} + \frac{\partial }{\partial x}\left( {uu} \right) + \frac{\partial }{\partial y}\left( {vu} \right) = \frac{1}{\rho }\frac{{\partial \sigma_{xy} }}{\partial y} + g\beta_{f} \left( {T - T_{\infty } } \right), $$
(2)
$$ \frac{\partial T}{{\partial t}} + \frac{\partial }{\partial x}\left( {uT} \right) + \frac{\partial }{\partial y}\left( {vT} \right) = - \frac{1}{{\rho c_{p} }}\frac{\partial Q}{{\partial y}}. $$
(3)
Fig. 1
figure 1

Physical model and coordinate system

Full size image

subject to the initial and boundary conditions:

$$ t \le 0: \, u = U_{\infty } , \, v = 0, \, T = T_{\infty } ;\;t > 0:\left\{ \begin{gathered} u = U_{\infty } , \, T = T_{\infty } {\text{ at }}x = 0; \hfill \\ u = 0, \, v = 0, \, T = T_{w} {\text{ at }}y = 0; \hfill \\ u \to U_{\infty } , \, T \to T_{\infty } {\text{ as }}y \to \infty . \hfill \\ \end{gathered} \right. $$

where u and v are the velocity components in the x- and y- direction, respectively, \(\rho\) is the density of the fluid, \(\sigma_{xy}\) is the shear stress component, g is the acceleration due to gravity, \(\beta_{f}\) is the thermal expansion coefficient, \(c_{p}\) is the specific heat capacity at constant pressure and Q is the heat flux.

The constitutive relation and modified Fourier’s law with spatial fractional derivatives are employed for the viscoelastic fluid. The Riemann–Liouville fractional derivative is defined as the derivative of the fractional integral (Kilbas et al. 2006), which has been quite frequently used in the description of viscoelasticity in non-Newtonian fluid flow by replacing the time derivative of an integer order (Makris et al. 1993; Tan et al. 2003; Yin and Zhu 2006; Fetecau et al. 2009; Pan et. al 2016b; Li and Liu 2020). Thus, the fractional relationship between the shear stress component and velocity gradient is given by:

$$ \sigma_{xy} = \tilde{\mu }\frac{{\partial^{\alpha } u}}{{\partial y^{\alpha } }}, $$
(4)

where \(\tilde{\mu }\) is the generalized dynamic viscosity with unit of \({\text{kg}} \cdot {\text{m}}^{\alpha - 2} \cdot {\text{s}}^{ - 1}\), \(\alpha\) is the velocity fractional derivative parameter with the Riemann–Liouville definition (Podlubny 1999):

$$ \frac{{\partial^{\alpha } }}{{\partial y^{\alpha } }}f(y) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{\partial }{\partial y}\int_{0}^{y} {\left( {y - \eta } \right)^{ - \alpha } } f(\eta ){\text{d}}\eta , \, 0 < \alpha < 1, $$
(5)

where \( \Gamma ()\) is the gamma function. The order of \(\alpha\) characterizes the dependence of viscoelastic moduli on the direction of shear at neighboring material points (Hanyga and Seredyńska 2012).

Similarly, the modified Fourier’s law with space-nonlocality is based on power kernels resulting in fractional differential operators in space coordinates (Povstenko 2015):

$$ Q = - \tilde{k}\frac{{\partial^{\beta } T}}{{\partial y^{\beta } }}, $$
(6)

where \(\tilde{k}\) is the generalized thermal conductivity with a unit of \({\text{J}} \cdot {\text{m}}^{\beta - 2} \cdot {\text{s}}^{ - 1} \cdot {\text{K}}^{ - 1}\), \(\beta\) is the temperature fractional derivative parameter that accounts for anomalous heat transport in nonlocal spatial distribution (Sumelka 2014). The constitutive relation and heat conduction law with spatial fractional derivatives are not local differential function but are affected by global field gradient in the nearby layers or even faraway layers from the particular single point.

Equations (1)–(3) are nondimensionalized by the following dimensionless variables:

$$ \begin{gathered} x^{*} = \frac{x}{{{\text{Re}} \cdot L}} = \frac{{x\tilde{\upsilon }_{f} }}{{U_{\infty } \cdot L^{\alpha + 1} }};\quad y^{*} = \frac{y}{L};\quad u^{*} = \frac{u}{{U_{\infty } }}; \quad v^{*} = {\text{Re}} \cdot \frac{v}{{U_{\infty } }} = \frac{{v \cdot L^{\alpha } }}{{\tilde{\upsilon }_{f} }}; \hfill \\ t^{*} = \frac{{t\tilde{\upsilon }_{f} }}{{L^{\alpha + 1} }};\quad\theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}; \quad {\text{Re}} = \frac{{U_{\infty } L^{\alpha } }}{{\tilde{\upsilon }_{f} }};\quad \lambda = \frac{{{\text{Gr}}}}{{{\text{Re}}}};\quad {\text{Gr}} = \frac{{g\beta_{f} \left( {T_{w} - T_{\infty } } \right)L^{2\alpha + 1} }}{{\tilde{\upsilon }_{f}^{2} }};\quad {\text{Pr}} = \frac{{\tilde{\mu }c_{p} }}{{\tilde{k}L^{\alpha - \beta } }} \hfill \\ \end{gathered} $$

where \(\tilde{\upsilon }_{f} = \tilde{\mu }/\rho\) is the generalized kinematic viscosity (\(m^{\alpha + 1} \cdot s^{ - 1}\)), \(L\) is the length of the plate, Re is the Reynolds number, Gr is the Grashof number, \(\lambda\) is the mixed convection parameter that \(\lambda > 0\) is for a heated plate and \(\lambda < 0\) for a cooled plate, respectively, Pr is the Prandtl number. It deserves to be mentioned that the x-coordinate and vertical velocity are nondimensionalized by a factor of Re, hence both coordinates and velocity components are of the same order of magnitude.

Dimensionless governing equations are obtained (for simplicity, the dimensionless mark “*” is omitted hereafter):

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$
(7)
$$\frac{\partial u}{{\partial t}} + \frac{\partial }{\partial x}\left( {uu} \right) + \frac{\partial }{\partial y}\left( {vu} \right) = \frac{\partial }{\partial y}\left( {\frac{{\partial^{\alpha } u}}{{\partial y^{\alpha } }}} \right) + \lambda \theta ,$$
(8)
$$ \frac{\partial \theta }{{\partial t}} + \frac{\partial }{\partial x}\left( {u\theta } \right) + \frac{\partial }{\partial y}\left( {v\theta } \right) = \frac{1}{{{\text{Pr}}}}\frac{\partial }{\partial y}\left( {\frac{{\partial^{\beta } \theta }}{{\partial y^{\beta } }}} \right). $$
(9)

The dimensionless initial and boundary conditions become:

\(t \le 0: \, u = 1, \, v = 0, \, \theta = 0; \quad t > 0:\left\{ \begin{array}{ll} u = 1, \, \theta = 0 & {\text{ at }}x = 0; \hfill \\ u = 0, \, v = 0, \, \theta = 1& {\text{ at }}y = 0; \hfill \\ u \to 1, \, \theta \to 0 & {\text{ as }}y \to \infty . \hfill \\ \end{array} \right.\)

3 Numerical technique

In this section, we develop the finite volume method combined with the shifted Grünwald-Letnikov formula to solve Eqs. (7)–(9). The computational domain is divided into discrete control volumes and Fig. 2 shows the collocated grid system. P denotes the general nodal point, then the neighbor points and side faces of the control volume are referred and described in the figure. The space step sizes in the x and y directions are identified by \(\Delta x\) and \(\Delta y\), respectively, while the time step is denoted as \(\Delta t\). Note \(A_{w} = A_{e} = \Delta y\), \(A_{n} = A_{s} = \Delta x\), \(\Delta V = \Delta x \cdot \Delta y\), where \(A\) represents the face area of the control volume and \(\Delta V\) is its volume. We define \(t_{k} = k \cdot \Delta t\), \(k = 0,1,2, \ldots ,R\); \(x_{i} = i \cdot \Delta x\), \(i = 0,1,2, \ldots ,X\); \(y_{j} = j \cdot \Delta y\), \(j = 0,1,2, \ldots ,Y\). The numerical solution at nodal point P is denoted as \(\left( {u_{i,j}^{k} ,v_{i,j}^{k} ,\theta_{i,j}^{k} } \right)\).

Fig. 2
figure 2

The grid system of the control volume at nodal point P

Full size image

To yield the discretized equation at nodal point P, the integration of Eq. (8) over a control volume augmented with a further integration over a finite time step is carried out as:

$$ \begin{gathered} \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial u}{{\partial t}}} } {\text{d}}V{\text{d}}t + \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial }{\partial x}\left( {uu} \right){\text{d}}V{\text{d}}t} } + \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial }{\partial y}\left( {vu} \right)} } {\text{d}}V{\text{d}}t \hfill \\ = \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial }{\partial y}\left( {\frac{{\partial^{\alpha } u}}{{\partial y^{\alpha } }}} \right){\text{d}}V{\text{d}}t} } + \int_{t}^{t + \Delta t} {\int_{\Delta V} {\lambda \theta {\text{ d}}V{\text{d}}t} } \hfill \\ \end{gathered} $$
(10)

The time term is approximated by first-order backward difference scheme:

$$ \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial u}{{\partial t}}} } {\text{d}}V{\text{d}}t = \int_{\Delta V} {\int_{t}^{t + \Delta t} {\frac{\partial u}{{\partial t}}{\text{d}}t{\text{d}}V = \left( {u_{i,j}^{k} - u_{i,j}^{k - 1} } \right) \cdot \Delta V} } , $$
(11)

The volume integrals of the convective terms are substituted by surface integrals and the first-order upwind difference format is introduced to calculate velocities on the control volume faces, where the first velocity in each parenthesis is linearized by the value of last time step at \(t_{k - 1}\). These results give Eqs. (12)–(13) as follows:

$$\int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial }{\partial x}\left( {uu} \right){\text{d}}V{\text{d}}t} } = \left[ {\left( {uAu} \right)_{e}^{k} - \left( {uAu} \right)_{w}^{k} } \right] \cdot \Delta t = \left( {u_{i,j}^{k - 1} u_{i,j}^{k} - u_{i - 1,j}^{k - 1} u_{i - 1,j}^{k} } \right) \cdot \Delta y\Delta t,$$
(12)
$$\int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial }{\partial y}\left( {vu} \right)} } {\text{d}}V{\text{d}}t = \left[ {\left( {vAu} \right)_{n}^{k} - \left( {vAu} \right)_{s}^{k} } \right] \cdot \Delta t = \left( {v_{i,j}^{k - 1} u_{i,j}^{k} - v_{i,j - 1}^{k - 1} u_{i,j - 1}^{k} } \right) \cdot \Delta x\Delta t,$$
(13)

To discretize the Riemann–Liouville derivative in the velocity diffusion term on the interface of the control volume, the shifted Grünwald–Letnikov formula is employed as \(0 < \alpha < 1\) for \(u = 0\) at \(y = 0\) (Liu et al. 2004):

$$ \frac{{\partial^{\alpha } u\left( {x_{i} ,y_{j - 1/2} ,t_{k} } \right)}}{{\partial y^{\alpha } }} = \frac{1}{{\Delta y^{\alpha } }}\sum\limits_{I = 0}^{j} {g_{I}^{(\alpha )} u\left( {x_{i} ,y_{j - I} ,t_{k} } \right)} + O\left( {\Delta y} \right), $$
(14)
$$ \frac{{\partial^{\alpha } u\left( {x_{i} ,y_{j + 1/2} ,t_{k} } \right)}}{{\partial y^{\alpha } }} = \frac{1}{{\Delta y^{\alpha } }}\sum\limits_{I = 0}^{j + 1} {g_{I}^{(\alpha )} u\left( {x_{i} ,y_{j + 1 - I} ,t_{k} } \right)} + O\left( {\Delta y} \right), $$
(15)

where \(g_{0}^{(\alpha )} = 1, \, g_{I}^{(\alpha )} = \left( { - 1} \right)^{I} \frac{{\alpha \left( {\alpha - 1} \right) \cdots \left( {\alpha - I + 1} \right)}}{I!}, \, I = 1,2, \ldots ,N.\) Thus, the integral of the spatial fractional derivative yields:

$$ \begin{gathered} \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial }{\partial y}\left( {\frac{{\partial^{\alpha } u}}{{\partial y^{\alpha } }}} \right){\text{d}}V{\text{d}}t} } = \Delta t \cdot \left\{ {\left[ {A\left( {\frac{{\partial^{\alpha } u}}{{\partial y^{\alpha } }}} \right)} \right]_{n}^{k} - \left[ {A\left( {\frac{{\partial^{\alpha } u}}{{\partial y^{\alpha } }}} \right)} \right]_{s}^{k} } \right\} \hfill \\ = \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\left( {\sum\limits_{I = 0}^{j + 1} {g_{I}^{(\alpha )} u_{i,j + 1 - I}^{k} - \sum\limits_{I = 0}^{j} {g_{I}^{(\alpha )} u_{i,j - I}^{k} } } } \right) = \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0}^{j + 1} {g_{I}^{(\alpha + 1)} u_{i,j + 1 - I}^{k} } \hfill \\ \end{gathered} $$
(16)

The source term is approximated by values of two consecutive time steps:

$$ \int_{t}^{t + \Delta t} {\int_{\Delta V} {\lambda \theta \, dVdt} } = \frac{\lambda \Delta V\Delta t}{2}\left( {\theta_{i,j}^{k} + \theta_{i,j}^{k - 1} } \right), $$
(17)

At last, the iteration equation at the nodal point P is obtained:

$$ a_{P} u_{i,j}^{k} = a_{W} u_{i - 1.j}^{k} + a_{S} u_{i,j - 1}^{k} + \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{j + 1} {g_{I}^{{\left( {\alpha + 1} \right)}} } u_{i,j + 1 - I}^{k} + \Delta V \cdot u_{i,j}^{k - 1} + S_{P} $$
(18)

where \(a_{P} = \Delta V + \Delta y\Delta t \cdot u_{i,j}^{k - 1} + \Delta x\Delta t \cdot v_{i,j}^{k - 1} - \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}g_{1}^{{\left( {\alpha + 1} \right)}}\), \(a_{W} = \Delta y\Delta t \cdot u_{i - 1,j}^{k - 1}\), \(a_{S} = \Delta x\Delta t \cdot v_{i,j - 1}^{k - 1}\), \(S_{P} = \frac{\lambda \Delta V\Delta t}{2}\left( {\theta_{i,j}^{k} + \theta_{i,j}^{k - 1} } \right)\).

Similar process is dealt with the temperature terms in Eq. (9). It is worth mentioning that the temperature boundary condition is \(\theta = 1\) at \(y = 0\), the truncation error of the shifted Grünwald–Letnikov formula for temperature fractional derivative is \(O\left( {\Delta y} \right) + O(1)\). Further, the difference of the fractional derivatives in the north and south side faces weakens the truncation error of the non-zero boundary. Thus, the integral of the temperature diffusion term with fractional derivative is dealt similar to Eq. (16).

The vertical velocity is solved by integration of the community Eq. (7) in the following:

$$ \begin{aligned} 0 &= \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial u}{{\partial x}}} } {\text{d}}V{\text{d}}t + \int_{t}^{t + \Delta t} {\int_{\Delta V} {\frac{\partial v}{{\partial y}}} } {\text{d}}V{\text{d}}t \hfill \\ &= \frac{\Delta t}{2}\left[ {\left( {uA} \right)_{n}^{k} - \left( {uA} \right)_{s}^{k} + \left( {uA} \right)_{n}^{k - 1} - \left( {uA} \right)_{s}^{k - 1} } \right] \\ & \quad + \frac{\Delta t}{2}\left[ {\left( {vA} \right)_{e}^{k} - \left( {vA} \right)_{w}^{k} + \left( {vA} \right)_{e}^{k - 1} - \left( {vA} \right)_{w}^{k - 1} } \right] \hfill \\ \end{aligned} $$
(19)
$$ v_{i,j}^{k} = v_{i,j - 1}^{k} + v_{i,j - 1}^{k - 1} - v_{i,j}^{k - 1} + \frac{\Delta y}{{\Delta x}}\left( {u_{i - 1,j}^{k} - u_{i,j}^{k} + u_{i - 1,j}^{k - 1} - u_{i,j}^{k - 1} } \right). $$
(20)

4 Theoretical analysis of the finite volume method

4.1 Stability

The stability of the iteration Eq. (18) by finite volume method will be discussed in the following section with the uniform boundary conditions \(u_{0,j}^{k} = u_{X,j}^{k} = u_{i,0}^{k} = u_{i,Y}^{k} = 0\), \(k = 0,1,2, \cdots ,R\). The numerical solution of Eq. (18) is denoted as \(u_{i,j}^{k}\). The source term \(\lambda \theta\) in Eq. (8) is denoted as \(f_{i,j}^{k}\), which represents the function value of \(f\left( {x,y,t} \right)\). Let \(\left\| {u^{k} } \right\|_{\infty } = \max_{1 \le i \le X - 1;1 \le j \le Y - 1} \left| {u_{i,j}^{k} } \right|\) and \(\left\| f \right\|_{\infty } = \max_{0 \le i \le X;0 \le j \le Y;0 \le k \le R} \left| {f_{i,j}^{k} } \right|\).

Lemma 1

Assume that \(u_{i,j}^{k} \ge 0\) and \(v_{i,j}^{k} \ge 0\). If \(\left| {u_{{i_{x} ,j_{y} }}^{k} } \right| = \max_{1 \le i \le X - 1;1 \le j \le Y - 1} \left| {u_{i,j}^{k} } \right|\), then \(\left\| {u^{k} } \right\|_{\infty } \le \left| {u_{{i_{x} ,j_{y} }}^{k - 1} + f_{{i_{x} ,j_{y} }}^{k} \cdot \Delta t} \right|\).

Proof

By Eq. (20), we obtain at the \(t_{k - 1}\) time step:

$$\Delta y \cdot u_{i,j}^{k - 1} - \Delta y \cdot u_{i - 1,j}^{k - 1} + \Delta x \cdot v_{i,j}^{k - 1} - \Delta x \cdot v_{i,j - 1}^{k - 1} = 0$$
(20)

,

Using \(\sum\limits_{I = 0}^{j + 1} {g_{I}^{{\left( {\alpha + 1} \right)}} } < 0\), \(g_{1}^{{\left( {\alpha + 1} \right)}} = - \alpha < 0\), \(g_{I}^{{\left( {\alpha + 1} \right)}} > 0 \quad \left( {I = 0,2,3, \ldots } \right)\), we have

$$ \begin{aligned} \left\| {u^{k} } \right\|_{\infty } & = \left| {u_{{i_{x} ,j_{y} }}^{k} } \right| \hfill \\& \le \frac{1}{\Delta V}\left( {a_{P} - a_{W} - a_{S} - \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{{j_{y} + 1}} {g_{I}^{{\left( {\alpha + 1} \right)}} } } \right)\left| {u_{{i_{x} ,j_{y} }}^{k} } \right| \hfill \\ \end{aligned} $$
$$ \begin{gathered} \le \frac{1}{\Delta V}\left( {a_{P} \left| {u_{{i_{x} ,j_{y} }}^{k} } \right| - a_{W} \left| {u_{{i_{x} - 1,j_{y} }}^{k} } \right| - a_{S} \left| {u_{{i_{x} ,j_{y} - 1}}^{k} } \right| - \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{{j_{y} + 1}} {g_{I}^{{\left( {\alpha + 1} \right)}} } u_{{i_{x} ,j_{y} + 1 - I}}^{k} } \right) \hfill \\ \le \frac{1}{\Delta V}\left| {a_{P} u_{{i_{x} ,j_{y} }}^{k} - a_{W} u_{{i_{x} - 1,j_{y} }}^{k} - a_{S} u_{{i_{x} ,j_{y} - 1}}^{k} - \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{{j_{y} + 1}} {g_{I}^{{\left( {\alpha + 1} \right)}} } u_{{i_{x} ,j_{y} + 1 - I}}^{k} } \right| \hfill \\ = \frac{1}{\Delta V}\left| {\Delta V \cdot u_{{i_{x} ,j_{y} }}^{k - 1} + S_{P} } \right| = \left| {u_{{i_{x} ,j_{y} }}^{k - 1} + f_{{i_{x} ,j_{y} }}^{k} \cdot \Delta t} \right|. \hfill \\ \end{gathered} $$

Hence, Lemma 1 is proved.

Remark 1

In the present physical problem, the horizontal velocity is positive, while the value of vertical velocity depends on \(\lambda\). When \(\lambda\) is large enough, the vertical velocity is negative.

Theorem 1

Assume that \(u_{i,j}^{k} \ge 0\) and \(v_{i,j}^{k} \ge 0\). Then, \(\mathop {\max }\nolimits_{1 \le J \le k} \left\| {u^{J} } \right\|_{\infty } \le \left\| {u^{0} } \right\|_{\infty } + k\left\| f \right\|_{\infty } \cdot \Delta t\). Moreover, \(\left\| {u^{k} } \right\|_{\infty } \le \left\| {u^{0} } \right\|_{\infty } + k\left\| f \right\|_{\infty } \cdot \Delta t\), \(k = 1,2,3, \ldots ,R\).

Proof

Let \(\left| {u_{{i_{x} ,j_{y} }}^{k} } \right| = \max_{1 \le i \le X - 1;1 \le j \le Y - 1} \left| {u_{i,j}^{k} } \right|\). According to Lemma 1, we can obtain.

$$\left\| {u^{k} } \right\|_{\infty } \le \left| {u_{{i_{x} ,j_{y} }}^{k - 1} + f_{{i_{x} ,j_{y} }}^{k} \cdot \Delta t} \right| \le \mathop {\max }\nolimits_{1 \le J \le k - 1} \left\| {u^{J} } \right\|_{\infty } + \left\| f \right\|_{\infty } \cdot \Delta t,$$

that is, \(\mathop {\max }\nolimits_{1 \le J \le k} \left\| {u^{J} } \right\|_{\infty } \le \mathop {\max }\limits_{1 \le J \le k - 1} \left\| {u^{J} } \right\|_{\infty } + \left\| f \right\|_{\infty } \cdot \Delta t\),

By recurrence, \(\mathop {\max }\nolimits_{1 \le J \le k} \left\| {u^{J} } \right\|_{\infty } \le \left\| {u^{0} } \right\|_{\infty } + k\left\| f \right\|_{\infty } \cdot \Delta t\).

Thus, Theorem 1 is proved (Li and Liu 2020).

Theorem 2

The fractional finite volume method presented by Eq. (18) is conditionally stable.

Proof.

Let \(\tilde{u}_{i,j}^{k}\) be the approximate solution of Eq. (18), the iteration error \(\tau_{i,j}^{k} = \tilde{u}_{i,j}^{k} - u_{i,j}^{k}\), which yields

$$a_{P} \tau_{i,j}^{k} = a_{W} \tau_{i - 1.j}^{k} + a_{S} \tau_{i,j - 1}^{k} + \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{j + 1} {g_{I}^{{\left( {\alpha + 1} \right)}} } \tau_{i,j + 1 - I}^{k} + \Delta V \cdot \tau_{i,j}^{k - 1} ,$$

Using Theorem 1 under the assumption that \(u_{i,j}^{k} \ge 0\) and \(v_{i,j}^{k} \ge 0\), we have

\(\left\| {\tau^{k} } \right\|_{\infty } \le \left\| {\tau^{0} } \right\|_{\infty } ,k = 1,2,3, \ldots ,R,\)

where \(\left\| {\tau^{k} } \right\|_{\infty } = \max_{1 \le i \le X - 1;1 \le j \le Y - 1} \left| {\tau_{i,j}^{k} } \right|\).

Thus, Theorem 2 is proved.

Remark 2

In the present physical problem, the horizontal and vertical velocity are both positive as \(\lambda\) is small. In this condition, the presented finite volume method in Eq. (18) is stable for different space and time steps.

4.2 Convergence

Theorem 3

Assume that \(u_{i,j}^{k} \ge 0\) and \(v_{i,j}^{k} \ge 0\). Then, the coefficient matrix of Eq. (18) is strictly diagonally dominant.

Proof

By Eq. (20), we obtain at the \(t_{k - 1}\) time step:

$$\Delta y \cdot u_{i,j}^{k - 1} - \Delta y \cdot u_{i - 1,j}^{k - 1} + \Delta x \cdot v_{i,j}^{k - 1} - \Delta x \cdot v_{i,j - 1}^{k - 1} = 0,$$

Using \(\sum\nolimits_{I = 0}^{j + 1} {g_{I}^{{\left( {\alpha + 1} \right)}} } < 0\), \(g_{1}^{{\left( {\alpha + 1} \right)}} = - \alpha < 0\), \(g_{I}^{{\left( {\alpha + 1} \right)}} > 0 \quad \left( {I = 0,2,3, \ldots } \right)\), we have

$$ \begin{aligned} \left| {a_{P} } \right| & = \left| {\Delta V + \Delta y\Delta t \cdot u_{i,j}^{k - 1} + \Delta x\Delta t \cdot v_{i,j}^{k - 1} - \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}g_{1}^{{\left( {\alpha + 1} \right)}} } \right| \hfill \\& = \left| {\Delta V + \Delta y\Delta t \cdot u_{i - 1,j}^{k - 1} + \Delta x\Delta t \cdot v_{i,j - 1}^{k - 1} - \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}g_{1}^{{\left( {\alpha + 1} \right)}} } \right| \hfill \\ & > \Delta V + \left| {a_{W} } \right| + \left| {a_{S} } \right| + \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{j + 1} {g_{I}^{{\left( {\alpha + 1} \right)}} }\\& > \left| {a_{W} } \right| + \left| {a_{S} } \right| + \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{j + 1} {g_{I}^{{\left( {\alpha + 1} \right)}} } . \hfill \\ \end{aligned} $$

Thus, Theorem 3 is proved.

Remark 3

Theorem 3 is a sufficient condition of convergence called bounded criterion.

Theorem 4

Let \(u\left( {x_{i} ,y_{j} ,t_{k} } \right)\) be the exact solution of the governing Eqs. (7)–(9). Then \(\left| {u\left( {x_{i} ,y_{j} ,t_{k} } \right) - u_{i,j}^{k} } \right| \le B\left( {\Delta x + \Delta y + \Delta t} \right)\), where \(B\) is a positive constant.

Proof

Let the truncation error \(\varepsilon_{i,j}^{k} = u\left( {x_{i} ,y_{j} ,t_{k} } \right) - u_{i,j}^{k}\). From Eq. (18), it yields

$$a_{P} \varepsilon_{i,j}^{k} = a_{W} \varepsilon_{i - 1.j}^{k} + a_{S} \varepsilon_{i,j - 1}^{k} + \frac{\Delta t \cdot \Delta x}{{\Delta y^{\alpha } }}\sum\limits_{I = 0,I \ne 1}^{j + 1} {g_{I}^{{\left( {\alpha + 1} \right)}} } \varepsilon_{i,j + 1 - I}^{k} + \Delta V \cdot \varepsilon_{i,j}^{k - 1} + \Phi \left( {x_{i} ,y_{j} ,t_{k} } \right) \cdot \Delta V \cdot \Delta t,$$

where \(\left| {\Phi \left( {x_{i} ,y_{j} ,t_{k} } \right)} \right| \le C\left( {\Delta x + \Delta y + \Delta t} \right)\), \(C\) is a positive constant.

Applying Theorem 1, we have \(\left\| {\varepsilon^{k} } \right\|_{\infty } \le \left\| {\varepsilon^{0} } \right\|_{\infty } + k\left\| \Phi \right\|_{\infty } \cdot \Delta t\), \(k = 1,2,3, \ldots ,R\).

Notice that \(\varepsilon_{i,j}^{0} = u\left( {x_{i} ,y_{j} ,t_{0} } \right) - u_{i,j}^{0}\), that is \(\left\| {\varepsilon^{0} } \right\|_{\infty } = 0\), and \(\left\| \Phi \right\|_{\infty } \le C\left( {\Delta x + \Delta y + \Delta t} \right)\).

Denote \(B = kC \cdot \Delta t\). Thus, Theorem 4 is proved.

4.3 Comparison with the exact solution

To validate the accuracy of the numerical techniques, we construct suitable exact solutions to the special case of the mixed convection flow with homogeneous boundary conditions, where two source terms are derived inversely by the manufactured solutions:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$
(21)
$$ \frac{\partial u}{{\partial t}} + \frac{\partial }{\partial x}\left( {uu} \right) + \frac{\partial }{\partial y}\left( {vu} \right) = \frac{\partial }{\partial y}\left( {\frac{{\partial^{\alpha } u}}{{\partial y^{\alpha } }}} \right) + \lambda \theta + f_{1} \left( {x,y,t} \right), $$
(22)
$$ \frac{\partial \theta }{{\partial t}} + \frac{\partial }{\partial x}\left( {u\theta } \right) + \frac{\partial }{\partial y}\left( {v\theta } \right) = \frac{1}{{{\text{Pr}}}}\frac{\partial }{\partial y}\left( {\frac{{\partial^{\beta } \theta }}{{\partial y^{\beta } }}} \right) + f_{2} \left( {x,y,t} \right). $$
(23)

where \(f_{{_{1} }} \left( {x,y,t} \right) = 2x^{2} \left( {1 - x} \right)^{2} y^{2} \left( {1 - y} \right)^{2} t + 2x^{3} \left( {1 - x} \right)^{3} \left( {1 - 2x} \right)y^{4} \left( {1 - y} \right)^{4} t^{4}\)

$$ \begin{gathered} \, - 4x^{3} \left( {1 - x} \right)^{3} \left( {1 - 2x} \right)y\left( {1 - y} \right)\left( {1 - 2y} \right)\left( {\frac{1}{3}y^{3} - \frac{1}{2}y^{4} + \frac{1}{5}y^{5} } \right)t^{4} \hfill \\ \, - x^{2} \left( {1 - x} \right)^{2} t^{2} \left[ {\frac{{\Gamma (5)y^{3 - \alpha } }}{{\Gamma \left( {4 - \alpha } \right)}} - \frac{{2\Gamma (4)y^{2 - \alpha } }}{{\Gamma \left( {3 - \alpha } \right)}} + \frac{{\Gamma (3)y^{1 - \alpha } }}{{\Gamma \left( {2 - \alpha } \right)}}} \right] - \lambda x^{2} \left( {1 - x} \right)^{2} y^{2} \left( {1 - y} \right)^{2} t^{2} , \hfill \\ \end{gathered} $$
$$ \begin{aligned} f_{{_{2} }} \left( {x,y,t} \right) & = 2x^{2} \left( {1 - x} \right)^{2} y^{2} \left( {1 - y} \right)^{2} t + 2x^{3} \left( {1 - x} \right)^{3} \left( {1 - 2x} \right)y^{4} \left( {1 - y} \right)^{4} t^{4} \hfill \\ \,& - 4x^{3} \left( {1 - x} \right)^{3} \left( {1 - 2x} \right)y\left( {1 - y} \right)\left( {1 - 2y} \right)\left( {\frac{1}{3}y^{3} - \frac{1}{2}y^{4} + \frac{1}{5}y^{5} } \right)t^{4} \hfill \\ \,& - \frac{1}{{{\text{Pr}}}}x^{2} \left( {1 - x} \right)^{2} t^{2} \left[ {\frac{{\Gamma (5)y^{3 - \beta } }}{{\Gamma \left( {4 - \beta } \right)}} - \frac{{2\Gamma (4)y^{2 - \beta } }}{{\Gamma \left( {3 - \beta } \right)}} + \frac{{\Gamma (3)y^{1 - \beta } }}{{\Gamma \left( {2 - \beta } \right)}}} \right]. \hfill \\ \end{aligned} $$

Subject to the homogeneous initial and boundary conditions:

$$ \begin{aligned} u\left( {x,y,0} \right) &= v\left( {x,y,0} \right) = \theta \left( {x,y,0} \right) = 0,\\ u\left( {0,y,t} \right)& = \theta \left( {0,y,t} \right) = 0,\;\;u\left( {x,0,t} \right) = v\left( {x,0,t} \right) = \theta \left( {x,0,t} \right) = 0,\\ u\left( {x,1,t} \right) & = \theta \left( {x,1,t} \right) = 0.\end{aligned} $$

The manufactured exact solutions are:

$$ \begin{aligned} u\left( {x,y,t} \right) &= x^{2} \left( {1 - x} \right)^{2} y^{2} \left( {1 - y} \right)^{2} t^{2} ,\\ v\left( {x,y,t} \right)& = - 2x\left( {1 - x} \right)\left( {1 - 2x} \right)\left( {\frac{1}{3}y^{3} - \frac{1}{2}y^{4} + \frac{1}{5}y^{5} } \right)t^{2} ,\\ \theta \left( {x,y,t} \right) &= x^{2} \left( {1 - x} \right)^{2} y^{2} \left( {1 - y} \right)^{2} t^{2}. \end{aligned} $$

Figure 3 presents the comparison between the exact solution and numerical solution of \(u/\theta\), which is obtained by the developed fractional finite volume method. The involved parameters are fixed as \({\text{Pr}} = 5\), \(\lambda = 1\), \(\alpha = \beta = 0.5\), \(t = 2\) and \(x = 1\). The space and time steps are \(\Delta x = \Delta y = 0.05\), \(\Delta t = 0.1\), respectively. The good agreement of the results validates the accuracy of the numerical technique and the calculations of the space fractional derivatives are effective in the following section.

Fig. 3
figure 3

Comparison between the numerical solution and exact solution of \(u/\theta\)

Full size image

5 Results and discussion

The numerical solutions of the mixed convection flow and heat transfer with space fractional derivatives are obtained. The boundary of the computational domain is chosen as \(Y_{\max } = 20\), which is corresponding to \(y \to \infty\). The iteration error is controlled within \(10^{ - 6}\). The effects of space fractional derivative parameters \(\alpha\) and \(\beta\), mixed convection parameter \(\lambda\) and Prandtl number Pr on velocities and temperature distributions are discussed graphically in detail.

Figure 4 illustrates horizontal velocity distributions for different \(\alpha\) at \(x = 1\). In the main region of the boundary layer, the horizontal velocity declines clearly with the rise of \(\alpha\). When \(\alpha = 1\), the fractional derivative is degenerated to Newtonian model and the Newtonian fluid has slowest horizontal velocity. The reason is that the viscous effect of the fluid enhances with the increase of \(\alpha\) and the flow slows down. However, on the edge of the boundary layer that is close to main stream, the horizontal velocity increases slightly as the velocity fractional derivative parameter rises. Vertical velocity distributions for different \(\alpha\) at \(x = 1\) are described in Fig. 5. Near the flat plate, the vertical velocity decreases with the augment of \(\alpha\). On the other hand, the vertical velocity rises as \(\alpha\) increases in the region that has a certain distance from the plate. The distance between two curves reduces and the sensitivity of vertical velocity weakens. The Newtonian fluid as \(\alpha = 1\) is at the bottom first then rises to the biggest value. It should be noted that both horizontal and vertical velocity profiles intersect with each other for different \(\alpha\). These results demonstrate that the viscoelastic fluid with spatial fractional derivative has evident stress relaxation with distance.

Fig. 4
figure 4

Horizontal velocity distributions for different \(\alpha\) at \(x = 1\)

Full size image
Fig. 5
figure 5

Vertical velocity distributions for different \(\alpha\) at \(x = 1\)

Full size image

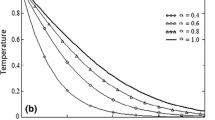
Figure 6 presents temperature distributions for different \(\beta\) at \(x = 1\). The temperature increases significantly with the augment of \(\beta\), but the thermal boundary layer become thicker. When \(\beta = 1\) the fractional derivative is simplified to normal Fourier’s law and the fluid has the thickest boundary layer. This phenomenon illustrates that the heat transfer efficiency reduces and the viscous dissipation enlarges. The viscoelastic performs shear-thickening property as fractional derivative \(\beta\) increases. Horizontal velocity distributions for different \(\beta\) at \(x = 1\) are shown in Fig. 7. As the temperature fractional derivative parameter rises, the horizontal velocity increases, but the momentum boundary layer thickness has almost no variation for different \(\beta\). The fluid with Fourier’s law develops fastest and the horizontal velocity profile is at the top. This result implies that the temperature fractional derivative parameter has a weak effect on horizontal velocity. Figure 8 depicts vertical velocity distributions for different \(\beta\) at \(x = 1\). The vertical velocity declines remarkably with the rise of \(\beta\). Moreover, the effects of \(\beta\) horizontal velocity and vertical velocity are totally opposite. It is worth mentioning that in Figs. 5 and 8, the vertical velocities are both positive and the stability of the numerical results is verified.

Fig. 6
figure 6

Temperature distributions for different \(\beta\) at \(x = 1\)

Full size image
Fig. 7
figure 7

Horizontal velocity distributions for different \(\beta\) at \(x = 1\)

Full size image
Fig. 8
figure 8

Vertical velocity distributions for different \(\beta\) at \(x = 1\)

Full size image

Figure 9 shows horizontal velocity distributions for different \(\lambda\) at \(x = 1\). As \(\lambda\) increases from negative to positive, the external body force originated from temperature gradient varies from opposing effect to assisting effect respectively. Thus, the horizontal velocity increases with the augment of the mixed convection parameter. Vertical velocity distributions for different \(\lambda\) at \(x = 1\) are presented in Fig. 10. On the contrary, the vertical velocity declines evidently as the mixed convection parameter increases. The distance between two profiles gradually reduce, which demonstrates that vertical velocity is less sensitive to larger mixed convection parameter. Figure 11 describes temperature distributions for different Pr at \(x = 1\). Near the plate surface, the temperature profiles are close to each other. Away from the plate, with the increase of Pr, the temperature decreases and the thermal boundary layer thickness reduces.

Fig. 9
figure 9

Horizontal velocity distributions for different \(\lambda\) at \(x = 1\)

Full size image
Fig. 10
figure 10

Vertical velocity distributions for different \(\lambda\) at \(x = 1\)

Full size image
Fig. 11
figure 11

Temperature distributions for different Pr at \(x = 1\)

Full size image

6 Conclusions

In this study, mixed convection boundary layer flow and heat transfer of viscoelastic fluid with spatial fractional derivatives are investigated. Nonlinear and coupled governing equations are formulated, which are discretized by developed finite volume method combined with the shifted Grünwald-Letnikov formula. The numerical scheme is proved to be conditionally stable and the convergence is also obtained. To validate the numerical solutions, a comparison with exact solutions of a special case is conducted. Results show that the viscoelastic fluid with fractional derivatives has evident stress relaxation and performs shear-thickening property. Effects of involved parameters on velocities and temperature distributions are concluded below:

  1. (i)

    With the rise of \(\alpha\), the horizontal and vertical velocity first declines but increases later.

  2. (ii)

    With the augment of \(\beta\), the temperature increases significantly and the horizontal velocity increases, but the vertical velocity declines remarkably.

  3. (iii)

    As \(\lambda\) increases, the horizontal velocity increases but the vertical velocity declines evidently. With the increase of Pr, the temperature decreases.