Thermal analysis of MHD convective slip transport of fractional Oldroyd-B fluid over a plate

Abstract

The prime concern of this study is to analyze the generalized time-dependent magnetohydrodynamic (MHD) slip transport of an Oldroyd-B fluid near an oscillating upright plate. The plate is nested in a porous media under the action of ramped heating and nonlinear thermal radiation. Caputo–Fabrizio (CF) and Atangana–Baleanu (ABC) derivatives are utilized to constitute fractional partial differential equations that establish slip flow, shear stress, and heat transfer phenomena. Primarily, Laplace transformation is applied to dimensionless fractional models, and later Stehfest’s numerical algorithm is invoked to anticipate solutions of momentum and heat equations in principal coordinates. Moreover, computed solutions of velocity and energy fields are authenticated by Durbin’s and Zakian’s Laplace inversion algorithms. The relations for skin friction and Nusselt number are evaluated in terms of velocity and temperature gradients to efficiently anticipate shear stress and rate of heat transfer at the solid–fluid interface. The respective outcomes are manifested through tables. A critical examination of the current model is carried out and repercussions of variation in implanted parameters on temperature and momentum profiles are graphically elucidated. For the sake of comparison, three limiting fractional models, named second grade, Maxwell, and viscous models, are proposed for the isothermal and ramped temperature cases. Consequently, the observed outcomes affirm that under the isothermal condition, a generalized Maxwell fluid performs the swiftest slip transport compared to other models. Inversely, a second grade fluid specifies the highest velocity profile under ramped temperature case.

1 Introduction

Traditionally, two types of limitation on the fluid at the boundary surface are implemented to efficiently model the fluid flow problems. These limit conditions are acknowledged as zero slip flow and nonzero slip flow. The zero slip flow condition indicates that a fluid in the immediate vicinity of the boundary and the boundary itself express no relative motion. In other words, an imbalance between cohesive and adhesive forces at the fluid–boundary interface leads to bringing down the fluid velocity to zero. Despite a few coupled constraints, this zero slip limitation is widely applied as it contributes to contract the intricacy of flow dynamics. For some sufficiently smooth boundaries, cohesive forces marginally suppress the attractive forces between solid boundary and fluid particles, and consequently fluid slips away from the boundary walls. In such scenarios, the zero slip condition is unable to provide reliable results. For instance, the zero slip limitation fails to accurately predict the blood flow in capillary tubes (Zhu and Granick 2002). However, Navier proposed the idea of a nonzero slip condition to overcome this obstacle more adequately, and therefore this condition is also regarded as the Navier condition (Navier 1823). The practical implications of the nonzero slip flow are found in industrial adhesives, medical fields, protrusion, specifically in the washing of fabricated heart valves, transportation of nanofluids and biological fluids via permeable closures, and soil degradation by erosion (Blake 1990; Pit et al. 1999).

In recent times, many researchers and scientists are interested in evaluating the physical and computational features of industrial fluids due to their growing critical utilization in mechanical and industrial sciences. These industrial fluids are generally recognized as non-Newtonian fluids and they involve whipped cream, silicone oils, drilling mud, clay, and lubricants as their subclassifications. The traditional Navier–Stokes model fails to accurately forecast the behavior of non-Newtonian fluids due to their rheological attributes and an additional nonlinear association of shear rate and shear stress. Therefore, several models are advised to suitably perceive the rheological properties of non-Newtonian fluids. Among them are Maxwell model (Farooq et al. 2019), Burgers viscoelastic model (Raza et al. 2019), Jeffery’s model (Kahshan et al. 2019), second grade fluid model (Haq et al. 2020), Sisko’s model (Khan et al. 2019), and Oldroyd-B model (Tanner 1962). Oldroyd-B model specifies the relaxation and retardation mechanisms, includes the flow records, and proficiently expresses the rheology of viscoelastic fluids. For the very first time, James G. Oldroyd advised this model with the key specification of preserving the rheological properties for unidirectional flows. Shakeel et al. (2016) applied slip condition on the boundary to analytically discuss the flow of Oldroyd-B fluid near a progressing boundary. Riaz et al. (2016) established the series form solutions of generalized Oldroyd-B fluid flowing inside a circular channel. Tahir et al. (2018) performed a theoretical study to examine the time-dependent fractional flow of Oldroyd-B model past a rotating closure. Wang et al. (2019) further expanded this analysis and computed the semianalytic solutions through modified Bessel functions and integral transformations. Heat transfer and hydromagnetic flow of the Oldroyd-B fluid through a horizontal channel with extending boundaries were inspected by Ali et al. (2016). Elhanafy et al. (2019) numerically scrutinized the Oldroyd-B model to anticipate the blood transport inside an abdominal aortic section. Recently, on the basis of Littlewood–Paley theory, Wan proved the global well-posed property of incompressible Oldroyd-B fluid corresponding to some usual initial conditions (Wan 2019).

For various real-world engineering problems, it was well acknowledged in the past decades that for differentiation fractional operators are more efficient compared to integral derivatives. Consequently, generalization of problems from the classical to fractional environment is an issue of interest for numerous researchers in recent times. The significant utilities of fractional calculus are found in viscoelasticity, electrochemistry, diffusion, control, and relaxation processes. The convolutions of a kernel of the fractional operator with ordinary derivative are utilized to establish the fractional operators. For this purpose, a variety of suggested kernels is present in the literature, however, the power-law kernel $x^{-\beta }$ is the basic and most common among them. It is employed to define the Caputo and Riemann–Liouville fractional operators (Podlubny 1998). Later, a modified fractional operator was constructed by Caputo and Fabrizio by using an exponential kernel $e^{-\beta x}$ (Caputo and Fabrizio 2015). Finally, the generalized Mittag-Leffler law $E_{\beta }(-\psi x^{\beta })$ was applied as a kernel by Atangana and Baleanu to construct a new version of the fractional operator (Atangana and Baleanu 2016; Atangana and Gómez-Aguilar 2017; Atangana 2018). Due to these novel fractional challenges and trends, many researchers are exploring some new directions in this field (Khan et al. 2017; Sheikh et al. 2017; Atangana and Baleanu 2017; Abro et al. 2019; Imran et al. 2017; Khan et al. 2016). Saqib et al. (2018) investigated the freely convective generalized flow of carbon nanotubes (CNTs) through a channel. Zafar and Fetecau (2016) employed Caputo–Fabrizio fractional operator to evaluate the exact solutions of viscous fluid flow near an infinite vertical plate. Ali et al. (2016) explored the fractionalized MHD convective motion of Walter’s-B fluid with the existence of an exponential kernel. A fractional model to analyze the blood flow under the influence of Lorentz force through a cylindrical tube was developed by Ali et al. (2017). The memory effect in the vicinity of an energy field established by a charge was numerically probed through various differential operators by Alkahtani and Atangana (2016). They provided some modern numerical approaches to solve the fractional systems of equations. Saqib et al. (2019) established a system of nonintegral order equations to comprehensively scrutinize the heat transfer phenomenon for some hybrid nanofluids. Shah and Khan (2016) utilized the Caputo–Fabrizio approach and integral transformation to provide an exact analysis of second grade fluid flow near an oscillating vertical surface. Recently, Siddique et al. (2020) applied Caputo–Fabrizio and Atangana–Baleanu derivatives for freely convective second grade fluid to forecast the heat transfer under Newtonian heating.

In light of the above-mentioned literature, the primary focus of this study is to generalize the time-dependent MHD convection slip flow of an Oldroyd-B fluid near an infinite vertical wall. The generalized model also incorporates the impacts of nonlinear radiative heat flux, wall oscillation, ramped heating, and porous material. The purpose of generalization is achieved by operating Caputo–Fabrizio and Atangana–Baleanu fractional operators. The temperature and momentum distributions are established through Laplace transform and Stehfest’s Laplace inversion algorithm. Durbin’s and Zakian’s algorithms are utilized to certify the computed solutions. At the boundary, the temperature and velocity gradients are calculated in terms of Nusselt number and skin friction as they have indispensable practical applications in mechanical and industrial fields. The graphs and tables are elucidated to critically evaluate the control of incipient parameters on temperature, velocity, skin friction, and heat transfer rate. Finally, a comparison between generalized velocity distributions of Oldroyd-B, second grade, Maxwell, and viscous fluid models for uniform (isothermal) and nonuniform (ramped) temperature conditions are graphically elucidated to have a critical view of the physics of the current model.

2 Problem description and model formulation

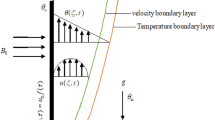
Consider the time-dependent flow of an electrically conducting Oldroyd-B fluid over an infinitely long upright wall subject to nonzero slip condition at the surface. At the start $\uptau =0$, the wall and surrounding fluid exhibit zero motion at a constant temperature $T_{\infty }$. For ${\uptau }=0^{+}$, the wall begins oscillating in its plane, and the temperature is lowered to $T_{\infty }+(T_{w}-T_{\infty })(\uptau /\uptau _{0})$ for ${\uptau } \leq {\uptau _{0}}$ and later it is raised to fixed temperature $T_{w}$ for ${\uptau } > {\uptau _{0}}$. Furthermore, nonlinear radiation thermal flux and magnetic effects are acting in the transverse direction to the wall (see Fig. 1). The equations to describe incompressible time-dependent MHD convection flow of Oldroyd-B fluid subject to standard Boussinesq’s approximation are provided as (Asghar et al. 2003; Anwar et al. 2020)

$$\mathbf{\nabla }\cdot \mathbf{q}=\mathbf{0},\rho \mathbf{g}{\beta }_T(T-T_{\mathrm{\infty }})+\mathbf{J}\times \mathbf{M}+\text{div}\mathbf{T}+\mathbf{R}=\rho [\frac{\partial \mathbf{q}}{\partial \mathrm{\tau }}+(\mathbf{q}.\mathbf{\nabla })\mathbf{q}].$$

(2.1)

Fig. 1

Geometrical configuration of the flow model

In the aforementioned expressions, $\textbf{q}$ specifies the velocity distribution, $\rho$ is the density, $\mathbf{g}$ is the force of gravity, $T$ is the fluid temperature, $T_{\infty }$ is the ambient temperature, $\uptau$ is the time, $\beta _{T}$ is the co-efficient of thermal volume expansion, $\mathbf{M}$ is the collective magnetic strength, $\mathbf{R}$ is the vector of Darcy resistance, and $\mathbf{J}$ is the electric density. The following expressions for $\mathbf{R}$ and $\mathbf{J} \times \mathbf{M}$ are generated by utilizing modified Darcy’s law and the set of Maxwell’s equations:

$$\begin{aligned} \mathbf{R}+\alpha \frac{\partial \mathbf{R}}{\partial \uptau }=- \left \{ \frac{\mu \varphi }{k_{0}}\mathbf{q}+\alpha _{r} \frac{\mu \varphi }{k_{0}}\frac{\partial \mathbf{q}}{\partial \uptau } \right \} , \quad \mathbf{J} \times \mathbf{M}=-\sigma _{0} M^{2}_{0} \mathbf{q}, \end{aligned}$$

(2.2)

where $M^{2}_{0}$ accounts for the imposed magnetic strength, $\varphi$ is the porosity of medium, $\sigma _{0}$ is the current conducting capacity of the fluid, and $k_{0}$ is the permeability of porous media. The velocity and stress fields for unidirectional flows are assumed as

$$\begin{aligned} \mathbf{q}=\left [V(y,{\uptau }),0,0 \right ], \quad \mathbf{S}= \mathbf{S}(y,\uptau ). \end{aligned}$$

(2.3)

The constitutive expressions of Cauchy stress tensor $\mathbf{{T}}$ and extra stress tensor $\mathbf{{S}}$ for an Oldroyd-B model are presented in the following manner:

$$\begin{aligned} \mathbf{T}=-p \mathbf{I}+\mathbf{S}, \qquad \left (1+\alpha \frac{D}{D \uptau } \right )\mathbf{S}=\mu \left (1+\alpha _{r} \frac{D}{D \uptau } \right ) \mathbf{B}, \end{aligned}$$

(2.4)

where $-p$I denotes the stress tensor’s indeterminate part, $\mu$ shows the dynamic viscosity, and $\alpha$ and $\alpha _{r}$ deal with the relaxation and retardation phenomenon respectively. The Rivlin–Ericksen tensor $\mathbf{B}$ and material time derivative $\frac{D}{D \uptau }$ are respectively expressed as

$$\begin{aligned} \mathbf{B}= {\nabla } \mathbf{q}+({\nabla } \mathbf{q})^{T}= \left ( \textstyle\begin{array}{c@{\quad }c} 0 & V_{y} \\ V_{y} & 0 \\ \end{array}\displaystyle \right ), \quad \frac{D}{D \uptau }&= \frac{\partial }{\partial \uptau }+V \frac{\partial }{\partial x}+U \frac{\partial }{\partial y}+W\frac{\partial }{\partial z}. \end{aligned}$$

(2.5)

After substituting Eqs. (2.2)–(2.5) into Eq. (2.1)₂ and using the classical Rosseland approximation, the principal equations establishing flow, stress field, and heat transfer for an Oldroyd-B model are described as (Martyushev and Sheremet 2012)

$$\begin{aligned} &\frac{\partial V(y,\uptau )}{\partial \uptau }{+}\alpha \frac{\partial ^{2} V(y,\uptau )}{\partial \uptau ^{2}}=\nu \frac{\partial ^{2} V(y,\uptau )}{\partial y^{2}}{+}\nu \alpha _{r} \frac{\partial ^{3} V(y,\uptau )}{\partial y^{2} \partial \uptau }- \left \{ \frac{\nu \varphi }{k_{0}}V(y,\uptau )+\alpha _{r} \frac{\nu \varphi }{k_{0}} \frac{\partial V(y,\uptau )}{\partial \uptau } \right \} \\ &\quad +g \beta _{T} \left (1+\alpha \frac{\partial }{\partial \uptau } \right ) (T-T_{\infty }) -\left \{ \frac{\sigma _{0} M^{2}_{0}}{\rho } V(y, \uptau )+\frac{\sigma _{0} M^{2}_{0}}{\rho } \alpha \frac{\partial V(y,\uptau )}{\partial \uptau } \right \} , \end{aligned}$$

(2.6)

$$\begin{aligned} &\left (1+\alpha \frac{\partial }{\partial \uptau } \right ) S(y,\uptau )= \mu \left (1+\alpha _{r} \frac{\partial }{\partial \uptau } \right ) \frac{\partial V(y,\uptau )}{\partial y}, \end{aligned}$$

(2.7)

$$\begin{aligned} &\left ( {\rho c_{p}} \right ) \frac{\partial T(y,\uptau )}{\partial \uptau }={k} \frac{\partial ^{2} T(y,\uptau )}{\partial y^{2}}- \frac{\partial q_{r}}{\partial y}, \\ &\left [q_{r}=-\frac{4 \sigma _{0}}{3 \beta _{0}} \frac{\partial T^{4}}{\partial y}, \quad T^{4} \approx (4 T_{\infty }^{3})T-3T_{\infty }^{4} \right ], \end{aligned}$$

(2.8)

where $\sigma _{0}$ is the Stefan–Boltzmann coefficient, $c_{p}$ is the specific heat at a fixed pressure, $\nu$ is the kinematic viscosity, $\beta _{0}$ is the coefficient of Rosseland absorption, and $k$ is the thermal conductivity. The initial and boundary conditions corresponding to modeled equations are

$$\begin{aligned} V(y,0)&=0, \quad T(y,0)=T_{\infty }, \quad V(0,\uptau )=b \frac{\partial V (0,\uptau )}{\partial y}+e^{(a \uptau )} , \end{aligned}$$

(2.9)

$$\begin{aligned} T(0,\uptau )&=(T_{w}-T_{\infty })\frac{\uptau }{\uptau _{0}}+T_{\infty }\quad \textrm{for} \quad \uptau \leq \uptau _{0} \quad \textrm{and} \\ \quad T(0,\uptau )&=T_{w} \quad \textrm{for} \quad \uptau > \uptau _{0} , \end{aligned}$$

(2.10)

$$\begin{aligned} V(y,\uptau )& \rightarrow 0, \quad T(y,\uptau ) \rightarrow T_{\infty }\quad \textrm{for} \quad y \rightarrow \infty . \end{aligned}$$

(2.11)

Some appropriate unitless quantities are introduced as

$$\begin{aligned} \zeta =\frac{V_{0}}{\nu } y, \quad V^{*}=\frac{V}{V_{0}} , \quad t= \frac{\uptau }{\uptau _{0}}=\frac{V^{2}_{0}}{\nu } \uptau , \quad \Theta =\frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \qquad \\ \alpha _{1}=\frac{V^{2}_{0}}{\nu }\alpha , \quad \alpha _{2}= \frac{V^{2}_{0}}{\nu }\alpha _{r}, \quad S^{*}= \frac{\nu }{\mu V^{2}_{0}}S, \quad Gr= \frac{g \beta _{T} (T_{w}-T_{\infty }) \nu }{V^{3}_{0}}, \\ a_{1}=\frac{\nu }{V^{2}_{0}}a, \quad b_{1}=\frac{V_{0}}{\nu }b, \quad Rd= \frac{16 \sigma _{0} T^{3}_{\infty }}{3 k \beta _{0}}, \quad Pr= \frac{\mu c_{p}}{k}, \qquad \\ M =\frac{\sigma _{0} M^{2}_{0} \mu }{\rho ^{2} V^{2}_{0}}, \quad K= \frac{k_{0} V^{2}_{0}}{\nu ^{2} \varphi }, \quad a_{2}=M+\frac{1}{K}, \quad b_{2}=\alpha _{1} M + \frac{\alpha _{2}}{K}. \end{aligned}$$

(2.12)

Operating these unitless quantities in Eqs. (2.6) and (2.7) and dropping the ∗ notation from $V^{*}$ and $S^{*}$ yield

$$\begin{aligned} \left (1+\alpha _{1} \frac{\partial }{\partial t} \right ) \frac{\partial V(\zeta ,t)}{\partial t}=\left (1+\alpha _{2} \frac{\partial }{\partial t} \right ) \frac{\partial ^{2} V(\zeta ,t)}{\partial \zeta ^{2}}-a_{2} V(\zeta ,t) \\ -b_{2} \frac{\partial V(\zeta ,t)}{\partial t}+Gr \left (1+\alpha _{1} \frac{\partial }{\partial t} \right ) \Theta (\zeta ,t), \end{aligned}$$

(2.13)

$$\begin{aligned} \left (1+\alpha _{1} \frac{\partial }{\partial t} \right ) S(\zeta ,t)= \left (1+\alpha _{2} \frac{\partial }{\partial t} \right ) \frac{\partial V(\zeta ,t)}{\partial \zeta }. \qquad \end{aligned}$$

(2.14)

The local form of thermal balance to describe the heat diffusion mechanism is

$$\begin{aligned} \rho c_{p} \frac{\partial T (y,\uptau )}{\partial \uptau }=- \frac{\partial q(y,\uptau )}{\partial y}, \end{aligned}$$

(2.15)

where $q(y,\uptau )$ denotes the local heat flux density. The Fourier principle expresses the heat flux in the following manner (Henry et al. 2010; Hristov 2016, 2017):

$$\begin{aligned} q(y,\uptau )=-k\left \{ \frac{\partial T(y,\uptau )}{\partial y} \right \} . \end{aligned}$$

(2.16)

On combining Eqs. (2.15) and (2.16), we get

$$\begin{aligned} \rho c_{p} \frac{\partial T (y,\uptau )}{\partial \uptau }=- \frac{\partial }{\partial y} \left [-k \left \{ \frac{\partial T(y,\uptau )}{\partial y} \right \} \right ]. \end{aligned}$$

(2.17)

On solving Eqs. (2.8) and (2.17) in the light of unitless quantities (2.12) and transforming the consequent expression to the fractional form, we acquire

$$\begin{aligned} Pr \big\{ D_{t}^{\gamma }\Theta (\zeta , t) \big\} = \left (1+Rd \right )\frac{\partial ^{2} \Theta (\zeta , t)}{\partial y^{2}}, \end{aligned}$$

(2.18)

where $D^{\gamma }_{t}$ denotes the fractional operator with order $\gamma$. In the present case, $D^{\gamma }_{t}$ is either Caputo–Fabrizio (CF) or Atangana–Baleanu (ABC) operator, and both operators are defined later to establish fractional models. The unitless version of initial and boundary conditions is secured as

$$\begin{aligned} &V(\zeta ,0)=0, \quad \Theta (\zeta ,0)=0, \quad V(0,t)=b_{1} \frac{\partial V (0,t)}{\partial \zeta }+e^{(a_{1} t)}, \end{aligned}$$

(2.19)

$$\begin{aligned} &\Theta (0,t)=t \quad \textrm{for} \quad t \leq 1 \quad \textrm{and} \\ &\Theta (0,t)=1 \quad \textrm{for} \quad t > 1, \end{aligned}$$

(2.20)

$$\begin{aligned} &V(\zeta ,t) \rightarrow 0, \quad \Theta (\zeta ,t) \rightarrow 0 \quad \textrm{for} \quad \zeta \rightarrow \infty . \end{aligned}$$

(2.21)

The CF $\left ({}^{CF} D^{\gamma }_{t} \{\cdot \} \right )$ and ABC $\left ({}^{ABC} D^{\gamma }_{t} \{\cdot \} \right )$ fractional derivatives are respectively defined as (Caputo and Fabrizio 2015; Atangana and Baleanu 2016)

$$\begin{aligned} {}^{CF} D^{\gamma }_{t} V(\zeta ,t)=\left (\frac{1}{1-\gamma }\right ) \int \limits _{0}^{t} \exp \left ( \frac{\gamma (t-z)}{\gamma -1} \right )V'(\zeta ,z)dz, \end{aligned}$$

(2.22)

$$\begin{aligned} {}^{ABC} D^{\gamma }_{t} V(\zeta ,t)=\left (\frac{1}{1-\gamma }\right ) \int \limits _{0}^{t} E_{\gamma }\left ( \frac{\gamma (t-z)^{\gamma }}{\gamma -1}\right )V'(\zeta ,z)dz. \end{aligned}$$

(2.23)

3 Solution of the problem

Laplace transformation (LT) (Le Page 1961) is considered an efficient technique to derive solutions of fractional order ordinary differential equations under nonuniform conditions on the boundary. The Laplace transform formula is stated as

$$\begin{aligned} \mathcal{L}[\psi ](\zeta ,t)=\int \limits _{0}^{\infty } \psi (\zeta ,t) e^{-q t}dt=\bar{\psi }(\zeta ,q). \end{aligned}$$

(3.1)

For the present problem, $\psi \in \{ V, \Theta , S \}$. The condition $Re(q)> \gamma _{0}$ guarantees the convergence of above integral. Moreover, $q=\gamma _{1}+\dot{\imath } \gamma _{2}$, where $\gamma _{0}$, $\gamma _{1}$, and $\gamma _{2}$ represent real numbers and $\dot{\imath }$ is usual complex unit. The transformed Laplace domain forms of CF and ABC fractional derivatives are respectively provided as

$$\begin{aligned} \mathcal{L} \left \{ {}^{CF} D^{\gamma }_{t} V(\zeta ,t)\right \} = \frac{q \mathcal{L}\left \{ {V}(\zeta ,t)\right \} -V(\zeta ,0)}{\gamma +(1-\gamma )q}, \quad \end{aligned}$$

(3.2)

$$\begin{aligned} \mathcal{L}\left \{ {}^{ABC} D^{\gamma }_{t} V(\zeta ,t)\right \} = \frac{q^{\gamma } \mathcal{L}\left \{ {V}(\zeta ,t)\right \} -q^{\gamma -1}V(\zeta ,0)}{\gamma +(1-\gamma )q^{\gamma }}. \end{aligned}$$

(3.3)

The Laplace transform inversion of $\bar{\psi }(\zeta ,q)$ is established as

$$\begin{aligned} \mathcal{L}^{-1}[\bar{\psi }](\zeta ,q)=\frac{1}{2\pi \dot{\imath } } \int \limits _{\gamma _{1}-\dot{\imath }\infty }^{{\gamma _{1}+ \dot{\imath }\infty }} \bar{\psi }(\zeta ,q)e^{q t}dq=\psi (\zeta ,t). \end{aligned}$$

(3.4)

3.1 CF fractional model and its solution

3.1.1 Temperature field subject to ramped temperature

The CF fractional version of temperature equation (Eq. (2.18)) is determined as

$$\begin{aligned} Pr \big\{ {}^{CF}D_{t}^{\gamma }{ \Theta (\zeta , t)} \big\} = \left (1+Rd \right )\frac{\partial ^{2} \Theta (\zeta , t)}{\partial \zeta ^{2}}. \end{aligned}$$

(3.5)

Employing the LT on Eq. (3.5) and substituting Eqs. (2.19)₂ and (3.2) in the consequent expression yields

$$\begin{aligned} \left [(1+Rd)\left \{ \frac{ \gamma +(1-\gamma )q }{\gamma }\right \} \right ] \frac{\partial ^{2} \bar{\Theta }(\zeta ,q)}{\partial \zeta ^{2}}= Pr \bar{\Theta } (\zeta ,q), \end{aligned}$$

(3.6)

where $\bar{\Theta }(\zeta ,q)$ follows the boundary conditions

$$\begin{aligned} \bar{\Theta }(0,q)=\frac{1-e^{-q}}{q^{2}}, \quad \textrm{and} \quad \bar{\Theta }(\zeta ,q)\rightarrow 0 \quad \textrm{for} \quad \zeta \rightarrow \infty . \end{aligned}$$

(3.7)

The solution of energy equation (3.6) subject to conditions (3.7) is derived as

$$\begin{aligned} \bar{\Theta }(\zeta ,q)=\left (\frac{1-e^{-q}}{q^{2}} \right ) e^{- \left (\sqrt{\frac{Pr \beta q}{(1+Rd)(\gamma \beta + q)}} \zeta \right )}, \end{aligned}$$

(3.8)

where $\beta =\frac{1}{1-\gamma }$.

3.1.2 Velocity field subject to ramped temperature

The CF fractional version of velocity equation (2.13) is determined as

$$\begin{aligned} \left (1+\alpha _{1} {}^{CF}D^{\gamma }_{t} \right ) \frac{\partial V( \zeta ,t)}{\partial t}&=\left (1+\alpha _{2} {}^{CF} D^{\gamma }_{t}\right ) \frac{\partial ^{2} V(\zeta ,t)}{\partial \zeta ^{2}}-a_{2} V(\zeta ,t) \\ &-b_{2} {}^{CF}D^{\gamma }_{t} V(\zeta ,t)+Gr \left (1+\alpha _{1} {}^{CF} D^{\gamma }_{t} \right ) \Theta (\zeta ,t). \end{aligned}$$

(3.9)

Employing the LT on Eq. (3.9) and substituting the initial condition (2.19)₁ yields

$$\begin{aligned} &\frac{\partial ^{2} \bar{V}(\zeta ,q)}{\partial \zeta ^{2}}-\left ( \frac{q^{2}(1+\alpha _{1} \beta )+q (\gamma \beta +a_{2} + b_{2} \beta )+a \gamma }{q(1+\alpha _{2} \beta )+\gamma \beta } \right ) \bar{V}(\zeta ,q) \\ &\quad =-Gr \left ( \frac{q(1+\alpha _{1} \beta )+\gamma \beta }{q(1+\alpha _{2} \beta )+\gamma \beta } \right ) \bar{\Theta }(\zeta ,q). \end{aligned}$$

(3.10)

The Laplace transformed boundary conditions for velocity field are

$$\begin{aligned} \bar{V}(0,q)=b_{1}\frac{\partial \bar{V} (0,q)}{\partial \zeta }+ \frac{1}{q-a_{1}} \quad \textrm{and} \quad \bar{V}(\zeta ,q) \rightarrow 0 \quad \textrm{for} \quad \zeta \rightarrow \infty . \end{aligned}$$

(3.11)

After substituting Eq. (3.8), the solution of Eq. (3.10) is determined as

$$\begin{aligned} \bar{V}(\zeta ,q)=&\, \frac{e^{-\left (\sqrt{f_{1}} \zeta \right )}}{(q-a_{1})(1+b_{1} \sqrt{f_{1}})} \\ &{}+ \left \{ \frac{Gr f_{2}}{f^{2}_{3}-f_{1}}\left ( \frac{1-e^{-q}}{q^{2}} \right ) \right \} \left [ \frac{1+b_{1} f_{3}}{1+b_{1} \sqrt{f_{1}}} e^{-\left (\sqrt{f_{1}} \zeta \right )}-e^{-\left ({f_{3}}\zeta \right )} \right ], \end{aligned}$$

(3.12)

where

$$\begin{aligned} f_{1} = \frac{q^{2}(1+\alpha _{1} \beta )+q (\gamma \beta +a_{2} + b_{2} \beta )+\gamma \beta a_{2}}{q(1+\alpha _{2} \beta )+\gamma \beta }, \quad \\ f_{2}= \frac{q(1+\alpha _{1} \beta )+\gamma \beta }{q(1+\alpha _{2} \beta )+\gamma \beta }, \quad f_{3}=\sqrt{\frac{Pr \beta q}{(1+Rd)(\gamma \beta + q)}}. \end{aligned}$$

3.1.3 Temperature field subject to isothermal temperature

The transformed energy equation and isothermal temperature condition are provided as

$$\begin{aligned} \left [ \frac{(1+Rd) (\gamma \beta +q)}{\beta q}\right ] \frac{\partial ^{2} \bar{\Theta }(\zeta ,q)}{\partial \zeta ^{2}}= Pr \bar{\Theta } (\zeta ,q), \end{aligned}$$

(3.13)

$$\begin{aligned} \bar{\Theta }(0,q)=\frac{1}{q}, \quad \bar{\Theta }(\zeta ,q) \rightarrow 0 \quad \textrm{for} \quad \zeta \rightarrow \infty . \end{aligned}$$

(3.14)

The solution of Eq. (3.13) is developed as

$$\begin{aligned} \bar{\Theta }(\zeta ,q)=\frac{1}{q} e^{-\left (\sqrt{ \frac{Pr \beta q}{(1+Rd)(\gamma \beta + q)}} \zeta \right )}. \end{aligned}$$

(3.15)

3.1.4 Velocity field subject to isothermal temperature

Plugging Eq. (3.15) into Eq. (3.10) yields the following velocity equation subject to isothermal temperature condition:

$$\begin{aligned} \frac{\partial ^{2} \bar{V}(\zeta ,q)}{\partial \zeta ^{2}}-f_{1} \bar{V}(\zeta ,q)&=-\left (\frac{Grf_{2}}{q} \right ) e^{-\left (f_{3} \zeta \right )}. \end{aligned}$$

(3.16)

The exact Laplace domain solution of Eq. (3.16) subject to the conditions (3.11) is

$$\begin{aligned} \bar{V}(\zeta ,q)= \frac{e^{-\left (\sqrt{f_{1}} \zeta \right )}}{(q-a_{1})(1+b_{1} \sqrt{f_{1}})}+ \left \{ \frac{Gr f_{2}}{q \left (f^{2}_{3}-f_{1} \right )} \right \} \left [\frac{1+b_{1} f_{3}}{1+b_{1} \sqrt{f_{1}}} e^{-\left (\sqrt{f_{1}} \zeta \right )}-e^{-\left ({f_{3}}\zeta \right )} \right ]. \end{aligned}$$

(3.17)

The rate of heat transfer corresponding to ramped surface temperature condition is calculated in terms of Nusselt number as

$$\begin{aligned} Nu&=-\frac{\partial \bar{\Theta }(0,q)}{\partial \zeta }=f_{3}\left ( \frac{1-e^{-q}}{q}\right ) . \end{aligned}$$

(3.18)

In industrial and mechanical fields, wall shear stress is of indispensable significance, and increasing shear stress is considered a disadvantage. To predict shear stress at the wall, the skin friction coefficient is evaluated as

$$\begin{aligned} \bar{C_{f}}&=\left [ \frac{q(1+\alpha _{2} \beta )+\gamma \beta }{q(1+\alpha _{1} \beta )+\gamma \beta } \right ] \frac{\partial \bar{V}(0,q)}{\partial \zeta } \\ &=\frac{Gr }{f^{2}_{3}-f_{1}}\left ( \frac{1-e^{-q}}{q^{2}} \right ) \left [f_{3}-\sqrt{f_{1}} \left ( \frac{1+b_{1} f_{3}}{1+b_{1} \sqrt{f_{1}}} \right ) \right ]- \frac{\sqrt{f_{1}}}{f_{2}(q-a_{1})(1+b_{1} \sqrt{f_{1}})}. \end{aligned}$$

(3.19)

3.2 ABC fractional model and its solution

3.2.1 Temperature field subject to ramped temperature

The ABC fractional version of temperature equation (2.18) is determined as

$$\begin{aligned} Pr \big\{ {}^{ABC}D_{t}^{\gamma }{ \Theta (\zeta , t)} \big\} = \left (1+Rd \right )\frac{\partial ^{2} \Theta (\zeta , t)}{\partial \zeta ^{2}}. \end{aligned}$$

(3.20)

Employing the LT on Eq. (3.20) and utilizing Eqs. (2.19)₂ and (3.3) yield

$$\begin{aligned} \left [ \frac{(1+Rd) (\gamma \beta +q^{\gamma })}{\beta q^{\gamma }} \right ] \frac{\partial ^{2} \bar{\Theta }(\zeta ,q)}{\partial \zeta ^{2}}= Pr \bar{\Theta } (\zeta ,q). \end{aligned}$$

(3.21)

The solution of Eq. (3.21) subjected to conditions (3.7) is derived as

$$\begin{aligned} \bar{\Theta }(\zeta ,q)=\left (\frac{1-e^{-q}}{q^{2}} \right ) e^{- \left (\sqrt{\frac{(1+Rd) (\gamma \beta +q^{\gamma })}{\beta q^{\gamma }}} \zeta \right )}. \end{aligned}$$

(3.22)

3.2.2 Velocity field subject to ramped temperature

The ABC fractional version of velocity equation (2.13) is determined as

$$\begin{aligned} \left (1+\alpha _{1} {}^{ABC}D^{\gamma }_{t} \right ) \frac{\partial V( \zeta ,t)}{\partial t}&=\left (1+\alpha _{2} {}^{ABC} D^{\gamma }_{t}\right ) \frac{\partial ^{2} V(\zeta ,t)}{\partial \zeta ^{2}}-a_{2} V(\zeta ,t) \\ &-b_{2} {}^{ABC}D^{\gamma }_{t} V(\zeta ,t)+Gr \left (1+\alpha _{1} {}^{ABC} D^{\gamma }_{t} \right ) \Theta (\zeta ,t). \end{aligned}$$

(3.23)

Employing the LT on Eq. (3.23) yields

$$\begin{aligned} &\frac{\partial ^{2} \bar{V}(\zeta ,q)}{\partial \zeta ^{2}}-\left ( \frac{q^{\gamma +1}(1+\alpha _{1} \beta )+q^{\gamma }(a_{2} + b_{2} \beta )+\beta _{1}}{q(1+\alpha _{2} \beta )+\gamma \beta } \right ) \bar{V}(\zeta ,q) \\ &\quad = -Gr \left ( \frac{q^{\gamma }(1+\alpha _{1} \beta )+\gamma \beta }{q^{\gamma }(1+\alpha _{2} \beta )+\gamma \beta } \right ) \bar{\Theta }(\zeta ,q), \end{aligned}$$

(3.24)

where $\beta _{1}=\gamma \beta q+ \gamma \beta a_{2}$. The solution of Eq. (3.24) in the presence of Eq. (3.22) is determined as

$$\begin{aligned} \bar{V}(\zeta ,q)=&\, \frac{e^{-\left (\sqrt{g_{1}} \zeta \right )}}{(q-a_{1})(1+b_{1} \sqrt{g_{1}})} \\ &{}+ \left \{ \frac{Gr g_{2}}{g^{2}_{3}-g_{1}}\left ( \frac{1-e^{-q}}{q^{2}} \right ) \right \} \left [ \frac{1+b_{1} g_{3}}{1+b_{1} \sqrt{g_{1}}} e^{-\left (\sqrt{g_{1}} \zeta \right )}-e^{-\left ({g_{3}}\zeta \right )} \right ], \end{aligned}$$

(3.25)

where

$$\begin{aligned} g_{1} = \frac{q^{\gamma +1}(1+\alpha _{1} \beta )+q^{\gamma }(a_{2} + b_{2} \beta )+\beta _{1}}{q(1+\alpha _{2} \beta )+\gamma \beta }, \\ g_{2}= \frac{q^{\gamma }(1+\alpha _{1} \beta )+\gamma \beta }{q^{\gamma }(1+\alpha _{2} \beta )+\gamma \beta }, \quad g_{3}=\sqrt{ \frac{(1+Rd) (\gamma \beta +q^{\gamma })}{\beta q^{\gamma }}}. \end{aligned}$$

For the ABC model, temperature and velocity field solutions under the isothermal temperature conditions can be obtained by following the same steps adopted for the CF model. The corresponding results are avoided to reduce mathematical expressions; however, relations for Nusselt number and skin friction coefficient are developed as

$$\begin{aligned} &Nu=g_{3} \left (\frac{1-e^{-q}}{q}\right ), \end{aligned}$$

(3.26)

$$\begin{aligned} &\bar{C}_{f}=\frac{Gr }{g^{2}_{3}-g_{1}}\left ( \frac{1-e^{-q}}{q^{2}} \right ) \left [g_{3}-\sqrt{g_{1}} \left ( \frac{1+b_{1} g_{3}}{1+b_{1} \sqrt{g_{1}}} \right ) \right ]- \frac{\sqrt{g_{1}}}{g_{2}(q-a_{1})(1+b_{1} \sqrt{g_{1}})}. \end{aligned}$$

(3.27)

For both CF and ABC fractional models, the derived temperature and velocity field solutions in Eqs. (3.8), (3.12), (3.15), (3.17), (3.22), (3.25) comprise multivalued combinations of Laplace frequency $q$. These multivalued functions restrict us to apply the analytic inverse Laplace transform, therefore for similar problems the numerical Laplace inversion is an effective way out to fetch the solutions in the primary domain. In recent times, Saqib et al. (2019) employed the numerical Laplace inversion to transform the solutions of fractional differential equations in the real-time domain. Tahir et al. (2017) established the results of fractional differential equations by applying the numerical inverse Laplace transformation. Sheng et al. (2011) declared that numerical Laplace inversion is a reliable and effective tool to anticipate solutions of nonintegral order differential equations in primary coordinates. On the basis of the above reports, we employed the numerical inverse Laplace transformation to anticipate temperature and velocity solutions of considered models. More precisely, we implicated Stehfest’s algorithm (Durbin 1974) to establish the results, and the authenticity of these results is further secured with the assistance of Fourier series expansion based Durbin’s algorithm (Stehfest 1970) and Zakian’s algorithm (Zakian 1969). The graphical verification for velocity and temperature solutions of CF and ABC fractional models are presented in Figs. 2 and 3, respectively. These solutions are in perfect agreement for both models. The formulas for the aforementioned algorithms are provided as

$$\begin{aligned} \textrm{(Stehfest's algorithm)} \\ V(\zeta ,t)&=\frac{\ln (2)}{t}\sum _{s=1}^{2k}d_{s} \bar{V} \left ( \zeta , s \frac{\ln (2)}{t}\right ), \quad \textrm{with} \qquad \\ d_{s}&=(-1)^{s+k} \sum _{j=\left [ \frac{s+1}{2}\right ]}^{\min (s,k)} \frac{j^{n} (2j)!}{(k-j)! j! (j-1)! (s-1)! (2j-s)!}; \\ \textrm{(Durbin's algorithm)} \\ V(\zeta ,t)&=\frac{e^{a_{1} t}}{T} \left [ -\frac{1}{2} \operatorname{\mathbb{R}e}\left \{ \bar{V}(\zeta ,a_{1})\right \} + \sum _{s=0}^{\infty } \operatorname{\mathbb{R}e}\left \{ \bar{V}\left ( \zeta ,a_{1}+\frac{s \pi }{T} \dot{\imath } \right )\right \} \cos \left (\frac{s \pi t}{T}\right ) \right . \\ & \left . -\sum _{s=0}^{\infty } \operatorname{\mathbb{I}m}\left \{ \bar{V}\left (\zeta ,a_{1}+\frac{s \pi }{T} \dot{\imath } \right ) \right \} \sin \left (\frac{s \pi t}{T}\right ) \right ]; \\ \textrm{(Zakian's algorithm)} \\ V(\zeta ,t)&=\frac{2}{t}\sum _{m=1}^{5}\operatorname{\mathbb{R}e} \left \{ K_{m} \bar{V}\left (\zeta ,\frac{\lambda _{m}}{t} \right ) \right \} , \end{aligned}$$

(3.28)

where $k$ specifies a positive integer, $[c]$ specifies the integer part of real constant $c$, and $\lambda _{m}$ and $K_{m}$ appear in terms of real constants or conjugate complex pairs.

Fig. 2

Authentication of temperature and velocity distributions for CF fractional operator

Fig. 3

Authentication of temperature and velocity distributions for ABC fractional operator

4 Limiting models

In this section, some special cases of the current model are deduced to compare the flow characteristics. These limiting models are presented for CF fractional derivative; however, adoption of the same trend leads to the ABC version of these models. The velocity solutions of these models are graphically compared with the velocity field of an Oldroyd-B model under ramped and isothermal temperature conditions.

4.1 Velocity field for Maxwell fluid

The velocity field solution for a fractional Maxwell fluid corresponding to slip flow and ramped heating can be traced out by substituting $\alpha _{2}=0$ into Eq. (3.12), which gives

$$\begin{aligned} \bar{V}(\zeta ,q)=&\, \frac{e^{-\left (\sqrt{f_{4}} \zeta \right )}}{(q-a_{1})(1+b_{1} \sqrt{f_{4}})} \\ &{}+ \left \{ \frac{Gr f_{5}}{f^{2}_{3}-f_{4}}\left ( \frac{1-e^{-q}}{q^{2}} \right ) \right \} \left [ \frac{1+b_{1} f_{3}}{1+b_{1} \sqrt{f_{4}}} e^{-\left (\sqrt{f_{4}} \zeta \right )}-e^{-\left ({f_{3}}\zeta \right )} \right ], \end{aligned}$$

(4.1)

where

$$\begin{aligned} f_{4} = \frac{q^{2}(1+\alpha _{1} \beta )+q (\gamma \beta +a_{2} + M \alpha _{1} \beta )+ \gamma \beta a_{2}}{q(1+\alpha _{2} \beta )+\gamma \beta }, \quad f_{5}= \frac{q(1+\alpha _{1} \beta )+\gamma \beta }{q+\gamma \beta }. \end{aligned}$$

(4.2)

4.2 Velocity field for second grade fluid

The solution for generalized momentum equation of second grade fluid is obtained by using $\alpha _{1}=0$ in Eq. (3.12) as

$$\begin{aligned} \bar{V}(\zeta ,q)=&\, \frac{e^{-\left (\sqrt{f_{6}} \zeta \right )}}{(q-a_{1})(1+b_{1} \sqrt{f_{6}})} \\ &{}+ \left \{ \frac{Gr f_{7}}{f^{2}_{3}-f_{6}}\left ( \frac{1-e^{-q}}{q^{2}} \right ) \right \} \left [ \frac{1+b_{1} f_{3}}{1+b_{1} \sqrt{f_{6}}} e^{-\left (\sqrt{f_{6}} \zeta \right )}-e^{-\left ({f_{3}}\zeta \right )} \right ], \end{aligned}$$

(4.3)

where

$$\begin{aligned} f_{6}= \frac{q^{2}+q (\gamma \beta +a_{2} + \frac{\alpha _{2}}{K} \beta )+\gamma \beta a_{2} }{q+\gamma \beta }, \quad f_{7}= \frac{q+\gamma \beta }{q(1+\alpha _{2} \beta )+\gamma \beta }. \end{aligned}$$

(4.4)

4.3 Velocity field for viscous fluid

The velocity distribution for viscous fluid is evaluated by choosing $\alpha _{1}=\alpha _{2}=0$ in Eq. (3.12) as

$$\begin{aligned} \bar{V}(\zeta ,q)=&\, \frac{e^{-\left (\sqrt{f_{8}} \zeta \right )}}{(q-a_{1})(1+b_{1} \sqrt{f_{8}})} \\ &{}+ \left \{ \frac{Gr}{f^{2}_{3}-f_{8}}\left (\frac{1-e^{-q}}{q^{2}} \right ) \right \} \left [\frac{1+b_{1} f_{3}}{1+b_{1} \sqrt{f_{8}}} e^{- \left (\sqrt{f_{8}} \zeta \right )}-e^{-\left ({f_{3}}\zeta \right )} \right ], \end{aligned}$$

(4.5)

where

$$\begin{aligned} f_{8}= \frac{q^{2}+q \left (\gamma \beta +a_{2} \right )+\gamma \beta a_{2}}{q+\gamma \beta }. \end{aligned}$$

(4.6)

5 Results and discussion

In this section, some critical findings are discussed and elaborated to deeply examine the physical aspects of the presented model. The generalization of the considered non-Newtonian fluid model is presented through CF and ABC fractional operators. The noteworthy contribution of rheological parameters in heat transfer and MHD convective slip flow of an Oldroyd-B fluid over an accelerating ramped wall is analyzed, and graphs are presented to explain the repercussions. The upright wall is nested in a porous media under thermal radiation effects. A tabular illustration of velocity and temperature gradients is provided to anticipate the impacts of incipient parameters on skin friction and rate of heat transfer at the wall. Graphical illustrations are supplied to validate the velocity and temperature solutions evaluated by Stehfest’s, Durbin’s, and Zakian’s Laplace reversion methods. A comparison is drawn for generalized Oldroyd-B fluid, Maxwell fluid, second grade fluid, and viscous fluid under ramped and isothermal wall temperature conditions. The incipient parameters significantly influencing the flow characteristics are named Grashof number $Gr$, porosity parameter $K$, Prandtl number $Pr$, relaxation parameter $\alpha _{1}$, fractional parameter $\gamma$, magnetic parameter $M$, slip parameter $b_{2}$, retardation parameter $\alpha _{2}$, and radiation parameter $Rd$.

Figure 4(a) encloses temperature distributions developed through CF and ABC fractional operators. Subject to ramped surface heating, the ABC operator-based model exhibits a higher temperature distribution. However, a reverse behavior is witnessed when isothermal temperature condition is considered, i.e., temperature curve for the CF model is higher than that of the ABC model. Furthermore, an identical trend for velocity distribution is analyzed in Fig. 4(b). The CF model exhibits a higher velocity field for isothermal temperature, whereas for ramped temperature this velocity curve declines and stays lower than the velocity curve associated with the ABC model. The prime physical argument for these trends is a dissimilarity between values of the time ($t$). The values of time associated with ramped and isothermal temperature cases are $t=0.9$ and $t=3.0$, respectively. This time nonuniformity influences velocity and thermal boundary layers independently and produces a variation in them. In the present study, this variation in connected boundary layers is opposite for isothermal and ramped surface heating conditions therefore, the acquired physical profiles behave inversely. In Fig. 5, the velocity profile of the current model and Haq et al. (2020) are compared for ramped and isothermal temperature cases. The solutions are found in good agreement, which justifies the reliability of our solutions.

Fig. 4

Temperature and velocity comparison between CF and ABC fractional operators

Fig. 5

Comparison between flow curve of Haq et al. (2020) and current model when $\alpha _{1}=Rd=M=\frac{1}{K}=0$

Figure 6 uncovers the control of fractional parameter $\gamma$ on temperature distribution. For a ramped surface, it is evident that temperature exhibits a decaying profile for increasing variation of $\gamma$. An augmentation in $\gamma$ strongly influences the thermal boundary layer and leads to a decrease in its thickness. Consequently, a decline in the temperature curve is perceived. On the contrary, the behavior of temperature profile under $\gamma$ variation reverses for the isothermal temperature condition due to the higher value of time. In the mainstream region, fluid temperature presents a significant behavior and asymptotically tends to zero as the fluid flows through the free stream region. The key role of radiation parameter $Rd$ in the temperature distribution is discerned in Fig. 7. A large value of $Rd$ specifies the ameliorated transfer of heat energy to the flow region, and therefore, the temperature distribution escalates. Corresponding to the increasing variation of $Rd$, the mean Rosseland absorptivity $\beta _{0}$ increases for invariant values of $T_{\infty }$ and $k$ (Eq. (2.12)). In the physical sense, the radiative transfer of heat from boundary to the flow region enhances due to dominant thermal radiation flux gradient ($\frac{\partial q_{r}}{\partial y}$). As a consequence, a higher temperature distribution is observed. Figure 8 reveals that temperature is elevated for dropping values of Prandtl number $Pr$. This diminishing behavior of fluid temperature is legitimized by the reason that the fluid with a small value of $Pr$ has greater thermal conductivity. The physical aspect of this phenomenon describes that the fluids associated with lower $Pr$ values are supportive for rapid transfer of heat from the boundary to the fluid due to their greater conduction potential and ultimately a rise in energy boundary layer thickness and temperature curve is witnessed.

Fig. 6

Temperature curve for diverse inputs of $\gamma$

Fig. 7

Temperature curve for diverse inputs of $Rd$

Fig. 8

Temperature curve for diverse inputs of $Pr$

The impact of the relaxation parameter $\alpha _{1}$ on fluid velocity accompanied by a variation of the fractional parameter $\gamma$ is revealed in Fig. 9. In this figure, velocity solutions are presented for ramped and isothermal temperature cases, and it is noted that fluid has a lower velocity for the former case. This result also highlights an important feature that the wall ramping technique can be implemented to attain better flow performance and control in highly-sensitive dynamical systems. For isothermal temperature, the fluid velocity exhibits an accelerating behavior subject to increasing variation of $\gamma$. However, $\gamma$ exerts inverse effects on the momentum boundary layer for the ramped condition and retards the fluid motion. Additionally, an augmentation in the variation of $\alpha _{1}$ upsurges the flow. The time required by the fluid to adjust its flow is specified by the parameter $\alpha _{1}$. A large value of $\alpha _{1}$ shows that fluid particles get more time to adjust, which allows them to express a smooth motion. Hence, the velocity profile increases.

Fig. 9

Flow curve for diverse inputs of $\alpha _{1}$ and $\gamma$

Figure 10 perceives the relative influence of buoyancy and viscous forces on velocity distribution in terms of Grashof number $Gr$. It is depicted that an increase in Grashof number accelerates the fluid flow. In the physical sense, a positive variation of $Gr$ is associated with greater heating of the fluid which leads to the occurrence of convection currents. These convection currents play their part to appreciate the supremacy of buoyancy force which suppresses the other flow retarding forces and consequently velocity of the fluid is augmented. The porosity parameter $K$ influence on fluid velocity is shown in Fig. 11. It is descried that the slip transport of an Oldroyd-B type fluid is accelerated with the amplifying magnitude of parameter $K$. The physical argument after this velocity variation is the reduction in the strength of dragging force. Corresponding to higher values of $K$, this reduction phenomenon appears because holes of the porous medium permit more amount of fluid to pass through them, and consequently flow velocity is accelerated. The influence of $K$ on velocity distribution is the same for ramped and isothermal temperature conditions. Figure 12 is provided to account for the magnetic parameter $(M)$ effects on velocity distribution for multiple values of $\gamma$. It is witnessed that flow is retarded due to a magnifying alteration of $M$. This figure characterizes the development of the Lorentz force that operates in an antiflow direction. Hence, it plays the role of dragging force and reduces the velocity of the fluid. In short, it is observed that the imposition of a magnetic field in the flow region significantly reduces the speed of fluid’s motion. These physical arguments justify observed behaviors of velocity boundary layer and velocity profile.

Fig. 10

Flow curve for diverse inputs of $Gr$ and $\gamma$

Fig. 11

Flow curve for diverse inputs of $K$ and $\gamma$

Fig. 12

Flow curve for diverse inputs of $M$ and $\gamma$

Figure 13 characterizes the impression of the retardation parameter $\alpha _{2}$ on the velocity profile. A reciprocal profile of fluid velocity for increasing variation of $\alpha _{2}$ is visualized when compared with the velocity profile developed for increasing relaxation parameter $\alpha _{1}$. Physically, resistive force dominates for larger values of $\alpha _{2}$ and establishes a significant resistance, which results in declination of fluid velocity. This profile is further endorsed by the Eq. (2.13), which presents that fluid velocity shares an inverse relationship with $\alpha _{1}$ and $\alpha _{2}$. The parameter $\alpha _{2}$ exerts identical effects on the boundary layer thickness for both the conditions of isothermal and ramped temperature. The contribution of radiative heat flux in flow distribution is surveyed in Fig. 14. An expansion in the inputs of $Rd$ depicts that heat transfer through radiation gradually increases. The force due to which fluid particles stick to each other becomes weak when more heat energy is transferred to the flow region. Therefore, the fluid particles are unable to produce significant resistance to flow and ultimately an augmented velocity distribution is attained. Figure 15 is prepared to emphasize the impacts of thermal and viscous forces on flow profile. For both cases of ramped and isothermal temperature, the flow is decelerated by maximized values of $Pr$. The physical reason behind this decelerating flow is the dominant nature of viscous forces, which drag the fluid and ultimately reduce the velocity of the fluid. The parameter $Pr$ is the relative contribution of momentum and thermal diffusivities in heat and flow profiles. For high $Pr$ values, momentum diffusivity dominates and reduces the thickness of momentum and thermal boundary layers.

Fig. 13

Flow curve for diverse inputs of $\alpha _{2}$ and $\gamma$

Fig. 14

Flow curve for diverse inputs of $Rd$ and $\gamma$

Fig. 15

Flow curve for diverse inputs of $Pr$ and $\gamma$

Figure 16 scrutinizes the behavior of velocity distribution for variation in slip parameter $b_{2}$. An interesting fact is observed that velocity is accelerated for isothermal temperature case subject to addition in the values of $b_{2}$. Contrarily, for the ramped temperature condition, the fluid is retarded due to greater values of $b_{2}$. Physically, the momentum boundary layer gets thicker for the evolution of time and fluid attains more speed in the immediate vicinity of the wall. Additionally, velocity in the case of slip transport is higher than the velocity of the fluid with a zero-slip condition for the isothermal temperature condition. This phenomenon reverses for ramped heating of the wall. Figure 17 is developed to draw a comparison between generalized velocity distributions of Oldroyd-B, Maxwell, second grade, and viscous models. The respective figure contains velocity distributions of all the aforementioned models for ramped and isothermal conditions at the boundary. It is worth mentioning that the second grade slippage flow has the highest velocity profile under the ramped heating condition. The velocity field of second grade fluid is followed by the velocity fields of viscous, Oldroyd-B, and Maxwell fluid, respectively. In the case of isothermal temperature, a reverse pattern is followed in such a way that the Maxwell fluid flows with the highest velocity, and second grade fluid exhibits the slowest flow profile.

Fig. 16

Flow curve for diverse inputs of $b_{2}$ and $\gamma$

Fig. 17

Velocity comparison between various fluid models

In Fig. 18, the Nusselt number generated through CF and ABC fractional models is demonstrated to analogize the heat transfer rate. Same as temperature and velocity distributions, the heat transfer rate specifies an inverse variation for both types of thermal conditions. More precisely, the CF derivative provides a better heat transfer rate under the ramped temperature condition, and for the isothermal condition, the ABC model appreciates the heat transfer rate. The impacts of fractional parameter $\gamma$ and Prandtl number $Pr$ on the rate of heat transfer are analyzed in Figs. 19 and 20. An interesting fact is explored that the parameter $\gamma$ influences the Nusselt number in an exactly opposite fashion for ramped surface condition and isothermal surface condition. Extensively, for ramped temperature ($0< t<1$), heat is swiftly transferred from the boundary to the fluid, whereas for isothermal temperature ($t>1$) the rate of heat transfer starts decreasing with time progression. Additionally, due to the dominance of the wall temperature gradient, the rate of heat transfer enhances for greater values of $Pr$. Generally, it is observed that the rate of heat transfer is exceptionally rapid for the ramped boundary condition. Figure 21 anatomizes how the radiative thermal flux controls the heat transfer rate. A decline in heat transfer rate is perceived due to higher values of $Rd$. Physically, intensification of radiation effects leads to enhance the Rosseland approximation, which results in temperature enhancement. Conclusively, the heat transfer phenomenon takes place at a lower rate.

Fig. 18

Nusselt number comparison between CF and ABC fractional operators

Fig. 19

Nusselt number for diverse inputs of $\gamma$

Fig. 20

Nusselt number for diverse inputs of $Pr$

Fig. 21

Nusselt number for diverse inputs of $Rd$

Table 1 is reported to numerically visualize the relative control of parameter $\gamma$ on velocity, temperature, and Nusselt number for CF and ABC fractional derivatives. In Table 2, a numerical comparison between slip and no-slip flow profiles is drawn for ramped and isothermal temperature conditions. The value $t=0.9$ is connected with the former boundary condition. In this case, a rapid fluid motion is observed in the absence of slip parameter $b_{2}$. However, in the case of constant temperature, the velocity of the fluid is higher for slippage flow. The physical justification after these inverse behaviors is that parameter $b_{2}$ produces an opposite variation in the velocity boundary layer. Numerical outcomes of fractionalized Nusselt number are accessible through Table 3. In this table, we have deeply inspected the significance of incipient parameters in the rate of heat transfer. Nusselt number is a decreasing function of $Rd$ while it shows an escalating variation in response to growing values of $Pr$. In the physical view, loosely connected intermolecular bonds and higher thermal conductivity amplify the heat conduction potential of fluid and resultantly rate of heat transfer grows. The effect of parameter $\gamma$ on Nusselt number is reversible for isothermal and ramped boundary conditions. In order to determine the behavior of wall shear stress, the variation of skin friction coefficient corresponding to dissimilar inputs of incipient parameters is presented in Table 4. Shear stress has abundant implications in industrial and mechanical sciences and its intensification is assumed to be a drawback in engineering exercises. The table specifies that shear stress at the boundary can be restrained by choosing augmented values of relaxation parameter $\alpha _{2}$ and magnetic parameter $M$. On the other hand, smaller inputs of $\alpha _{1}$, $Gr$, and $b_{2}$ are useful to achieve the desired outcomes.

Table 1 Control of fractional parameter $\gamma$ on temperature, velocity, and Nusselt number for CF and ABC fractional operators

Table 2 Numerical velocity profile comparison for slip and no-slip boundary flows

Table 3 Numerical computations of Nusselt number for diverse inputs of implanted parameters

Table 4 Numerical computations of skin friction for diverse inputs of implanted parameters

6 Conclusion

The motive of this theoretical study is to investigate the influence of CF and ABC fractional derivatives on heat transfer enhancement in MHD convective Oldroyd-B fluid slip flow with ramped wall heating. The plate exhibits an oscillatory motion in a porous material and encounters the radiation effects. Laplace transformation is operated to establish the solutions of principal unitless fractional equations. The dominance of several nested parameters on flow and energy distributions is surveyed to grasp the dynamics of the present problem. The effects of ramped boundary heating and stepped boundary heating on heat transfer rate, velocity, and energy fields are also compared and discussed. Additionally, the generalized models of Oldroyd-B, Maxwell, second grade, and viscous fluids are studied for isothermal and ramped temperature conditions to distinguish the flow characteristics.

The noteworthy outcomes of this investigation are enlightened as follows:

• For ramped boundary temperature, the rate of heat transfer is an increasing function of the fractional parameter $\gamma$ while it specifies a reciprocal behavior for isothermal boundary temperature.

• Heat transfer takes place at a rapid rate for ramped wall temperature but for isothermal wall temperature, heat transfer rate exhibits a gradual decay against time evolution.

• ABC fractional derivative maximizes the heat transfer rate under constant surface temperature, while CF derivative serves this purpose for ramped plate temperature.

• The velocity and temperature profiles under the ramped boundary condition are higher for the ABC model. Inversely, for the isothermal condition, these physical quantities are better explained by the CF operator.

• Fluid velocity is controlled by wall ramping technique, magnetic effects, and retardation parameter $\alpha _{2}$.

• The dominant convection currents ($Gr$), thermal radiation ($Rd$), relaxation parameter $\alpha _{1}$, and porosity parameter $K$ upsurge the fluid motion. Additionally, the oscillated Oldroyd-B fluid performs a rapid motion for the nonzero slip condition under constant temperature.

• Shear stress enhances for growing variation of parameters $b_{2}$, $Gr$, $K$, and $\alpha _{1}$, while it reduces for higher values of retardation parameter $\alpha _{2}$ and magnetic parameter $M$.

• The role of the parameter $\gamma$ is reversible for ramped and stepped temperature conditions.

• The generalized slip flow of Maxwell fluid possesses greater velocity subject to constant boundary temperature. Under the ramped heating condition, second grade fluid exhibits the augmented slip transport to the remaining models.

• For each parameter, energy and momentum distributions associated with the isothermal condition are always in a leading position.

• The solutions computed through Stehfest’s, Durbin’s, and Zakian’s numerical methods are in excellent agreement.