Comparison of hidden and explicit resources in ecoepidemic models of predator–prey type

Abstract

This paper investigates mathematical models of predator-prey systems where a transmissible disease spreads only among the prey species. Two mathematical models are proposed, analysed and compared to assess the influence of hidden or explicit resources for the predator. The predator is assumed to be a generalist in the first model and a specialist on two prey species in the second one. Existence and boundedness of the solutions of the models are established, as well as local and global stability and bifurcations. The equilibria of two systems possessing the same biological meaning are compared. The study shows that the relevant ecosystem behaviour including stability switching, extinction and persistence for any species depends on four important parameters, viz., the reproduction rate and the infection rate of the main prey, the mortality rate of infected prey and the reproduction rate of the alternative prey. This study ultimately indicates that the simpler formulation with the hidden resource already captures the salient features of the ecosystem. Therefore, modeling explicitly the substitute prey is not needed unless a particular emphasis is placed on the alternative resource behaviour. In such case, the extended model is preferable, at the expenses of a more complicated formulation and analysis. Ultimately, the choice of the model to be used should be guided by the reasons of its formulation and the answers that are sought.

1 Introduction

Currently, mathematical models in ecoepidemiology play an important tools in the analysis of the spread and control of infectious diseases among interacting animal communities (Anderson and May 1986; Hadeler and Freedman 1989; Venturino 1994). Most models dealing with the transmission of infectious diseases descend from the classic SIR model (Haque and Venturino 2006; Kermack and McKendrick 1927; Venturino 2016). However, in this paper we consider models only of type SI, Venturino (2011), to keep the presentation simple without obscuring the main goals with unnecessary mathematical complications.

The main focus of this investigation concerns the fact that in modeling some selected features in nature are chosen as being part of the general picture one wants to set in the mathematical framework, while necessarily some others are neglected. The situation is similar to a well-known story that cartographers were asked to produce a very accurate map of the terrain, and to obtain that any scale smaller than the 1:1 would be insufficient. But the result was that such a map would cover completely the ground and, therefore, be absolutely useless. When looking at ecological situations, apart from including or excluding particular features of the ecosystem at hand, it is important to decide which dependent variables are essential for the effective description of the picture. In that respect, including too many may lead to a full illustration of the system dynamics, which can be simulated via numerical devices but excludes any sort of mathematical qualitative analysis, in view of its complexity. Needless to say, the simulations must be repeated over and over again giving each time different values to the relevant parameters, to obtain qualitative information on the future system behaviour. On the contrary, the mathematical analysis, if it can be carried out, would answer these evolution questions in a relatively easy fashion. When it comes to quantitative predictions, the roles reverse, and it is the numerical simulations that could provide more or less reliable answers, but those would depend on the accurate measurements of the parameters of the model, which may not all be known or available.

Setting our perspective from the qualitative viewpoint, sometimes of the many actors on the scene, i.e. the several species interacting in a natural scenery, some should be excluded in order to render the mathematical description analytically tractable. It may thus happen that some populations are judged to play a less relevant role and are not, therefore, modeled as system’s variables. For instance, a (generalist) predator may subsist on several prey, but to reduce the number of interacting populations in the dynamical system formulation, only the main one is explicitly taken into account. But in so doing, something is lost and it is not clear if this entails relevant consequences for the ensuing analysis. Here, we would like to consider exactly this issue, and exploring namely what are the implications of omitting one explicit (prey) population from the dynamical formulation of a predator–prey interaction. We thus compare two models, one in which the omission is compensated by some “generic” alternative resources available for the predator, and a second one in which the previously omitted population is instead explicitly accounted for as a system variable. In nature there are very many such instances, we mention for instance the pine marten Martes martes L., that can feed possibly on grey squirrel Sciurus carolinensis and the European hare Lepus Europaeus, both now invasive species in Northern Italy, Gosso et al. (2012), La Morgia and Venturino (2017). Either one could be forgotten, if the focus of the model is for instance finding eradication measures for the other one.

The main objective of this paper is, therefore, the comparative study of two predator–prey ecoepidemic models, an example of which is discussed in Bravo and Tamburino (2011); Haque et al. (2013), although food webs can also be considered, see for instance Jiang and Niu (2017). We assume that the disease spreads among the prey population. The difference between the models is represented by the predator having an alternative food source, which is implicit in the first formulation and explicit in the second one. Thus, the predator is assumed to be generalist in the first model, while in the second model, because of this explicitly accounted for alternative food resource, the predator is regarded as specialist on both prey species. In the papers de Assis et al. (2018), Khan et al. (1998), Turchin (2003), purely demographic systems are analysed, in this work, we extend some of those systems to the Ecoepidemic situation, there is, we include the dynamics of a disease in the prey population.

The presentation is organized as follows: In Sect. 2, we present the model for the generalist predator and, we present the corresponding model with two prey and the specialist predator in Sect. 3. In both situations, we show that the systems trajectories remain confined within a compact set; we study local and global stability, and determine existing bifurcations between the equilibria of the model. The outcomes of the two models are compared in Sect. 4 and a final discussion concludes this paper.

2 The model with hidden resources

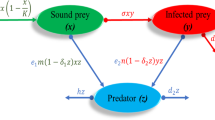
Let the prey population be denoted by X, the infected prey population U, which is assumed to be weakened by the disease so as not to be able to reproduce nor to interfere with the susceptibles, and the predator population Z. The predator population has an alternative food supply, indicated by a suitable logistic growth term. The model, in which all the parameters are nonnegative, reads

$$\begin{aligned} \frac{{\text{ d }}X}{{\text{ d }}t}= & {} r X \left( 1- \frac{X}{K} \right) - a ZX - \lambda XU,\nonumber \\ \frac{{\text{ d }}U}{{\text{ d }}t}= & {} \lambda XU - c ZU - \mu U,\\ \frac{{\text{ d }}Z}{{\text{ d }}t}= & {} u Z \left( 1- \frac{Z}{L} \right) + eZ (a X + cU).\nonumber \end{aligned}$$

(1)

The first equation of model (1) describes the healthy prey population dynamics. The first term on the right-hand side expresses logistic growth with r being the per capita net reproduction rate and K the carrying capacity of the environment. The second term models the hunting process of predators on healthy individuals at rate a and the third term describes the infection process by “successful” contacts with an infected individual via a simple mass action law, with contact rate $\lambda$. The second equation describes the infected prey evolution, recruited by the infection process at rate c, hunted via a classical mass action term and subject to natural plus disease-related mortality $\mu$. The third equation contains the dynamics of the predators, who in the absence of both healthy and infected prey have an alternative resource, that is hidden in the model and originating a logistic growth, with per capita net reproduction rate u and the carrying capacity of the environment L. The term $eZ(aX+cU)$ instead accounts for the reward obtained by hunting healthy and infected prey, respectively, e denoting the conversion factor. The equilibria of this model are denoted by the superscript $[p\_ehp]$, the first “p” referring to predators and the second one to prey, “e” standing for “epidemics” and “h” for “hidden”.

In shorthand notation, the model (1) can be rewritten in a vector form

$$\begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}t} = f(P), \quad P = (X,U,Z)^T, \quad f = (f_1,f_2,f_3)^T, \end{aligned}$$

(2)

with the components of f given by the right-hand side of model (1).

2.1 Boundedness

To obtain a well-posed model, we need to show that the trajectories of the system remain confined within a compact set. Consider the total environment population $\varphi (t)=X(t)+U(t)+Z(t)$. Taking an arbitrary $0< \eta < \mu$, summing the equations in model (1), we obtain

$$\begin{aligned} \frac{\mathrm{d}\varphi (t)}{\mathrm{d}t}=rX \left( 1-\frac{X}{K}\right) +uZ \left( 1-\frac{Z}{L}\right) -\mu U+(e-1)(aXZ+cUZ). \end{aligned}$$

(3)

Since $e\le 1$, from (3) we can obtain

$$\begin{aligned} \frac{\mathrm{d}\varphi (t)}{\mathrm{d}t}= & {} rX \left( 1-\frac{X}{K}\right) +uZ \left( 1-\frac{Z}{L}\right) -\mu U+(e-1)(aXZ+cUZ) \nonumber \\\le & {} rX \left( 1-\frac{X}{K}\right) +uZ \left( 1-\frac{Z}{L}\right) -\mu U. \end{aligned}$$

(4)

Adding $\eta \varphi (t)$ on both sides of inequality (4), we find the estimate

$$\begin{aligned} \frac{\mathrm{d}\varphi (t)}{\mathrm{d}t}+\eta \varphi (t)\le & {} rX \left( 1-\frac{X}{K}+\frac{\eta }{r}\right) +uZ \left( 1-\frac{Z}{L}+\frac{\eta }{u}\right) \\&+ (\eta - \mu ) U \le p_1(X)+p_2(Z), \\ p_1(X)= & {} rX \left( 1-\frac{X}{K}+\frac{\eta }{r}\right) , \quad p_2(X)=\left( 1-\frac{Z}{L}+\frac{\eta }{u}\right) . \end{aligned}$$

The functions $p_1(X)$ and $p_2(Z)$ are concave parabolae, with maxima located at $X^*$, $Z^*$, and corresponding maximum values

$$\begin{aligned} M_1=p_1(X^*)=\frac{rK}{4}\left( 1+\frac{\eta }{r} \right) ^2, \quad M_2=p_2(Z^*)=\frac{uL}{4}\left( 1+\frac{\eta }{u}\right) ^2. \end{aligned}$$

Thus

$$\begin{aligned} \frac{\mathrm{d}\varphi (t)}{\mathrm{d}t}+\eta \varphi (t) \le M; \quad M_1+M_2=M. \end{aligned}$$

Integrating the differential inequality, we find

$$\begin{aligned} \varphi (t) \le \left( \varphi (0) - \frac{M}{\eta } \right) e^{-\eta t} + \frac{M}{\eta } \le \max \left\{ \varphi (0), \frac{M}{\eta } \right\} . \end{aligned}$$

(5)

From this result, since $0\le X,U,Z \le \varphi$, the boundedness of the original ecosystem populations is immediate. Thus, for model (1) the solutions are always non-negative, in view of the existence and uniqueness theorem Perko (2001), and contained within a compact set.

2.2 Local stability analysis

The Jacobian matrix of the system (1) is given by

$$\begin{aligned} J^{[p\_ehp]} = \left( \begin{array}{c@{\quad }c@{\quad }c} J_{11}^{[p\_ehp]} &{} - \lambda X &{} -aX\\ \lambda U &{} -cZ + \lambda X - \mu &{} - cU\\ aeZ &{} ceZ &{} J_{33}^{[p\_ehp]} \\ \end{array} \right) \end{aligned}$$

(6)

with

$$\begin{aligned} J_{11}^{[p\_ehp]}=- \lambda U - aZ + r \left( 1 - \frac{2X}{K}\right) , \quad J_{33}^{[p\_ehp]}=u - 2u \frac{Z}{L} + eaX + ecU, \end{aligned}$$

There are 7 equilibria for model (1), but four must be rejected. At first, the two are always feasible but unstable points: the origin $P_1^{[p\_ehp]}=(0,0,0)$, with eigenvalues $r, -\mu , u$, and $P_2^{[p\_ehp]}=(K,0,0)$, with eigenvalues $-r, K \lambda -\mu , u+aeK$. In addition, for the equilibrium point $P_3^{[p\_ehp]}=(\mu \lambda ^{-1}, r \lambda ^{-1} (1-\mu \lambda ^{-1} K^{-1}) ,0)$ the feasibility condition requires $U_3^{[p\_ehp]}\ge 0$ which explicitly is given by $1\ge \mu \lambda ^{-1} K^{-1}$. Furthermore, the Jacobian matrix (6) evaluated at $P_3^{[p\_ehp]}$ gives one explicit eigenvalue which should be negative to ensure stability, i.e. $u+ae\mu \lambda ^{-1}+cer\lambda ^{-1}(1-\mu \lambda ^{-1}K^{-1})<0$ must be satisfied. Clearly, if the condition for feasibility of $P_3^{[p\_ehp]}$ holds, this eigenvalue is positive and thus $P_3^{[p\_ehp]}$ is unstable whenever feasible. Finally, the point $P_4^{[p\_ehp]}=(0,-(u \mu + ucL)e^{-1}c^{-2}L^{-1},-\mu c^{-1})$ is not feasible.

The equilibrium point $P_5^{[p\_ehp]}=(0,0,L)$ is always feasible and stable if

$$\begin{aligned} \frac{r}{a}<L. \end{aligned}$$

(7)

The point $P_6^{[p\_ehp]}=(X_6^{[p\_ehp]},0,Z_6^{[p\_ehp]})$, with explicit populations levels:

$$\begin{aligned} X_6^{[p\_ehp]}= \frac{urK-auKL}{a^2eKL+ur}, \quad Z_6^{[p\_ehp]}= \frac{L(aerK+ur)}{a^2eKL+ur}, \end{aligned}$$

is feasible if

$$\begin{aligned} \frac{r}{a} \ge L. \end{aligned}$$

(8)

The characteristic equation of the Jacobian matrix (6) evaluated at $P_6^{[p\_ehp]}$ can be factorized into the product of one linear equation and one quadratic equation providing one explicit eigenvalue producing the following condition, written both in implicit and explicit forms:

$$\begin{aligned} \lambda X_6^{[p\_ehp]}< c Z_6^{[p\_ehp]} + \mu , \quad \lambda < \frac{acerKL + ucrL+u \mu r + a^2 e \mu KL}{uK(r-aL)}, \end{aligned}$$

(9)

while the Routh–Hurwitz conditions for the remaining minor

$$\begin{aligned} \overline{J}_{P_6}^{[p\_ehp]}= \left( \begin{array}{c@{\quad }c} -\frac{ru(r-aL)}{ur+a^2eKL} &{} -\frac{auK(r-aL)}{ur+a^2eKL} \\ \frac{aerL(aeK+u)}{ur+a^2eKL} &{} -\frac{ru(aeK+u)}{ur+a^2eKL}\\ \end{array} \right) \end{aligned}$$

are always satisfied, if the feasibility condition (8) holds sharply, namely

$$\begin{aligned} {\text {tr}}(\overline{J}_{P_6}^{[p\_ehp]})=\frac{-ru(r -aL)-ruaeK-ru^2}{ur+ a^2eKL}< 0 \end{aligned}$$

(10)

and

$$\begin{aligned} {\text {det}}(\overline{J}_{P_6}^{[p\_ehp]})=\frac{(r-aL)(aeK+u)(a^2 uerKL+r^2 u^2)}{(a^2 eKL+ru)^2}>0. \end{aligned}$$

(11)

Thus, if the condition (9) is satisfied, equilibrium $P_6^{[p\_ehp]}$ is stable.

For the coexistence $P_7^{[p\_ehp]}=(X_7^{[p\_ehp]}, U_7^{[p\_ehp]}, Z_7^{[p\_ehp]})$, we find

$$\begin{aligned} X_7^{[p\_ehp]}= \frac{cZ_7^{[p\_ehp]}+\mu }{\lambda }, \quad U_7^{[p\_ehp]}= \frac{r}{\lambda } \left( 1 - \frac{\mu }{\lambda K}\right) - \frac{Z_7^{[p\_ehp]}}{\lambda } \left( a + \frac{rc}{\lambda K} \right) \end{aligned}$$

and

$$\begin{aligned} Z_7^{[p\_ehp]}= \frac{L}{K\lambda ^2 u + c^2 e rL} ( ae \mu \lambda K + u \lambda ^2 K + cer \lambda K - cer \mu ). \end{aligned}$$

Feasibility requirements for $U_7^{[p\_ehp]} \ge 0$ and $Z_7^{[p\_ehp]} \ge 0$ are given, respectively, by

$$\begin{aligned} \lambda\ge & {} \frac{au \lambda KL +rcuL+acerKL+a^2 e \mu KL+\mu r u}{u r K},\\ \mu\le & {} \frac{ae\mu \lambda K + u \lambda ^2 K + cer\lambda K}{cer}. \end{aligned}$$

which in turn reduce to

$$\begin{aligned} uk(r-aL) \lambda \ge rcuL+acerKL+a^2 e \mu KL+\mu r u, \end{aligned}$$

(12)

which is satisfied for

$$\begin{aligned} \lambda \ge \lambda _*, \quad \lambda _* = \frac{rcuL+acerKL+a^2 e \mu KL+\mu r u}{uk(r-aL)}, \end{aligned}$$

(13)

where $\lambda _*$ is the root of the equality associated to (12) when (8) holds, while in the opposite case no solution exists and $P_7^{[p\_ehp]}$ in unfeasible, and

$$\begin{aligned} \Psi (\lambda )= u \lambda ^2 K + e(aK\mu + crK) \lambda - cer \mu \ge 0 \end{aligned}$$

for which, denoting by $\lambda _{\pm }$ the roots of $\Psi (\lambda )$, the quadratic inequality is satisfied for

$$\begin{aligned} 0 \le \lambda \le \lambda _{\pm }. \end{aligned}$$

(14)

For stability, the diagonal entries in the generic Jacobian (6) simplify to

$$\begin{aligned} J^{[p\_ehp]}_{11}= -\frac{r}{K} X_7^{[p\_ehp]}, \quad J^{[p\_ehp]}_{22}= 0, \quad J^{[p\_ehp]} _{33}= -\frac{u}{L} Z_7^{[p\_ehp]}. \end{aligned}$$

Evaluating all the principal minors of the opposite of the Jacobian at coexistence, $-J(P_7^{[p\_ehp]})$, we find that it is positive definite. Thus, whenever feasible, $P_7^{[p\_ehp]}$ is stable:

$$\begin{aligned}&\frac{r}{K} X_7^{[p\_ehp]}>0, \quad \lambda ^2 U_7^{[p\_ehp]} X_7^{[p\_ehp]}>0,\\&\left( \frac{c^2 e r}{K} + \frac{u\lambda ^2}{L}\right) X_7^{[p\_ehp]} U_7^{[p\_ehp]} Z_7^{[p\_ehp]} > 0. \end{aligned}$$

In Table 1, we summarize the behaviour of the equilibrium points of model (1).

Table 1 Behaviour and feasibility and stability conditions of the equilibria of model (1)

2.3 Global stability for the equilibria of model (1)

Table 1 shows that of the seven equilibria in model (1), only three may be stable. In this section, we prove that their local stability, as proved through the analysis of the eigenvalues, also implies their global stability as well. To accomplish this task, suitable Lyapunov functions are constructed.

We now prove that feasibility of $P_7^{[p\_ehp]}$ implies its global asymptotic stability. Consider the following function:

$$\begin{aligned} V_7^{[p\_ehp]}(X(t),U(t),Z(t))= & {} \alpha _2 \left( X-X_7^{[p\_ehp]}-X_7^{[p\_ehp]}\ln \frac{X}{X_7^{[p\_ehp]}}\right) \\&+\,\alpha _1\left( U-U_7^{[p\_ehp]}-U_7^{[p\_ehp]}\ln \frac{U}{U_7^{[p\_ehp]}}\right) \\&+\,\alpha _0\left( Z-Z_7^{[p\_ehp]}-Z_7^{[p\_ehp]}\ln \frac{Z}{Z_7^{[p\_ehp]}}\right) , \end{aligned}$$

where $\alpha _2$, $\alpha _1$ and $\alpha _0$ are arbitrary positive constants. Differentiating along the solution trajectories of (1), we find

$$\begin{aligned} \frac{\mathrm{d}V_7^{[p\_ehp]}}{\mathrm{d}t}= & {} -\alpha _2 \frac{r}{K}\left( X-X_7^{[p\_ehp]}\right) ^2 -\alpha _0 \frac{u}{L} \left( Z-Z_7^{[p\_ehp]}\right) ^2 \\&+ \, \lambda (\alpha _1 -\alpha _2)\left( X-X_7^{[p\_ehp]}\right) \left( U-U_7^{[p\_ehp]}\right) \\&+ \, a (\alpha _0 e -\alpha _2)\left( X-X_7^{[p\_ehp]}\right) \left( Z-Z_7^{[p\_ehp]}\right) \\&+ \, c (\alpha _0 e -\alpha _1)\left( U-U_7^{[p\_ehp]}\right) \left( Z-Z_7^{[p\_ehp]}\right) . \end{aligned}$$

If we choose $\alpha _2=\alpha _1=\alpha _0 e$, then the above derivative is negative definite except at the equilibrium point $P_7^{[p\_ehp]}$, so it is a Lyapunov function. Hence, $P_7^{[p\_ehp]}$ is a globally stable equilibrium point whenever it is feasible.

Analogous results can be shown for the remaining two equilibria, $P_6^{[p\_ehp]}$ and $P_7^{[p\_ehp]}$.

For $P_5^{[p\_ehp]}$, we need to choose

$$\begin{aligned} V_5^{[p\_ehp]}(X(t),U(t),Z(t))=\beta _2 X + \beta _1 U +\beta _0\left( Z-Z_5^{[p\_ehp]}-Z_5^{[p\_ehp]}\ln \frac{Z}{Z_5^{[p\_ehp]}}\right) , \end{aligned}$$

with $\beta _2$, $\beta _1$ and $\beta _0$ positive constants to be determined. Differentiation along the system trajectories leads to

$$\begin{aligned} \frac{dV_5^{[p\_ehp]}}{dt}= & {} -\beta _2 \frac{r}{K}X^2 -\beta _0 \frac{u}{L} \left( Z-Z_5^{[p\_ehp]}\right) ^2 + a (\beta _0 e -\beta _2)XZ \\&+ \, \lambda (\beta _1 -\beta _2) XU + c (\beta _2 e -\beta _1) UZ + (\beta _2 r -\beta _0 e aL)X \\&+ \, (-\beta _1 \mu -\beta _0 e cL)U \end{aligned}$$

so that choosing $\beta _2=\beta _1=\beta _0 e$ and using the local stability condition (7), the above derivative of $V_5^{[p\_ehp]}$ is negative definite and the equilibrium point $P_5^{[p\_ehp]}$ is globally asymptotically stable.

Similarly, for equilibrium point $P_6^{[p\_ehp]}$ consider the following candidate Lyapunov function:

$$\begin{aligned} V_6^{[p\_ehp]}(X(t),U(t),Z(t))= & {} \gamma _2\left( X-X_6^{[p\_ehp]}-X_6^{[p\_ehp]}\ln \frac{X}{X_6^{[p\_ehp]}}\right) \\&+ \, \gamma _1 U + \gamma _0\left( Z-Z_6^{[p\_ehp]}-Z_6^{[p\_ehp]}\ln \frac{Z}{Z_6^{[p\_ehp]}}\right) , \end{aligned}$$

where $\gamma _2, \gamma _1$ and $\gamma _0$ are positive constants to be determined. Once more, differentiating $V_6^{[p\_ehp]}$ along the trajectories of (1) we find, after some algebraic manipulations,

$$\begin{aligned} \frac{dV_6^{[p\_ehp]}}{dt}= & {} -\gamma _2 \frac{r}{K}\left( X-X_6^{[p\_ehp]}\right) ^2 -\gamma _0 \frac{u}{L} \left( Z-Z_6^{[p\_ehp]}\right) ^2 \\&+\, a (\gamma _0 e -\gamma _2)\left( X-X_6^{[p\_ehp]}\right) \left( Z-Z_6^{[p\_ehp]}\right) + \lambda (\gamma _1 -\gamma _2) XU \\&+ \,c (\gamma _0 e -\gamma _1) UZ + \left( \gamma _2 \lambda X_6^{[p\_ehp]} -\gamma _0 e c Z_6^{[p\_ehp]} - \gamma _1 \mu \right) U. \end{aligned}$$

Choosing $\gamma _1=\gamma _2=\gamma _0 e$ and using the local stability condition (9), we find that the derivative of $V_6^{[p\_ehp]}$ is negative definite except at $P_6^{[p\_ehp]}$. Thus, the equilibrium point $P_6^{[p\_ehp]}$ is globally asymptotically stable.

Remark 1

These results indicate that if feasible, the equilibria $P_5^{[p\_ehp]}$, $P_6^{[p\_ehp]}$ and $P_7^{[p\_ehp]}$ of the system (1) are globally asymptotically stable. Indeed these three equilibria are mutually exclusive. This statement for $P_5^{[p\_ehp]}$ and $P_6^{[p\_ehp]}$ follows by comparing their respective feasibility and stability conditions in Table 1. Further, for $r< aL$, $P_5^{[p\_ehp]}$ is stable and $P_7^{[p\_ehp]}$ is unfeasible, because (12) does not hold. Conversely, for $r\ge aL$, $P_6^{[p\_ehp]}$ is feasible but then (9) and (12), (13) contradict each other, so that $P_6^{[p\_ehp]}$ and $P_7^{[p\_ehp]}$ are also excluding each other. These remarks suggest the existence of transcritical bifurcations linking these equilibria, a question that will be investigated analytically in the next section.

2.4 Transcritical bifurcations

To study the local bifurcations of the equilibrium points of model (1), we use Sotomayor’s theorem Perko (2001). The general second-order term of the Taylor expansion of f in (2) is given by

$$\begin{aligned}&D^2 f(P,\psi )(V,V) \nonumber \\&\quad = \left( \begin{array}{c} \frac{\partial ^2 f_1}{\partial X^2} \xi _1^2+\frac{\partial ^2 f_1}{\partial U^2} \xi _2^2 +\frac{\partial ^2 f_1}{\partial Z^2} \xi _3^2+2\frac{\partial ^2 f_1}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_1}{\partial X \partial Z} \xi _1 \xi _3+2\frac{\partial ^2 f_1}{\partial U \partial Z} \xi _2 \xi _3\\ \frac{\partial ^2 f_2}{\partial X^2} \xi _1^2+\frac{\partial ^2 f_2}{\partial U^2} \xi _2^2 +\frac{\partial ^2 f_2}{\partial Z^2} \xi _3^2+2\frac{\partial ^2 f_2}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_2}{\partial X \partial Z} {\xi _1}{\xi _3}+2\frac{\partial ^2 f_2}{\partial U \partial Z} {\xi _2}{\xi _3}\\ \frac{\partial ^2 f_3}{\partial X^2} \xi _1^2+\frac{\partial ^2 f_3}{\partial U^2} \xi _2^2 +\frac{\partial ^2 f_3}{\partial Z^2} \xi _3^2+2\frac{\partial ^2 f_3}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_3}{\partial X \partial Z} {\xi _1}{\xi _3}+2\frac{\partial ^2 f_3}{\partial U \partial Z} {\xi _2}{\xi _3} \end{array} \right) , \end{aligned}$$

(15)

where $\psi$ represents the parametric threshold and $\xi _1,\xi _2,\xi _3$ are the components of the eigenvector $V=(\xi _1,\xi _2,\xi _3)^T$ of the variations in X, U and Z.

2.4.1 Bifurcation of the equilibrium point $P_6^{[p\_ehp]}$

The axial equilibrium point $P_6^{[p\_ehp]}$ coincides with the equilibrium $P_5^{[p\_ehp]}$ at the parametric threshold $r^\dagger$ and with equilibrium $P_7^{[p\_eep]}$ at the parametric threshold $\lambda ^\dagger$, where

$$\begin{aligned} r^\dagger =aL, \quad \lambda ^\dagger = \frac{aeKL(cr+a \mu )+ur(\mu +cL)}{uK(r-aL)} \end{aligned}$$

(16)

when we compare the feasibility condition (8) of $P_6^{[p\_ehp]}$ together with the stability condition (7) of $P_5^{[p\_ehp]}$ as well as, respectively, the stability condition (9) of $P_6^{[p\_ehp]}$ and the feasibility condition (12) of the equilibrium $P_7^{[p\_ehp]}$.

The Jacobian matrix of the system (1) evaluated at $P_6^{[p\_ehp]}$ and at $r^\dagger$ is

$$\begin{aligned} J_{P_6}^{[p\_ehp]}(r^ \dagger ) = \left( \begin{array}{c@{\quad }c@{\quad }c} 0&{} 0 &{} 0\\ 0 &{} -cL-\mu &{} 0 \\ aeL &{} ceL &{} -u \\ \end{array} \right) . \end{aligned}$$

Its right and left eigenvectors, corresponding to the zero eigenvalue, are given by $V_1=\varphi _1(1, 0, aeL/u)^T$ and $Q_1=\omega _1(1, 0, 0)^T$, where $\varphi _1$ and $\omega _1$ are any nonzero real numbers. Differentiating partially the right-hand sides of the Eq. (1) with respect to r and calculating its Jacobian matrix, we find, respectively

$$\begin{aligned} f_r = \left( \begin{array}{c} X_6^{[p\_ehp]} (1- X_6^{[p\_ehp]} /K) \\ 0 \\ 0 \end{array} \right) , \quad Df_r = \left( \begin{array}{c@{\quad }c@{\quad }c} 1-\frac{1}{K} X_6^{[p\_ehp]} &{} 0 &{} 0 \\ 0 &{} 0&{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

After calculating $D^2 f$ in (15) evaluated at $P_6^{[p\_ehp]}$, the parametric threshold $r^\dagger$ and the eigenvector $V_1$, we can verify the following three conditions:

$$\begin{aligned}&\displaystyle {Q_1}^T f_r(P_6^{[p\_ehp]}, aL)=0, \\&\displaystyle {Q_1}^T[Df_r(P_6^{[p\_ehp]}, aL)V_1]=\varphi _1 \omega _1 \ne 0, \\&\displaystyle Q_1^T[D^2f_ r(P_6^{[p\_ehp]}, aL)(V_1,V_1) ]= -\omega _1 {\varphi _1}^2 \left( \frac{aL}{K}+\frac{2a^2 eL}{u} \right) \ne 0. \end{aligned}$$

When $P_6^{[p\_ehp]}$ coincides with the equilibrium $P_7^{[p\_ehp]}$ at the threshold $\lambda ^\dagger$, the Jacobian matrix of the system (1) is

$$\begin{aligned} J_{P_6}^{[p\_ehp]}(\lambda ^ \dagger ) = \left( \begin{array}{c@{\quad }c@{\quad }c} -\frac{ru(r-aL)}{ur+a^2eKL} &{} -\frac{L(acerK+a^2 e \mu K+cru)+ru \mu }{ur+a^2eKL} &{} \frac{a^2 u KL-aruK}{ur+a^2eKL} \\ 0 &{} 0 &{} 0 \\ \frac{L(a^2 e^2 rK+aeru)}{ur+a^2eKL} &{} \frac{L(ac e^2 rK+ceru)}{ur+a^2eKL}&{} -\frac{aeruK+ru^2}{ur+a^2eKL} \\ \end{array} \right) .\qquad \end{aligned}$$

(17)

For the zero eigenvalue in (17), the corresponding eigenvector is $V_2=\varphi _2(1,v_1,v_2)^T$, where $\varphi _2$ is any nonzero real number and $v_1$ and $v_2$ are

$$\begin{aligned} v_1=\frac{-a^3eKL^2-L(aru-a^2erK)+r^2u)}{a^2ceKL^2+L(-2acerK-a^2e\mu K-cru)-\mu ru} \end{aligned}$$

and

$$\begin{aligned} v_2=\frac{L^2(a^2ce^2rK+a^3e^2\mu K+2aceru)+uL(ae\mu r-cer^2)}{a^2ceuKL^2+L(-2aceruK-a^2e\mu uK-cru^2)-\mu ru^2}. \end{aligned}$$

(18)

Besides that, $Q_2=\omega _2(0,1,0)^T$ represents the eigenvector corresponding to the zero eigenvalue of $(J_{P_6}^{[p\_ehp]}(r^ \dagger ))^T$, where $\omega _2$ is any nonzero real number. Differentiating partially the right hand sides of (1) with respect to $\lambda$ and calculating its Jacobian matrix, we respectively find

$$\begin{aligned} f_{\lambda } = \left( \begin{array}{c} -X_6^{[p\_ehp]} U_6^{[p\_ehp]} \\ X_6^{[p\_ehp]} U_6^{[p\_ehp]} \\ 0 \end{array} \right) , \quad Df_{\lambda } = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} {-X_6}^{[p\_ehp]} &{} 0 \\ 0 &{} {X_6}^{[p\_ehp]} &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

After calculating $D^2 f$ in (15) evaluated at $P_6^{[p\_ehp]}$, the parametric threshold $\lambda ^\dagger$ and the eigenvector $V_2$ we can verify the following three conditions, the latter being satisfied in view of (18) and (16):

$$\begin{aligned}&{Q_2}^T f_{\lambda }(P_6^{[p\_ehp]}, \lambda ^\dagger )=0, \quad {Q_2}^T[Df_{\lambda }(P_6^{[p\_ehp]},\lambda ^\dagger )V_2]=\varphi _2 \omega _2 v_1 {X_6}^{[p\_ehp]} \ne 0,\\&Q_2^T[D^2f_{\lambda } (P_6^{[p\_ehp]}, \lambda ^\dagger )(V_2,V_2) ]= 2 v_1 \omega _2 {\varphi _2}^2 \left( \lambda ^\dagger - c v_2 \right) \ne 0. \end{aligned}$$

Thus, all the conditions for transcritical bifurcation are satisfied. Figure 1 illustrates the simulation explicitly showing the transcritical bifurcation between $P_6^{[p\_ehp]}$ and $P_5^{[p\_ehp]}$ for the chosen parameter values (see the caption of Fig. 1a) when the parameter r crosses a critical value $r^\dagger =aL = 1$ given by (16) and the transcritical bifurcation between $P_6^{[p\_ehp]}$ and $P_7^{[p\_ehp]}$ for the chosen parameters values (see the caption of Fig. 1b) when the parameter $\lambda$ crosses a critical value $\lambda ^\dagger \approx 1.072$ given by (16).

Fig. 1

a Transcritical bifurcation between $P_6^{[p\_ehp]}$ and $P_5^{[p\_ehp]}$ for the parameter values: $\mu =0.01$, $K = L = a= u=1$, $e = c = 0.3$ and $\lambda =1.01$. Initial conditions $X_0 = U_0 = Z_0 = 0.01$. The equilibrium $P_5^{[p\_ehp]}$ is stable for $\lambda \in [0.1, 1.01]$ and $P_6^{[p\_ehp]}$ is stable past $\lambda =1.01$. The vertical line shows the transcritical bifurcation threshold. b Transcritical bifurcation between $P_6^{[p\_ehp]}$ and $P_7^{[p\_ehp]}$ for the parameter values: $\mu =0.01$, $K = L = a= u=1$, $e = c = 0.3$ and $r=1.6$ and the same initial conditions. The equilibrium $P_{6}^{[p\_ehp]}$ is stable for $\lambda \in [0.1, 1.072]$ and $P_{7}^{[p\_ehp]}$ is stable past $\lambda =1.072$. The vertical line has the same meaning as in (a)

3 The mathematical model with explicit resources

Now, we render the hidden resource for the predator explicit, naming it Y. The model is denoted with the superscript $[p\_eep]$, where the first “p” refers to predators and the last one to prey, the first “e” stands for “epidemics” (in the prey) and the second one stands for explicit resource for the predator. The model, in which all the parameters are nonnegative, reads

$$\begin{aligned}&\displaystyle \frac{\mathrm{d}X}{\mathrm{d}t}=r X \left( 1- \frac{X}{K} \right) - a ZX - \lambda XU,\nonumber \\&\displaystyle \frac{\mathrm{d}U}{\mathrm{d}t}=\lambda XU - c ZU - \mu U,\nonumber \\&\displaystyle \frac{\mathrm{d}Y}{\mathrm{d}t}=s Y \left( 1- \frac{Y}{H} \right) - b YZ,\nonumber \\&\displaystyle \frac{\mathrm{d}Z}{\mathrm{d}t}= -m Z^2 + e (aXZ + bYZ + cUZ). \end{aligned}$$

(19)

The first and second equations of model (19), respectively representing the healthy and infected prey, have the same meaning as described for model (1). The third equation describes the alternative prey population dynamics. The first term on the right-hand side expresses logistic growth with s being the per capita net reproduction rate and H the environment carrying capacity. The second term models hunting of Y by the predator at rate b. The fourth equation describes the predator population dynamics and is essentially the same as described for (1), with an additional gain due to the hunting of the alternative prey.

3.1 Boundedness

The proof for system (19) follows a similar pattern as in Sect. 2.1 and is, therefore, omitted. Setting $\psi (t)=X(t)+U(t)+Y(t)+Z(t)$, for an arbitrary $0<\eta < \mu$, we find an estimate similar to the one in Eq. (5), where only the definition of M slightly changes, again ensuring boundedness of all the ecosystem populations.

3.2 Local stability analysis of the model (19)

The Jacobian matrix of system (19) is given by

$$\begin{aligned} J^{[p\_eep]} = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} J_{11}^{[p\_eep]} &{} - \lambda X &{} 0 &{} -aX \\ \lambda U &{} - cZ + \lambda X - \mu &{} 0 &{} -cU\\ 0 &{} 0 &{} s- \frac{2s}{H}Y - bZ &{} -bY\\ aeZ &{} ceZ &{} beZ &{} J_{44}^{[p\_eep]} \end{array} \right) \end{aligned}$$

(20)

with

$$\begin{aligned} J_{11}^{[p\_eep]}=r - \frac{2r}{K}X - aZ - \lambda U, \quad J_{44}^{[p\_eep]}=eaX + ebY + ecU - 2mZ. \end{aligned}$$

There are 13 possible equilibria for model (19). The four always unstable points are the origin $P_1^{[p\_eep]}=(0,0,0,0)$, with eigenvalues $r, \mu ,$ s, 0, $P_2^{[p\_eep]}=(K,0,0,0)$, with eigenvalues $-r, -\mu , s, eaK$, $P_3^{[p\_eep]}=(0,0,H,0)$, with eigenvalues r, $-\mu$, $-s$, ebH and $P_4^{[p\_eep]}=(K,0,H,0)$, with eigenvalues $-r, -s, -\mu +\lambda K, aeK+ebH$.

Further, the point $P_5^{[p\_eep]}=(X_5^{[p\_eep]}, U_5^{[p\_eep]}, 0, 0)$, where $X_5^{[p\_eep]}=\mu \lambda ^{-1}$ and $U_5^{[p\_eep]}= r \lambda ^{-1} - r \mu \lambda ^{-2} K^{-1}$, which is feasible if $\mu \le \lambda K$ is unconditionally unstable because the Jacobian (20) evaluated at the $P_5^{[p\_eep]}$ has two explicit eigenvalues, $ea \mu \lambda ^{-1} + ecr \lambda ^{-1} - ecr \mu \lambda ^{-2} K^{-1}$ and $s>0$. Similarly, the equilibrium $P_8^{[p\_eep]}=(\mu \lambda ^{-1}, - r \lambda ^{-1} + r \mu \lambda ^{-2} K^{-1}, H, 0)$ is feasible if

$$\begin{aligned} \mu \ge \lambda K, \end{aligned}$$

(21)

but unconditionally unstable when feasible, since one of the two explicit eigenvalues of the Jacobian at $P_8^{[p\_eep]}$ is positive in view of (21):

$$\begin{aligned} -s<0, \quad ebH + \frac{ea \mu }{\lambda } - \frac{ecr}{\lambda } \left( 1-\frac{\mu }{\lambda K} \right) >0. \end{aligned}$$

There are also two unconditionally unfeasible points:

$$\begin{aligned} P_6^{[p\_eep]}= \left( 0, - \frac{m \mu }{ec^2}, 0, - \frac{\mu }{c} \right) , \quad P_7^{[p\_eep]}=(0, U_7^{[p\_eep]}, Y_7^{[p\_eep]}, Z_7^{[p\_eep]}), \end{aligned}$$

with

$$\begin{aligned} U_7^{[p\_eep]}= \frac{ecsbH - e \mu b^2 H - ms \mu }{c^2 es}, \quad Y_7^{[p\_eep]}=\frac{\mu b H + csH}{cs}, \quad Z_7^{[p\_eep]}= - \frac{\mu }{c}. \end{aligned}$$

The equilibrium $P_9^{[p\_eep]}=(X_9^{[p\_eep]}, 0, 0, Z_9^{[p\_eep]})$, where

$$\begin{aligned} X_9^{[p\_eep]}=\frac{mrK}{a^2 eK+mr}, \quad Z_9^{[p\_eep]}=\frac{aerK}{a^2eK+mr} \end{aligned}$$

is always feasible and conditionally stable, because two explicit eigenvalues of the Jacobian at $P_9^{[p\_eep]}$ give the stability conditions

$$\begin{aligned} s< \frac{aberK}{a^2eK+mr}, \quad \lambda < \frac{aeK(a \mu + cr)+mr \mu }{mrK}. \end{aligned}$$

(22)

while the Routh–Hurwitz conditions for the remaining minor $\overline{J}_{P_9}^{[p\_eep]}$ hold

$$\begin{aligned} -\text {tr}(\overline{J}_{P_9}^{[p\_eep]})= & {} \frac{r}{K}X_9^{[p\_eep]} + mZ_9^{[p\_eep]}>0, \\ \det (\overline{J}_{P_9}^{[p\_eep]})= & {} \frac{mr}{K}X_9^{[p\_eep]} Z_9^{[p\_eep]}+a^2eX_9^{[p\_eep]}Z_9^{[p\_eep]}>0. \end{aligned}$$

The point $P_{10}^{[p\_eep]}=(0, 0, Y_{10}^{[p\_eep]}, Z_{10}^{[p\_eep]})$, with

$$\begin{aligned} Y_{10}^{[p\_eep]}=\frac{msH}{b^2eH+ms}, \quad Z_{10}^{[p\_eep]}=\frac{ebsH}{b^2eH+ms} \end{aligned}$$

is similarly always feasible and conditionally stable. From the Jacobian at ${P_{10}}^{[p\_eep]}$, one explicit eigenvalue is $- c Z_{10}^{[p\_eep]} - \mu < 0$ while another explicit eigenvalue provides the stability condition

$$\begin{aligned} Z_{10}^{[p\_eep]}= \frac{abesH}{b^2eH+ms} > \frac{r}{a}. \end{aligned}$$

(23)

The Routh–Hurwitz criterion on the remaining minor $\overline{J}_{P10}^{[p\_eep]}$ holds

$$\begin{aligned} -\text {tr}(\overline{J}_{P_{10}}^{[p\_eep]})= & {} \frac{s}{H}Y_{10}^{[p\_eep]} + mZ_{10}^{[p\_eep]}>0, \\ \det (\overline{J}_{P_{10}}^{[p\_eep]})= & {} \frac{ms}{H}Y_{10}^{[p\_eep]}Z_{10}^{[p\_eep]} +b^2eY_{10}^{[p\_eep]}Z_{10}^{[p\_eep]}>0.\\ \end{aligned}$$

The equilibrium $P_{11}^{[p\_eep]}=(X_{11}^{[p\_eep]}, 0, Y_{11}^{[p\_eep]}, Z_{11}^{[p\_eep]})$, with

$$\begin{aligned} X_{11}^{[p\_eep]}= & {} K - \frac{aK}{r}Z_{11}^{[p\_eep]}, \quad Y_{11}^{[p\_eep]}=H - \frac{bH}{s}Z_{11}^{[p\_eep]}, \\ Z_{11}^{[p\_eep]}= & {} \frac{rs(beH+aeK)}{a^2esK+b^2erH+mrs} \end{aligned}$$

is feasible if

$$\begin{aligned} r \ge aZ_{11}^{[p\_eep]}=\frac{abesH}{b^2eH+ms}, \quad s \ge bZ_{11} ^{[p\_eep]} =\frac{aberK}{a^2 eK+mr}. \end{aligned}$$

(24)

The second condition can be rewritten giving either an upper bound on r or no bound at all, respectively, if $abeK>ms$ holds or not. In the former case, the condition is

$$\begin{aligned} r \le \frac{a^2eKs}{abeK-ms}, \quad abeK>ms. \end{aligned}$$

(25)

Its Jacobian has one explicit eigenvalue, providing the stability condition

$$\begin{aligned} \lambda X_{11}^{[p\_eep]} < \mu + c Z_{11}^{[p\_eep]}, \end{aligned}$$

(26)

which explicitly becomes

$$\begin{aligned} r [ces (aK+bH) + (\mu -\lambda K) (b^2 e H + ms)] > -aes K (bH \lambda + a\mu ), \end{aligned}$$

(27)

so that if $ces (aK+bH) + (\mu -\lambda K) (b^2 e H + ms)>0$ no constraint on r arises, while conversely we must have

$$\begin{aligned} r< \frac{aes K (bH \lambda + a\mu )}{(\lambda K - \mu ) (b^2 e H + ms) - ces (aK+bH)}, \\ \nonumber \quad ces (aK+bH) + \mu (b^2 e H + ms)<\lambda K (b^2 e H + ms). \end{aligned}$$

(28)

Besides that, the remaining submatrix of the Jacobian, $-\overline{J}_{P_{11}}^{[p\_eep]}$, is positive definite, since its principal minors are all positive, so no further stability conditions arise

$$\begin{aligned}&\displaystyle \frac{r}{K}X_{11}^{[p\_eep]}> 0, \quad \frac{rs}{HK}X_{11}^{[p\_eep]} Y_{11}^{[p\_eep]}> 0, \\&\displaystyle \quad \left( \frac{mrs}{HK} +\frac{a^2es}{H}+\frac{b^2er}{K}\right) X_{11}^{[p\_eep]}Y_{11}^{[p\_eep]}Z_{11}^{[p\_eep]} > 0,\\ \end{aligned}$$

The equilibrium $P_{12}^{[p\_eep]}=(X_{12}^{[p\_eep]}, U_{12}^{[p\_eep]}, 0, Z_{12}^{[p\_eep]})$, with

$$\begin{aligned} X_{12}^{[p\_eep]}= & {} \frac{c^2 erK + ace \mu K + m \mu \lambda K}{c^2er+ m \lambda ^2 K}, \quad Z_{12}^{[p\_eep]}=- \frac{\mu }{c} + \frac{\lambda }{c}X_{12}^{[p\_eep]},\\ \quad U_{12}^{[p\_eep]}= & {} \frac{a \mu }{c \lambda } + \frac{r}{\lambda }- \frac{r}{\lambda K}X_{12}^{[p\_eep]} - \frac{a}{c} X_{12}^{[p\_eep]} \end{aligned}$$

is feasible if

$$\begin{aligned} \lambda \ge \frac{a^2 e \mu K+mr \mu +acerK}{mrK} \end{aligned}$$

(29)

and $\mu \le \lambda K(rc + a \mu ) (rc)^{-1}$. The latter can be rewritten as

$$\begin{aligned} \mu \le \frac{cr \lambda K}{cr-a \lambda K}, \quad cr > a \lambda K, \end{aligned}$$

(30)

while in the case for which the second inequality in (30) does not hold, no solution exists for $\mu$ and the equilibrium $P_{12}^{[p\_eep]}$ is, therefore, unfeasible.

Again, one eigenvalue is explicit, to give the stability condition

$$\begin{aligned} \lambda > \frac{cer(cs+b \mu )+ms \lambda ^2 K}{beK(cr+a \mu )}. \end{aligned}$$

(31)

The explicit condition (31) in terms of $\lambda$ hinges on the roots $\lambda _{\pm }$ of the quadratic

$$\begin{aligned} \Phi (\lambda )=msK \lambda ^2 - beK (cr+a \mu )\lambda + cer(cs+b \mu ) <0. \end{aligned}$$

(32)

If the discriminant of $\Phi (\lambda )$ is negative, no solution of (32) exists, while in the opposite case we find that the stability conditions become

$$\begin{aligned} \lambda _{-} \le \lambda \le \lambda _{+}, \quad b^2eK(cr+a\mu )^2 \ge 4cmrs(cs+b\mu ). \end{aligned}$$

(33)

Also, no further stability conditions arise, as the submatrix

$$\begin{aligned} \overline{J}_{P_{12}}^{[p\_eep]} = \left( \begin{array}{c@{\quad }c@{\quad }c} -\frac{r}{K} X_{12}^{[sp\_ep]} &{} - \lambda X_{12}^{[sp\_ep]} &{} -aX_{12} ^{[sp\_ep]} \\ \lambda U_{12}^{[sp\_ep]} &{} 0 &{} -cU_{12} ^{[sp\_ep]} \\ aeZ_{12}^{[sp\_ep]} &{} ceZ_{12}^{[sp\_ep]} &{} -mZ_{12}^{[sp\_ep]} \\ \end{array} \right) \end{aligned}$$

is positive definite:

$$\begin{aligned}&\displaystyle \frac{r}{K}X_{12}^{[p\_eep]}> 0, \quad \lambda ^2 X_{12}^{[p\_eep]} U_{12}^{[p\_eep]}> 0,\\&\displaystyle \quad \left( m\lambda ^2 + \frac{c^2 er}{K}\right) X_{12}^{[p\_eep]} U_{12}^{[p\_eep]} Z_{12}^{[p\_eep]} > 0. \end{aligned}$$

The coexistence equilibrium $P_{13}^{[p\_eep]}=(X_{13}^{[p\_eep]}, U_{13}^{[p\_eep]}, Y_{13}^{[p\_eep]}, Z_{13}^{[p\_esp]})$ can also be explicitly evaluated

$$\begin{aligned} X_{13}^{[p\_eep]}= & {} \frac{\lambda K(bcesH+b^2 e \mu H + ms \mu )+c^2 ersK+aces \mu K}{\lambda ^2 K(b^2 eH+ms)+ers c^2},\\ U_{13}^{[p\_eep]}= & {} \left[ \lambda ^2 K(b^2 eH+ms)+ers c^2 \right] ^{-1} [\lambda K(b^2 erH +mrs-abesH) \\&-aesK(rc+a \mu ) - berH(sc + b \mu ) - mrs \mu ] , \\ Y_{13}^{[p\_eep]}= & {} \frac{\lambda HK(-bcer -abe \mu )+c^2ersH+bcer \mu H+ms \lambda ^2 HK}{\lambda ^2 K(b^2 eH+ms)+ers c^2},\\ Z_{13}^{[p\_eep]}= & {} \frac{aes \mu \lambda K + cers \lambda K +bes \lambda ^2 HK-cers \mu }{\lambda ^2 K(b^2 eH+ms)+ers c^2}. \end{aligned}$$

The feasibility requirements are

$$\begin{aligned}&r \ge \frac{aes K (bH \lambda + a\mu )}{(\lambda K - \mu ) (b^2 e H + ms) - ces (aK+bH)}, \nonumber \\&\quad ces (aK+bH) + \mu (b^2 e H + ms)<\lambda K (b^2 e H + ms); \end{aligned}$$

(34)

$$\begin{aligned}&\lambda \le \frac{cer(cs+b \mu )+ms \lambda ^2 K}{beK(cr+a \mu )}; \end{aligned}$$

(35)

$$\begin{aligned}&\mu \le \frac{\lambda K(b \lambda H+cr+a \mu )}{rc}. \end{aligned}$$

(36)

These conditions can be made explicit in terms of $\lambda$ by considering $\Phi _1(\lambda )\ge 0$

$$\begin{aligned} \Phi _1(\lambda )= [ rK (b^2 e H + ms) -aes K bH] \lambda - a^2es K \mu - r [\mu (b^2 e H + ms) +ces (aK+bH)] \end{aligned}$$

whose root $\lambda _0$ is positive if

$$\begin{aligned} r (b^2 e H + ms) \ge aes bH \end{aligned}$$

(37)

in which case the inequality is satisfied for $\lambda >\lambda _0$, while in the opposite case, for which (37) does not hold, no solution exists, and we have to consider the following inequalities:

$$\begin{aligned} \Phi _2(\lambda )= & {} mKs \lambda ^2 - \lambda beK(cr+a \mu ) + cer(cs+b \mu ) \ge 0, \\ \Phi _3(\lambda )= & {} b KH \lambda ^2 + \lambda K(cr+a \mu ) - cr \mu \ge 0. \end{aligned}$$

If the respective roots of the associated equalities are denoted by $\lambda _{\pm }^{(k)}$, $k=2,3$, feasibility is ensured for $\lambda \ge \lambda _0$, $\lambda _-^{(2)} \ge \lambda \ge 0$ or $\lambda \ge \lambda _+^{(2)}$, $0 \le \lambda \le \lambda _+^{(3)}$, i.e. in the interval

$$\begin{aligned} \min \left\{ \lambda _+^{(3)}, \lambda _-^{(2)} \right\} \ge \lambda \ge \max \left\{ \lambda _0, \lambda _+^{(2)} \right\} . \end{aligned}$$

(38)

The diagonal of the Jacobian at $P_{13}^{[p\_eep]}$ simplifies using the equilibrium equations:

$$\begin{aligned} J_{11}=-\frac{r}{K}X_{13}^{[p\_eep]}, \quad J_{33}=- \frac{s}{H} Y_{13}^{[p\_eep]} , \quad J_{44}= -mZ_{13} ^{[p\_eep]}. \end{aligned}$$

Now, $-J_{P_{13}}^{[p\_eep]}$ is positive definite because its principal minors are

$$\begin{aligned}&\displaystyle \frac{r}{K} X_{13}^{[p\_eep]}> 0, \quad \lambda ^2 U_{13}^{[p\_eep]} X_{13}^{[p\_eep]}> 0, \quad \frac{\lambda ^2 s}{H}X_{13}^{[p\_eep]} U_{13}^{[p\_eep]} Y_{13}^{[p\_eep]}> 0,\\&\displaystyle \left( \frac{s}{H}\left( \lambda ^2 m+\frac{rec^2}{K}\right) + b^2m\lambda ^2\right) X_{13}^{[p\_eep]} U_{13}^{[p\_eep]} Y_{13}^{[p\_eep]} Z_{13}^{[p\_eep]} > 0. \end{aligned}$$

Thus, whenever feasible, coexistence is unconditionally stable. In Table 2, we summarize the behaviour of the equilibrium points of model (19).

Table 2 Behaviour and feasibility and stability conditions of the equilibria of model (19)

3.3 Global stability for the equilibria of model (19)

We prove the global stability for the equilibria of (19) following the pattern of Sect. 2.3. For this reason, we just summarize the results.

For each equilibrium, se select the following Lyapunov functions candidates, using always the same positive coefficients $\delta _3$, $\delta _2$, $\delta _1$ and $\delta _0$, whose specific choice will possibly be different for each equilibrium, though:

$$\begin{aligned} W_{13}^{[p\_eep]}(X(t),U(t),Y(t),Z(t))= & {} \delta _3 \left( X-X_{13}^{[p\_eep]}-X_{13}^{[p\_eep]}\ln \frac{X}{X_{13}^{[p\_eep]}}\right) \\&+\,\delta _2\left( U-U_{13}^{[p\_eep]}-U_{13}^{[p\_eep]}\ln \frac{U}{U_{13}^{[p\_eep]}}\right) \\&+\,\delta _1\left( Y-Y_{13}^{[p\_eep]}-Y_{13}^{[p\_eep]}\ln \frac{Y}{Y_{13}^{[p\_eep]}}\right) \\&+\,\delta _0\left( Z-Z_{13}^{[p\_eep]}-Z_{13}^{[p\_eep]}\ln \frac{Z}{Z_{13}^{[p\_eep]}}\right) , \end{aligned}$$

Differentiating along the trajectories we find

$$\begin{aligned} \frac{\mathrm{d}W_{13}^{[p\_eep]}}{\mathrm{d}t}= & {} -\delta _3 \frac{r}{K}\left( X-X_{13}^{[p\_eep]}\right) ^2 -\delta _1 \frac{s}{H} \left( Y-Y_{13}^{[p\_eep]}\right) ^2 \\&- \,m\delta _0 \left( Z-Z_{13}^{[p\_eep]}\right) ^2 + \lambda (\delta _2 -\delta _3)\left( X-X_{13}^{[p\_eep]}\right) \left( U-U_{13}^{[p\_eep]}\right) \\&+ \,a (\delta _0 e -\delta _3)\left( X-X_{13}^{[p\_eep]}\right) \left( Z-Z_{13}^{[p\_eep]}\right) \\&+ \, b (\delta _0 e -\delta _1)\left( Y-Y_{13}^{[p\_eep]}\right) \left( Z-Z_{13}^{[p\_eep]}\right) \\&+ \, c (\delta _0 e - \delta _2)\left( U-U_{13}^{[p\_eep]}\right) \left( Z-Z_{13}^{[p\_eep]}\right) . \end{aligned}$$

which is negative definite, giving global stability, if we choose

$$\begin{aligned} \delta _3=\delta _2=\delta _1=\delta _0 e. \end{aligned}$$

(39)

The Lyapunov function candidates for the remaining equilibria are

$$\begin{aligned}&W_9^{[p\_eep]}(X(t),U(t),Y(t),Z(t))\\&\quad =\delta _3 \left( X-X_{9}^{[p\_eep]}-X_{9}^{[p\_eep]}\ln \frac{X}{X_{9}^{[p\_eep]}}\right) \\&\qquad +\,\delta _2 U +\delta _1 Y +\delta _0\left( Z-Z_{9}^{[p\_eep]}-Z_{9}^{[p\_eep]}\ln \frac{Z}{Z_{9}^{[p\_eep]}}\right) ,\\&W_{10}^{[p\_eep]}(X(t),U(t),Y(t),Z(t))\\&\quad = \delta _1\left( Y-Y_{10}^{[p\_eep]}-Y_{10}^{[p\_eep]}\ln \frac{Y}{Y_{10}^{[p\_eep]}}\right) \\&\qquad + \, \delta _3 X + \delta _2 U +\delta _0\left( Z-Z_{10}^{[p\_eep]}-Z_{10}^{[p\_eep]}\ln \frac{Z}{Z_{10}^{[p\_eep]}}\right) ,\\&W_{11}^{[p\_eep]}(X(t),U(t),Y(t),Z(t))\\&\quad =\delta _3 \left( X-X_{11}^{[p\_eep]}-X_{11}^{[p\_eep]}\ln \frac{X}{X_{11}^{[p\_eep]}}\right) +\delta _2 U \\&\qquad + \, \delta _1\left( Y-Y_{11}^{[p\_eep]}-Y_{11}^{[p\_eep]}\ln \frac{Y}{Y_{11}^{[p\_eep]}}\right) \\&\qquad + \, \delta _0\left( Z-Z_{11}^{[p\_eep]}-Z_{11}^{[p\_eep]}\ln \frac{Z}{Z_{11}^{[p\_eep]}}\right) ,\\&W_{12}^{[p\_eep]}(X(t),U(t),Y(t),Z(t))\\&\quad =\delta _3 \left( X-X_{12}^{[p\_eep]}-X_{12}^{[p\_eep]}\ln \frac{X}{X_{12}^{[p\_eep]}}\right) +\delta _1 Y \\&\qquad + \, \delta _2\left( U-U_{12}^{[p\_eep]}-U_{12}^{[p\_eep]}\ln \frac{U}{U_{12}^{[p\_eep]}}\right) \\&\qquad + \, \delta _0\left( Z-Z_{12}^{[p\_eep]}-Z_{12}^{[p\_eep]}\ln \frac{Z}{Z_{12}^{[p\_eep]}}\right) \end{aligned}$$

and upon differentiation, they are all seen to produce negative definite derivatives using always the choice (39).

Remark 2

These results indicate that there is no possibility of Hopf bifurcations at all the equilibria also of the system (19).

3.4 Transcritical bifurcations

Similar to what was done in Sect. 2.4, we also verify the transversality conditions required for the transcritical bifurcations involving the equilibria of model (19).

3.4.1 The pairs $P_{11}^{[p\_eep]}-P_9^{[p\_eep]}$ and $P_{11}^{[p\_eep]}-P_{10}^{[p\_eep]}$

The equilibrium point $P_{11}^{[p\_eep]}$ coincides with the equilibrium $P_9^{[p\_eep]}$ and with equilibrium $P_{10}^{[p\_eep]}$, respectively, at the parametric thresholds

$$\begin{aligned} s^*=\frac{aberK}{a^2 eK+mr}, \quad r^*= \frac{abesH}{b^2eH+ms}, \end{aligned}$$

(40)

when we compare the second feasibility condition (24) and the first stability condition (22) and, similarly, the second feasibility condition (24) and the stability condition (23).

The Jacobian of (19) evaluated at $P_{11}^{[p\_eep]}$ with $s=s^*$ is

$$\begin{aligned} J_{P_{11}}^{[p\_eep]}(s^ *) =\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -\frac{mr^2}{mr+a^2eK}&{} -\frac{mr\lambda K}{mr+a^2eK} &{} 0 &{} -\frac{amrK}{mr+a^2eK} \\ 0 &{} \frac{mr\lambda K +mr\mu -acerK -a^2 e\mu K}{mr+a^2eK} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \frac{a^2 e^2 rK}{mr+a^2eK} &{} \frac{ace^2rK}{mr+a^2eK} &{} \frac{abe^2rK}{mr+a^2eK} &{} - \frac{aemrK}{mr+a^2eK}\\ \end{array} \right) \end{aligned}$$

and its right and left eigenvectors, corresponding to zero eigenvalue, are given by $V_3=\varphi _3(1, 0, -(mr+a^2eK)/abeK, -r/aK)^T$ and $Q_3=\omega _3(0, 0,1, 0)^T$, where $\varphi _3$ and $\omega _3$ are any nonzero real number. Differentiating partially the right-hand sides of the system equations (19) with respect to s and calculating its Jacobian matrix we find

$$\begin{aligned} f_s = \left( \begin{array}{c} 0 \\ 0\\ Y_{11}^{[p\_eep]} (1- Y_{11}^{[p\_eep]} /H) \\ 0 \end{array} \right) , \quad Df_s = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0&{}0 \\ 0 &{} 0 &{} 0&{}0 \\ 0 &{} 0 &{} 1-\frac{2}{H} Y_{11}^{[p\_eep]} &{}0\\ 0 &{} 0&{} 0&{} 0 \end{array} \right) . \end{aligned}$$

Denoting by $P = (X, U, Y,Z)^T$ the population vector and by $f = (f_1,f_2,f_3,f_4)^T$ the right-hand side of (19), by $\psi$ a generic threshold parameter and by $\xi _1,\xi _2,\xi _3,\xi _4$ the components of the eigenvector $V=(\xi _1,\xi _2,\xi _3,\xi _4)^T$ of variations in X, U, Y and Z, let us define $D^2 f(P,\psi )(V,V)$ by

$$\begin{aligned} D^2 f(P,\psi )(V,V)=\left( \begin{array}{c} D^2_{11} \\ D^2_{21} \\ D^2_{31} \\ D^2_{41} \end{array} \right) , \end{aligned}$$

(41)

where

$$\begin{aligned} D^2_{11}= & {} \frac{\partial ^2 f_1}{\partial X^2} \xi _1^2+\frac{\partial ^2 f_1}{\partial U^2} \xi _2^2 +\frac{\partial ^2 f_1}{\partial Y^2} \xi _3^2+\frac{\partial ^2 f_1}{\partial Z^2} \xi _4^2+2\frac{\partial ^2 f_1}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_1}{\partial X \partial Y} {\xi _1}{\xi _3} \\&+ \, 2\frac{\partial ^2 f_1}{\partial X \partial Z} {\xi _1}{\xi _4} + 2\frac{\partial ^2 f_1}{\partial U \partial Y} \xi _2{\xi _3}+2\frac{\partial ^2 f_1}{\partial U \partial Z} {\xi _2}{\xi _4}+2\frac{\partial ^2 f_1}{\partial Y \partial Z} {\xi _3}{\xi _4},\\ D^2_{21}= & {} \frac{\partial ^2 f_2}{\partial X^2} \xi _1^2+\frac{\partial ^2 f_2}{\partial U^2} \xi _2^2+\frac{\partial ^2 f_2}{\partial Y^2} \xi _3^2+\frac{\partial ^2 f_2}{\partial Z^2} \xi _4^2+2\frac{\partial ^2 f_2}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_2}{\partial X \partial Y} {\xi _1}{\xi _3} \\&+ \, 2\frac{\partial ^2 f_2}{\partial X \partial Z} {\xi _1}{\xi _4} + 2\frac{\partial ^2 f_2}{\partial U \partial Y} {\xi _2}{\xi _3}+2\frac{\partial ^2 f_2}{\partial U \partial Z} {\xi _2}{\xi _4}+2\frac{\partial ^2 f_2}{\partial Y \partial Z} {\xi _3}{\xi _4},\\ D^2_{31}= & {} \frac{\partial ^2 f_3}{\partial X^2} \xi _1^2+\frac{\partial ^2 f_3}{\partial U^2} \xi _2^2+\frac{\partial ^2 f_3}{\partial Y^2} \xi _3^2+\frac{\partial ^2 f_3}{\partial Z^2} \xi _4^2+2\frac{\partial ^2 f_3}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_3}{\partial X \partial Y} {\xi _1}{\xi _3} \\&+ \, 2\frac{\partial ^2 f_3}{\partial X \partial Z} {\xi _1}{\xi _4} + 2\frac{\partial ^2 f_3}{\partial U \partial Y} {\xi _2}{\xi _3}+2\frac{\partial ^2 f_3}{\partial U \partial Z} {\xi _2}{\xi _4}+2\frac{\partial ^2 f_3}{\partial Y \partial Z} {\xi _3}{\xi _4},\\ D^2_{41}= & {} \frac{\partial ^2 f_4}{\partial X^2} \xi _1^2+\frac{\partial ^2 f_4}{\partial U^2} \xi _2^2+\frac{\partial ^2 f_4}{\partial Y^2} \xi _3^2+\frac{\partial ^2 f_4}{\partial Z^2} \xi _4^2+2\frac{\partial ^2 f_4}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_4}{\partial X \partial Y} {\xi _1}{\xi _3} \\&+ \, 2\frac{\partial ^2 f_4}{\partial X \partial Z} {\xi _1}{\xi _4} + 2\frac{\partial ^2 f_4}{\partial U \partial Y} {\xi _2}{\xi _3}+2\frac{\partial ^2 f_4}{\partial U \partial Z} {\xi _2}{\xi _4}+2\frac{\partial ^2 f_4}{\partial Y \partial Z} {\xi _3}{\xi _4}. \end{aligned}$$

After calculating $D^2 f$ from (41) evaluated at $P_{11}^{[p\_eep]}$, at the threshold $s^*$ and using the eigenvector $V_3$ we can verify the following three conditions:

$$\begin{aligned}&{Q_3}^T f_s(P_{11}^{[p\_eep]}, s^*)=0, \quad {Q_3}^T[Df_s(P_{11}^{[p\_eep]}, s^*)V_3]=-\varphi _3 \omega _3 \left( \frac{mr+a^2eK}{abeK}\right) \ne 0\\&Q_3^T[D^2f_ s(P_{11}^{[p\_eep]}, s^*)(V_3,V_3) ] = -2\omega _3 {\varphi _3}^2 \left( \frac{bmr^2}{a^2beK^ 2} +\frac{r}{K}+\frac{mr^2}{abeHK}+\frac{ar}{bH} \right) \ne 0. \end{aligned}$$

Now, a similar calculation when $P_{11}^{[p\_eep]}$ coincides with $P_{10}^{[p\_eep]}$ for $r= r^*$, using the Jacobian

$$\begin{aligned} J_{P_{11}}^{[p\_eep]}( r^*) =\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{-bcesH-b^2e\mu H+ms\mu }{b^2eH +ms} &{} 0 &{} 0 \\ 0&{} 0 &{} -\frac{ms^2}{b^2eH+ms} &{} -\frac{bmsH}{b^2eH+ms} \\ \frac{abe^2 sH}{b^2eH+ms} &{} \frac{abce^2HK}{(a^2 beH+amr)K+bmrH}&{} \frac{b^2e^2sH}{b^2eH+ms} &{} -\frac{bems}{b^2eH+ms} \\ \end{array} \right) , \end{aligned}$$

the right and left eigenvectors of the zero eigenvalue $V_4=\varphi _4(1,0,-abeH/(b^2eH+ms),aes/(b^2eH+ms))^T$ and $Q_4=\omega _4(1, 0,0,0)^T$ produces

$$\begin{aligned} f_{r} = \left( \begin{array}{c} X_{11}^{[p\_eep]} (1-X_{11}^{[p\_eep]}/K) \\ 0 \\ 0 \\ 0 \end{array} \right) , \quad Df_{r} = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1-\frac{2}{K}X_{11}^{[p\_eep]} &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0 &{} 0&{} 0 \\ 0 &{} 0&{} 0&{} 0 \end{array} \right) \end{aligned}$$

so that evaluating $D^2 f$ from (41) the following three conditions are satisfied:

$$\begin{aligned}&{Q_4}^T f_{r}(P_{11}^{[p\_eep]}, r^*)=0, \quad {Q_4}^T[Df_{r}(P_{11}^{[p\_eep]},r^*)V_4]=\varphi _4 \omega _4 \ne 0,\\&Q_4^T[D^2f_{r} (P_{11}^{[p\_eep]},r^*)(V_4,V_4) ]= 2 \omega _4 {\varphi _4}^2 \left( \frac{abesH}{msK+b^2eHK}\right) \ne 0. \end{aligned}$$

These transcritical bifurcations are illustrated, respectively, in Fig. 2 which occur for $s^*\approx 0.6$, $r^*\approx 0.6$, (40).

Fig. 2

a Transcritical bifurcation between $P_{11}^{[p\_eep]}$ and $P_{9}^{[p\_eep]}$ for the parameters values $r=K=a=c=\mu =H=b=m=e=1.1$, $\lambda = 0.5$. The equilibrium $P_9^{[p\_eep]}$ is stable for $s\in [0.1, 0.602]$ while $P_{11}^{[p\_eep]}$ is stable for $s>0.602$. The vertical line indicates the threshold. b Transcritical bifurcation between $P_{11}^{[p\_eep]}$ and $P_{10}^{[p\_eep]}$ for $s = K = a = c = \mu = H = b = m = e = 1.1$, $\lambda = 0.5$. The equilibrium $P_{10}^{[p\_eep]}$ is stable for$r\in [0.1 , 0.603]$, $P_{11}^{[p\_eep]}$ is stable for $r> 0.603$; the vertical line indicates the threshold

3.4.2 The pairs $P_{13}^{[p\_eep]}-P_{11}^{[p\_eep]}$ and $P_{13}^{[p\_eep]}-P_{12}^{[p\_eep]}$

$P_{13}^{[p\_eep]}$ coincides with $P_{11}^{[p\_eep]}$ at the threshold $\lambda ^*$ and with $P_{12}^{[p\_eep]}$ at the threshold $b^*$, comparing (34) and the stability condition (27) of $P_{11}^{[p\_eep]}$, as well as (34) with the stability condition (31) of $P_{12}^{[p\_eep]}$, respectively.

The transcritical bifurcations proofs at $P_{13}^{[p\_eep]}$ are analogous to those presented earlier in this section and therefore omitted.

Figure 3 illustrates the simulation explicitly showing the transcritical bifurcation between $P_{13}^{[p\_eep]}$ with, respectively, $P_{11}^{[p\_eep]}$ and $P_{12}^{[p\_eep]}$ for the parameters values given in the caption of Fig. 3, respectively, for $\lambda ^*\approx 1.57$, $b^*\approx 2.7$ (40).

Fig. 3

a Transcritical bifurcation between $P_{13}^{[p\_eep]}$ and $P_{11}^{[p\_eep]}$ for $s = K = b = e =r= 0.5$, $a = 0.6$, $c= \mu = 0.4$, $H = m = 0.9$. The point $P_{11}^{[p\_eep]}$ is stable for $\lambda \in [0.1, 1.572]$ and $P_{13}^{[p\_eep]}$ is stable for $\lambda >1.572$. The vertical line indicates the threshold. b Transcritical bifurcation between $P_{13}^{[p\_eep]}$ and $P_{12}^{[p\_eep]}$ for $r=K=a=H=m=e=s=0.5$, $\mu =0.2$, $c=0.3$ and $\lambda = 0.9$. $P_{13}^{[p\_eep]}$ is stable for $b\in [0.1, 2.7]$, $P_{12}^{[p\_eep]}$ is stable for $b>2.7$; the vertical line indicates the threshold

In Table 3, we summarize the transcritical bifurcations of the models (1) and (19).

Table 3 Trancritical bifurcations of the models (1) and (19)

4 Comparison between the models with hidden and explicit resources

In this section, we investigate the behaviour of the models (1) and (19) from the comparison of their equilibrium points.

In Table  4, we present all the possibilities of comparison between equilibria.

Table 4 Comparison between similar equilibria of systems (1) and (19) which have the same biological behaviour and u unstable, s stable, cs conditionally stable, i unfeasible, uf unstable if feasible, sf stable if feasible

The populations in both ecosystems cannot completely disappear, as the origin in both systems is unstable. Note that the equilibria with the presence only of infected prey and predators, while the healthy prey population is absent, are impossible in both models. This is illustrated in Table 4 by the comparison of points $P_4^{[p\_ehp]}$ with $P_6^{[p\_eep]}$ and $P_7^{[p\_eep]}$.

The predator-free environment, with endemic disease in the prey, is feasible but unstable in both models, comparing equilibria $P_3^{[p\_ehp]}$ with $P_5^{[p\_eep]}$ and $P_8^{[p\_eep]}$.

Observe that the healthy-prey-only equibrium $P_2^{[p\_ehp]}$ in (1) has several counterparts in the system with alternative resources, namely $P_2^{[p\_eep]}$, healthy-prey-only environment, $P_3^{[p\_eep]}$, alternative resource-only point, and $P_4^{[p\_eep]}$ healthy-prey and alternative resource equilibrium. All these states are, however, unachievable, since they all are unconditionally unstable.

The predator-only state arises at $P_5^{[p\_ehp]}$ in the simpler model, and has its counterpart in the point $P_{10}^{[p\_eep]}$. Both are always feasible. The stability conditions (7) and (23) express the same idea that the prey reduced growth rate, i.e. the ratio between the reproduction rate of the healthy prey and the rate at which they are captured by the predators is bounded above by the predators’ population size at equilibrium.

The disease-free equilibrium in (1) is $P_6^{[p\_ehp]}$. Two points could be related to it, namely $P_9^{[p\_eep]}$ and $P_{11}^{[p\_eep]}$. The former, however, does not contain the alternative resource, so it is not really comparable. This would be possible only if in the model with alternative food supply we let $L\rightarrow 0$, but in such case $P_6^{[p\_ehp]}$ reduces to $P_2^{[p\_ehp]}$.

For feasibility of $P_6^{[p\_ehp]}$ and $P_{11}^{[p\_eep]}$ in both cases, the opposite conditions that ensure stability for $P_5^{[p\_ehp]}$ and $P_{10}^{[p\_eep]}$ are required, thereby indicating transcritical bifurcations among the pairs of points belonging to the same model.

Analogously, we can compare the equilibria $P_6^{[p\_ehp]}$ and $P_{11}^{[p\_eep]}$ with the pair $P_7^{[p\_ehp]}$ and $P_{13}^{[p\_eep]}$. The stability conditions of $P_6^{[p\_ehp]}$ and $P_{11}^{[p\_eep]}$ are the opposite conditions that ensure stability for the coexistence equilibria $P_7^{[p\_ehp]}$ and $P_{13}^{[p\_eep]}$, thereby indicating transcritical bifurcations among the pairs of points belonging to the same model (see Table 5).

The coexistence equilibrium $P_7^{[p\_ehp]}$ of the hidden resource system has two counterparts in the explicit resource model, $P_{12}^{[p\_eep]}$ and $P_{13}^{[p\_eep]}$, the difference being that in the former the alternative resource is absent, so in reality is not really a “coexistence” equilibrium of the explicit resource model. But in all three equilibria, the first prey with endemic disease and the predators persist.

Table 5 Transcritical bifurcations among the pairs of equilibria belonging to the same model

5 Results and conclusions

In this paper, we have compared the dynamics between two predator–prey models where the predator is generalist in the first model and specialist on two prey species in the second one; further, a transmissible disease spreads among the primary population resource. The alternative prey for the predator is implicit in the first model, but in the second one we have made it explicit.

In the first model, the infection rate $\lambda$ on the healthy prey population and the mortality rate of infected prey $\mu$ determine the stable coexistence of healthy prey, infected prey and predator when the predator has an alternative resource, see condition (12). However, in the second model, when we consider the explicit resource for the predator species, in addition to the infection rate $\lambda$ and the mortality rate $\mu$, also an extra condition involving the growth rate r of the healthy prey X plays an essential role for the stable coexistence; compare conditions (34), (35) and (36). In these cases, the ranges of possible values for the contact rate are, respectively, provided in (14) and (38).

Due to the presence of the alternative food resource for the generalist predator in model (1), we cannot observe any predator’s extinction scenario because the equilibria $P_2^{[p\_ehp]}$ and $P_3^{[p\_ehp]}$ are unstable. The same scenario exists in model (19) because the equilibria with no predators, namely $P_2^{[p\_eep]}$, $P_3^{[p\_eep]}$, $P_4^{[p\_eep]}$, $P_5^{[p\_eep]}$ and $P_8^{[p\_eep]}$, are all always unstable.

The main features in the behaviour of the systems (1) and (19) include switching of stability, extinction and persistence for the various populations. The bifurcation analysis and the comparison of the results of these models, summarized in Table 3, indicate that the most important parameters in these systems are the reproduction rate of the main prey r, the infection rate of the main prey $\lambda$, the mortality rate of infected prey and the reproduction rate of the alternative prey s. Note, however, that the last two, in particular, appear only in system (19). This remark shows that the more comprehensive formulation allows a finer tuning for the ecosystem behaviour. Indeed this has already been observed earlier, see Table 4, when we found that the equilibrium $P_9^{[p\_eep]}$ of (19) with neither disease nor alternative prey does not have any counterpart in the hidden resource model (1).

Table 6 Systems dynamics considering an environment with and without a transmissible disease among individuals of the main prey X

If the reproduction rate r of the prey X is low, it will cause the simultaneous extinction of the healthy prey X and the infected prey U in both systems (1) and (19). This situation is represented by equilibria $P_5^{[p\_ehp]}$ and $P_{10}^{[p\_eep]}$ for which the stability conditions are, respectively, given by (7) and (23). However, if the main prey growth rate r is high, the primary prey invade the system and the models will display the infected-prey-only extinction (equilibria $P_6^{[p\_ehp]}$ and $P_{11}^{[p\_eep]}$); compare their feasibility conditions (8) and the first condition in (24), respectively.

In addition, when the growth rate s of the alternative prey Y is low in model (19), extinction of U and Y occurs (see the first condition of (22)). However, if this rate is high, only the infected prey disappears (see the second condition of (24)).

A further consideration concerns the infection rate among prey $\lambda$. If it is low, extinction of the infected prey U occurs in both ecosystems (equilibria $P_6^{[p\_ehp]}$ and $P_{11}^{[p\_eep]}$), see (9) and (26), but otherwise both ecosystems will exhibit a coexistence scenario with all the species present, equilibria $P_7^{[p\_ehp]}$ and $P_{13}^{[p\_eep]}$. For both situations, see Figs. 1b and 3a. In models (1) and (19), feasibility and local asymptotic stability of the equilibria imply also their global asymptotic stability. Thus, if disease eradication is the goal, a low transmission rate $\lambda$ is desirable.

Another result that we can highlight is associated with the purely demographic system presented in de Assis et al. (2018), where the same dynamical systems are investigated, but excluding the possibility of an epidemic in the main prey X. As in our present situation, the models proposed in de Assis et al. (2018) present a logistic growth for both the X and Y prey populations and a quadratic mortality for the Z predator population when the alternative resource is explicit. When it is hidden, to take it into account, also the predators exhibit logistic growth. Table 6 illustrates the comparison between models with hidden and explicit prey for the predator, considering an environment with and without the possibility of a transmissible disease among individuals of prey population X. There is no possibility of a scenario in which in the ecoepidemic models, i.e. with a transmissible disease affecting the first prey, the infected prey thrive without the presence of the susceptible prey. This occurs both in the case of the hidden prey as well as of the explicit prey. This situation is represented by the healthy-prey-free equilibria. Note that this remark of course hinges on the assumption that the infected prey do not reproduce.

The scenario in which the predator Z survives is possible in both scenarios, i.e. with and without the infected population U. In both cases, clearly this result is guaranteed in the models (1) and (19). Finally, the existence of a transmissible disease among individuals X does not compromise the coexistence of prey and predator species. In addition, the disease-free equilibrium points represented by $P_6^{[p\_ehp]}$ and $P_{11}^{[p\_eep]}$, when represented in the same dynamic but without a transmissible disease among individuals X, clearly reduce to the equilibria representing coexistence.

This study ultimately indicates that the simpler formulation with the hidden resource already captures the salient features of the ecosystem. Therefore, modeling explicitly the substitute prey is not necessary unless a particular emphasis is placed on the behaviour and the possible consequences that involve the alternative resource. In such case, the extended model is preferable, but this of course as expected complicates the model formulation and entails a rather more complicated analysis. The bottom line of these remarks is, therefore, that the model to be used should be guided by the questions that prompt its formulation and the answers that are sought.